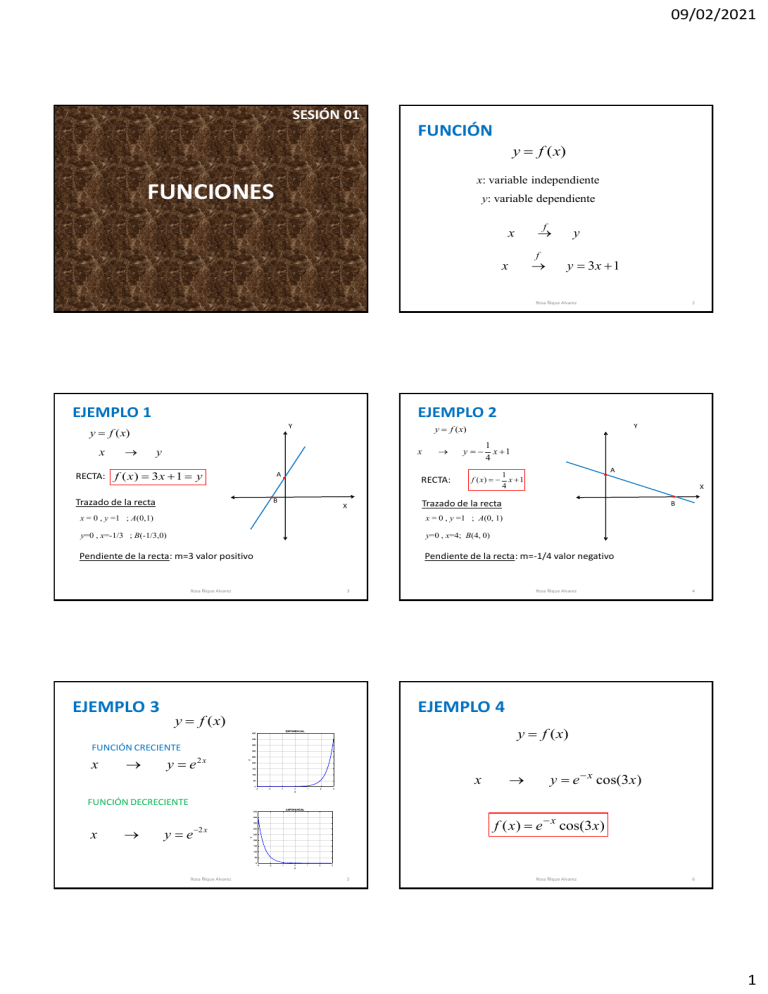
09/02/2021 SESIÓN 01 FUNCIÓN y f (x) x: variable independiente FUNCIONES y: variable dependiente f x f x y y 3x 1 Rosa Ñique Alvarez EJEMPLO 1 EJEMPLO 2 Y y f (x) x 2 y x RECTA: f ( x ) 3 x 1 y A B Trazado de la recta Y y f (x) RECTA: X 1 y x 1 4 A 1 f ( x) x 1 4 X Trazado de la recta B x = 0 , y =1 ; A(0,1) x = 0 , y =1 ; A(0, 1) y=0 , x=-1/3 ; B(-1/3,0) y=0 , x=4; B(4, 0) Pendiente de la recta: m=3 valor positivo Pendiente de la recta: m=-1/4 valor negativo Rosa Ñique Alvarez EJEMPLO 3 3 Rosa Ñique Alvarez 4 EJEMPLO 4 y f (x) y f (x) FUNCIÓN CRECIENTE x y e2 x x y e x cos(3 x) FUNCIÓN DECRECIENTE x f ( x) e x cos(3 x) y e 2 x Rosa Ñique Alvarez 5 Rosa Ñique Alvarez 6 1 09/02/2021 EJEMPLO 5 EJEMPLO 6 Graficar la siguiente función f ( x) e x sen(2 x), f ( x) e x cos(3 x) , 2 x 2 0 x 2 Rosa Ñique Alvarez 7 EJEMPLO 7 EJEMPLO 8 y h(t ) y f (t ) t y 3t e 4t t Rosa Ñique Alvarez 8 Rosa Ñique Alvarez 10 y ln 5t f (t ) ln(5t ) h(t ) 3te 4t Rosa Ñique Alvarez 9 2