Clase Unidad 3 Modelo

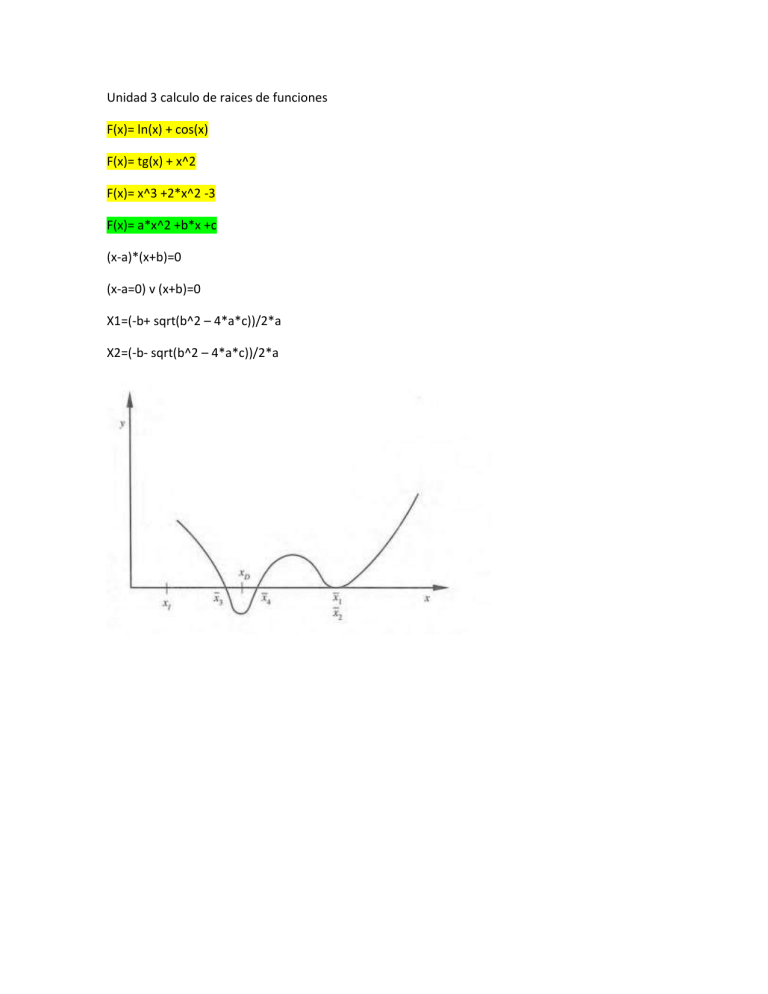
Unidad 3 calculo de raices de funciones
F(x)= ln(x) + cos(x)
F(x)= tg(x) + x^2
F(x)= x^3 +2*x^2 -3
F(x)= a*x^2 +b*x +c
(x-a)*(x+b)=0
(x-a=0) v (x+b)=0
X1=(-b+ sqrt(b^2 – 4*a*c))/2*a
X2=(-b- sqrt(b^2 – 4*a*c))/2*a
i
0
1
2
3
4
𝑥𝑖
0.5
1.62
1.3859
1.3688
1.3688
|𝑥𝑖+1- 𝑥𝑖 |<0.001
----------------1.12
0.2341
0.0171
0.0000
f(x)= x^3 +2*x^2 +10*x -20 ; f’(x)= 3*x^2 +4*x + 10
F(x)=0
𝑥𝑖+1 = 𝑥𝑖 - f(𝑥𝑖 )/f’(𝑥𝑖 )
Primera iteraccion
i=0
𝑥1 = 𝑥0 - f(𝑥0 )/ f’(𝑥0 )
xo=0.5
𝑥1 = 𝑥0 – (xo^3 +2*xo^2 +10*xo -20)/ (3*xo^2 +4*xo + 10)
X1 = 0.5 - (0.5^3 + 2*0.5^2 + 10*0.5 - 20)/(3*0.5^2 + 4*0.5 +10)
X1=1.62
Segunda iteración
i=1
𝑥2 = 𝑥1 - f(𝑥1 )/ f’(𝑥1 )
𝑥2 = 𝑥1 – (x1^3 +2*x1^2 +10*x1 -20)/ (3*x1^2 +4*x1 + 10)
X2= 1.62 - (1.62^3 + 2*1.62^2 +10*1.62 - 20)/(3*1.62^2 + 4*1.62 + 10)
X2=1.3859
Tercera iteración
i=2
X3= 𝑥 2 - f(𝑥 2)/ f’(𝑥 2)
𝑋3= 𝑥 2 – (x2^3 +2*x2^2 +10*x2 -20)/ (3*x2^2 +4*x2 + 10)
X3=1.3688
Cuarta iteraccion0
i=3
X4=1.3688
Resolver por newton rapshon
F(x)= ln(x)- x^2
F(x)= ln(x)- x^2 ; F’(x)= 1/x – 2x
i
0
1
2
3
𝑥𝑖
0.5
0.647715727
0.652916872
0.65291864
|𝑥𝑖+1- 𝑥𝑖 |<0.001
----------------0.147715727
0.005201145
0,0000018
Primera iteraccion
i=0
𝑥1 = 𝑥0 - f(𝑥0 )/ f’(𝑥0 )
xo=0.5
𝑥1 = 𝑥0 – (ln(xo)- xo^2) / 1/xo – 2xo)
𝑥1 =
Método de la secante
Metodo con base en dos valores iniciales o con base en dos puntos
𝑥𝑖+1 = 𝑥𝑖 - f(𝑥𝑖 )/f’(𝑥𝑖 )
F´(xi)= (f(xi) – f(𝑥𝑖−1 ))/( 𝑥𝑖 - 𝑥𝑖−1 )
𝒙𝒊+𝟏 =𝑥𝑖 − (𝒙𝒊 - 𝒙𝒊−𝟏 )* f(xi)/( f(xi) – f(𝒙𝒊−𝟏 )) (algoritmo de la secante)
f(x)= x^3 +2*x^2 +10*x -20
i
0
1
2
3
4
5
𝑥𝑖
0.5
1.5
1.333333
1.367478
1.368822
1.368808
|𝑥𝑖+1- 𝑥𝑖 |<0.001
----------------1.0
0.1667
0.034145
0,001344
0,000014
Primera iteraacion i=1
𝒙𝟐 =𝑥1 − (𝒙𝟏 - 𝒙𝟎 )* f(x1)/( f(x1) – f(𝒙𝟎 )) (algoritmo de la secante)
𝒙𝟐 =𝑥1 − (𝒙𝟏 - 𝒙𝟎 )* (x1^3 + 2*x1^2+ 10*x -20)/( (x1^3 + 2*x1^2+ 10*x -20)– (𝐱𝐨^𝟑 + 𝟐 ∗ 𝐱𝟎^𝟐 + 𝟏𝟎 ∗ 𝐱𝐨 − 𝟐𝟎))
X2= 1.333333
Segunda Iteración i=2
𝒙𝟑 =𝑥2 − (𝒙𝟐 - 𝒙𝟏 )* f(x2)/( f(x2) – f(𝒙𝟏 ))
𝒙𝟑 =𝑥2 − (𝒙𝟐 - 𝒙𝟏 )* (x2^3 + 2*x2^2+ 10*x2 -20)/( (x2^3 + 2*x2^2+ 10*x2 -20)– (𝐱𝟏^𝟑 + 𝟐 ∗ 𝐱𝟏^𝟐 + 𝟏𝟎 ∗ 𝐱𝟏 − 𝟐𝟎))
X3= 1.367478
Tercera Iteraccion i=3
𝒙𝟒 =𝑥3 − (𝒙𝟑 - 𝒙𝟐 )* f(x3)/( f(x3) – f(𝒙𝟐 ))
𝒙𝟒 =𝑥3 − (𝒙𝟑 - 𝒙𝟐 )* (x3^3 + 2*x3^2+ 10*x3 -20)/( (x3^3 + 2*x3^2+ 10*x3 -20)– (𝐱𝟐^𝟑 + 𝟐 ∗ 𝐱𝟐^𝟐 + 𝟏𝟎 ∗ 𝐱𝟐 − 𝟐𝟎))
X4 =1.368822
Cuarta Iteraccion i=4
𝒙𝟓 =𝑥4 − (𝒙𝟒 - 𝒙𝟑 )* f(x4)/( f(x4) – f(𝒙𝟑 ))
𝒙𝟓 =𝑥4 − (𝒙𝟒 - 𝒙𝟑 )* (x4^3 + 2*x4^2+ 10*x4 -20)/( (x4^3 + 2*x4^2+ 10*x4 -20)– (𝐱𝟑^𝟑 + 𝟐 ∗ 𝐱𝟑^𝟐 + 𝟏𝟎 ∗ 𝐱𝟑 − 𝟐𝟎))
X5 =1.368808
RESOLVER LOS 10 EJERCICIOS CON EL METODO DE LA SECANTES
BUSCAR LOS ALGORITMOS DEL METODO DE NEWTON RAPHSON Y LA SECANTE
Punto fijo
𝒙𝒊 =g(𝒙𝒊 )
f(x)= x^3 +2*x^2 +10*x -20=0
1. Despejando la variable independiente en todas sus formas posibles
a) X= (20 – 2*x^2 -10*x)^(1/3)
b) X= ((20-10*x – x^3)/2)^(1/2)
c) X=(20-2*x^2 –x^3)/10
2. Factorizando la función
x^3 +2*x^2 +10*x -20=0
x*(x^2+2*x +10)=20
x=20/(x^2+2*x +10)
3. Sumando x en ambos lados de la expresión
x^3 +2*x^2 +10*x -20+x=0+x
x= x^3 +2*x^2 + 11*x -20
f(x)= x^3 +2*x^2 +10*x -20=0
a) X= (20 – 2*x^2 -10*x)^(1/3)
i
0
1
2
3
4
5
6
𝑥𝑖
0.5
2.438
-2.5338
g(𝒙𝒊 )
xxxx
xxxx
xxxx
xxxx
2.438
-2.5338
3.1911
|𝑥𝑖+1- 𝑥𝑖 |<0.001
------------------1.938
5.72
|f( 𝑥𝑖 )|<0.001
14.37
30.7587
48.76
|𝑥𝑖+1- 𝑥𝑖 |<0.001
-------------------
|f( 𝑥𝑖 )|<0.001
xxxx
xxxxxx
b)X= ((20-10*x – x^3)/2)^(1/2)
i
0
1
𝑥𝑖
0.5
xxxxx
g(𝒙𝒊 )
xxxxx
xxxxx
2
3
4
5
6
xxxx
xxxx
xxxx
xxxx
Primera iteración
i=1
xo=0.5
x1= 1.5
𝒙𝒊+𝟏 =𝑥𝑖 − (𝒙𝒊 - 𝒙𝒊−𝟏 )* f(xi)/( f(xi) – f(𝒙𝒊−𝟏 )) (algoritmo de la secante)
𝒙𝟐 = 𝑥1 - (𝒙𝟏 -𝒙𝟎 )*f(x1)/(f(x1) –f(xo))
𝒙𝟐 = 𝒙𝟏 - ((𝒙𝟏 -𝒙𝟎 )*( x1^3 +2*x1^2 +10*x1 -20))/(( x1^3 +2*x1^2 +10*x1 -20)-( xo^3 +2*xo^2 +10*xo -20))
X2=1.33
Segunda iteración
i=2
𝒙𝟑 = 𝒙𝟐 - ((𝒙𝟐 -𝒙𝟏 )*( x2^3 +2*x2^2 +10*x2 -20))/(( x2^3 +2*x2^2 +10*x2 -20)-( x1^3 +2*x1^2 +10*x1 -20))
X3=1.3674