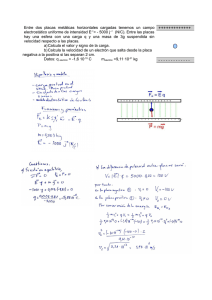
UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS FACULTAD DE CIENCIAS FÍSICAS ELECTROMAGNETISMO I Segundo examen parcial Advertencia: El examen es personal, está prohibido el uso de cuadernos, copias o libros. Solo se permite el uso de calculadoras y tablas de integración en forma personal. En la calificación influye el orden y la propiedad gramatical. 1.- Una esfera conductora de radio R y carga neta Q está sumergida en un medio dieléctrico de gran extensión cuya permitividad puede expresarse en la forma: ℰ(𝑟𝑟)=ℰ0(1+𝑎𝑎𝑎𝑎) r: distancia desde el centro de la esfera a cualquier punto del espacio. a) Determine el potencial electrostático en cualquier punto del espacio b) Halle las cargas de polarización. 2.- Un condensador de placas paralelas conductoras tiene sus dos placas perpendiculares a la dirección del eje z. Una de las placas localizada en z=0, tiene un potencial V=0, la otra placa localizada en z=d tiene un potencial V=V0 , V0 es una constante. El espacio entre las placas esta lleno de un dieléctrico de permitividad ε, la densidad de carga libre esta dada por 𝜌𝜌(𝑧𝑧) = 𝜌𝜌0 𝑒𝑒 −𝛼𝛼𝛼𝛼 , donde 𝜌𝜌0 y α son constantes. a) Demuestre que el potencial entre las placas está dado por 𝑉𝑉(𝑧𝑧) = 𝐴𝐴 + 𝐵𝐵𝐵𝐵 − donde A y B son constantes. 𝜌𝜌0 εα2 𝑒𝑒 −𝛼𝛼𝛼𝛼 b) Determine las constantes A y B. c) Determine el vector campo eléctrico entre las placas. 3.- Una esfera de radio a centrada en el origen está hecha de un material óhmico de conductividad g. El potencial en la superficie es mantenido a los valores expresados en coordenadas esféricas por: 𝜙𝜙 = 𝜙𝜙0𝐶𝐶𝐶𝐶𝐶𝐶 𝜃𝜃. Encontrar la densidad de corriente en cualquier punto en el interior de la esfera. 4.- Dos electrodos planos semi infinitos están dispuestos paralelamente separados una distancia d. Entre ellos existe un medio de conductividad g. Si la diferencia de potencial entre los electrodos es 𝜙𝜙0, hallar: a) el vector densidad de corriente en cualquier punto del medio de conductividad g. b) el valor de la densidad superficial de carga en cualquier punto de la armadura conectada a tierra.