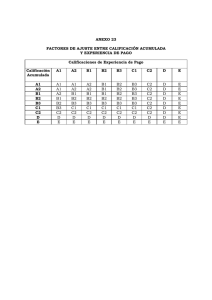
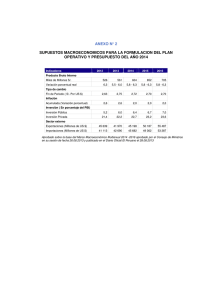
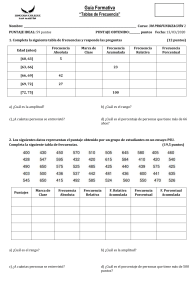
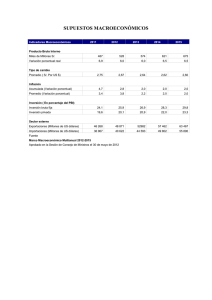
Introducción a la estadística El papel de la Estadística es extraer información de los datos para adquirir el conocimiento necesario para tomar decisiones. La estadística es imprescindible en cualquier disciplina científica o técnica donde se manejen datos, especialmente si son grandes volúmenes de datos, como por ejemplo en Física, Química, Medicina, Psicología, Economía o Ciencias Sociales. ALGUNOS CONCEPTOS DE ESTADÍSTICA Datos Población : conjunto total de individuos (personas, animales, cosas) sobre la cuál se estudia una determinada característica. Muestra : es una parte representativa de la población . Cuando el tamaño de una población es muy grande, se trabaja con una parte de ella llamada muestra Individuo : Cada elemento de la población o la muestra Variable: es el tema (característica ) es objeto de estudio o análisis de una población determinada. Datos son las observaciones de la variable EJEMPLO 1 Se requiere realizar una encuesta, sobre la estatura en cm de los alumnos de 8vo EGB de la ciudad de puyo, que en total son 6578 alumnos. Para ello, se elije a 63 alumnos de 8vo EGB del colegio “Vicentino” . Determinar: la población y la muestra • Población : Los 6578 alumnos de 8vo EGB de la ciudad de puyo • Muestra : 63 alumnos de 8vo EGB del colegio “Vicentino” • Individuo : Cada alumno de 8vo EGB • Variable : estatura en cm EJEMPLO 2 Estudio a fondo de las varibles Variables estadísticas Todo estudio estadístico comienza por la identificación de las características que interesa estudiar en la población y que se medirán en los individuos de la muestra. Definición - Variable estadística. Una variable estadística es una propiedad o característica medida en los individuos de la población Los datos son los valores observados en las variables estadísticas. ALGUNOS CONCEPTOS DE ESTADÍSTICA EJEMPLO 1 EJEMPLO 2 EJEMPLO 3 EJEMPLO 4 EJEMPLO 5 TABLAS DE FRECUENCIAS PARA VARIABLES DISCRETAS La tabla de frecuencias es una herramienta que permite ordenar los datos de manera que se presentan numéricamente las características de la distribución de un conjunto de datos o muestra. ALGUNAS COLUMNAS PRESENTES EN UNA TABLA DE FRECUENCIAS Y SU SIGNIFICADO. SIMBOLO SIGNIFICADO DATOS FRECUENCIA ABSOLUTA FRECUENCIA ACUMULADA 𝑿¡ f¡ 𝑭¡ Son los diferentes valores que toma la variable Es el número de veces que se repite un dato. Es el acumulado o suma de las frecuencias absolutas FRECUENCIA RELATIVA FRECUENCIA RELATIVA ACUMULADA 𝒉¡ 𝑯¡ Es el cociente (división) entre las frecuencia absoluta y el numero total de datos Es el acumulado o suma de las frecuencias relativas FRECUENCIA PORCENTUAL 𝒉¡ (%) Es la frecuencia relativa expresada en porcentaje FRECUENCIA PORCENTUAL ACUMULADA 𝑯¡ (%) Es el acumulado o suma de la frecuencia porcentual EJEMPLO 1 Se ha realizado una encuesta a 20 miembros de un club sobre su peso en kg, al término del año 2019, los siguientes resultados: 50, 65,80,85,50,85,60,85,55,80,80,65,55,65,80,50,60,85,85,60 Hallar la tabla de frecuencias. DATOS X¡ FRECUENCIA ABSOLUTA FRECUENCI A RELATIVA f¡ h¡ 50 3 55 2 60 3 65 3 80 4 85 5 20 3 = 0,15 20 2 20 = 0,10 3 = 0,15 20 3 = 0,15 20 4 = 0,2 20 5 = 0,25 20 1 FRECUENCIA ABSOLUTA ACUMULADA FRECUENCIA RELATVA ACUMULADA FRECUENCIA PORCENTUAL F¡ H¡ 3 0,15 0,15 x 100= 15 % 15 % 5 0,25 10 % 25 % 8 0,40 15 % 40 % 11 0,55 15 % 55 % 15 0,75 20 % 75 % 20 1 25 % 100 % h¡(%) FRECUENCIA PORCENTUAL ACUMULADA H¡(%) 100 % EJEMPLO 2 Elaborar una tabla de frecuencias a partir de las temperaturas máximas registradas en el mes de agosto en la ciudad de PUYO: DATOS X¡ temperat ura FRECUENCI A ABSOLUTA f¡ FRECUENC IA RELATIVA h¡ FRECUENCIA ABSOLUTA ACUMULADA F¡ FRECUENCIA RELATVA ACUMULADA H¡ FRECUENCIA PORCENTUAL h¡(%) FRECUENCIA PORCENTUAL ACUMULADA H¡(%) 15 4 0,129 4 0,129 12,9 % 12,9 % 16 5 0,161 9 0,290 16,1 % 29,0 % 17 5 0,161 14 0,451 16,1 % 45,1 % 18 7 0,226 21 0,677 22,6% 67,7 % 19 6 0,194 27 0,871 19,4 % 86,1 % 20 4 0,129 31 1 12,9 % 100 % 31 1 100 %