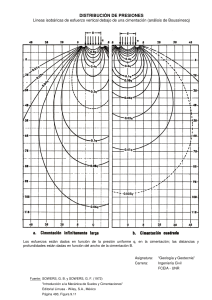
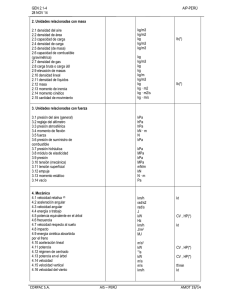
Interacción está-ca suelo-­‐ estructura en cimentaciones someras Agus5n Deméneghi Colina Profesor Facultad de Ingeniería UNAM La interacción suelo-estructura es aquella parte de la ingeniería que estudia las deformaciones del terreno de cimentación cuando éstas se ven afectadas por la presencia y rigidez de la propia estructura. La influencia de la estructura puede ser en condiciones estáticas, lo cual es tratado por la interacción estática suelo-estructura, o puede ser en condiciones dinámicas, lo cual cae en el campo de la interacción dinámica suelo-estructura. Se conocen como métodos de interacción estática suelo-estructura aquellos procedimientos que para el cálculo de las deformaciones del terreno de cimentación toman en cuenta la rigidez de la estructura. Todos estos métodos están basados en el principio de que en el contacto cimiento-terreno los desplazamientos tanto de la subestructura como los del terreno son iguales, es decir, existe compatibilidad de deformaciones entre estructura y suelo. En términos generales, el procedimiento de cálculo para la interacción suelo-estructura consiste en tres pasos: (a) se calculan los desplazamientos de la subestructura, (b) se calculan los desplazamientos del terreno de cimentación, y (c) se establece la compatibilidad de deformaciones entre estructura y suelo. Podemos distinguir dos clases de situaciones en relación con la interacción: (i) cuando los cimientos están suficientemente separados, de tal forma que la carga sobre un apoyo no ejerce influencia sobre los desplazamientos de los apoyos vecinos (este fenómeno se presenta usualmente en zapatas aisladas), y (ii) cuando se trata de un cimiento continuo donde el desplazamiento de un punto de dicho cimiento está afectado por la carga repartida en toda la subestructura (es el caso de zapatas corridas o losas de cimentación). Definamos el módulo de reacción o rigidez lineal vertical de un cimiento de la siguiente forma Kv = Qv/δv (1) donde Qv es la fuerza vertical aplicada al cimiento y δv es el asentamiento vertical ocasionado por Qv. Se define la rigidez lineal horizontal de un cimiento Kh = Qh/δh (2) donde Qh es la fuerza horizontal aplicada al cimiento y δh es el desplazamiento horizontal producido por Qh. Se define la rigidez a la rotación de un cimiento Kr = M/θ (3) donde M es el momento aplicado al cimiento y θ el ángulo –en radianes- producido por dicho momento. Utilizaremos el método de rigideces para el análisis de la estructura (véase el anexo 1), en el que se debe cumplir K δ + Pe + Pc = 0 (4) donde K = matriz de rigidez de la estructura δ = vector de desplazamientos Pe = vector de cargas de empotramiento Pc = vector de cargas concentradas La rigidez del terreno de cimentación se puede incluir en el vector de cargas concentradas Pc, de la siguiente forma: las fuerzas Qv, Qh y M se pueden obtener con las ecs 1 a 3 Qv = Kv δv (5) Qh = Kh δh (6) M = Kr θ (7) Determinación de los módulos de reacción del suelo La determinación de las rigideces Kv, Kh y Kr se lleva a cabo usando su definición dada por las ecs 1 a 3. Por ejemplo, el módulo Kv se obtiene aplicando a la zapata una carga vertical Qv y calculando el asentamiento que produce dicha carga. Dado el carácter no lineal de los suelos, es necesario que tanto la carga sobre el cimiento, como sus dimensiones, sean lo más cercano posible a sus magnitudes definitivas en la estructura, pues de otro modo la determinación de las rigideces será sólo aproximada. Ejemplo Determinar la rigidez lineal vertical Kv de la zapata de la fig E-1, utilizando para ello la fórmula de Burland y Burbridge. El subsuelo está formado por una arena normalmente cargada, N = 15 golpes. Solución El asentamiento en milímetros de la zapata está dado por (Burland y Burbridge, 1985): δ = qn B0.7 Ic Ic = 1.17/N1.4 qn = incremento neto de presión, en kPa B = ancho de la cimentación, en metros Sustituyendo valores qn = 26/1.7(2) = 7.647 t/m2 = 74.995 kPa Ic = 0.0264 B = 1.7 m δ = 2.870 mm = 0.00287 m El módulo Kv vale (ec 1) Kv = 26/0.00287 = 9059.2 t/m La teoría de la elasticidad proporciona los siguientes valores de los módulos de reacción, para un cimiento somero de planta circular Kv = 2ER/(1-ν2) (12) Kh = 32(1-ν)GR/(7-8ν) (13) Kr = 8GR3/3(1-ν) (14) Estas fórmulas se pueden usar en zapatas rectangulares cuando B < L < 2.5B, mediante el siguiente artificio: Sea A = BL el área del cimiento rectangular, R = √ A/π (15) Para calcular Kv y Kh usamos las ecs 12 y 13 con R obtenida de la ec 15. Sea I = momento de inercia del cimiento alrededor del eje que se desea calcular Kr R= 4√ 4I/π (16) Kr se computa con la ec 14, con R obtenida de la ec 16. Por lo ya señalado antes, los cálculos de los módulos de reacción con las ecs 12 a 14 son sólo aproximados, pues el comportamiento real de los suelos es no lineal. Otra forma aproximada de obtener los módulos de reacción es mediante la realización de pruebas de placa (Zeevaert, 1973). Sea kv el módulo de rigidez unitario, definido como kv = Qv/δvA (17) Siendo A = área del cimiento. Si ks1 es el módulo de rigidez vertical determinado con una prueba de placa de un pie de lado, se puede emplear la siguiente fórmula (Terzaghi, 1955) kv = ks1 [(B+0.3)/2B]2 (18) donde B es el ancho de la zapata en metros. En el caso de arcillas kv = ks1 [(n+0.5)/1.5n)] (19) donde n = L/B, siendo L la longitud del cimiento. Sea un cimiento totalmente flexible con carga uniforme apoyado en un suelo cohesivo totalmente saturado. El asentamiento a largo plazo toma la forma indicada en la fig 7a (Sowers, 1962); el diagrama de reacción del terreno en este caso es igual al de la carga, es decir, la reacción es uniforme. Si dicho cimiento se apoya sobre un suelo friccionante, el asentamiento se distribuye como se indica en la fig 7b (Sowers, 1962); por ser el cimiento totalmente flexible, la reacción del suelo es también uniforme. Sea ahora una placa de una rigidez infinita apoyada en una arcilla totalmente saturada (fig 8a). El hundimiento es uniforme, pero el diagrama de reacción a largo plazo toma la forma indicada en la fig 8a (Sowers, 1962). Si la placa se apoya sobre un suelo friccionante, el diagrama de reacción toma la forma de la fig 8b (Sowers, 1962). Vemos entonces que los diagramas de asentamientos y de reacciones del terreno dependen de la clase de suelo y de la rigidez de la estructura. Un cimiento real puede quedar entre los dos casos extremos señalados, pues su rigidez no necesariamente es nula o infinita. Interacción suelo-zapata corrida Consideremos un marco estructural con una cimentación a base de una zapata corrida (fig 9a), en el cual se trata de obtener los diagramas de asentamientos y de reacciones del terreno de cimentación (fig 9, b y c). Comencemos con el diagrama de reacciones. En el caso general, la forma del diagrama es diferente de una reacción uniforme (fig 9b). Sustituyamos la curva de reacción del terreno por una serie de reacciones uniformes r1, r2, ... , rn (fig 10a); el análisis estructural lo llevamos a cabo utilizando el método de rigideces, considerando las reacciones ri como incógnitas. A continuación, aplicando la tercera ley de Newton, aplicamos las cargas ri sobre el terreno (fig 10b), y obtenemos los hundimientos de éste en función de las ri, empleando el método de Chamecki (1956). El problema de la interacción se resuelve estableciendo la compatibilidad de deformaciones entre estructura y suelo, es decir, si el suelo está en contacto con la estructura de cimentación, las deformaciones de ambos medios deben ser iguales. Zapata corrida MARCO ESTRUCTURAL (a) DIAGRAMA DE ASENTAMIENTOS (b) DIAGRAMA DE REACCIONES (c) (Acisef3) MARCO ESTRUCTURAL CON CIMENTACIÓN A BASE DE ZAPATA CORRIDA FIGURA 9 Zapata corrida r4 r3 r5 r2 r6 r1 r7 (a) REACCIONES DEL TERRENO r1 r7 r2 r6 r3 r5 r4 r7 (b) CARGAS SOBRE EL TERRENO CARGAS SOBRE LA ESTRUCTURA Y EL SUELO FIGURA 10 El incremento de esfuerzo vertical vale σzijk = Izijk rkdk/ak (21) donde Izijk es el valor de influencia vertical, el cual es igual al esfuerzo normal vertical en el punto ij, producido por una presión unitaria actuando en el área ak (Zeevaert, 1973). Los esfuerzos normales vertical y horizontales se obtienen aplicando la ec 21 para todas las cargas rk, es decir nr σzij = Σ Izijk rkdk/ak (24) k=1 nr σxij = Σ Ixijk rkdk/ak (25) k=1 nr σyij = Σ Iyijk rkdk/ak k=1 (26) Comportamiento lineal En forma aproximada, se puede resolver la interacción considerando que la deformación bajo el punto i de un estrato de suelo de espesor Hj está dada por δij = (Hj/Eij) [σzij - ν(σxij +σyij)] (47) donde Eij es el módulo de deformación del suelo y ν su relación de Poisson. Sustituyendo las ecs 24 a 26 en la ec 47 nr δij = (Hj/Eij) Σ [ Izijk-ν(Ixijk+Iyijk) ] rkdk/ak k=1 Sea Iijk = Izijk-ν(Ixijk+Iyijk) (48) nr δij = (Hj/Eij) Σ Iijk rkdk/ak k=1 Tomando en cuenta todos los estratos de subsuelo, y una posible deformación previa δoi, la deformación del punto i es ne nr δi = δoi + Σ (Hj/Eij) Σ Iijk rkdk/ak j=1 k=1 (49) En el suelo, desarrollamos la ec 49 para i = 1: δ1 = (H1/E11) (I111r1d1/a1 + I112r2d2/a2 + I113r3d3/a3) + (H12/E12) (I121r1d1/a1 + I122r2d2/a2 + I123r3d3/a3) En la tabla 11 se muestran los valores de influencia para este problema. 3.2 m 3.2 m 2m PLANTA 35 t 50 t 35 t 3.7 t/m En la estructura: E = 1,130,000 t/m2 I = 0.05163 m4 0.5 m Estrato 1 0.8 m Estrato 2 1.6 m Roca ELEVACIÓN CARACTERÍSTICAS DE ESTRUCTURA Y TERRENO DE CIMENTACIÓN FIGURA 13 (EJEMPLO 3) 3.2 m 3.2 m Área 1 1 Área 2 Área 3 2 1.6 m 3 3.2 m 2m 1.6 m PLANTA 0.5 m Estrato 1 (1,1) (2,1) (3,1) 0.8 m Estrato 2 (1,2) (2,2) (3,2) 1.6 m Roca ELEVACIÓN CÁLCULO DE LOS VALORES DE INFLUENCIA FIGURA 16 (EJEMPLO 3) Comportamiento lineal En forma aproximada, se puede resolver la interacción considerando que la deformación bajo el punto i de un estrato de suelo de espesor Hj está dada por δij = (Hj/Eij) [σzij - ν(σxij +σyij)] (47) donde Eij es el módulo de deformación del suelo y ν su relación de Poisson. Sustituyendo las ecs 24 a 26 en la ec 47 nr δij = (Hj/Eij) Σ [ Izijk-ν(Ixijk+Iyijk) ] rkdk/ak k=1 Sea Iijk = Izijk-ν(Ixijk+Iyijk) (48) nr δij = (Hj/Eij) Σ Iijk rkdk/ak k=1 Tomando en cuenta todos los estratos de subsuelo, y una posible deformación previa δoi, la deformación del punto i es ne nr δi = δoi + Σ (Hj/Eij) Σ Iijk rkdk/ak j=1 k=1 (49) 3.2 m 3.2 m 2m (a) 35 t PLANTA 50 t 35 t 3.7 t/m En la estructura: E = 1,130,000 t/m2 I = 0.05163 m4 0.5 m NAF Estrato 1 Eu = 500 t/m2 Arcilla totalmente saturado 0.8 m Estrato 2 Eu = 560 t/m2 Arcilla totalmente saturado 1.6 m (b) ELEVACIÓN Roca CARACTERÍSTICAS DE ESTRUCTURA Y TERRENO DE CIMENTACIÓN FIGURA 17 (EJEMPLO 4) En el suelo, desarrollamos la ec 49 para i = 1: δ1 = (H1/E11) (I111r1d1/a1 + I112r2d2/a2 + I113r3d3/a3) + (H12/E12) (I121r1d1/a1 + I122r2d2/a2 + I123r3d3/a3) En la tabla 11 se muestran los valores de influencia para este problema. TABLA 11 VALORES DE INFLUENCIA (EJEMPLO 4) RELACIÓN DE POISSON = 0.5 Punto 1,1,1 1,1,2 1,1,3 1,2,1 1,2,2 1,2,3 2,1,1 2,1,2 2,1,3 2,2,1 2,2,2 2,2,3 3,1,1 3,1,2 3,1,3 3,2,1 3,2,2 3,2,3 Izijk 0.4868711 0.0017431 0.0000189 0.2791369 0.0402185 0.0009920 0.0016360 0.9737421 0.0016360 0.0355775 0.5582739 0.0355775 0.0000189 0.0017431 0.4868711 0.0009920 0.0402185 0.2791369 Ixijk 0.3181542 0.0526524 0.0034808 0.0579433 0.0912394 0.0114948 0.0431202 0.6363085 0.0431202 0.0649898 0.1158866 0.0649898 0.0034808 0.0526524 0.3181542 0.0114948 0.0912394 0.0579433 Iyijk 0.2659320 0.0031307 0.0000384 0.0297519 0.0048027 0.0001265 0.0029179 0.5318640 0.0029179 0.0042220 0.0595037 0.0042220 0.0000384 0.0031307 0.2659320 0.0001265 0.0048027 0.0297519 nu 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 Iijk 0.1948280 -0.0261484 -0.0017408 0.2352893 -0.0078026 -0.0048186 -0.0213830 0.3896559 -0.0213830 0.0009717 0.4705787 0.0009717 -0.0017408 -0.0261484 0.1948280 -0.0048186 -0.0078026 0.2352893 δ1 = (0.8/500)[(0.194828/2)r1-(0.02614844/2)r2 -(0.00174077/2)r3] + (1.6)/(560)[(0.23528931/2)r1 -(0.00780255/2)r2-(0.00481864/2)r3] Tomando en cuenta que r1 = r3 δ1 = 0.000483712 r1 – 0.00003206525 r2 (50) En forma análoga se obtiene δ2 = -0.000031436 r1 + 0.00098398 r2 (51) Resolviendo el sistema de ecuaciones 27, 28, 29, 50 y 51: δ1 = 0.014285 m, δ2 = 0.013224 m θ4 = 0.00075212 r1 = 30.487 t/m, r2 = 14.413 t/m Interacción estructura-­‐suelo plás-co parcialmente saturado (arcilla expansiva) Interacción estructura-suelo plástico parcialmente saturado En un suelo plástico parcialmente saturado, además de los asentamientos producidos por las cargas de una estructura, se presentan deformaciones debidas a cambios de humedad en el suelo. Un ejemplo de esta clase de fenómeno lo constituyen las arcillas expansivas, que sufren fuertes cambios volumétricos al variar su humedad natural. Habíamos obtenido: δ1 = 0.000817668 r1 + 0.0000349723 r2 δ2 = 0.0000634471 r1 + 0.00163405 r2 (55) (56) Resolviendo el sistema de ecuaciones 52 a 56 obtenemos δ1 = 0.021759 m, δ2 = 0.020075 m θ4 = 0.0010381 r1 = 26.129 t/m, r2 = 11.271 t/m Supongamos que por un aumento de humedad en el suelo, en campo libre la arcilla sufre una expansión de 3 cm en los puntos 1 y 3, y de 5 cm en el punto 2 (fig 16). Aplicando la ec 49 en las ecs 55 y 56 obtenemos δ1=-0.03+0.000817668r1+0.0000349723r2 (57) δ2 =-0.05+0.0000634471r1+0.00163405r2 (58) Resolviendo el sistema de ecuaciones 52, 53, 54, 57 y 58 δ1 = -0.013950 m, δ2 = -0.018469 m θ4 = 0.0020384 r1 = 18.835 t/m, r2 = 18.565 t/m Método itera-vo La interacción suelo-estructura se puede resolver mediante un método iterativo. Esto tiene aplicación en la práctica cuando se dispone de un paquete o un programa de computadora que sustituye al terreno de cimentación por “resortes”, que representan el módulo de reacción de dicho terreno. Dado que no se conoce a priori la “constante del resorte”, pues depende del diagrama de reacción del suelo, que es lo que justamente se está buscando, se tiene que recurrir a un procedimiento iterativo (Chamecki, 1956), que consiste en suponer valores iniciales de las “constantes de los resortes”, y con ellas computar por una parte las deformaciones de la estructura, y por otra las deformaciones del suelo; la diferencia entre deformaciones de estructura y suelo permite ajustar la “constante del resorte”; el proceso se repite hasta que coinciden las deformaciones de estructura y terreno. El método se usa de la siguiente forma: a) En el terreno se entra con las cargas ri y se determinan las deformaciones δi con la matriz de flexibilidades del suelo (se puede iniciar con la reacción uniforme); los módulos de reacción (o “constantes de los resortes”) se obtienen Kvi = ri di / δi (59) b) En la estructura se entra con las Kvi y se calculan las deformaciones ; las reacciones ri por unidad de longitud (en t/m) se obtienen ri = Kvi δi / di (60) donde di es la longitud en que actúa ri. Con estos valores de ri se entra nuevamente al suelo (inciso a), y el proceso se repite hasta que coinciden las deformaciones de estructura y suelo. Ilustremos el proceso anterior con la zapata de la fig 19 (ejemplo 6). Los datos de estructura y suelo son los mismos del ejemplo 3 (fig 13). De acuerdo con la ec 4 K δ + Pe + Pc = 0 Las reacciones del terreno se pueden incorporar en el vector de cargas concentradas Pc (fig 19b). De esta forma, obtenemos el siguiente sistema de ecuaciones (δ1): (21365.442+Kv1)δ1–21365.442δ2-34184.707θ4 – 5.92 – 35 = 0 (61) (δ2): -42730.884δ1+(42730.884+Kv2)δ2+68369.414θ4 –11.84 – 50 = 0 (62) (θ4): -34184.707δ1 +34184.707δ2+72927.375θ4 + 3.15733 = 0 (63) En el terreno de cimentación habíamos obtenido la siguiente matriz de flexibilidades (ecs 50 y 51) δ1 = 0.000483712 r1 – 0.00003206525 r2 (64) δ2 = -0.000031436 r1 + 0.00098398 r2 (65) Las iteraciones se realizan de la siguiente forma 1ra iteración Iniciamos el proceso considerando una reacción uniforme r1 = r2 = r3 = 22.45 t/m 1ra iteración Terreno de cimentación. Aplicando las ecs 64, 65 y 59 Kv1 Kv2 δ1 δ2 m m t/m t/m 0.010139 0.021385 3542.592 3359.425 Estructura. Con los Kvi anteriores, y aplicando las ecs 61, 62, 63 y 60 r1 r2 δ1 δ2 m m t/m t/m 0.013295 0.014729 29.437 15.463 2da iteración Terreno de cimentación. Con los ri anteriores y aplicando las ecs 64, 65 y 59 Kv1 Kv2 δ1 δ2 m m t/m t/m 0.013743 0.014290 3427.089 3462.699 Estructura. Con los Kvi anteriores, y aplicando las ecs 61, 62, 63 y 60 r1 r2 δ1 δ2 m m t/m t/m 0.013498 0.014775 28.912 15.988 4ta iteración Terreno de cimentación. Aplicando las ecs 64, 65 y 59 Kv1 Kv2 δ1 δ2 m m t/m t/m 0.013495 0.014779 3433.069 3452.402 Estructura. Con los Kvi anteriores, y aplicando las ecs 61, 62, 63 y 60 r1 r2 δ1 δ2 m M t/m t/m 0.013493 0.014782 28.952 15.948 Interacción suelo-­‐losa de cimentación Una losa de cimentación se puede modelar como una retícula de barras ortogonales entre sí. La solución es más precisa a medida que se incrementa el número de éstas. Para una retícula de barras horizontales Ejemplo de diseño de una zapata corrida Hacer el diseño geotécnico y el diseño estructural de la zapata corrida de concreto reforzado de la figura A, de acuerdo con las Normas de Cimentaciones del RCDF-2004. Terreno de cimentación: zona II, FR ≤ 0.7 En la estructura: Concreto: fc’ = 25 MPa Acero: fy = 420 MPa Considerar una vida útil de 50 años Asentamiento permisible = 10 cm 4m 4m 0.3 m B PLANTA 320 kN 640 kN 320 kN 10 kN/m NAF Arcilla preconsolidada cu = 52 kPa Eu = 2316 kPa, As' = 78, Aske = 0.3 cv = 0.00082 cm2/s, Φ' = 28°, OCR = 2 γsat = 16 kN/m3 Estrato 1 Eu = 3724 kPa, As' = 86, Aske = 0.3 cv = 0.00076 cm2/s, Φ' = 30°, OCR = 2 γsat = 18 kN/m3 Estrato 2 Arcilla preconsolidada cu = 64 kPa Roca ELEVACIÓN 0.8 m 0.6 m 1.4 m SOLUCIÓN Estados límite de falla Se debe verificar qult ≤ qR qR = 5.14 cu fc FR + pv (33) fc = 1 + 0.25 B/L + 0.25 D/B (34) para D/B < 2 y B/L < 1 . En caso de que D/B y B/L no cumplan con las desigualdades anteriores, dichas relaciones se tomarán iguales a 2 y 1, respectivamente. 0.35 ≤ FR ≤ 0.70 Para condiciones normales se recomienda 0.45 ≤ FR ≤ 0.55 qult = Σ Q Fc / A Suponemos ancho de la zapata B = 1.4 m, y un peralte de la losa de la zapata h = 25 cm qult = 189.97 kPa < qR = 194.08 kPa ∴ Cumple Estados límite de servicio Asentamiento inmediato Trabajamos bajo el centro de la zapata, y a la mitad de cada estrato. Usando la ley de Hooke: δu = σ z −ν (σ x + σ y ) Eu (Δzo ) Estrato 1 ν = 0.5, q = 137.17 kPa, z = 0.3 m σz = 133.43 kPa σx = 100.13 kPa σy = 70.19 kPa Eu = 2316 kPa δu = 133.43 − 0.5(100.13 + 70.19) (0.6) 2316 δu = 0.0125 m Procediendo en forma análoga para el estrato 2, con Eu = 3724 kPa, obtenemos δu = 0.0217 m δuT = 0.0125 + 0.0217 = 0.0342 m Asentamiento a largo plazo Δδ Pcon 1 − ⎡ ⎤ A ' s ⎛ ⎞ p +σz ⎟⎟ ⎥ Δzo = ⎢1 − ⎜⎜ veo ⎢ ⎝ pveo ⎠ ⎥ ⎢⎣ ⎦⎥ pveo = pcie + pvo’ pvo’ = 0.8(16)+(16-9.81)(0.3) = 14.657 kPa pveo = pvo’ = 14.657 kPa Δδ Pcon 1 − ⎤ ⎡ ⎛ 14.657 + 133.43 ⎞ 78 ⎥ (0.6) = 0.01753m = ⎢1 − ⎜ ⎟ ⎢ ⎝ 14.657 ⎠ ⎥ ⎣ ⎦ Δδ Pcpo = µ (Δδ Pcon ) (18) Por lo tanto, ya se completó la consolidación primaria, y Δδ Pcpo ,50 años = 0.0131(1) = 0.0131m Procediendo en forma similar para el estrato 2: δ50 años = 0.0120 m δ50 años = 1.31 + 1.20 = 2.51 cm (Zapata corrida con Skempton.xls) Asentamiento total El asentamiento total es la suma del hundimiento inmediato más el diferido, es decir δT = 3.43 + 2.51 = 5.94 cm < 10 cm ∴ Cumple Diseño estructural Interacción suelo-estructura Método directo (Deméneghi, 1996) El análisis estructural se lleva a cabo empleando el método de rigideces. El cálculo de deformaciones del suelo se realiza usando la siguiente fórmula ne nr j=1 k=1 δi = δoi + Σ (Δzj/Esij) Σ Iijk rkdk/ak (49) Donde Iijk = Izijk-ν(Ixijk+Iyijk) (48) Izijk es el valor de influencia vertical, el cual es igual al incremento de esfuerzo normal vertical en el punto ij, producido por una presión unitaria actuando en el área ak (Zeevaert, 1973). Las demás cantidades Ixijk e Iyijk se obtienen en forma similar, usando los incrementos de esfuerzo normal horizontal. 8m 1 2 3 4 5 7 7 8 9 1.4 m PLANTA 1 Distancias 0 0 0.5 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8m 1.5 2.5 3.5 4.5 5.5 6.5 7.5 m Estrato 1 (1,1) (2,1) (5,1) (9,1) Estrato 2 (1,2) (2,2) (5,2) (9,2) DETERMINACIÓN DE LA MATRIZ DE FLEXIBILIDADES FIGURA B ELEVACIÓN Método iterativo El análisis de interacción se puede llevar a cabo en forma iterativa (Ccmaflx02.for; Mafdatx0210). Aplicamos la ecuación 49, considerando, para iniciar los cálculos, una reacción uniforme, la cual vale r = ΣQ/longitud de la zapata r = 1536.32/8 = 192.04 kN/m Usando la matriz de flexibilidades del terreno de cimentación (ecuación 49), la cual se exhibe en el anexo 1, se calculan las deformaciones del suelo. En el anexo 3 se exhiben los resultados de este primer cálculo del análisis a corto plazo (primera iteración). El módulo de reacción vertical o “constante del resorte” es Kvi = ri di / δi (I) Sustituyendo valores se obtienen los valores de Kv mostrados en el anexo 3. Con estos módulos de reacción iniciamos el análisis estructural de la zapata (Ejemplo A E zapata corrida 0210.SDB; SAP 2000). Con los desplazamientos de la estructura δEi se calculan las nuevas cargas rEi sobre el terreno rEi = K viδ Ei di (J) A continuación se hace ri = rEi, y se vuelven a calcular las deformaciones del terreno con la ecuación 49. El proceso se repite hasta que las deformaciones del suelo igualan a las de la estructura. En el anexo 3 se presentan los resultados de la última iteración. Con los valores de Kv de esta última iteración se lleva a cabo el análisis estructural y se obtienen los elementos mecánicos sobre la zapata corrida (Ejemplo A E zapata corrida 0210.SDB; SAP 2000). Se encuentran los siguientes valores máximos Momento negativo, kN.m Momento positivo, kN.m Cortante centro, kN Cortante extremos, kN CORTO PLAZO 179.04 181.23 265.72 168.91 Estas magnitudes son similares a las halladas con el método directo. Las diferencias se deben básicamente a que en el procedimiento directo se aplican reacciones repartidas sobre la estructura, mientras que con el método iterativo las reacciones sobre la estructuras son cargas puntuales (a través de los resortes). 162.91 (+) (-) -177.5 (-) -200.5 -200.5 -177.5 -207.6 -207.6 c) DIAGRAMA DE MOMENTO FLEXIONANTE, kN.m 320 320 181.5 (+) (+) 87.7 44.1 (-) -87.7 (-) -44.1 -181.5 -320 -320 d) DIAGRAMA DE FUERZA CORTANTE, kN DIAGRAMAS DE ASENTAMIENTOS, DE REACCIONES Y DE ELEMENTOS MECÁNICOS CORTO PLAZO FIGURA E 207.4 (+) (-) (-) -167.8 -159.4 -167.8 -159.4 -179.4 -179.4 c) DIAGRAMA DE MOMENTO FLEXIONANTE, kN.m 320 320 187.5 (+) (+) 67.8 55.43 (-) -67.8 (-) -55.43 -187.5 -320 -320 d) DIAGRAMA DE FUERZA CORTANTE, kN DIAGRAMAS DE ASENTAMIENTOS, DE REACCIONES Y DE ELEMENTOS MECÁNICOS LARGO PLAZO FIGURA F Magnitudes aproximadas del módulo de reacción Para análisis preliminares de interacción suelo-estructura, se pueden usar los siguientes valores del módulo de reacción vertical Kv = kv = Qv δv Kv Q q = v = v a aδ v δ v Corto plazo Bajo el centro de la zapata corrida kvc = qv δv = 137.17 = 4010.82kN / m3 0.0342 K vc = kvc a = 4010.82(1)(1.4) = 5615.1kN / m En las orillas de la zapata se puede usar kvo = 2.1kvc k vo = 2.1(4010.82) = 8422.7 kN / m 3 K vo = kvo a = 8422.7(0.5)(1.4) = 5895.9kN / m Largo plazo Se toma el asentamiento total de la zapata δ = δu + δ’ = 3.43 + 2.37 = 5.80 cm qv 137.17 k vc = = = 2365kN / m 3 δ v 0.0580 K vc = kvc a = 2365(1)(1.4) = 3311kN / m kvo = 2.1(2365) = 4966.5kN / m 3 K vo = kvo a = 4966.5(0.5)(1.4) = 3476.55kN / m Ejemplo de cimentación compensada NAF Ee kPa Eu kPa Ep kPa Ecs kPa cv cm2/s ξ Gdin kPa 2 m Limo arcilloso sensitivo Gamma = 17 kN/m3 4m 4955 3980 6200 11295 2x10-3 5 3400 Arcilla limosa sensitiva Gamma = 14 kN/m3 4m 4905 4000 6795 12400 1.2x10-3 5 3300 Arcilla limosa sensitiva Gamma = 12 kN/m3 5m 5005 Lentes permeables 3890 7200 12805 1x10-3 5 3200 Arena muy compacta (Cc cimentación compensada ejemplo 130901) ESTRATIGRAFÍA Y PROPIEDADES FIGURA A 30.6 m 109 110 111 112 113 114 115 116 117 100 101 102 103 104 105 106 107 108 91 92 93 94 95 96 97 98 99 82 83 84 85 86 87 88 89 90 73 74 75 76 77 78 79 80 81 64 65 66 67 68 69 70 71 72 55 56 57 58 59 60 61 62 63 46 47 48 49 50 51 52 53 54 37 38 39 40 41 42 43 44 45 28 29 30 31 32 33 34 35 36 19 20 21 22 23 24 25 26 27 10 11 12 13 14 15 16 17 18 1 2 3 4 5 6 7 8 9 20 m NUMERACIÓN DE NUDOS DE LA CIMENTACIÓN FIGURA B (Cc cimentación compensada ejemplo 0210) 97 204 98 205 89 195 90 81 177 178 168 179 169 57 159 170 58 160 49 150 141 132 123 114 105 20 11 21 12 13 109 4 5 20 m NUMERACIÓN DE BARRAS FIGURA C 131 24 121 15 111 6 32 23 14 140 130 120 110 40 31 22 149 139 129 119 48 39 30 158 148 138 128 118 108 3 29 56 47 38 167 157 147 137 127 117 107 2 28 19 10 37 64 55 46 176 166 156 146 136 126 116 106 1 135 125 115 145 175 165 155 185 72 63 54 45 36 27 18 9 144 134 124 154 184 174 164 194 80 71 62 53 44 35 26 17 153 143 133 163 193 183 173 203 88 79 70 61 52 43 34 25 162 152 142 172 202 192 182 212 96 87 78 69 60 51 42 33 171 161 151 181 211 201 191 104 95 86 77 68 59 50 41 180 210 200 190 103 94 85 76 67 209 199 189 102 93 84 75 66 208 198 188 101 92 83 74 65 207 197 187 100 91 82 73 30.6 m 206 196 186 99 122 16 112 7 113 8 Magnitudes aproximadas de los módulos de reacción Para análisis preliminares de interacción suelo-estructura, se pueden usar los siguientes valores del módulo de reacción vertical Kv = kv = Qv δv Kv Q q = v = v a aδ v δ v Corto plazo Bajo el centro de la losa de cimentación kvc = q 83 = = 1114kN / m3 δ e + δ u 0.0415 + 0.0330 K vc = kvc a = 1114(2.5)(2.55) = 7102kN / m En las orillas de la losa se puede usar k vo ≅ 2.3 − 2.8k vc k vo ≅ 2.8(1114) = 3119.2kN / m 3 K vo = k vo a = 3119.2(1.25)(2.55) = 9942.4kN / m En las esquinas kve ≅ 6 − 7kvc k ve ≅ 7(1114) = 7798kN / m 3 K ve = k ve a = 7798(1.25)(1.275) = 12428.1kN / m Largo plazo Se toma el asentamiento total de la zapata δ = 0.0415 + 0.0330 + 0.0594 = 0.1339 m kvc = q δ = 70 = 522.8kN / m 3 0.1339 K vc = kvc a = 522.8( 2.5)(2.55) = 3332.8kN / m k vo ≅ 2.3 − 2.8k vc k vo ≅ 2.8(522.8) = 1463.8kN / m 3 K vo = k vo a = 1463.8(1.25)(2.55) = 4666kN / m k ve ≅ 6 − 7 k vc k ve ≅ 7(522.8) = 3659.6kN / m 3 K ve = k ve a = 3659.6(1.25)(1.275) = 5832.5kN / m Gracias por su atención Agus5n Deméneghi Colina [email protected]