UNIDAD II (TORNILLOS)

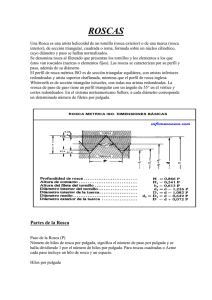
Diseño Mecánico II
UNIDAD II.- TORNILLOS
2.1.- INTRODUCCIÓN Y NOMENCLATURA.
Un tornillo es un dispositivo que se utiliza en la maquinaria para convertir un giro o desplazamiento angular en un
desplazamiento rectilíneo, y transmitir así, la acción de una fuerza o potencia mecánica.
Cada uno de los elementos de máquinas tiene una terminología única. En la figura (2.1) se describen la terminología y
las dimensiones de las partes roscadas.
Figura (2.1).- Parámetros que se emplean para definir la terminología de un perfil roscado.
De la figura anterior tenemos que:
d = diámetro mayor
d c = diámetro de la cresta
d p = diámetro de paso
d r = diámetro de la raíz
h t = altura más grande de la rosca
 = ángulo de la rosca
Dos términos importantes son:
a).- Paso (p).- Es la distancia desde un punto sobre una rosca hasta el mismo punto en una rosca adyacente.
En la nomenclatura americana
p
1
N
(2.1)
en donde
p
= paso en pulgadas.
N = número de roscas por pulgada.
Pág. 1
Diseño Mecánico II
b).- Avance (l).- Es la distancia que el tornillo avanzaría en relación con la tuerca en una revolución.
l  Np
De ésta manera para un tornillo de rosca sencilla l = p y para un tornillo de rosca doble
(2.2)
l = 2p, etc. En la figura
(2.2) se observan las diferencias entre tornillos de rosca sencilla, doble y triple.
Figura (2.2).- Tornillos de rosca a) simple, b) doble, c) triple.
Se pueden usar diferentes perfiles de rosca para una amplia variedad de aplicaciones. En la figura (2.3) se presentan
dos tipos. El perfil Acme se utiliza en los tornillos de potencia y en roscas de máquinas herramientas. Otro perfil es el unificado
(UN) que se utiliza también con mucha frecuencia. El perfil Acme tiene un ángulo de rosca de 29 o , mientras que el unificado
(UN) tiene un ángulo de rosca de 60 o . El perfil métrico (M) es popular y muy similar al perfil UN.
Figura (2.3).- Perfiles de rosca. a) Acme; b) UN.
En la siguiente figura se muestran detalles de los perfiles de rosca M y UN.
Figura (2.4).- Detalles de los perfiles de rosca M y UN.
Por medio de la figura anterior se obtiene lo siguiente:
Pág. 2
Diseño Mecánico II
ht 
0.5 p
tan 30 o
 0.866p
(2.3)
Una vez que se conocen el paso p y la altura máxima posible de la rosca h t , se pueden obtener las diferentes
dimensiones de los perfiles de rosca UN y M.
El término “series de rosca” se puede aplicar a las roscas de cualquier tamaño. Cada una de las series de rosca tiene el
mismo número de roscas por pulgada. Las ocho series de rosca UN de paso constante son 4, 6, 8, 12, 16, 20, 28 y 32 roscas por
pulgada.
Además de las series de rosca, los perfiles de rosca se clasifican por la basteza, la cual se refiere a la calidad y al
número de roscas por pulgada producidas sobre un diámetro común del sujetador. Las designaciones que siguen después de las
siglas UN significan lo siguiente:
1.- C = roscas de paso basto
2.- F = roscas de paso fino
3.- EF = roscas de paso extrafino
Después de la designación de la basteza se continúa con el diámetro medio en pulgadas y con el número de roscas por
pulgada. Por ejemplo, UNF 1/2 x 16 significa un perfil de rosca UN con roscas de paso fino, un diámetro de cresta de 1/2 pulg,
y 16 roscas por pulgada.
En el caso de las roscas métricas generalmente se consideran solo las designaciones basta o fina. Por ejemplo, MF 6x1
significa un perfil de rosca M con roscas de paso fino, un diámetro de cresta de 6 mm y una distancia de paso de 1 mm.
Las clasificaciones anteriores solo son aplicables para roscas individuales pero no se toma en cuenta como se ajustan
las partes macho y hembra del sujetador. En las unidades inglesas las roscas externas se designan por medio de la letra A,
mientras que las internas por la letra B. Existen tres clases de ajuste: 1 (ajuste más suelto), 2 (ajuste normal) y 3 (ajuste
apretado). Por ejemplo UNC 2x8 - 1B significa un perfil de rosca UN con rosca de paso basto, un diámetro de cresta de 2 pulg,
8 roscas de paso constante por pulg y un ajuste suelto, especificando la parte interna del sujetador.
TORNILLOS DE POTENCIA.
Los tornillos de potencia son dispositivos que transforman un movimiento angular en un movimiento lineal y se
utilizan generalmente para transmitir potencia. Estos dispositivos se utilizan para:
a)
Obtener una ventaja mecánica mayor al levantar una carga.
b) Ejercer fuerzas de gran magnitud, como en compactadores.
c)
Obtener un posicionamiento preciso de un movimiento axial.
En los tornillos de potencia se usa el perfil de rosca Acme el cual se detalla más ampliamente en la siguiente figura:
Pág. 3
Diseño Mecánico II
Figura (2.5).- Detalles del perfil de rosca Acme.
En la tabla (2.1) que se muestra a continuación, se proporciona el diámetro de la cresta, el número de roscas por
pulgada, y las áreas de esfuerzo de tensión y compresión para las roscas de tornillos de potencia Acme.
Diámetro de
cresta,
d c , pul
Número
de roscas
por pulgada, N
Área del esfuerzo de
tensión,
Áreas,
de los esfuerzos
At , pul2
cortantes, As , pul2
16
14
12
12
10
8
6
6
5
5
5
4
4
4
4
3
3
3
2
2
2
2
2
0.02632
0.04438
0.06589
0.09720
0.1225
0.1955
0.2732
0.4003
0.5175
0.6881
0.8831
1.030
1.266
1.811
2.454
2.982
3.802
4.711
5.181
7.330
9.985
12.972
16.351
0.3355
0.4344
0.5276
0.6396
0.7278
0.9180
1.084
1.313
1.493
1.722
1.952
2.110
2.341
2.803
3.262
3.610
4.075
4.538
4.757
5.700
6.640
7.577
8.511
1/4
5/16
3/8
7/16
1/2
5/8
3/4
7/8
1
11/8
11/4
13/8
11/2
13/4
2
21/4
21/2
23/4
3
31/2
4
41/2
5
Tabla (2.1).- Diámetros de cresta, roscas por pulgada y esfuerzos para rosca Acme.
El área del esfuerzo de tensión es:
Pág. 4
Diseño Mecánico II
dr dp
A t  4  2 


2
(2.4)
El diámetro de paso de una rosca de tornillo de potencia Acme es:
d p  d c  0.5p  0.01
(2.5.a)
d p  d c  0.5p  0.254
(2.5.b)
para d c y p en pulgadas.
para d c y p en mm.
En la figura siguiente se muestra una carga W dentro de la cual se rosca el tornillo de soporte y la cual se puede elevar
o bajar girando el tornillo. En ésta figura se muestra también el ángulo de la rosca de un tornillo Acme  , el cual es de 29o, y el
ángulo de avance  .
Figura (2.6).- Dimensiones y ángulos de un tornillo de potencia con collarín.
El ángulo de avance  relaciona el avance con la circunferencia de paso por medio de la siguiente expresión:
  tan 1  dl 
 p
(2.6)
donde
l = avance = mp
m = 1, tornillo de roscado sencillo
m = 2, tornillo de roscado doble
m = 3, tornillo de roscado triple
d p = diámetro de paso
La distancia recorrida en la dirección axial se determina como sigue:
Pág. 5
Diseño Mecánico II
d s  n o l  n o ( mp )
(2.7)
n o = número de revoluciones
La figura (2.7) nos muestra las fuerzas que actúan al levantar una carga con un tornillo de potencia.
(c)
Figura (2.7).- Fuerzas para elevar una carga con un tornillo de potencia.
En esta figura se tiene:
(a) Fuerzas que actúan sobre el paralelepípedo.
(b) Fuerzas que actúan sobre la sección axial.
(c) Fuerzas que actúan sobre un plano tangencial.
ELEVACIÓN DE LA CARGA.
Observando las figuras (2.7a) y (2.7b) obtenemos la siguiente relación:
Pág. 6
Diseño Mecánico II
senn  cos n cos  tan  / 2 
 n  tan 1 (cos  tan  / 2)
(2.8)
Sumando las fuerzas verticales de la figura (2.7c) se obtiene la siguiente expresión:
Pn 
W
cos n cos  sen
(2..9)
El par de torsión que se requiere para elevar la carga es,
T  W

( d p / 2 )(cos n tan    )
cos  n   tan 
 rc c 

(2.10)
en donde
 = coeficiente de fricción entre las roscas
 c = coeficiente de fricción para el collarín
rc = radio del collarín
BAJADA DE LA CARGA.
Al sumar las fuerzas verticales debe tenerse en cuenta el signo de las componentes de la fuerza de fricción, ya que
éstas cambian de signo. La expresión que se obtiene es:
Pn 
W
cos n cos  sen
(2.11)
 rc  c 

(2.12)
El par de torsión que se requiere para bajar la carga es,
T   W

( d p / 2 )( cosn tan  )
cosn  tan 
POTENCIA Y EFICIENCIA.
Potencia.
Pág. 7
Diseño Mecánico II
Una vez que se conoce el par de torsión T , podemos determinar la potencia que se transfiere por el tornillo mediante la
siguiente expresión:
H
Tn a
63025
(2.13)
En donde,
H = potencia en hp
n a = rpm del tornillo
T = par de torsión en lb-pul
En el sistema internacional,
H  T
(2.14)
En donde,
H = potencia en Watts
T = par de torsión en N–m
 = velocidad angular en rad/seg
EFICIENCIA.
La eficiencia de un mecanismo de tornillo es la razón entre el trabajo de salida y el trabajo de entrada, o

Wl
2 T
x100
(2.15)
 = eficiencia en %
l = avance, m, pul
W = carga, N, lb-pul
SUJETADORES ROSCADOS.
Pág. 8
Diseño Mecánico II
Un sujetador es un dispositivo que sirve para conectar o unir dos o más elementos. El sujetador más común es el
roscado, el cual se utiliza para sujeciones no permanentes; es decir, que puede ser desensamblado fácilmente sin recurrir a su
destrucción como ocurriría con otro tipo de uniones tales como las remachadas o soldadas.
Tipos de sujetadores roscados.
La siguiente figura representa tres tipos de sujetadores roscados: a).- De perno y tuerca, b).- Tornillo de cabeza, c).Birlo.
Figura (2.8).- Tres tipos de sujetadores roscados. (a) Perno y tuerca;
(b) Tornillo de cabeza; (c) Birlo.
2.3.2.- ANÁLISIS DE CARGA DE PERNOS Y TUERCAS.
El perno y la tierca se pueden considerar como un sistema de resortes como se presenta en la figura siguiente:
Figura (2.9).- Ensamble de perno y tuerca,
Simulado mediante un resorte de perno y junta.
El perno se considera como un resorte de tensión con una rigidez k b . La junta que une varios miembros, se considera
como un resorte de rigidez k j .
Pág. 9
Diseño Mecánico II
Figura (2.10).- Fuerzas contra deflexión del perno y junta
cuando se aplica una carga externa.
(extensión del perno = reducción en la contracción de la junta)
De la figura (2.10) se tiene que:
Pb = carga sobre el perno
P j = carga sobre la junta
Pi = precarga
P = incremento en Pb más la disminución en P j
De acuerdo con la figura anterior se obtiene lo siguiente:
P  Pi  k je k  Pi  k b e k  0 
ek 
P
k b k j
(2.16)
La carga sobre el perno es:
Pb  Pi  k b e k  Pi 
Pk b
kb k j
 Pi  C k P
(2.17)
En donde
Ck 
kb
k b k j
(2.18)
(parámetro adimensional de la rigidez)
La carga sobre la junta es:
Pj  Pi  k je k  Pi 
Pk j
k j kb
 Pi  (1  C k )P
(2.19)
Pág. 10
Diseño Mecánico II
RIGIDEZ DEL PERNO.
El perno se trata como un resorte en serie cuando se consideran el cuerpo y la sección roscada. El perno también puede
tener diámetros diferentes debido a otras especificaciones, por lo que su rigidez se determina como sigue:
1  1  1  1  .........
kb kb1 kb2
kb3
(2.20)
De acuerdo con la figura (2.11) la rigidez del perno se calcula mediante la expresión
1  4  Lse  Lte   4  Ls  0.4 d c  Lt  0.4 d r 

 d2

kb E  d 2
d r2  E 
d r2
c
 c

(2.21)
donde
d c = diámetro de la cresta, m
d r = diámetro de la raíz, m
Figura (2.11).- Perno y tuerca. (a) Ensamble, (b) Representación del eje escalonado del
cuerpo y la sección roscada.
Para roscas estandarizadas la longitud roscada se calcula por las siguientes expresiones:
Pág. 11
Diseño Mecánico II
L  125
 2d c  6

Lt   2d c  12 125  L  200
2d  25
L  200
 c
(roscas métricas)
( 2.22)
2d  0.25 pul
Lt   c
2d c  0.50 pul
(serie en pulgadas)
(2.23)
L  6 pul
L  6 pul
donde
Lt = longitud roscada, mm
L = longitud total del perno
d c = diámetro de la cresta, mm
RIGIDEZ DE LA JUNTA.
El cálculo de la rigidez de la junta es mucho más complicado que la determinada para el perno. Una de las
aproximaciones más frecuentes es que el esfuerzo que se induce en la junta es uniforme en toda la región que rodea al agujero
del perno, con un esfuerzo nulo fuera de esa región. Con frecuencia se emplean dos troncos cónicos simétricos alrededor del
plano medio de la junta; cada uno con un ángulo del vértice
 . En la figura siguiente
cónico de la junta en un ensamble de perno y tuerca. Debemos notar que
dw
se representa el esfuerzo del tronco
es el diámetro de la arandela.
Figura (2.12).- Ensamble de perno y tuerca con representación del esfuerzo del tronco
cónico de la junta.
Para determinar la rigidez de la junta, se recomienda la siguiente expresión:
Pág. 12
Diseño Mecánico II
k ji 
E i d c tan 
(2.24)
 2 L i tan   d i  d c )( d  d ) 
2 ln  ( L tan   d  d )( di  dc ) 
i
c
i c 
 i
donde
Li = longitud axial del tronco cónico, m
d i = diámetro del tronco cónico, m
Siempre se usa el más pequeño de los diámetros de los troncos cónicos. Para el miembro más cercano a la cabeza del
perno o de la tuerca
d i  d w  1.5d c
.
La rigidez resultante de la junta es
1  1  1  1  .......
k j k j1 k j2
k j3
(2.25)
RESISTENCIA.
Carga de prueba de un perno ( Pp ) .- Es la carga máxima que un perno puede soportar sin adquirir una deformación
permanente.
Resistencia de prueba (Sp ) .- Es el valor límite del esfuerzo que se determina usando la carga de prueba y el área de
esfuerzo de tensión; esto es,
Sp 
Pp
At
(2.26)
La resistencia de prueba define los grados de los pernos o clases en la que se especifica el material, el tratamiento
térmico y la resistencia de prueba mínima para el perno o el tornillo. En las tablas (2.2) y (2.3) se proporciona la información
de la resistencia para pernos grados SAE y métricos respectivamente.
Grado
Rango de los
Resistencia a la
diámetros de
rotura por
Resistencia a
Resistencia
de prueba,
Pág. 13
Diseño Mecánico II
SAE
la cresta d c ,
tensión, Sut , kpsi la fluencia, S y ,
pul
Sp ,
kpsi
kpsi
1
¼ - 11/2
60
36
33
2
¼-¾
74
57
55
1
> ¾ - 1 /2
60
36
33
4
¼ - 11/2
115
100
65
5
¼-1
120
92
85
1
> 1 - /2
105
81
74
7
¼ - 11/2
133
115
105
8
¼ - 11/2
150
130
120
Tabla (2.2).- Resistencia de pernos de acero para varios tamaños en pulgadas.
Grado
Diámetro de la
Resistencia a la
Resistencia a
Resistencia
cresta d c , mm
rotura por
la fluencia, S y ,
de prueba,
tensión, Sut ,
MPa
Sp ,
métrico
MPa
MPa
4.6
M5-M36
400
240
225
4.8
M1.6-M16
420
340
310
5.8
M5-M24
520
415
380
8.8
M17-M36
830
660
600
9.8
M1.6-M16
900
720
650
10.9
M6-M36
1040
940
830
12.9
M1.6-M36
1220
1100
970
Tabla (2.3).- Resistencia de pernos de acero para varios tamaños en milímetros.
En la tabla (2.4) se dan las dimensiones y las áreas de esfuerzo de tensión para roscas bastas y finas UN. La ecuación
para las áreas de esfuerzo es
Pág. 14
Diseño Mecánico II

A t  (0.7854) d c  0.9743
n

2
(2.27)
en donde
d c = diámetro de la cresta
n = número de roscas por pulgada
Diámetro
de la cresta
d c , pul
0.0600
0.0730
0.0860
0.0990
0.1120
0.1250
0.1380
0.1640
0.1900
0.2160
0.2500
0.3125
0.3750
0.4735
0.5000
0.5625
0.6250
0.7500
0.8750
1.0000
1.1250
1.2500
1.3750
1.5000
1.7500
2.0000
Roscas bastas (UNC)
Área del
Número
esfuerzo
de roscas
de tensión,
por pulgada,
At ,
n
pul2
64
0.00263
56
0.00370
48
0.00487
40
0.00604
40
0.00796
32
0.00909
32
0.0140
24
0.0175
24
0.0242
20
0.0318
18
0.0524
16
0.0775
14
0.1063
13
0.1419
12
0.182
11
0.226
10
0.334
9
0.462
8
0.606
7
0.763
7
0.969
6
1.155
6
1.405
5
1.90
41/2
2.50
Roscas finas (UNF)
Área del
Número
esfuerzo
de roscas
de tensión,
por pulgada,
At ,
n
pul2
80
0.00180
72
0.00278
64
0.00394
56
0.00523
48
0.00661
44
0.00830
40
0.01015
36
0.01474
32
0.0200
28
0.0258
28
0.0364
24
0.0580
24
0.0878
20
0.1187
20
0.1599
18
0.203
18
0.256
16
0.373
14
0.509
12
0.663
12
0.856
12
1.073
12
1.315
12
1.581
-
Tabla (2.4).- Dimensiones y áreas del esfuerzo a tensión
para roscas UN bastas y finas.
En la tabla (2.5) se dan las dimensiones y las áreas de esfuerzo de tensión para perfiles de rosca M. La ecuación
correspondiente para las áreas de esfuerzo es
Pág. 15
Diseño Mecánico II
A t  (0.7854 )( d c  0.9382 p) 2
En ésta ecuación tanto el diámetro de la cresta
d c como el paso p están en milímetros.
Roscas bastas (MC)
Roscas finas (MF)
Área
Área
Diámetro de la
cresta, d c , mm
(2.28)
del esfuerzo de
Paso, p, mm
tensión, A t ,
del esfuerzo
Paso, p, mm
de tensión, A t ,
mm2
mm2
1
0.25
0.460
-
-
1.6
0.35
1.27
0.20
1.57
2
0.40
2.07
0.25
2.45
2.5
0.45
3.39
0.35
3.70
3
0.50
5.03
0.35
5.61
4
0.70
8.78
0.50
9.79
5
0.80
14.20
0.50
16.1
6
1.00
20.10
0.75
22
8
1.25
36.6
1.00
39.2
10
1.50
58.0
1.25
61.2
12
1.75
84.3
1.25
92.1
16
2.00
157
1.50
167
20
2.50
245
1.50
272
24
3.00
353
2.00
384
30
3.50
561
2.00
621
36
4.00
817
3.00
865
42
4.50
1121
-
-
48
5.00
1473
-
-
Tabla (2.5).- Dimensiones y áreas de esfuerzo a tensión
para roscas métricas bastas y finas.
PERNO PRECARGADO (CARGA ESTÁTICA).
La ecuación (2.17) se puede escribir en términos del esfuerzo como sigue:
Pág. 16
Diseño Mecánico II
b 
Pb
At

Pi
At
Sp 
Pi
At

Pmáx n s C k
At
 Ck
P
At
(2.29)
La resistencia de prueba se determina por
(2.30)
donde
A t = área del esfuerzo de tensión
Pi = Precarga
A partir de la ecuación (2.30) se obtiene el factor de seguridad de la falla del perno:
n sb 
A tSp  Pi
Pb , máx Ck
(2.31)
donde
Pb ,máx = carga máxima aplicada sobre el perno
SEPARACIÓN DE LA JUNTA.
Pág. 17
Diseño Mecánico II
La separación ocurre cuando en la ecuación (2.19) P j = 0. De esta forma, el factor de seguridad que protege contra la
separación es:
n sj 
Pi
Pj, máx (1Ck )
(2.32)
en donde
Pj,máx = carga máxima aplicada a la junta
La cantidad de precarga que se aplica a los pernos bajo condiciones estáticas, es un término medio entre la sobrecarga
del perno y la separación. La precarga se da para conexiones reutilizables y permanentes como
Pi  0.75 Pp para conexiones reutilizables
Pi  0.90 Pp para conexiones permanentes
En la práctica las precargas raramente se especifican debido a que éstas son muy difícil de medir durante el ensamble
de las conexiones con pernos; sin embargo se tienen dos alternativas:
1.
Se especifica un par de torsión para su aplicación durante el apriete, el cual se controla mediante un torquímetro.
2.
Se define un número de rotaciones de un “estado ajustado”, como el de una media vuelta.
PERNO PRECARGADO (CARGA DINÁMICA).
El efecto de la precarga es mayor para las juntas cargadas dinámicamente que para las cargadas estáticamente. Como
es más probable que la falla por carga cíclica ocurra para el perno, solo se analiza éste elemento. Las cargas alternante y media
que actúan sobre el perno se determinan por las expresiones siguientes:
Pba 
Pb ,máx  Pb ,min
2

C k ( Pmáx  Pmin )
2
 Ck Pa
(2.33)
Pág. 18
Diseño Mecánico II
Pbm 
Pb ,máx  Pb ,min
2
 Pi 
C k ( Pmáx  Pmin )
2
 Pi  Ck Pm
(2.34)
Los esfuerzos alternante y medio se expresan como
a 
m 
C k Pa n s
At
(2.35)
Pi  C k Pm n s
At
(2.36)
El factor de seguridad no se aplica a la precarga.
El factor de seguridad se determina mediante el criterio de falla por fatiga de Goodman.
La teoría de Goodman se expresa como sigue:
K f a
Se
ns 

 Sm  1
(2.37)
ut
S ut   i
C k  K f

Pa
At
(2.38)
 Sut   Pm 
 Se  A t 
K f = factor de concentración de esfuerzos por fatiga
Grado
Grado
Roscas
Roscas
Filete
SAE
métrico
laminadas
cortadas
0-2
3.6 – 5.8
2.2
2.8
2.1
4-8
6.6 – 10.9
3.0
3.8
2.3
Tabla (2.6).- Factores de concentración de esfuerzos por fatiga K f
para elementos roscados.
Problema 2.1.- Un tornillo de potencia Acme ( 
 29 o ) de rosca doble se usa para levantar una carga de 1350 lb.
El diámetro exterior del tornillo es de 1.25 pul y el diámetro medio del collarín es de 2 pul. Los coeficientes de fricción son
0.13 para la rosca y 0.16 para el collarín. Determinar lo siguiente:
a)
Las dimensiones geométricas del tornillo.
b) El par de torsión requerido para levantar y bajar la carga.
c)
La eficiencia al levantar la carga.
d) La carga correspondiente a la eficiencia, si la eficiencia al levantar la carga es de 18 %.
Solución:
Pág. 19
Diseño Mecánico II
a). De la tabla (2.1) para un diámetro de la cresta de 1.25 pul, N = 5 roscas por pulgada.
El paso p = 1/N = 1/5 = 0.2
Para rosca doble el avance es l = mp = 2(0.2) = 0.4 pul
El diámetro de paso es d p  d c  0.5p  0.01 = 1.25 – 0.5(0.2) – 0.01 =1.14 pul
Ec (2.6):   tan 1  dl   tan 1
 p
   6.373
o
0.4
1.14 


Ec (2.8):  n  tan 1 (cos  tan  / 2)  tan 1 (cos 6.373 o )(tan 14 .5o ) = 14.414o
b).- Para elevar la carga:
T  W

( d p / 2 )(cos n tan    )
cos  n   tan 
 rcc   Ec (2.10):

 1.14 (cos14.41o tan 6.373o  0.13)

T  1350 2
 (1)(0.16)   408 lb-pul
cos14.414 o  0.13 tan 6.373o


Para bajar la carga:
T  W

( d p / 2 )(  cos  n tan  )
cos  n   tan 
 rcc   Ec (2.12):

 1.14 ( 0.13 cos14.41o tan 6.373o )

T  1350 2
 (1)(0.16)   233 lb-pul
cos14.414 o  0.13 tan 6.373o


c).- Ec (2.15):
d).-  
Wl
2 T

Wl
2 T
x100  W 
x 0.4
x100  1350
x100  21.06 %
2  ( 408)
2  ( 408)(18)
100 x 0.4
 1153.59 lb
Problema 2.2.- Un perno M12 de paso basto, clase 5.8 ensamblado con una tuerca hexagonal sirve para mantener
unidas dos partes de una máquina, como se muestra en la figura., determinar:
a)
La rigidez del perno y el miembro.
b) La carga externa máxima que el conjunto puede soportar para un factor de seguridad de la carga de 2.5.
c)
El factor de seguridad que protege contra la separación de los miembros.
d) El factor de seguridad que protege contra la fatiga si una carga externa repetida de 10 KN se aplica al conjunto de
ensamble.
Pág. 20
Diseño Mecánico II
Solución:
a). Rigidez del perno y el miembro:
Los módulos de elasticidad son:
Para el aluminio: Eal = 72 GPa
Para el acero: Eac = 207 GPa,
De la tabla 2.5 de tiene que: d c =12mm, p = 1.75 mm, A t = 84.3 mm2
De la figura del problema: L t = 20 mm, L s = 40 mm
ht 
0.5 p
tan 30o
 0.866p = 1.5155 mm
De la figura (2.4) se obtiene el diámetro de la raíz:
d r  d c  2(0.625 h t )  12  2(0.625 x1.5155 )  10 .1056 mm
La rigidez del perno se obtiene como sigue:
1
kb
1
kb


4
 ( 207 x10 9 )
4
E
 L s  0.4d c
 d c2 
L t  0.4 d r
d 2r

 
 0.04  0.4( 0.012)  0.02  0.4( 0.0101056)  
 ( 0.012) 2

( 0.0101056) 2
k b  297 .468 MN/m
La rigidez de la junta se obtiene a partir de la ecuación (2.24):
Pág. 21
Diseño Mecánico II
k ji 
E i d c tan 
(a)
 ( 2 L i tan d i d c )( d d ) 
ln  ( 2 L tan d d )( di dc ) 
i c
i c 
 i
Tramo I, E1 = Eal =72 GPa, d1  1.5d c  1.5(12 )  18 mm, L1 = 30 mm = 0.03 m
En la ecuación (a) se tiene:
k j1 
 ( 72 x109 )(0.012) tan 30o
 ( 0.06 tan 30 o 0.0180.012 )( 0.0180.012 ) 
ln 

o
 ( 0.06 tan 30 0.0180.012 )( 0.0180.012 ) 
= 1,368.226 MN/m
Tramo II, EII = E1 = 72 GPa, d 2 = 2(25)tan30o + 18 = 46.87 mm = 0.04687 m
k j2 
 ( 72 x109 )(0.012) tan 30o
= 26,269.07 MN/m
 ( 0.01 tan 30 o 0.046870.012 )( 0.046870.012 ) 
ln 

o
 ( 0.01 tan 30 0.046870.012 )( 0.046870.012 ) 
Tramo III, EIII = Eac = 207 Gpa, d 3  d1  18 mm = 0.018 m
k j3 
1
kj

1
k j1
 ( 207 x109 )(0.012) tan 30o
 ( 0.05 tan 30 o 0.0180.012 )( 0.0180.012 ) 
ln 

o
 ( 0.05 tan 30 0.0180.012 )( 0.0180.012 ) 
 4,149.80 MN/m
1
1
 k1  k1  1,3681.226  26, 269
 4,149

.07
.8
j2
j3
k j = 990.18
MN/m
El parámetro de la rigidez de la unión es:
Ck 
kb
kb k j

297.468
297.468  990.18
= 0.231
(b).- Carga externa máxima que puede soportar el conjunto:
Tabla (2.3) para un perno de grado 5.8, S p = 380 MPa, Sut = 520 MPa, S y = 415 MPa
Pi  0.75 Pp = 0.75(380x106)(84.3x10-6) = 24.025 KN
n sb 
A t S p  Pi
Pb ,máx C k
 Pb , máx 
(84.3 x10 6 )(380 x10 6 )  24, 025
0.231x 2.5
= 13,868.4 KN
(c).- Factor de seguridad contra la separación de la junta:
Pág. 22
Diseño Mecánico II
n sj 
Pi
Pj,máx (1 C k )
 13,868.4 x (1 0.231) =2.25
24, 025
(d).- Factor de seguridad que protege contra la fatiga:
Pa
At

Pmáx  Pmin
2A t

Pm
At

Pmáx  Pmin
2A t

i 
Pi
At

10, 000  0
2 x 84.3 x10 6
10, 000  0
2 x 84.3 x10 6
24, 025
84.3 x10 6
= 59.31 MPa
= 59.31 MPa
= 285 MPa
Se  k a k b k c k r k dSe  (1)(1)(1)(1)(1)( 0.45 x 520 )  234 Mpa
Tabla (2.6) para roscas laminadas K f  2.2
ns 
S ut   i
C k  K f

Pa
At
 Sut   Pm 
 Se  A t 

520  285
( 0.231) 2.2 x 59.31 520
 59.31
234

 
 = 2.9
Pág. 23