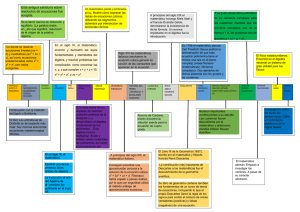
Historia del Álgebra: Personajes Clave y sus Contribuciones
Anuncio

Papiro de Rhind: fue comprado en el año de 1858 por Henry Rhind. Se sabe que este papiro pudo ser escrito entre los años 2000 y 1800 a. C, en este papiro se encuentran ecuaciones de primer grado como las ecuaciones de la forma x + ax = b ò x + ax + bx = c, donde a, b, c, son números conocidos y x un numero desconocido, se puede ver en el papiro que las ecuaciones planteadas no se refieren a objetos concretos y específicos como pan o cerveza, ni tampoco piden el resultado de operaciones con números conocidos. La solución que se da en el Papiro de Rhind, de los problemas de carácter algebraico planteados no es la que podría verse en los libros de texto modernos, sino que es característica de un procedimiento que conocemos hoy como el “método de la falsa posición. Los babilónicos solucionaron tanto ecuaciones lineales como ecuaciones cuadráticas sin ninguna dificultad y algunos ejemplos de ecuaciones cúbicas, no tenían ningún reparo en sumar una longitud con un área o un volumen. Actualmente, las ecuaciones cuadráticas se clasifican en tres tipos que reducidos a sus formas canónicas son: 1) X^2 + pX = q 2) X^2 = pX + q 3) X^2 + q = pX Todos estos tipos nos los encontramos en los viejos textos babilónicos -tablillas de arcilla- de hace unos 4000 años. Los babilónicos no conocían los números negativos por lo tanto daban solo soluciones de las posibles raíces positivas. También aparecen problemas que conducen a raíces cúbicas: XYZ = V, Donde V es un volumen dado. Recordando que a través de la geometría los helenos llegaron a muchos planteamientos algebraicos, a Tales se le atribuyen 5 teoremas de la geometría elemental: 1. Los ángulos de la base de un triángulo isósceles son iguales. 2. Un circulo es bisecado por algún diámetro. 3. Los ángulos entre dos líneas rectas que se cortan son iguales. 4. Dos triángulos son congruentes si ellos tienen dos ángulos y un lado igual. 5. Todo ángulo inscrito en una semicircunferencia es recto. Pitágoras de Samos 570 a. C. después de 510 a. C. Debemos a los pitagóricos el perfeccionamiento del álgebra y de la aritmética, la clasificación de los poliedros regulares, el teorema de Pitágoras y su corolario, la inconmensurabilidad de la diagonal y del lado de un cuadrado 1.Su doctrina consiste en la teoría de los números . 2.Creyeron en la esferidad de la tierra y el movimiento alrededor de un fuego central. 3.Explicaron los elipses y las fases lunares. 4.Aplicación de las aritmética y la geometría. 5.Fundo una comunidad religiosa, política y científica 6.la relación entre los sonidos y la longitud de la cuerda vibrante 7. el teorema de Pitágoras 8. la tabla de multiplicar 9. la relación de la música y las matemáticas 10. nace la idea de la “armonía de las esferas”, sostenían la relación que existe entre el diámetro de la orbita de los astros es proporcionar a las longitudes que existe en las cuerdas musicales. Fue discípulo de Arquitas de Tarento. Su trabajo sobre la teoría de la proporción denota una amplia comprensión de los números y permite el tratamiento de las cantidades continuas, no únicamente de los números enteros o números racionales. Cuando esta teoría fue resucitada por Tartaglia y otros estudiosos en el siglo XVI, se convirtió en la base de cuantitativas obras de ciencias durante un siglo, hasta que fue sustituida por los métodos algebraicos de Descartes. Eudoxo demostró que el volumen de una pirámide es la tercera parte del de un prisma de su misma base y altura; y que el volumen de un cono es la tercera parte del de un cilindro de su misma base y altura, teoremas ya intuidos por Demócrito Una curva algebraica lleva su nombre, la kampyle de Eudoxo: Ciertos autores árabes afirman que Euclides era hijo de Naucrates y se barajan tres hipótesis: Euclides fue un personaje matemático histórico que escribió Los elementos y otras obras atribuidas a él. Euclides fue el líder de un equipo de matemáticos que trabajaba en Alejandría. Todos ellos contribuyeron a escribir las obras completas de Euclides, incluso firmando los libros con el nombre de Euclides después de su muerte. Las obras completas de Euclides fueron escritas por un equipo de matemáticos de Alejandría quienes tomaron el nombre Euclides del personaje histórico Euclides de Megara, que había vivido unos cien años antes. Los Elementos es un compendio, en lenguaje geométrico, de todos los conocimientos de la matemática elemental, es decir, por una parte la geometría sintética plana (puntos, rectas, polígonos y círculos) y espacial (planos, poliedros y cuerpos redondos); y por otra parte, una aritmética y un álgebra, ambas con una indumentaria geométrica. La obra de Euclides está formada por trece libros, de los cuales el Libro II y el V son casi completamente algebraicos; pero a diferencia de nuestra álgebra actual, que es simbólica, el álgebra de Los Elementos es un álgebra geométrica. De la Esfera y el Cilindro" donde introduce el concepto de concavidad y convexidad. "De los Conoides y Esferoides" donde define las figuras engendradas por la rotación de distintas secciones planas de un cono. "De las espirales" donde analiza estas curvas y sus elementos más característicos. "De la cuadratura de la parábola" donde obtiene el área limitada por un segmento parabólico en el intervalo [0,1], mediante la suma de las áreas de los rectángulos inscritos y circunscritos. Sólo dos obras de Apolonio han llegado hasta nuestros días: Secciones en una razón dada y Las Cónicas . Esta última obra junto con los Elementos de Euclides es uno de los libros más importantes de matemáticas. Las Cónicas está formado por 8 libros. El libro I: trata de las propiedades fundamentales de estas curvas. El libro II trata de los diámetros conjugados y de las tangentes de estas curvas. El libro III: trata de los tipos de conos. El libro IV: trata de las maneras en que pueden cortarse las secciones de conos. El libro V: estudia segmentos máximos y mínimos trazados respecto a una cónica. El libro VI: trata sobre cónicas semejante. El libro VII: trata sobre los diámetros conjugados. El libro VIII: se ha perdido, se cree que era un apéndice. En esta obra realiza sus estudios de ecuaciones con variables que tienen un valor racional, aunque no es una obra de carácter teórico sino una colección de problemas. Importante fue también su contribución en el campo de la notación; si bien los símbolos empleados por DIOFANTO no son como los concebimos actualmente, introdujo importantes novedades como el empleo de un símbolo único para la variable desconocida (στ) y para la sustracción, aunque conservó las abreviaturas para las potencias de la incógnita (δς) para el cuadrado, (δδς) para el duplo del cuadrado, (χς)para el cubo, (δχς) para la quinta potencia, etc. Como matemático, escribió la obra La Métrica, donde estudia las áreas y volúmenes de distintas superficies y cuerpos. Desarrolla también técnicas de cálculo, tomadas de los babilonios y egipcios, como el cálculo de raíces cuadradas mediante iteraciones. Pero sin duda su logro más famoso en el campo de la geometría es la conocida como la fórmula de Herón, que relaciona el área de un triángulo con la longitud de sus lados. Chien o “Espejo Precioso de los Cuatro elementos” escrito por Chu Shih- Chieh en 1303, donde los cuatro elementos a los que se refiere el título, son el cielo ,la tierra, el hombre y la materia, representan las cuatro incógnitas de una ecuación. Este libro marca la cota más alta que alcanzó el desarrollo del álgebra china, y en él se estudian tanto sistemas de ecuaciones simultáneas como ecuaciones individuales de grados tan altos como catorce. CHU SHIH-CHIEH explica un método de transformación para ecuaciones, que él llama el fan fa y cuyo fundamento debe de haber aparecido en China mucho tiempo atrás. Este método suele conocerse en occidente con el nombre de “método de HORNER”, matemático que vivió medio milenio más tarde, y consiste en evaluar de manera eficiente polinomios de una forma monomial. Un ejemplo que viene en el libro de CHU SHIH-CHIEH es resolver la ecuación x" + 252x – 5292 = 0 CH’IN CHIU- SHAO donde su obra SHU-SHU CHIUCHANG o “Tratado matemático en nueve secciones” marca el punto culminante del análisis indeterminado chino con la invención de reglas rutinarias para resolver sistemas de congruencias simultáneas y el cálculo de la raíz cuadrada por etapas, paralelamente a lo que se hace en el “método de HORNER”. Li Ye fue un matemático chino que vivió durante la dinastía SONG, dejó como legado dos importantes libros acerca de cálculo de la superficie y perímetro del círculo, así como métodos de cálculo para reducir a ecuaciones algebraicas los problemas geométricos. Se reconoce también su aporte a la definición de los números negativos y su método de solución de ecuaciones se asemeja mucho al enfoque conocido mucho más tarde como algoritmo de HORNER. La primera obra que se conoce de este periodo fue la del matemático ARYBHATA que es ARYABHATIYA, libro bastante análogo a los Elementos de Euclides. Ambas obras son recopilaciones de desarrollos anteriores compiladas por un único autor. Pero a diferencia de los Elementos, ARYABHATIYA está compuesta por 123 estrofas métricas y no tiene ninguna relación con la metodología deductiva. El método de inversión para resolver ecuaciones algebraicas aparece en el ARYABHATIYA donde hay algunas ecuaciones algebraicas resueltas por el método de inversión, que consiste en partir del resultado e ir haciendo las operaciones inversas en sentido contrario a como se dan en el enunciado. La obra más famosa de Brahmagupta es su BRAHMASPHUTASIDDHANTA. Compuesta en verso elíptico, practica común en las matemáticas hindúes, la obra tiene en consecuencia un cierto halo poético, como en ella no se dan demostraciones no se sabe como BRAHMAGUPTA obtenía los resultados matemáticos. BRAHMAGUPTA da la solución de la ecuación lineal general en el capítulo dieciocho de BRAHMASPHUTASIDDHANTA, que aunque expresada en el libro en palabras, viene a ser equivalente a la siguiente expresión algebraica: Además, dio dos soluciones equivalentes para la ecuación general de segundo grado, que vienen a ser equivalentes, respectivamente, a las siguientes expresiones algebraicas: BHASKARA resolvió algunos casos particulares de la ecuación DIOFANTICA cuadrática, x" =1+py". BHASKARA, último matemático medieval importante en la India, plasmó las contribuciones hindúes anteriores a su época , en especial los problemas planteados por BRAHMAGUPTA, en su tratado más conocido y en otra obra menos conocida llamada Vija-ganita. BHASKARA sabia que las ecuaciones cuadráticas tenían dos raíces e incluían las negativas y las irracionales. Los tres tipos de ecuaciones Cuadráticas ax" +bx =c , ax" =bx +c , ax" +c =bx con a, b, c positivos estudiados por DIOFANTO, de manera independiente, fueron tratados por dos de los matemáticos BRAHMAGUPTA y BHASKARA como un solo caso px" +qx +r =o porque admitían que algunos coeficientes podían ser negativos. Para ello utilizaban el método de completar cuadrado. Es considerado un gran matemático y astrónomo de la edad media islámica el cual transmitió al mundo árabe los fundamentos de la matemática hindú y el concepto del cero. El mérito de AL-BATTANIS gira en torno a la trigonometría, fue el primero en utilizar el seno en lugar de las cuerdas, halló y demostró por primera vez el teorema del seno, así como el hecho de que la tangente representa la relación entre el seno y el coseno. La palabra álgebra viene de un libro escrito en el año 830 por el astrónomo AL-KHOWÂRIZMÎ, titulado AL-JABR W´AL MUQÂBALA, que significa restauración y simplificación. El libro de AL-KHOWÂRIZMÎ empieza exponiendo, en seis breves capítulos, la solución de los seis tipos de ecuaciones que resultan al considerar simultáneamente en presencia los tres posibles tipos de cantidades: cuadrados, raíces y números, es decir, x", x y constante. El libro de AL-KHOWÂRIZMÎ contiene además de la resolución de ecuaciones, que ocupa aproximadamente la mitad del libro, reglas para operar con expresiones binómicas, incluyendo productos tales como (10+x)(10-x), demostraciones geométricas para la resolución de ecuaciones, y por último una gran variedad de problemas que sirven para ilustrar los casos tratados en los seis capítulos. AL-KHOWÂRIZMÎ introdujo de la matemática hindú la cifra cero en el sistema arábigo y con ello en todos los sistemas numéricos modernos. En sus libros expone estrategias de solución sistemáticas para ecuaciones lineales y cuadráticas. Fue un matemático y astrónomo persa, halló la solución para las ecuaciones de tercer grado y sus raíces a través de su expresión geométrica. Se dedicó principalmente al problema de las paralelas y a los números irracionales. Los desarrollos de su obra prevalecieron en álgebra durante mucho tiempo. conocido también como SACROBOSCO, fue un maestro inglés que contribuyó con su obra ALGORISMUS VULGARIS, manual práctico de cálculo que rivalizó en popularidad con su otra famosa obra: SPHAERA, un tratado sobre astronomía que se usó en las escuelas a lo largo de la edad media tardía. Más conocido como FIBONACCI o “hijo de Bonaccio”, en 1202 escribió su LIBER ABACI (el libro del ábaco), un tratado muy completo sobre métodos y problemas algebraicos en el que se recomienda con gran insistencia el uso de los numerales hindú-arábigos. La característica nueva más significativa del trabajo de Leonardo es la observación de que la clasificación de Euclides de los irracionales en el libro X de los Elementos no incluía todos los irracionales. mostró que las raíces de la ecuación x^3+2x" +10x =20 no pueden construirse con regla y compás. quien tradujo del árabe los Elementos de EUCLIDES, el Almagesto de PTOLOMEO y el Álgebra de AL-KHOWARIZMI. Fue uno de los autores que origino el arranque matemático en Europa principalmente por la difusión de sus obras en universidades como Oxford, París, Viena y Erfurt (estas dos últimas fundadas en los años 1365y 1392 respectivamente). También llamado REGIOMONTANUS, fue un matemático, astrónomo y editor de la Baja Edad Media. REGIOMONTANUS destaca como el fundador de la trigonometría moderna En Roma, acompañando al cardenal BESARION, llegó a adquirir un gran conocimiento del griego, con lo que enlazó el conocimiento clásico preservado en Constantinopla y el movimiento renacentista. Al regresar a Alemania estableció una imprenta y un observatorio en NUREMBERG, con la esperanza de imprimir traducciones de ARQUÍMEDES, APOLONIO, HERON, PTOLOMEO y otros, pero murió joven (probablemente envenenado) y el proyecto quedó incompleto. La lista de libros que planeaba imprimir se conserva, lo que indica que el desarrollo de las matemáticas se habría acelerado si hubiera sobrevivido. Matemático italiano, su principal obra SUMMA de ARITHMETICAGEOMETRIA, PROPORZIONI E PROPORZIONALITA se publicó en 1494 y está dividida en dos partes: la primera trata de aritmética y álgebra, donde la parte dedicada al álgebra incluye las soluciones de las ecuaciones lineales y algunas soluciones de las cuadráticas pero principalmente describe reglas de las cuatro operaciones básicas y un método para extracción de raíces. La segunda parte está dedicada a temas de geometría. Se le atribuye gran importancia histórica por ser este el primer libro impreso de matemáticas y con ello, la primera sistematización de la aritmética el álgebra y la geometría que alcanza una muy amplia difusión. Médico, filósofo y matemático italiano, CARDANO hizo importantes descubrimientos en el cálculo de probabilidades, así como también fue el primero en sugerir la existencia de números imaginarios. Sin embargo en al año 1545 divulgó la solución no sólo de la ecuación cúbica, sino también de la cuártica, gracias a la publicación del ARS MAGNA, no obstante, Cardano afirma en su libro que no fue el descubridor original de la solución de la ecuación cúbica ni de la cuártica. fue un matemático veneciano, especialmente conocido por sus relevantes aportes en el tema de las ecuaciones de tercer grado y por la gran controversia en la que se vio envuelto en torno a la solución de las 13 ecuaciones de este tipo que entonces se distinguían. En la actualidad se considera una única forma de la ecuación de tercer grado: x³ + ax² + bx + c = 0, pero esta formulación única es posible gracias a que a, b y c pueden ser números negativos o cero. En la época de TARTAGLIA aún no se aceptaban los números negativos y por ello existían trece ecuaciones distintas, de las cuales siete eran completas (todas las potencias representadas), tres sin término lineal y tres sin término cuadrático. La tercera de estas ecuaciones tiene una solución principal negativa, de modo que no se trataba. RAFAEL BOMBELLI fue un matemático e ingeniero italiano. En su libro L'ALGEBRA, publicado en 1572 introduce los números negativos e incluso números imaginarios. Desarrolló las ampliaciones, que la consideración de los números negativos implican en las soluciones propuestas por NICOLO TARTAGLIA y GEROLAMO CARDANOS para las ecuaciones algebraicas de tercer grado. Se le atribuye la introducción de los paréntesis en la notación algebraica. Abogado francés cuyo interés por las matemáticas era puro Entretenimiento, él escribe IN ARTEM ANALYTICAM ISAGOGE como la obra del análisis matemático restaurado. VIÈTE traza la línea divisoria entre la aritmética y el álgebra y propone utilizar una vocal para representar una cantidad que se supone en álgebra desconocida o indeterminada, y una constante para representar una magnitud o un número que se supone conocido o dado. Esta distinción entre el concepto de parámetro y la idea de incógnita fue un paso previo a la matemática moderna. Sitúa a Francia en el centro del mundo matemático, durante el último tercio del siglo XVII. Dio un avance importante en el álgebra, se trata de símbolos para las incógnitas, para las operaciones y potencias algebraicas. Debido a este avance, el Libro III de la Geometría (1637), escrito por el matemático y filósofo francés René Descartes se parece bastante a un texto moderno de álgebra. Sin embargo, la contribución más importante de Descartes a las matemáticas fue el descubrimiento de la geometría que reduce la resolución de problemas geométricos a la resolución de problemas algebraicos. Su libro de geometría contiene también los fundamentos de un curso de teoría de ecuaciones, incluyendo lo que el propio Descartes llamó la regla de los signos para contar el número de raíces verdaderas (positivas) y falsas (negativas) de una ecuación. En su memoria es llamada geometría cartesiana la cual es el estudio de la geometría mediante un sistemas de coordenadas y en el algebra propuso un teorema importante que permite hallar el residuo de una división de polinomios por simple evaluación. Isaac Newton fue un físico, matemático, astrónomo, alquimista, filósofo y alto funcionario administrativo inglés. En 1707 aparece DE ANÁLYSIS de ISAAC NEWTON ,la esencia de la obra consiste en reducir cualquier problema a la formación de una ecuación algebraica, cuya raíz será la solución del problema. En el libro, NEWTON enuncia un teorema que permite determinar el número de raíces reales de un polinomio, así como una regla con la que es posible dar una cota superior de las raíces positivas. De ANÁLYSIS termina con los resultados de la teoría general de ecuaciones y además la resolución gráfica de éstas mediante la construcción geométrica de las raíces. Filósofo, científico, matemático, diplomático, físico, historiador y bibliotecario alemán. En 1672 Leibniz construyó una máquina calculadora, que podía multiplicar, dividir y extraer la raíz cuadrada. Entre los años 1672 y 1676, desarrolló los fundamentos del cálculo infinitesimal. A Leibniz se debe la notación (hasta hoy en uso) del diferencial así como el signo para la integral. Además descubrió el criterio que lleva su nombre, un criterio matemático de convergencia para series infinitas, como asimismo la fórmula de Leibniz que se usa para el cálculo de determinantes en matrices. Fue uno de los matemáticos más importantes y prolíficos de la historia. Escribió en total 866 publicaciones y sus resultados fundamentales crearon nuevos campos de la matemática. Una gran parte de la actual simbólica matemática se debe a EULER. Además de su dedicación al cálculo diferencial e integral, trabajó, entre otros temas, con ecuaciones diferenciales, geometría diferencial, ecuaciones recurrentes, integrales elípticas, así como también en la teoría de las funciones gamma y beta. Muchos conceptos y teoremas matemáticos llevan su nombre. El número de EULER e = 2,7182818284590452... cuenta entre los más conocidos. Fue un matemático y astrónomo italiano. Trabajó en el problema de los tres cuerpos de la mecánica celeste, en el cálculo de variaciones y en la teoría de funciones complejas. LAGRANGE realizó aportes a la teoría de las ecuaciones en álgebra y a la teoría de las formas cuadráticas en la teoría de números. Entre otras contribuciones, la función que lleva su nombre («LAGRANGIANO»), particularmente importante en la mecánica, se debe a su obra. ÉVARISTE GALOIS fue un matemático francés. A pesar de su corta vida de sólo 20 años, GALOIS alcanzó reconocimiento póstumo por sus trabajos sobre la solución de ecuaciones algebraicas de la así llamada teoría de GALOIS. A él se deben algunos teoremas fundamentales de la teoría de grupos, Esta idea del estudio de la estructura de los campos algebraicos y la comparación con ellos de la estructura de los grupos de un número finito de sustituciones, fue la base de lo que hoy se denomina “álgebra moderna”. Fue un matemático, astrónomo, geodésico y físico alemán. En 1799, GAUSS publica su tesis en la Universidad de HELMSTÄDT que lleva el título de Nueva Demostración del Teorema Que Toda Función Algebraica Racional y Entera de Una Variable Puede Resolverse en Factores Reales de Primero o de Segundo Grado. La tesis doctoral de GAUSS demostraba que toda ecuación polinómica f(x) =0 tiene al menos una raíz, ya sean los coeficientes reales o complejos. GAUSS publicó su libro más conocido, un tratado de teoría de números en latín, DISQUISITIONES ARITHMETICAE. Esta obra es la responsable del desarrollo del lenguaje y de las notaciones de la parte de la teoría de números conocida como el álgebra de las congruencias. La notación que adoptó GAUSS en su obra es la misma que utilizamos en la actualidad, b≡c(mod a) y procedió a construir un álgebra para la relación análoga al álgebra usual expresada en el lenguaje de la igualdad. Matemático Noruego que en álgebra lleva su nombre el grupo ABELIANO. En 1824 publicó un ensayo titulado Sobre la Resolución Algebraica de Ecuaciones. En su obra, Abel llega a la conclusión de la insolubilidad de la quíntica, es decir, demuestra que no puede existir ninguna fórmula general expresada en términos de operaciones algebraicas explícitas que nos de las raíces de la ecuación si el grado del polinomio es mayor que cuatro. En 1833 Hamilton presenta un importante artículo en la IRISH ACADEMY, en el que introduce y estudia un álgebra formal de parejas de números reales cuyas reglas de combinación eran las que se dan en la actualidad para el sistema de los números complejos. La importante regla que definía la multiplicación de parejas era (a , b) · (( α , β )) = ((a α – b β ) , (a α + b β) ) Hamilton interpreta este producto como una operación en la que interviene una rotación. Primero las definió como pares y luego como cuádruplas, para estas cuádruplas se debería tomar i" +j"+ k" =-1, ij=k, ji=-k, análogamente para el resto, perdiendo la propiedad conmutativa. Sus ideas las plasmó en su obra ELEMENTS OF QUATERNIONS. Matemático ingles que vivió gran parte de su vida en Estados Unidos, CAYLEY fue uno de los primeros matemáticos en estudiar las matrices, como peculiar forma y estructura algebraica. Definió la suma, multiplicación de matrices y la matriz identidad. FÉLIX HAUSDORFF fue un matemático alemán. Se le considera cofundador de la topología moderna y realizó contribuciones esenciales a la teoría de conjuntos (general y descriptiva), a la teoría de la medida, al análisis funcional y al álgebra. En su honor se denomina en topología, entre otros conceptos, el espacio de HAUSDORFF. El álgebra HOMOLÓGICA es una rama del álgebra abstracta que se ocupa de resultados válidos para tipos de espacios muy diferentes, una invasión de la topología algebraica en el dominio del álgebra pura. La gran rapidez con la que se produjo este cruce fue gracias a los artículos publicados en el MATHEMATICAL REVIEWS al libro HOMOLOGICAL ÁlLGEBRA publicado en 1956 por el francés HENRI CARTAN y el polaco, SAMUEL EINLENBERG. LUIS ALEJANDRO SIERRA ANA BEATRIZ NARANJO Historia de la Matemática U.P.T.C. Duitama 2012