cuerpo libre

1
TEMAS DE FÍSICA I
DIAGRAMAS DE CUERPO LIBRE DE PARTÍCULAS
Profr. Abelardo Rodríguez Soria et al
TRIMESTRE 11‐P
1. La importancia de los diagramas de cuerpo libre.
El comportamiento mecánico de los cuerpos materiales está gobernado por las fuerzas a que están
sometidos. Hacer el diagrama de cuerpo libre del cuerpo material bajo estudio consiste precisamente en
hacer una identificación y representación gráfica de las fuerzas que solicitan al cuerpo. Como se advierte,
la confección del DCL constituye un primer paso imprescindible en la aplicación de las leyes de la
mecánica.
Definición. El diagrama de cuerpo libre (DCL) de un cuerpo es una figura donde se muestra
únicamente el cuerpo en cuestión (aislado conceptualmente de los demás cuerpos a su alrededor), junto
con todas y cada una de las fuerzas que actúan sobre él.
Antes de hacer un diagrama de cuerpo libre es preciso especificar cuál es el cuerpo (o conjunto de
cuerpos) al que pertenecerá este DCL. En otros términos, hay que especificar cuál es el “sistema físico”
que estamos considerando.
Definición. El sistema físico es aquel cuerpo material (o conjunto de cuerpos materiales)
estipulado expresamente para aplicarle las leyes de la mecánica.
Inicialmente trataremos sistemas físicos compuestos de un solo cuerpo. Más adelante
explicaremos cómo hacer los DCL’s de sistemas que incluyen varios cuerpos.
•
•
•
•
•
Etc.
La obtención del DCL de un cuerpo (es decir, de un sistema) es el paso previo para:
Estudiar el estado de equilibrio del sistema.
Estudiar el estado de movimiento del sistema.
Decidir sobre la aplicabilidad de las leyes de conservación de energía mecánica, o formular la
ecuación de balance de energía mecánica.
Decidir sobre la aplicabilidad de las leyes de conservación del momento lineal o del momento
angular, o formular la ecuación de balance del momento lineal o angular.
Estudiar el estado de esfuerzos y deformaciones del sistema.
Saber hacer DCL’s le allanará el camino en muchas materias de su carrera de ingeniería.
Regla 1. Dé un nombre (o asigne un símbolo) a cada cuerpo que figure en el conjunto
considerado. Esto facilitará la definición del sistema físico.
Regla 2. Siempre debe estar claro cuál es el cuerpo (o conjunto de cuerpos) que constituye el
sistema físico en consideración. Asimismo, debe estar claro cómo son las uniones o acoplamientos del o
los cuerpos del sistema con los demás cuerpos ajenos a su alrededor. Es decir, el sistema físico debe
especificarse con precisión.
2
Notación. Un sistema físico que conste de varios cuerpos, digamos los cuerpos A, B, C y D, se
escribirá poniendo el o los cuerpos constituyentes encerrados entre llaves, así: {A, B, C, D}.
EJEMPLO 1. Observe el conjunto de cuerpos en equilibrio mostrado en la figura 1a. Conforme a la regla 1,
hemos asignado un nombre a cada cuerpo del conjunto.
El resorte está elongado; los contactos entre el Bloque‐1 y el Bloque‐2, y entre cada uno de estos
bloques y el plano inclinado, son simples (es decir, estos cuerpos simplemente descansan uno junto o sobre
el otro, sin estar unidos fijamente entre sí); la polea es lisa y está fija a una pared no mostrada.
Figura 1a
Figura 1b (DCL del Bloque‐1)
Consideremos el sistema {Bloque‐1}. Su DCL se muestra en la figura 1b. De las fuerzas que actúan
sobre el Bloque‐1, mostradas en este DCL, la fuerza W1 es el peso del bloque. Las demás fuerzas son
debidas al contacto del Bloque‐1 con los siguientes cuerpos: el Resorte (fuerza R), la Cuerda (fuerza T), el
Bloque‐2 (fuerza normal N1), y el Plano inclinado (fuerza normal N2).
¿Cómo llegamos al DCL de la figura 1b? Paciencia.
Regla 3. Las fuerzas no surgen de la nada. Toda fuerza sobre un cuerpo A es debida siempre a
algún otro cuerpo, ya sea la Tierra (que ejerce la fuerza llamada peso) o bien otro cuerpo que esté en
contacto con el cuerpo A considerado.
Si Ud examina un DCL (quizás hecho por otra persona) y descubre en él alguna fuerza que no
pueda asociar con algún cuerpo que la produzca, ello significa que dicha fuerza no debería figurar en el
DCL
Regla 4. El símbolo que se pone junto a un vector fuerza en un DCL indica la magnitud de la
fuerza (la dirección de la misma ya está indicada en el DCL mediante la punta de flecha).
Así por ejemplo, en la figura 1b, los símbolos de las fuerzas (R, T, W1, N2, N1, T) no llevan ningún
uur
tilde ni formato que denote carácter vectorial, como serían W, W , W , T , etc.
Otros sistemas que podríamos considerar en relación con el conjunto de la figura 1a son los
siguientes: {Bloque‐2}, {Bloque‐3} y {Bloque‐1, Bloque‐2}. Este último consta de dos cuerpos.
3
2. Partícula.
Decimos que un cuerpo se considera una partícula cuando podemos suponer que todas las
fuerzas sobre él actúan en un mismo punto de aplicación. En otros términos: las fuerzas se pueden
suponer concurrentes, sin que ello afecte sensiblemente el fenómeno físico bajo estudio (como serían las
magnitudes de las fuerzas, la aceleración del cuerpo, etcétera.).
En este escrito consideraremos solamente DCL’s de cuerpos (o conjuntos de cuerpos)
considerados como partículas. Por el momento nuestros sistemas físicos serán partículas individuales.
Más adelante explicaremos cómo hacer el DCL de un sistema compuesto por varias partículas.
Regla 5. En el DCL de un cuerpo modelado como partícula, el cuerpo se puede representar por un
punto (de hecho un pequeño círculo lleno, como “ • “).
EJEMPLO 2. En la figura 2a se tiene un collarín (cilindro acanalado) ensartado en una guía recta fija,
sobre el que actúan, además de la guía, un resorte estirado y una cuerda que remata en un bloque.
Figura 2a
Figura 2b
En la figura 2b se muestra el DCL del collarín (la línea a rayas representa la guía recta). En este DCL el
collarín se ha representado por un punto “ • “.
Otro ejemplo: el DCL del Bloque‐1 considerado en el Ejemplo 1 de la página precedente
(reproducido aquí en la figura 3a) pudo haberse hecho como se muestra en la figura 3b, en la que el
Bloque‐1 se ha representado por un punto.
Figura 3a (DCL del Bloque‐1)
Figura 3b (Mismo DCL de la figura 3a)
Esta representación por un punto puede ser más conveniente a la hora de calcular las
componentes de las diversas fuerzas. Sin embargo, con objeto de que se reconozca más fácilmente cuál es
el sistema considerado, nosotros dibujaremos la imagen del cuerpo tal como se presenta inicialmente.
4
3. Clasificación de las fuerzas.
Las fuerzas sobre todo cuerpo se pueden clasificar en 2 categorías:
Primera. Fuerzas de acción a distancia (o fuerzas de acción por campo).
A esta categoría pertenecen las fuerzas gravitatorias, las eléctricas y las magnéticas, de
importancia fundamental en ingeniería.
Segunda. Fuerzas de contacto (llamadas también fuerzas mecánicas o macroscópicas).
Estas son fuerzas debidas al contacto del cuerpo considerado con otros cuerpos en
su vecindad inmediata.
En este curso no trataremos fuerzas eléctricas ni magnéticas. Nuestra fuerza de acción por campo
por excelencia será la fuerza gravitatoria ejercida sobre todo cuerpo por el planeta Tierra, denominada el
peso del cuerpo.
Un asunto muy importante: cuando hablamos de fuerzas de contacto sobre un cuerpo nos
estamos refiriendo a contactos directos o inmediatos (permítasenos la redundancia) del cuerpo
considerado (o sistema) con otros cuerpos en su vecindad.
He aquí un ejemplo muy drástico de lo que queremos decir.
EJEMPLO 3. Considere el conjunto de 3 bloques acomodados en una pila, como vemos en la figura 4.
Figura 4
PREGUNTA: ¿Sufre el Bloque‐3 alguna fuerza debida al Bloque‐1?
RESPUESTA: NO, puesto que el Bloque‐3 no está en contacto con el Bloque‐1.
A primera vista la respuesta puede parecer extraña, pues dado que el Bloque‐1 está encima del
Bloque‐3, ¿cómo es que no ejerce fuerza sobre éste?
Quizás podríamos decir que “el Bloque‐1 ejerce indirectamente una fuerza sobre el Bloque‐3, a
través (o por intermedio) del Bloque‐2”. Sin embargo, en los DCL’s no figuran fuerzas ejercidas
indirectamente, ni fuerzas ejercidas a traves de cuerpo intermedio alguno. En ellos figuran solamente
fuerzas debidas a los contactos directos del cuerpo considerado con otros cuerpos.
La cosa está así: el Bloque‐3 tiene contactos (directos) con el Bloque‐2 y con la Mesa, y éstos dos
son los únicos cuerpos (aparte de la Tierra, por supuesto) que ejercen fuerzas sobre el Bloque‐3.
5
Siguiendo la misma tónica, observe la figura 5a. Un amigo sostiene un bloque mediante una
cuerda.
Figura 5a
Figura 5b
¿Ejerce el Amigo fuerza alguna sobre el Bloque?
De nuevo, en el lenguaje cotidiano informal quizás podríamos decir que sí. Sin embargo, en el
lenguaje usado en el trazado de los DCL’s (el lenguaje técnico que usaremos siempre en este escrito), el
Amigo
no ejerce fuerza sobre el Bloque. Es la Cuerda la que ejerce fuerza sobre el Bloque (porque la
Cuerda sí está en contacto con el Bloque, no así el Amigo).
Análogamente, en la situación de la figura 5b, el Bloque‐1 no ejerce fuerza sobre el Bloque‐3.
¿Captó la idea? Felicidades; ha dado Ud un gran paso en el asunto del trazado de DCL’s.
Con lo discutido hasta el momento podemos dar ya la regla más importante de todas:
4. La regla maestra.
•
•
Regla 6. (Regla Maestra: Cómo trazar el DCL de un cuerpo‐partícula).
Para trazar el DCL de un cuerpo‐partícula:
Trace primeramente el peso del cuerpo.
Recorra visualmente el cuerpo considerado por todo su contorno y su interior, haciendo una lista
(mentalmente o por escrito) de todos aquellos cuerpos vecinos con los que el cuerpo considerado
esté en contacto. Incluya en el DCL la fuerza existente en cada uno de estos contactos.
Ahora bien, ¿cómo podemos estar seguros que un DCL está trazado correctamente?
A este respecto son dos cosas las que importan:
Primera. Que en el DCL no se haya omitido ninguna fuerza que debiera estar incluida en él, y
además que no se haya incluido alguna fuerza (superflua) que no debiera figurar en él.
Segunda. Que cada una de las fuerzas del DCL se haya trazado tomando en cuenta sus
direcciones y propiedades correctas.
En este curso introductorio de Física I trataremos exclusivamente los siguientes tipos de fuerzas:
Un tipo de fuerza de acción por campo:
• La fuerza denominada peso, ejercida por la Tierra sobre todo cuerpo en su superficie.
Cuatro tipos de fuerzas de contaco (o mecánicas o macroscópicas):
• La fuerza de tensión, debida a contacto con cuerdas o cables, o resortes estirados, o barras o
varillas rígidas ligeras estirados.
6
•
•
•
La fuerza de compresión, debida a contacto con resortes comprimidos, o barras o varillas rígidas
ligeras comprimidos.
La fuerza normal, debida al contacto simple de un cuerpo con otro.
La fuerza de fricción o rozamiento, debida al contacto simple de un cuerpo con otro relativamente
al cual el primero tiende a deslizarse.
Regla 6. Los símbolos que usaremos para denotar estos tipos de fuerzas son:
W para el peso
T para tensión de cuerdas o cables
R para tensión de resortes
C para compresión de resortes
V para tensión de barras o varillas
K para compresión de barras o varillas
N para fuerza normal
f y fm para fuerza de fricción.
Usaremos subíndices cuando sea necesario para distinguir fuerzas de un mismo tipo.
Obviamente, no todos los tipos de fuerzas figurarán en un DCL particular. La presencia o
ausencia de algún tipo de fuerza en el DCL depende de la situación física del cuerpo.
5. Estudio de las fuerzas.
Emprenderemos a continuación una breve descripción (eminentemente práctica) de los diversos
tipos de fuerzas citados en el párrafo anterior. Si Ud desea profundizar en el asunto, le recomendamos el
libro “Elementos de álgebra vectorial y estática en el plano”, por los autores Sergio Becerril H. y sus 4
amigos, publicación de la UAM‐Azcapotzalco (disponible en la librería de la Unidad).
(A) Peso.
Definición. El peso de un cuerpo es la fuerza gravitatoria que ejerce el planeta Tierra sobre él.
El peso es una fuerza que actúa verticalmente hacia abajo (hacia el centro de la Tierra) en la
localidad terrestre supuesta.
Dada la masa m del cuerpo (en kilogramos), su peso W (en newtons) se calcula con la fórmula
(1)
W=mg
donde g = 9.8 m/s2 es la aceleración de caída libre (o aceleración de la gravedad) en la Tierra.
En los DCL’s, el peso es una fuerza omnipresente, pues ningún cuerpo es capaz de sustraerse a la
acción de la Tierra. De todas maneras, el peso de cierta clase de cuerpos, como las cuerdas, resortes,
barras, varillas y otros, se suele despreciar cuando es muy pequeño en comparación con las demás fuerzas
relevantes; hablamos entonces de cuerpos ligeros o ingrávidos.
7
El vector que representa el peso de un cuerpo puede trazarse en cualquier lugar junto o en el
interior del cuerpo, como se muestra en las figuras 6a,b,c para el peso W de un bloque: Esto lo podemos
hacer porque estamos tratando al cuerpo como una partícula.
Figura 6a
Figura 6b
Figura 6c
(B) Fuerza de tensión en cuerdas o cables.
Para poner una cuerda en tensión, hay que jalarla de sus extremos, a manera de elongarla.
Figura 7a
Figura 7b. Estado de tensión simple
Por ejemplo, en la figura 7a tenemos dos amigos (designados como “Amigo 1” y “Amigo 2”) que
jalan de los extremos de una cuerda con iguales fuerzas “T”. La cuerda se pone tirante bajo la acción de
ambas fuerzas “T”, y su diagrama de cuerpo libre sería el que vemos en la figura 7b (hemos despreciado
aquí el peso de la cuerda). En la situación de la figura 7b decimos que la cuerda se halla en un estado de
tensión simple.
Otros cuerpos notables que pueden hallarse en un estado de tensión simple son los resortes y las
varillas o barras rígidas ligeras. En las figuras 8a y 8b se muestran respectivamente un resorte y una
varilla recta en tal estado. Estas figuras serían los DCL’s del resorte y varilla, si se desprecia su peso. Los
símbolos R y V denotan las fuerzas aplicadas sobre cada uno, respectivamente.
Figura 8a
Figura 8b
Las fuerzas T, R y V que aparecen en las figuras 7b, 8a y 8b se denominan la tensión de la cuerda,
del resorte y de la varilla rígida, respectivamente.
8
Volvamos a la cuerda. Del DCL de la figura 7b se sigue que su ecuación de equilibrio es
simplemente
(2)
T–T=0
Análogamente las ecuaciones de equilibrio del resorte y la varilla son
(3)
R – R = 0,
(4)
V–V=0
Las ecuaciones (2), (3) y (4) son unas grandes verdades pero no tienen ninguna utilidad práctica. De ahí la
siguiente regla.
Regla 7. Excepto en casos especiales, para resolver un problema de estática o dinámica no es
necesario hacer los DCL’s de las cuerdas o cables que figuren en el problema.
Tampoco es necesario hacer los DCL’s de resortes ligeros en tensión o compresión, o varillas o
barras ligeras en tensión o compresión. Asimismo, no hacemos DCL’s de apoyos fijos (cuerpos masivos
unidos firmemente a Tierra) como serían Mesa fija, Techo, Pared, Soporte fijo, Bastidor, etc.
En el caso de las cuerdas, lo que sí nos interesa son las fuerzas que una cuerda tirante ejerce sobre
los cuerpos atados a sus extremos, pues estas fuerzas figurarán en los DCL’s de estos últimos. La
respuesta viene dada por la tercera ley de Newton.
Figura 9
La cosa está así: la cuerda ejerce sobre los Amigos 1 y 2 la misma fuerza T que ellos ejercen sobre
aquella, en las direcciones mostradas en la figura 9.
Advirtamos que la fuerza de tensión T sobre cada Amigo es un vector que emana del punto de
sujeción o atadura de la cuerda, y corre a lo largo de la cuerda. La punta de este vector está dirigida hacia
lo lejos del punto de sujeción.
Esto es general, así que tenemos la siguiente regla:
Regla 8. Para trazar la fuerza de tensión ejercida por una cuerda sobre un cuerpo:
1. Ubique el punto de atadura (o sujeción) de la cuerda al cuerpo considerado.
2. Desde este punto trace un vector que corra a lo largo de la cuerda, apuntando
hacia lo lejos del punto de atadura.
9
EJEMPLO 4. La figura 10 muestra dos bloques que penden de dos cuerdas.
Figura 10
Hagamos los DCL’s de los sistemas {Bloque‐1} y {Bloque‐2}.
Para el Bloque‐1:
De acuerdo con la Regla Maestra (Regla 6, página 5), sobre el Bloque‐1 actúan la Tierra y además
la Cuerda‐1 y la Cuerda‐2, que son los cuerpos en contacto con dicho bloque.
Denotaremos el peso del Bloque‐1 con el
símbolo W1.
Dibujemos el Bloque‐1 (Véase la figura 11),
incluyendo en la figura unos tramitos de las cuerdas
1 y 2.
Ubiquemos los puntos de atadura de las
cuerdas 1 y 2 al Bloque‐1 (los hemos señalado en la
figura 11 mediante puntos “ • “).
Tracemos
cada
fuerza
de
tensión
simplemente añadiendo a ambos tramitos sendas
puntas de flecha dirigidas hacia lo lejos del
respectivo punto de atadura. Llegamos al DCL de la
figura 12a.
Figura 12a
Figura 11
Figura 12b
Procediendo de la misma manera trazamos el DCL del Bloque‐2, quedando como se muestra en la
figura 12b.
10
Toda cuerda tirante posee en sus extremos 2 puntos de sujeción a otros cuerpos. Dos cuerdas se
consideran distintas si poseen al menos un punto de sujeción distinto.
Regla 9. El número de fuerzas de tensión que figuran en un problema dado (al hacer los DCL’s
individuales de los cuerpos a que están atadas) es igual al número de cuerdas distintas que existen en el
problema.
Se sugiere numerar las cuerdas según Cuerda‐1, Cuerda‐2, Cuerda‐3, .. etc., o bien C1, C2, C3, …,
etc. y designar sus tensiones respectivas mediante T1, T2, T3, …, etcétera.
Definición. Un nodo es un punto material (de masa insignificante) donde confluyen 3 o más
cuerdas. Un nodo puede constituir por sí solo un sistema físico válido que posee su propio DCL.
EJEMPLO 5. Observe el conjunto representado en
la figura 13. Se tiene un nodo donde confluyen las
cuerdas C1, C2 y C3, y un Bloque que cuelga de la
cuerda C3.
Dado que existen 3 cuerdas, de acuerdo con
la Regla 9 figurarán tres fuerzas de tensión que
denotaremos con T1, T2 y T3, respectivamente.
Conviene aquí definir un sistema físico que
conste solamente del nodo (el sistema {Nodo}). En
la figura 14a se muestra la acción de las cuerdas
sobre el Nodo, y en la figura 14b separadamente
sobre el Bloque.
Figura 13
Hemos añadido el peso W del Bloque, con objeto de que la figura 14b sea ya el DCL del Bloque (el cual
debe incluír todas las fuerzas sobre él).
{Nodo}
{Bloque}
Figura 14a (DCL del Nodo)
Figura 14b (DCL del Bloque)
11
EJEMPLO 6. En el conjunto ilustrado en la figura 15a se tiene una pesa, un bloque y una sola cuerda que
parte desde la pesa, bordea la polea fija izquierda, pasa bordeando la polea 3 móvil y remata en el techo.
¿Cómo actúa la cuerda sobre las poleas fija y móvil? Suponga poleas lisas.
Figura 15a
Figura 15b (No son DCL’s)
Para resolver este ejemplo necesitamos un par de reglas útiles más:
Regla 10. Al bordear una cuerda una polea o perno lisos, la tensión de la cuerda no se altera.
Regla 11. Una cuerda bajo tensión T, que pasa por el canal periférico de una polea lisa (fija o
móvil) produce sobre ésta una acción equivalente a dos fuerzas de magnitudes iguales a T, aplicadas
tangencialmente a la polea en los puntos donde la cuerda deja de hacer contacto con aquella. Véase la
figura 16.
Figura 16
Note que, según la Regla 10, la tensión de la cuerda es la misma a ambos lados de la polea lisa.
Note también que uno podría imaginarse que la (única) cuerda está “atada” a los puntos “a” y “b”, y usar
la Regla 8 de la página 11 para trazar las tensiones T.
Prosigamos con el ejemplo. Primeramente notemos que, en virtud de que existe solamente una
cuerda (y las poleas son lisas), habrá una sola tensión T en el problema.
Según la regla 11, la acción de la cuerda sobre las poleas fija y móvil es la que se muestra en la
figura 15b. Como vemos, la tensión de la cuerda actúa tangencialmente a cada polea en los puntos donde
la cuerda entra y sale de cada polea. En esta figura hemos puesto el comentario “No son DCL’s” puesto
que no se han incluido todas las fuerzas sobre las poleas (solamente las debidas a la cuerda).
12
EJEMPLO 7. Observe el conjunto de bloques, poleas y cuerdas mostrado en la figura 17a. ¿Qué fuerzas
actúan sobre la polea móvil inferior, debidas a las cuerdas?
Figura 17a
Figura 17b
Fíjese que existen 3 cuerdas distintas en el conjunto, cuyas tensiones se designarán T1, T2 y T3.
Las fuerzas de las cuerdas sobre la polea móvil inferior se muestran en la figura 17b. Si se
desprecia el peso de esta polea, la figura 17b es el DCL de la misma.
EJEMPLO 8. Observe la figura 18. Tenemos 3 bloques, designados B1, B2 y B3. Al bloque B1 se le ata una
cuerda (designada Cuerda 1) que corre hacia la izquierda, pasa bordeando una polea lisa (la Polea fija 1),
y finaliza en el bloque B2. Existe otra cuerda (la Cuerda 2) que parte desde el bloque B2 hacia la derecha,
bordea la Polea fija lisa 2, y remata en el bloque B3 que pende verticalmente.
Trazar las fuerzas sobre cada bloque debidas a las cuerdas.
Figura 18
En la figura 19 se muestra la acción de las
cuerdas sobre cada bloque. Estas son algunas de las
fuerzas que figurarían en los DCL’s individuales de
los sistemas {B1}, {B2} y {B3}.
Note que como estamos suponiendo lisas
ambas poleas, la tensión en la Cuerda 1 es la misma
a ambos lados de la Polea 1, y lo mismo podemos
decir sobre la tensión a ambos lados de la Polea 2.
Figura 19 (No son DCL’s)
13
Ejercicios.
Ejercicio 1. Para el dispositivo de poleas mostrado, hacer el DCL de cada polea, así como el DCL del
bloque. Suponer poleas sin peso, y peso W para el bloque.
Ejercicio 2. Para el tendedero de la figura, hacer el DCL de cada nodo y bloque.
Ejercicio 3. Una cuerda pasa por un anillo liso, como se ve en la figura. El peso del anillo es W. Hacer su
DCL.
Sugerencia. Note que existe solamente una cuerda en el problema.
Ejercicio 4. Trazar las fuerzas que ejerce la cuerda sobre cada polea fija lisa, y sobre cada bloque.
14
(C) Fuerza de tensión en resortes estirados, o barras o varillas rígidas estiradas.
Sabiendo ya cómo trazar la fuerza de tensión debida a una cuerda o cable, es inmediato hacer lo
propio para los rersortes o barras o varillas rígidas elongadas.
La regla es similar a la regla 8 de la página 8. La expresaremos en estos términos:
Regla 8. Para trazar la fuerza de tensión ejercida por un resorte elongado (de peso despreciable):
1. Ubique el punto de sujeción del resorte al cuerpo considerado.
2. Desde este punto trace un vector que corra a lo largo del resorte, apuntando
hacia lo lejos del punto de sujeción.
(O sea: imagine que el resorte fuera una cuerda)
Denote la tensión de resortes con el símbolo genérico R.
Misma cosa con respecto a las barras o varillas rígidas ligeras elongadas.
EJEMPLO 9. El bloque está sujeto a dos barras y dos resortes. Las barras están elongadas (es decir, en
tensión), lo mismo que los resortes. Todos estos cuerpos son de masa despreciable, excepto el bloque.
Figura 20
En la figura 21 se muestra el DCl del bloque, representado por un punto “ • “.El DCL sería el
mismo si sustituyésemos las barras y los resortes por cuerdas tirantes, y los símbolos R’s (tensión de
resortes) y V’s (tensión de barras) por T1, T2, T3 y T4 (tensión de cuerdas).
Figura 21
15
(D) Fuerza normal debida al contacto simple entre dos cuerpos.
Definición. Dos cuerpos están en contacto simple si los cuerpos solamente se “tocan” en el punto
o región de contacto, sin estar unidos por pegamento, soldadura, tornillos u otros.
Un tipo de contacto simple muy común en las aplicaciones es el de un bloque y una superficie
plana (como por ejemplo una mesa o pared, un plano inclinado, etc.). En las figuras 22a,b se muestran
ejemplos.
Dos cuerpos en contacto simple siempre se presionan mutuamente. No ofrecen resistencia a ser
separados el uno del otro, pero sí gran resistencia a compenetrarse. En el contacto simple surgen las
fuerzas denominadas fuerza normal y fuerza de fricción (o rozamiento). Por el momento supondremos
que las superficies de los cuerpos en contacto son lisas, lo cual significa que no habrá fuerza de fricción.
Figura 22a
Figura 22b
Con respecto al contacto simple Bloque‐Mesa de la figura 22a tenemos lo siguiente:
El DCL individual del Bloque incluye una fuerza normal N debida a la Mesa. Por la tercera ley de
Newton, el DCL de la Mesa incluye también una fuerza N debida al Bloque. Esta pareja de fuerzas N son
de acción‐reacción: tienen iguales magnitudes y direcciones opuestas, como vemos en la figura 23a.
Figura 23a. (No son DCL’s)
Figura 23b. (No son DCL’s)
Cosa análoga sucede en relación con el contacto simple Bloque‐Plano inclinado de la figura 22b.
Tanto el DCL del Bloque como el DCL del Plano inclinado incluirán una fuerza normal N, en las
direcciones mostradas en la figura 23b.
Advierta que las fuerzas normales acción‐reacción tienden a separar ambos cuerpos en contacto.
16
Regla 9. Fuerza normal N en el contacto simple entre un Bloque y una Superficie plana.
La fuerza normal N que experimenta un bloque debida al contacto simple con una superficie
plana (Mesa, Pared, Otro bloque, etc.) es un vector perpendicular a la superficie plana con la que el bloque
está en contacto simple. Esta fuerza normal N tiene una dirección tal que tiende a alejar el bloque de la
superficie.
Convencionalmente, el vector que representa la fuerza N lo trazaremos con su punta sobre la cara
de contacto del bloque.
No está de más especializar la Regla 9 al caso particular del contacto simple entre dos bloques,
que aparece frecuentemente en los problemas. Tendremos así la siguiente regla:
Regla 10 (= Regla 9 aplicada a dos bloques).
Cuando dos bloques A y B están en contacto simple, la fuerza normal N que el bloque A sufre,
debida al otro bloque B, debe aparecer también en el DCL del bloque B, con el mismo valor N y con
sentido contrario (figura 24).
Figura 24
He aquí otra regla útil:
Regla 11. El número total de fuerzas normales distintas que figuran en los DCL’s individuales de
todos los cuerpos considerados es igual al número de contactos simples distintos que hay en el problema.
EJEMPLO 10. Dos bloques de pesos W1 y W2 son empujados por una fuerza constante F a lo largo de una
mesa horizontal lisa. Hacer el DCL de cada bloque (Figura 25).
Figura 25
‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
Veamos cuántos contactos simples existen en este problema. Son los siguientes:
Contacto simple entre el Bloque‐1 y el bloque‐2
Contacto simple entre el Bloque‐1 y la Mesa.
Contacto simple entre el Bloque‐2 y la Mesa.
Según la Regla 11 recién dada, figurarán entonces 3 fuerzas normales en el problema, que denotaremos
así: N, entre Bloque‐1 y Bloque‐2; N1, entre Bloque‐1 y Mesa; N2, entre Bloque‐2 y Mesa.
17
Figura 26
Los DCL’s de los bloques se muestran en la figura 26. Note lo siguiente:
•
•
•
Los bloques se ejercen entre sí la misma fuerza N, en las direcciones mostradas en la figura 26.
El sistema no está en equilibrio. La fuerza F acelera a ambos bloques hacia la derecha.
La fuerza que empuja al Bloque‐2 hacia la derecha es la fuerza normal N que le ejerce el Bloque‐1.
‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
EJEMPLO 11. Tres bloques de pesos 50 N, 80 N y 120 N están apilados sobre una mesa, como se muestra en
la figura 27. Hacer el DCL de cada bloque.
Figura 27
En este problema aparecerán 3 fuerzas normales, pues existen los 3 contactos simples siguientes:
Bloque‐1 con Bloque‐2
Bloque‐2 con Bloque‐3
Bloque‐3 con la Mesa.
Denotaremos las fuerzas respectivas con N1, N2 y N3.
He aquí los DCL’s de los sistemas {Bloque‐1}, {Bloque‐2} y {Bloque‐3} (estúdielos bien):
Figura 28a (DCL del Bloque‐1)
Figura 28b (DCL del Bloque‐2)
Figura 28c (DCL del Bloque‐3)
18
Vamos ahora a formular la regla para trazar la fuerza normal en el caso general de un contacto
simple entre superficies arbitrarias (no solamente superficies planas).
Sean “Cuerpo A” y “Cuerpo B” dos cuerpos en contacto simple (figura 29a). Por el punto de
contacto tracemos una recta (de hecho un plano) que sea tangente a ambos cuerpos (figura 29b).
Figura 29a
Figura 29b
Regla 12. La fuerza normal N que experimenta cada uno de los cuerpos A y B en contacto simple
es perpendicular al plano tangente común a ambos cuerpos en el punto (o región) de contacto. La fuerza
N sobre cada uno de estos cuerpos actúa en una dirección que tiende a separar cada cuerpo del otro, como
se ve en la figura 30.
Figura 30
La pareja de fuerzas N que vemos en la figura 30 son fuerzas de acción‐reacción. Estamos aquí
ante un claro ejemplo de la tercera ley de Newton.
19
El contacto simple entre dos cuerpos puede ocurrir en una esquina o pico, como en el caso que
vemos en la figura 31, donde el bloque se apoya sobre una pared vertical y un plano inclinado (esto
cuenta como dos contactos simples). En este caso no podemos trazar un plano tangente a un pico, pero sí
al otro cuerpo sobre el que el pico se apoya, y esto es lo que determina la dirección de la fuerza normal.
Figura 31
(E) Fuerza de compresión debida a resortes comprimidos, o barras o varillas ligeras
comprimidas.
En la página 7 definimos lo que es el estado de tensión simple de un resorte o una barra o varilla
rígida (Véanse las figuras 8a,b en dicha página).
Los resortes y barras o varillas pueden estar también en un estado de compresión simple. En este
estado estos cuerpos sufren en sus extremos fuerzas encontradas que tienden a comprimirlos. Las figuras
32a,b son los DCL’s de estos cuerpos en el estado de compresión simple (despreciando el peso de los
mismos).
La fuerza C se denomina la compresión del resorte; la fuerza K es la compresión de la barra o
varilla rígida.
Figura 32a
Figura 32b
Lo que aquí nos interesa son las fuerzas que un resorte o barra comprimidos ejercen sobre los
cuerpos sujetos a sus extremos, que son los cuerpos que ponen al resorte o barra en compresión. Estas
fuerzas son las reacciones de las fuerzas mostradas en la figura 32a,b.
Regla 13. La fuerza de compresión C ejercida por un resorte comprimido sobre un cuerpo sujeto a
uno de sus extremos es una fuerza que incide sobre el cuerpo en el punto de sujeción del resorte, viniendo
desde el exterior del cuerpo considerado a lo largo del eje longitudinal del resorte.
Lo análogo es válido para la fuerza de compresión K debida a una barra o varilla comprimida.
20
EJEMPLO 12. Una bola de peso W está sostenida por dos resortes, como se muestra en la figura 33a.
Hacer el DCL de la bola.
Figura 33a
Figura 33b. DCL de la Bola
En la figura 33b se muestra el DCL del sistema {Bola}. En él, C1 y C2 son las fuerzas de
compresión debidas al Resorte‐1 y al Resorte‐2, respectivamente. Note que los vectores C1 y C2 vienen
desde fuera de la Bola y se “clavan” en la misma (o sea: las puntas de los vectores inciden en los puntos de
sujeción de los resortes a la bola).
EJEMPLO 13. Los dos bloques mostrados en la figura 34a descansan sobre superficies lisas. Los bloques
están unidos por una barra ligera. Se aplica una fuerza P sobre el bloque izquierdo. Hacer el DCL de cada
bloque.
Figura 34a
Figura 34b
Está claro que la barra está en compresión.
Vea los DCL’s de los bloques individuales en la figura 34b. Fíjese especialmente cómo actúa la
barra comprimida sobre cada bloque (fuerza de compresión K).
21
(E) La fuerza de fricción o rozamiento.
En general, la interacción entre dos superficies en contacto simple es más complicada de lo que
hemos descrito hasta ahora. En realidad consta no solamente de la conocida fuerza normal “N” −que
como sabemos actúa perpendicularmente a las superficies contactantes−, sino adicionalmente de una
componente que es tangencial a dichas superficies: la llamada fuerza de fricción o rozamiento.
Las propiedades principales de la fuerza de fricción pueden deducirse a partir de una experiencia
muy simple. Coloquemos una caja pesada sobre una superficie horizontal (Mire la figura 35) y tratemos
de ponerla en movimiento aplicándole cierta fuerza horizontal F. Por ahora apartemos de la discusión las
fuerzas verticales del peso y la normal, que se cancelan.
Figura 35
Sabemos por experiencia que si F es muy pequeña la caja no se moverá. De la condición de
equilibrio se deduce entonces que, al mismo tiempo que se aplica F, se genera otra fuerza igual y opuesta,
“f ”, que contrarresta su efecto. Esta es la fuerza de fricción.
Incrementemos poco a poco la fuerza aplicada F (mire la figura 36), todavía sin que la caja se mueva.
Debe ocurrir que la fricción f se incremente en la misma proporción que F, a modo de mantener la
igualdad f = F que garantice el equilibrio observado.
Figura 36. La fricción aumenta con F hasta llegar
a su valor máximo fm.
Sin embargo, sabemos que sí es posible mover la caja empujándola con una fuerza F
suficientemente grande. Esto significa que se llega a una situación en que la fricción ya no puede
compensar la fuerza aplicada F, de tal manera que el equilibrio se rompe.
La fricción es la resistencia que oponen las superficies al deslizamiento relativo mutuo. Pero las
superficies no pueden desarrollar esta oposición más allá de cierto valor máximo fm. En tanto F es menor
que fm, hay equilibrio. Si F es justamente igual a fm, la caja está a punto de moverse (su movimiento es
inminente), esto es, cualquier cosa que aumente F por encima de fm motivará que la caja se mueva (“se
deslice” o “resbale”), por leve que sea su movimiento. Si F sobrepasa el valor fm la caja se moverá
aceleradamente.
Relacionemos lo anterior con el DCL completo de la caja, supuesta en equilibrio.
22
El contacto de la caja con la superficie horizontal genera sobre aquella una fuerza perpendicular a
la superficie de contacto (o sea la conocida fuerza normal N) y además una fuerza tangencial a la
superficie de contacto (la fuerza de fricción f).
Figura 37
En general,
Regla 14. El contacto simple de un cuerpo y una superficie da lugar a una fuerza normal N y, si
existe tendencia de deslizamiento entre ambas superficies, adicionalmente una fuerza de fricción f. La
dirección de la fuerza de fricción se opone a la dirección de deslizamiento del cuerpo considerado.
Recordemos entonces que toda normal N viene acompañada en general de una fuerza de fricción
o rozamiento f.
Propiedades de la fricción máxima.
De nuevo hay que recurrir al experimento a fin de obtener las características de la fricción máxima
fm. Esta vez investigamos cómo depende el estado de movimiento inminente con la normal N, las
dimensiones y los materiales de fabricación de la caja. He aquí las observaciones experimentales:
•
fm es proporcional a su normal asociada N:
fm = μ N
El factor de proporcionalidad μ se denomina el coeficiente de fricción. Es un número puro (sin
dimensiones físicas) que depende de la naturaleza de las superficies en contacto y del estado de
dichas superficies (pulcritud, lubricación, pulimento, corrosión, oxidación, humedad, etc.).
•
fm no depende del área de contacto.
El contacto simple puede ser de punto, como en los casos representados en las figuras. 38a y 38b. La
fricción máxima que se desarrolla en estos contactos también obedece la relación fm = μ N.
Figura 38a
Figura 38b
23
La fricción es una fuerza muy compleja. Los modelos atómicos de la fricción no explican ciento
por ciento las observaciones macroscópicas. Incluso la fricción macroscópica puede depender de la
“historia” del contacto, es decir, del modo como ambos cuerpos hayan llegado al equilibrio.
En la tabla que sigue se muestran valores típicos del coeficiente de fricción.
Materiales
Condiciones de superficies
Metal sobre Metal
Limpias
Bien lubricadas
No‐metal sobre No‐metal
No lubricadas
Bien lubricadas
Metal sobre No‐metal
No lubricadas
Bien lubricadas
Coeficiente
de fricción
0.4 − 1.0
0.2 − 0.4
0.4 − 0.9
0.1 − 0.2
0.4 − 0.6
0.05 − 0.12
Las tablas de valores de coeficientes de fricción no son muy confiables. Los óxidos e impurezas
presentes en las superficies afectan apreciablemente el valor de μ. Es mejor determinar este coeficiente
experimentalmente en cada escenario, para lo cual el procedimiento más simple es el dado en el Ejemplo
15 un poco más adelante.
Definición. Una superficie lisa es aquella cuyo coeficiente de fricción relativo a cualquiera otra
superficie vale cero. Se trata obviamente de un caso ideal (muy utilizado en la práctica). En este caso no
existe fuerza de fricción sobre los cuerpos en contacto.
En la situación de movimiento inminente, la fuerza de fricción sobre el cuerpo es la máxima, dada
por fm = μN. Apenas el cuerpo empieza a moverse, la fricción disminuye abruptamente desde su valor
máximo fm hasta otro valor fk denominado la fricción cinética (figura 39). Ésta obedece siempre la relación
fk = μk N, donde μk es el coeficiente de fricción cinética. Grosso modo tenemos que μk ≈ 0.75 μ.
En los problemas donde intervienen fuerzas de fricción debe tomar en consideración que la
fricción posee un rango de valores, desde 0 hasta su valor máximo μN. Solamente en la situación de
movimiento inminente puede usarse la relación fm = μ N; en cualquiera otra situación no existe relación
empírica alguna entre la fuerza de fricción f y la normal N.
movimiento inminente
Figura 39
moviéndose
24
EJEMPLO 14. Se presiona un bloque de 50 N de peso contra una pared (figura 40 superior). El coeficiente
de fricción pared − bloque vale μ = 0.4. (a) ¿Con qué fuerza mínima F debe presionarse para que el bloque
no se mueva ? (b) Si se presiona con el doble de la fuerza anterior, ¿cuánto vale la fuerza de fricción?
Figura 40
La figura 40 central muestra el DCL del bloque correspondiente al inciso (a). Si deseamos que el
bloque no se mueva, la fricción debe equilibrar el peso de 50 newton. Supongamos que aplicáramos una
fuerza F bastante grande; entonces la fricción se ajustaría fácilmente al valor requerido de 50. Vayamos
disminuyendo esa fuerza. Lo podemos hacer hasta la situación de movimiento inminente del bloque, es
decir, la mínima fuerza F requerida corresponderá al valor máximo de f, o sea fm = μ N.
Tenemos así que
N=
fm 50
=
= 125 = F
μ 0.4
En el inciso (b), si F = 250 la fricción máxima sería fm = μ N = 0.4 × 250 =100. Esta fricción sería
suficiente para mantener un bloque de 100 newton. En este caso la fricción no alcanza a llegar a su valor
máximo, sino que toma el valor necesario para sostener el bloque de 50 N, es decir, f = 50 newton (figura
40 inferior).
25
EJEMPLO 15. Un procedimiento muy simple para determinar el coeficiente de fricción entre dos
superficies 1 y 2 consiste en utilizar un bloque del material 1 y una barra giratoria del material 2. Luego se
colocan como se muestra en la figura 41 y se va aumentando el ángulo θ hasta que se observe un leve
movimiento del bloque. Esto corresponderá aproximadamente a la situación de movimiento inminente o
sea de fricción máxima.
Figura 41
De las ecuaciones de equilibrio del bloque,
fm = mg sen θ
N = mg cos θ
junto con
fm = μ N
se deduce que
μ = tan θ
Midiendo θ obtenemos μ.
26
EJEMPLO 16. El pony puede jalar a lo más con fuerza de 2000 N. El peso de la caja es 5000 N y su
coeficiente de fricción con el suelo es μ = 0.5.
(a) ¿Qué fuerza vertical mínima debe ejercer el hombre en la situación de la figura 42 para que la caja esté
a punto de deslizarse?
(b) ¿Cuánto valdría esta fuerza si se aplicara horizontalmente?
Figura 42
(a) Para poder mover la caja, el pony debe vencer la máxima fuerza de fricción caja‐suelo. Si el hombre no
jalara la cuerda, la normal sobre la caja sería igual al peso de la misma, o sea N = 5000, y la fricción
máxima sería
fm = μ N = 0.5 x 5000 = 2500
Como el pony puede aplicar a lo más 2000 newton, no logra mover la caja en esta situación.
El hombre coopera jalando la caja hacia arriba, de modo que disminuya la normal y con ello
también la fricción máxima. Deseamos que la fricción máxima sea de 2000, valor al que corresponde una
normal de N = fm/μ = 2000/0.5 = 4000. Para que la normal se reduzca a este valor el hombre debe jalar con
una fuerza de 1000.
(b) Hacer las cosas como en la figura 41 no es eficiente. Es mejor que el hombre empuje horizontalmente la
caja con una fuerza de 500. Entonces entre el pony y el hombre producirán una fuerza de 2000 + 500 =
2500, que iguala la fricción máxima a vencer.
A continuación están los DCL’s correspondientes a (a) y (b) junto con la resolución matemática
detallada del problema.
Inciso (a)
Inciso (b)
fm – 2000 = 0
F + 2000 − fm = 0
N + T – 5000 = 0
fm = 0.5 N
N – 5000 = 0
fm = 0.5 N
N = 4000
T = 1000
fm = 2500
F = 500
27
6. Algunos ejemplos de equilibrio.
EJEMPLO 14.
Introduciremos una regla más, en el contexto de un problema concreto de equilibrio. Resolve‐
remos el problema representado en la figura 43.
He aquí los datos del problema:
− La tensión de la cuerda vale 40 newton.
− El peso del Bloque1 es de 60 newton.
− La fuerza del Resorte no se conoce ni en
magnitud ni en dirección (no se sabe si está en
tensión o en compresión).
− El peso del Bloque2, W2, es otra incógnita.
− La normal Bloque2−Bloque3, N1, también es
incógnita.
− La normal Bloque3−Piso vale 200 newton.
− El peso del Bloque3 vale 80 newton.
Figura 43
Las cantidades a determinar son tres: la fuerza del resorte, N1 y W2.
¿Qué hacer en un problema como éste en que interviene un resorte cuyo estado (tensión o
compresión) no se conoce de antemano? He aquí la regla al respecto:
Regla 15. Si no conoce a priori el estado de un resorte (tensión o compresión):
− Haga una hipótesis de trabajo: trace la fuerza del resorte hacia alguna dirección supuesta.
Desígnela con “R” o “C”, según la haya supuesto de tensión o compresión, respectivamente.
− Resuelva el problema bajo semejante hipótesis. Si obtiene un valor positivo de R o C, acertó a la
dirección correcta. Si obtiene un valor negativo (absurdo) de R o C, entonces la hipótesis queda invalidada
y la dirección de R o C es en realidad la contraria de la supuesta al comienzo (la tensión era realmente
compresión, o viceversa, así que hay que modificar el DCL y replantear las ecuaciones de equilibrio).
Supongamos que el Resorte esté en tensión. Tendríamos los DCL’s de las figuras 44a,b,c.
Figura 44a
Figura 44b
Las ecuaciones de equilibrio son inmediatas:
40 – 60 – R = 0
N1 + R – W2 = 0
200 – N1 – 80 = 0
Figura 44c
28
Su solución es
R = − 20
N1 = 200 − 80 = 120
W2 = N1 + R = 120 + (−20) = 100.
El valor negativo absurdo de R significa que el resorte realmente está en compresión,
contradiciendo nuestra hipótesis. Debemos corregir los DCL’s, invirtiendo la dirección de la fuerza R que
aparece en ellos y renombrándola “C”. Luego debemos replantear las ecuaciones de equilibrio y
resolverlas de nuevo. Se encuentran los valores correctos
La Regla 15 recién dada es de utilidad no solamente con resortes. Existen otros tipos de fuerzas
(fricción, fuerzas en una varilla, fuerza normal, etc.) cuyas direcciones no siempre son conocidas de
partida, para las que también habría que hacer una hipótesis acerca de su dirección.
EJEMPLO 15. Resolvamos ahora un caso en que aparece una fuerza normal de dirección desconocida a
priori. En la figura 45a tenemos un collarín (cilindro acanalado) que encaja dentro de una guía cilíndrica
recta. El peso del collarín es de 50 newtons, la tensión de la cuerda se ha prefijado al valor de 100 newtons,
y el resorte tiene una tensión de 300 newtons. Se trata de calcular la fuerza normal en el contacto simple
collarín−guía.
Figura 45a
Figura 45b
En la Figura 45b podemos ver el contacto con más detalle. Imagine que el collarín no ajusta
perfectamente en la guía, sino que hay cierta holgura o juego en el canal. Si el contacto canal–collarín tiene
lugar en la parte de arriba del collarín, la normal N apuntaría hacia arriba (la normal incide en el punto de
contacto con el cuerpo considerado −el collarín−, viniendo desde el cuerpo externo o actuante −la guía−).
La dirección de N se invierte si el contacto es en la superficie inferior del collarín.
29
Hagamos el DCL del collarín, bajo la hipótesis de que N apunta hacia arriba (figura 46).
Figura 46
De la ecuación de equilibrio,
N +100 –50 –300 = 0
obtenemos N = 250. El hecho de que N haya salido positiva indica que efectivamente apunta hacia arriba,
es decir, que el contacto collarín−guía tiene lugar en la parte superior del canal.
Si el resorte estuviera en compresión, la fuerza de 300 en el DCL estaría dirigida hacia arriba. El
valor resultante para N sería N = −350, que correspondería a un contacto en la parte inferior del canal del
collarín.
EJEMPLO 16. Fuerzas negativas.
De las fuerzas que hemos introducido las siguientes tienen dirección conocida de antemano:
– El peso W (vector que apunta siempre verticalmente hacia abajo)
– La tensión de cables, resortes o varillas, T o R o V
(vector que siempre “emana” del cuerpo)
– La compresión de resortes o varillas, C ó K
(vector que se “clava” en el cuerpo paciente, viniendo desde el cuerpo agente).
Entre ellas se contaría la normal N a condición de que se conozca el punto de contacto, en cuyo caso incide en el
cuerpo pasivo en este punto, viniendo desde el cuerpo activo.
Tip. Una fuerza cuya dirección ya es conocida antes de resolver el problema siempre debe resultar
positiva. Un resultado negativo significa que existe un error en la resolución, o que los datos usados no
son consistentes con la situación física.
Ilustremos con un ejemplo muy simple.
En el conjunto en equilibrio de la figura 47a, el resorte superior tiene tensión de 120 N y el inferior
tiene compresión de 80 N. La fuerza normal entre el Bloque2 y el Piso vale 380 N. Queremos calcular los
pesos de los bloques. Digamos que hiciéramos los DCL’s como vemos en la figura 47b, donde la fuerza de
tensión del resorte superior no está trazada correctamente.
30
Figura 47a
Figura 47b
Las ecuaciones serían
80 – 120 – W1 = 0
y
380 – W2 – 80 = 0
de donde obtendríamos
W1 = −40 ( ! )
y
W2 = 300
El signo negativo de W1 señala un error en el problema, pues indicaría que el peso del Bloque1
actúa en dirección opuesta a la que tiene en los DCL’s, o sea, ¡actúa verticalmente hacia arriba!
Corrigiendo la fuerza de 120 del resorte superior en el DCL del Bloque1 (trazándola hacia arriba) y
volviendo a plantear las ecuaciones y a hacer los cálculos obtenemos los valores correctos:
W1 = 200, W2 = 300.
31
7. Diagramas de cuerpo libre de sistemas compuestos de dos o más cuerpos.
Por supuesto, un sistema físico puede constar de 2 o más cuerpos. Con miras a hacer los DCL’s de
tales tipos de sistemas, introduciremos la siguiente terminología:
Definición. Se denomina contactos internos de un sistema formado por varios cuerpos a los
contactos que tienen lugar entre los propios cuerpos pertenecientes al sistema. Por otra parte, los contactos
externos de un sistema son los que tienen lugar entre al menos un cuerpo del sistema y algún cuerpo no
perteneciente (ajeno) al sistema.
EJEMPLO 17. En la figura 48 se muestra un conjunto de cuerpos en equilibrio. Está formado por un
amigo que jala hacia arriba una cuerda atada a un bloque; el bloque descansa sobre una tabla, que a su vez
presiona un resorte, comprimiéndolo contra el piso.
Figura 48
En la figura 49 hemos señalado con puntos
gruesos a, b, c, d, e y f los contactos entre los
diversos cuerpos del conjunto, así como los
contactos con el piso.
Definamos el sistema que consta de todos
los cuerpos mostrados (excepto el Piso).
LLamémosle sistema global:
Sistema global ≡
{Amigo, Cuerda, Bloque, Tabla, Resorte}
Para este sistema, todos los contactos son internos,
excepto los contactos con el Piso, que es un cuerpo
Figura 49
no perteneciente al sistema global (La Tierra
también es un cuerpo ajeno al sistema global).
32
Regla 16. El DCL de un sistema formado por varios cuerpos incluye, además de los pesos de tales
cuerpos, las fuerzas debidas solamente a los contactos externos del sistema (llamadas fuerzas externas).
NO incluye fuerzas que surgen en los contactos internos del sistema (llamadas fuerzas internas).
Apliquemos la Regla 16 para hacer el DCL del sistema global {Amigo, Cuerda, Bloque, Tabla,
Resorte}.
El DCL del sistema global incluirá, aparte de las fuerzas debidas a la Tierra (los pesos), las fuerzas
debidas solamente al Piso, que es el único contacto externo del sistema. Vea el DCL en la figura 50.
Figura 50
En este DCL, W1, W2 y W3 son los pesos del bloque, el amigo y la tabla, respectivamente, y C y N2
son las fuerzas del piso sobre el resorte y el amigo, respectivamente. Note que en el DCL no aparecen
fuerzas que se ejerzan entre sí el amigo, la cuerda, el bloque, la tabla y el resorte, puesto que estos cuerpos
son los que forman el sistema, así que sus contactos mutuos son internos.
Solamente en los contactos externos del sistema es donde existen fuerzas que aparecen en su DCL.
PREGUNTA. ¿Cuáles son los contactos externos del sistema {Bloque, Tabla}?
RESPUESTA. La Cuerda y el Resorte.
(El contacto simple Bloque‐Tabla es interno, pues ambos cuerpos pertenecen al sistema).
PREGUNTA. ¿Qué cuerpos ejercen fuerzas sobre el sistema {Amigo, Cuerda, Bloque}?
RESPUESTA. Aparte de la Tierra, son: la Tabla y el Piso.
PREGUNTA. ¿Ejerce fuerza el Resorte sobre el sistema {Cuerda, Bloque}?
RESPUESTA. No, porque aunque el Resorte es un cuerpo externo al sistema dado, no tiene
contacto ni con la Cuerda ni con el Bloque.
33
EJEMPLO 18. Se tienen 2 bloques, B1 y B2, acoplados a unos resortes R1 y R2 (figura 51a). El resorte R1
está elongado, y el R2 comprimido. Hacer el DCL del sistema {B1, B2} formado por los dos bloques.
Figura 51a
Figura 51b
Para el sistema de 2 bloques {B1, B2} de la figura 51a, el contacto simple entre ambos bloques es
interno, y los contactos de B1 con el resorte R1, y de B2 con el resorte B2, son externos. En otras palabras,
los resortes R1 y R2 son ajenos (no pertenecen) al sistema {B1, B2}. Naturalmente, la Tierra también es un
cuerpo ajeno al sistema {B1, B2}. Por la Regla 16, los cuerpos que ejercen fuerzas sobre el sistema {B1, B2}
son: la Tierra, el resorte R1 y el resorte R2.
Observe bien el DCL del sistema {B1, B2} en la figura 51b. Incluye las fuerzas debidas al resorte R1
(fuerza R), al resorte R2 (fuerza C) y a la Tierra (fuerzas W1 y W2). No incluye la fuerza de interacción
normal entre ambos bloques, pues esta surge en el contacto interno entre los mismos.
EJEMPLO 19. Para el conjunto de cuerpos mostrados en la figura 52, ¿Cuáles son los contactos internos y
externos del sistema {Bloque‐1, Bloque‐2, Bloque‐3, Cuerda}?
Figura 52
Note que los contactos
Bloque‐1 ↔ Bloque‐2,
Bloque‐2 ↔ Cuerda, y
Cuerda ↔ Bloque‐3
son internos del sistema, pues todos los cuerpos implicados en ellos pertenecen al sistema dado. Los
contactos externos del sistema son: el Agente que ejerce la fuerza P, el Piso y la Pared.
34
EJEMPLO 20. Determinar la fuerza con que debe jalar
la cuerda el obrero para sostenerse a sí mismo. El obrero
pesa 700 N y el andamio 100 N. Suponer poleas ideales
(lisas y ligeras).
‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
Asignemos nombres a los diversos cuerpos del
conjunto, tal como vemos en la figura 54a.
Haremos los DCL’s de los sistemas {Polea A},
{Polea B} y {Obrero, Andamio}. Los dos primeros son
inmediatos (figura 54b), recordando cómo es la acción
de cuerdas sobre poleas, explicada en la Regla 11 dada
en la página 11.
Figura 53
Figura 54a
Figura 54b
Con respecto al DCL del sistema {Obrero, Andamio},
notamos que dicho sistema tiene contactos externos solamente
con la cuerda 3 y con la cuerda 2. Entonces, aparte de los pesos
del obrero (700 N) y del andamio (100 N), debemos incluir las
fuerzas T3 y T2 debidas a estas cuerdas, tal como vemos en la
figura 55.
Hemos usado aquí el hecho que el contacto simple entre
el obrero y el andamio es interno al sistema {Obrero, Andamio},
de tal manera que la fuerza normal que ambos cuerpos se
ejercen allí no aparece en el DCL de dicho sistema.
Figura 55
He aquí las ecuaciones de equilibrio:
{Polea A}
{Polea B}
{Obrero, Andamio}
2T1 = T3
2T2 = T1
T2 + T3 = 100 + 700
35
La fuerza con que se soporta el Obrero, o sea T2, resulta igual a
T2 =
⇒
1
(100 + 700) = 160
5
T1 = 320
T3 = 640
Aprovechemos este problema para introducir otra regla útil:
Regla 17. Para poder calcular una fuerza debemos definir un sistema para el cual esta fuerza sea
externa, de modo que aparezca en su DCL.
Para ilustrar esta regla, supongamos que deseamos calcular la interacción Obrero−Andamio. No
podemos valernos del sistema {Obrero, Andamio} ya que la fuerza a calcular es interna a ese sistema
(Mire en la Figura 56a los tres contactos existentes).
Podemos usar cualquiera de los dos sistemas simples {Obrero} o {Andamio}, cuyos DCL’s son las
figuras 56b y 56c,, respectivamente.
Figura 56a
Figura 56b
Figura 56c
El sistema {Obrero} tiene contacto solamente con la Cuerda 2 (fuerza T2) y con el Andamio (fuerza
normal N)
Por otra parte, el sistema {Andamio} tiene contacto solamente con la Cuerda 3 (fuerza T3) y con el
Obrero (fuerza normal N)
Las ecuaciones de equilibrio de {Obrero} y {Andamio} son respectivamente
T2 + N = 700
T3 = N + 100
⇒
N = 700 − 160 = 540
T3 = 540 + 100 = 640
mismo resultado que antes.
36
8. Problemas.
Hacer los DCL’s de los bloques individuales y demás partículas que intervienen en cada conjunto
en equilibrio.
1. Por medio de una cuerda se aplica una fuerza de
100 N al bloque superior, como se ve en la figura.
Hacer el DCL de cada bloque y calcular las fuerzas
desconocidas.
2. Dos bloques, de 8 kg y 12 kg, son empujados
contra una pared mediante una fuerza de 200 N
aplicada sobre el primero. Del segundo bloque
pende otro bloque de masa 6 kg. Hacer el DCL de
cada bloque y calcular las fuerzas desconocidas.
3. El hombre, que pesa 600 newton, trata de
levantar (infructuosamente) una mesa fija al piso,
con el fin de aliviar una comezón en el pie. La
fuerza que aplica a la mesa vale 120 newton.
¿Cuánto vale la fuerza normal
hombre ↔ piso antes de aplicar dicha fuerza y
después de aplicarla? Explique con ayuda del DCL del
hombre y de las ecuaciones de equilibrio. Haga el
experimento.
Ahora el hombre presiona sobre la mesa hacia abajo
con sus manos, con una fuerza de 80 newton, con
el fin de aliviar el dolor en un callo. Analizar este
caso.
Resp. 600 N, 720 N; 520 N.
4. Malú Mora sube a la báscula con un bastón de peso despreciable. Supongamos que el peso de Malú es
de 800 newtons, y que el plato de la báscula no pesa nada. ¿Cuál es la lectura de la báscula si Malú
presiona el bastón contra el plato con una fuerza de 50 newtons? Haga el DCL de los sistemas {Malú} y
{Plato, Resorte}.
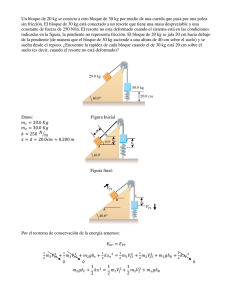
Resp. 800 N.
37
5. Pancho se sostiene de dos cables jalándolos con sendas fuerzas de 100 newtons. Está parado sobre una
plataforma de 50 newtons de peso, la cual descansa sobre un muelle sujeto a un baúl de 400 newtons de
peso. El peso de Pancho es de 600 newtons.
Intente deducir mentalmente los valores de las siguientes fuerzas:
– La fuerza de contacto entre Pancho y la Plataforma.
– La compresión del resorte.
– La fuerza de contacto Baúl – Piso.
Resp. 400; 450; 850.
6. Determinar la tensión en todas las cuerdas del colgadijo mostrado en la figura. El peso del bloque es de
600 N. La polea grande pesa 100 N, y las pequeñas pesan 40 N cada una.
Resp. 480, 126.6, 213.3, 213.3, 386.6
7. Calcular la fuerza que debe aplicar Elmer Homero para sostenerse a sí mismo. Elmer pesa 800 N y el
andamio 200 N. Calcular también la fuerza con que pisa el andamio.
38
Resp. 100; 700
8. El sistema está sometido a las fuerzas indicadas. Sin usar lápiz y papel, compruebe que está en
equilibrio.
9. Calcule la fuerza normal guía−collarín. El resorte superior está en compresión (200 N), el inferior en
tensión (300 N). El peso del collarín es 100 N.
Resp. 600 N
10. Hay en total 9 fuerzas sobre el cuerpo A mostrado abajo. ¿Cuáles son?
39
11. Haga el DCL de cada bloque de los conjuntos mostrados.
(Resortes en tensión.)
(Resorte superior en tensión, inferior en compresión)
(Resorte izquierdo en compresión, derecho en tensión)
(Resorte en compresión, cuerda en tensión.)
40
12. ¿Qué fuerza F es necesaria para mantener a la esferita de masa 6 kg en equilibrio? La esferita descansa
sobre una superficie cilíndrica lisa.
41
Resp. 40.22 N.
13. La esfera de peso 46 N pende de una varilla rígida ligera y recta, y descansa sobre una superficie lisa.
Calcular la tensión de la varilla, “K”.
Resp. K = 33.38 N.
14. La esferilla de peso 50 N se apoya sobre la superficie parabólica. El resorte forma un ángulo de 20° con
la vertical. Calcular su tensión, así como la normal sobre la esfera.
Resp. R = 44.6; N = 17.3.
15. Calcular las fuerzas normales entre todas las superficies. Pesos: esfera menor, 200 N; esfera mayor, 500
N.
42
Resp. 666.66; 700; 833.33; 666.66.
16. Calcular la tensión del cable y la fuerza normal con el plano inclinado.
Resp. 29.8; 45.7.
17. ¿Qué fuerza aplicada (a) horizontalmente, (b) a lo largo del plano, es necesaria para mantener al
bloque en equilibrio? Suponer superficies lisas.
Resp. 28.3 N; 24.5 N.
18. El peso de la esfera es 300 N, la tensión del resorte es 500 N. Calcular la normal y la fuerza F.
Resp. 182; 376.
19. Calcular las fuerzas normales sobre la esfera de peso 100 N. El resorte tiene una compresión de 50 N.
43
Resp. 81.2 N, 111.1 N.
20. Se pasa una cuerda por un anillo liso de peso W. Se aplica al anillo una fuerza horizontal P de modo
que esté en equilibrio en la configuración mostrada. Calcular la tensión de la cuerda y el valor de la fuerza
F en términos del peso W.
Resp. T = 0.732W; F = 0.268 W.
21. Calcular el peso W que produce el equilibrio en el sistema mostrado. Todas las superficies son lisas.
Calcular la reacción en el apoyo de articulación de la polea, supuesta de masa despreciable.
22. Calcular las tensiones en todas las cuerdas. El peso del bloque es 120 newton.
Resp. 121.8; 21.1; 138.5; 90.4; 120.
23. Un aparato para levantar pesos consiste de una barra ligera rígida AB de 100 cm de largo, que está
atada al punto C por un cable BC de 60 cm de largo. Un peso de 600 N está suspendido por otro cable en B.
Calcular las fuerzas en la cuerda BC y la barra AB.
44
Resp. 500 N, 300 N.
Resp. (77.25 N ∠ – 29.52°), (136.45 N ∠ – 119.52°)
Resp. 4.8 kgf, 3.6 kgf, 6.4 kgf.
24. Un pequeño collarín de peso W, que puede deslizarse a lo largo de un anillo vertical liso, se mantiene
fijo mediante una cuerda atada al punto más alto del anillo. Calcular la reacción del anillo sobre el
collarín.
Resp. W.
45
25. La barra rígida AD soporta un bloque de 5000 N mediante una polea lisa en D y un cable fijo en C y D.
Calcular la fuerza en la barra y en el cable CD.
Resp. T = 4090 N, C = 12100 N.
26. Con los datos m1 = 28 kg, m2 = 22 kg, θ1 = 30° y
θ2 = 32°, calcular la fuerza F necesaria para mantener el equilibrio de los dos cuerpos.
Resp. F = 148.2 N.
27. El collarín de peso 20 N es guiado por una barra circular vertical. El resorte tiene constante elástica
k = 1000 N/m y su elongación es δ = 22 mm. Calcular el ángulo α que forma el resorte con la vertical.
46
Resp. 25°.
28. Calcular el valor de la masa M para que exista equilibrio en el sistema mostrado.
Resp. M = 324.7 kg.
29.
47
Resp. 344 N; Permanece.
30. Una barra rígida y ligera se acopla mediante pasadores lisos a dos bloques de pesos 50 N y 36 N como
se muestra en la figura. El coeficiente de fricción entre los bloques y la superficie es 0.325. Calcular la
fuerza P que motivará que el sistema esté a punto de resbalar hacia la derecha.
Resp. 57 N.
31. Para el sistema mostrado, suponer conocidas las cantidades M, m, y θ. ¿Cuánto vale el coeficiente de
fricción μ si el bloque grande está a punto de resbalar (a) hacia abajo; (b) hacia arriba?