691-MA26 - Funciones - 2020 (5)

Matemáticas
Material : MA-26
CUADERNO DE EJERCICIOS N° 23
FUNCIONES
1.
¿Cuál(es) de
]a, b[?
I)
los siguientes gráficos representa(n) una función en el intervalo
II)
y
III)
y
a
a
a
A)
B)
C)
D)
E)
2.
b
x
y
b x
b
Solo I
Solo I y II
Solo I y III
Solo II y III
I, II y III
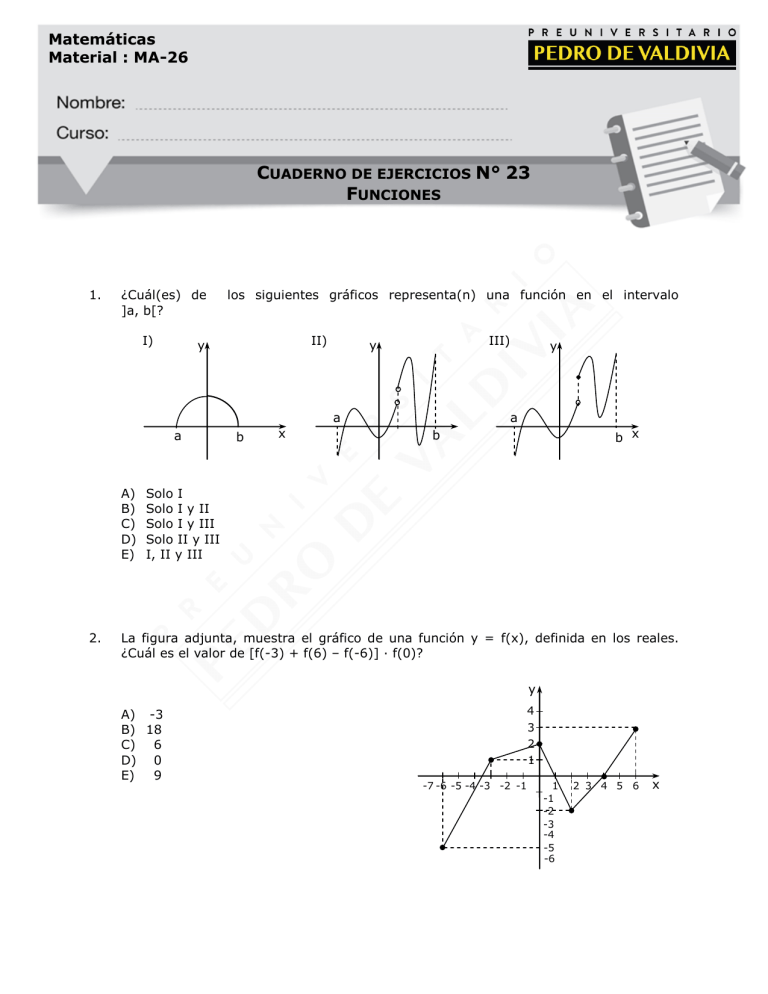
La figura adjunta, muestra el gráfico de una función y = f(x), definida en los reales.
¿Cuál es el valor de [f(-3) + f(6) – f(-6)] · f(0)?
y
A) -3
B) 18
C) 6
D) 0
E)
9
4
3
2
1
-7 -6 -5 -4 -3 -2 -1
1
-1
-2
-3
-4
-5
-6
2 3 4 5 6
x
3.
De acuerdo al gráfico de la función h(x) de la figura adjunta, se puede afirmar que
I)
II)
III)
La función es creciente en [-2,4].
Dom h = [-2,4]
Rec h = [-2,3]
y
3
h(x)
2
A)
B)
C)
D)
E)
4.
1
-2
E)
g(x) = x2 – 2, entonces f(g(2)) es
2
-2
10
-14
1
10
Si f(x) = x2 – 1
A)
B)
C)
D)
E)
-1
-1
-2
Si f(x) = 3x – 8, y
A)
B)
C)
D)
5.
Solo I
Solo I y II
Solo I y III
Solo II y III
I, II y III
y
g(x) = 2x + 1, entonces f(g(x)) es igual a
4x2 + 4x
4x2 – 4x
2x2 – 1
4x2
2x
2
1 2 3 4 x
6.
Si f(x) = x
y
g(x) = 3, ¿cuál es el valor de
g(x + 3)  g(x)
?
f (x + 3)  f (x)
A) 3
B) 2
C) 1
D) 0
E) -3
7.
Sea f(x) = x + 3 y g(x) = x – 2, el gráfico que mejor representa f (g(x)) es
A)
y
y
B)
3
y
C)
3
1
-2
2
x
x
-2
D)
E)
y
x
-2
-3
y
3
3
2
1
x
-2
8.
2
-1
2
x
Sea f una función, con dominio el conjunto de los números reales, definida por
f(x) = (x – 5)3 + 3. Si g, h, k, m y n son funciones, todas con dominio el conjunto de
los números reales, ¿con cuál de las siguientes traslaciones se obtiene la gráfica de f ?
A) Trasladar la gráfica de g(x) = x3 + 3, cinco unidades horizontalmente hacia la
izquierda.
B) Trasladar la gráfica de h(x) = (x – 2)3 + 3, tres unidades horizontalmente hacia la
izquierda.
C) Trasladar la gráfica de m(x) = x3, cinco unidades horizontalmente hacia la izquierda
y tres unidades verticalmente hacia arriba.
D) Trasladar la gráfica de k(x) = (x – 5)3 – 1, cuatro unidades verticalmente hacia
arriba.
E) Trasladar la gráfica de n(x) = x3 – 5, tres unidades verticalmente hacia arriba.
(Fuente: DEMRE, Publicación 2019)
3
9.
Sean las funciones f, g y h, todas con dominio el conjunto de los números reales,
3
definidas por f(x) =
x, x – 2g(x) + 2 = 0, 5x + 6h(x) – 30 = 0. ¿Cuál de las
4
siguientes afirmaciones es verdadera?
A) h(x) es inversamente proporcional a x.
B) g(x) es directamente proporcional a x.
C) Las rectas que representan a las gráficas de las funciones f y g tienen la misma
pendiente.
D) g(2x) = 2g(x)
1
E) g(0) = h(0)
5
(Fuente: DEMRE, Publicación 2017)
10. Sea f(x) = x + 2, entonces la gráfica de la función g que es simétrica a f(x) con
respecto al eje y es
y
A)
y
B)
2
1
-2 -1
y
C)
2
1
1
2
3
x
2
1
-2 -1
-2
1
2
3
x
-2 -1
-2
D)
E)
y
2
2
1
1
1
2
3
2
-2
y
-2 -1
1
x
-2
-2 -1
-2
4
1
2
3
x
3
x
11. ¿Cuál(es) de los siguientes gráficos representa(n) a una función f y su función
inversa f-1?
I)
II)
y
f
y
y
III)
f
f
4
5
4
f-1
3
1
2
-1
-2
1
-4 -3 -2 -1
1 2 3 4
x
1
1
4
x
2
f-1
-1
1
-1
x
f-1
A)
B)
C)
D)
E)
Solo
Solo
Solo
Solo
Solo
I
II
III
I y III
II y III
12. Sea g: lR  lR definida por g(x) =
x
 5 . ¿Cuál(es) de las siguientes afirmaciones
3
es (son) verdadera(s)?
I)
II)
III)
A)
B)
C)
D)
E)
g es inyectiva.
g es epiyectiva.
La función inversa de g es g–1: lR  lR definida por g–1(x) = 3x – 15.
Solo I
Solo II
Solo I y II
Solo II y III
I, II y III
13. Sea g una función, cuyo dominio es lR – {-3}, definida por g(x) =
siguientes funciones corresponde a su inversa?
A) f(x) =
B) t(x) =
C) q(x) =
D) r(x) =
E) s(x) =
x+3
1 
, con dominio lR –  
4x  1
4
3  2x
, con dominio lR – {-5}
x+5
3x + 1
, con dominio lR – {4}
4  x
x+3
1
, con dominio lR –
, -3
4x  1
4
3x + 1
1

, con dominio lR – 4, - 
4  x
3

 
5
4x  1
. ¿Cuál de las
x+3
14. Dada la función g(x) =
2
x  1 , definida de lR en lR, entonces g–1(g(x)) es
5
A) g–1(g(x)) = 1
B) g–1(g(x)) = -1
1
C) g–1(g(x)) =
x
D) g–1(g(x)) = x
5x + 5
E) g–1(g(x)) =
2
15. Se pone a hervir agua que inicialmente estaba a una temperatura de 10 °C. Si su
temperatura sube uniformemente durante los primeros 7 minutos hasta alcanzar los
100 °C, estabilizándose la temperatura después de este tiempo, ¿cuál de los siguientes
gráficos representa mejor este fenómeno?
A)
B)
Temperatura (°C)
C)
Temperatura (°C)
Temperatura (°C)
100
100
100
10
10
10
0
7
0
Minutos
D)
7
Minutos
0
7
Minutos
E)
Temperatura (°C)
Temperatura (°C)
100
100
10
0
10
7
Minutos
0
7
Minutos
(Fuente: DEMRE. Publicación 2011)
6
16. Un técnico cobra un cargo fijo de $ 17.000 más $ 1.500 por hora de trabajo. ¿Cuál de
las siguientes funciones modela el cobro, en pesos, para un trabajo de n horas de este
técnico?
A)
B)
C)
D)
E)
g(n) = 17.000n + 1.500
p(n) = 17.000 ∙ 1.500n
h(n) = 18.500n
f(n) = 17.000 + 1.500n
q(n) = n + 18.500
(Fuente: DEMRE, Publicación 2014)
17. La tarifa de cierta compañía de telefonía consta de un cargo fijo mensual de $ 9.000
más un cargo de $ 50 por minuto que se habla. Si durante los primeros 240 minutos
esta tarifa se modela mediante una función de la forma f(x) = mx + n, ¿cuál de las
siguientes gráficas representa mejor a la gráfica de f?
A)
f(x)
B)
f(x)
9.000
240
240
C)
x
D)
f(x)
9.000
x
240
x
f(x)
9.000
50
E)
240
x
240
x
f(x)
9.000
(Fuente: DEMRE. Publicación 2020)
7
18. En la figura adjunta se muestran las gráficas de tres funciones f, g y h que representan
el costo correspondiente a kilogramos de peras, plátanos y manzanas,
respectivamente. ¿Cuál de las siguientes afirmaciones es FALSA en relación a la
información entregada en el gráfico?
A)
B)
C)
D)
E)
El kilogramo de plátanos es más caro que el kilogramo de manzanas.
2 kg de peras tienen el mismo costo que 3 kg de manzanas.
Con $ 1.200 es posible comprar 5 kg de fruta.
Con $ 1.000 se puede comprar 1 kg de manzanas y 1 kg de peras.
El costo total de 2 kg de cada fruta son $ 3.000.
(Fuente: DEMRE. Publicación 2015)
19. Un modelo para la temperatura T, en grados Celsius (°C), de un líquido recién vertido
en un recipiente está dado por T(t) = 90 – 10t, donde t es el tiempo transcurrido en
minutos, desde el instante en que fue vertido, ¿cuál(es) de las siguientes afirmaciones
es (son) verdadera(s)?
I)
II)
III)
A)
B)
C)
D)
E)
La temperatura disminuye en función del tiempo.
El líquido fue vertido a 90 °C.
La temperatura del líquido disminuye a razón de 10 °C por minuto.
Solo I
Solo II
Solo I y III
Solo II y III
I, II y III
(Fuente: DEMRE. Publicación 2015)
8
20. En un cuadrado, la mitad de la medida de la diagonal es P. ¿Cuál de las siguientes
funciones describe el perímetro del cuadrado en función de P?
A) f(P) = 4 2 P
B) g(P) = 2 2 P
C) h(P) = 2 P
D) r(P) = 4P
E) q(P) = 2P
(Fuente: DEMRE. Publicación 2018)
21. Si M(x) = x – [x] es la función mantisa, que hace corresponder a cada número el
mismo número menos su parte entera, entonces ¿cuál es el valor de
M(8,75) + M(-3,75)?
A) 7
B) 1
C) 0,5
D) 0
E) -7
22. Si 3 < x < 4, entonces f(x) = |x – 3| + |x – 5| +|4 – x| equivale a
A)
B)
C)
D)
E)
x–4
x+6
12 – 3x
6–x
x – 12
9
23. Sea la función f(x) = x  h + k, con dominio el intervalo [h, [. Si h y k son números
reales, ¿cuál(es) de las siguientes afirmaciones es (son) siempre verdadera(s)?
I)
II)
III)
A)
B)
C)
D)
E)
El recorrido de f es el intervalo [h, [.
Si k > 0 y h < 0, entonces la gráfica de f se encuentra solo en el segundo
cuadrante.
El mínimo valor que alcanza f es k.
Solo I
Solo II
Solo III
Solo I y III
I, II y III
(Fuente: DEMRE. Publicación 2018)
24. Una función h, cuyo dominio son los números naturales, verifica la propiedad
h(n + 1)
h(n) =
, para todo n perteneciente al dominio de h. Si h(1) = 3, entonces
2
h(20)=
A)
B)
C)
D)
E)
220 · 3
219 · 3
(2 · 3)19
60
57
25. Sea f una función afín, tal que f: lR  lR y f -1 es su función inversa. Si f(2) = 4 y
f -1(3) = 5, ¿cuál es el valor de f -1(4) + f(5) + f -1(f(4))?
A) 6
B) 7
C) 9
D) 10
E) 13
(Fuente: DEMRE. Publicación 2020)
10
26. Si f(x) = mx + n es una función afín, se puede determinar el punto de intersección de
la gráfica de f(x) con el eje de las abscisas, si se sabe que:
(1) f(0) = 2
(2) f(1) = 0
A)
B)
C)
D)
E)
(1) por sí sola
(2) por sí sola
Ambas juntas, (1) y (2)
Cada una por sí sola (1) ó (2)
Se requiere información adicional
27. Sea f(x) = ax3, la función representada en la figura adjunta, se puede determinar el
valor de a, si se sabe que:
y
(1) b = 16
b
(2) f(2) = 16
A)
B)
C)
D)
E)
(1) por sí sola
(2) por sí sola
Ambas juntas, (1) y (2)
Cada una por sí sola (1) ó (2)
Se requiere información adicional
2
x
28. En una cuenta de agua potable se consigna un cargo fijo de $ 900. Sabiendo que el
modelo de cálculo es lineal, se puede determinar cuánto paga una persona que
consume 200 m3, si se sabe que:
(1) una persona que consume 100 m3 de agua paga $ 20.900.
(2) una persona que no consume agua paga $ 900.
A)
B)
C)
D)
E)
(1) por sí sola
(2) por sí sola
Ambas juntas, (1) y (2)
Cada una por sí sola (1) ó (2)
Se requiere información adicional
11
29. Sea f(x) = n · ax, con a > 0. Si (3, b) es un punto de la gráfica de la función f(x), se
puede determinar el valor de b, si:
(1) el punto (2,9) pertenece a la gráfica de la función f(x).
(2) el punto (0,1) pertenece a la gráfica de la función f(x).
A)
B)
C)
D)
E)
(1) por sí sola
(2) por sí sola
Ambas juntas, (1) y (2)
Cada una por sí sola (1) ó (2)
Se requiere información adicional
30. Sea f(x) = |x – a|+ b, se puede determinar los valores de a y b, si se sabe que:
(1) la gráfica de la función intersecta al eje x en (-1,0) y (3,0).
(2) la gráfica de la función intersecta al eje y en (0, -1).
A)
B)
C)
D)
E)
(1) por sí sola
(2) por sí sola
Ambas juntas, (1) y (2)
Cada una por sí sola (1) ó (2)
Se requiere información adicional
RESPUESTAS
1.
2.
3.
4.
5.
6.
C
B
D
B
A
D
7.
8.
9.
10.
11.
12.
E
D
E
A
C
C
13.
14.
15.
16.
17.
18.
C
D
E
D
A
C
19.
20.
21.
22.
23.
24.
E
A
B
D
C
B
25.
26.
27.
28.
29.
30.
C
B
D
A
C
A
MA-26
Puedes complementar los contenidos de esta guía visitando nuestra web
http://www.pedrodevaldivia.cl/
12