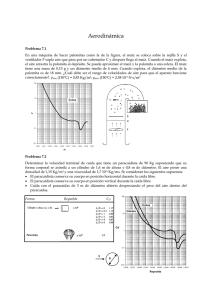
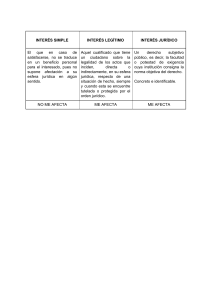
Aerodinámica Problema 8.1 En una máquina de hacer palomitas como la de la figura, el maíz se coloca sobre la rejilla S y el ventilador F sopla aire que pasa por un calentador C y después llega al maíz. Cuando el maíz explota, el aire arrastra la palomita al depósito. Se puede aproximar el maíz y la palomita a una esfera. El maíz tiene una masa de 0,15 g y un diámetro medio de 6 mm. Cuando explota, el diámetro medio de la palomita es de 18 mm. ¿Cuál debe ser el rango de velocidades de aire para que el aparato funcione correctamente?. ρaire (150ºC) = 0,83 Kg/m3; µaire (150ºC) = 2,38⋅10-5 N⋅s/m2 100 10 CD Esfera T = 150º C 1 S C 0,1 F 0,01 1,E-02 1,E-01 1,E+00 1,E+01 1,E+02 1,E+03 1,E+04 1,E+05 1,E+06 1,E+07 Re Problema 8.2 Determinar la velocidad terminal de caída que tiene un paracaidista de 90 Kg suponiendo que su forma corporal se asimila a un cilindro de 1,6 m de altura y 0,8 m de diámetro. El aire posee una densidad de 1,15 Kg/m3 y una viscosidad de 1,7 10-5 Kg/ms. Se consideran los siguientes supuestos: • El paracaidista conserva su cuerpo en posición horizontal durante la caída libre. • El paracaidista conserva su cuerpo en posición vertical durante la caída libre. • Caída con el paracaídas de 3 m de diámetro abierto despreciando el peso del aire dentro del paracaídas. Forma Reynolds 100 CD Esfera 10 Cilindro Cd 1 0.1 V D 0.01 1.E-02 1.E-01 1.E+00 1.E+01 1.E+02 1.E+03 1.E+04 1.E+05 1.E+06 1.E+07 Reynolds VIII. Aerodinámica Problema 8.3 La esfera lisa de la figura de diámetro D=15 cm tiene un peso W=3,5 N y cuelga de un alambre sin peso de longitud L=60 cm. Sobre la esfera sopla una corriente de aire de velocidad V∞=17 m/s. Sabiendo que el ángulo de inclinación es θ=20º y que se desprecia la resistencia del aire sobre el alambre, calcular el coeficiente de arrastre de la esfera. L g θ V∞ D Problema 8.4 Un avión ligero pesa 10000 N y está diseñado para transportar una carga útil de 2000 N. Se considera que la superficie aerodinámica es convencional con una envergadura de 12 m y una cuerda de 1,8 m. Calcular: a) la velocidad de despegue si se desea un ángulo de ataque de 8°. b) la velocidad de pérdida de sustentación cuando aterriza. c) la potencia necesaria a una velocidad de crucero de 50 m/s, si se requiere un 45% de la potencia para mover la superficie aerodinámica (asumir que la velocidad de crucero se alcanza en las condiciones de diseño con un ángulo α ≅ 2°). Problema 8.5 Una corriente de aire incide sobre dos esferas del mismo tamaño (una rugosa y otra lisa) que están sujetas en los extremos del brazo de una balanza, como se indica en la figura. Cuando la velocidad u = 0 m/s, la balanza está equilibrada. Calcular la mínima velocidad u que hace que la balanza gire en el sentido de las agujas del reloj. Esfera lisa 0,1 m Esfera rugosa -2 ε/D = 1,25·10 0,3 m 0,5 m U Problema 8.6 Se lanza un balón de fútbol desde un helicóptero sobre un estadio. Para que la velocidad del balón al llegar al público no sea muy elevada se utiliza un paracaídas. ¿Qué diámetro D debe tener el paracaídas para que el balón llegue a una velocidad no superior a 2 m/s? Datos: • Masa del balón: 850 gramos • Despreciar el arrastre y el empuje del aire sobre el balón • Propiedades del aire: νaire = 1,5·10-5 m2/s y ρaire = 1,2 kg/m3. • Coeficiente de arrastre del paracaídas basado en el área frontal (πD2/4): CD = 0,8 – 0,1·log (Re+1) 0 < Re < 106 Re > 106 CD = 0,2 2 Uva – Dpto. I.E.F. – Mecánica de Fluidos (Ene-2013) VIII. Aerodinámica Problema 8.7 a) Las torres de transmisión eléctrica están separadas 400 m y un cable conductor liso de 1,3 cm de diámetro cuelga entre ellas. Si un viento de 30 m/s sopla transversalmente al cable conductor, calcular la fuerza total de arrastre sobre el cable en el tramo entre las dos torres. b) Calcular la velocidad terminal de una barra cilíndrica de diámetro 1,3 cm y densidad 1500 kg/m3 asumiendo que desciende horizontalmente en un depósito de agua dulce. Problema 8.8 Se considera un aeroplano ultraligero cuyo peso máximo es 7780 N. El ala tiene un área de 16.6 m2 y su coeficiente de sustentación máximo es 2,1 con los flaps activados. Se pide: a) Calcular la velocidad de despegue a nivel del mar (Presión 760 mm Hg y temperatura 20ºC)) b) Calcular la velocidad de despegue en La Paz (Bolivia) a 3600 m de altura (Presión 495 mm Hg y Temperatura 20ºC) c) Razonar que implicaciones tendría alterar la relación de aspecto de las alas o el ángulo de ataque con objeto de mantener la velocidad del apartado (a) en despegues en La Paz. Problema 8.9 Se consideran partículas de polvo esféricas de densidad ρs en presencia de un flujo de aire que se opone a la fuerza de la gravedad. Datos: Ds=5 10-5 m, ρs=2,5 103 kg/m3, ρa=1,25 kg/m3 y µa=1,875 10-5 kg/m/s. Se asume que las partículas de polvo no se ven afectadas por la presencia de otras y que el coeficiente de arrastre viene dado por la expresión: Se pide: a) La velocidad del aire para la que las partículas están suspendidas b) La velocidad de las partículas cuando la velocidad del aire es 3 m/s. Uva – Dpto. I.E.F. – Mecánica de Fluidos (Ene-2013) 3