VOLUMEN MOLAR PARCIAL

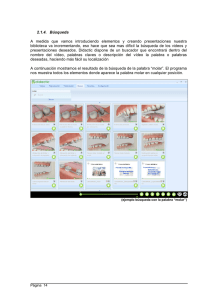
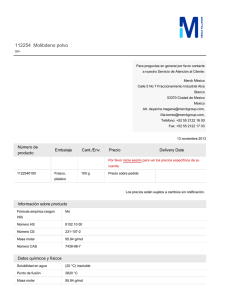
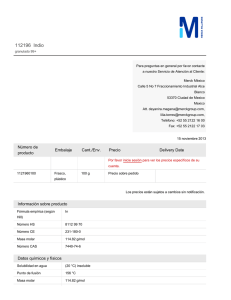
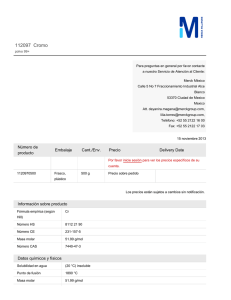
[INFORME DE LABORATORIO DE FISICOQUÍMICA] Práctica #5: Volumen molar parcial
VOLUMEN MOLAR PARCIAL
F. Vega-Piedras*, L. Torres-Hernández, A. Iniesta-Hernández, P Ávila Gómez, G. Santiago
Emeterio, A. Valdez Rivera
Laboratorio 4. Facultad de Química Unidad El Cerrillo. Campus Universitario El Cerrillo, UAEM.
Cerrillo Piedras Blancas, C.P. 50200, Toluca, Estado de México, México.

ABSTRACT
The results shown in this work were obtained with an experimental session to
determinate the molar partial volume of a two components mixture; the
measurements were taken at constant temperature and pressure (20°C and 1 atm)
working with two ideal liquids: water and ethanol it was determinate the density of a
liquid mixture only depends on the molar fraction of solute and dissolvent.

INTRODUCCIÓN
Si se mezclan dos sustancias
1 y 2 para obtener una
disolución con n1, n2,…, nr
moles de las sustancias 1 y 2 a
temperatura
y
presión
constantes y se consideran
𝑉̅1, 𝑉̅2 los volúmenes molares
de los componentes puros y a
V* como el volumen total de
los componentes (puros) no
mezclados a T y P constantes,
entonces:
𝑉 = 𝑛1 𝑉̅1 + 𝑛2 𝑉̅2 + ⋯ + 𝑛𝑖 𝑉̅𝑖
𝑟
𝑉 = ∑ 𝑛𝑖 𝑉̅𝑖
𝑖=1
Si mezclamos dos sustancias,
al fina se encuentra que el
volumen V de la disolución no
es en general igual al volumen
total de los componentes no
mezclados; 𝑉 ≠ 𝑉 ∗ . Esto se
atribuye
a
que
las
interacciones intermoleculares
Realizado: 09/10/12
Revisado: 16/10/12
en la disolución difieren en
aquellas de los componentes
puros. Una situación similar se
observa
para
otras
propiedades extensivas como
U, H, S, A y G. cada una de
estas
propiedades
termodinámicas es función de
estado de la temperatura de la
disolución,
que
puede
especificarse por las variables
T, P y 𝑛𝑖 . Por lo tanto:
𝑉 = 𝑉[𝑇, 𝑃, 𝑛𝑖 … 𝑛𝑟 ]
𝑈 = 𝑈[𝑇, 𝑃, 𝑛𝑖 … 𝑛𝑟 ]
Con ecuaciones similares para
H, S y G, etc. La diferencial
total de V, esta dado por la
siguiente ecuación:
𝜕𝑉
𝜕𝑉
𝜕𝑉
𝑑𝑉 = ( ) 𝑑𝑇 + ( ) 𝑑𝑃 + ( ) 𝑑𝑛𝑖 el
𝜕𝑇 𝑃,𝑛
𝜕𝑃 𝑇,𝑛
𝜕𝑛 𝑃,𝑇
𝑖
𝑖
subíndice 𝑛𝑖 en las dos
primeras derivadas parciales
indica que todos los números
de moles
se mantienen
[INFORME DE LABORATORIO DE FISICOQUÍMICA] Práctica #5: Volumen molar parcial
constantes; el volumen molar
parcial se puede considerar
como
el incremento del
volumen obtenido al adicionar
una mol del componente i a
una muestra infinita de la
muestra. Cuando se relaciona
este volumen molar con la
primera y segunda ley de la
termodinámica y se toma en
cuenta además el potencial
químico. Castellan 1983 «Si
suponemos que se añade una
cantidad
infinitesimal
de
cualquier sustancia a una
masa homogénea cualquiera
en
un
estado
de
tensión hidrostática, que la
masa permanece homogénea
y
su entropía y
volumen
permanecen constantes, el
incremento
de
la energía
interna de la masa dividida por
la cantidad de la sustancia
añadida es el potencial para
esa sustancia en la masa
considerada.» y además se
toman consideraciones de T y
P constantes la ecuación de V*
es :
𝑑𝑉 = 𝑉̅1 𝑑𝑛1 + 𝑉̅2 𝑑𝑛2 + ⋯ + 𝑉̅𝑟 𝑑𝑛𝑟
De modo que al integrarla
entre los límites del número de
especies resulta:
𝑉 = 𝑉̅1 𝑛1 + 𝑉̅2 𝑛2 + ⋯ + 𝑉̅𝑟 𝑛𝑟
̅ 𝑟 𝑛𝑟
∑𝑟𝑖=1 𝑉
Por lo que se sabe desde un
principio que al mezclar 1 litro
de agua con 1 litro de etanol el
volumen de la mezcla no será
2 litros, esto como ya se
Realizado: 09/10/12
explicó por las interacciones
intermoleculares agua-etanol.

SESIÓN EXPERIMENTAL
Equipos:






1 balanza analítica o digital
1 picnómetro
1 termómetro de 0 a 110 °C
1 baño María
2 buretas de 50mL.
1 matraz Erlenmeyer o vaso de
precipitados de 1L.
Reactivos:


Metanol, acetona o etanol.
Agua destilada
Procedimiento:
Se eligió entre el soluto con el que se
quería trabajar, se limpio y secó el
picnómetro y se peso. Después de
lleno este último con la cantidad
suficiente de etanol para que saliera
una pequeña gota por el capilar sin
derramarse y se peso nuevamente en
la balanza. Inmediatamente después
de lleno de agua con el mismo
principio y se pesó, obteniendo así la
masa del mismo volumen de soluto y
disolvente.
Se colocó 55mL de etanol en un vaso
de precipitados de 1L y se añadió
3mL de agua destila obteniéndose así
una disolución al 94.8% de etanol, se
lleno el picnómetro con esta mezcla y
se registro la masa de la misma. Se
repitieron estas acciones pero ahora
cambiando de 3 a 100mL de agua por
Revisado: 16/10/12
[INFORME DE LABORATORIO DE FISICOQUÍMICA] Práctica #5: Volumen molar parcial
cada titulación y registrándose el
peso del picnómetro lleno de cada
una de estas mezclas; después de 9
titulaciones se llegó a un volumen de
900mL de agua con los respectivos
pesos del picnómetro.

Resultados y Discusión
T (°C) [constante]
20
Vi (mL)
55
Tabla 1. Composición en volumen de
componentes
#mix
V total (mL)
%Vi
Vi (mL)
Vj (mL)
0
55
100
55
0.0
1
58
94.83
52.16
2.84
2
155
35.48
19.52
35.48
3
255
21.57
11.86
43.14
4
355
15.49
8.52
46.48
5
455
12.09
6.65
48.35
6
555
9.91
5.45
49.55
7
655
8.40
4.62
50.38
8
755
7.28
4.01
50.99
m pic (g)
35.9
9
855
6.43
3.54
51.46
m pic c/i (g)
75.5
10
955
5.76
3.17
51.83
m pic c/j (g)
85.7
p j (g/mL)
0.9982
p i (g/mL)
0.7937
PMj (g/mol)
18
PMi (g/mol)
46.07
Utilizando los volúmenes de los
componentes obtenidos en la Tabla 1
y con la densidad calculada (con la
masa del picnómetro vacío y lleno de
cada componente y con su capacidad
volumétrica)
se
obtienen
las
respectivas masas y fracciones
másicas de cada una de las mezclas
Tabla 2. Fracciones másicas por
componentes
Para determinar la densidad de cada
una de las mezclas se utiliza la
ecuación:
𝜌 = 𝑥𝑖 𝜌𝑖 + 𝑥𝑗 𝜌𝑗
Realizado: 09/10/12
#mix
mi (g)
mj (g)
xi
xj
0
43.65
0.0
1.0
0.0
1
41.40
2.84
0.936
0.064
2
15.49
35.42
0.304
0.696
3
9.42
43.06
0.179
0.821
4
6.76
46.40
0.127
0.873
5
5.28
48.26
0.099
0.901
6
4.33
49.46
0.080
0.920
7
3.67
50.29
0.068
0.932
8
3.18
50.90
0.059
0.941
9
2.81
51.37
0.052
0.948
10
2.51
51.74
0.046
0.954
Revisado: 16/10/12
[INFORME DE LABORATORIO DE FISICOQUÍMICA] Práctica #5: Volumen molar parcial
Posteriormente con las fracciones
másicas y con las densidades de los
componentes puros se calcularon las
densidades de cada una de las
disoluciones (Tabla 3).
Tabla 4. Número de moles de cada
componente en las disoluciones
#mix
ni (mol)
nj (mol)
0
0.948
0.00
1
0.899
0.158
2
0.336
1.968
Tabla 3. Densidades de cada disolución
#mix
xi
xj
p mix (g/mL)
3
0.204
2.392
0
1.0
0.0
0.7937
4
0.147
2.578
1
0.936
0.064
0.8068
5
0.115
2.681
2
0.304
0.696
0.9360
6
0.094
2.748
3
0.179
0.821
0.9615
7
0.080
2.794
4
0.127
0.873
0.9722
8
0.069
2.828
5
0.099
0.901
0.9780
9
0.061
2.854
6
0.080
0.920
0.9818
10
0.055
2.874
7
0.068
0.932
0.9843
8
0.059
0.941
0.9862
9
0.052
0.948
0.9876
10
0.046
0.954
0.9887
Para calcular el volumen molar
parcial es necesario conocer el
número
de
moles
de
cada
componente en cada una de las
disoluciones, para ello se empleo la
ecuación:
𝑛𝑟 =
𝑚𝑟
𝑃𝑀𝑟
Vm j (mL/mol)
18.032
Vm i (mL/mol)
58.04
Obteniéndose los resultados de la
tabla 5 para las disoluciones
preparadas.
Tabla 5. Vol. en la mezcla y por
componente
#mix
Obteniéndose
los
resultados
mostrados en la Tabla 4 para cada
una de las disoluciones preparadas.
Realizado: 09/10/12
Para el volumen molar se utilizaron
los valores de los volúmenes molares
parciales para cada uno de los
componentes en su estado puro
(Summers pp 48)
0
1
2
3
4
5
6
7
8
Revisado: 16/10/12
Vm mix
(mL)
52.11
47.31
76.38
105.61
121.05
130.41
136.66
141.13
144.48
Vm i (mL)
Vm j (mL)
55.00
52.15
19.51
11.86
8.52
6.65
5.45
4.62
4.01
0.00
2.84
35.48
43.14
46.48
48.35
49.55
50.38
50.99
[INFORME DE LABORATORIO DE FISICOQUÍMICA] Práctica #5: Volumen molar parcial
9
10
147.08
149.16
A continuación
gráficas:




3.54
3.17
se
muestran
51.46
51.83
las
Volumen molar de mezcla vs
fracción de etanol (Fig. 1).
Volumen molar de etanol vs
fracción de etanol (Fig. 2).
Volumen molar de agua vs
fracción de etanol (Fig. 3).
Fig 2. Vm i VS xi
Fig 1. Vm vs xi
Fig 3. Vm j VS xi
Realizado: 09/10/12
Revisado: 16/10/12
[INFORME DE LABORATORIO DE FISICOQUÍMICA] Práctica #5: Volumen Molar Parcial


CONCLUSIONES
Al
realizar
este
trabajo
experimental se llegó a la
conclusión de que la densidad de
una mezcla binaria de dos líquidos
ideales solo depende en sí, de la
concentración
de
soluto
y
disolvente de la mezcla. Cuando
se lleva a cabo este trabajo a
temperatura constante y presión
atmosférica, estas dos variables
no tienen influencia significativa
en la densidad de la mezcla.
i= Etanol
j= agua
Vm= volumen molar parcial
ρi = densidad del componente
xi = fracción másica de etanol
xj= fracción másica de agua
ni= moles de etanol
nj= moles de agua
Vi= volumen de etanol
Vj= volumen de agua
PMi= masa molar de etanol
PMj= masa molar de agua
Se determinó que a mayor
concentración de soluto o de
solvente la densidad de la mezcla
alcanzará prácticamente el valor
de la densidad del componente
puro que se encuentre en mayor
proporción.
Para los cálculos del volumen
molar parcial se tuvo que recurrir
al cálculo primero del número de
moles
presentes
de
cada
componente en cada una de las
disoluciones y a los valores
reportados en la bibliografía de los
volúmenes molares de cada
especie pura; para así poder
obtener el valor del volumen molar
de cada mezcla líquida.
Realizado: 09/10/12
SIMBOLOGIA
Revisado: 16/10/12
[INFORME DE LABORATORIO DE FISICOQUÍMICA] Práctica #5: Volumen Molar Parcial

AUTOR RESPONSABLE
F. Vega Piedras: Lázaro Cárdenas, #67, Colonia Centro; San Pedro Tlaltizapan.
Edo. de México Tel. 1319309, Cel. 7221136098, Correo electrónico:
paco.876@hotmailcom
*

REFERENCIAS
 Smith, Van Ness & Abbott (2005) Introducción a la termodinámica en
ingeniería química. Editorial Mc Graw-Hill, 7ª edición, México, D.F.
 Summers, Donald B., Manual de Química, Editorial Grupo Editorial
Iberoamérica, 1983.
 ANEXOS
A: Bitácora firmada.
Realizado: 09/10/12
Revisado: 16/10/12