elasticidad

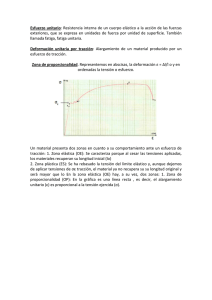
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
UNIVERSIDAD NACIONAL DE SAN CRISTÓBAL DE
HUAMANGA
DEPARTAMENTO ACADÉMICO DE MATEMÁTICA Y FÍSICA
FISICA II
Elasticidad
Kléber Janampa Quispe
[email protected]
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
I.
ELASTICIDAD
1. INTRODUCCIÓN
Los diferentes objetos como una silla, el televisor, así como edificios, puentes, etc. disponen de una estructura
que les permite proporcionar forma y protección para resistir fuerzas externas. Las estructuras están formadas
por varias piezas o elementos y cada uno de ellos contribuye, a evitar que la estructura se rompa. Por ejemplo
para diseñar adecuadamente edificios, puentes u otras construcciones, es necesario conocer profundamente como
es la relación que existe entre las acciones externas (viento, sismo, cargas fijas y móviles, etc.) y la respuesta
interna del material que constituye la estructura. Ello nos plantea caracterizar el comportamiento del material
sometido a la acción de fuerzas externas.
En el estudio de cuerpos rígidos, se definió un cuerpo rígido como un cuerpo ideal formado por un sistema de
partículas donde las distancias entre ellas permanecen invariables; en consecuencia un cuerpo rígido no sufre
deformaciones por efecto de fuerzas externas aplicadas. En la práctica todo cuerpo se deforma por efecto de una
fuerza externa, deformaciones que aun siendo muy pequeñas tienen un efecto macroscópico importante.
La capacidad de un sólido de sufrir cambios depende de su estructura molecular y de las características de los
enlaces intermoleculares.
Los sólidos pueden caracterizarse como cristalinos o amorfos. En un sólido cristalino sus átomos, moléculas o
iones están en un arreglo ordenadamente tridimensional, formando una red periódica tridimensional llamada
red cristalina. Cada átomo vibra respecto a su posición fija y no tiene libertad para moverse por la red.
Un sólido compuesto de un solo átomo o molécula (Monocristal) se caracteriza por ser anisotrópico debido a las
características de la estructura cristalina regular no presenta las mismas propiedades en todas las direcciones. En
tanto que los policristales se caracterizan por ser isotrópicos, es decir presentan las mismas propiedades en todas
las direcciones.
Los sólidos amorfos, no presentan una estructura microscópica regular, por lo que se parecen más a los líquidos,
sus átomos y moléculas se encuentran en un estado aleatorio y vibran respecto a posiciones fijas. El vidrio, el
alquitrán, los polímeros de alta masa molecular como el plexiglás son ejemplos de sólidos amorfos.
Los sólidos resisten a cambiar de volumen y forma en tanto que los líquidos resisten a cambiar de volumen pero
no de forma.
Fig. 1 Estructuras diversas
2. PROPIEDADES ELÁSTICAS DE LOS SÓLIDOS
La elasticidad, relaciona el comportamiento de los cuerpos que tienen la propiedad de recuperar su tamaño y
forma cuando cesan las fuerzas que producen dichas deformaciones. Todos los cuerpos sólidos presentan
propiedades elásticas en cierta medida. Al aplicar fuerzas externas sobre un cuerpo éste se deforma, aunque
dichas deformaciones no se observan a gran escala, las fuerzas que resisten la deformación se vuelven fuerzas
de corto alcance a nivel molecular. El comportamiento elástico del material está determinado por su estructura
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
molecular y las fuerzas intermoleculares. La distancia intermolecular de un material no sometido a fuerzas
externas depende del equilibrio entre las fuerzas moleculares de atracción y repulsión, las moléculas ocupan
posiciones que hacen mínima la energía potencial. Cuando se aplica una fuerza externa aparece tensión en el
interior del material, las distancias moleculares cambian y el material se deforma. Si las moléculas están
firmemente unidas entre sí, la deformación no será muy grande incluso con una tensión intensa. En cambio, si las
moléculas están poco unidas, una tensión relativamente pequeña causará una deformación grande.
Cuando sobre un sólido deformable actúan fuerzas exteriores y éste se deforma (al modificar la posición de las
moléculas del sólido) se produce un trabajo de estas fuerzas que se almacena en el cuerpo en forma de energía
potencial y por tanto se producirá un aumento de la energía interna. El sólido se comportará elásticamente si
este incremento de energía puede realizarse de forma reversible, de modo que cuando se deja de aplicar la
fuerza, las moléculas vuelven a su posición de equilibrio y el sistema tiende a adoptar la configuración de
mínima energía potencial y el material elástico recupera su forma original debido a las fuerzas internas que
producen el reajuste de las posiciones moleculares. Más allá del límite de elasticidad, la fuerza aplicada separa
tanto las moléculas que no pueden volver a su posición de partida, la energía no se recupera, y el material queda
permanentemente deformado o se rompe.
La deformación de un sólido puede caracterizarse en base a los siguientes conceptos:
Esfuerzo: El esfuerzo es una consecuencia de las fuerzas internas de corto alcance que se producen en un cuerpo
por la aplicación de fuerzas exteriores, por fuerzas internas se entienden fuerzas entre elementos macroscópicos
con dimensiones pequeñas en relación con aquellas típicas del sólido considerado, pero grandes en comparación
con las dimensiones típicas de los cristales. El esfuerzo es proporcional a la fuerza que produce la deformación,
y se define como la relación entre la intensidad de la fuerza externa por unidad de área de la sección transversal.
F
Fig. 2 Un cuerpo en equilibrio
Los átomos tienen una posición
donde la energía interna es mínima
F
Fig. 3 El trabajo realizado por F
aumenta la energía potencial interna
y cambia la configuración de los átomos
Deformación: medida del grado de deformación, variación relativa de la forma o dimensión de un cuerpo
sometido a esfuerzo. Depende del material que se deforma y de la naturaleza de la deformación:(estiramiento,
aplastamiento, compresión, torsión).
Módulo de elasticidad: para esfuerzos pequeños, se encuentra que el esfuerzo es proporcional a la deformación,
la constante de proporcionalidad se denomina módulo de elasticidad, que se puede expresar como:
Módulo elástico= (esfuerzo)/(deformación)
Coeficiente de elasticidad: Si el esfuerzo es lo suficientemente pequeño la deformación es proporcional al
esfuerzo, denominándose la constante de proporcionalidad coeficiente de elasticidad.
El coeficiente de elasticidad nos cuantifica la facilidad que tiene un objeto para deformarse y el módulo de
elasticidad la resistencia que opone al ser deformado. Un material es, por tanto, más elástico cuando menor sea
su módulo de elasticidad.
En los sólidos reales los coeficientes de elasticidad pueden depender también de la dirección en que es aplicado
el esfuerzo, no son por tanto, isótropos en lo que a propiedades elásticas se refiere. Sin embargo, en este tema se
considerarán sólo sólidos isótropos.
2.1 ELASTICIDAD DE LONGITUD: TENSIÓN
La elasticidad de longitud mide la resistencia del sólido al cambio de longitud.
Consideremos una barra que está sometida a dos fuerzas opuestas que actúan perpendicularmente a las caras del
sólido como ilustra la figura 4 y tienden a estirarlo (tracción) o a comprimirlo (contracción). Las fuerzas
aplicadas pasan por el centroide de la sección considerada (fuerzas axiales). En cada caso las fuerzas internas de
nivel molecular se resisten a la deformación longitudinal de tracción o contracción. Si evaluamos la distribución
de fuerzas internas en una porción de la barra, las fuerzas internas se hallan uniformemente distribuidas sobre la
sección transversal, la resultante de las fuerzas aplicadas pasa por el centroide de la sección considerada. Puesto
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
que cada porción está en equilibrio, la resultante de las fuerzas que actúan en direcciones contrarios deben tener
igual valor F, a dicha fuerza resultante interna se denomina tensión.
l
l
F
F
F
F
F
F
F
F
Fig. 4. a Barra sometida a tensión de tracción
l
l
F
F
F
F
F
F
F
F
Fig. 4.b Barra sujeta a tensión de compresión
En la porción de la barra sometida a tensión uniaxial, definimos el esfuerzo de tensión sobre la sección
transversal como:

F
F
A
l
l+ l
Fig. 5. Distribución de esfuerzos de tensión
donde σ es el esfuerzo unitario (N/m2), F es la fuerza aplicada (N) y A es el área sobre la cual actúa la fuerza
(m2).
El cambio de longitud que sufre la barra bajo esfuerzo de tensión uniaxial, se conoce como deformación
longitudinal  l. La deformación unitaria se define como el cambio en la longitud por unidad de longitud, esta
magnitud es adimensional (no tiene unidades):

l
l
El módulo de elasticidad de longitud, que relaciona el esfuerzo y la deformación unitaria se define como:

Y

Y
F
l
A
l
El módulo de elasticidad de longitud Y mide la resistencia del sólido al cambio de longitud, es decir es una
medida de la rigidez del material de cuan deformable sea; entre mayor sea el valor de Y, mayor es la rigidez del
material. Este valor fue calculado a principios del siglo XIV por Thomas Young; por lo que se le llama módulo
de Young. El módulo de Young de un material cualquiera puede cambiar con la temperatura.
Esta ley es válida para la tracción y la contracción. Hay materiales para los que el módulo de Young para un
esfuerzo de tracción es diferente al de contracción, por ejemplo el cemento.
El cemento MDF (Macro-Defect Free) tiene una resistencia a la compresión 300 MPa, se encuentra que la
resistencia a la tracción es muy baja, aproximadamente se encuentra entre 5% a 15% de la resistencia de
comprensión. Un porcentaje óptimo puede considerarse en el orden del 10%. La deformación también se
encuentra en el mismo rango correspondiente a la resistencia a la tracción.
Cuando se somete un sólido a un esfuerzo de tensión no sólo cambia longitudinalmente sino también se modifica
las otras direcciones, se observa que su sección transversal disminuye en tracción y aumenta en el caso de
contracción.
Experimentalmente, se observa que la deformación transversal es proporcional a la deformación longitudinal,
cumpliendo,
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
a h
l

 u
a
h
l
a
F
h
L
Fig. 6 Deformación lateral
El signo menos de la ecuación anterior refleja que cuando la sección longitudinal aumenta, las otras dimensiones
disminuyen. La constante u se denomina coeficiente de Poisson y es un parámetro adimensional. Aunque se le
denomina coeficiente por razones históricas hay que tener presente que no es un coeficiente de elasticidad en el
sentido habitual. En la mayoría de metales el coeficiente de Poisson está comprendido entre 0.25 y 0.45,
pudiendo utilizarse como regla práctica u ≈1/3 para metales. En un sólido isótropo, sólo hay dos constantes
elásticas independientes, de modo que las constantes elásticas se pueden expresar en función del módulo de
Young y del coeficiente de Poisson.
CURVA ESFUERZO DE TENSIÓN Y DEFORMACIÓN UNITARIA
Experimentalmente se realizan ensayos de tensión, donde la muestra se somete a un esfuerzo de tracción axial a
lo largo de su eje longitudinal. La figura 7 muestra la curva a típica del esfuerzo de tensión con respecto a la
deformación unitaria, ésta curva permite evaluar varias propiedades mecánicas de los materiales, característica
inherente del material que permite diferenciar uno de otro bajo fuerzas externas.
En la figura 7 se distinguen claramente dos tipos de comportamiento:
b
c
d
λ
λo
Fig. 7 Relación entre esfuerzo y deformación.
Deformación Elástico: Ocurre hasta que el esfuerzo aplicado alcance un valor en (c) de la Fig. 7, llamado límite
de elasticidad. En esta zona, si el material es sometido a esfuerzo, al suprimir el mismo, éste retoma su forma
original sin sufrir deformación permanente. Al principio del estiramiento, para esfuerzos suficientemente
pequeños, la deformación es proporcional al esfuerzo, es en esta zona que es válida la Ley de Hooke. Esta zona
de proporcionalidad elástica ocurre hasta que el esfuerzo aplicado alcanza un valor llamado “límite de
proporcionalidad” (punto b). Más allá del límite de proporcionalidad, la gráfica se desvía de la recta y no existe
una relación sencilla entre el esfuerzo y deformación. Sin embargo la deformación es reversible y cuando cesa el
esfuerzo el material recupera su estado original.
Deformación plástica o flujo plástico: Si la muestra se somete más allá del límite elástico (Fig. 7), entra la zona
plástica en donde si quitamos el esfuerzo aplicado el material no vuelve a su estado original y queda
permanentemente deformado, esto es el material presenta efectos de histéresis (líneas punteadas donde muestra
una deformación permanente λo cuando cesa el esfuerzo aplicado). Si el esfuerzo continúa incrementándose, el
punto final de esta zona es en el que se produce la fractura o ruptura del material, por ello se le denomina punto
de fractura (d). El esfuerzo necesario para causar la fractura recibe el nombre de esfuerzo de ruptura, o
resistencia límite. Entre el límite elástico y el punto de ruptura, a menudo existe una zona de fluencia, donde el
material se deforma fácilmente, sin necesidad de aumentar el esfuerzo (región plana de la curva). Dependiendo
del tipo de material, esta región de fluencia puede o no existir, si esta región es pequeña o inexistente, el material
es frágil, si esta región es amplia, el material es dúctil.
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
σm
E
s
f
u
e
r
z
o
d
Deformación
Fig. 8 Procesos, hasta la ruptura de la muestra
Es de vital importancia para los ingenieros que el diseño de estructuras por ejemplo, se
realice dentro de la zona elástica lineal o proporcional, para evitar que las estructuras
fallen.
Fig. 9. Curvas esfuerzos- deformación a la tensión, para distintos materiales. Los gráficos son cualitativos.
Tabla 1. Valores comunes para módulos elásticos
Sustancia
Módulo de Young
(N/m2)
Módulo de corte
(N/m2)
Módulo
volumétrico (N/m2)
Aluminio
7.0 x 1010
2.5 x 1010
7.0 x 1010
Latón
9.1 x 1010
3.5 x 1010
6.1 x 1010
Cobre
11 x 1010
4.2 x 1010
14 x 1010
Acero
20 x 1010
8.4 x 1010
16 x 1010
Tungsteno
35 x 1010
14 x 1010
20 x 1010
Vidrio
6.5 –7.8 x 1010
2.6 – 3.2 x 1010
5.0 – 5.5 x 1010
Cuarzo
5.6 x 1010
2.6 x 1010
2.7 x 1010
Agua
0.21 x 1010
Mercurio
2.8 x 1010
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
Tabla 2. Resistencia a la tensión de varios sólidos
Material
Alambre de acero para piano
Acero
Resistencia a la tensión
(MN/m2)
3000
400 – 1500
Hierro colado
70 – 250
Aluminio puro
70
Aleaciones de aluminio
Cobre
Aleaciones de titanio
Vidrio
140 – 550
140
700 – 1400
30 – 170
Seda de araña
250
Tendón humano
100
Licuación de los suelos por un sismo
Básicamente afecta a suelos como arenas de baja compacidad o arcillas débiles en presencia de agua
(saturadas o sumergidas); ocurre cuando la presión del fluido contenido en los espacios intergranulares
aumenta repentinamente como consecuencia de la presión inducida por el paso de ondas sísmicas,
haciendo que el contacto entre los granos disminuya a tal grado que el cuerpo llega a comportarse, por
unos instantes, como un líquido denso. Lo anterior ocasiona deslizamientos en laderas o que los
edificios pierdan la verticalidad en mayor o menor grado aunque sin sufrir, en muchos casos, daño
considerable en su estructura.
Es este caso, el suelo pierde toda su resistencia a corte y se comporta como un líquido. Los rellenos
aún compactados son materiales muy susceptibles a licuación.
Teoría del rebote elástico en un sismo.
En la corteza de la Tierra se acumula energía, gracias a procesos de deformación elástica. La figura 10 ilustra el
proceso de liberación de esa energía, muestra cómo se produce la ruptura de una capa de rocas, después de
superar el límite elástico. Allí resulta un conjunto de bloques desplazados a lo largo de las líneas de ruptura. La
corteza terrestre está prácticamente, siempre y en todas partes, sometida a algún tipo de tensión. Las mayores
concentraciones de tensiones se producen a lo largo de los límites entre las placas corticales, e incluso en su
interior donde pueden producirse acumulaciones de tensiones que superen la competencia elástica de las rocas.
La ruptura de las rocas debajo de los volcanes se produce debida a los movimientos de ascenso de magma y a la
liberación explosiva de gases volcánicos. Siendo esto así, en todo momento existen en el mundo diversos
sectores, grandes o pequeños, en que los esfuerzos elásticos acumulados en la corteza terrestre hacen que las
rocas que allí se encuentran estén muy próximas a su punto de rotura probable.
En estas circunstancias, basta un pequeño esfuerzo adicional para desencadenar un terremoto, comprendiéndose,
por tanto, que los cambios causados por la tensión consecuente de un gran terremoto pueden provocar una
reacción en cadena que se traducirá en una serie de sacudidas grandes o pequeñas.
También es factible que las pequeñas alteraciones en el campo de esfuerzos de la corteza, generadas por el paso
de depresiones ciclónicas profundas o por los ciclos de mareas terrestres, puedan desencadenar auténticas
sacudidas.
Fig. 10. Teoría del rebote elástico: 1. deformación elástica, 2. fisuras de tensión, 3. fisuras de tensión y
compresión, 4. fallamiento y liberación de la energía de deformación por ruptura
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
Concreto
La gráfica esfuerzo deformación del concreto (fig.11) nos muestra que el concreto posee una mayor capacidad
para resistir esfuerzos de compresión que para soportar esfuerzos de tracción. Debido a este comportamiento, el
concreto se emplea dentro de las estructuras para resistir esfuerzos de compresión y la parte de los esfuerzos de
tensión o tracción es absorbida por el acero de refuerzo con que van armadas las estructuras. La resistencia a
tracción del concreto se encuentra entre 5 a 15% de la resistencia a compresión, tomándose como porcentaje
óptimo el 10%.
El concreto presenta un comportamiento frágil bajo esfuerzos de tracción y de corte. Por esta razón, el esfuerzo
de tensión que pueda soportar es casi siempre despreciable en el diseño de estructuras.
Resistencia a la compresión = 20x106 N/m2
Fig. 11. Gráfica Esfuerzo - Deformación del Concreto Simple
La curva característica de esfuerzo-deformación del acero permite visualizar la manera en que se comporta el
material ante esfuerzos de tensión (figura 12).
Fig.12. Gráfica característica esfuerzo – deformación del acero. Cabe decir que, para las diferentes clases de
aceros, esta curva varía en función de la cantidad de carbón que poseen las barras
Ley de HOOKE
Podemos expresar la ley de Hooke a partir de la expresión del módulo de Young. Para esfuerzos pequeños hay
una proporcionalidad entre el esfuerzo de tensión y la deformación unitaria:
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
  Y
F
l
Y
A
l
 YA 
F    l
 l 
La cantidad de estiramiento o de compresión (cambio de longitud), es directamente proporcional a la fuerza
aplicada.
El trabajo realizado en la deformación de un cuerpo se acumula en forma de energía elástica interna en el cuerpo.
Para aumentar la longitud un una barra de longitud inicial l en un diferencial d(∆l), se realiza un diferencial de
trabajo dW, dado por:
dW  F d (l )
YA
W   ( l )d (l )
l
1 YA
W
( l ) 2
2 l
1
l
W  Y ( Al )( ) 2
2
l
1
W  YV  2  U
2
U 1 2
 Y
V
2
a
F
h
l
l
La última expresión, determina la energía potencial acumulada por unidad de volumen.
Ejemplo
Se tiene un muro sometido a una carga de 150 kN por metro de longitud y soportado por una cimentación de
concreto la cual a la vez se apoya sobre el suelo. Calcular los esfuerzos actuantes en el muro, la cimentación y el
suelo y compararlos con los esfuerzos máximos (admisibles) del muro, concreto y suelo respectivamente son:
,
,:
150 kN
150 kN=F
muro
30cm
concreto
50cm
F
Solución
Muro
suelo
F
concreto
que es menor que el
esfuerzo máximo de 3.92 M Pa, por tanto el muro es seguro.
Concreto
que es menor que el
esfuerzo máximo de 4.83 M Pa, por tanto el concreto es seguro
F
F
suelo
Luego es esfuerzo en el concreto es igual a la del suelo, pues el área de contacto es el mismo y la acción de
fuerza igual. El esfuerzo en el suelo es 0.3 MPa menor que el máximo 0.38 MPa.
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
2.2 ELASTICIDAD DE LA FORMA: MÓDULO DE CORTE
Los esfuerzos de tensión están relacionados con esfuerzos normales porque las fuerzas actúan
perpendicularmente a la superficie. Ahora evaluaremos los esfuerzos generados por fuerzas aplicadas en
dirección tangencial a la caras sobre las que actúan, cuando se aplica fuerzas transversales a una barra o pieza,
esta experimenta fuerzas internas en el plano de la sección cuya resultante es F. Estas fuerzas internas son
llamadas fuerzas cortantes. Las fuerzas distribuidas tangencialmente se denominan esfuerzos tangenciales,
esfuerzos de corte o de cizalladura. El sólido reacciona inclinándose, de modo que el volumen del cuerpo
permanece constante y la deformación correspondiente se denomina de deslizamiento.
La fig. 13 muestra, que cuando se aplica una fuerza tangencial F a la cara superior del bloque éste se desliza,
inclinándose la cara vertical un ángulo θ, mientras que la otra cara horizontal se mantiene fija. El deslizamiento
del bloque lo podemos explicar asumiendo que está constituido por sucesivas placas planas o láminas (fig. 13),
de modo que cuando se aplica la fuerza tangencial en la cara superior, éste desliza a la placa inferior y así
sucesivamente entre las otras placas.
F
Δx
y
F
F
θ
F
A
A
F
(a)
(b)
(c)
Fig. 13 (a) Fuerza tangencial sobre un bloque (b) Deslizamiento de las placas que constituyen el bloque (c)
distribución uniforme de fuerzas internas en una lámina interna del bloque
El deslizamiento entre las placas se da debido a las fuerzas internas de fricción entre placas, estas fuerzas
internas dan lugar al esfuerzo cortante o de cizalladura. La placa en contacto con la superficie permanece en
reposo, y como el bloque permanece deformado en equilibrio la fuerza de la superficie de apoyo sobre ella es de
igual valor y dirección contraria a F.
Para una distribución uniforme de las fuerzas internas se define el esfuerzo de corte o de cizalladura como:
s 
F
A
Donde F es la resultante tangencial de las fuerzas internas que actúan sobre la superficie de área A.
La deformación de corte o cizalladura o deformación angular, se define como la tangente del ángulo de
deformación
s  tan 
s 
x
y
Para ángulos θ muy pequeños se puede aproximar a:
s  tan   
s  
La relación entre el esfuerzo de corte σs y su deformación λs se llama módulo de elasticidad de corte G:
G
G
s
s
F

A
Fig. 14 Relación entre el esfuerzo de corte y de tensión
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
El módulo de corte (también llamado Coeficiente de rigidez) mide la resistencia al movimiento de los planos de
un sólido a deslizar uno sobre otro, mide la resistencia del sólido a deformarse.
Consideramos un bloque cúbico (fig. 15) sometido a esfuerzo de corte, que se distribuye de la siguiente forma
F
n
n σ
σ
F
F
m
D/2
p
p
m
σ
σ
q
F
(a)
(b)
q
(c)
Fig. 15. Bloque cúbico sometido a esfuerzo de corte
Una deformación por cizalladura se pude considerar que es una combinación de:
 Esfuerzo de tracción
 Contracción lateral
Es decir en una deformación de corte se puede considerar que se aplican simultáneamente fuerzas de tracción en
un par de caras opuestas y fuerzas de compresión en otro par.
Consideremos un cubo sometido a esfuerzo de corte Fig. 15a, en ella evaluamos el cubo mnpq Fig.15.b, que bajo
la acción del esfuerzo de corte se desliza, dicho efecto se considera como el resultado de esfuerzos de tracción y
comprensión como ilustra la Fig. 15c.
Ahora determinemos la deformación longitudinal por tracción del cubo de lado mn igual a l = D/2
1 
l1 

D
Y
2
Por efecto de la compresión el lado np tiene una deformación unitaria λ

l


D
Y
2
La compresión estira más el lado mn, la que se deduce mediante:
2 
l2
 u
D
2
2  u

Y
La deformación unitaria total del lado nm resulta
l1 l2 


 u
D
D
Y
Y
2
2
l  (1  u )

D
Y
2
1  2 
La deformación unitaria, para una longitud D resulta:
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
D 2l

D
D
D l  (1  u )


D
D
Y
2
D  (1  u )

D
Y
ΔD
F
Δx
Q
45º
D
l
La deformación de corte del bloque cúbico resulta:
θ
s  tan 
F
x
s 
y
Fig. 16. Desplazamiento ∆x
Para desplazamientos muy pequeños, el ángulo en Q de la Fig. 16 tiende a ser perpendicular a la prolongación
del diámetro D, por lo que resulta:
x  2 D
y
D
2
D
D
 (1  u )
s  2
Y
s  2
Luego, el módulo de corte o de cizalladura, al igual que el módulo de compresibilidad, se puede expresar en
función del módulo de Young y del coeficiente de Poison:
G
s


s 2 (1  u )
G
Y
Y
2(1  u )
De los valores del coeficiente de Poisson se deduce que el valor del módulo de cizalladura suele estar
comprendido entre Y/3 e Y/2.
Esfuerzo cortante doble:
En este caso, el corte, en la barra central se resiste a través de 2 áreas
De manera que:
Ejemplo:
Calcular los esfuerzos normales en las barras AB y CB y los esfuerzos cortantes en los pasadores en A y C, cuyo
diámetro es de 1.2 cm. La sección transversal de las barras es de 8cm2.
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
2m
TCB
TAB
TAB
TAB
37º
B
B
A
9KN
TCB
B
TCB
Desarrollo
Del DCL:
9KN
C
Esfuerzos normales de tensión en los alambres
, compresión
En cada barra
⁄
, tracción
Esfuerzos de corte en los pasadores, el área de los pasadores
En A hay esfuerzo de cortante doble
En C esfuerzo contante simple
2.3 MÓDULO VOLUMÉTRICO. ELASTICIDAD DE VOLUMEN:
El módulo volumétrico caracteriza la respuesta de un cuerpo a una fuerza uniforme aplicada perpendicularmente
sobre toda su superficie.
Si consideramos un sólido de forma cúbica (Fig. 17), al cual se aplican fuerzas uniformes en todas sus caras; este
es el caso, por ejemplo, cuando sumergimos un sólido en un recipiente lleno de un líquido; el esfuerzo de
volumen, llamado en este caso presión, se define como:
p 
F
A
La deformación de relativa del volumen del cuerpo, es:
V
V
El Módulo volumétrico β, que mide la resistencia que sólidos o líquidos presentan a los cambios de volumen, se
define como:
p
V
V
F
  A
V
V
 
F
Fig. 17. Esfuerzo volumétrico
A
El signo menos garantiza que β sea positivo, en razón que ΔV es menor que cero puesto que el cubo se
comprime. Al recíproco del módulo volumétrico se denomina módulo de comprensibilidad del material.
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
Para el sólido cúbico, se demuestra la siguiente relación que vincula el módulo de Young y el coeficiente de
Poisson

Y
3(1  2u )
En el cubo de la Fig. 18, se muestra el cambio de volumen cuando es sometido a esfuerzo de volumen
Las variaciones de sus lados serán respectivamente a , l y h
l
Determinemos el cambio de volumen del cubo:
El volumen inicial es:
a
V  lha
El volumen final
a  a h  h l  l
)(
)(
)
a
h
l
h
a
h
l
V ´ V (1  )(1  )(1  )
a
h
l
a h a h l a l h l a h l
V ´ V (1 


 


)
a
h
a h
l
a l
h l
a h l
V ´ lha(
Fig. 18. Cambio de volumen del cubo sujeto a presión
La variación de volumen resulta:
V  V ´V
V a h l a h a l h l a h l


 



V
a
h
l
a h
a l
h l
a h l
V a h l



V
a
h
l
Ahora determinemos la variación longitudinal de un lado del cubo, el lado de longitud l; para ello
consideraremos la variación de la longitud de l es el efecto de la compresión directa l1 más el efecto de
alargamiento por la comprensión de los lados a y h que denominaremos l2 y l3 respectivamente
l
De modo que
∆l1
l  l1  l2  l3
Calculemos
l1 por la comprensión del lado l
(l1 )
F
Y
A
l
l1
F

l
YA
F
A
Fig. 19. Deformación longitudinal en l
La variación del lado h por comprensión es
F
(h2 )
F
Y
A
h
∆l2
A
Comprensión que genera el alargamiento del dado por
l2
h
 u 2
l
h
Resultando
∆h2
h
l2
F
u
l
YA
Fig. 20. Deformación longitudinal en h
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
De igual manera para el lado a, la comprensión de a genera un alargamiento de l dado por
l3
F
u
l
YA
De modo que la variación longitudinal total de l es:
l l1 l2 l3



l
l
l
l
l
F
F
F

u
u
l
YA
YA
YA
l
F
  (1  2 )
l
YA
Por simetría para un cuerpo homogéneo la variación longitudinal de los lados h y a son respectivamente
h
F
  (1  2u )
h
YA
a
F
  (1  2u )
a
YA
De donde podemos obtener: el cambio de volumen total
V a h l



V
a
h
l
V
F
  3(1  2u )
V
YA
Reemplazando en la expresión del módulo volumétrico obtenemos la relación con el coeficiente de Poisson
 
F
V
A

V
F
A
F
3(1  2u )
YA

Y
3(1  2u )
Relación que es válida para un sólido isotrópico de forma cualquiera ya que siempre podemos considerar que
todo sólido está formado por cubos infinitesimales. De la última expresión, podemos deducir que el coeficiente
de Poisson debe ser menor que 1/2 para que β sea positivo.
Incidentalmente, si u tiende a 0.5, β tiende al infinito, o sea el material sería incompresible.
3. FLEXIÓN
Los cuerpos pueden experimentar esfuerzos de tensión y compresión al mismo tiempo, así tenemos por ejemplo,
una viga horizontal apoyada en sus extremos, este se flexiona por su propio peso (pandea). Encontramos, que la
parte superior de la viga disminuye de longitud en consecuencia está sujeto a compresión y la parte inferior
aumenta de longitud y está en tracción. Para minimizar el esfuerzo y por consiguiente la deformación por
flexión, las partes superior e inferior, de la viga deben tener una sección transversal grande. Los esfuerzos
máximos de compresión o tracción se encuentran en los extremos de la viga (Fig. 21) y van disminuyendo
conforme se acercan a la línea central (zona neutra) de la viga, zona que no está sujeta ni a compresión ni
tracción, así que esta parte puede tener una sección pequeña; esto ayuda a minimizar el peso de la viga y reducir
el esfuerzo. Es decir si se quiere una barra que se flexione poco para un esfuerzo dado, será preciso disponer la
materia de manera que esté lo más alejada posible del hilo neutro. De ahí la forma de doble T de las secciones de
las vigas y la forma que se les da a los carriles de ferrocarril.
F
θ
r
Compresión
θ
dF
y
L
Tracción
Fig. 21. Viga sujeta a flexión y zona neutra
∆L
Fig. 22 Porción de una viga sujeta a flexión
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
En la Fig. 22 se muestra una porción de una viga flexionada. La longitud no deformada de un sección de la viga
a una distancia y de la zona neutra es L=r θ, la longitud sujeta a compresión será
Como
, luego
De modo que el esfuerzo de compresión resulta:
L dF

L
dA
r  (r  y ) dF
Y

r
dA
y dF
Y

r dA
y2
Y
dA  ydF
r
YI
M
r
Y
Fig. 23. Viga sujeta a flexión. Esfuerzos de compresión y tracción debidos al
momento flector M que surge.
4. TORSIÓN
Consideremos una barra sujeta rígidamente en un extremo y sometida en el otro a una cupla aplicado en un plano
perpendicular el eje, como se muestra en la figura, se dice que la barra está sometida a torsión simple.
Una torsión simple se presenta muy pocas veces, en general aparece la torsión combinada con flexión y corte.
Sin embargo, aplicando el principio de superposición de efectos, a partir de la torsión simple se puede llegarse a
otros casos de torsión compuesta.
Para una torsión simple consideraremos que las secciones normales al eje de la barra permanecen planas y
paralelas a sí misma luego de la deformación por torsión y las secciones transversales mantienen su forma.
Como consecuencia, resulta que las secciones tienen rotaciones relativas, de modo que las rectas trazadas sobre
ellas continúan siendo rectas y los ángulos mantienen su medida. Por otro lado, las generatrices rectilíneas de la
superficie lateral del cilindro se transforman en hélices. En estas condiciones determinaremos qué tipo de
esfuerzos genera la torsión simple y cuál es su distribución.
La presencia de esfuerzos normales σ a la sección transversal de la barra, en caso de tener una distribución
uniforme haría que exista una deformación resultante longitudinal lo cual no se muestra en una torsión simple;
por lo que la distribución del esfuerzo no debería ser uniforme, sin embargo ello generaría deformaciones
especificas longitudinales variables de punto a punto, y la sección trasversal de la barra no continuaría siendo
normal al eje y no se mantendría plana. En consecuencia en una torsión sólo debe haber esfuerzos tangenciales.
Si tomamos un elemento diferencial, el esfuerzo tangencial a la sección deberá ser tangente a la circunferencia,
ya que de no ser así existirá una componente de radial que originaría variaciones del tamaño del área de la
sección.
En resumen en una torsión simple: sólo existen tensiones tangenciales, la distribución a lo largo de un diámetro
es antimétrica y su dirección es normal al radio
A continuación trataremos de establecer la ley de distribución de las tensiones. Para ello consideramos que
aislamos un tubo de espesar ∆r torsionada y de ella tomamos un paralelepípedo de longitud ∆L (Fig. 25). El
ángulo que giran será θ, a este ángulo la denominaremos “ángulo específico de torsión”.
σs
γ
θ
R
R
L
Fig. 24 Torsión de una barra y distribución de esfuerzo de corte
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
Δr
Δs
γ
r
θ
Δl
Δs
γ
ΔL
Fig. 25. Evaluación del esfuerzo de corte en una porción cúbica de la barra
Así tenemos geométricamente:
L  s  r
L  r
∆A= ∆l∆r
El esfuerzo de corte que desplaza un ∆s es
F

G
r
A
L
F  G

L
Fr  G
M  G
r A

L

L
r 2 A
dM  G

L
r 2 dA

 dM  G L  r dA
M G
r 2 A

L
2
I
Reemplazando en esta última expresión el esfuerzo de corte:
El esfuerzo cortante máximo debe ser igual a:
Por ejemplo, para una barra circular maciza:
entonces
LA PLASTICIDAD MODELA PAISAJES
Flujo “plástico” de tierras
El hielo fluye plásticamente en los glaciares.
La corteza, el manto y hasta el núcleo sólido de la tierra están en un continuo proceso de deformación plástica
Las arrugas plásticas de la corteza terrestre crean las grandes cordilleras, como el Himalaya.
Internamente, las rocas y minerales muestran también signos microscópicos de las deformaciones plásticas
La plasticidad está casi siempre presente en la rotura, incluso, localmente, en las roturas frágiles.
MATERIALES DÚCTILES Y FRÁGILES
Los materiales como el acero dulce, que alcanzan una gran deformación antes de alcanzar la rotura, se denominan
“dúctiles” y los materiales como el acero duro donde la rotura se produce sin grandes deformaciones se denominan
“frágiles”.
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
ELASTICIDAD: NOTAS BASICAS
 Plasticidad: El cambio de disposición de los átomos en el mismo elimina la energía elástica y por ello
conserva la deformación. Plasticidad, capacidad de cambiar de forma y conservarlo.
 El límite elástico depende de las impurezas, por ejemplo el aluminio monocristal tiene un límite elástico de
40N/cm2 y =10-5, el aluminio comercial tiene 10000N/cm2
 Endurecimiento. Si se somete a deformación plástica el límite de elasticidad se eleva. Ejemplo. El
monocristal zinc tiene un límite elástico menor que luego de doblar fácilmente con los dedos se hace difícil
enderezar puesto que su límite elástico aumenta. La propiedad del metal al elaborarlo en frío implica
endurecimiento por deformación plástica.
 El vidrio no es capaz de deformarse plásticamente.
 Fluencia. Bajo una tensión igual al límite de fluencia, el cuerpo aumentará indefinidamente la deformación
fluirá como un líquido.
 Un metal en que se produce muy poca deformación plástica antes de su ruptura se denomina frágil.
 Si se deforma un objeto, los esfuerzos pueden ser altos al principio, pero decaen lentamente con el tiempo.
Además si van a esfuerzos altos, no hasta el punto de ruptura, cuando baja la deformación el esfuerzo
retornará siguiendo una curva diferente llamado Histéresis. La histéresis es una indicación de que parte del
trabajo mecánico se pierde durante el ciclo de estiramiento y contracción.
 Cuando se consideran ciertos materiales, como por ejemplo el cobre, donde la curva de tensión-deformación
no tiene ningún tramo lineal, aparece una dificultad ya que no puede usarse la expresión anterior. Para ese
tipo de materiales no lineales pueden definirse magnitudes asimilables al módulo de Young de los materiales
lineales, ya que la tensión de estiramiento y la deformación obtenida no son directamente proporcionales.
 La tiza: presenta mayor resistencia al esfuerzo de corte que al de tensión.
 Concreto: Esfuerzo o resistencia a la tensión = 2x106 N/m2
Resistencia a la compresión = 20x106 N/m2
Resistencia al corte = 2x106 N/m2
 En general el concreto es quebradizo cuando se moldea en secciones delgadas
 Losas pre-esforzadas: El concreto se refuerza aún más pre esforzándolo con varillas de acero bajo tensión.
 CONCRETO: Los esfuerzos generados en los pavimentos de concreto tienen diferentes orígenes. Algunos se
deben a las características mismas del concreto y se presentan como consecuencia de las reacciones del
cemento con el agua y se conocen como esfuerzos de retracción por secado, otros esfuerzos que se presentan
en las losas se deben a las cargas a que se ven sometidas durante la vida útil, otro tipo de esfuerzos son los
que se presentan por los cambios térmicos y de humedad en las losas.
 El acero es un ejemplo de normalidad: su módulo de Young es el mismo en tracción que en compresión, y las
resistencias a la tracción y a la compresión también son iguales.
 El hormigón, sin embargo, aunque tiene el mismo módulo de Young en ambos casos, presenta una resistencia
a la tracción de 2 MN/m2, pero tiene una resistencia a la compresión de 17 MN/m2.
 Y el hueso humano tiene un módulo de Young de 16 GN/m2 en tracción, que baja a 9 GN/m2 en compresión,
con una resistencia en tracción de 200 MN/m2 y de 270 MN/m2 en compresión.
 Esfuerzos debido al alabeo: Durante el día cuando la temperatura en la parte superior de la losa es más alta
que en la inferior, la superficie superior tiende a expandirse con respecto al eje neutro mientras que la inferior
tiende a contraerse. Sin embargo, el peso de la losa restringe tanto la expansión como la contracción;
entonces, se inducen esfuerzos de compresión en la parte superior y de tracción en la inferior. En la noche
cuando la temperatura en la parte superior de la losa es más baja que la de la inferior y así se inducen
esfuerzos de tensión en la parte superior y de compresión en la inferior.
 Fatiga: la fatiga de materiales se refiere a un fenómeno por el cual la rotura de los materiales bajo cargas
dinámicas cíclicas (fuerzas repetidas aplicadas sobre el material) se produce ante cargas inferiores a las
cargas estáticas que producirían la rotura. Un ejemplo de ello se tiene en un alambre: flexionándolo
repetidamente se rompe con facilidad, pero la fuerza que hay que hacer para romperlo en una sola flexión es
muy grande. La fatiga es una forma de rotura que ocurre en estructuras sometidas a tensiones dinámicas y
fluctuantes (puentes, automóviles, aviones, etc.). Su principal peligro es que puede ocurrir a una tensión
menor que la resistencia a tracción o el límite elástico para una carga estática, y aparecer sin previo aviso,
causando roturas catastróficas. Es un fenómeno muy importante, ya que es la primera causa de rotura de los
materiales metálicos (aproximadamente el 90%), aunque también está presente en polímeros (plásticos,
composites,...), y en cerámicas.
 RESISTENCIA (oposición a la rotura) y RIGIDEZ (oposición a las deformaciones)
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
Pregunta:




Compare la resistencia a la flexión de una barra de sección transversal cuadrada, circular y triangular
equilátero, considerando que tienen el mismo valor de área.
¿Cómo es más fácil romper un espagueti que está crudo: estirándolo o doblándolo? ¿Por qué?
¿Podrías romper un alambre estirándolo? ¿Y retorciéndolo? ¿Por qué?
En muchas construcciones se usan elementos que tienen una gran anchura y longitud y poco grosor, a estos
se les llama láminas. Consiguen ser resistentes debido a la forma que puedan tomar. Se usan para cubiertas
de edificios, las carrocerías de los coches, depósitos de fluidos. Algunas veces las láminas se refuerzan con
unos nervios o costillas. Explíquelos.
EJERCICIOS RESUELTOS
1. Una barra de cobre de 90cm de longitud y sección transversal 3.2cm2 está unida, extremo con extremo a una
barra de acero de longitud L y sección 6.4cm2. La barra compuesta es sometida a sus extremos a tensiones
iguales y opuestas de 30000N (a) calcular la longitud L de la barra de acero si son iguales los alargamiento de
ambas barras (b) ¿cuál es el esfuerzo en cada barra? (c) y ¿la deformación específica?
F
F
Lcu=90cm
Solución
Lac= L
F
F
ΔLcu
Lcu=90cm
(a) La deformación de cada material es:
Y
F
A
L
L
 L 
Lcu 
F
Lcu
Ycu Acu
Lac 
F
Lac
Yac Aac
Igualando
F
L
YA
Lac= L
ΔLac
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
Lcu  Lac
F
F
Lcu 
Lac
Ycu Acu
Yac Aac
Lac 
Yac Aac
Lcu
Ycu Acu
20.6 x1010 Nm 2 x6.4cm 2
Lac 
90cm
8.2 x1010 Nm 2 x3.2cm 2
Lac  452.2cm
(b) el esfuerzo en cada barra
 ac 
F
Aac
30000 N
 4.69 x107 Nm 2
4
2
6.4 x10 m
F

Acu
 ac 
 cu
 ac 
30000 N
 2.34 x107 Nm 2
4
2
3.2 x10 m
(c) la deformación específica
Lcu 
F
Lcu
Ycu Acu
Lcu 
30000 N
90cm  0.102cm
8.2 x10 Nm2 x3.2 x104 m 2
10
2. Suponga que para generar un agujero en la placa de 8mm se usa un punzón de diámetro d=20mm tal como se
muestra en la figura. Si se requiere una fuerza de 110kN para realizar el agujero. ¿Cuál es el esfuerzo
cortante promedio en la placa y el esfuerzo de compresión en el punzón?
Solución
Para determinar el esfuerzo de corte sobre la placa, debemos identificar el área sobre la que actúa las fuerzas
cortantes, dicha área es el área lateral dada por
A  ( d )t
A   x 20 x103 x8 x103 m 2
A  5, 02 x104 m2
El esfuerzo de corte resulta
P
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
F
A
110 x103 N
c 
 2, 2 x108 Nm2
4
2
5, 02 x10 m
c 
P
El esfuerzo de presión en el punzón se da en el área
A  ( d ) / 4
2
A
 x(20 x103 ) 2
4
A  3,14 x104 m 2
m2
El esfuerzo de compresión resulta
P
F

A
110 x103 N

 3,5 x108 Nm2
4
2
3,14 x10 m
3. Un tubo de acero de L=4pies de longitud, diámetro externo d2=6pulg y diámetro interno d1=4,5 pulg se
comprime con una fuerza axial P= 140klb. El módulo de elasticidad del material es Y= 30x10 6 lb/pul2 y la
relación de Poisson es u=0,3. Determine las siguientes variables para el tubo:
a) el acortamiento
b) la deformación unitaria lateral
c) el aumento del diámetro interior y exterior
d) el aumento del espesor de la pared
Solución
Esfuerzo de tensión
A

(d 22  d12 )  A 

[62  (4,5) 2 ]  12,36 pul 2
4
4
3
F
140 x10 lb
   
 1,13x104 lb / pul 2
2
A
12,36 pul
Determinamos
a) Acortamiento longitudinal


Y
 
1,13x104 lb / pul 2
 3, 7 x104
30 x106 lb / pul 2
l  l   l  3, 7 x104 x 4 pies  1, 48 x103 pies
b) La deformación unitaria lateral

d
 u    0,3x(3, 7 x104 )  1,1x104
d
c) Aumento del diámetro interior y exterior

d 2
d2
d 2   d 2  d 2  1,1x104 (6 pul )  6, 6 x104 pul
d1   d1  d1  1,1x104 (4,5 pul )  5, 0 x104 pul
P=140klb
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
d) Aumento del espesor de la pared
d 2   d 2
d1   d1
t 
d 2  d1
6, 6 x104  5, 0 x104
 t 
 8 x105 pu l
2
2
4. En el interior de un cilindro de acero absolutamente rígido, de radio interior r = 0.10m, se introduce un
cilindro de caucho del mismo radio (coeficiente de Poisson = 0.4), según se indica en la figura. Mediante una
fuerza de F = 20000N que actúa sobre un pistón de peso y rozamiento despreciable colocado sobre el caucho,
se comprime este. Calcula la presión existente entre el caucho y acero.
Solución
u=0.4
Ycaucho= 0.001 GN/m2 =1x106 N/m2
r= 0.10m
F= 20000N
A= πr2
F
Al comprimir el cilindro mediante la fuerza F, el cilindro
tiende a aumentar de radio, por lo que la pared de acero
al ser rígida impide dicho incremento por lo que ejerce
una fuerza lateral FL que ejerce presión sobre la superficie
lateral del cilindro de goma.
ΔL
FL
FL
L
Determinamos la deformación unitaria de la altura L
del cilindro
F
L
 A
L
Y
20000
 (0.10) 2 
L

L
106
L
 0.64
L
F
El aumento de r resultaría
r
L
 u
r
L
r
 0.4 x(0.64)
r
r
 0.26
r
Las fuerzas del cilindro de acero generan comprensión en el orden que debiera aumentar la dimensión de r.
r

r
FL
AL
Y
r P

r Y
P Y
r
r
P  2.6 x105 N / m2
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
5. Una barra supuestamente rígida está sustentada por dos barras circulares articuladas con la anterior, según la
disposición siguiente:
La barra A tiene una resistencia a tensión de 1000 kg/cm2 y sección 10 cm2, mientras que la barra B tiene
una resistencia a tensión de 1200 kg/cm2 y sección 8 cm2. Ambas barras tienen idéntico módulo de
elasticidad. Hallar los valores máximos de las cargas puntuales P y Q para que la barra permanezca
horizontal.
Solución
Como la barra horizontal sujeta a la carga P y Q, mantiene su horizontalidad, lo que genera igual alargamiento
longitudinal de las barras A y B y, consecuente mente igual deformación unitaria λ.
Luego, igualamos el módulo de Young de A y B:
TA
Y
AA

TB  TA
TB

M
P
0
3.5Q  2.5TB  0.5TA  0
AB
2.5TB  0.5TA
3.5
2.5(8000)  0.5(10000)
Q
3.5
Q  7142.89 Kg

Q
AB
8
 10000  8000 Kg
AA
10
P  TA  TB  Q
P  10857.14 Kg
6. Un péndulo de torsión está formado por un alambre de cierto material que lleva a su extremo un disco
homogéneo de plomo. Si el alambre es de acero, tiene una longitud de 80 cm y un diámetro de 1 mm, siendo
el disco de plomo de un diámetro de 12 cm y de 1 cm de espesor. a) ¿Qué esfuerzo soportará el alambre? ¿Se
superará el límite elástico? b) Si se gira el disco de plomo cierto ángulo y después se abandona de modo que
realice oscilaciones. Sabiendo que el tiempo empleado en realizar 100 oscilaciones es de 315 s determinar la
constante de torsión de este péndulo c) Determinar el módulo de rigidez del acero que constituye el alambre.
L=80cm
Solución
Densidad del plomo: ρ=11.3g/cm3
Diámetro: D=12cm
r=6cm
Espesor: e= 1cm
D=12cm
(a) Calculamos la masa de plomo y el esfuerzo en el alambre de acero
m   e r 2
A
2
2 2
m  11.3x10 x10 x3.14 x(6 x10 )  1.277 Kg
3
F
12.77 N
 
 16.3x106 N / m2
4 2
A 3.14 x(5 x10 )
F=mg
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
De tablas encontramos que el límite elástico del acero está en el orden de 25Kg/mm2=25x107N/m2, de manera
que el esfuerzo a que está sometido no supera el límite elástico.
(b) El péndulo de torsión tiene una frecuencia angulas de oscilación dado por (MAS: torsión):
√
Dónde: k es la constante de torsión del péndulo
I es el momento de inercia del disco de plomo respecto al eje axial de oscilación
T periodo de oscilación
De modo que
El momento recuperador en el alambre sujeto a torsión está dado por:
M  (G
Ia
)
L
d 2
dt 2
M  k  I

k 2

I
T
Ia
 2 
k 
 I G
L
 T 
2
2
2


4
L
 2  L  2 
G
I

(  pb e r )

2  r4

 T  I a  315
(
)
100 

2
2
 2 
2 4
0.8
 (11.3 x103 x102  (6 x10 ) )
G
 74.5 x109 N / m 2
4 4
2
315
 (5 x10 )


100 

2
7. Obtener las distribuciones de fuerza cortante y momento flector a lo largo de la viga uniforme de longitud L
y peso W, representada en la figura 2(b), la cual se halla empotrada por uno de sus extremos
10000N
2m
4m
Solución
Calculamos las reacciones en A y B
∑⃗
10000N
A  B  10000
3m
A
4m
B
4 B  1x10000
B  2500 N
A  7500 N
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
Fuerza cortante V y momento flector M sobre una longitud x de la barra x <2
5000x
5000x
V
Sistema
equivalente
M
A
x/2
x
V
x/2
M
A
V(N)
7500
∑⃗
5000 x  V  7500
V  7500  5000 x
1.5 2
-2500
∑
5000
5625
M(Nm)
X
)  (7500  5000 X ) X
2
M  7500 X  2500 X 2
M  5000 X (
Para 2<x<4
10000N
10000  V  7500
V  2500 N
V
1m
M  2500 X  10000
M
A
x
(*) Podemos hallar el momento flector evaluando en el extremo donde está la fuerza cortante
( )
Para x <2
Para 2<x<4
8. Obtener las distribuciones de fuerza cortante y momento flector a lo largo de la viga uniforme que se muestra
en la figura.
P
P
d
RA
d
B
C
Determinamos las reacciones en A y B
M
A
RD  P
  Pd  P( L  d )  RD L  0
RD
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
 F  P  P  R
D
 RA  0
RA  P
V
Momento flector entre A y B: x<d
x
 F  P V  0
M
V P
M
A
RA
 Vx  M  0
M  Px
P
V
d
M
Momento flector entre A y B: d < x < L-d
RA=P
 F  P  P V  0
x
V 0
M
A
  Pd  M  0
M  Pd
P
Momento flector entre A D: L-d <x<L
M
V  P
A
V
d
 F  P  P  P V  0
M
P
x
RA=P
  Pd  P( L  d )  Px  M  0
L-d
M  P( L  x)
9. Dos alambres de acero con un área de sección transversal de 0.2 cm2, sostienen un letrero cuya masa es de 2
10 kg. (a) ¿cuál es el esfuerzo sobre cada alambre? (b) ¿en cuánto se alargará cada alambre? (Ignore su masa.
Ver Fig ). Si la resistencia a la tensión del acero es de 480Mpa, determine el máximo peso de la carga que
puede soportar y cuál podrá romperse primero? Yac=20x1010 N/m2
A
4B/5
4B/5
B
3B/5
4B/5
Cálculo de las tensiones
7B
 2100
5
B  1500 N
A  1200 2 N  1697.06 N
Deformación unitaria
1697.0.6
N / m2  8.48 x107 N / m 2
5
2 x10
1500
A 
N / m2  7.5 x107 N / m2
5
2 x10
A 
FISICA II
INGENIERÍA CIVIL
A
KLÉBER JANAMPA Q.
8.48 x107
 4.24 x104
10
Y
20 x10

7.5 x107
B  B 
 3.75 x104
10
Y
20 x10
A 

Peso máximo
B  4.8 x108 x 2 x105  9600 N
7B
W
5
W  13440 N
10. La barra AB de la figura articulada en A, es sostenida por la varilla de acero EB y por la de cobre CD. La
longitud de CD es de 1m y la de EB 2m, la sección de CD es de 2cm2 y la de EB 3cm2, determinar (a) la
tensión y esfuerzo en cada varilla vertical; considerando la barra absolutamente rígida y horizontal antes de
aplicar la carga de 400kN (b) la ecuación de la distribución de fuerza cortante y momento flector en la barra
AB. Despreciar el peso de AB. Para el cobre, E cu=1,2x106 kg/cm2 y para el acero EA=2,1x106 kg/cm2.
E
D
A
1m
2m
C
B
400kN
Solución
(a)
∑⃗
TA
A
TBE
TCD
1m
2m
∑
ΔlBE
ΔlCD
….(I)
Las deformaciones longitudinales de CD y BE están en la relación
Elásticamente
Reemplazando en la ecuación anterior
…. (II)
De I y II
400kN
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
(b) Mostramos las fuerzas sobre la barra AB
TBE
TCD
A
1m
2m
TA
400kN
V
Para x<1
x
M
A
Para 1<x<3 m
TCD
V
1m
M
x
A
11. Hallar los diagramas de fuerzas cortantes y momentos flectores de la siguiente estructura, sabiendo que M
está en el plano de XY con valor 800Nm.
2m
1m
1m
2m
Solución
A=B
Evaluando momento en A
M=2B
Luego:
B= 400N
A= 400N
Para x<2m
V=A
A
B
V
x
Mf
A
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
V
Para 1<x<3 m
x
A
Mf
2m
V(N)
400
2
3
x(m)
3
x(m)
-800
2
M(Nm)
12. Calcular el incremento de longitud que tendrá un pilar de hormigón de 50 x 50 cm2 de sección y de 3m de
longitud, que se encuentra apoyado en su base inferior, debido a su propio peso. Datos: E= 25 GPa, peso
específico del hormigón= 24 KN/m3
Solución
Evaluamos el esfuerzo sobre un diferencial de volumen de espesor dy
Sobre él actúa la fuerza del peso del hormigón superior de altura y
La deformación que produce F en la porción de hormigón de
longitud dy, es un diferencial, dado por:
y
F
dy
Integrando
∫
∫
13. La estructura articulada de la figura está formada por dos barras de sección circular de acero. Si la estructura
ha de soportar una carga de 30 kN en el nudo C, se pide: 1) Calcular las tensiones en ambas barras 2)
Calcular el desplazamiento del nudo C. Datos: barra AC: R = 1 cm; barra BC: R = 1,2 cm.; E = 210000
N/mm2
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
Solución
A
TAC
ΔLBC
TBC
θ=33.7º
C1
B
∑⃗
θ
C
y1
C2
θ y
2
ΔLAC
Cf
La deformación de cada barra
⁄
⁄
⁄
Para hallar la posición final de C, asumimos que BC se contrae ΔLBC y C pasa a la posición C1, luego gira a la
posición Cf, equivalentemente AC gira de modo que C pasa a C2 y luego se estira ΔLAC hasta Cf. Luego la
posición: tiene coordenadas:
x= - ΔLBC= - 0.71 mm
y=-3.7mm
14. La barra rígida AB, sujeta a dos varillas verticales como se muestra en la figura, está en posición horizontal
antes de aplicar la carga P. Si P = 80 kN, determine: el movimiento vertical del punto C, de aplicación de la
fuerza. Acero: L=3m, A= 300mm2 Yac= 200 GPa; Aluminio: L=4m, A= 500mm2 Yb= 70 GPa
Bronce
Acero
A
B
2m
3m
P
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
Solución
Bronce
Acero
TB
TA
A
B
2m
A
ΔLA
3m
B
2m
yc
3m
ΔLB
P
Aplicando suma de momentos en A:
∑
Luego
∑
Las deformaciones
⁄
⁄
⁄
En el trapecio que se ilustra:
yc =2,9 mm
15. El eje de acero de una llave matraca tiene 0.5plg. de diámetro y 18 plg. de longitud (véase figura). si el
esfuerzo permisible cortante es 10 000 Psi. ¿cuál es el par máximo permisible que puede aplicarse con la
llave? ¿a qué ángulo θ se torcerá la barra bajo la acción del par máximo? (suponer G = 11x106 Psi)
0.5 plg
τ
18 plg
Solución
El máximo torque permisible corresponde al esfuerzo permisible cortante según la expresión obtenida
De donde: (Psi=lb/plg2)
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
(
)
Hallamos el ángulo de torsión
PREGUNTAS
1.
2.
3.
4.
5.
6.
7.
8.
¿Cuáles son los tipos fundamentales de tensión?
¿Qué caracteriza el módulo de Poisson?
¿Es posible que haya esfuerzos sin la aplicación de fuerzas externas?
Por qué la mayor parte del acero en una viga en forma de I está en los patines superior e inferior
Diferencie desde un punto de vista microscópico, el comportamiento elástico y plástico de un cuerpo
Una columna vertical de concreto armado soporta una carga axial, explique en ella qué significa estar
sujeto a esfuerzos de compresión. Luego, indique en qué condiciones la columna estará en posibilidad
de pandearse y en estas condiciones a qué tipos de esfuerzo está sometido
Una viga apoyada sobre sus extremos, se flexiona debido a su peso ¿A qué tipos de esfuerzo está
sometido? Explique.
La tabla muestra, valores de módulos de elasticidad y resistencias de algunos materiales. Analice
comparativamente el significado de cada valor.
M
B
Rest. compresión
(Cizalladura) (Volumétrico)
6
2
x10 N/m
x109 N/m2
x109 N/m2
Material
Y (Young)
x109 N/m2
Rest. Tracción
x106 N/m2
Acero
200
520
520
84
160
Hierro
190
390
-
70
100
EJERCICIOS PROPUESTOS
1- Un cable de acero se encuerda entre dos apoyos adjuntos al techo (Figura). Inicialmente, no hay ninguna
tensión en el cable cuando está horizontal. Entonces, desde el centro del cable se cuelga un cuadro de 96N,
como el dibujo ilustra, formando un ángulo de 26º con respecto a la horizontal. ¿Cuál es el radio del cable?
E=200x109 N/m2.
26º
96N
2- Un conjunto de barra BC puntal y cable AB (véase figura) sostiene una carga vertical P = 20 kN. El cable
tiene una sección transversal efectiva de 150 mm2. Calcular: los esfuerzos normales en el cable y el puntal, e
indicar si son de tensión o compresión. Área del puntal es 200 mm2. SOL: σa b = 111.1 MPa (tracción) , σbc
= 83.3 MPa ( compresión )
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
A
1.5 m
B
1.5 m
P
C
2m
3- La barra rígida de masa despreciable está articulada en un extremo y suspendida de una varilla de acero y
una de bronce, según se muestra en la figura. Cuánto vale la máxima carga P que se puede aplicar sin
exceder un esfuerzo en el acero de 140 MN/ m2 y en el bronce de 80 MN/ m2? Acero: L=3m, A= 900mm2
Yac= 200 GPa; Bronce L=2m, A= 300mm2 Yb= 83 GPa
Acero
Bronce
Soluc: 35436 N
O
2m
3m
1m
4- Dos barras AB y BC de aluminio 6061 – T6 (E= 70 G Pa) de sección rectangular (5 cmx2cm)
P y longitud L =
50cm conforman la armadura mostrada. Si la carga P = 50000 N, la longitud d = 40 cm, halle los esfuerzos
que soportan las barras, su deformaciones axiales y el desplazamiento del punto B.
5- Cuál es el diámetro mínimo requerido "d" para una barra circular maciza sometida a un par torsional de τ=
461kgm. El esfuerzo cortante permisible es 1054.5 kg/cm². (Suponer G = 7.73x105 kg/cm2) Solución: dmin =
6,1cm
Τ=461kgm
d
6- Sea la barra AB de la figura 2 articulada en A y soportada por la varilla de acero EB y por la de cobre CD.
Considérese absolutamente rígida y horizontal antes de aplicar la carga de 20000kg. La longitud de CD es
de 90cm y la de EB 150cm. Si la sección CD es de 5 cm2 y la de EB 3 cm2, determinar la tensión y esfuerzo
en cada varilla vertical y el alargamiento de la de acero. Despreciar el peso de AB. Para el cobre, E=1,2x10 6
kg/cm2 y para el acero E=2,1x106 kg/cm2.
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
7- Un paralelepípedo de un material elástico, con módulo de Young Y y módulo de Poisson u y de
dimensiones a, b y c, se introduce en una cavidad de anchura b de paredes completamente rígidas, planas y
perfectamente lisas, como se indica en la figura. Se aplica sobre la cara superior, perpendicularmente a ella,
una fuerza constante p por unidad de superficie. Se pide: (a) esfuerzos a los que está sometido; (b)
deformaciones sufridas por el paralelepípedo; (c) variación de la longitud de cada uno de sus lados.
8- Dos miembros se unen mediante un tornillo AB de aluminio como se muestra en la figura 4, si la carga P =
36 000N, y el esfuerzo cortante permisible es de 90 MPa. , halle el diámetro mínimo requerido del tornillo
para el cual no falle.
9- Una barra de sección variable y peso despreciable está empotrada en su extremo inferior y sometido a las
cargas que se indican en la figura 5. Se pide determinar: Tensión máxima, indicando donde se dará, e
incremento de longitud de cada barra sin son de igual longitud inicial. Datos: Y = 210000 N/mm2.
2000N
1 cm2
1000N
2cm2
4 cm2
2000N
2m
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
10- En la barra prismática suspendida verticalmente cuya sección es A= 40cm2 cuya densidad relativa es de 7,8
se coloca la carga Q=100MN, según ¿qué ley varía la tensión de tracción en la barra a la distancia x del
punto de actuación de la carga?
11- En un cable de sección A= 20cm2 se coloca una carga de Q=5MP ¿cuál es la longitud del cable admisible
considerando el peso propio como carga estática, si la tensión de tracción en el cable junto al tambor ha de
ser σ =3000kp/cm2, densidad relativa del cable 7,8.
12- Una varilla redonda de acero de 8 pies de longitud está sujeta a una carga axial de tensión de 8000 lb. ¿Qué
diámetro debe tener la varilla si el esfuerzo de tensión no debe exceder de 16 000lb/plg2 y el alargamiento
debe ser menor que 0,075plg? Supóngase que se consiguen varillas con incrementos de 1/16plg de diámetro.
El módulo de elasticidad de acero es de 30 000klb/ plg2.
13- Una varilla de acero de 10mm de diámetro y 2m de longitud está sujeta a una fuerza de tensión de 18000 N.
El módulo de elasticidad del acero es de 200Gpa. Determinar a) la deformación unitaria en la varilla, b) la
deformación total de la varilla.
14- Determinar la carga máxima de tensión que puede soportar una barra de aluminio de 1,5 m de longitud y de
10mm x 30mm de sección transversal. El esfuerzo de tensión no debe exceder de 100Mpa y el alargamiento
debe ser menor que 2mm.
15- Se usa aceite lubricante de densidad relativa 0,88 como fluido de trabajo en un sistema hidráulico de alta
presión. Estime el cambio porcentual en la densidad del aceite cuando su presión se eleva de las condiciones
ambiente hasta 300atm (manométrica). ¿Suponer fluido incompresible es una buena hipótesis para este
aceite en esas condiciones? Aceite: β = 1,44 GN/m2. Sol. : 2.1 %
16- Un pequeño poste construido con un tubo circular hueco de aluminio, soporta una carga de compresión de
26klb. Los diámetros internos y externos del tubo son d 1 = 4,0pulg y d2 = 4,5pulg respectivamente y su
longitud es de 16 pulg. Se mide el acortamiento del poste debido a la carga y resulta ser de 0,012 pulg.
Determinar el esfuerzo y la deformación unitaria de compresión en el poste (no tenga en cuenta el peso del
poste miso y suponga que el poste no se pandea bajo la carga).
17- Una varilla redonda de acero de longitud L y diámetro d cuelga en un tiro de mina y sostiene una canasta de
mineral con peso W en su extremo inferior. a) deducir la fórmula del esfuerzo máximo σmax en la varilla,
teniendo en cuenta el peso de la varilla misma. b) calcular el esfuerzo máximo si L=40 m, d = 8mm y W =
1,5kN
18- En el sistema de la figura se pide determinar los esfuerzos en los cables a, b y c, en términos de P y A,
siendo A el área de la sección transversal de cada cable y estos son del mismo material. Módulo de Young
G.
(a)
(b)
L
L
L
L
(c)
L/2
(a)
(b)
ΔLa
ΔLb
(c)
ΔLc
P
19- Obtener las distribuciones de fuerza cortante y momento flector a lo largo de la viga uniforme que se
muestra en la figura sujeta a las cargas que se indican.
(a)
10000N
2m
(b)
4m
FISICA II
INGENIERÍA CIVIL
KLÉBER JANAMPA Q.
20- La viga en voladizo de la figura está sujeto a la distribución de fuerza mostrada, las distribuciones de
fuerza cortante y momento flexor a lo largo de la viga uniforme, de peso despreciable. Distribución de
fuerza por unidad de longitud q.
q
L
21- Los músculos de las patas de un insecto se contraen 0,2 mm antes de saltar. La longitud inicial del
músculo es de 0,60 mm, su diámetro es 0,10 mm y su módulo de Young 2x10 6Nm-2. ¿Hallar con qué
velocidad inicial saltará el insecto si se impulsa con dos patas y su masa es de 2gr? Rpta: 3,24cm/ s
22- Un ciclista de 75 kg apoya todo su peso sobre un pedal. El diámetro del eje de éste mide 1,5 cm. (a)
Hallar el esfuerzo cortante sobre dicha barra. (b)Hallar la razón de este esfuerzo al máximo esfuerzo
cortante, de 108 N· m-2.
23- Una barra cilíndrica de sección circular se carga a tracción con una fuerza P = 85KN. La barra tiene una
longitud L = 3m y un diámetro d=30mm y es de aluminio con un módulo de elasticidad de E = 70 000
MPa y módulo de poisson μ = 1/3. Calcular el alargamiento, la disminución de diámetro y el
incremento de volumen de la barra.
24- Dado el sistema de la figura, formado por cables y barras, donde el área de la sección de cada cable es
A = 0,78 cm2y las barras son imponderables y rígidas; en el extremo C se aplica una carga puntual P =
30kN. El módulo de elasticidad del material de los cables es E = 2×106 kg/cm2. Determine el esfuerzo
en los cables GF, HD, EB y sus respectivas deformaciones.
G
H
2m
1.5 m
D
E
F
1.5 m
B
C
1.5 m
A
1m
P
Nunca consideres el estudio como una obligación, sino como una oportunidad
para penetrar en el bello y maravilloso mundo del saber.
Hay una fuerza motriz más poderosa que el vapor, la electricidad y la energía
atómica: la voluntad.
Dos cosas son infinitas: la estupidez humana y el universo; y no estoy seguro de
lo segundo.
El que no posee el don de maravillarse ni de entusiasmarse más le valdría estar
muerto, porque sus ojos están cerrados.
— Albert Einstein