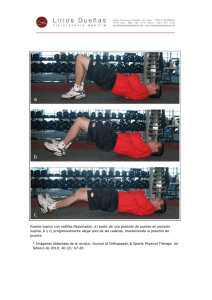
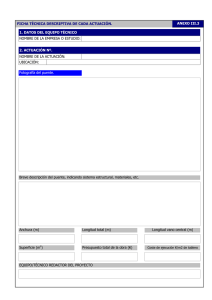
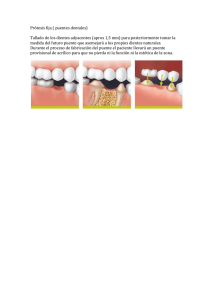
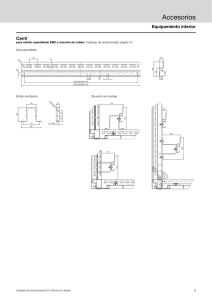
CHABERT Y ENGELDINGER (1956) ( Jesmerth) Los investigadores realizaron el estudio más antiguo y completo sobre socavación en pilas, una de las canaletas usadas tenía un ancho de 0.80 m, con 4 diámetros diferentes de pilas desde 0.05 m hasta 0.15 m, cuatro sedimentos uniformes con diámetros entre 0.26 y3.2 mm y 3 profundidades de flujo:0.10, 0.20, 0.35m el segundo canal tenía un ancho de 3.0m con sedimento uniforme de 3 m de diámetro además de una pila cilíndrica de 0.15m de diámetro, se ensayaron 6 formas diferentes, lo mismo que algunas medidas para atenuar la socavación se desarrollaron unos 300 experimentos con duraciones desde unas horas hasta días. la máxima socavación se presentó en la transición entre la condición de agua clara y lecho activo. ANÁLISIS Como ya se mencionó, la socavación local ocurre debido a la presencia de algún obstáculo al flujo, y provoca una disminución de la elevación del fondo únicamente en la zona alrededor del obstáculo. La rapidez de la socavación local puede expresarse como la diferencia entre la capacidad del flujo de extraer el material que se encuentra en la olla de socavación y la aportación de sedimentos a ésta. Así que: la profundidad de socavación local Ds, depende solo de los siguientes parámetros: Ds f v, d 0 , w ,V , D, S , b, g Esta relación puede cambiarse por la siguiente: Ds f v, d 0 , ,V , D, b, g Ds = profundidad de socavación local. Donde: s w peso especifico sumergido de los granos. w Por análisis dimensional pueden obtenerse los siguientes parámetros adimensionales ya expresados en forma de ecuación: vD v 2 ds d0 D f , , , , b b b V D • El primer parámetro, ds/b, se justifica porque se ha comprobado experimentalmente que puede relacionarse la profundidad de socavación local con el tirante. • El segundo parámetro, vD/ʋ, es el número de Reynolds relativo a los granos del sedimento, del cual es función la fuerza del arrastre del sedimento por el flujo. • El tercer parámetro adimensional, v2 /∆gd, se obtiene de la relación que permite estimar la velocidad crítica de arrastre en función del diámetro del grano y demás variables. • El cuarto parámetro, ∆, es el peso específico relativo sumergido de los granos. Los últimos 2 parámetros relacionan el ancho de la pila con el tirante y con el diámetro del sedimento. APLICACIÓN (Ejemplo Puente Trilce) N° Puente Luz (m) Altura libre (m) n Cota de Fondo (m.s.n.m) cota (Tr=175) (m.s.n.m) 1 Trilce 15.00 4.50 0.035 690.93 691.22 ECUACION V * Rh v Q(caudal) V A(area ) Re 0.29 22.01 0.33 27.14 90 v = viscosidad del fluido=0.0000010070 Re<2000 Transcisional 2000<Re<4000 Turbulento V vD/V=Re 691.26 TALUD α (°) Rh = radio hidraulico de la seccion que fluye el caudal=0.30 Laminar vD v 2 ds d D f , , , 0 , b b b V D cota (Tr=500) Tirante 175 Tirante 500 Q175 (m3/s) Q500 (m3/s) (m.s.n.m) (m) (m) Re > 4000 27.14 0.90 32 Re 0.90 * 0.30 269.19 0.001003 V * Rh v 2 ds d D f , , , 0 , b D b b v ds V * Rh f 0.33 v ds 0.90 * 0.30 f 0.33 0.01003 ds f 269.19 0.33 d s 88 .83 cm d s profundidad de socavacion izquierdo 0 derecho 0 CONCLUSION • El cálculo de la socavación local en pilas de puentes, es de significativa importancia debido a que la mayoría de las fallas de puentes en el mundo es debido a la socavación local. • Para el cálculo de la socavación local en pilas, a la fecha no existe ninguna solución robusta, la mayor parte de los métodos que se emplean, están basados en datos de laboratorio. • En el cauce se pueden encontrar distintos tipos de materiales, ya sean cohesivos, como arcillas; y no cohesivos, como gravas o arenas, con sus respectivas propiedades, de acuerdo con su estructura, el parámetro d no es suficiente para caracterizar a todos los tipos de suelo que se pueden encontrar en el fondo del cauce. • Este método es aplicable para cauces con grandes caudales, con diferentes tipos de suelo. INTRODUCCION Para llegar a un diseño adecuado y óptimo se necesitan realizar diferentes cálculos, obteniendo así datos sustanciales que servirán para un posterior manejo y diseño. Uno de los tantos datos que se necesitan y que de alguna manera resulta esencial, es la altura de socavación que ejerce el agua sobre la estructura. Para el presente informe se calculara la altura de socavación según el método Liu, Chang y Skiner, para este fin se realizara la toma de datos según la información brindada por el docente, como por ejemplo el caudal máximo, la sección transversal del rio, el tirante del flujo, entre otros. Además este informe se determinara la altura de socavación para 5 distintos puentes (Buenos Aires, La curva, Trilce, Cuchilla I, Cuchilla II), este método calcula la profundidad de socavación tipo contracción, las fórmulas y el cálculo correspondiente se realizará en una hoja de Excel de manera detallada. Las ecuaciones para el cálculo de la socavación en estribos se basan en información de laboratorio y muy poca información de campo existe para su verificación. Casi todas las ecuaciones dan como resultado valores muy conservadores de socavación debido a que consideran que el estribo está en el cauce principal formado por lechos aluviales y asumen que caudal de agua obstruido es proporcional a la longitud del estribo, local raramente ocurre en la realidad. La socavación locales de tipo lecho móvil (vivo), dependiendo en muchos casos si el estribo se ubica en las márgenes o si está dentro del cauce principal. • Socavación en lecho móvil • Estribos que se proyectan dentro del cauce principal • No existe flujo sobre la llanura de inundación • Usado en suelos Granulares • El largo del estibo es menor que 25 veces la profundidad media del agua (L/h <25) • Flujo subcrítico • Lecho del cauce arenoso • Las ecuaciones deben ser ajustadas por un factor de corrección Kф para considerar el ángulo de ataque del flujo. Este método de Liu, Chang y Skiner, según las consideraciones y teoría presentada, se da la socavación en un lecho móvil, por lo cual es aplicable para suelos granulares en ríos no montañosos, donde la socavación es por tipo local en estribos, donde los principales datos a considerar son: la velocidad según el caudal máximo del rio, profundidad media del flujo aguas arriba, longitud del estribo y accesos al puente que se opone al paso del agua, estos datos son principales para determinar la profundidad de socavación.” DONDE REFERENCIA 1 𝑑𝑠 𝐿 = 𝐾𝑓 ∗ ℎ ℎ e= 𝐾𝐿 𝑦 Profundidad de socavación h Profundidad media del flujo aguas arriba en el cauce principal L 0.4 ∗ 𝐹𝑟 0.33 Fr= 𝑉 𝑔ℎ REFERENCIA 2 0.4 0.6 ds ∗ 𝐹𝑟 Longitud del estribo y accesos al puente que se opone al paso del agua V Velocidad media del flujo aguas arriba Kf 1.1 para estribos con pared inclinada hacia el cauce 0.33 Fr= 𝑉 𝑔ℎ kf 2.15 para estribos con pared vertical Fr Numero de Froude en la sección de aguas arriba. g Gravedad. e Erosión Máxima y Profundidad de Aproximación del Rio PUENTE BUENOS AIRES RESULTADOS DE ALTURA DE SOCAVACION DE LOS 5 PUENTES • El método Liu, Ching y Skiner calcula la profundidad de socavación de tipo local en estribos, dependiendo del flujo del rio, características del sedimento y las secciones transversales. • Es aplicable para suelos granulares (No cohesivos) y para ríos no montañosos. • Los datos obtenidos son netamente confiables, lo cual la mayor parte de la información es brindada por el docente, en este caso solo asumimos el área de la sección del rio que corresponde a mi trabajo N° 1 del Rio Limon- Tabaconas – Cajamarca (mostrado en el Excel correspondiente al método Liu, chang y skinner), así como también la longitud del estribo y accesos al puente que se opone al paso del agua. • La altura de Socavación para el puente “La Curva” es 3.00 m, siendo el puente con mayor altura de socavación debido al flujo transitado por el rio (Q= 242.7m3/s) con velocidad de 5.98 m/s. MÉTODO DE FROEHLICH (Claudio) INTRODUCCIÓN Es muy importante poder predecir la magnitud de la erosión que un flujo dado puede provocar al pie de las diferentes obras hidráulicas tales como puentes, vertederos, espigones, etc. El presente trabajo se pretende analizar el método que se ha desarrollado desde hace algunas décadas por el investigador Dr. David Froehlich (1991) de igual manera es utilizada por el software HEC-RAS como alternativa a la ecuación de la Universidad de Colorado (CSU), para estimar la profundidad de socavación local al pie de pilas de puentes sobre material no cohesivo. Dicha socavación ocasiona que las pilas queden sin apoyo, se asienten y provoquen la falla de la superestructura. FUENTE: Dr. Humberto Salinas Tapia Se entiende por Erosión Generalizada al descenso del lecho del río que se produce al presentarse una creciente debido al aumento de la capacidad de arrastre de material sólido que en ese momento adquiere la corriente, en virtud de su mayor velocidad. MÉTODO DE FROEHLICH INTRODUCCIÓN Fuente: Caída del puente sobre el río Reque (1998) Fuente: BridgeSe failures”que realizo FUENTE: Dueñas (Río Rímac). observa la D. W. Smith sobre numero de fallas, de FUENTE:Puente http://www.dipromin.com/noticias/balta-vs-solidaridadacuerdo a su origen, ocurridas en 143 puentes de todo el mundo obtuvo los profundización del cauce (1983). siguientes resultados: determina-la-duracion-puente/ MÉTODO DE FROEHLICH MARCO TEÓRICO FORMAS DE SOCAVACIÓN 1. SOCAVACIÓN EN LECHO MÓVIL Ó LECHO VIVO 2. SOCAVACIÓN EN AGUA CLARA Se presenta cuando no hayhay transporte de de sedimentos desde aguas arriba hasta la zona de estudio, decir puente. Se da cuando transporte sedimentos desde aguas arriba hasta el puente, por lo es tanto noel hay los sedimentos se quedan del atrapados en el hueco de socavación alcanzando cantidad de un reabastecimiento hueco socavado (Guevara Álvarez 2013). Existeun unequilibrio equilibriocuando en estelatipo de material que es transportado y depositado la más cantidad de material que es removido en la zona. socavación cuando el flujo no puede iguala remover partículas ni transportarlas. FUENTE: Humberto Salinas Tapia MÉTODO DE FROEHLICH REVISIÓN BIBLIOGRÁFICA MARCO TEÓRICO REFERENCIA 1 ECUACIÓN DE FROEHLICH PARA LA ESTIMACIÓN DE LA SOCAVACIÓN EN UNA PILA Se basa en análisis dimensional y análisis de regresión de 170 mediciones de socavación en lecho móvil en canales de laboratorio, HEC-RAS utiliza para sus cálculos, así mismo recomienda usarla tanto para agua clara como para lecho móvil, para estribos que se proyectan dentro del cauce principal o no. Fuente: Bridge failures”que realizo D. W. Smith sobre numero de fallas, de acuerdo a su origen, ocurridas en 143 puentes de todo el mundo obtuvo los siguientes resultados: MÉTODO DE FROEHLICH REVISIÓN BIBLIOGRÁFICA REFERENCIA 1 MÉTODO DE FROEHLICH MÉTOD E EFROEHLICH MÉTOD OODDEEO FROEHLICH MÉTOD OD D FROEHLICH MÉTOD FROEHLICH PARA PUENTE BUENOS AIRES PARA PUENTE BUENOS AIRES MÉTOD O D E FROEHLICH PARA PUENTE BUENOS AIRES PARAen PUENTE BUENOS AIRES Mediciones de socavació lecho móvil en canales de laboratorio,HEC-RAS utiliza para sus cálculos, usado para Mediciones deMediciones socavació en lecho móvilPUENTE enlecho canales de en laboratorio,HEC-RAS utiliza para susutiliza cálculos, para usado para de socavació en móvil canales de laboratorio,HEC-RAS parausado sus cálculos, PARA BUENOS AIRES ANALISIS PUENTE BUENOS AIRES Mediciones de clara socavació en lecho móvil en canales de laboratorio,HEC-RAS utiliza para sus cálculos, usado PUENTE PUENTE CUCHILLA TRILCE III CUCHILLA agua como para lecho móvil, para estribos que se dentro proyectan dentro del cauce principal o no.para aguaMediciones clara como para lecho móvil, para estribos que seestribos proyectan del cauce principal ocálculos, no. agua clara como para lecho móvil, para que se proyectan dentro del cauce principal o no. de socavació en lecho móvil en canales de laboratorio,HEC-RAS utiliza para sus usado para agua clara como para lecho móvil, para estribos que se proyectan dentro del cauce principal o no. PUENTE LA CURVA 𝑑 estribos𝐿 que se proyectan 𝐿 agua clara como para lecho dentro del cauce principal o no. 𝑑 móvil, para 0.43 0.43 𝑠 0.43 0.61 0.43 𝑠𝑑 𝑑 0.61𝐿 = 2.27𝐾 𝐾 𝐹 +1 𝑠 𝐿 𝑓 𝜃 𝑠= 2.27𝐾 𝐹𝑟𝑒 0.43 𝜃 = 2.27𝐾 ℎ𝑒𝑓 𝐾 ℎ𝑒0.61++11𝑟𝑒𝐹𝑟𝑒 0.61 + 1 𝑓𝐾 𝜃 𝐾 𝐹 𝐿 ℎ𝑒ℎ𝑑𝑠= 2.27𝐾 ℎ 𝑓 𝜃 𝑟𝑒 𝑒 ℎ ℎ 0.61 𝑒 𝑒 ℎ 𝐹𝑟𝑒 +1 𝑒 = 2.27𝐾𝑓 𝐾𝜃 𝑒 ℎ𝑒 ℎ𝑒 REFERENCIA REFERENCIA 1 1 = longitud del estribo y accesos al puente que se opone al paso del agua proyectada normalmente al flujo (m). = 0.33 = longitud del estribo y accesos al puente que se opone al paso del agua proyectada normalmente al flujo (m). estribo y accesos puente que sehidráulica) opone aguadedel proyectada normalmente al flujo (m). profundidad media del flujoal en ladel zona inundación obstruida por el estribo aguas del estribo y(profundidad accesos al puente que al se paso opone al paso agua proyectada normalmente al flujo (m). arriba del puente (m). = = longitud 0.33 =dellongitud = coeficiente quededepende de la estribo forma del estribo Tabla N° 1N° , Figura N° 1 = =coeficiente N° =que coeficiente de formaTabla del estribo N°N° 1 1,1Figura N° 1 coeficiente quedepende dependeque deladepende laforma formadel dellaestribo Tabla N°11, Tabla ,Figura Figura = coeficiente que depende de la forma del estribo Tabla N° 1 , Figura N° 1 = longitud del estribo y accesos al puente que se opone al paso del agua proyectada normalmente al flujo (m). = 0.33= 0.35del 0.33 profundidad media flujom(profundidad hidráulica) en la zona de inundación obstruida por el estribo aguas arriba del puente (m). = 0.50 profundidadprofundidad media del flujo (profundidad hidráulica) en la zonaendelainundación obstruidaobstruida por el estribo puente (m). (m). del flujo hidráulica) de inundación por el aguas estriboarriba aguas del arriba del puente Número de Froude enmedia la sección de(profundidad aproximación obstruida por zona el estribo. 2.04 m profundidad media del flujo (profundidad hidráulica) en la zona de inundación obstruida por el estribo aguas arriba del puente (m). 1.48 m 0.35 m Número de Froude en la sección0.29 de aproximación obstruida por el estribo. m Número deNúmero Froude en sección desección aproximación obstruidaobstruida por el estribo. de la Froude en la de aproximación por el estribo. Número de Froude en la sección de aproximación obstruida por el estribo. Velocidad media del flujo obstruido por el estribo y accesos al puente en la sección de aguas arriba (m/s). = =1 1 =1 = caudal media obstruido estribo o los medido aguasalarriba delenpuente Velocidad del por flujoelobstruido poraccesos el estribo y accesos puente la sección de aguas arriba (m/s). Velocidad media del flujo obstruido por el estribo y accesos al en la de sección aguas(m/s). arriba (m/s). Velocidad media del flujo obstruido por el estribo y accesos al puente enpuente la sección aguasdearriba Velocidad media del flujo obstruido por elaguas estribo y accesos al puente en la sección de aguas arriba (m/s). = área del flujo de la de aguas arribamedido obstruida porarriba los estribos = caudal obstruido por el sección estribo o los accesos del puente = caudal obstruido pores estribo o losmedido accesos medido aguas arriba del el tirante hidráulico cual una variable en la ecuación para calcular el puente número de Froude. = T=caudal obstruido por elelestribo oellos accesos aguas arriba del puente = caudal obstruido por el estribo o los accesos medido aguas arriba del puente Q= del 27.14 m3/s = área flujo de la sección de aguas arriba obstruida por los estribos = área flujo de la de aguas arriba obstruida por los estribos m2dedel =A=área del3.44 flujo la el sección desección aguas arriba obstruida por lospara estribos T= el tirante hidráulico cual variable en la arriba ecuación calcular el número de Froude. = tirante área del flujo es de una laelsección porpara los calcular estribos T=m/s2 el hidráulico cual es de unaaguas variable en obstruida la ecuación el número de Froude. g= 9.81 T= el tirante hidráulico el cual es una variable en la ecuación para calcular el número de Froude. Q= 242.70 m3/s T= el tirante hidráulico el cual es una variable en la ecuación para calcular el número de Froude. =1 =1 Q=m 21.85 m3/s 9.47 77.90 m3/s A=Q=T= 120.44 m2 m3/s A=Q= 22.77 3.12 m2 A= 40.44 m2 g= 9.81 m/s2 m2 g= A= 9.81 3.21 m/s2 0.36 m 9.81 m/s2 T= g= 9.47 mT= g= 9.47 9.81 m m/s2 T= 9.47 m T= 9.47 m Reemplazando elmcaudal 12.72 0.33 my el tirante hidráulico en la ecuación del número de Froude se obtiene: 4.27 m 0.34 m 4.17938775 Reemplazando caudal y elhidráulico tirante hidráulico en la ecuación del número de Froude se obtiene: Reemplazando el caudal yel el tirante en la ecuación del número de Froude se obtiene: el caudal y el el caudal tirante yhidráulico en la ecuación número Froude obtiene: Reemplazando el tirante hidráulico en la del ecuación delde número dese Froude se obtiene: = coeficiente quedel depende del ángulo del de ataque del flujo. Ecuación 3 óN°2 Figura N°2 Reemplazando = =coeficiente que depende ángulo de ataque flujo. Ecuación 3 ó Figura que del ángulo Ecuación óó Figura = coeficiente que depende del ángulodel deflujo. ataque del flujo.33Ecuación ó Figura N°2 =coeficiente coeficiente quedepende depende del ángulode deataque ataque del flujo. Ecuación Figura3N°2 N°2 3.89547154 0.18040731 0.29761939 3.88996745 = == = 1.00 1.00 = 1.00 Ө=Ө=Ө= Ө= 90 9090 Ө= 1.00 1.00 90 90 Dejando la profundidad de socavación (ds) de la ecuación de Froehlich (Ver Ecuación 1) y luego reemplazando se obtiene: Dejando la profundidad de socavación (ds) de la ecuación de Froehlich (Ver Ecuación 1) y luego reemplazando se obtiene: Dejando lalaprofundidad socavación de la laecuación ecuación Froehlich (Ver Ecuación y luego se obtiene: Dejando lade profundidad de(ds) socavación (ds) de la ecuación de(Ver Froehlich (Ver1) Ecuación 1) y reemplazando luego reemplazando se obtiene: Dejando profundidad de socavación (ds) de dede Froehlich Ecuación y1)luego reemplazando se obtiene: 2.12233226 2.17110725 2.19553468 2.32133581 2.78437379 MÉTODO DE FROEHLICH REVISIÓN BIBLIOGRÁFICA REFERENCIA 2 MÉTODO DE FROEHLICH ANÁLISIS REFERENCIA 2 𝒅𝒔 = 𝟎. 𝟑𝟐𝑲𝒇 𝒂′ 𝟎.𝟔𝟐 𝟎.𝟒𝟕 𝒉 𝑭𝒓 𝟎.𝟐𝟐 𝑫𝟓𝟎 −𝟎.𝟗𝟗 + 𝒂 = factor de corrección en base el perfil de la nariz de la pila. Φ= 1,3 Φ= 1,0 Φ= 0,7 para pilas con nariz cuadrada. para pilas con nariz redondeada. para pilas con nariz triangular. PARA PUENTE BUENOS AIRES PARA PUENTE LA CURVA PARAPUENTE PUENTECUCHILLA TRILCE I PARA PARA PUENTE CUCHILLA II = profundidad del flujo directamente aguas arriba de la pila (m) = profundidad del flujo directamente aguas arriba de la pila (m) = =profundidad del flujo directamente pila profundidad flujodirectamente directamenteaguas aguasarriba arribade dela pila(m) (m) 1.48 m deldel == profundidad flujo aguas arriba de lalapila (m) = 0.33 m = 0.50 0.35m de == =número 2.04 mmFroude en la sección directamente aguas arriba de la pila = número de Froude en la sección directamente aguas arriba de la pila = número de Froude enenlalasección número Froudeen seccióndirectamente directamenteaguas aguasarriba arribade delalalapila pila = =número dede Froude la sección directamente aguas arriba de pila = velocidad media del flujo directamente aguas arriba de la pila (m/s) = velocidad media flujom/s directamente aguas arriba de la pila (m/s) = del1.93 = =velocidad media flujo directamente = del 7.89 m/s velocidad media del flujo directamenteaguas aguasarriba arribadedelalapila pila(m/s) (m/s) = velocidad media del flujo directamente aguas arriba de la pila (m/s) 1.3 == 7.09 m/s 7.00 m/s = 2.02 m/s = 0.505546315 = 4.38490236 = = 3.20286396 3.77944754 de la partícula de lecho en una mezcla cuyo 50% es menor (m) == diámetro 0.450452957 = diámetro de la partícula de lecho en una mezcla cuyo 50% es menor (m) = =diámetro diámetrodedelalapartícula partículadedelecho lechoenenuna unamezcla mezclacuyo cuyo50% 50%esesmenor menor(m) (m) 0.50 m == diámetro de la partícula de lecho en una mezcla cuyo 50% es menor (m) = 0.50 m = = 0.50 0.50mm La profundidad de socavación (ds) de la ecuación de Froehlich (Ver Ecuación 4) y reemplazando se obtiene: = 0.50 m = ancho proyectado de la pila con relación al ángulo de ataque del flujo (m) La profundidad de socavación (ds) de la ecuación de Froehlich (Ver Ecuación 4) y reemplazando se obtiene: factor de corrección por la forma de la pila. Tabla N°2 = 3.00 m = ancho de la pila, adicionado como un factor de seguridad (m) 1.50 m = profundidaddedesocavación socavación(ds) (ds)dedelalaecuación ecuacióndedeFroehlich Froehlich(Ver (VerEcuación Ecuación4)4)yyreemplazando reemplazandoseseobtiene: obtiene: LaLaprofundidad La profundidad de socavación (ds) de la ecuación de Froehlich (Ver Ecuación 4) y reemplazando se obtiene: 2.41 m 2.22 m 2.22mm 2.32 2.53 m MÉTODO DE FROEHLICH CONCLUSIONES Froehlich REFERENCIA 1 propone una fórmula para estimar la profundidad de socavación al pie de estribos en lecho móvil, condiciones de socavación en agua clara según la clasificación de ríos para cuencas jóvenes, maduros y viejos tranquilamente se puede aplicar esta referencia 1. Esta cuya ecuación es dependiente de la longitud del estribo, tirante del flujo, Número de Froude, forma de estribos y ángulo de taque del flujo; denegando el tamaño y densidad de los sólidos del lecho, cuya influencia es determinante en el proceso de la socavación al pie de estribos de puentes. Froehlich REFERENCIA 2 también propone una ecuación solamente para condiciones de socavación en agua clara según la clasificación de ríos para cuencas jóvenes, pero tiende a dar valores muy bajos y propone una fórmula para estimar la profundidad de socavación al pie de estribos en lecho móvil, cuya ecuación es dependiente de ancho de pilar Número de Froude, forma de estribos y ángulo de ataque del flujo; influyendo el tamaño 𝐷50 de los sólidos del lecho, cuya influencia es determinante en el proceso de la socavación al pie de estribos de puentes. MÉTODO DE FROEHLICH CONCLUSIONES El estudio del comportamiento del transporte de sedimentos se deriva a partir de las condiciones hidrodinámicas del flujo en estudio, así como algunas condiciones específicas tales como tamaño medio de las partículas 𝐷50 . Debido a que no se pudo obtener ese dato asumimos 0.50m de diámetro medio. Asimismo el área de la sección del flujo, espejo del agua (T) ha sido indispensable para adecuar las condiciones iniciales y de contorno para los diversos escenarios de flujo. Algunos datos asumimos por falta de datos como también el ancho y forma de pila, forma estribo y ancho proyectado de la pila con relación al ángulo de ataque del flujo. Los resultados obtenidos para el cálculo de profundidad de socavación bajo el estribo del puente sobre cada uno de los ríos no se pueden comparar, debido a que cada una de las referencias utilizadas se basa en diferentes principios. Pero los resultados tanto de referencia 1 y referencia 2 en 𝐝𝐬 si se asemejan como que por ahí va no varía mucho. METODO ARTAMONOV (Rider) El método K. F. Artamonov permite estimar no solo la profundidad de socavación al pie de estribos, sino además al pie de espigones. Esta erosión depende del gasto que teóricamente es interceptado por el espigón, relacionando con el gasto total que escurre por el río, del talud que tienen los lados del estribo y del ángulo que el eje longitudinal de la obra forma con la corriente. El tirante incrementado al pie de un estribo medido desde la superficie libre de la corriente, esta dada por: FORMULA DE LA ALTURA DE SOCAVACION (St) St = Pa x Pq x PR x Ho Pa = coeficiente que depende del ángulo a que forma el eje del puente con la corriente, como se indica en la figura siguiente; su valor se puede encontrar en la tabla N° 4 Pq = coeficiente que depende de la relación Q1/Q, en que Q1 es el gasto que teóricamente pasaría por el lugar ocupado por el estribo si éste no existiera y Q, es el gasto total que escurre por el río. El valor de Pq puede encontrarse en la tabla N° 5 PR = coeficiente que depende del talud que tienen los lados del estribo, su valor puede obtenerse en la tabla N° 6 Ho = tirante que se tiene en la zona cercana al estribo antes de la erosión Valores de coeficientes Pa, Pq, PR TABLA N° 4 VALORES DEL COEFICIENTE CORRECTIVO Pa EN FUNCION DE a a (°) 30 60 90 120 Pa 0.84 0.94 1 1.07 Q1/Q Pq 150 1.19 TABLA N° 5 VALORES DEL COEFICIENTE CORRECTIVO Pq EN FUNCION DE Q1/Q 0.1 0.2 0.3 0.4 0.5 0.6 0.7 2 2.65 3.45 3.22 3.67 3.87 4.06 0.8 4.2 TABLA N° 6 VALORES DEL COEFICIENTE CORRECTIVO PR EN FUNCION DE R TALUD R 0 0.5 1 1.5 2 3 PR 1 0.91 0.85 0.83 0.61 0.5 PUENTE BUENOS AIRES ANALISIS: Datos hidráulicos: Tirante 500 (m) 1.48 Q500 (m3/s) 77.9 α (°) 90 TALUD izquierdo derecho 0 0 Estribo margen izquierda y derecho St = tirante incrementado al pie del estribo debido a la socavación en mts. Ho = tirante que se tiene en la zona cercana al estribo antes de la erosion Qd = caudal de diseño 1.48 77.90 m m3/seg Q1 = caudal que teóricamente pasaría por el lugar ocupado el 10% del caudal de diseño (10%Qd) Q1/Q = Pq = coeficiente que depende de la relación Q1/Q. Ver tabla N° 5 a = ángulo que forma el eje del estribo con la corriente Pa = coeficiente que depende del ángulo a . Ver tabla N° 4 R = talud que tiene el estribo PR = coeficiente que depende del talud que tiene el estribo. Ver tabla N° 6 7.79 0.10 2.00 90.00° 1.00 0.00 1.00 m3/seg 𝑺 𝒕 = 𝑷 𝒂 ∗ 𝑷 𝒒 ∗ 𝑷 𝑹 ∗ 𝑯𝒐 𝑺 𝒐 = 𝑺 𝒕 − 𝑯𝒐 St = 2.96 So = 1.48 Asumimos = So = 1.50 Resumen general de los 5 puentes METODO DE ARTAMONOV INTERPRETACION H. socavación (m) PUENTE E. IZQUIERDO E. DERECHO BUENOS AIRES 1.5 1.5 LA CURVA 2 2 TRILCE 0.35 0.35 CUCHILLA I 0.35 0.35 CUCHILLA II 0.5 0.5 Sin embargo, en el presente estudio de cada puente se ha encontrado caudales demasiados altos como lo es en el puente “la Curva” con un caudal de 242.7 m3/s para un periodo de 500 años dando como consecuencia una altura de socavación de 2 m, la cual esta propenso a colapsar sino se llega a diseñar estructuras hidráulicas que contrarrestan el fenómeno. CONCLUSIÓN EL Método de Artamonov define una ecuación dependiente de los siguientes parámetros: caudal interceptado por el estribo, ángulo de incidencia del flujo, talud de inclinación del estribo y tirante normal del flujo aguas arriba del estribo; dejando de lado la influencia del tamaño y densidad de los sólidos del lecho y forma del estribo; se puede definir como un método poco confiable por falta de parámetros importantes como es el estudio de las partículas de sedimentación. INGLIS POONA (1949) La Estación Central de Investigaciones de Agua y Fuerza en Poona, India, realizó una serie de ensayos en laboratorio con el fin de encontrar la profundidad de socavación para un sólo pilar rectangular colocado en el centro de una corriente, con material de fondo formado por arena uniforme de diámetro medio de 0,29 mm. Al concluir el estudio se encontró la siguiente expresión para la profundidad de socavación a partir del lecho sin erosión(socavación total). La socavación y erosión de suelo es un tema o problema como lo catalogan ciertos autores, que ha estado presente desde tiempos remotos, así no es un tema nuevo. Su uso resulta nuevo aunque ahora no tanto, es la forma y métodos brillantes aplicados para solucionarlo. Diversos autores han contribuido a lo largo de la historia con fórmulas que desde su perspectiva ayudan al manejo y control de la socavación. Ahora bien, se denomina socavación a la excavación profunda causada por el agua. Uno de los tipos de erosión hídrica, puede deberse al embate de las olas contra un acantilado, a los remolinos del agua, especialmente allí donde se encuentran algún obstáculo la corriente, y al roce con las márgenes de las corrientes que han sido desviadas por los lechos sinuosos. En este último caso es más rápida en la primera fase de las avenidas. La socavación provoca el retroceso de las cascadas y de los acantilados que, al ser privados de apoyo en su base, se van desplomando progresivamente. También representa un papel esencial en la formación y migración de los meandros. Los objetivos del método son los siguientes: Objetivo General : Calcular la altura de socavación de forma rápida y sencilla teniendo en cuenta las consideraciones. Objetivo Específico: Aplicar el método para realizar el calculo de la altura de socavación siguiendo las condiciones de método comparando variables Recopilar información mediante datos iniciales y alcanzar así la altura de socavación Facilitar el calculo INGLIS POONA (1949) FÓRMULA PARA DETERMINAR LA ALTURA DE SOCAVACIÓN: 𝑌𝑠 = 1.70𝑏( 𝑞 2 3 𝑏 0.78 ) − 𝑌𝑛 Donde: Ys Profundidad de socavación en metros medida desde el lecho de erosión (socavación total) b : Ancho del pilar en metros (m) q : Caudal unitario (m3/s) Yn : Tirante Normal del flujo de aproximación (m) Los datos necesarios son el caudal unitario para lo cual antes debemos de tener un caudal con el que trabajar este dato es propio y particular del puente o rio tratado, además de esllo necesitamos el dato de la base y el tirante normal. Cabe resaltar que estos datos pudieron ser obtenidos y trabajados de acuerdo al Excel que se impartió en clase (Caudales). A continuación presentaremos los datos puente por puente: Puente Buenos Aires: MÉTODO INGLIS POONA (1949) CUADRO DE DATOS MANEJADOS PUENTE Q (m3/s) Qu (m3/s) Buenos Aires 63.18 0.36 Yn (m) 1.48 b (m) 25 Puente la Curva: MÉTODO INGLIS POONA (1949) CUADRO DE DATOS MANEJADOS PUENTE Q (m3/s) Qu (m3/s) La Curva 208.2 1.19 Yn (m) 2.04 b (m) 25 Puente Trilce : MÉTODO INGLIS POONA (1949) CUADRO DE DATOS MANEJADOS PUENTE Q (m3/s) Qu (m3/s) Trilce 22.01 0.13 Yn (m) 0.33 b (m) 25 Puente la Cuchilla I: MÉTODO INGLIS POONA (1949) CUADRO DE DATOS MANEJADOS PUENTE Q (m3/s) Qu (m3/s) Cuchilla I 17.72 0.10 Yn (m) 0.35 b (m) 25 Puente la Cuchilla II: MÉTODO INGLIS POONA (1949) CUADRO DE DATOS MANEJADOS PUENTE Q (m3/s) Qu (m3/s) Cuchilla II 18.47 0.11 Yn (m) 0.5 b (m) 25 A continuación se muestra el cuadro general de resultados luego de aplicar el método: MÉTODO INGLIS POONA (1949) CUADRO DE RESÚMENES DE LOS RESULTADOS PUENTE Ys Buenos Aires 0.55m La Curva 1.74m Trilce 0.8 6 m Cuchilla I 0.69m Cuchilla II 0.60m INTERPRETACIÓN: una vez mostrados los datos podemos percibir que el rango de variación similitud entre todos os puentes es peqeño excepto el del puente la Curva siendo este el puente con una mayor profundidad de socavación. El resultado obtenido es muy coherente y se encuentra directamente relacionado con el caudal que tiene el caucel del rio que corre en ese punto. • Si bien es cierto el método se desarrolló en Poona – la India, tras una serie de experimentos como se menciona en la investigación del ingeniero Cuba, Alejandro León (2000). Se experimentó en un puente sobre un río de cauce variable, el cual no presente mucha presencia de erosión. • Los suelos en la India según la página de “Digfineart”, son clasificables en seis grandes grupos estando entre ellos los siguientes: suelo negro, suelo aluvial, suelo rojo, laterita, suelo del desierto y finalmente suelo de montaña. Al igual que Perú se encuentran también una variedad, pero el método en si es aplicable para suelos costeros con un fondo de cimentación de arena uniforme. • Los resultados obtenidos a partir de este método aplicable en los cinco puentes designados son los siguientes: Puente Buenos Aires: Ys= 0.79 m Puente La Curva: Ys= 3.63 m Puente Trilce: Ys= 0.90 m Puente Cuchilla I: Ys= 0.73 m Puente Cuchilla II: Ys= 0.65 m De los resultados obtenidos podemos realizar ciertas conclusiones: -El puente que tiene mayor caudal y por ende mayor distancia de socavación es el puente la Curva, debido a que esta distancia se encuentra en relación a su caudal unitario que es el mayor de todos y de su tirante normal que se encuentra en promedio a los demás. Por lo que se concluye que este puente debería aumentar ya sea su tirante normal como fortalecerlo de alguna forma, lo que implica un mayor análisis y diseño riguroso. -Recordemos también la ubicación de los puentes lo que juega un papel muy importante en cuanto a la aplicación de los métodos desarrollados; por ejemplo este método se desarrolló con diferentes tipos de suelo al que se encuentra en el lugar de ubicación del puente La Curva, por lo que es lógico que los resultados varíen progresivamente por así decirlo. -Quizá se deba de aplicar un método diferente para este puente. • Método Inglis Poona (1949) SOCAVACION DE PUENTES, Capitulo IV. Cálculo de Erosión. Universidad del Cauca.URL:http://www.hidrojing.com/wpcontent/uploads/Bibliografia/19_SOCAVACION_PUENTES_3_CALCULO.pdf METODOLOGIA PARA CALCUAR LA PROFUNDIDAD DE SOCAVACIÓN GENERAL EN RÍOS DE MONTAÑA (LECHO DE GRAVAS). Barbosa, Sebastián (2013). Universidad Nacional de Colombia: URL/ http://www.bdigital.unal.edu.co/11674/1/1128416170.2013.pdf MODELACIÓN NUMÉRICA DE LA SOCABACIÓN LOCAL EN LOS ESTRIBOS DEL PUENTE RÍO SUNUBA SEGÚN LAS CARACTERISTICAS HIDRODINÁMICAS DE LA ZONA. Bedoya, Sebastián & Cerón, Santiago (2015). Universidad de Colombia. Bogotá, Octubre 26. URL/ https://repository.javeriana.edu.co/bitstream/handle/10554/21400/BedoyaCristanchoJuanSebastian2015.pdf?sequence=1 https://repository.javeriana.edu.co/bitstream/handle/10554/21400/BedoyaCristanchoJuanSebastian2015.pdf?sequence=1 SOCA V ACION ALREDEDOR DE PILARES CILINDRICOS EN LECHOS NO COHESIVOS. León, Arturo.(2000). Universidad Nacional de Ingeniería.URL/ http://cybertesis.uni.edu.pe/handle/uni/1353.