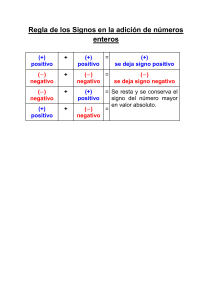
CENTRO EDUCATIVO JARDIN DE AMOR SANTA MARÍA DE JESÚS SACATEPÉQUEZ Guía de trabajo No. 2 PRIMERO BÁSICO Prof. Miguel Sánchez Instrucciones: resuelva en hojas adicionales, cada una de las series que se le presentan a continuación. Trabaje de forma clara y ordenada. Respuestas a lapicero. Coloque sus datos completos para tener un control de los trabajos que ha realizado. Operaciones Suma: - Caso 1 (igual signo): se suman los números a operar, y se mantiene el signo. Ejemplo: - 5+4= 9 −5 − 4 = −9 Caso 2 (distinto signo): se restan ambos valores, sin tener en consideración el signo. El signo del resultado, lo definirá el valor más alto. Ejemplo: −5 + 4 = Por un momento nos olvidamos de los signos, teniendo a los números 4 y 5, y los restamos 5−4=1 Finalmente, si comparamos los números 4 y 5, el número más grande es el 5, y en el ejercicio es un número negativo, por lo tanto, el resultado será negativo −5 + 4 = −1 Para explicarlo de mejor forma, hemos de representar las sumas realizadas, en la recta numérica: −5 − 4 = −9 −5 + 4 = −1 Resta: Una resta de números enteros se puede resolver como si se tratara de una suma, pero con una particularidad: El símbolo de la resta le cambia el signo a la cifra que le sigue, por lo que: Si el número que se resta es positivo lo convierte en negativo. Si el número que se resta es negativo lo convierte en positivo. Vamos a ver a continuación cuatro posibles casos: a) A un número positivo le restamos otro número positivo: 3-2 Lo tratamos como si fuera una suma, pero a la cifra que se resta (2) le tenemos que cambiar el signo = 3 + (-2) Por un lado, sumamos los números positivos: 3 Por otro lado, sumamos los números negativos: (-2) Ahora el resultado positivo suma y el negativo resta: 3-2=1 b) A un número positivo le restamos un número negativo: 3 - (-4) Lo tratamos como si fuera una suma, pero a la cifra que se resta (-4) le tenemos que cambiar el signo = 3 + (4) Se trataría ya de una suma normal: = 3 + (4) = 7 c) A un número negativo le restamos otro número negativo: (-3) - (-4) Lo tratamos como si fuera una suma, pero a la cifra que se resta (-4) le tenemos que cambiar el signo = (-3) + (4) Por un lado sumamos los números positivos: 4 Por otro lado sumamos los números negativos: (-3) Ahora el resultado positivo suma y el negativo resta: 4-3=1 d) A un número negativo le restamos un número positivo: (-3) - 4 Lo tratamos como si fuera una suma, pero a la cifra que se resta (4) le tenemos que cambiar el signo (-4) = (-3) + (-4) Se trataría de una suma de dos números negativos. Es una suma normal pero el resultado tiene signo negativo: = (-3) + (-4) = -7 1. Resuelve las siguientes operaciones: 1 + 5 + (-2) + (-3) = 2 + (-2) + 1 + (-6) = 5 + 8 + (-2) + (-1) = 8 + (-1) + 9 + (-5) = 7 + 6 + (-8) + 9 = 9 + (-8) + 9 + (-8) = 6 + 9 + (-4) + (-1) = 5 + 3 + (-7) + (-6) = 4 + (-1) + 4 + (-2) = 2 + (-9) + (-2) + 8 = CENTRO EDUCATIVO JARDÍN DE AMOR SANTA MARÍA DE JESÚS SACATEPÉQUEZ Guía de trabajo No. 2 SEGUNDO BÁSICO Prof. Miguel Sánchez Instrucciones: resuelva en hojas adicionales, cada una de las series que se le presentan a continuación. Trabaje de forma clara y ordenada. Respuestas a lapicero. Coloque sus datos completos para tener un control de los trabajos que ha realizado. 1. ¿Qué es un número entero? Recordad que los números naturales, NN, son los números que usamos para contar (sin decimales): Los números enteros, ZZ, son los números naturales con signo (positivo y negativo), excepto el número 00, que no tiene signo: Es habitual escribir los enteros positivos sin signo, a no ser que sea necesario. Observad que el conjunto de los números naturales está contenido en el conjunto de los números enteros: 2. Suma de números enteros Si los dos enteros a sumar tienen el mismo signo, se suman los números (sin signo) y se conserva el signo. Ejemplo 1 Sumamos los enteros +3+3 y +5+5: Sumamos los enteros −3−3 y −5−5: Si los dos enteros tienen signos distintos, se restan los números (sin signo) y se conserva el signo del número que sea mayor (sin signo). Ejemplo 2 Sumamos los enteros +4+4 y −5−5: Sumamos los enteros −3−3 y +5+5: En una suma de enteros, podemos omitir el signo positivo de la suma (y los paréntesis). Ejemplo 3 Reescribimos las sumas del ejemplo anterior: También, podemos omitir el signo positivo en la primera suma ya que no aporta información: 3. Resta de números enteros Cuando tenemos una resta de enteros, podemos transformarla en una suma cambiando el signo del segundo sumando. Ejemplo 4 Restamos los enteros 44 y −5−5: Restamos los enteros −5−5 y −7−7: Restamos los enteros −3−3 y 77: 4. Regla de los signos La regla de los signos proporciona el signo del resultado de la multiplicación/división de dos enteros: • • • El resultado es positivo si los dos factores tienen el mismo signo. El resultado es negativo si los dos factores tienen signo distinto. El resultado es neutro si alguno de los factores es 00. Podemos resumir la regla como sigue: 5. Multiplicación/división de enteros La multiplicación de dos enteros se calcula multiplicando los números (sin signo) y aplicando la regla de los signos. Ejemplo 5 Multiplicamos los enteros 22 y −3−3: Multiplicamos los enteros −3−3 y −3−3: Multiplicamos los enteros −2−2 y 55: Multiplicamos los enteros 22 y 44: La división de enteros se calcula dividiendo los números (sin signo) y aplicando la regla de los signos. Ejemplo 6 Dividimos los enteros 44 y −2−2: Dividimos los enteros −12−12 y −3−3: (-70) + (+86) = (+61) × (-8) = (-60) × (-47) = (-60) × (-50) = (+3944) ÷ (+58) = (+43) + (-94) = (-51) × (-97) = (+95) + (-86) = (+87) + (+52) = (-38) - (+91) = (-86) × (+4) = (+87) - (-45) = (-10) + (-37) = (-2) - (+63) = (+93) × (+14) = (-5340) ÷ (-89) = (+25) + (-81) = (-34) × (+16) = (+60) - (+85) = (+63) - (-48) = (+4712) ÷ (+62) = (-13) - (-10) = (+41) - (-58) = (+27) × (-67) = (+90) + (-75) = (+71) × (+14) = (+61) × (-98) = (-42) + (+81) = (-920) ÷ (+23) = (+65) - (-10) =