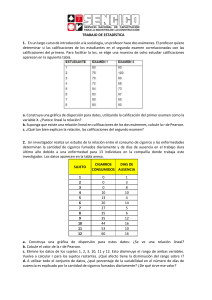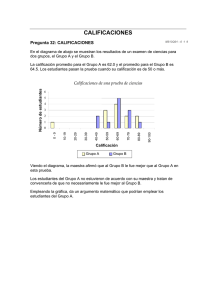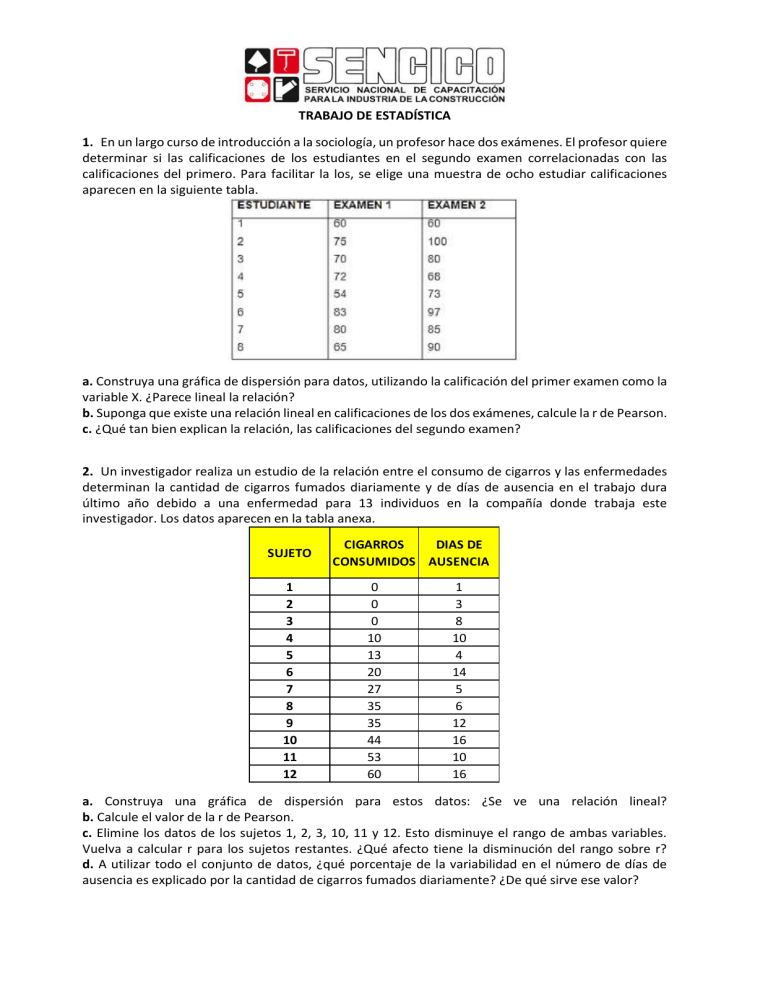
TRABAJO DE ESTADÍSTICA 1. En un largo curso de introducción a la sociología, un profesor hace dos exámenes. El profesor quiere determinar si las calificaciones de los estudiantes en el segundo examen correlacionadas con las calificaciones del primero. Para facilitar la los, se elige una muestra de ocho estudiar calificaciones aparecen en la siguiente tabla. a. Construya una gráfica de dispersión para datos, utilizando la calificación del primer examen como la variable X. ¿Parece lineal la relación? b. Suponga que existe una relación lineal en calificaciones de los dos exámenes, calcule la r de Pearson. c. ¿Qué tan bien explican la relación, las calificaciones del segundo examen? 2. Un investigador realiza un estudio de la relación entre el consumo de cigarros y las enfermedades determinan la cantidad de cigarros fumados diariamente y de días de ausencia en el trabajo dura último año debido a una enfermedad para 13 individuos en la compañía donde trabaja este investigador. Los datos aparecen en la tabla anexa. SUJETO 1 2 3 4 5 6 7 8 9 10 11 12 CIGARROS DIAS DE CONSUMIDOS AUSENCIA 0 0 0 10 13 20 27 35 35 44 53 60 1 3 8 10 4 14 5 6 12 16 10 16 a. Construya una gráfica de dispersión para estos datos: ¿Se ve una relación lineal? b. Calcule el valor de la r de Pearson. c. Elimine los datos de los sujetos 1, 2, 3, 10, 11 y 12. Esto disminuye el rango de ambas variables. Vuelva a calcular r para los sujetos restantes. ¿Qué afecto tiene la disminución del rango sobre r? d. A utilizar todo el conjunto de datos, ¿qué porcentaje de la variabilidad en el número de días de ausencia es explicado por la cantidad de cigarros fumados diariamente? ¿De qué sirve ese valor? 3. Un educador ha construido un examen para las aptitudes mecánicas y desea determinar si éste es confiable, mediante dos administraciones con un lapso de 1 mes entre ellas. Se realiza un estudio en el cual 10 estudiantes reciben dos administraciones del examen, donde la segunda administración ocurre un mes después que la primera. Los datos aparecen en la tabla. a. Construya una gráfica de dispersión para las parejas de datos. b. Determine el valor de r. c. ¿Sería justo decir que éste es un examen confiable? Explique esto al utilizar. SUJETO 1 2 3 4 5 6 7 8 9 10 ADMINISTRACIÓN 1 ADMINISTRACIÓN 2 10 12 20 25 27 35 43 40 32 47 10 15 17 25 32 37 40 38 30 49 4. Para determinar si alguna de ellas se puede utilizar como dispositivo de selección, elige 10 empleados representativos de la sección de manufactura, garantizando que un amplio rango de desempeño quede representado en la muestra, y realiza las dos pruebas con cada empleado. Los datos aparecen en la siguiente tabla. Mientras mayor sea la calificación, mejor será el desempeño. Las calificaciones de desempeño en el trabajo. Las calificaciones de desempeño fabricados por cada empleado por semana, promediados durante los últimos 6 meses. a. Construya una gráfica de dispersión del desempeño en el trabajo y la primera prueba, utilizando la prueba 1 como la variable X. ¿Parece lineal la relación? b. Suponga que la relación anterior es lineal y calcule el valor de la r de Pearson. c. Construya una gráfica de dispersión del desempeño en el trabajo y la segunda prueba, utilizando la prueba 2 como la variable X. ¿Parece lineal la relación? d. Suponga que la relación anterior es lineal, calcule el valor de la r de Pearson. e. Si sólo pudiera utilizar una de las pruebas para la selección de los empleados, ¿utilizaría alguna de ellas? En tal caso, ¿cuál de ellas? Explique.