Guia PYE 2020 v6

PROBABILIDAD Y ESTADÍSTICA Versión 6 - año 2020 CONTENIDO: F Espacios de probabilidad F Variables Aleatorias y Modelos F Pares de Variables Aleatorias F Estadı́stica Probabilidad y Estadı́stica - 2020 Página 1 de 86 Sección 1 PREFACIO Estas notas pretenden ser una referencia para el curso Probabilidad y Estadı́stica de la Facultad de Ingenierı́a de la Universidad ORT Uruguay, tanto para estudiantes como para docentes. Este material contiene notas del curso y un set de ejercicios del curso, que serán la referencia para los exámenes. Estas notas son resumidas por lo que se recomienda, para abundar más sobre el tema, aclarar algún concepto que no quedó suficientemente claro o mejorar sus conocimientos con otros puntos de vista, utilice los libros y materiales que en muy buena cantidad y calidad se ofrecen. Marzo del 2020 Ing. Freddy Rabı́n Catedrático de Matemática Responsable de esta edición Probabilidad y Estadı́stica - 2020 Página 2 de 86 Sección 2 ÍNDICE PREFACIO Página 2 ÍNDICE Página 3 ESPACIOS DE PROBABILIDAD Página 6 . Modelos deterministas vs. probabilistas Página 6 . Espacios de probabilidad Página 6 . Espacios de probabilidad finitos Página 11 . Calculando probabilidades (primera parte) Página 13 . Probabilidad condicional e independencia de suceso Página 19 . Calculando probabilidades (segunda parte) Página 25 PRÁCTICO: ESPACIOS DE PROBABILIDAD (primera parte) Página 27 PRÁCTICO: ESPACIOS DE PROBABILIDAD (segunda parte) Página 29 PRÁCTICO: ESPACIOS DE PROBABILIDAD (tercera parte) Página 32 . EVALUACIÓN DE ESPACIOS DE PROBABILIDAD VARIABLES ALEATORIAS Página 35 Página 37 . Variables aleatorias discretas y continuas Página 37 . “Composición” de una variable aleatoria Página 40 . Valor esperado, una medida de exactitud Página 41 . Varianza, una medida de dispersión Página 42 . Distribuciones de probabilidad con nombre Página 43 Probabilidad y Estadı́stica - 2020 Página 3 de 86 PRÁCTICO: VARIABLES ALEATORIAS (1a. parte) Página 45 PRÁCTICO: VARIABLES ALEATORIAS (2a. parte) Página 48 PRÁCTICO: VARIABLES ALEATORIAS (3a. parte) Página 49 PRÁCTICO: VARIABLES ALEATORIAS (4a. parte, modelos) Página 51 PRÁCTICO: VARIABLES ALEATORIAS (5a. parte, problemas con v.a.) Página 56 DOS VARIABLES ALEATORIAS Página 60 . Par aleatorio discreto Página 60 . Par aleatorio continuo Página 61 . Ejemplos con pares aleatorios Página 62 . Independencia de variables aleatorias Página 63 . Más ejemplos con pares aleatorios Página 64 PRÁCTICO: DOS ALEATORIAS . EVALUACIÓN DE VARIABLES ALEATORIAS ESTADÍSTICA Página 66 Página 70 Página 72 . Muestras y estadı́sticos Página 72 . Máximo y Mı́nimo Página 72 . El promedio Página 72 . La desviación estándar Página 75 . Estimación puntual Página 76 . Estimación por intervalos (Intervalos de confianza) Página 76 Probabilidad y Estadı́stica - 2020 Página 4 de 86 PRÁCTICO: ESTADÍSTICA (primera parte) Página 77 PRÁCTICO: ESTADÍSTICA (segunda parte) Página 80 PRÁCTICO: ESTADÍSTICA (tercera parte) Página 83 . EVALUACIÓN DE ESTADÍSTICA Probabilidad y Estadı́stica - 2020 Página 85 Página 5 de 86 Sección 3 Tema (I) : ESPACIOS DE PROBABILIDAD I.1 MODELOS DETERMINISTAS vs. PROBABILISTAS Para introducir el concepto de probabilidades podrı́amos decir en forma no formal que “cuánta chance tiene de salir” y debemos distinguir entre modelos deterministas, al que estamos más acostumbrados, y probabilistas, que estamos proponiendo. Decimos que el modelo que estamos realizando de un experimento es un modelo determinista si las condiciones en que se realiza el experimento determina el resultado del mismo. Decimos que el modelo que estamos realizando de un experimento es un modelo probabilı́stico o estocástico si las condiciones en las que se realiza el experimento determinan la distribución de probabilidades de obtener cada resultado posible. I.2 ESPACIOS DE PROBABILIDAD Definición I.1 (Espacios de probabilidad). Diremos que (Ω , A , P ) es un espacio de probabilidad donde: F Ω es el conjunto de resultados posibles del experimento aleatorio. A Ω lo llamaremos espacio muestral. F A es el conjunto de sucesos (eventos), en definitiva conjunto de subconjuntos de Ω. F P es la función de probabilidad, P : A → [0, 1], que cumple: • P (Ω) = 1. +∞ +∞ P n=1 n=1 • P ( ∪ An ) = P (An ) si los sucesos {An }+∞ n=1 son disjuntos 2 a 2 (Ai ∩ Aj = ∅ si i 6= j). Observación I.2. Diremos que el espacio de probabilidad es: F Discreto: Si es finito o infinito numerable (se pueden enumerar sus elementos). F Continuo: Si es infinito no numerable (por ejemplo Ω = IR o Ω = [a, b] ⊂ IR). Observación I.3. El conjunto de sucesos A debe cumplir determinadas propiedades, las lógicas, pero no entraremos a describirlas. En este curso consideraremos A = P(Ω) = 2Ω (todos los subconjuntos del espacio muestral) Probabilidad y Estadı́stica - 2020 Página 6 de 86 Por ejemplo: Si Ω = { a , b , c }, P(Ω) = { ∅ , { a } , { b } , { c } , { a , b } , { a , c } , { b , c } , Ω } Observación I.4 (Interpretación de las operaciones de conjuntos). Las operaciones entre sucesos (entre conjuntos) se interpretan con los nexos lógicos: Operación A∪B A∩B Ac Interpretación A y/o B AyB no sucede A y los diagramas de Venn dan una posible representación y visualización de los sucesos asociando la probabilidad con el “área del conjunto”. Observación I.5. La correctitud del modelo elegido para el problema planteado es algo a analizar con cuidado. Veamos algunas propiedades que se cumplen en todo espacio de probabilidad. Probabilidad y Estadı́stica - 2020 Página 7 de 86 Propiedad I.6. En cualquier espacio de probabilidad se cumple: P (∅) = 0. Demostración: Aplicando la segunda condición de la definición de la función probabilidad: +∞ P (∅) = P ( ∪ ∅) = n=1 +∞ X P (∅) n=1 De donde se concluye que P (∅) = 0. L.Q.Q.D. Propiedad I.7 (“Ley de la suma” (parte 1 de 2)). En cualquier espacio de probabilidad se cumple: P (A ∪ B) = P (A) + P (B) si A y B son disjuntos (A ∩ B = ∅) Demostración: P (A ∪ B) = P (A ∪ B ∪ ∅ ∪ ∅ ∪ ∅ ∪ ∅... ∪ ∅...) y ahora, como A y B son disjuntos, aplicando la segunda condición de la definición de la función probabilidad, se tiene: P (A ∪ B) = P (A) + P (B) + P (∅) + P (∅) + P (∅) + ... + P (∅) + ... y como P (∅) = 0: P (A ∪ B) = P (A) + P (B) L.Q.Q.D. Observación I.8. La propiedad anterior se puede generalizar fácilmente: N P ( ∪ An ) = n=1 N X P (An ) n=1 si los sucesos {An }N n=1 son disjuntos 2 a 2. Ası́ queda probada la ley de la suma o ley de adición para cantidad finita de sucesos. Probabilidad y Estadı́stica - 2020 Página 8 de 86 Propiedad I.9. En cualquier espacio de probabilidad se cumple: F P (B − A) = P (B) − P (A ∩ B) y se concluye P (B − A) ≤ P (B) y P (A ∩ B) ≤ P (B). F En particular, si A ⊂ B entonces P (B − A) = P (B) − P (A) y se concluye P (A) ≤ P (B). Demostración: Para probar que P (B − A) = P (B) − P (A ∩ B) podemos recurrir a los diagramas de Venn: o podemos hacer un desarrollo analı́tico: Aplicando la propiedad I.7, como B = (A ∩ B) ∪ (B − A) y A ∩ B y B − A son disjuntos, se tiene: P (B) = P (A ∩ B) + P (B − A) Despejando se tiene la igualdad de la tesis: P (B − A) = P (B) − P (A ∩ B). Si observamos que P (A ∩ B) ≥ 0 y P (B − A) ≥ 0, concluimos la desigualdad de la tesis: P (B − A) ≤ P (B) y P (A ∩ B) ≤ P (B) Se puede observar fácilmente que la segunda parte del teorema es efectivamente un caso particular. L.Q.Q.D. Propiedad I.10 (“Ley de la suma” (parte 2 de 2)). En cualquier espacio de probabilidad se cumple: P (A ∪ B) = P (A) + P (B) − P (A ∩ B). Demostración: Para probar que P (A ∪ B) = P (A) + P (B) − P (A ∩ B) podemos recurrir a los diagramas de Venn: Probabilidad y Estadı́stica - 2020 Página 9 de 86 o podemos hacer un desarrollo analı́tico: Aplicando la propiedad I.7, como A ∪ B = A ∪ (B − A) y A y B − A1 son disjuntos, se tiene: P (A ∪ B) = P (A) + P (B − A) Además, usando la propiedad I.9: P (B − A) = P (B) − P (A ∩ B) Sustituyendo una igualdad en la otra y despejando se tiene la tesis: P (A ∪ B) = P (A) + P (B) − P (A ∩ B) L.Q.Q.D. Observación I.11. La propiedad anterior, en que los sucesos no son disjuntos, es algo más complejo de generalizar. En este caso se cumple el llamado “Principio de Inclusión - Exclusión” que en el caso de tres sucesos A, B y C se enuncia: P (A ∪ B ∪ C) = P (A) + P (B) + P (C) − P (A ∩ B) − P (A ∩ C) − P (B ∩ C) + P (A ∩ B ∩ C) Dejamos al lector demostrarlo. Propiedad I.12. En cualquier espacio de probabilidad se cumple: P (Ac ) = 1 − P (A). Demostración: Basta tomar B = Ω, A ⊂ Ω, en la propiedad I.9. P (Ω − A) = P (Ω) − P (A) Ahora, como Ω − A = Ac y P (Ω) = 1 se tiene la tesis: P (Ac ) = 1 − P (A) o recurriendo a los diagramas de Venn: L.Q.Q.D. 1 La diferencia de conjuntos B − A, también anotada B\A, denota el conjunto {ω ∈ B / ω ∈ / A} Probabilidad y Estadı́stica - 2020 Página 10 de 86 Propiedad I.13 (Continuidad de las probabilidades). F Si (An ) es una sucesión creciente de sucesos (A1 ⊂ A2 ⊂ ... ⊂ An ⊂ An+1 ⊂ ...), entonces +∞ N P ( ∪ An ) = lim P (AN ) = lim P ( ∪ An ) N →+∞ n=1 N →+∞ n=1 F Si (An ) es una sucesión decreciente de sucesos (A1 ⊃ A2 ⊃ ... ⊃ An ⊃ An+1 ⊃ ...), entonces +∞ N P ( ∩ An ) = lim P (AN ) = lim P ( ∩ An ) N →+∞ n=1 N →+∞ n=1 Demostración (la omitiremos). I.3 ESPACIOS DE PROBABILIDAD FINITOS En este caso el espacio muestral es finito: Ω = {ω1 , ω2 , ... ωr } La función probabilidad quedará determinada asignando la probabilidad a cada suceso elemental (a cada resultado) pj = P ({wj }) (a veces se abusa de la notación pj = P (wj )) y se tiene: F p1 + p2 + ... + pr = 1. F P ({ωj1 , ωj2 , ... ωjk }) = k P p ji = i=1 k P P ({wji }). i=1 Como caso particular tenemos la definición clásica de probabilidad, donde los resultados son equiprobables y se tiene 1 pj = cte = r P ({ωj1 , ωj2 , ... ωjk }) = k X 1 i=1 Probabilidad y Estadı́stica - 2020 r = k Cantidad de casos f avorables = r Cantidad de casos posibles Página 11 de 86 Ejemplo I.14. Lanzamos una moneda equilibrada y anotamos el resultado: cara (C) o número (N ). Como espacio muestral podemos tomar el conjunto finito: Ω = { C , N }. El conjunto de sucesos lo consideramos: A = P(Ω) = { ∅ , { C } , { N } , Ω } Para determinar la función de probabilidad observemos que estamos en un caso en el que cada resultado (suceso elemental) tiene la misma posibilidad de ocurrir, decimos que estamos en un “espacio de equiprobabilidad”. Usemos entonces: Cantidad de casos f avorables Cantidad de casos posibles 1 ; P (C, N ) = 1 2 Notemos que dicha función toma valores reales no negativos, menores o iguales a 1 y que la suma de las probabilidades de los sucesos individuales es 1, lo que caracterizan a una función probabilidad discreta. P (∅) = 0 ; P ( {C} ) = P ( {N } ) = Ejemplo I.15. Se lanza un dado equilibrado y se anota el número que sale. Como espacio muestral podemos tomar el conjunto finito: Ω = { 1 , 2 , 3 , 4 , 5 , 6 }. El conjunto de sucesos lo consideramos: A = P(Ω) que tiene 26 = 64 elementos. Como en el ejemplo anterior cada resultado individual presenta la misma posibilidad de ocurrir. Como la suma de todas las probabilidades individuales es 1 y son 6 sucesos individuales se concluye: P ( {1} ) = P ( {2} ) = P ( {3} ) = P ( {4} ) = P ( {5} ) = P ( {6} ) = 1 6 Expresemos algunos sucesos en forma verbal y otros en forma de operaciones entre conjuntos: A = { salga par } B = { salga 1 o 2 } Usando las leyes de probabilidad: P (A) = P ( { 2 , 4 , 6 } ) = P ( {2} ) + P ( {4} ) + P ( {6} ) = 1 1 1 1 + + = 6 6 6 2 o usando (“espacio de equiprobabilidad”) Cantidad de casos f avorables Cantidad de casos posibles P (A) = P ( { 2 , 4 , 6 } ) = Probabilidad y Estadı́stica - 2020 3 1 = 6 2 Página 12 de 86 P (B) = P ( { salga 1 o 2 } ) = P ( { 1 , 2 } ) = 1 2 = 6 3 A ∩ B = { [ salga par ] y [ salga 1 o 2 ] } A ∪ B = { [ salga par ] o [ salga 1 o 2 ] } P (A ∩ B) = P ( { 2 } ) = 1 6 P (A ∪ B) = P ( { 1 2 , 4 , 6 } ) = 4 2 = 6 3 y verificamos que: P (A ∪ B) = P (A) + P (B) − P (A ∩ B) 2 1 1 1 4 3 2 1 = + − o más evidente = + − 3 2 3 6 6 6 6 6 I.4 CALCULANDO PROBABILIDADES (primera parte) En esta sección presentaremos varios ejemplos para mostrar distintas técnicas de cálculo de probabilidades con los elementos vistos. Ejemplo I.16. En una carrera participan tres competidores a, b y c. Se estima que el corredor a tiene el doble de probabilidad de ganar que el corredor b y este a su vez tiene el triple de probabilidad de ganar que el corredor c. Queremos calcular las respectivas probabilidades de ganar de cada corredor (se sobreentiende que debe haber un y solo un ganador). Se consideran los sucesos disjuntos dos a dos: A = { gana el corredor a } , B = { gana el corredor b } , C = { gana el corredor c } Tenemos entonces que Ω = A ∪ B ∪ C, de donde usando la definición de probabilidad se cumple que: 1 = P (Ω) = P (A) + P (B) + P (C) Por hipótesis: P (A) = 6 P (C) y P (B) = 3 P (C) y sustituyendo en la igualdad anterior se tiene: 10 P (C) = 1 luego P (A) = 6 3 3 1 = , P (B) = y P (C) = . 10 5 10 10 Probabilidad y Estadı́stica - 2020 Página 13 de 86 Ejemplo I.17. Se lanza en forma sucesiva, una moneda equilibrada, 8 veces, y queremos calcular la probabilidad de que salgan 5 caras y 3 cruces. Primeramente describamos un espacio muestral para este experimento: Ω = { { x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8 } / xi ∈ { C , X } } Planteamos ver los resultados sin orden indicando la cantidad de caras y cantidad de cruces. El problema de este planteo es que los resultados no tienen todos la misma probabilidad. Si consideramos: Ω = { ( x1 , x 2 , x 3 , x 4 , x 5 , x 6 , x 7 , x 8 ) / xi ∈ { C , X } } Resultados ordenados (por ejemplo en el orden de realización de las 8 tiradas), ahora sı́ tienen la misma probabilidad y podemos calcular: P (“5 caras y 3 cruces”) = Cantidad de casos f avorables C8 = 85 Cantidad de casos posibles 2 Los casos favorables son C58 , la forma de ubicar las 5 caras en los 8 lugares mientras los casos posibles son 28 (2 opciones para cada uno de los 8 lugares). Ejemplo I.18. En una ciudad se publican tres periódicos que designaremos A, B y C. Se tienen los siguientes datos: F El 20 % de la ciudad lee el A. F El 16 % de la ciudad lee el B. F El 14 % de la ciudad lee el C. F El 8 % de la ciudad lee el A y el B. F El 5 % de la ciudad lee el A y el C. F El 4 % de la ciudad lee el B y el C. F El 4 % de la ciudad lee el A el B y el C. Si se elige al azar una persona de la ciudad, calcular la probabilidad de que: 1. No lea ninguno de los periódicos. 2. Lea exactamente uno de los tres periódicos. 3. Lea el periódico A o lea el periódico B, entendiendo el “o” no excluyente. 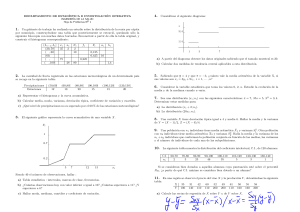Probabilidad y Estadı́stica - 2020 Página 14 de 86 Representando los datos en diagramas de Venn obtenemos el siguiente diagrama: donde las probabilidades se indican como porcentajes. Podemos ahora contestar las preguntas, identificando la probabilidad requerida que esta expresada en forma verbal, lo escribimos en lenguaje de conjuntos: 1. No lea ninguno de los periódicos. P ( Ac ∩ B c ∩ C c ) = P ( [ A ∪ B ∪ C ]c ) = 0, 63 2. Lea exactamente uno de los tres periódicos. P ( [ A ∩ B c ∩ C c ] ∪ [ Ac ∩ B ∩ C c ] ∪ [ Ac ∩ B c ∩ C ] ) = 0, 11 + 0, 08 + 0, 09 = 0, 28 3. Lea el periódico A o lea el periódico B, entendiendo el “o” no excluyente. P ( A ∪ B ) = 0, 11 + 0, 01 + 0, 04 + 0, 04 + 0, 08 = 0, 28 o usando propiedades: P (A ∪ B) = P (A) + P (B) − P (A ∩ B) = 0, 20 + 0, 16 − 0, 08 = 0, 28 Ejemplo I.19. En un ómnibus de 8 asientos dispuestos en 2 filas de dos asientos pegados a cada lado del pasillo, vacı́o, suben dos personas y se sientan, ¿cuál es la probabilidad de sentarse uno al lado del otro?. Tener en cuenta que: F se sientan en asientos distintos y no tienen en cuenta dónde se sentó el otro más que para no sentarse encima. F la siguiente tabla muestra las preferencias para sentarse, de cualquiera de ellos, si el ómnibus está vacı́o, dando la probabilidad de cada asiento. Probabilidad y Estadı́stica - 2020 Página 15 de 86 fila 1 2 ventana 0.2 0.2 pasillo 0.05 0.05 pasillo 0.05 0.05 ventana 0.2 0.2 De la tabla sabemos que cada asiento junto a una ventana tiene la misma probabilidad de ser elegido, a su vez cada asiento sobre el pasillo también y entre ellos tenemos que la probabilidad de elegir cada una de las cuatro ventanas es cuatro veces la de elegir el asiento contiguo. Podemos llevar nuestro modelo a uno de equiprobabilidad considerando cada asiento junto a la ventana como cuatro asientos junto al pasillo. Tenemos pues 20 asientos con igual probabilidad de ser elegidos, 16 sobre ventana y 4 sobre pasillo. En este contexto podemos calcular en forma más sencilla la probabilidad pedida. Supongamos que la primer persona se sienta en una ventana, para que la segunda se siente junto a la primera tenemos el siguiente cálculo: 16 1 ∗ 20 16 | {z } | {z } elijo una ventana elijo el asiento contiguo Para elegir el asiento contiguo quedan 16 asientos porque saco las 4 ventanas que corresponden al asiento de la primer persona. Si ahora suponemos que la primer persona se sienta en un pasillo, para que la segunda se siente junto a la primera tenemos el siguiente cálculo: 4 4 ∗ 20 19 | {z } | {z } elijo un pasillo elijo el asiento contiguo Para elegir el asiento contiguo quedan 4 ventanas que están al lado del pasillo en el que se sentó la primer persona. 16 1 4 4 7 Finalmente la probabilidad pedida vale: ∗ + ∗ = . 20 16 20 19 76 El siguiente diagrama de árbol representa el problema, “en dos etapas”, que formalizaremos aún más en la sección siguiente (“los valores de una rama se multiplican” (ley del producto) mientras “las distintas ramas se suman” (ley de la suma)). Probabilidad y Estadı́stica - 2020 Página 16 de 86 Ejemplo I.20. En una urna hay 6 bolas blancas, 8 bolas azules y 16 bolas rojas, todas de igual medida. Se extraen en forma conjunta un conjunto de tres bolas. Se pide calcular las probabilidades de los siguientes sucesos: F A = { Sacar las tres bolas azules }. F B = { Sacar las tres bolas de diferentes colores }. F C = { Sacar dos bolas azules y una roja }. F D = { Sacar al menos una bola azul }. Si pensamos que cada extracción es una selección de tres elementos diferentes, de un conjunto de 30 posibles, donde en cada selección no distinguimos el orden de los elementos que la conforman. Tenemos entonces que estamos en un espacio de equiprobabilidad donde el cardinal del espacio muestral es C330 (combinaciones sin repetición de 30 elementos formados de a 3). En cada caso pues, usaremos herramientas combinatorias para determinar el números de casos favorables a cada suceso. Tenemos: F En el caso de A los casos favorables son C38 (mismo razonamiento que para el espacio muestral restringiéndonos a bolas azules). Luego: P (A) = C38 C330 Con razonamientos parecidos tenemos: F En el caso de B los casos favorables son 8 ∗ 6 ∗ 16 y por lo tanto: P (B) = Probabilidad y Estadı́stica - 2020 8 ∗ 6 ∗ 16 C330 Página 17 de 86 F En el caso de C los casos favorables son C28 ∗ 16 y por lo tanto: P (C) = C28 ∗ 16 C330 F Para contar los casos favorables en el caso de D lo podemos hacer considerando los sucesos disjuntos, separando en casos: • Sacar las tres bolas azules. • Sacar dos bolas azules y otra que no lo sea. • Sacar una bola azul y otra dos que no lo sean. para luego sumarlas cantidades o, más sencillo, contar lo contrario: Los casos no favorables son C222 y por lo tanto: P (D) = 1 − C222 C330 Ejemplo I.21. Se lanzan dos dados equilibrados de diferente color y se anotan sus resultados. 1. Calcular la probabilidad de que la suma de los resultados de los dos dados sea siete. 2. A dos amigos Pablo y Juan, se les propone el siguiente juego: F Se lanzan los dados de la primer parte. F Comienza tirando Juan y luego se alternan el turno de lanzar. F Gana el primero que sume siete en su tirada. Se pide calcular la probabilidad de los siguientes sucesos: A = { gana Juan } ; B = { gana P ablo } ; C = { empatan } Primero considera el lanzamiento de los dos dados. En este caso el espacio muestral se puede mostrar en la siguiente figura (tabla de la izquierda), donde cada pareja de resultados tiene la misma posibilidad de salir. Los casos favorables se indican en la misma figura (tabla de la derecha): Tenemos entonces: P ( salga 7 ) = Probabilidad y Estadı́stica - 2020 6 1 = 36 6 Página 18 de 86 El juego que realizan los dos amigos Pablo y Juan puede representarse mediante el siguiente árbol: Ası́ la probabilidad de ganar de Juan puede calcularse: +∞ 1 5 5 1 5 5 5 5 1 1X P (A) = + ∗ ∗ + ∗ ∗ ∗ ∗ + ... = 6 6 6 6 6 6 6 6 6 6 n=0 5 6 2n +∞ 1X = 6 n=0 25 36 n = 6 11 Dejamos al lector calcular las probabilidades de B y C. I.5 PROBABILIDAD CONDICIONAL E INDEPENDENCIA DE SUCESOS Definición I.22 (Probabilidad condicional). Sean A, B ∈ A con P (B) > 0. Definimos la probabilidad condicional de A dado B como df P (A/B) = P (A ∩ B) P (B) Observación I.23. Los diagramas de Venn permiten interpretar la probabilidad condicional. En el caso general, cuando calculamos la probabilidad condicional de A dado B, lo que estamos haciendo es calcular la probabilidad de que ocurra el suceso A, tomando como conjunto de referencia al conjunto B. Podemos verlo como el peso relativo del suceso A (la parte A dentro de B), con respecto al peso de B. Esto no se observa directamente en el diagrama (un poco más si hiciéramos los diagramas a escala), pero podemos “verlo abstractamente”, directamente en la definición: P (A/B) = Probabilidad y Estadı́stica - 2020 P (A ∩ B) P (B) Página 19 de 86 Veamos algunos casos particulares que nos van a marcar la interpretación y la idea intuitiva de la probabilidad condicional. Casos particulares: F Si A ∩ B = ∅, entonces: P (A/B) = 0. Para demostrarlo basta observar que P (A/B) = P (A ∩ B) P (∅) 0 = = = 0. P (B) P (B) P (B) Lógico: Si ocurrió B y A y B son disjuntos, seguro que no ocurrió A. F Si B ⊂ A, entonces: P (A/B) = 1. Para demostrarlo basta observar que A ∩ B = B, luego P (A/B) = P (A ∩ B) P (B) = = 1. P (B) P (B) Lógico: Si ocurrió B y B está incluido en A, seguro que también ocurrió A. F Si A ⊂ B, entonces P (A/B) > P (A). Para demostrarlo basta observar que A ∩ B = A, luego P (A/B) = P (A ∩ B) P (A) = > P (A). P (B) P (B) Lógico: Si ocurrió B y A está incluido en B, la probabilidad de A aumenta (A se ve más grande, “los mismos casos favorables, pero eventualmente disminuyeron los casos posibles”). Ejemplo I.24. Se lanza un dado equilibrado. Calcular la probabilidad de que: F salga el número 2. F salga el número 2, sabiendo que salió un número par. Estamos en el caso de un espacio de equiprobabilidad donde hay 6 casos posibles, ası́: P ( “salga el número 2” ) == P ( “salga par” ) == 1 Cantidad de casos f avorables = Cantidad de casos posibles 6 Cantidad de casos f avorables 3 1 = = Cantidad de casos posibles 6 2 P ( “salga el número 2” / “salga par” ) = = P ( “salga el número 2” ∩ “salga par” ) = P ( “salga par” ) P ( “salga el número 2” ) 1/6 1 = = P ( “salga par” ) 1/2 3 Es como si la población total se reduce a tres de los cuales uno solo es favorables. Probabilidad y Estadı́stica - 2020 Página 20 de 86 Propiedad I.25. Si dejamos B fijo P (A/B) es una probabilidad, o sea: (Ω , A , PB ), donde PB (A) = P (A/B) es un espacio de probabilidad. Demostración: Primero probemos que 0 ≤ PB (A) ≤ 1 para todo suceso A. PB (A) = P (A/B) = P (A ∩ B) . P (B) PB (A) ≥ 0 por ser cociente de dos números no negativos. Como (A ∩ B) ⊂ B, se tiene P (A ∩ B) ≤ P (B), por lo que PB (A) ≤ 1. Luego hay que probar las dos propiedades que definen una función probabilidad: (i) P (Ω/B) = 1. P (Ω/B) = P (B) P (Ω ∩ B) = =1 P (B) P (B) Ahora probemos: +∞ +∞ P (ii) P ∪ An /B = P (An /B) si los sucesos {An }+∞ n=1 son disjuntos 2 a 2 (Ai ∩ Aj = ∅ si i 6= j). n=1 n=1 Demostración: P +∞ ∪ An /B n=1 +∞ P = P (B) P (An ∩ B) P (B) = ∩B n=1 = n=1 ∪ An P +∞ P = +∞ X P (An ∩ B) n=1 P (B) +∞ ∪ (An ∩ B) n=1 P (B) = +∞ X = P (An /B) n=1 +∞ donde se usó que los sucesos {An ∩ B}+∞ n=1 son disjuntos 2 a 2 por también serlo los sucesos {An }n=1 (hipótesis), conjuntamente con que P es una función de probabilidad. L.Q.Q.D. Propiedad I.26 (“Ley del producto”). F Si A y B son dos sucesos, con P (B) > 0, entonces P (A ∩ B) = P (B) P (A/B). F Si A1 , A2 , ... Ak son k sucesos, con P (Ai ) > 0 para todo i = 1, 2, ..., k, entonces: P (A1 ∩ A2 ∩ ... ∩ Ak ) = P (A1 ) P (A2 /A1 ) P (A3 /A1 ∩ A2 ) ... P (Ak /A1 ∩ A2 ∩ ... ∩ Ak−1 ) Probabilidad y Estadı́stica - 2020 Página 21 de 86 Demostración: La primera igualdad resulta de despejar P (A ∩ B) en la definición de probabilidad condicional. Veamos la segunda igualdad para k = 3: P (A1 ) P (A2 /A1 ) P (A3 /A1 ∩ A2 ) = P (A1 ) P (A1 ∩ A2 ) P (A1 ∩ A2 ∩ A3 ) = P (A1 ∩ A2 ∩ A3 ) P (A1 ) P (A1 ∩ A2 ) L.Q.Q.D. Observación I.27. Esta “Ley del producto” justifica los diagramas de árbol utilizados antes. Además nos dice que sobre las flechas debe colocarse la probabilidad condicional de pasar del estado anterior al siguiente: Ejemplo I.28. Se considera el siguiente experimento: F Extraemos una bola de una urna que contiene 12 bolas idénticas, 4 azules y 8 blancas. F Sin reponer la bola extraı́da, se realiza una nueva extracción. Llamaremos: A = { “sale una bola azul en la primer extracción” } B = { “sale una bola blanca en la segunda extracción” } Calculemos P ( B / A ) y P ( A / B ). Podemos resumir la situación en el siguiente diagrama de árbol: Probabilidad y Estadı́stica - 2020 Página 22 de 86 La probabilidad P ( B / A ) fue parte del armado del árbol (para la segunda extracción queda una urna con 3 azules y 8 blancas): 8 P(B /A) = 11 Mientras P ( A / B ) podemos calcularla de la siguiente forma: P(A/B ) = P(A)P(B /A) P (A ∩ B) = P (B) P ( A ) P ( B / A ) + P ( Ac ) P ( B / Ac ) o sea: P(A/B ) = 1 3 ∗ 1 3 8 11 8 ∗ 11 + 32 ∗ 7 11 = 8 4 = 22 11 Propiedad I.29 (“Fórmula de la probabilidad total”). N Si {Bj }N j=1 es una partición de Ω, o sea ∪ Bj = Ω y los sucesos son disjuntos 2 a 2, entonces: j=1 P (A) = N X P (Bj ) P (A/Bj ) j=1 Demostración: P (A) = P (Ω ∩ A) = P +∞ ∪ Bj j=1 ∩A =P X +∞ N X ∪ (Bj ∩ A) = P (Bj ∩ A) = P (Bj ) P (A/Bj ) +∞ j=1 n=1 j=1 +∞ donde se usó que los sucesos {Bj ∩ A}+∞ n=1 son disjuntos 2 a 2 por también serlo los sucesos {Bj }j=1 L.Q.Q.D. Observación I.30. El siguiente diagrama puede ayudar para visualizar la demostración de la “Fórmula de la probabilidad total” (N = 3). Probabilidad y Estadı́stica - 2020 Página 23 de 86 Propiedad I.31 (“Fórmula de Bayes”). F P (B/A) = P (A/B) P (B) . P (A) N F Si {Bj }N j=1 es una partición de Ω, o sea ∪ Bj = Ω y los sucesos son disjuntos 2 a 2, entonces: j=1 P (Bk /A) = P (A/Bk ) P (Bk ) N P P (Bj ) P (A/Bj ) j=1 Demostración: Para demostrar la primera igualdad, por la definición definición de probabilidad condicional o la ley del producto (propiedad I.26) se tiene: P (B/A)P (A) = P (A ∩ B) = P (A/B)P (B) y despejando se tiene la tesis. Para demostrar la segunda igualdad combinamos la primer igualdad: P (Bj /A) = P (A/Bj ) P (Bj ) P (A) con la fórmula de la probabilidad total (propiedad I.29): P (A) = N X P (Bj ) P (A/Bj ) j=1 y simplemente sustituyendo se concluye: P (Bk /A) = P (A/Bk ) P (Bk ) N P P (Bj )P (A/Bj ) j=1 L.Q.Q.D. Definición I.32 (Sucesos independientes). A, B ∈ A son independientes sii P ( A ∩ B ) = P ( A ) P ( B ). Observación I.33. Si P (A) > 0, A y B son independientes sii P (B/A) = P (B) (esta condición es más intuitiva). Probabilidad y Estadı́stica - 2020 Página 24 de 86 Propiedad I.34. Si A y B son independientes, entonces: F Ac y B son independientes. F Ac y B c son independientes. Demostremos que Ac y B son independientes: Tenemos que probar que P ( Ac ∩ B ) = P ( Ac ) P ( B ), sabiendo que P ( A ∩ B ) = P ( A ) P ( B ). P ( Ac ∩B ) = P ( B−A ) = P ( B )−P ( A∩B ) = P ( B )−P ( A ) P ( B ) = [ 1−P ( A ) ] P ( B ) = P ( Ac ) P ( B ) L.Q.Q.D. El lector debe justificar cada paso ası́ como demostrar la segunda igualdad. Definición I.35 (Sucesos independientes, generalización). Los sucesos de la colección {Ai } son independientes sii para cualquier elección finita Ai1 , Ai2 , ... , Air se verifica P (Ai1 ∩ Ai2 ∩ ... ∩ Air ) = P (Ai1 )P (Ai2 )...P (Air ) En la siguiente sección veremos algunos ejemplos más de cálculo de probabilidades. I.6 CALCULANDO PROBABILIDADES (segunda parte) Ejemplo I.36. Un grupo de 40 estudiantes, de los cuales 8 son altos, 24 intermedios y 8 bajos, va a dar una prueba de matemática. La probabilidad de que un estudiante alto apruebe la prueba es de 0,8, si es intermedio es de 0,9 y si es bajo es de 0,5. Se pide: 1. Si se elige al azar un estudiante del grupo, ¿cuál es la probabilidad de que apruebe la prueba?. 2. Se elige al azar un estudiante de este grupo que salvó la prueba: a) ¿cuál es la probabilidad de que sea alto?. b) ¿cuál es la probabilidad de que sea intermedio?. c) ¿cuál es la probabilidad de que sea bajo?. Probabilidad y Estadı́stica - 2020 Página 25 de 86 3. ¿Son independientes los sucesos “ser alto” y “aprueba la prueba”? 4. ¿Son independientes los sucesos “ser intermedio” y “aprueba la prueba”? 5. ¿Son independientes los sucesos “ser bajo” y “aprueba la prueba”? Ejemplo I.37. Un examen que consta de 6 ejercicios múltiple opción, los cuáles se contestan bien o mal (no hay resultados intermedios), con cinco opciones cada uno. Tres de los ejercicios podemos considerarlos fáciles y los otros tres difı́ciles. El examen se aprueba con 5 o más preguntas bien contestadas. La probabilidad de que Juan conteste bien una pregunta fácil es la probabilidad de contestarla bien es 15 . 2 3 mientras que si la pregunta es difı́cil Se pide: 1. ¿Por qué no es lógico pensar que la probabilidad de contestar una pregunta sea menor que 15 ?. ¿Cómo se interpreta que Juan tenga probabilidad 51 de contestar bien una pregunta difı́cil?. 2. Calcular la probabilidad de que Juan salve el examen. 3. Si Juan salvó el examen, ¿cuál es la probabilidad de que haya contestado exactamente 5 preguntas bien?. Ejemplo I.38. Un niño, que no sabe matemática, ordena cuatro fichas que tienen grabados números, más precisamente los números son 3, 4, 8 y 9, armando números de cuatro cifras. 1. ¿Cuál es la probabilidad de que el número obtenido sea menor de 4000 o par?. 2. ¿Cuál es la probabilidad de que el número obtenido sea menor de 4000 y par?. 3. ¿Son independientes los sucesos “menor de 4000” y “par”? 4. Si el número obtenido es menor de 4000 o par, ¿cuál es la probabilidad de que sea par?. 5. Si el número obtenido es menor de 4000 o par, ¿cuál es la probabilidad de que sea menor de 4000?. Nota: El “o” en todos los casos es no excluyente (equivale al “y/o”). Probabilidad y Estadı́stica - 2020 Página 26 de 86 Sección 4 Práctico (I) : ESPACIOS DE PROBABILIDAD (1a. parte) Ejercicio I.1. Sean A, B y C tres sucesos asociados a un mismo experimento. Expresar las siguientes proposiciones verbales en notación de conjuntos. 1. Al menos uno de los sucesos ocurre. 2. Exactamente uno de los sucesos ocurre. 3. Exactamente dos de los sucesos ocurren. 4. No ocurren más de dos de los sucesos. 5. No ocurren ninguno de los tres sucesos. Ejercicio I.2. Determinar el espacio muestral asociado a cada uno de los siguientes experimentos aleatorios, y en el caso que sea finito, indicar su cardinal (cantidad de elementos). 1. Lanzar al aire una moneda tres veces. 2. Extraer dos fichas sucesivamente y sin reposición de una bolsa que contiene fichas numeradas con los dı́gitos pares. 3. Lanzar una moneda finalizando el experimento si sale número; si sale cara, tirar además un dado. 4. Seleccionar al azar dos alumnos de una clase de 20. 5. Duración de un componente electrónico en un sistema hasta que falla. Ejercicio I.3. Si se lanzan tres monedas equilibradas, calcular la probabilidad de obtener: 1. Todas salgan cara. 2. Salga una cara y dos cruces. 3. Salga dos caras y una cruz. 4. Todas salgan cruces. Ejercicio I.4. Si en un ómnibus de 10 asientos dispuestos en 5 filas de dos asientos pegados suben dos personas y se sientan aleatoriamente, ¿cuál es la probabilidad de sentarse uno al lado del otro? (se supondrá que se sientan en asientos distintos!). Probabilidad y Estadı́stica - 2020 Página 27 de 86 Ejercicio I.5. Una caja fuerte se abre mediante una combinación de 5 dı́gitos que pueden estar repetidos. Alberto intenta robar el contenido de dicha caja fuerte probando al azar la combinación. 1. ¿Cuál es la probabilidad de que Alberto logre sus propósitos si la caja explota si la combinación es errónea?. 2. ¿Cómo mejora la probabilidad de que Alberto logre sus propósitos si Juan, portero del banco, le comenta que el primer dı́gito de la combinación es 0 o 1?. Ejercicio I.6. Si se ordenan al azar las letras de la palabra PROBABILIDAD, ¿cuál es la probabilidad de que efectivamente se lea la palabra probabilidad?. Ejercicio I.7. Un semáforo tiene ciclos de trabajo de 75 segundos. La luz roja dura 30 segundos, la amarilla 5 y la verde 40 segundos. Si un conductor llega al semáforo en un momento arbitrario de tiempo, ¿cuál es la probabilidad de encontrar el semáforo en cada uno de los estados?. Ejercicio I.8. Se considera el experimento “elegir un punto al azar en el cuadrado [0, 1] × [0, 1]”. 1. Describa un espacio muestral para este experimento. 2. Discuta una posible medida de probabilidad adecuada para las regiones del cuadrado. 3. ¿Cuál es la probabilidad de que el punto elegido este dentro del cı́rculo unitario? 4. Indique cómo podrı́a usarse este experimento de manera repetida para estimar el valor de π. Ejercicio I.9. Sean A y B dos sucesos, probar que se cumple: P ((A ∩ B c ) ∪ (Ac ∩ B)) = P (A) + P (B) − 2 P (A ∩ B) Ejercicio I.10. 1. Sean A y B dos sucesos con A ⊂ B, probar que: P (A) ≤ P (B). 2. Sean A y B dos sucesos cualesquiera, probar que: P (A ∩ B) ≤ mı́n{P (A), P (B)}, Probabilidad y Estadı́stica - 2020 P (A ∪ B) ≥ máx{P (A), P (B)} Página 28 de 86 Sección 5 Práctico (II) : ESPACIOS DE PROBABILIDAD (2a. parte) En esta segunda parte queremos introducir la noción de variable aleatoria buscando modelizar distintos espacios de probabilidad en forma más abstracta. Definición: Una variable aleatoria (v.a.) X es una función X : Ω → IR tal que a cada resultado posible de un experimento en el espacio muestral le asigna un número real. Si el recorrido de X es un conjunto discreto RX = { x1 , x2 , . . . , xn , . . . } decimos que es una variable aleatoria discreta, y su ley de probabilidad está dada por pX (xi ) = P (X = xi ) para cada elemento del recorrido. Ejercicio II.1. 1. Se consideran el experimento “lanzar un dado equilibrado” y la v.a. X = “número obtenido” Hallar el recorrido y la ley de probabilidad de X. 2. Si ahora se lanzan dos dados y se considera X =“suma de los resultados”. Hallar el recorrido y la ley de probabilidad de X. 3. Si ahora, para el mismo experimento de la parte anterior, se considera: Y = “el mayor de los resultados” Hallar el recorrido y la ley de probabilidad Y . Ejercicio II.2. 1. Se lanzan tres monedas equilibradas y se considera la v.a. X =“cantidad de caras obtenidas”. Hallar el recorrido y la ley de probabilidad de X. 2. Se lanzan n monedas equilibradas y se considera la v.a. X =“cantidad de caras obtenidas”. Hallar el recorrido y la ley de probabilidad de X. Ejercicio II.3. 1. Un productor tiene almacenados 9 motores, de los cuales 2 están fallados. Si vende 3 motores en forma aleatoria, ¿cuál es la probabilidad de que venda los dos fallados?. 2. Sea X =“cantidad de motores fallados en la venta”. Hallar el recorrido y la ley de probabilidad de X. Probabilidad y Estadı́stica - 2020 Página 29 de 86 Ejercicio II.4. El servicio de radio taxis tiene 12 Volkswagen y 8 Renaults. Si 5 de estos autos están en reparación y tanto el Volkswagen como el Renault tiene la misma probabilidad de fallar, encuentre la probabilidad de que en el taller se encuentren: 1. 3 Volkswagen y 2 Renaults. 2. Por lo menos 3 Volkswagen. 3. 5 Volkswagen o 5 Renaults. Sugerencia: Considere la v.a. X =“cantidad de Renaults en reparación”. Ejercicio II.5. Un minorista ha verificado que la demanda de cajones de cada semana es una variable aleatoria X con la siguiente ley: P (X = n) = e−µ µn n! n = 0, 1, 2, . . . con µ = 2 cajones Esta ley se conoce como distribución de Poisson de parámetro µ = 2 cajones. 1. Verificar que la ley de probabilidad anterior está bien definida. 2. El minorista produce 4 cajones por semana. Al efectuar un análisis de la actividad del negocio, se le plantean las siguientes preguntas: a) ¿Cuál es la probabilidad de vender toda la producción?. b) ¿Cuál es la probabilidad de que sea incapaz de cumplir con un pedido por lo menos?. c) ¿Cuántos cajones deberá producir por semana a fin de que cumpla con todos los pedidos con probabilidad mayor al 95 %?. Nota: Se recuerda que +∞ P 0 µn = eµ . n! Ejercicio II.6. En una población de N = 160 personas se decide hacer una encuesta para determinar cuántos son hinchas de un determinado equipo de fútbol. Se estima que D = 81 (la mitad más uno) son hinchas de un equipo determinado. Se decide consultar a n = 5 personas al azar. Se considera la variable aleatoria X =“no. de personas del equipo en la muestra”. 1. Hallar y graficar la ley de probabilidad X si la muestra se hace sin reposición. 2. Hallar y graficar la ley de probabilidad X si la muestra es con reposición. Compare los resultados. ¿A qué se debe esto? Probabilidad y Estadı́stica - 2020 Página 30 de 86 Ejercicio II.7. Se considera el juego de la ruleta en el cual se elige un número al azar entre 0 y 36 con igual probabilidad. En este juego hay 18 números negros e igual cantidad de rojos. Si una persona apuesta al color negro, en el caso de salir, se le paga el doble de lo apostado y si el número que sale no es negro pierde lo apostado. Si una persona apuesta $1 al color negro, sea X =“ganancia de la persona”. Calcular la ley de probabilidad de X (recuerde que el 0 no es de ningún color). Ejercicio II.8. Se considera el siguiente experimento: lanzar una moneda equilibrada hasta que salga cara. 1. Construya un espacio muestral adecuado para este experimento. 2. Sea X =“no. de tiradas necesarias para que salga cara”. Hallar y graficar la ley de probabilidad de X. 3. Calcular P (X > k), es decir, la probabilidad de que sean necesarias más de k tiradas. Probabilidad y Estadı́stica - 2020 Página 31 de 86 Sección 6 Práctico (III) : ESPACIOS DE PROBABILIDAD (3a. parte) Ejercicio III.1. Se consideran los sucesos A y B tales que: P (A) = 3 5 3 , P (B) = y P (A ∪ B) = 8 8 4 Calcular: P ( A / B ) y P ( B / A) e indicar si los sucesos son independientes o no. Ejercicio III.2. Finalizados los cursos el 25 % de los estudiantes perdieron matemática, el 15 % perdieron fı́sica y 10 % perdieron las dos materias. Se selecciona un estudiante al azar. 1. Si perdió fı́sica, ¿cuál es al probabilidad de que haya perdido matemática?. 2. Si perdió matemática, ¿cuál es la probabilidad de que haya perdido fı́sica?. Ejercicio III.3. Una caja contiene 5 bolas negras y 4 blancas. Se extraen dos bolas sucesivamente. Resolver las partes siguientes considerando dos casos: la primer bola se vuelve a colocar en la caja (“muestreo con reposición”) o no (“muestreo sin reposición”). 1. Si se observa que la primera es blanca, ¿cuál es la probabilidad que la segunda también sea blanca?. 2. Sin saber el resultado de la primer extracción, ¿cuál es la probabilidad que la segunda sea blanca?. 3. Indicar si los sucesos “la primer bola es blanca” y “la segunda bola es blanca” son independientes o no. Ejercicio III.4. La policı́a caminera planea reforzar el control de los lı́mites de velocidad colocando cuatro radares en cuatro rutas distintas. Por razones económicas los radares no estarán en funcionamiento todo el tiempo. El radar 1 funciona el 40 %, el radar 2 el 30 %, el radar 3 el 30 % y el radar 4 el 20 % del tiempo. Una persona que se dirige a su trabajo lo hace por alguna de las rutas, y lo hace siempre a más velocidad de la permitida, tiene una probabilidad de 0,2 de pasar por la ruta del radar 1, de 0,1 por la del 2, de 0,5 por del 3 y de 0,2 por del 4. Calcular la probabilidad que tiene la persona de ser multado. Probabilidad y Estadı́stica - 2020 Página 32 de 86 Ejercicio III.5. Se lanza una moneda cargada de modo que la probabilidad de obtener cara es 23 . Si sale cara se elige un número al azar de 1 al 9 y si sale cruz, del 1 al 5. ¿Cuál es la probabilidad de obtener un número par?. Ejercicio III.6. Tres máquinas A, B y C producen respectivamente el 50 %, 30 % y 20 % del número total de artı́culos de una fábrica. Los porcentajes de producción de defectuosos de cada máquina son 3 %, 4 % y 5 % respectivamente. Se toma al azar un artı́culo de la producción total. 1. Hallar la probabilidad de que el artı́culo sea defectuoso. 2. Si el artı́culo seleccionado es defectuoso, hallar la probabilidad de que haya sido producido por A. Ejercicio III.7. Se tiene dos urnas. La primera contiene 5 bolas blancas y 7 negras mientras que la segunda contiene 3 blancas y 9 negras. Una bola es escogida al azar de la primera urna y transferida a la segunda. Luego, una bola es extraı́da al azar de la segunda urna. Calcular la probabilidad de que la bola transferida haya sido negra dado que la bola extraı́da fue negra. Ejercicio III.8. Se tiene un tablero de ajedrez clásico del cual se eligen 3 casillas al azar. 1. Calcular la probabilidad de que dos casillas sean de un color y la restante del color opuesto. 2. Calcular la probabilidad de que las tres casillas estén alineadas, es decir, que se encuentren en la misma fila o columna. 3. ¿Son independientes los sucesos de las dos partes anteriores?. Justifique. Ejercicio III.9. Juan, Santiago y Magdalena juegan el siguiente juego. Empiezan jugando Juan y Santiago, eligen un lado de una moneda equilibrada cada uno, tiran la moneda y resulta un triunfador de la tirada 1. El ganador juega con Magdalena, nuevamente eligen un lado de una moneda cada uno, tiran la moneda y resulta un triunfador de la tirada 2. El ganador juega con quien está esperando (no está jugando) y ası́ sucesivamente. Se realizan hasta 4 tiradas y el ganador del juego es el primero que resulta triunfador en dos tiradas consecutivas. Si no hay un ganador diremos que el juego terminó empatado. Se pide: Probabilidad y Estadı́stica - 2020 Página 33 de 86 1. Hallar las probabilidades de que: (i) gane Juan (ii) gane Santiago (iii) gane Magdalena (iv) empaten. 2. Hallar la probabilidad de que Juan gane en la segunda tirada y la probabilidad de que Juan gane en la segunda tirada sabiendo que Juan ganó. 3. Hallar la probabilidad de que Magdalena gane en la tercer tirada y la probabilidad de que Magdalena gane en la tercer tirada sabiendo que Magdalena ganó. Comente lo lógico del último resultado. Ejercicio III.10. Se descubre una nueva enfermedad que se sabe afecta al 1 % de la población. La misma no presenta ningún tipo de sı́ntomas. Por lo tanto, un especialista ha diseñado un estudio para determinar si un paciente dado sufre o no de dicha enfermedad. Se ha comprobado que el estudio tiene una precisión del 98 % sobre resultados positivos y del 97 % sobre resultados negativos. Es decir que si un paciente está enfermo, el estudio le dará positivo con una probabilidad del 98 %. De manera similar, si el paciente no está enfermo, el estudio dará negativo con 97 % de probabilidad. Usted se hace este estudio y obtiene un resultado positivo. ¿Cuál es la probabilidad de que efectivamente esté enfermo?. Ejercicio III.11 (“Contraejemplo de independencia de tres sucesos”). Se extrae al azar una bolilla de una urna que contiene 9 bolillas de las cuales 3 son blancas, 3 son negras y 3 son rojas, numeradas en cada color del 1 al 3. Además las siguientes bolillas son rayadas (la demás no): número 1 de color blanco, número 2 de color negro y número 3 de color rojo. Sean los siguientes sucesos: F A - La bolilla extraı́da tiene el número 1. F B - La bolilla extraı́da es de color blanco. F C - La bolilla extraı́da es rayada. 1. ¿A, B y C son independientes dos a dos?. 2. ¿A, B y C son independientes?. Probabilidad y Estadı́stica - 2020 Página 34 de 86 Sección 7 Evaluación (I) : ESPACIOS DE PROBABILIDAD Ejercicio I.1 (Parcial Octubre 2015). En un espacio de probabilidad se consideran tres sucesos A, B y C. Probar que: P (A ∩ B c ) + P (B ∩ C c ) + P (C ∩ Ac ) = P (A ∪ B ∪ C) − P (A ∩ B ∩ C) Ejercicio I.2 (Examen Febrero 1999). Se consideran tres sucesos A, B y C que cumplen simultáneamente: F A y B son sucesos independientes. F B y C son sucesos mutuamente excluyentes (disjuntos). F La probabilidad de que se cumpla A y no se cumplan ni B ni C vale 0,2. F La probabilidad de que se cumpla B es 0,35. F La probabilidad de que se cumpla C y no se cumpla A vale 0,15. F La suma de las probabilidades de los tres sucesos vale 0,9. 1. Calcular la probabilidad de que no se cumplan ninguno de los tres sucesos. 2. Calcular la probabilidad de se cumpla A dado que se cumple C. ¿Son A y C independientes?. Justificar. Ejercicio I.3 (Examen Mayo 1998). 1. Se considera el siguiente experimento: F Se lanza una moneda cargada de modo que la probabilidad de obtener cara es 0,65. F Si sale cara se tira un dado perfecto y si sale cruz se tiran dos dados perfectos. F Se considera como resultado el puntaje obtenido (el valor del dado o la suma de los valores según corresponda). ¿ Cuál es la probabilidad de que el resultado sea 6?. 2. Si se repite el experimento de la parte anterior 5 veces en forma independiente y se miran los resultados, a) ¿Cuál es la probabilidad de que el resultado nunca sea 6?. b) ¿Cuál es la probabilidad de que el resultado sea 6 por lo menos 3 veces?. Probabilidad y Estadı́stica - 2020 Página 35 de 86 Ejercicio I.4. Un inspector de control de calidad seleccionará productos para realizarse distintas pruebas en 9 lı́neas de montaje distribuidas en tres fábricas A, B y C, de una determinada empresa. Los porcentajes de producción de cada fábrica en relación a la producción total de la empresa y los porcentajes de fallas en la lı́nea de montaje respecto a la producción de dicha lı́nea se presentan en la siguiente tabla: Fábrica A Fábrica B Fábrica C Lı́nea Lı́nea Lı́nea Lı́nea Lı́nea Lı́nea Lı́nea Lı́nea Lı́nea 1 2 3 4 5 6 7 8 9 Porcentaje de producción 25 % 15 % 10 % 15 % 10 % 5% 10 % 5% 5% Porcentaje de falla 0.5 % 1% 1.5 % 0.5 % 1.5 % 2% 1% 2% 2% 1. Durante 5 dı́as, el inspector selecciona al azar una de las lı́neas para ser inspeccionada ese dı́a. a) ¿Cuál es la probabilidad que seleccione una lı́nea más de una vez durante los 5 dı́as?. b) ¿Cuál es la probabilidad de que nunca inspeccione la fábrica A?. 2. Posteriormente decide seleccionar un artı́culo al azar de la producción total de las tres fábricas. a) ¿Cuál es la probabilidad de que esté fallado?. b) Si el artı́culo seleccionado resultó fallado, ¿cuál es la probabilidad de que haya sido producido por la fábrica A?. Probabilidad y Estadı́stica - 2020 Página 36 de 86 Sección 8 Tema (II) : VARIABLES ALEATORIAS II.1 VARIABLES ALEATORIAS DISCRETAS Y CONTINUAS Definición II.1 (Variable aleatoria). En (Ω , A , P ), un espacio de probabilidad, llamaremos variable aleatoria (v.a.) a: X : Ω → IR tal que X −1 (I) ∈ A ∀ I intervalo en IR Definición II.2 (Variables aleatorias discretas). Decimos que la variable aleatoria X es discreta si su recorrido (los valores que toma) es discreto (finito o infinito numerable), x1 , x2 , ... , xn , .... Ası́ la variable aleatoria queda determinada por el recorrido y las probabilidades de tomar esos valores. Llamamos cuantı́a o función de probabilidad a: pj = pX (xj ) = P (X = xj ) j = 1, 2, ..., n, ... Decimos que X presenta probabilidades concentradas en los puntos xj con valores pj . Propiedades II.3. F ¿Cuándo está bien definida?: {pj } es cuantı́a ⇔ 0 ≤ pj ≤ 1 ∀ j = 1, 2, ..., n, ... y P pj = 1. j F ¿Cómo calcular probabilidades?: P (X ∈ B) = X pj j / xj ∈B Caracterización de las variables aleatorias. Función distribución acumulada FX . Definición II.4 (Función distribución acumulada o simplemente distribución). En (Ω , A , P ), llamaremos función distribución acumulada de la variable aleatoria X (o simplemente distribución de X) a la función FX : IR → [0, 1] tal que nt FX (x) = P ({ω ∈ Ω / X(ω) ≤ x}) = P (X −1 ((−∞, x])) = P (X ≤ x) Probabilidad y Estadı́stica - 2020 Página 37 de 86 Ejemplo II.5. Sea X la variable aleatoria discreta que toma los valores 1, 2 y 5 con P (X = 1) = 0,2 y P (X = 2) = 0,5. 1. Calcular P (X = 5) y representar X. 2. Hallar y graficar la distribución acumulada de probabilidades de X (FX ). Propiedades II.6. F FX (+∞) = lim FX (x) = 1 y FX (−∞) = lim FX (x) = 0. x→+∞ x→−∞ F FX es creciente (no necesariamente estrictamente creciente, x1 < x2 ⇒ FX (x1 ) ≤ FX (x2 )). F FX es continua por la derecha y tiene lı́mite por la izquierda. Observación II.7. F Estas tres propiedades determinan una función distribución de probabilidades y por lo tanto una variable aleatoria. F En el caso de una variable aleatoria discreta FX resulta una función “escalonada” o “escalera”, donde los saltos se producen en los xj y tienen el valor pj . Propiedades II.8. F P (a < X ≤ b) = FX (b) − FX (a). − F P (X = x0 ) = FX (x0 ) − FX (x− 0 ), o lo que es lo mismo FX (x0 ) = P (X < x0 ). Observación II.9. F Estas tres propiedades muestran cómo calcular probabilidades usando la función distribución de probabilidades y reafirman que la variable aleatoria quedó bien definida. Definición II.10 (Variables aleatorias continuas o absolutamente continuas). Decimos que la variable aleatoria X es continua o absolutamente continua sii existe fX : IR → IR, función seccionalmente continua (continua a trozos), llamada densidad de probabilidades (o simplemente densidad), tal que: Zx fX (x) ≥ 0 ∀ x ∈ IR y FX (x) = fX (t) dt −∞ Probabilidad y Estadı́stica - 2020 Página 38 de 86 Propiedades II.11. F ¿Cuándo está bien definida?: fX es densidad de probabilidades ⇔ fX (x) ≥ 0 ∀ x ∈ IR y +∞ R fX (x) dx = 1. −∞ F ¿Cómo calcular probabilidades?: Para calcular probabilidades: Zb P (a < X ≤ b) = P (a ≤ X ≤ b) = P (a < X < b) = P (a ≤ X < b) = fX (x) dx a o más general Z P (X ∈ B) = fX (x) dx B F P (X = x0 ) = 0. F FX resulta una función continua. F Si fX es continua en x0 , FX es derivable en x0 y FX0 (x0 ) = fX (x0 ). Ejemplo II.12. Sea X es una variable aleatoria con densidad de probabilidades: k ∗ x3 si x ∈ [1, 3] fX (x) = k ∈ IR 0 en otro caso 1. Hallar k y calcular P (0 ≤ X ≤ 2). 2. Hallar y graficar la distribución acumulada de probabilidades de X (FX ). Variables aleatorias mixtas Llamaremos ası́ a aquellas variables aleatorias que tengan probabilidades concentradas en algunos puntos xj (numerable, P (X = xj ) > 0) y el resto de la probabilidad se reparta según una densidad de probabilidades. Observar que aquı́ la suma de las probabilidades concentradas más la integral de la densidad es lo que da uno. Probabilidad y Estadı́stica - 2020 Página 39 de 86 Ejemplo II.13. Sea X una variable aleatoria cuya función distribución acumulada de probabilidades está dada por  0 si x < 0  x 1 + si x ∈ [0, 2) FX (x) = 3  12 −x 1−e si x ≥ 2 1. ¿Está bien definida?. ¿Qué tipo de v.a. es?. (hallar cuantı́a y/o densidad según corresponda). 2. Calcular P (1 ≤ X ≤ 3). II.2 “COMPOSICIÓN” DE UNA VARIABLE ALEATORIA Si X : Ω → IR es una variable aleatoria y g : IR → IR continua entonces g(X) : Ω → IR es una nueva variable aleatoria (g(X) = g ◦ X).2 ¿Cómo calcular la distribución de Y = g(X)? En el caso continuo calculemos la distribución de probabilidades de Y = g(X): FY (y) = P (Y ≤ y) = P (g(X) ≤ y) = P (X ∈ g −1 ((−∞, y])) y complementamos calculando la densidad de probabilidades mediante fY (y) = FY0 (y). Ejemplo II.14 (Uniforme). X ∼ U ni(0, 1) Calculemos las densidades de Y = 3 X + 1 y Z = X − 1 2 . En el caso discreto calculemos directamente la cuantı́a de Y = g(X). Ejemplo II.15. Sea X la variable aleatoria discreta que toma los valores −1, 13 , 32 , 2 y 5 con: 1 2 P (X = −1) = 0,1 P X = = 0,15 P X = = 0,35 P (X = 2) = 0,1 y P (X = 5) = 0,3 3 3 Calculemos las densidades de Y = 3 X + 1 y Z = X − 2 1 2 . Trabajaremos sin utilizar mayor formalidad con las condiciones de regularidad necesarias para g. Probabilidad y Estadı́stica - 2020 Página 40 de 86 II.3 VALOR ESPERADO, UNA MEDIDA DE EXACTITUD Definición II.16 (Valor esperado). El valor esperado (E(X)) de una variable aleatoria X valor representativo del modelo que lo definiremos a partir la forma de calcularlo (omitimos las condiciones de regularidad): Para el caso discreto, con cuantı́a pj = P (X = xj ): E(X) = X xj pj j Para el caso absolutamente continuo, con densidad fX (x): +∞ Z E(X) = x fX (x) dx −∞ En general puede calcularse: +∞ Z Z0 E(X) = [1 − FX (x)] dx − FX (x) dx 0 −∞ Propiedades II.17. F Si X ≥ 0, entonces E(X) ≥ 0. F Linealidad: E(λ X + µ Y ) = λ E(X) + µ E(Y ) F E(11A ) = P (A) ∀ A ∈ A, donde 11A es la indicatriz del suceso A o sea 11A (ω) = 1 si ω ∈ A y 11A (ω) = 0 si ω ∈ / A. Estas tres propiedades definen al valor esperado. Propiedades II.18. F Si X = a constante, entonces E(X) = a. F Si X es una variable acotada, E(X) < ∞. F Si X ≤ Y , entonces E(X) ≤ E(Y ). F Si X cualquiera, X = X + − X − donde X + es la parte positiva3 y X − es la parte negativa4 de X, entonces E(X) = E(X + ) − E(X − ). F |E(X)| ≤ E(|X|). 3 4 X + (ω) = max{X(ω), 0} X − (ω) = max{−X(ω), 0} Probabilidad y Estadı́stica - 2020 Página 41 de 86 F E(g(X)) puede calcularse con las siguientes expresiones: Para el caso discreto, con cuantı́a pj = P (X = xj ): X E(g(X)) = g(xj ) pj j Para el caso absolutamente continuo, con densidad fX (x): +∞ Z E(g(X)) = g(x) fX (x) dx −∞ II.4 VARIANZA, UNA MEDIDA DE DISPERSIÓN Definición II.19 (Varianza). Si E(X) < ∞, definimos la varianza mediante: V ar(X) = E [X − E(X)]2 = E(X 2 ) − [E(X)]2 Probemos que las dos expresiones resultan en el mismo número: V ar(X) = E [X − E(X)]2 = E X 2 − 2 E(X) X + [E(X)]2 = = E X 2 − 2 E(X) E(X) + E [E(X)]2 = E X 2 − 2 [E(X)]2 + [E(X)]2 = E(X 2 ) − [E(X)]2 La primera muestra a la varianza como una medida de dispersión del modelo, es el “error cuadrático medio” del modelo. Propiedades II.20. F V ar(X) ≥ 0, de donde se deduce que E(X 2 ) ≥ ( E(X) )2 . F Si X = a constante, entonces V ar(X) = 0. F Si V ar(X) = 0, entonces X = E(X) constante. F Si a constante, entonces V ar(X + a) = V ar(X). F La varianza no es lineal. • Si a constante, entonces V ar(a X) = a2 V ar(X). • NO vale V ar(X + Y ) = V ar(X) + V ar(Y ) (a veces sı́, a veces no) (sı́ cuando son independientes, condición que se verá más adelante). Definición II.21 (Momentos de una variable aleatoria). Llamamos momento de orden k de la variable aleatoria X respecto del origen a E(X k ). Llamamos momento centrado de orden k de la variable aleatoria X a E [X − E(X)]k . Probabilidad y Estadı́stica - 2020 Página 42 de 86 II.5 DISTRIBUCIONES DE PROBABILIDAD CON NOMBRE Observación II.22. Las siguientes tablas resumen los datos principales (distribución, valor esperado y varianza de algunas variables aleatorias con nombre. Variables aleatorias discretas Distribución Bernoulli Ber(p) 0≤p≤1 Binomial Bin(n, p) n ∈ IN , 0 ≤ p ≤ 1 Geométrica Geo(p) 0≤p≤1 Hipergeométrica Hip(N, r, n) N, r, n ∈ IN 1≤r≤N , 1≤n≤N de P oisson P oi(λ) λ>0 Cuantı́a Valor esperado Varianza P (X = 1) = p P (X = 0) = 1 − p p p(1 − p) pj = Cjn pj (1 − p)n−j j = 0, 1, 2, ..., n np np(1 − p) pj = p(1 − p)j−1 j = 1, 2, ... 1 p 1−p p2 N −r Crj Cn−j CnN j = 0, 1, 2, ..., n si n ≤ r j = 0, 1, 2, ..., r si n > r nr N r N −r N −n n N N N −1 j −λ pj = λ e j! j = 0, 1, 2, ... λ λ pj = Probabilidad y Estadı́stica - 2020 Página 43 de 86 Variables aleatorias absolutamente continuas Distribución U nif orme U ni(a, b) a, b ∈ IR , a < b N ormal N (µ, σ) µ, σ ∈ IR , σ > 0 Exponencial Exp(λ) λ ∈ IR , λ > 0 ( fX (x) = Densidad 1 si x ∈ [a, b] b−a 0 en otro caso fX (x) = √1 σ 2π fX (x) = λ e−λ x 0 x−µ σ 2 e −1 Valor esperado Varianza a+b 2 (b − a)2 12 µ σ2 1 λ 1 λ2 2 si x ≥ 0 en otro caso Propiedades II.23. F Bin(n, p) corresponde al experimento de muestreo con reposición (se extrae una muestra de tamaño n de una urna con N bolas, r blancas y N − r azules, p = Nr , donde X mide la cantidad de bolas blancas de la muestra). F Hip(N, r, n) corresponde al experimento de muestreo sin reposición (se extrae una muestra de tamaño n de una urna con N bolas, r blancas y N − r azules, donde X mide la cantidad de bolas blancas de la muestra). F Si N es grande y p = r N ≈ constante, entonces Hip(N, r, n) ≈ Bin(n, p). i=n variables aleatorias independientes F Si {Xi }i=1 5 con Xi ∼ Ber(p), entonces n P Xi ∼ Bin(n, p). i=1 F Si n es grande y p pequeño (np ≥ 1 y p < 0,1), entonces Bin(n, p) ≈ P oi(np). F Si X ∼ N (µ, σ), entonces 5 X−µ σ ∼ N (0, 1). Más adelante se definirá con precisión este concepto, aquı́ apelamos al sentido común Probabilidad y Estadı́stica - 2020 Página 44 de 86 Sección 9 Práctico (IV) : VARIABLE ALEATORIA (1a. parte) Variables aleatorias discretas Ejercicio IV.1. Un embarque de 8 computadoras similares que se envı́a a un distribuidor contiene 3 aparatos defectuosos. Una escuela realiza una compra de 2 de estas computadoras. Sea X una variable aleatoria cuyos valores son el número de computadoras defectuosas compradas por la escuela. 1. Indicar cuáles son los valores que toma esta variable aleatoria discreta. 2. Hallar la función de probabilidad puntual pX . 3. Calcular la probabilidad de que X resulte impar. Ejercicio IV.2. Sea X una variable aleatoria discreta que toma con probabilidad los valores 0, 1 y 2 cuya función de probabilidades está dada por: pX (0) = a 5 , pX (1) = , pX (2) = a2 6 6 1. Hallar a. 2. Calcular P (1 < X < 2), P (1 < X ≤ 2), P (1 ≤ X < 2) y P (1 ≤ X ≤ 2). 3. Hallar y graficar la función distribución acumulativa FX . 4. Hallar FX (2) − FX (1) y comparar con los resultados obtenidos en la segunda parte. Ejercicio IV.3. Se considera la siguiente función de distribución  0    1   2 5 FX (x) = 8  7     8 1 acumulativa: si si si si si x < −1 1 x ∈ −1, √3 1 x ∈ √ 3 , 2 x∈ 2, 4 x≥4 1. Graficar FX . Mostrar que FX es efectivamente una función distribución acumulativa y observar que se trata de una distribución de probabilidades discreta. 2. Hallar la función de probabilidad puntual pX . √ √ 3. Calcular P (0 < X < 2) y P (0 < X ≤ 2). Probabilidad y Estadı́stica - 2020 Página 45 de 86 Variables aleatorias continuas Ejercicio IV.4. Se sabe que el error en la medición de la temperatura en un experimento controlado de un laboratorio es una variable aleatoria X que tiene la función de densidad: x2 si x ∈ (−1, 2) 3 fX (x) = 0 en otro caso 1. Verificar que fX es efectivamente una densidad. 2. Calcular P (0 < X < 1). 3. Hallar y graficar la función distribución acumulativa FX . Ejercicio IV.5. Se considera la función f : IR → IR tal que: f (x) = k x2 si x ∈ [1, +∞) en otro caso 0 1. Hallar k para que f sea una densidad de probabilidades. 2. Se considera una variable aleatoria X con densidad f (con el valor de k hallado). a) Hallar y graficar la función distribución acumulativa FX . b) Calcular P (−1 < X < 2). Ejercicio IV.6. Un transmisor inalámbrico emite una señal con cierta potencia. Debido al ruido y a las reflexiones que sufre la señal en el camino, la señal recibida puede modelarse como una variable aleatoria X cuya densidad está dada por: ( 2 fX (x) = x x − 2σ2 e σ2 0 si x > 0 en otro caso donde σ > 0 es un parámetro relacionado con la potencia de transmisión. 1. Calcular P (X > x) para x ∈ IR. 2. Usando lo anterior, calcular y bosquejar la función de distribución acumulada FX (x) de la variable X. 3. Para que el mensaje sea recibido correctamente, se requiere X > 1. Calcular el mı́nimo valor de σ tal que P (X > 1) ≥ 0, 9. 4. Para el valor de σ hallado, calcule P (1 < X < 2). Probabilidad y Estadı́stica - 2020 Página 46 de 86 Variables aleatorias mixtas Ejercicio IV.7. Sea X una variable aleatoria cuya función distribución  0 si     x si  1 si FX (x) = 2  1 x  + si    2 2 1 si acumulada de probabilidades está dada por x < 0 x ∈ 0, 31 x ∈ 13 , 23 x ∈ 23 , 1 x≥1 1. Graficar la función distribución acumulativa FX y verificar sus propiedades. 2. Muestre que se trata de variable aleatoria mixta indicando los puntos de probabilidad acumulada y la densidad de probabilidades que la determinan. Calcular la integral de la densidad en todos los reales y verificar que sumada a las probabilidades concentradas da uno. 3. Calcular P X> 12 , P X ≥ 21 , P 13 ≤ X ≤ 23 , P 13 < X ≤ 23 , P 13 ≤ X < 23 y P 31 < X < 23 . Probabilidad y Estadı́stica - 2020 Página 47 de 86 Sección 10 Práctico (V) : VARIABLE ALEATORIA (2a. parte) Composición con una variable aleatoria Ejercicio V.1. Hallar la función distribución acumulativa y la densidad de probabilidades de la variable aleatoria Y = L(X), donde X es una variable aleatoria con densidad 1 si x ∈ [1, +∞) x2 fX (x) = 0 en otro caso Ejercicio V.2. Sea X es una variable aleatoria con densidad de probabilidades: 1 si x ∈ (0, 1) fX (x) = 0 en otro caso distribución Uniforme en (0, 1). Hallar la función distribución acumulativa y la densidad de probabilidades de la variable aleatoria Y siendo: 1) Y = 3X + 1 2) Y = −3X + 1 3) Y = X 2 + 1 Ejercicio V.3. Si X es una variable aleatoria con distribución discreta que toma los valores −3, 1 y 3 dada por la función de probabilidad: 1 1 1 pX (−3) = pX (1) = pX (3) = 3 6 2 Hallar la función la función de probabilidad de la variable aleatoria Y donde: 1) Y = 2X − 1 2) Y = X 2 3) Y = |X| Ejercicio V.4. El porcentaje de alcohol de un cierto compuesto quı́mico se puede considerar una variable aleatoria X con la siguiente densidad de probabilidades: 20x3 (1 − x) si x ∈ (0, 1) fX (x) = 0 en otro caso El precio de venta del compuesto anterior depende del contenido de alcohol. Especı́ficamente si 1 2 3 < X < 3 el precio es 100 $/litro y en otro caso 50 $/litro. En todos los casos el costo de producción es de 30 $/litro. Hallar la función de probabilidad de la ganancia por litro. Ejercicio V.5. Sea X ∼ U ni(0, 1). Se considera Y = min X , 21 . Hallar la distribución acumulada de probabilidades. Muestre que se trata de una variable aleatoria mixta indicando dónde hay densidad no nula y dónde probabilidad concentrada. Probabilidad y Estadı́stica - 2020 Página 48 de 86 Sección 11 Práctico (VI) : VARIABLE ALEATORIA (3a. parte) Valor esperado y varianza Ejercicio VI.1. Si X es una variable aleatoria con distribución de Bernoulli de parámetro p (X toma los valores 1 y 0 con probabilidad p y 1 − p respectivamente), probar que: 2) V ar(X) = p(1 − p) 1) E(X) = p Ejercicio VI.2. Si X es una variable aleatoria con densidad de probabilidades: 1 si x ∈ (0, 1) fX (x) = 0 en otro caso distribución Uniforme en (0, 1), probar que: 1) E(X) = 1 2 2) V ar(X) = 1 12 Ejercicio VI.3. Si X es una variable aleatoria con distribución discreta que toma los valores −3, 1 y 3 dada por la función de probabilidad: 1 1 1 pX (1) = pX (3) = pX (−3) = 3 6 2 Hallar: E(X) , E(2X + 5) , E(X 2 ) , E((X + 1)2 ) , E(X 4 ) , V ar(X) y V ar(X 2 ) Ejercicio VI.4. Si X es una variable aleatoria cuya función distribución acumulativa es: 1 − e−x si x ≥ 0 FX (x) = 0 si x < 0 decimos que X es una variable aleatoria con distribución Exponencial de parámetro 1. Hallar E(X) y V ar(X). Probabilidad y Estadı́stica - 2020 Página 49 de 86 Ejercicio VI.5. Si X es una variable aleatoria que verifica E((X −1)2 ) = 10 y E((X −2)2 ) = 6, hallar E(X) y V ar(X). Ejercicio VI.6. Si X es una variable aleatoria con E(X) = µ y V ar(X) = σ 2 probar que Y = y V ar(Y ) = 1. X −µ verifica E(Y ) = 0 σ Ejercicio VI.7. Sea X es una variable aleatoria con E(X) = µ y V ar(X) = σ 2 . 1. Si c es una constante cualquiera, evaluar E((X − c)2 ) en términos de µ y σ 2 . 2. ¿Para qué valor de c, E((X − c)2 ) es mı́nimo?. Interpretar el resultado. Ejercicio VI.8. Hallar el valor esperado de X, variable aleatoria definida en el ejercicio V.4. Ejercicio VI.9. Hallar el valor esperado de Y , variable aleatoria definida en los ejercicios V.5. Probabilidad y Estadı́stica - 2020 Página 50 de 86 Sección 12 Práctico (VII) : VARIABLE ALEATORIA (4a. parte, modelos) Algunas distribuciones de probabilidad discretas Ejercicio VII.1 (Distribución de Bernoulli). Sea X con distribución de Bernoulli, o sea: X ∼ Ber(p) con 0 ≤ p ≤ 1 si y solo si P (X = 1) = p P (X = 0) = 1 − p 1. Explique un experimento que sea modelado por X. 2. Hallar el valor esperado y la varianza de X comprobando que: E(X) = p , V ar(X) = p(1 − p) 3. Hallar la distribución de X n (n ∈ IN , n ≥ 2) y deducir los valores de los momentos, E(X n ). Ejercicio VII.2 (Distribución Binomial). 1. Sea X con distribución Binomial, o sea: X ∼ Bin(n, p) con n ∈ IN , 0 ≤ p ≤ 1 si y solo si pj = P (X = j) = Cjn pj (1 − p)n−j j = 0, 1, 2, ..., n a) Explique un experimento que sea modelado por X. b) Hallar directamente (sin usar la parte siguiente) el valor esperado y la varianza de X comprobando que: E(X) = np , V ar(X) = np(1 − p) Nota: Puede ser conveniente hallar E(X(X − 1)). c) Mostrar, a través del experimento planteado en la primer parte, que podemos escribir: Yi ∼ Ber(p) , i = 1, 2, ..., n X = Y1 + Y2 + ... + Yn con variables aleatorias independientes Nota: Asumiremos la noción de variables aleatorias independientes intuitiva. Utilizar este hecho para volver a encontrar que el valor esperado y la varianza de X valen: E(X) = np , V ar(X) = np(1 − p) Nota: Asumiremos que si son variables aleatorias independientes, se cumple que la varianza de la suma es la suma de las varianzas. Probabilidad y Estadı́stica - 2020 Página 51 de 86 2. Una compañı́a petrolera va a hacer 10 pozos y cada uno de ellos tiene probabilidad 0,1 de producir petróleo. a) ¿Cuál es la probabilidad de que por lo menos un pozo produzca petróleo?. Hallar el valor esperado y la varianza de cantidad de pozos que producen petróleo. b) Si cada perforación cuesta 10000 dólares y de él se extrae petróleo por valor de 50000 dólares si produce,calcular: 1) la ganancia esperada de la empresa. 2) la desviación estándar de esa ganancia. Ejercicio VII.3 (Distribución Geométrica). Se considera una variable aleatoria X con distribución Geométrica de parámetro p, 0 ≤ p ≤ 1 , X ∼ Geo(p) , es decir con función de cuantı́a: pj = pX (j) = P (X = j) = p (1 − p)j−1 j = 1 , 2 , ... 1. Explique un experimento que sea modelado por X. 2. Hallar el valor esperado y la varianza de X comprobando que: E(X) = 1 1−p , V ar(X) = p p2 Analice lo razonable del resultado para el valor esperado. 3. Calcular P ( X > k ) para k ∈ IN , k ≥ 1. 4. Probar la propiedad de “pérdida de memoria”: P ( X > k + h / X > k ) = P ( X > h ) ∀ k, h ∈ IN , k, h ≥ 1 Ejercicio VII.4 (Distribución Hipergeométrica). Se considera una variable aleatoria X con distribución Hipergeométrica de parámetros N, r, n, ∈ IN , 1 ≤ r ≤ N , 1 ≤ n ≤ N , X ∼ Hip(N, r, n) , es decir con función de cuantı́a: pj = pX (j) = P (X = j) = N −r Cjr Cn−j CnN j = 0 , 1 , 2 , ... , min( n , r ) 1. Explique un experimento que sea modelado por X y concluir que: min( n , r ) X N −r Cjr Cn−j j=0 CnN =1 2. Analice que sucede (a qué otra distribución se asemeja) si se consideran N y r muy grandes (respecto de n) y utilice esto para justificar en algo que el valor esperado y la varianza de X valen: r N − r N − n nr , V ar(X) = n E(X) = N N N N −1 Probabilidad y Estadı́stica - 2020 Página 52 de 86 Ejercicio VII.5 (Distribución de Poisson). Se considera una variable aleatoria X con distribución de Poisson de parámetro µ ∈ IR , µ > 0 , X ∼ P oi(µ) , es decir con función de cuantı́a: pX (k) = P (X = k) = e−µ µk k! k = 0 , 1 , 2 , ... Calcular E(X), E[X(X − 1)] y deducir el valor de V ar(X). Algunas distribuciones de probabilidad continuas Ejercicio VII.6 (Distribución Uniforme). Sea X una variable aleatoria con distribución uniforme en el intervalo [a, b] , X ∼ U ni(a, b) , es decir con función densidad: ( 1 si x ∈ [a, b] b−a fX (x) = 0 en otro caso 1. Explique un experimento que sea modelado por X. 2. Hallar el valor esperado y la varianza de X comprobando que: E(X) = a+b (b − a)2 , V ar(X) = 2 12 Analice lo razonable de los resultados. 3. ¿Cuál es la máxima distancia, en términos de la desviación estándar (raı́z de la varianza), a la que puede encontrarse un valor X del valor esperado?. Ejercicio VII.7 (Distribución Exponencial). Sea X una variable aleatoria con distribución exponencial de parámetro λ , X ∼ Exp(λ) , λ ∈ IR , λ > 0 , es decir con función densidad: λ e−λ x si x ≥ 0 fX (x) = 0 en otro caso 1. Hallar el valor esperado y la varianza de X comprobando que: E(X) = 1 1 , V ar(X) = 2 λ λ 2. Calcular P ( X > x ) para x ∈ IR , x ≥ 0. 3. Probar la propiedad de “pérdida de memoria”: P ( X > x + y / X > x ) = P ( X > y ) ∀ x, y ∈ IR , x, y ≥ 0 Probabilidad y Estadı́stica - 2020 Página 53 de 86 4. Las duraciones de los neumáticos para automóviles se pueden modelar por una distribución exponencial de valor medio 30000 km. a) Hallar la probabilidad de que un neumático dure más de 30000 km. b) Hallar la probabilidad de que un neumático dure más de 60000 km si se sabe que duró más de 30000 km. La distribución Normal ( N ( µ , σ )) Nota: Utilizaremos la notación X ∼ N ( µ , σ ) para decir que X es una variable aleatoria con distribución Normal con media (valor esperado) µ y varianza σ 2 ). Su densidad es: x−µ −1 1 σ 2 fX (x) = √ e σ 2π 2 µ, σ ∈ IR , σ > 0 Ejercicio VII.8. Sea X una variable aleatoria continua con densidad fX y valor esperado finito. 1. Probar que el valor esperado de X es el único número real α que verifica +∞ Z [x − α] fX (x) dx = 0 −∞ 2. Probar que si fX es par respecto de α (o sea fX (α − t) = fX (α + t) ∀ t > 0), entonces el valor esperado de X es α. 3. Pruebe, utilizando la segunda parte de este ejercicio, que si X ∼ N (µ, σ 2 ), entonces E(X) = µ. 2 k ex +4x+8 si x ∈ (−4, 0) 4. Si fX (x) = , con k una constante positiva, 0 en otro caso ¿cuál es el valor esperado de X?. Justifique su respuesta. Nota: No se pide hallar k. Ejercicio VII.9 (Usando la tabla de la Distribución Normal). 1. Si X ∼ N ( 0 , 1 ), calcular P (X ≤ 1,96) , P (X < 1,96) , P (X > 1,96) y P (−0,53 < X < 1,78). 2. Si X ∼ N ( 0 , 1 ), hallar x1 , x2 , x3 y x4 tal que P (X ≤ x1 ) = 0,75, P (X ≤ x2 ) = 0,23, P (X ≥ x3 ) = 0,77 y P (−x4 ≤ X ≤ x4 ) = 0,58. 3. Si X ∼ N ( 200 , 20 ), calcular P (185 ≤ X < 210), P (215 ≤ X ≤ 250) y P (X > 240). 4. Si X ∼ N ( −25 , 10 ), calcular P (X ≤ 0) y hallar x1 , x2 y x3 tales que P (X ≤ x1 ) = 0,1251, P (X ≥ x2 ) = 0,834 y P (−x3 ≤ X ≤ x3 ) = 0,58. Probabilidad y Estadı́stica - 2020 Página 54 de 86 Ejercicio VII.10. Una fábrica produce pistones cuyos diámetros siguen una distribución normal con un diámetro promedio de 5 cm y una desviación estándar igual a 0,001 cm. Para que el pistón sirva su diámetro debe encontrarse entre 4,998 y 5,002 cm. Si el diámetro del pistón es menor que 4,998 cm se desecha mientras que si es mayor que 5,002 cm el pistón puede reprocesarse. 1. ¿Qué porcentaje de pistones servirá?. 2. ¿Qué porcentaje será desechado?. 3. ¿Qué porcentaje será reprocesado?. Ejercicio VII.11. La demanda mensual de cierto producto A tiene una distribución normal con una media de 200 unidades y desviación estándar igual a 40 unidades. La demanda de otro producto B también tiene una distribución normal con media de 500 unidades y desviación estándar igual a 80 unidades. Un comerciante que vende estos productos tiene en su almacén 280 unidades de A y 650 de B al comienzo de mes. ¿Cuál es la probabilidad de que, en el mes, se vendan todas las unidades de ambos productos?. Puede suponer independencia entre la venta de artı́culos. Probabilidad y Estadı́stica - 2020 Página 55 de 86 Sección 13 Práctico (VIII) : UNA VARIABLE ALEATORIA (5a. parte, problemas con variables aleatorias) Ejercicio VIII.1. Sea f (x) = ex 2 e−x 2 si x ≤ 0 si x > 0 1. Graficar f (x) y verificar que es una posible función densidad de probabilidades. Sea X una variable aleatoria continua con densidad f (x). 2. Calcular E(X) y V ar(X). 3. Sea Y = |X| a) Calcular la densidad de probabilidad de la variable aleatoria Y . b) Calcular E(Y ) y V ar(Y ). c) Comparar E(X) y E(Y ). ¿Se pudo predecir este resultado antes de calcular E(Y )?. d ) Comparar V ar(X) y V ar(Y ). ¿Se pudo predecir este resultado antes de calcular V ar(Y )?. Ejercicio VIII.2. En una fábrica cuya producción se supone muy grande (o de producción continua) la proporción de defectuosos es 0,02. Se toma una muestra de tamaño n. 1. Hallar la probabilidad de que haya al menos 2 defectuosos. 2. ¿El resultado de la parte anterior es diferente si el muestreo se realiza con o sin reposición?. Justificar. Ejercicio VIII.3. Un fabricante de aceite tiene el siguiente problema: Por cada una unidad (mil litros) de aceite vendida obtiene una ganancia de $ 300, mientras que por cada unidad producida y no vendida tiene una pérdida de $ 100. Si la demanda de aceite al fabricante tiene una distribución uniforme en [2, 4] (medida en unidades = miles de litros), ¿cuánto debe producir para maximizar la utilidad esperada?. Probabilidad y Estadı́stica - 2020 Página 56 de 86 Ejercicio VIII.4. Suponga que el aumento en la demanda de energı́a eléctrica, expresada en millones de KWh durante los próximos dos años en un área particular, es una variable aleatoria X cuya densidad está dada por: 1 3 si 0 < x < 4 64 x fX (x) = 0 en otro caso 1. Verifique que es una densidad válida. 2. Calcule la distribución acumulativa de X y úsela para determinar la probabilidad de que el aumento de la demanda sea a lo sumo de 2 millones de KWh. 3. Si el área sólo tiene capacidad para generar 3 millones de KWh adicionales, ¿cuál es la probabilidad de que la demanda sea mayor que la oferta?. 4. Calcule el aumento promedio de la demanda. Ejercicio VIII.5 (Distribución Binomial Negativa). Se considera una variable aleatoria X con distribución Binomial Negativa de parámetros r ∈ IN , r ≥ 1 , 0 ≤ p ≤ 1 , es decir con función de cuantı́a: j−1 r pj = pX (j) = P (X = j) = Cr−1 p (1 − p)j−r j = r , r + 1 , r + 2 , ... 1. Muestre que X modela la cantidad de tiradas de una moneda, moneda con probabilidad p de salir cara, hasta que sale cara por r-ésima vez y concluir que: +∞ X j−1 r p (1 − p)j−r = 1 Cr−1 j=r 2. Vincular X con una cierta cantidad de variables aleatorias con distribución Geométrica para determinar el valor esperado de X y concluir que: +∞ X j−1 r p (1 − p)j−r = j Cr−1 j=r r p Ejercicio VIII.6. √ Un blanco está formado por tres cı́rculos concéntricos de radios √13 , 1 y 3. Los disparos dentro del cı́rculo interior valen 4 puntos, dentro del anillo siguiente valen 3 puntos, dentro del tercer anillo valen 2 puntos y fuera del blanco valen 0. Llamamos R es la variable aleatoria que representa la distancia del impacto al centro la cual se supone con densidad de probabilidades f tal que: f (r) = Probabilidad y Estadı́stica - 2020 2 con r > 0 π(1 + r2 ) Página 57 de 86 1. Verificar que f es una densidad de probabilidades. 2. Describir la distribución del puntaje en un tiro. 3. Calcular el valor esperado del puntaje en un tiro. 4. Calcular el valor esperado del puntaje después de cinco tiros. 5. Calcular el valor esperado de R. Ejercicio VIII.7. Se tiran dos dados de forma independiente y sea X la diferencia en valor absoluto de los dos resultados. 1. Identificar los valores posibles que toma X. 2. Hallar la función de probabilidad (cuantı́a) pX . 3. Hallar la esperanza E(X). 4. Hallar la varianza V ar(X). Ejercicio VIII.8. La duración de los artı́culos producidos por dos empresas (1 y 2) siguen distribución exponencial de valor esperado 4 y 5 dı́as respectivamente. Se supone que ambas empresas pueden producir un amplio stock. Si se eligen 5 artı́culos de la empresa 1 y 3 de la empresa 2, calcular las siguientes probabilidades: 1. Entre los 8 elegidos hayan 4 que duren más de tres dı́as. 2. Dado que 4 artı́culos duran más de tres dı́as, ¿cuál es la probabilidad de que de esos, 2 sean de la fábrica 1 y 2 sean de la fábrica 2?. Ejercicio VIII.9. Los jugadores, Daniel y Mauricio tienen 200 $ cada uno. Se lanza una moneda con probabilidad p ∈ (0, 1) de salir cara. Si sale cara Daniel recibe 100 $ de Mauricio y si sale número Daniel le paga 100 $ a Mauricio. Sea N el número de lanzamientos hasta que el juego termina (uno de los jugadores se queda sin dinero). Hallar E(N ). Probabilidad y Estadı́stica - 2020 Página 58 de 86 Ejercicio VIII.10. El peso del cereal que contiene una caja se aproxima a una distribución normal con una media de 600 gramos. El proceso de llenado de las cajas está diseñado para que, en promedio, el peso de una de cada 100 cajas se encuentre fuera del intervalo 590-610 gramos. ¿Cuál es el valor máximo de la desviación estándar para alcanzar este requerimiento?. Ejercicio VIII.11. El número de personas que llegan (n) a una caja registradora de un supermercado en el intervalo [ 0 , t ] es una variable aleatoria que tiene una distribución de probabilidades de Poisson con una media λ t (λ es un parámetro, al igual que t), o sea: P (n = k) = e−λ t (λ t)k k! k = 0 , 1 , 2 , ... 1. Dar una interpretación para el parámetro λ. 2. Sea T el tiempo transcurrido hasta la primer persona que llega a la caja registradora. Hallar la función densidad de probabilidades de T . Concluir E(T ) y reafirmar la interpretación dada en la parte anterior. Nota: Observar que P (T > t) = P (n = 0) (para los parámetros λ y t), ¿por qué?. Ejercicio VIII.12. Una empresa fabrica tornillos mediante dos máquinas A y B que producen el 75 % y el 25 % del total respectivamente. El largo de los tornillos es una variable aleatoria con distribución normal que, para la máquina A, tiene media 4 cm y varianza 1 cm2 mientras que, para la máquina B tiene media 5 cm y varianza 4 cm2 . Un tornillo se considera defectuoso si su largo es mayor que 6 cm. Si se extrae un artı́culo al azar de la producción total, ¿cuál es la probabilidad de que sea defectuoso?. Probabilidad y Estadı́stica - 2020 Página 59 de 86 Sección 14 Tema (III) : DOS VARIABLES ALEATORIAS III.1 PAR ALEATORIO DISCRETO Definición III.1 (Par aleatorio discreto). La probabilidad se concentra en una cantidad finita o infinita numerable, de puntos. El par aleatorio queda determinado por la cuantı́a conjunta (también llamada función de probabilidad): rij = pX,Y (xi , yj ) = P (X = xi , Y = yj ) i , j = 1, 2, ... es decir los puntos que toman probabilidades concentradas y dichas probabilidades. Propiedades III.2. F ¿Cuándo está bien definida?: {rij } es una cuantı́a conjunta ⇔ 0 ≤ rij ≤ 1 ∀ i , j = 1, 2, ... y P rij = 1. i,j F ¿Cómo calcular probabilidades?: P ((X, Y ) ∈ B) = X X rij = i , j / (xi ,yj )∈B P (X = xi , Y = yj ) (xi ,yj )∈B F El cálculo de la distribución de probabilidades de Z = g(X, Y ) puede realizarse en forma similar al caso de una sola variable aleatoria (calculando los valores que toma la nueva variable aleatoria y luego “transferimos” las probabilidades). F Las cuantı́as marginales: (son las cuantı́as de cada variable aleatoria sola) vienen dadas por: pi = P (X = xi ) = X rij = X j qj = P (Y = yj ) = X P (X = xi , Y = yj ) j rij = X i P (X = xi , Y = yj ) i F Los valores esperados E(g(X, Y )) pueden calcularse con expresiones análogas a las correspondientes a una sola variable aleatoria: X X E(g(X, Y )) = g(xi , yj ) rij = g(xi , yj ) P (X = xi , Y = yj ) i,j Probabilidad y Estadı́stica - 2020 i,j Página 60 de 86 Ejemplo III.3. Sean X e Y variables aleatorias discretas con cuantı́a conjunta dada por la siguiente tabla: X /Y 1 2 3 0 0,1 0,15 0 1 0,2 0,15 0,4 1. Verificar está bien definida. 2. Calcular P ( X 2 + Y 2 ≤ 4 ). 3. Calcular las cuantı́as marginales. 4. Calcular la cuantı́a de Z = X − 2Y . 5. Calcular E(Z). III.2 PAR ALEATORIO CONTINUO Definición III.4 (Par aleatorio continuo). Decimos que el vector aleatorio (X, Y ) es continuo sii existe fX,Y : IR2 → IR, función seccionalmente continua, llamada densidad conjunta de probabilidades, tal que: RR P ((X, Y ) ∈ B) = fX,Y (x, y) dx dy B Propiedades III.5. F ¿Cuándo está bien definida?: fX,Y es densidad de probabilidades ⇔ +∞ +∞ R R RR fX,Y (x, y) dx dy = dx fX,Y (x, y) dy = 1. ⇔ fX,Y (x, y) ≥ 0 ∀ (x, y) ∈ IR2 y 2 −∞ −∞ IR F ¿Cómo calcular probabilidades?: (ya lo dice la definición) RR P ((X, Y ) ∈ B) = fX,Y (x, y) dx dy B En particular: P (X = x0 , Y = y0 ) = 0 y si área(B) = 0 , entonces P ((X, Y ) ∈ B) = 0 F El cálculo de la distribución de probabilidades de Z = g(X, Y ) puede realizarse en forma similar al caso de una sola variable aleatoria (calculando la distribución acumulada de probabilidades y luego derivar para tener la densidad). Probabilidad y Estadı́stica - 2020 Página 61 de 86 F Las densidades marginales: (son las densidades de cada variable aleatoria sola) vienen dadas por: +∞ +∞ Z Z fX (x) = fX,Y (x, y) dy y fY (y) = fX,Y (x, y) dx −∞ −∞ F Los valores esperados E(g(X, Y )) pueden calcularse con expresiones análogas a las correspondientes a una sola variable aleatoria: +∞ Z RR E(g(X, Y )) = IR g(x, y) fX,Y (x, y) dx dy = 2 −∞ +∞ Z dx g(x, y) fX,Y (x, y) dy −∞ Ejemplo III.6. Sean X e Y variables aleatorias continuas con densidad de probabilidades conjunta dada por: k (x + y) si x ∈ (0, 1) e y ∈ (0, 1) fX,Y (x, y) = 0 en otro caso 1. Hallar k. 2. Calcular P X ≤ 1 2 ,Y ≤ 1 2 . 3. Calcular las densidades marginales. 4. Hallar E(X + Y ). III.3 EJEMPLOS CON PARES ALEATORIOS Ejemplo III.7. Juan y Pedro van a cazar patos todos los fines de año. Se sabe que la siguiente tabla representa las posibles cantidad de patos cazados y las respectivas probabilidades conjuntas (función de probabilidad conjunta). Llamemos J y P a la variable aleatoria cantidad de patos cazados por Juan y Pedro respectivamente. P /J 0 1 2 0 0,05 0,01 0,01 1 0,08 0,01 0,01 2 0,20 0,08 0,01 3 0,26 0,12 0,02 4 0,12 0,01 α 1. Hallar α. 2. Hallar las probabilidades de cada cazador de cada una de sus posibles cantidades a cazar, por separado (funciones de probabilidad marginales). Probabilidad y Estadı́stica - 2020 Página 62 de 86 3. Calcular la distribución de probabilidades (función de probabilidad) de la cantidad de patos cazados con que vuelven Juan y Pedro de su cacerı́a. Ejemplo III.8. Se consideran dos variables aleatorias X e Y con densidad conjunta: k si 0 ≤ x ≤ 1 y x ≤ y ≤ 1 fX,Y (x, y) = 0 en otro caso 1. Hallar k. 2. Hallar las densidades marginales fX y fY . 3. Hallar la distribución de probabilidad de Z = Y − X y su densidad. 4. Hallar el valor esperado de Z = Y − X. III.4 INDEPENDENCIA DE VARIABLES ALEATORIAS Definición III.9 (Variables aleatorias independientes). Diremos que las variables aleatorias X e Y son independientes si y solo si X −1 (I) y Y −1 (J) son sucesos independientes para todo I y J intervalos de números reales, es decir: P ( X ∈ I , Y ∈ J ) = P ( X ∈ I ) P ( Y ∈ J ) ∀ I , J intervalos Propiedades III.10. F X e Y variables aleatorias discretas, son independientes si y solo si P (X = xi , Y = yj ) = P (X = xi )P (Y = yj ) ∀ i , j o sea ri,j = pi qj ∀ i , j F X e Y variables aleatorias continuas, son independientes si y solo si fX,Y (x, y) = fX (x)fY (y) ∀ (x, y) ∈ IR2 Ejemplo III.11. 1. Analizar si en los pares aleatorios de los ejemplos anteriores se tienen variables aleatorias independientes. 2. ¿Pudo deducirse sin realizar ningún cálculo?. Teorema III.12. Si X e Y son independientes, entonces E(XY ) = E(X)E(Y ). Probabilidad y Estadı́stica - 2020 Página 63 de 86 Definición III.13 (Covarianza y coeficiente de correlación). Llamaremos covarianza de las variables aleatorias X e Y al número: Cov(X, Y ) = E ((X − E(X))(Y − E(Y ))) Llamaremos coeficiente de correlación de las variables aleatorias X e Y al número: Cov(X, Y ) p ρ(X, Y ) = p V ar(X) V ar(Y ) También podemos calcular la covarianza como: Cov(X, Y ) = E(XY ) − E(X)E(Y ) Observación III.14. Sea X una variable aleatoria no constante. Cov(X, X) = V ar(X) > 0 y por lo tanto X no es independiente con X (¡¡OBVIO!!). Teorema III.15. V ar(X + Y ) = V ar(X) + V ar(Y ) + 2 Cov(X, Y ) Propiedades III.16. Si X e Y son independientes, entonces: F Cov(X, Y ) = 0. F V ar(X + Y ) = V ar(X) + V ar(Y ). Estas propiedades no garantizan la independencia de las variables aleatorias (no vale el recı́proco). III.5 MÁS EJEMPLOS CON PARES ALEATORIOS Ejemplo III.17. Sean las variables aleatorias: X ∼ U ni(0, 1) e Y ∼ U ni(0, 1) , independientes Hallar la densidad de probabilidades de Z = X + Y . Probabilidad y Estadı́stica - 2020 Página 64 de 86 Ejemplo III.18. Sean X e Y variables aleatorias discretas independientes. La siguiente tabla representa la función de probabilidad conjunta y las funciones de probabilidad marginales. X /Y 0 1 pY 1 2 4 0,1 0,3 0,6 pX 0,3 0,7 1 1. Completar la tabla. 2. Calcular Cov(X, Y ) y V ar(X + Y ). Probabilidad y Estadı́stica - 2020 Página 65 de 86 Sección 15 Práctico (IX) : DOS VARIABLES ALEATORIAS Ejercicio IX.1. Se consideran dos variables aleatorias, X que toma los valores −1 y 1 e Y que toma los valores 2, 4 y 6 con las probabilidades conjuntas dada por la siguiente tabla: X /Y −1 1 2 0,2 0,1 4 0,25 a 6 0,15 0,25 1. Hallar a. 2. Calcular P ( X < 1 , Y ≤ 4 ). 3. Hallar las funciones de probabilidad de X + Y , X 2 Y y |X − Y |. 4. Hallar el valor esperado de X + Y y X 3 Y 2 . Ejercicio IX.2. Se consideran dos variables aleatorias X e Y con densidad conjunta: 1 k e− 5 x−10 y si x > 0 e y > 0 fX,Y (x, y) = 0 en otro caso 1. Hallar k. 2. Calcular P ( X < 3 , Y ≤ 2 ). 2 3. Hallar el valor esperado de XY . Ejercicio IX.3. Sean X e Y variables aleatorias con densidad conjunta: 2 ( x + y − 2 x y ) si x ∈ (0, 1) e y ∈ (0, 1) fX,Y (x, y) = 0 en otro caso 1. Hallar las densidades marginales correspondientes. 2. Hallar E(X), E(Y ), E(XY ) y Cov(X, Y ). 3. ¿Son independientes X e Y ?. 4. Dada las densidades de dos variables aleatorias, ¿es única la distribución conjunta?. Justifique e interprete su respuesta. Probabilidad y Estadı́stica - 2020 Página 66 de 86 Ejercicio IX.4. Sean X e Y variables aleatorias discretas que toman los valores 1, 2 y 3 con la función de probabilidad representada en la siguiente tabla: X /Y 1 2 3 1 2 1 12 1 6 1 9 1 4 0 1 18 3 0 1 5 2 15 1. Calcular las funciones de probabilidad marginales. 2. ¿Son independientes X e Y ?. ¿Pudo deducirse mirando la tabla?. Ejercicio IX.5. Sean X e Y dos variables aleatorias que toman los valores −1, 0 y 1 con la función de probabilidad conjunta dada por la siguiente tabla: X /Y −1 0 1 −1 0,1 0,05 0,1 0 0,05 0,1 0,2 1 0,1 0,2 0,1 1. Hallar las funciones de probabilidad marginales. 2. ¿Son independientes X e Y ?. Justificar. 3. Hallar la función de probabilidad, el valor esperado y la varianza de Z = X 2 Y 2 . Ejercicio IX.6. Considere el siguiente experimento: se tira un dado de 6 caras (no cargado). Si el resultado es par, se toma una moneda cargada tal que P (cara) = p y se lanza. Si el resultado es impar, se toma una moneda distinta cargada tal que P (cara) = q y se lanza. Sean X =“No. que sale en el dado” e Y = 1 si la moneda sale cara e Y = 0 si no. 1. Exprese mediante una tabla la ley conjunta de X e Y . 2. Calcule las distribuciones marginales en función de p y q. 1 3. ¿Qué relación deben cumplir p y q para que P (Y = 1) = ?. 2 4. Para p y q que cumplen la relación anterior, ¿son X e Y independientes?. Probabilidad y Estadı́stica - 2020 Página 67 de 86 Ejercicio IX.7. Se considera el experimento “elegir un punto al azar del cı́rculo unitario”. Sean X =“abscisa del punto elegido” e Y =“ordenada del punto elegido”. 1. Exprese la densidad conjunta de (X, Y ) y calcule las densidades marginales de X e Y . ¿Son X e Y independientes?. Justificar. 2. Calcular la distribución acumulada y la densidad de R = “distancia del punto al origen”. Calcular E(R). 3. Calcular la distribución acumulada y la densidad de θ = “ángulo del punto con el eje x” (medido de 0 a 2 π). Interpretar el resultado. 4. ¿Son R y θ independientes?. Justificar. Ejercicio IX.8. Se considera el par de variables aleatorias continuas (X, Y ) con distribución uniforme en el dominio D = [ 0 , 3 ] × [ 0 , 1 ]. 1. Escribir la densidad conjunta del par aleatorio (X, Y ). Explique cómo se obtuvo. 2. Hallar la densidad de probabilidades de Z = X + Y . A partir de la densidad calculada, calcular E(Z). 3. Hallar la densidad de probabilidades de W = X + 2 Y . A partir de la densidad calculada, calcular E(W ). 4. Corroborar los valores esperados calculado en las partes anteriores calculando primero E(X) y E(Y ) para luego deducir E(Z) y E(W ). Ejercicio IX.9. Se consideran dos variables aleatorias X e Y que toman los valores 1, 2 y 3 con las probabilidades conjuntas dadas en la siguiente tabla: X /Y 1 2 3 1 0,02 a 0,06 2 0,08 0,08 b 3 c 0,10 0,30 1. Hallar a, b y c sabiendo que X e Y son independientes. 2. Hallar la función de probabilidad de X 2 Y 2 y, a partir de esta, su valor esperado. 3. Hallar los valores esperados de X 2 y de Y 2 . Comprobar que el producto de ellos da el valor esperado calculado en la parte anterior. Explique por qué este resultado era esperado. Probabilidad y Estadı́stica - 2020 Página 68 de 86 Ejercicio IX.10. Sean X e Y variables aleatorias con densidad conjunta: k si (x, y) ∈ D fX,Y (x, y) = 0 en otro caso donde D es el triángulo de vértices (0, 0), (1, 0) y (0, 1). 1. Hallar k. 2. a) Hallar las densidades marginales correspondientes. b) Deducir a partir de este resultado que X e Y no son independientes. c) ¿Pudo deducirse sin hacer ningún cálculo, solo mirando la densidad conjunta?. Justifique su respuesta. 3. Hallar la densidad de probabilidades de Z = X + Y . Calcular E(Z). −1 si x + y ≤ 21 e y ≤ x 2 4. Sea g : IR → IR tal que g(x, y) = . 1 en otro caso Calcular el valor esperados y la varianza de Z = g(X, Y ). Probabilidad y Estadı́stica - 2020 Página 69 de 86 Sección 16 Evaluación (II) : VARIABLES ALEATORIAS Ejercicio II.1. Un Shopping Center tiene un departamento de marketing que estudia la venta semana de diferentes productos. Se sabe que los ingresos por semana de una cierta baterı́a de productos es una variable aleatoria X con distribución Normal con media (valor esperado) µ = 75567,5 pesos y desvı́o estándar σ = 1235,5 pesos. Se pide: 1. Hallar valores de α y β tal que P ( α ≤ X ≥ β ) = 0,95. 2. Hallar valores de u y v tal que P ( u ≤ X ≥ v ) = 0,99. 3. Si en una semana los ingresos fueron de 71123,5 pesos, y en la semana siguiente fueron de 70211 pesos. Según su opinión, ¿cómo van las ventas semanales?. 4. Calcular la probabilidad de que la venta semanal supere los 77000 pesos. 5. Calcular la probabilidad de que, en 5 semanas consecutivas, la venta, por lo menos una semana, supere los 77000 pesos. Ejercicio II.2. La ganancia que reporta un artı́culo depende de dos parámetros que son variables aleatorias: X ∼ U ni(0, 1) e Y ∼ U ni(1, 5) , independientes Si X + Y ≥ 3 y X 2 + Y < 5 la ganancia es 1500 $ mientras que en otro caso la ganancia es 300 $. 1. Hallar el valor esperado de la ganancia. 2. Consideremos la variable aleatoria Z que: F toma el valor 1 si X + Y ≥ 3 y X 2 + Y < 5. F toma el valor 0 en todo otro caso. a) ¿Cuál es la distribución de Z?. (dar el nombre y valor de el/los parámetros y su valor esperado) b) Observar que la ganancia se puede escribir G = 300 + 1200 Z y deducir de aquı́ el valor esperado de la ganancia, verificando el resultado anterior. Probabilidad y Estadı́stica - 2020 Página 70 de 86 Ejercicio II.3 (Segundo Parcial julio 2012). Luis tira penales. En la siguiente figura se muestra el arco y las probabilidades de que el tiro de Luis esté en cada una de las zonas (supondremos que el tiro cae en alguna de las zonas o afuera). Rodolfo es golero y ante cada penal elige una de tres posiciones finales en el arco, que identificaremos como derecha, izquierda y centro. La siguiente figura muestra las tres posiciones y la probabilidad de que Rodolfo elija cada una, la cual es independiente de la decisión de Luis. El penal que tira Luis es atajado por Rodolfo si la elección de la zona de Luis está dentro de elección de la posición final de Rodolfo. 1. Calcular la probabilidad de que Luis tire el penal afuera. 2. Calcular la probabilidad de que el penal sea gol. Sugerencia: Puede ser útil definir una variable aleatoria que determine dónde va el tiro de Luis, separando en las zonas en que se posiciona Rodolfo. Ejercicio II.4. Una empresa generadora de energı́a dispone de dos plantas solares cercanas entre sı́. La energı́a (en porcentaje respecto al máximo posible) producida por cada una de las plantas en un dı́a cualquiera puede modelarse como variables aleatorias X e Y respectivamente, con la siguiente densidad conjunta: k ( x2 + y 2 ) si x ∈ [0, 1] , y ∈ [0, 1] fX,Y (x, y) = 0 en otro caso 1. Hallar k para que fX,Y sea efectivamente una densidad. 2. Hallar las distribuciones marginales de X e Y . 3. Hallar E(X), E(Y ) y E(XY ). 4. Hallar Cov(X, Y ) y concluir que las variables no son independientes. ¿Puede interpretar este resultado intuitivamente?. Probabilidad y Estadı́stica - 2020 Página 71 de 86 Sección 17 Tema (IV) : ESTADÍSTICA IV.1 MUESTRAS Y ESTADÍSTICOS 1. Muestras. 2. Muestra aleatoria simple. 3. Estadı́sticos. IV.2 MÁXIMO Y MÍNIMO FALTA. IV.3 EL PROMEDIO 1. Valor esperado y varianza. 2. Desigualdad de Chebyshev. Teorema IV.1 (Desigualdad de Chebyshev). Si X es una variable aleatoria con valor esperado y varianza finitas y ε > 0, entonces: P ( | X − E(X) | ≥ ε ) ≤ V ar(X) ε2 o escribiendo: E(X) = µ , V ar(X) = σ 2 y ε = k σ: P(|X − µ| ≥ k σ ) ≤ o P X −µ ≥k σ ≤ 1 k2 1 k2 Observación IV.2. F Conociendo valor esperado y varianza no conocemos la distribución de probabilidades de la variable aleatoria pero podemos acotar las probabilidades. F Permite interpretar la varianza como medida de dispersión. Probabilidad y Estadı́stica - 2020 Página 72 de 86 3. Leyes débil y fuerte de los grandes números. Definición IV.3 (Convergencia débil o convergencia en probabilidad). Sea {Xn } una sucesión de variables aleatorias y X una variable aleatoria, todas en (Ω, A, P ), espacio de probabilidad. Diremos que {Xn } converge débilmente o converge en probabilidad a X si P ( | Xn − X | > ε ) −→ 0 ∀ ε > 0 n→+∞ Notación: Xn −→ X. p Definición IV.4 (Convergencia fuerte o convergencia casi segura). Sea {Xn } una sucesión de variables aleatorias y X una variable aleatoria, todas en (Ω, A, P ), espacio de probabilidad. Diremos que {Xn } converge fuertemente o converge casi seguramente a X sii: P (Xn −→ X) = 1 n Notación: Xn → X c.s. Observación IV.5. Como lo hace suponer sus nombres la convergencia fuerte es más potente que la convergencia débil, es decir: Xn → X c.s. ⇒ Xn −→ X p Definición IV.6 (Convergencia cuadrática). Sea {Xn } una sucesión de variables aleatorias y X una variable aleatoria, todas en (Ω, A, P ), espacio de probabilidad. Diremos que {Xn } converge cuadráticamente a X sii E ( Xn − X )2 −→ 0 n→+∞ Observación IV.7. La convergencia cuadrática es más potente que la convergencia débil, es decir: Xn → X cuadráticamente ⇒ Xn −→ X p Probabilidad y Estadı́stica - 2020 Página 73 de 86 Teorema IV.8. Si E (Xn ) −→ c y V ar (Xn ) −→ 0 , entonces Xn → c cuadráticamente. n→+∞ n→+∞ Teorema IV.9 (Ley débil de los grandes números). Si {Xn }n≥1 es una sucesión de variables aleatorias independientes idénticamente distribuidas (notación reducida v.a.i.i.d.) con E(Xi ) = µ < ∞ y V ar(Xi ) = σ 2 < ∞, entonces: Xn = Sn X1 + X2 + ... + Xn = −→ µ p n n o sea P ( | X n − µ | > ε ) −→ 0 ∀ ε > 0 n→+∞ donde: X n es el promedio y Sn es la suma de las variables aleatorias X1 , X2 , ... , Xn . Observación IV.10. Si las variables aleatorias no tienen igual varianza (V ar(Xi ) = σi2 < ∞) alcanza con pedir que V ar X n = V ar Sn n = n 1 X 2 σi −→ 0 n→+∞ n2 i=1 para que la ley débil siga valiendo. Teorema IV.11 (Ley fuerte de los grandes números (Kolmogorov)). Si {Xn }n≥1 es una sucesión de variables aleatorias independientes idénticamente distribuidas, con momento de primer orden finito (E(|Xi |) < ∞), entonces: Sn −→ 0 c.s. n n→+∞ Observación IV.12. Si las variables aleatorias no tienen igual varianza (V ar(Xi ) = σi2 < ∞) alcanza con pedir que n X σ2 i i=1 i2 −→ 0 n→+∞ para que la ley fuerte siga valiendo. Observación IV.13. En el caso particular que las variables aleatorias sean con distribución de Bernoulli se concluye que la frecuencia relativa de un suceso converge a la probabilidad del suceso casi seguramente. Probabilidad y Estadı́stica - 2020 Página 74 de 86 4. Teorema Central de Lı́mite. Aproximación de la distribución Binomial por la distribución Normal. Teorema IV.14 (Teorema Central del Lı́mite). Si {Xn }n≥1 es una sucesión de variables aleatorias independientes idénticamente distribuidas con E(Xi ) = µ < ∞ y V ar(Xi ) = σ 2 < ∞, entonces: P O, como Sn √ −nµ σ n = X n −µ √σ n Sn − n µ √ a≤ ≤b σ n 1 −→ √ n→+∞ 2π Zb e− x2 2 dx a , queda: P a≤ Xn − µ √σ n ! ≤b 1 −→ √ n→+∞ 2π Zb e− x2 2 dx a Observación IV.15. En las condiciones del teorema: p √ F n µ = E(Sn ) y σ n = V ar(Sn ). −nµ es aproxiPor lo tanto el teorema plantea que para n grande la distribución de Sσn√ n madamente N (0, 1) (normal con valor esperado 0 y varianza 1), o dicho de otra manera, √ Sn ≈ N ( n µ , σ n ). q F µ = E X n y √σn = V ar X n . Por lo tanto el teorema plantea que para n grande la distribución de X n −µ √σ n es aproximadamente N (0, 1) (normal con valor esperado 0 y varianza 1), o dicho de otra manera, X n ≈ N ( µ , √σn ). F Observando que las distribuciones binomiales son suma de v.a.i.i.d. con distribución de Bernoulli, se concluye que la binomial se aproxima por la normal para n grande: p Bin(n, p) ≈ N ( n p , n p (1 − p) ) para n grande IV.4 LA DESVIACIÓN ESTÁNDAR (s2 ) 1. Valor esperado. 2. Distribución Chi-cuadrado. Probabilidad y Estadı́stica - 2020 Página 75 de 86 IV.5 ESTIMACIÓN PUNTUAL 1. Estimadores insesgados, eficiencia relativa y estimadores consistentes. 2. Cálculo del tamaño de la muestra para acotar errores en probabilidad. 3. Estimadores de máxima verosimilitud. IV.6 ESTIMACIÓN POR INTERVALOS (INTERVALOS DE CONFIANZA) 1. Planteo general. 2. Casos de muestra de tamaño n = 1. 3. Casos de muestras grandes. 4. Intervalos de confianza para la la media y desviación de una distribución Normal. Probabilidad y Estadı́stica - 2020 Página 76 de 86 Sección 18 Práctico (X) : ESTADÍSTICA (1a. parte) Muestras y Estadı́sticos Ejercicio X.1. Sean X1 , X2 , ... , Xn , n v.a.i.i.d. con distribución uniforme en (0, 1). 1. Hallar las densidades de probabilidad de: Mn = max{ X1 , X2 , ... , Xn } y mn = min{ X1 , X2 , ... , Xn } 2. Hallar los respectivos valores esperados y varianzas. Interpretar los resultados. Ejercicio X.2. Sean X1 , X2 , ... , Xn , n v.a.i.i.d. con distribución exponencial, Xi ∼ Exp(λi ) para i = 1, 2, ..., n, es decir con densidad λi e−λi x si x ≥ 0 fXi (x) = con λi > 0 0 en otro caso Probar que mn = min{ X1 , X2 , ... , Xn } ∼ Exp(λ1 + λ2 + ... + λn ). Ejercicio X.3. Conteste las siguientes preguntas utilizando la desigualdad de Chebyshev. 1. La producción diaria de motores eléctricos en una fábrica es (en promedio) µ = 120 con una desviación estándar de σ = 10. Hallar un intervalo que contenga por lo menos el 90 % de la cantidad diaria de motores producidos. 2. Una empresa de electrónica se encarga de suministrar tarjetas de impresoras a una fábrica de montaje de microcomputadoras. Se estudió la demanda mensual de tarjetas durante algunos meses y se vio que el promedio era µ = 280 con una desviación estándar de σ = 4. ¿Cuál es el stock de tarjetas que debe tener la empresa de electrónica al principio de cada mes para que la demanda sea mayor que la oferta cuando mucho con una probabilidad de 0.10?. Ejercicio X.4. Este ejercicio describe el método de Montecarlo para el cálculo de integrales. 1. Sean (Ui )i∈IN ∼ U ni[a, b], v.a.i.i.d. y f es integrable Riemann en [a, b]. Mostrar que: n 1X f (Ui ) n i=1 Probabilidad y Estadı́stica - 2020 −→ n→+∞ 1 b−a Zb f (x) dx a Página 77 de 86 2. Mediante la generación de 100 números aleatorios, obtenga una estimación de 1 Z 0 x2 e− 2 √ dx. 2π Comparar el resultado obtenido con el provisto por las tablas de la distribución N (0, 1). 3. Sea D una región arbitraria de [0, 1] × [0, 1] y sean ( X1 , Y1 ) , ( X2 , Y2 ) , . . . , ( Xn , Yn ) pares aleatorios independientes e idénticamente distribuidas con distribución uniforme en [0, 1] × [0, 1], es decir que se cumple que: P ( ( Xi , Yi ) ∈ A ) = área ( A ∩ [0, 1] × [0, 1] ) Sea an = # { i / 1 6 ( Xi , Yi ) ∈ D } n Probar que: an −→ n→+∞ área(D) Ejercicio X.5. Una pieza de una máquina se verifica al final de cada hora de producción y se cambia por una nueva en caso de encontrarse rota. El tiempo de vida en horas de la pieza se puede modelar con una variable aleatoria T con distribución exponencial de parámetro λ (T ∼ exp(λ)), por lo tanto el tiempo en horas que transcurre hasta el recambio de la pieza se puede modelar con una variable aleatoria X = [T ] + 1, donde [T ] es la parte entera de T (esto es, X = n si y sólo si n − 1 ≤ T < n). 1. Hallar la función de probabilidad de la variable aleatoria X y probar que tiene distribución geométrica de parámetro 1 − e−λ (X ∼ Geo(1 − e−λ )). 2. A partir de los tiempos en los que se realiza el recambio de las piezas se desea estimar el parámetro λ del tiempo de vida de dichas piezas. a) Calcular λ en función de µ siendo µ = E(X). b) ¿Cómo estimarı́a µ a partir de las observaciones X1 , X2 , . . . , Xn de los tiempos de recambio de las piezas, utilizando la ley de grandes números? c) Construir un estimador para λ en función de las observaciones X1 , X2 , . . . , Xn de los tiempos de recambio de las piezas. Ejercicio X.6. Se lanza una moneda 1000 veces. Calcular la probabilidad de que la cantidad de caras esté entre 400 y 600. Indicar la forma en que se resolverı́a tomando p = probabilidad de resultar cara en una tirada de la moneda y calcular efectivamente el valor para el caso de la moneda equilibrada. Ejercicio X.7. Se lanza un dado perfecto 100 veces. Calcular la probabilidad de que salgan más de 20 veces el número seis. Probabilidad y Estadı́stica - 2020 Página 78 de 86 Ejercicio X.8. Se considera una población que tiene una distribución con valor esperado 5 y varianza 400. Se toma una muestra de tamaño n muy grande y se considera el promedio: Xn = X1 + X2 + ... + Xn n Calcular la probabilidad de que el promedio se encuentre entre 4,5 y 5,5 considerando el tamaño de la muestra: a) n = 100 , b) n = 1000 , c) n = 10000 ¿A cuánto tiende la probabilidad hallada al hacer tender n a infinito?. Comentar. Ejercicio X.9. Conteste las preguntas del Problema X.3 pero suponiendo ahora que la distribución es normal y compare la precisión obtenida. Ejercicio X.10. Se midió el pH de 30 muestras de agua de una planta industrial obteniéndose un promedio de 6,8 y una desviación estándar de 0,9. Intuitivamente, ¿le parece razonable pensar que la planta trata de mantener el pH del agua en 7,0?. Ejercicio X.11. Se dice que una variable aleatoria X es una variable de spin de parámetro h, y se denota X ∼ S(h), si X toma los valores −1 y 1 con la siguiente probabilidad: P (X = x) = ehx , eh + e−h x ∈ {−1, 1}, h > 0 1. Calcule E[X] y V ar(X). 2. Considere una sucesión de variables aleatorias X1 , X2 , . . . , Xn iid ∼ S(h). ¿Cómo estimarı́a h a partir de las observaciones utilizando la ley de grandes números?. 3. El spin total de un conjunto de n partı́culas está definido por: M= n X Xi i=1 Se dice que un sistema de n partı́culas presenta magnetización (positiva) cuando M > 2 n. 3 a) Si se supone que el número total de partı́culas es n = 9000 y que h = L(2), estime la probabilidad de que el sistema presente magnetización. b) Suponiendo como antes que n = 9000, calcule el mı́nimo valor de h para el cual se cumple 1 que la probabilidad de que el sistema presente magnetización es superior a . 2 Probabilidad y Estadı́stica - 2020 Página 79 de 86 Sección 19 Práctico (XI) : ESTADÍSTICA (2a. parte) Estimación puntual Ejercicio XI.1. Sean X1 , X2 , X3 y X4 cuatro variables aleatorias independientes con el mismo valor esperado y varianza. Consideramos los siguientes estimadores del valor esperado: X1 + X4 2 X1 + 2 X4 3 4 X1 − 2 X3 + X4 3 X1 + X2 + X4 3 1. Indicar si los estimadores son insesgados. 2. ¿Cuál es el estimador más eficiente entre los insesgados?. 3. Proponer otro estimador del valor esperado que sea insesgado y más eficiente que los anteriores. Comente los resultados. Ejercicio XI.2. Sean X1 y X2 dos variables aleatorias independientes con la misma distribución. (X1 − X2 )2 ¿Es Z = un estimador insesgado de la varianza de la distribución?. 2 Ejercicio XI.3. Sean X1 , X2 , ..., Xn , n v.a. iid. 1. Demostrar que los estimadores a1 X1 + a2 X2 + ... + an Xn son insesgados de la media de la población si y solo si a1 + a2 + ... + an = 1. 2. Demostrar que de todos los estimadores de la parte anterior el más eficientes es el promedio. Sugerencia: Recordar la desigualdad de Cauchy-Schwartz: n X i=1 !2 x i yi 6 n X i=1 ! x2i n X ! yi2 i=1 donde la igualdad se da cuando xi = λ yi ∀ i = 1 , 2 , 3 , ... , n. Y aplicarla considerando xi = ai e yi = 1 ∀ i = 1 , 2 , 3 , ... , n. Probabilidad y Estadı́stica - 2020 Página 80 de 86 Ejercicio XI.4. Suponer que θ̂1 y θ̂2 son estimadores insesgados del mismo parámetro θ, independientes, con varianzas σ12 y σ22 respectivamente. Se considera un nuevo estimador del mismo parámetro θ de la siguiente forma: θ̂3 = a θ̂1 + (1 − a) θ̂2 con a < 1 1. Probar que θ̂3 es un estimador insesgado de θ. 2. ¿Cómo debe elegirse a para que el estimador sea el más eficientes de los ası́ definidos?. Ejercicio XI.5. Llamamos p a la porción de autos defectuosos de cierta empresa. 1. Se elige de la producción una muestra aleatoria simple al azar de tamaño n. Hallar el estimador de máxima verosimilitud de p a partir de la muestra. Sugerencia: Llamar Xi a la variable aleatoria de Bernoulli, indicatriz del suceso ser defectuoso en el i-ésimo auto de la muestra (toma el valor 1 si resulta defectuoso y 0 en caso contrario) y observar que podemos escribir: P (Xi = x) = px (1 − p)1−x donde x = 0 o 1 2. Si en una muestra de 50 autos resultan 2 defectuosos, ¿cuál serı́a el valor estimado por máxima verosimilitud de la proporción de autos defectuosos?. Ejercicio XI.6. En los siguientes casos hallar el estimador de máxima verosimilitud, a partir de una muestra aleatoria simple X1 , . . . , Xn con la distribución indicada. 1. Xi ∼ N (µ, 1), se desea estimar µ. 2. Xi ∼ exp(λ), se desea estimar λ. 3. Xi ∼ U ni(0, a), se desea estimar a. 4. Xi ∼ N (µ, σ), se desea estimar µ y σ 2 . Nota: Para maximizar una función de dos variables tiene que considerar anular las dos derivadas (respecto de las dos variables) simultáneamente. 5. Xi ∼ P oi(µ), se desea estimar µ. Probabilidad y Estadı́stica - 2020 Página 81 de 86 Ejercicio XI.7. Se tiene una urna con 9 bolas siendo b bolas blancas y 9 − b rojas. Se retiran 3 bolas obteniéndose la primer bola blanca, la segunda roja y la tercera blanca. 1. Estimar por máxima verosimilitud el valor de b (cantidad de bolas blancas de la urna) si las bolas se retiran con reposición. 2. Estimar nuevamente considerando que las bolas se retiran sin reposición. Ejercicio XI.8. Hallar el estimador de máxima verosimilitud de θ a partir de una muestra aleatoria simple de una θ−1 θ+1 población con distribución U ni 2 , 2 . Comente los resultados obtenidos. Ejercicio XI.9. Una variable aleatoria X tiene distribución N (µ, 1). Se hacen 20 observaciones de X, pero en vez de anotar su valor, sólo observamos si X es negativa o no. Utilizar que el suceso { X < 0 } sucedió exactamente 14 veces para estimar por el método de máxima verosimilitud el valor de µ. Sugerencia: Observar que si â es el estimador de máxima verosimilitud de a entonces g(â) es el estimador de máxima verosimilitud de g(a). Probabilidad y Estadı́stica - 2020 Página 82 de 86 Sección 20 Práctico (XII) : ESTADÍSTICA (3a. parte) Estimación por intervalos. Intervalos de confianza Ejercicio XII.1. Una máquina de refrescos está ajustada de tal manera que la cantidad de lı́quido despachada se distribuye aproximadamente en forma normal con una desviación estándar igual a 0,15 decilitros. 1. Encontrar un intervalo de confianza al nivel 0,05 para la media de todos los refrescos que sirve esta máquina si una muestra aleatoria de 36 refrescos tiene un contenido promedio de 2,25 decilitros. 2. ¿Qué tan grande tiene que ser la muestra si se desea tener una confianza del 95 % de que la media muestral no difiere en más de 0,03 decilitros de la media real µ?. Ejercicio XII.2. Los estudiantes de una muestra de tamaño 12 sorteados entre los que se han presentado a un cierto examen obtuvieron los siguientes puntajes: 48 70 72 44 39 80 57 66 70 54 61 55 Si suponemos que la distribución de puntajes es normal y que las calificaciones de los estudiantes son variables aleatorias independientes, construir un intervalo de confianza al 95 % para la media de puntaje. Ejercicio XII.3. Un fabricante de baterı́as para automóvil asegura que sus baterı́as duran, en promedio, 3 años con una varianza de un año. Si 5 de estas baterı́as tienen duraciones de 1,9, 2,4, 3,0, 3,5 y 4,2 años, determine un intervalo de confianza al nivel 0,05 para σ 2 (varianza) e indique si es válida la afirmación del fabricante de que σ 2 = 1. Se supone que la población de las duraciones de las baterı́as se distribuye aproximadamente en forma normal. Ejercicio XII.4. De una lı́nea de producción se extraen independientemente 200 artı́culos, de los cuales se encuentra que 26 son defectuosos. 1. Obtener un intervalo de confianza al 90 % para la probabilidad de ser defectuoso un artı́culo de la lı́nea de producción. 2. ¿De qué tamaño hay que tomar la muestra para que el intervalo de confianza calculado en la parte anterior tenga longitud menor o igual que 0,02?. Probabilidad y Estadı́stica - 2020 Página 83 de 86 Ejercicio XII.5. En un hospital se desea estimar el valor esperado de la cantidad de dı́as de internación. Para ello se determina el número de dı́as que permanecen internados los pacientes de una muestra extraı́da al azar de 800 individuos. El promedio y la varianza de la muestra son respectivamente 6,2 dı́as y (3,3 dı́as)2 . Indicar un intervalo de confianza al 99 % del valor esperado de la cantidad de dı́as de internación. Ejercicio XII.6. Al probar 100 barras de acero que fabricó la compañı́a A se encuentra que 12 no cumplieron con las especificaciones. 1. Determinar un intervalo de confianza al nivel 95 % para la proporción verdadera de las barras de acero que no cumplen las especificaciones. 2. Si se desea estimar la proporción verdadera que no cumple con las especificaciones con una exactitud de 0,05 y a un nivel de confianza de 95 %. ¿Cuántas barras se deben muestrear?. Ejercicio XII.7. Se está considerando un nuevo sistema de montaje industrial. El sistema actual tiene una probabilidad de montaje “perfecto” del 80 %. Se realiza una muestra de 40 montajes experimentales con el nuevo sistema y 34 de ellos son “perfectos”. Hallar un intervalo de confianza al nivel 95 % para la probabilidad de éxito (montaje “perfecto”) del nuevo sistema. ¿Puede concluir que el nuevo sistema es mejor? Probabilidad y Estadı́stica - 2020 Página 84 de 86 Sección 21 Evaluación (III) : ESTADÍSTICA Ejercicio III.1 (Examen Febrero 2007). Se considera el par de variables aleatorias discretas (X, Y ) con función de probabilidad (cuantı́a) conjunta dada por la siguiente tabla: X /Y 0 1 0 0,25 + α 0,25 − α 1 0,25 − α 0,25 + α con −0,25 ≤ α ≤ 0,25. 1. Hallar las funciones de probabilidad (cuantı́as) marginales. Probar que X e Y son independientes si y solo si α = 0 y en este caso se tiene todos los resultados con la misma probabilidad. 2. Estimar α por máxima verosimilitud si los resultados de una muestra de tamaño 3 fueron (0, 0), (1, 0) y (0, 1). 3. a) Hallar pindep = P (Y = 1 / X = 0) si X e Y independientes. b) Hallar pestim = P (Y = 1 / X = 0) si α es el valor estimado en la segunda parte. c) Verificar que pestim > pindep . ¿Es lógico este resultado?. Explicar. Ejercicio III.2 (Examen Octubre 2006). Sea X una variable aleatoria discreta con parámetro a > 0, que toma los valores a, 6a y 10a con probabilidades 0,2, 0,3 y 0,5 respectivamente. 1. Hallar el valor esperado y la varianza de X. 2. Dada una muestra aleatoria simple, X1 , X2 , ... , Xn (variables aleatorias independientes idénticamente distribuidas), con la distribución de X, indicar un estimador insesgado y consistente del parámetro, probando que efectivamente lo es. 3. Dada una muestra aleatoria simple, X1 , X2 , ... , X300 (variables aleatorias independientes idénticamente distribuidas), con la distribución de X, de tamaño 300, donde se obtuvo X1 + X2 + ... + X300 = 1500 hallar un intervalo de confianza al 98 % para a. Ejercicio III.3 (Examen Febrero 2015). Consideremos una empresa que fabrica globos que supondremos esferas perfectas. El radio de las esferas es una variable aleatoria X con distribución normal (llamaremos µ al su valor esperado y σ 2 a su varianza). Se miden los radios de una muestra aleatoria simple de tamaño 7 de la producción (muestra aleatoria simple, variables aleatorias independientes idénticamente distribuidas, de la variable aleatoria X), resultando un promedio de X̄ = 10 y una desviación estándar s = 3, todo medido en metros. Probabilidad y Estadı́stica - 2020 Página 85 de 86 1. Hallar un intervalo de confianza para µ, con una confianza del 95 % en base a los resultados de la muestra. Explique en detalle cómo lo obtuvo y tenga en cuenta la pregunta de la última parte para elegir el tipo de intervalo de confianza. 2. Hallar un intervalo de confianza para σ, con una confianza del 95 % en base a los resultados de la muestra. Explique en detalle cómo lo obtuvo y tenga en cuenta la pregunta de la última parte para elegir el tipo de intervalo de confianza. 3. El gerente de la empresa doce: “La empresa fabrica globos con una probabilidad mayor 95 % de que el radio de los globos esté entre 10 y 11 metros”. ¿Qué opinión le merece la frase del gerente de la empresa?. Justifique su respuesta en base a los resultados de las partes anteriores, en términos probabilı́sticos/estadı́sticos. Ejercicio III.4. Una planta textil elabora un producto cuya concentración de tinta es una variable aleatoria X con distribución Normal (X ∼ N (µ , σ)). 1. Una consultora contratada por la empresa le indica al ingeniero de la misma que se constató que P (X ≤ 150) = 0,5 y P (X ≥ 120) = 0,975. ¿Puede usted ayudar al ingeniero a determinar los valores de µ y σ a partir de los datos brindados por la consultora?. 2. Como el ingeniero de la empresa desconfı́a de los resultados brindados por la consultora decide tomar una muestra aleatoria simple de la producción y mide la concentración de tinta obteniendo los siguientes resultados: 154,5 149,3 148,2 147,1 146,0 148,3 150,1 152,0 139,9 145,3 Como el ingeniero no sabe qué hacer con los diez valores que obtuvo, te pide que le calcules los valores de µ y σ usando los diez valores medidos. Debes utilizar estimadores insesgados para hacerlo. Nota: Si los estimadores utilizados son los usuales alcanza con probar que uno de los dos es insesgado y si no lo son debes probar que ambos son insesgados. Probabilidad y Estadı́stica - 2020 Página 86 de 86

Guia PYE 2020 v6

Documentos relacionados

Productos

Apoyo

Guia PYE 2020 v6

Documentos relacionados

Añadir este documento a la recogida (s)

Añadir a este documento guardado

Sugiéranos cómo mejorar StudyLib