LIMITE DE UNA VARIABLE O FUNCION:

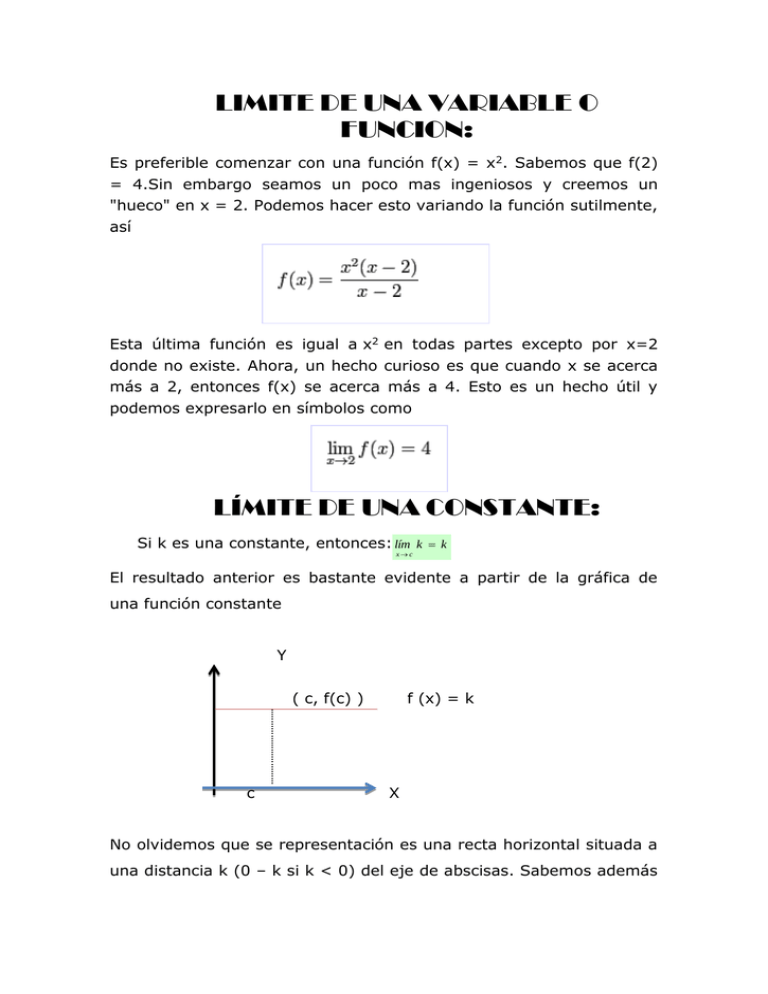
LIMITE DE UNA VARIABLE O
FUNCION:
Es preferible comenzar con una función f(x) = x2. Sabemos que f(2)
= 4.Sin embargo seamos un poco mas ingeniosos y creemos un
"hueco" en x = 2. Podemos hacer esto variando la función sutilmente,
así
Esta última función es igual a x2 en todas partes excepto por x=2
donde no existe. Ahora, un hecho curioso es que cuando x se acerca
más a 2, entonces f(x) se acerca más a 4. Esto es un hecho útil y
podemos expresarlo en símbolos como
LÍMITE DE UNA CONSTANTE:
Si k es una constante, entonces: lím k  k
x c
El resultado anterior es bastante evidente a partir de la gráfica de
una función constante
Y
( c, f(c) )
c
f (x) = k
X
No olvidemos que se representación es una recta horizontal situada a
una distancia k (0 – k si k < 0) del eje de abscisas. Sabemos además
que cualquier función constante está definida para todo número real
por lo que si f(x) = k.
lím k  f ( c )  k
x c
Dentro del producto de funciones existe un caso especial; el producto
de una constante con cualquier función arbitraria. Si g(x) = k
f(x), cuando existe lím f ( x ) , entonces:
x c
= lím kf ( x )
lím g ( x )
x c
x c
y en virtud del teorema A (III):
lím kf ( x )
x c
=
lím k lím f ( x )
x c
x c
, o bien:
LÍMITE DEL PRODUCTO DE UNA
CONSTANTE POR UNA FUNCIÓN.
Si lím f ( x ) existe, entonces:
x c
lím kf ( x ) = k  lím f ( x )
x c
x c
Es decir, las constantes que multiplican a una función “entran” o
“salen” del límite, sin que esto lo altere.La función g(x) = xn (nN)
está definida en todo el eje real.
LÍMITES AL INFINITO
Se trata ahora de calcular cuál es el valor, en caso de que exista y
sea finito, al que se acerca una sucesión según vamos avanzando
términos. Usaremos un ejemplo muy ilustrativo para introducir esta.
Considérese la siguiente sucesión:
Si escribimos algunos términos, nos haremos rápidamente una idea
de hacia qué valor real se acercan los mismos:
Como podemos comprobar, los términos se van haciendo cada vez
menores, por lo que es de esperar que, de existir realmente un
último término de la sucesión, éste sería 0. Esto nos da una idea
intuitiva de lo que significa el límite de una sucesión cuando tiende a
infinito; ésto es, aventurar de algún modo a qué valor se acercan los
términos de la sucesión según vamos avanzando sobre la misma.
Con la sucesión anterior, podemos escribir
nos podemos tomar la siguiente licencia:
, y de hecho,
.
INDETERMINACIONES
Hay límites QUE evaluándolos directamente, se obtiene alguna de las
siguientes expresiones:
A estas expresiones se les denomina indeterminaciones, ya que, a
simple vista, no está claro cual puede ser el límite (si es que
existe).Por ejemplo, en la segunda de estas ecuaciones, el límite
pudiese valer 0, 1 o infinito. En algunos casos, simplificando las
expresiones u obteniendo expresiones equivalentes a las iniciales,
mediante racionalización o factorización se puede resolver la
indeterminación y calcular el límite.
EJERCICIOS EN CLASE
𝐲 = 𝐱𝟐
y + ∆y = (x + ∆x)2
y + ∆y = (x)2 + 2(x)(∆x) + (∆x)2
y + ∆y = x 2 + 2x∆x + (∆x)2
∆y = x 2 + 2x∆x + (∆x)2 − x 2
∆y = ∆x(2x + ∆x)
∆y ∆x(2x + ∆x
=
∆x
∆x
∆y
= 2x + ∆x
∆x → 0
y , = 2x + 0
y , = 2x
𝐟(𝐱 + ∆𝐱) − 𝐟(𝐱)
∆𝐱→𝟎
∆𝐱
𝐟 , (𝐱) = 𝐥𝐢𝐦
(x + ∆x)2 − x 2
∆x→0
∆x
f , (x) = lim
x 2 + 2x∆x + (∆x)2 − x 2
∆x→0
∆x
f , (x) = lim
2x∆x + (∆x)2
∆x→0
∆x
f , (x) = lim
∆x(2x + ∆x)
∆x→0
∆x
f , (x) = lim
f , (x) = 2x + 0
f , (x) = 2x
𝐲 = 𝟓𝐱 𝟐 + 𝟐𝐱
y + ∆y = 5(x + ∆x)2 + 2(x + ∆x)
y + ∆y = 5[(x)2 + 2x∆x + (∆x)2 ] + 2x + 2∆x
y + ∆y = 5x 2 + 10x∆x + 5(∆x)2 + 2x + 2∆x
−y + y + ∆y = 5x 2 + 10x∆x + 5(∆x)2 + 2x + 2∆x − 5x 2 − 2x
∆y
∆x(10x + 5∆x + 2)
=
∆x → 0
∆x
∆y
= 10x + 5∆x + 2
∆x → 0
∆y
= 10x + 5(0) + 2
∆x
y , = 10x + 2
𝐟(𝐱 + ∆𝐱) − 𝐟(𝐱)
∆𝐱→𝟎
∆𝐱
𝐟 , (𝐱) = 𝐥𝐢𝐦
[5(x + ∆x)2 + 2(x + ∆x)] − 5x 2 − 2x
∆x→0
∆x
f , (x) = lim
[5(x)2 + 2x∆x + (∆x)2 ] + 2x + 2∆x] − 5x 2 − 2x
∆x→0
∆x
f , (x) = lim
5x 2 + 10x∆x + 5(∆x)2 + 2x + 2∆x − 5x 2 − 2x
∆x→0
∆x
f , (x) = lim
f
, (x)
10x∆x + 5(∆x)2 + 2∆x
= lim
∆x→0
∆x
∆x(10x + 5∆x + 2)
∆x→0
∆x
f , (x) = lim
f , (x) = lim 10x + 5∆x + 2
∆x→0
f , (x) = 10x + 5(0) + 2
f , (x) = 10x + 2
𝐟 , (𝐱) = 𝟑𝐱 𝟐 − 𝟐𝐱 + 𝟏
f(x + ∆x) − f(x)
∆x→0
∆x
f , (x) = lim
[3(x + ∆x)2 − 2(x + ∆x)] + 1 − 3x 2 + 2x − 1
∆x→0
∆x
f , (x) = lim
3x 2 + 6x∆x + 3(∆x)2 − 2x − 2∆x + 1 − 3x 2 + 2x − 1
∆x→0
∆x
f , (x) = lim
f
, (x)
6x∆x + 3(∆x)2 − 2∆x
= lim
∆x→0
∆x
∆𝑥(6𝑥 + 3∆𝑥 − 2)
∆𝑥→0
∆𝑥
f , (𝑥) = 𝑙𝑖𝑚
𝑓 , (𝑥) = 𝑙𝑖𝑚 6𝑥 + 3∆𝑥 − 2
∆𝑥→0
𝑓 , (𝑥) = 6𝑥 + 3(0) − 2
𝑓 , (𝑥) = 6𝑥 − 2
𝒇(𝒙) = 𝟑𝒙𝟑 − 𝟓𝒙
3(𝑥 + ∆𝑥)3 − 5(𝑥 + ∆𝑥) − 3𝑥 3 + 5𝑥
𝑓′(𝑥) = 𝑙𝑖𝑚
∆𝑥→0
∆𝑥
3(𝑥 2 + 3𝑥 2 ∆𝑥 + 3𝑥∆𝑥 2 + ∆𝑥 3 ) − 5𝑥 − 5∆𝑥 − 3𝑥 3 + 5𝑥
𝑓′(𝑥) = 𝑙𝑖𝑚
∆𝑥→0
∆𝑥
3𝑥 2 + 9𝑥 2 ∆𝑥 + 9𝑥∆𝑥 2 + 9∆𝑥 3 − 5∆𝑥 − 3𝑥 3
∆𝑥→0
∆𝑥
𝑓′(𝑥) = 𝑙𝑖𝑚
9𝑥 2 ∆𝑥 + 9𝑥∆𝑥 2 + 9∆𝑥 3 − 5∆𝑥
∆𝑥→0
∆𝑥
𝑓′(𝑥) = 𝑙𝑖𝑚
∆𝑥(9𝑥 2 + 9𝑥∆𝑥 + 9∆𝑥 2 − 5)
∆𝑥→0
∆𝑥
𝑓′(𝑥) = 𝑙𝑖𝑚
𝑓′(𝑥) = 𝑙𝑖𝑚 9𝑥 2 − 9 𝑥∆𝑥 + 9∆𝑥 2 − 5
∆𝑥→0
𝑓′(𝑥) = 9𝑥 2 − 9𝑥(0) + 9(0) − 5
𝑓(𝑥) = 9𝑥 2 − 5
𝑓(𝑥) = 5𝑥 3 − 3𝑥 2 + 12𝑥 + 8
5(𝑥 + ∆𝑥)3 − 3(𝑥 + ∆𝑥)2 + 12(𝑥 + ∆𝑥) − 8
𝑓′(𝑥) = 𝑙𝑖𝑚
∆𝑥→0
∆𝑥
5(𝑥 3 + 3𝑥 2 ∆𝑥 + 3𝑥∆𝑥 2 + ∆𝑥 3 ) − 3(𝑥 2 + 2𝑥∆𝑥 + ∆𝑥 2 ) + 12𝑥 − 8 + 12∆𝑥 − 5𝑥 3 + 3𝑥 2 − 12𝑥 + 8
∆𝑥→0
∆𝑥
𝑓′(𝑥) = 𝑙𝑖𝑚
5𝑥 3 + 15𝑥 2 ∆𝑥 + 15𝑥∆𝑥 2 + 5∆𝑥 3 − 3𝑥 2 − 6𝑥∆𝑥 − 3∆𝑥 2 + 12∆𝑥 − 5𝑥 3 + 3𝑥 2
∆𝑥→0
∆𝑥
𝑓′(𝑥) = 𝑙𝑖𝑚
15𝑥 2 ∆𝑥 + 15∆𝑥 2 + 5∆𝑥 3 − 6𝑥∆ − 3∆𝑥 2 + 12∆𝑥
∆𝑥→0
∆𝑥
𝑓′(𝑥) = 𝑙𝑖𝑚
∆𝑥(15𝑥 2 + 15∆𝑥 + 5∆𝑥 2 − 6 − 3∆𝑥 + 12)
𝑓′(𝑥) = 𝑙𝑖𝑚
∆𝑥→0
∆𝑥
𝑓 ′ (𝑥) = 15𝑥 2 + 15(0) + 5(0) − 6 − 3(0) + 12
𝑓 ′ (𝑥) = 15𝑥 2 − 6 + 12
𝑦=
3𝑥 − 1
5 − 2𝑥
3(𝑥+∆𝑥)−1
𝑦′ = 𝑙𝑖𝑚
∆𝑥
∆𝑥→0
3𝑋+3∆𝑥−1
𝑦′ = 𝑙𝑖𝑚
3𝑥−1
− 5−2𝑥
5−2(𝑥+∆𝑥)
5−2𝑥−2∆𝑥
3𝑥−1
− 5−2𝑥
∆𝑥
∆𝑥→0
(5−2𝑥)(3𝑥 2 +6𝑥∆𝑥+2∆𝑥 2 )−(5−2𝑥−2∆𝑥)(3𝑥−1)
(5−2𝑥−2∆𝑥)(5−2𝑥)
𝑦′ = 𝑙𝑖𝑚
∆𝑥
∆𝑥→0
15𝑥+15∆𝑥−5−6𝑥 2 −6𝑥∆𝑥+2𝑥−(15𝑥−6𝑥 2 −6𝑥∆𝑥−5−2𝑥−2∆𝑥)
(5−2𝑥−2∆𝑥)(5−2𝑥)
𝑦′ = 𝑙𝑖𝑚
∆𝑥
∆𝑥→0
15𝑥+15∆𝑥−5−6𝑥 2 −6𝑥∆𝑥+2𝑥−15𝑥+6𝑥 2 +6𝑥∆𝑥+5+2𝑥+2∆𝑥
(5−2𝑥−2∆𝑥)(5−2𝑥)
𝑦′ = 𝑙𝑖𝑚
∆𝑥
∆𝑥→0
13∆𝑥
𝑦′ = 𝑙𝑖𝑚
(5−2𝑥−2∆𝑥)(5−2𝑥)
∆𝑥→0
∆𝑥
13∆𝑥
∆𝑥→0 ∆𝑥(5 − 2𝑥 − 2∆𝑥)(5 − 2𝑥)
𝑦′ = 𝑙𝑖𝑚
𝑦′ =
13(0)
(5 − 2𝑥 − 2(0))(5 − 2𝑥)
𝑦′ =
13
(5 − 2𝑥)(5 − 2𝑥)
𝑦′ =
13
(5 − 2𝑥)2
𝑦=
2𝑥 2
𝑥+3
𝑦´ = 𝑙𝑖𝑚
2(𝑥+∆𝑥)2
(𝑥+∆𝑥)+3
2𝑥 2
− 𝑥+3
∆𝑥
∆𝑥→0
2(𝑥 2 +2𝑥∆𝑥+∆𝑥 2 )
𝑦´ = 𝑙𝑖𝑚
𝑥+∆𝑥+3
∆𝑥
∆𝑥→0
2𝑥 2 +4𝑥∆𝑥+2∆𝑥 2
𝑦´ = 𝑙𝑖𝑚
2𝑥 2
− 𝑥+3
𝑥+∆𝑥+3
2𝑥 2
− 𝑥+3
∆𝑥
∆𝑥→0
(𝑥+3)(2𝑥 2 +4𝑥∆𝑥+2∆𝑥 2 )−(𝑥+∆𝑥+3)(2𝑥 2 )
(𝑥+∆𝑥+3)(𝑥+3)
𝑦´ = 𝑙𝑖𝑚
∆𝑥
∆𝑥→0
𝑦´ = 𝑙𝑖𝑚
∆𝑥→0
𝑦´ = 𝑙𝑖𝑚
∆𝑥→0
𝑦´ = 𝑙𝑖𝑚
∆𝑥→0
𝑦´ = 𝑙𝑖𝑚
2𝑥 3 +4𝑥 2 ∆𝑥+2𝑥∆𝑥 2 +6𝑥 2 +12𝑥∆𝑥+6∆𝑥 2 −(2𝑥 3 +2𝑥 2 ∆𝑥+6𝑥 2 )
(𝑥+∆𝑥+3)(𝑥+3)
∆𝑥
2𝑥 3 +4𝑥 2 ∆𝑥+2𝑥∆𝑥 2 +6𝑥 2 +12𝑥∆𝑥+6∆𝑥 2 −2𝑥 3 −2𝑥2 ∆𝑥−6𝑥 2 )
(𝑥+∆𝑥+3)(𝑥+3)
2𝑥 2 ∆𝑥+12𝑥∆𝑥+6∆𝑥 2
(𝑥+∆𝑥+3)(𝑥+3)
∆𝑥
2𝑥 2 ∆𝑥+12𝑥∆𝑥+6∆𝑥 2
(𝑥+∆𝑥+3)(𝑥+3)
∆𝑥→0
𝑦´ =
∆𝑥
∆𝑥
∆𝑥(2𝑥 2 +12𝑥+6∆𝑥)
(𝑥+∆𝑥+3)(𝑥+3)
𝑙𝑖𝑚
∆𝑥
∆𝑥→0
1
2
∆𝑥(2𝑥 + 12𝑥 + 6∆𝑥)
∆𝑥→0 ∆𝑥(𝑥 + ∆𝑥 + 3)(𝑥 + 3)
2𝑥 2 + 12𝑥 + 6(0)
𝑦´ =
(𝑥 + 0 + 3)(𝑥 + 3)
2𝑥 2 + 12𝑥
𝑦´ =
(𝑥 + 3)(𝑥 + 3)
𝑦´ = 𝑙𝑖𝑚
𝑦´ =
2𝑥(𝑥 + 6)
(𝑥 + 3)2
𝑥 4 − 16 24 − 16 0
= 3
=
𝑥→2 𝑥 3 − 8
2 −8
0
𝑙𝑖𝑚
𝑥 4 − 16
𝑙𝑖𝑚 3
𝑥→2 𝑥 − 8
(𝑥 2 + 4)(𝑥 2 − 4)
𝑙𝑖𝑚
𝑥→2 (𝑥 − 2)(𝑥 2 + 2𝑥 + 4)
(𝑥 2 + 4)(𝑥 − 2)(𝑥 + 2)
𝑙𝑖𝑚
𝑥→2 (𝑥 − 2)(𝑥 2 + 2𝑥 + 4)
(𝑥 2 + 4)(𝑥 + 2)
𝑥→2 (𝑥 2 + 2𝑥 + 4)
𝑙𝑖𝑚
𝑥 3 + 2𝑥 2 + 4𝑥 + 8
𝑥→2
(𝑥 2 + 2𝑥 + 4)
𝑙𝑖𝑚
23 + 2(2)2 + 4(2) + 8
22 + 2(2) + 4
8 + 8 + 8 + 8 32 8
=
=
4+4+4
12 3
𝑥 2 − 5𝑥 + 4 16 − 20 + 4 0
=
=
𝑥→4 𝑥 2 − 2𝑥 − 8
16 − 8 − 8
0
𝑙𝑖𝑚
𝑥 2 − 5𝑥 + 4
𝑥→4 𝑥 2 − 2𝑥 − 8
𝑙𝑖𝑚
(𝑥 − 4)(𝑥 − 1)
𝑥→4 (𝑥 − 4)(𝑥 + 2)
𝑙𝑖𝑚
(𝑥 − 1)
𝑥→4 (𝑥 + 2)
𝑙𝑖𝑚
4−1 3 1
= =
4+2 6 2
𝑥 2 + 3𝑥 + 2 1 − 3 + 2 0
=
=
𝑥→(−1)
𝑥2 − 1
1−1
0
𝑙𝑖𝑚
𝑥 2 + 3𝑥 + 2
𝑙𝑖𝑚
𝑥→(−1)
𝑥2 − 1
(𝑥 + 2)(𝑥 + 1)
𝑥→4 (𝑥 − 1)(𝑥 + 1)
𝑙𝑖𝑚
(𝑥 + 2)
𝑥→4 (𝑥 − 1)
𝑙𝑖𝑚
−1 + 2
1
=−
−1 − 1
2
𝑥 2 − 25
𝑙𝑖𝑚
𝑥→5 𝑥 − 5
(𝑥 − 5)(𝑥 + 5)
𝑥→5
𝑥−5
𝑙𝑖𝑚
𝑙𝑖𝑚 𝑥 + 𝑙𝑖𝑚 5
𝑥→5
𝑥→5
5 + 5 = 10
𝑥 2 + 2𝑥 − 15
𝑙𝑖𝑚
𝑥→3
𝑥−3
(𝑥 + 5)(𝑥 − 3)
𝑥→3
𝑥−3
𝑙𝑖𝑚
𝑙𝑖𝑚(𝑥 + 5)
𝑥→3
𝑙𝑖𝑚 𝑥 + 𝑙𝑖𝑚 5
𝑥→3
𝑥→3
3+5=8
3𝑥 2 − 4𝑥 + 2
𝑥→∝
6𝑥 2 − 1
𝑙𝑖𝑚
3𝑥 2
𝑙𝑖𝑚
𝑥→∝
𝑥2
4𝑥
6𝑥 2
𝑥2
1
− 𝑥2
4
𝑙𝑖𝑚
𝑥→∝
2
− 𝑥2 + 𝑥2
2
3 − 𝑥 + 𝑥2
1
6 − 𝑥2
𝑙𝑖𝑚 4
𝑥→∝
𝑙𝑖𝑚 3 − 𝑙𝑖𝑚
𝑥→∝
𝑥→∝
lim 6 −
x→∝
+
𝑥
𝑙𝑖𝑚 2
x→∝
( lim x)
x→∝
lim 1
x→∝
( lim x)
2
x→∝
3−0+0 3 1
= =
6−0
6 2
4
2
=
2
3 − ∝ + ∝2
1
6 − ∝2
=