Metapoblaciones

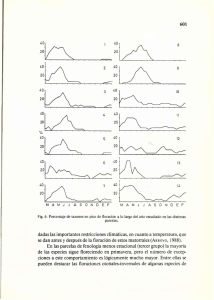
Metapoblaciones
Fragmentación de hábitats. Poblaciones: entidades formados por ind de cierta especie en un mismo lugar.
Tienen una probabilidad mucho mayor de entrecruzarse entre ellos que con miembros de otras poblaciones. Se
consideró que está cerrada a los movimientos migratorios, la dinámica poblacional está determinada por las
características demográficas de la población y los factores ambientales.
Los ind de una población habitualmente se distribuyen de forma aleatoria, o contagiosa en un hábitat con cierta
heterogeneidad espacial, pero la intensa movilidad de los ind, el intenso flujo a lo largo y ancho del hábitat,
permite considerarlos una población continua, la capacidad de dispersión entre las manchas donde se agregan es
tan elevada que no cabe la posibilidad de extinción local.
Puede que (de modo natural o promovido por el hombre) la fragmentación de un hábitat transforme un espacio
continuo en manchas, es actualmente una de las principales amenazas para la diversidad biológica. La
destrucción de un hábitat suele reducir el tamaño del hábitat y dejar un mosaico de fragmentos separados por una
matriz de paisaje muy modificado o degradado. Funcionan como islas en un “mar” inhóspito antropogénico, pero
también puede haber fragmentación sin reducción significativa de área, como en la construcción de carreteras,
cortafuegos, canales...
Los fragmentos de hábitats difieren del original, aumenta la relación perímetro/S. Tienen más longitud de hábitat
de borde o margen (hábitat más adyacente a las actividades humanas) con respecto al área total del hábitat. La
fragmentación aumenta drásticamente la cantidad de margen respecto a de hábitat interior, y en ellos las
características ambientales son netamente diferentes a las del interior...
La fragmentación de un hábitat transforma un espacio continuo en parcelas (parches, islas de hábitats...), áreas
con los recursos necesarios para la persistencia de una subpoblación: población local. Están inmersas en un
hábitat inadecuado, en una matriz inhóspita. Cada parcela puede estar ocupada o vacía de ind, así una población
grande y más o menos continua se transforma en subpoblaciones, poblaciones residuales. Cuando el tamaño
poblacional en estos fragmentos es bajo, las poblaciones locales tienden a extinguirse gradualmente y la
recolonización se dificulta.
Estas poblaciones locales pueden quedar interconectadas por pasillos o corredores ecológicos (naturales o
fabricados) que facilitan el trasiego de ind entre parcelas, ayuda a aliviar el peligro de extinción local (una
subpoblación o población local desaparece) inherente a las poblaciones peq, y contribuye a estabilizar a la
población a una escala regional, donde cobra importancia el proceso de extinción, extinción regional, cuando
desaparecen todas las poblaciones locales de la metapoblación.
Las perturbaciones antropogénicas severas que dificultan gravemente o imposibilitan esos movimientos
migratorios (cercados, autovías, presas…) pueden reducir la I entre manchas de hábitats y reducir o eliminar la
probabilidad de recolonización tras una extinción local.
Estas subpoblaciones más o menos interconectadas son metapoblaciones o población de poblaciones. Mosaico
de subpoblaciones que, como un caleidoscopio, es cambiante, estando estas subpoblaciones vinculadas por algún
grado de intercambio de ind a través de fenómenos migratorios y, eventualmente, con el espacio exterior.
Cada subpoblación exhibe sus propias fluctuaciones poblacionales, posee sus propias tasas de natalidad y
mortalidad, probabilidad de colonización y extinción, aunque ahora no lo consideraremos así. Las parcelas se
asumen con características muy similares, homogéneas en forma, tamaño, distancia entre manchas...
A diferencia de los modelos poblacionales anteriores, que trataban de predecir los tamaños poblacionales en el
eq en términos de nº de ind, los modelos de metapoblaciones pretenden predecir la persistencia de la
población en términos del nº o fracción de parcelas ocupadas.
Lo que interesa al estudiar el comportamiento dinámico de una metapoblación no es cómo aumenta o disminuye
el tamaño, sino el nº (%) de parcelas ocupadas por las subpoblaciones. La variable a utilizar es la fracción de
espacios ocupados (p)
Si p = 1, todas las parcelas están ocupadas, (1 – p): fracción de espacios vacíos.
La escala para reconocer una situación de eq es la regional (o de paisaje) A esta escala, el foco de estudio no es
la población local, se buscan modelos que describan la persistencia de la metapoblación a escala regional.
Los modelos de metapoblaciones tratan de predecir la persistencia de la población, expresada mediante el nº o
fracción de parcelas ocupadas, este, en una situación de eq se manifiesta como un eq dinámico entre la I, nº de
parcelas ocupadas por unidad de tiempo, y la E, nº de parcelas abandonadas por unidad de tiempo, expresadas en
función de los espacios ocupados (p)
Podríamos expresar I como I(p) y E como E(p) , pero por simplificar solo I y E: dp/dt = I - E
En el eq, cuando I = E → dp/dt = 0, y p permanece cte (p*), pero en un eq dinámico, necesita renovación
continua de poblaciones locales.
I opera sobre las parcelas vacías y depende de ellas, puede asumirse proporcional a la fracción de espacios
vacíos (1 – p): a más parcelas vacías y aptas para su colonización, mayor I.
E opera sobre las parcelas ocupadas, es proporcional a p.
Ambos términos de proporcionalidad [α y β] pueden hacerse funciones de p, aún sin especificar, que
representarán las probabilidades de inmigración y extinción local (tasas intrínsecas de inmigración y extinción
local) α y β: probabilidades (o tasas intrínsecas) de inmigración y extinción local
I = α (1 – p)
E = β·p
Sea cuál sean las formas de α y β, se cumple que:
I = 0 si p = 1
E = 0 si p = 0
(todos los espacios ocupados)
(todos los espacios vacíos)
No confundir las tasas de inmigración y extinción (I, E) con sus probabilidades (o tasas intrínsecas) de
colonización y extinción (α y β)
Caso 1. Lluvia de propágulos o modelo continente-isla.
Asunciones simplificadoras, las probabilidades de colonización y extinción [α y β]:
.Las mismas para todas las parcelas, homogéneas, sin diferencias en tamaño, aislamiento, calidad del hábitat,
nivel de recursos u otros factores que puedan afectarles.
.No dependen de p, no están afectadas por la fracción de parcelas ocupadas, ni por su disposición espacial, en un
modelo más realista, la probabilidad de colonización (α) para una parcela dependerá del total de parcelas
ocupadas y, más concretamente, de la ocupación de parcelas cercanas.
.Son ctes en el tiempo.
También asume que (y esto es extensible a todos los modelos siguientes):
.No hay retardo en el tiempo, la metapoblación responde inmediatamente a los cambios en la fracción de
parcelas ocupadas.
.No hay destrucción de parcelas. Las parcelas donde ocurre una extinción local están disponibles para su
recolonización (la extinción de una población local muy a menudo conlleva una destrucción del hábitat, la
parcela queda disponible tras su regeneración)
De entre ellas la asunción más importante es:
Las probabilidades de inmigración y extinción local son ctes e independientes de p.
α = cte = i
Si cada parcela es colonizada independientemente, esta probabilidad depende solo de sus
condiciones físicas y biológicas (tamaño, disponibilidad de recursos, ausencia de predadores…)
β = cte = e
Así, I y E son funciones lineales de p.
p = 0, I = i
p = 1, I = 0
I = i (1 – p) = i – ip
Todas las parcelas inicialmente vacías.
Todas las parcelas ocupadas.
La I también será 0 si la probabilidad de colonización local (i) es 0. Mismo razonamiento para E: E = e · p,
p = 0, E = 0
Todas las parcelas inicialmente desocupadas.
p = 1, E = e
Todas las parcelas ocupadas.
La E también será 0 si la probabilidad de extinción local (e) es 0.
Modelo completo: dp/dt = I – E = i(1 – p) – e · p
En el eq, cuando dp/dt = 0, i – i · p* = e · p*, i = ip* + ep* = p* (i + e)
p* = i/(i + e)
I disminuye y E aumenta con la fracción de espacios ocupados. El punto de corte es el valor de eq p*.
Aunque la probabilidad de extinción (e) sea muy grande y la de inmigración (i) muy peq, nunca se extinguirá la
metapoblación (p > 0)
La metapoblación es siempre subvencionada desde una fuente inagotable de inmigrantes (el "continente") que
pueden potencialmente colonizar las parcelas vacías, así I ≠ 0 ni cuando ninguna parcela es ocupada (p = 0)
(“lluvia de propágulos”) Por su analogía con el modelo de MacArthur & Wilson, también: “modelo islacontinente”.
Caso 2. Si la metapoblación carece de fuente externa e inagotable de inmigrantes potenciales, la ocupación
de los espacios vacíos solo es a partir de las parcelas ya ocupadas mediante colonización interna. La
persistencia de la metapoblación no está garantizada, si p = 0 no hay ninguna posibilidad de
recolonización y la población se extinguirá a escala regional.
Si las parcelas están conectadas por procesos migratorios, la probabilidad de colonización no dependerá solo de
las condiciones físicas y biológicas de las parcelas, también de la presencia de poblaciones en otras parcelas,
cada parcela ocupada aporta por emigración un pool de ind capaces de colonizar otras vacías.
La probabilidad de colonización (α) ya no es cte e independiente de p, es proporcional (asumimos que la
dependencia es lineal) a p, α = i · p
La tasa de colonización será I = α (1 – p) = i · p (1 – p) = ip – ip2
Si p = 0 (todas las parcelas vacías) → I = 0
Si p = 1 (todas las parcelas ocupadas) → I = 0
Si todas las poblaciones locales se extinguen (p = 0), I es 0, no hay otra fuente de colonizadores. Cuando la
probabilidad de inmigración depende de la fracción de espacios ocupados, I toma una forma parabólica
(ec cuadrática) con un máx de 0,25i cuando p = 0,5
Si p es peq, I incrementa con el nº de parcelas ocupadas y emisarias de ind migrantes, cuando p = 0,5, I
comienza a disminuir porque cada vez quedan menos sitios vacíos y es progresivamente más difícil encontrar
parcelas sin ocupar.
Si no se modifican las asunciones relativas a la probabilidad de extinción (β = cte = e), el eq es definido por:
dp/dt = 0 → I = E → i p (1 – p) = ep → i (1 – p) = e → i – ip = e → ip = i – e
p = (i – e)/i = p* = 1 – (e/i)
La persistencia de la población (p* > 0) no está asegurada siempre, requiere que i > e.
Esta combinación de asunciones para las probabilidades de colonización y extinción constituye el Modelo de
Levins o de "colonización interna".
Caso 3. Efecto rescate. Asumimos que cada parcela ocupada por una población local produce un exceso de
propágulos que llegan solo a otras parcelas ocupadas (si llegan a una parcela vacía sería colonización interna,
pero aún no lo contemplamos)
Incrementa el tamaño de la población ya establecida, disminuye la probabilidad de extinción local frente a
perturbaciones demográficas o ambientales. Efecto Rescate (reposición de las pérdidas de ind): reducción de la
probabilidad de extinción local por la llegada a parcelas ocupadas de migrantes de subpoblaciones
cercanas.
Hasta ahora se consideró la probabilidad de extinción local cte [β = cte = e], independiente de p (fracción de
parcelas ocupadas)
Ahora la relacionamos con la porción de parcelas ocupadas, así disminuye al aumentar la fracción de parcelas
emisarias de ind, hasta 0 cuando todas las parcelas están ocupadas: β = e – ep = e (1 – p)
Si p = 0 → β = e
Si p = 1 → β = 0
La tasa de extinción es: E = β·p = e (1 – p)·p = ep – ep2, una ec cuadrática o parabólica, así E = 0 cuando p = 0
y p = 1, y alcanzará un valor máx cuando p = 0,5
E es 0 cuando no hay ninguna parcela ocupada, incrementa con el aumento de la ocupación hasta un valor máx
a partir del cual disminuye por el efecto rescate, siendo 0 cuando todos los asentamientos están ocupados.
Si respecto a I seguimos considerando el caso de “lluvia de propágulos”, la probabilidad de colonización es
una cte i, e I disminuye linealmente con el incremento de la fracción de espacios ocupados, el modelo queda:
dp/dt = i (1 – p) – e (1 – p)·p
En el eq, cuando dp/dt = 0 → i (1 – p) = e (1 – p) · p → i = e · p → p* = i/e
La persistencia de la metapoblación está asegurada. Si la probabilidad de inmigración i es mayor que la de
extinción e, la metapoblación en el eq tendrá todos sus espacios ocupados (p* tiende a 1)
Caso 4. Colonización interna y efecto rescate (the core-satellite hypothesis)
Asumimos que las probabilidades de inmigración y extinción son dependientes de p y combinamos la
colonización interna con el efecto rescate el modelo queda:
dp/dt = I – E = β (1 – p) – β p = ip (1 – p) – e (1 – p) p = (ip – ip2) - (ep – ep2)
colonización interna
efecto rescate
I y E son expresiones cuadráticas, pudiendo ocupar ambas parábolas distintas posiciones relativas, la situación de
eq no tiene una solución única. El resultado depende de los valores relativos de i y e.
i > e → dp/dt > 0 para cualquier p, p tenderá a 1, todos los espacios ocupados. I siempre > E.
i < e → dp/dt < 0 para cualquier p, p tenderá a 0, extinguiéndose la población. E siempre > I.
i = e → dp/dt = 0 para cualquier p. Eq neutro: cualquier p es en teoría un valor de eq p*. El sistema
permanecerá indefinidamente en cualquier situación, a no ser que actúe algún factor no considerado.
Modelo global. Los modelos se diferenciaban en la existencia de lluvia de propágulos o colonización interna
para la colonización, y en la existencia o no de efecto rescate para la extinción.
Esas cuatro opciones derivaban de la dependencia o independencia de las probabilidades de colonización y
extinción respecto a la situación regional, respecto a p. Son casos particulares de un modelo general de
metapoblación.
El modelo de Lluvia de Propágulos y Efecto Rescate asume que solo es posible la colonización externa de
parcelas vacías, y que la dispersión entre parcelas solo previene las extinciones locales.
El modelo de Colonización Interna implica que el sistema es cerrado, los ind colonizadores pueden generarse
solo desde parcelas ocupadas en la metapoblación. Aunque esta situación puede ser la válida para muchos casos
de metapoblaciones de especies "emblemáticas", no siempre es así.
El modelo de Colonización Interna y Efecto Rescate implica que el efecto rescate es tan elevado que la
probabilidad de extinción local se aproxima a 0 cuando todas las parcelas están ocupadas.
Es más real un modelo donde la colonización de parcelas deriva de propágulos generados en el sistema y
fuera, y cada parcela tenga una probabilidad intrínseca de extinción que no se reduzca a 0 por el efecto
rescate, aunque el paisaje esté saturado (p = 1)
Presentamos un modelo general de metapoblaciones que incorpore funciones más reales para las probabilidades
de inmigración y extinción local. Asumimos que la probabilidad de colonización es una función lineal de la
fracción de parcelas ocupadas: α = a + bp
El punto de corte con la ordenada (a) cuantifica la inmigración externa, la pendiente positiva b representa el
refuerzo que la colonización interna supone para el valor anterior.
Podemos asumir que la probabilidad de extinción local es también función lineal de p: β = c – dp
La pendiente no coincide con el punto de corte con ordenadas como en el efecto rescate. Entonces veíamos que
como p = 1, la pendiente c/p = c/1 = c; por lo cual la pendiente b era c – cp = c (1 – p)
Si cada parcela tiene una probabilidad intrínseca de extinción que se reduce a 0, por el efecto rescate la
pendiente negativa (d) es un factor que, en forma de efecto rescate, disminuye la probabilidad de extinción
conforme aumenta p, pero no llega a 0 cuando todos los espacios están ocupados, siempre tiene cierto valor.
El modelo global queda: dp/dt = (a + bp) (1 – p) – (c – dp) p
Bajo ciertas restricciones (a, b, c y d ≥ 0, y c ≥ d), la persistencia de la población está garantizada si hay alguna
colonización externa (a > 0) Si no hay, la persistencia podría alcanzarse si b es muy superior a c y d.
El modelo global de dinámica de metapoblaciones describe los cambios en la porción de parcelas ocupadas
según cuatro parámetros: dos para la inmigración (a y b) y dos para la extinción (c y d) Los casos vistos son
solo particulares de este modelo general.
Si b = 0 y d = 0 → Lluvia de propágulos → dp/dt = a(1 – p) – c·p
Si a = 0 y d = 0 → Colonización interna → dp/dt = bp(1 – p) – c·p
Si b = 0 y c = d → Lluvia de Propágulos y Efecto Rescate → dp/dt = a(1 – p) – c(1 – p)p
Si a = 0 y c = d → Colonización interna y efecto rescate → dp/dt = bp(1 – p) – d(1 – p p
Para este modelo general, si hay alguna colonización externa (a > 0), p siempre alcanza un eq estable (p* > 0)
Si no hay, puede alcanzarse un eq si la colonización interna (b) puede contrarrestar el efecto de los parámetros de
extinción (c y d)