ASENTAMIENTOS

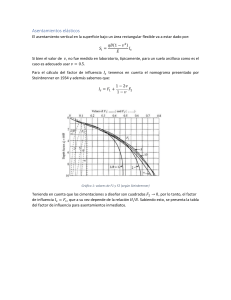
ASENTAMIENTOS
INTRODUCCIÓN:
Cuando aplicamos cargas a una masa de suelo, se inducen esfuerzos adicionales, por encima
de los que originalmente existen, el suelo pasa de un estado de reposo a un estado o condición
geostatica.
Debido a la compresión inducida en el suelo, se producirán deformaciones en la masa de
suelo, que se traducen en un asentamiento o desplazamiento vertical.
Para poder evaluar estos asentamientos debemos determinar los esfuerzos que se inducen por
las cargas aplicadas.
σ
1
∆σ
∆ε
Modulo de la tangente
Inicial Ei
0
ε
Diagrama Esfuerzo Deformación.
Para calcularlo utilizamos la Teoría de la Elasticidad y las condiciones de borde.
Da buenos resultados en suelos cohesivos saturados o parcialmente saturados sometidos a
incrementos de esfuerzos moderados, no es muy aplicable en suelos granulares sin cohesión ya
que el modulo de elasticidad varia marcadamente con la presión confinante.
Los esfuerzos calculados por la teoría de la elasticidad pueden estar errados en +/- 25%, por lo
que su aplicación debe hacerse con buen juicio.
Generalmente vamos a tener dos tipos de asentamientos:
1.- Asentamientos Elásticos: Características:
a) Son instantáneos.
b) Son directamente proporcional a la magnitud de la carga.
c) Son reversibles.
d) Se producen en todos los suelos.
e) En suelos granulares y suelos cohesivos no saturados constituyen la totalidad del
asentamiento que se van ha producir.
1
Prof. Jorge Rojas
2.- Asentamientos por Consolidación: son importantes en suelos finos (arcillas y limos)
saturados características:
a) No se producen instantáneamente.
b) No son totalmente irreversibles si no una pequeña parte.
c) Son asentamientos catastróficos (falla por corte).
Causas de los Asentamientos.
-
Aplicación de la carga.
Vibraciones en suelos granulares.
Cambio de la cota del nivel freático.
Deterioros de la fundación.
Presencia de arcillas expansivas (lluvias y evaporación).
Construcciones adyacentes.
Por lo tanto el cálculo del asentamiento será:
ST = Se + Scons
Asentamiento Elástico: “Teoría de la Elasticidad” “Ley de Hooke”.
Asentamiento elástico en cimentación Superficial.
Asentamiento elástico de cimentaciones
flexibles y rígidas
1 H
( ∆σ z − µ s ∆σ x − ∆σ y )dz
0
E s ∫0
Se = Asentamiento Elástico.
Es = Modulo de Elasticidad del suelo.
H = Espesor del estrato del suelo.
H
Se = ∫ ε z dz =
2
Prof. Jorge Rojas
µ s = Relación de Poisson del suelo.
∆σ x ; ∆σ y ; ∆σ z = Incremento de esfuerzos.
Si la cimentación es perfectamente flexible (Bowles 1.987)
1 − µ s2
S e = q 0 (αB´)(
)I s I f
Es
Donde:
qo = presión aplicada por la cimentación.
µ s = relación de Poisson del suelo
Es = Modulo de Elasticidad promedio del suelo bajo la cimentación medido de z = 0 a z = 4B
B´ = B/2 para el centro de la cimentación.
= B para una esquina de la cimentación.
Is = factor de forma (Staiembrener 1934)
 1 − 2µ s 
 F2
I s = F1 + 
 1 + µs 
F1 y F2 Tabla (5.4) dependen de (m´y n´)
If = factor de profundidad (Fox 1948) (Tabla 5.5)
α = factor que depende de la posición de la cimentación donde el asentamiento esta siendo
calculado.
Para calcular el asentamiento en el centro de la fundación:
α = 4; m´= L/B y n´= H / (B/2)
Para calcular el asentamiento en una esquina de la cimentación:
α = 1; m´= L/B y n´= H/B
If = (Tabla 5.5) depende de (Df / B y µ s ) Cuando Df = 0 => If = 1.
El Asentamiento Elástico de una cimentación rígida puede estimarse como:
Se(rígida) = 0,93 Se(flexible, centro)
Bowles (1987) recomienda usar un promedio ponderado para (Es).
Es =
∑E
si
∆z
−
z
Esi = modulo de elasticidad del suelo en una profundidad ∆z
3
Prof. Jorge Rojas
−
z = H ó 5B la que sea más pequeña.
Asentamiento sobre un área circular uniformemente cargada. (1999, Mayne, Poulos)
Presentaron formula mejorada para calcular asentamientos elásticos; toman en consideración,
la rigidez de la cimentación, la profundidad, el incremento del modulo de elasticidad con la
profundidad y la localización del estrato rígido.
Para utilizar la ecuación se requiere determinar el diámetro equivalente “Be” de una
cimentación cuadrada.
Be =
4 BL
π
;
Para cimentación circular Be = B = diámetro.
Parámetros para la ecuación mejorada.
Es = E0 + Kz
Se =
(
q 0 Be I G I F I E
1 − µ s2
E0
)
E0 H
) (figura 5.17)
;
KBe Be
IF = factor de corrección por rigidez de la cimentación f (KF = factor de flexibilidad)
IG = factor de influencia para la variación Es con la profundidad f ( β =




Ef

 2t
KF =
Be  Be

K
 E0 +
2 




3
(figura 5.16)
IE = factor de corrección por profundidad f (Df / B; µ s ) (figura 5.19)
4
Prof. Jorge Rojas
Asentamiento en suelo arenoso. (Schmertman y Hartman 1978)
Se evalúa usando un factor de influencia de la deformación unitaria.
z2
Iz
∆z
0 Es
Iz = factor de influencia de la deformación unitaria.
C1 = factor de corrección para la profundidad de fundación.
_
S e = C1C 2 (q − q)∑


q 
C1 = 1 − 0,5 _


 q− q 
C2 = factor de corrección para tomar en cuenta el flujo plástico en el suelo
 tiempoenaños 
C 2 = 1 + 0,2 Log 

0,1


_
q = esfuerzo a nivel de la cimentación.
q = γD f
Calculo de asentamiento elástico usando el factor de influencia de la deformación unitaria
5
Prof. Jorge Rojas
Para cimentaciones cuadradas o circulares
Iz = 0,1 para z = 0
Iz = 0,5 para z = z1 = 0,5B
Iz = 0 para z = z2 = 2B
Para cimentaciones con L / B > 10
Iz = 0,2 para z = 0
Iz = 0,5 para z = z1 = B
Iz = 0 para z = z2 = 4B
Asentamiento por consolidación Primaria.
Se da a lo largo del tiempo, ocurre en suelos arcillosos saturados cuando son sometidos a
cargas crecientes.
Asentamiento por consolidación
S c ( p ) = ∫ ε z dz
donde ε z = deformación unitaria vertical.
6
Prof. Jorge Rojas
εz =
∆e
1 + e0
∆ e = cambio de la relación de vacíos f ( σ o´ , σ c´´ y∆σ ´ )
Para arcillas normalmente consolidadas
S c( p)
 σ o, + ∆σ ,prom
Cc H c
log
=

1 + e0
σ o,





Para arcillas preconsolidadas con σ o´ + ∆σ ´prom < ∆σ c´
S c( p) =
 σ o, + ∆σ ,prom
Cs H c
log

1 + e0
σ o,





Para arcillas preconsolidadas con σ o, < σ c, + ∆σ ,prom
S c( p)
σ , C H
C H
= s C log c, + c c
1 + e0
 σ o 1 + e0
,
,
  σ 0 + ∆σ prom

 log

σ c,
 




Donde:
σ 0, = presión efectiva promedio sobre el estrato de arcilla antes de la construcción de la
cimentación.
∆σ ,prom = incremento promedio de la presión efectiva sobre el estrato de arcilla causado por la
construcción de la cimentación.
σ c, = presión de preconsolidación.
eo = relación de vacíos inicial del estrato de arcilla.
Cc = índice de compresibilidad.
Cs = índice de expansión.
Hc = espesor del estrato de arcilla.
Como el incremento de la presión efectiva no es constante con la profundidad, el incremento
promedio se puede determinar por:
(
)
1
∆σ t, + 4∆σ m, + ∆σ b,
6
,
,
Donde ( ∆σ t ; ∆σ m ; ∆σ b, ) son los incrementos de presión efectiva arriba, en el medio y en el
fondo del estrato de arcilla causado por la construcción de la cimentación. Estos incrementos
se calculan con los métodos antes señalados.
∆σ ,prom =
7
Prof. Jorge Rojas
Pruebas de Carga de Campo.
La capacidad de carga ultima, así como la capacidad admisible basada en consideraciones de
asentamientos tolerables, se puede determinar con la prueba de carga de campo o “prueba de
carga de placa” (ASTM – 2000) (D-1194-94).
Se utiliza placas de acero e = 1” (25mm) φ = (150 – 762) mm (6 – 30)” ó cuadradas de (305 x
305) mm (12 x 12)”.
Prueba de la placa de carga.
La carga de aproximadamente un cuarto o un quinto de la carga última estimada se aplican
paulatinamente, se mide el asentamiento con el extensómetro y debe transcurrir una hora para
cada etapa de aplicación de la carga.
La prueba debe llevarse hasta la falla, o por lo menos hasta que la placa se haya asentado 25
mm (1”).
Con la grafica obtenemos la carga última por área unitaria o esfuerzo ultimo.
Para pruebas en arcillas:
qu(F) = qu(p)
donde:
qu(F) = capacidad de carga última de la cimentación propuesta.
qu(p) = capacidad de carga última de la placa de pruebas.
8
Prof. Jorge Rojas
Para pruebas en suelos arenosos:
B
qu ( F ) = qu ( p ) F
Bp
Donde:
BF = ancho de la cimentación.
Bp = ancho de la placa de prueba.
La capacidad de carga admisible de una cimentación basada en consideraciones de
asentamientos y para una intensidad de carga “qo” es:
B
S F = S p F (Suelo arcilloso).
Bp
 2 BF
SF = S p 
B +B
p
 F




2
(Suelos arenosos).
Asentamientos diferenciales y tolerables.
(Skempton y Mac Donald 1956) basado en estudios de 98 edificios propusieron para
asentamientos totales:
Fundaciones aisladas en arcillas:
6,5 cms.
Fundaciones aisladas en arenas:
4,0 cms.
Losas en arcillas:
(6,5 a 10) cms.
Losas en arenas:
(4 a 6,5) cms.
(Bjerrum 1963) para evitar daños en la estructura propuso los siguientes limites para la
relación ( δ / L )
δ /L
1/750
1/600
1/500
1/300
1/250
1/150
Tipo de Daño
Dificultades con maquinarias sensibles
Peligro para pórticos con diagonales.
Limites seguro para edificios donde no se permiten grietas.
Agrietamiento de paredes, problemas con grúas
Inclinación de altas edificaciones es visible
Agrietamiento considerable en paneles y paredes de ladrillo.
9
Prof. Jorge Rojas