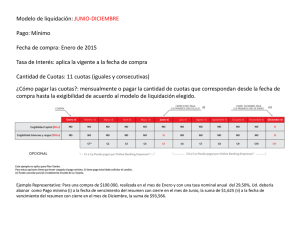
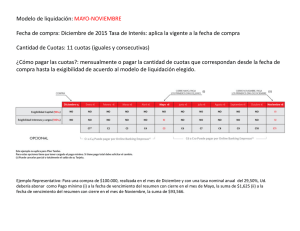
Ejercicios Gradientes Por Ana Milena Cardona 1. Se le proporciona el siguiente diagrama de flujo de caja de un crédito bancario: 60.000.000 trim 0 2% trimestral trim 1 … trim 24 trim 25 Cuota periodo n = 3.000.000 + G*(n-1) Realice una tabla de amortización y determine el valor de G. 2. Usted tiene una cuenta por pagar que asciende hasta 30.000.000. Ha decidido pagar de la siguiente forma: los primeros 6 meses cuotas mensuales iguales. Luego (después de los 6 meses), estará 4 quincenas sin pagar nada. Seguidamente, empezará a pagar cuotas mensuales que aumentan en 10.000 periodo a periodo, donde la primera será el doble del monto de las cuotas iguales. El interés de la operación es de 3,5% quincenal. Realice la tabla de amortización y calcule el valor de las cuotas de los primeros 6 meses. 3. Suponga que usted adquirió una activo de 250.600.000 y decide amortizarlo durante 30 trimestres con una tasa del 5% trimestral de la siguiente forma: Un abono en el periodo cero de 3.000.000 Las primeras 8 cuotas serán trimestrales y en la modalidad de abono constante a capital (o sea, amortización constante) de 2'000.000 cada periodo. Luego, los periodos del 9 al 20 dará cuotas de 20.000.000 Un abono extra PACTADO en el trimestre 10 del 15% de la cuota correspondiente a ese periodo Por último, los periodos que queden, dará cuotas que disminuyan periodo a periodo en 50.000, empezando por un valor desconocido. Desarrolle la tabla de amortización y encuentre el valor de la cuota #1 de su gradiente. 4. Cuánto habré de demorarme saldando una deuda de 100.000.000, si he acordado con mi acreedor una tasa del 15%NM, y saldarla así: El primer año pagaré cuotas mensuales IGUALES de un valor desconocido tal que al finalizar el primer año el saldo a deber sea exactamente la mitad del inicial. Luego, los siguientes 2 meses serán un periodo de gracia donde pagaré una cuota reducida. Después, del periodo 15 en adelante daré unas cuotas iguales de 4.191.049,966 hasta llegar a saldo 0.