38

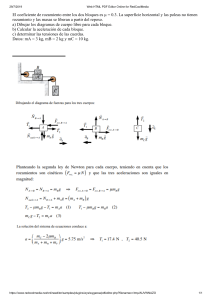
ESTÁTICA
Rama de la mecánica, cuyo objetivo es estudiar las
condiciones que deben de cumplir las fuerzas que actúan
sobre un cuerpo, para que éste se encuentre en
equilibrio.
Concepto de fuerza. Cuando realizamos un esfuerzo
muscular para empujar o tirar de un objeto, le estamos
comunicando una fuerza; una locomotora ejerce una fuerza
para arrastrar los vagones de un tren; un chorro de agua
ejerce una fuerza para hacer funcionar una turbina. Así,
todos tenemos intuitivamente la idea de lo que es una
fuerza. Analizando los ejemplo que acabamos de citar, es
posible concluir que para que el efecto de una fuerza
quede bien definido, será necesario especificar su
magnitud, su dirección y su sentido. en otras palabras
es una magnitud vectorial y podrá, por tanto, ser
representada con un vector. Otro ejemplo de fuerza, con
la cual tratamos con frecuencia, es la acción atractiva
de la Tierra sobre los cuerpos situados cerca o en su
superficie. Esta fuerza se conoce como peso de un
cuerpo. Entonces peso de un cuerpo es la fuerza con que
la Tierra atrae a dicho cuerpo. Naturalamente, el peso
es una cantidad vectorial y se puede representar por un
vector. La fuerza de atracción de la Tierra sobre un
objeto, así como las fuerzas eléctricas o las magnéticas
(fuerza de un imán sobre un clavo, por ejemplo) son
ejercidas sin que haya necesidad de contacto entre los
cuerpos (son de acción a distancia). Se diferencian así
de las fuerzas citadas al inicio de esta sección, las
cuales sólo pueden ser ejercidas si existe contacto
entre los cuerpos.
I) EQUILIBRIO.
Un cuerpo cualquiera se encuentra en equilibrio cuando
carece de todo tipo de aceleración (a = 0).
ESTATICA
Vectores: Son modelos matemáticos.
Sea el vector V, representa una cantidad física y, se compone de:
1.
Módulo: (magnitud) valor numérico y absoluto
del mismo, expresa la cantidad que representa el
mismo y se le asigna una unidad.
2.
Dirección: recta de acción, que según el
sistema de referencia posee una inclinación .
3.
Sentido: según el sistema de referencia, tendrá signo positivo o
negativo.
4.
Origen: punto de aplicación.
Fuerza
Magnitud física que se representa con un vector y su unidad puede ser Newton
(N), kilogramo fuerza (kgr) o dina (din).
Resultante
Es la suma vectorial de todas las fuerzas aplicadas y no aplicadas a un
sistema.
Momento de una fuerza
El momento de una fuerza es el producto de dicha fuerza por la distancia
perpendicular a un determinado eje de giro. Cuando se
aplica una fuerza a una puerta pesada para abrirla, la
fuerza se ejerce perpendicularmente a la puerta y a la
máxima distancia de las bisagras. Así se logra un momento
máximo. Si se empujara la puerta con la misma fuerza en un
punto situado a medio camino entre el tirador y las
bisagras, la magnitud del momento sería la mitad. Si la
fuerza se aplicara de forma paralela a la puerta (es
decir, de canto), el momento sería nulo.
Sea el vector distancia, un vector perpendicular a una fuerza, de magnitud
igual a la distancia entre un punto A y la recta de acción de la fuerza, se
define como vector momento de la fuerza con respecto al punto A:
El producto vectorial entre el vector fuerza y el vector distancia, cuya
dirección es perpendicular al plano que forman el punto A y la fuerza y, el
sentido dependerá del vector fuerza (horario –
antihorario).
Vista tridimensional según la regla del tirabuzón
(para la mano izquierda)
Las unidades del vector momento son: N.m,
kilográmetro (kgrm) ó din.cm. por ser éste un
producto vectorial.
1ª Condición de Equilibrio
"Un cuerpo se encontrará en equilibrio cuando la fuerza
resultante que actúa sobre él sea igual a cero; para
eso, las fuerzas componentes deben ser necesariamente
coplanares y concurrentes".
Condición algebraica.
Condición gráfica.
Si la resultante de un sistema de vectores es nula, el
polígono que se forma será cerrado.
II) LEYES DE NEWTON.
1ª Le de Newton (Ley de la Inercia)
Al estructurar los principios de la Mecánica, Newton se
basó en los estudios realizados por los físicos que lo
precedieron, entre ellos Galileo. Así la primera ley de
Newton no es más que una síntesis de las ideas de
Galileo referentes a la inercia, y por eso mismo,
también se le denomina ley de la inercia:
"Un cuerpo de masa constante permanece en estado de
reposo o movimiento con una velocidad constante en línea
recta, a menos que sobre ella actue una fuerza"
3ª Ley de Newton
En sus estudios de Dinámica, Newton se dio cuenta de que
las fuerzas siempre aparecen como resultado de la
interacción de dos cuerpos. En otras palabras, la acción
de una fuerza sobre un cuerpo no se puede manifestar sin
que haya otro cuerpo que lo provoque. Además Newton pudo
comprobar que en la interacción de dos cuerpos, als
fuerzas siempre aparecen en pares: para cada acción de
un cuerpo sobre otro siempre existirá una reacción igual
y contraria de éste sobre el primero. tales
observaciones de Newton se pueden sintetizar en el
enunciado de su tercera ley, que también se conoce como
ley de la acción y la reacción:
"Si un cuerpo le aplica una fuerza a otro (Acción);
entonces el otro le aplica una fuerza igual y en sentido
contrario al primero (Reacción)".
Ejemplo:
Si soltamos desde una altura una pelotita de jebe, esta
llega al suelo aplicándole una fuerza
; pero en ese
instante el suelo reacciona y le aplica otra fuerza
la pelotita (en sentido contrario y de una misma
magnitud y dirección).
a
Si colocamos un clavo y
un imán sobre una mesa. Sabemos que el imán atrae al clavo
con una fuerza
. Por la tercera ley de Newton, el clavo
reacciona y atrae al imán con una fuerza
de misma magnitud
y misma dirección, pero en sentido contrario a
.
La tierra atrae a la Luna con fuerza
. La Luna atrae también a la Tierra con
fuerza
, pero en sentido contrario.
Tener en cuenta que la acción y
reacción no se anulan porque no actúan en el mismo cuerpo.
III) FUERZAS INTERNAS.
Son los que mantienen juntos a las partículas que forman
un sólido rígido. Si el sólido rígido esta compuesto
estructuralmente de varias partes, las fuerzas que
mantienen juntas a las partes componentes se definen
también como fuerzas internas. Entre las fuerzas
internas más conocidas, tenemos: La tensión y la
compresión.
1. Tensión (T). Es aquella fuerza que aparece en el
interior de un cuerpo flexible (cuerda, cable); debido a
fuerzas externas que tratan de alargarla.
2. Compresión (C). Es aquella fuerza que aparece en el
interior de un sólido rígido cuando fuerzas externas
tratan de comprimirlo.
IV) TEOREMA DE LAMY.
Tenemos un cuerpo en equilibrio bajo la acción de tres
fuerzas coplanares y concurrentes, el valor de cada una
de las fuerzas es directamente proporcional al seno del
ángulo que se le opone.
V) DIAGRAMA DE CUERPO LIBRE.
Hacer el D.C.L. de un cuerpo es representar gráficamente
las fuerzas que actúan en él.
Para esto se sigue los
siguientes pasos.
1.- Se aísla al cuerpo, de todo el sistema
2.- Se representa al peso del cuerpo mediante un vector
dirigido siempre hacia el centro de la Tierra.
3.- Si existiesen superficies en contacto, se representa
a la reacción mediante un vector perpendicular a dichas
superficies y empujando siempre al cuerpo.
4.- Si hubiesen cuerdas o cables, se representa a la
tensión mediante un vector que está siempre jalando al
cuerpo, previo corte imaginario.
5.- Si existiesen barras comprimidas, se representa a la
compresión mediante un vector que está siempre empujando
al cuerpo, previo corte imaginario.
Ilustraciones:
Método
para
la
Resolución de Ejercicios (M. Algebraico)
1.- Aislar al objeto bajo estudio.
2.- Mostrar en un diagrama, las fuerzas que actúan sobre
el objeto aislado (D.C.L).
3.- Encontrar las componentes rectangulares de cada
fuerza.
4.- Escribir la primera condición de equilibrio en forma
de ecuación.
5.- Resolver para determinar las cantidades requeridas.
1º Dos barras homogéneas OA y OB, articuladas en O, tienen la
misma longitud l = 2 m. y sus pesos respectivos son P = 4 Kg
y P’ = 5 Kg. Los extremos A, B se apoyan sin rozamiento en el
suelo horizontal y están unidos por medio de un hilo
elástico. La tensión del hilo es T = K(x-xo) siendo xo = 3 m.
la longitud natural del hilo. Suponiendo que el sistema se
encuentra en equilibrio cuando el ángulo entre ambas barras
es 120 º. ¿ Qué valor ha de tener K en esas condiciones ?
¿Cual es valor de las reacciones en el suelo ? Sol : 8,4 kg/m
2º Un cigarrillo sin filtro de longitud L = 5l esta apoyado
en un soporte tal como indica la figura. Encendemos el
cigarrillo por un extremo y empieza a formarse ceniza
uniformemente a una velocidad de v= 0,2 mm/s, según el eje
del mismo. Suponiendo que la sección no varia y siendo la
densidad de la ceniza 3/8 de la parte sin quemar, calcular el
tiempo que tardará en caerse.
Sol: 200 seg.
3º Se dobla el alambre homogéneo ABC como se indica en la
figura y se un a una articulación C. Hallar L para la cual el
tramo BC del alambre es horizontal.
Sol : 942,57 mm.
1-Calcular el peso P
necesario para mantener
el equilibrio en el
sistema mostrado en la
figura. En el cual A pesa
100 kg, Q pesa 10 kg. El
plano y las poleas son
lisas. La cuerda AC es
horizontal y la cuerda AB
es paralela al plano.

Calcular también la
reacción del plano
sobre el cuerpo A.
2-Dos cilindros
macizos y
homogéneos de
pesos 6 y 10 kg se
apoyan sin
rozamiento sobre
los planos
inclinados de la
figura. Calcular:


El ángulo que
forma con la
horizontal la
línea que une
los centros
de los dos
cilindros.
La reacción
de los planos
inclinados
3.-Una viga uniforme tiene 4 m
de larga y pesa 100 Kg. Un
hombre de 75 kg está situado a 1
m del apoyo A.

Calcula las reacciones en
los apoyos A y B.
4.-Una varilla de
6 kg y 0.8 m de
longitud está
apoyada sobre un
ángulo recto liso,
como se muestra en
la figura.
Calcular :


El ángulo de
equilibrio
que forma la
varilla con
la
horizontal.
Las
reacciones en
los apoyos.
5.-a escalera, de masa 40 kg y
6 m de longitud, está apoyada
sobre una pared lisa vertical y
sobre un suelo horizontal

La fuerza de rozamiento
cuando el un hombre de 80
kg ha subido 3 m a lo
largo de la escalera.
La longitud máxima a lo
largo de la escalera a la
que puede ascender, antes
de que comience a
deslizar.

6.-Queremos arrastrar una
silla a velocidad constante
sobre el suelo horizontal,
siendo el coeficiente dinámico
de rozamiento entre las patas
y el suelo 0.3. La silla pesa
25 kg.

¿Cuál es la fuerza
horizontal F, aplicada a
0.6 m de altura sobre el
suelo, necesaria para
arrastrarla?. ¿Cuánto
vale la reacción del
suelo sobre las patas
delanteras y traseras?.

¿A qué altura máxima se
podrá aplicar la fuerza
de arrastre sin que
vuelque la silla?
7-Una pluma de 4 m de la
grúa de la figura pesa 200
kg y está sosteniendo una
carga de 1000 kg. Calcular:

La tensión del cable AB
y las componentes de la
fuerza sobre la
articulación C.
.8.-Calcular el peso máximo del disco
de la figura, sabiendo que la tensión
máxima que puede soportar la cuerda es
de 15 kg.


Calcular también la reacción en
la articulación A
Datos: peso de la barra 6 kg,
longitud 40 cm; radio del disco
20 cm.
9.-En el problema
esquematizado en la
figura, la barra
tiene una longitud de
5 m y pesa 20 kg, el
cilindro tiene un
peso de 30 kg y un
radio de 0.5 m.
Suponer que no hay
rozamiento entre la
barra y el cilindro,
y que el coeficiente
est tico de
rozamiento entre el
extremo derecho de la
barra y el plano
horizontal es 0.3. La
esfera está sujeta, a
su vez, por una
cuerda de 1.3 m de
longitud.

Calcular la
fuerza de
rozamiento y la
tensión de la
cuerda cuando el
ángulo entre la
barra y el plano
horizontal es de
15º.
 ¿Deslizará o no
la barra?,
razonar la
respuesta.
10.-Una barra OA de
30 kg de peso y 2 m
de longitud,
articulada en O, se
apoya sobre una caja
rectangular de 10 kg
de peso y de
dimensiones 0.75 y
0.5 m. La caja puede
deslizar sobre el
plano horizontal.
Sabiendo que el
ángulo entre la barra
y el plano horizontal
es de 30º, calcular:



La fuerza sobre
la articulación
O
La fuerza que
ejerce plano
horizontal sobre
la caja y su
punto de
aplicación.
¿Deslizará o no
la caja?. Razona
la respuesta.
Dato: el coeficiente
estático de
rozamiento entre la
caja y el plano
horizontal vale 0.5
11.-Dos escaleras CA
y DA de 40 kg y 30
kg, respectivamente,
se apoyan sobre un
suelo liso y se
articulan en el
vértice A, están
sujetas por una
cuerda paralela al
suelo situada a 0.9 m
del mismo. Las
escaleras forman
entre sí un ángulo
recto. Calcular:



Las reacciones
en los apoyos C
y B.
La tensión de la
cuerda.
Las componentes
horizontal y
vertical de la
fuerza que una
escalera ejerce
sobre la otra a
través de la
articulación A.
La primera ley de newton
Antes que nada recordemos el enunciado de la primera
ley:
Es decir, nadie hace o deja de hacer algo si no lo
obligan.
¿Qué quiere decir esto?.
Bueno, para empezar debemos pensar las leyes de
Newton, como Newton quiere
que las pensemos.
Cuando nos referimos a un
cuerpo, él será el único
existente. En otras
palabras, el universo está
formado por los cuerpos
que estamos considerando y
no habrá otros.
Es igual que cuando se ama profundamente, la persona
amada es todo lo que importa, no hay nadie más. Ósea,
cuando se ama, no se montan cachos.
En el universo existen también fuerzas que actúan
sobre los cuerpos. Éstas fuerzas representan
(resumen), la interacción de nuestro universo con
otrosuniversos desconocidos. No debemos estar celosos
de esos universos.
Si en el universo existe un solo cuerpo, nadie
puede interferir con su movimiento. Y si no hay
fuerzas sobre él, es muy razonable pensar que no
se mueva nunca si no se estaba moviendo, o que no
se detenga nunca si se estaba moviendo. Esto
último es en el sentido intuitivo, coloquial, de
fuerza. Puesto que con esta ley solamente Newton
no ha definido lo que es la fuerza. Esta ley es
parte de esa definición.
Leyendo de nuevo el enunciado podemos concluir:
Las fuerzas son las cosas responsables de los
cambios en el movimiento de los cuerpos.
Los cuerpos son cosas más fáciles de definir.
Tienen extensión, materia y
si son muy lindos, por regla general no piensan
mucho.
Para determinar veamos un ejemplo de la vida
Cuando empujamos una
carretilla, sentimos que la
primera ley de Newton no es tan
cierta como nos dicen.
Para que la carretilla se mueva
a velocidadconstante, debemos
estar empujándola
constantemente. Así que parece
mentiraque sobre un cuerpo que
se mueve a velocidad constante
no actúa ningunafuerza.
En este caso no hemos pensado las cosas como están
planteadas en la primera ley. Hemos sido un poco
egoístas. No consideramos que la gravedad, la
reacción del piso y la resistencia del aire también
son fuerzas que están actuando sobre la
carretilla.
Entonces,
para
evaluar la
veracidad
de
la
primera ley
debemos
considerar
el
efecto
conjunto de
todas
la
fuerzas
como
una
sola, y a
la
carretilla
como
el
único
objeto del
universo.
En
este
caso
podemos
someter
a
prueba
el
enunciado
con éxito.
La sumatoria de las fuerzas que actúan sobre la
carretilla es nula y ésta se mueve con velocidad
constante.
2. Tercera Ley De Newton
La tercera ley de Newton explica las fuerzas de acción y
reacción. Estas fuerzas las ejercen todos los cuerpos que
están en contacto con otro, así un libro sobre la mesa ejerce
una fuerza de acción sobre la mesa y la mesa una fuerza de
reacción sobre el libro. Estas fuerzas son iguales pero
contrarias; es decir tienen el mismo modulo y sentido, pero
son opuestas en dirección.
Esto significa que siempre en que un cuerpo ejerce una fuerza
sobre otro este también ejerce una fuerza sobre él.
Se nombra fuerza de acción a la que es ejercida por el primer
cuerpo que origina una fuerza sobre otro, por lo tanto se
denomina fuerza de reacción a la es originada por el cuerpo
que recibe y reacciona (De allí el nombre) con esta otra
fuerza sobre el primer cuerpo.
¿Pero qué pasa cuando ningún cuerpo origino primariamente la
fuerza, como en el ejemplo del libro sobre la mesa?
Cualquiera puede ser denominada fuerza de acción y obviamente
a la otra se le denominará como fuerza de reacción.
Ejemplos
En la siguiente imagen se encuentran cinco ejemplos más de
las fuerzasa de acción y reacción:
La fuerza que ejerce la bala sobre la pistola y la que ejerce la pistola sobre la bala
provocando el disparo de esta.




La fuerza que ejerce el avión sobre el aire, provoca que
el aire reaccione sobre el avión provocando el
desplazamiento de este.
La fuerza del misil hacia el aire y la del aire sobre el
misil provoca el movimiento del misil.
La fuerza que la mano ejerce sobre la mesa y la que esta
ejerce de vuelta no da como resultado el movimiento
debido a que las fuerzas son muy leves como para
provocarlo.
La fuerza que ejerce el remo sobre el muelle no es
suficiente como para moverlo pero la fuerza de reacción
del muelle si es suficiente como para mover al remo
hacia atrás, llevando al hombre hacia atrás, por lo que
el bote es arrastrado hacia atrás.
Otros ejemplos:




Al patear una pelota, el pie ejerce una fuerza sobre
ésta; pero, al mismo tiempo, puede sentirse una fuerza
en dirección contraria ejercida por la pelota sobre el
pie.
Si una persona empuja a una pared la pared. La persona
ejerce una fuerza sobre la pared y la pared otra fuerza
sobre la persona.
Cuando una persona camina empuja hacia atrás el suelo,
la reacción del suelo es empujarlo hacia adelante, por
lo que se origina un movimiento de la persona hacia
adelante. Lo mismo sucede con un auto en movimiento, las
ruedas empujan el camino y este la empuja hacia
adelante.
Un objeto colgando de una cuerda ejerce una fuerza sobre
la cuerda hacia abajo, pero la cuerda ejerce una fuerza
sobre este objeto hacia arriba, dando como resultado que
el objeto siga colgando y no caiga
Como referencia, he aquí de nuevo las tres leyes:
(1) En ausencia de fuerzas, un cuerpo en reposo
seguirá en reposo, y un cuerpo moviéndose a
velocidad constante en línea recta continuará
haciéndolo indefinidamente.
(2) Cuando se aplica una fuerza a un objeto
("cuerpo") se acelera en la dirección de la fuerza.
La aceleración es directamente proporcional a la
intensidad de la fuerza e inversamente proporcional
a la masa a mover:
a = F/m
ó
F = ma
(3) Las fuerzas son siempre producidas en pares,
teniendo direcciones opuestas e igual magnitud. Si
el cuerpo nº 1 actúa con una fuerza F sobre el
cuerpo nº 2, el cuerpo nº 2 actuará sobre el nº 1
con una fuerza de igual intensidad y dirección
opuesta.
La segunda ley proporciona una fórmula explícita y por ello
es una de las más útiles. Pero también puede ser una de las
que los estudiantes de física encuentren más confusa. Su
problema se enuncia como sigue:
Una fórmula en la que todas las cantidades están
definidas puede usarse para deducir a una de las
otras. Una fórmula donde una cantidad no está
definida puede, en el mejor de los casos, servir
como definición: aísle esa cantidad en el lado de
signos "iguales" y lo definirá en los términos de
los otros. Una fórmula en la cual dos cantidades
están sin definir, llamadas A y B, es poco menos
que inútil. No nos dice nada sobre esas cantidades,
puesto que cualquier valor que se escoja para A ó
B puede siempre ajustarse para que la ecuación se
cumpla.
Ese parece el caso en F = ma. La aceleración a es
una cantidad bien definida, el cambio por segundo
en la velocidad (y también tiene una dirección).
Pero, ¿que pasa con m y F?. ¿Como se puede usar la
ecuación sin definirlas por independiente?
Buena pregunta. Generaciones de estudiantes de física
lucharon con eso y a menudo, también sus profesores. Algunos
retrocedieron definiendo la masa como peso, usando la
gravedad como una herramienta. Un profesor que yo conozco, un
físico distinguido, blandió su brazo al frente de la clase y
definió la fuerza con la analogía de que era como la
producida por sus músculos.
La formulación de las leyes de Newton por Mach Ernest Mach,
que vivió en Alemania dos siglos después que Newton, dio la
que puede ser la respuesta más satisfactoria. Mach
argumentaba que las leyes de Newton se unían en una sola:
"Cuando dos objetos compactos ("puntos masa" en
palabras de física) actúan uno sobre el otro,
aceleran en direcciones opuestas y la relación de
sus aceleraciones es siempre la misma".
Léalo de nuevo: no menciona fuerzas ó masas, solo
aceleración, la cual puede medirse. Cuando una pistola actúa
sobre una bala, un cohete sobre su chorro, el Sol sobre la
Tierra (en la escala de la distancia que los separa, el Sol y
la Tierra pueden ser vistos como objetos compactos), las
aceleraciones son siempre directamente opuestas.
La masa y la fuerza se derivan ahora fácilmente. Si uno de
los objetos es un litro de agua, su masa se define como un
kilogramo. Si luego actúa sobre otro objeto (quizás, para el
experimento, con el agua convertida en hielo), la relación de
su aceleración awcon la aceleración del otro objeto nos da la
masa del objeto m:
aw /a
=
m /1 kg
=
m
Luego
m a
=
1 kg. aw
esto se puede interpretar diciendo que una unidad de fuerza
de magnitud aw existe entre las dos
F
=
m a
=
1 kg. aw
Esa unidad de fuerza será la fuerza que causa que 1 kg se
acelere a 1 m/s2, esto es, su velocidad se incrementa cada
segundo en 1 m/s. Parece correcto llamar a esa unidad el
newton. Después de todo, Newton fue quien, con esa fórmula,
hizo que fuese posible calcular todos los movimientos y la
aplican por doquier los ingenieros todos los días con
finalidades prácticas. No extraña que el poeta Alexander
Pope, quien vivió en tiempos de Newton, escribiera:
La Naturaleza y sus leyes yacían
escondidas en la noche
Dios dijo: "¡Hagamos existir a Newton!"
y se hizo la luz.
Gravedad
Oh si, la gravedad. Un cuerpo cayendo, tanto si es ligero
como si es pesado, tiene la misma aceleración g: unos 10
m/s2. ¿Donde entra F = ma aquí?
Newton llamó a la fuerza que produce la citada aceleración
gravitación, y propuso que era proporcional a la masa. Esa
fuerza, medida en newtons, con m en kilos, es
F
=
m g
Sustituyendo esto en la fórmula F = m a
nos da
m g = m a
ó
a = g
La última línea indica que la aceleración de un objeto
cayendo siempre es igual a g, tanto si es un guijarro como
una gran roca. La fuerza que tira de la roca hacia abajo, su
"peso", es mucho mayor: no obstante su masa, la inercia que
deberá vencer para moverla, es grande también, con el mismo
factor. La conclusión es que, grande ó pequeña, la
aceleración siempre es igual a g.
Eso era lo que confundía a los científicos antes de Newton.
Cuando veían caer a las piedras, pesadas o ligeras, con la
misma velocidad, la función de la masa no estaba nada clara.
Estamos ahora en bellas y serias dificultades. Obviamente, la
masa de un objeto puede ser medida de dos maneras diferentes
(comparándola con la masa de un litro de agua). Una usando la
gravedad, pesándola obtenemos la masa gravitatoria;
indiquémosla como m. Ó se puede prescindir de la gravedad,
como los astronautas abordo del Skylab y medir la "masa
inercial", llamándola M. Se puede visualizar un universo
donde las dos sean diferentes, pero nuestro Universo no
parece comportarse así. El físico húngaro Roland Eötvös
(Lorand en húngaro) comparó las dos a lo largo de un siglo
usando instrumentos muy sensibles y llegó a la conclusión que
eran las mismas con una precisión de varios decimales. Esta
igualdad se convirtió en una de las bases de la física, en
especial de la teoría general de la relatividad .
Objetos en Descanso
Cuando está de pié en el suelo, la gravedad continúa tirando
su cuerpo hacia abajo con fuerza
F = +mg (hacia abajo)
¿Por qué no cae? ¡Porque el suelo no le deja! Las partículas
integrantes del suelo están juntas y no permiten a su piés
bajar más (como lo haría si estuviera sobre arenas
movedizas). El hecho de que la fuerza F no produzca
aceleración es la evidencia de que otra fuerza, opuesta al
movimiento, es producida por el suelo:
F' = -mg (hacia arriba)
Conjuntamente, F y F' se suman y su resultado es cero, y el
resultado es que sus pies y su cuerpo continúan quietos.
Esta es una regla general: si nada cambia, las fuerzas
sumaran cero. Se dice que está "en equilibrio", un concepto
que será muy útil en la próxima sección. Tome nota de que no
tiene nada que ver con la 3ª ley de Newton: la 3ª ley se
ocupa de las fuerzas que producen el movimiento, mientras que
aquí todas las fuerzas se cancelan.
unidades
La observación de un fenómeno es en
general incompleta a menos a menos que dé
lugar a una información cuantitativa. Para
obtener dicha información se requiere la
medición de una propiedad física. Así, la
medición constituye una buena parte de la
rutina diaria del físico experimental.
La medición es la técnica por medio de la
cual asignamos un número a una propiedad
física, como resultado de una comparación
de dicha propiedad con otra similar tomada
como patrón, la cual se ha adoptado como
unidad.
Supongamos una habitación cuyo suelo está
cubierto de baldosas, tal como se ve en la
figura, tomando una baldosa como unidad, y
contando el número de baldosas medimos la
superficie de la habitación, 30
baldosas. En la figura inferior, la
medida de la misma superficie da una
cantidad diferente 15 baldosas.
La medida de una misma magnitud física
(una superficie) da lugar a dos cantidades
distintas debido a que se han empleado
distintas unidades de medida.
Este ejemplo, nos pone de manifiesto la
necesidad de establecer una única unidad
de medida para una magnitud dada, de modo
que la información sea comprendida por
todas las personas. Este es el espíritu
del Sistema Internacional de Unidades de
medida, obligatorio en España y vigente en
la Unión Europea.
Unidades SI básicas.
Magnitud
Nombre
Símbolo
Longitud
metro
m
Masa
kilogramo kg
Tiempo
segundo
s
Intensidad de corriente
eléctrica
ampere
A
Temperatura termodinámica
kelvin
K
Cantidad de sustancia
mol
mol
Intensidad luminosa
candela
cd
Unidad de
longitud: metro
(m)
El metro es la longitud de trayecto
recorrido en el vacío por la luz durante
un tiempo de 1/299 792 458 de segundo.
Unidad de masa
El kilogramo (kg) es igual a la masa del
prototipo internacional del kilogramo
Unidad de tiempo
El segundo (s) es la duración de 9 192
631 770 periodos de la radiación
correspondiente a la transición entre los
dos niveles hiperfinos del estado
fundamental del átomo de cesio 133.
Unidad de
intensidad de
corriente
eléctrica
El ampere (A) es la intensidad de una
corriente constante que manteniéndose en
dos conductores paralelos, rectilíneos,
de longitud infinita, de sección circular
despreciable y situados a una distancia
de un metro uno de otro en el vacío,
produciría una fuerza igual a 2.10-7
newton por metro de longitud.
Unidad de
temperatura
termodinámica
El kelvin (K), unidad de temperatura
termodinámica, es la fracción 1/273,16 de
la temperatura termodinámica del punto
triple del agua.
Observación: Además de la temperatura
termodinámica (símbolo T) expresada en
kelvins, se utiliza también la
temperatura Celsius (símbolo t) definida
por la ecuación t = T - T0 donde T0 =
273,15 K por definición.
El mol (mol) es la cantidad de sustancia
de un sistema que contiene tantas
entidades elementales como átomos hay en
0,012 kilogramos de carbono 12.
Unidad de
cantidad de
sustancia
Cuando se emplee el mol, deben
especificarse las unidades elementales,
que pueden ser átomos, moléculas, iones,
electrones u otras partículas o grupos
especificados de tales partículas.
La candela (cd) es la unidad luminosa, en
una dirección dada, de una fuente que
emite una radiación monocromática de
frecuencia 540 1012 hertz y cuya
intensidad energética en dicha dirección
es 1/683 watt por estereorradián.
Unidad de
intensidad
luminosa
Unidades SI suplementarias.
Magnitud
Nombre
Ángulo plano
Radián
Ángulo sólido Estereorradián
Símbolo
Expresión en
unidades SI
básicas
rad
mm-1= 1
sr
m2m-2= 1
Unidad de ángulo
plano
El radián (rad) es el ángulo plano
comprendido entre dos radios de un
círculo que, sobre la circunferencia de
dicho círculo, interceptan un arco de
longitud igual a la del radio.
Unidad de ángulo
sólido
El estereorradián (sr) es el ángulo
sólido que, teniendo su vértice en el
centro de una esfera, intercepta sobre
la superficie de dicha esfera un área
igual a la de un cuadrado que tenga por
lado el radio de la esfera.
Unidades SI derivadas
Las unidades SI derivadas se definen de forma que sean
coherentes con las unidades básicas y suplementarias, es
decir, se definen por expresiones algebraicas bajo la forma
de productos de potencias de las unidades SI básicas y/o
suplementarias con un factor numérico igual 1.
Varias de estas unidades SI derivadas se expresan simplemente
a partir de las unidades SI básicas y suplementarias. Otras
han recibido un nombre especial y un símbolo particular.
Si una unidad SI derivada puede expresarse de varias formas
equivalentes utilizando, bien nombres de unidades básicas y
suplementarias, o bien nombres especiales de otras unidades
SI derivadas, se admite el empleo preferencial de ciertas
combinaciones o de ciertos nombres especiales, con el fin de
facilitar la distinción entre magnitudes que tengan las
mismas dimensiones. Por ejemplo, el hertz se emplea para la
frecuencia, con preferencia al segundo a la potencia menos
uno, y para el momento de fuerza, se prefiere el newton metro
al joule.
Unidades SI derivadas expresadas a partir de unidades básicas
y suplementarias.
Magnitud
Nombre
Símbolo
Superficie
metro cuadrado
m2
Volumen
metro cúbico
m3
Velocidad
metro por segundo
m/s
Aceleración
metro por segundo
cuadrado
m/s2
Número de ondas
metro a la potencia
menos uno
m-1
Masa en volumen
kilogramo por metro
cúbico
kg/m3
Velocidad
angular
radián por segundo
rad/s
Aceleración
angular
radián por segundo
cuadrado
rad/s2
Unidad de
velocidad
Un metro por segundo (m/s o m s-1) es la
velocidad de un cuerpo que, con
movimiento uniforme, recorre, una
longitud de un metro en 1 segundo
Unidad de
aceleración
Un metro por segundo cuadrado (m/s2 o m
s-2) es la aceleración de un cuerpo,
animado de movimiento uniformemente
variado, cuya velocidad varía cada
segundo, 1 m/s.
Unidad de número
de ondas
Un metro a la potencia menos uno (m-1) es
el número de ondas de una radiación
monocromática cuya longitud de onda es
igual a 1 metro.
Un radián por segundo (rad/s o rad s-1)
Unidad de
velocidad angular es la velocidad de un cuerpo que, con
una rotación uniforme alrededor de un
eje fijo, gira en 1 segundo, 1 radián.
Unidad de
aceleración
angular
Un radián por segundo cuadrado (rad/s2 o
rad s-2) es la aceleración angular de un
cuerpo animado de una rotación
uniformemente variada alrededor de un
eje fijo, cuya velocidad angular, varía
1 radián por segundo, en 1 segundo.
Unidades SI derivadas con nombres y símbolos especiales.
Magnitud
Nombre
Símbolo Expresión Expresión en
en otras
unidades SI
unidades
básicas
SI
Frecuencia
hertz
Hz
s-1
Fuerza
newton
N
m kg s-2
Presión
pascal
Pa
N m-2
m-1 kg s-2
Energía,
trabajo,
cantidad de
calor
joule
J
N m
m2 kg s-2
Potencia
watt
W
J s-1
m2 kg s-3
Cantidad de
coulomb C
electricidad
carga eléctrica
Potencial
eléctrico
fuerza
electromotriz
volt
Resistencia
eléctrica
ohm
Capacidad
eléctrica
farad
V
s A
W A-1
m2 kg s-3 A-1
V A-1
m2 kg s-3 A-2
F
C V-1
m-2 kg-1 s4 A2
Flujo magnético weber
Wb
V s
m2 kg s-2 A-1
Inducción
magnética
tesla
T
Wb m2
kg s-2 A1
Inductancia
henry
H
Wb A-1
m2 kg s-2 A-2
Unidad de
frecuencia
Un hertz (Hz) es la frecuencia de un
fenómeno periódico cuyo periodo es 1
segundo.
Unidad de fuerza
Un newton (N) es la fuerza que, aplicada
a un cuerpo que tiene una masa de 1
kilogramo, le comunica una aceleración
de 1 metro por segundo cuadrado.
Unidad de presión Un pascal (Pa) es la presión uniforme
que, actuando sobre una superficie plana
de 1 metro cuadrado, ejerce
perpendicularmente a esta superficie una
fuerza total de 1 newton.
Unidad de energía, Un joule (J) es el trabajo producido por
trabajo, cantidad una fuerza de 1 newton, cuyo punto de
de calor
aplicación se desplaza 1 metro en la
dirección de la fuerza.
Unidad de
potencia, flujo
radiante
Un watt (W) es la potencia que da lugar
a una producción de energía igual a 1
joule por segundo.
Unidad de cantidad Un coulomb (C) es la cantidad de
de electricidad,
electricidad transportada en 1 segundo
carga eléctrica
por una corriente de intensidad 1
ampere.
Unidad de
potencial
eléctrico, fuerza
electromotriz
Un volt (V) es la diferencia de
potencial eléctrico que existe entre dos
puntos de un hilo conductor que
transporta una corriente de intensidad
constante de 1 ampere cuando la potencia
disipada entre estos puntos es igual a 1
watt.
Unidad de
resistencia
eléctrica
Un ohm
que existe entre dos puntos de un
conductor cuando una diferencia de
potencial constante de 1 volt aplicada
entre estos dos puntos produce, en dicho
conductor, una corriente de intensidad 1
ampere, cuando no haya fuerza
electromotriz en el conductor.
Unidad de
capacidad
eléctrica
Un farad (F) es la capacidad de un
condensador eléctrico que entre sus
armaduras aparece una diferencia de
potencial eléctrico de 1 volt, cuando
está cargado con una cantidad de
electricidad igual a 1 coulomb.
Unidad de flujo
magnético
Un weber (Wb) es el flujo magnético que,
al atravesar un circuito de una sola
espira produce en la misma una fuerza
electromotriz de 1 volt si se anula
dicho flujo en un segundo por
decaimiento uniforme.
Unidad de
inducción
magnética
Una tesla (T) es la inducción magnética
uniforme que, repartida normalmente
sobre una superficie de 1 metro
cuadrado, produce a través de esta
superficie un flujo magnético total de 1
weber.
Unidad de
inductancia
Un henry (H) es la inductancia eléctrica
de un circuito cerrado en el que se
produce una fuerza electromotriz de 1
volt, cuando la corriente eléctrica que
recorre el circuito varía uniformemente
a razón de un ampere por segundo.
Unidades SI derivadas expresadas a partir de las que tienen
nombres especiales
Magnitud
Nombre
Símbolo
Expresión
en
unidades
SI básicas
Viscosidad dinámica
pascal segundo
Pa s
m-1 kg s-1
Entropía
joule por kelvin
J/K
m2 kg s-2
K-1
Capacidad térmica
másica
joule por
kilogramo kelvin
J(kg K)
m2 s-2 K-1
Conductividad
térmica
watt por metro
kelvin
W(m K)
m kg s-3 K-
Intensidad del
campo eléctrico
volt por metro
V/m
Unidad de viscosidad
dinámica
1
m kg s-3 A1
Un pascal segundo (Pa s) es la
viscosidad dinámica de un fluido
homogéneo, en el cual, el movimiento
rectilíneo y uniforme de una
superficie plana de 1 metro cuadrado,
da lugar a una fuerza retardatriz de
1 newton, cuando hay una diferencia
de velocidad de 1 metro por segundo
entre dos planos paralelos separados
por 1 metro de distancia.
Unidad de entropía
Un joule por kelvin (J/K) es el
aumento de entropía de un sistema que
recibe una cantidad de calor de 1
joule, a la temperatura termodinámica
constante de 1 kelvin, siempre que en
el sistema no tenga lugar ninguna
transformación irreversible.
Unidad de capacidad
térmica másica
Un joule por kilogramo kelvin (J/(kg
K) es la capacidad térmica másica de
un cuerpo homogéneo de una masa de 1
kilogramo, en el que el aporte de una
cantidad de calor de un joule,
produce una elevación de temperatura
termodinámica de 1 kelvin.
Unidad de
conductividad térmica
Un watt por metro kelvin (W m/K) es
la conductividad térmica de un cuerpo
homogéneo isótropo, en la que una
diferencia de temperatura de 1 kelvin
entre dos planos paralelos, de área 1
metro cuadrado y distantes 1 metro,
produce entre estos planos un flujo
térmico de 1 watt.
Unidad de intensidad
del campo eléctrico
Un volt por metro (V/m) es la
intensidad de un campo eléctrico, que
ejerce una fuerza de 1 newton sobre
un cuerpo cargado con una cantidad de
electricidad de 1 coulomb.
Unidades definidas a partir de las unidades SI, pero que no
son múltiplos o submúltiplos decimales de dichas unidades.
Magnitud
Nombre
Ángulo
plano
vuelta
Símbolo
Relación
rad
grado
º
minuto de ángulo '
rad
Tiempo
segundo de
ángulo
"
minuto
min
60 s
hora
h
3600 s
día
d
86400 s
rad
Unidades en uso con el Sistema Internacional cuyo valor en
unidades SI se ha obtenido experimentalmente.
Magnitud
Nombre
Símbolo
Valor en unidades
SI
Masa
unidad de masa
atómica
u
1,6605402 10-27 kg
Energía
electronvolt
eV
1,60217733 10-19 J
Múltiplos y submúltiplos decimales
Factor
Prefijo
Símbolo
Factor
Prefijo
Símbolo
1018
exa
E
10-1
deci
d
1015
penta
P
10-2
centi
c
1012
tera
T
10-3
mili
m
109
giga
G
10-6
micro
u
106
mega
M
10-9
nano
n
103
kilo
k
10-12
pico
p
102
hecto
h
10-15
femto
f
101
deca
da
10-18
atto
a
EQUILIBRIO ESTATICO
El equilibrio de un sólido sometido a la acción de un
sistema de fuerzas coplanarias no paralelas se puede decir a
la estudio de dos sistemas de fuerzas paralelas , sin más que
tener en cuenta las componentes horizontales y verticales .
Se pueden aplicar ,los métodos
, a las componentes
horizontales y verticales por separado . Las dos condiciones
de equilibrio se expresarán en la forma :
1)
Fuerzas
La resultante o suma vectorial de todas las
fuerzas
aplicadas al cuerpo debe ser cero .
Equivale a decir que
la suma algebraica de
las fuerzas o de sus componentes
aplicadas
a
un
cuerpo en una dirección cualquiera debe
ser
cero :
a) La suma algebraica de las componentes horizontales es
cero; esto es ,
Fx = 0.
b) La suma algebraica de las componentes verticales es cero ;
esto es , Fy = 0.
Descomponiendo
cada
una
de
las
fuerzas
en
sus
proyecciones horizontal y vertical
se tendrán dos sistemas
de fuerzas paralelas mutuamente perpendiculares Así , pues ,
Fx = 0 y Fy = 0 .
2)
Momentos L a suma algebraica de los momentos de todas
las
fuerzas , con respecto a un eje
cualquiera perpendicular
al plano de las mismas
debe ser cero ( es decir
Un cuerpo esta en equilibrio respecto a la traslación
cuando esta en reposo o cuando se halla animado de un
movimiento rectilinio y uniforme .
Un cuerpo sobre el que actúa un sistema de fuerza esta
en equilibrio cuando dicho sistema - fuerzas aplicadas
simultáneamente - no produce cambio alguno ni en su
movimiento de traslación (rectilineo) ni en el de rotación .
Las fuerzas actuan en varias direcciones , suelen ser
conveniente resolverlas en componentes paralelos a un par de
ejes perpendiculares que simplificarán los cálculos. por
ejemplo, para las fuerzas en un solo plano , la técnica más
útil
es resdolverlas en componentes horizontales y
verticales.
CINEMATICA LINEAL. SISTEMAS DE REFERENCIA. DESCRIPCION
GRAFICA DEL
MOVIMIENTO LINEAL. DESPLAZAMIENTO. VELOCIDAD Y ACELERACION.
ECUACIONES DEL
MOVIMIENTO. MOVIMIENTO DE UNA DIMENSION CON ACELERACION
VARIABLE. ECUACION
DEL MOVIMIENTO UNIFORMEMENTE ACELERADO. ECUACION DEL
MOVIMIENTO EN CAIDA
LIBRE.
DINAMICA. CONCEPTO DE MASA Y FUERZA. LEVES DE LA
MECANICA. SISTEMA
INERCIAL DE REFERENCIA. METODOS ESTATICOS Y DINAMICOS PARA
MEDIR FUERZAS.
FUERZA DE ROZAMIENTO. LEY DE GRAVITACION UNIVERSAL. PESO Y
MASA. VARIACION
DE LA ACELERACION DE LA GRAVEDAD CON LA ALTURA. DIFERENTES
SISTEMAS DE
UNIDADES.
ESTATICA. EQUILIBRIO MECANICO. CONDICIONES DE
EQUILIBRIO.
MOVIMIENTO EN EL PLANO. DESPLAZAMIENTO. VELOCIDAD Y
ACELERACION.
ACELERACION NORMAL Y TANGENCIAL. MOVIMIENTO DE UN PROYECTIL.
MOVIMIENTO
CIRCULAR. DINAMICA DEL MOVIMIENTO CIRCULAR. FUERZA
CENTRIPETA. LEYES DE
KEPLER. MOVIMIENTO DE UNA CIRCUNFERENCIA VERTICAL. MOVIMIENTO
RELATIVOS.
SISTEMAS NO INERCIALES.
TRABAJO Y ENERGIA. DEFINICIONES. TEOREMA TRABAJO Y
ENERGIA. FUERZAS
CONSERVATIVAS Y NO CONSERVATIVAS. ENERGIA POTENCIAL. SISTEMAS
CONSERVATIVOS
EN UNA DIMENSION. ENERGIA POTENCIAL GRAVITATORIA. POTENCIA.
CANTIDAD DE MOVIENTO. DEFINICION. CONSERVACION DE LA
CANTIDAD DE
MOVIMIENTO. TEOREMA IMPULSO CANTIDAD DE MOVIENTO. CHOQUES.
COEFICIENTE DE
RESTITUCION. CHOQUE ELASTICO E INELASTICO.
MODULO 2
SISTEMAS DE PARTICULAS. DINAMICA DE UN SISTEMA DE
PARTICULAS. CENTRO
DE MASA. CANTIDAD DE MOVIMIENTO DE UN SISTEMA DE PARTICULAS.
SISTEMAS DE
ORDENADAS CON ORIGEN EN EL CENTRO DE MASA. CANTIDAD DE
MOVIMIENTO CON
REFERENCIA A ESE SISTEMA. ENERGIA CINETICA DE UN SISTEMA DE
PARTICULAS.
TEOREMA TRABAJO Y ENERGIA
CUERPO RIGIDO. MOVIMIENTO DE ROTACION. CINEMATICA DE LA
ROTACION.
ROTACION CON ACELERACION CONSTANTE. CANTIDADES ROTACIONALES
CON VECTORES.
RELACION ENTRE LA CARACTERISTICAS CINEMATICAS, LINEALES, Y
ANGULARES EN EL
MOVIMIENTO CIRCULAR. MOMENTO DE UNA FUERZA. EQUILIBRIO DE
ROTACIONES.
EJEMPLOS. DINAMICA DE LA ROTACION MOMENTO DE INERCIA.
CALCULO. RADIO DE
GIRO. TEOREMA DE STEINER. ENERGIA CINETICA. TRABAJO Y
POTENCIA PARA EL
MOVIMIENTO CIRCULAR.
MOVIMIENTO GENERAL DE UN CUERPO RIGIDO. MOVIMIENTO
CONVINADO DE
TRASLACION Y ROTACION. RODADURA SIN DESLIZAMIENTO. EJE
INSTANTANEO DE
ROTACION. ENERGIA CINETICA PARA LA ROTACION-TRASLACION
COMBINADA.
MOMENTO CINETICO. DEFINICION DE MOMENTO CINETICO DE UNA
PARTICULA.
MOMENTO DE UN SISTEMA DE PARTICULAS Y DE UN CUERPO RIGIDO.
TEOREMA
IMPULSION ANGULAR-MOMENTO CINETICO. CONSERVACION DE UN
MOMENTO CINETICO.
PRECESION. GIROSCOPICO.
MOVIMIENTO PERIODICO. MOVIMIENTO ARMONICO SIMPLE.
CINEMATICA, DINAMICA
Y CONSIDERACIONES ENERGETICAS DEL MAS. COMBINACION DE
MOVIMIENTOS
ARMONICOS. FIGURAS LISSANJOUS. MOVIMIENTO ARMONICO
AMORTIGUADO Y FORZADO.
RESONANCIA. PENDULO SIMPLE O MATEMATICO. MOVIMIENTO ARMONICO
DE ROTACION.
PENDULO FISICO Y DE TORSION. CENTRO DE OSCILACION.
ELASTICIDAD ESTATICA.ESFUERZOS Y DEFORMACIONES
ESPECIFICAS. RELACION
ESFUERZO-DEFORMACION. MODULO DE ELASTICIDAD. LEY DE HOOKE.
MODULO 3
CALOR Y TEMPERATURA. EQUILIBRIO TERMICO. CONCEPTO DE
CANTIDAD DE CALOR
Y TEMPERATURA. MEDIDADE TEMPERATURA. TERMOMETRO. ESCALAS
TERMOMETRICA.
DILATACION DE SOLIDOS Y LIQUIDOS. ESFUERZOS DE ORIGEN
TERMICO.
CALORIMETRIA. CAPACIDAD CALORIFICA Y CAPACIDAD CALORIFICA
ESPECIFICA.
MODULO 3
CALOR ESPECIFICO. CALOR ESPECIFICO MOLAR. CALORIMETROS Y
METODOS DE
MEDICION. CONDUCCION DEL CALOR. FLUJO ESTACIONARIOS DE CALOR.
EJEMPLOS.
TERMODINAMICA. EQUIVALENTE MECANICO DEL CALOR. CALOR,
TRABAJO Y
SISTEMA TERMODINAMICO. PRIMERA LEY DE LA TERMODINAMICA.
ENERGIA INTERNA.
DILATACION DE GACES. LEY DE BOYLE-MARIOTTE Y GUY LUSSAC.
GASES IDEALES.
TRANSFORMACIONES DE GASES IDEALES. ECUACIONES DE ESTADO DE UN
GAS IDEAL.
CAMBIOS ISOTERMICOS Y ADIABATICOS. GASES REALES.ISOTERMAS DE
UN GAS REAL.
DIAGRAMA DE ANDREWS. SUPERFICIE PVT PARA UN GAS REAL. TEORIA
CINETICA.
ECUACION DE VAN DER WAALS. MAQUINAS TERMICAS. PROCESOS
REVERSIBLES E
IRREVERSIBLES. CICLO CARNOT. ENUNCIADOS DE SEGUNDO PRINCIPIO
DE LA
TERMODINAMICA. TEOREMA DE CARNOT. ESCALA KELVIN DE
TEMPERTURA. ENTROPIA.
HIDROSTATICA. PRESION DE UN FLUIDO. LEY DE EQUILIBRIO.
PRINCIPIO DE
PASCAL. TEOREMA GENERAL DE LA HIDROSTATICA. PRINCIPIO DE
ARQUIMEDES.
MEDIDAS DE LA PRESION. BAROMETRO Y MANOMETRO. SUPERFICIE
LIBRE DE UN
LIQUIDO. TENSION SUPERFICIAL. COEFICIENTE DE TENSION
SUPERFICIAL. FORMACION
DE GOTAS. ELEVACION CAPILAR. EXCESO DE PRESION DE BURBUJAS.
HIDRODINAMICA. FLUJO ESTACIONARIO. ECUACION DE
CONTINUIDAD. TEOREMA
DE BERNOULLI. APLICACIONES. VISCOSIDAD. COEFICIENTE DE
VISCOSIDAD. FLUJOS
LAMINAR EN TUBOS CILINDRICOS. LEY DE POISEUILLE. LEY DE
STOKES.
SUSTENTACION DINAMICA. MOVIMIENTO TURBULENTO. RESISTENCIA DE
PRESION.
NUMERO DE REYNOLDS.
ESTATICA DE ROZAMIENTO
El rozamiento entre dos superficies en contacto ha sido
aprovechado por nuestros antepasados más remotos para hacer
fuego frotando maderas. En nuestra época, el rozamiento tiene
una gran importancia económica, se estima que si se le
prestase mayor atención se podría ahorrar muchísima energía y
recursos económicos.
Históricamente, el estudio del rozamiento comienza con
Leonardo da Vinci que dedujo las leyes que gobiernan el
movimiento de un bloque rectangular que desliza sobre una
superficie plana. Sin embargo, este estudio pasó
desapercibido.
En el siglo XVII Guillaume Amontons, físico francés,
redescubrió las leyes del rozamiento estudiando el
deslizamiento seco de dos superficies planas. Las
conclusiones de Amontons son esencialmente las que estudiamos
en los libros de Física General:



La fuerza de rozamiento se opone al movimiento de un
bloque que desliza sobre un plano.
La fuerza de rozamiento es proporcional a la fuerza
normal que ejerce el plano sobre el bloque.
La fuerza de rozamiento no depende del área aparente de
contacto.
El científico francés Coulomb añadió una propiedad más

Una vez empezado el movimiento, la fuerza de rozamiento
es independiente de la velocidad.
Explicación del origen del
rozamiento por contacto
La mayoría de las superficies, aún las que se consideran
pulidas son extremadamente rugosas a escala microscópica. Los
picos de las dos superficies que se ponen en contacto
determinan el área real de contacto que es una pequeña
proporción del área aparente de contacto (el área de la base
del bloque). El área real de contacto aumenta cuando aumenta
la presión (la fuerza normal) ya que los picos se deforman.
Los metales tienden a soldarse en frío, debido a las fuerzas
de atracción que ligan a las moléculas de una superficie con
las moléculas de la otra. Estas soldaduras tienen que
romperse para que el deslizamiento se presente. Además,
existe siempre la incrustación de los picos con los valles.
Este es el origen del rozamiento estático.
Cuando el bloque desliza sobre el plano, las soldaduras en
frío se rompen y se rehacen constantemente. Pero la cantidad
de soldaduras que haya en cualquier momento se reduce por
debajo del valor estático, de modo que el coeficiente de
rozamiento cinético es menor que el coeficiente de rozamiento
estático.
Finalmente, la presencia de aceite o de grasa en las
superficies en contacto evita las soldaduras al revestirlas
de un material inerte.
La explicación de que la fuerza de rozamiento es
independiente del área de la superficie aparente de contacto
es la siguiente:
En la figura, la superficie más pequeña de un bloque está
situada sobre un plano. En el dibujo situado arriba, vemos un
esquema de lo que se vería al microscopio: grandes
deformaciones de los picos de las dos superficies que están
en contacto. Por cada unidad de superficie del bloque, el
área de contacto real es relativamente grande (aunque esta es
una pequeña fracción de la superficie aparente de contacto,
es decir, el área de la base del bloque).
En la figura, la superficie más grande del bloque está
situada sobre el plano. El dibujo muestra ahora que las
deformaciones de los picos en contacto son ahora más pequeñas
por que la presión es más pequeña. Por tanto, un área
relativamente más pequeña está en contacto real por unidad de
superficie del bloque. Como el área aparente en contacto del
bloque es mayor, se deduce que el área real total de contacto
es esencialmente la misma en ambos casos.
Ahora bien, las investigaciones actuales que estudian el
rozamiento a escala atómica demuestran que la explicación
dada anteriormente es muy general y que la naturaleza de la
fuerza de rozamiento es muy compleja (Véase el artículo
titulado "Rozamiento a escala atómica" en la bibliografía de
este capítulo.
La fuerza normal
La fuerza normal, reacción del plano o fuerza que ejerce el
plano sobre el bloque depende del peso del bloque, la
inclinación del plano y de otras fuerzas que se ejerzan sobre
el bloque.
Supongamos que un bloque de
masa m está en reposo sobre
una superficie horizontal, las
únicas fuerzas que actúan
sobre él son el peso mg y la
fuerza y la fuerza normal N.
De las condiciones de
equilibrio se obtiene que la
fuerza normal N es igual al
peso mg
N=mg
Si ahora, el plano está inclinado un ángulo
, el bloque
está en equilibrio en sentido perpendicular al plano
inclinado por lo que la fuerza normal N es igual a la
componente del peso perpendicular al plano, N=mg·cos
Consideremos de nuevo el bloque sobre la superficie
horizontal. Si además atamos una cuerda al bloque que forme
un ángulo
con la horizontal, la fuerza normal deja de ser
igual al peso. La condición de equilibrio en la dirección
perpendicular al plano establece N=mg - F·sen
Fuerza de rozamiento estático
También existe una fuerza de rozamiento entre dos objetos que
no están en movimiento relativo.
Como vemos en la figura la fuerza F aplicada sobre el bloque
aumenta gradualmente, pero el bloque permanece en reposo.
Como la aceleración es cero la fuerza aplicada es igual y
opuesta a la fuerza de rozamiento estático Fe.
F=Fe
La máxima fuerza de rozamiento corresponde al instante en el
que el bloque está a punto de deslizar.
Fe
máx
eN
La constante de proporcionalidad
de rozamiento estático.
e
se denomina coeficiente
Los coeficientes de rozamiento estático y dinámico dependen
de las condiciones de preparación y de la naturaleza de las
dos superficies y son casi independientes del área de la
superficie de contacto.
Comportamiento de un cuerpo que
descansa sobre un plano horizontal
Dibujemos una gráfica en la que en el eje horizontal
representamos la fuerza F aplicada sobre el bloque y en el
eje vertical la fuerza de rozamiento.
1. Desde el origen hasta el punto A la fuerza F aplicada
sobre el bloque no es suficientemente grande como para
moverlo. Estamos en una situación de equilibrio estático
F= Fe
eN
En el punto A, la fuerza de rozamiento Fe alcanza
su máximo valor eN
F= Fe
máx
eN
2. Si la fuerza F aplicada se incrementa un poquito más, el
bloque comienza a moverse. La fuerza de rozamiento
disminuye rápidamente a un valor menor e igual a la
fuerza de rozamiento cinético, Fk k N
Si la fuerza F no cambia, punto B, y permanece
igual a Fe máx el bloque comienza moviéndose con una
aceleración
a=(F-Fk)/m
Si incrementamos la fuerza F, punto C, la fuerza
neta sobre el bloque F-Fk se incrementa y también se
incrementa la aceleración.
En el punto D, la fuerza F aplicada es igual a Fk
por lo que la fuerza neta sobre el bloque será
cero. El bloque se mueve con velocidad constante.
En el punto E, se anula la fuerza aplicada F, la
fuerza que actúa sobre el bloque es - Fk, la
aceleración es negativa y la velocidad decrece
hasta que el bloque se para
LA ESTÁTICA DE FLUIDOS
La estática de fluidos estudia el equilibrio de gases y
líquidos. A partir de los conceptos de densidad y de
presión se obtiene la ecuación fundamental de la
hidrostática, de la cual el principio de Pascal y el de
Arquímedes pueden considerarse consecuencias. El hecho
de que los gases, a diferencia de los líquidos, puedan
comprimirse hace que
el estudio de ambos tipos de fluidos tengan
características diferentes. En la atmósfera
fenómenos de presión y de empuje que pueden
estudiados de acuerdo con los principios de
de gases.
algunas
se dan los
ser
la estática
Se entiende por fluido un estado de la materia en el
que la forma de los cuerpos no es constante, sino que se
adapta a la del recipiente que los contiene. La materia
fluida puede ser trasvasada de un recipiente a otro, es
decir, tiene la capacidad de fluir. Los líquidos y los
gases corresponden a dos tipos diferentes de fluidos.
Los primeros tienen un volumen constante que no puede
mortificarse apreciablemente por compresión. Se dice por
ello que son fluidos incompresibles. Los segundos no
tienen un volumen propio, sino que ocupan el del
recipiente que los contiene; son fluidos compresibles
porque, a diferencia de los líquidos, sí pueden ser
comprimidos.
El estudio de los fluidos en equilibrio constituye el
objeto de la estática de fluidos, una parte de la física
que comprende la hidrostática o estudio de los líquidos
en equilibrio, y la aerostática o estudio de los gases
en equilibrio y en particular del aire.
LA DENSIDAD DE LOS CUERPOS
Densidad
Los cuerpos difieren por lo general en su masa y en su
volumen. Estos dos atributos físicos varían de un cuerpo
a otro, de modo que si consideramos cuerpos de la misma
naturaleza, cuanto mayor es el volumen, mayor es la masa
del cuerpo considerado. No obstante, existe algo
característico del tipo de materia que compone al cuerpo
en cuestión y que explica el porqué dos cuerpos de
sustancias diferentes que ocupan el mismo volumen no
tienen la misma masa o viceversa.
Aun cuando para cualquier sustancia la masa y el volumen
son directamente proporcionales, la relación de
proporcionalidad es diferente para cada sustancia. Es
precisamente la constante de proporcionalidad de esa
relación la que se conoce por densidad y se representa
por la letra griega r
m = cte · V
es decir:
m = r · V
Despejando r de la anterior ecuación resulta:
ecuación que facilita la definición de r y también su
significado físico.
La densidad r de una sustancia es la masa que
corresponde a un volumen unidad de dicha sustancia. Su
unidad en el SI es el cociente entre la unidad de masa y
la del volumen, es decir kg/m3 o kg · m-3.
A diferencia de la masa o el volumen, que dependen de
cada objeto, su cociente depende solamente del tipo de
material de que está constituido y no de la forma ni del
tamaño de aquél. Se dice por ello que la densidad es una
propiedad o atributo característico de cada sustancia.
En los sólidos la densidad es aproximadamente constante,
pero en los líquidos, y particularmente en los gases,
varía con las condiciones de medida. Así en el caso de
los líquidos se suele especificar la temperatura a la
que se refiere el valor dado para la densidad y en el
caso de los gases se ha de indicar, junto con dicho
valor, la presión.
Densidad y peso específico
La densidad está relacionada con el grado de acumulación
de materia (un cuerpo compacto es, por lo general, más
denso que otro más disperso), pero también lo está con
el peso. Así, un cuerpo pequeño que es mucho más pesado
que otro más grande es también mucho más denso. Esto es
debido a la relación P = m · g existente entre masa y
peso. No obstante, para referirse al peso por unidad de
volumen la física ha introducido el concepto de peso
específico pe que se define como el cociente entre el
peso P de un cuerpo y su volumen:
El peso específico representa la fuerza con que la
Tierra atrae a un volumen unidad de la misma sustancia
considerada.
La relación entre peso específico y densidad es la misma
que la existente entre peso y masa. En efecto:
siendo g la aceleración de la gravedad.
La unidad del peso específico en el SI es el N/m3 o N ·
m-3.
Densidad relativa
La densidad relativa de una sustancia es el cociente
entre su densidad y la de otra sustancia diferente que
se toma como referencia o patrón:
Para sustancias líquidas se suele tomar como sustancia
patrón el agua cuya densidad a 4 ºC es igual a 1 000
kg/m3. Para gases la sustancia de referencia la
constituye con frecuencia el aire que a 0 ºC de
temperatura y 1 atm de presión tiene una densidad de
1,293 kg/m3. Como toda magnitud relativa, que se obtiene
como cociente entre dos magnitudes iguales, la densidad
relativa carece de unidades físicas.
EL FUNDAMENTO DEL DENSÍMETRO La determinación de densidades
de líquidos tiene importancia no sólo en la física, sino
también en el mundo del comercio y de la industria. Por el
hecho de ser la densidad una propiedad característica -cada
sustancia tiene una densidad diferente- su valor puede
emplearse para efectuar una primera comprobación del grado de
pureza de una sustancia líquida.
El densímetro es un sencillo aparato que se basa en el
principio de Arquímedes. Es, en esencia, un flotador de
vidrio con un lastre de mercurio en su parte inferior
-que le hace sumergirse parcialmente en el líquido- y un
extremo graduado directamente en unidades en densidad. El
nivel del líquido marca sobre la escala el valor de su
densidad.
En el equilibrio, el peso P del densímetro será igual al
empuje E:
P = E
Si se admite, para simplificar el razonamiento, que su forma
es la de un cilindro, E será igual, de acuerdo con el
principio de Arquímedes, al peso del volumen V del líquido
desalojado, es decir:
donde h es la altura sumergida y S la superficie de la base
del cilindro.
Dado que el peso del densímetro es igual a su masa m por la
gravedad g, igualándolo al empuje resulta:
es decir:
donde m y S son constantes, luego es inversamente
proporcional a la altura sumergida. Midiendo alturas
sumergidas pueden, por tanto, determinarse densidades.La
determinación de la pureza de la leche de vaca es una de las
aplicaciones industriales del densímetro.
LA PRESIÓN
El concepto de presión
Cuando se ejerce una fuerza sobre un cuerpo deformable,
los efectos que provoca dependen no sólo de su
intensidad, sino también de cómo esté repartida sobre la
superficie del cuerpo. Así, un golpe de martillo sobre
un clavo bien afilado hace que penetre mas en la pared
de lo que lo haría otro clavo sin punta que recibiera el
mismo impacto. Un individuo situado de puntillas sobre
una capa de nieve blanda se hunde, en tanto que otro de
igual peso que calce raquetas, al repartir la fuerza
sobre una mayor superficie, puede caminar sin
dificultad.
El cociente entre la intensidad F de la fuerza aplicada
perpendicularmente sobre una superficie dada y el área S
de dicha superficie se denomina presión:
La presión representa la intensidad de la fuerza que se
ejerce sobre cada unidad de área de la superficie
considerada. Cuanto mayor sea la fuerza que actúa sobre
una superficie dada, mayor será la presión, y cuanto
menor sea la superficie para una fuerza dada, mayor será
entonces la presión resultante.
La presión en los fluidos
El concepto de presión es muy general y por ello puede
emplearse siempre que exista una fuerza actuando sobre
una superficie. Sin embargo, su empleo resulta
especialmente útil cuando el cuerpo o sistema sobre el
que se ejercen las fuerzas es deformable. Los fluidos no
tienen forma propia y constituyen el principal ejemplo
de aquellos casos en los que es más adecuado utilizar el
concepto de presión que el de fuerza.
Cuando un fluido está contenido en un recipiente, ejerce
una fuerza sobre sus paredes y, por tanto, puede
hablarse también de presión. Si el fluido está en
equilibrio las fuerzas sobre las paredes son
perpendiculares a cada porción de superficie del
recipiente, ya que de no serlo existirían componentes
paralelas que provocarían el desplazamiento de la masa
de fluido en contra de la hipótesis de equilibrio. La
orientación de la superficie determina la dirección de
la fuerza de presión, por lo que el cociente de ambas,
que es precisamente la presión, resulta independiente de
la dirección; se trata entonces de una magnitud escalar.
Unidades de presión
En el SI la unidad de presión es el pascal, se
representa por Pa y se define como la presión
correspondiente a una fuerza de un newton de intensidad
actuando perpendicularmente sobre una superficie plana
de un metro cuadrado. 1 Pa equivale, por tanto, a 1
N/m2.
Existen, no obstante, otras unidades de presión que sin
corresponder a ningún sistema de unidades en particular
han sido consagradas por el uso y se siguen usando en la
actualidad junto con el pascal. Entre ellas se
encuentran la atmósfera y el bar.
La atmósfera (atm) se define como la presión que a 0 ºC
ejercería el peso de una columna de mercurio de 76 cm de
altura y 1 cm2 de sección sobre su base.
Es posible calcular su equivalencia en N/m2 sabiendo que
la densidad del mercurio es igual a 13,6 · 103 kg/m3 y
recurriendo a las siguientes relaciones entre
magnitudes:
Peso (N) = masa (kg) · 9,8 m/s2
Masa = volumen · densidad
Como el volumen del cilindro que forma la columna es
igual a la superficie de la base por la altura, se
tendrá:
es decir: 1 atm = 1,013 · 105 Pa.
El bar es realmente un múltiple del pascal y equivale a
105 N/m2. En meteorología se emplea con frecuencia el
milibar (mb) o milésima parte del bar · 1 mb = 102 Pa.
1 atm = 1 013 mb
LA HIDROSTÁTICA
La ecuación fundamental de la hidrostática
Todos los líquidos pesan, por ello cuando están
contenidos en un recipiente las capas superiores oprimen
a las inferiores, generándose una presión debida al
peso. La presión en un punto determinado del líquido
deberá depender entonces de la altura de la columna de
líquido que tenga por encima suyo.
Considérese un punto cualquiera del líquido que diste
una altura h de la superficie libre de dicho líquido. La
fuerza del peso debido a una columna cilíndrica de
líquido de base S situada sobre él puede expresarse en
la forma
Fpeso = mg = · V · g = · g · h · S
siendo V el volumen de la columna y r la densidad del
líquido. Luego la presión debida al peso vendrá dada
por:
La presión en un punto
La definición de la presión como cociente entre la
fuerza y la superficie se refiere a una fuerza constante
que actúa perpendicularmente sobre una superficie plana.
En los líquidos en equilibrio las fuerzas asociadas a la
presión son en cada punto perpendiculares a la
superficie del recipiente, de ahí que la presión sea
considerada como una magnitud escalar cociente de dos
magnitudes vectoriales de igual dirección: la fuerza y
el vector superficie. Dicho vector tiene por módulo el
área y por dirección la perpendicular a la superficie.
Cuando la fuerza no es constante, sino que varía de un
punto a otro de la superficie S considerada, tiene
sentido hablar de la presión en un punto dado. Para
definirla se considera un elemento de superficie DS que
rodea al punto; si dicho elemento reduce enormemente su
extensión, la fuerza DF que actúa sobre él puede
considerarse constante. En tal caso la presión en el
punto considerado se definirá en la forma matemática
esta expresión, que es la derivada de F respecto de S,
proporciona el valor de la presión en un punto y puede
calcularse si se conoce la ecuación matemática que
indica cómo varía la fuerza con la posición.
Si la fuerza es variable y F representa la resultante de
todas las fuerzas que actúan sobre la superficie S la
fórmula
define, en este caso, la presión media.
Si sobre la superficie libre se ejerciera una presión
exterior adicional po, como la atmosférica por ejemplo,
la presión total p en el punto de altura h sería:
Esta ecuación puede generalizarse al caso de que se
trate de calcular la diferencia de presiones Dp entre
dos puntos cualesquiera del interior del líquido
situados a diferentes alturas, resultando:
es decir:
que constituye la llamada ecuación fundamental de la
hidrostática.
Esta ecuación indica que para un líquido dado y para una
presión exterior constante la presión en el interior
depende únicamente de la altura. Por tanto, todos los
puntos del líquido que se encuentren al mismo nivel
soportan igual presión. Ello implica que ni la forma de
un recipiente ni la cantidad de líquido que contiene
influyen en la presión que se ejerce sobre su fondo, tan
sólo la altura de líquido. Esto es lo que se conoce como
paradoja hidrostática, cuya explicación se deduce a modo
de consecuencia de la ecuación fundamental.
El principio de Pascal y sus aplicaciones
La presión aplicada en un punto de un líquido contenido
en un recipiente se transmite con el mismo valor a cada
una de las partes del mismo.
Este enunciado, obtenido a partir de observaciones y
experimentos por el físico y matemático francés Blas
Pascal (1623-1662), se conoce como principio de Pascal.
El principio de Pascal puede ser interpretado como una
consecuencia de la ecuación fundamental de la
hidrostática y del carácter incompresible de los
líquidos. En esta clase de fluidos la densidad es
constante, de modo que de acuerdo con la ecuación p = po
+ r· g · h si se aumenta la presión en la superficie
libre, por ejemplo, la presión en el fondo ha de
aumentar en la misma medida, ya que r · g · h no varía
al no hacerlo h.
La prensa hidráulica constituye la aplicación
fundamental del principio de Pascal y también un
dispositivo que permite entender mejor su significado.
Consiste, en esencia, en dos cilindros de diferente
sección comunicados entre sí, y cuyo interior está
completamente lleno de un líquido que puede ser agua o
aceite. Dos émbolos de secciones diferentes se ajustan,
respectivamente, en cada uno de los dos cilindros, de
modo que estén en contacto con el líquido. Cuando sobre
el émbolo de menor sección S1 se ejerce una fuerza F1 la
presión p1 que se origina en el líquido en contacto con
él se transmite íntegramente y de forma instantánea a
todo el resto del líquido; por tanto, será igual a la
presión p2 que ejerce el líquido sobre el émbolo de
mayor sección S2, es decir:
p1 = p2
con lo que:
y por tanto:
Si la sección S2 es veinte veces mayor que la S1, la
fuerza F1 aplicada sobre el émbolo pequeño se ve
multiplicada por veinte en el émbolo grande.
La prensa hidráulica es una máquina simple semejante a
la palanca de Arquímedes, que permite amplificar la
intensidad de las fuerzas y constituye el fundamento de
elevadores, prensas, frenos y muchos otros dispositivos
hidráulicos de maquinaria industrial.
El principio de los vasos comunicantes
Si se tienen dos recipientes comunicados y se vierte un
líquido en uno de ellos en éste se distribuirá entre
ambos de tal modo que, independientemente de sus
capacidades, el nivel de líquido en uno y otro
recipiente sea el mismo. Éste es el llamado principio de
los vasos comunicantes, que es una consecuencia de la
ecuación fundamental de la hidrostática.
Si se toman dos puntos A y B situados en el mismo nivel,
sus presiones hidrostáticas han de ser las mismas, es
decir:
luego si pA = pB necesariamente las alturas hA y hB de
las respectivas superficies libres han de ser idénticas
hA = hB.
Si se emplean dos líquidos de diferentes densidades y no
miscibles, entonces las alturas serán inversamente
proporcionales a las respectivas densidades. En efecto,
si pA = pB, se tendrá:
Esta ecuación permite, a partir de la medida de las
alturas, la determinación experimental de la densidad
relativa de un líquido respecto de otro y constituye,
por tanto, un modo de medir densidades de líquidos no
miscibles si la de uno de ellos es conocida.
APLICACIÓN DE LA ECUACIÓN FUNDAMENTAL DE LA HIDROSTÁTICA
Un submarinista se sumerge en el mar hasta alcanzar una
profundidad de 100 m. Determinar la presión a la que está
sometido y calcular en cuántas veces supera a la que
experimentaría en el exterior, sabiendo que la densidad del
agua del mar es de 1 025 kg/m3.
De acuerdo con la ecuación fundamental de la hidrostática:
Considerando que la presión po en el exterior es de una
atmósfera (1 atm = 1,013 · 105 Pa), al sustituir los datos en
la anterior ecuación resulta:
p = 1,013 · 105 + 1025 · 9,8 · 100 = 11,058 · 105 Pa
El número de veces que p es superior a la presión exterior po
se obtiene hallando el cociente entre ambas:
APLICACIÓN DEL PRINCIPIO DE PASCAL
El elevador hidráulico de un garaje funciona mediante una
prensa hidráulica conectada a una toma de agua de la red
urbana que llega a la máquina con una presión de 5 · 105
N/m2. Si el radio del émbolo es de 20 cm y el rendimiento es
de un 90 %, determinar cuál es el valor en toneladas de la
carga que como máximo puede levantar el elevador.
De acuerdo con el principio de Pascal:
p1 = p2
que para una prensa hidráulica se transforma en:
En este caso el dato que correspondería al émbolo pequeño de
la prensa se facilita en forma de presión, de modo que
combinando las ecuaciones anteriores se tiene:
Como el rendimiento es del 90 % el valor efectivo de la carga
máxima expresado en newtons será:
Una tonelada métrica equivale al peso de un cuerpo de 1 000
kg de masa, es decir:
luego:
EQUILIBRIO DE SÓLIDOS EN EL ...
Empuje hidrostático: principio de Arquímedes
Los cuerpos sólidos sumergidos en un líquido
experimentan un empuje hacia arriba. Este fenómeno, que
es el fundamento de la flotación de los barcos, era
conocido desde la más remota antigüedad, pero fue el
griego Arquímedes (287-212 a. de C.) quien indicó cuál
es la magnitud de dicho empuje. De acuerdo con el
principio que lleva su nombre, todo cuerpo sumergido
total o parcialmente en un líquido experimenta un empuje
vertical y hacia arriba igual al peso del volumen de
líquido desalojado.
Aun cuando para llegar a esta conclusión Arquímedes se
apoyó en la medida y experimentación, su famoso
principio puede ser obtenido como una consecuencia de la
ecuación fundamental de la hidrostática. Considérese un
cuerpo en forma de paralelepípedo, las longitudes de
cuyas aristas valen a, b y c metros, siendo c la
correspondiente a la arista vertical. Dado que las
fuerzas laterales se compensan mutuamente, sólo se
considerarán las fuerzas sobre las caras horizontales.
La fuerza F1 sobre la cara superior estará dirigida
hacia abajo y de acuerdo con la ecuación fundamental de
la hidrostática (ec. 5.5) su magnitud se podrá escribir
como
siendo S1 la superficie de la cara superior y h1 su
altura respecto de la superficie libre del líquido.
La fuerza F2 sobre la cara inferior estará dirigida
hacia arriba y, como en el caso anterior, su magnitud
vendrá dada por:
La resultante de ambas representará la fuerza de empuje
hidrostático E.
pero, dado que S1 = S2 = S y h2 = h1 + c, resulta:
que es precisamente el valor del empuje predicho por
Arquímedes en su principio, ya que V = c · S es el
volumen del cuerpo, r la densidad del líquido, m = r · V
la masa del liquido desalojado y finalmente m · g es el
peso de un volumen de líquido igual al del cuerpo
sumergido.
Equilibrio de los cuerpos sumergidos
De acuerdo con el principio de Arquímedes, para que un
cuerpo sumergido en un líquido esté en equilibrio, la
fuerza de empuje E y el peso P han de ser iguales en
magnitudes y, además, han de aplicarse en el mismo
punto. En tal caso la fuerza resultante R es cero y
también lo es el momento M, con lo cual se dan las dos
condiciones de equilibrio. La condición E = P equivale
de hecho a que las densidades del cuerpo y del líquido
sean iguales. En tal caso el equilibrio del cuerpo
sumergido es indiferente.
Si el cuerpo no es homogéneo, el centro de gravedad no
coincide con el centro geométrico, que es el punto en
donde puede considerarse aplicada la fuerza de empuje.
Ello significa que las fuerzas E y P forman un par que
hará girar el cuerpo hasta que ambas estén alineadas.
Equilibrio de los cuerpos flotantes
Si un cuerpo sumergido sale a flote es porque el empuje
predomina sobre el peso (E>P). En el equilibrio ambas
fuerzas aplicadas sobre puntos diferentes estarán
alineadas; tal es el caso de las embarcaciones en aguas
tranquilas, por ejemplo. Si por efecto de una fuerza
lateral, como la producida por un golpe de mar, el eje
vertical del navío se inclinara hacia un lado, aparecerá
un par de fuerzas que harán oscilar el barco de un lado
a otro. Cuanto mayor sea el momento M del par, mayor
será la estabilidad del navío, es decir, la capacidad
para recuperar la verticalidad. Ello se consigue
diseñando convenientemente el casco y repartiendo la
carga de modo que rebaje la posición del centro de
gravedad, con lo que se consigue aumentar el brazo del
par.
LA ESTÁTICA DE LOS GASES
La aerostática frente a la hidrostática
Desde un punto de vista mecánico, la diferencia
fundamental entre líquidos y gases consiste en que estos
últimos pueden ser comprimidos. Su volumen, por tanto,
no es constante y consiguientemente tampoco lo es su
densidad. Teniendo en cuenta el papel fundamental de
esta magnitud física en la estática de fluidos, se
comprende que el equilibrio de los gases haya de
considerarse separadamente del de los líquidos.
Así, la ecuación fundamental de la hidrostática no puede
ser aplicada a la aerostática. El principio de Pascal,
en el caso de los gases, no permite la construcción de
prensas hidráulicas. El principio de Arquímedes conserva
su validez para los gases y es el responsable del empuje
aerostático, fundamento de la elevación de los globos y
aeróstatos. Sin embargo, y debido a la menor densidad de
los gases, en iguales condiciones de volumen del cuerpo
sumergido, el empuje aerostático es considerablemente
menor que el hidrostático.
La compresibilidad de los gases. Ley de Boyle.
El volumen del gas contenido en un recipiente se reduce
si se aumenta la presión. Esta propiedad que presentan
los gases de poder ser comprimidos se conoce como
compresibilidad y fue estudiada por el físico inglés
Robert Boyle (1627-1691).
Si se dispone de un cilindro con un émbolo móvil que
puede modificar el volumen de aquél y se introduce un
gas en su interior, el volumen ocupado por el gas
variará con la presión del émbolo de tal modo que su
producto se mantiene constante si la temperatura es
constante durante el experimento. Es decir:
Ello significa que a temperatura constante la presión y
el volumen de un gas son magnitudes inversamente
proporcionales
y por tanto la representación gráfica de p frente a V
corresponde a una hipérbola equilátera.
Este resultado se conoce como ley de Boyle y describe de
forma aproximada el comportamiento de un gas en un
amplio rango de presiones y volúmenes. No obstante, a
temperaturas elevadas o a presiones elevadas, para las
cuales el gas se aproxima bastante al estado líquido, la
ley de Boyle deja de cumplirse con una precisión
razonable.
La presión atmosférica
Del mismo modo que existe una presión hidrostática en
los líquidos asociada al peso de unas capas de líquido
sobre otras, las grandes masas gaseosas pueden dar lugar
a presiones considerables debidas a su propio peso. Tal
es el caso de la atmósfera. La presión del aire sobre
los objetos contenidos en su seno se denomina presión
atmosférica.
La ley de variación de la presión atmosférica con la
altura es mucho más complicada que la descrita por la
ecuación fundamental de la hidrostática p = po + r g h.
Al tratarse de un fluido compresible, la densidad no es
constante, sino que varía con la presión; pero además,
para variaciones importantes de la altura el valor de g
tampoco se mantiene constante. Esta dependencia mutua de
las variables que aparecen en la anterior ecuación hace
que el cálculo preciso de la presión atmosférica en un
punto determinado sea una tarea compleja que proporciona
tan sólo resultados aproximados.
La primera comprobación experimental de la existencia de
una presión asociada al aire fue efectuada por
Evangelista Torricelli (1608-1647). El experimento de
Torricelli consistió en llenar de mercurio un tubo de
vidrio de más de un metro de largo, cerrarlo
provisionalmente e invertirlo sumergiéndolo en una gran
cubeta con mercurio. Cuando abrió el extremo del tubo
sumergido observó que éste sólo se vaciaba en parte,
quedando en su interior una columna de mercurio de unos
setenta y seis centímetros.
Este resultado fue interpretado como una prueba de que
la presión del peso del aire actuando sobre la
superficie libre del mercurio de la cubeta era capaz de
soportar el peso de la columna. En el espacio restante
del tubo se había producido el primer vacío de la
historia de la física que se conoce como vacío de
Torricelli. La presión correspondiente a una columna de
mercurio de 760 mm de altura define, precisamente, la
atmósfera (atm) como unidad de presión.
Además de con la altura, la presión atmosférica varía
con la temperatura y con la humedad y, en general, con
el estado del tiempo, por lo que constituye una magnitud
decisiva en el análisis y en la predicción
meteorológicos. Las primeras variaciones de la presión
atmosférica de un día a otro fueron observadas por el
propio Torricelli con su dispositivo, que fue precursor
de los actuales barómetros.
Manómetros y barómetros
Un manómetro es un aparato que sirve para medir la
presión de los gases contenidos en recipientes cerrados.
Existen, básicamente, dos tipos de manómetros: los de
líquidos y los metálicos.
Los manómetros de líquidos emplean, por lo general,
mercurio que llena un tubo en forma de J. El tubo puede
estar o abierto por ambas ramas o abierto por una sola.
En ambos casos la presión se mide conectando al
recipiente que contiene el gas el tubo por su rama
inferior y abierta y determinando el desnivel h de la
columna de mercurio entre ambas ramas. Si el manómetro
es de tubo abierto entonces es necesario tomar en cuenta
la presión atmosférica po en la ecuación p = po ± rgh.
Si es de tubo cerrado, la presión vendrá dada
directamente por p = rgh. Los manómetros de este segundo
tipo permiten, por sus características, la medida de
presiones elevadas.
En los manómetros metálicos la presión del gas da lugar
a deformaciones en una cavidad o tubo metálico. Estas
deformaciones se transmiten a través de un sistema
mecánico a una aguja que marca directamente la presión
del gas sobre una escala graduada.
El barómetro es el aparato con el que se mide la presión
atmosférica. Como en el caso de los manómetros, los hay
también de mercurio y metálicos. Los primeros se basan
en el dispositivo utilizado por Torricelli en sus
experimentos. El llamado barómetro de fortín es, de
hecho, una reproducción mejorada del aparato de
Torricelli. Su cubeta posee un fondo compuesto de un
material flexible, por lo que puede ser alterado
mediante un tornillo auxiliar con el fin de conseguir
ajustar el nivel del mercurio de la cubeta al cero de la
escala graduada cada vez que se efectúa una medida. Los
barómetros de sifón son simples manómetros de tubo
cerrado en los cuales la rama corta del tubo en J hace
las veces de cubeta y la rama larga de tubo de
Torricelli.
Los barómetros metálicos o aneroides constan de una caja
metálica de paredes relativamente elásticas, en cuyo
interior se ha efectuado el vacío. Un resorte metálico
hace que las paredes de la caja estén separadas. En su
ausencia dichas paredes tenderían a aproximarse por
efecto de la presión exterior. Por igual procedimiento
variaciones en la presión atmosférica producen cambios
en la forma de la caja que se transmiten al resorte y
éste los indica, a través de un mecanismo de
amplificación, sobre una escala graduada en unidades de
presión. Los barómetros metálicos pueden mortificarse de
forma que sus resultados queden registrados en un papel.
De este modo se puede disponer de información sobre cómo
varía la presión atmosférica con el tiempo.
APLICACIÓN DEL PRINCIPIO DE ARQUÍMEDES
Un globo de goma tiene 8 g de masa cuando está vacío. Para
conseguir que se eleve se infla con gas ciudad. Sabiendo que
la densidad del aire es de 1,29 kg/m3 y la del gas ciudad
0,53 kg/m3 determinar el volumen que, como mínimo, ha de
alcanzar el globo para que comience a elevarse.
Para que el globo inicie el ascenso, la fuerza del empuje ha
de ser superior a la del peso:
E > P
En virtud del principio de Arquímedes:
ya que en este caso el fluido desalojado es el aire.
Por otra parte, el peso P será la suma del peso del globo más
el peso del gas ciudad que corresponde al volumen V, es
decir:
Por tanto:
es decir:
El volumen mínimo será, por tanto, de 10,5 litros.