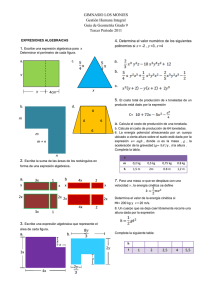
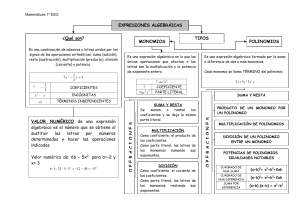
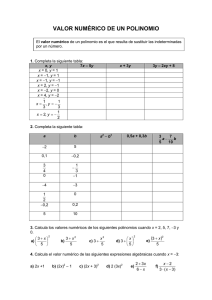
Servicio 2: Desarrollo de contenidos pedagógicos y educativos La innovación educativa para las instituciones educativas de Fe y Alegría Colombia. Ambiente Cualificar. Formación de docentes y equipos de dirección. Del lenguaje numérico al literal Área: Matemáticas Guía N°: 73 Duración: 13 horas Año: 2019 Meta (s) de Aprendizaje: Explico fenómenos de la vida real que involucran variación y cambio, selecciono correctamente reglas generales para hacer deducciones y resuelvo problemas de la cotidianidad y distintos campos disciplinares basado en la investigación realizada través de herramientas digitales y establezco la pertinencia y utilidad de la solución adoptada. Preguntas Esenciales: ¿Como las expresiones algebraicas me permiten comprender situaciones de mi contexto que involucran el uso de sumas y restas? ¿Cómo crees que las expresiones algebraicas ayudan a ciencias diferentes a la matemática (física, química, astronomía entre otras), para dar respuesta a interrogantes y teorías propias de esas disciplinas? ¿Cómo los programas creados para cálculos numéricos y modelación le han ayudado a los científicos de la NASA y a científicos de otras especialidades, a cumplir con sus proyectos, como por ejemplo llevar un robot a marte? ¿En qué situaciones puede surgir la necesidad de expresar un problema a través de expresiones algebraicas? Evidencias Construyo expresiones algébricas equivalentes a una expresión algebraica dada. Grafica la información que brinda un enunciado o situación por medio de expresiones algebraicas. Utiliza herramientas tecnológicas para realizar ejercicios de aplicación de expresiones algebraicas. Comunica información por medio de expresiones algebraicas. Infiere a partir de una gráfica compuesta por varias figuras, y conociendo algunas medidas, la expresión algebraica que la representa. Actividad 1 Actividad 2 Actividad 3 Actividad 4 Actividad 5 Actividad 6 Desarrollando mis competencias ¿Cuánto sé? Amplio mis conocimientos Aplico lo aprendido Aprendo y me divierto Descompongo expresiones Servicio 2: Desarrollo de contenidos pedagógicos y educativos La innovación educativa para las instituciones educativas de Fe y Alegría Colombia. Ambiente Cualificar. Formación de docentes y equipos de dirección. Actividad 1: desarrollando mis competencias. Sabías que… El lenguaje algebraico sirve para expresar situaciones relacionadas con la vida cotidiana, utilizando letras y números de forma combinada. La realización de estas operaciones ha de hacerse al principio paso a paso, pero después se agilizarán y simplificarán las distintas fases en la resolución de ecuaciones. El estudio de las expresiones algebraicas fomentará la agilidad en las operaciones aritméticas con números naturales y enteros, así como el empleo de técnicas de resolución por tanteo, ensayo-error y específicas, como la transposición y reducción de términos. Una expresión algebraica es una combinación de números y letras relacionadas por los signos de las operaciones aritméticas. Las letras se llaman variables, incógnitas o indeterminadas. Ejemplo: Longitud de la circunferencia: = 2 , donde es el radio de la circunferencia. Área del cuadrado: = 2, donde es el lado del cuadrado. Volumen del cubo: = 3, donde es la arista del cubo. Expresiones algebraicas1. En la vida cotidiana puedes encontrarte con expresiones como: a) Un número cualquiera b) El doble de un número c) La mitad de una cantidad d) Ya tengo el triple de la edad de mi hijo 1. Como ves, aunque todas se refieren a un número, ninguna lo presenta, entonces, ¿cómo podrías representar una cantidad que desconoces? Un número cualquiera, que no conozco, lo puedo expresar con una letra cualquiera, por ejemplo M. Si eso es así, aplícalo a la siguiente situación: ¿Cómo calculas la mitad de 10? _____________________________ http://aprende.colombiaaprende.edu.co/sites/default/files/naspublic/ContenidosAprende r/G_8/M/MG/MG_M_G08_U02_L01.pdf 1 Servicio 2: Desarrollo de contenidos pedagógicos y educativos La innovación educativa para las instituciones educativas de Fe y Alegría Colombia. Ambiente Cualificar. Formación de docentes y equipos de dirección. ¿Cómo calculas el triple de 10? ____________________________ ¿Cómo calculas el doble de 10? ____________________________ Pero si no sabemos que el número es el 10, y por ello lo reemplazamos por una letra, por ejemplo, la M, ¿cómo expresarías las operaciones anteriores? ¿Cómo calculas la mitad de M? ___________________________ ¿Cómo calculas el triple de M? ___________________________ ¿Cómo calculas el doble de M? ___________________________ 2. Escribe las expresiones algebraicas correspondientes La suma de tres números consecutivos. La suma de tres números pares consecutivos Área de un cuadrado de lado Área de un triángulo de base y altura Perímetro de un rectángulo de lados y . 3. El largo y ancho de una piscina son datos desconocidos, pero se sabe que el largo es el doble que el ancho. Escribe las expresiones algebraicas que dan el perímetro y el área de la piscina Enlaces de interés: Ver los siguientes videos y realiza un resumen sobre el lenguaje algebraico. https://www.youtube.com/watch?v=z902TyTcC2Y Servicio 2: Desarrollo de contenidos pedagógicos y educativos La innovación educativa para las instituciones educativas de Fe y Alegría Colombia. Ambiente Cualificar. Formación de docentes y equipos de dirección. Actividad 2: ¿Cuánto sé? Recordemos que: Una expresión algebraica es un conjunto de números y letras (variables) que se relacionan con los signos de las operaciones aritméticas, donde las letras representan cantidades desconocidas. En una expresión algebraica las letras también se denominan variables, ya que al ser cantidades desconocidos pueden tomar cualquier valor. Por el contrario, aquello valores que son conocidos dentro de la expresión, se llaman constantes, ya que son valores dados, así: en las expresiones 1. Con base en lo anterior resuelve el siguiente ejercicio: En la siguiente expresión algebraica identifica cuáles son las constantes, cuáles las variables y cuáles son los signos de las operaciones aritméticas que se encuentra en la expresión algebraica. Escribe tus respuestas dentro de los recuadros de la imagen teniendo en cuenta lo que señalan las flechas en la misma 2. En las expresiones algebraicas que se presentan en la siguiente tabla, identifica las variables, las constantes, y las operaciones que hay en las expresiones. Escríbelas en los espacios de la tabla. Expresión Variables Constantes Operaciones que hay en la Servicio 2: Desarrollo de contenidos pedagógicos y educativos La innovación educativa para las instituciones educativas de Fe y Alegría Colombia. Ambiente Cualificar. Formación de docentes y equipos de dirección. algebraica 3a +4 y expresión ab-4c+ 3xy-5y+2+3x -2a +x +4cd+3ac 3abcxyz 3. Ahora responde: a) ¿Qué características tienen las letras que se presentan en una expresión algebraica? b) De acuerdo con sus características, dichas letras reciben el nombre de ____________. c) Aquellas magnitudes que representan cantidades conocidas se denominan ___________ Clasificación y grado de los polinomios algebraicos Los polinomios algebraicos se clasifican en las siguientes categorías, así: Monomio Es una expresión algebraica que representa el producto de un número por una o varias variables, elevadas a distintos exponentes. Partes del monomio: 4. Del monomio - 4 5 2 9 , identifica cada una de las partes de este. Para ello escribe cada una de las partes dentro del siguiente cuadro, en la fila que corresponda. Partes del monomio monomio - 4 5 2 9 Signo Coeficiente numérico Parte literal Exponentes Para una mejor comprensión de los elementos del monomio, veamos los siguientes ejemplos: Servicio 2: Desarrollo de contenidos pedagógicos y educativos La innovación educativa para las instituciones educativas de Fe y Alegría Colombia. Ambiente Cualificar. Formación de docentes y equipos de dirección. http:/ /tananyag.geomatech.hu/m/2137469 Además si en la expresión algebraica la parte literal no tiene exponente o coeficiente, es porque ambos valores son iguales a uno. Polinomios Se puede definir como: Expresión algebraica formada por la suma o la resta de dos o más monomios, los cuales reciben el nombre de términos algebraicos. Ejemplos: Están conformados por términos algebraicos, los cuales están separados por el signo más (+) o el signo menos (-). Su clasificación depende del número de términos que tenga, ejemplo: 5a2b+3ab= binomio 3x5 + 4xy3z4 - 5x5y= Trinomio Lo que significa que en este caso tenemos un polinomio de dos términos, y un polinomio de tres términos respectivamente. Para la clasificación de los polinomios utilizamos los sufijos: mono = un término, bi = 2 términos, tri = tres términos, y terminamos con la palabra nomio. Cuando hay más de tres términos se le llama polinomio, simplemente. 5. Ahora resuelve: Servicio 2: Desarrollo de contenidos pedagógicos y educativos La innovación educativa para las instituciones educativas de Fe y Alegría Colombia. Ambiente Cualificar. Formación de docentes y equipos de dirección. Completa la siguiente tabla, escribiendo los datos que se solicitan en cada columna de la tabla. En la columna titulada Términos escribe cuántos términos tiene el polinomio. Expresión Clase de algebraica polinomio Grado absoluto Grado relativo del polinomio del polinomio Términos 3 x2 + 5xy 3 2 abc 2d 5 5 x4+ y3 + 4a 5 -2 a 2y 2 3 + a 5 x2 - 7ax 3 + 4x 2 2a5 3 a 3-2c 3 + 4abc Actividad 3: Amplio mis conocimientos. Valor numérico de un polinomio El valor numérico de un polinomio se obtiene al realizar las operaciones que indica el polinomio, una vez se reemplazan las variables o letras por un valor numérico asignado. 1. Teniendo en cuenta el valor numérico de las variables y los signos de agrupación, determina cuál es el valor de los siguientes polinomios, si el valor de cada variable es: a) 2a2 x3-[3az-(5xz-3x3) +2bx2] = _________________________ b) 2a2 x3-3az- [-5xz-(3x3 +2bx2)] = _________________________ 2. Observa que los polinomios tienen los mismos términos, pero los signos de agrupación están ubicados en diferentes posiciones, ¿el resultado será igual? Escribe tu respuesta. ___________________________________________________________________ _________________________________________________________________ 3. Halla el área sombreada de las siguientes dos figuras, si a= 6; b=2,54; c = Servicio 2: Desarrollo de contenidos pedagógicos y educativos La innovación educativa para las instituciones educativas de Fe y Alegría Colombia. Ambiente Cualificar. Formación de docentes y equipos de dirección. Para la figura A, primero define: a) ¿Cuál es el área de uno de los cuadrados pequeños de la figura? ____________ b) ¿Cuánto suma el área de los cuatro cuadrados pequeños? ____________ c) Con base en la pregunta anterior ¿cuánto suma el área de los cuatro cuadrados pequeños? __________________________________________________________ d) ¿Cuál es el área del rectángulo mayor? ____________ e) ¿Qué área da la resta de las áreas? ________________ f) El área resultante de la pregunta anterior ¿a qué corresponde? ________________ Para la figura B, determina a) ¿Cuál es el área total del rectángulo? ______________ b) ¿Cuál es el área del triángulo en blanco? _____________ c) Ahora con las medidas anteriores, determina, ¿cuál es el área de la parte sombreada? ____________ A) Área del rectángulo= b. h B) Área del triángulo= (b•h) /2 a+ b C C C C C C b+ c a C a+b+ c Ingresa al enlace para ampliar tus conocimientos y socializa con tu docente lo observado en el video. https://www.youtube.com/watch?v=zRlJgiDVcPo&t=39s Actividad 4: Aplico lo aprendido Servicio 2: Desarrollo de contenidos pedagógicos y educativos La innovación educativa para las instituciones educativas de Fe y Alegría Colombia. Ambiente Cualificar. Formación de docentes y equipos de dirección. El álgebra ha sido de gran ayuda para generalizar situaciones en cualquier ámbito o ciencia, contrario a la aritmética que habla de casos específicos. Con el uso de las expresiones algebraicas podemos pasar de un lenguaje común a un lenguaje algebraico. Teniendo en cuenta la información de la imagen resuelve los siguientes ejercicios: 1. Lee la siguiente conversación: Tomado: Libro editorial Santillana Entonces la expresión algebraica con la que podríamos representar lo dicho en el diálogo anterior podría ser: 3X + Y = 500 o 3X + = 500, donde las variables son X y Y. En este caso X, representa la producción del juguete uno, y Y representa la producción del juguete dos. Ten en cuenta lo siguiente: La expresión algebraica del ejemplo pudo ser también, por ejemplo: 3L + (½) A = 500, dependiendo de las variables que hayan elegido, que bien pudieron ser letras o símbolos. También ten en cuenta que las dos variables elegidas se colocaron en este orden, por la forma como se presenta el diálogo entre las personas, pero también se pudieron organizar así: Y + 3X = 500 Ahora haz tú lo mismo con las siguientes oraciones: Servicio 2: Desarrollo de contenidos pedagógicos y educativos La innovación educativa para las instituciones educativas de Fe y Alegría Colombia. Ambiente Cualificar. Formación de docentes y equipos de dirección. Escribe la expresión algebraica que representa cada oración, y define cuales son las variables de dicha expresión, e indica que representan las variables inmersas en ellas, según el contexto de la frase: 1. El perímetro de un cuadrado cuyo lado mide 2XY3. Expresión algebraica _________________ variables_________________ que representan_________________ 2. Compré 3 jeans y 7 camisetas por un valor de $230.000 Expresión algebraica __________________variables_________________ que representan_________________ Actividad 5: Aprendo y me divierto 1. Identifica los elementos que se piden: Los términos de 5r +s Los términos de 5xy2 +2y –7w Los factores de 5z La base en 3xy2 El coeficiente numérico en 2xy 2. Considerando que un monomio es un número variable o producto de números y variables, explique por qué las siguientes expresiones no son monomios: a) 5 + b) 7xy3+h c) x- 2y 3. Considere las siguientes expresiones y completa. a) 14x + 10 y –3 d) x + y b) –17x5y3z2 e) 5x4z –1/2 x2 z2 + xz3 –7z6 c) 7x5y f) x+4 De acuerdo con las expresiones algebraicas anteriores, completa: Identifique los polinomios: Identifique los monomios: Identifique los binomios: _ Para cada polinomio, que no sea monomio, especifique los términos Servicio 2: Desarrollo de contenidos pedagógicos y educativos La innovación educativa para las instituciones educativas de Fe y Alegría Colombia. Ambiente Cualificar. Formación de docentes y equipos de dirección. 4. Dados los polinomios A: 2b2c –3b + 6c B: 4b - c2b + 12 b2c C: 4 – 2c Ejecute las siguientes operaciones: a) A + B= b) A - C= c) B - A= 5. Calcular el perímetro de la siguiente figura: x2 +x 2x2 +x x 3x2 +x –3 6. El perímetro de un rectángulo es 8x –6 y un lado es 3x +7 ¿Cuánto mide el otro lado? Actividad 6: Descompongo expresiones Sabías que… los términos de un polinomio tienen un factor común. Ejemplos: a) 3 a + 5 ab - 4 ac = a (3 + 5 b – 4 c) b) a2 + 2 a = a (a + 2) c) 10 a2 – 5 a + 15 a3 = 5 a (2 a – 1 + 3 a2) d) x4 + x3 - x2 = x2(x2 + x – 1) 1. De acuerdo con los ejemplos del recuadro, resuelve: a. 3x2-15 Servicio 2: Desarrollo de contenidos pedagógicos y educativos La innovación educativa para las instituciones educativas de Fe y Alegría Colombia. Ambiente Cualificar. Formación de docentes y equipos de dirección. b. c. d. e. f. g. 8x3 - 8x2 - 16x 3mn3 + 3mn -6m 3x3-9xy+3x2y2-3x2y 3a2b + 6ab – 5a3b2 + 8a2bx + 4ab2m 34ax2 + 51a2y – 68a y2 4x2 – 8x + 2 Sabías que…. Ahora vas a ver como se soluciona un Trinomio cuadrado perfecto. Pero antes Pide a tu ayuda a tú tutor y soluciona los ejercicios planteados. Ejemplos: a) m2 + 2m + 1 = (m + 1) (m + 1) = (m + 1)2 b) 4x2 – 20xy + 25y2 = (2x – 5y) (2x- 5y) = (2x – 5y)2 2. Ahora, practica: 9 – 6x + x2 a2 – 10a + 25 16 + 40x2 + 25x4 4x2 – 12xy + 9y2 9b2 – 30a2b + 25a4 9a2+6a+1 25m2-70mn +49n2 Vamos avanzado ahora seguimos con el Trinomio de la forma x2 + bx +c. Observa el ejemplo: x2 + 5x + 6 = (x + 3) (x + 2) Ahora, resuelve: 1) x2 – 5x – 14 2) x2 – 13x + 40 3) y2 – 9y + 20 4) n2 – 6n – 40 5) x2 – 7x – 30 6) n2 – 14n + 5 7) x2 + 4x – 21 8) x2 + 7x – 60 9) x2 + x – 240 10) x4 + 5x2 + 4 Para ampliar tus conocimientos, también puedes tener como punto de referencia los siguientes libros: Servicio 2: Desarrollo de contenidos pedagógicos y educativos La innovación educativa para las instituciones educativas de Fe y Alegría Colombia. Ambiente Cualificar. Formación de docentes y equipos de dirección. Secuencias matemáticas 8°. Editorial Libros y libros. 2016. Saberes matemáticas 8°. Editorial Santillana. Busca a 2 compañeros que hayan terminado esta guía, luego realiza preguntas sobre las temáticas y contenidos que aprendiste luego de resolver la guía. Una vez termines de socializar con tus compañeros busca al docente para realizar la sustentación. MUCHOS EXITOS