Fisica ejercicios

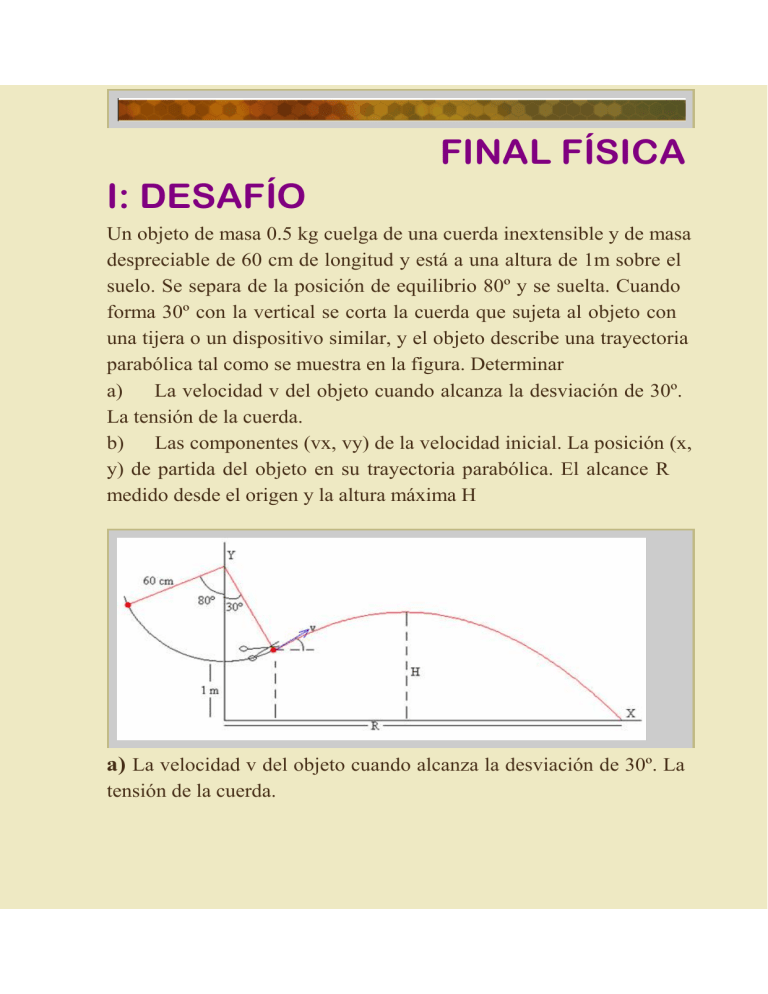
FINAL FÍSICA
I: DESAFÍO
Un objeto de masa 0.5 kg cuelga de una cuerda inextensible y de masa
despreciable de 60 cm de longitud y está a una altura de 1m sobre el
suelo. Se separa de la posición de equilibrio 80º y se suelta. Cuando
forma 30º con la vertical se corta la cuerda que sujeta al objeto con
una tijera o un dispositivo similar, y el objeto describe una trayectoria
parabólica tal como se muestra en la figura. Determinar
a)
La velocidad v del objeto cuando alcanza la desviación de 30º.
La tensión de la cuerda.
b) Las componentes (vx, vy) de la velocidad inicial. La posición (x,
y) de partida del objeto en su trayectoria parabólica. El alcance R
medido desde el origen y la altura máxima H
a) La velocidad v del objeto cuando alcanza la desviación de 30º. La
tensión de la cuerda.
La Energía Mecánica se define como la suma de la Energía Cinética mas la
Energía Potencial, esto es:
Em = Ec + Ep
Para demostrarlo partimos de la Segunda Ley de Newton:
2
desafio final.nb
La Energía Mecánica se define como la suma de la Energía Cinética mas la
Energía Potencial, esto es:
Em = Ec + Ep
Para demostrarlo partimos de la Segunda Ley de Newton:
F = m.a
También debemos saber la cinemática relacionada con la posición del cuerpo
y su aceleración:
Vf2 = Vo2 + 2.a.(X-Xo)
Si aplicamos la Ley de Newton tenemos que:
SF= m.a
m.g.senΒ = m.a
La relación entre las velocidades vo y vf del cuerpo cuando estan en las
alturas hf y ho es:
vf2 = vo2 + 2. a.HX - XoL -> a =
vf2 -vo2
2. HX -XoL
Introduciendo esto en 4 tenemos:
2
2
m. 2.vfHX-vo
= m.g.sen.Β
-XoL
Como
m.Ivf2 -voM
2
= mg(ho - hf)
y separando los momentos iniciales y finales llegamos a que:
1
1
vf = vo + 2. a.HX - XoL -> a =
2. HX -XoL
desafio final.nb
3
Introduciendo esto en 4 tenemos:
2
2
m. 2.vfHX-vo
= m.g.sen.Β
-XoL
Como
m.Ivf2 -voM
2
= mg(ho - hf)
y separando los momentos iniciales y finales llegamos a que:
1
2
mVo2 + mgho =
1
2
mVf2 + m.g.hf
Teniendo en cuenta el principio de conservaciòn de la energía y la última
ecuación planteamos la primera parte del problema teniendo en cuenta que es
un péndulo simple.
Para calcular la velocidad tenemos en cuenta la posición inicial donde el
objeto se encuentra a un ángulo de 80º. Teniendo en cuenta el teorema de
pitágoras ya que se desconoce h se tendra que y= 0.6.Cos[80] por lo que h=
1,60-0.6Cos[80] y de la misma manera obtenemos h2= 1,6-0.6Cos[30]
Utilizando la ecuación
1
2
mVo2 + mgho =
1
2
mVf2 + m.g.hf
4
desafio final.nb
In[1]:=
e1 =
1
2
m v12
Out[1]=
-
Out[2]=
In[3]:=
2
e2 = m * g * h1 - m * g * h2
g h1 m - g h2 m
e3 = e1 Š e2
-
m v22
+
2
In[4]:=
Out[4]=
2
m Hv1L2
m v22
m v12
Out[3]=
1
+
2
In[2]:=
* m * Hv2L2 -
Š g h1 m - g h2 m
2
s = Solve@e3, v2D . 8m ® 0.5<
::v2 ® -
2 g h1 - 2 g h2 + v12 >, :v2 ®
2 g h1 - 2 g h2 + v12 >>
desafio final.nb
In[5]:=
Out[5]=
In[6]:=
Out[6]=
In[7]:=
Out[7]=
In[8]:=
Out[8]=
5
s1 = s . 8g ® 9.8<
::v2 ® -
19.6 h1 - 19.6 h2 + v12 >, :v2 ®
19.6 h1 - 19.6 h2 + v12 >>
s2 = s1 . :h1 ® 1.6 - 0.6 * CosB
4
::v2 ® -
29.3179 - 19.6 h2 + v12 >>
29.3179 - 19.6 h2 + v12 >, :v2 ®
s3 = s2 . :h2 ® 1.6 - 0.6 * CosB
::v2 ® -
8.14236 + v12 >, :v2 ®
1
ΠF>
6
8.14236 + v12 >>
s4 = s3 . 8v1 ® 0<
88v2 ® -2.85348<, 8v2 ® 2.85348<<
La velocidad del objeto es:
ΠF>
9
6
desafio final.nb
V = s4@@2, 1, 2DD
In[9]:=
2.85348
Out[9]=
Diagrama de Cuerpo libre, para calcular la tensión T
Fy = T + - m g CosB
In[10]:=
1
ΠF Š m a
6
1
-
Out[10]=
3 gm+TŠam
2
Ya que el movimiento del objeto es una trayectoria circular se utilizara la aceleración del movimiento circular uniforme arad=
V2
R
In[11]:=
donde V es la velocidad, y R el radio.
a1 =
V2
R
8.14236
Out[11]=
R
desafio final.nb
In[12]:=
Out[12]=
In[13]:=
Out[13]=
In[14]:=
Out[14]=
7
Tension = Solve@Fy, TD . 8a ® a1<
::T ®
1
16.2847 m
3 gm+
2
R
>>
Tension1 = Tension . 8m ® 0.500<
::T ®
1
8.14236
0.866025 g +
2
R
>>
Tension2 = Tension1 . 8R ® 0.6<
::T ®
1
2
H13.5706 + 0.866025 gL>>
La tensión de la cuerda es:
In[15]:=
Out[15]=
Tension3 = Tension2 . 8g ® 9.8<
88T ® 11.0288<<
b) Las componentes (vx, vy) de la velocidad inicial. La posición (x,
y) de partida del objeto en su trayectoria parabólica. El alcance R
medido desde el origen y la altura máxima H
Al cortarse la cuerda, el objeto se convierte en un proyectil
La posición en Y del Objeto es:
In[16]:=
Y = V SinB
1
ΠF t -
6
Out[16]=
1
9.8 t2
2
1.42674 t - 4.9 t2
La posición inicial en Y es:
In[17]:=
Yo = 1.6 - 0.6 CosB
1
6
Out[17]=
1.08038
Posición en X del Objeto
In[18]:=
X = V CosB
1
6
Out[18]=
2.47119 t
Posicion Inicial en Y
ΠF t
ΠF
8
In[19]:=
desafio final.nb
Xo = SinB
1
ΠF 0.6
6
Out[19]=
0.3
Componente en X de la velocidad:
In[20]:=
Vx = V CosB
1
ΠF
6
Out[20]=
2.47119
Componente de la velocidad en Y:
In[21]:=
Vy = V SinB
1
ΠF - 9.8 t
6
Out[21]=
1.42674 - 9.8 t
Su altura máxima se produce cuando Vy=0
In[22]:=
Out[22]=
Vy1 = Vy Š 0
1.42674 - 9.8 t Š 0
Tiempo en el que el objeto esta en su punto máximo en Y
In[23]:=
Out[23]=
In[24]:=
Out[24]=
t1 = Solve@Vy1, tD
88t ® 0.145586<<
tmax = t1@@1, 1, 2DD
0.145586
Al conocer t reemplazo en Y para conocer la altura máxima
In[25]:=
Out[25]=
Ymax = Y . 8t ® tmax<
0.103857
Conociendo la Yo la Hmax será
In[26]:=
Out[26]=
Hmax = Ymax + Yo
1.18424
Para conocer a que distancia está la altura máxima reemplazo t en X
desafio final.nb
In[27]:=
Out[27]=
In[28]:=
Out[28]=
Xmax = X . 8t ® tmax<
0.35977
DHmax = Xo + Xmax
0.65977
El objeto llega al suelo cuando Y=0
In[29]:=
Out[29]=
In[30]:=
tf = Y Š 0
1.42674 t - 4.9 t2 Š 0
tf0 = Solve@tf, tD
Out[30]=
88t ® 0.<, 8t ® 0.291172<<
In[31]:=
tf1 = tf0@@2, 1, 2DD
Out[31]=
0.291172
El alcance máximo R desde la posición en que se corta la cuerta:
In[32]:=
Out[32]=
Alcance = X . 8t ® tf1<
0.71954
Alcance desde el origen de coordenadas
In[33]:=
Out[33]=
Alcancemax = Xo + Alcance
1.01954
Para conocer su Alcance desde que el objeto está en equilibrio se calcula la distancia del objeto al origen de coordenas que es
In[34]:=
Out[34]=
In[35]:=
Out[35]=
Alcanceobj = -Sin@80D 0.6
0.596333
Alcancetotal = Alcancemax + Alcanceobj
1.61587
9