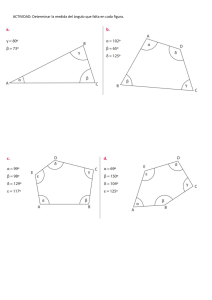
En nuestro entorno podemos encontrar una variedad de objetos en la cual notamos la presencia de los ángulos. Ángulos Definición Bisectriz de un ángulo Según su medida Clasificación de ángulos Según la posición de sus lados Según la suma de sus medidas Definición Es aquella figura geométrica formada por dos rayos que tienen el mismo origen. A dichos rayos se le denomina lados y al origen común vértice del ángulo. B O Elementos Lados : OA y OB Vértice : O A Notación: Ángulo AOB: Medida del ángulo AOB: m m AOB = AOB AOB Es aquel rayo ubicado en la región interior del ángulo cuyo origen es el vértice de dicho ángulo y que forma con sus lados, ángulos de igual medida. A O P B En la figura OP: bisectriz del ángulo AOB. Entonces: m AOP = m POB Si OC es bisectriz del BOD, además m m AOD = 80º , Calcula m AOC . AOB= 20º y Solución: A A B O O C B 200 800 C 2 = 30º Nos piden: m AOC = 20º+ m D D Rpta: La medida del ángulo AOC es 50º + 20º = 80º AOC =50º Según su medida Ángulo agudo: Es aquel ángulo cuya medida es mayor que 0º pero menor que 90º . A Ángulo recto: Es aquel ángulo cuya medida es igual a 90º . Ángulo obtuso: Es aquel ángulo cuya medida es mayor que 90º pero menor que 180º. A A O B En el gráfico el ángulo AOB es agudo; luego: 00 90º O B En el gráfico el ángulo AOB es recto; luego: O B En el gráfico el ángulo AOB es obtuso; luego: = 90º 90º 180º Ángulo llano: Es aquel ángulo cuya medida es igual a180º. A B C Ángulo no convexo: Es aquel ángulo cuya medida es mayor que 180º pero menor que 360º. Ángulo convexo: Es aquel ángulo cuya medida es mayor que 0º pero menor que 180º.Son ángulos convexos, el agudo, recto y obtuso. (Ángulo no convexo) 230º 130º (Ángulo convexo) Ángulo de una vuelta: Es aquel ángulo cuya medida es igual a 360º. 360º A B Según la posición de sus lados Ángulos adyacentes.Son dos ángulos que tienen el mismo vértice y además están situados a distinto lado de un lado común. B A Ángulos consecutivos.Se denomina así a dos o más ángulos que son adyacentes con su ángulo inmediato. B A β C β O O D C En el gráfico los ángulos En la figura los ángulos AOB y BOC son AOB, BOC y COD son adyacentes. consecutivos. Entonces: Se cumple: =+ m AOE= + + Ángulos opuestos por el vértice.- Son dos ángulos que tienen el mismo vértice y además los lados de uno de ellos son las prolongaciones de los lados del otro en sentido contrario. M A O β N B En la figura los ángulos AOB y MON son opuestos por el vértice. Se cumple: m AOE = m Es decir: = MON Ejemplucho: 1. En los ángulos consecutivos AOB y BOC se cumple que m m AOC = 4m AOB. Calcula m AOB BOC = 48º, Solución: Sea: m AOB = x Del dato: m AOC = 4m AOB = 4X De la figura: 4x = x + 480 3x = 480 x = 160 B A x 4x 48º O C Por la suma de sus medidas Ángulos complementarios Ángulos suplementarios Son dos ángulos cuya suma de sus medidas es igual a 90º . A Son dos ángulos cuya suma de sus medidas es igual a 180º . M B A M O Q y x β N En la figura se tienen los ángulos complementarios AOB y MQN. Entonces: + β = 900 Sea C(): complemento de . Entonces: C() = 900 - B O Q N En la figura se tienen los ángulos suplementarios AOB y MQN. Entonces: x + y = 1800 Sea S(): suplemento de x. Entonces: S(x) = 1800 - x Ejempluchos: C(37°) = 90° - 37° = 53° C( 60°) = 90° - 60° = 30° C(10°) = 90° - 10° = 80° S(135°) = 180° - 135° = 45° S(120°) = 180° - 120° = 60° S(80°) = 180° - 80° = 100° Problemas propuestos 1. Si: OM es bisectriz del AOB, calcula “°”. M B 5° C A ° 48° O 2. Calcula el valor de “°” en el gráfico mostrado. 3. Si: m AOB = 30° y mBOC = 80°,además OM es bisectriz del ángulo BOC, calcula m BOM. M B C A O 4. Calcula el valor de “°”, si m AOD = 80°. A B ° O 3° C ° D 5. Calcula el complemento de 26°. 6. Calcula el suplemento de 83°. 7. Calcula el complemento de 72°. 8. Calcula el complemento de 54°. 9. Calcular el suplemento de 114°. 10. Calcula el suplemento de 123°. 11. Calcula el complemento de 48°. 12. Calcula el suplemento de 100° más el complemento de 50°. 13. Calcula el suplemento de 80° menos el complemento de 60°. 14. Calcula el complemento de 70° más el suplemento de 130°.