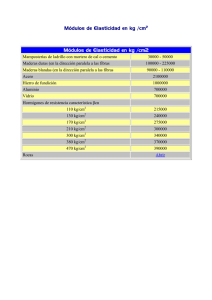
ESTRUCTURAS I PROPIEDADES GEOMÉTRICAS DE LAS SECCIONES PLANAS, CON APLICACIONES MECÁNICAS F.A.D.U. / UdelaR AÑO 2018 CENTRO DE GRAVEDAD MOMENTO ESTÁTICO MOMENTO DE INERCIA - SECCIONES IRREGULARES - SECCIONES COMBINADAS Recordemos: DIMENSIONADO: • ELEGIDO UN MATERIAL ( ACERO, MADERA, etc.) • DEFINIDA LA FORMA DE LA SECCIÓN (RECTANGULAR, PERFILERÍA NORMALIZADA DE ACERO, etc.) DETERMINAR LAS DIMENSIONES MÍNIMAS DE MODO QUE EN NINGÚN PUNTO DE LA PIEZA SE SUPERE LA TENSIÓN DE DIMENSIONADO. En todas las verificaciones tenemos una ecuación que nos relaciona: En todas las verificaciones tenemos una ecuación que nos relaciona: - el material; definido por su tensión admisible y su módulo de elasticidad. En todas las verificaciones tenemos una ecuación que nos relaciona: - el material; definido por su tensión admisible y su módulo de elasticidad. - las solicitaciones; obtenidas a partir del equilibrio, en función de las acciones y los vínculos de la estructura. En todas las verificaciones tenemos una ecuación que nos relaciona: - el material; definido por su tensión admisible y su módulo de elasticidad. - las solicitaciones; - la sección; obtenidas a partir del equilibrio, en función de las acciones y los vínculos de la estructura. definida por su área, su momento de inercia y su módulo resistente. En todas las verificaciones tenemos una ecuación que nos relaciona: - el material; definido por su tensión admisible y su módulo de elasticidad. - las solicitaciones; - la sección; obtenidas a partir del equilibrio, en función de las acciones y los vínculos de la estructura. definida por su área, su momento de inercia y su módulo resistente. Verificación de tensiones normales en tracción N N M fd σmáx wAr A En todas las verificaciones tenemos una ecuación que nos relaciona: - el material; definido por su tensión admisible y su módulo de elasticidad. - las solicitaciones; - la sección; obtenidas a partir del equilibrio, en función de las acciones y los vínculos de la estructura. definida por su área, su momento de inercia y su módulo resistente. Verificación de tensiones normales en tracción N N M fd σmáx wAr A Donde: fd -tensión admisible N A -esfuerzo axil - área de la sección En todas las verificaciones tenemos una ecuación que nos relaciona: - el material; definido por su tensión admisible y su módulo de elasticidad. - las solicitaciones; - la sección; obtenidas a partir del equilibrio, en función de las acciones y los vínculos de la estructura. definida por su área, su momento de inercia y su módulo resistente. Verificación de tensiones normales en compresión f d N _ _ σreal= A ≤ σeuler= ω En todas las verificaciones tenemos una ecuación que nos relaciona: - el material; definido por su tensión admisible y su módulo de elasticidad. - las solicitaciones; - la sección; obtenidas a partir del equilibrio, en función de las acciones y los vínculos de la estructura. definida por su área, su momento de inercia y su módulo resistente. Verificación de tensiones normales en compresión Donde: fd -tensión admisible f d N _ _ σreal= A ≤ σeuler= ω N A -esfuerzo axil w -coeficiente de pandeo -área de la sección En todas las verificaciones tenemos una ecuación que nos relaciona: - el material; definido por su tensión admisible y su módulo de elasticidad. - las solicitaciones; - la sección; obtenidas a partir del equilibrio, en función de las acciones y los vínculos de la estructura. definida por su área, su momento de inercia y su módulo resistente. Verificación de tensiones normales en flexión M N fd σmáx wr A En todas las verificaciones tenemos una ecuación que nos relaciona: - el material; definido por su tensión admisible y su módulo de elasticidad. - las solicitaciones; - la sección; obtenidas a partir del equilibrio, en función de las acciones y los vínculos de la estructura. definida por su área, su momento de inercia y su módulo resistente. Verificación de tensiones normales en flexión Donde: fd -tensión admisible M N fd σmáx wr A M N W A -momento flector -esfuerzo axil -módulo resistente - área de la sección En todas las verificaciones tenemos una ecuación que nos relaciona: - el material; definido por su tensión admisible y su módulo de elasticidad. - las solicitaciones; - la sección; obtenidas a partir del equilibrio, en función de las acciones y los vínculos de la estructura. definida por su área, su momento de inercia y su módulo resistente. Verificación de tensiones tangenciales en flexión En todas las verificaciones tenemos una ecuación que nos relaciona: - el material; definido por su tensión admisible y su módulo de elasticidad. - las solicitaciones; - la sección; obtenidas a partir del equilibrio, en función de las acciones y los vínculos de la estructura. definida por su área, su momento de inercia y su módulo resistente. Verificación de tensiones tangenciales en flexión Donde: T V SLN b I -tensión admisible -esfuerzo cortante -momento estático -ancho de la sección - inercia En todas las verificaciones tenemos una ecuación que nos relaciona: - el material; definido por su tensión admisible y su módulo de elasticidad. - las solicitaciones; - la sección; obtenidas a partir del equilibrio, en función de las acciones y los vínculos de la estructura. definida por su área, su momento de inercia y su módulo resistente. Verificación de deformaciones en flexión Zmáx ≤ Zadm En todas las verificaciones tenemos una ecuación que nos relaciona: - el material; definido por su tensión admisible y su módulo de elasticidad. - las solicitaciones; - la sección; obtenidas a partir del equilibrio, en función de las acciones y los vínculos de la estructura. definida por su área, su momento de inercia y su módulo resistente. Verificación de deformaciones en flexión Zmáx ≤ Zadm L L ó Zadm = 500 300 En todas las verificaciones tenemos una ecuación que nos relaciona: - el material; definido por su tensión admisible y su módulo de elasticidad. - las solicitaciones; - la sección; obtenidas a partir del equilibrio, en función de las acciones y los vínculos de la estructura. definida por su área, su momento de inercia y su módulo resistente. Verificación de deformaciones en flexión Donde: z es la deformación Zmáx ≤ Zadm L L ó Zadm = 500 300 y en ella intervienen : • Las acciones • L: el largo de la barra • E: el módulo de elasticidad del material • I : el momento de inercia de la sección - GEOMETRÍA DE LA SECCIÓN GEOMETRÍA DE LA SECCIÓN: Vimos que en las ecuaciones, las y propiedades geométricas de la sección que intervienen son: • El área x h • El momento de inercia respecto a un eje baricéntrico b • El módulo resistente para una sección rectangular: - área: A = b x h 3 - inercia (baricéntrica) I = b x h / 12 - módulo resistente W = I / 0,5 h = b x h2 / 6 Geometría de la sección: y - área: x h b A=bxh - inercia (baricéntrica): I = b x h3 /12 2 - módulo resistente : W = b x h /6 Cuantificar la inercia baricéntrica, implica tener ubicado el centro de gravedad de la sección. En caso de existir un eje de simetría, el centro de gravedad se encuentra sobre dicho eje. En el caso del rectángulo se obtiene de inmediato, por estar en el cruce de las medianas. (que son ejes de simetría) En otro tipo de secciones, debemos hallar esa ubicación, la que no siempre es inmediata. En caso de existir un eje de simetría, el centro de gravedad se encuentra sobre dicho eje. - SECCIÓN IRREGULAR Ubicación del centro de gravedad: Ubicación del centro de gravedad: Utilizamos el MOMENTO ESTÁTICO o de 1er. ODEN y el Teorema de VARIGNON. Ubicación del centro de gravedad: Utilizamos el MOMENTO ESTÁTICO (o de 1er. ODEN) y el Teorema de VARIGNON. MOMENTO ESTÁTICO Ubicación del centro de gravedad: Utilizamos el MOMENTO ESTÁTICO (o de 1er. ODEN) y el Teorema de VARIGNON. MOMENTO ESTÁTICO Ubicación del centro de gravedad: Utilizamos el MOMENTO ESTÁTICO (o de 1er. ODEN) y el Teorema de VARIGNON. MOMENTO ESTÁTICO Ubicación del centro de gravedad: b2 h2 h1 b1 Podemos descomponer la figura total en otras figuras regulares, de las que conozcamos la posición de su centro de gravedad. Ubicación del centro de gravedad: b2 h2 h1 b1 Podemos descomponer la figura total en otras figuras regulares, de las que conozcamos la posición de su centro de gravedad. Consideramos las áreas parciales como “vectores”, ubicados en el centro de gravedad de cada una de ellas, y ubicamos la resultante mediante una toma de momentos, aplicando el Teorema de Varignon. Ubicación del centro de gravedad: b2 h2 h1 A2 = b2 x h2 A1 = b1 x h1 b1 Podemos ubicar los ejes baricéntricos, considerando las áreas parciales como “vectores”, y ubicando la resultante mediante una toma de momentos Ubicación del centro de gravedad: b2 y h2 h1 A2 = b2 x h2 A1 = b1 x h1 b1 eje baricéntrico eje baricéntrico Podemos ubicar los ejes baricéntricos, considerando las áreas parciales como “vectores”, y ubicando la resultante mediante una toma de momentos Ubicación del centro de gravedad: b2 y h2 h1 A2 = b2 x h2 A1 = b1 x h1 b1 eje baricéntrico eje baricéntrico Podemos ubicar los ejes baricéntricos, considerando las áreas parciales como “vectores”, y ubicando la resultante mediante una toma de momentos Esto lo hacemos para el eje horizontal y para el eje vertical, obteniendo el centro de gravedad donde se cruzan dichos ejes. Ubicación del centro de gravedad: b2 P y h2 h1 A2 = b2 x h2 A1 = b1 x h1 b1 eje baricéntrico Podemos ubicar los ejes baricéntricos, considerando las áreas parciales como “vectores”, y ubicando la resultante mediante una toma de momentos Esto lo hacemos para el eje horizontal y para el eje vertical, obteniendo el centro de gravedad donde se cruzan dichos ejes. Para esto tomamos momento, por ej., en P A1 x h1 /2 + A2 x h2 /2 = (A1 + A2 ) x y y= A1 x h1 /2 + A2 x h2 /2 (A1 + A2 ) Cálculo del Momento de Inercia, (o Momento de 2º orden): b2 y dI x = dA. y 2 x h2 A2 = b2 x h2 Cálculo del Momento de Inercia, (o Momento de 2º orden): b2 y dI x = dA. y 2 x h2 A2 = b2 x h2 Cálculo del Momento de Inercia, (o Momento de 2º orden): b2 y s dIx = dA. y2 x h2 A2 = b2 x h2 X eje baricéntrico Cálculo del Momento de Inercia, (o Momento de 2º orden): b2 y s dIx = dA. y 2 x h2 A2 = b2 x h2 X eje baricéntrico dIX= dA. (y + s) 2 Cálculo del Momento de Inercia, (o Momento de 2º orden): b2 y s dIx = dA. y2 x h2 A2 = b2 x h2 X eje baricéntrico dIX= dA. (y + s)2 = dA. (y2 + 2sy + s2 ) Cálculo del Momento de Inercia, (o Momento de 2º orden): b2 y s dIx = dA. y2 x h2 A2 = b2 x h2 X eje baricéntrico dIX= dA. (y + s)2 = dA. (y2 + 2sy + s2 ) I X = dA. y2 + 2s dA. y + s2 dA Cálculo del Momento de Inercia, (o Momento de 2º orden): b2 y s dIx = dA. y2 x h2 A2 = b2 x h2 X eje baricéntrico dIX= dA. (y + s)2 = dA. (y2 + 2sy + s2 ) I X = dA. y2 + 2s dA. y + s2 dA Expresión general del Teorema de STEINER Cálculo del Momento de Inercia, (o Momento de 2º orden): b2 y s dIx = dA. y2 x h2 A2 = b2 x h2 X eje baricéntrico dIX= dA. (y + s)2 = dA. (y2 + 2sy + s2 ) I X = dA. y2 + 2s dA. y + s2 dA Expresión general del Teorema de STEINER Cuando uno de los ejes es baricéntrico: Cálculo del Momento de Inercia, (o Momento de 2º orden): b2 y dIx = dA. y2 x h2 s A2 = b2 x h2 X eje baricéntrico dIX= dA. (y + s)2 = dA. (y2 + 2sy + s2 ) I X = dA. y2 + 2s dA. y + s2 dA Expresión general del Teorema de STEINER Cuando uno de los ejes es baricéntrico: dA. y2 = I x Cálculo del Momento de Inercia, (o Momento de 2º orden): b2 y dIx = dA. y2 x h2 s A2 = b2 x h2 X eje baricéntrico dIX= dA. (y + s)2 = dA. (y2 + 2sy + s2 ) I X = dA. y2 + 2s dA. y + s2 dA Expresión general del Teorema de STEINER Cuando uno de los ejes es baricéntrico: dA. y2 = I x dA. y = 0 Cálculo del Momento de Inercia, (o Momento de 2º orden): b2 y dIx = dA. y2 x h2 s A2 = b2 x h2 X eje baricéntrico dIX= dA. (y + s)2 = dA. (y2 + 2sy + s2 ) I X = dA. y2 + 2s dA. y + s2 dA Expresión general del Teorema de STEINER Cuando uno de los ejes es baricéntrico: dA. y2 = I x dA. y = 0 s 2 dA = s2 . A Cálculo del Momento de Inercia, (o Momento de 2º orden): b2 y dIx = dA. y2 x h2 s A2 = b2 x h2 X eje baricéntrico dIX= dA. (y + s)2 = dA. (y2 + 2sy + s2 ) I X = dA. y2 + 2s dA. y + s2 dA Expresión general del Teorema de STEINER Cuando uno de los ejes es baricéntrico: dA. y2 = I x dA. y = 0 s 2 dA = s2 . A Se obtiene la expresión más utilizada: I X = Ix + s2 A Steiner Cálculo del Momento de Inercia, (o Momento de 2º orden): b2 y dIx = dA. y2 x h2 s A2 = b2 x h2 X eje baricéntrico dIX= dA. (y + s)2 = dA. (y2 + 2sy + s2 ) I X = dA. y2 + 2s dA. y + s2 dA Expresión general del Teorema de STEINER Cuando uno de los ejes es baricéntrico: dA. y2 = I x dA. y = 0 s 2 dA = s2 . A Se obtiene la expresión más utilizada: I X = Ix + s2 A Steiner En nuestro ejemplo, la Inercia total será la suma de las inercias parciales (1 y 2) trasladadas por Steiner al eje baricéntrico del conjunto de la sección. PERFILES METÁLICOS Los perfiles estructurales son productos fabricados para la construcción de estructuras, son perfiles de sección cerrada, conformado en frío y soldado eléctricamente por alta frecuencia, formando elementos tubulares de sección cuadrada, circular, rectangular, T, TT, vienen en longitudes de 12metros, estos productos son realizados según normas ASTM - SECCIÓN COMBINADA Ejemplo: Formamos una sección mediante la unión de un PNI Nº 14, unido mediante soldadura a un PNC Nº 6 y ½ uno encima del otro, según la figura adjunta. Ejemplo: Formamos una sección mediante la unión de un PNI Nº 14, unido mediante soldadura a un PNC Nº 6 y ½ uno encima del otro, según la figura adjunta. Debemos cuantificar el área de los perfiles y ubicar la posición de su centro de gravedad. Ambos tienen una simetría vertical, por lo que uno de los ejes baricéntricos es el eje de simetría. A1 A2 Ejemplo: Formamos una sección mediante la unión de un PNI Nº 14, unido mediante soldadura a un PNC Nº 6 y ½ uno encima del otro, según la figura adjunta. Debemos cuantificar el área de los perfiles y ubicar la posición de su centro de gravedad. Ambos tienen una simetría vertical, por lo que uno de los ejes baricéntricos es el eje de simetría. Obtenemos los datos en la tabla correspondiente. A1 A2 perfil PNI Nº 14, unido, mediante soldadura, a un perfil PNC Nº 6 y 1/2 Ejemplo: 6,5 cm Ubicación del centro de gravedad 2,78 cm 4,2 cm 1,42 cm 9,03 cm2 y= 9,03 cm2 x 2,78 cm + 18,2 cm2 x 11,2 cm (9,03 cm2 + 18,2 cm2 ) 3 7 cm 2 18,2 cm 14 cm 6,6 cm y= 3 25,1 cm + 203,84 cm (27,23 cm2) = 8,408 cm perfil PNI Nº 14, unido, mediante soldadura, a un perfil PNC Nº 6 y 1/2 Centro de gravedad: 6,5 cm Ubicación del centro de gravedad 2,78 cm 4,2 cm 1,42 cm 9,03 cm2 y= 8,408 cm 9,03 cm2 x 2,78 cm + 18,2 cm2 x 11,2 cm (9,03 cm2 + 18,2 cm2 ) 3 7 cm 2 18,2 cm 14 cm 6,6 cm y= 3 25,1 cm + 203,84 cm (27,23 cm2) = 8,408 cm perfil PNI Nº 14, unido, mediante soldadura, a un perfil PNC Nº 6 y 1/2 Centro de gravedad: 6,5 cm Ubicación del centro de gravedad 2,78 cm 4,2 cm 1,42 cm 9,03 cm2 y= 8,408 cm 2 18,2 cm 14 cm 6,6 cm (9,03 cm2 + 18,2 cm2 ) 3 (27,23 cm2 ) 7 cm 9,03 cm2 x 2,78 cm + 18,2 cm2 x 11,2 cm y= 3 25,1 cm + 203,84 cm (27,23 cm2) = 8,408 cm perfil PNI Nº 14, unido, mediante soldadura, a un perfil PNC Nº 6 y 1/2 Centro de gravedad: 9,03 cm2 s1 Ubicación del centro de gravedad 8,408 cm y= 2 (27,23 cm ) s2 18,2 cm2 9,03 cm2 x 2,78 cm + 18,2 cm2 x 11,2 cm (9,03 cm2 + 18,2 cm2 ) 3 y= 3 25,1 cm + 203,84 cm (27,23 cm2) = 8,408 cm s 1=8,408 cm - 2,78 cm = 5, 628 cm s 2= 7 cm + 4,2 cm - 8,408 cm = 2, 792 cm perfil PNI Nº 14, unido, mediante soldadura, a un perfil PNC Nº 6 y 1/2 Inercia: 9,03 cm2 s1 = 5,628 cm Ubicación del centro de gravedad 8,408 cm y= 2 (27,23 cm ) s2 = 2,792 cm 18,2 cm2 9,03 cm2 x 2,78 cm + 18,2 cm2 x 11,2 cm (9,03 cm2 + 18,2 cm2 ) 3 y= 3 25,1 cm + 203,84 cm (27,23 cm2) = 8,408 cm s 1=8,408 cm - 2,78 cm = 5, 628 cm s 2= 7 cm + 4,2 cm - 8,408 cm = 2, 792 cm perfil PNI Nº 14, unido, mediante soldadura, a un perfil PNC Nº 6 y 1/2 Inercia: 9,03 cm2 s1 = 5,628 cm Ubicación del centro de gravedad 8,408 cm y= 2 (27,23 cm ) s2 = 2,792 cm 18,2 cm2 9,03 cm2 x 2,78 cm + 18,2 cm2 x 11,2 cm (9,03 cm2 + 18,2 cm2 ) 3 y= 3 25,1 cm + 203,84 cm (27,23 cm2) = 8,408 cm s 1=8,408 cm - 2,78 cm = 5, 628 cm s 2= 7 cm + 4,2 cm - 8,408 cm = 2, 792 cm Cálculo de la Inercia (STEINER) IX = Ix + s2 A perfil PNI Nº 14, unido, mediante soldadura, a un perfil PNC Nº 6 y 1/2 Inercia: 9,03 cm2 s1 = 5,628 cm Ubicación del centro de gravedad 8,408 cm y= 2 (27,23 cm ) s2 = 2,792 cm 18,2 cm2 9,03 cm2 x 2,78 cm + 18,2 cm2 x 11,2 cm (9,03 cm2 + 18,2 cm2 ) 3 y= 3 25,1 cm + 203,84 cm (27,23 cm2) = 8,408 cm s 1=8,408 cm - 2,78 cm = 5, 628 cm s 2= 7 cm + 4,2 cm - 8,408 cm = 2, 792 cm Cálculo de la Inercia (STEINER) IX = Ix + s2 A IX = (573 cm4 + 18,2 cm 2x 2,792 2cm 2) + (14,1 cm 4+ 9,03 cm 2x 5,628 2cm 2) perfil PNI Nº 14, unido, mediante soldadura, a un perfil PNC Nº 6 y 1/2 Inercia: 9,03 cm2 s1 = 5,628 cm Ubicación del centro de gravedad 8,408 cm y= 2 (27,23 cm ) s2 = 2,792 cm 18,2 cm2 9,03 cm2 x 2,78 cm + 18,2 cm2 x 11,2 cm (9,03 cm2 + 18,2 cm2 ) 3 y= 3 25,1 cm + 203,84 cm (27,23 cm2) = 8,408 cm s 1=8,408 cm - 2,78 cm = 5, 628 cm s 2= 7 cm + 4,2 cm - 8,408 cm = 2, 792 cm Cálculo de la Inercia (STEINER) IX = Ix + s2 A IX = (573 cm4 + 18,2 cm 2x 2,792 2cm 2) + (14,1 cm 4+ 9,03 cm 2x 5,628 2cm 2) IX = 573 cm4 + 141,9 cm4+ 14,1 cm4 + 286 cm4 perfil PNI Nº 14, unido, mediante soldadura, a un perfil PNC Nº 6 y 1/2 Inercia: 9,03 cm2 s1 = 5,628 cm Ubicación del centro de gravedad 8,408 cm y= 2 (27,23 cm ) s2 = 2,792 cm 18,2 cm2 9,03 cm2 x 2,78 cm + 18,2 cm2 x 11,2 cm (9,03 cm2 + 18,2 cm2 ) 3 y= 3 25,1 cm + 203,84 cm (27,23 cm2) = 8,408 cm s 1=8,408 cm - 2,78 cm = 5, 628 cm s 2= 7 cm + 4,2 cm - 8,408 cm = 2, 792 cm Cálculo de la Inercia (STEINER) IX = Ix + s2 A IX = (573 cm4 + 18,2 cm 2x 2,792 2cm 2) + (14,1 cm 4+ 9,03 cm 2x 5,628 2cm 2) IX = 573 cm4 + 141,9 cm4+ 14,1 cm4 + 286 cm4 IX = 1015 cm4 Módulo resistente: perfil PNI Nº 14, unido, mediante soldadura, a un perfil PNC Nº 6 y 1/2 9,03 cm2 s1 = 8,408 cm 8,408 cm (27,23 cm2 ) 18,2 cm2 s2 = 9,792 cm IX = 1015 cm4 WX = I cm4 / y0 cm Módulo resistente: perfil PNI Nº 14, unido, mediante soldadura, a un perfil PNC Nº 6 y 1/2 9,03 cm2 s1 = 8,408 cm 8,408 cm (27,23 cm2 ) 18,2 cm2 s2 = 9,792 cm IX = 1015 cm4 WX = I cm4 / y0 cm y0 es la distancia a la fibra mas alejada de la línea neutra Módulo resistente: perfil PNI Nº 14, unido, mediante soldadura, a un perfil PNC Nº 6 y 1/2 9,03 cm2 s1 = 8,408 cm 8,408 cm (27,23 cm2 ) 18,2 cm2 s2 = 9,792 cm IX = 1015 cm4 WX = I cm4 / y0 cm y0 es la distancia a la fibra mas alejada de la línea neutra WX = 1015 cm4 / 9,792 cm Módulo resistente: perfil PNI Nº 14, unido, mediante soldadura, a un perfil PNC Nº 6 y 1/2 9,03 cm2 s1 = 8,408 cm 8,408 cm (27,23 cm2 ) 18,2 cm2 s2 = 9,792 cm IX = 1015 cm4 WX = I cm4 / y0 cm y0 es la distancia a la fibra mas alejada de la línea neutra WX = 1015 cm4 / 9,792 cm WX = 103,6 cm3 Análisis de tensiones: perfil PNI Nº 14, unido, mediante soldadura, a un perfil PNC Nº 6 y 1/2 9,03 cm2 s1 = 8,408 cm 8,408 cm (27,23 cm2 ) 18,2 cm2 s2 = 9,792 cm IX = 1015 cm4 WX = I cm4 / y0 cm y0 es la distancia a la fibra mas alejada de la línea neutra WX = 1015 cm4 / 9,792 cm WX = 103,6 cm3 M N fd σmáx wr A Análisis de tensiones: perfil PNI Nº 14, unido, mediante soldadura, a un perfil PNC Nº 6 y 1/2 9,03 cm2 s1 = 8,408 cm 8,408 cm (27,23 cm2 ) 18,2 cm2 s2 = 9,792 cm IX = 1015 cm4 WX = I cm4 / y0 cm y0 es la distancia a la fibra mas alejada de la línea neutra WX = 1015 cm4 / 9,792 cm WX = 103,6 cm3 M N fd σmáx wr A fd = Tensión de diseño M y N = Solicitaciones A = 27,23 cm2 Wr = 103,6 cm3 Verificación de tensiones tangenciales: Sabemos que el valor máximo se da a la altura de la Línea Neutra. Verificación de tensiones tangenciales: Sabemos que el valor máximo se da a la altura de la Línea Neutra. Utilizaremos la expresión de Jourawsky: 𝑉 ∙ 𝑆𝐿𝑁 𝜏= 𝑏 ∙ 𝐼𝑥 Verificación de tensiones tangenciales: Sabemos que el valor máximo se da a la altura de la Línea Neutra. Utilizaremos la expresión de Jourawsky: Necesitamos hallar el momento estático de la zona de la sección que queda por encima de la línea neutra con respecto a la misma. 𝑉 ∙ 𝑆𝐿𝑁 𝜏= 𝑏 ∙ 𝐼𝑥 Verificación de tensiones tangenciales: Sabemos que el valor máximo se da a la altura de la Línea Neutra. Utilizaremos la expresión de Jourawsky: Necesitamos hallar el momento estático de la zona de la sección que queda por encima de la línea neutra con respecto a la misma. Cuando un perfil queda todo entero de un lado de la Línea neutra, es muy sencillo. Pero si un perfil queda cortado, se complica un poco porque resulta una figura no regular. Nos aproximamos al perfil de la sección, descomponiendo en figuras regulares aproximadas. 𝑉 ∙ 𝑆𝐿𝑁 𝜏= 𝑏 ∙ 𝐼𝑥 Vamos a considerar un rectángulo A, correspondiente al alma, y dos rectángulos B, correspondientes al ala, con la altura promedio. SL.N. (del perfil C – 6,5) = 9,03 x 5,628 SL.N. (del rectáng. A) = 0,57 x 4,208 x 4,208/2 SL.N. (de los rect. B) = (6,60 – 0,57) x 0,86 x (4,208 – 0,86/2) SL.N. = 9,03x5,628 + 0,57x4,208²/2 + 6,03x0,86x3,778 = 75,46 cm³ V x 75,46 τ máx. = 0,57 x 1015 Por lo general, cuando se trata del acero, la tensión tangencial máxima es muy inferior a la admisible, y en la mayoría de los casos no es necesario verificarla. Por lo general, cuando se trata del acero, la tensión tangencial máxima es muy inferior a la admisible, y en la mayoría de los casos no es necesario verificarla. Resulta, sí, interesante determinar la tensión tangencial en la superficie de contacto entre ambos perfiles, porque nos permiten dimensionar los elementos de unión, sean bulones, sea soldadura, para que el trabajo conjunto resulte exitoso. Por lo general, cuando se trata del acero, la tensión tangencial máxima es muy inferior a la admisible, y en la mayoría de los casos no es necesario verificarla. Resulta, sí, interesante determinar la tensión tangencial en la superficie de contacto entre ambos perfiles, porque nos permiten dimensionar los elementos de unión, sean bulones, sea soldadura, para que el trabajo conjunto resulte exitoso. SL.N. (del perfil C – 6,5) = 9,03 x 5,628 = 50,82 cm³ V x 50,82 τ (4,208) = 6,5 x 1015 Por lo general, cuando se trata del acero, la tensión tangencial máxima es muy inferior a la admisible, y en la mayoría de los casos no es necesario verificarla. Resulta, sí, interesante determinar la tensión tangencial en la superficie de contacto entre ambos perfiles, porque nos permiten dimensionar los elementos de unión, sean bulones, sea soldadura, para que el trabajo conjunto resulte exitoso. SL.N. (del perfil C – 6,5) = 9,03 x 5,628 = 50,82 cm³ V x 50,82 τ (4,208) = 6,5 x 1015 Si queremos hallar la fuerza de deslizamiento que se produce en 1 m, deberemos multiplicar la tensión hallada por la superficie de contacto. Por lo general, cuando se trata del acero, la tensión tangencial máxima es muy inferior a la admisible, y en la mayoría de los casos no es necesario verificarla. Resulta, sí, interesante determinar la tensión tangencial en la superficie de contacto entre ambos perfiles, porque nos permiten dimensionar los elementos de unión, sean bulones, sea soldadura, para que el trabajo conjunto resulte exitoso. SL.N. (del perfil C – 6,5) = 9,03 x 5,628 = 50,82 cm³ V x 50,82 τ (4,208) = 6,5 x 1015 Si queremos hallar la fuerza de deslizamiento que se produce en 1 m, deberemos multiplicar la tensión hallada por la superficie de contacto. F deslizamiento = τ (4,208) x A (6,5 x 100) Con esta fuerza determinamos los elementos de unión en cada metro de tramo. Verificación de la deformación: Para la verificación de las deformaciones, sólo va a intervenir el momento de inercia de la sección, que ya fue determinado antes. DE DOS MATERIALES DIFERENTES: -SECCIONES COMPUESTAS Se denominan vigas compuestas a aquellas vigas elaboradas con más de un material. Algunos ejemplos de este tipo de vigas son las llamadas sandwich, bimetálicas, los tubos recubiertos con plásticos o las escuadrías de madera reforzadas con perfiles o planchuelas de acero. Se pueden distinguir, a efectos de su análisis mecánico, dos tipos de vigas compuestas: A- aquellas formadas por la superposición vertical de capas de distintos materiales. B- aquellas formadas por piezas de distintos materiales unidas lateralmente. Se supondrá que los materiales que componen este tipo de vigas cumplen con la ley de Hooke y que las distintas partes de la viga están unidas entre sí de modo que pueda suponerse que se comportan como una única unidad estructural. Estudiaremos la distribución de tensiones en secciones compuestas para el caso de piezas en que el plano de flexión es un plano de simetría de la sección. Estudiaremos la distribución de tensiones en secciones compuestas para el caso de piezas en que el plano de flexión es un plano de simetría de la sección. Trabajaremos bajo la hipótesis de que las secciones planas se mantienen planas y perpendiculares al eje de la viga luego de la flexión (hipótesis de Bernouilli), con lo cual las deformaciones unitarias serán proporcionales a las distancias a la línea neutra. Estudiaremos la distribución de tensiones en secciones compuestas para el caso de piezas en que el plano de flexión es un plano de simetría de la sección. Trabajaremos bajo la hipótesis de que las secciones planas se mantienen planas y perpendiculares al eje de la viga luego de la flexión (hipótesis de Bernouilli), con lo cual las deformaciones unitarias serán proporcionales a las distancias a la línea neutra. Sea una sección genérica como la que muestra la figura 2, compuesta por un material 1 de módulo de elasticidad E1 y un material 2 de módulo de elasticidad E2; Supondremos: E1 < E2. Sea una sección genérica como la que muestra la figura 2, compuesta por un material 1 de módulo de elasticidad E1 y un material 2 de módulo de elasticidad E2; Supondremos: E1 < E2. Las deformaciones unitarias producidas en la misma se pueden expresar, en función de la distancia de cada fibra a la línea neutra, como: ε = ky Sea una sección genérica como la que muestra la figura 2, compuesta por un material 1 de módulo de elasticidad E1 y un material 2 de módulo de elasticidad E2; Supondremos: E1 < E2. Las deformaciones unitarias producidas en la misma se pueden expresar, en función de la distancia de cada fibra a la línea neutra, como: ε = ky donde: ε = Deformación unitaria; k = Curvatura; y = Distancia a LN. Sea una sección genérica como la que muestra la figura 2, compuesta por un material 1 de módulo de elasticidad E1 y un material 2 de módulo de elasticidad E2; Supondremos: E1 < E2. Las deformaciones unitarias producidas en la misma se pueden expresar, en función de la distancia de cada fibra a la línea neutra, como: ε = ky Luego, admitiendo que los materiales 1 y 2 cumplen con la ley de Hooke, tenemos que las tensiones en cada material serán: 𝜎1 = 𝐸1 ∙ 𝜀 = 𝐸1 ∙ 𝐾 ∙ 𝑦 𝜎2 = 𝐸2 ∙ 𝜀 = 𝐸2 ∙ 𝐾 ∙ 𝑦 Sea una sección genérica como la que muestra la figura 2, compuesta por un material 1 de módulo de elasticidad E1 y un material 2 de módulo de elasticidad E2; Supondremos: E1 < E2. Las deformaciones unitarias producidas en la misma se pueden expresar, en función de la distancia de cada fibra a la línea neutra, como: ε = ky Luego, admitiendo que los materiales 1 y 2 cumplen con la ley de Hooke, tenemos que las tensiones en cada material serán: 𝜎1 = 𝐸1 ∙ 𝜀 = 𝐸1 ∙ 𝐾 ∙ 𝑦 𝜎2 = 𝐸2 ∙ 𝜀 = 𝐸2 ∙ 𝐾 ∙ 𝑦 Para determinar la ubicación de la línea neutra y la constante k, igualamos los esfuerzos internos a los externos en la sección: Para determinar la ubicación de la línea neutra y la constante k, igualamos los esfuerzos internos a los externos en la sección: Definiendo , relación entre los módulos de elasticidad de los materiales que componen la sección, podemos escribir las ecuaciones de equilibrio anteriores como: Esta sección la podemos diseñar multiplicando el ancho de la zona 2 por n. De esta forma el problema original con dos materiales puede ser sustituido por un problema equivalente tomando una sección de módulo de elasticidad constante (en este caso E1) y área igual a A1 + A2’, como se indica en la figura 3, problema que es más sencillo y que sabemos resolver. Esta sección la podemos diseñar multiplicando el ancho de la zona 2 por n. De esta forma el problema original con dos materiales puede ser sustituido por un problema equivalente tomando una sección de módulo de elasticidad constante (en este caso E1) y área igual a A1 + A2’, como se indica en la figura 3, problema que es más sencillo y que sabemos resolver. Esta sección la podemos diseñar multiplicando el ancho de la zona 2 por n. De esta forma el problema original con dos materiales puede ser sustituido por un problema equivalente tomando una sección de módulo de elasticidad constante (en este caso E1) y área igual a A1 + A2’, como se indica en la figura 3, problema que es más sencillo y que sabemos resolver. Debemos hallar el baricentro de cada sección y, a partir de ellos, el baricentro del conjunto. Esta sección la podemos diseñar multiplicando el ancho de la zona 2 por n. De esta forma el problema original con dos materiales puede ser sustituido por un problema equivalente tomando una sección de módulo de elasticidad constante (en este caso E1) y área igual a A1 + A2’, como se indica en la figura 3, problema que es más sencillo y que sabemos resolver. Debemos hallar el baricentro de cada sección y, a partir de ellos, el baricentro del conjunto. Para esto, aplicamos lo desarrollado a partir de la lámina 9, ubicando el baricentro, y, a través de la aplicación de Steiner, la inercia total.