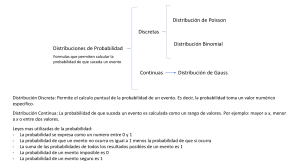
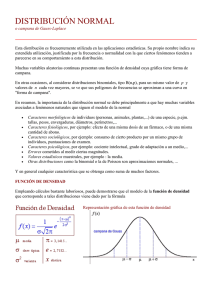
LDA El método LDA (Loss Distribution Approach) es un método aplicado en el campo actuarial y combina la distribución de probabilidad de la severidad y la distribución de probabilidad de la frecuencia del evento y uno de los métodos a través del cual se puede llevar a cabo esta operación es la Simulación de Montecarlo. La aplicación que se le dará al modelo será para el cálculo de pérdida por Riesgo Operacional. Para las distribuciones de frecuencia se utilizan distribuciones de probabilidad discretas, en las cuales se utilizan comúnmente: Distribución Binomial Distribución de Poisson Distribución Binomial Negativa Para la elección de la distribución de probabilidad discreta que más se asemeje con la distribución observada de las frecuencias, se realizan pruebas de bondad de ajuste, donde se utilizan primordialmente la media µ y la varianza de las frecuencias. Los criterios utilizados son los siguientes: Si µ = σ los datos se comportan como una distribución de Poisson. Si µ > σ los datos se comportan como una distribución Binomial. Si µ < σ los datos se comportan como una distribución Binomial negativa. Para las distribuciones de severidad se utilizan distribuciones de probabilidad continuas, en las cuales se utilizan comúnmente: Distribución Weibull Distribución Exponencial Distribución Gamma Distribución LogNormal Para la elección de la distribución de probabilidad continua que más se asemeje con la distribución observada de las severidades, se realizan pruebas de bondad de ajuste. Las pruebas de bondad de ajuste más comunes son: Kolmogorov Smirnov Anderson Darling Cramer–Von Mises Para las pérdidas agregadas se utilizará el método de simulación de Montecarlo, donde se realizarán con N cantidad de iteraciones y con un nivel de confianza (1-α). Basilea II ha fijado un nivel de confianza (1-α) igual a 99.9% y con una corrida no menor a 1000 iteraciones. El método de simulación de Montecarlo multiplicará los valores de la frecuencia por la severidad para cada iteración, donde la media de los resultados obtenidos por el método de Montecarlo será la pérdida esperada proyectada por riesgo operacional, y la pérdida máxima por riesgo operacional se calcula en el percentil (1-α). El proceso del calculo de reservas por pérdida de riesgo operacional se muestra en la siguiente figura: