Vectores y proyectiles

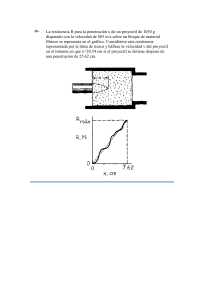
Vectores y proyectiles
Navegue a: Revisar Inicio de la Sesión/ Listado de Temas Vectores y proyectiles - Inicio Versión
imprimible? Preguntas y enlaces Respuestas a las preguntas: Todos los #1-9 #10-45 #46-55
#56-72
Parte A: Opción Múltiple-Múltiple
1. ¿Cuáles de las siguientes afirmaciones son verdaderas para los escalares y vectores?
Enumere todos los que son VERDADEROS.
a. Una cantidad vectorial siempre tiene una dirección asociada.
b. Una cantidad escalar puede tener una dirección asociada.
c. Los vectores se pueden agregar juntos; cantidades escalares no pueden.
d. Los vectores se pueden representar mediante una flecha en un diagrama a escala; la
longitud de la flecha representa la magnitud del vector y la dirección que apunta representa la
dirección del vector.
Respuesta: AD
a. TRUE - Los vectores se definen como cantidades que se describen completamente por su
magnitud y dirección. Por definición, un vector tiene una dirección asociada. Si no lo hizo,
entonces NO sería un vector.
b. FALSO - Los escalares se definen como cantidades que se describen completamente por su
magnitud solamente. Los escalares no tienen en cuenta la dirección y no tiene sentido asociar
una dirección con tal cantidad. Si una cantidad tuviera una dirección asociada, esa cantidad no
sería un vector.
c. FALSE - Tanto los vectores como los escalares se pueden agregar juntos. Las reglas para
agregar vectores juntos son exclusivas de los vectores y no se pueden usar al agregar escalares
juntos. La dirección de un vector debe tenerse en cuenta al agregar dos vectores juntos. La
dirección no tiene importancia al agregar escalares.
d. VERDADERO - Este es exactamente el caso y exactamente lo que se hace en toda la unidad.
2. ¿Cuáles de las siguientes cantidades son vectores? Incluya todos los que correspondan.
a. distancia recorrida
b. desplazamiento
c. Velocidad media
d. velocidad media
e. velocidad instantánea
f. aceleración
Respuesta: BDEF
De las cinco cantidades cinemáticas enumeradas aquí (distancia, desplazamiento, velocidad,
velocidad y aceleración), tres de ellas son vectores. El desplazamiento, la velocidad (tanto
media como instantánea) y la aceleración requieren la mención de una dirección para describir
completamente la cantidad.
3. Los valores numéricos y las direcciones se indican para una variedad de cantidades. ¿Cuál de
estas declaraciones representa una descripción vectorial? Incluya todos los que correspondan.
a. 20 metros, oeste
b. 9,8 es/diccionario
c. 35 mi/hr, sur
d. 16 años
e. 60 minutos
f. 3,5 m/s, sur
g. -3,5 es/diccionari
h. +20 grados C
Respuesta: ACFG
Las expresiones de cantidades vectoriales incluirían una magnitud (número, valor, etc.) y una
dirección. La dirección podría describirse como norte, sur, este, oeste o izquierda, derecha,
arriba, abajo. En ocasiones, se utiliza un "+" o "-" para describir la dirección. Dado que los
cálculos matemáticos en las calculadoras no funcionan bien con la escritura de "sur", un signo a menudo se sustituye por una dirección dada. En el caso de g, las unidades indican una
cantidad de aceleración. El signo "-" indica una dirección. Uno debe tener cuidado al asumir
que un signo "+" o "-" es un signo seguro de que una cantidad es una dirección para otras
cantidades no vectoriales puede utilizar tales signos también (como es el caso en h).
4. ¿Cuáles de las siguientes declaraciones son verdaderas de la adición vectorial, la resta de
vectores y los diagramas de adición vectorial? Enumere todo lo que corresponda.
a. Los vectores A, B y C se agregan juntos como A + B + C. Si el orden en el que se agregan se
cambia a C + B + A, entonces el resultado sería diferente.
b. Los vectores A, B y C se agregan juntos como A + B + C. Si el orden en el que se agregan se
invierte a C + B + A, entonces el resultado sería un vector con la misma magnitud pero la
dirección opuesta.
c. Al construir un diagrama vectorial para A + B + C, no es absolutamente necesario que los
vectores B y C utilicen la misma escala que utiliza el vector A.
d. El resultado en un diagrama de adición vectorial siempre se extiende desde la cabeza del
último vector hasta la cola del primer vector.
e. Si los vectores A y B se añaden en ángulo recto entre sí, entonces uno puede estar seguro de
que el resultado tendrá una magnitud mayor que las magnitudes de cualquiera de los vectores
individuales A y B.
f. Si los vectores A y B se añaden en ángulo recto entre sí, entonces uno puede estar seguro de
que el resultado tendrá una magnitud que es menor que la suma aritmética de las magnitudes
de A y B.
g. Los diagramas de adición vectorial no se pueden utilizar para determinar el resultado
cuando hay una operación de resta de vectores.
Respuesta: EF
a. FALSE - Alterar el orden en el que se agregan tres vectores no altera el resultado del proceso
de adición. A + B + C a C + B + A. Cada orden de operación produce un resultado con la misma
magnitud y dirección.
b. FALSE - Como se mencionó anteriormente en un, alterar el orden en el que se agregan tres
vectores no altera el resultado del proceso de adición. Invertir el orden produce un resultado
con la misma magnitud y la misma dirección.
c. FALSE - Al construir un diagrama de adición vectorial, se debe elegir y adherir una escala. La
escala que se utiliza para dibujar el vector A también debe utilizarse para los vectores B y C. No
se pueden cambiar caballos en medio del arroyo.
d. FALSE - El resultado en un diagrama de adición vectorial se extrae desde la cola del primer
vector (el punto inicial) hasta la cabeza del último vector (el punto final).
e. VERDADERO - Supongamos que A 3 unidades y B - 4 unidades y que los dos vectores están
dirigidos en ángulo recto entre sí. La suma vectorial o resultante de A + B es 5 unidades, que es
claramente mayor que cualquiera de los vectores que se agregan. En general, el resultado en
tal caso se representará en un diagrama de adición vectorial como la hipotenusa de un
triángulo derecho. La hipotenusa es siempre mayor que las otras dos patas del triángulo. Así
que esta declaración siempre es verdadera.
f. VERDADERO - Supongamos que A 3 unidades y B a 4 unidades y que los dos vectores están
dirigidos en ángulorecto entre sí. La suma vectorial o resultante de A + B es 5 unidades,
mientras que la suma aritmética es de 7 unidades. En este caso y en todos los casos, la suma
vectorial de dos vectores de ángulo recto siempre será menor que la suma aritmética. Es decir,
Sqrt(a2 + b2) siempre será menor que a + b.
g. FALSE - Cuando se realiza una operación de resta vectorial, por lo general es aconsejable
simplemente convertirla en una operación de adición vectorial. Esto se logra agregando el
negativo del vector que se está restando. Así que A - B sería equivalente a A + (-B). Al hacerlo,
se puede utilizar un diagrama de adición vectorial para determinar el resultado.
5. ¿Cuál de las siguientes descripciones de objetos en movimiento retrata con precisión un
proyectil? Enumere todo lo que corresponda.
a. un objeto que se mueve a través del aire y no toca ninguna superficie
b. un paracaidista que cae con un paracaídas abierto
c. cualquier objeto sobre el cual la resistencia al aire sea insignificante
d. un objeto de caída libre
e. un objeto sobre el cual la única fuerza significativa es la fuerza de la gravedad
f. una pluma que cae
g. una pluma que cae en una cámara de vacío
h. una pluma que cae en una cámara de vacío que cae.
Respuesta: DEGH
Un proyectil es un objeto sobre el cual la única fuerza es la gravedad. La resistencia al aire
debe ser insignificante o inexistente. Otras fuerzas resultantes de personas o cosas tirando o
empujando, ataduras o contacto con superficies no deben estar presentes.
a. NO - Un avión se mueve a través del aire y no está tocando ninguna superficie. Sin embargo,
un avión claramente no es un proyectil.
b. NO - Un paracaidista que cae típicamente experimenta una considerable resistencia al aire.
Es popular describir tales paracaidistas como estar en caída libre. Este es un uso erróneo del
término.
c. NO - Mientras se sente en su silla, la resistencia al aire es insignificante. Ciertamente no eres
un proyectil (al menos, esperamos que no).
d. SÍ - Un proyectil es un objeto en caída libre.
e. SI - Un objeto sobre el cual la única fuerza significativa es la gravedad se ajusta a la
definición de un proyectil (siempre que significa significativa "tener una influencia").
f. NO - Las plumas que caen encuentran resistencia al aire que impide la aceleración hacia
abajo y hace que la pluma caiga a una velocidad casi constante.
g. SI - Cuando se permite que una pluma caiga en el vacío, se elimina la resistencia al aire y la
pluma puede caer libremente.
h. SI - Cuando se permite que una pluma caiga en el vacío y el vacío también caiga libremente,
se elimina la resistencia al aire y un observador notará que tanto la cámara de vacío como la
pluma están en caída libre.
6. ¿Cuáles de las siguientes afirmaciones son verdaderas con los proyectiles? Enumere todo lo
que corresponda.
a. Un proyectil es un objeto que cae libremente.
b. Un proyectil experimenta una resistencia al aire insignificante o nula.
c. Un proyectil debe moverse en la dirección descendente.
d. Un proyectil debe estar acelerando en la dirección descendente.
e. Un proyectil no tiene que tener movimiento horizontal.
f. Un proyectil podría comenzar su movimiento de proyectiles con una velocidad descendente.
g. Un proyectil no necesita "caer".
Respuesta: ABDEF y posiblemente G
a. VERDADERO - Los objetos que caen libremente, como los proyectiles, son objetos sobre los
que la única fuerza significativa es la gravedad.
b. VERDADERO - La única fuerza en un proyectil es la gravedad; la resistencia al aire no debe
estar presente o no debe influir en el movimiento del proyectil.
c. FALSO - Los proyectiles pueden moverse hacia arriba o hacia abajo o en un ángulo a la
vertical. Sin embargo, deben estar acelerando hacia abajo, consistente con el efecto de la
gravedad sobre un objeto.
d. TRUE - La fuerza de gravedad actúa directamente hacia abajo sobre un objeto, causando una
aceleración hacia abajo. Cualquier proyectil debe estar acelerando hacia abajo
independientemente de otras características de su movimiento.
e. TRUE - Un proyectil podría estar moviéndose estrictamente en una dirección vertical sin
movimiento horizontal. Una pelota lanzada directamente en el aire sería un caso.
f. TRUE - No hay ninguna regla sobre qué dirección debe moverse un proyectil en el instante en
que se proyecta. Podría comenzar su movimiento con una velocidad inicial hacia abajo.
g. VERDADERO - La palabra "caer" puede significar cosas diferentes para diferentes personas.
Si "caer" implica moverse en la dirección descendente en todos los instantes en el tiempo,
entonces un proyectil no necesita estar "cayendo". Para muchos, "caer" significa ser arrastrado
hacia abajo por la fuerza de la gravedad. En este caso, un proyectil debe estar "cayendo".
7. ¿Cuáles de las siguientes afirmaciones son verdaderas del movimiento horizontal de los
proyectiles? Enumere todo lo que corresponda.
a. Un proyectil no tiene una velocidad horizontal.
b. Un proyectil con un componente hacia la derecha del movimiento tendrá un componente
hacia la derecha de la aceleración.
c. La velocidad horizontal de un proyectil cambia 9,8 m/s cada segundo.
d. Un proyectil con un componente horizontal de movimiento tendrá una velocidad horizontal
constante.
e. La velocidad horizontal de un proyectil es de 0 m/s en el pico de su trayectoria.
f. La velocidad horizontal de un proyectil no se ve afectada por la velocidad vertical; estos dos
componentes de movimiento son independientes entre sí.
g. El desplazamiento horizontal de un proyectil depende del tiempo de vuelo y de la velocidad
horizontal inicial.
h. La velocidad horizontal final de un proyectil es siempre igual a la velocidad horizontal inicial.
i. A medida que un proyectil se eleva hacia el pico de su trayectoria, la velocidad horizontal
disminuirá; al caer desde el pico de su trayectoria, su velocidad horizontal disminuirá.
j. Considere un proyectil lanzado desde el nivel del suelo a una velocidad de lanzamiento fija y
un ángulo variable y aterrizaje a nivel del suelo. El desplazamiento horizontal (es decir, el
rango) del proyectil siempre aumentará a medida que el ángulo de lanzamiento se incremente
de 0 grados a 90 grados.
k. Considere un proyectil lanzado desde el nivel del suelo en un ángulo de lanzamiento fijo y
una velocidad de lanzamiento variable y aterrizaje a nivel del suelo. El desplazamiento
horizontal (es decir, el rango) del proyectil siempre aumentará a medida que se aumente la
velocidad de lanzamiento.
Respuesta: DFGHK
a. FALSO - Muchos proyectiles se están moviendo de izquierda a derecha y de derecha a
izquierda a medida que simultáneamente se cae libre. Estos proyectiles tienen un movimiento
horizontal. Mientras que un proyectil puede tener un movimiento horizontal, no puede tener
una aceleración horizontal. Cualquier movimiento que tenga en la dimensión horizontal, debe
ser movimiento con una velocidad constante.
b. FALSO - Un proyectil con un movimiento hacia la derecha (además de un movimiento
vertical) tendrá una velocidad constante en la dirección derecha. Esto quiere decir que no
tiene aceleración horizontal.
c. FALSE - Un proyectil tiene una velocidad horizontal constante. La velocidad vertical cambiará
en 9,8 m/s cada segundo.
d. VERDADERO - ¡Absolutamente cierto! Los proyectiles son objetos sobre los que se actúa
solo por la gravedad. Como tal, hay una aceleración vertical pero no una aceleración
horizontal. La velocidad horizontal de un proyectil es cero o un valor constante distinto de
cero.
e. FALSO - La velocidad vertical de un proyectil es de 0 m/s en el pico de su trayectoria; pero el
componente horizontal de la velocidad en el pico es cualquiera que era el valor cuando se
lanzó por primera vez.
f. VERDADERO - Para cualquier movimiento bidimensional (ya sea movimiento de proyectiles o
problemas de bote fluvial o ...), los componentes perpendiculares del movimiento son
independientes entre sí. Cualquier alteración en un componente vertical no afectará a los
componentes horizontales del movimiento.
g. VERDADERO - El desplazamiento horizontal (x) se puede calcular con la fórmula x - vox • t,
donde vox es la velocidad horizontal inicial y t es el tiempo. Estas son las dos variables que
afectan el desplazamiento horizontal de un proyectil.
h. VERDADERO - Puesto que no hay aceleración horizontal para un proyectil, la velocidad
horizontal inicial es igual a la velocidad horizontal final.
i. FALSE - Esta es una verdadera descripción para el componente vertical de la velocidad. La
velocidad horizontal es invariable a lo largo de la trayectoria de un proyectil.
j. FALSO - El rango (o desplazamiento horizontal) aumentará a medida que el ángulo se
incremente de 0 grados a 45 grados. El rango máximo se produce a 45 grados. A medida que el
ángulo aumenta aún más a valores superiores a 45 grados, el desplazamiento horizontal
disminuye.
k. TRUE - A medida que aumenta la velocidad de lanzamiento, los componentes de la velocidad
inicial (tanto horizontal como vertical) también aumentan. Esto hace que el proyectil
permanezca en el aire durante un período de tiempo más largo y se mueva más rápido en la
dirección horizontal. El resultado es que el aumento de las velocidades de lanzamiento
siempre conduce a un aumento de los desplazamientos horizontales.
8. ¿Cuáles de las siguientes afirmaciones son verdaderas del movimiento vertical de los
proyectiles? Enumere todo lo que corresponda.
a. El componente vertical de la velocidad de un proyectil es un valor constante de 9,8 m/s.
b. El componente vertical de la velocidad de un proyectil es constante.
c. El componente vertical de la velocidad de un proyectil está cambiando.
d. El componente vertical de la velocidad de un proyectil está cambiando a una velocidad
constante.
e. Un proyectil con un componente ascendente de movimiento tendrá un componente
ascendente de aceleración.
f. Un proyectil con un componente de movimiento hacia abajo tendrá un componente
descendente de aceleración.
g. La magnitud de la velocidad vertical de un proyectil cambia en 9,8 m/s cada segundo.
h. La velocidad vertical de un proyectil es de 0 m/s en el pico de su trayectoria.
i. La velocidad vertical de un proyectil no se ve afectada por la velocidad horizontal; estos dos
componentes de movimiento son independientes entre sí.
j. La velocidad vertical final de un proyectil es siempre igual a la velocidad vertical inicial.
k. La aceleración vertical de un proyectil es de 0 es/diccionario/espanol-ingles/m_1'
target='blank_' title='Entry of "m"'>m/es/diccionario/espanol-ingles/s_1' target='blank_'
title='Entry of "s"'>s/es/diccionario/espanol-ingles/s_1' target='blank_' title='Entry of "s"'>s
cuando está en el pico de su trayectoria.
L. A medida que un proyectil se eleva hacia el pico de su trayectoria, la aceleración vertical
disminuirá; al caer desde el pico de su trayectoria, su aceleración vertical disminuirá.
m. A medida que un proyectil se eleva hacia el pico de su trayectoria, la aceleración vertical se
dirige hacia arriba; al caer desde el pico de su trayectoria, su aceleración vertical se dirige hacia
abajo.
n. La altura máxima a la que un proyectil se eleva por encima de la ubicación de lanzamiento
depende de la velocidad vertical inicial.
o. A medida que un proyectil se eleva hacia el pico de su trayectoria, la velocidad vertical
disminuirá; a medida que cae desde el pico de su trayectoria, su velocidad vertical disminuirá.
p. Considere un proyectil lanzado desde el nivel del suelo a una velocidad de lanzamiento fija y
un ángulo variable y aterrizaje a nivel del suelo. El desplazamiento vertical del proyectil
durante la primera mitad de su trayectoria (es decir, la altura máxima) siempre aumentará a
medida que el ángulo de lanzamiento aumente de 0 grados a 90 grados.
q. Considere un proyectil lanzado desde el nivel del suelo en un ángulo de lanzamiento fijo y
una velocidad de lanzamiento variable y aterrizaje a nivel del suelo. El desplazamiento vertical
del proyectil durante la primera mitad de su trayectoria (es decir, la altura máxima) siempre
aumentará a medida que aumente la velocidad de lanzamiento.
Respuesta: CDFGHINPQ
a. FALSO - El componente vertical de la velocidad de un proyectil está cambiando
constantemente. Es la aceleración que tiene un valor de 9,8 es/diccionario/espanolingles/m_1' target='blank_' title='Entry of "m"'>m/es/diccionario/espanol-ingles/s_1'
target='blank_' title='Entry of "s"'>s/s.
b. FALSO - Los proyectiles son objetos sobre los que se actúa solo por gravedad. Como tal, hay
una aceleración vertical; la velocidad vertical no es constante, sino cambiante.
c. VERDADERO - Véase la parte b anterior.
d. TRUE - Un proyectil tiene una aceleración vertical de 9,8 es/diccionario/espanol-ingles/m_1'
target='blank_' title='Entry of "m"'>m/es/diccionario/espanol-ingles/s_1' target='blank_'
title='Entry of "s"'>s/es/diccionario/espanol-ingles/s_1' target='blank_' title='Entry of "s"'>s a
lo largo de toda la trayectoria. Este valor de aceleración es constante. Esto significa que la
velocidad vertical cambia en la misma cantidad - 9,8 m / s - durante cada segundo de su
movimiento. Hay un cambio en la velocidad vertical en una cantidad constante.
e. FALSO - Todos los proyectiles experimentan una aceleración hacia abajo, ya sea que se estén
moviendo hacia arriba o hacia abajo. Los proyectiles que se mueven hacia arriba tienen una
velocidad ascendente, pero los valores de velocidad reales son cada vez más pequeños; es
decir, el proyectil se está desacelerando en el camino a su pico.
f. TRUE - Esta es una declaración verdadera. También se podría decir que un proyectil con un
componente ascendente de movimiento también tiene una aceleración hacia abajo. Todos los
proyectiles aceleran en la dirección descendente. Período.
g. VERDADERO - Esto es absolutamente cierto.
h. VERDADERO - En el pico de su trayectoria, un proyectil está en el proceso de cambiar de
dirección. La velocidad vertical debe cambiar de un valor positivo (+ para arriba) a un valor
negativo (- para abajo). Esta transición significa que el valor de la velocidad vertical debe estar
en algún momento entre un número + y -. El número intermedio es 0 m/s y esto ocurre en el
pico.
i. VERDADERO - Para cualquier movimiento bidimensional (ya sea movimiento de proyectiles o
problemas de bote fluvial o ...), los componentes perpendiculares del movimiento son
independientes entre sí. Cualquier alteración en un componente vertical no afectará a los
componentes horizontales del movimiento.
j. FALSE - Un proyectil lanzado en ángulo forma una trayectoria parabólica. Supongamos que
uno debía rastrear el movimiento de un proyectil hacia adelante en el tiempo desde el pico y
hacia atrás en el tiempo desde el pico. Si se hace, uno encontraría que el valor de velocidad
vertical tiene la misma magnitud para cantidades iguales de veces trazadas hacia adelante y
hacia atrás desde el pico. Así que por el mismo tiempo antes y después del pico, un proyectil
tiene la misma velocidad. Sin embargo, algunos proyectiles no se lanzan desde la misma altura
a la que aterrizan. La altura final no es la misma que la altura inicial y como tal el tiempo para
subir al pico no es igual al tiempo para caer desde el pico. En tales casos, la velocidad vertical
inicial no es igual a la velocidad vertical final.
k. FALSO - ¡No! ¡No! ¡No! La velocidad vertical es de 0 m/s en el pico y la aceleración vertical es
de -9,8 es/diccionario/espanol-ingles/m_1' target='blank_' title='Entry of
"m"'>m/es/diccionario/espanol-ingles/s_1' target='blank_' title='Entry of
"s"'>s/es/diccionario/espanol-ingles/s_1' target='blank_' title='Entry of "s"'>s a lo largo de toda
la trayectoria.
l. FALSE - Esta sería una verdadera descripción de la velocidad vertical. Pero la aceleración
vertical es un valor constante de 9,8 es/diccionario/espanol-ingles/m_1' target='blank_'
title='Entry of "m"'>m/es/diccionario/espanol-ingles/s_1' target='blank_' title='Entry of
"s"'>s/es/diccionario/espanol-ingles/s_1' target='blank_' title='Entry of "s"'>s a lo largo de toda
la trayectoria.
m. FALSE - La magnitud de la aceleración vertical no sólo es un valor constante a lo largo de la
trayectoria de un proyectil, la dirección también es constante. Los proyectiles en todo
momento, independientemente de cualquier otra variable, se acelerarán hacia abajo a 9,8
es/diccionario/espanol-ingles/m_1' target='blank_' title='Entry of
"m"'>m/es/diccionario/espanol-ingles/s_1' target='blank_' title='Entry of "s"'>s/s. Esta es
quizás la verdad más importante a digerir sobre los proyectiles.
n. VERDADERO - La velocidad vertical inicial tiene un efecto en el tiempo que tarda un proyectil
en elevarse hacia su pico. También afecta a la velocidad media del proyectil a medida que se
eleva hacia su pico. Como resultado, cualquier alteración en la velocidad vertical alterará la
altura máxima del proyectil.
o. FALSE - Los proyectiles ascendentes tienen una aceleración hacia abajo; esto significa que se
están desacelerando a medida que se elevan. La magnitud de su velocidad está disminuyendo.
Los proyectiles que se mueven hacia abajo también tienen una aceleración hacia abajo; esto
significa que se están acelerando. La magnitud de su velocidad está aumentando.
p. TRUE - Un aumento en el ángulo de lanzamiento (de 0 a 90 grados) siempre aumentará el
componente vertical de la velocidad inicial (viy). Este aumento de la viy conducirá a un
aumento de los tiempos para que el proyectil suba hacia su pico. Y un ángulo mayor hace que
el proyectil se mueva con una mayor velocidad media durante su camino hacia su pico. Ambos
efectos conducen al resultado de que la altura máxima de un proyectil aumentará a medida
que el ángulo de lanzamiento aumenta de 0 a 90 grados.
q. TRUE - A medida que aumenta la velocidad de lanzamiento, los componentes de la
velocidad inicial (tanto horizontal como vertical) también aumentan. Esto hace que el proyectil
permanezca en el aire durante un período de tiempo más largo y se mueva más rápido en la
dirección vertical. El resultado es que el aumento de las velocidades de lanzamiento siempre
conduce a mayores alturas para los proyectiles.
9. ¿Cuáles de las siguientes afirmaciones son ciertas con el tiempo de vuelo de un proyectil?
Enumere todo lo que corresponda.
a. El tiempo que un proyectil está en el aire depende del componente horizontal de la
velocidad inicial.
b. El tiempo que un proyectil está en el aire depende del componente vertical de la velocidad
inicial.
c. Para un proyectil que aterriza a la misma altura desde la que se proyecta, el tiempo para
subir al pico es igual al tiempo para caer desde su pico hasta la altura original.
d. Para los mismos ángulos de lanzamiento hacia arriba, los proyectiles permanecerán en el
aire más tiempo si se aumenta la velocidad inicial.
e. Supongamos que una pelota pateada en el fútbol es un proyectil. Si la pelota tarda 3
segundos en subir al pico de su trayectoria, entonces tomará 6 segundos para caer desde el
pico de su trayectoria hasta el suelo.
Respuesta: BCD
a. FALSO - El tiempo para que un proyectil suba verticalmente a su pico (y posteriormente
vuelva al suelo) depende de la velocidad vertical inicial. La alteración en la velocidad horizontal
sólo hará que el proyectil tenga un mayor desplazamiento horizontal (x).
b. VERDADERO - Absolutamente cierto. Los proyectiles con un mayor componente vertical de
la velocidad inicial estarán en el aire durante más tiempo (suponiendo que las direcciones de
los víveres sean hacia arriba). Una alteración en el valor viy alterará el tiempo de vuelo del
proyectil, independientemente de la dirección de la víy.
c. TRUE - Para los proyectiles lanzados en ángulos ascendentes y aterrizando a la altura
original, el tiempo hasta el pico es igual al tiempo para caer desde el pico. Si tarda 3 segundos
en subir, tardará 3 segundos en caer.
d. TRUE - Para un ángulo de lanzamiento constante, un aumento en la velocidad inicial (vi)
aumentará la velocidad vertical (viy). Esto se traduce en un mayor tiempo para que el proyectil
se desacelere a 0 m/s a medida que se eleva hacia su pico. Así que el proyectil tarda más en
llegar al pico, más tiempo para caer desde el pico y en general está en el aire durante más
tiempo.
e. FALSO - Cerrar, pero muy falso. Si tarda 3 segundos en subir al pico, entonces toma 3
segundos para caer del pico; Los 6 segundos es el tiempo total de vuelo del proyectil.
Parte B: Elección múltiple
10. Si se agregan dos vectores de desplazamiento de 6 metros y 8 metros (con diferentes
direcciones), entonces el resultado podría oscilar entre ___ metros y ___ metros.
a. 0, 48
b. 1.33, 48
c. 0, 14
d. 2, 14
e. ... ¡Tonterías! No se puede hacer tal predicción.
F.... ¡Tonterías! Se puede hacer una predicción, pero ninguna de estas opciones es correcta.
Respuesta: D
La suma vectorial de 6,0 metros y 8,0 metros será la mayor si se suman en la misma dirección;
que produciría un resultado de 14 metros. La suma vectorial de 6,0 metros y 8,0 metros será la
más pequeña si se suman juntas en la dirección opuesta; que produciría un resultado de 2,0
metros. Una animación que representa los diversos resultados de 6,0 metros añadidos a 8,0
metros en diferentes direcciones se muestra en una página separada. Ver animación.
11. Se añaden tres vectores siguiendo las reglas de adición de vectores. Un cuarto vector se
extrae desde la cola del primer vector hasta la cabeza del último vector. Este cuarto vector se
conoce como ____.
a. el equilibrio
b. la hipotenusa
c. el resultado
d. un error
Respuesta: C. El resultado representa el resultado de agregar dos o más vectores. En un
diagrama de adición vectorial escalado, el resultado siempre se extrae desde la cola del primer
vector hasta la cabeza del último vector.
12. VERDADERO o FALSO:
a. Verdadero
El orden en que se agregan vectores afectará al resultado final.
b. Falso
Respuesta: B. El orden en que se agregan vectores no afecta a la magnitud o dirección del
resultado. A + B + C da el mismo resultado que B + C + A y el mismo resultado que A + C + B.
Una animación que representa la adición de cabeza a cola de cinco vectores en tres órdenes
diferentes se muestra en una página separada. Ver animación.
13. El vector A se dirige hacia el norte y el vector B se dirige hacia el este. ¿Cuál de los
siguientes diagramas de adición de vectores representa mejor la adición de vectores A y B y el
resultado posterior?
Respuesta: E
Si se utiliza el método de cabeza a cola (a veces denominado método de triángulo), entonces la
cola de B se debe dibujar comenzando en la cabeza de A. Ambos diagramas D y E muestran
esto. A continuación, el resultado debe extraerse de la cola de A a la cabeza de B (que no se
muestra en el diagrama D). También hay un método de paralelogramo para agregar vectores.
En este método, las colas de los dos vectores se colocan juntas (como en los diagramas A y B).
A continuación, se debe dibujar un paralelogramo con los dos vectores que forman los lados
adyacentes del paralelogramo. El resultado se extrae de las colas de los vectores a la esquina
opuesta del paralelogramo. Esto no se hace correctamente en los diagramas A y B. Los
diagramas C y F no se asemejan a ningún método de adición vectorial (preciso) conocido por la
humanidad.
14. Al agregar el vector B al vector A geométricamente (o gráficamente) utilizando el método
de cabeza a cola, el resultado se extrae de ____ al ____.
a. cabeza de A, cola de B
b. cola de A, cabeza de B
c. cabeza de B, cola de A d. cola de B, cabeza de A
Respuesta: B
Agregar el vector B al vector A equivale a decir A + B. En tal caso, A se dibuja primero, luego Se
dibuja B con su cola en la cabeza de A. Finalmente, el resultado se extrae de la cola del primer
vector (A) a la cabeza del último vector (B).
Utilice los siguientes diagramas de adición de vectores para Preguntas #15-#20.
15. ¿Cuál de las siguientes ecuaciones de adición vectorial se muestra en el Diagrama 1?
a. A + B = C
f. C + A = B
b. A + C = B
c. B + C = A
g. Ninguno de estos
d. B + A = C
e. C + B = A
16. ¿Cuál de las siguientes ecuaciones de adición vectorial se muestra en el Diagrama 2?
a. A + B = C
f. C + A = B
b. A + C = B
c. B + C = A
g. Ninguno de estos
d. B + A = C
e. C + B = A
17. ¿Cuál de las siguientes ecuaciones de adición vectorial se muestra en el Diagrama 3?
a. A + B = C
f. C + A = B
b. A + C = B
c. B + C = A
g. Ninguno de estos
d. B + A = C
e. C + B = A
18. ¿Cuál de las siguientes ecuaciones de adición vectorial se muestra en el Diagrama 4?
a. A + B = C
f. C + A = B
b. A + C = B
c. B + C = A
g. Ninguno de estos
d. B + A = C
e. C + B = A
Respuestas a preguntas #15-#18:
15. B
16. A
17. E
18. G
Los vectores se agregan mediante un método de cabeza a cola y el resultado se extrae desde la
cola del primer vector hasta la cabeza del último vector. Así que si se añaden dos vectores digamos B se agrega a A (como en A + B) - entonces primero se dibuja A y la cola de B se coloca
en la cabeza de A. El resultado se dibuja con la cola en la cola de A y su cabeza en la cabeza de
B. Por lo tanto, cuando las colas de dos vectores se ven conectadas, uno de los vectores es el
resultante y el otro es el primer vector que se agrega. Y cuando las cabezas de dos vectores se
ven conectadas, uno de los vectores es el resultante y el otro es el segundo vector que se está
agregando. Estos principios se pueden aplicar para responder a las preguntas anteriores.
Tenga en cuenta que en la pregunta 18, no hay un solo vector que se extraiga de la cola de un
vector a la cabeza de otro vector. Por lo tanto, no se dibuja ningún resultado. Se podría decir
que el diagrama muestra que A + B + C - 0.
19. Considere la magnitud y la dirección de los vectores A y B como se muestra en el Diagrama
1 anterior. ¿Cuál de los diagramas siguientes representaría B - A = R?
Respuesta: B
La resta de A de B equivale a añadir el negativo de A a B. Es decir, B - A = B + (-A). El negativo
de un vector es simplemente el mismo vector dibujado en la dirección opuesta. La respuesta
correcta debe ser un diagrama que muestre B que se está dibujando primero. Luego, en la
cabeza de B, se debe dibujar la cola de un vector que apunta en la dirección opuesta de A. Esto
se muestra en los diagramas B y C. El resultado debe entonces ser extraído de la cola de B a la
cabeza de -A. Esto no se muestra en el diagrama C.
20. Considere la magnitud y la dirección de los vectores B y C como se muestra en el Diagrama
2 anterior. ¿Cuál de los diagramas siguientes representaría C - B = R?
Respuesta: C
La resta de B de C equivale a añadir el negativo de B a C. Es decir, C - B a C + (-B). El negativo de
un vector es simplemente el mismo vector dibujado en la dirección opuesta. La respuesta
correcta debe ser un diagrama que muestre C que se está dibujando primero. A continuación,
en la cabecera de C, se debe dibujar la cola de un vector que apunta en la dirección opuesta a
B. Esto se muestra en los diagramas B y C. El resultado debe entonces ser extraído de la cola de
C a la cabeza de -B. Esto no se muestra en el diagrama B.
21. La suma vectorial (sólo magnitud) de 25,0 m, norte + 18,0 m, este es ___ m.
a. 7.00
g. 949
b. 21,5
c. 30,8
h. Ninguno de estos
d. 35,8
e. 43,0
f. 54,2
Respuesta: C
Estos dos vectores se dirigen en ángulo recto entre sí. En tales casos, la suma vectorial se
puede determinar utilizando el teorema de Pitágoras. El resultado (R) es igual a la raíz
cuadrada de la suma de los cuadrados de los dos vectores que se agregan.
Es decir, R - Sqrt (A2 + B2) donde A y B son los dos vectores que se agregan juntos. Así
R = Sqrt [ (25.0 m)2 + (18.0 m)2 ] = Sqrt [ (625 m2) + (324 m2) ] = Sqrt (949
m2)
R = 30.805 m = ~30.8 m
22. La suma vectorial (sólo magnitud) de 32,0 m, norte + 41,0 m, oeste es ___ m.
a. 9.00
b. 36.5
c. 38.0
d. 52.0
e. 73.0
f. 128
g. 2.70 x 103
h. Ninguno de estos
Respuesta: D
Al igual que la pregunta #21 anterior, estos dos vectores están dirigidos en ángulo recto entre
sí. El teorema de Pitágoras se puede utilizar para determinar el resultado de su suma. El
resultado (R) es igual a la raíz cuadrada de la suma de los cuadrados de los dos vectores que se
agregan.
R = Sqrt (A2 + B2)
R = Sqrt [ (32.0 m)2 + (41.0 m)2 ] = Sqrt [ (1024 m2) + (1681 m2) ] = Sqrt
(2705 m2)
R = 52.010 m = ~52.0 m
Utilice el diagrama siguiente para responder a las preguntas #23 #28. Cada cuadrado del
diagrama representa un área de 20 metros x 20 metros.
23. Si una persona camina de D a H a G a C, entonces la distancia recorrida es ____ metros.
a. 128
b. 180
c. 401
d. 460
e. 480
f. 533
g. 620
h. Ninguno de estos
Respuesta: F
La distancia es una cantidad escalar y sumar tres escalares es tan simple como agregar los tres
números aritméticamente. Sin embargo, dado que la primera de las tres patas de este viaje no
se debe al este, oeste, norte o sur, la determinación de la distancia para esta etapa requiere
que se utilice el teorema de Pitágoras. Es decir, caminar de D a H equivale a caminar 140
metros al este (7 cuadrados) y 160 metros (8 cuadrados) al sur. La distancia de D a H es así
212.6 metros - Sqrt [ (140 m)2 + (160 m)2 ]. El paseo de H a G es una distancia de 80 metros (4
cuadrados) y el paseo de G a C es de 240 metros (12 cuadrados). La distancia total a pie es la
suma de 212,6 m + 80 m + 240 m = 532,6 m = 533 m.
24. Si una persona camina de D a H a G a C, entonces la magnitud del desplazamiento es ____
metros.
a. 128
b. 180
c. 401
d. 460
e. 480
f. 533
g. 620
h. Ninguno de estos
Respuesta: A
El desplazamiento es una cantidad vectorial que indica hasta qué punto nuestro lugar está un
objeto al final del movimiento en relación con el principio del movimiento. El desplazamiento
no depende de la trayectoria tomada desde la posición inicial hasta la posición final, sino solo
de la distancia de un vector dibujado de principio a fin. El resultado de los tres segmentos de
este paseo simplemente se dibuja de D a C. La distancia de este resultado se encuentra
mediante el uso del teorema de Pitágoras. El resultado se extiende hacia el sur 80 metros (4
cuadrados) y el oeste 100 metros (5 cuadrados). El resultado tiene una magnitud de Sqrt [ (80
m)2 + (100 m)2 ] o 128 metros.
25. Si una persona camina de D a H a G a C, entonces la dirección del desplazamiento es ___
grados (medidos en sentido contrario a las agujas del reloj desde el este).
a. 39
b. 51
c. 53
d. 217
e. 219
f. 231
g. 233
h. Ninguno de estos
Respuesta: E
Como se discutió en el problema anterior, el resultante se extiende
hacia el sur 80 metros (4 cuadrados) y el oeste 100 metros (5 cuadrados). Esto se muestra en el
diagrama de la derecha. Estas dos partes del vector resultante se pueden combinar con una
función trigonométrica para determinar el ángulo theta. El ángulo theta es de
aproximadamente 38,7 grados. Esta no es la dirección del desplazamiento resultante, sino
simplemente el ángulo entre el vector de desplazamiento y el oeste debido. La convención
utilizada para expresar la dirección del vector es medir el ángulo de rotación en sentido
contrario a las agujas del reloj desde el presente. Por lo tanto, en este caso, la dirección es 180
grados + 38,7 grados o 219 grados.
26. Si una persona camina de H a E a C a G, entonces la distancia recorrida es ____ metros.
a. 80.
b. 240.
c. 253
d. 333
e. 493
f. 560.
g. 640.
h. Ninguno de estos
Respuesta: E
La distancia es una cantidad escalar y sumar tres escalares es tan simple como añadir las
distancias individuales de las tres patas es tan simple como añadir las distancias. Aritmético. El
problema se simplifica en que los dos primeros tramos del viaje están a lo largo del mismo
segmento de línea. La parada en E puede ser ignorada ya que su es simplemente un punto en
la línea de la ubicación H a la ubicación C. Es decir, HE + EC = HC. Dado que el segmento de la
línea HC no se extiende debido a Este, Oeste, Norte o Sur, determinar la distancia para esta
etapa requiere que se utilice el teorema de Pitágoras. Es decir, caminar de H a C equivale a
caminar 240 metros al oeste (12 cuadrados) y 80 metros (4 cuadrados) al norte. La distancia de
D a H es así de 253,0 metros - Sqrt [ (240 m)2 + (80 m)2 ]. El paseo de H a E a C es una distancia
de 253 metros y el paseo de C a G es de 240 metros (12 cuadrados). La distancia total a pie es
la suma de 253 m + 240 m = 493 m.
27. Si una persona camina de H a E a C a G, entonces la magnitud del desplazamiento es ____
metros.
a. 80.
b. 240.
c. 253
d. 333
e. 493
f. 560.
g. 640.
h. Ninguno de estos
Respuesta: A
El desplazamiento es una cantidad vectorial que indica hasta qué punto nuestro lugar está un
objeto al final del movimiento en relación con el principio del movimiento. El desplazamiento
no depende de la trayectoria tomada desde la posición inicial hasta la posición final, sino solo
de la distancia de un vector dibujado de principio a fin. El resultado de los tres segmentos de
este paseo simplemente se dibuja de H a G. La distancia de este resultado es simplemente 80
metros (4 cuadrados), norte.
28. Si una persona camina de H a E a G, entonces la dirección del desplazamiento es ___
grados (medidoen en sentido contrario a las agujas del reloj desde el este).
a. 0
b. 18.
c. 72
d. 90.
e. 108
f. 162
g. 342
h. Ninguno de estos
Respuesta: D
El destino final G se debe al norte de la ubicación inicial. Por lo tanto, el desplazamiento se
dirige hacia el norte (a 90 grados).
Utilice el siguiente diagrama para Preguntas #29 #33. En el diagrama, se muestra un bote
fluvial comenzando en la posición A en la orilla este de un río. El barco se dirige hacia la
posición B (un punto directamente a través del río desde A) con una velocidad de 3,8 m/s. Pero
debido a una corriente con una velocidad de 1,8 m/s, el barco aterriza en la orilla oeste del río
en la posición C, un lugar aguas abajo de B. La anchura del río (dacross) es de 86,4 metros.
29. La magnitud de la velocidad resultante del barco es ____ m/s.
a. 1.8
b. 2.0
c. 3.4
d. 3.8
e. 4.2
f. 5.6
g.11
h. Ninguno de estos
Respuesta: E
Este es el caso de un barco cruzando un río por el uso de su motor. El motor permite que el
barco viaje 3,8 metros hacia la orilla opuesta en cada segundo. El río fluye hacia el sur,
llevando el barco a una distancia de 1,8 metros por el río cada segundo. La velocidad
resultante es simplemente la suma vectorial de estas dos velocidades individuales. Dado que
estas dos velocidades están en ángulo recto entre sí, la suma vectorial se puede determinar
utilizando el teorema de Pitágoras.
vresultant2 = (3.8 m/s)2 + (1.8 m/s)2
vresultant = Sqrt[ (3.8 m/s)2 + (1.8 m/s)2 ]
vresultant = 4.2 m/s
30. La dirección de la velocidad resultante del barco es ____ m/s.
a. 0
b. 18.
c. 712
d. 90.
e. 108
f. 162
g. 342
h. Ninguna de estos
Respuesta: H
La dirección de la velocidad resultante está en dirección sureste.
Eso coloca el vector en el tercer cuadrante con una dirección en algún lugar entre 180 grados y
270 grados. El ángulo exacto se puede determinar si el ángulo theta se encuentra usando
trigonometría. Theta es el ángulo que la velocidad resultante (el vector rojo en el diagrama a la
derecha) hace con el oeste debido. Este ángulo se puede encontrar demandando la función
tangente. La obra se muestra a la derecha. El ángulo theta se encuentra en 25,3 grados. La
dirección real medida como el ángulo de rotación en sentido antihorario con el este debido es
de 180 grados más 25,3 grados. Esto sería 205.3 grados.
31. El tiempo necesario para que el barco cruce el río de 86,4 m de ancho es de ___ segundos.
a. 4.2
b. 15
c. 21
e. 48
f. Ninguno de estos
d. 23
Respuesta: D
El motor permite que el barco viaje 3,8 metros hacia la orilla opuesta en cada segundo. El
barco tiene 86,4 metros para viajar de costa a costa. (La presencia de la corriente no altera la
anchura ni la distancia de la costa a la orilla.) El tiempo para cruzar el río se puede calcular a
partir de la anchura del río y la velocidad del barco utilizando la ecuación v - d/t.
Reorganización de la ecuación para resolver los rendimientos t
t = d/v
t = (86.4 m) / (3.8 m/s) = ~23 s (unrounded 22.7 s)
32. La ubicación C es el lugar donde el barco finalmente aterriza en la orilla
opuesta. ¿Cuál es la distancia desde la ubicación B hasta la ubicación C.
a. 37
b. 41
c. 78
d. 86
e. 96
f. 180
g. 2.0 x 102
h. Ninguno de estos
Respuesta: B
La distancia que la ubicación C es aguas abajo de B está matemáticamente
relacionada con la velocidad del río y el tiempo para cruzar el río. La distancia
se puede calcular multiplicando la velocidad actual por el tiempo para cruzar el
río
ddownstream = vriver • t
ddownstream = (1.8 m/s) • (22.7 s)
ddownstream = ~41 m
33. Si la corriente en un día en particular fluyecon dos veces la velocidad,
entonces el tiempo para cruzar el río sería ____.
a. dos veces mayor
b. la mitad de grande
c. mayor, pero no dos veces mayor
d. menos, pero no la mitad de la hora original
e. lo mismo que era cuando la corriente fluyó a 1,8 m/s.
Respuesta: E
Para esta situación de un barco que se dirige directamente a través del río, la
velocidad actual se dirige perpendicular a la velocidad del barco. Estos dos
componentes del movimiento resultante de los barcos son independientes entre
sí. La velocidad del barco hace la única contribución a la capacidad del barco
para cruzar el río. La velocidad del río sólo lleva el barco hacia el sur por el río.
Así que una alteración de la velocidad del río no tendría ningún efecto en el
tiempo necesario para que el barco cruzara el río.
34. Un objeto está experimentando movimiento de caída libre. A medida que
cae, el ____del objeto.
a. la velocidad aumenta
b. la aceleración aumenta
c. ambos de estos
d. ninguno de estos
Respuesta: A
Como un objeto cae en caídas libres, su velocidad (y también su velocidad)
cambia en aproximadamente 10 m/ s cada segundo. Esto significa que la
aceleración es un valor constante de 10 m/s/s. Un objeto tiene una velocidad
cambiante (o velocidad) y una aceleración constante si la velocidad cambia en
la misma cantidad (una "cantidad constante") en cada segundo consecutivo de
su movimiento.
35. Un balón de fútbol se patea en el aire en un ángulo de 45 grados con el
horizontal. En la parte superior de la trayectoria de la pelota, su velocidad es
_______.
a. totalmente vertical
b. totalmente horizontal
c. tanto vertical como horizontal
d. no se proporciona suficiente información para saber.
Respuesta: B
A medida que un proyectil se eleva hacia su pico, su velocidad horizontal
permanece constante mientras que su velocidad vertical disminuye. En su pico,
su velocidad vertical se convierte en 0 m/s. En este instante en el tiempo, la
velocidad es totalmente horizontal; no hay ningún componente vertical a la
velocidad.
36. Un balón de fútbol se patea en el aire en un ángulo de 45 grados con el
horizontal. En la parte superior de la trayectoria de la pelota, su aceleración es
_______. (Descuide los efectos de la resistencia al aire.)
a. totalmente vertical
b. totalmente horizontal
c. tanto vertical como horizontal
d. no se proporciona suficiente información para saber.
Respuesta: A
A medida que un proyectil se eleva hacia su pico, su velocidad horizontal
permanece constante mientras que su velocidad vertical disminuye. Esto quiere
decir que la aceleración del objeto es vertical, no horizontal. En el pico y en
todas partes a lo largo de la trayectoria, hay una aceleración vertical (hacia
abajo). De hecho, un proyectil es un objeto sobre el cual la única fuerza es la
gravedad. Esta fuerza provoca una aceleración que está en la misma dirección
que la fuerza - hacia abajo
37. Un balón de fútbol se patea en el aire en un ángulo de 45 grados con el horizontal. En la
parte superior del camino de la pelota, la fuerza neta que actúa sobre ella es _______.
(Descuide los efectos de la resistencia al aire.)
a. totalmente vertical
b. totalmente horizontal
c. tanto vertical como horizontal d. no se proporciona suficiente información para saber.
Respuesta: A
Un proyectil es un objeto sobre el cual la única fuerza es la gravedad. Dado que ninguna otra
fuerza actúa sobre el objeto, la fuerza neta sería hacia abajo.
38. ¿En qué momento de su camino es el componente horizontal de la velocidad (vx) de un
proyectil el más pequeño?
a. En el instante en que se lanza.
b. A mitad de camino a la cima.
c. En la parte superior.
d. A medida que se acerca a la parte superior.
e. Es lo mismo en todo el camino.
Respuesta: E
A medida que un proyectil se eleva hacia su pico, su velocidad horizontal permanece constante
mientras que su velocidad vertical disminuye. Esto quiere decir que la aceleración del objeto es
vertical, no horizontal. Al tener una velocidad horizontal constante, no hay ningún punto a lo
largo de la trayectoria donde el valor vx es más pequeño que en otros puntos.
39. ¿En qué momento de su camino es el componente vertical de la velocidad (vy) de un
proyectil el más pequeño?
a. En el instante en que se lanza.
b. A mitad de camino a la cima.
c. En la parte superior.
d. A medida que se acerca a la parte superior. e. Es lo mismo en todo el camino.
Respuesta: C
A medida que un proyectil se eleva hacia su pico, su velocidad horizontal permanece constante
mientras que su velocidad vertical disminuye. Durante la porción ascendente de su trayectoria,
el vy disminuye continuamente hasta que se convierte en 0 m/s en el pico. Por lo tanto, el vy
es tan pequeño como siempre lo será cuando está en el pico de la trayectoria.
40. Un avión que vuela a 100 km/h en un viento cruzado huracán de 100 km/h tiene una
velocidad (en relación con el suelo) de ____.
a. 0 km/h
b. 100 km/h
c. 141 km/h
d. 200 km/h
Respuesta: C
Cuando un objeto como un avión o un barco se mueve dentro de un medio que se mueve en
relación con el suelo, la velocidad del avión o barco (medida por su velocímetro) no será la
misma que la velocidad medida por una persona en el suelo (velocidad del suelo). La velocidad
del suelo (es decir, la velocidad resultante producida por la combinación de la velocidad del
avión y la velocidad del viento) se puede determinar añadiendo la velocidad del avión y la
velocidad del viento como vectores. En este caso, los dos vectores están en ángulo recto, por
lo que la velocidad resultante se puede determinar utilizando el teorema de Pitágoras.
R2 = (100 km/hr)2 + (100 km/hr)2
R = SQRT( (100 km/hr)2 + (100 km/hr)2 )
R = 141 km/hr
41. Un avión se mueve a 141 km/h hacia el noreste (45 grados). ¿Cuál es la velocidad de su
componente en la dirección norte?
a. 41 km/h
b. 100 km/h
c. 110 km/h
d. 141 km/h
Respuesta: B
Para determinar el componente de un vector en una dirección determinada, se deben aplicar
principios de resolución de vectores. Este vector de velocidad está dirigido a 45 grados y tiene
una magnitud de 141 km/h. El componente vertical (hacia el norte) de este vector se puede
encontrar utilizando la función sinusoi.
vy = v * sine(theta)
vy = (141 km/hr)*sine(45 degrees)
vy = 100 km/hr
42. Enrolle una bola de bolos del borde de una mesa. A medida que cae, su
componente horizontal de velocidad ___.
a. disminuye
b. permanece constante
c. aumenta
Respuesta: B
Una vez que la pelota sale del borde de la mesa, se convierte en un proyectil. A
medida que cae, su velocidad horizontal permanece constante mientras su
velocidad vertical disminuye. Esto quiere decir que la aceleración del objeto es
vertical, no horizontal. De hecho, un proyectil es un objeto sobre el cual la
única fuerza es la gravedad. Esta fuerza provoca una aceleración que está en la
misma dirección que la fuerza - hacia abajo.
43. Una bala se dispara horizontalmente y golpea el suelo en 0,5 segundos. Si
se hubiera disparado con el doble de velocidad en la misma dirección, habría
golpeado el suelo en ____. (No suponga resistencia al aire.)
a. menos de 0,5 s.
b. más de 0,5 s.
c. 0,5 s.
Respuesta: C
Una vez que la bala sale del hocico, se convierte en un proyectil (suponiendo
que no haya resistencia al aire). A medida que cae, su velocidad horizontal
permanece constante mientras su velocidad vertical disminuye. La fuerza de
gravedad actúa sobre la bala para causar su aceleración hacia abajo. El
movimiento de la bala en la dirección descendente es independiente del
movimiento en la dirección horizontal. Es decir, cualquier alteración en un
aspecto horizontal de su movimiento no afectará el movimiento en la dirección
vertical. El tiempo para caer verticalmente al suelo no se ve realizado por la
velocidad horizontal del proyectil. Todavía tardaría 0,5 segundos en caer al
suelo desde esta altura, independientemente de la velocidad horizontal.
44. Se lanza un proyectil en un ángulo de 15 grados por encima de la horizontal
y aterriza hacia abajo. Para la misma velocidad, ¿qué otro ángulo de proyección
produciría la misma distancia de rango descendente?
a. 30 grados.
d. 75 grados
b. 45 grados.
e. 90 grados.
c. 50 grados.
Respuesta: D
Para los proyectiles lanzados en ángulos, un ángulo de lanzamiento de 45
grados proporcionará el desplazamiento horizontal más grande. Los dos
ángulos de lanzamiento separados de 45 grados por la misma cantidad (por
ejemplo, 40 grados y 50 grados, 30 grados y 60 grados y 15 grados y 75
grados) proporcionarán el mismo desplazamiento horizontal.
45. Dos proyectiles se disparan a velocidades iguales pero diferentes ángulos.
Uno se dispara en un ángulo de 30 grados y el otro a 60 grados. El proyectil
que golpee primero el suelo será el que se dispare (resistencia al aire de
negligencia) ____.
a. 30 grados
b. 60 grados
c. ambos golpearon al mismo tiempo
Respuesta: A
Para los proyectiles lanzados en ángulos, un ángulo de lanzamiento de 45
grados proporcionará el desplazamiento horizontal más grande. Los ángulos de
lanzamiento superiores a 45 grados dan como resultado grandes componentes
verticales de velocidad; estos permanecen en el aire más tiempo y se elevan a
alturas más altas. Los ángulos de lanzamiento inferiores a 45 grados dan como
resultado pequeños componentes verticales de velocidad; estos no se elevan
tan alto y terminan cayendo al suelo en tiempos más cortos.
Parte C: Diagramación y análisis
46. Exprese la dirección de cada uno de los siguientes vectores en el siguiente diagrama.
A: 0 deg
B: 90 deg
C: 135 deg
D: 205 deg
E: 270 deg
F: 340 deg
Respuesta: Vea las respuestas anteriores.
Se utiliza la convención de que la dirección de un vector se mide como el ángulo de rotación en
sentido contrario a las agujas del reloj de ese vector desde el sureste. Como tal, un vector
hacia el este (A) tiene una dirección de 0 grados; un vector hacia el norte (B) tiene una
dirección de 90 grados; y un vector hacia el sur (E) tiene una dirección de 270 grados. Se debe
utilizar un transportador para determinar las direcciones de C, D y F. Vector C está en el
segundo cuadrante, por lo que su dirección está entre 90 grados y 180 grados. El ángulo entre
el este y el vector C se puede medir. El vector D está en el tercer cuadrante; su dirección está
entre 180 grados y 270 grados. Un transportador se puede utilizar para medir el ángulo entre
El oeste (180 grados) y el vector D. Esta medida de ángulo se puede agregar a 180 grados para
obtener la respuesta. Un procedimiento similar se repite con Vector F.
47. En los diagramas siguientes, se añaden dos vectores y se dibuja el resultado. Para cada
diagrama, identifique qué vector es el resultante y escriba la ecuación (por ejemplo, A + B = C).
a.
b.
The resultant is vector B.
The resultant is vector B.
The equation is C + A = B.
The equation is A + C = B.
c.
d.
The resultant is vector A.
The equation is C + B = A.
The resultant is vector C.
The equation is A + B = C.
Respuesta: Vea las respuestas anteriores.
Los vectores se agregan mediante un método de cabeza a cola y el resultado se extrae desde la
cola del primer vector hasta la cabeza del último vector. Así que si se añaden dos vectores digamos B se agrega a A (como en A + B) - entonces primero se dibuja A y la cola de B se coloca
en la cabeza de A. El resultado se dibuja con la cola en la cola de A y su cabeza en la cabeza de
B. Por lo tanto, cuando las colas de dos vectores se ven conectadas, uno de los vectores es el
resultante y el otro es el primer vector que se agrega. Y cuando las cabezas de dos vectores se
ven conectadas, uno de los vectores es el resultante y el otro es el segundo vector que se está
agregando. Estos principios se pueden aplicar para responder a las preguntas anteriores.
48. Considere los cinco vectores que se muestran a continuación; están etiquetados como A, B,
C, D y E.
Utilice la magnitud y la dirección indicadas de estos vectores para esbozar un diagrama de
adición vectorial para las siguientes operaciones vectoriales y determinar el resultado. Sólo es
necesario construir un croquis aproximado; no hay necesidad de hacer un diagrama escalado.
A+B+C
A+C+B
A+E+D
E+D+C
C-D
B+E-C
Respuesta: Consulte los diagramas anteriores.
Los vectores se agregan mediante un método de cabeza a cola. La magnitud y la dirección de
los vectores se mantienen cuando se realizan las operaciones de suma (y resta). En los
diagramas esbozados, debe asegurarse de:
• coloque la cola del segundo vector en la ecuación en la cabeza del primer vector en la
ecuación
• etiquetar cada vector (A, B, C ...)
• dibujar el resultante de la cola del primer vector a la cabeza del último vector
• etiquetar el resultado
Una operación de resta es lo mismo que agregar el negativo de un vector. Así que si D se va a
restar de C, a continuación, simplemente agregue un vector cuya magnitud es la misma que D,
pero se dirige en la dirección opuesta.49. El movimiento de un excursionista puede describirse
mediante los tres vectores de desplazamiento siguientes.22,0 km, 45 grados + 16,0 km, 135
grados + 12,0 km, 270 grados
Agregue los tres vectores de desplazamiento utilizando el método de cabeza a cola de adición
vectorial. A continuación, responda las dos preguntas siguientes.
(a) ¿Cuál es la distancia recorrida por el excursionista?
(b) ¿Cuál es el desplazamiento resultante del excursionista?
Respuesta: Distancia a 50,0 km; Desplazamiento a 15,5 km, 74 grados
La distancia es una cantidad escalar y no considera que la dirección de las patas individuales
de la caminata sea importante. Así que la distancia es simplemente la suma aritmética de las
distancias de las tres patas individuales de la caminata. Distancia 22,0 km + 16,0 km + 12,0 km
a 50,0 km
El desplazamiento es una cantidad vectorial que es igual a la suma vectorial de los
desplazamientos individuales de la caminata de tres patas. Un diagrama de adición vectorial
escalado sirve como una herramienta útil para determinar esta suma. Se elige una escala
conveniente (por ejemplo, 1 cm a 4 km o 1 cm a 5 km o 1 cm a 8 km) y los vectores se añaden
utilizando el método de cabeza a cola. Esto se muestra en el siguiente diagrama.
Una vez dibujado el resultado, se puede medir la magnitud (en cm) y la escala se puede utilizar
para convertir a kilómetros. La dirección se puede medir desde el diagrama como el ángulo de
rotación en sentido contrario a las agujas del reloj desde el este. El desplazamiento es de 15,5
km a 74 grados.
50. Resuelva el siguiente problema utilizando un diagrama de adición vectorial.
Un excursionista camina por 12,0 km, al oeste. Luego hace un giro y camina en línea recta
hasta llegar a su destino final. Si el desplazamiento resultante es de 21,0 km a 147 grados,
¿cuál fue el desplazamiento (magnitud y dirección) de la segunda etapa de la caminata?
Respuesta: 12,7 km, 116 grados
Este es un problema único en que se da el resultado y se da uno de los dos vectores. El
problema solicita la magnitud y la dirección del segundo vector. En el diagrama siguiente, se
dibuja el primer vector y el resultante se dibuja comenzando en la cola del primer vector. El
segundo vector se extendería desde la cabeza del primer vector hasta la cabeza del resultado.
Esto se puede dibujar en el diagrama y se puede determinar su magnitud y dirección.
51. Considere el diagrama de trayectoria que se muestra a continuación para un proyectil
lanzado horizontalmente. En el diagrama, dibuje flechas vectoriales que representen los
componentes de velocidad vx y vy durante el transcurso del movimiento. La longitud de las
flechas debe representar la magnitud de los componentes de velocidad. Etiquete cada
componente. (Tenga en cuenta que los componentes de velocidad ya se muestran para la
primera posición.)
Respuesta: Consulte el diagrama anterior.
Un proyectil tiene una aceleración hacia abajo. No hay aceleración horizontal; más bien, la
velocidad horizontal permanece constante. Por lo tanto, el vector vx es de longitud constante
(es decir, magnitud) a lo largo de la trayectoria. La aceleración hacia abajo significa que el
vector vy cambiará. A medida que el objeto cae, se acelera. Por lo tanto, el vector vy aumenta
su longitud (es decir, magnitud) a lo largo de la trayectoria. Esto se muestra en el diagrama
anterior.
52. Considere el diagrama de trayectoria que se muestra a continuación para un proyectil no
lanzado horizontalmente. En el diagrama, dibuje flechas vectoriales que representen los
componentes de velocidad vx y vy durante el transcurso del movimiento. La longitud de las
flechas debe representar la magnitud de los componentes de velocidad. Etiquete cada
componente. (Tenga en cuenta que los componentes de velocidad ya se muestran para la
primera posición.)
Respuesta: Consulte el diagrama anterior.
Un proyectil tiene una velocidad horizontal constante y una velocidad vertical cambiante. El
componente vertical cambiante de la velocidad es consistente con el hecho de que hay una
aceleración vertical. A medida que el proyectil se eleva hacia el pico de su trayectoria, la
velocidad vertical disminuye hasta alcanzar 0 m/s en el pico mismo de la trayectoria. A medida
que el proyectil se eleva hacia el pico de su trayectoria, la velocidad vertical aumenta. La
velocidad vertical al caer es de la misma magnitud y la dirección opuesta que cualquier
ubicación correspondiente de la misma altura durante el movimiento ascendente. La velocidad
horizontal permanece constante durante toda la trayectoria. Estos principios se muestran en el
diagrama anterior.
53. Considere el siguiente diagrama. El trazado azul representa la trayectoria de un proyectil
caído del reposo desde la parte superior del trazado. (Cada ubicación de bola representa la
ubicación después de un intervalo de tiempo de 1 segundo.) La trayectoria roja representa la
trayectoria de la misma bola lanzada horizontalmente en ausencia de gravedad. Construir una
tercera trayectoria que muestre con precisión la trayectoria de un proyectil lanzado con la
misma velocidad horizontal que la bola roja. Muestre la ubicación durante los primeros cuatro
segundos de movimiento. Finalmente, la posición de coordenada (x, y) de la ubicación 1 es (0
m, -5 m) y la posición de coordenada (x, y) de la ubicación 2 es (15 m, 0 m). Determine las
posiciones de coordenadas (x, y) de las cuatro ubicaciones de su trayectoria. (Supongamos que
g a 10 m/s/s.)
Respuesta: Consulte el diagrama anterior.
Un proyectil como este tiene un componente horizontal y vertical de movimiento. Estos dos
componentes de movimiento son independientes entre sí. El movimiento estrictamente
vertical de la bola (el camino azul arriba) representa el desplazamiento vertical en intervalos
de 1 segundo. Si se imparte un movimiento horizontal a la bola, su desplazamiento vertical no
se efectuará ya que estos dos componentes son independientes entre sí. El movimiento
estrictamente horizontal de la pelota (el camino rojo de arriba) retrata el movimiento de la
pelota en ausencia de gravedad. La presencia de gravedad haría que la pelota se acelerara
hacia abajo. Este movimiento vertical no afecta al movimiento horizontal, ya que estos dos
componentes son independientes entre sí. El camino verde representa el movimiento del
proyectil cuando la gravedad actúa sobre él y se le imparte un movimiento horizontal. La
ubicación horizontal en cada instante de 1 segundo en el tiempo es la misma posición que
estaba en el camino rojo por encima de ella. Y la ubicación vertical en cada instante de 1
segundo en el tiempo es la misma posición que estaba en el camino azul a la izquierda de la
misma. Las posiciones de coordenadas reales se pueden determinar utilizando las ecuaciones
cinemáticas y el tiempo dado. Para la coordenada x, el desplazamiento es el mismo cada
segundo - es decir, hay una velocidad horizontal constante. Puesto que la ubicación 2 tiene
una coordenada x de 15 m, cada ubicación consecutiva será 15 m más allá de la anterior. La
coordenada y se determina utilizando la expresión 0.5•a•t2 con tiempos de 1 s, 2 s, 3 s y 4 s.
La simplificación de que g es de 10 m/s2 se utiliza para simplificar las matemáticas y resaltar el
concepto.
54. Considere el mapa de los Estados Unidos a la derecha. Dada la escala que 1 cm a 500 km,
utilice un transportador y una regla para determinar el desplazamiento de un viajero para los
viajes enumerados. Un par de viajes incluyen dos "piernas". Indique tanto la magnitud como la
dirección (utilizando el sentido contrario a las agujas del reloj de la convención Este) para el
vector de desplazamiento resultante del viajero.
Dirección de magnitud de viaje
a. De Chicago (CHI) a Washington, DC (WSH)
b. De Chicago (CHI) a Seattle (SEA)
c. De Jackson Hole (JXH) a Houston (HST)
d. De Denver (DEN) a Phoenix (PHX) a Washington (WSH)
e. De Salt Lake City (SLC) a Reno (REN) a Miami (MIA)
Respuesta: Véase la tabla anterior.
a. La distancia de CHI a WSH es de 2,6 cm. Según la escala, esto equivaldría a 1300 km. La
dirección de este vector de desplazamiento se mide como el ángulo de rotación en sentido
contrario a las agujas del reloj desde el este debido a 341 grados.
b. La distancia de CHI a SEA es de 6,7 cm. Según la escala, esto equivaldría a 3400 km. La
dirección de este vector de desplazamiento se mide como el ángulo de rotación en sentido
contrario a las agujas del reloj desde el este de 165 grados.
c. La distancia de JHX a HST es de 4,3 cm. Según la escala, esto equivaldría a 220 km. La
dirección de este vector de desplazamiento se mide como el ángulo de rotación en sentido
contrario a las agujas del reloj desde el este de vencimiento - 312 grados.
d. Este es un viaje de dos patas. Sin embargo, el desplazamiento sólo depende de las
ubicaciones inicial y final. Cuando el viajero ha terminado con el viaje, es desplazado por una
cantidad igual a la distancia de DEN a WSH. Esto es de 6,4 cm en el mapa. Según la escala, esto
equivaldría a 3200 km. La dirección de este vector de desplazamiento se mide como el ángulo
de rotación en sentido contrario a las agujas del reloj desde el este debido a 356 grados.
e. Una vez más, el desplazamiento sólo depende de las ubicaciones inicial y final. Cuando el
viajero ha terminado con el viaje, es desplazado por una cantidad igual a la distancia de SLC a
MIA. Esto es de 7,7 cm en el mapa. Según la escala, esto equivaldría a 3900 km. La dirección de
este vector de desplazamiento se mide como el ángulo de rotación en sentido contrario a las
agujas del reloj desde el este de 334 grados.
55. Una bala de cañón se lanza desde la parte superior de un acantilado de 125 metros de
altura con una velocidad horizontal inicial de 20 m/s. La posición de coordenada (x, y) de la
ubicación de lanzamiento se designa como la posición (0, 0). Determine las posiciones de
coordenadas (x, y) de la bola de cañón a intervalos de 1 segundo durante su ruta hacia el
suelo. Supongamos que g a 10 m/s/s, abajo.
Respuesta: Consulte el diagrama anterior.
La velocidad horizontal es de 20 m/s a lo largo de la trayectoria. Así que el proyectil se moverá
una distancia de 20 metros en cada segundo. Este desplazamiento horizontal se combina con
un movimiento de caída que deja caer el proyectil una cierta distancia vertical por debajo de la
altura inicial del cañón. El desplazamiento vertical se da mediante la expresión 0.5•a•t2 donde
el valor a se indica como 10 m/s2. Los tiempos de 1 s, 2 s, 3 s, etc. se pueden sustituir en esta
expresión para determinar los desplazamientos verticales de -5 m, -20 m, -45 m, -80 m, -125
m.
Parte D: Solución de problemas
56. En el Laboratorio de Adición de Vectores, Anna comienza en la puerta del aula y camina:
• 2,0 metros, Oeste
• 12,0 metros, Norte,
• 31,0 metros, Oeste,
• 8,0 metros, Sur
• 3,0 metros, Este
Usando un diagrama escalado o una calculadora, determine la magnitud y la dirección del
desplazamiento resultante de Anna.
Respuesta: 30,3 metros, 172 grados
Para asegurar la solución más precisa, este problema se resuelve mejor utilizando una
calculadora y principios trigonométricos. El primer paso es determinar la suma de todos los
desplazamientos horizontales (este-oeste) y la suma de todos los desplazamientos verticales
(norte-sur).
Horizontal: 2,0 metros, Oeste + 31,0 metros, Oeste + 3,0 metros, Este a 30,0 metros, Oeste
Vertical: 12,0 metros, Norte + 8,0 metros, Sur a 4,0 metros, Norte
La serie de cinco desplazamientos equivale a dos desplazamientos de 30 metros, Oeste y 4
metros, Norte. El resultado de estos dos desplazamientos se puede encontrar utilizando el
teorema de Pitágoras (para la magnitud) y la función tangente (para la dirección). Un croquis
sin escalas es útil para visualizar la situación.
La aplicación del teorema de Pitágoras conduce a la magnitud del resultado (R).
R2 = (30.0 m)2 + (4.0 m)2 = 916 m2
R = Sqrt(916 m2)
R = 30.3 metros
El ángulo theta en el diagrama anterior se puede encontrar utilizando la función tangente.
tangent(theta) = opposite/adjacent = (4.0 m) / (30.0 m)
tangent(theta) = 0.1333
theta = invtan(0.1333)
theta = 7.59 degrees
Este ángulo theta es el ángulo entre el oeste y el resultante. Las direcciones de los vectores se
expresan como el ángulo de rotación en sentido contrario a las agujas del reloj en relación con
el este. Así que la dirección es 7.59 grados menos de 180 grados. Es decir, la dirección es de
172 grados.
57. En una tienda de comestibles, un comprador camina 36,7 pies por un pasillo. Luego gira a
la izquierda y camina 17,0 pies rectos. Finalmente, gira a la derecha y camina 8,2 pies hasta un
destino final. (a) Determinar la magnitud del desplazamiento global. (b) Determinar la
dirección del vector de desplazamiento en relación con la línea de movimiento original.
Respuesta: (a) 48,0 pies; (b) 21 grados desde la línea de movimiento original
Este problema se aborda mejor mediante un diagrama de la situación física. Los tres
desplazamientos se muestran en el siguiente diagrama a la izquierda. Dado que los tres
desplazamientos se pueden hacer en cualquier orden sin afectar al desplazamiento resultante,
estas tres patas del viaje se reorganizan convenientemente en el diagrama de abajo a la
derecha.
Ahora es obvio en el diagrama de la derecha que los tres vectores de desplazamiento son
equivalentes a dos vectores de desplazamiento perpendiculares de 44,9 pies y 17 pies. Estos
dos vectores se pueden agregar juntos y el resultado se puede dibujar desde la ubicación
inicial hasta la ubicación final. A continuación, se muestra un boceto.
Dado que estos vectores de desplazamiento están en ángulo recto entre sí, la magnitud del
resultado se puede determinar utilizando el teorema de Pitágoras. La obra se muestra a
continuación.
R2 = (44.9 ft)2 + (17.0 ft)2 = 2305 ft2
R = Sqrt(2305 ft2)
R = 48.0 feet
El ángulo theta en el diagrama anterior se puede encontrar utilizando la función tangente.
tangent(theta) = opposite/adjacent = (17.0 ft) / (44.9 ft)
tangent(theta) = 0.3786
theta = invtan(0.3786)
theta = 20.7 degrees
Este es el ángulo que el resultado hace con la línea de movimiento original (el vector de
desplazamiento de 36,7 pies).
58. Un excursionista camina 12,4 km, al sur. El excursionista entonces hace un giro hacia el
sureste y termina en el destino final. El desplazamiento total del viaje de dos patas es de 19,7
km a 309 grados. Determine la magnitud y la dirección de la segunda etapa del viaje.
Respuesta: 12,7 km, 347 grados
Al igual que el problema anterior (y la mayoría de los otros problemas en la física), este
problema se aborda mejor usando un diagrama.
El primer desplazamiento se debe al sur y el desplazamiento resultante (a 309 grados) está en
algún lugar del cuarto cuadrante. (Es en el cuarto cuadrante porque 309 grados se encuentra
entre 270 grados o debido al sur y 360 grados o debido al este.) Por el bien de la
comunicación, nos referiremos al primer desplazamiento como A y el segundo desplazamiento
como B. Tenga en cuenta que A + B = R. Dado que se conoce la magnitud y la dirección del
resultado, los componentes x e y se pueden determinar mediante funciones trigonométricas.
Dado que el ángulo de 309 grados se expresa como un ángulo de rotación en sentido contrario
a las agujas del reloj con el presente, se puede utilizar como Theta en la ecuación.
Rx = R•cos(theta) = 19.7 km • cos(309 deg) = 12.398 km
Ry = R•sin(theta) = 19.7 km • sin(309 deg) = -15.310 km (the "-" means
South)
Cualquiera que sea la magnitud y la dirección de B, debe añadirse al vector A para dar un
desplazamiento hacia el sur de 15.310 km y un desplazamiento hacia el este de 12.398 km.
Esto podría expresarse mediante ecuaciones matemáticas como
Ax + Bx = 12.398 km, east
Ay + By = 15.310 km, south
Pero Ax está a 0 km y Ay está a 12 km, al sur. Al sustituir estos dos valores en
las ecuaciones anteriores, se pueden determinar los valores de los
componentes x e y del desplazamiento desconocido:
Bx = 12.398 km, east and By = 2.910 km, south
Conocer los componentes Bx y By nos permitirá determinar
la magnitud y la dirección de B. Otro diagrama ayudaría a visualizar la
situación. La magnitud de B se puede encontrar usando el teorema de
Pitágoras. B es la hipotenusa de un triángulo recto con patas de 12.398 km y
2.910 km. La suma de los cuadrados de los lados es igual al cuadrado de la
hipotenusa.
B2 = (12.398 km)2 = (2.910 km)2
B2 = 162.179 km2
B = Sqrt(162.179 km2)
B = 12.735 km
La dirección de B es cercana a los 360 grados. Como se muestra en el
diagrama, es menos de 360 grados por una cantidad igual a theta. El ángulo
theta se puede determinar utilizando la función tangente y la longitud de los
dos lados del triángulo derecho.
Tangent (Theta) = (2.910 km) / (12.398 km)
Tangent (Theta) = 0.2347
Theta = Invtan (0.2347)
Theta = 13.2 degrees
The direction of B is 360 degrees - 13.2 degrees = ~347 degrees.
59. Un barco se dirige directamente a través de un río que es 100. metros de
ancho. Para las dos combinaciones siguientes de velocidades de barco y
velocidades actuales, determine la velocidad resultante, el tiempo necesario
para cruzar el río y la distancia recorrida aguas abajo.
a.
Given:
b.
Given:
Boat velocity = 10.0 m/s, East
Boat velocity = 8.0 m/s, East
River velocity = 4.0 m/s, North
River velocity = 5.0 m/s, South
Calculate:
Calculate:
Resultant Vel. (mag. & dir'n): 11 m/s, Resultant Vel. (mag. & dir'n): 9.4 m/s,
22 deg.
328 deg.
Time to cross river: 10.0 s
Time to cross river: 13 s
Distance traveled downstream: 40. m
Distance traveled downstream: 63 m
Respuesta: Véase la tabla anterior.
Los dos vectores de velocidad (barco y río) se dirigen perpendiculares entre sí.
Se pueden añadir usando el teorema de Pitágoras. La dirección se encuentra
utilizando la función tangente; se expresa como el ángulo de rotación en
sentido contrario a las agujas del reloj desde el debido este. El tiempo para
cruzar el río depende de la anchura del río y la velocidad del barco. Y la
distancia aguas abajo depende del tiempo que el barco se está moviendo y la
velocidad a la que se mueve aguas abajo - la velocidad del río.
a.
Resultant Vel. (mag. & dir'n):
b.
Resultant Vel. (mag. & dir'n):
R2 = (10.0 m/s)2 + (4.0 m/s)2
R2 = (8.0 m/s)2 + (5.0 m/s)2
R = SQRT ( (10.0 m/s)2 + (4.0 m/s)2 )
R = SQRT ( (8.0 m/s)2 + (5.0 m/s)2 )
R = SQRT(116 m2/s2) = 11
m/s (rounded from 10.8 m/s)
R = SQRT(89 m2/s2) = 9.4
m/s (rounded from 9.43 m/s)
dir'n = invtan(4.0/10.0) = 22 degrees
dir'n = 360 deg. - invtan(5.0/8.0)
= 328 degrees
Time to cross river:
d = v*t ---> t = d/v
t = (100. m)/(10.0 m/s) = 10.0 s
Distance traveled downstream:
d = v*t = (4.0 m/s)*(10.0 s) = 40. m
Time to cross river:
d = v*t ---> t = d/v
t = (100. m)/(8.0 m/s)
= 13 s (rounded from 12.5 s)
Distance traveled downstream:
d = v*t = (5.0 m/s)*(12.5 s) = ~63 m
60. El diagrama de la derecha muestra un proyectil lanzado horizontalmente
dejando un acantilado de altura y con una velocidad horizontal (vix) y
aterrizando una distancia x de la base del acantilado. Exprese su comprensión
de la cinemática de proyectiles rellenando los espacios en blanco en la siguiente
tabla. Para simplificar los cálculos, utilice el valor aproximado para la
aceleración del valor de gravedad de -10 m/s/s.
vix
y
(m/s)
(m)
a.
15.0 m/s
20.0 m
b.
15.0 m/s
45.0
c.
45.0 m
15.0
d.
12.0
31.3
e.
74.0 m
17.2
Respuesta: Véase la tabla anterior.
t
(s)
2.00
3.00 s
3.00
2.50 s
3.85
x
(m)
30.0
45.0
45.0 m
30.0 m
66.0 m
Las soluciones a los cinco problemas de los proyectiles implican el uso de
ecuaciones cinemáticas y una estrategia adecuada de resolución de problemas.
Las ecuaciones cinemáticas y su uso en problemas de proyectiles se enumeran
y discuten en otros lugares. La idea básica de la estrategia es identificar tres
variables cinemáticas para el movimiento horizontal o para el movimiento
vertical. Una vez, se conocen tres cantidades en una dirección, se pueden
encontrar todas las demás cantidades en esa dirección (o se puede encontrar la
hora del vuelo). A menudo, el tiempo se utiliza con cantidades cinemáticas para
la segunda dimensión con el fin de determinar todas las demás cantidades
desconocidas para esa dimensión.
En cada uno de estos problemas, se sabe que ax = 0 m/s/s, ay = -10 m/s/s, and
viy = 0 m/s. Cuando estos tres conocidos se combinan con los otros conocidos
dados se obtienen las siguientes respuestas:
Answers
a.
t = 2.0 s and x = 30.0 m
Method
Use y, viy, and ay to calculate t; then use
t, vix and ax to calculate x.
b.
y = 45.0 m and x = 45.0 m
Use t, vix and ax to calculate x; and use t,
viy, and ay to calculate y.
c.
Use y, viy, and ay to calculate t; then use
vix = 15.0 m/s and t = 3.00 s t, x and ax to calculate vix.
d.
Use t, x and ax to calculate vix; and use t,
vix = 12.0 m/s and y = 31.3 m viy, and ay to calculate y.
e.
Use y, viy, and ay to calculate t; then use
vix = 17.2 m/s and t = 3.85 s t, x and ax to calculate vix.
61. La velocidad y el ángulo de lanzamiento se indican para tres proyectiles
diferentes. Utilice funciones trigonométricas para resolver los vectores de
velocidad en componentes de velocidad horizontal y vertical. A continuación,
utilice ecuaciones cinemáticas para determinar el tiempo que el proyectil está
en el aire, la altura a la que viaja (cuando está en su pico) y la distancia
horizontal que recorre. (Para simplificar los cálculos, utilice una aceleración del
valor de gravedad de -10 m/s/s.)
a.
Given:
b.
Given:
c.
Given:
Launch Vel. = 30.0 m/s
Launch Vel. = 30.0 m/s
Launch Vel. = 30.0 m/s
Launch angle = 30.0
degrees
Launch angle = 45.0
degrees
Launch angle = 50.0
degrees
Calculate:
vix = 26.0 m/s
Calculate:
vix = 21.2 m/s
Calculate:
vix = 19.3 m/s
viy = 15 m/s
viy = 21.2 m/s
viy = 23.0 m/s
tup = 1.5 s
tup = 2.12 s
tup = 2.35 s
ttotal = 3.0 s
ttotal = 4.24 s
ttotal = 4.69 s
y at peak = 11.3 m
y at peak = 22.5 m
y at peak = 26.9 m
x = 77.9 m
x = 89.9 m
x = 90.4 m
Respuesta: Véase la tabla anterior.
Las soluciones a los tres problemas de proyectiles no lanzados horizontalmente
implican el uso de ecuaciones cinemáticas y una estrategia adecuada de
resolución de problemas. Las ecuaciones cinemáticas y su uso en problemas de
proyectiles se enumeran y discuten en otros lugares. En cada uno de estos
problemas, se sabe que ax = 0 m/s/s and ay = -10 m/s/s los valores de vix y viy
se pueden determinar utilizando funciones trigonométricas:
vix = vi * cos(theta)
viy = vi * sin(theta)
Una vez que se conocen la vix y la víy, las otras incógnitas se pueden calcular.
El tiempo hasta el pico (tup) se puede determinar usando la ecuación
vfy = viy + ay *t
donde el vfy = 0 m/s (no hay velocidad vertical para un proyectil cuando está en
su pico) y ay = -10 m/s/s. Una vez que se conoce el tup, el ttotal (tiempo para
recorrer toda la trayectoria -tanto arriba como abajo) se puede determinar
duplicando la tup. El desplazamiento horizontal del proyectil (x) se puede
calcular de la manera habitual utilizando la ecuación
x = vix*t + 0.5*ax*t2
donde t es el valor ttotal, ax = 0 m/s/s y vix fue el primer valor calculado
(utilizando las funciones trigonométricas). Finalmente, la y en el pico (es decir,
la altura máxima) se puede calcular utilizando la ecuación
y = viy*t + 0.5*ay*t2
donde t es el valor tup, ay = -10 m/s/s y viy fue uno de los primeros valores
calculados (utilizando la función trigonométrica). El valor t en la ecuación es tup
porque la altura máxima se alcanza cuando el proyectil ha viajado durante la
mitad de su tiempo total; tup es ese momento. Este método producirá las
respuestas dadas en la tabla anterior.62. Si un proyectil se pone en marcha
horizontalmente con una velocidad de 12,0 m/s desde la parte superior de un
edificio de 24,6 metros de altura. Determinar el desplazamiento horizontal del
proyectil.
Respuesta: x a 27,0 m
Este problema de proyectiles lanzado horizontalmente puede resolverse (y
debe) resolverse de la misma manera que la solución a #60 anteriormente.
Mientras que #60 se desglosa para usted en buenos pasos, este problema no
es tan fácil de usar. Se recomienda encarecidamente que comience
enumerando los valores conocidos para cada una de las variables en las
ecuaciones cinemáticas. Es útil organizar la información en dos columnas: una
columna de información horizontal conocida y una columna de información
vertical conocida.
Horizontal Motion
x = ???
Vertical Motion
y = -24.6 m (- means moving down)
vix = 12.0 m/s
viy = 0.0 m/s (its launched horizontally)
ax = 0 m/s/s (true for all projectiles)
ay = -9.8 m/s/s (true for all projectiles)
Dado que ahora se conocen tres partes de la información y, se puede emplear una
ecuación y para encontrar el tiempo.
y = viy*t + 0.5*ay*t2
Enchufar y tirar los valores anteriores en esta ecuación produce un tiempo de 2,25
segundos. Ahora el valor t se puede combinar con el valor vix y hacha y se puede
utilizar en una ecuación x
x = vix*t + 0.5*ax*t2
para dar la respuesta 27,0 m. Más ejemplos y discusión de este tipo de problemas de
proyectiles se discuten en otros lugares.63. Se lanza un proyectil con una velocidad
inicial de 21,8 m/s en un ángulo de 35,0 grados por encima de la horizontal.
(a) Determinar la hora de vuelo del proyectil.
(b) Determinar la altura máxima del proyectil.
(c) Determinar el desplazamiento horizontal del proyectil.
Respuesta: (a) 2.55 s; (b) 7,98 m; (c) 45,7 m
Este problema de proyectiles no lanzado horizontalmente puede resolverse (y debe)
resolverse de la misma manera que la solución a #61 anteriormente. Mientras que #61
se desglosa para usted en pasos bien estructurados, este problema no es tan fácil de
usar. Se recomienda encarecidamente que comience resolviendo la velocidad inicial y
el ángulo en los componentes de velocidad inicial utilizando las ecuaciones:
vix = vi * cos(theta)
viy = vi * sin(theta)
Esto produce valores de vix = 17,9 m/s y viy = 12,5 m/s. Una vez hecho esto, enumere
los valores conocidos para cada una de las variables en las ecuaciones cinemáticas. Es
útil organizar la información en dos columnas: una columna de información horizontal
conocida y una columna de información vertical conocida.
Horizontal Motion
Vertical Motion
x = ???
y = 0 m (it rises and falls to original height)
vix = 17.9 m/s (from trig. function)
viy = 12.5 m/s (from trig. function)
ax = 0 m/s/s (true for all projectiles)
ay = -9.8 m/s/s (true for all projectiles)
Dado que ahora se conocen tres partes de la información y, se puede emplear una
ecuación y para encontrar el tiempo. Una ecuación útil es
y = viy*t + 0.5*ay*t2
en cuyo caso habrá dos soluciones: t = 0 s y t = 2,55 s. Estas dos soluciones a la
ecuación indican que el tiempo es 0 s cuando el desplazamiento vertical (y) es 0 m.
Esto es cierto antes de ser lanzado (t = 0 s) y en el instante en que aterriza (t=2.55 s).
La última de las dos soluciones se puede utilizar para determinar el desplazamiento
horizontal (x). Utilice la ecuación:
x = vix*t + 0.5*ax*t2
donde t es 2.55 s, ax = 0 m/s/s y vix fue el primer valor calculado (utilizando las
funciones trigonométricas). Enchufar un chugging los valores anteriores en esta
ecuación produce la respuesta de 45,7 m.
Encontrar las demandas de desplazamiento vertical en el pico (ypeak) utilizando la
ecuación y original con un tiempo de 1,28 segundos (tup). Este tiempo corresponde a
la hora de la mitad de la trayectoria - el tiempo en el que el proyectil estará en su
posición más alta o pico. Sustituir los valores viy, ay y t en la ecuación
ypeak = viy*tup + 0.5*ay*tup2
produce un valor de 7,98 m para la altura máxima.
Más ejemplos y discusión de este tipo de problemas de proyectiles se discuten en
otros lugares.64. Un proyectil se lanza horizontalmente desde la cima de un acantilado
de 45,2 metros de altura y aterriza a una distancia de 17,6 metros de la base del
acantilado. Determine la magnitud de la velocidad de lanzamiento.
Respuesta: 5,79 m/s
El mejor medio para iniciar este problema es enumerar los valores conocidos para cada
una de las variables en las ecuaciones cinemáticas. Es útil organizar la información en
dos columnas: una columna de información horizontal conocida y una columna de
información vertical conocida.
Horizontal Motion
Vertical Motion
x = 17.6 m (the distance horizontally y = -45.2 m (it falls down from the cliff
from cliff base)
to the ground)
vix = ??? m/s
viy = 0 m/s (it is horizontally launched)
ax = 0 m/s/s (true for all projectiles)
ay = -9.8 m/s/s (true for all projectiles)
Dado que ahora se conocen tres partes de la información y, se puede emplear una
ecuación y para encontrar el tiempo. Una ecuación útil es:
y = viy*t + 0.5*ay*t2
en cuyo caso habrá dos soluciones: t = 3.0372 s y t = -3.0372 s. Una parábola completa
que sigue a la función anterior tendría a lugares donde la coordenada y es de -45,2 m.
Uno sería "avanzar en el tiempo" a 3.0372 segundos; y la otra solución está en una
ubicación trazada "hacia atrás en el tiempo" desde el momento de lanzamiento. Por
supuesto, la respuesta positiva es la que necesitamos; se puede utilizar para
determinar la velocidad horizontal inicial (vix). Utilice la ecuación:
x = vix*t + 0.5*ax*t2
donde t es 3.0372 s, ax = 0 m/s/s y x = 17,6 m. Enchufar y tirar los valores anteriores en
esta ecuación produce la respuesta de 5.7948 m/s.
65. Dos estudiantes de física se paran en la parte superior de su cubierta de 3,29
metros de segundo piso y lanzan un globo de agua desde un extremo casero. El globo
se lanza hacia arriba a una velocidad de 45,2 m/s y un ángulo de 39,1 grados. El globo
aterriza en un estanque de retención cuya superficie está 2,92 metros por debajo del
grado. Determine la distancia horizontal desde la ubicación de lanzamiento hasta la
ubicación de aterrizaje.
Respuesta: 211 m
Se trata de un problema de proyectiles no lanzado horizontalmente en el que se dan la
velocidad inicial y el ángulo de lanzamiento. Tres pasos iniciales siempre se toman
sabiamente antes de iniciar un problema de este tipo. En primer lugar, determine los
componentes de velocidad iniciales (vix e viy) utilizando funciones trigonométricas. En
segundo lugar, construya un diagrama de la situación física. Y en tercer lugar, organizar
información conocida (y desconocida) en una "tabla x-y". Estos tres pasos se toman
aquí. Rápidamente irrumpir en una solución antes de dar al problema un cierto análisis
previo a menudo conduce a una pérdida de mucho tiempo y, en última instancia, una
gran cantidad de confusión.
La velocidad inicial y el ángulo se pueden resolver en componentes de velocidad inicial
utilizando las ecuaciones:
vix = vi * cos(theta)
viy = vi * sin(theta)
Esto produce valores de vix = 35.077 m/s y viy = 28.507 m/s.
Se muestra un diagrama de la situación física.
Ahora los valores conocidos para cada una de las variables en las ecuaciones
cinemáticas se enumeran en una tabla utilizando una columna para información
horizontal conocida y una columna para información vertical conocida.
Horizontal Motion
x = ???
vix = 35.077 m/s (from trig.
function)
ax = 0 m/s/s (true for all
projectiles)
Vertical Motion
y = -5.49 m (from initial + to height to final height)
viy = 28.507 m/s (from trig. function)
ay = -9.8 m/s/s (true for all projectiles)
Dado que ahora se conocen tres partes de la información y, se puede emplear una
ecuación y para encontrar el tiempo. Una ecuación útil es
y = viy*t + 0.5*ay*t2
en cuyo caso habrá dos soluciones: t= -0,1867 s y t = 6,004 s. Una parábola completa
que sigue a la función anterior tendría dos ubicaciones donde la coordenada y es de
-5,49 m. Una ubicación sería "adelante en el tiempo" en 6.004 segundos; y la otra
solución está en una ubicación trazada "hacia atrás en el tiempo" desde el momento
de lanzamiento. Por supuesto, la respuesta positiva es la que necesitamos; se puede
utilizar para determinar el desplazamiento horizontal (x).
Ahora usa la ecuación:
x = vix*t + 0.5*ax*t2
donde t = 6.004 s, ax = 0 m/s/s y vix = 35.077 m/s (como se calculó originalmente
utilizando las funciones trigonométricas). Enchufar y tirar los valores anteriores en esta
ecuación produce la respuesta de 211 m. (Wow! Será mejor que esos chicos tengan
cuidado.)
66. Un pateador de lugar patea un balón desde 39,6 metros desde los postes de la
portería. La patada sale del suelo con una velocidad de 24,8 m/s en un ángulo de 49,6
grados. Los postes de la portería tienen 3,10 metros de altura.
(a) Determinar la cantidad por la cual la patada borra los postes de la portería.
b) Para esta velocidad de lanzamiento dada, ¿cuál es el gol de campo más largo (en
yardas) que podría haber sido pateado? Supongamos que el balón golpea el travesaño
horizontal de los postes y rebota a través. Dado: 1.00 metros a 3,28 pies.
Respuesta: (a) 13,7 m; (b) 64,7 m (medidos desde la ubicación de la patada hasta los
puestos de gol)
(a) En parte de este problema, la tarea consiste en encontrar la altura de la pelota
(y) cuando ha recorrido una distancia de 39,6 metros. La altura de los postes de
objetivo se puede restar de este valor para determinar la cantidad de espacio
libre.
(b) Como es el caso en todos los problemas de proyectiles no lanzados
horizontalmente, debe iniciarse resolviendo la velocidad inicial y el ángulo en
los componentes de velocidad inicial utilizando las ecuaciones:
vix = vi * cos(theta)
viy = vi * sin(theta)
Esto produce valores de vix = 16.073 m/s y viy = 18.886 m/s. Una vez hecho esto,
enumere los valores conocidos para cada una de las variables en las ecuaciones
cinemáticas. Es útil organizar la información en dos columnas: una columna de
información horizontal conocida y una columna de información vertical conocida.
Horizontal Motion
x = 39.6 m (horiz. distance to goal
posts)
Vertical Motion
y = ??? (we need to calculate this)
vix = 16.073 m/s (from trig. function)
ax = 0 m/s/s (true for all projectiles)
viy = 18.886 m/s (from trig. function)
ay = -9.8 m/s/s (true for all
projectiles)
Dado que ahora se conocen tres piezas de información x, se puede emplear una
ecuación x para encontrar el tiempo para que el fútbol viaje la distancia horizontal a
los postes de la portería. Una ecuación útil es
x = vix*t + 0.5*ax*t2
en cuyo caso el tiempo es de 2.4637 s. El tiempo ahora se puede combinar con una
secuacion y para encontrar el desplazamiento vertical (es decir, la altura sobre el
suelo) cuando el fútbol ha viajado horizontalmente a los postes de la portería. Utilice la
ecuación:
y = viy*t + 0.5*ay*t2
donde t = 2.4637 s, ay a -9,8 m/s/s y viy = 18.886 m/s. Enchufar un chugging los valores
anteriores en esta ecuación produce la respuesta de 16.788 m.
Cuando la pelota ha recorrido una distancia horizontal de 39,6 m, está a 16,8 m sobre
el suelo. Los postes de gol son 3,10 m de altura; por lo que el balón despeja los postes
de la portería en 13,7 metros.
(b) La parte b de este problema se puede hacer de manera similar. La tarea consistirá
primero en encontrar el tiempo para que la pelota suba a su pico y luego caiga de
nuevo a una altura de 3,10 metros. A continuación, el desplazamiento horizontal se
puede calcular para este tiempo. La respuesta final deberá convertirse en yardas. Se
pueden utilizar los mismos valores vix y viy. Dado el nuevo contexto del problema, el
valor de y ahora se conoce y x es desconocido. La información se puede organizar en la
tabla x e y habitual.
Horizontal Motion
x = ???
Vertical Motion
y = 3.10 m (the height of the goal posts)
vix = 16.073 m/s (from trig. function)
viy = 18.886 m/s (from trig. function)
ax = 0 m/s/s (true for all projectiles)
ay = -9.8 m/s/s (true for all projectiles)
Dado que ahora se conocen tres partes de la información y, se puede emplear una
ecuación y para encontrar el tiempo. Una ecuación útil es
y = viy*t + 0.5*ay*t2
en cuyo caso habrá dos soluciones: t = 0,1718 s y t = 3,6825 s. La primera solución
corresponde al primer punto a lo largo de la parábola (durante el ascenso del balón)
cuando el fútbol está a una altura de 3,10 m y la segunda solución es el segundo punto
a lo largo de la parábola (durante la caída del fútbol) cuando el fútbol está a una altura
de 3,10 m. La segunda respuesta se puede utilizar para determinar el desplazamiento
horizontal (x) del fútbol. Utilice la ecuación:
x = vix*t + 0.5*ax*t2
donde t = 3.6825 s, ax = 0 m/s/s y vix = 16.073 m/s. Enchufar un chugging los valores
anteriores en esta ecuación produce la respuesta de x a 59.189 m. Este valor x se
puede convertir en pies multiplicando por la relación de conversión de 3,28 ft/m y
luego convertirse en yardas dividiendo por la relación de conversión de 3,00 ft/yd. El
pateador puede patear como un gol de campo de 64,7 yardas. (En el fútbol, se le
conocería como gol de campo de 47 yardas ya que los postes de la portería se colocan
a 10 yardas detrás de la línea de gol y el balón es pateado desde unas 7 yardas detrás
de la línea de scrimmage. Las distancias de los objetivos de campo se miden desde la
línea de meta hasta la línea de scrimmage.)
67. Un avión comienza en el punto A y vuela 210. km a 311 grados hasta el punto B. El
avión vuela 179 km a 109 grados hasta el punto C. Finalmente, el avión vuela 228 km a
29 grados hasta el punto D. Determinar el desplazamiento resultante (magnitud y
dirección) de los puntos A a D.
Respuesta: R a 304 km, 24 grados
Al igual que la mayoría de los problemas de adición de vectores, este problema se
inicia mejor mediante la construcción de un boceto aproximado de la situación física.
Este boceto se muestra a continuación. Hay tres desplazamientos separados tomados
por el avión para dar lugar a un único desplazamiento desde el punto A al punto D.
La solución real se realiza mejor utilizando funciones trigonométricas para
determinar los componentes X e Y de cada vector de desplazamiento. A
continuación, estos componentes se agregan para determinar el componente x
e y del resultante. El trabajo se organiza en una tabla a continuación.
X-component
Y-Component
210. km • cos(311)
210 km • sin(311)
A to B
= 137.772 km, East
= 158.489 km, South
B to C
179 km • cos(109)
179 km • sin(109)
= 58.277 km, West
= 169.248 km, North
C to D
228 km • cos(29)
199.413 km, East
228 km • sin(29)
110.537 = km, North
Resultant
278.909 km, East
121.295 km, North
Una vez conocidos los componentes, el teorema de Pitágoras se puede utilizar
para determinar el resultado. El resultado tiene componentes de 278.909 km,
Este y 121.295 km, Norte. La magnitud y la dirección del resultado se pueden
determinar agregando estos componentes. Puesto que están en ángulo recto
entre sí, la magnitud se puede determinar usando el teorema de Pitágoras
como se muestra a continuación.
R2 = Rx2 + Ry2
2
2
R = (278.909 km) + (121.295 km)2 = 92502.800 km2
R = SQRT(92502.800 km2)
R = 304 km
La dirección se indicaría como el ángulo de rotación en sentido contrario a las
agujas del reloj desde el presente. Este es simplemente el ángulo Theta. Theta
se puede determinar mediante la función tangente. La obra se muestra a
continuación.
Tangent(theta) = Ry/Rx
Tangent(theta) = (121.295 km) / (278.909 km) = 0.43489
Theta = Invtan(0.43489)
Theta = 23.5 degrees
68. Sammy Sosa coloca un jonrón que navega 421 pies y aterriza en un balcón
de apartamentos situado a una distancia vertical de 59,0 pies por encima del
nivel de la ubicación de contacto entre pelota y murciélago. Un observador
multiplica el vuelo al balcón para tomar 3.40 segundos.
(a) Determinar la velocidad (magnitud y ángulo) a la que la pelota sale del
bate.
(b) Determinar la velocidad de la pelota (en millas/hora) cuando aterriza en las
gradas.
Dado: 1.00 m/s = 2,24 mi/hr; 1.00 metros = 3,28 pies.
Respuesta: a) = 43,7 m/s = 30,2 grados; (b) 88,3 mi/h
(a) Para cualquier problema de proyectiles, siempre es una buena idea comenzar la
solución con una lista de información conocida y desconocida en una "tabla x-y". Esto
se muestra a continuación.
Horizontal Motion
Vertical Motion
x = 421 ft = 128.35 m (horiz. distance y = 59.0 ft = 17.99 m (vert. distance
to balcony)
to balcony)
vix = ???
viy = ???
ax = 0 m/s/s (true for all projectiles)
ay = -9.8 m/s/s (true for all projectiles)
t = 3.40 s (the ball is a projectile for this t = 3.40 s (the ball is a projectile for
long)
this long)
Tenga en cuenta que se conoce la hora del vuelo. El tiempo es una cantidad escalar y
no tiene ningún componente direccional asociado; no se puede hacer referencia al
tiempo horizontal o al tiempo vertical. Se enumera en ambas tablas ya que se puede
utilizar con ecuaciones cinemáticas tanto para la dirección x como para la dirección y.
Dado que se conocen tres partes de la información x, se puede emplear una ecuación x
para encontrar la velocidad horizontal inicial. Una ecuación útil es
x = vix*t + 0.5*ax*t2
La velocidad horizontal inicial (vix) es de 37.751 m/s.
También hay tres piezas de información y conocidas. Por lo tanto, se puede utilizar una
ecuación y para determinar la velocidad vertical inicial (viy). Una buena ecuación es
y = viy*t + 0.5*ay*t2
Enchufar un chugging los valores anteriores en esta ecuación produce un valor de
velocidad vertical inicial (viy) de 21.951 m/s.
La pelota deja el bate de Sammy Sosa moviéndose hacia arriba con una velocidad de
21.951 m/s y moviéndose horizontalmente con una velocidad de 37.751 m/s. Estos dos
componentes de la velocidad inicial se pueden utilizar para determinar la velocidad
inicial y el ángulo de la pelota de béisbol después del contacto con el bate. Un
diagrama se muestra a la derecha. La velocidad inicial de la bola está representada por
la hipotenusa de un triángulo derecho con lados iguales a los valores de componente.
Por lo tanto, el teorema de Pitágoras se puede utilizar para determinar la velocidad
inicial de la pelota de béisbol.
vi 2 = (vix)2 + (viy) 2
vi2 = (37.751 m/s)2 + (21.951 m/s)2
vi 2 = 1906.97 m2/s2
vi = SQRT (1906.97 m2/s2 ) = 43.7 m/s
El ángulo (theta) de la velocidad inicial se puede determinar mediante una función
trigonométrica. La función tangente se utiliza aquí.
Tangent(theta) = opposite / adjacent
Tangent(theta) = (21.951 m/s) / (37.751 m/s) = 0.58145
Theta = Invtan (0.58145) = 30.2 degrees
(b) En la parte a) de este problema, se determinó que la velocidad horizontal inicial era
de 37.751 m/s. Para los proyectiles, esta velocidad horizontal no cambia durante el
vuelo del proyectil. Por lo tanto, el proyectil golpea el balcón moviéndose con una
velocidad horizontal final (vfx) de 37.751 m/s. Si se puede determinar la velocidad
vertical final (vfy), entonces se puede utilizar con el valor vfx para determinar la
velocidad final (vf). Varias ecuaciones cinemáticas son útiles para encontrar la
velocidad vertical final (vfy). Se utilizará la siguiente ecuación:
vfy = viy + ay•t
vfy = 21.951 m/s + (-9.8 m/s/s)•(3.4 s)
vfy = 21.951 m/s - 33.32 m/s
vfy = -11.369 m/s
Con los componentes x e y de la velocidad final (vf)
conocidos, el teorema de Pitágoras se puede utilizar para determinar el valor de
velocidad final. Un diagrama se muestra a la derecha y los cálculos se muestran a
continuación.
vf 2 = (vfx)2 + (vfy) 2
vf2 = (37.751 m/s)2 + (-11.369 m/s)2
vf 2 = 1554.41 m2/s2
vf = SQRT (1554.41 m2/s2) = 39.43 m/s
Este valor se puede convertir a millas/hora utilizando el hecho de que 1,00 m/s = 2,24
millas/hora. La respuesta a la parte b es 88.3 mi/hr.
69. Se produjo un desafortunado accidente en el camino de peaje. Un conductor
accidentalmente pasó a través de una barricada defectuosa en un puente (bastante
por desgracia). y aterrizó en una pila de heno (bastante afortunadamente). Las
mediciones en la escena del accidente revelan que el conductor se hundió a una
distancia vertical de 8,26 metros. El coche llevaba una distancia horizontal de 42,1
metros desde el lugar donde salió del puente. Si el conductor estaba en una zona de
velocidad de 65 millas/h, entonces determine la cantidad por la cual el conductor
estaba excediendo el límite de velocidad en el momento del accidente. Supongamos
que el contacto con la barricada no frenó el coche. (1,00 m/s = 2,24 mi/h)
Respuesta: 72,6 mi/hr
Este es un ejemplo de un problema de proyectiles lanzado horizontalmente. Al igual
que todos los problemas de proyectiles, el mejor medio para iniciar el problema es
enumerar los valores conocidos para cada una de las variables en las ecuaciones
cinemáticas. Es útil organizar la información en dos columnas: una columna de
información horizontal conocida y una columna de información vertical conocida.
Horizontal Motion
x = 42.1 m (the horizontal distance
which is traveled)
Vertical Motion
y = -8.26 m (it falls down from the cliff
to the ground)
vix = ??? m/s
viy = 0 m/s (it is horizontally launched)
ax = 0 m/s/s (true for all projectiles)
ay = -9.8 m/s/s (true for all projectiles)
Dado que ahora se conocen tres partes de la información y, se puede emplear una
ecuación y para encontrar el tiempo. Una ecuación útil es
y = viy*t + 0.5*ay*t2
en cuyo caso habrá dos soluciones: t = 1.2983 s y t = -1.2983 s. Una parábola completa
que sigue a la función anterior tendría dos ubicaciones donde la coordenada y es de 8,26 m. Uno sería "avanzar en el tiempo" a 1.2983 segundos; y la otra solución está en
una ubicación trazada "hacia atrás en el tiempo" desde el momento de lanzamiento.
Por supuesto, la respuesta positiva es la que necesitamos; se puede utilizar para
determinar la velocidad horizontal inicial (vix). Utilice la ecuación:
x = vix*t + 0.5*ax*t2
donde t = 1.2983 s, ax = 0 m/s/s y x = 42,1 m. colocar los valores anteriores en esta
ecuación produce la respuesta de 32.426 m/s. Esta es la velocidad a la que el coche
sale del puente al inicio de su movimiento de proyectil. Convertir esto a mi/hr implica
multiplicar por la relación de conversión (2.24 mi/hr) / (1 m/s). El resultado es 72.6
mi/hr.
(En realidad, el coche viajaba más rápido que esta velocidad, ya que la colisión con el
riel de protección probablemente frenó el coche antes de salir del puente y comenzó
su movimiento de proyectiles.)
70. Cupido desea disparar una flecha a través de la ventana abierta de un edificio alto.
La ventana está a 32,8 metros sobre el suelo y Cupido se encuentra a 63,6 metros de la
base del edificio. Si Cupido apunta la flecha en un ángulo de 51,5 grados por encima de
la horizontal, ¿con qué velocidad mínima debe disparar la flecha para que entre en la
ventana?
Respuesta: 32,7 m/s
Este es un ejemplo de un problema de proyectiles lanzado no horizontalmente en el
que se da el ángulo, pero no se conoce la velocidad de lanzamiento. Por lo tanto, no se
pueden encontrar los componentes x e y de la velocidad inicial. No obstante, las
expresiones que relacionan estos componentes con la velocidad inicial todavía se
pueden escribir y utilizar en el problema.
vix = vi * cos(theta)
viy = vi * sin(theta)
Se toma el procedimiento habitual de enumerar la información conocida en una "tabla
x-y":
Horizontal Motion
Vertical Motion
x = 63.6 m (horizontal distance to
y = 32.8 m (vertical distance from ground
building)
to window)
vix = vi * cos(51.5 deg) = 0.6225 •
viy = vi * sin(51.5 deg) = 0.7826 • vi
vi
ay = -9.8 m/s/s (true for all projectiles)
ax = 0 m/s/s (true for all projectiles)
Como se muestra en la tabla, sólo hay dos piezas de información x y dos piezas de
información y dadas en el problema. Por lo tanto, parecería al principio que no se
proporciona suficiente información. Pero como suele ocurrir en un problema real, se
puede avanzar utilizando variables con la esperanza de que haya un medio para
introducir otra ecuación que ayude en la solución. Así que se escribirá una ecuación de
desplazamiento horizontal y vertical. (Tenga en cuenta que las unidades se han
eliminado forman la solución con el fin de mejorar la claridad de la solución.)
Horizontal Displacement
x = vix*t + 0.5*ax*t2
63.6 = (0.6225 • vi ) •
t
Vertical Displacement
y = viy*t + 0.5*ay*t2
32.8 = (0.7826 • vi) •t + 0.5 • (-9.8) •
t2
Ahora hemos generado dos ecuaciones con dos incógnitas y se puede encontrar una
solución para la velocidad inicial de la flecha. La ecuación 1 se utiliza para generar una
expresión para t en términos de vi. Esta expresión se sustituye a continuación en la
ecuación 2 con el fin de resolver la velocidad inicial (vi). La obra se muestra a
continuación.
From equation 1: t = (63.6) / (0.6225 • vi )
Substituting into equation 2: 32.8 = (0.7826 • vi) •[(63.6) / (0.6225 • vi )] +
0.5 • (-9.8) • [(63.6) / (0.6225 • vi )]2
32.8 = (0.7826 • vi) •[(63.6) / (0.6225 • vi )] + 0.5 • (-9.8) • [(63.6) / (0.6225
• vi )]2
32.8 = 79.956 - 51145.94/(vi)2
-47.956 = -51145.94/(vi)2
(vi)2 = (-51145.94) / (-47.956)
(vi)2 = 1066.52
vi = 32.7 m/s
71. En una demostración de Física, se lanza un proyectil desde una altura de 1,23 m
sobre el suelo con una velocidad de 10,6 m/s en un ángulo de 30,0 grados por encima
de la horizontal.
a) ¿A qué distancia horizontal desde la ubicación de lanzamiento aterrizará el
proyectil?
b) ¿Con qué velocidad aterriza el proyectil?
Respuesta: (a) x = 11,7 m; (b) vf = 11,7 m/s
(a) Como es el caso en todos los problemas de proyectiles no lanzados
horizontalmente, debe iniciarse resolviendo la velocidad inicial (10,6 m/s) y el ángulo
(30,0 grados) en los componentes de velocidad inicial utilizando las ecuaciones:
vix = vi * cos(theta)
viy = vi * sin(theta)
Esto produce valores de vix = 9,180 m/s y viy = 5,30 m/s. Una vez hecho esto, enumere
los valores conocidos para cada una de las variables en las ecuaciones cinemáticas. Es
útil organizar la información en dos columnas: una columna de información horizontal
conocida y una columna de información vertical conocida.
Horizontal Motion
x = ??? (the unknown in part a)
Vertical Motion
y = -1.23 m (vert. distance to floor)
vix = 9.180 m/s (from trig. function)
viy = 5.30 m/s (from trig. function)
ax = 0 m/s/s (true for all projectiles)
ay = -9.8 m/s/s (true for all projectiles)
Dado que ahora se conocen tres piezas de información y, se puede emplear una
ecuación y para encontrar el tiempo para que el proyectil se eleve y, en última
instancia, caiga al suelo. Una ecuación útil es
y = viy*t + 0.5*ay*t2
en cuyo caso hay dos soluciones para la época: t = 1.2780 s y t = -0.1964 s. Una
parábola completa que sigue a la función anterior tendría dos ubicaciones donde la
coordenada y es de -1,23 m. Una ubicación sería "adelante en el tiempo" en 1.2780
segundos; y la otra solución está en una ubicación trazada "hacia atrás en el tiempo"
desde el momento de lanzamiento. Por supuesto, deseamos utilizar el valor de tiempo
positivo en nuestros cálculos. Así que t = 1.2780 segundos.
El tiempo ahora se puede combinar con una x-ecuaciones para encontrar el
desplazamiento horizontal (x). Utilice la ecuación:
x = vix*t + 0.5*ax*t2
donde t = 1,2780 s, ax = 0 m/s/s y vix = 9,180 m/s. colocar los valores anteriores en
esta ecuación produce la respuesta de 11.739 metros para el desplazamiento
horizontal.
(b) La velocidad de aterrizaje (vf) del proyectil se puede determinar a partir de los
valores del componente x e y de la velocidad final. Dado que el objeto que se está
analizando es un proyectil, no hay aceleración horizontal y la velocidad horizontal final
(vfx) es la misma que la velocidad horizontal inicial (vix) - 9.180 m/s. La velocidad
vertical final (vfx) se puede determinar utilizando la siguiente ecuación cinemática:
vfy = viy + ay•t
vfy = 5.3 m/s + (-9.8 m/s/s)•(1.2780 s)
vfy = -7.2244 m/s
Con los componentes x e y de la velocidad final (vf)
conocidos, el teorema de Pitágoras se puede utilizar para determinar el valor de
velocidad final. Un diagrama se muestra a la derecha y los cálculos se muestran a
continuación.
vf 2 = (vfx)2 + (vfy) 2
vf = (9.180 m/s)2 + (-7.2244 m/s)2
2
vf 2 = 136.462 m2/s2
vf = SQRT (136.462 m2/s2) = 11.7 m/s
72. Un coche está aparcado en un acantilado con vistas al mar. El acantilado está
inclinado en un ángulo de 29,0 grados por debajo de la horizontal. El conductor
negligente deja el coche en punto muerto y comienza a rodar desde el resto hacia el
borde del acantilado con una aceleración 4,50 m/s/s. El coche se mueve una distancia
lineal de 57,2 m hasta el borde del acantilado antes de sumergirse en el océano de
abajo. El acantilado está a 42,2 m sobre el mar.
(a) Encontrar la velocidad (en m/ s) del coche en el momento en que sale del
acantilado.
(b) Encontrar el tiempo (en segundos) que tarda el coche en caer al agua por debajo
del borde del acantilado.
(c) Encontrar la posición (en metros) del coche en relación con la base del acantilado
cuando aterrice en el mar.
Respuesta: (a) vf = 22,7 m/s; (b) t = 2,02 segundos; (c) x = 40,1 metros)
La primera tarea consiste en utilizar una ecuación cinemática para determinar la
velocidad del coche después de acelerar desde el reposo a 4,5 m/s/s para una
distancia de 57,2 m. La mejor ecuación es
vf2 = vi2 + 2•a•d
vf2 = (0 m/s)2 + 2•(4.5 m/s2)•(57.2 m) = 514.8 m2/s2
vf = SQRT(514.8 m2/s2) = 22.689 m/s
(b) Una vez que el coche llega al borde del acantilado y se despliega, se convierte en un
proyectil con una aceleración vertical de 0 m/s2. La segunda tarea consiste en
determinar el tiempo de vuelo del proyectil desde el borde del acantilado hasta el agua
de abajo. Al igual que todos los proyectiles lanzados no horizontalmente, el punto de
partida es determinar la velocidad horizontal inicial (vix) y la velocidad vertical inicial
(viy). La velocidad inicial (22,7 m/s) y el ángulo (-29,0 grados) se pueden resolver en
componentes de velocidad inicial utilizando las ecuaciones:
vix = vi * cos(theta)
viy = vi * sin(theta)
Esto produce valores de vix = 19.844 m/s y viy = -10.999 m/s. Una vez hecho esto,
enumere los valores conocidos para cada una de las variables en las ecuaciones
cinemáticas. Es útil organizar la información en dos columnas: una columna de
información horizontal conocida y una columna de información vertical conocida.
Horizontal Motion
x = ???
Vertical Motion
y = -42.2 m (vert. distance to water)
vix = 19.844 m/s (from trig. function)
viy = -10.999 m/s (from trig. function)
ax = 0 m/s/s (true for all projectiles)
ay = -9.8 m/s/s (true for all projectiles)
Dado que ahora se conocen tres piezas de información y, se puede emplear una
ecuación y para encontrar el tiempo para que el proyectil se eleve y, en última
instancia, caiga al suelo. Una ecuación útil es
y = viy*t + 0.5*ay*t2
en cuyo caso hay dos soluciones para la época: t = 2.0196 s y t = -4.2644 s. Una
parábola completa que sigue a la función anterior tendría dos ubicaciones donde la
coordenada y es de -42,2 m. Una ubicación sería "adelante en el tiempo" en 2.0196
segundos; y la otra solución está en una ubicación trazada "hacia atrás en el tiempo"
desde el momento de lanzamiento. Por supuesto, deseamos utilizar el valor de tiempo
positivo en nuestros cálculos. Así que t = 2.0196 segundos.
(c) El tiempo ahora se puede combinar con una x-ecuaciones para encontrar el
desplazamiento horizontal (x). Utilice la ecuación:
x = vix*t + 0.5*ax*t2
donde t = 2,02 s, ax = 0 m/s/s y vix = 19,8 m/s. colocar los valores anteriores en esta
ecuación produce la respuesta de 40,1 metros para el desplazamiento horizontal.