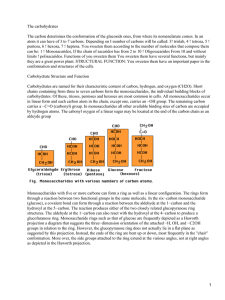
8628 J. Phys. Chem. B 1999, 103, 8628-8638 Quantum Mechanical Study of β-Lactam Reactivity: The Effect of Solvation on Barriers of Reaction and Stability of Transition States and Reaction Intermediates Irina Massova and Peter A. Kollman* Department of Pharmaceutical Chemistry, UniVersity of California, San Francisco, California 94143-0446 Downloaded via UNIV DEL DESARROLLO on October 22, 2018 at 18:24:19 (UTC). See https://pubs.acs.org/sharingguidelines for options on how to legitimately share published articles. ReceiVed: July 12, 1999 β-Lactams are widely used in medicine as potent antibacterials and in chemistry as synthetic intermediates. The investigation of the intrinsic reactivity of β-lactams is important for the understanding of the mechanisms of action and inactivation of β-lactamases and penicillin-binding proteins. Ab initio quantum mechanical calculations using a polarizable continuum model to estimate solvation effects have been utilized to analyze the hydrolysis and methanolysis of selected β-lactams and simple amides. The roles of four-membered ring strain, reduced amide resonance, substituent and ring fusion effects on hydrolysis, and methanol-mediated hydrolysis of these compounds have been studied by reconstructing the corresponding reaction pathways in gas and solution. Strong correlations have been found between the calculated kinetic, structural, and electronic properties of these compounds and the experimental data. The findings in this paper shed light on the contributions of the various structural elements to the reactivity of β-lactams. Insights into this reactivity could prove very useful in the design of novel potent antimicrobials. Introduction The antimicrobial function of the β-lactam antibiotics is determined by their ability to bind specifically and covalently to the bacteria cell-wall-synthesizing enzymes (penicillin-binding proteins or PBPs). PBPs catalyze the cross-linking reaction of the peptidoglycans, a major structural component of the bacteria cell wall, rendering it into a three-dimensional rigid network which allows the bacteria to survive in a harsh environment. Deprived of active PBPs, bacteria cannot sustain the rigidity of their cell walls and are ruptured by osmotic forces. To defend against β-lactam antibiotics, such as penicillins and cephalosporins, bacteria have developed β-lactamases. These enzymes protect the bacteria from β-lactam antibiotics by hydrolyzing their β-lactam ring and converting them into inactive compounds. The products of β-lactam hydrolysis by β-lactamases have no noticeable affinity for the PBPs. Thus, β-lactamases destroy the antimicrobial function of the antibiotic and provide the bacteria with resistance to it. The widespread use of β-lactam antibiotics in hospitals, agriculture, and household products has caused the emergence of new multiple antibiotic resistant strains of bacteria that carry β-lactamase genes (MAR).1-4 Nevertheless, β-lactam pharmaceuticals still remain extremely useful for many infections.5 One of the solutions to the MAR problem is to develop new β-lactamase inhibitors.6,7 These molecules can then be administered together with older antibiotics to protect them from hydrolytic inactivation by β-lactamases. Full knowledge about the mechanism of β-lactamase catalysis is important for understanding the function and interactions of these enzymes with substrates and inhibitors. This kind of information should assist the development and evaluation of novel β-lactams to overcome the resistance problem. The hydrolytic reactivity of β-lactams is related to their activity with β-lactamases. Nonenzymatic methanol-mediated * To whom correspondence should be addressed:, Peter A. Kollman, Department of Pharmaceutical Chemistry, University of California, San Francisco, California 94143-0446. Phone: (415) 476-4637. FAX: (415) 476-0688. E-mail: [email protected]. hydrolysis (e.g. methanolysis followed by hydrolysis) of β-lactams mimics the enzymatic pathway and could be studied in the gas phase and solution as a model reaction for hydrolysis of β-lactams by β-lactamases. The methanol molecule corresponds to a truncated version of the catalytic serine residue of β-lactamases. The energy profile for this reaction is expected to be similar to the enzyme catalyzed reaction with some differences in relative depths of the wells and heights of the hills on the potential surface and with the exception that there is no analogue for the Michaelis complex in β-lactam methanolmediated hydrolysis reactions. It has been suggested that the strain in the four-membered β-lactam ring increases the reactivity of β-lactams.8 β-Lactams of slightly basic amines display 30-500-fold rate increase and β-lactams of basic amines show ∼10 times rate acceleration for hydroxide ion catalyzed hydrolysis compared to corresponding acyclic amides.9,10 However, as it has been pointed out in refs 9 and 10, this rate enhancement cannot be solely attributed to the ring strain. Another contribution to β-lactams increased reactivity is the reduced amide resonance as a result of ring fusion.11 Furthermore, the change in the carbonyl acidity and ring nitrogen basicity caused by deviation of their geometries from their equilibrium values in unstrained structures can also lead to a decrease in β-lactam ring stability.9,10 In addition, an ambiguity exists about the direction of nucleophilic attack.10 The theory of stereoelectronic control predicts an approach of the nucleophile from the β-side of β-lactam, requiring the lone pair of the ring nitrogen and the lone pair of the nucleophile to be in an anti-periplanar orientation. However, several observations, such as the nonplanar shape of the fused ring system, steric hindrance of the β-side, and the absence of the product for intramolecular aminolysis of penicillins containing a primary amino group at C-6β side chain, suggest that the nucleophilic approach is from the R-side, at least for penicillins.10 This issue remains controversial. More planar cephalosporins with a primary amino group in their C-7β side chain undergo intramolecular aminolysis,12 and a similar reaction has been observed 10.1021/jp9923318 CCC: $18.00 © 1999 American Chemical Society Published on Web 09/15/1999 Quantum Mechanical Study of β-Lactam Reactivity J. Phys. Chem. B, Vol. 103, No. 40, 1999 8629 SCHEME 1 in 6-epi-ampicillin, a penicillin.13 In any case, the approach of the nucleophile occurs from the R-side of β-lactams during the enzymatic catalysis. We have investigated all these and other β-lactam-activity related issues in our current work. β-Lactams, known from the early 1940s, always were a subject of thorough study not only for their antimicrobial properties but also for their importance as synthetic intermediates. One of the first semiempirical molecular modeling studies of β-lactams was conducted by Boyd. His work helped one to understand the major steps of enzymatic catalysis, transition state structures, and the effect of the leaving group on the inhibitory activity of cephalosporins.14,15 Several semiempirical calculations using a supermolecular approach and polarizable continuum dielectric models implemented in AMSOL have recently been done by Frau et al.16 to study the hydroxide-ion attack on the carbonyl of N-methyl-2-azetidinone. That group has also evaluated the reaction barriers for the hydroxide-ion attack on the carbonyl of 2-azetidinone in gas using ab initio calculations. Frau et al. have observed the preferential pathway for the proton abstraction rather than an addition of the hydroxyl to the carbonyl, which has forced Frau et al. to constrain the N-H distance during the ab initio calculations. This problem has been later overcome by using the reaction field method (SCRF).17 Similar work has been conducted by Pitarch et al.18 on neutral and alkaline hydrolyses of N-methyl-2-azetidinone. Del Rı́o et al.19 have studied the first step of methanolysis of 2-azetidinone as a part of the reverse reaction of enolate-imine condensation using high level ab initio calculations and the polarizable continuum dielectric model. All of the above studies considered only the first stepsan addition of a nucleophilesin the reaction pathway of methanolysis/hydrolysis of azetidinones in solution. The common limitation of these previous studies was that they did not study the subsequent ring-opening step of the β-lactam by protonation, which is the accepted mechanism for this step in solution and in β-lactamases and PBPs.10 The work presented in this manuscript is the first comprehensive attempt to study a more complete reaction pathway for hydrolysis/methanolysis of a variety of β-lactams and variants and correlate the experimental results with their structural and physicochemical data. The series of reactions (1-16) have been designed to evaluate the effect of ring strain, substituents and loss of amide resonance on the reactivity of selected β-lactams (Scheme 1). The reaction pathways in gas and in solution for the reactions in Scheme 1 have been modeled to investigate these issues. The differences in the barriers of activation for the reactions of Scheme 1 as well as relative stability of the reactants, intermediates, and products helped to correlate reactivity with structures. Methods The GAUSSIAN94 and 98 ab initio modeling software have been used for the geometry optimization and the energy evaluation for each compound (reactions in Scheme 1). The HF/ 8630 J. Phys. Chem. B, Vol. 103, No. 40, 1999 Massova and Kollman TABLE 1. reaction 1/2 (H2O + H2O f HO + H3O ) - + ∆Gsolv, kcal/mol, used for ∆Gwater calculations (calcd)b (exptl) basis set ∆Ggas, kcal/mol gas (calcd) HF/6-31+G* HF/6-31+G* HF/6-31+G* G1 G2 G2MP2 CBS-Q CBS-4a CBS-Q 115.96 115.96 115.96 112.28 112.71 112.95 113.97 113.63 113.97 -100.54 HF/6-31+G* 41.54 -23.61 HF/6-31+G* rank of pKa, ∆Greaction, ∆Gwater, kcal/mol ∆Gwater pKa kcal/mol pH units, water (calcd) water water calcd water ∆Ggas + ∆Gsolv (exptl) (calcd) (exptl) (exptl) 2(3) 11.30 12.65 15.88 8.61 8.92 9.09 9.84 9.59 14.56 19.11 14.01 -94.1d 15.42 17.26 21.66 11.74 12.17 12.41 13.43 13.09 19.87 -23.0 17.93 3(2) 13.14 12.62 9.25 222.05 -187.65 -187.6 34.40 4(4) 25.22 ∼21 ∼15.5 HF/6-31+G* 203.96 -164.17 39.79 5(5) 29.17 ∼34 ∼25 HF/6-31+G* 185.03 -170.41 -168 14.62 1(1) 10.72 -98.7c -94.3d -100.54 -100.54 -100.54 -100.54 -100.54 NA 6.49 4.75 a Foresman, J. B.; Frisch, Æ. Exploring Chemistry with Electronic Structure Methods; Gaussian, Inc: Pittsburgh, PA 1996; p 159. b Calculated as described in the Methods section. c The experimental values were taken from Barone, V.; Cossi, M.; Tomasi, J. J. Chem. Phys. 1997, 107, 3210-3221. d ∆Gsolv calculated from the experimental data (Franks, F. Water: A ComprehensiVe Treatise. Aqueous Solutions of Simple Electrolytes; Plenum Press: New York, 1973; Vol. 3, pp 55, 56. ∆Gsolv(H+) ) -260.5 kcal/mol; ∆Gsolv(HO-) ) -90.6 kcal/mol). The rest was calculated from the reaction H3O+aq f H2Oaq + H+aq; pKa ) -1.7 which was adjusted for an activity of water ) 1. The free energy for H+ was calculated as ∆G(H+) ) RT - ST, whereas S ) Rln (e5/2kBT)/(p°Λ3); Λ ) (h2/2πmkBT)1/2, h is Planck’s constant and kB is the Boltzmann constant. 6-31+G* basis set has been used. The first step, the formation of tetrahedral intermediate during the nucleophilic attack on carbonyl, usually has a late transition state (TS) with the energy comparable to that of the intermediate (ITS).20 The application of the Hammond’s rule for the reactions in Scheme 1 leads to the assumption that any energy change in the barrier heights for transition species and a change in the free energies of their corresponding tetrahedral intermediates are approximately linearly related. Therefore, the energies of tetrahedral species (ITS1) were used to estimate the relative changes in the activation barriers for the first step along the reaction pathways. All products and most of the starting materials and intermediates have several rotatable bonds. Only a few conformations have been evaluated for each reaction in order to reduce the computational time. Calculations showed that the species ITS2 represented merely a point on the energy surface rather than a stationary state. Energy minimization of ITS2 resulted in a structure which could be characterized as being obtained from the species ITS1 by following the “reaction coordinate path” and representing the structural conformer of a product. Thus, we produced an additional conformation of a product by energyminimized the structure of ITS1 protonated at the ring nitrogen (ITS2). The TS2 structure is expected to be similar to that of ITS1. It has not been determined for the following reasons: (i) The formation of the tetrahedral intermediate is a rate-limiting step for alkaline hydrolysis of β-lactams.9,10 (ii) On the other hand, nucleophilic hydrolysis of penicillin G catalyzed by weakly acidic alcohols showed that a breakdown of the tetrahedral species is a slower step.21 (iii) Furthermore, Bakowies and Kollman20 demonstrated that TS1 and TS2 are similar in structure and energy and both have a barrier height very close to the energy of ITS1. The products (PR) of the acylation step of the reactions had their starting structures chosen as close as possible to the conformation of penicillin G in the acyl-enzyme complex of Glu166Asn mutant of TEM-1 β-lactamase from Escherichia coli.22 The polarizable continuum dielectric model (PCM)23,24 currently implemented in GAUSSIAN98 was used to evaluate the solvation free energies. The structures 17, 18, and 19 were energy-minimized in gas and solution to estimate the effect of the solvation on geometries. The structures determined in gas and in water were essentially identical with the standard deviation of 0.07, 0.03, and 0.04 Å, respectively. These results are in a good agreement with the findings of Barone et al.23,25 Furthermore, it has been shown in ref 25 for the ring-opening reaction of cyclobutene radical that the values for the barriers and the free energies of all the species which were energy-minimized in solution were never higher than 0.4 kcal/mol from those determined for the structures energyminimized in gas and reevaluated by single-point calculation in solution. Moreover, all values shifted in the same direction. To estimate the possible systematic errors due to imperfection of the PCM model, we evaluated the pKa’s for five small molecules using different levels of ab initio calculations (Table 1). The PCM/UAHF model with Icomp ) 4 has been employed to calculate the free energy changes in water. The differences vary for each case, although overall trends were predicted correctly (cf. rank column in Table 1). The free energy difference of 4.4 kcal/mol (per one water molecule) was observed when the free energy of formation of HO- and H3O+ from 2 H2O was calculated using the experimental values reported in refs 23 and 26 (the second and the third entries in Table 1). A considerable discrepancy has been found for the experimental free energy of hydration of hydroxide ion reported in ref 26 (-90.6 kcal/mol) and used in ref 23 (-106 kcal/mol) to derive the new definition cavity parameters for ab initio calculations of the solvent effect. Even though this potentially dramatic difference could result in shift of as much as 15.4 kcal/ mol in the free energy values, the relative differences between energies would still be the same because the same species (e.g., HO-) occurs in all reactions. The effect of the geometry change in solution, electron correlation, and the basis set were further investigated in evaluation of the pKa of water using different protocols listed in Table 1 and two additional ones. The structures of a water Quantum Mechanical Study of β-Lactam Reactivity molecule, hydroxyl anion and hydronium ion were first energy minimized in water using PCM/UAHF parameter set and Icomp ) 2 for two basis sets HF/6-31+G* and B3LYP/6-31+G* then the single point calculations have been carried out on the optimized structures with Icomp ) 4, which has been shown better to account for the solute escaped electron density outside the cavity.23 None of the methods was able to achieve the precision of the approach used by Barone et al.23 to develop UAHF parameters. Similar results have been found by Schüürmann et al.27 who used an additional four basis sets with polarization and/or diffuse functions (6-31G**, 6-31+G**, 6-311G(2d,2p), 6-311+G(2d,2p)) and with and without inclusion of the correlation effect (HF and MP2 levels). None of the basis sets was able to predict the pKa’s of 16 carboxylic acids better than the protocol developed by Barone et al.23 Therefore, the following strategy has been used in this work: first, the geometry was optimized in gas with HF/6-31+G* basis set, and second the zero-point frequencies and the thermal energy corrections were calculated in gas phase for 298.15 K; all the structures of SM, ITS1, ITS2, and PR species were found to have no imaginary frequencies and were true minimum structures; ultimately, a single-point energy calculation in water using PCM/UAHF was conducted to evaluate the solvation free energies with HF/6-31+G* basis set for anions and HF/6-31G* basis set for cations and neutral molecules. J. Phys. Chem. B, Vol. 103, No. 40, 1999 8631 SCHEME 2 Results and Discussion In general, amides require harsher conditions for their hydrolysis than esters, which is due to an amide resonance stabilizing a ground state of the starting materials. This stabilization can be lost in β-lactams, since four-membered ring strain can partially destroy the amide resonance.11 However, the crystallographic data shows planarity of the ring nitrogen in monobactams, which is an indication that amide resonance still exists in monocyclic β-lactams. Both penicillins and cephalosporins have two fused ring systems. One is a β-lactam ring and another, a thiazolidine or dihydrothiazine ring, respectively. The rings share a common amide nitrogen and a carbon atom. Additional strain along the ring fusion causes the amide torsion angle to be nonplanar, and this can contribute to the loss of amide resonance. It can result in a lower activation barriers for methanolysis/hydrolysis reactions of β-lactams than those for reactions of similar acyclic amides. The four-membered β-lactam ring could also have an effect on ring nitrogen basicity and carbonyl acidity because of the deviation of bond angles from their unstrained geometries, which could, in turn, effect the stability of β-lactams. The reactions we studied (Scheme 1) have been designed to evaluate all these factors. Reactions in Scheme 1 shows progressive increase in complexity of the system, with the penicillin G shown under 14. Reactions 1, 2, 6, and 7 vs 3 and 8 give insight into ring strain issue, since they compare analogous peptide and β-lactam reactants. Reactions 8 and 9, 11 and 12 show the effect of nitrogen basicity. Comparing reactions 9 with 10 and 12 with 13 helps one estimate the influence of the adjacent five-membered ring and substituents on this ring on the stability of the reactant and tetrahedral intermediate during hydrolysis or methanolysis. The methanol-mediated hydrolysis of β-lactams mimics the enzymatic pathway, with methanol acting as a catalyst and representing a surrogate side chain of the catalytic serine residue of β-lactamases. The acylation step has been studied in the current work. The hypothetical energy profile is shown in Scheme 2, whereas SM are the starting materials, TS is a transition state, ITS1 is a tetrahedral intermediate, and PR are the products. Assuming a linear dependency between the activation barriers (TS1) and the free energies of ITS1, we have used the latter as an estimate for the relative heights of the activation barriers. The calculations showed that ITS2 was not a stationary point on energy surface but rather was merely a point on the reaction pathway between the transition state 2 (TS2) and the products. The ITS2 geometry optimization resulted in one of the rotamers of the product. It is impractical to do a full search for the transition state along the reaction coordinate for such complicated models as 4, 5, and 11-16. Thus, we rely on the experimental and theoretical studies that the structure and the free energy of TS1 are very close to that of ITS1.10,20 Therefore, we compare the barriers for the wide variety of molecules using the ITS1 free energies. Formation of the Tetrahedral Intermediate. The PCM formalism has been used to evaluate the free energy changes in solution for the reactions discussed above. The results are presented in Tables 2-4. Table 2 shows the activation barriers for the first step of acylation of methanol by β-lactam in gas and solution and the hydration free energies. For base-catalyzed hydrolysis of β-lactams, the first step, the formation of tetrahedral intermediate, is a rate-limiting step. In contrast, protonation of the nitrogen is a rate-limiting step for hydrolysis in noncyclic amides.10 Therefore, the activation barrier for that step (∆G2,water) can be related to the observed kinetic rates of the reactions. Interestingly, the numbers ∆G2,water are within the range of the experimental values of 20-30 kcal/mol for the activation barriers reported for simple amides,28,29 and the experimental value of 16.7 kcal/mol has been determined for the hydroxide-ion attack on 2-azetidinone.30 These numbers are comparable to the barriers given in Table 2. The data in Table 8632 J. Phys. Chem. B, Vol. 103, No. 40, 1999 Massova and Kollman TABLE 2: Barriers for the First Step of Neutral Hydrolysis/Methanolysis of β-Lactams ∆G1 ∆G2 SM + ROH + H2O 98 SM + RO- + H3O+ 98 ITS1+ H3O+ a Two conformations of ITS1 with the different torsion angles around C-N rotatable bond have been considered. b The Boltzmann weighted thermodynamic average ∆G2,water energy for 3 is ) 24.04 kcal/mol and for 17 is 21.05 kcal/mol. c The energies (∆G2,water) are less than the values of the previous column (∆G1,water + ∆G2,water) by 30.84 kcal/mol for hydrolysis and 34.40 kcal/mol for methanolysis (Table 1). The barrier for the hydrolysis of water is underestimated by 3.69 kcal/mol (Table 1; the first line). This could give rise a systematic error of as much as 7.38 kcal/mol in overestimation of the values of ∆G2,water. 2 show several important trends. First, a 30-500-fold increase10 in rates of hydrolysis of β-lactams compared to the corresponding acyclic amides has been reproduced by our calculations. That change corresponds to a 2.0-3.7 kcal/mol decrease in the activation barrier. Our calculations gave a 4.2 kcal/mol decrease in the barrier for hydrolysis (reactions 2 and 3) and a 3.5 kcal/ mol decrease in barrier for methanolysis (reactions 8 and 7) in water. This effect was a combination of two changes: a decrease the gas-phase barrier for β-lactam reaction and in the solvation free energies, as the starting materials are converted to tetrahedral intermediates. The result was not due to the relief of a ring strain, because the ring was still closed in the ITS1 Quantum Mechanical Study of β-Lactam Reactivity J. Phys. Chem. B, Vol. 103, No. 40, 1999 8633 TABLE 3: Free Energy Changes for the Second Step of the Reactions reaction number ITS1+H3O+ f PR+H2O ∆Ggas kcal/mol ∆Gsolv kcal/mol ∆Gwater kcal/mol 1a 2a 6b 7b,c 7b 8b,d 8b 9b,d 9b 10b,d 10b 10b,e 11b,d 11b 12b,d 12b 13b,d 13b 14b 15b 16b,d 16b -226.43 -229.18 -229.62 -232.13 -231.61 -232.72 -231.75 -303.01 -301.90 -293.01 -296.45 -298.52 -217.34 -216.79 -283.86 -286.91 -278.45 -283.29 -284.52 -300.21 -281.19 -283.29 171.63 167.58 171.08 163.49 168.85 171.37 171.58 239.22 240.56 238.01 235.07 238.60 157.78 158.11 221.24 223.94 221.56 222.85 229.20 230.7 219.88 224.65 -54.80 -61.59 -58.54 -68.64 -62.76 -61.35 -60.17 -63.79 -61.34 -55.00 -61.38 -59.92 -59.56 -58.68 -62.62 -62.97 -56.89 -60.44 -55.32 -69.51 -61.31 -58.64 TABLE 4: Free Energies of the Reactions for the Selected β-Lactams a Hydrolysis reaction. b Methanolysis reaction. c See footnote a of Table 2. d Several PR conformations have been considered, as discussed in the Methods section. The top entry corresponds to the structure resulting after energy minimization of the ITS1 species protonated at nitrogen and the next entry corresponds to the structure similar to the conformation of penicillin G in the acyl-enzyme complex.22 e An additional conformer with the different thiazolidine ring puckering has been investigated. species. It was caused by relief of the strain on the carbonyl carbon as it converts from a three-coordinated sp2-hybridized carbon to a four-coordinated sp3-center.10 The introduction of an electron-rich group at the nitrogen side increases the activation barrier. In contrast, when one esterifies the carboxylate group, the rate accelerates by 130-fold (2.9 kcal/mol decrease in the activation barrier).31 The data in Table 2 show the substantial barrier increase of 69.8-72.3 kcal/mol in the gas phase when the carboxylic group is introduced at the nitrogen side, (reactions 8 and 9; 11 and 12). Though this group contributes favorably to the solvation energy, the activation barrier in solution is calculated to increase by 1.5-5.5 kcal/ mol. The electron-rich carboxylate group destabilizes the growing negative charge on the center of the nucleophilic attack, resulting in an increased activation barrier. The introduction of the second ring increases the rates of hydrolysis 280-3900-fold which corresponds to 3.3-4.9 kcal/ mol decrease in the activation barriers.10 That was supported by our calculations, which showed barriers decreased by 8.713.8 kcal/mol in the gas phase and 1.6-8.8 kcal/mol in solution (reactions 9 and 10; 12 and 13; 16 and 14). The second ring introduces an additional strain at the ring juncture resulting in the elevated energy of the starting materials and therefore in the smaller barriers to hydrolysis. An electron-withdrawing group next to the carbonyl carbon is known to have an inductive effect on reaction center, which results in rate enhancement.10 Modeling these reactions in the gas-phase did show a significant rate enhancement (reactions 8 and 11; 9 and 12; 10 and 13; a 14.8-17.7 kcal/mols decrease in the activation barriers). However, the opposite trend for the solvation free energies of the species canceled this effect, resulting in almost the same or sometimes even higher barriers for the reactions in water. These discrepancies with the experimental observations could be due to a number of factors. a Hydrolysis reaction. b Methanolysis reaction. c See footnote d of Table 3. d See footnote e of Table 3. First, it could be caused by inaccuracies in the solvent model. A second possible source of error was that all possible conformers were not sampled. We have chosen the conformation of our compounds to be as close as possible to that of penicillin G in the crystal structure of the acyl-enzyme intermediate.22 A third possible source of the discrepancy is that a change in the reaction mechanism could occur when a substituent was introduced. The approach of the nucleophile could be from the less crowded R-side for β-lactams. The approach for the less substituted compounds may occur from the β-side as suggested by the theory of stereoelectronic control. 8634 J. Phys. Chem. B, Vol. 103, No. 40, 1999 Massova and Kollman Figure 1. The reaction profiles for the attack of the hydroxide ion on carbonyl of N-methyl-3β-hydroxy-2-azetidinone (17) for syn-periplanar (gray lines) and anti-periplanar (black lines) approaches in the gas phase (A, C) and in water (B, D). All energies are shown relative to the sum of the electronic energy of the starting materials in the gas phase and their solvation free energies in water. The tick mark on the vertical axis at 22.16 kcal/mol corresponds to the total Gibbs free energy for 18. To investigate this issue we modeled reactions 3 and 17 in gas and solution accounting for all possible conformers. The hydroxyl group has been chosen as a model substituent at carbon side of 17 because of its small size and similarity to an amide nitrogen in terms of its hydrogen bond donating ability and the inductive and field effects on the reaction center. The Boltzmann weighted thermodynamic average energies were calculated based on all conformers for 3 and 17. The free energy change for the first step of the reaction was 21.05 kcal/mol for 17 and 24.04 kcal/mol for 3. That corresponds to a 160-fold rate enhancement for 17, in agreement with the trends seen in the experiments for similar β-lactams. The analysis of the tetrahedral intermediate revealed that the C-3β-hydroxyl substituent of 17 participated in hydrogen bonding to the carbonyl oxygen, thus stabilizing the growing negative charge on it. Interestingly, this hydrogen bond formed in all tetrahedral species which had a β-acylamino substituent at the carbon neighboring to the carbonyl of the β-lactam ring. This hydrogen bond provided by the amide of C-3(6,7)β-side chain of β-lactams/monobactams is reminiscent of the oxyanion hole in proteins, with the difference that only one amide is available to hydrogen bond to the oxygen on the tetrahedral center. Hence, these results for 3 and 17 suggest that the most likely explanation for the discrepancies between the calculated free energies for 8 vs 11, 9 vs 13, 10 vs 13, and experiment is incomplete conformational sampling. The Approach of Nucleophile. We have also studied the direction of nucleophilic approach, exploring the attack for all possible conformers of 17. We started our study with the approach from the less hindered R-side of 17. Compound 17 can serve as a minimal model for a β-lactam with a β-side chain. It has an almost planar nitrogen and the hydroxyl at C-3β creates the preference for the nucleophile to attack from the opposite side. The theory of stereoelectronic control suggests that the incipient C-O bond should be anti-periplanar to the nitrogen lone pair. The ITS1 product of such approach is 18, though this conformation is slightly less thermodynamically favorable than 19 (Table 2, 0.61 kcal/mol difference) which can be formed in a syn-periplanar approach of the hydroxide ion. The direction of the nucleophilic approach for 18 and 19 is from the less hindered R-side. It is analogous to the direction of the attack on β-lactams with fused ring systems for which the approach is dictated by the shape of the molecules, with the difference that structures such as 18 cannot form for such lactams because of the rigidity of their nitrogen at the ring fusion juncture. The energy profiles for the reaction of hydroxide ion with 17 converting to 18 and 19 in the gas phase and in water are shown in Figure 1,A-D. The current PCM solvation model implemented in GAUSSIAN was not ideal for the calculations of free energies of solvation for the transition states and intermediate structures between the stationary states because of their transient nature and mixed hybridization on the reaction center and adjacent atoms. This made it difficult to fully validate such models. The spike seen in Figure 1B is probably related to a reassignment of cavity parameters as the assumed hybridization on atoms changes during transition state formation. Nevertheless, the plots shown in Figures 1,A-D seemed to be reasonable and applicable for further analysis. The energy profiles for hydroxide-ion addition to 17 (Figures 1A,B) are very similar to ones calculated for hydroxide ion addition to formaldehyde in the gas phase and aqueous solution.32 The calculation showed Quantum Mechanical Study of β-Lactam Reactivity J. Phys. Chem. B, Vol. 103, No. 40, 1999 8635 Figure 2. Stereoviews of the energy-minimized structures of the starting material 17, transition states, and tetrahedral intermediates for 18 and 19. The two right structures could be viewed with stereoglasses and the left combination represents the crossed eye projections. the preference in the reaction pathway leading to the formation of structure 18 (Figures 1,A-D). The investigation of both pathways suggested that the barrier for the anti-periplanar approach (18) was 2.6 kcal/mol lower in energy than for the syn-periplanar attack (19). The relatively small difference in barrier heights for 18 and 19 indicates that structure 19 will form under thermodynamically controlled conditions and 18 will be the major product for kinetically controlled reactions. The transition state corresponded to the structure with a C-O bond length of 1.85 Å for both pathways (Figure 2). Some interesting structural changes could be seen. Thus, the C-O bond of the former CdO bond in TS1 and ITS1 species originated during syn-periplanar approach of nucleophile has more single bond character than that of similar structures formed during anti attack (TS: 1.245 Å (19) vs 1.233 Å (18); Figure 2). We studied the hysteresis of the nucleophile approach/ departure by reconstructing the direct approach from the starting materials and gradually decreasing the distance between hydroxide ion and the carbonyl carbon. The modeling in the direction from the starting materials to the tetrahedral intermediates always resulted in species 18. We also modeled the reaction pathway in the opposite direction from the tetrahedral intermediates 18 and 19, when the distance between the carbonyl carbon and the nucleophilic oxygen was gradually increased. As the distance got larger, both the carbonyl carbon and the nitrogen became more planar, and at a distance of 2.1 Å the structure 8636 J. Phys. Chem. B, Vol. 103, No. 40, 1999 that originated from 19 collapsed to that one from 18, as a demonstration for the preference of the anti-periplanar approach. We have investigated the possibility of β-side attack of HOon 17 and our calculations demonstrated that the nature of this attack for the simple compound was dominated by steric hindrance. The β-side approach resulted in proton abstraction rather than the addition of the hydroxyl to the carbonyl in the gas phase. It is likely that β-side approach in water would not abstract the 3β-OH proton, but still would be involved hydrogen bond formation between the proton on the hydroxyl and the nucleophile. This process would lower the basicity of the nucleophile, which should result in a higher barrier for β-side attack. This would also occur in monobactams with the C-3β side chain and penicillins and cephalosporins with the C-6(7)β side chain where the amide proton on the side chain can act as a proton donor, stabilize the nucleophile, and inhibit it from attacking the carbonyl bond. The addition of the hydroxyl to the carbonyl bond of 17 occurred without barrier in the gas-phase resulting in an ITS1 species with the energy of 34.0 kcal/mol (syn-periplanar approach) and of 37.6 kcal/mol (anti-periplanar approach) lower than that of the SM. A small hill was observed at a 2.1 Å C-O distance due to the HO- interaction with the proton at C-4. The desolvation of the hydroxide ion in water resulted in a barrier of 27.3 kcal/mol for the reaction in solution. The energies plotted at vertical axes of Figures 1B and 1D are the sum of the electronic energies and the solvation free energies (∆Ee + ∆Gsolv, whereas Ee is an electronic energy, and Gsolv is a solvation free energy). The total Gibbs free energy differs from this term by the sum of zero point energies and thermal corrections: Gtotal ) Ee + Gsolv + E1; E1 ) ZPE + Ee298 + Ev298 + Er298 + RT - ST, whereas ZPE is a zero point energy, Ee298, Ev298, and Er298 are the thermal corrections to electronic, vibrational and rotational energies and S is an entropy. The inclusion of the ∆E1 will result in an increase for the free energy of the tetrahedral intermediate by 14.25 kcal/mol for the synperiplanar approach and by 13.67 kcal/mol for the anti-attack. We illustrated this in Figure 1B by a the mark at the vertical axis at 22.16 kcal/mol which corresponds to the total free energy of 18. Most of this change, ∼12.5 kcal/mol, is contributed by the entropy loss that occurs at the latest stages of the addition of the hydroxide making the value of the free energy of the intermediate even more comparable to that of the transition state. This quantitative evaluation supports the validity of the application of Hammond’s rule to the reactions considered here, and, as a consequence, the use of the free energies of the tetrahedral intermediates for the analysis of the activation barriers and reaction rates discussed in this work. The preference for the R-side approach of the hydroxide ion for 17 leads to the more general support for R-side approach of the nucleophile in reactions with penicillins with C-6β-side chains and monobactams with C-3β-side chains, in which the side-chain amide can participate in a hydrogen bond with the negatively charged oxygen. This process will stabilize the tetrahedral species. Another aspect favoring R-side approach is the repulsion between the negatively charged oxygen on the tetrahedral center and the carboxylate at C-3 of the thiazolidine ring of penicillins (or C-4 of the dihydrothiazine ring of cephalosporins) and the sulfonate group on nitrogen of some monobactams. All these factors support the R-side approach of the nucleophile for the basic and neutral methanolysis and hydrolysis of β-lactams. The Breakdown of the Tetrahedral Species. The energies for the second step of the reaction are given in Table 3. The Massova and Kollman cleavage of the β-lactam ring of the cyclic compounds in the gas phase is accompanied by the release of slightly more energy than C-N bond cleavage in amides because of the relief of ring strain. But the ring strain adds only fractions of a kcal/mol to the energy released in the gas phase (reactions 7 and 8) and this effect is masked in solution because of the opposite trend in solvation free energies (Table 3). These numbers are quite different from the estimate of 26-29 kcal/mol of ring strain,33 in agreement with findings of ref 10. Many β-lactams actually release even less energy than N,N-dimethylacetamide upon C-N bond cleavage. The cleavage of the monobactams is more favorable than the ring-fused systems, despite one’s expectation that the strain energy is larger in the latter. The second step is not a rate-limiting step for the reactions of β-lactams; therefore, it does not influence the overall rate of the reaction. The Thermodynamics of the Overall Reaction. The total free energy changes for reactions 1-16 are given in Table 4. Calculations showed that most of the analyzed reactions of β-lactams are exothermic, in contrast to what is observed for the acetamide reaction, which is endothermic. The β-lactams are less stable than peptides. The free energy of the reaction is correlated with the barrier height for the first step. Monobactam 8 has a 3.5-kcal/mol lower barrier than 7 (Table 2). The total difference in solubilities of the products and starting materials for reactions 7 and 8 is about 1 kcal/mol (3.89 vs 4.77/4.98 kcal/mol, respectively, Table 4). As a result the methanolysis of monobactam 8 releases 2 kcal/mol more free energy than that of acetamide 7. This is the direct consequence of the destabilization of the starting materials because of strain energy in 8. Another effect on reaction free energies is ring strain because of ring fusion. The addition of the ring(s) lowers the free energy of reaction (reactions 10, 13, and 15). The fusion of the second ring increases the strain along the ring juncture which is relieved when the β-lactam ring opens, and the reaction of monobactams on average has a less negative/more positive ∆G(reaction) than that of bicyclic penicillins (reactions 9 and 10; 12 and 13). One can thus relate the release of ring strain to the calculated free energy for the reaction. In addition, the methanolysis reactions involve a less negative/more positive ∆G(reaction) than hydrolysis (compare reactions 6 and 1; 7 and 2). The Ground-State Effect. The geometrical parameters for compounds 1-16 are shown in Table 5. The calculations with HF/6-31+G* basis set result in overestimated vibrational frequencies.34 All the frequencies in Table 5 have been scaled to 87% to represent the experimental value for acetamide (1). The frequencies were then in reasonable agreement with experiment (Table 6). To evaluate the ground state and kinetic effects on hydrolysis of β-lactams, we determined the correlation of their geometrical parameters and energies with the experimental kinetic data10 available only for compounds 3, 4, 5, and 14 of those molecules studied by us. An excellent correlation was found (99%, r2 ) 0.978; Figure 3) between the β-lactam CdO bond length and the observed second-order rate constants for hydroxide ion catalyzed hydrolysis of β-lactams, thus relating the stability of the starting materials to the activation barrier height for the first step of the reaction. The CdO bond length represents the cumulative effect of the various factors such as ring strain, ring fusion, substituent on nitrogen and carbon sides on the stability of SM. Interestingly, the monobactams have the CdO bond length comparable to that of noncyclic amides, in contrast to the bicyclic β-lactams, which is clear indication that amide resonance still exists in the monocyclic system. The mechanisms for the hydroxide ion and the methoxide-ion Quantum Mechanical Study of β-Lactam Reactivity J. Phys. Chem. B, Vol. 103, No. 40, 1999 8637 TABLE 5: Some Geometrical Parameters and Vibrational Frequencies of the Selected β-Lactams TABLE 6: Experimental and Calculated Amide Vibrational Frequencies compound acetamide primary amides secondary amides tertiary amides β-lactam (monocyclic) β-lactam (multiple-ring system) amide I band CdO amide I band CdO stretching frequency stretching frequency (experiment, cm-1) (calculated, cm-1) 1694a,b 1650a,b 1640a,b,c 1680-1630a,b 1760-1730d 1810-1750d 1695 na 1680-1662 1658 1739-1699 1742-1727 a Solid. b Silverstein, R. M.; Bassler, C. G.; Morrill, T. C.; Robert M. Spectrometric Identification of Organic Compounds; Wiley: New York, 1991; p 419. c 1700-1680 in solution. d Various conditions of measurements. Page, M. I. The Chemistry of β-Lactams; Blackie Academic & Professional: New York, 1992; p 351. catalyzed hydrolysis reactions should be similar. Therefore, we expect to see a linear relationship between the activation barrier heights and the β-lactam CdO bond length for methoxide-ion Figure 3. The dependence of the second-order rate constants for hydroxide-ion catalyzed hydrolysis of β-lactams on the ground-state effect. Numbers near diamonds correspond to the compounds. kobs is the observed second-order rate constant (M-1 s-1, experiment).10 catalyzed reactions just like we observed for hydroxide-ion catalyzed hydrolysis. Probably the largest source of error in our models is the imperfections of the solvation model used. The deviation from the linearity between the calculated activation barriers and the calculated β-lactam CdO bond lengths could 8638 J. Phys. Chem. B, Vol. 103, No. 40, 1999 Massova and Kollman References and Notes Figure 4. The correlation of the barriers for the methoxide-ion catalyzed hydrolysis of β-lactams with the ground-state effect. ∆Gcalc, is the calculated activation barrier for the first step of the reaction in water (∆G2,water from Table 2). serve as a measure for how well the PCM/UAHF method reproduces the real solvation energies. The correlation of 77% (r2 ) 0.598, Figure 4) has been found, which is indicative of a reasonably good solvent model. As has been pointed out in ref 10, the pyramidal shape of amide nitrogen does not necessary mean the loss of an amide resonance in the case when the overlap of the lone pair orbital on the nitrogen still can be achieved with the π orbital on the carbonyl. The length of the β-lactam CdO bond is a good estimate of the degree of such loss of amide resonance, which may be caused by ring strain, ring fusion, substituent effects and other factors. Figure 3 shows the strong correlation between the reactivity of β-lactams and the loss of amide resonance (ground-state effect). The PCM model has provided reasonable estimates for the solvation energies in qualitative agreement with the experimental data (Figure 4). Conclusions This work represents the first attempt to correlate the experimental data to the geometrical and electronic structures of a broad set of the important β-lactams as well as related amides. The study has been done with the use of ab initio methods and the PCM/UAHF solvent model. Generally good agreement has been found between calculated barriers of reactions and the kinetic parameters for the selected compounds. The validity of the application of the PCM/UAHF model for the estimate of the solvent contribution has been demonstrated. The CdO bond length has been shown to correlate to the β-lactam hydrolytic stability. It can be used as a criteria for evaluation of the β-lactam susceptibility toward hydrolysis/ methanolysis and, as a consequence, toward hydrolysis by β-lactamases and may relate to the β-lactam inhibitory activity with PBPs. The findings in this paper shed light on the contributions of the various structural elements to the reactivity of β-lactams. That information can prove very useful in the design of novel potent antimicrobials. Acknowledgment. The authors thank the National Institutes of Health for research support (Grant GM-29072 to P.A.K. and Grant AI-09998 to I.M.). We thank Jed Pitera and Jim Caldwell for their helpful comments on this manuscript. (1) Levy, S. B. The Antibiotic Paradox. How Miracle Drugs Are Destroying the Miracle; Plenum Press: New York, 1992; p 279. (2) Garrett, L. The Coming Plague: Newly Emerging Diseases in a World out of Balance; Farrar, Straus and Giroux Press: New York, 1994; pp 411-456. (3) Spach, D. H.; Black, D. Ann. Allergy Asthma Immunol. 1998, 81, 293-302. (4) Jones, R. N. Diagn. Microbiol. Infect. Dis. 1998, 31, 461-466. (5) Quinn, J. P. Diagn. Microbiol. Infect. Dis. 1998, 31, 389-395. (6) Livermore, D. M. J. Antimicrob. Chemother. (Suppl. D) 1998, 41, 25-41. (7) Rosen, H.; Hajdu, R.; Silver, L.; Kropp, H.; Dorso, K.; Kohler, J.; Sundelof, J. G.; Huber, J.; Hammond, G. G.; Jackson, J. J.; Gill, C. J.; Thompson, R.; Pelak, B. A.; Epstein-Toney, J. H.; Lankas, G.; Wilkening, R. R.; Wildonger, K. J.; Blizzard, T. A.; DiNinno, F. P.; Ratcliffe, R. W.; Heck, J. V.; Kozarich, J. W.; Hammond, M. L. Science 1999, 283, 703706. (8) Strominger, J. L. Antibiotics 1967, 1, 706. (9) Proctor, P.; Gensmantel, N. P.; Page, M. I. J. Chem. Soc., Perkin Trans. 2 1982, 1185-1192. (10) Page, M. I. The Chemistry of β-Lactams; Blackie Academic & Professional: London, 1992; p 351. (11) Jonhnson, J. R.; Woodward, R. B.; Robinson, R. The Chemistry of Penicillin; Princeton University Press: Princeton, 1949; p 443. (12) Tsuji, A.; Nakashima, E.; Deguchi, Y.; Nishide, K.; Shimizu, T.; Horiuchi, S.; Ishikawa, K.; Yamana, T. J. Pharm. Sci. 1981, 70, 11201128. (13) Llinás, A.; Vilanova, B.; Frau, J.; Muñoz, F.; Donoso, J.; Page, M. I. J. Org. Chem. 1998, 63, 9052-9060. (14) Boyd, D. B.; Hermann, R. B.; Presti, D. E.; Marsh, M. M. J. Med. Chem. 1975, 18, 408-417. (15) Boyd, D. B.; Heron, D. K.; Lunn, W. H. W.; Spitzer, W. A. J. Am. Chem. Soc. 1980, 102, 1812-1814. (16) Frau, J.; Donoso, J.; Muñoz, F.; Vilanova, B.; Garcia-Blanco, F. HelV. Chim. Acta 1996, 79, 353-362. (17) Frau, J.; Donoso, J.; Muñoz, F.; Vilanova, B.; Garcia-Blanco, F. HelV. Chim. Acta 1997, 80, 739-747. (18) Pitarch, J.; Ruiz-López, M. F.; Silla, E.; Pascual-Ahuir, J. L.; Tunon, I. J. Am. Chem. Soc. 1998, 120, 2146-2155. (19) Del Rı́o, E.; López, R.; Menéndez, M. I.; Sordo, T. L.; Ruiz-López, M. F. J. Comput. Chem. 1998, 19, 1826-1833. (20) Bakowies, D.; Kollman, P. A. J. Am. Chem. Soc. 1999, 121, 57125726. (21) Page, M. I. Philos. Trans. R. Soc. London, Ser. B 1991, 332, 149156. (22) Strynadka, N. C. J.; Adachi, H.; Jensen, S. E.; Johns, K.; Sielecki, A.; Betzel, C.; Sutoh, K.; James, M. N. G. Nature 1992, 359, 700-705. (23) Barone, V.; Cossi, M.; Tomasi, J. J. Chem. Phys. 1997, 107, 32103221. (24) Barone, V.; Cossi, M.; Tomasi, J. J. Comput. Chem. 1998, 19, 404417. (25) Barone, V.; Rega, N.; Bally, T.; Sastry, G. N. J. Phys. Chem. 1999, 103, 217-219. (26) Franks, F. Water: A ComprehensiVe Treatise. Aqueous Solutions of Simple Electrolytes; Plenum Press: New York, 1973; Vol. 3, pp 55, 56. (27) Schüürmann, G.; Cossi, M.; Barone, V.; Tomasi, J. J. Phys. Chem. 1998, 102, 6706-6712. (28) Guthrie, J. P. J. Am. Chem. Soc. 1974, 96, 3608-3615. (29) Slebocka-Tilk, H.; Bennet, A. J.; Hogg, H. J.; Brown, R. S. J. Am. Chem. Soc. 1991, 113, 1288-1294. (30) Bowden, K.; Bromley, K. J. Chem. Soc., Perkin Trans. 2 1990, 12, 2103-2109. (31) Laws, A. P.; Page, M. I. J. Chem. Soc., Perkin Trans. 2 1989, 10, 1577-1581. (32) Madura, J. D.; Jorgensen, W. L. J. Am. Chem. Soc. 1986, 108, 2517-2527. (33) Page, M. I. Chem. Soc. ReV. 1973, 295. (34) Foresman, J. B.; Frisch, Æ. Exploring Chemistry with Electronic Structure Methods; Gaussian Inc: Pittsburgh, PA, 1996.