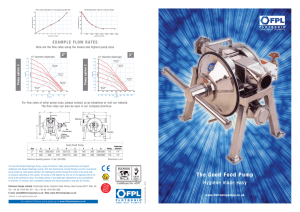
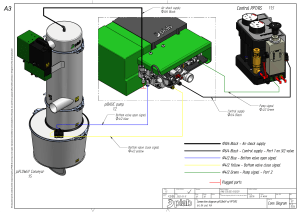
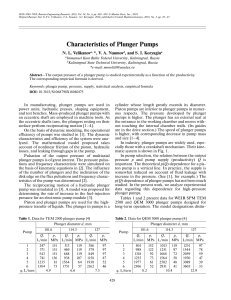
![[Igor J. Karassik, Terry McGuire (auth.)] Centri(BookZZ.org)](http://s2.studylib.es/store/data/008900592_1-7fce22d32f06f46da4d1f3efd08c02c6-768x994.png)
PUMPS Sec 0 n d Ed it ion Dedicated to the memory of Igor J. Karassik, an engineer of note whose career contributed handsomely to the general comprehension of pumps, hence their benefit to society at large. PUMPS Second Edition Igor J. Karassik (Deceased) formerly Senior Consulting Engineer Ingeool-Dressor Pump Comp;!flY Liberty Comer, New Jersey Terry cGuire Consulting Engineer and Director, AlhllOCes IngersoIl-Dressor Pump ComP<!flY Liberty Comer, New .Jmey CHAPMAN & HAll I JlONAI. THOMSON PUBUSHING Thomson SctenCf: New YorI> • AlbGny • 80m • Boston • ClIlOmlltI • DetrOit laldon • M!Idod • Mdbolme • Meloco CIty . Poclflc GrO'<'e PIYl5 • Sen FrllnClSCO • SI09IlPOI'I! • Tokyo • Torooto • Wasn'l19too Join Us on the Internet WWW: EMAIL: http://www.thomson.com findit®kiosk.thomson.com thomson.com is the on-line portal for the products, services and resources available from International Thomson Publishing (ITP). This Internet kiosk gives users immediate access to more than 34 ITP publishers and over 20,000 products. Through thomson.com Internet users can search catalogs, examine subject-specific resource centers and subscribe to electronic discussion lists. You can purchase ITP products from your local bookseller, or directly through thomson.com. Visit Chapman & Hall's Internet Resource Center for information on our new publications, links to useful sites on the World Wide Web and an opportunity to join our e-mail mailing list. Point your browser to: http://www.chaphaIl.com or http://www.thomson.comlchaphalllmecheng.htmi for Mechanical Engineering A service of I®p® Copyright © 1998 by Chapman & Hall Softcover reprint of the hardcover 2nd edition 1998 Chapman & Hall 115 Fifth Avenue New York, NY 10003 Chapman & Hall 2-6 Boundary Row London SEl 8HN England Thomas Nelson Australia 102 Dodds Street South Melbourne, 3205 Victoria, Australia Chapman & Hall GmbH Postfach 100 263 D-69442 Weinheim Germany International Thomson Editores Campos Eliseos 385, Piso 7 Col. Polanco 11560 Mexico D.F Mexico International Thomson Publishing-Japan Hirakawacho-cho Kyowa Building, 3F 1-2-1 Hirakawacho-cho Chiyoda-ku, 102 Tokyo Japan International Thomson Publishing Asia 221 Henderson Road #05-10 Henderson Building Singapore 0315 All rights reserved. No part of this book covered by the copyright hereon may be reproduced or used in any form or by any means-graphic, electronic, or mechanical, including photocopying, recording, taping, or information storage and retrieval systems-without the written permission of the publisher. 1 2 3 4 5 6 7 8 9 10 XXX 01 00 99 98 Library of Congress Cataloging-in-Publication Data Karassik, Igor T., 1911Centrifugal pumps: selection, operation, and maintenance I by Igor J. Karassik, J.T. MtGuire. -- 2nd ed. p. em. Includes index. ISBN 978-1-4615-6606-9 ISBN 978-1-4615-6604-5 (eBook) DOI 10.1007/978-1-4615-6604-5 1. Centrifugal pumps. I. MCGuire, J. T., 1947TJ919.K3 19% 621.6'7--dc20 II. Title. 96-1819 CIP British Library Cataloguing in Publication Data available "Centrifugal Pumps" is intended to present technically accurate and authoritative information from highly regarded sources. The publisher, editors, authors, advisors, and contributors have made every reasonable effort to ensure the accuracy of the information, but cannot assume responsibility for the accuracy of all information, or for the consequences of its use. To order this or any other Chapman & Hall book, please contact International Thomson Publishing, 7625 Empire Drive, Florence, KY 41042. Phone: (606) 525-6600 or 1-800-842-3636. Fax: (606) 525-7778. e-mail: [email protected]. For a complete listing of Chapman & Hall titles, send your request to Chapman & Hall, Dept. BC, 115 Fifth Avenue, New York, NY 10003. Contents Preface to the Second Edition Foreword (First Edition) vii IX PUMP TYPES AND CONSTRUCTION 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. II Classification and Nomenclature Casings and Diffusers Multistage Pump Casings Impellers and Wearing Rings Axial Thrust in Single- and Multistage Pumps Hydraulic Balancing Devices Shafts and Shaft Sleeves Stuffing Boxes Mechanical Seals Breakdown Seals Bearings Couplings Baseplates and Other Pump Supports Special Designs: Vertical Pumps Special Designs: Self-Priming Pumps Special Effect Pumps Materials of Construction PUMP PERFORMANCE 18. 19. 20. 21. Heads, Conditions of Service, Performance Characteristics, and Specific Speed Suction Conditions and Limitations on Suction Performance System-Head Curves Pumps and Energy Conservation 3 18 44 62 91 104 116 136 161 195 211 272 298 311 347 352 367 399 401 473 506 545 v vi Contents 22. III CONTROLS, DRIVERS, AND PRIMING 23. 24. 25. IV Services Procuring Centrifugal Pumps INSTALLATION, OPERATION, MAINTENANCE, AND DIAGNOSTICS 28. 29. 30. 31. 32. VI Controls Drivers Priming SERVICES AND SELECTION OF PUMPS 26. 27. V Pump Operation at Off-Design Conditions Installation Operation Monitoring and Performance Testing Maintenance Diagnostics of Field Problems DEVELOPMENT 33. The Centrifugal Pump of Tomorrow 558 593 595 621 686 715 717 800 831 833 882 893 916 927 947 949 Data Section 957 Index 975 Preface to the Second Edition New Yorkers woke up to face a dismal morning, at least the New Yorkers who did not depend on electric alarm clocks. It was cold, with the temperature hovering around 20 degrees. The electricity was off and so was the heat. No hot water, no water of any kind issued from the faucets. No radio, no news. Even battery-operated radios were no help, because the stations were not broadcasting. No gas to cook breakfast. Badly shaven or not shaven at all, hungry, grumpy, and bewildered, men issued into the streets to find no subways running, no traffic except for an occasional horse-drawn peddler's wagon. Those who tried to start their cars had no success. A few men took off for their offices on foot. Most congregated on street corners and asked each other questions. There were no newspapers because there was no way of delivering them. Before long, all sorts of rumors were flying. A little later, rioting and looting broke out allover New York. The police were handicapped by the fact that all normal communication had failed. By noon, emergency telephone communication operated by batteries had been reestablished between critical points in the city. But by noon, the situation itself had become critical. Elsewhere in the world the picture was essentially the same in the cities and small towns, although the smaller the towns, the less panic. In the country, matters were simpler. When farmers found that there was no water, they went to the rivers, lakes, and ponds with buckets and brought some water back. Just like their ancestors had done hundreds of years before. All this happened because on that morning all the pumps in the world stopped running. But of course this could not have happened. For had all the pumps stopped, I would not be writing this, nor would you be reading it, because the human heart is also a pump and it too would have stopped. Every industrial process that underlies our modern civilization involves the transfer of liquids from one level of pressure or static energy to another level, and as a result, pumps have become an essential part of all industrial processes. Carried farther, this means that pumps are an integral part of all modern economic and social development. At the same time, as I have said in one of my papers, the role of the pump industry should be much more than the development of new lines of pumps, the manufacturing of these pumps, and their selling. It should also include making efforts to build more efficient and longer lived equipment, to do so with less expenditure of natural resources, and, especially, to educate pump users in practices that consume less energy, provide trouble-free operation for longer periods, and reduce the incidence of premature failure. vii viii Preface to the Second Edition This last, the education of pump users, is precisely what this book was intended to do. To what extent we must have achieved our purpose, our readers must decide. My good friend and associate, J. T. (Terry) McGuire, and I have been working very closely together for a long time. Our view of engineering problems and of their solutions coincide to an astonishing degree. When I was asked to prepare a second edition of my book Centrifugal Pumps, it was logical that I turned to Terry and suggested that he be my coauthor on this project. He agreed to do so, and his cooperation has been most valuable, both in improving the resultant work and in easing my burden. It would be presumptuous on my part to pretend that nothing has changed in the technology of centrifugal pumps during the 30 years since I prepared the manuscript for the first edition of this book. Let me, then, speak of some of these changes. In the area of pump hydraulics, the most important addition to our knowledge has been the understanding of the phenomena that take place in a pump impeller as the capacity of a pump is reduced below that at which best efficiency is achieved. These phenomena can lead to pntssure pulsations, vibrations, and damage to the impeller and to certain adjacent pump areas. The understanding of the causes of these phenomena has, in turn, led to a better evaluation of what should be the minimum operating flows for centrifugal pumps. This subject is treated in a completely new chapter (Chapter 22). Greater understanding exists today with respect to conditions at the pump suction and of the effect of liquid properties on the behavior of pumps under cavitating conditions. The part of the book dealing with this subject has been much expanded and is now covered separately in Chapter 19. The portion of the chapter discussing guidelines for pump suction conditions recommended by the Hydraulic Institute has been revised in a much simplified form. Some improvements have been made in the range of attainable efficiencies, and means are now available to correct these attainable efficiencies when pump design practices depart from certain preselected standard constraints. These more refined guidelines are incorporated in Chapter 18. In pump construction, the last 30 years have seen the application of finite element analysis to the design of pump components, resulting in better hydraulic designs, refinement of the technology of rotor dynamics, more effective pressure containing parts, and a significant increase in the service life of mechanical seals. The emerging technological improvements in the area of variable frequency motors will have a very marked influence on the selection of drivers for centrifugal pumps and in the availability of pump speeds other than the synchronous speeds at 60 and 50 cycles. Pump applications have shown a trend to higher capacities, pressures, and, consequently, power levels. There has also been a greater tendency to use centrifugal pumps to handle a variety of slurries and other solids-laden liquids. Finally, two new chapters are devoted to pumps and energy conservation and to the centrifugal pump of tomorrow. As in the case of the first edition of this book, we have tried to avoid using this as a vehicle to discuss subjects that are possibly of great interest to pump designers but can contribute nothing but confusion to pump users. We have guarded ourselves against the temptation to discuss the theoretical intricacies of velocity diagrams, vane angles, or other similar design details. A doctorate in fluid dynamics should not, we firmly believe, be a prerequisite to understanding what the user must do to achieve a successful pump installation. This second edition is dedicated to Henry R. Worthington. We've done this to mark the 150th anniversary, albeit now 6 years ago, of the development of the direct acting steam pump by Henry R. Worthington-an invention that laid the foundation for the entire pump industry. Igor J. Karassik Foreword (First Edition) The subject of centrifugal pumps has received much attention in technical literature both here and abroad. However, the authors felt that most of this literature placed greatest emphasis on centrifugal pump theory, with insufficient stress on the more practical side of the problem. This practical side is more important to most engineers and users, as these people put centrifugal pumps to use while only a small minority actually design the equipment. One aim of this book is to guide the centrifugal pump user in system design and equipment selection for the most satisfactory combination of the two. It is also intended to provide useful information about equipment already installed as a guide to maximum service with minimum maintenance and unscheduled outage. The structural details and component parts of centrifugal pumps are described and methods are recommended for restoring each component to its initial condition after deterioration in service. In addition, special chapters are devoted to vertical pumps, self-priming units, and the so-called regenerative pumps. These are followed by a discussion of construction materials. A detailed presentation is given on the concept of "heads," conditions of service, and performance characteristics of various types of centrifugal pumps. System-head curves and their effect on pump output and selection are also fully discussed. An important factor in centrifugal pump application and operation that has often been neglected is the controls. This subject has been given special attention. Because successful pump application also depends on a harmonious combination of pump and driver, a chapter is included on pump drivers. Another important subject, priming, is discussed in great detail. Nearly all centrifugal pumping services have their individual problems and requirements. These services range from general water supply, sewage, drainage, and irrigation to power plant, process work, and other specialized applications. Growth and change in processes and industries have contributed to the development of new designs for the ever-increasing number of pumps. Many special designs are therefore available today that may be severely limited in application flexibility. Centrifugal pump users should have a general knowledge of specialized designs to help assure proper application. The chapter on services covers these special types and presents related operational information. It is supplemented by a chapter on the preparation of inquiries and ordering procedures. One important section of the book is devoted to the installation, operation, and maintenance of ix x Foreword centrifugal pumps. Finally, to make this book as useful as possible, a general Data Section contains valuable data required for engineering pumping installations and analyzing the performance of existing units. The authors have attempted to avoid complex technical explanations and involved theoretical discussions having little practical value to centrifugal pump users. Theoretical design data would only suggest that the user is expected to judge the excellence of the designer. This aim is not part of, nor compatible with, the objectives of the book, which are to provide practical and useful knowledge of centrifugal pump construction, application, control, installation, operation, maintenance, and trouble-shooting. The data in this book apply to all makes and types of centrifugal pumps. Wherever possible, therefore, illustrations have been selected from a wide group of manufacturers. For obvious reasons, however, we had greatest access to the extensive files of the Worthington Corporation. For many subjects-for example, individual pump parts-the illustrations would be similar, regardless of source, and therefore most of these were selected from the Worthington files. Wherever photographs of complete pumps or sectional drawings that are not from Worthington are reproduced, the captions give credit to the pump manufacturer responsible for the design. The authors wish to extend their thanks to the Worthington Corporation, the Allis-Chalmers Mfg. Co., Byron-Jackson Co., the DeLaval Steam Turbine Co., IngersollRand Co., Pacific Pump Co., and many others who very graciously granted the right to reproduce equipment photographs and drawings. The authors also wish to thank numerous magazines including Air Conditioning, Heating and Ventilating, Power, Power Engineering, Southern Power and Industry, Water and Sewage Works, and many others for their kind permission to utilize material from articles by the authors that had originally appeared in their pages. We are indebted to the Hydraulic Institute for the permission to reproduce a number of charts and data from its Standards. Finally, the authors wish to express their thanks to Messrs. A. H. Borchardt, G. F. Habach, L. H. Garnar, W. C. Krutzsch, C. J. Tullo, and many other associates at Worthington Corporation for providing valuable advice and constructive criticism. Roy Carter and I decided to undertake this book a number of years ago. Unfortunately, Mr. Carter did not live to see it completed. He passed away unexpectedly in September 1958. I decided that the book should be completed and therefore continued the task alone. I hope it measures up to our mutual expectations. Because its writing reflects our many discussions, and its chapters contain much that we had conceived together as articles for technical magazines, this book carries both our names as coauthors. Igor J. Karassik PUMPS Sec 0 n d Ed i tiD n I PUMP TYPES and CONSTRUCTION 1 Classification and Nomenclature Pumping can be defined as the addition of energy to a fluid to move it from one point to another. It is not, as frequently thought, the addition of pressure. Because energy is capacity to do work, adding it to a fluid causes the fluid to do work, normally flowing through a pipe or rising to a higher level. A centrifugal pump is a kinetic device, meaning that it adds energy to the pumped liquid by increasing its velocity. Because the addition of energy depends on liquid velocity, the amount of energy added varies with the rate of flow through the pump. These are the fundamental physics behind the usual head versus capacity characteristic of the centrifugal pump (Fig. 1.1). It is important to note the distinct difference between the head (energy added) versus flow characteristic of a centrifugal pump and that of a displacement pump (Fig. 1.1). Centrifugal pumps have low "flow regulation"; their flow varies widely with variations in system resistance, a characteristic that lends itself to easy flow control. Displacement pumps exhibit high flow regulation; their flow is largely independent of variations in system resistance, making them ideal for services where a constant flow is necessary over varying system conditions. The limitations of displacement pumps are machine size versus capacity and mechanical complexity. A centrifugal pump is a simple machine consisting of a set of rotating vanes enclosed within a housing or casing. Torque applied by the pump's driver is converted to total head by the action of the vanes on the pumped liquid, and these vanes are the only component that adds energy to the liquid. This action follows Euler's equation faithfully, provided it is recognized that the effective liquid velocities, magnitude, and direction cannot be determined directly from the geometry of the vanes. That determination is part of the centrifugal pump designer's "art." Stripped of all refinements then, a centrifugal pump has just two main parts: (1) a rotor, made up of the vaned component, known as an impeller, and a shaft, and (2) a stator, made up of the impeller enclosure, known as a casing, some form of seal where the shaft passes thru the casing, and bearings to support the rotor. The structural details of these parts and all refinements applied in modern pump construction are covered in Chapters 2 through 17. Most people find it difficult to visualize the path of the liquid passing through a centrifugal pump. Figure 1.2 shows this path for a single-stage end-suction pump operating at its design capacity, that at which best efficiency is obtained. The liquid, forced by either atmospheric or other pressure, enters the impeller vanes at a relatively low velocity, is accelerated to a high velocity as it passes through the 3 I. J. Karassik et al., Centrifugal Pumps © Chapman & Hall 1998 4 Classification and Nomenclature Displacement I "'i Energy Added @ Constant Speed Flow Fig. 1.1 Head-capacity characteristic of centrifugal (kinetic) versus displacement pumps. impeller. then is discharged into the casing, where the high velocity is converted into pressure, a process known as "diffusion." One of the most important factors contributing to the increasing use of centrifugal pumps has been the universal development of electric power. This century has seen electricity replacing small steam plants as the main industrial power source. Although reciprocating pumps were ideal for steam drive, the development of the electric motor permitted use of the much lighter and cheaper direct-connected centrifugal pump. Even though early centrifugal pumps would be considered inefficient by modem performance standards, their lower first cost more than compensated for this shortcoming. The centrifugal pump also immediately demonstrated other important advantages over the reciprocating pump. For example, the centrifugal pump gives steady flow at uniform pressures without pressure surges. It provides the greatest possible flexibility, developing a specific maximum discharge pressure under any operating condition with delivery controlled by either speed variation or throttling. Naturally, manufacturers working to widen the field of centrifugal pump applications through experience and research have greatly improved the operating range of pressures, the efficiency, and the mechanical and hydraulic design of their product. Concurrently, electric motor builders improved their designs, permitting pump manufacturers to use higher rotative speeds and develop pumps suitable for higher heads. So, over the last 80 years, the application of centrifugal pumps has been greatly extended in both pressure and capacity. Centrifugal pumps have been built in sizes ranging from tiny swimming pool pumps handling a few gallons per minute to the very large reversible pump turbines at Bath County, which deliver 116 m3/s (1.8 million gpm) against 387 m (1,270 ft) total head and absorb 410 MW (549,000 hp) when running in pump mode. The range of differential pressures is just as wide, starting with a single-stage cellar drainer pump which develops around 0.3 bar (5 psi), and rising to the multistage pumps used for oil field water injection, which develop as much as 360 bar (5,250 psi) in a single casing. And centrifugal pumps have been designed to run at speeds as high as 25,000 rpm for industrial applications. Compounding all that, the centrifugal pumps used in the space shuttle for fuel supply are the highest energy density machines yet made: 3,400 m3Jhr (15,000 gpm), 56,700 m (186,000 ft), 52,000 '" () f 6i 2 2t 3,500 166 200 GPM FT TOTAL HEAD RPM IN. SUCTION DIAM IN. DISCHARGE OIAM IN. IMPELLER DIAM IN. IMPELLER WIDTH PUMP Fig. 1.2 1 rPICAt 60 80 50 1\ SUCT ION VANE TIP -1-1-' SUC TION FL ANGE o 10 20 r/ V / V V ./ DE VELOP E 0 --- PATH ..:>, OISCHARGE VANE TIP f"-. I I I I I I I I VOLU TE THROAT I I FLOW SURFAt.~ --f- Flow path and velocity variation through an end-suction volute pump. " CD ~ ...'":> ~ ..J g 30 I- ,: z - 40 ...t:l ... i!i0. 8w 70 '" ~ SECTION THROUGH IMPELLER ANO VOLUTE "LONG "'E"~ SECTION FLOW LINE \. OISCHARGE FLANG E I- 1-1- 6 Classification and Nomenclature 100,000 Capacity, m3/h 10 100 ""T"""~,r-.,......L.. " 10,000 - 1000 10,000 _ _ _.J..-_ _--L_ _ _..L..-_ _---L----, "" Reciprocating -----~'" 1000 Centrifugal .... III .0 100 1000 - ~ ::J CJ) CJ) ~ Q.. I I I I I I i 100 10 ~ i 10;----r_---,----r--~r_--~ 10 100 1000 Capacity U.S. gpm 10,000 100,000 Fig. 1.3 Approximate upper limit of pressure and capacity by pump class. (Reprinted with permission/rom "Pump Handbook," Me-Graw Hill, NY, 1976.) kW (70,000 hp) at 37,000 rpm in a machine weighing 780 kg (1720 lb) including the integral gas turbine driver. Although the coverage of centrifugal pumps is very broad, it is not unlimited. For high-differential pressures at low capacities, reciprocating pumps are necessary. Similarly for some services within the normal coverage of centrifugal pumps, a displacement pump, either rotary or reciprocating and in that order, may be the better choice for the service conditions. Figure 1.3 shows the approximate upper limits of energy added (pressure rise) and flow for each of the three basic pump classes. MODERN PRACTICE IN SMALL- AND MEDIUM-CAPACITY RANGE In small- and medium-size centrifugal pumps, about 60 percent of all pumps in use are of centrifugal design and over 75 percent of these are in a head capacity range that can be met by standardized endsuction pumps. A typical example of this standardization is a line of pumps consisting of a number of liquid ends, all suitable for mounting (1) on a motor in a close-coupled arrangement, (2) on a bearing frame for separately coupled or belt drive, or (3) on a turbine in a close-coupled arrangement, although the last is rare today. Many standard alternatives are then incorporated into the basic plan, both in materials selected and mechanical construction, thereby eliminating "specials." The use of such an integrated line can result in better delivery service, a wider selection of standardized units, and dollar savings through the maximum use of interchangeable parts. In one typical case, some 100 sizes of pumps, using interchangeable parts, can produce over 60,000 different, standard combinations to suit almost any user's needs. Classification and Nomenclature 7 CENTRIFUGAL PUMP CLASSIFICATION Centrifugal pumps are produced in a wide range of design variations. To bring some order to these variations, several classification systems are in use. The original system is based on the form of the collector that surrounds the impeller and then the geometry of the impeller itself. Pumps employing a volute collector (Fig. 1.2) are generally called volute pumps, and those having a multiple vane diffuser (Fig. 1.4) are called diffuser pumps. Diffuser pumps were once quite commonly called turbine pumps, but this term has become more selectively applied to vertical deep-well centrifugal diffuser pumps, now called vertical turbine pumps. The impellers, in tum, are classified as radial flow, mixed flow, and axial flow, now usually called propeller type. The impeller classifications are further subdivided by suction arrangement, single or double, and vane closure (see Chap. 4). Associated with classification based on the hydraulic components, there are terms related to the arrangement of those components. If the pump is one in which the total head is developed by a single impeller, it is called a single-stage pump. Often the total head to be developed requires the use of two or more impellers in series, each taking its suction from the discharge of the preceding impeller. For this purpose, two or more single-stage pumps may be connected in series, or all the impellers may be incorporated in a single casing. The machine is then called a multistage pump. In the early development of centrifugal pumps, birotor pumps (Fig. 1.5) and even trirotor pumps were fairly common. In effect, these were two one-half capacity or three one-third capacity pumps built into Casing Fig. 1.4 Typical diffuser pump. 8 Classification and Nomenclature Fig. 1.5 Birotor pump. the one casing and operated in parallel. Modem versions of such designs, typically used for pipeline service, are generally a series-parallel arrangement, for example, a three-impeller two-stage pump (two single-suction first-stage impellers in series with a double-suction second-stage impeller; Fig. 1.6) or a four-impeller two-stage pump (two single-suction first-stage impellers in series with two single-suction second-stage impellers; Fig. 1.7. The mechanical design of the casing provides the added classification of axially split or radially split, and the orientation of the axis of rotation determines whether the pump is horizontal, vertical, or (occasionally) inclined. Horizontal pumps are classified still further according to suction and discharge nozzle locations, the more common arrangements being Fig. 1.6 Two-stage, three-impeller pump. (Courtesy Sulzer.) Classification and Nomenclature Fig. 1.7 1. End suction, top discharge 2. Top suction, top discharge 3. Side suction, side discharge 4. Bottom suction, side discharge. 9 Two-stage, four-impeller pump. Some pumps operate with the total liquid flow conducted to and from the unit by piping. Other pumps, most often vertical types, are submerged in their suction supply. Vertical pumps are therefore either dry-pit or wet-pit types. If the wet-pit pumps are axial flow, mixed flow, twin volute, or vertical turbine types, the liquid is discharged up through the supporting drop or column pipe to a point either above or below the supporting floor. These pumps are consequently designated as above-ground or below-ground discharge units. An alternative to the classification system described here has been developed by the Hydraulic Institute [1.1]. Figure 1.8 shows a subtle variation of this system, which first differentiates between the various classes of kinetic pumps, of which the centrifugal pump is one. Centrifugal pumps are then classified by their basic rotor construction, their drive arrangement, and finally their casing configuration. The virtue of this system is that it focuses on pump configuration versus use, thereby leaving the choice of hydraulic detail to the designer. Because the basic rotor construction has a significant effect on the balance of a pump's design, having it as the first distinguishing feature means several fundamental design issues are settled once the class of rotor is selected. .... <:) Pumps----i Fig. 1.8 Displacement ,Kineuc Between Induced Vortex Viseous Shear (Tesla) Barske Reversible Centrifugal Rowllng Casing (Pilot) Bearings E t C VerIIeaI Tu_ ",-,Ie, SIngle SIage L _0$'- Sepandely SIIIge Mulll-Slllge c:: Single r-SingIeSlllge Overhung - - - - - - - i L - MuItI-"- Vertical Diffuser Between BearIng. Classification of kinetic pumps (after Hydraulic Institute). Effect Special I L -----i Regenerative Turbine Centrifugal CIIIIing CasIng c:: _ _ SplIt SpIll C A*I _ SpIt SpItCasIng CIIIIing ~_ PIt Vol Suppooted Overhung-{-~_~~~ BlIICket E ~ MouI*d ---, - Classification and Nomenclature 11 CENTRIFUGAL PUMP COMPONENT NOMENCLATURE The basic elements of a centrifugal pump are its impeller, casing, shaft, and bearings, but there are other necessary parts. Various names have been given to these parts by different manufacturers, often leading to confusion. Figures 1.9, 1.10, 1.11, 1.12 and 2.9 show typical constructions of a horizontal overhung pump, a horizontal double-suction volute pump, a horizontal multistage pump (radially split), the bowl section of a single-stage axial-flow propeller pump, and a vertical overhung pump. Names recommended by the Hydraulic Institute for the various parts are given in Table 1.1. EVOLUTION The reader may be interested in comparing centrifugal pumps of the 1900s with their modem counterparts. These are illustrated in Figs. 1.13 through 1.19, which clearly show many of the changes in mechanical construction that were necessary for improved service life and maintenance. Other changes simply reflect refinements in design, foundry, or machine shop practice. Table 1.1 Recommended Names of Centrifugal Pump Parts These parts are called out in Figs. 1.9, 1.10, 1.11, 1.12 and 2.9 Item no. I IA IB 2 5 5A 5B 6 7 8 8A 8B 9 11 13 14 15 16 17 18 19 20 22 24 25 27 29 31 32 Name of part Casing Casing (lower half) Casing (upper half) Impeller Diffuser Diffuser, first stage Diffuser, discharge Shaft Ring, casing Ring, impeller Ring, impeller, eye Ring, impeller, hub Cover, suction Cover, casing Packing Sleeve, shaft Discharge bowl Bearing, inboard Gland Bearing, outboard Frame Nut, shaft sleeve Locknut, bearing Nut, impeller Ring, suction cover Ring, casing cover Seal cage Housing, bearing, inboard Key, impeller Item no. 35 37 39 40 40A 40B 50 55 56 59 60 63 65 72 73 73A 73B 73C 73D 78 80 85 86 89 99 101 103 115 123 Name of part Cover, bearing, inboard Cover, bearing, outboard Bushing, bearing Deflector Deflector, inboard Deflector, outboard Locknut, coupling Bell, suction Drum, balancing Cover, handhole Ring, oil Bushing, seal housing Seal, mechanical, stationary element Collar, thrust Gasket Gasket, casing Gasket, bearing cover, inboard Gasket, bearing cover, outboard Gasket, compensator Bearing spacer Seal, mechanical, rotating element Tube, shaft enclosing Ring, thrust, split Seal Housing, bearing Pipe, column Bearing, connector Bushing, balancing Cover, bearing, end 12 Classification and Nomenclature 22 46 6 7 2 27 63 80 65 40A 16 60 37. Fig. 1.9 Horizontal sil tgle-stage overhung refinery pump. (Numbers refer 0 parts listed in Table 1.1.) Fig. 1.10 Horizontal single-stage double-suction volute pump. (Numbers n(er to parts listed in Table 1.1.) Classification and Nomenclature 25 Fig. 1.11 Horizontal multistage double casing (barrel) diffuser pump. (Numbers refer to parts listed in Table 1.1.) Fig. 1.12 Vertical wet-pit diffuser pump bowl. (Numbers refer to parts listed in Table 1.1.) 13 14 Classification and Nomenclature Fig. 1.13 Old double-suction pump with separately cast suction elbows. Fig. 1.14 Double-suction pump evolved from that in Fig. 1.13. (Features integrally cast suction and discharge passages, separate casing heads, and radially split casing.) Classification and Nomenclature Fig. 1.15 Modern double-suction single stage pum p with an axially split casing. Fig. 1.16 Old style multistage pump with radially split casing. 15 16 Classification and Nomenclature Fig. 1.17 Modem high-speed high-pressure multistage pump (for over 175 bar gauge [2,500 psig)) with a radially split casing. Fig. 1.18 Early motor-mounted pump (around 1905). Classification and Nomenclature Fig. 1.19 Modem close-coupled pump. BIBLIOGRAPHY [1.1] ANSI/HI 1.1-1.5, 1994, Centrifugal Pumps, Hydraulic Institute, Parsiopany, NJ, USA. 17 2 Casings and Diffusers The term "casing" is generally used to describe the component that "contains" the pump. In practice a pump's casing has five functions: 1. Provide pressure containment. Incorporate the collector, either as an integral part of the casing or as a separate piece. 2. 3. Permit rotor installation and removal. 4. Support the pump or provide a structural connection to the pump's support. 5. Maintain alignment of the pump and its rotor under the action of pressure and reasonable piping loads. Traditionally pump casings have been classified by the type of collector used, so that aspect is dealt with first. The purpose of the collector is to gather and diffuse the high velocity liquid discharged by the impeller. This process is necessary to (1) slow the liquid to a usable velocity and (2) convert the kinetic energy into pressure energy, thus recovering more of the pump's energy input. Two basic forms of collector are in use: the volute and the diffuser. The volute-casing pump (see Fig. 1.2) derives its name from the spiral-shaped casing surrounding the impeller. This casing section collects the liquid discharged by the impeller and converts velocity energy into potential energy. A centrifugal pump volute increases in area from its initial point until it encompasses the full 360 deg around the impeller and then flares out to the final discharge opening. The wall dividing the initial section and the discharge nozzle portion of the casing is called the tongue of the volute, or the "cut-water." The diffusion vanes and concentric casing of a diffuser pump fill the same function as the volute casing in energy conversion. In propeller and other pumps in which axial-flow impellers are used, it is not practical to use a volute casing; rather, the impeller is enclosed in a pipe-like casing. Normally, diffusion vanes are used behind the impeller proper, but in certain extremely low head units, these vanes may be omitted. A diffuser-type centrifugal pump was illustrated in Fig. 1.4. The development of the diffuser appreciably improved the efficiency of the rather crude volute forms characteristic of the early days of centrifugal 18 I. J. Karassik et al., Centrifugal Pumps © Chapman & Hall 1998 Casings and Diffusers 19 pump construction. Later improvements in the hydraulic desigJ I of impellers and volute casings made the diffuser of little, if any, value in increasing pump efficiency. It is therefore seldom applied to a single-stage volute pump, although it possesses structural as '",ell as hydraulic advantages that may sometimes be useful. The principal advantages of a diffuser-type collector are that °or a given stage performance, it allows a smaller stage volume than an equivalent volute-type collector, and, with appropriate design and construction, produces negligible radial reaction on the rotor. As a consequence, diffuser-type collectors are used for all propeller and vertical turbine pumps (Fig. 2. L), most high-pressure, double-casing, multistage pumps (Fig. 1.11), and some special design of meditm head pumps (Figs. 1.6 and 2.13). Against the advantage of a smaller pump, a poorly designed diffuser can impair the hydraulic characteristics of the pump. The fast-moving liquid from the inlpeller can meet the fixed vanes of the diffuser without shock only when the pump is operating at rated capacity, for only then does the angle of the vanes correspond to the angle at which the liquid leaves 1he impeller. At all other rates of flow, the multiple vanes cause shock and turbulence, so that the pumr may operate in an unstable condition. As a matter of fact, when flow is restricted to as low as 5-10 peJcent of normal capacity, the shock and turbulence may become sufficiently severe to reduce the total llead generated. As a result, the head- Fig. 2.1 Vertical mixed-flow pump with diflusion vanes. 20 Casings and Diffusers capacity curve of diffuser-type pumps could easily acquire a "droop" in the shut-off capacity area, making the pump unsatisfactory for parallel operation. Do not interpret this to mean that a diffuser pump always produces a drooping characteristic. However, such a curve can result from this design unless extreme care is taken in layout of the impeller and diffuser combination. Pump manufacturers have long tried to stabilize diffuser pump head-capacity curves, and various solutions are available, based on proper selection of impeller vane angles, curvature of the impeller blades, and careful design of diffuser passageways. Another problem arising from the use of diffusers is potential pump flexibility. Obviously, pump manufacturers try to obtain as much coverage from a single pump pattern as possible, to keep the number of patterns comprising a complete line of pumps at a minimum and to reduce the necessary number of parts in stock. With a volute pump, the impeller diameter may be decreased as much as 20 percent from its maximum value without appreciably reducing the pump efficiency caused by increased hydraulic losses. On the other hand, similar reduction in diameter of a diffuser-type pump impeller would produce unacceptable performance. The increased gap between the impeller periphery and the diffuser inlet vanes would result in excessive hydraulic losses. For this reason, a maximum-diameter impeller can be cut only from 5 to 10 percent. Further reduction requires a different diffuser pattern with a smaller inlet vane diameter. Impeller cutdown restrictions necessitate an increased parts inventory. Also, the flexibility of constructed units is limited because a change in conditions of service, otherwise taken care of by an impeller cutdown, may also require a new diffuser for satisfactory performance. RADIAL THRUST In a single-volute pump casing design (Fig. 2.2), uniform or near-uniform pressures act on the impeller when the pump is operated at design capacity (which coincides with the best efficiency). At other capacities (Fig. 2.3), the pressures around the impeller are not uniform, and there is a resultant radial Fig. 2.2 Zero radial reaction in single-volute casing. Pressure distribution is uniform at design capacity. Fig. 2.3 Radial reaction in a single-volute casing. Pressure distribution is not uniform at off-design capacity. Casings and Diffusers 21 100 80 Radial Thrust % Thrust @O% Flow 60 40 20 20 40 60 80 100 120 140 160 180 Flow-% BEP Fig. 2.4 Characteristic of radial reaction in a single-volute casing. F decreases from shutoff to design capacity and then increases with overcapacity. At overcapacity, the reaction is roughly in the opposite direction from that at partial capacity. reaction (F). A graphical representation of the typical change in this force with pump capacity is shown in Fig. 2.4; note that the force is greatest at shutoff 1 For any pt>r(,~!l!::gc of ~apacIty, radial reaction is a function of the total head and of the width and diameter of the impeller. The magnitude of the reaction, Fr in kN (16), can be estimated using the following relationship: Fr = where: kD 2W 2H(SG) . . . F kD2WzH(SG). US . 10.21(104) III metnc umts or r = 2.31 III umts k = radial thrust factor D2 = impeller diameter, mm (in) W2 = impeller width, induding the shrouds, mm (in) H =pump total head, m (ft) The radial thrust factor k is determined by experiment, and varies with both percentage of design capacity and pump specific speed (see Fig. 2.5). Zero radial reaction is not often realized. The more usual characteristic is that shown in Fig. 2.4, in which the reaction is greatest at shutoff, least in the region of best efficiency point (BEP). To complicate matters a little further, the direction of radial reaction varies with capacity, typically being 90 deg away from the tongue at shutoff, moving to approximately 270 deg away at flows on the order 140 percent of BEP (see Fig. 2.6). In a centrifugal pump design, shaft diameter and bearing size can be affected by allowable deflection as determined by shaft span, impeller weight, radial reaction forces, and the torque to be transmitted. Formerly, standard designs with maximum diameter impeller were only suitable for operation down to lIn Fig. 2.2, 2.3, 2.4, and 2.7, no attempt has been made to show correct quantitative force values for a specific example nor to locate the exact resultant force. The magnitude and direction of forces vary with the type of pump, casing design, and many other factors. 22 Casings and Diffusers 0.4 .. 0.3 u: ~ c5 0.2 a... ::.::: 0.1 o ". .... • 20 40 60 80 100 120 --- ".".".".~ 100% 140 160 N5 - Specific Speed Fig. 2.5 Radial thrust factor k. 90° 0° 0% 180° -------------------4~----------------- 140% Ns = 1,700 Fig. 2.6 Direction of radial thrust. 50 percent of design capacity. For sustained operations at lower capacities, the pump manufacturer, if properly advised, would supply a heavier shaft, usually at a much higher cost. More recently, sustained operation at extremely low flows without informing the manufacturer at the time of purchase became a common practice. The result-broken shafts, especially on high-head units. Because of the increasing operation of pumps at reduced capacities, it has become desirable to design Casings and Diffusers 23 standard units to accommodate such conditions. One solution is to use heavier shafts and bearings. Except for low-head pumps in which only a small additional load is involved this solution is not economical. The only practical answer is a casing design that develops a much smaller radial reaction force at partial capacities. One of these is the double-, olute casing design, also called twin-volute or dual-volute. The application of the double-volute design principle to neutralize reaction forces at reduced capacity is illustrated in Fig. 2.7. Basically, this design consists of two 1S0-deg volutes; a passage external to the second joins the two into a common discharge. Although a pressure unbalance exists at partial capacity through each ISO-deg arc, forces F, and F2 are approximately equal and opposite, thereby producing little, if any, radial force on the shaft and bearings. Although the double-volute casing design principle has been known for a long time, broad use of it had to await the development of improved foundry techniques. The problems were two. In axially split casings, the second volute or "splitter" spanned the split joint, and so casting accuracy had to be improved to avoid mismatch between the casing halves. (Fig. 2.S) In all casings, there was a lower limit to the size of the cored passage that had to be cast to produce the second volute. By the 1960's, these difficulties were overcome to the extent that double volute construction became feasible in a commercial line of intermediate and large-size double suction pumps. At the current state of the art, double volute construction is generally available in pumps of 100 mm (4 in) discharge and larger. The double-volute design has many "hidden" advantages. For example, in large-capacity mediumand high-head single-stage vertical pump applications, the rib forming the second volute and separating it from the discharge waterway of the first volute strengttens the casing (Fig. 2.9). When the principle of the double volute is applied t< I individual stages of a multistage pump, it becomes a twin-volute. The question has been broached wbether this design should be called twin-volute or a two-vane diffuser, but the first has become the accepted form. A typical twin-volute is illustrated in Fig. 2.10. The kinetic energy of the water discharged from the impeller must be transformed into pressure energy, then turned back ISO deg to enter the impeller of the next stage. The twin-volute, therefore, also acts as a return channel. The back view in Fig. 2.10 shows this, as well as the guide vanes used to straighten the flow into the next stage. A double volute is not always practicable. In small low· specific-speed designs the second or hidden DOUBLE-VOLUTE WALL Fig. 2.7 Radial reactions in double-volute pump. Fig . 2.8 Transverse view of double-volute casing pump. 24 Casings and Diffusers Fig. 2.9 Sectional view of vertical-shaft end-suction pump with a double-volute casing. Numbers refer to parts listed in Table 1.1. passage can become too small for reliable casting and cleaning. There may be a need to line the casing waterway for corrosion or erosion resistance. The nature of the liquid pumped may preclude small passages or fine tongues. In these cases, an alternative is a modified single volute. The modification entails making part or all of the volute concentric. Figure 2.11 compares the shape and radial thrust characteristic of these two modified forms with that of a conventional single volute. The third approach to reducing radial thrust is to use a diffuser instead of a volute. Because a diffuser is analogous to a series of small volutes spread equally around the impeller, any hydraulic reactions on the impeller tend to be balanced. There are, however, limitations. Diffusers can develop quite high values of radial reaction (Fig. 2.12) if there are irregularities in the vanes, if the impeller is not concentric with the vanes or, in some designs, when the flow is reduced to the point where the diffuser develops rotating Casings and Diffusers 25 Fig. 2.10 Twin-volute of a mul :istage pump. Front view (left) and back view (right). Spiral Volute (conventional) Semi-concentric t t Head Head 100% 100% I I 0-100% 1-110 . ...\i....... . ........, t " ." Concentric ...f.".#. ~ '.'. t .................,.,., I "'" 100% .'./,1 I,,.,, m"" Head HlO. 0-100% '" 0-100% Note: Radial force plotted as a percentage of the force at thrust off for spiral volute. Fig. 2.11 Characteristic of radial reaction in modified volutes (semi-concentric and concentric) versus normal single volute. 26 Casings and Diffusers R . egular@10-15%N ( I. . .>---'-----t·..· r .. ,,---, , , I Radial Force , , Irregular ~ , , Rotating Force (Diffuser Stall) ~ / ,, ~ ,, ~ , ,, ,, ~ Stationary Force (Rotor Eccentricity) I 100 Flow-%BEP Fig. 2.12 Possible radial reactions in a diffuser. stall (Fig. 2.12). The first two reactions are generally stationary, the third rotates at a low frequency, typically 10-15 percent of running speed. Efficiency can also influence the choice of collector design. Taking a well designed single volute as a basis, the following general observations can be made: 1. Double volute-lower peak efficiency in small sizes, comparable in larger; characteristic similar. 2. Modified volute-lower peak efficiency in all sizes; characteristic broader thus offering comparable overall power consumption in pumps running over a wide flow range. 3. Diffuser-higher peak efficiency in all sizes; efficiency characteristic narrower, thus tending to offset the advantage of higher peak efficiency in pumps running over a wide flow range. Some designs have a collector arrangement incorporating a diffuser discharging into a single volute (Fig. 2.13). Resorting to this arrangement offers two advantages. First, in small- and middle-size pumps the higher peak efficiency of the diffuser is realized. Second, the point of peak efficiency can be shifted while maintaining high peak efficiency by changing both the impeller and the diffuser. Because the ~ Fig. 2.13 Single stage pump with a separate diffuser discharging into a single volute casing. (Courtesy Sulzer.) 28 Casings and Diffusers diffuser is discharging into a volute, this collector arrangement still exhibits radial thrust but of lower magnitude than a volute alone. Volutes can be either an integral part of the casing (Figs. 2.8 and 2.9) or separate and bolted into the casing (Fig. 2.10). Except in very large pumps, diffusers are separate (Fig. 2.13), a consequence of the care needed to produce their small passages. SOLID AND SPLIT CASINGS Solid casing is a design in which the discharge waterways that lead to the discharge nozzle are all in one casting or fabricated piece. It must have one side open so that the impeller can be introduced into the casing; however, it cannot be completely solid, and designs normally called solid casing are really radially split (Figs. 2.14, 2.16, 2.17, and 2.18). Split casing is a casing made of two or more parts. The term "horizontally split" had regularly been used to describe horizontal double-suction pumps, indicating that the casing was divided by a horizontal plane through the shaft centerline or axis (Fig. 2.15). That designation was an unfortunate choice because applications of the same pump design for vertical use or with the nozzle position rotated caused confusion. The term "axially split" is now preferred. Since both the suction and discharge nozzles of axially split pumps are usually in the same half of the casing, the other half may be removed (upper half in the case of horizontal pumps) for inspection without disturbing the bearings or piping. Like its counterpart, "horizontally split," the term "vertically split" is unfortunate. It refers to a casing split in a plane perpendicular to the axis of rotation. The term "radially split" is now preferred. Fig. 2.14 Radially split, foot mounted, overhung pump with stuffing box head or cover for back-pull-out capability. Casings and Diffusers Fig. 2.15 Axially split casing, horizontal, double suction volute pump. Fig. 2.16 Vertical overhung pump with an elbow t) pe suction nozzle. 29 30 Casings and Diffusers Fig. 2.17 Horizontal overhung process pump with a fiat elbow type suction nozzle. A now obsolete casing configuration for horizontal pumps had an axial split but with the joint surface inclined to the horizontal. The virtue claimed for this construction was the utility of top discharge combined with the convenience of an axial split. Whether to split a casing radially or axially depends on the impeller configuration, whether the pump is single or multistage, the pressure to be contained, and to some degree the shaft orientation. Pressure containment is influenced by liquid specific gravity (SG) and temperature, low SG or high temperature or both tending to increase the split joint design pressure necessary to ensure a tight seat. Shaft orientation reflects the influence of gravity on assembling the impeller or element into the pump's casing. For the various combinations of these factors there is a casing split that represents the lesser manufacturing cost. Usual casing splits for the more common pump arrangements and how the various factors influence the choice is shown in Table 2.1. When factors beyond those previously listed have a bearing on the design, the choice of casing split can be quite different. SUCTION NOZZLE Centrifugal pumps are sensitive to the flow distribution at the impeller inlet, and the sensitivity increases with specific speed. Depending on its design, the suction nozzle can have a significant influence on the flow distribution at the impeller inlet, thus it is an important part of a casing. In many instances, the suction nozzle arrangement that provides the easiest installation also penalizes pump performance, raising Casings and Diffusers Table 2.1 31 Typical Casing Split for Various Pump Configurations and Pressure Ratings Impeller Number of Stages Pressure Single Suction l Single All Double Suction Multi Single Low & Medium High I~ Shaft Orientation Either Horiz. Vertical Either Casing Split Radial Axial Radial Radial the net positive suction head required (NPSHR) and lowering efficiency. When this occurs, it is necessary to strike a compromise between installation cost and energy wnsumption. With only subtle variations, all pumps use one of three basic suction nozzle arrangements: end, elbow, or flat elbow. End suction (Fig. 2.14) has the liquid entering the impeller eye without any turning. Because the liquid approach is so direct, this arrangement offt~rs the best potential for low NPSHR and high efficiency, and is therefore widely used in pumps with single-suction impellers. An elbow suction is used for vertical single-suction pumps when the piping arrangement make it desirable to tum the flow through 90 degrees before entering the impeller (see Chapter 14). With proper design (large radius and tapered), these elbows do not seriously affect the pump's NPSHR and efficiency. Refinement of the elbow suction to a flat elbow (Figs. 2.16 and 2.17) significantly shortens the axial space required for the nozzle with only a minor effect on pump NPSHR and efficiency. Flat elbow suction nozzles are particularly important for reducing bearing span when the impeller is located between bearings (Figs. 2.13 and 2.15). 32 Casings and Diffusers PREROTATION AND STOP PIECES On occasion, the liquid in the suction pipe may swirl for some distance ahead of the actual impeller entrance. This phenomenon is called "prerotation." When this occurs there are two possible causes: One is that the pump is operating below its suction recirculation capacity and the prerotation is being induced by same (see Chap. 22). The second is that the incoming flow is being distorted by the suction entrance, piping, or nozzle. In the first case, the effect on pump performance is evident from test results, and can only be corrected by changing the pump's impeller design. In the second case, the pump's performance is often impaired (high NPSHR, low head and efficiency) because the liquid is not entering the impeller as the design intended. To confer some tolerance of flow distortions introduced by suction piping, most pump suction nozzles include a stop vane or vanes to straighten the flow as it approaches the impeller. An exception to this is pumps intended for services such as sewage and paper stock, in which solids in the liquid would likely buildup on the stop vane and block the pump. RADIALLY SPLIT CASINGS At least one side of a radially split casing must be removable so the impeller or element can be installed in the casing. Single-stage end-suction pumps are the most common example of radially split casings and are built with one of three cover arrangements. If the cover is on the suction side, it becomes the casing sidewall and contains the suction opening or nozzle (Fig. 2.18). This is called the suction cover or casing suction head. Other designs are made with a stuffing box cover (Fig. 2.14), whereas still others have both a suction cover and a stuffing box cover (Fig. 2.19). For general service, the end-suction single-stage pump design is used extensively for both close coupled (motor mounted) and separately coupled pumps up to 8-in. discharge size. In all of these, the small size makes it feasible to cast the volute and one side integrally. Whether the stuffing box or suction side is made integrally with the casing is usually determined by the service for which the pump is intended. Designs for general, chemical, and process service have a so-called stuffing box or casing Fig. 2.18 Section of frame-mounted end-suction pump with radially split casing. Note the suction cover. Casings and Diffusers Fig. 2.19 33 Section of radially split, foot mounted end-suction pump with two covers (suction and stuffing box). Fig. 2.20 Section of frame mounted, radially split, end-suction slurry pump with stuffing box cover and replaceable casing liners. 34 Casings and Diffusers cover (Fig. 2.14). For separately coupled pumps, provided the appropriate spacer coupling is furnished, the virtue of this arrangement is the ability to remove the entire bearing frame, cover, and impeller assembly without disturbing the pump's driver or suction and discharge piping connections. Such an arrangement is often referred to as "back pull-out." When the casing is prone to high wear, as in slurry service, or there is an advantage to being able to vary the discharge nozzle orientation (see nozzle locations), the casing is frame mounted with a suction cover (Figure 2.18) or a stuffing box cover (Fig. 2.20). Dismantling pumps of this arrangement without disturbing the driver or the pump's bearing frame requires a spool in the suction piping. Radially split casings for other than end suction are available (see under nozzle locations). For pumps of two or more stages, radially split casings are necessarily more complicated than for a single stage. A detailed treatment of such casings is given in Chapter 3. AXIALLY SPLIT CASINGS Most axially split casings are designed with their mounting feet integral with the lower half (Fig. 2.15) or with the fixed half in the case of pumps mounted with the split vertical. By being built in this way, Fig. 2.21 Section of single stage volute pump with axially split casing and separate stuffing boxes. Casings and Diffusers 3S the pump can be dismantled without disturbing the driver (provided the coupling halves will separate normal to the shaft axis) or the pump's suction and discharge connections. Single-stage designs for general service usually have the stuffing boxes cast integrally with the casing (Fig. 2.15), since that is an economical arrangement. For more severe service, where stuffing box cooling or a special mechanical shaft seal is necessary, it is often better to employ a separate stuffing box (Fig. 2.21), to avoid the difficulty of having to cast a complex shape as part of the casing. Bearing support is either by integral brackets (Fig. 2.15) or by brackets built into the bearing housings and bolted to the casing sidewall (Fig. 2.21). CASING CONSTRUCTION FOR OPEN IMPELLER PUMPS In the simplest open impeller pump, the close axial clearances needed to seal the impeller are formed by the casing and cover or head directly (Fig. 2.22). Such construction is employed in low-cost pumps because it is simple; and in many chemical pumps, because it has the least number of potential crevice corrosion sites. When the service is abrasive, the casing and in severe services the head are equipped with a replaceable liner or wear plate (Figs. 2.20 and 2.23). Adopting this construction allows the wear plate to be of a more abrasion-resistant material when necessary and enables ready replacement of the wearing surface. Except in very rare instances, the use of wear plates is limited to single-suction impellers. Early designs extended this construction to double-suction impellers, but the difficulty of setting up and maintaining the close axial clearances had rendered such arrangements obsolete. Fig. 2.22 End suction chemical pump with semi-open impeller running directly against casing. 36 Casings and Diffusers I -1---- -j- l [ -- - - - - -.- - - - - - - ] 1 : Discharge --- , I: I Fig. 2.23 End suction chemical and stock pump with semi-open impeller running against a wear-plate. NOZZLE LOCATIONS End suction single stage horizontal pumps are usually arranged for top-vertical discharge (see Figs. 2.14, 2.18, 2.20, and 2.22). Other positions, however, may be obtained when necessary. The most common variations are top-horizontal (overshot), bottom-horizontal (undershot), and bottom-vertical. Figure 2.24 A B o F Fig. 2.24 Possible positions of discharge nozzles for horizontal end-suction solid-casing frame mounted pump. Rotation illustrated is counterclockwise from suction end. Casings and Diffusers 37 shows these positions plus intermediate positions (inclined) that may be available if the casing attachment allows. Generally, the alternate nozzle positions are employed to simplify piping arrangements, save space, or reduce pipeline erosion by the elimination of an elbow. Unless the casing is frame mounted (Figs. 2.18 & 2.20), the provision of alternative nozzle locations requires a change in casting or a casing with multiple mounting pads. With some older frame-mounted designs, interference between the discharge flange and the bearing frame or base precludes the two bottom nozzle locations. In other instances, access to auxiliary connections, such as stuffing box sealing, limits casing rotation. Single-stage radially split horizontal pumps with an elbow or flat elbow suction are usually arranged with both suction and discharge top-vertical (Fig. 2.17). Such an arrangement is generally known as "top-top," referring to the suction first, then the discharge. Top-top nozzles are separated axially in single-suction pumps (Fig. 2.17) and are in the same axial plane in double-suction pumps (Fig. 2.25). When the piping arrangement dictates it, pumps of the form in Fig. 2.25 can be furnished with "sideside" instead of top-top nozzles. Axially split casings always have the nozzles in the lower half, or what is termed the fixed half when the pump axis is vertical, so the pump can be dismantled without breaking the suction and discharge piping connections. Horizontal pumps, whether single or double suction, almost invariably have a side discharge nozzle and either side or a bottom suction nozzle. If the suction nozzle is placed on the side of the pump casing with its axial centerline at right angles to the vertical centerline (see Fig. 2.15), the pump is classified as a side-suction pump. If its suction nozzle points vertically downward (Fig. 2.26), the pump is called a bottom-suction pump. Single-stage bottom-suction pumps are rarely made in sizes below lO-in. discharge nozzle diameter. Fig. 2.25 Centerline supported, radially split single stage pump with top suction and discharge nozzles. 38 Casings and Diffusers Fig. 2.26 Bottom-suction single stage axially split casing, single stage pump. Special nozzle positions can sometimes be provided for double-suction axially split casing pumps to meet special piping arrangements, for example, a vertically split casing with bottom suction and top discharge in one half of the casing. As these special designs are usually costly, they should be avoided. CENTRIFUGAL PUMP ROTATION The direction of rotation of a centrifugal pump is a fundamental element of its specification; there are only two directions, and running a pump in the wrong direction has dire consequences on its performance. In many designs, the direction of rotation also affects the location of the suction and discharge nozzles, so it's important in this discussion of casings to address the means used to define the direction of rotation. According to Hydraulic Institute Standards, rotation is defined as clockwise or counterclockwise by looking at the driven end of a horizontal pump or looking down on a vertical unit. Some manufacturers still designate rotation of a horizontal pump from its outboard end. Therefore, to avoid misunderstanding, clockwise or counterclockwise rotation should always be clarified by including the direction from which one looks at the pump. Casings and Diffusers 39 The tenns "inboard end" and "outboard end" are used only with horizontal pumps. Inboard end is the one closest to the driver, whereas the outboard end is the one farthest away. The tenns lose their significance with dual-driven pumps and are not then used. Many centrifugal pump casings produced from one pattern can be built into a pump of either clockwise or counterclockwise rotation. One such design is the axially split, single-stage double suction pump (Fig. 2.15). Other designs such as endsuction and some radially split double suction pumps have an integral head on one side, and therefore require separate directional casing patterns. CASING HAND HOLES Casing hand holes are furnished primarily on pumps handling sewage or stringy materials that may become lodged on the impeller suction vane edges or on the tongue of the volute. They pennit removal of this material without dismantling the complete pump. End-suction pumps used for handling such liquids are provided with hand holes for access to the suction side of the impellers. These are located on the suction head or in the suction elbow. Hand holes are also included in drainage, irrigation, circulating, and supply pumps if foreign matter may become lodged in the waterways. On very large pumps, manholes provide access to the interior for both cleaning and inspection. MECHANICAL FEATURES OF CASINGS Most single-stage centrifugal pumps are intended for service with moderate pressures and temperatures. As a result, pump manufacturers usually design a special line or lines of pumps for high operating pressures and temperatures rather than make their standard line unduly expensive by having it cover too wide a range of operating conditions. Casings for higher pressure or temperature or both tend to be radially split, despite the difficulties this arrangement entails in double-suction pumps and large horizontal pumps of either single- or doublesuction configuration. Axially split casings have inherent limitations, which generally restrict their economical use to low and intennediate pressures. The two principal limitations are both products of casing deflection under the action of pressure. First, when the bearing brackets are attached to the casing sidewall, as they are in double-suction pumps (Fig. 2.15), "ballooning" or bulging of the casing sidewalls rotates the brackets slightly, which raises the pump's rotor. In extreme cases, the rotor can be raised to the extent it contacts the internal running clearances, thus rendering the pump inoperable. For the usual design pressures, internal or external ribbing is used to avoid this deficiency. Second, deflection of the casing, the bolting flange, and the bolting itself reduces the residual gasket load, with the greatest reduction at the innennost diameter of the joint. If the gasket load is reduced too much, the gasket is washed out, allowing internal leakage and eventually casing erosion. Chapter 3 discusses this problem and its solution in detail. Most pumps are supported directly by feet on their casing or indirectly by feet on a frame or pedestal. The virtue of this arrangement is a simple connection to the foundation, whether through a baseplate or directly to the foundation. For higher pumping temperatures, the change in rotor position caused by thennal expansion of the casing or frame poses a major coupling alignment problem. To avoid this difficulty, pumps for higher temperatures are usually supported by feet located at or very close to the casing centerline (Figs. 2.17 and 2.25). The temperature at which centerline support is necessary varies with casing height and coupling misalignment capacity; a commrnon industry standard is 175°C (350°F). With centerline support, the base or foundation must include pedestals to reach the pump's feet. 40 Casings and Diffusers Contrary to past opinion, practicality and more sophistication in piping design mean that pump casings now must also withstand moderate loads from the connected piping. Two effects should be considered in assessing a particular design's piping load capability: distortion of the pump casing proper, leading to contact at the internal clearances, and distortion of the pump as a whole, leading to misalignment at the coupling. Close-coupled pumps are not, of course, influenced by the second effect, because driverto-pump alignment does not depend on a connection through earth. This feature affords close-coupled pumps a notable advantage. Casing distortion from piping loads is a function of pressure rating, material, and the path of load transmission to the foundation. In general, casings designed for higher pressures will have relatively higher piping load capability. The importance of material is stiffness, because for the same stress, bronze and cast iron deflect about twice as much as steel. Thus, changing to a stiffer material offers lower distortion if the stress levels are similar. Ideally, piping loads should pass directly from the nozzle to a mounting foot and thence to the foundation. By doing this, the extent of the casing subjected to higher loads is minimized, hence casing distortion is minimized. A casing with feet on its nozzles (Fig. 2.15 & 2.21) has the path of piping load transmission approaching the ideal. Centerline-supported pumps can also approach the ideal provided the design seeks to realize a direct structural connection between the nozzles and mounting feet rather than through the casing. To maintain coupling alignment, the prime distinction is the number of points of support, whether two, three, or four points. Most centerline-supported overhung pumps (Fig. 2.17) and some hightemperature foot-supported pumps are two-point supported. Because even relatively small deflections of the feet and pedestal are usually magnified substantially as displacement of the shaft at the coupling, two-point-supported pumps generally have the lowest piping load capability. Depending on the stiffness of the pump and its bearing frame, three-point support (Fig. 2.14) can significantly increase piping load capacity, a result of the third support close to the shaft end. The difficulty with this design is that it turns the bearing frame and the bracket connecting it to the casing into structural elements subject to part of the piping loads. Provided the bearing frame is sufficiently stiff to accommodate the additional loading while maintaining bearing, seal, and running clearance alignment, this arrangement is quite viable. For high-temperature pumps, three-point support with a foot-mounted casing requires care lest differences in thermal expansion of the supports cause bearing frame distortion. To a lesser degree, but still of some consequence, the same concern exists for centerline-supported casings. Four-point support (Fig. 2.25) offers the greatest piping load capability, and although more expensive, should be given serious consideration for services where high piping loads are likely. Two factors account for this. First, the greater piping load capability may allow a less expensive piping layout. Second, the pump will likely require less maintenance than an equivalent two- or three-point-supported overhung pump. SERIES UNITS For large-capacity, medium-high-head service conditions that require such an arrangement, two singlestage double-suction pumps can be connected in series on one baseplate with a single driver. Such an arrangement is very common in waterworks applications for heads of 75 to 120 m (250 to 400 ft). One series arrangement uses a double-extended shaft motor in the middle, driving two pumps connected in series by piping (Fig. 2.27). In a second type, a standard motor is used with one pump having a doubleextended shaft (Fig. 2.28). This latter arrangement may be limited, because the shaft of the pump next to the motor must be strong enough to transmit the total pumping horsepower. If the total pressure generated by such a series unit is relatively high, the casing of the second pump may require ribbing. Casings and Diffusers Fig. 2.27 Fig. 2.28 Series unit (motor in middle). Series unit (motor at end). 41 42 Casings and Diffusers CASING MAINTENANCE Pumps that handle noncorrosive water or liquids are not usually subject to extensive casing wear. However, the casing waterways should always be thoroughly cleaned and repainted during a complete overhaul. A suitable paint should be used that finnly adheres to the metal so that the water velocity will not wash or jet it off. An enamel-like finish is the most efficient. A program of casing cleaning and repainting should be established on the basis of local conditions. This will prevent the protective coat from ever fully eroding before replacement, thereby preventing corrosion. Pumps handling gritty or sandy water naturally are more subject to casing troubles. Erosion can be reduced by selecting pumps with low-liquid velocities-that is, low head per stage-or employing more erosion resistant materials, or a combination of both. Caution is needed, however, because conventional water pump designs and materials can tolerate only relatively low concentrations of sand or silt. As a general guide, special materials should be investigated if the concentration exceeds 1 percent, and a pump designed for slurry should be used if the concentration exceeds 2-3 percent. Progress has recently been made in processes of rubber-coating pump waterways, and this technique may be desirable in some applications. If the casings of pumps handling sandy or gritty water are to be protected primarily by periodic painting, a suitable type pump should be carefully selected for local water conditions and a special maintenance schedule established. In these difficult pumping applications, the casing should be regularly examined for corrosion, which will be indicated by cast-iron graphitization. This occurs when the ferrous particles are washed out by electrolytic action and deposited on bronze pump parts. If severe graphitization takes place, the manufacturer should be consulted on the possibility of substituting materials more impervious to the pumped liquid. If the casing is pitted or eroded in places, it can be restored by welding, brazing, silver soldering, or metal spraying, depending on the material and the facilities available. The authors know of several large centrifugal pumps in waterworks service in which corroded areas, located where water velocities are low, are actually filled with properly anchored concrete. Special care must be taken to examine and recondition meta1-to-metal fits where stationary parts such as casing rings, diffusers, or stage-pieces seat in the casing. If the casing is steel, and these fits show signs of erosion, it might be advantageous to face them with 18-8 stainless steel and refinish. Frequently, the cut-water, or volute tongue as it is also called, becomes eroded, for example, when a pump handles water with some sand in suspension or when the periphery of the impeller is located too close to the tongue. Another fairly common cause of erosion in this area is galvanic action between a cast-iron casing and bronze fittings. The cast iron graphitizes and wears away most perceptibly in areas of high velocity, like those near the volute tongue. The best way to correct this condition is to cut back the tongue so that it is straight across .and then file it to a smooth rounded edge (Fig. 2.29). This cut back does not affect pump capacity unfavorably; on the contrary, it is often used to squeeze out an extra small percentage of capacity without putting in an impeller of larger diameter. The added capacity comes from the increase in the casing throat area, which causes an increase for a given casing velocity. If the pump is double volute, it is prudent to cut back both the tongues so they are 180 deg apart after correction. Doing this helps to ensure there is minimal radial thrust after correction. In cases where this is not feasible, consult the manufacturer to detennine whether asymmetric tongues can be tolerated. Care should be taken not to distort or warp the casing during overhaul. After repairs are completed, the horizontal flanges of an axially split casing should be finished to a flat surface with hand tools. Of course, if the repairs are very serious, the pump is serviced at the manufacturer's shop. The casing flanges may have to be refinished at that time and the casing rebored. Except for some special designs, every pump has gaskets that are subject to damage when the pump Casings and Diffusers Fig. 2.29 43 Method of filing worn volute tongue. is opened. If the old gasket adheres to the lower half of the casing and is in good condition, it is not necessary to replace it. However, it should be replaced if it is damaged in any way, and for this reason a new gasket should always be available. The new gasket should be of the same thickness as the original and, if possible, of the same type of material so that it will have the same compression characteristics. Too thick a gasket usually leads to leakage. If the gasket is thinner than the original, tightening of the two casing halves may exert undue force on casing wearing rings and distort them. In installing a new gasket, the inner edge must be accurately trimmed along the edge of the stuffing box bore. At all points where the gasket abuts on the outer diameter and the sides of stationary parts, the edges must be trimmed squarely and neatly, allowing sufficient gasket overlap. Tightening the upper half of the casing will effectively press the gasket edges against the stator parts, insuring proper sealing. This trimming operation is best accomplished by first cementing the gasket to the upper casing half with shellac (this makes for easier gasket removal at the next overhaul) and then cutting all edges square with a razor blade. Of course, all foreign matter must be removed from the casing flanges before the gasket is applied to the lower casing half. In reassembling the pump, it is recommended that powdered graphite be rubbed into the gasket before the top casing half is replaced. This action will prevent the gasket from sticking to the lower half when the casing is next dismantled. 3 Multistage Pump Casings Although most single-stage pumps have volute casings, both volute and diffuser casings are used in multistage pumps. Advantages of the volute casing are described in Chapter 2. However, the diffuser casing or collector is a very strong competitor of the volute design in high-pressure applications. The principal reason for this is that for the same pump capacity, a diffuser design is smaller (occupies less volume) than a volute, thus making a diffuser pump less expensive to manufacture. When compared to integrally cast volutes, the volume advantage of a diffuser design is compounded by symmetry, an absence of complicated castings, suitability for radially split construction, and more uniform expansion in high-temperature service. Arranging twin volutes in the same manner as diffusers (Fig. 2.10) overcomes all the advantages except that of lower volume for the same capacity. At that point, the choice between twin volutes and diffusers must be made based on pump cost versus operating cost, the broader efficiency characteristic of the volute being an advantage when the pump has to run over a wide flow range. There is evidence, too, that at conditions far from BEP, twin volutes produce lower rotor forces than diffusers. In smaller, lower pressure multistage pumps, the cost advantage of diffusers is not so significant. At the same time, ease of manufacturing favours volute pumps, at least down to around 2-in. discharge, so most such pumps have volute casings. In all but the smallest sizes, twin volutes are used. The smallest sizes use single volutes to avoid the casting problems inherent in small double volutes, and balance radial thrust by staggering successive volutes 180 deg. apart. Figure 3.1 shows the principle for a twostage pump. Older designs successfully used staggered single volutes in larger sizes than is generally done today. The advantage these designs had was a relatively robust shaft, able to withstand the moment produce between impeller pairs. Modem designs tend to use more slender shafts in the interests of higher efficiency and lower NPSHR, and have therefore had to use a twin volute at each stage. AXIALLY AND RADIALLY SPLIT CASINGS Both axially and radially split casings are used for multistage centrifugal pumps. Variety in pump design is based on these two successful solutions for casing construction problems, which were arrived at in 44 I. J. Karassik et al., Centrifugal Pumps © Chapman & Hall 1998 Multistage Pump Casings 45 Radial Thrust Stage 1 Fig. 3.1 Multistage volute pump arrangement for radial thrust balance. the early days of the centrifugal pump. Each of these designs, incorporated in pump models over many years, has followed its own separate evolution. Although the radially split casing design might logically seem to be a recent development motivated by higher pressure requirements, it is really a reversion to the original type. The first centrifugal pumps had a vertically split casing, with radial joints in a plane perpendicular to the shaft axis. Radially split casings have been in continuous use both here and abroad ever since, especially in high-pressure multistage centrifugal pumps. The idea of splitting the casing axially, or parallel to the axis of rotation, was introduced to overcome radially split casing limitations on accessibility for inspection and repairs. The casing suction and discharge connections were located in the lower half. The upper half could be lifted and the rotor laid bare for inspection or removal without disconnecting the pump proper either from its foundations or from the suction and discharge piping. This was the key influence in the development of the axially split casing. The change was made solely for reasons of cost. Less machining was deemed likely to reduce the manufacturing cost, and the greater convenience of dismantling and reassembly would certainly reduce maintenance costs. As long as pump working pressures remained within modest limits, axially split casings proved satisfactory. Higher working pressures, however, exposed a basic weakness. As pressures increased, it became more and more difficult to maintain a tight axial split flange. The consequences of this were intemalleakage between the stages with subsequent casing erosion and occasional axial thrust problems at the least; leakage of the pumped liquid to the atmosphere at the worst. Distortion of the joint flange 46 Multistage Pump Casings was recognized as the problem. The first remedies were to increase the flange thickness, stiffen the casing with ribs, and increase the number and size of casing bolts. Although these remedies increased the allowable working pressures to some extent, there was still an upper limit beyond which reliable axial split operation could not be ensured. Axially split against radially split pump casings was one of the most eontroversial design topics until late in the nineteen-thirties. Then, the 1938 to 1948 period produced a definite trend, with 85 bar gauge (1,250 psig) becoming the average working pressure at which a user changed from axially to radially split casings. For some time after that, designer opinion on the proper pressure limits for the two casing designs varied considerably, with some favoring a reduction in the changeover point to as low as 70 bar gauge (1,000 psig) and others convinced that the axially split casing limit could be safely increased to 110 bar gauge (1,600 psig). The limiting factor in the history of axially split casings was the difficulty in making even rough estimates of the stress and strain (distortion) in such a complex shape (see the discussion later). An entirely satisfactory design could be realized by "cut and try" methods, but usually at greater expense than was commercially tolerable. To realize consistently well behaved axial split joints at reasonable cost, it was necessary for the technique known as "finite element analysis" (FEA) to come into general use. With this technique, the casing is modeled as many connected blocks, and its stress and strain contours are calculated for a given set of loads, including piping loads and constraints. The beauty of FEA is that it takes account of the interdependence between stress and strain and allows the casing to be "tested" while it is still just a design. The drawback is that the solutions can only be run on a computer; the extent of calculation is well beyond manual techniques. With FEA the working pressure limit for axially split casings has risen to 275 bar gauge (4,000 psig). Such casings, however, tend to be more expensive than an equivalent radially split design, so are used only when other circumstances, such as floor space or ease of maintenance, dictate them. The general economical limit of axially split casings in services such as boiler feed is 170 bar gauge (2,500 psig). For applications handling petroleum based liquids, the limit can be lower. API-61O [3.1], taking account of the consequence of casing leakage in oil refineries, the greater risk of leakage when handling petroleum products at elevated temperatures, and the difficulty of remaking axial split joints in the field, limits axially split casings to rated pressures of 100 bar gauge (1,450 psig), pumping temperatures of 230°C (450°F) and liquids of SG 0.7 and higher at the pumping temperature. These are conservative limits and there are many axially split casings operating reliably beyond them. In contemplating axially split casings beyond the limits of API-61O, the pump user needs to consider the ratio of the casing's maximum allowable working pressure to the rated pressure (the higher the better), actual operating experience with the same casing in similar conditions, and finally the availability of the skills necessary to successfully remake the casing joint. CASING UPPER PRESSURE LIMITS To analyze a bolted and gasketed flange joint, we must visualize the phenomena occurring during the initial tightening process and when internal pressure is applied. As the flanges are pulled tight by bolt action, the bolts are subjected to a tensile stress. The gasket itself is subjected to a compression stress determined by the bolt stress and the relative bolt and gasket areas. As internal pressure is applied, the bolt stress increases and the bolts stretch. Assuming that the deformation of the gasket under initial tightening is not permanent, gasket thickness will increase by the same amount that the bolts are increased in length. This requires that the gasket stress not exceed the yield strength of the gasket material and Multistage Pump Casings 47 that the material possess sufficient resiliency. Although the gasket compression stress is thus reduced under internal pressure, it remains sufficiently high to prevent leakage between the flanges. This analysis assumes that the flange surfaces are sufficiently smooth to give relatively uniform gasket stress under internal pressure, the stress never falling below the minimum required for effective sealing. If flange surfaces are rough, large local stresses may develop in the gasket at flange high spots during the initial tightening. Conversely, the gasket may have low-stress areas at flange depressions even when high stress is applied during the initial tightening. When internal pressure is applied, highly stressed gasket areas may not match the increase in gasket thickness found in other areas, and low flange areas not sufficiently stressed initially may fail to hold the internal pressure, causing leakage. For these reasons, planed or milled flange surfaces are only suitable for low or medium pressures. If a satisfactory flange joint is desired in a high-pressure range, the flange surfaces must be very carefully ground and low spots eliminated. Analyses of the tightness of bolted flange joints vary in complexity. If the flange is symmetrical (for example, a pipe flange), the bolt load distributed uniformly over the entire gasket contact area, and the gasket material perfectly homogeneous, it is relatively easy to calculate initial bolt and gasket stress, elongation of bolts caused by internal pressure, and the resulting increase in gasket thickness. If the restoration characteristics of the gasket material are known, it can then be determined whether the joint is sufficiently tight for its intended service. Axially split casing flanges in multistage pumps do not, however, lend themselves to simple analysis. Figure 3.2 shows the horizontal flange of a six-stage pump. The bolting distribution is usually very complex, making it necessary to use finite element analysis to study overall joint quality under varying pressure at the individual stages. By definition any "model" of a part is an approximation, so prudence requires that FEA be occasionally verified or calibrated by experiment. Stress is checked using strain gages, and gross strain or deflection by checking the actual movement, or joint separation, at critical Fig. 3.2 Horizontal flange of an axially split six-stage pump casing. 48 Multistage Pump Casings areas within the casing under working pressure. The critical areas, of course, are the projecting casing tongues that separate the various pump stages and that are farthest removed from the bolting. These data must be supplemented by stress-deflection tests on the gasket material to permit comparison between the casing deflection under internal pressure and restoration of gasket thickness under reduced stress. The comparison will indicate whether the flange joint will remain tight under pressure or leak. Special gages (Fig. 3.3) permit experimental measurement of casing stretch. One or more such gages are clamped to the internal ring bores on the lower casing half. They are so arranged that the spring pushes the soft copper wedges into the split at the adjacent tongue. The gage plunger is retracted before installation and secured with the holding screw. To determine gasket compression induced by the initial bolting, small pieces of gasket are removed at the tongues. The measurement is obtained by using feeler gages. After the casing stretch gages are installed, the upper half of the casing is put in place and the bolts tightened. As the shaft and impellers are not in place for this test, it is possible to reach into the stuffing Holding Screw ___"""""--__ Slot Clamp Fig. 3.3 Casing flange deflection gage. Used in experimental analysis of axially split casing pump designs. Multistage Pump Casings 49 box opening and release the gage-holding screws. The soft copper wedges are thereby pressed against the closed split under spring pressure, free to advance as casing deflection occurs. It is also possible at this stage to reach in with a feeler gage and measure gasket compression under initial tightening. Endplates are fastened over the stuffing box opening, and the casing subjected to the desired hydrostatic test pressure. The copper wedges penetrate into the split as far as it is opened up. After the casing has been held at test pressure for the required length of time, the pressure is released. The two casing halves resume their original position, and an indentation is made on the soft copper wedges at an easily measurable point. When the casing is opened and the gages removed, this indentation permits exact determination of casing deflection. Comparison of this measurement with the restoration curve of the gasket material under varying stresses will indicate whether the selection of the size, number, and location of the bolting material, the stiffening ribbing on the casing, and the gasket material will assure a pump casing that will remain tight under working pressure conditions. Interstage pump leakage along the horizontal flange with accompanying annoyance, maintenance expense, and pump outage were common characteristics of multistage pumps for many years. They were previously accepted as an unavoidable consequence of man's attempt to generate hydraulic pressures in excess of those provided by the free state of nature. Fortunately, designs have today improved to the point that an axially split casing pump need not develop this leakage. Fig. 3.4 Two-stage axially split casing volute pump. For small capacities and pressures up to 17.5 bar gauge (250 psig). SO Multistage Pump Casings Fig. 3.5 Two-stage axially split casing volute pump. For pressures up to 27.5 bar gauge (400 psig). Note the outline of integrally cast interstage passages. Fig. 3.6 Five stage axially split casing volute pump. For pressures up to 110 bar gauge (1,600 psig). Multistage Pump Casings 51 Fig. 3.7 Ten stage axially split casing volute pump. For pressures up to 175 bar gauge (2,500 psig). AXIALLY SPLIT CASING DESIGN The design and arrangement of stages within a casing is discussed in more detail later. Whatever the arrangement, it is necessary to connect the successive stages of a multistage pump. In the low and medium pressure and capacity range, these interstage passages are cast integrally with the casing (Figs. 3.4 and 3.5). Older designs for higher capacities and pressures used external crossovers (Fig. 3.6) to keep casing dimensions small and avoid sudden changes in flow velocity or direction, hence higher hydraulic losses. Improved understanding of casing flow, particularly in the crossover region between stages, has yielded modern designs that realize equal or better efficiency without the added cost of external crossovers (Fig. 3.7). Interstage Construction A multistage pump inherently has adjacent chambers at different pressures. These chambers must be isolated from one another so that leakage from high to low pressure will occur only at the clearance joints between stationary and rotating pump parts and will thus remain minimal. The isolating wall used to separate two adjacent chambers of a multistage pump is called a stage-piece, a diaphragm, or an interstage diaphragm. The stage-piece can be a single piece, or it may be fitted with a renewable stagepiece bushing at the rotor section immediately inside the stage-piece. The stage-pieces, which are usually solid, are assembled onto the rotor along with impellers, sleeves, bearings, and similar components to make the pump's element. It is important to note the distinction between rotor and element; the former is the assembly of all the rotating components, the latter is the rotor plus the removable stationary parts. A typical element for an axially split pump is shown in Fig. 3.8. 52 Multistage Pump Casings Fig. 3.8 Inner element of six-stage opposed-impeller axially split casing pump. Stage-pieces are assembled on the rotor between the impellers. Upper Half Locking Surface .... / OfCasing " Lower Half Of Casing Fig. 3.9 Locked tongue-and-groove joint in lower half of axially split casing. Multistage Pump Casings 53 To prevent the stage-pieces from rotating, a locked tongue-and-groove joint is provided in the lower half of the casing (Fig. 3.9). (This tongue-and-groove is clearly visible in Fig. 3.8.) Clamping the upper casing half to the lower half securely holds the stage-piece and prevents rotation. Proper seating of a solid stage-piece against an axially split casing has given designers considerable trouble not only because it presents alignment problems of a three-way joint but also because the joint must be tight and leakproof under a pressure differential without bolting the stage-piece directly to the casing. A small-diameter casing is an important pump design factor in combatting stage-piece leakage. It helps ensure a seal fitting of the two casing halves adjacent to the stage-piece when the casing bolting is pulled tight. The small diameter also helps eliminate stage-piece cocking, which leaves leakage clearance in the upper casing half when it is pulled down tight. No matter how rigidly the stage-piece may be seated in the lower casing half, there must be a sliding fit between the seat faces of the stagepiece and the upper casing half so that the upper half may be pulled down. Also, each stage-piece must be arranged so that pumping pressure differential will tend to seat it tightly against the casing (Fig. 3.10) rather than open up the joint. Some designs incorporated an elastic seal ring in the stage-piece and wearing ring (Fig. 3.11) to try to ensure pressure tightness at the face despite minor machining variations, indifferent assembly, or thermal distortion. These worked as intended, but with better machining and materials, the simpler arrangement shown in Fig. 3.10 has proved more cost effective. The use of elastomer seals at axially split pump interstage joints is now limited to stage pieces with a radial seal only or those with a very high pressure drop, where even minor leakage would quickly cause wiredrawing of the casing. Although simplification of interstage joints is highly desirable, it should not extend to the point where Low Pressure High Pressure Seating --t-::n"''--t---f---t:--,tI''''V Surface Fig. 3.10 Stage - Piece Arrangement of stage-piece between pump pressure stages. S4 Multistage Pump Casings Neoprene Seal Ring Fig. 3.11 Arrangement of stage-piece elastic seal-ring. joint perfonnance is impaired. To do so risks interstage leakage with a consequent reduction in pump perfonnance and element service life. The heads per stage being developed in modem designs are a product of the need for higher pressure and practical limitations on the number of stages. That these higher heads can be developed reliably is in part the result of careful design and development of the interstage joints. General Considerations Axially split casing pumps are used routinely for pressures up to 170 bar gauge (2,500 psig). Such pressures introduce the extremely important subject of proper choice of material. High-pressure piping systems, of which pumps fonn a part, are invariably made of steel because this material is stronger and stiffer than iron, and is ductile, that is, it yields significantly before fracturing. Considerable piping strain occurs in these systems, some of which is transmitted to the pump casing. The latter is essentially an axially split barrel flanged at the split and fitted with two necks to serve as inlet and discharge openings. Under the action of piping strain, these necks are the highest stressed regions of the casing and if not made of a strong, ductile material they may fracture. Steel (or chrome steel; see materials in Chap. 17) is therefore the safest material for pump casings whenever working pressures exceed 70 bar gauge (1,000 psig). This discussion points up a very important feature in suction and discharge flange design. Whereas raised face flanges are perfectly satisfactory for steel casing pumps, their use is extremely dangerous with cast-iron pumps. A lack of ductility in cast iron leads to flange breakage when the bolts are tightened because the bending moment fulcrum is located inside the bolt circle. Therefore, be sure to avoid raised face flanges on cast-iron casings, as well as the use of a raised-face flange pipe directly. against a flatface cast-iron flange. Multistage Pump Casings 55 If a cast-iron pump casing is used, it remains possible to use a steel adapter piece in the shape of either a straight pipe extension or an elbow. This adapter piece should have a flat flange face at the pump discharge flange connection. Most specifications are very conservative in specifying the type of discharge flange, but they frequently overlook the most elementary safety requirements in describing the suction flange. Obviously, the latter should be suitable for the pump casing hydrostatic test pressure. Therefore, if the hydrostatic test pressure is over 35 bar gauge (500 psig), it would be improper to use an ANSI 150 flange. Location of the pump casing support is not critical in smaller units operating under 17.5 bar gauge (250 psig) and at moderate temperatures (see Fig. 3.4). Very little distortion is likely in this small unit, whatever the support foot location. However, in larger units operating at higher pressures and perhaps higher temperatures, it is most important to support the casing as close as possible to the horizontal centerline and immediately below the bearings (Figs. 3.5-3.7). Certain pump requirements are basic and normally accepted by all reputable pump manufacturers. However, it is good practice to include them when preparing pump specifications. 1. 2. 3. 4. 5. 6. 7. The analysis and physical characteristics of the recommended casing material should be outlined. The manufacturer should specify the casing hydrostatic test pressure. Usually this pressure is 1.5 times the casing design pressure, which equals or exceeds the maximum allowable working pressure at 38°C (lOO°F). Because the pressure increment between standard flanges is large in the high pressure range, the maximum allowable working pressure of multistage pump casings is often less than that of its suction and discharge flanges. If the casing joint is axially split, it should be provided with dowels for accurate reassembly after opening. The casing should be provided with a suitable vent at the suction of the first stage impeller. Suitable valved openings should be provided for venting the high points of the casing and for draining. Necessary pressure instrument taps should be provided at suction and discharge flanges. If shaft seal leakage can accumulate in the brackets connecting the bearings to the casing, the bracket should have a suitable drain connection and overflow holes should be provided to prevent flooding of a bearing if a drain becomes blocked. RADIALLY SPLIT DOUBLE-CASING DESIGN The oldest form of radially split casing multistage pump is that commonly called the "ring-casing" or the "doughnut" type. When it was originally found necessary to use more than one stage to generate higher pressures, two or more single-stage units of the prevalent radially split casing type were bolted together. Figure 3.12 shows this type of two-stage pump, about 1907 vintage. This is a far cry from a modem radially split casing pump, but it clearly illustrates the origin of today's design principles. In later radially split casing pump designs (Fig. 3.13), the individual stage sections and separate suction and discharge heads were held together with large through-bolts. These pumps, still basically an assembly of bolted-up sections, had serious dismantling and reassembly problems because suction and discharge connections had to be broken each time the pump was opened. The double-casing pump retained the advantages of the radially split casing design and solved the dismantling problem. The development of the double-casing high-pressure pump has been most interesting. Like the evolution of several related but different animal families, it has evolved into several types, similar in principle but different in conception. The basic principle consists in enclosing the working parts of a multistage centrifugal pump in an inner casing and in building a second casing around this inner casing. The space between the two casings is usually maintained at the discharge pressure of the last stage. Some newer designs, however, effectively 56 Multistage Pump Casings Discharge Suction Fig.3.12 Two-stage radially split "ring section casing" pump (around 1907). revert to single casing construction by sealing each stage directly to the outer casing. The objective of this arrangement is to reduce the size of the outer casing. That it does, but at the expense of casing material and manufacturing complexity since the casing must now have a sealing fit for each stage. The inner casing design follows one of two basic principles: (1) axially split (Fig. 3.14) or (2) radially split (Fig. 3.15). The first of the two is a simple evolutionary step from the usual axially split casing for low-pressure pumps. This type of single casing will distort and breathe, with consequent leakage at the axial split and between stages, whenever final discharge pressure exceeds certain design limits because practical flange thickness and bolting strength maximums are not adequate. To help prevent the leakage at the axial split, the casing is enclosed in a solid barrel of cast or forged steel. As the outside of the axially split casing is subjected to a pressure greater than the average internal pressure, the inner casing is under compression and the axial flanges will remain tight. The inner casing is usually of volute design. The main shortcomings of this particular design are as follows: (1) it lacks the symmetry of a radially split inner casing and (2) it eliminates possible leakage at the axial joint without ensuring against interstage leakage at the stage pieces, or leakage at the threecornered joint where the axial split meets the main sealing face in the outer casing. The principal advantage of this design is that the rotors of high-speed pumps, those running at more than 4,000 rpm, can be dynamically balanced, then installed without subsequent dismantling and reassembly. The double-casing pump with radially split inner casing is an evolution of the ring-casing pump, with added provisions for ease of dismantling. After assembly, it is inserted inside a cast or forged cylindrical casing and supported by one of two basic means (see later discussion) to remain aligned within the pump yet be free to expand under temperature changes. Multistage Pump Casings 57 Fig. 3.13 Multistage radially split "ring section casing" pump of the 1930s. Radial joints between the stages offer the advantage of greater accuracy in the manufacture of the hydraulic passages, and because all the joints are ring-type, lower risk of leakage between the stages or across the element-to-casing sealing face. The one disadvantage is that after the rotor is balanced it must be dismantled, then reassembled with the inner casing pieces to make up the complete inner assembly or element. With the appropriate construction (see Ch. 7), the rotor's balance can be maintained as the element is assembled. The difference in construction and assembly sequence of axially and radially split inner casings can lead to confused terminology. A rotor is defined as the assembly of all the rotating parts of a pump, and an element as the assembly of the rotor plus the stationary internal parts. In a single casing axially split pump, the element is the rotor plus the wearing rings, stage pieces, and interstage bushings (Fig. 3.8). In a double casing pump with an axially split inner casing, the same assembly exists, but it is now only a sub-assembly of the complete inner element which necessarily includes the inner casing. 58 Multistage Pump Casings Byron Jackson Double Case Pump Fig. 3.14 .... .. Double-casing pump with axially split inner casing. (Courtesy BW/IP International Inc.) . . -':i..-- .t I I ',~- Fig. 3.15 Double-casing pump with radially split inner casing. Multistage Pump Casings 59 The assembled inner element is inserted into a cylindrical casing or "barrel", which is usually a weldment of forgings. Support of the element within the casing and provision for its thermal expansion are generally achieved by either: 1) a radial fit at the suction end of the casing and stay bolts through the element to casing sealing face (Fig. 3.15), or 2) a radial fit at each end of the casing and a spring or "compensator gasket" between the element and casing head to maintain contact at the casing sealing face (Figs. 1.11 and 3.14). Of the two methods, the latter is less expensive, has proven reliable, and is therefore used in most modem designs. In Fig. 3.16 the inner element (radially split) of a double casing pump is being installed in the outer casing. Fig. 3.17 shows the external appearance of this type of unit (see also Fig. 11.56). The suction and discharge nozzles are an integral part of the outer casing, and the inner element can therefore be withdrawn without disturbing piping connections. The most important advantages of this design are symmetry of the outer casing and ring-type outer casing joints, both of which make for more reliable sealing at high pressures and temperatures. Taking advantage of this, double casing pumps have been built for pressures to 965 bar gauge (14,000 psig) and temperatures to 425°C (800°F). CASING MAINTENANCE Axially split single casings are maintained following the principles set out in Ch. 2. In double casing pumps, the maintenance of axially split inner casings broadly follows the principles for single casings, but does require special techniques to reduce the risk of leakage between the stages and across the element-to-casing seal. Most axially split inner casings have opposed impeller rotors, which means there is a second important seal, with a differential pressure equal to about half the pump's pressure rise, between the inner casing and the casing head. The maintenance of radially split inner casings typically involves checking the ring joint surfaces for damage, checking that the locating fits between the pieces are correct, and inspecting waterway surfaces for damage (erosion, cracks). Joint face damage and loss of fit between the pieces is repaired by welding, stress relieving where necessary, and remachining to new dimensions. Any damage to the waterway surfaces should first be investigated to determine and correct the cause. Once that is done, the damage can usually be repaired by excavating to sound material, then welding, stress relieving where necessary, and refinishing to the original surface contour. Although the outer casings of double casing pumps usually do not require maintenance, this being one of the objectives of the design, the following should be checked each time the pump is opened: • Inner surfaces for corrosion (or casing wall thickness). • Waterway overlays for substrate corrosion. • Element-to-casing sealing face for mechanical damage and erosion or "wire drawing". • Casing and head gasket faces for damage. • Fillet adjacent to the element-to-casing sealing face for cracks. Local corrosion can be repaired by welding and refinishing the surface to the original contour. Major corrosion of the casing inner surfaces (beyond the design corrosion allowance) or substrate corrosion under overlays is most efficiently done by machining out to sound material, building up with automatic welding, stress relieving, then remachining to new dimensions. The build-up can include a corrosion resistant overlay if required by the original design or deemed necessary from the actual corrosion rate in service. Damage to sealing surfaces is repaired by welding, usually with austenitic stainless steel, then remachining. Cracking in the casing is serious. Whether it can be repaired depends on the cause 60 Multistage Pump Casings Fig. 3.16 Inner element of radially split double-casing pump being inserted into its outer casing. Fig. 3.17 Multistage radially split double-casing pump. Multistage Pump Casings 61 of the cracking and the extent of it. Extensive cracking caused by low cycle thennal fatigue should not be repaired because there is a risk that all the material through the section has been damaged. For other than minor repairs such as local corrosion or damage to sealing surfaces, the casing must be disconnected from its piping and moved to a repair shop. BIBLIOGRAPHY [3.1] API-61O, 8th Edition, Centrifugal Pumps for Heavy-Duty Chemical, Gas Processing, and Refinery Service, 1995, American Petroleum Institute, Washington, D.C. 4 Impellers and Wearing Rings --- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - IMPELLER TYPES The function of the impeller is to convert torque applied to the pump shaft to pressure and kinetic energy in the pumped liquid. It does this by the action of its vanes on the liquid and is the only component of a centrifugal pump that does so. The other components, even those that convert kinetic energy to pressure, absorb some energy from the liquid. Given its unique function, the impeller can be considered the fundamental component of a centrifugal pump. Impellers are classified by the following four design distinctions: 1. 2. Shaft mounting Inlet or suction arrangement 3. 4. Vane shape and form Vane closure. Before discussing classification in detail, it is beneficial to address impeller nomenclature. Referring to Fig. 4.1, liquid enters the impeller through the "suction eye," the minimum area just ahead of the vanes, passes through the waterways formed by the "vanes," "hub," and "shroud," and leaves at the "discharge tip." Torque is transmitted from shaft to vanes through the "hub." Leakage of high-pressure liquid from the impeller discharge back to suction is limited by a close-running clearance at the "outer hub" or "wearing ring hub." Shaft mounting, although nominally a mechanical feature, has a bearing on impeller hydraulics and so is dealt with first. When the impeller is attached to one end of the shaft, such that the shaft does not extend into the impeller eye, the impeller is termed overhung. For hydraulics, this is the ideal arrangement, because the shaft does not block the impeller eye. The alternative is to have the shaft passing through the impeller eye, an arrangement usually referred to as shaft through eye. Because the shaft now blocks the impeller eye, the eye diameter must be larger than that of an overhung impeller with the same eye area. The larger eye diameter increases the NPSHR for an otherwise equal design. A further possible 62 I. J. Karassik et al., Centrifugal Pumps © Chapman & Hall 1998 Impellers and Wearing Rings Outer Hub or 63 Center dividing wall of Double Suction Impeller Wearing Ring Hub Suction Eye Suction Vane edge or tip Hub Shroud Fig. 4.1 Nomenclature of double suction impeller. effect is lower pump efficiency as the ratio of eye diameter to impeller diameter increases, a consequence of overloading the vanes (trying to add too much energy over too short a vane). There are two inlet or suction arrangements: single suction and double suction (Fig. 4.1). As the terms imply, a single-suction impeller has one eye; a double suction, two. Pumps with double-suction impellers normally have the two casing suction passages joined to a common suction nozzle and flange. Whether to use single- or double-suction impellers depends on a number of factors. Small, radially split pumps, either horizontal or vertical shaft, almost invariably have single-suction impellers, because it is an economical arrangement and the NPSHR is tolerable. Very large verticalshaft pumps, too, invariably have single-suction impellers, the choice in this case being a product of structural considerations (vertical) and realizing the highest possible efficiency (overhung impeller). In medium and large pumps, the use of double-suction impellers has two advantages. First, it allows lower NPSHR than a single-suction impeller of equal capacity. Second, double-suction impellers are theoretically in axial hydraulic balance, thus reducing the size of the necessary thrust bearing (but see Chap. 22 for cautionary remarks). When the service conditions allow an axially split casing (see Chap. 2), the added casing complexity is fairly easily accommodated. For those services requiring a radially split casing, the construction is more complex but often employed for both lower NPSHR and the advantage of a between bearings rotor. Multistage pumps usually have single-suction impellers to avoid the casing complexity associated with getting liquid to and from a series of double-suction impellers. The only exception is the first stage of sizes 3-in. discharge and larger, which is sometimes double suction to avoid having to provide additional NPSH. 64 Impellers and Wearing Rings Pumps designed to handle liquids laden with solids or abrasives incorporate special leakage restriction arrangements to avoid binding and allow for adjustment (see wearing rings). These arrangements are not suited to double-suction impellers, so such pumps also normally have single-suction impellers. Vane shape and form are generally divided into four groups: 1. Plain vane (Figs. 4.2 and 4.9-4.11) 2. Francis vane (Figs. 4.3-4.5) 3. Mixed flow (Fig. 4.6) 4. Propeller or axial flow (Fig. 4.7). In a plain vane impeller, the vanes are of single curvature, with all vane surfaces straight lines parallel to the axis of rotation. The vane surfaces in a Francis-vane impeller have a double curvature. This impeller is also often called the Francis screw-vane or screw-vane impeller. An impeller design that has both a radial and axial flow component is called a mixed-flow impeller. It is generally restricted to single-suction designs with a specific speed above 4,200. Types with lower specific speeds are called Francis-vane impellers (see Chap. 18). Mixed-flow impellers with a very small radial flow component are usually referred to as "propellers." In a true propeller or axial-flow impeller, the flow strictly parallels the axis of rotation. In other words, it moves only axially. The relation of impeller profiles to specific speed for single-suction impellers is shown in Fig. 4.8. Impeller classification according to vane shape is arbitrary, because impeller types overlap in various pump types. For example, impellers in single- and double-suction pumps of low specific speed have vanes extending across the suction eye. This arrangement provides a mixed flow pattern at the impeller entrance for low pickup losses at high rotative speeds, but allows the discharge portion to follow the plain vane principle. In pumps of higher specific speed operating against low heads, impellers have double-curvature vanes extending over the full vane surface. They are therefore full Francis-type impellers. The mixed-flow impeller, usually a single-suction type, is essentially one-half of a double-suction highspecific-speed Francis-vane impeller. Vane closure refers to the means used to "close" the waterways of the impeller. Some means of closure is necessary lest the pressure difference across the impeller vanes (between the pressure and suction sides, an inherent aspect of impeller action) cause leakage and a consequent drop in pump performance. Three closure arrangements are generally recognized: (1) open, (2) semiopen, and (3) closed. An open impeller (Figs. 4.6 and 4.9) essentially consists of vanes connected to a hub. Leakage across the vane ends is limited by a close axial clearance at each side, formed by the casing and cover wall. The design has two mechanical limitations. First, the vanes are weak in bending, and if at all long must be stiffened with a rib or partial shroud. Second, either the casing or cover surface must be adjustable or readily replaceable to allow economical restoration of running clearances. With the appropriate vane design, open impellers are able to pump liquid containing significant solids without suffering blockage of the waterways or binding between the impeller and casing. This capability is a consequence of having a "cutting edge" at each end of the vane and not having a shroud, which can accumulate material between itself and the adjacent casing walls. Open impellers are better suited to stringy or bulky solids than abrasive materials, the latter being handled with longer service lives by semi-open or closed impellers. Combined with the mechanical limitations, this restricts the normal use of open impellers to small, general service solids-handling pumps. In a semi-open impeller (Fig. 4.10), one side of the impeller waterway is closed by a shroud, usually on the back side of the impeller, occasionally on the front side. With this refinement, the mechanical limitations of the open impeller are largely overcome; vane bending strength is adequate and the impeller Fig. 4.2 Plain-vane single-suction closed impeller. Fig. 4.4 High-specific-speed Francis-vane doublesuction closed impeller. Fig. 4.6 Open mixed-flow impeller. Fig. 4.3 Fig. 4.5 Francis-vane double-suction closed impeller. Low-specific-speed Francis-vane singlesuction closed impeller. Fig. 4.7 Axial-flow impeller. 65 66 Impellers and Wearing Rings I 0 0 ... ,- - ..... 0 0 CD 0 ,... 0 Radi al ' 0 0 IJI ~an, 0 0 '" 0 0 ~- li,ld o o "'. o o q '" Fr anc:is - o o ~ ler.. f ie ld o o o. o o o ¢- '" o o q '" o o ~ MI.,d-fIO" f i' ld o o 0 0 0 0 0_ q q CD '" 0 Al i a l - f1aoo l i,'d Fig. 4.8 Variation in impeller profiles showing approximate range of specific speeds (US units). Fig. 4.9 Open impellers. Impellers at left and right strengthened by a partial shroud. Fig. 4.10 Semi-open impeller. o o .., 0. Impellers and Wearing Rings 67 Fig. 4.11 Semi-open impeller. Front view (left); back view (right) shows pump-out vanes. to casing clearance can be maintained by an adjustable rotor. The shroud side normally has pump-out vanes (Fig. 4.11) to (1) lower the pressure at the shaft seal and (2) keep the region between the shroud and the casings free of any solids. When the shroud has balance holes in the region of the vane inlet edge, the pump-out vanes also serve to minimize the leakage flow down the back shroud. The compromise made by using a semi-open impeller is lower solids-handling capability than an open impeller. For all but the most difficult services, the compromise is of little consequence, thus semiopen impellers are widely used in pumps for chemical, paper, slurry, and severe industrial services. An argument made frequently for their use in such services, aside from resistance to blockage, is that clearance wear, hence pump performance, can be restored to a worthwhile degree without having to open the pump. A closed impeller (Figs. 4.2-4.5) has both sides of its waterways closed with a shroud, an arrangement that eliminates leakage across the ends of the vanes. Of course high-pressure liquid still tends to leak back to lower pressure, so some form of cylindrical or axial restriction is incorporated between the casing and the shroud at a convenient location to minimize the leakage (see wearing rings). For a given pump, except in very small sizes, a closed-impeller design is more economical to make for high efficiency than either an open- or a semi-open-impeller design. The reasons for this are the sensitivity of the latter two designs to clearance at the ends of their impeller vanes and the need for clearance adjustment. Sensitivity to end clearance requires additional care in machining to achieve consistently high performance. The need for clearance adjustment complicates pump construction. Closed impellers are also sensitive to leakage, but not to the same degree as open and semi-open impellers (the leakage is around the impeller rather than back into the succeeding channel), and the close clearances used to limit leakage are easier to manufacture accurately. Given this advantage, closed impellers are used almost exclusively for clean liquid services, the exception being small, low-cost, nonadjustable pumps designed to be replaced when worn out. 68 Impellers and Wearing Rings SPECIAL DESIGNS Given the myriad services to which centrifugal pumps are applied, there are many impellers designed for specific applications. Details of some of the more prevalent are given here. Liquids containing rags, stringy material, and solids like sewage will quickly clog the inlet region of conventional impellers. The preferred solution is a closed impeller with large waterways and thick, rounded vane inlet edges (Fig. 4.12), a variation known as a nonclog impeller. For pumps up to 12- to 16-in. discharge, such impellers usually have only two vanes, larger sizes have three and four vanes. With hydraulic design compromised to allow the passage of large solids, nonclog impellers are not quite as efficient as conventional designs and are prone to noisy operation at capacities below design (see Chap. 22). Solids-laden liquids that cannot be handled by nonclog impellers are often pumped with what is known as afree-flow or induced-vortex impeller (Fig. 4.13). In this arrangement, the impeller is recessed into the back of the casing, out of the pumped flow to give a free-flow path. The impeller is a simple, radial vaned, semiopen design. Head is produced in the pumped flow by momentum exchange. Low momentum liquid enters the impeller near the hub, is accelerated through the impeller, then issues as high momentum liquid into the pumped flow where it gives up energy to the flow. Pump efficiency is lower th.an conventional designs, but the performance characteristics are similar. Closed impellers for liquids containing abrasive solids follow the usual slurry pump practices of simple vane shape, thick vanes and shrouds for tolerance of wear, and pump-out vanes on the back shroud. To both restrict leakage down the front shroud and keep the region free of solids, the front shroud also has pump-out vanes (Fig. 4.14). For high-energy impellers (head above 200 m [600 ft] and power more than 225 kW [300 hpJ) or when low-pressure pulsations and low noise are important, it becomes necessary to modify conventional impeller designs. The essential objective is to reduce the pressure pulsation produced as the impeller vanes pass the stationary volute tongue or diffuser vanes. Although it is really a casing design consideration, a good start is to have a certain minimum clearance between the impeller and collector vanes (Fig. 4.15). How much is still a matter of some controversy Fig. 4.12 Phantom view of radial-vane non-clogging impeller. Fig. 4.13 Induced vortex impeller. Impellers and Wearing Rings Fig. 4.14 Closed impeller for slurry pump (rough casting). HIGH ENERGY PUMPS DEFINITION STAGE PERF GREATER THAN: 200 M (650 FT) COLLECTOR TYPE CLEARANCE 225 KW (300HP) DIFFUSER :3 VOLUTE 6 & " R2 LEARANCE I ~ ql % R2,,(R J - R2 R,l 100 1,1t III, II'I :('1:, I I t \ , • Fig. 4.15 Radial clearance between impeller and stationary vanes (gap "B"). 69 70 Impellers and Wearing Rings Fig. 4.16 Double suction impeller with split and staggered vanes. because it is influenced by the head being developed, the impeller design, and the form of the stationary vanes. There is, however, general agreement that values of diametral clearance equal to 1-2 percent of impeller diameter are too small, and that increasing the clearance to 3-5 percent benefits both pump efficiency and behavior (see Chap. 22 for further discussion). Within the impeller itself, the objective is to minimize variations in the velocity of the liquid being discharged. The most beneficial approach is to sacrifice efficiency and use a conservative design; one with a relatively low discharge recirculation capacity (see Chap. 22). Further refinement involves such measures as split and staggered vanes (Fig. 4.16), which is commonly used for double-suction impeller on fan pump and similar service, and has also been used for single-suction impellers when circumstances warranted it. The virtue claimed for split and staggered vanes is that the velocity variation (wake) associated with each vane is halved, hence the pressure pulse caused by its passing is also halved. In very high energy impellers (typically 750 m [2,500 feet] and 13,500 kW [18,000 hp)), split and staggered vanes have proven necessary to ensure the bending strength of the vanes between the shrouds was sufficient. An inducer (Fig. 4.17) is a special version of the propeller pump. Its function is to operate in series with a conventional impeller and produce enough head to raise the net positive suction head available (NPSHA) at the impeller to at least that required by the impeller. Being designed for only a very low head, the inducer has inherently lower NPSHR and, to compound the benefit, is able to run with quite a degree of cavitation without suffering damage or materially affecting the pump head. Correctly designed and applied, an inducer enables pumping to higher heads with the same NPSHA or to the same heads with lower NPSHA. In either case, the pumping installation is less expensive. There is need. however. for emphasis on correct design and application. Inducers have a limited flow over which they operate Impellers and Wearing Rings Fig. 4.17 71 Inducer. well. At higher flows, the head produced is not enough to provide the NPSH required by the impeller. Recirculation (see Chap. 22) sets in at flows below the lower limit. Operation outside the "stable" flow range therefore results in cavitation or noise and vibration or all three. MANUFACTURE In the past most impellers were cast. Usually the casting was one piece unless small size and low specific speed dictated casting in two pieces and permanently assembling after machining. Modem practice has fabrication and molding making notable inroads into impeller manufacture. Small, closed impellers for mass-produced standard pumps are now routinely spot welded together from stainless steel pressings. The justification for this approach is better performance (accuracy of shape and finish) and lower cost provided the production runs are high enough. Using a combination of cast and wrought (pressed) pieces, very large impellers for pumps and pump/turbines are also being fabricated. Adopting this approach has 72 Impellers and Wearing Rings improved the accuracy of shape and lowered cost, while maintaining mechanical integrity equal to or better than that of a one-piece casting. Casting is, of course, still an entirely valid means of making impellers, but it is a skill that is becoming more concentrated, hence more expensive, and so is fostering the development of alternatives. Molding is the means used to produce plastic impellers. For small water pumps and severe service chemical pumps, plastic is being used with increasing frequency. The need to separate the mold limits one-piece molding to semi-open plain-vane impellers. Closed impellers can be made in two pieces and bonded together, but the vane shape is still limited to plain. IMPELLER TYPE SELECTION From the preceding text it is evident there are many possible configurations of centrifugal pump impeller. Figure 4.18 is intended as a broad guide to selecting or identifying the most appropriate basic impeller type. It does not address, to any extent, special designs, and it obviously cannot be more than a broad guide given the variations in service conditions and available product. WEARING RINGS Wearing rings provide an easy and economically renewable running clearance between the impeller and casing. A running clearance without renewable parts is illustrated in Fig. 4.19. To restore original clearances after wear, the operator must either (1) build up the worn surfaces by welding, metal spraying, or other means, and then true up the part; or (2) buy new parts. The new parts are not very costly in small pumps, especially if the stationary casing element is a simple suction cover. As a matter of fact, the cost of a renewable stationary ring would sometimes differ very little from that of a totally new suction cover for these units. This would not be true for larger pumps of course, nor if the stationary element is part of a complicated casting. If the first cost of a pump is of prime importance, the designer can benefit the operator by providing means for both stationary parts and the impeller to be remachined. Renewable casing and impeller rings can then be installed (Figs. 4.20 and 4.21). A preferable approach, now common practice for large pumps, is to furnish the new pump with single-ring construction (Fig. 4.20). This simplifies pump construction, provides a readily renewable wearing surface in the component of lesser material (casing typically iron or steel), and recognizes the durability of the impeller wearing surface (typically 13 chrome or 13/4 chrome nickel steel). Nomenclature for the casing or stationary part that forms the leakage joint surface varies as follows: (1) "casing ring" (if mounted in the casing); (2) "suction cover ring" or "suction head ring" (if mounted in a suction cover or head); and (3) "casing cover ring" or "head ring" (if mounted in the casing cover or head). Some engineers like to identify the part further by prefixing the word "wearing" to the word "ring," for example, "casing wearing ring." A renewable part for the impeller wearing surface is called the "impeller ring." Pumps with both stationary and rotating rings are said to have "double-ring" construction. WEARING RING TYPES There are various types of wearing ring designs, and selection of the most desirable type depends on the liquid being handled, the pressure differential across the running clearance, the rubbing speed, and the particular pump design. In general, centrifugal pump designers use the ring construction they have found most suitable for each particular pump service. The most common ring constructions are the flat Impellers and Wearing Rings 73 CLEAN LIQUIDS PUMP SIZE I SMALL MEDIUM LARGE 'STAGES 'STAGES SHAFT AXIS I I I MULTI SINGLE I ® ® I CD 0 I I I I MULTI SINGLE I I 0 ® I I I HORIZONTAL VERTICAL I I 0 CD SOLIDS LADEN UQUIDS ABRASIVENESS NONE TO LOW I MODERATE HIGH @ ® PUMP SIZE I SMALL I @ ® o I MEDIUM I ® o ® o Fig. 4.18 Impeller type selection chart. KEY: 1. Overhung, single-suction, closed. 2. Shaft through eye, single suction, closed. 3. As 2 but with doublesuction first stage. 4. Shaft through eye, double-suction, closed. 5. Overhung, single-suction, open. 6. Overhung, single-suction, semiopen. 7. Overhung, single-suction, special design for service. type (Figs. 4.20 and 4.21) and the L type. The leakage path in the fonner is a straight annular clearance. In the L-type ring illustrated in Fig. 4.22 the axial clearance between the impeller and casing ring is large so that the velocity of the liquid flowing into the stream entering the suction eye of the impeller is low. The L-type casing rings shown in Fig. 4.22 and 4.23 have the additional function of guiding the liquid into the impeller eye; they are called "nozzle rings." Impeller rings of the L type shown in Fig. 4.23 also furnish protection for the face of the impeller wearing ring hub. 74 Impellers and Wearing Rings IMPELLER SUCTION RING SUCTION HEA SUCTION HEAD Fig. 4.19 Plain flat running clearance (no rings). Fig. 4.20 Single flat casing ring construction. SUCTION RING SUCTION HEAD Fig. 4.21 Double flat ring construction. Impellers and Wearing Rings CASING ---....\" 7S CASING RING CASING CASING RING-__>/ IMPELLER ~~~LLER_+--_-++, Fig.4.22 Casing ring with "L-nozzle". Fig.4.23 Double ring with "L-nozzle". CASING--ooooOoooo\l/ CASING----i" RELIEF CHAMBER CASING RING IMPELLER RING -+----+-+' Fig. 4.24 Single labyrinth of intenneshing type. Double ring construction with nozzle-type casing ring. r-t-"-"''"---.J-IMPELLER Fig. 4.25 Double labyrinth ring construction. In the past, some designers favored labyrinth type rings (Figs. 4.24 and 4.25). The objective of these designs was lower leakage for a given pressure drop. This was to be realized by two features: first, the series of close clearances followed by expansions would increase the overall friction coefficient. Second, the reentrant feature of the design increased the total length of close clearance. The objective was often realized, but many pumps also suffered vibration problems, the cause of which was finally traced to labyrinth type rings. By virtue of the liquid flow and pressure distribution within it, a leakage restriction with both inside and outside close clearances is self-disturbing; that is, radial displacement of the rotor develops a force causing even more radial displacement. As a result of this finding, labyrinth type rings have been modified to have either inside or outside close clearances but not both. With this modification, the single labyrinth (Fig. 4.24) offers little advantage. Double, or even more, labyrinth rings (Fig. 4.25) are employed when space permits and the complexity is justified. Wearing ring designs employing only intermediate expansions to raise the overall friction coefficient are also used. One example is the stepped ring, which can be single step (Fig. 4.26) or multiple steps. Another example is the serrated ring (Figure 4.27), in which a series of grooves serve as the intermediate expansions. In addition to reducing leakage losses, serrating one of the surfaces of a radial running clearance serves to significantly increase the clearance's resistance to galling in the event of internal contact. For many applications, particularly those where materials with low galling resistance must be 76 Impellers and Wearing Rings RELIEF CHAMBER Fig. 4.26 Single step-type running clearance (double rings). Fig. 4.27 Serrated casing wearing ring. used, the anti-galling characteristic of a serrated ring is more important than any improvement in pump performance, the logic being that a pump not running has zero performance. Wearing ring grooves or serrations can be either normal to the axis or helical. There are arguments advanced that helical grooving which acts to pump against the leakage flow, improves pump efficiency by reducing the leakage. Considering that such a pumping arrangement is relatively inefficient, any reduction in leakage would be offset by an increase in power. This leads to the suggestion that it is better to allow the leakage to be repumped by the more efficient impeller. In those cases where reverse pumping wearing rings have yielded higher efficiency, the change in leakage rate must have been enough to affect impeller performance. Helical grooving does seem to offer better resistance to damage from incidental contact between the surfaces. This is attributed to the helical groove "wiping" across the adjacent surface rather than "scoring" into it. For raw water pumps in water works service and large pumps in sewage service in which the liquid contains sand and grit, water-flushed rings have become popular (Fig. 4.28). Clear water under a pressure greater than that on the discharge side of the rings is piped to the inlet and distributed by the cored ~ ___________ IMPELLER ,.--_ _ _ _ IMPELLER RING ,..-------- SUCTION HEAD RING z----SUCTION HEAD ~---CI_E~,R WATER INLET Fig.4.28 Water-flushed wearing ring. Impellers and Wearing Rings 77 passage, the holes through the stationary ring, and the groove to the clearance. Ideally, the clear water should fill the clearance with some flow both to the suction and discharge sides to prevent any sand or grit from getting into the clearance space. To realize this, the pressure drop across the downstream portion of the ring considering the flush flow alone, must be greater than the difference between the static pressure at the pump suction and that just upstream of the running clearance. In all but very low head pumps, this requires a flush flow higher than is usually practicable, which is why flushed wearing rings have not always performed as expected. Similar difficulties have been encountered in the petroleum industry, and are often remedied by adding pump-out vanes to the impeller shrouds to lower the pressure adjacent to the joint. That solution has the disadvantage of noticeably increasing the pump's power, a consequence of the power absorbed by the pump-out vanes. The trend today is to avoid the complexity of flushing and employ wearing materials or coatings able to yield acceptable service lives running in the pumped liquid. In large pumps (roughly 36-in. discharge, or larger), particularly vertical end-suction single-stage volute pumps, mere size alone permits some refinements not found in smaller pumps. One example is the inclusion of inspection ports for measuring ring clearance (Fig. 4.29). These ports can be used to check the impeller centering after the original installation as well as to observe ring wear without dismantling the pump. The lower rings of large vertical pumps handling liquids containing sand and grit on intermittent service are highly susceptible to wear. During shutdown periods, the grit and sand settle out and naturally accumulate in the region in which these rings are installed, as it is the lowest point on the discharge side of the pump. When the pump is started again, this foreign matter is washed into the clearance and causes wear. To prevent this action in medium and large pumps, a dam-type ring is often used (Fig. 4.30), for it permits the pocket on the discharge side of the dam to be periodically flushed. One trouble with the simple water-flushed ring previously described (Fig. 4.28) is its failure to provide uniform pressure in the stationary ring groove. If the pump size and design permit, two sets of regular flat wearing rings in tandem and separated by a large water space (Fig. 4.31) provide the best solution. The large water space allows uniform distribution of the flushing water to the full 360 deg of each running clearance. For pumps handling gritty or sandy water, the ring construction should provide an apron on which the stream leaving the clearance can impinge, as sand or grit will erode any surface it hits. Thus, a form of L-type casing ring similar to that shown in Fig. 4.28 should be used. STUFFING BOX HEAD STUFFING BOX HEAD RING IMPELLER RING IMPELLER Fig.4.29 Wearing ring design with inspection hole. 78 Impellers and Wearing Rings IMPELLER----------~ I't-.------SUCTION HEAD Fig. 4.30 Dam-type ring construction. IMPELLER IMPELLER RING NO.2 SUCTION HEAD RING NO.2 FULL CIRCLE CORED PASSAGE CLEAR WATER INLET HEAD SUCTION HEAD RING NO. I Fig. 4.31 Two sets of rings with space for flushing water. WEARING RING LOCATION In some designs used by one or two sewage pump manufacturers, leakage is controlled by an axial clearance (Fig. 4.32). Usually this design requires a means of adjustment of the shaft position for proper clearance. Then, if uniform wear occurs over the two surfaces, the original clearance can be restored Impellers and Wearing Rings 79 IMPELLER ----~ Fig. 4.32 Axial running clearance. Fig. 4.33 Adjustable axial-clearance ring construction. simply by adjusting the impeller position. This method does have its limitations, however, for the impeller must be nearly central in the casing waterways. Axial running clearances are not overly popular for double-suction pumps because a very close tolerance is required in machining the ring fit in reference to the centerline of the volute waterways. Radial clearances, however, allow some shifting of the impeller for centering. The only adverse effect is a slight inequality in the lengths of the leakage paths on the two impeller sides. An ingenious ring construction that overcomes this objection is illustrated in Fig. 4.33. However, this design is more expensive than the conventional radial-clearance ring. Also, if it must be adjustable after wear, the threaded parts must be corrosion proof for the liquid being handled. So far, this discussion has treated only those running clearances located adjacent to the impeller eye or at the smallest outside shroud diameter. Sometimes, however, the running clearance is located at the impeller periphery (Fig. 4.34). In a vertical pump, this design is advantageous because the space between the joint and the suction waterways is open and sand or grit cannot accumulate. But the design is impractical in regular pump lines because of increased area and rubbing speed and because the impeller diameters used in the same casing vary over a wide range. There are, however, advantages to having some form of leakage restriction at or near the impeller outside diameter (OD) in addition to the usual hub running clearance (Fig. 4.35). As used today, the restriction is typically two-three times the clearance of the wearing ring and is not made up of renewable surfaces. In solids-handling services such as sewage pumping, the restriction serves to minimize accumulation of solids in the region between the shroud and casing or cover wall. A second advantage is partial isolation of the shroud region from pressure pulsations occurring at the impeller discharge during off design operation (see Chap. 22). In high-head pumps this can be an important factor in realizing reliable 80 Impellers and Wearing Rings IMPELLER CASING Fig.4.34 Running clearance at periphery of impeller. operation over wide flow ranges. A disadvantage of the arrangement is a reduction in efficiency caused by not being able to recover part of the energy put into disk friction as useful head. STATIONARY WEARING RING MOUNTING In small single-suction pumps with suction heads, a stationary wearing ring is usually pressed into a headbore and can be locked securely by several set screws located half in the head and half in the ring (see Fig. 4.21). Larger pumps often use an L-type ring with the flange held against a face on the head (see Fig. 4.36). Single-suction radially split pumps designed for rings on the stuffing box side usually have either a flat or L-type ring located in a shouldered bore in the cover (Fig. 4.29). Ring retention can be by a shrink fit, an interference fit with pins, or a slide fit with machine screws, from either the liquid or atmospheric side (Fig. 4.36). In the interests of reliability, it is desirable to minimize the use of fasteners for wearing rings. Internal pins and machine screws can and do work loose. External screws are easier to secure, but are a potential source of leakage unless sealed carefully. For service temperatures up to 200°C (400°F), a simple shrink fit has proven reliable. Higher service temperatures or the need for easier removal have been accommodated by using several short welds to retain interference fit rings. In axially split casing pumps, the cylindrical casing bore (in which the casing ring will be mounted) should be slightly larger than the outside diameter of the ring. Unless some clearance is provided, ring distortion may occur when the two casing halves are assembled. However, the joint between the ring and the casing must be tight enough to prevent leakage. This is usually accomplished with a radial metal-to-metal joint (like the one marked "J" in Fig. 4.23) so arranged that the discharge pressure will press the ring against the casing surface. Impellers and Wearing Rings r "A" 2-3 TIMES "CLA" t CLR + t Fig. 4.35 Shroud space isolation (gap "A"). Fig. 4.36 Double ring construction with machine screw fasteners. Screws fasten wearing rings to casing and impeller. 81 82 Impellers and Wearing Rings If the pressure differential is very high, leakage may occur between the casing and the ring, eroding the casing. A sealed casing ring (Fig. 4.37) may be required, especially on multistage pumps with high stage pressures. As it is not desirable for the casing ring of an axially split design to be pinched by the casing, the ring will not be held tightly enough to prevent its rotation (due to the impeller torque transmitted through the liquid in the clearance space) unless special provisions are made to keep it in place. One common way of preventing rotation is to place a pin in the casing that extends into a clearance hole in the ring (Fig. 4.38). The same basic arrangement can be reversed, placing the pin in the ring, with equal effectiveness. Pin-type anti-rotation devices are suitable for low-cost low-energy stages. They are not really adequate for high-energy stages, often suffering pin or hole failure, and should not be used in vertical-shaft axially split pumps, the single shoulder making for difficulty assembly. An alternative, and very reliable, antirotation arrangement is to have a tongue on the casing ring, extending around 180 deg and engaging a corresponding groove in the one half of the casing (Fig. 4.39). This method can be used with casing rings having a central flange (see Fig. 4.33) by making the flange of larger diameter for 180 deg and cutting a deeper groove in that half of the casing. Many methods are used to retain impeller rings. A shrink fit is the simplest, and has proven reliable for temperatures to 150°C (300°F). At higher temperatures, there is a risk the ring may loosen and turn should the pump be started from cold with hot liquid. In these circumstances, a legitimate question is whether an impeller ring should be used at all. Many believe they should. Usual practice is to mount the ring with an interference fit, then secure it with threaded axial pins (Fig. 4.21), machine screws (Fig. 4.36), or a number of short welds. The first two methods involve internal fasteners. Great care must be taken to ensure the fasteners are locked, l~st they back out and cause premature failure (see comment on casing rings also). Threaded axial pins can only be used when the impeller and ring materials are of similar alloy and hardness. If the ring is appreciably harder than the impeller, a common requirement, the tap drill will drift off center into the softer impeller. Short welds must be made with care to ._--IMPELLER CASING RING -----SEAL RING ASING Fig. 4.37 Sealed casing ring. Impellers and Wearing Rings 83 UPPER HALF CASING ~.-J.-~ LOWER HALF CASING CASING Fig. 4.38 "Pin-in-casing hole-in-ring" locking device. Fig. 4.39 Tongue-and-groove casing ring design. avoid cracking in the weld or adjacent material. Provided this is done, it is a simple and reliable ring retention method. Impeller rings of brittle materials such as cast iron, Ni-resist and fully hardened 13 chrome steel, should not be mounted in tension. One solution in older designs was to thread the hub and ring and screw the parts together but is rarely used today because it is deemed too complicated. When a hard surface is required on the impeller, it is really better to avoid a ring altogether and apply a hard coating directly to the hub. Hard coating offers simpler construction and better use of resources by applying exotic materials only where necessary. This technology has been proven in other forms of turbomachinery, and although its adoption into centrifugal pump practice has been slow, its use will increase. In impeller ring design, ring stretch due to centrifugal force must be considered, particularly if the pump is a high-speed unit. For example, some boiler feed pumps operate at speeds that would loosen the rings if only a press fit were used. For such pumps shrink fits should be used or, preferably, the impeller rings eliminated. IMPELLER MAINTENANCE An impeller removed from a pump casing should be carefully examined on all surfaces for unusual wear, such as from abrasion, corrosion, or cavitation. Most pumps for general service use bronze impellers, which have a reasonably long life. Occasionally, these pumps operate on high suction lifts or at part capacities, both of which affect impeller life. Manufacturers can suggest a more suitable impeller design for such conditions. Pumps handling water containing low concentrations of sand or silt may use bronze, cast-iron, nickelcast iron, or even chrome-steel impellers, depending upon the amount of sand, its abrasiveness, and the character of the water. Generally, impeller materials that form a protective coating or film, which adheres firmly to the underlying metals and is not washed off by the water stream, should always be used. However, abrasive material naturally erodes this protective film on many metals, making their use undesirable. 84 Impellers and Wearing Rings Abrasion wear can be best tested by a sedimentation test. Some of the pumped liquid is allowed to stand in a glass container for a few hours, and the settled particles are examined for grit. A chemical laboratory analysis of the pumped liquid is usually necessary to determine whether corrosion is responsible for undue wear. Of course, if corrosion wear is detected, the substitution of better materials becomes necessary. Cavitation is often accompanied by pitting in the impeller suction areas and can be detected by a crackling noise during operation. If impellers rapidly become pitted or eroded, check the NPSHA then the range of flows over which the pump is being operated (see Chap. 22). Unless the original impeller was cast iron, changing to a better material usually is not sufficient to correct rapid cavitation erosion. In small pumps, impeller wear is best corrected by replacement of the impeller, because the pump size does not permit its being rebuilt. Whereas rebuilding by brazing, soldering, welding, and the like, is feasible, the cost is high, and so replacement is usually the better solution. Most large impellers will provide many years of service, regardless of abrasion, if eroded areas are treated by "building up" the metal. Although unlikely, wear may sometimes occur in the impeller hub over the shaft mounting or at the keyway. The first may be caused by a porosity in the impeller casting, permitting water to seep from the higher pressure region to the fit between the shaft and impeller. Sometimes, the shaft material is the one more readily attacked. Wear at the keyway may occur if the impeller fits loosely on the shaft or the key is not properly fitted. Finally impeller cracks may develop, the usual causes being vibration caused by pressure pulsations associated with internal recirculation or vane passing (see Chap. 22) or subsurface defects not detected during manufacture. Whether to repair or replace cracked impellers depends on their size, the material, and the location and extent of the cracking. If repair is elected, the method must respect that an impeller is a dynamic part, subject to cyclic stresses, and prone to catastrophic failure if a critical crack develops. Impeller balance should be rechecked whenever the impeller is removed from the pump rotor during overhaul. Whether to balance statically or dynamically depends on the impeller's width-to-diameter ratio and the pump's rotative speed. One widely used guide is to dynamically balance whenever the diameter to width ratio is less than 6 or the rotative speed above 3,600 rpm. If there is any doubt, consult the manufacturer. When dynamic balancing is required, note that an impeller in dynamic balance is necessarily in static balance, but the reverse is not the case. In fact, an impeller in static balance can easily be so badly out of dynamic balance that correction is impossible. The significance of this is that impellers requiring dynamic balancing should not be balanced statically first. Metal removal for balancing must be done in a manner that will not affect the pump's hydraulic performance or mech;prical reliability. This means not removing metal from impeller waterways unless there is an obvious variation in thickness or profile, and not drilling or milling. Both techniques produce sharp corners, which can lead to erosion or initiate cracking. For balancing a shrouded impeller, the best practice is to mount the impeller off-center in a lathe and take a cut (which will be deepest at the periphery) from the shroud (Fig. 4.40). The cut can be taken from both shrouds, depending on their actual thicknesses and the amount of metal to be removed. In semiopen impeller pumps, the removed metal can be taken from the shroud if the design permits or from underneath the vanes if those on the heavy side are thicker than the others. The latter method is the one used for balancing open impellers. WEARING RING MAINTENANCE Installation Most rings are now pressed on the impeller. As distortion may occur during the mounting process, it is advisable to check the shaft and impeller assembly on centers to see if the new ring surfaces are Impellers and Wearing Rings 8S Fig. 4.40 Metal removal for balancing impeller. true and, if not, to true them up. If the proper facilities are available, it would be just as easy to get slightly oversize rings and turn their wearing surface to the proper diameter after mounting. Clearance One manufacturer's clearance and tolerance standards for nongalling wearing joint metals in general service pumps are shown in Fig. 4.41. They apply to the following combinations: (1) bronze with a dissimilar bronze, (2) cast iron with bronze, (3) steel with bronze, (4) monel metal with bronze, and (5) cast iron with cast iron. If the metals gall easily (like the chrome steels), the values given should be increased by about 0.050 mm (0.002 in.). In mUltistage pumps, the basic diameter clearance should be increased by 0.075 mm (0.003 in.) for larger rings. The tolerance indicated is "plus" (+) for the casing ring and "minus" (-) for the impeller hub or impeller ring. In a single-stage pump with a running clearance of nongalling components, for example, the correct machining dimension for a casing ring diameter of 225.000 mm (9.000 in.) would be 225.000 plus 0.075 and minus 0.000 (9.000 plus 0.003 and minus 0.000 in.) and for the impeller hub or ring, 225.000 minus 0.450, or 224.550 plus 0.000 and minus 0.750 mm (9.000 minus 0.018, or 8.982 plus 0.000 and minus 0.003 in.). Actual diametral clearances would be between 0.450 and 0.600 mm (0.018 and 0.024 in.). Naturally, the manufacturer's recommendation for ring clearance and tolerance should be followed. A widely used industry standard for we~ng ring clearances is given in American Petroleum Institute (API) Standard 610. These clearances are intended for pumping temperatures up to 260°C (500°F), so are somewhat larger than those in Fig. 4.38 to allow for thermal distortion. The standard provides for pumping temperatures above 260°C (500°F) and the use of materials with low galling resistance by requiring an increment over the standard clearance. There is also provision for closer than standard clearances in multistage pump balancing devices and similar critical components. Allowable Wear It is difficult to generalize on the amount of wear allowable before a pump should be dismantled and the running clearances renewed, because too many factors are involved. Internal leakage through the rings naturally means an efficiency loss. Ring renewal should be such that the overhaul cost will be offset by the power savings. Thus, with constant use and high power costs, more frequent renewal can be justified. The power lost to leakage decreases with increasing specific speed. At the same time it is higher in multistage pumps of a given specific speed because of the need to balance axial thrust (see 86 Impellers and Wearing Rings DIAMETER - MM 50 70 100 I 0.040 150 200 300 400 SOO J L 700 L I 1,000 1,500 2,000 _J 1.00 I , ~ ::i! ~z et -~ 0.030 ! UU ZZ etet a:: a:: et UJ UJ..J ~ 0.020 CLEARANCE d .... ..J(!) et Z a::z ...,j • l5 o:t etet - . 3 4 5 6 ,- ~-- f-'-- DIAMETRAL / CLEARANCE? Fig.4.41 I .+- -~ g O!I W (,) J Z <C a: 0.25 <C w ..J _. (,) -t' 15 20 RUNNING CLEARANCE DIAMETER, IN. 0--/ O.SO , -- TOLERANCE s,_ ! I 8 10 <C a: w ..J ~ 0.010 -f- Z •• 1-- ~ ui 0.75 (,) I UJUJ 30 40 50 60 80 CASING RING \ RADIAL I CLEARANCE' Wearing-ring clearances for single-stage pumps using nongalling materials. Chap. 5). A general rule of thumb is to renew the running clearances in single stage pumps when they have increased 100 percent (leakage about 3 times higher), and in multistage pumps when they have increased 50 percent (leakage about 2 times higher). Even though the clearance is not excessive and the pump can be reassembled without renewing the components, always check the impeller hub diameter and the inside diameter of the stationary wearing ring for eccentricity of wear. Measurement of Clearances Wearing ring clearances may sometimes be measured by inserting a feeler gage between the stationary and rotating parts. If the wearing ring is L type and the lip of the L prevents inserting the gage, the clearance may be approximately checked without dismantling the element in the following manner: 1. Mount a dial indicator on the impeller (Fig. 4.42), and with the stationary ring resting on the impeller wearing-ring hub, set the dial reading to zero. Impellers and Wearing Rings 87 I"'QICA'TOR SUPPORT MO\.lNTED ON IMPEI.I.ER Fig. 4.42 Measuring wearing ring clearances in a multistage pump with a dial indicator. 2. Without moving the impeller or dial indicator, push up on the stationary ring from below and record the maximum dial reading. This corresponds to the diametral clearance. 3. Repeat this operation for every clearance joint and make a record of all readings. This operation is best carried out, however, with the element removed from the pump casing. It is best suited to multistage pumps because once the element is out of the casing of single-stage pumps, the stationary rings may be freely removed and the clearance determined by measuring the two diameters and calculating the difference. One note of warning: This short-cut method gives no clue to the condition of adjacent clearance surfaces. In other words, burrs, grooves, or indentations caused by foreign matter passing through the clearances will go undetected, as will the resultant damage to the surfaces. If the pump has been dismantled, normal procedure is to measure independently the inside diameter (ID) of the wearing ring fit and the OD of the impeller wearing ring hub. Use inside and outside micrometers, respectively (Figs. 4.43 and 4.44) Several measurements will determine whether or not the wearing ring or impeller has become worn in an egg-shaped manner. The clearance is considered to be the maximum difference between the maximum ID and the minimum OD readings. Clearances may also be measured directly by placing the impeller within the wearing ring (Fig. 4.45) and moving it laterally against a dial indicator to determine total diametral clearance. To determine inequality in wear around the circumference, the impeller should be rotated and the dial indicator attached to several points of the stationary part. If the pump has been dismantled, however, the "difference" method is more reliable. The impeller and wearing rings should be the same temperature before measurements are made. Some high-pressure and high-temperature pumps use shrunk-on impellers that must be heated before removal from the shaft to at least 200°C (400°F) and possibly to as much as 260 to 320°C (500 to 600°F). These should be allowed to cool down to about 50°C (l20°F) so that measurements can be made comfortably. But if the wearing ring is at 28°C (80°F), say, there will be a 22°C (40°F) difference between the two parts and this difference can be quite significant. If the coefficient of thermal expansion is taken as 11.7 X 10-6 mm per mm per degree Celsius (6.5 x 10-6 in per in per degree Fahrenheit), and if the wearing ring fit diameter is 200 mm (8 in.), the apparent clearance will be about 0.05 mm (0.002 in.) less than 88 Impellers and Wearing Rings Fig. 4.43 Measuring wearing ring bore with an inside micrometer. Fig. 4.44 Measuring OD of impeller hub with outside micrometer. Impellers and Wearing Rings Fig. 4.45 89 Measuring wearing ring clearance with dial indicator. the true clearance. This error will, of course, be magnified if the impeller diameter is measured when its temperature is even higher than the 50°C (120 0 P) we have assumed. This possibility of error is frequently overlooked, as many people assume that such a small difference in metal temperatures is not of consequence. Restoring Clearances When No Rings are Used To restore the clearance between impeller and casing when no ring is provided, the operator must (1) buy new parts, (2) build up the worn surfaces by welding, metal spraying, or other means, or (3) install a wearing ring or rings if sufficient metal is available in the casing part or on the impeller hub. Restoring Clearances of Pumps with Single Rings There are three ways to restore the clearance of a pump with single flat or L-type wearing ring construction: 1. Obtain a new casing ring bored undersize from the manufacturer. Then, true up the impeller wearing ring hub by turning down in a lathe. 2. Build up the worn surface of the wearing ring by welding or metal spraying so that it can be bored undersize. Then, true up the impeller wearing ring hub. True up the wearing ring by boring oversize, build up the impeller wearing ring hub, and machine to give correct clearance with the rebored ring. 3. Of these, the first is the best approach. With impeller hubs sized for say 3 undersizes, the time between having to restore the impeller hubs to original size can be 20 years or more. Once the impeller hub has 90 Impellers and Wearing Rings been worn below its minimum undersize, it is built up by welding and remachined to its standard maximum size. When the impeller is a material that cannot be welded, such as cast iron, double-ring construction is preferred for all but small pumps. Restoring Clearances of Pumps with Double Rings If the pump has double flat or L-type wearing rings, clearances may be renewed, by one of the following methods: 1. 2. 3. 4. Obtain a new oversize impeller ring and use the old casing ring bored out larger. Obtain a new casing ring bored undersize and use the old impeller ring turned down. Renew both rings if necessary. Build up either the casing or impeller ring by welding or metal spraying and machine the other part. By altering the ring buildup, the original leakage joint diameter can be closely maintained. The relative merits of various methods for renewing clearances in single-ring pumps mentioned earlier in this chapter also apply to double-ring construction. For rings other than the flat type, the manufacturer's recommendations for maintenance should be followed. In axial running clearances (see Fig. 4.32) the stationary part, the impeller, or both may be altered to accommodate rings. The complicated labyrinth rings (see Figs. 4.24 and 4.25) do not generally permit either the building up of worn surfaces or the remachining of parts. Replacement of both labyrinth rings is thus advisable. 5 Axial Thrust in Singleand Multistage Pumps AXIAL THRUST IN SINGLE-STAGE PUMPS The pressures generated by a centrifugal pump exert forces on both its stationary and rotating parts. The design of these parts balances some of these forces, but separate means may be required to counterbalance others. Axial hydraulic thrust is the summation of unbalanced impeller forces acting in the axial direction. As reliable large-capacity thrust bearings are now readily available, axial thrust in single-stage pumps remains a problem only in larger units. Theoretically, a double-suction impeller is in hydraulic axial balance with the pressures on one side equal to and counterbalancing the pressures on the other (Fig. 5.1). In practice, this balance may not be achieved for the following reasons: 1. 2. 3. 4. 5. The suction passages to the two suction eyes may not provide equal or uniform flows to the two sides. External conditions, such as an elbow being too close to the pump suction nozzle, may cause unequal flows to the suction eyes. The two sides of the discharge casing may not be symmetrical, or the impeller may be located off-center. These conditions will alter the flow characteristics between the impeller shrouds and casing, causing unequal pressures on the shrouds. Unequal leakage through the two leakage joints will tend to upset the balance. The pump is operating with discharge recirculation, which causes random, unequal fluctuations in the effective pressure acting on each impeller shroud (see chapter 22). Combined, these factors create definite axial unbalance. To compensate for this, all centrifugal pumps, even those with double-suction impellers, incorporate thrust bearings. The ordinary single-suction radial-flow impeller with the shaft passing through the impeller eye (Fig. 5'!), is subject to axial thrust because a portion of the front wall is exposed to suction pressure, thus exposing relatively more backwall surface to discharge pressure. If the net pressure generated by the impeller were equal to the stage pressure rise, and the pressure at the impeller discharge were uniform 91 I. J. Karassik et al., Centrifugal Pumps © Chapman & Hall 1998 92 Axial Thrust in Single- and Multistage Pumps 1II -------, IUW "ex It -- ___I -I ::J _-_ _-_ 11l "0:----_ 1:(/')--------<001 UIll _ _ _ ____1 l6-a:1L1 - - - - - - - I 1~-------I 4:(/') (/')0: li 0. -------I 00..-------4 nr.,---,~ r - - - - - - III / 1 t - - - - - - ct / J t - - - - - - :J At------ ~ /11------1L1 J I - - - - - ct a. ~II;:~~----------- ~ A""-----(( t------< t------0 .1......_----1/) ", ..._ _ _ _ _ 0 DOUBLE. SUCTION IMPELLER Fig. 5.1 -~----. .-~~- SINGLE SUCTION IMPELLER Origin of pressure acting on impeller shrouds to produce axial thrust. over all the surfaces exposed to impeller discharge pressure, the axial force acting toward the suction would be equal to the product of the net pressure generated by the impeller and the unbalanced annular area. In reality this is not the case, for two reasons. First, the net pressure generated by the impeller is lower than the stage pressure rise by the pressure recovered in diffusion (see Chap. 2). Typically this pressure recovery is equivalent to 20-25 percent of stage head at BEP, and about 10 percent at shutoff. Second, the pressure on the single-suction impeller shrouds is not uniform. The liquid between the impeller shrouds and casing walls is in rotation, and the pressure at the impeller periphery is normally appreciably higher than at the impeller hub. Although we need not be concerned with the theoretical calculations for this pressure variation, Fig. 5.2 describes it qualitatively. Generally speaking, axial thrust toward the impeller suction is about 20 to 30 percent less than the product of the net pressure and the unbalanced area. Beyond pressure distribution over the impeller shrouds, two further factors can affect the axial thrust in centrifugal pumps. The first is momentum. In any design where the flow changes direction as it passes through the impeller, that is all designs other than axial flow, the change in direction produces a momentum force. This force acts away from the suction (see Fig. 5.3), and its magnitude, Fm , is estimated from where m=mass flow rate through impeller em! = velocity at impeller inlet cp = angle through which flow is turned. Momentum is often neglected, with little ill effect, in small low-flow pumps. In larger pumps, particularly those developing relatively low net pressure, momentum can be the major component of axial thrust and therefore cannot be neglected. The second factor is the axial component of the vane force exerted in accelerating the liquid into the impeller vane cascade. This force acts toward the suction, and exists only in those impellers whose inlet vanes reach into the impeller eye. Acceleration thrust is well understood in mixed- and axial-flow impellers (discussed later), but it can also be of consequence in medium specific speed radial flow impellers. Its magnitude is a function of specific speed (impeller shape; Fig. 4.8), then the detail design of the particular impeller. At the current state of the "art", the magnitude of acceleration thrust can only Axial Thrust in Single- and Multistage Pumps 93 Pr'SWry Dcf,,., on ,1ft/WII,r shroud. / ! / / _ _~ ~------ ------ - -- '---- Fig. 5.2 - Actual pressure distribution on front and back shrouds of single-suction impeller with shaft through impeller eye. Fm Fig. 5.3 • Axial thrust produced by change in momentum of flow through impeller. 94 Axial Thrust in Single- and Multistage Pumps Dischar~ / prrssvre Fronr wrorlng ring ......... " Balancing ...... hoI. " ........ Sud/on pressure ~fr-- t I I Svcfion prrssv~ --f--- Fig. 5.4 Balancing axial thrust of single-suction impeller with wearing ring on the back and balancing holes. be detennined with any accuracy from test data. Experience suggests attention be paid to it with radial flow, single suction impellers of specific speed 2,000 and higher, and absorbing more than 300 kW (400 HP). To eliminate the axial thrust of a single-suction impeller, a pump can be provided with both front and back wearing rings. To equalize thrust areas, the inner diameter of both rings is made the same (Fig. 5.4). Pressure approximately equal to the suction pressure is maintained in a chamber located on the impeller side of the back wearing ring by drilling so-called balancing holes through the impeller. Leakage past the back wearing ring is returned into the suction area through these holes. However, with large-single-stage single-suction pumps, balancing holes are considered undesirable because leakage back to the impeller suction opposes the main flow, creating disturbances. In such pumps, a piped connection to the pump suction replaces the balancing holes. Another way to eliminate or reduce axial thrust in single-suction impellers is by use of pump-out vanes on the back shroud. The effect of these vanes is to reduce the pressure acting on the back shroud of the impeller (Fig. 5.5). Because axial thrust is reduced without additional leakage, such as occurs with back wearing rings, pump out vanes are sometimes thought to offer higher efficiency. To realize the pressure reduction the vanes absorb extra power, the net result being no notable difference in efficiency. For this reason, plus the need to maintain a relatively close axial clearance, pump out vanes are generally used only in pumps handling solids, where the design helps keep the space between the impeller shroud and casing free of foreign material. So far, our discussion of the axial thrust has been limited to single-suction impellers with a shaft passing through the impeller eye and located in pumps with two shaft seals, one on either side of the impeller. In these pumps, suction pressure magnitude does not affect the resulting axial thrust. On the other hand, axial forces acting on an overhung impeller with one shaft seal (Fig. 5.6) are definitely affected by suction pressure. In addition to the unbalanced force found in a single-suction, two-box design (see Fig. 5.2), there is an axial force equivalent to the product of the equivalent shaft area through Axial Thrust in Single- and Multistage Pumps /' 95 ,,--Pump-ouf van~s - / / R~ducflon In pr~ssur~ cau~d by pump - ouf van~s Fig. 5.5 Reducing axial thrust of single-suction impeller with pump-out vanes. the seal (shaft area for packed box seals; area of balance diameter for mechanical seals) and the difference between suction and atmospheric pressure. This force acts toward the impeller suction when the suction pressure is less than the atmospheric or in the opposite direction when it is higher than the atmospheric. When an overhung impeller pump handles a suction lift, the additional axial force is very low. For example, if the shaft diameter through the seal is 50 mm ([2 in.] area 19.6 cm2 [3.14 in.2])-and if the suction lift is 6.1m (20 ft) of water (pressure 0.42 bar (abs) [6.06 psia]), the axial force caused by the .. Adddional thrust ..,dh suction I,f't ac fs In thiS dlr~c tlon Addtf,onal fhrust ..,dh pOJlftv~ suctIon acts In th,s dlr~ctlon _=J t=~:j --~~W~~~r2~~~~--~ ~=~j / ,,-- ./ ./ / Afmosph~rlc pr~ssur~ Fig. 5.6 Axial thrust problem with single-suction overhung impeller and single stuffing box. 96 Axial Thrust in Single- and Multistage Pumps overhung impeller and acting toward the suction will be only 116 N (27 lb). On the other hand, if the suction pressure is 6.9 bar gauge (100 psig), the force will be 1352 N (314 lb) and acts in the opposite direction. Therefore, as the same pump may be applied for many conditions of service over a wide range of suction pressures, the thrust bearing of pumps with single-suction overhung impellers must be arranged to take thrust in either direction. They must also be selected with sufficient thrust capacity to counteract forces set up under the maximum suction pressure established as a limit for that particular pump. Special Applications Special applications may induce extremely high axial thrusts, in boiler circulating pumps, for example. To reduce shaft seal maintenance, these pumps are usually the single-suction, single-stage overhung impeller type. Figure 5.7 shows that the force acting on the shaft toward the right is the product of 82.8 bar gauge (1,200 psig) (the difference between suction and atmospheric pressures) and 78.5 cm2 (12.56 sq in.) the unbalanced area of 10 cm (4-in. shaft), or 65 kN (15,072lb). Note that with such a high suction pressure there is no condition which produces a thrust toward the left of the impeller. It is true that providing the impeller with a back wearing ring would reduce stuffing box pressure by an amount equal to the net pump pressure. But as this pressure is only 4.14 bar (60 psi), the back wearing ring would reduce the sealed pressure by only 5 percent, which is negligible on a nominal 80 bar gauge (1,200-psig) boiler circulating pump. On the other hand, the partial balance of the axial thrust obtained by eliminating the back wearing ring is very useful. If the unbalanced area ofthe single-suction impeller is 258 cm2 (40 in.2), the net pressure, 4.14 bar (60 psi), and the average pressure acting on the back shroud 80 percent of the net pressure rise, then the unbalanced thrust acting to the left is 8.5 kN (1,920 lb) and the net force acting to the right is reduced to 56.5 kN (13,152Ib), or almost 13 percent less. When the pump is standing idle on standby duty, however, this partial reduction disappears, and the end thrust returns to its former value of 65 kN (15,072lb). The pump thrust bearing, therefore, must accommodate this higher thrust. Except for very large units and certain special applications, the maximum thrust developed by mixedflow and axial-flow impellers is not of consequence because the operating heads are relatively low. With axial-flow impellers, axial thrust is caused by the pressure on the vanes as they act on the liquid. In addition, there is a difference in pressure acting on the two shaft ends, the end in the pump subject to suction pressure and the other to atmospheric pressure. Occasionally, provision is made in an axial- Line - VI ,;a;;;..;,.,.w- Q. - .... () ~ ..... . -,- -- _ . b~or,ng - -- - - - - - " Tltrusf bearlflg _ _ ____ / -t~I/lrust • IJ.l521b \ ' 4 m sit art af sfurrmg box Fig. 5.7 Axial thrust in single-suction boiler circulating pump. Axial Thrust in Single- and Multistage Pumps 97 flow pump for a running clearance at or near the discharge hub periphery, with balancing holes through the hub. This construction is used mainly in vertical wet-pit pumps with covered shaft designs so that the seal at the lower end of the cover pipe will be subject to suction rather than discharge pressure. With mixed-flow impellers, axial thrust is a combination of forces caused by action of the vanes on the liquid and those arising from the difference in the pressures acting on the various surfaces. Wearing rings are often provided on the back of mixed-flow impellers, with either balancing holes through the impeller hub or an external balancing pipe leading back to the suction. In the past, some large mixed-flow impeller designs and some high-head vertical pumps with singlesuction radial-type impellers had a running clearance on the back side of the impeller that was larger in diameter than the leakage joint on the suction side. This disparity caused the axial thrust to act upward, balancing the dead weight of the rotor. This practice was discarded once more reliable thrust bearings became available. The use of wearing rings on the back of large-capacity sewage pumps with mixed-flow impellers has not met with general approval. Therefore, larger capacity thrust bearings must be used. AXIAL THRUST IN MULTISTAGE PUMPS It might seem that the advantages of balanced axial thrust and greater available suction area in a double- suction impeller would warrant applying such impellers to multistage pumps. But, there are definite shortcomings to this practice. The average multistage pump has relatively low capacity when compared to the entire range covered by modem centrifugal pumps. It is seldom necessary, therefore, to use doublesuction impellers just to reduce the net positive suction head required for a given capacity. Even if a double-suction impeller is desirable for the first stage of a large-capacity multistage pump, it is hardly necessary for the remaining stages. As to the advantage of the axial balance it provides, it must be considered that a certain amount of axial thrust is actually present in all centrifugal pumps and the necessity of a thrust bearing is therefore not eliminated. Most important, the use of double-suction impellers in a multistage pump adds needless length to the pump shaft span. Additional space is required for the extra passage leading to the second inlet of each successive stage. In a pump with four or more stages (Fig. 5.8), this increase becomes quite appreciable and causes additional casting difficulties. If shaft diameter is increased to compensate for the longer span so as to maintain reasonable shaft deflection, the impeller inlet areas are correspondingly reduced. The result is that the advantage of superior suction conditions usually offered by double-suction impellers is considerably reduced. Finally, as it is impractical to arrange the various double-suction impellers in any but the ascending order of the stages, the impeller at one end of the casing becomes the last stage impeller and the pressure acting on the adjacent stuffing box becomes the discharge pressure of the next-to-Iast stage. To reduce this pressure, a pressure-reducing bushing must be interposed between the last-stage impeller and the stuffing box, and this bushing further increases the overall length. The result of all these considerations is that most multistage pumps are built with single-suction impellers. Two obvious single-suction impeller arrangements for a multistage pump are as follows: 1. Several single-suction impellers may be mounted on one shaft, each having its suction inlet facing in the same direction and its stages following one another in ascending order of pressure (Fig. 5.9), an arrangement known as "in-line" or "tandem" impellers. The axial thrust is then balanced by a hydraulic balancing device (see Chap. 6). 2. An even number of single-suction impellers can be mounted on one shaft, one half of these facing in an opposite direction to the second half. With this arrangement, axial thrust on the one half is compensated by the thrust in the opposite direction on the other half (Fig. 5.10). This mounting of singlesuction impellers back-to-back is frequently called "opposed impellers." 98 Axial Thrust in Single- and Multistage Pumps ....,'" .... ... <;> <!) <I 0- III III Sl UF F ING BOX UNDER s ue T 0, 111 PRE SS u RE ..... ... .., .,.... <;> <;> ....<I III '" Slur riNG BOl( UNDER STAGE ;, PRE SSuRE Fig. 5.8 Four-stage pump with double-suction impellers. Fig. 5.9 Multistage pump with single-suction impellers facing in one direction (tandem) and hydraulic balancing device. An uneven number of single-suction impellers can be used with this arrangement, provided the correct shaft and interstage bushing diameters are used to give the effect of a hydraulic balancing device that will compensate for the hydraulic thrust on one of the stages. Intuition suggests that opposed impeller rotors inherently have zero axial thrust. In current practical designs this is not achieved; there is normally some residual thrust when the pump is new, and it either increases or is developed as the pump's running clearances increase with wear. To explain why this is Axial Thrust in Single- and Multistage Pumps 99 OP POS ED IMPELLERS Fig. 5.10 Four-stage pump with opposed impellers. the case, it's useful to first state the conditions needed to achieve zero axial thrust with an opposed impeller rotor. These are: 1. The pump must have two shaft seals of equal size. 2. The opposing stages must be of identical configuration. 3. The major pressure breakdowns within the pump must be the same diameter. 4. There must be no leakage between the stages. Except for some special pumps that have an internal product lubricated bearing at one end, and therefore only one shaft seal, most multistage pumps fulfill the first condition. The second requirement is also met in most designs, unless the pump has a special first stage impeller or an odd number of stages. And when it does, the third requirement, which is normally met too, is varied to compensate as noted earlier in this chapter. The practical difficulty arises with the fourth condition because there is leakage between the stages. This has its greatest effect between the back-to-back impeller pairs, because the direction of the leakage over the impeller shrouds affects the average pressure acting on the impellers' back shroud. When the flow is radially inward, as it is for the higher pressure impeller, the average pressure is lower than normal (Fig. 5.11). Similarly, when the flow is radially outward, as it is for the lower pressure impeller, the average pressure is higher than normal (Fig. 5.11). The net result is that each pair of backto-back impellers has some residual thrust, whose magnitude increases with the leakage flow between the stages. This residual thrust can be balanced for one condition with different diameter pressure breakdowns, but for simplicity it is usually carried by the pump's thrust bearing. Good design practice is to size the bearing to accommodate the thrust produced with internal running clearances worn to 2-3 times their new values. 100 Axial Thrust in Single- and Multistage Pumps Residual Thrust .. '--"-- Theoretical L Effect of Ql Outward Fig. 5.11 Effect of QL Inward Residual thrust in back-to-back opposed impeller pair. The effect on axial thrust of wear at the pressure breakdown between back-to-back opposed impellers can be reduced in 2 stage pumps by using a face-to-face arrangement (Fig. 5.12). Because the residual thrust in this arrangement is produced by a small difference in head per stage, the result of leakage across the interstage bushing raising the gross capacity of the first stage impeller, the increase in axial thrust with wear at the clearances is much lower. In the pump shown in Figure 5.12, the pressure at the shaft seals is equal to impeller discharge pressure less the pressure reduction down the back shroud. For many applications this is quite acceptable. When it is not, various combinations of impeller axial balancing (back wearing ring and balancing holes) and breakdown bushings, with appropriately sized bleed-offs, can be used to lower the pressure at the shaft seals. Axial Thrust in Single- and Multistage Pumps Fig. 5.12 101 Two stage pump with face-to-face opposed impellers. ARRANGEMENT OF STAGES IN OPPOSED·IMPELLER MULTISTAGE PUMPS Once a multistage pump is balanced by an opposed-impeller design, the best sequence in which the individual stages are to be arranged within the pump casing must be determined. This problem is not simple, as illustrated by analyzing the best arrangement for a six-stage pump. The total number of possible arrangements is the permutation of 6, that is, 6 x 5 x 4 x 3 x 2 xl, or 720. Of course, half this number are duplicates, because they describe the same arrangement as viewed in a mirror. The problem is actually simplified by the fact that most potential sequences are rather complicated and can be eliminated entirely. Figure 5.13 illustrates four of the most logical possibilities for a six-stage pump. Three factors enter into the analysis of a satisfactory stage arrangement, and the final solution must be a compromise between the "best" individual solutions, each satisfying the following requirements: 1. The arrangement of stages provides the minimum possible leakage at the running clearances and maintains this minimum over a long period of time. 2. The various stage impellers are arranged so that the shaft seals are subject to the lowest pressure in the pump. 3. The sequence of stages precludes excessive complications in the forming of interstage passages. Running Clearance Leakage To minimize internal leakage, the pump designer must determine whether it is preferable to keep a single breakdown under relatively high pressure (as arrangement I in Fig. 5.13, in which breakdown A 102 Axial Thrust in Single- and Multistage Pumps n , . - ---- - - - -- - - _.. - - :- - --, ~ -- - - -r- -- \ ~ :JI-o-~~ i\J m 5 - 4 --- -- - ;-- -) lkj c 6 - ..... , I j1J 3 2 --': ;-- - - ~:..-=-:-..=- :::.-_-___..:- =- ::. ~-_=_.:-~ =-:::. ~-~ _~ .:::.:::- =- -=---~~ ~ ~_~-~:~! --:-rJil~~) ~ J E 6 4 III ( ---~_. -_-~~ ~ ~ ..: =.=.;- ==::. 2 5 = ~_-_-~_--.... ---', \ I I 5 - - - - - _.. - -_.---Fig. 5.13 -- - -- 4 ~j : 2 Stage arrangements for six-stage axially balanced pump. (I.) Breakdown A subject to three-stage pressure differential; one shaft seal under high pressure at B. (1/.) Arrangement with two high-pressure breakdowns, including four-stage pressure differential at C and two-stage differential at D. (Ill.) Breakdowns E and F under two-stage pressure differential. (IV.) All running breakdowns subject to only one-stage pressure differential. is subject to a three-stage pressure differential) or to have many breakdowns under a moderate pressure differential (such as the five interstage breakdowns in arrangement IV (Figs. 5.13 and 5_14). Experimental data show that the latter alternative allows the lowest internal leakage, hence the best hydraulic preference. Before the development of more erosion resistant materials, operating experience showed multiple breakdowns (arrangement IV in Fig. 5.13) was the arrangement most resistant to wear at the internal clearances, thereby allowing longer periods between overhauls to restore hydraulic performance or correct high axial thrust (see the discussion earlier in this chapter). As materials have improved, it has been established that the simpler stage arrangement I, a single breakdown, relatively longer and with a closer clearance to account for the higher differential pressure, yields comparable hydraulic performance and achieves adequate periods between overhauls in most applications. The one exception is applications in which the pumped liquid contains abrasive solids. For these, past experience suggests that the classic stage arrangement IV, with essentially the same pressure differential across each running clearance, would still achieve a longer period between overhauls. The difficulty with this solution is that the design is very expensive to produce; see later discussion in this chapter. Axial Thrust in Single- and Multistage Pumps 103 Fig. 5.14 Section of six-stage opposed-impeller pump. Suction pressure equals zero; pressure generated by each impeller is indicated by P. Shaft Seal Pressures In all but one (arrangement I) of the stage arrangements shown in Fig. 5.13, the pressure at the shaft seals is satisfactory. By placing the two lowest pressure stage impellers at the two ends of the pump, the seals are subjected to only the lowest pressures in the pump, namely suction and first-stage discharge pressures. For stage arrangement I, a second breakdown, B, is added to lower the pressure at the adjacent shaft seal. The leakage from breakdown B is usually returned to pump suction, so the pressure at the seals is nominally equal. To account for friction losses in the bleed-off piping, it is usual to say the pressure at the seal adjacent to the breakdown is 1 bar (15 psi) above suction pressure. Casing Simplicity Comparing the four possible stage arrangements of a six-stage pump shown in Fig. 5.13, it can be seen that arrangement I has two high pressure breakdowns, A and B, each with a pressure differential of three stages, and requires only one casing crossover. Arrangement II has two high-pressure breakdowns: C with a pressure differential of four stages, D with two, and requires two casing crossovers. Similarly, arrangement III has two high pressure breakdowns, E and F, both with a pressure differential of two stages, but requires five casing crossovers to achieve it. Arrangement IV achieves the ideal of having only the differential pressure of one stage across each of its running clearances, but also requires five casing crossovers to do so. Casings with multiple external crossovers (Figs. 3.6 and 5.13) are far more expensive to produce than those with a single integral crossover (Fig. 3.7). It is for this reason that pump manufacturers pursued the development of running clearance materials to make stage arrangement I in Figure 5.13 viable, and as a result established it as the dominant arrangement in modem opposed impeller multistage pumps. 6 Hydraulic Balancing Devices A single-suction impeller is subject to axial hydraulic thrust caused by the pressure differential between its two faces. If all the single-suction impellers of a multistage pump face in the same direction, the total theoretical hydraulic axial thrust acting toward the suction end of the pump will be the sum of the individual impeller thrusts. The thrust magnitude (in pounds) will be approximately equal to the product of the net pump pressure (in pounds per square inch) and the annular unbalanced area (in square inches). Actually the axial thrust turns out to be about 70 to 80 percent of this theoretical value (see Chap. 5). Some form of hydraulic balancing device must be used to balance the axial thrust and to reduce the pressure on the shaft seal adjacent to the last-stage impeller. This hydraulic balancing device may be a balancing drum, a balancing disk, or a combination of the two. In estimating axial thrust and assessing hydraulic balancing devices, there is a fundamental point to be noted: axial thrust is only produced by pressures acting over the normal areas between rotating and stationary surfaces. Figure 6.1 shows a simple axial thrust model. The thrust developed is equal to P multiplied by the area between D3 and D2, and acts to the left. A much larger force, equal to P multiplied p Retention Nut _______ Fig. 6.1 104 I. J. Karassik et al., Centrifugal Pumps © Chapman & Hall 1998 t D1 Elementary axial thrust model. Hydraulic Balancing Devices 105 by the area between D2 and Db acts on the retention nut. This larger force is of great consequence to rotor design but not to axial thrust. BALANCING DRUMS The simplest balancing device is a single diameter balancing drum (Fig. 6.2). This design produces a balancing force by lowering the pressure acting on part of the back of the last stage impeller to close to suction pressure. To do this the balancing drum, which is keyed to the shaft and therefore rotates with it, runs with a close radial clearance in the stationary "balancing drum head" or "balancing bushing." The balancing drum head is installed in a casing diaphragm or partition that separates the region behind the last stage impeller from the balancing leak-off chamber. The balancing leak-off chamber is connected either to the pump suction or to the vessel from which the pump takes its suction. Thus, the back pressure in the balancing chamber is only slightly higher than the suction pressure, the difference between the two being equal to the friction losses between this chamber and the point of return. The leakage between the drum head is, of course, a function of the differential pressure across the drum and of the clearance area. To assess the effect of a balancing drum, the last-stage impeller and balancing drum can be considered as a single piece (the pressure between the impeller and drum affects the separating force between them but not the rotor axial thrust). Looking at Fig. 6.2, the thrusts acting on the balancing drum and last stage impeller are 1. Toward the discharge end-last stage suction pressure multiplied by the net thrust area at the last stage impeller inlet (area "A"). 2. Toward the suction end--discharge pressure multiplied by the last stage unbalanced area (area "B"), plus the back pressure in the balancing chamber multiplied by the back balancing area (area "C"). The first force is greater than the second, thereby counterbalancing the axial thrust exerted upon the single-suction impellers. Actually, the drum diameter can be selected to balance axial thrust completely or within 90 to 95 percent, depending on the desirability of carrying any thrust bearing loads. [" --- --- --- --- --[Area'S' Area 'A' Fig. 6.2 Balancing drum. rhL Area 'C' 106 Hydraulic Balancing Devices It has been assumed in the preceding simplified description that the pressure acting on the impeller walls is constant over their entire surface and that the axial thrust is equal to the product of the total net pressure generated and the unbalanced area. The actual pressure distributions are more complex. They are not constant over the shrouds and generally not equal at two corresponding points on opposite impeller shrouds (D and E, Fig. 6.2). Broadly, three factors account for this: 1. 2. 3. Rotation of the liquid adjacent to the impeller shrouds produces a pressure reduction in the radial direction (see Fig. 5.2). Leakage flow direction and velocity affect the pressure distribution over the impeller shroud. Flow outward increases the average pressure, whereas flow inward decreases it. For all but the last stage impeller of tandem impeller pumps (Fig. 6.2), the leakage flow is outward over the back shroud, inward over the front, giving a higher average pressure on the back shroud, hence higher axial thrust. As clearances increase with wear, the higher leakage velocities act to further increase axial thrust. Figure 6.3 illustrates the point. The clearance between impeller shroud and casing wall influences the average angular velocity of the liquid in that region, hence the pressure reduction due to centrifugal action. Reducing the clearance tends to increase the pressure reduction, thus lowering the average pressure over the shroud. Depending on the position of the impeller, this effect may reinforce or oppose that of leakage. The effects just described are for a given flow. As flow through the pump varies, there are two additional effects: 1. The static pressure at the impeller discharge varies, ranging from 75-80 percent of stage pressure rise at best efficiency point to about 90 percent at shutoff. As the static pressure at the impeller discharge varies so does the average pressure over the shrouds. - - - - - Centrifugal Force Only - - - - With Influence of Leakage, QL, Direction - - - - - Effect of Wear at Clearances Pi Pi ,~ \~ .\ p. sf- \ . \\ \ \ . I Fig. 6.3 Effect of leakage direction on shroud pressure distribution. Hydraulic Balancing Devices 2. 107 Axial thrust produced by the momentum of the liquid entering the impeller varies. Specifically, reducing the flow lowers the momentum, thus increasing thrust toward the suction. By drawing correction factors from actual thrust measurements and allowing for tolerable manufacturing variations, axial thrust can be estimated with acceptable accuracy over the range of normal operating flows. Because the thrust developed by the balancing drum is nearly constant, varying only with pump differential pressure, the design task becomes one of trying to insure the thrust is always inboard over the pump's operating flow range and its magnitude within the thrust bearing's capacity. The latter requirement dictates care, as the thrust magnitude is the small difference between two large forces. Figure 6.4 shows a typical axial thrust characteristic. Depending On the actual pump design, the onset of secondary flows at the impeller discharge as flow is reduced can significantly alter the shroud pressure distributions. The greater effect is usually over the front shroud (inward leakage flow) and can produce thrust reversal (see Fig. 6.4). Being a product of an unstable flow regime, these conditions also tend to fluctuate, which poses the possibility of fatigue failure of the rotor or thrust bearing. When this problem is anticipated, designing the impeller and adjacent casing wall to isolate the shroud space (Fig. 4.35) is an effective solution. Most balancing drum designs incorporate some form of grooving on the drum. This is done to (1) decrease the leakage flow by raising the friction coefficient and (2) reduce the risk of seizure at the clearance should there be metal-to-metal COntact between the parts. The form of the grooves varies markedly, a product of the degree of hydraulic rotor support sought by the design. A balancing drum, correctly sized, satisfactorily balances most of the axial thrust of single suction impellers and reduces the pressure at the discharge side shaft seal. It does this at some expense to efficiency because the leakage is usually relatively high, but with the advantage of simplicity since there is no close axial clearance to be set during assembly. What it lacks, however, is the virtue of automatic Bypass Bearing Capacity + (positive) Toward Suction Axial Thrust Q Osap - (negative) Toward Discharge CD Ideal: Flat characteristic, no thrust reversal ® Acceptable: Steep characteristic, thrust reversal at part load ® Undesireable: Sudden thrust reversal at part load Fig. 6.4 Typical axial thrust characteristics with balancing drum. 108 Hydraulic Balancing Devices compensation for any changes in axial thrust caused by variations in pressure distribution over the impeller shrouds (see earlier discussion). The net result is a fairly wide variation in residual thrust over the pump's operating flow range (Fig. 6.4). To achieve automatic compensation for changes in impeller thrust, it is necessary to have a balancing device whose balancing force varies with the rotor's axial position. The simplest of these devices is the balancing disk. BALANCING DISKS The operation of the simple balancing disk is illustrated in Fig. 6.5. The disk is fixed to and rotates with the shaft. It is separated from the balancing disk head installed as a casing part, by a small axial clearance. The leakage through this clearance flows into the balancing chamber and from there either to the pump suction or to the vessel from which the pump takes its suction. The back of the balancing disk is subject to the balancing chamber back pressure whereas the disk face experiences a range of pressures. These vary from discharge pressure at its smallest diameter to back pressure at its periphery. The inner and outer disk diameters are chosen so that the difference between the total force acting on the disk face and that acting on its back will balance the impeller axial thrust. If the axial thrust of the impellers should exceed the thrust acting on the disk during operation, the latter is moved toward the disk head, reducing the axial clearance between the disk and the disk head. The amount of leakage through the clearance is reduced so that the friction losses in the leakage return line are also reduced, lowering the back pressure in the balancing chamber. This automatically increases the pressure difference acting on the disk and moves it away from the disk head, increasing the clearance. Now, the pressure builds up in the balancing chamber, and the disk is again moved toward the disk head until an equilibrium is reached. To ensure proper balancing disk operation, the change in back pressure in the balancing chamber 4 -- Restricting Orifice To Suction---... Balancin Balancing Chamber Disk Head Fig. 6.5 Simple balancing disk. Hydraulic Balancing Devices 109 must be of an appreciable magnitude. Thus, with the balancing disk wide open with respect to the disk head, the back pressure must be substantially higher than the suction pressure to give a resultant force that restores the normal disk position. This can be accomplished by introducing a restricting orifice in the leakage return line that increases back pressure when leakage past the disk increases beyond normal. The disadvantage of this arrangement is that the pressure on the shaft seal is variable-a condition that will shorten the life of the seal and is therefore to be avoided. Many older pump designs used a balancing disc without a supplementary thrust bearing to limit the rotor's axial movement. Under stable operating conditions, this simple design demonstrated adequate reliability. The same was not so during transient conditions (flow swings, cavitation, or similar), which usually resulted in serious damage to the balancing disc and often the rest of the pump. It is for this reason that the use of a balancing disc without a thrust bearing is now generally limited to small pumps. COMBINATION DISK AND DRUM For the reasons just described, the simple balancing disk is seldom used. The combination balancing disk and balancing drum (Fig. 6.6) was developed to obviate the shortcomings of the disk while retaining the advantage of automatic compensation for axial thrust changes. The rotating component of this balancing device is a long cylinder with a wide-faced flange. Acting with the stationary component, known as a "disk head," the cylinder forms a balancing drum, the flange a balancing disk. In this design, radial clearance remains constant regardless of disk position, whereas t 1B -+ A -+ Axial Clearance Radial Clearance + ---1----+ L..::~O-=:::I Intermediate Relief Chamber Fig. 6.6 Combination balancing disk and drum. 1 E 110 Hydraulic Balancing Devices the axial clearance varies with the pump rotor position. The following thrusts are developed by this device acting in conjunction with the last stage impeller: 1. 2. Toward the discharge end-last stage suction pressure multiplied by area A, plus the intermediate pressure multiplied by area C, plus the average pressure across the axial clearance multiplied by area D. Toward the suction end-last stage discharge pressure multiplied by area B, plus the back pressure multiplied by area E. Whereas the "position-restoring" feature of the simple balancing disk required an undesirably wide variation of the back pressure, it is now possible to depend on a variation of the intermediate pressure to achieve the same effect. Here is how it works. When the pump rotor moves toward the suction end (to the left in Fig. 6.6) because of increased axial thrust, the axial clearance is reduced, and pressure builds up in the intermediate relief chamber, increasing both the value of the intermediate pressure acting on area C and the average pressure acting on area D. In other words, with reduced leakage, the pressure drop across the radial clearance decreases, increasing the pressure drop across the axial clearance. The increase in intermediate pressure forces the balancing disk towards the discharge end until eqUilibrium is reached. Movement of the pump rotor toward the discharge end would have the opposite effect of increasing the axial clearance and the leakage and decreasing the intermediate pressure acting on area C and the average pressure on area D. Figure 6.7 illustrates the pressure distribution in a combination balancing disk and drum. No attempt is made to describe the exact manner in which the pressure decreases between any two points, although this curve is not necessarily a straight line. Also, this illustration is not quantitatively correct. It only serves to show that changes in the balancing device position vary the internal pressure distribution without altering the back pressure. The only possible variation may be caused by pressure changes at the point where the balancing device leakage is returned to the system. An orifice may still be located in the return line. Its function now, however, is not that of changing back pressure but rather of gaging the volume of leakage flow. This flow should not be throttled outside the balancing device; the orifice pressure drop is negligible, ranging from about 0.15 to 1.5 bar (2 to 20 psi). Balancing device modifications Most pumps employing a combination disc drum to balance axial thrust also have a thrust bearing to limit rotor movement (see Balancing Disks). The bearing is typically sized for the residual thrust produced with the disc faces at some minimum clearance determined by the pump manufacturer. In high temperature applications, such as hot charge in refining, there have been instances where differential expansion during thermal transients increased the minimum disc clearance to the point where the thrust bearing became overloaded and failed. Various modifications of hydraulic balancing devices are now in use. All try to retain the selfcompensating feature of the disk or combined disk and drum, while avoiding the risk of face contact and scoring inherent in a close running axial clearance (typically 0.050 to 0.125mm [0.002 to 0.005 in.]). One means of realizing this is to soften the restoring action by lowering the proportion of the total pressure drop taken across the axial clearance. This is done by narrowing the disk face of a combined disk and drum, and either leaving the disk at the end of the drum (Fig. 6.6) or locating it between two drum regions (Fig. 6.8). The latter design, often referred to as a stepped drum, has the added virtues of a substantial back pressure at the disk, hence no flashing across the disk, and the ability to "fine-tune" net thrust by changing the clearance at one drum. In some pumps using stepped balancing drums, the design axial clearance is fairly large, typically 0.4Omm (0.015 in.), to further reduce the risk of contact at the disk faces. Set this way, the disk's self-restoring action is normally inactive, serving only as backup protection to control rotor position should the thrust bearing cease doing so. Hydraulic Balancing Devices 111 Pel w a:: ::;) (/) (/) Pe2 w a:: 11. Pc RADIAL CLEARANCE ALANCING CHAMBER Fig. 6.7 Pressure distribution in combination balancing disk and drum. Key: PA = discharge pressure; PB = pressure at intermediate relief chamber; Pc = back pressure; I = normal pressure distribution; II = pressure distribution after disk moves away from disk head; PA - PB = pressure drop through drum portion; PB - Pc = pressure drop through disk portion. Another approach to the problem of a close-running axial clearance is to change its detail configuration so the restoring action is more stable. Tapering one of the faces so the axial clearance converges in the flow direction (Fig. 6.9) achieves this. It does so by increasing the rate of pressure drop as the clearance decreases. Materials selection for balancing devices will be treated in a subsequent section. However, it is imperative to remember that both the material and the design are extremely important. If the balancing device wears appreciably, problems can develop, the nature of which depends on the type of balancing device. With a single diameter balancing drum (Fig. 6.2), pump performance will deteriorate (from increased leakage), and eventually axial thrust will increase as the back pressure in the balancing leakoff chamber rises. A balancing disk (Fig. 6.5) or combination disk and drum (Fig. 6.6) without a thrust bearing poses the risk of contact between the impellers and some internal pump part as the rotor moves axially to compensate for wear. When a thrust bearing is used, rotor axial movement to compensate for wear is limited, and so wear leads to a drop in performance (from higher leakage) and higher thrust bearing loads as the disk portion becomes less effective. INDIVIDUAL AXIAL THRUST BALANCING A design sometimes used to balance the axial thrust of single-suction impellers without the use of a hydraulic balancing device is illustrated in Fig. 6.10. It provides the individual impellers with wearing 112 Hydraulic Balancing Devices Fig. 6.8 Combination balancing disk and drum with disk located in center portion of drum. - 11- Disc Clearance Parallel Faces Press Drop Convergent Faces "- ~ Clearance Fig. 6.9 Balancing disk modification for improved stability. Hydraulic Balancing Devices 2nd Stage Discharge 113 3rd Stage Discharge Fig. 6.10 Balancing axial thrust of single suction impellers with back wearing rings. rings both in front and back, the inner diameter of both rings being the same to equalize the thrust areas. Balancing holes are drilled through the impellers to equalize the pressures from front to back. This prevents the leakage water that flows across the back sealing surface from collecting in the annular space back of the impeller and building up the pressure at that point. For convenience, the back wearing ring may form an integral part with the diffuser or stage-piece bushing. This design theoretically provides axial balance. Although the pressures on the two impeller sides may not be exactly equal in practice (because of unequal wearing ring leakage), the amount of unbalance is rather small and can usually be accommodated by the thrust bearing. Unfortunately, the use of a back wearing ring becomes less justifiable when one considers the effects of this construction on multistage pump internal leakage and mechanical design. Normally, pumps with impellers arranged in ascending stage order enjoy almost negligible pressure difference and leakage across the stage-piece separating two consecutive stages. However, with a wearing ring at the back of the impeller, this difference becomes equivalent to the pressure generated by one stage. Thus, two additional clearance joints subject to a full one-stage pressure difference are now used, namely, the back wearing ring and the stage-piece joints. A back wearing ring design is lacking in one other respect, compared to a hydraulic balancing device. That is, it does not reduce the pressure on the discharge-end shaft seal which is now subjected to the suction pressure of the last stage. Unless this pressure can be reliably sealed (a pronounced improbability in other than low pressure pumps), it is necessary to provide some form of pressure-reducing mechanism ahead ofthe box. This requirement, in addition to the space needed for the back wearing rings, substantially increases the total shaft span of a multistage pump and makes the design even less desirable. COMPARISON OF BALANCING DEVICES AND OPPOSED IMPELLERS On the surface, it would appear that the choice between using a balancing device and arranging impellers in opposed sequence to balance axial thrust reflects a basic difference in design philosophy. Consequently, this choice has always been controversial among designers and users. The argument supporting each 114 Hydraulic Balancing Devices 111 ~ 111 2 A 'If? --3'------1.4- ----'-------'6---7'------'8'- - - - - - - - Fig. 6.11 Balancing axial thrust with balancing device in eight-stage pump. Breakdown A is subject to a differential pressure of eight stages. method centers on the presence or absence of a balancing device subject to a differential pressure equal to the total pressure generated by the pump, and the effect that it has on potential wear rate, rotor dynamics, and sensitivity to wear. The argument over potential wear rate is strictly semantic. To balance axial thrust and keep the pressure at the seals low, the total differential pressure has to be broken down in either case. Whether this is accomplished across a single breakdown (Fig. 6.11) or the balancing device is split into two separate portions distributed throughout the pump (Fig. 6.12) and given a different name is immaterial so long as the running joints in each case are of proper length. Wear is essentially a function of the pressure drop per unit length of break down and if the lengths of the breakdowns are chosen to maintain the same pressure drop unit length the wear will not be affected by the number of breakdowns nor by the pressure differential across them. This assumes the risk of rubbing contact at the major breakdowns is similar, since contact within clearances is also a factor in wear rate. There is a significant difference between the two designs in their effect on rotor dynamics. Because the major pressure breakdowns also act as hydrostatic bearings (see the Lomakin effect in Chapter 7), their position along the rotor becomes important. The center bushing in an opposed impeller arrangement (Fig. 6.12) is located close to rotor midspan, effectively halving the bearing span when the pump is running with liquid in it, and so changing the rotor's dynamics considerably. It is this effect that allows the satisfactory operation of slender shaft rotors. The balancing device of tandem impeller rotors also acts as a hydrostatic bearing, but because it is located relatively close to one end of the pump, its effect on the rotor's dynamics is much less. See Chapter 7 for further discussion on rotor dynamics. Sensitivity to wear at the running clearances has two aspects: residual thrust and rotor dynamics. In pumps with tandem impellers, the impeller thrust increases with wear. Balancing discs and combined disc drums compensate for this up to the point where the disc clearance is controlled by the thrust bearing. Balancing drums cannot compensate for the additional impeller thrust, and so the thrust balance changes. The residual thrust mayor may not increase depending on whether the original balance produced reverse thrust at some capacity (Fig. 6.4). Opposed impellers develop additional residual thrust at the opposed impeller pair (see Chapter 5) and from any differences in flow within the pump caused by B 2 3 4 8 7 6 5 Fig. 6.12 Balancing axial thrust with opposed impellers in eight-stage pump. Breakdowns A & B are each subject to a differential pressure of four stages, for a total of eight stages. Hydraulic Balancing Devices 115 uneven wear at the clearances. For most designs within the limits of nonnal wear at the clearances, the increase in residual thrust is quite small. Unless the running clearances have been intentionally designed to maximize the Lomakin effect, the rotor dynamics of pumps with balancing devices are not very sensitive to wear at the clearances. Opposed impeller pumps, on the other hand, are very sensitive, particularly those with slender rotors. As the major breakdowns in these designs wear, the stiffness of the hydrostatic bearing at rotor midspan decreases, thereby significantly changing the rotor's dynamic characteristics (see Chapter 7). With some sensitivity to wear in both designs, it is useful to be able to measure the leakage through the major breakdowns. These data give a direct indication of the condition of the major breakdowns, and an indirect indication of the condition of the other clearances which nonnally wear at about the same rate. Pumps with a balancing device have only one major breakdown at one end of the pump (Fig. 6.11), where the leakage from it can be easily measured. The same can be done with the end or balance bushing in the usual opposed impeller arrangement (Fig. 6.12), but it is not practical to measure the leakage through the center bushing, the other major breakdown in this design. The various points of this comparison between balancing devices and opposed impellers as means of balancing hydraulic thrust are summarized in Table 6.1. Despite all that can be stated in comparing the two designs, there are, in the history of multistage pump applications, many instances in which a pump with a balancing device perfonned better than one with opposed impellers and vice versa. Many factors besides those already discussed can account for this, hydraulic design, rotor stiffness, materials, and casing construction to name four, but from the pump user's point of view one design perfonned better than the other, and therefore personal preference often makes the choice between the two designs. Table 6.1 Comparison of Balancing Devices and Opposed Impellers Balancing Device Factor Suitable for high temperature Wear rate Effect on rotor dynamics Residual thrust Effect of wear on: -residual thrust -rotor dynamics Measure leakage Drum Yes Small(3) Moderate(4) Disc Drum Opposed Impellers Nd 1) Yes All approximately equal(2) Minor Major Negligible Small Negligible(5) Minor Yes Varies(6) Major No(7) Notes: 1. Differential thermal expansion during thermal transients can open disc clearance leading to thrust bearing failure from overload. 2. Provided pressure drop per unit length similar and no rubbing contact. 3. Residual thrust low at design capacity; generally increases as flow reduced. 4. Depends on thrust characteristic and original thrust balance. 5. Within limits of rotor movement allowed by thrust bearing. 6. Depends on number of stages, number of opposed impellers pairs, and equal wear at high pressure breakdowns. 7. Leakage through the center bushing (Fig. 6.12) cannot be measured 7 Shafts and Shaft Sleeves The primary function of a centrifugal pump shaft is to transmit torque to the impeller. At the same time, the shaft and its support arrangements must maintain alignment of the rotor within its running clearances and through the shaft seal. These functions lead to the following design requirements: First, the shaft must be strong enough to withstand sudden starting, such as occurs when a motor is started across the line. It should also tolerate the higher power associated with expected abnormal operation such as starting a hot service pump on cold liquid, variations in the process (resulting in high liquid sa or viscosity), reduced system head (allowing the pump to run to high capacity), or, in axial flow pumps, increased system head (causing the pump to run back at lower capacity, hence higher power). Second, the shaft must be designed for tolerable deflection under the weight of the rotor and any hydraulic loads, either radial or axial. Third, the shaft must not be liable to any significant response to a resonant condition (excitation of a critical speed), lest it develop destructive vibration. CRITICAL SPEEDS As critical speed is a key factor in the selection of shaft diameters, the centrifugal pump user ought to have a general knowledge of this subject. Developments in pump design have compounded the need. Smaller pumps running at higher speeds have brought about a significant improvement in the understanding of pump rotor dynamics. Applied correctly, this improved understanding results in better pumps. Applied generally, it can result in unduly restrictive, hence expensive, specifications for quite simple pumps. Any object made of an elastic material has an infinite number of natural frequencies, each of a different mode shape. When a pump rotor or shafting system rotates at any speed corresponding to a natural frequency, the vibration produced by minor unbalance will be magnified. These speeds are called the critical speeds. In conventional pump designs, the rotating assembly is theoretically uniform around the shaft axis, and the center of mass should coincide with the axis of rotation. This theory will not hold for two 116 I. J. Karassik et al., Centrifugal Pumps © Chapman & Hall 1998 Shafts and Shaft Sleeves 117 reasons. First, there are always minor machining or casting irregularities, and second, there will be variations in metal density of each part. Thus, no matter how carefully a rotor is made, there will always be some eccentricity of the center of mass to produce centrifugal force and therefore deflection as the assembly rotates. A critical condition is reached when the rotative speed is such that the centrifugal force equals the shaft's elastic restoring force. With these opposing forces equal, the only force restraining the shaft, neglecting effects at the running clearances, is that produced by viscous friction within the shaft material. If the rotor is allowed to run at this condition without external restraint, there is a high risk that vibration will increase until the shaft fails. On occasion, the same phenomenon can occur at a speed above or below the pump's rotative speed. For this to happen, the rotor must be excited by a disturbing force rotating at or close to a critical speed. To rotate at a speed other than the pump speed, the disturbing force must be of hydraulic origin. Rigid and Flexible Shaft Designs The lowest critical speed is called the first critical speed; the next higher is called the second, and so forth. In centrifugal pump nomenclature, a "stiff shaft" means one with an operating speed lower than its first critical speed, whereas a flexible shaft is one with an operating speed higher than its first critical speed. ROTOR MECHANICAL STIFFNESS In the simplest analysis, the rotor of a centrifugal pump (Fig. 7.1) is considered running in air and supported by infinitely stiff bearings (Fig. 7.2[a]). By taking the equation for the natural frequency of a single mass rotor: ......:.... ............ _~~-~::~----- -- ---~~~ ':~~~.~~ ---- --- ---':'~_:~:'[~_ J Fig. 7.1 Rotor assembly of a single-stage double-suction pump. 118 Shafts and Shaft Sleeves (8) (b) Fig.7.2 Rotor support models. a) Rotor supported by infinitely stiff bearings; critical speed determined by rotor mass and stiffness alone. b) Rotor supported by bearings offinite stiffness and having damping, with additional support and damping at internal clearances; critical speeds determined by motor mass, rotor stiffness, support stiffness, and support damping. O)n = (k/m)D.5 where k is stiffness and m is mass, both in consistent units, and rearranging it, the first bending critical speed, NCh can be estimated from NCI where = 946/(Y,,)D.5 in metric units or NCI = 188/(y,,)D.5 in US units NCI = critical speed in rpm y" = rotor static deflection in mm (in). The rotor static deflection Yst is that resulting from rotor weight alone, and is therefore a measure of the rotor's mechanical stiffness. Under the action of radial hydraulic forces, the running rotor deflection Shafts and Shaft Sleeves 119 may well be higher. That is of consequence to the shaft seal and running clearances, but has no bearing on critical speeds unless seal or clearance considerations dictate a change in shaft geometry. For all but the simplest shafts, calculating a rotor's static deflection requires either a reliable approximation for manual work or use of a computer routine if greater accuracy is necessary. The significance of mechanical stiffness can be gleaned by considering two rotor designs, one to run at 1,800 rpm, the other at 3,600 rpm, both to be "stiff." A usual margin for rigid motors is to have the critical speed at least 20 percent above of the running speed, giving critical speeds of 2,160 and 4,320 rpm for the two rotors being considered. The corresponding static deflections are 0.193 and 0.048mm (0.0076 and 0.0019 in.) A rotor whose static deflection is 0.193mm (0.0076 in.) is relatively easy to design, and, in fact, would likely be somewhat stiffer to avoid contact at the running clearances. Except for pumps of only one or two stages, limiting the static deflection to 0.048mm (0.0019 in.) makes the rotor design a great deal more difficult unless unusual proportions are resorted to. Most 3,600-rpm multistage pumps, therefore, have rotors that are "flexible" when analyzed on the basis of mechanical stiffness alone. HYDRAULIC STIFFNESS (LOMAKIN EFFECT) While analyzing critical speeds considering only rotor mechanical stiffness is simple, it is not sufficiently accurate for many designs, because other factors significantly affect the actual dynamic behavior. The dynamic behavior of all pump rotors is influenced to some degree by the following factors: 1. Finite bearing stiffness, with sleeve bearings having the lowest stiffness of the arrangements used 2. Additional rotor support and damping from radial type shaft seals such as packed box and breakdown bushings 3. Additional rotor support and damping from hydraulic effects at internal running clearances 4. Increased effective mass from motion of the liquid adjacent to the vibrating rotor. These factors change the rotor support arrangement from the simple two infinitely stiff bearings arrangement in Fig. 7.2(a) to the much more complicated series of springs and dashpots in Fig. 7.2(b). The net effect of these factors varies with pump detail design. In most cases where the net effect is of consequence, typically multistage and high-speed pumps, the dominant component is that produced by a hydraulic effect at the internal running clearances. This effect is known as the Lomakin effect after its discoverer and can be termed hydraulic stiffness for comparison with a rotor's mechanical stiffness. Under the action of significant Lomakin effect, the rotor's running critical speed is raised to a higher value (additional support or stiffness) and the response through the critical speed reduced (damping; see Fig. 7.3). Note that in very large low-speed pumps, the dominant factor tends to be increased effective mass, leading to a reduction in the running critical speed. The Lomakin effect is a product of hydrostatic (pressure) and hydrodynamic (velocity and viscosity) action as liquid passes through a pump's internal running clearances under the action of a differential pressure. As such, the magnitude of the Lomakin effect depends on the pressure drop across the running clearances, the surface speed at them, their geometry (length, clearance, and surface form), and the liquid viscosity. Given these dependencies, there is very little Lomakin effect until the pump is running at say 75 to 80 percent of rated speed. For the same fundamental reasons, clearances with a large length-toclearance ratio and smooth surfaces develop more Lomakin effect than those with a low length-toclearance ratio and one surface serrated. From the same reasoning, it is evident running clearance wear will reduce the Lomakin effect. Tests show the reduction is greater in arrangements designed to produce high Lomakin effect (Fig. 7.4). 120 Shafts and Shaft Sleeves 0.8 a. I J!1 'E ai 6 / "0 ::I :t::: Without Lomakin Effect a.. E c: <C 4 0 ... .0 ~ :> 2 I 1000 2000 3000 r With Lomakin Effect 4000 5000 Pump Speed, rpm Fig. 7.3 Influence of Lomakin effect on rotor dynamic response. (I. J. Karrasik et ai, Pump Handbook, 1st Edition, 1976. Reproduced with permission of the McGraw-Hill Companies) Computer routines are used to estimate the running dynamic behavior of rotors, but the accuracy of their estimates depends on how well the running clearances can be modeled, a process that does not yet yield entirely consistent results. To check the accuracy of a prediction it is necessary to determine the rotor's natural frequencies while it is running. Measurements during rundown give an approximation, but they are on the low side since the Lomakin effect is decreasing rapidly as the pump's speed drops. Measurements at running speed require some form of external excitation. Variable-speed shaking or calibrated impact are two available methods; the second, with the appropriate instrumentation, is the easier. To differentiate between the two approaches to analyzing rotor dynamics, the terms "dry critical" and "wet critical" have been introduced. The former refers to an analysis assuming the rotor is supported by infinitely stiff bearings alone, the latter refers to an analysis recognizing the influence of the Lomakin effect, liquid around the impeller, shaft seal support, and the finite stiffness of bearings. Both values tend to be used in pump evaluations because the difference gives a measure of the pump's sensitivity to wear at its running clearances. As a general rule, it is prudent to require rotors with low Lomakin effect to have at least a 20 percent margin separating running and critical speeds. When the Lomakin effect is high, the rotor's relative response to excitation at the critical speed becomes the governing criterion. This is necessary because the high damping spreads the region of response (Fig. 7.3), making a clear separation hard to define. The response of such rotors should always be calculated for both new and worn clearances, to reduce the risk of destructive rotor vibration as the clearances increase with wear. TORSIONAL CRITICAL SPEEDS Two or more masses connected by a torsionally elastic shaft (Fig. 7.5), have n - I natural frequencies, where n is the number of masses connected by the shaft. In a manner similar to lateral or bending critical Shafts and Shaft Sleeves 121 7000 \. 6500 \\ 6000 ~ a. ~ al ~ 5500 \. "iii o +=' 8 " - oo~ (/J 5000 ........ r--...... 4500 c: Ol ·iii 4000 Q) 0 3500 Q) 0 ~ D,. (3 .01 0 ~O\led c: co Q) .02 ~ " ~- ~ P across wear ring I = 300 PSI .03 .04 .05 Diametral Clearance (Inches) Fig. 7.4 Effect of running clearance wear on wet critical speed. 12 (Driver) (P ump) 11 r--""-'- - - - -- -- Fig. 7.5 I t---- - - l- kt Shaftin 9 Torsional critical speed model. speeds, sustained operation of a rotor under conditions where one of its torsional natural frequencies is close to an exciting frequency, can lead to large amplitude torsional vibration with consequent shaft failure. In centrifugal pump practice, torsional critical speeds are usually of consequence only when the rotor has low torsional stiffness (long and slender) and the drive has a pulsating characteristic, for example, an engine or variable-frequency-controlled motor. Since torsional natural frequencies are a product of connected masses, they are a property of the pump plus its drive train, including couplings, and can only be determined as such. A potential torsional resonance problem is best corrected by changing 122 Shafts and Shaft Sleeves the stiffness of the connection, usually by modifying the coupling. In the rare instances where resonance cannot be easily avoided, torsional stress analysis is carried out to determine whether the resonance can be tolerated. SHAFT SIZING Sizing a shaft is an iterative process. In general, a minimum diameter is determined for strength, steps to enable assembly are added, deflection is checked, then the dynamic characteristics are predicted. The process is then repeated until an acceptable solution is realized. Pump designers, of course, have various methods to enable them to quickly develop an approximate solution. Sufficient shaft strength requires that the shaft not fail by fatigue, taking account of the loads imposed during starting, normal operation, and any specified abnormal operation. This means that the endurance strength of the shaft material, in the pumped liquid if that is the case, must be above the combined stress at the critical point in the shaft. How far above (how big a design factor) depends on the certainty of loading, liquid condition, shaft detail at the critical point, and material condition. Loading should assume lO percent torsional fluctuation and make provision where applicable for some coupling misalignment. Nominal torsional stress at the smallest diameter is a common evaluation approach. Conservative, but not absolutely safe, values for nominal torsional stress are Shaft Material Carbon steel Alloy steel, chrome steel 316 stainless steel Typical Torsional Stress-MPa (psi) 48 (7,000) 55 (8,000) 35 (5,000) A discussion of deflection and dynamics is easiest if the two basic rotor configurations, overhung and between bearings, are considered separately. For overhung rotors accepted design practice now requires the following: 1. Deflection, static plus that caused by imposed forces under the worst expected operating conditions, should be less than the available internal clearance. 2. Deflection at the shaft seal should be less than 0.050 mm (0.002 in). 3. First bending critical speed (dry basis) should be at least 20 percent above the running speed (except for high-speed pumps). These requirements have become accepted practice, because they have been proven reliable (running clearance wear, seal, and bearing life), are simple to design for, usually do not exact any performance penalty, and do not cause an undue increase in pump cost. Determining all the data necessary to verify a rotor meets the preceding design requirements is quite an extensive task. A simpler, and generally sufficiently accurate, alternative approach is to employ a factor that is proportional to static deflection but can be calculated from shaft geometry alone. By comparing factors or using an upper limit based on experience, a series of offers or a troublesome pump can be quickly evaluated. For cantilever rotors of the form shown in Fig. 7.6, the deflection is proportional to Shafts and Shaft Sleeves IMP <t BRG <t BRG <t 1-.-~1--·1- L2-1 Fig. 7.6 IMP <t BRG <t 123 BRG <t ~ Li -1- ~2---1 Cantilever shafts. where Ll is the impeller overhang, Lz is the bearing span, Dl is the shaft diameter under the shaft sleeve, and D2 is the shaft diameter between the bearings. Common practice for shafts with the larger diameter between the bearings (Fig. 7.6(a)) is to evaluate them using the first term of the equation just given, specifically since the .error introduced by this simplification is quite small. When Dl is greater than D2 (Fig. 7.6(b)), the error can be significant thus the result quite misleading. Acceptable values of the simplified shaft flexibility factor, L I3/D14, decrease with increasing pump size. Figure 7.7 shows the characteristic of shaft flexibility factor over the normal range of process pumps for designs that meet API-610 [3.1] and for designs intended to have shafts 2 times as stiff as required by API-61O. The latter is an informal standard that has evolved in the United States over the past decade from the oil industry's emphasis on shaft stiffness (see Chap. 27). Between bearings, rotors for one- and two-stage pumps are usually relatively short and therefore easily made to meet the simple requirements for cantilever rotors. Between bearings rotors for pumps, having three or more stages, cannot be designed to withstand any appreciable radial thrust, so twin volutes, diffusers, or staggered single volutes (see Chaps. 2 and 3) are employed to reduce radial thrust to negligible values. The design of the rotors themselves is controversial. One philosophy, resting on lower cost and higher efficiency, advocates low mechanical stiffness (slender shaft) and high hydraulic stiffness (Lomakin effect). The opposing philosophy, claiming that reliability is more important than first cost and efficiency (the efficiency of a failed pump is zero) calls for high mechanical stiffness (large shaft) and low hydraulic stiffness. In a more general sense, it is worth noting that this controversy is peculiar to liquid handling turbomachines; those handling gases must rely on mechanical stiffness because the hydraulic stiffness is very low. Slender shaft rotors are sized for torque, then stepped up to permit assembly and perhaps reflect some empirical stiffness requirement. Their static deflection is greater than the available internal clearance and the dry first bending critical speed is consequently well below the running speed. As the pump is accelerated, the Lomakin effect rapidly increases the hydraulic stiffness such that at 100 percent speed the rotor is classically "stiff' (Fig. 7.8). Most successful slender shaft pumps have opposed impeller rotors (see Chap. 5), an arrangement whose center bushing is ideally suited to developing the high Lomakin effect necessary for success. Large shaft rotors, on the other hand, are designed for static deflection less than the available internal clearance. The dry first bending critical speed is therefore 124 Shafts and Shaft Sleeves QH N 5 100 = USGPM(FT) RPM 50 10 100 500 1,000 50 1,000 500 10 250 ~&~. l~ , 5.0 ..........<.\"-4,0 ~.s' ~ 'ISfiftJ ~ ...... 1.0 0.5 - 100 L3/D4 (in· 1 ) 50 25 10 0.1 0.1 0.5 5.0 1.0 QH N = 10 50 100 M3/HR {M} RPM Fig. 7.7 Typical values of cantilever shaft flexibility factor UID" versus pump size factor. significantly higher. There is also an increase in critical speed as the pump is brought up to speed, but by design, it is small and the rotor typically remains classically "flexible" (Fig. 7.8). Relying on high Lomakin effect to produce acceptable dynamics in slender shaft rotors is not an unmixed blessing. Given the Lomakin effect's dependence on pressure differential and running clearance condition, there are two cautionary comments. First, rubbing contact at the running clearances whenever the pump speed is significantly below design (at startup and shutdown) dictates care in the choice of materials for these clearances if damage is to be minimized, and even that may not prevent rapid wear under frequent start/stop operation. Second, the dynamic behavior of such rotors may be quite sensitive to running clearance conditions. In the worst case, the reduction in critical speed as clearances wear can be sufficient to allow coincidence between the critical and running speeds. If this happens when the clearances are worn to the point where damping is also significantly reduced, there is a risk the rotor will develop severe vibration and further damage the pump. As with overhung rotors, a factor proportional to static deflection is frequently used to quicldy evaluate between bearings rotors. Various factors in use, with the most common being Shafts and Shaft Sleeves 125 LOW MECHANICAL STIFFNESS, HIGH HYDRAULIC EFFECT OF WEAR Cl~ UJ{!) UJ~ a..Cl C/)Z ...,JUJ «al Q 1-- 100% RUNNING ------------ SPEED I-C/) -a: a:_ O!:S HIGH MECHANICAL STIFFNESS, LOW HYDRAULIC 100 PERCENTAGE OF RUNNING SPEED Fig. 7.8 Multistage pump rotor characteristics: variation of critical speed with running speed and running clearance wear. where L is the bearing span and D is the nominal shaft diameter. This factor is based on the stiffness of the shaft alone and neglects the weight of components mounted on it. Such an approach is justified on the grounds that the shaft provides most of a rotor's mechanical stiffness. The only published guideline for L4/D 2 is a demarcation for rotor runout and balancing in the 8th edition of APlO-61O: rotors with L4/D2 above 1.9x109 mm2 (3.0x106 in2) have higher allowable runout and are identified as difficult to balance for operating speeds above 3,800 rpm. Beyond this, the choice of a limiting value of L4/D2 must rely on the evaluator's experience. There is opinion that neglecting the weight of the mounted components distorts the evaluation, particularly for slender shaft rotors whose mounted components usually weigh more than the shaft, and therefore have a significant influence on static deflection and dry critical speeds. A useful alternative factor, one that is proportional to the rotor's first dry bending critical speed, is where W is rotor weight and D and L are before. A notable advantage of this factor is that some guidelines for limiting values have been published (Fig. 7.9). These allow a rotor to be classified as "too slender," "slender," suitable for "wet operation only," or capable of "running dry." Although a correlation such as this can never be the last word on a particular design, it is consistent with the authors' experience. Whether to use a slender or heavy shaft rotor is not a clear choice but depends on many factors. To provide a starting point, the more significant factors are • Neither design can tolerate high radial hydraulic forces, so the hydraulic design and selection must be good or pump life will be short. 126 Shafts and Shaft Sleeves 1000 \ , 900 U'l SLENDER SHAFTS c:i ;;t -- Cl 800 II 700 '"...J ~ :::.::: + I" \ - Possible Difficulties In Achieving Rub - Free Initial Build \ \ W(N) W ::1! 600 « a: - Unduly Affected By Out Of Balance and Lack Of Initial Straightness. Possibility Of Premature Wear Of Internal Clearances \ i\. ~~ " I":~ w - SLENDER SHAFTS \ I- ~ (m,f::::::: r.:::: :~ :-'\ a: CJ) CJ) Om L(mm)~ ~ - - Recommended Design Line ----For Wet Running Pumps 500 w Z LL LL 400 i= CJ) l- '" " LL « 300 I ~ CJ) Recommended Upper Limit For - - - Pumps With Dry - Running Capability 200 ~ ~~ - r::::::~ ............... r--- 100 o 2 3 4 5 6 7 8 9 N = (RPM/100) MAX OPERATING SPEED Fig. 7.9 Guidance chart for stiffness of between-bearing rotors [7.1]. • At a given rotative speed, slender shaft pumps require less NPSH and are usually more efficient than large shaft pumps. In modem designs, the latter advantage derives almost solely from slender shaft pumps having more stages and consequently a higher specific speed. Hydraulic design refinements have overcome the loss of efficiency traditionally associated with increasing the shaft size in a given impeller. The higher specific speed of slender shaft pumps also makes them less expensive as cost varies with the 2nd or 3rd power of diameter but only linearly with length, making a long, slender pump less expensive than one that is shorter and larger in diameter. • The service life (time between need to open the casing and renew internal clearances) varies markedly with the application. Table 7.1 shows typical service lives for the two broad classes of multistage pump rotors in various applications. Shafts and Shaft Sleeves Table 7.1 127 Typical Multistage Pump Service Lives in Various Applications Typical Service Life-Hours - - - - --- - - Slender Shaft Large Shaft - - - _.- Application Continuous operation at essentially constant flow pumping benign liquid Frequent start/stop operation with wide flow swings, pumping liquid of low lubricity or containing low concentration of abrasive solids Frequent start/stop operation with wide flow swings, pumping liquid with high concentration of abrasive solids - - - - -- - -- - - - - 50,000-75,000 150,000-200,000 7,500-10,000 30,000-40,000 Normally not used 7,500-10,000 ROTOR CONSTRUCTION A centrifugal pump's rotor comprises the shaft plus impeller or impellers, balancing device if applicable, sleeves, and some retention devices, usually nuts. The design and mounting of these parts is of consequence to the rotor's integrity and sometimes even influences shaft sizing. Mounting and retention of the impeller or impellers is determined by power, speed, and impeller material. The most common arrangement is to center the impeller with a cylindrical slide fit, drive it with a key, and locate it axially with a shoulder and nut or snap rings (Fig. 7.1). Small low-cost pumps, some chemical pumps, and most slurry pumps have the impeller threaded onto the shaft and locked against a shoulder (Fig. 7.10). Although the centering is not as accurate as a cylinderical slide fit, this Fig. 7.10 Thread mounted impeller. 128 Shafts and Shaft Sleeves arrangement does offer simplicity; low cost; and, for slurry pumps, a practicable means of mounting hard metal, rubber-lined, or ceramic impellers. At high rotative speeds, dynamic balance requirements dictate more accurate centering than can easily be achieved with slide fits. Taper mounting (single stage only) or shrink fits are used to achieve this. Good practice requires that shrink fit multistage rotors have the fits stepped to ease assembly. Most taper- and shrink-fit-mounted impellers have a key for torque transmission. When the interference in the fit is high, the key serves as a backup device only, to prevent rotation should the fit loosen during a thermal transient or similar event. At high powers or in severe services, it is important that the impeller is not able to move on the shaft or its mounting fit could suffer fretting corrosion. Medium-size pumps typically employ a tapered fit in these circumstances, large pumps use a bolted flange (Fig. 7.11), in which the impeller is centered on a rabbet fit and the coupling is held tight by fitted bolts. Most rotors have renewable shaft sleeves to protect the shaft, locate parts on it, or both (see discussion later in this chapter). There are, however, circumstances where sleeves are not desirable. For reasons of manufacture and installation, shaft sleeves have a certain minimum thickness, typically 2.5mm (0.10 in.) for shafts to about lOOmm (4 in.) diameter. In small pumps, adding a minimum thickness sleeve to a shaft sized for adequate stiffness usually results in an abnormally large diameter at the shaft seal. The alternative is to make the shaft of a material able to offer reasonable wear resistance or hard-coat the shaft with chrome or ceramic in the region of the seal. Figure 7.12 shows such a shaft, often referred to as "solid" shaft construction. Solid shafts cost less to make than a shaft plus a sleeve. Taking account of this and the simpler maintenance procedure, solid shafts are often the most cost-effective solution for small pumps. In multistage pumps, particularly those of large shaft design, the minimum thickness of a sleeve would aggravate the effect of shaft size on impeller proportions. The prevailing practice, therefore, is to make the shaft of a material able to resist erosion and corrosion of the exposed regions between the impellers. Fig. 7.11 Section of large vertical pump-turbine. Note flange mounted impeller. tilting pad guide bearing. rigid line shaft coupling. (Courtesy: Voith) Shafts and Shaft Sleeves Fig. 7.12 129 Section of small centrifugal pump without shaft sleeves. How the impeller and other rotor parts are mounted affects the rotor's mechanical stiffness. Parts mounted with a shrink fit increase the effective diameter, hence the stiffness, in the region of the fit. In most designs, however, the total length of shrink fits is a fairly small fraction of the rotor's bearing span, so the overall increase in stiffness is not great. Slide fit parts held in compression with nuts, such as the rotor in Fig. 7.1, often increase the stiffness significantly, although with notable dependence on the tightness of the nuts. In multistage rotors, where such construction has many faces butting together, the benefit in stiffness is usually offset by extreme difficulty in building and maintaining a straight rotor. Most good specifications now require individually located impellers for multistage rotors to avoid this vexing problem. Slide fit parts retained at one end, such as the hook-type shaft sleeve prevalent in chemical and overhung process pumps, do not increase stiffness. SHAFT MAINTENANCE Except for small pumps with solid shafts, it is unusual to have to replace a centrifugal pump shaft. Typically the shaft will last the life of the pump, unless damaged as a consequence of some other failure or problem within the pump. Given this, any shaft failure should be investigated carefully to find the cause, so it can be corrected and further failures prevented. Although the shaft is nominally a lifetime component, it should be carefully cleaned and inspected at each pump overhaul, and where necessary and feasible, repaired to ensure it is suitable for further service. The important points in this process are 1. Check for straightness, supporting the shaft on rollers at its bearing journals (next to the journals when they are chrome plated). Avoid checking for straightness with the shaft between centers; the centers are often 130 Shafts and Shaft Sleeves damaged during assembly and dismantling. The allowable shaft runout depends on the pump's design and service and should be specified in the manufacturer's manual. As a general rule, bent shafts should be replaced rather than attempting to straighten them. The usual straightening techniques (e.g., pressing, peening, hot spotting) rely on local residual stresses. During operation, vibration tends to relieve the residual stresses, thus allowing the shaft to assume its original bent shape. Compounding this, some of the techniques leave sufficient residual stress to become the site of subsequent fatigue failure. Shafting for vertical turbine pumps is the one exception to the general "no straightening" rule. This long, slender shafting is routinely and successfully straightened by repeated pressing and subsequent stress relief. The procedure appears simple, but is best carried out by a shop experienced in doing it. 2. Inspect the shaft, paying attention to at least the following aspects: • Coupling and antifriction bearing fits for fretting and scoring • Impeller and sleeve fits for corrosion, erosion (from leakage), and scoring • Wetted regions for corrosion and erosion (from liquid impingement) • Keyways for wear, distortion, and corrosion • Threads for corrosion and damage (e.g., torn or cracked threads) • Fillets for damage (tool marks, scratches) and cracking. Inspection for cracks can be visual, using some magnification, or by the various non-destructive evaluation (NOE) methods (liquid penetrant, magnetic particle, ultrasonic). 3. Take measurements to determine the exact extent of any damage found during the inspection. Whether to replace or repair a shaft depends on the nature and extent of the damage, the availability of a new shaft, and the available repair processes. Refinishing to remove scoring, scratching, and minor corrosion is acceptable provided it does not leave the shaft undersize at a critical location. Machining down and building up by plating (chrome or nickel) or spraying (flame or plasma) are viable processes to repair local corrosion, scoring, and wear, provided they are carried out correctly. The major risks are weakening of the shaft, leading to fatigue failure and spalling of the plating or coating in areas of rubbing contact or heavy press fits. Welding is generally not a suitable repair technique. This is not to say shafts are not welded, those for large pumps sometimes are, it just recognizes that the materials used for most centrifugal pump shafts are not readily welded or require postweld heat treatment, a process that would distort the shaft. Because welding is not usually viable, cracks in a shaft are cause for its replacement. 4. If the shaft has been repaired, it should be checked again for straightness and the repaired areas carefully inspected. It is well to note the location and extent of repair and the final inspection results in the pump's maintenance file so there is some history should a problem develop later. SHAFT SLEEVES Pump shafts are usually protected from erosion, corrosion, and wear at stuffing boxes, running clearances, internal bearings, and in the waterways by renewable sleeves. The most common shaft sleeve function is that of protecting the shaft from wear at a stuffing box. Thus shaft sleeves serving other functions are given specific names to indicate their purpose. For example, a shaft sleeve used between two multistage pump impellers in conjunction with the interstage bushing to form an interstage running clearance is called an interstage or distance sleeve. In medium-size centrifugal pumps with two external bearings on opposite sides of the casing (the common double-suction and multistage varieties), the favored shaft sleeve construction uses an external shaft nut to hold the sleeve in axial position against the impeller hub. Sleeve rotation is prevented by a key, usually an extension of the impeller key (Fig. 7.13). If the axial thrust exceeds the frictional grip of the impeller on the shaft, it is transmitted through the sleeve to the external shaft nut. In larger high-head pumps, a high axial load on the sleeve is possible, and a design like that in Fig. 7.14 may be favored. This design has the commercial advantages of simplicity and low replacement Shafts and Shaft Sleeves IMPELLER KEY -=::;"-_j~ IMPELLER Fig. 7.13 SLEEvE SHAF NUT Sleeve with external lock nut and impeller key. IMPELLER SHAFT GLAND SHAFT NUT IMPELLER NUT SLEEVE SET SCREW Fig. 7.14 Sleeve with internal impeller nut, external shaft sleeve nut, and separate key. 131 132 Shafts and Shaft Sleeves IMPELLER SHAFT GLAND SLEEVE Fig. 7.15 Sleeve threaded onto shaft with no external lock nut. cost. Some manufacturers favor the sleeve shown in Fig. 7.15, in which the impeller end of the sleeve is threaded and screwed to a matching thread on the shaft. A key cannot be used with this type of sleeve and right- and left-hand threads are substituted so that the frictional grip of the packing on the sleeve will tighten it against the impeller hub. In the sleeve designs shown in Figs. 7.13 and 7.14, right-hand threads are usually used for all shaft nuts because keys prevent the sleeve from rotating. As a safety precaution, the external shaft nuts (Figs. 7.13 and 7.14) and the sleeve itself (Fig. 7.15) use set screws for a locking device. In pumps with overhung impellers, various types of sleeves are used. Often, stuffing boxes are placed close to the impeller, and the sleeve actually protects the impeller hub from wear (Fig. 7.16). As a portion of the sleeve in this design fits directly on the shaft, the impeller key can be used to drive the shaft sleeve. Part of the sleeve is clamped between the impeller and a shaft shoulder to maintain its axial position. Shaft sleeve seals Older designs relied on a metal-to-metal joint between the sleeve and impeller hub (see Fig. 7.13) to prevent leakage under the sleeve. For pumps handling water at moderate pressures with a packed box shaft seal, in which a little leakage did not matter, this simple arrangement performed well. Most modem designs are intended to be applied over a wide range of services, with a variety of shaft seals, thus have to employ a means of ensuring there is no leakage under the sleeve. A common arrangement for sleeves on between bearings rotors is shown in Fig. 7.17. Hook-type shaft sleeves (Fig. 7.18), are retained at one end and sealed with a gasket or "0" ring. Retention at one end reduces the risk of bending the shaft and allows for differential thermal expansion. In services where there is a risk of scaling or carbonizing under the sleeve if the pumped liquid gets into the fit, making sleeve removal difficult, it is better to seal the inner end of the sleeve. This is an inherent feature with hook-type sleeves on overhung rotors. When sleeves are used to protect a shaft against corrosion, it is crucial to ensure the shaft does not Shafts and Shaft Sleeves SHAFT GL Fig. 7.16 133 STUFFING BOX 0 SLEEVE IMPELLER Sleeve for pumps with overhung-impeller hubs extending into stuffing box. RUBBER "0" RING SLEEVE Fig. 7.17 SHAFT NUT Shaft sleeve seal to prevent leakage along shaft. get wet, or it could suffer crevice or concentration cell corrosion. Many users feel the added maintenance procedures necessary to ensure this are time consuming and risky, so they insist on shafts that are able to survive without protection. Material for shaft seal sleeves Most pumps are now equipped with mechanical seals. Many of these seals are assembled and mounted as a cartridge, of which the shaft sleeve is an integral part. See Chap. 9 for details of the shaft sleeves used with mechanical seals. The rest of this section, including Maintenance, deals with shaft sleeves for packed box shaft seals, and has some relevance to breakdown-type seals (Chap. 10). 134 Shafts and Shaft Sleeves Fig. 7.18 Hook-type sleeve for pump with overhung impeller. Stuffing box shaft sleeves are surrounded in the stuffing box by packing; the sleeve must be smooth so that it can tum without generating too much friction and heat. Thus the sleeve materials must be capable of taking a very fine finish, preferably a polish. Cast iron is therefore not suitable. A hard bronze is generally used for pumps handling clear water, but chrome or other stainless steels are sometimes preferred. For services subject to grit, hardened chrome or other stainless steels give good results. For more severe conditions, Stellite coated sleeves are often used and occasionally sleeves that are chromium plated at the packing area. Sleeves made entirely of a hardened chrome steel are usually the most economical and satisfactory. SHAFf SLEEVE MAINTENANCE Shaft sleeves are usually the fastest wearing pump part and the one most frequently requiring replacement. Once sleeves are worn appreciably, the packing cannot be adjusted to prevent excessive leakage. As a matter of fact, excessively worn sleeves frequently tear and score any new packing as soon as it is inserted. Thus, sleeves frequently require repair or replacement when no other pump overhaul is necessary. Sleeves of single-stage and low-head multi-stage pumps can be removed quite easily. As the long sleeves sometimes used in high-pressure multistage pumps may be harder to remove, they are often fabricated with external grooves so that a sleeve puller can be used (Fig. 7.19). In a design that uses an impeller nut between the sleeve and the impeller (see Fig. 7.14), a tight sleeve can often be loosened by backing off the impeller nut. Shaft sleeves are occasionally reconditioned by welding or metal spraying and final grinding. This procedure is not recommended for a pump on severe service, or if existing facilities for the final grinding are inadequate. It is necessary to assure both concentricity of grinding and the perpendicularity of the sleeve radial faces to the sleeve bores. Concentricity should be double checked after reassembly on the rotor. Although it may be easier to pack a pump with brand new shaft sleeves, the sleeves do not have to Shafts and Shaft Sleeves Fig. 7.19 135 Shaft sleeve puller. be replaced each time new packing is installed. The degree of permissible sleeve wear grooving depends on the type of grooving. Usually, the sleeve surface is highly polished under the packing action, and the grooving is undulated rather than composed of sharp separate grooves under each individual packing ring. Sometimes, slight grinding of these worn sleeves is permissible to permit reuse if the pump service is not too severe. The controlling factors are the availability of the necessary tools, shop facilities, and trained shop personnel. Restored sleeves must have a good, smooth surface, and the refinished parts should neither be run-out nor distorted. If the facilities are available, it may be advisable to try regrinding and reusing one set of worn sleeves to establish the practicability of this procedure. The shaft sleeve OD should not be reduced to a point at which excessive clearance at the bottom of the stuffing box permits any packing to be squeezed inside the pump when the glands are tightened. As a rule, sleeves for packed boxes should not be ground down more than 0.65 to 0.75mm (25 to 30 thousandths) on the diameter and should be given a 0.40 micron (l6-microinch) finish. Worn sleeves, however, are ordinarily replaced rather than reconditioned. Hammering to expand or crack the material will facilitate their removal, but extra care should be taken to prevent shaft damage. BIBLIOGRAPHY [7.1] A. B. Duncan and 1. F. Hood, The Application of Recent Pump Developments to the Needs of the Offshore ai/Industry, Proc. of the Conference on Pumps and Compressors for Offshore Oil and Gas, London, UK, June 29-July 1, 1976, pp. 7-24. 8 Stuffing Boxes INTRODUCTION Strictly, the term "stuffing box" is related to the packed box shaft seal, long the principal device used to seal a pump's casing where the shaft passes through it. Although the number and variety of devices used for this purpose has increased significantly as processes and the pumps used have evolved, the term stuffing box is still widely understood to mean the shaft seal, regardless of the type. For this reason, retaining the existing title of this chapter uses a familiar term to introduce a very important subject. The sealing of a pump is a crucial aspect of its design. Although it is not always obvious, even a relatively minor deterioration in sealing performance can render a pump inoperable. Sensitivity to sealing performance has increased with environmental concerns, with many services now being the subject of legislation limiting allowable leakage. Even where specific leakage limits do not exist, there are often implicit limits in general environmental legislation. All centrifugal pumps are sealed, either to keep the pumped liquid in the pump or, if the internal pressure adjacent to the seal is below atmospheric, to keep the atmosphere out of the pump. Most seals are some form of dynamic liquid or gas device where the shaft passes through the casing. All these seals leak to some degree, although in many designs, the rate is so low the leakage is not obvious. Generally, the leakage passes to atmosphere. In those services where leakage to atmosphere cannot be tolerated or a dynamic liquid seal is difficult to realize, a so-called "sealless" pump is used. Such pumps are not actually sealless; they are either arranged so seal leakage is returned to the suction vessel or they are hermetically sealed. The types of shaft sealing devices and sealing arrangements commonly used in modern centrifugal pumps are listed next. For quick reference, the chapter in this book dealing with the particular type or arrangement is also listed. Seal Type or Arrangement Packed box (soft packing) Fixed packing Hydrodynamic 136 I. J. Karassik et al., Centrifugal Pumps © Chapman & Hall 1998 Chapter 8 8 8 Stuffing Boxes Axial face (mechanical) Breakdown bushing 137 9 10 Sealless; leakage to suction 14 Sealless; hermetically sealed 24 Sealless pumps involve special construction of either the pump or its drive arrangement, and are therefore covered in the chapters dealing with the appropriate construction. SEAL SELECTION The various sealing devices and arrangements used in centrifugal pumps have different capabilities. Selecting the most appropriate type of arrangement therefore depends on an accurate specification of the conditions prevailing at the seal. All too frequently, this fundamental step is overlooked, only to become the reason for a badly behaved or inoperable seal once a pump is put into service. A comprehensive specification of sealing conditions, often referred to as seal environment, requires the following: 1. Pressure at the seal, taking account of the pump's internal arrangement, and including any range in pressure likely from operating conditions or wear at the pump's running clearances 2. Temperature at the seal, noting whether cooling or heating is being applied to the seal, and if so the estimated temperature drop or rise 3. Liquid being sealed, its properties (pH, SG, viscosity, specific heat) if not common knowledge, its condition (presence of solids or contaminants), and any unusual characteristics (e.g., tendency to crystallize, precipitate solids) 4. Surface speed at the sealing interface 5. Rotor displacements, radial and axial, likely under expected operating conditions 6. Operating mode (Le., intermittent, continuous, frequent stop/start) 7. Allowable leakage rate. Note that the only reference to size is the surface speed at the seal interface. This is intentional. Given the importance of sealing, it is better if the appropriate device or arrangement determines the space required rather than having the space available limit the seal design. To a degree, some of the more modern pump specifications now recognize this by specifying minimum space provisions for certain types of seals. For the more difficult applications, selecting the sealing device or arrangement is an iterative process, involving repeated checks of sealing feasibility against the prevailing sealing conditions or environment. Figure 8.1 illustrates the process. Unless the pump selection or basic construction are changed, the only characteristics of the sealing conditions that can be changed in this iterative process are pressure at the seal, temperature at the seal, and liquid condition. Details of how these can be changed vary, to some extent, with the seal type, and thus are addressed in the specific seal sections. Selecting the appropriate sealing device or arrangement is a complex task. In a general sense, it is possible to narrow the choices by first considering allowable leakage, then the liquid and service conditions (see Figs. 8.2 and 8.3). Once the choice of seal types is narrowed, refinement of the selection depends on the specific conditions, available seal capabilities and personal preference. Sealing technology is, of course, continually evolving, so any selection guide is only approximate. 138 Stuffing Boxes ACCURATELY DETERMINE SEAL ENVIRONMENT IS SEALING FEASIBLE? NO CHANGE SEAL ENVIRONMENT FINAL SEAL SELECTION Fig. 8.1 Seal selection-fundamental. Moderate-Soft Packing (packed box) Allowable Leakage Minimum - [ None i Fixed Packing Axial Face (mechanical) Hydrodynamic* (1) Breakdown (to pump suction) Axial Face (double) (2) Hermetically Sealed (isolated from atmosphere) (1) *Zero Leakage when running (2) Barrier Fluid Leakage to atmosphere Fig. 8.2 Seal type versus allowable leakage. Stuffing Boxes 139 Water at Low Temp. Intermittent Operation - - Soft Packing Water, Continuous Operation -{ Axial Face Soft Packing Hydrocarbon (1) - { Axial Face Continuous Operation Hermetically Sealed Liquid and Service Liquid Difficult to Seal - { Breakdown Suction at Atmospheric Pressure Hydrodynamic Dry Running Possible Liquid Difficult to Seal Toxic, Isolation from - - Hermetically Sealed Atmosphere Required Hydrodynamic High Solids Content { Soft Packing Fixed Packing Axial Face (1) Seal Selection depends on allowable leakage Fig. 8.3 Seal type for liquid and service conditions. PACKED BOX SEAL In its elementary fonn, a packed box shaft seal consists of a number of rings of soft, compressible packing in a cylindrical recess, generally known as a "stuffing box," around the pump shaft sleeve (Figs. 8.4 and 8.5). The packing is compressed axially by an adjustable gland to produce a close radial clearance with the shaft, thereby minimizing leakage through the seal. To prevent extrusion of the packing into the pump, it is necessary to have a close clearance at the bottom of the stuffing box. This clearance can be an integral part of the casing (Fig. 7.16), a separate bottom ring (Fig. 8.5), or a separate throat bushing (Fig. 8.4). The last arrangement is used as a manufacturing aid (it allows a larger boring bar) or when it is considered necessary to be able to restore the close clearance (a legacy from pumps whose shafts were too slender). Separate throat bushings are generally one piece and when the casing is axially split are located with a tongue and groove fit. To function correctly, a packed box seal must leak. The purpose of the leakage is twofold: First, it lowers the friction between the shaft or sleeve and the packing, thus minimizing the heat generated. Second, it helps remove the heat that is generated. See "Stuffing box maintenance" for instructions and cautionary remarks on packing adjustment. 140 Stuffing Boxes SLEEVE STUFFING 80X THROAT BUSHING SEAL CAGE GLAND Fig. 8.4 Conventional stuffing box with throat bushing. SEALING LIQUID BOTTOMING RING Fig. 8.5 PACKING Conventional stuffing box with bottoming ring. Stuffing Boxes o 141 m/sec 10 20 30 100 1000 10 iu III i; 100 CD en II) II) en ...u 0 a.. « ~ :::l II) II) 10 ~ a.. 0.1 01234567 Relative Velocity @ Seal-1000 FtiMin Fig. 8.6 Packed box seal capabilities (after Durametallic). Figure 8.6 shows the general upper limit of packed box seal capability in terms of pressure versus surface speed at the seal interface. It is possible to exceed these limits, but unless the design, manufacture, installation, and operation of the seal are all carried out very carefully, the seal is likely to be a continual source of operating difficulty. SEAL CAGES Most pumps are designed to have the region adjacent to their shaft seal at or very close to suction pressure. When a pump so designed operates with negative suction head, the inner end of the stuffing box is under vacuum, and air tends to leak into the pump. For this type of service, packing is usually separated into two sections by a lantern ring or seal cage (Fig. 8.4). Water or some other sealing fluid is introduced under pressure into the space, causing flow of sealing fluid in both axial directions. This construction is useful for pumps handling flammable or chemically active and dangerous liquids since it prevents outflow of the pumped liquid. To ensure adequate lubrication of the packing, it is also advisable to use a seal cage when the pressure at the seal is 0.3 bar gauge (5 psig) or lower. Seal cages are usually axially split for ease of installation and removal (Fig. 8.7). Some installations involve variable suction conditions, the pump operating part time with head on suction and part time with suction lift. When the operating pressure inside the pump exceeds the atmospheric pressure, the liquid seal cage becomes inoperative (except for lubrication). However, it is maintained in service so that when the pump is primed at starting, all air can be excluded. 142 Stuffing Boxes Fig. 8.7 Lantern ring or seal cage. Sealing liquid arrangements When a pump handles clean, cool water, sealing liquid is usually taken from the pump discharge, or, in multistage pumps, from an intermediate stage. An independent supply of sealing water should be provided if any of the following conditions exist: 1. 2. 3. 4. 5. 6. A suction lift in excess of 4.5 m (15 ft) A discharge pressure under 0.7 bar or 7.0 m (10 psig or 23-ft) Hot water (over 120°C [250°F]) being handled without adequate cooling (except for boiler feed pumps, in which seal cages are not used) Muddy, sandy, or gritty water being handled For all hotwell pumps The liquid being handled is other than water-such as acid, juice, molasses, or sticky liquids-without special provision in the stuffing box design for the nature of the liquid. When sealing water is taken from the pump discharge, an external connection may be made through small diameter piping (Fig. 8.8) or internal passages. In some pumps, these connections are arranged so that a sealing liquid can be introduced into the packing space through an internal drilled passage either from the pump casing or an external source (Fig. 8.9). When the pumped liquid is used for sealing, the external connection is plugged. If sealing liquid from an external source is required, it is connected at the external pipe tap and the internal connection is plugged. Because the leakage flow from a correctly adjusted packed box is relatively low, seals with sealing liquid supplied from the pump discharge (Figs. 8.8 and 8.9) are normally subject to a pressure close to pump discharge. For pressures up to 1.4-1.7 bar (20-25 psig) this is quite acceptable. At higher pressures, it is advisable to use only external piping (Fig. 8.8) and to carry out most the adjustment of seal leakage using the needle valve provided. Not taking this precaution generally results in operating difficulty with the seal, the difficulty increasing with pump discharge pressure. Stuffing Boxes Fig. 8.8 Fig. 8.9 Piping connections from the pump discharge. Arrangements for sealing liquid supply in an end-suction pump. A. Internal seal. B. External seal. 143 144 Stuffing Boxes Radial Clearance P1 Throat Bushing Fig. 8.10 Packed box arrangment with throat bushing and seal cage for pump handling gritty or dirty liquid. Abrasive solids in the pumped liquid will cause accelerated seal wear (packing rings and sleeve) if the liquid passes through the seal. To prevent this, pumps handling abrasive laden liquids and sealed with a packed box often have a throat bushing and seal cage at the bottom of the stuffing box (Fig. S.10). Clean liquid, compatible with the pumped liquid, is brought from an external source and injected into the seal. The injection flow required is that to produce a liquid velocity through the throat bushing clearance of 3-4.6 m/s (10-15 ftls). Experience shows velocities on this order are necessary to ensure there is minimal mixing of pumped liquid and injection flow within the seal. The drawback of an injected throat bushing is dilution of the pumped liquid, often a concern in mineral processing and petroleum refining. When dilution is a concern, the choice is a seal cage located farther into the packing set (Fig. S.4) and a higher rate of seal wear, or a different type of shaft seal (consult Fig. S.3). In some services, pumps handle liquids containing low concentrations of fine solids, not sufficient to erode the casing or impeller but enough to shorten sleeve and packing life if used as sealing liquid. Fine filters can be used to remove the solids. The arrangement is complex, however, because filters tend to plug, and therefore have to be monitored for pressure drop and arranged in duplex if on line cleaning is required. This difficulty can be overcome in many instances by using cyclone separator to remove the fine solids. Figure S.11 shows the flow diagram for such an arrangement. See Chapter 9 for a detailed description of cyclone separators and the precautions necessary in their installation and use. If clean, cool water is not available (as with drainage and irrigation pumps) or cannot be connected directly to the pump (as with sewage pumps), grease or oil seals are often used. Most pumps for sewage service have a single stuffing box subject to discharge pressure and are located below the liquid in the suction reservoir. It is therefore not necessary to seal these pumps against air leakage, but forcing grease into the sealing space and packing helps to exclude grit. An automatic oil sealer that exerts discharge pressure in a cylinder on one side of a plunger, with oil or light grease on the other side, is available for sewage service. The oil or grease line is connected to the seal connection, which is near discharge pressure. As the inner end of the stuffing box would be at about SO percent discharge pressure, there is a slow flow of grease or oil into the pump when the unit is in operation. No flow takes place when the pump is out of service. Some pumps handle water in which there are small, even microscopic, solids. Using water of this kind as a sealing liquid introduces the solids into the leakage path, shortening the life of the packing and sleeves. It is sometimes possible to remove these solids by installing small pressure filters in the sealing water piping from the volute to the stuffing box. Stuffing Boxes 145 Clean liquid to seal cage connection Dirty liquid to pump suction Fig. 8.11 Cyclone separator for packed box seal. WATER-COOLED STUFFING BOXES High temperatures or pressures or both complicate the operation of packed box seals by raising the temperature of the leakage. Should the temperature rise to the point that the leakage flashes within the packing set as the pressure drops (Fig. 8.12; from Ref. [8.1]), damage to the packing and the sleeve will quickly render the seal inoperable. Direct injection with cool liquid is the most efficient means of controlling seal temperature, but is not always acceptable for reasons of pumped liquid contamination (e.g., boiler feed) or the availability of liquid at the correct condition. Therefore usual practice is to provide pumps for the more difficult services with jacketed, water-cooled stuffing boxes. The cooling water removes heat from the liquid leaking through the stuffing box and heat generated by friction in the box, thus improving packing service conditions. In some special cases, oil or gasoline may be used in the cooling jackets instead of water. Two water-cooled stuffing box designs are available. The first (Fig. 8.13) provides cored passages in the casing casting. These passages, which surround the stuffing box, are arranged with in-and-out connections. The second type uses a separate cooling chamber combined with the stuffing box proper, the whole assembly being inserted into and bolted to the pump casing (Fig. 8.14). The choice between the two is based on manufacturing preferences. Pressure and temperature conditions With a more thorough understanding of the interrelation of stuffing box pressures, rubbing speeds, and leakage temperatures, improved water-cooled stuffing boxes have been built for temperatures up to 200°C (400°F), and stuffing box pressures up to 35 bar (500 psig), without pressure-reducing breakdowns or labyrinths. This type of stuffing box is illustrated in Fig. 8.15. For greatest cooling efficiency, the temperature difference between the cooling liquid and the leakage through the box must be kept to a maximum at all points. In this design (Fig. 8.15), the cooling water is introduced nearer to the outside of the stuffing box. Before moving axially toward the interior of the pump, the cooling water is circulated completely around that portion of the stuffing box which surrounds the packing. A cored passage is 146 Stuffing Boxes Outer Ih ell cooliq - ---- Frictional bell Dot removed - - Frictional beal removed Precoolin. sec:1ion Fig. 8.12 Sb.ftleal Pressure and temperature profile through packed box. (Courtesy Sulzer) provided from this annular chamber toward the interior of the pump. The cooling water then circulates in a secondary annular chamber extending inside the pump beyond the packing. This allows precooling of stuffing box leakage before it reaches the packing. The cooling water then escapes through a second cored passage to the cooling chamber exit. In this design, the coldest cooling water is adjacent to the coldest leakage. Having picked up some heat, the cooling water flows into the pump at a higher temperature and cools a higher temperature leakage. One such unit has operated continuously for over a year without renewing the packing, under stuffing box operating conditions of 22 bar (325 psig) and 200°C (400 0 P). The shaft diameter at the stuffing box was 100 mm (4 in), and the operating speed 3,600 rpm. Stuffing box pressure and temperature limitations vary with the pump type, because it is generally not economical to use expensive stuffing box construction for infrequent high-temperature or high- Stuffing Boxes QUENCHING UOIJID STUFFING BOX BUSHING Fig. 8.13 COOLING WATER INLET Jacketed stuffing box with cored cooling passage cast in casing. SECTION A-A , LE"MOF' TO COO"' ... W"TlEIt OUTLlT ! LOWE~ ~1t[SSUIt[ t SlUFFING C~I'" Fig. 8.14 W"TlEIt CMAMIER Separate jacketed stuffing box assembly with pressure-reducing stuffing box bushing. 147 148 Stuffing Boxes COOLING WATER OUTLET CORED PASSAGE INTO PRECOOLING ANNULAR SPACE PRECOOLING OF LEAKAGE "f-E~ - --- ---~I- ~ INTERIOR ANNULAR COOLING AREA AROUND PACKING Fig. 8.1S Special water-cooled stuffing box for high pressures and high temperatures. pressure applications. Therefore, whenever the manufacturer's stuffing box limitations for a given pump are exceeded, the only solution is the application of pressure-reducing devices ahead of the stuffing box. PRESSURE·REDUCING DEVICES Essentially, pressure-reducing devices consist of a bushing or meshing labyrinth, ending in a relief chamber located between the pump interior and the stuffing box. The relief chamber is connected to some suitable low-pressure point in the installation, and the leakage past the pressure-reducing device is returned to this point. The only drawback to application of these devices is the necessity of bleeding a part of the effective pump capacity back to a lower pressure level, and the resultant reduction in installation efficiency. If the pumped liquid must be salvaged, as with treated feed-water, it is returned back into the pumping cycle. If the liquid can be wasted, the relief chamber can be connected to a drain. There are many different pressure reducing device designs. Figure 8.14 illustrates a design for limited pressures. A short, serrated stuffing box bushing is inserted at the bottom of the stuffing box, followed by a relief chamber. The leakage past the serrated bushing is bled off to a low-pressure point. With relatively high-pressure units, intermeshing labyrinths may be located following the balancing device and ahead of the stuffing box (Fig. 8.16). Piping from the chamber following pressure-reducing Stuffing Boxes 149 BALANCING DEVICE LEAKOFF TO SUCTION LAST IMPEL Fig. 8.16 LEAKOFF TO LOWER PRESSURE Labyrinth-type pressure reducing bushing on the discharge side of a pump equipped with a balancing device. devices should be amply sized so that as wear increases leakage, piping friction will not increase stuffing box pressure. Mining and mineral processing occasionally require slurry pumps arranged in series to develop heads beyond the capability of a single pump. When the pumps are next to each other, one of the major problems is sealing the latter pumps against leakage of high pressure slurry. One successful approach is to provide a clear liquid breakdown bushing (Fig. 8.17) ahead of a conventional packed box. Highpressure clear liquid, generally water, is provided by a small reciprocating pump. 150 Stuffing Boxes SEAL WATER Pi I I INLET Pi + SEAL WATER OUTLET P21.LOW PRESSURE) ILAND RADIAL CLEARANCE PRESSURE BREAKDOWN IUSHING Fig. 8.17 Breakdown bushing injected with clear liquid for pumps handling gritty or dirty liquid. STUFFING BOX PACKING Basically, stuffing box packing is a pressure breakdown device. The packing must be somewhat plastic so that it can be adjusted for proper operation. It must also absorb energy without failing or damaging the rotating shaft or shaft sleeve. In a breakdown of this nature, friction energy is liberated. This generates heat that must be dissipated in the fluid leaking past the breakdown or by means of cooling water jacketing or both. There are numerous stuffing box packing materials, each adapted to some particular class of service. Until recently asbestos, lubricated with graphite or inert oil, was one of the principal materials. Now that asbestos is a proven carcinogen, it is no longer used to any significant extent as a packing material. Although there is no one alternative material possessed of all the properties of asbestos, research has produced materials able to outperform asbestos on specific services. These developments have led to the simple packed box being again considered a viable shaft seal for modern pumps. Some of the principal packing materials now in use are described in the following summary and their typical properties set out in Table 8.1. Note that the pressure and PV limitations in Table 8.1 are below those shown in Figure 8.6. The lower values reflect a conservative approach by the packing manufacturers, the likely intention being to avoid those applications where success is so dependent upon the pump operator's skill. 1. Plastic-a mixture of short strand synthetic fiber and lubricant, the latter usually graphite or mica and oil or grease. Occasionally metal particles are added to act as a lubricant reservoir. Used alone, plastic packing produces a low-leakage seal for moderate pressures and high temperatures. At higher pressures, the allowable temperature decreases and back up rings of braided or metallic packing are recommended to avoid extrusion. Chemical resistance is limited. 2. Synthetic fibers-a wide variety of materials has been developed in the pursuit of non-asbestos packings. Those currently in general use are Teflon®, aramid, and graphite. Teflon (PTFE) is an attractive material because it is inert in most pumped liquids. Developing a suitable packing, however, has been hampered by the material's low thermal conductivity and high coefficient of thermal expansion. PTFE yam treated with colloidal PTFE as a lubricant and a silicon compound for improved heat dissipation is a viable packing for high pressures, moderate to high temperatures and moderate surface speeds. Flitney [8.2] reports expanded PTFE with 50 percent encapsulated graphite further improves thermal conductivity and allows surface speeds on the order of 23 mls (4,500 ft/min). Aramid fiber is serviceable to moderate temperatures but has less chemical resistance than PTFE. The virtue of aramid fiber is high strength and abrasion resistance, making it a packing suitable for pumps handling slurries or solids laden liquids. The packing itself tends to be Stuffing Boxes Table 8.1 151 Properties of Common Packing Materials Material Plastic PTFE yarn Aramid fiber Graphite filament Graphite foil Lead foil Aluminum or copper foil Pressure bar (psig) PV (Note 1) Temperature °C (OF) pH 7.0(100) 17.5(250) 17.5(250) 10.5(150) 17.5(250) 17.5(250) 17.5(250) 17.5(250) 70(190xI0 3) 165(470) 165(470) 116(380) 165(470) 165(470) 165(470) 165(470) 315(600) 65(150) 260(500) 65(150) 400(750) 400(750) 230(450) 400(750) 4.8 4.8 0-14 3-10 0-14 0-14 2-10 3-10 Notes 2 3 Notes I. PV factor based on (m/s) x (bar) left/min) x (psi)]. 2. Maximum surface speed 9.1 m/s (1,800 ft/min). 3. Maximum surface speed 6.6 m/s (1,900 ft/min); performance lowest of published values. 4. Values of pressure, PV, and temperature are maximum. abrasive, and so is limited to moderate surface speeds and must run on a very hard shaft sleeve (Brinell hardness 650 minimum, where BHN is the Brinell hardness number) shaft sleeve. Graphite or carbon filament packings have wide chemical resistance, high temperature capability, and high pressure/speed capacity. The material is expensive, however, and is therefore normally used only for severe chemical or high-temperature service. All the synthetic fiber packings are interbraid or interlace construction. This affords high flexibility and enables the packing to remain intact even when individual strands wear through at the working surface. 3. 4. Graphite foil-known generically as "exfoliated graphite" or more commonly as Graphol ®, graphite foil realizes high thermal conductivity, which allows for a seal with very low leakage rates, nominally 50 percent of that for asbestos packing. Chemical resistance and service capabilities are the same as for graphite filament, the only notable difference being better thermal conductivity, therefore the capability of running with slightly less leakage. Metallic-composed of flexible metallic strands or foil with graphite or oil lubricant impregnation and with either a synthetic or plastic core. The impregnation makes this packing self-lubricating for its start-up period. The foils are made of babbitt or lead, copper, and aluminum. Babbitt or lead is used on water and oil service for low and medium temperatures (up to 230°C or 450°F) and medium to high pressures. Copper is used for medium to high temperatures and pressures with water and low-sulfur-content oils. Aluminum is used mainly on oil service for medium to high temperatures and pressures. Babbitt or lead packing is not suitable for operation on brass or bronze shaft sleeves. Cooper and aluminum packings require a shaft sleeve whose Brinell hardness is at least 500. Packing is supplied either in continuous coils of square cross section or in prefonned die-molded rings. Plastic packing is sometimes supplied in bulk or in cartridges for injection by gun. Graphite foil packing is produced as ribbon, but for pump packings, it is usually supplied as split die-fonned rings. When coil-type packing (Figs. 8.18 and 8.19) is used, it is cut in lengths that make up individual rings. The ends are cut with a diagonal, or scarf joint, and with a slight clearance to provide for expansion and avoid buckling. The rings have a tendency to swell from the liquid action and the rise in temperature. The scarf joint allows the ends to slide and laterally absorb expansion. It is preferable, where possible, to use die-molded packing rings (Fig. 8.20), which are available to 152 Stuffing Boxes Fig. 8.18 Synthetic fiber packing in continuous coil form. (Courtesy John Crane Co.) Fig. 8.19 Metallic packing in spiral form. (Courtesy John Crane Co.) exact size and in sets. A molded ring insures an exact fit to the shaft or shaft sleeve and to the stuffing box bore and also establishes equal packing density throughout the stuffing box. Hard packing such as metallic is not as resilient as fiber or plastic and is, therefore, more sensitive to changes in operating conditions. One common means of improving seal performance under these conditions is to use a combination of hard and soft packing, for example metallic and fiber or plastic (Fig. 8.21). Combination packing sets always have the end rings of hard material to minimize extrusion. Such sets are available in standard die-formed ring combinations from most packing manufacturers. The pressure drop across a packed box seal is not linear. Figure 8.12 shows a five-ring arrangement in which more than 50 percent of the pressure drop occurs across the outer ring, while the inner ring Stuffing Boxes Fig. 8.20 Metallic packing in ring fonn. (Courtesy John Crane Co.) Fig. 8.21 Combination of hard and soft packing. (Courtesy John Crane Co.) 153 154 Stuffing Boxes has essentially zero pressure drop. From the meager data available it seems this characteristic increases with the number of rings, so there is little to be gained from using more than four or five rings of packing for even the most severe services. In some instances, low pressure, for example, extra rings can cause difficulties by limiting leakage through the packing. Packing size typically ranges from 10 to 30 percent of the shaft or sleeve diameter. The minimum practicable size is generally considered 6 mm (0.25 in.) square. Some industry standards, however, dictate a larger minimum, API-610 [3.1] for instance, requiring 10 mm (0.38 in.) square minimum in refinery pumps. Packed box seal performance is influenced significantly by the shaft or sleeve surface, both hardness and finish, and any cyclic radial motion of the surface during pump operation. Considering sealing surface hardness first, good practice based on past experience suggests the following: For sealed pressures below 2.5 bar (35 psig) conventional packing running on a soft sleeve (bronze or equal hardness) will give good service. Raising the pressure to 5.2 bar (75 psig) requires a harder sleeve, the usual material being 13 chrome steel (Brinell hardness 300-500 depending on grade and heat treatment). Conventional packing will give reasonable service but the best results will be realized with metal foil and plastic or graphite. At pressures above 5.2 bar (75 psig), the packing should be either metal foil and plastic or graphite, and the sleeve fully hardened 13 chrome (Brinell hardness 450 minimum) or hard coated. Usual hard coating materials are ColmonoyTM 6 or ceramic, either chrome oxide or tungsten carbide. Ceramic is harder than ColmonoyTM but has lower resistance to thermal shock. In services involving abrasives, both the nature of the liquid and the type of packing (aramid fiber or similar) dictate ceramic coated sleeves. In all cases the sealing surface should be finished to Ra 0.8~m (32 ~in) or better. Shaft or sleeve runout and vibration produce cyclic radial motion of the sealing surface. The packing is not able to follow this motion so it runs with a larger clearance, hence more leakage. Flitney [8.2] reports a linear increase in leakage with sealing surface runout. Good practice requires that sealing surface runout not exceed 0.075 mm (0.003 in.) total indicated runout (TIR). Alignment of the shaft or sleeve within the stuffing box is not as critical as runout and vibration because the packing is flexible enough to accommodate small static eccentricities on the order of 0.25 mm (0.010 in). Care is necessary, however, in high-pressure service where the risk of extrusion is higher. STUFFING BOX GLANDS Stuffing box glands may assume several forms, but basically they can be classified into two groups: 1. 2. Solid glands (Fig. 8.22). Split glands (Fig. 8.23). Split glands are made in halves so that they may be removed from the shaft without dismantling the pump, thus providing more working space when the stuffing boxes are being repacked. Split glands are desirable for pumps that have to be repacked frequently, especially if the space between the box and the bearing is restricted. The two halves are generally held together by bolts (Fig. 8.23), although other methods are also used. Split glands are generally a construction refinement rather than a necessity, and they are rarely used in smaller pumps. They are commonly furnished for large single-stage pumps, for some multistage pumps, and for refinery pumps. Another common refinement is the use of swing bolts in stuffing box glands. Such bolts may be swung to the side, out of the way, when the stuffing box is being repacked. Stuffing box leakage into the atmosphere might, in some services, seriously inconvenience or even endanger the operating personnel-for example, when such liquids as hydrocarbons are being pumped Stuffing Boxes Fig. 8.22 ISS Solid stuffing box gland . • Fig. 8.23 Split stuffing box gland. at vaporizing temperatures or temperatures above their flash point. As this leakage cannot always be cooled sufficiently by a water-cooled stuffing box, smothering glands are used (see Fig. 8.13). Provision is made in the gland itself to introduce a liquid-either water or another hydrocarbon at low temperaturethat mixes intimately with the leakage, lowering its temperature, or, if the liquid is volatile, absorbing it. Stuffing box glands are usually made of bronze, although cast iron or steel may be used for all ironfitted pumps. Iron or steel glands are generally bushed with a nonsparking material like bronze in refinery 156 Stuffing Boxes service to prevent the ignition of flammable vapors by the glands sparking against a ferrous metal shaft or sleeve. STUFFING BOX MAINTENANCE Stuffing box maintenance primarily consists of packing replacement. Although this sounds simple, it must be done correctly, or pump operation will not be satisfactory. The following procedure should be followed in repacking a stuffing box: 1. 2. Never try to add one or two rings to the old packing. This is false economy. Remove the old packing completely, using a packing puller, if available, and thoroughly clean the box. Inspect the sleeve to make sure it is in acceptable condition. Putting new packing in a box against a rough or badly worn sleeve will not give satisfactory service. . Be sure that the new packing is a proper type for the liquid, operating pressure, and temperature. Unless the packing comes preformed in sets, make sure that each ring is cut square on a mandrel of correct size. 3. Insert each ring of packing separately, pushing it squarely into the box and firmly seating it, using split pusher rings of proper length, fitting the box nicely. Successive rings of packing should be rotated so the joints are 120 or 180 deg apart. 4. When a seal cage is used, make sure to install it between the proper two packing rings so it will correctly handle the sealing liquid supply when the box is fully packed and adjusted. 5. After all the required packing rings have been inserted, install the gland and firmly tighten the gland nuts. Make sure that the gland enters the stuffing box squarely and without cocking, so the full periphery of the packing is under uniform pressure. 6. After the first tightening of the gland, back off the nuts until they are only finger tight. Start the pump with the gland loose, so that there will be excessive initial leakage. Tighten up slightly and evenly on the gland nuts, at 15 or 20 min intervals, so the leakage is reduced to normal after several hours. Normal seal leakage is not easily defined. In principle, the leakage necessary for a particular seal depends on the amount of heat generated and how that can be dissipated. The heat generated is, in tum, a function of sealed pressure, surface speed at the seal, packing type, and sleeve condition. Data on the relative influence of these factors are meager and often conflicting. As a practical guide, Table 8.2 shows the range of usual leakage rates for various sealed pressures. These data are for conventional packing and typical conditions. With carbon or graphite packing (self-lubricating) and well-finished sleeves running with minimum vibration, lower leakage rates are attainable. Take care when adjusting the packing. Unless enough liquid leaks through the seal to remove the heat generated, the packing will be burned and the sleeve scored. (On pumps with quenching glands, stop the supply of quenching water at intervals, and observe actual leakage through the box, otherwise, visual inspection cannot distinguish between leakage past the packing and the quenching liquid supply.) Repacking and adjusting stuffing boxes should only be done by experienced personnel. Others assigned Table 8.2 Packing Leakage Rates Sealed pressure bar (psig) 4.0 (60) 4.0 to 7.0 (60 to 100) 7.0 to 17 (100 to 250) Leakage rate liter/hr (gal/hr) 0.2-6.8 (0.06-1.8) 0.8-11 (0.20-3.0) 1.9-28 (0.50-7.4) Stuffing Boxes 157 this work should be cautioned against putting too much pressure on the gland. It should be made clear that excessive leakage is not as hannful as too little. Packing removed from a stuffing box being repacked, should be examined in order to obtain as much information as possible on the cause of packing wear. Often, correctable operating conditions or inadequate packing procedures are revealed by this examination. Some of the more frequently encountered symptoms are the following: Excessive wear on rings nearest to the gland, while the bottom rings remain in good condition, is caused by overtightening of the packing in one adjustment or by not inserting rings one at a time, and pushing each home before inserting the following ring. 2. Charring or glazing of the inner circumference of the rings is caused by excessive heating, insufficient lubrication, or inadequate packing material for the pressure and temperature conditions. 3. Wear on the outer circumference of the rings occurs when they rotate within the stuffing box. 4. Heavy packing ring wear on one selective portion of the inner circumference may be caused by excessively worn bearings or eccentric rotor operation. 5. If some rings are cut too short or shrink excessively, the adjacent rings will bulge and be extruded into the open space. 1. FIXED PACKING Conventional packed box seals using soft packing suffer from two distinct disadvantages. First, the packing requires periodic adjustment to maintain acceptable leakage rates. Second, in pumps handling abrasive laden liquids, the flush water necessary to realize reasonable seal life is a source of pumped liquid dilution. Quite often, pumped liquid dilution is the greater of the two disadvantages, particularly as energy costs increase. Responding to both these problems, several manufacturers have developed fixed packing type seals; arrangements designed for zero adjustment and minimum pumped liquid dilution. Three recent developments in the mining industry, reported by Pearse [8.4], are typical of the arrangements used: 1. Hydrostatic gland-two feather-edged rubber seals are arranged with a seal cage between them (Fig. 8.24). Water at a pressure above that inside the pump at the seal is injected into the region between the lip seals. For typical slurry pumps, the injection pressure is approximately 75 percent of pump discharge pressure. Leakage into the pump is reportedly on the order of 0.2 m3/hr (1 gpm). Water @ 75% Pump Discharge ~ Rubber Seal Ring J...../ = 0.2 m3 /hr (1 gpm) into pump (Wilkinson Rubber Linatex) Fig. 8.24 Hydrostatic gland (diagrammatic). 158 Stuffing Boxes Actual Seal Pressure Reducing Element Sand Barrier Fig. 8.25 IHe Liquidyne seal. (Courtesy [HC Holland) 2. "Simmering" seal-using the same principle as the hydrostatic gland, the Simmering seal employs two opposed lip seals and has oil injected between them to effect a seal. 3. "Liquidyne" seal:-three sealing elements are retained in a four-piece bolted housing (Fig. 8.25). Flushing water at a pressure above that inside the pump is applied between the inner and intermediate sealing elements (sand barrier and pressure reducing elements). A small part of this flush flow passes into the pump, thus excluding the pumped liquid from the seal. The balance of the flush liquid flows through the pressurereducing element, then to an atmospheric drain. The outer seal serves only to contain leakage passing to the drain. All three of these designs rely on resilient radial sealing elements and a flush or injection liquid source at a pressure above that inside the pump. The first two differ from the third in that leakage from the pressure reducing element passes directly to atmosphere instead of being collected and passed to a drain. HYDRODYNAMIC SEALS Although the construction and operation of hydrodynamic seals is quite different from packing, their frequent use in place of packing for difficult services and their reliance on some form of packing when the pump is shut down are deemed sufficient reasons to justify their inclusion in this chapter. Stuffing Boxes 159 A hydrodynamic seal is a device that produces, by hydrodynamic action, a pressure below atmosphere at the shaft opening. Since the pressure inside the pump is below atmosphere, the seal has to be arranged to maintain a stable liquid/air interface while the pump is operating. Because the pump configuration suits it, hydrodynamic seals are generally applied to single suction, overhung impellers. Figure 8.26 shows an arrangement employing a "sealing impeller," or "expeller" as it more commonly known. Operation of the seal can be determined from the pressure profiles through the pump (see Fig. 8.27). At the impeller periphery there exists a static pressure rise (less than the total head-see Chap. 4) across the impeller. Pump-out vanes on the back shroud of the impeller (see Chap. 4) produce a pressure drop down the back shroud (PPOy) to yield a lower pressure Ph at the impeller hub. The plain side of the expeller causes a small increase in pressure P L resulting in a slightly higher pressure P, at the expeller periphery. Provided the pump is operating within the seal's capability, the vaned side of the expeller lowers the static pressure to atmosphere part way down the vanes at rio Unless unusual proportions are resorted to (e.g., expeller or pump-out vanes at larger diameter than the impeller vanes), expeller-sealed pumps are limited to suction pressures on the order of 15 percent of the pump's differential pressure. Some early hydrodynamic seals were developed for high-speed pumps, there being at the time no other suitable sealing device. More recently, most applications are for pumps handling abrasive laden Fig. 8.26 Expeller seal. 160 Stuffing Boxes - constant XT.D.H. I Ppov- ..... , 1- r Pg ! 't' f 'i --1-_ SHAFT CENTERLINE EXPELLER Fig. 8.27 IMPELLER Pressure profiles in pump with expeller seal. or other difficult to seal liquids. The expeller has few parts and no close running clearances, and is therefore well suited to such applications. Beyond their tolerance of solids laden and other difficult liquids, hydrodynamic seals are often justified on the basis of not having to provide a flush water system (difficult and expensive for a remote, arid site), and the elimination of pumped liquid dilution. Hydrodynamic seals have zero leakage while the pump is running. But when the pump is shut down some form of auxiliary seal is necessary to prevent leakage if the suction pressure is above atmosphere. Most designs use some form of packed seal, either soft packing grease lubricated or fixed packing such as a lip seal. More sophisticated arrangements include pneumatic bushings (inflated once the pump is shutdown) and centrifugally activated closures. Being a pumping device, hydrodynamic seals absorb power, therefore their inclusion in a pump is not a free means of effecting a seal. In most cases, however, the cost of additional power for the seal probably equals that of a flush water system, so it is not significant in the total cost of the plant, and may even be a saving in some cases. The one problem the seal power can cause is vaporization of volatile liquids, In such cases, it is necessary to ensure a small circulation of liquid from the seal back to the pump proper, so the heat generated is dissipated. BIBLIOGRAPHY [8.1] Schoffler, W. & Florjancic, D., Packed Stuffing Boxes in Pumps Circulating Hot Water, Sulzer Technical Review, 3/1981, pp 99-103. [8.2] Flitney, R. K., Soft Packings, Tribology International, vol. 19, #4, August '86, pp 181-183. [8.3] Pearse, G., Pumps for the Mineral Industry, Mining Magazine, V152, #4, April '85, pp 299, 301, 303, 305, 307-309,311,313. 9 Mechanical Seals - ~---~~------ Mechanical seals are widely considered superior to the other forms of shaft seals employed in centrifugal pumps, particularly packed stuffing boxes and breakdown-type seals. This is generally correct, but there are applications for which mechanical seals represent "too much technology," and services for which they are not suitable (see the introduction to Chap. 8). The general superiority of mechanical seals over packed boxes and breakdown seals derives from the orientation of their sealing elements. Before proceeding with a detailed treatment of mechanical seals themselves, it is worthwhile to develop the details of this fundamental difference. Packed boxes and breakdown seals are classified as radial seals, those that act on the circumference of the shaft (Fig. 9.1[aD. As such, these seals must be designed to accommodate variations in shaft dimensions and radial position. Such variations result from manufacturing tolerances or movements within the pump produced by operating loads or thermal expansion or both. Whether this accommodation is provided by a resilient material, packing, or a specific clearance between shaft and seal, the seal inherently has a certain amount of leakage. Compounding that, designs employing packing are limited in surface speed, sealed pressure, and the nature of the sealed liquid. Mechanical seals, sometimes referred to as face seals, are arranged so the seal acts against an axial face (Fig. 9.1 [b D. With the sealing interface now normal to the shaft axis, it no longer has to accommodate variations in radial dimensions and shaft position. Freed of this need, the sealing interface can now run with a very close clearance and its design (proportions and materials) has only to consider wear resistance. The advantages offered by mechanical seals are: 1. 2. Greater sealing capability (defined as pressure containment with tolerable leakage and service life). With appropriate face geometry and materials, acceptable leakage and seal life can be realized at surface speeds on the order of SOmis (10,000 ft/min) and sealed pressures on the order of 140 bar (2,000 psi). Lower leakage. Because the sealing interface can run with a very close clearance, the leakage from a mechanical seal is significantly less than from an equivalent packed box seal. In most cases, the leakage is so little it evaporates on coming into contact with the atmosphere and is therefore not obvious to an observer. It is important, however, to recognize that there is some leakage from all mechanical seals, a fact of consequence to plant safety and the more stringent pollution limitations coming out of environmental considerations. 161 I. J. Karassik et al., Centrifugal Pumps © Chapman & Hall 1998 162 Mechanical Seals Pa ---'----+- a) Radial seal acts on cylindrical surface to produce pressure drop in axial direction. Fig. 9.1 3. 4. b) Axial seal acts on plane surface to produce pressure drop in radial direction. Fundamental seal arrangements for rotating shafts. Tolerance of liquids. Many of the liquids handled by pumps in modern refining, petrochemical, and chemical processing have little or no lubricity and act as solvents to the lubricants used in most packings. To seal these liquids with a packed box requires the introduction of a compatible seal oil into the packing, a requirement that complicates the installation and causes dilution or contamination of the pumped liquid. No adjustment. Mechanical seals are self-compensating for wear, therefore they do not have to be adjusted over the course of their service life. In a large, complex plant this confers a substantial advantage to overall pump maintenance costs. The advantages of mechanical seals have led to their playing a fundamental role in the evolution and development of processes employed by mankind to raise the standard of living. It is true to say that many of the processes now taken for granted would not have been possible without mechanical seals for the pumps used in them. Despite this contribution to modem technology, the mechanical seal is not a new device. Mayer [9.1] reports the use of mechanical seals "about 1900" for difficult services, and Fig. 9.2 shows a design patented in 1915. As is so often the case with mechanical devices, the 1915 seal contains features that are now considered in the forefront of design. Although they were obviously known early in pump history, mechanical seals remained a relative novelty until general service conditions started to really tax the capability of packed box seals. To quite a degree, this was entirely rational; the packed box is a simple seal, and there is no real advantage to using more technology than is necessary for a particular duty. Where a mechanical seal was necessary, however, the legacy of the packed box unduly influenced seal design for a long time, a circumstance that impaired mechanical seal performance and has only recently been overcome. PRINCIPLES OF MECHANICAL SEALS Although there are a number of mechanical seal arrangements and a great many detailed design variations, all incorporate the same fundamental elements. The sliding seal interface is effected between the fiat, Mechanical Seals Fig.9.2 163 Mechanical seal patented in 1915. polished mating faces of two rings, one connected and sealed to the pump's rotor, the other to its casing. To accommodate manufacturing tolerances, minor axial movement of the pump's rotor, and wear of the seal faces, one of the rings is flexibly mounted and provided with a means of ensuring the sealing faces remain in contact. In much the same manner as sleeve bearings, mechanical seals depend on some form of lubrication between the seal faces to lower the coefficient of friction and help remove the heat generated. Without this lubrication, the faces will come into intimate contact and wear rapidly. The presence and quality of face lubrication depends on a number of interrelated factors, namely: sealed pressure, nominal surface speed, mechanical distortion of the seal faces, seal face materials, heat generated at the faces, heat dissipation, proximity of sealed liquid to its boiling point, and thermal distortion of the seal faces. Resolving all these issues to produce a reliable seal is the seal designer's problem. There is merit, however, in briefly reviewing the principles behind these factors. All mechanical seals derive their face lubrication from leakage of the sealed fluid, be it a liquid or a gas between the seal faces. Seal leakage, and therefore the quality of face lubrication, is influenced significantly by the sealed pressure and the characteristic of that pressure drop across the seal faces. The pressure drop characteristic depends on face orientation in the running seal. Figure 9.3 shows the three basic pressure distributions and the face orientation associated with each. In general, seal capability and leakage rate both increase as the pressure drop characteristic moves from concave to convex (or as seal face orientation changes from divergent to convergent in the direction of leakage flow). For a mechanical seal to function, the forces tending to close its faces must exceed those tending to open the faces. This net closing force gives rise to what is termed face loading. The significance of face loading is that it has an upper limit, largely dependent on face materials and the sealed liquid conditions, beyond which the lubricating film between the faces breaks down. From the simple seal shown in Fig. 9.4, the net force tending to close the faces is the resultant of the hydrostatic closing force (FH), the hydrostatic opening force (F0), the flexible element compression force (F d, and the dynamic gasket friction force (F/). Neglecting flexible element seal friction for the time being (see Design), the least certain of these forces is the hydrostatic opening force. The usual assumption is that the pressure drop 164 Mechanical Seals 70 60 ~ System Pressure, 50 Percent ~) 40 30 20 10 00 Flat Seal Faces H L Low Pressure Side 10 20 Face Width, Percent Fig. 9.3 Seal face orientation (exaggerated) versus pressure drop profile. (Courtesy Durametallic Corp.) (+ ve to left) -Face load ~n~ ~------~I-.--· Ff Face load = Fe FH - Fa + Fe - Ff FH = PSAH Fa = PA F P= rL Fe Mean effective pressure between seal faces = Load from compression device Ff = Friction force@ dynamic gasket (if used) Fig. 9.4 Force balance at mechanical seal faces. Mechanical Seals 165 across the seal faces is linear, giving a mean effective pressure pi equal to half the pressure drop. If, however, the pressure drop is concave, a result of the faces being divergent (Fig. 9.3), the opening force will be lower and the net face loading higher, possibly to the extent that the face load capacity is exceeded. At the other extreme, a convex pressure drop, the opening force will be higher and the net face loading lower. To a certain extent this is desirable because it increases seal capacity, although at the expense of higher leakage; but if the face loading is too low, the seal can become unstable with the risk that its faces may "blow apart" and allow gross leakage. As already noted, the face loading capacity of a seal is affected by the condition of the sealed liquid. In its passage through the seal surface, the leakage flow of sealed liquid undergoes a pressure drop from sealed pressure to atmospheric and a temperature rise, the latter from seal friction and the pressure drop. When the sealed liquid is already close to its vapor pressure, the seal leakage may vaporize as it passes through the seal interface. If vaporization occurs only a short distance across the seal face (Fig. 9.S[a]), the liquid film may not be sufficient to support the face loading, a condition that will cause the seal to wear rapidly. Three approaches are used to try to avoid this difficulty. The classical solution is to avoid any tendency to vaporize by ensuring the temperature of the leakage is below its atmospheric boiling point (Fig. 9.5 [c]). When this approach is feasible and its expense can be accommodated, it represents an excellent solution. In this connection, it is of particular importance for sealing hot water, where by reducing the temperature of the water at the seal to 70°C (160°F), good sealing performance can be achieved with quite straightforward seal designs. It is not always feasible to cool the liquid below its atmospheric boiling point, and in other cases it is not deemed viable. In these circumstances, the approach taken is to raise the pressure at the seal or cool the liquid or both to ensure vaporization occurs closer to the face ID (Fig. 9.S[b]), thus providing nearly full face load capacity. Two criteria are used to determine the conditions necessary to ensure this behavior. The pressure at the seal is required to be above the liquid vapor pressure by some margin (e.g. 3.S bar or SO psi minimum per API-682 [9.2]). Alternatively, the temperature of the liquid at the seal must be below its boiling point, at the sealed pressure, by some margin whose value is dependent on the sealing conditions and the seal face materials (Fig. 9.6). Careful examination of Fig. 9.S reveals an apparent paradox: vaporization between the seal faces raises the mean effective pressure acting between them, thus raising the opening force, Fo, and lowering the net face loading. This has been confirmed by testing but the difficulty is that while the net face loading is decreasing so is the extent of the liquid film and thereby the face load capacity. Seal operation in this region is therefore dependent on a delicate balance between net face loading and load capacity and is not a desirable state, particularly for a single component liquid such as water. When the sealed liquid cannot be cooled sufficiently, the pump cannot be rearranged to raise the pressure at the seal, or the sealing conditions exceed the capability of these two approaches, the third approach is to modify the characteristic of the pressure drop across the seal faces. Two means are employed to do this: shaped grooves in the rotating face to promote hydrodynamic or convergent face orientation for a convex pressure drop (Fig. 9.3). These are dealt with in more detail in the following discussion of face lubrication technology. Because the performance of mechanical seals has not always been as good as expected, particularly in severe services, there has been a great deal of research into the precise nature of seal face lubrication. The present state of the art identifies three classes of face lubrication: boundary, mixed film, and full film. At the same time, there now exist computer routines able to predict the class of face lubrication likely to prevail in a given seal whose operating conditions are known. Figure 9.7 shows the general limits of seal capability for these three classes of face lubrication. Most mechanical seals run with boundary lubrication, and as Fig. 9.7 shows, this class of face lubrication provides broad capabilities. Boundary lubrication is largely a product of a favorable pressure 166 Mechanical Seals Ps -I E7fvaJ~t~n--F I. Pv Face load capacity LuqUid vapor pressure @ TL a) Vaporization close to seal face 0.0. Ps,Ts Ts -t~{' Path .1TL I- Ps I. Pv_ -I Vaporization P b) Vaporization close to seal face 1.0. Sealed pressure, Ps, typically equivalent to margin of 14°C (2S0F) over Ts; varies with liquid, face materials, & sealed pressure. Ps,Ts I--_l~l' V Path Ps AT~I I-Pv D T L < atmospheric boiling point c) No vaporization across seal face. Fig. 9.5 Effect of vaporization across seal faces. Mechanical Seals 167 Product Water 30 \Silicon \ carbide \ 25 20 \ Alumina ceramic -~ 10 ,, \ ,, ,, \ 5 o \ 50 Vapour pressure curve (water) \, \ , \ 100 150 200 250 Temperatu ref" C Fig. 9.6 Variation in required" (temperature margin below boiling point) with sealing conditions and seal face materials. Operating limits for alumina ceramic, tungsten carbide, and silicon carbide inserted balanced seals (stationary face-carbon): size 80 mm, speed 4,000 rpm. (Courtesy Flexibox) "~T drop (from sealed pressure to atmospheric), which forces liquid between the faces. Once the liquid is between the faces, minor surface irregularities and face porosity serve to develop boundary lubrication conditions. For conditions beyond the capability of boundary-lubricated seals, mixed-film lubrication offers a worthwhile improvement in capability (Fig. 9.7). All seals designed for gases (sometimes used in pumps as backup seals or for sealing cyrogenic liquids in the vapor phase) rely on mixed-film lubrication. The distinguishing feature of mixed-film seals is the incorporation of specially shaped grooves in one of the faces (Fig. 9.8), whose function is to develop mixed-film lubrication by hydrodynamic action. Most designs have the face grooves at the pressure side of the face (usually the 00), and therefore act on the sealed fluid to develop face lubrication. The difficulties with all mixed-film seals are performance prediction (much of the design methodology is still largely empirical) and the accumulation of debris in the grooves, which can result in unexpected wear. 168 Mechanical Seals c- 0, 6, PACKED BOX APPLICATIONS mls 20 10 so 40 30 60 70 soo ~ ~ooo 1---"" ~ : i ~ 0_0_.,\. \ 100 •MIXED FILM LUBRICAnON BREAKDOWN BUSHING . OR \ . MECHANICAL SEAL- \ . '" *BOUNDARY~.\ ~a . f 100 so 20 10 a: I::-----T--lr-----·~" '\ 200 s 2 .\ LUBRICATION 1.0 10~-----------I--------------~\-.--~~~----~ \ ~ \ \. 0\ O.S 0.2 0.1 10~-L--~~~-L~~--~~-~~--~~~~~~ 3 4 5 6 7 RELATIVE VELOCITY Fig. 9.7 8 9 10 11 12 13 14 15 @ SEAL-1,OOO FT/MIN Seal capabilities (After Durametallic). Full-film lubrication offers the highest sealing capability, and because the faces are separated by a full-fluid film, such seals also offer long service lives. Two means are employed to develop full-film lubrication. The older approach is to inject lubricating fluid directly between the faces (Fig. 9.9). This arrangement is generally known as a hydrostatic seal. With the advent of computer analysis (finite element methods), it is now possible to design a seal so that at operating conditions it runs with its/aces convergent in the direction of leakage. From the earlier discussion of seal face orientation, this arrangement allows the pressure gradient to force liquid between the faces thus ensuring full face load capacity. At the same time, the convex face pressure distribution (Fig. 9.3) lowers the face loading. Leakage from both designs of full-tilm-Iubricated seals is higher than from boundary- and mixed-film designs, but is still lower than from alternative seal types. Hydrostatic seals have the disadvantage of relying on a separate lubricating fluid system. Convergent face seals avoid this, but their design must take account of the actual range of operating conditions, and their manufacture and installation must accurately reproduce the design configuration. Mechanical Seals 169 5 1. 2. 3. 4. 5. Fig. 9.8 Lubrication Flats Lubrication Slots Spiral Grooves, Unidirectional Lubrication Slots Lubrication Grooves Various seal face groove fonns used to develop mixed-film face lubrication. (Courtesy Durametallic Corp.) HYDRAULIC BALANCE In the discussion of face loading, the hydrostatic force tending to close the seal faces was identified as one of the major components in that force balance. The magnitude of this force under a given pressure depends on the seal's hydraulic balance. Two terms are in general use to classify this aspect of seal design: unbalanced or balanced. The seal in Fig. 9.1O(a) has the sealed pressure PSI acting over an annulus AH , bounded by the OD of the face contact region and the ID of the flexible element gasket. As such, the area producing the hydrostatic closing force is equal to or greater than AF , the area producing the opening force. A seal with this ratio of effective hydrostatic force areas is termed unbalanced. Recognizing that the opening hydrostatic force is produced by the average pressure acting over the face contact area AF , it is evident the face loading in unbalanced seals increases significantly as the sealed pressure rises. This characteristic limits the pressures and liquids that can be successfully sealed with unbalanced seals. Many users seek to avoid the complexity of assessing whether an unbalanced seal will work in a particular service, and instead specify a conservative upper limit on sealed pressure, or specify that all pusher-type seals are to be balanced, as does API-682. 170 Mechanical Seals 9 Fig. 9.9 Axial face seal with hydrostatic injection. (Courtesy Voith) (8) ~ Fe Fe-E::V (b) L Fe lL!::~~~ BALANCE DIAMETER AH AF < 1.0 Fig.9.10 Mechanical seal hydraulic balance-a) unbalanced, b) balanced. Mechanical Seals PUMPED LIQUID SIDE 171 ATMOSPHERIC SIDE Fig. 9.11 Internal mechanical seal. As the sealed pressure rises beyond the capability of unbalanced seals, it is necessary to lower the hydrostatic closing force to keep the seal face loading within the capacity of the seal faces. This is done by making the hydrostatic closing force area less than that for the opening force (Fig. 9.1O(b». Such a seal is termed balanced. The actual degree of balance is defined by the ratio of hydrostatic force areas, AH/AF' and typically ranges from 0.6 to 0.9 depending primarily on service conditions and face materials. Balance ratios below 0.6 offer lower face loading, hence longer seal life, but at the expense of higher leakage and lower seal stability (the risk of a minor fluctuation in operating conditions causing the seal to "blow open"). SEAL ARRANGEMENTS There are two aspects to seal arrangements. The first deals with fundamental arrangements of the basic parts and the second with various arrangements of complete seals. Fundamental arrangements of the basic parts considers the location of the rotating element. Internal seals (Fig. 9.11) have their rotating element inside the seal housing and the sealed liquid at the OD of the seal interface, therefore leakage is normally inward toward the shaft. Centrifugal action in the liquid tends to oppose leakage across the seal interface. External seals (Fig. 9.12) are the opposite; the rotating element is outside the seal housing and the sealed liquid is at the ID of the seal interface. Leakage is therefore normally outward away from the shaft, with centrifugal action in the liquid tending to promote leakage, and to promote the centrifuging of any solids in the liquid into the sealing interface. ROTATING ELEMENT ATMOSPHERIC SIDE t SHAFT Fig. 9.12 External mechanical seal. 172 Mechanical Seals PUMPED LIQUID SIDE ATMOSPHERIC SIDE \::i SHAFT Fig. 9.13 Double mechanical seal. Most centrifugal pumps equipped with mechanical seals employ a single seal, either intemal or external. With this arrangement there is direct leakage of the sealed liquid to the atmosphere. This is not always tolerable, for reasons of seal face life, liquid toxicity, liquid cost, or environmental pollution. One solution is to use multiple seals, either double or tandem depending on the particular circumstance. When the service is such that the pumped liquid cannot be allowed to leak into the atmosphere (toxic or polluting) or must be kept out of the seal interface (abrasive solids in the liquid), a double seal offers one solution (Fig. 9.13). The seal is made up of two single seals mounted either back to back (Fig. 9.14) or face to face. The region between the seals is maintained at a pressure greater than the sealed liquid pressure with a barrier fluid. By doing this, the sealed liquid is excluded from the seal, since the leakage flow at the inner seal is from the barrier fluid to the sealed liquid. Until recently, the barrier fluid was always a liquid. With a liquid, the heat generated at the seal faces is often high enough to require that the liquid be cooled by circulation through some form of heat exchanger. For a long time, a double seal with a liquid barrier was the only available solution for toxic, polluting, or abrasive pumped liquids. This arrangement is complex, however, and somewhat unreliable as a consequence, a circumstance that has lead to the development of better solutions for most services. Drawing from centrifugal compressor technology, double seals using an inert gas as the barrier fluid (Fig. 9.14) have simplified the total sealing system considerably. Such designs are now used quite extensively in pumps handling toxic and polluting liquids, limited only by compatibility of the barrier gas with the pumped liquid. Similarly, research into the behavior of seals in abrasive liquids has precipitated the development of specially designed single seals for these applications; see Seal environment later in this chapter. The objective of a tandem seal is to provide a backup so failure of the main or primary seal does not result in gross leakage and the need to immediately shut down the pump. In services such as hydrocarbon or crude oil, safety and pollution requirements alone can warrant tandem seals to prevent even short-term gross leakage. A tandem seal has two or more single seals arranged in series, with each successive seal serving to backup the preceding seal. The most common arrangement has two seals (Fig. 9.15), the inner acting as the primary, the outer as the secondary. Under normal conditions, the primary seal contains the pumped liquid, whereas the secondary seal runs at a pressure below the sealed pressure, usually atmospheric, in an inert buffer fluid. Leakage beyond a certain rate causes a pressure rise in the secondary seal lubrication system, a condition that is used to close off the lubrication system vent, and hence contain the primary seal leakage and sound an alarm. For services where a high pressure must be sealed with the utmost reliability, staged mechanical seals Mechanical Seals Fig. 9.14 173 Section, non-contacting double seal with inert gas barrier. (Courtesy John Crane, Inc.) are sometimes used. The seals are arranged in tandem, but unlike in the tandem seal, the total pressure drop is shared approximately equally between the seals. This is achieved by bleeding a small flow through a throttling orifice in each seal housing (Fig. 9.16), and returning the flow to a point of lower pressure in the system. The primary use for staged mechanical seals has been in nuclear reactor primary coolant circulating pumps (see Chap. 26). Buffer Seal Flush I Liquid (circulated) I Atmospheric Side Pumped Liquid Side Shaft Rotating Elements ct- - - - - - - - - - Fig. 9.15 Tandem mechanical seals. 174 Mechanical Seals If Req'd: Buffer Liquid P1 > P2 > P3 at P > P1 Bleed-off to point at P = P3 ~ Os Atmospheric Side Pumped Liquid Side Fig. 9.16 Staged mechanical seals. SEAL DESIGN Most who review this section on seal design will either be seeking to apply a seal or determine why a particular seal is misbehaving. A mechanical seal cannot be looked at in isolation; a pump depends on a seal to prevent leakage, but the design and ultimate performance of the seal is influenced significantly by the design of the pump itself. It is better if the pump design is looked at first, because doing so can save a great deal of wasted effort and expense. The aspects that need to be investigated and finally quantified are 1. What is the pressure at the seal? Does it change with operating conditions or pump wear or both? The pump design needs to be studied carefully, and perhaps the manufacturer consulted, to determine the answers to these questions. Sometimes the pressure at the seal is normally a vacuum. As already noted, mechanical seals designed for liquids will suffer rapid face wear if run under conditions that do not produce a lubricating liquid film. Therefore if the pressure is normally a vacuum, it is necessary to either change the pump design to raise the pressure or resort to a more complicated seal, for example, a double seal. 2. Does rotor deflection under some operating conditions produce significant angular misalignment through the seal? Mechanical seals, particularly those with rotating flexible elements (see detailed seal design), are susceptible to premature failure if run with high angular misalignment. Several industry specifications address this problem by limiting rotor deflection at the seal to 0.050 mm (0.002 in.) under the worst expected operating conditions. 3. Is there significant axial rotor movement during pump operation? Pumps with hydrodynamic thrust bearings (Kingsbury type; see Chap. 11) typically have 0.30 to 0.40 mm (0.012- to 0.Q15-in.) rotor endplay. Similarly, but as a result of manufacturing tolerances rather than bearing clearance, pumps with antifriction type thrust bearings can have as much as 0.50 mm (0.020-in.) rotor endplay. Most mechanical seals can accommodate axial movements of this magnitude, provided the movement is slow and relatively infrequent. Usually this is the case, but under adverse operating conditions (see Chap. 22) pump rotors can shuttle rapidly, a condition that usually causes excessive seal leakage and premature failure. When this condition is the product of operating flows alone, meaning that it is not influenced by an extreme hydraulic design, the better solution is to avoid operating the pump down to such low flows. 4. What is the housing arrangement available for the seal? It is now well recognized that the space for conventional packing has little radial room for optimum seal geometry and heat dissipation, resulting in seals that fail frequently and prematurely. Two industry standards, ANSI B73.1[9.3] and API 610, now Mechanical Seals 175 mandate minimum radial dimensions for mechanical seal housings as one facet of an effort to improve seal life in chemical and refinery pumps. An extension of this concept is the arrangement generally known as an open seal housing (Fig. 9.17). The rationale behind this design is to provide as much room as possible for free circulation of the pumped liquid around the seal, thus allowing optimum heat removal and avoiding any tendency for the housing geometry to force solids into the improved heat dissipation. Experience in the chemical- and mineral-processing industries has shown that pumps employing this housing arrangement have longer seal lives than those with more conventional arrangements. There are myriad variations in detailed mechanical seal design, far too many to cover in this text. Compounding that, the design of mechanical seals is still changing rapidly, so the best course for this text is to address the function of the basic parts and the fundamental differences in design, paying attention to the points that are thought to have a significant effect on seal performance and life. When a need arises for more detailed information, the reader should consult the literature (e.g. Mayer [9.1], Lebeck [9.4]), or the seal manufacturers. Beyond a seal face design able to maintain an adequate lubricant film under the expected operating conditions, the design of a mechanical seal must also address the following basic functions: 1. Sealing the flexibly mounted face; keeping it in contact with its mating face and driving it (resisting the torque developed by friction between the faces). Fig. 9.17 Open seal housing. 176 2. 3. 4. Mechanical Seals Whether to have the face loading or compression device rotating or stationary; wet or dry. How to mount the seal. How to introduce liquid into the seal housing for cooling. Sealing the flexibly mounted face (secondary sealing), keeping it in contact with its mating face, and driving it are the functions of what is generally termed the compression unit or flexible element. Sealing is difficult because the design must effect a positive seal while allowing the sealed face to move freely. This is accomplished by one of two basic methods: a dynamic gasket, frequently an O-ring (Fig. 9.18), between the flexibly mounted face and its sleeve or housing, or a bellows, either elastomer (Fig. 9.19) or metal (Fig. 9.20). Seals employing a dynamic gasket are often referred to as pusher seals, a term derived from the gasket being pushed along the sleeve or housing to compensate for face wear. Although a bellows provides the flexible seal, it still must be sealed to the sleeve or housing. Elastomer bellows do this with a metal-banded, tight-fitting sleeve or nose at the end of the bellows (Fig. 9.19). A metal bellows relies on some form of static gasket (Fig. 9.20), the form and material dependent on the service conditions. Each of the means of secondary sealing has advantages for particular service conditions. As an aid to selection, Table 9.1 summarizes the salient features of the two basic designs. The means of secondary sealing is a principal distinction between mechanical seal design, and can therefore be used as a basis for classifying seal designs (Fig. 9.21). Springs are the usual means of energizing or compressing the seal to keep its faces in contact. Most designs use coil springs, either a large single spring or an arrangement of multiple small springs. A large single spring (Fig. 9.19) is simpler, has a low spring constant (making it tolerant of setting variations Compression Springs Coil Fig. 9.18 "Pusher" type mechanical seal with dynamic gasket. (Courtesy Durametallic Corp.) Mechanical Seals Fig. 9.19 Fig. 9.20 Elastomer bellows type mechanical seal. (Courtesy John Crane, Inc.) Stationary metal bellows type mechanical seal. (Courtesy EG & G Sealo/) 177 178 Mechanical Seals Table 9.1 Mechanical seal capability versus secondary seal type Bellows Secondary seal Dynamic gasket Compression Size range Pressure limit Temperature range Balance Hysteresis Risk of fretting Special designs Special materials Number of parts Cost ! Elastomer polymer Single or multiple Broad; 12-500 mm (0.5 to 20 in.) High; to 200 bar (3,000 psig) Intermediate; -57 to 150°C (-70 to 300°F) Available Moderate High! Available Available More Base Metal springs Broad Bellows Narrower; 20-125 mm (0.75 to 5.0 in.) Low; to 2 bar Intermediate; to 35 bar (30 psig) (500 psig) High; -270 to 425°C Low; -18 to 50°C (0 to 120°F) (-450 to 800°F) Available Inherent Negligible None Not available Limited Not available Limited More Fewer Usually lower Usually higher Reduced with stationary compression unit. and face wear), and is less likely to become clogged with foreign material that may be in the sealed liquid. Size, rotative speed, and available materials determine the limits of single springs. A multiple spring arrangement (Fig. 9.18) allows a more compact seal, is said to apply more even face loading, can tolerate higher rotative speeds, and the smaller springs are easily made in the more exotic alloys. The smaller springs have a high spring constant, making the seal more sensitive to setting variations and face wear, and are more likely to clog if there is foreign material in the sealed liquid (there are design variations to avoid this; see dry compression units). Elastomer bellows seals are generally spring energized (Fig. 9.19), the bellows typically being too resilient for this function. Metal bellows seals, however, have as one of their virtues a bellows that serves as both the secondary seal and the means of energizing the seal (Fig. 9.20). The spring constant of metal bellows is high, thus they are sensitive to setting variations and face wear in the same manner as multiple spring seals. Coil springs are not the only device employed to energize mechanical seals. Wave washers are used 'O'Ring g 'i,v'Rin DynamiC Wedge gasket 'U'Ring Seal { 'C'Ring Bellows Unbal'd Balance Comp'n 't { ."'"',,•.} ,m { 1 ,~"""' Rotating Stationary FI 'bl Wt eXI e D' } ry Single spring Mit' . U I spring Wave washer E"""",,,_ wosh" Elastomer washer LElastomer Polymer Metal -+-Inherently balanced-+ comPt 'n -{ SRt °t~ating }- Flexible -l Metal Bellows Un! a lonary Element L Fig. 9.21 Mechanical seal design classification. Based on form of secondary seal. Mechanical Seals 179 in some designs instead of multiple coil springs; the characteristics are similar. Some seals designed for abrasive-laden liquids have used a plastic encapsulated Belleville washer or a rubber block in shear as both the compression device and the secondary seal (Fig. 9.22). These have very high spring constants, requiring that the seal be adjusted periodically to compensate for wear. Very large seals have used sealed pressure, or some fraction of it, applied to a piston built into the moving face (Fig. 9.23) to energize it by hydrostatic force. A novel design for small seals uses magnetic attraction (Fig. 9.24). The magnetic materials limit the services to which this elegantly simple design can be applied. Torque is transmitted through the compression unit by one of three basic designs. The most common is an arrangement of drive pins (Fig. 9.18) or tabs and grooves (Fig. 9.19). Although a little complicated, these arrangements have the advantage of being bidirectional. An alternative design for pusher seals is to use a single coil spring to both energize the seal and transmit the face torque (Fig. 9.25). This arrangement has the virtue of simplicity but the seal is now unidirectional, requiring care in specification and installation to ensure the applied torque tends to extend (unwind) the spring. In metal bellows seals (Fig. 9.20), the torque is generally transmitted through the bellows. At the time of this writing, the more common arrangement is to have the compression unit rotating. By and large that is a legacy of seals designed to fit in the space provided for packing and a belief that rotating the compression unit improved heat dissipation from the seal faces. Once the requirement to have mechanical seals and packing interchangeable is dispensed with, the better design is to have the compression unit stationary. There are two distinct advantages. First, a stationary compression unit accommodates angular misalignment between the rotor axis and seal housing face by taking a "set," whereas a rotating compression unit is subject to continual cycling in this circumstance (Fig. 9.26). Second, a stationary compression unit does not have its action influenced by inertia effects caused by rotation. For seals operating at nominal surface speeds above 250 mls (4500 ft/min), a stationary compression unit is mandatory to avoid operating problems due to inertia effects. In the case of metal bellows seals sealing solids-laden liquids, the point is moot. One argument is that rotating the bellows ensures that it does not become clogged with solids. Another argument is that a stationary bellows is less likely to be eroded by the solids. On balance, the better solution is probably to have the bellows stationary and ensure adequate circulation within the seal housing (see pump design). For clean, innocuous liquids, the simpler arrangement is to have the compression unit wet (Figs. 9.18, 9.19,9.20, and 9.26). When the liquid contains solids likely to clog the seal parts, the compression unit needs to be a special design (Fig. 22) or arranged so it is dry (Fig. 9.27). Metal bellows seals, by way of their construction, always have the compression unit wet. Seals are mounted in one of two ways: direct or cartridge. In direct mounting (Figs. 9.18, 9.19, and 9.20), the major components of the seal (compression unit, faces, sleeve and flange) are assembled into the pump separately or as subassemblies. The setting of the seal is therefore dependent on locating surfaces within the pump or the mechanic's skill in positioning the parts correctly. On top of this, the parts are all susceptible to damage and contamination until the seal is finally closed up. By preassembling the seal, sleeve, and flange into a unit, an arrangement known as cartridge mounting, these problems can be eliminated as possible causes of premature seal failure. Cartridge-mounted seals (Figs. 9.25 and 9.27) are set with locking tabs between the flange and sleeve. These keep the cartridge assembled as it is installed into the pump. Once the cartridge is installed and the sleeve and flange secured, the lock tabs are removed. A further advantage of cartridge mounting, one not related to reliability, is greatly reduced tum around time for seal changing (provided, of course, that a spare cartridge is available). Not by any means a new idea, cartridge mounting awaited a critical need to improve seal reliability before its inherently greater expense became acceptable. The usual means used to introduce liquid into the seal housing is a tapped connection in the housing or flange. When the sole purpose of doing this is to cool the seal, the flow necessary is quite low and provided the flow is controlled, a simple flange tapping (Fig. 9.20) is adequate. For cooling, it is important ISO Mechanical Seals (a) 3 Fixed ring a Ring insert LO L3 3 4 Rotating ring b Ring insert 5 Cone spring membrane 6 Drive rings 7 Sleeve 2 Shaft (b) Rotating unit clamped between Virtually Indestructible Rubber-In-Shear element with smooth contours Clamping plate for quick seal readjustment impeller and sleeve for easy installation Fig. 9.22 Mechanical seals for slurry applications using two alternative compression devices. a) Encapsulated conical spring. (Courtesy Cefilac) b) Rubber in shear. (Type RIS; BWIIP International Inc.) Mechanical Seals 181 1. Rotating Face (Composite) 2. Stationary Face 3. Inner Housing 4. Outer Housing Shaft Flange 5. Retaining Ring 6. Wear Indicator 7. Head Cover 8. Static Seal (Air Operated) Shaft Fig. 9.23 Axial face seal with hydrostatic loading. (Courtesy Sterling) that the flush liquid be directed into the region of the seal faces. If the flush or injection flow is intended to both cool the seal and raise the pressure in the seal housing by pressure drop across a throat bushing, the flow needed can be quite high. In this case, the velocity of liquid issuing from a simple flange tapping may easily be high enough to disturb the bahavior of the seal by impact or eventually erode the seal parts. This problem is avoided by either diffusing the flow through the flange connection (Fig. 9.28) or adding a second connection in the housing proper and introducing most of the flow through that. Of the two approaches, the former is the preferred because it is simpler. It is not always possible, however. (1) stationary seat (2) carbide-ceramic sealing head (3) magnetic ring (4) a-ring static seal, also transmits the torque Fig. 9.24 Magnetic axial face seal showing magnetic circuit. 182 Mechanical Seals Fig. 9.25 Single spring, spring driven, and cartridge mounted seal. (Courtesy Flexibox International) ~I''''~ 9 ¢ -Static Angularity Between Rotor & Stationary Face (a) Rotating Compression Unit-Cycles Every Revolution to Compensate Rotating Face Square To Shaft Axis (b) Stationary Compression Unit-Adopts Set Position To Compensate ¢-Static Angularity Between Rotor & Stationary Unit Mounting Face Fig. 9.26 Effect of angular misalignment on compression unit: a) rotating, b) stationary. Mechanical Seals Fig. 9.27 183 Seal for general purpose or slurry applications with stationary, external spring. (Courtesy Flexibox International) Materials Face materials are chosen based on wear and corrosion resistance in the sealed liquid, heat dissipation, and cost, there being a distinct connection between good performance and cost. The usual combination is hard against soft, and the materials range from reinforced phenolic against cast iron to carbon against silicon carbide (possibly zirconium carbide by the time this is published). As noted in the discussion of vaporization at the faces, the choice of the hard face material can significantly affect the conditions required for satisfactory operation of the seal (Fig. 9.6). General practice is to rotate the face with the higher thermal conductivity. In some difficult hydrocarbon services (e.g., light ends), there are instances where having the better conductor stationary seems to materially aid the development of a stable liquid film between the faces. Seals for slurries employ hard against hard faces, typically silicon carbide against tungsten carbide. This choice is dictated by the need for abrasion resistance; it is tolerable because the surface speeds are relatively low. Corrosion and endurance strength govern the selection of materials for the metal parts in mechanical seals. Corrosion needs particular care because the relatively small parts usually cannot tolerate the degree of metal loss that would be quite acceptable in, say, a pump casing. Metal parts are at least type 316 stainless steel. Welded metal bellows are typically Hastelby C® or similar materials suitable for hightemperature service. Shaft sleeves are frequently hard coated in the region under the dynamic gasket in pusher seals to reduce the risk of fretting corrosion. Seal flanges are at least chrome steel for adequate corrosion resistance at the critical sealing and locating surfaces. Dynamic gasket materials range from neoprene to Teflon.™ Resilience is an important characteristic 184 Mechanical Seals Multi-Point Flush Injection Fig. 9.28 "Multipoint" injection to diffuse injection flow. (Courtesy Flexibox International) or the seal may either leak (too loose) or have high hysteresis (too tight). For this reason when the service conditions require Teflon,TM it is only used in a form (C ring, encapsulated a-ring) where its lack of resilience is compensated for. Static gaskets are chosen for chemical and temperatures resistance. Materials range from neoprene through GraphojlTM to soft iron or stainless steel. Auxiliary Seals Many mechanical seals are equipped with some sort of auxiliary seal. These can function to allow the introduction of a quench fluid (often low-pressure steam) to remove deposits formed at the atmospheric Mechanical Seals 185 side of the seal, or to contain leakage for a short time should the seal fail (similar to a tandem seal but without the sophistication and durability). Designs range from a simple close clearance bushing, lip seal or packed box for quench fluid, to dry running (gas type) mechanical seals (Fig. 9.29) and abeyant mechanical seals (faces not normally in contact; Fig. 9.30) to contain leakage should the main seal fail. Seal Environment The importance of providing the correct seal environment cannot be overstated. Attention to this aspect of seal application ensures the best seal choice in the selection phase and avoids the extremely high costs that can be associated with a chronically unreliable mechanical seal. From the discussion of vaporization at the seal faces, it is clear that dissipation of the frictional heat generated at the faces is important. If the liquid being sealed is at a temperature well below its boiling point at the sealed pressure and the housing design allows good natural circulation, (Fig. 9.17), the prevailing seal environment is satisfactory. Should the housing design not allow good circulation, piping a small flow from the pump discharge (API Plan 11, Fig. 9.31) to the seal flange will correct the deficiency to an acceptable degree. When the liquid is being sealed at conditions close to its boiling point, the requirements for satisfactory operation become more complex. Depending on the seal face design selected (see face lubrication), it will be necessary to cool the sealed liquid below the pumping temperature or raise the pressure in the seal housing. Lowering the temperature can be achieved by injecting cool liquid from an external source (API plan 32; Fig. 9.32), by cooling a small flow from the pump discharge (API plan 21; Fig. 9.33), or by limiting the heat flow from the pump into the seal housing and circulating liquid from the housing through a heat exchanger and returning it across the seal faces (API plan 23; Fig. 9.34). Of these three approaches, the third, plan 23, has the highest thermal efficiency; that is, it dissipates the least amount of energy to provide the environment needed for the seal. Plan 23 is expensive, although not significantly more than plan 21, and requires a certain minimum peripheral speed to effect adequate circulation of the sealed liquid. Despite these limitations, plan 23 is used extensively because it is reliable and does not rely on exotic seal face materials. Raising the pressure in the seal housing is achieved by either eliminating the balance holes in a singlesuction impeller (see Chap. 4) and circulating liquid from the seal housing back to the pump suction (API plan 13; Fig. 9.35), or taking a large flow from the pump discharge (API plan 11) or an external source (API plan 32) and developing the required pressure drop across a throat bushing. The former is the better design since the seal housing pressure is not influenced by pump wear. It is not always feasible, however, because the resultant axial thrust can easily exceed bearing capacity. The flows required for plan 11 or 32 are often larger than expected, particularly when the liquid has low SG (see seal design for cautionary comments on introducing large flows into mechanical seal housings). Liquids pumped at high temperatures but still below their atmospheric boiling point, e.g. heat transfer oil and refinery bottoms), can be sealed at or close to the pumping temperature using metal bellows seals. The heat developed by seal friction is dissipated with small flow from the pump discharge (API plan 11). Seal face life will be longer, however, if the temperature at the seal is lowered. Some users have achieved a moderate reduction in temperature by adding a liquid to air heat exchanger (making it plan 21; Fig. 9.33) located in the motor cooling air draft. A still more conservative approach, one that is yielding very long seal face lives, is to keep the seal both cool and clean by injecting cool light cycle oil from an external source (API plan 32) during normal operation. Modern pump designs has all but eliminated the jacketed seal housing as a means of cooling seals. When new their effectiveness was relatively low; once in service for a while, particularly at high temperature, scaling on the water side reduced their effectiveness still further. Given this, the simplification realized by eliminating this cooling more than offset the small advantage. There is perhaps some advantage 186 Mechanical Seals INJECTION THRU CAGE RING TAP CAUTION: BOll HOLES MUST ClEAR OIA "W" A MIN t - - - - - - - - J- - - - - -- + -- -C - - - G-2 Fig. 9.29 Dry running (gas type) auxiliary seal. (Courtesy BWIIP Inc.) Fig. 9.30 Abeyant auxiliary seal. (Courtesy Flexibox International) Mechanical Seals 187 Orifice; Min. dia. 0.12 in. Fig. 9.31 Seal flush from pump discharge; API plan 11. From external source Fig. 9.32 Seal flush from external source; API plan 32. in some form of cooling jacket to act as an additional thermal barrier in pumps employing self-circulating seals (API plan 23). If by way of pump construction and suction pressure, the pressure at the seal would normally be less than 0.35 bar (5 psig), the seal housing pressure must be increased (see face lubrication). Two approaches are used: The first is to use one of the methods previously described for raising the sealed pressure when pumping liquids close to their boiling point. Note that unless plan 32 is used, seals pressurized by these methods will be at suction conditions in pumps on standby, and may therefore suffer considerable "airin" leakage if the suction pressure is a high vacuum. The alternate is a double seal, a complex solution most users try to avoid. With modem mechanical seals, it is generally not necessary to lower the pressure at the seal. Should 188 Mechanical Seals Heat exchanger Fig. 9.33 Seal flush from discharge through heat exchanger; API plan 21. Heat Exchanger Seal Water In Fig. 9.34 Circulation of sealed liquid through heat exchanger; API plan 23. Mechanical Seals 189 Fig. 9.35 Seal flush from within pump back to suction; API plan 13. doing so be necessary for some reason, a breakdown bushing with bleed-off to a point of low pressure (see Chap. 8) is the method used. Solids-laden liquid cannot be sealed effectively with conventional mechanical seals. Slurries are being sealed with varying degrees of success, using seals designed specifically for several abrasive service (Figs. 9.22 and 9.27). Unless legislation dictates otherwise, slurry seals have all but replaced double seals for these duties. Installing a throat bushing in the bottom of the seal housing and injecting clean liquid from an external source, thus excluding the pumped liquid from the seal housing, will allow a conventional seal to work. The drawback is the loss of plant efficiency caused by product dilution or returning refined product to the cycle. In services where the liquid is merely contaminated with solids, a simple means of cleaning up the flush liquid is to use a cyclone separator (API plan 31; Fig. 9.36). These devices (Fig. 9.37) function by accelerating a liquid stream to high velocity through an orifice, then feeding it into a cone. The highvelocity swirling in the cone centrifuges those solids heavier than the liquid to the outside of the liquid body. Clean liquid is drawn from the center of the cone (outlet C) and piped to the seal flush connection. The concentrated dirty liquid is piped from the bottom of the cyclone (outlet B) back to the pump suction. For cyclone separators to function correctly, the pressures at outlets B and C need to be within 1.4 bar (20 psi) of each other. If the sealed pressure is more than 1.4 bar (20 psi) above suction pressure, an orifice (not a valve) should be added in the line back to the pump suction to raise the pressure at the cyclone outlet. By their very action, cyclone separators will not separate solids whose sa is lower than that of the liquid. Their action is also impaired by high viscosity; the drag on the solids reduces the degree of separation, particularly of the finer solids. To avoid having the cyclone plug at the inlet orifice and stop all flow to the seal, it is prudent to install a Y-type strainer upstream (Fig. 9.37). The strainer can be arranged for manual backflushing if on-line cleaning is deemed necessary. Double mechanical seals, by definition, have the region between them filled with a barrier fluid that is maintained at a pressure above that of the sealed liquid. When the barrier is a liquid, it is generally necessary to circulate and cool it to dissipate the heat generated at the seal faces. In most cases, this function is realized using an external, pressurized reservoir (API plan 53; Fig. 9.38). Circulation is by a pumping device on the seal if that is feasible, otherwise by a separate pump. Multiple installations of double seals are sometimes served by a single, central circulation system (API Plan 54; Fig. 9.39). 190 Mechanical Seals 'Y' type strainer Cyclone separator Fig.9.36 Seal flush from discharge through cyclone (abrasives) separator; API plan 31. Note addition of "Y" type strainer. Clean Flow Outlet .......... :>"'.......1.......... . . .' . .......:.;-- Inlet .' Dirty Flow Outlet Fig. 9.37 Abrasives separator; a) connections, b) principle of operation. (Courtesy John Crane, Inc.) Mechanical Seals IJ:NII PRESSURE 9 191 lOW LEVl:L ALARM o AlARM IlELIEF IALVI: FU I I I I I I IJ:NII PRESSUflE SWITCH PUMP SHAFT DOUBLE SEAL Fig. 9.38 API plan 53 system for double (pressurized dual) seals. (Courtesy Flexibox International) Barrier liquid is circulated by the system; the pressure at the seal is maintained by an orifice or regulator in the common return line. The primary seal in a tandem mechanical seal arrangement has its environment maintained as if it were a single seal (see earlier discussion). The secondary seal is lubricated and cooled by a buffer liquid at atmospheric pressure. This function is carried out by an external, nonpressurized reservoir (API plan 52, Fig. 9.40). Practice for circulating and cooling the barrier liquid follows that for plan-53 systems. 192 Mechanical Seals 1_ _ _ .__ .._._. Fig. 9.39 Central circulator for double seals with liquid barrier fluid; API plan 54: a) circulator unit, b) flow diagram. (Courtesy Durametallic Corp.) In addition to lubricating and cooling the secondary seal, plan-52 systems must also detect primary seal leakage and isolate it. This function is achieved with an orifice and motorized valve in the reservoir's vent line. A high flow through the vent line will cause a measurable pressure rise in the reservoir. A pressure switch in the reservoir detects this, sound an alarm, and closes the motorized vent line valve to contain the primary seal leakage. From this point on, the pump is being sealed by the secondary seal until it is shut down and the seal assembly replaced. So far the discussion of mechanical seal environment has centered on the sealed liquid side of the interface. This is by far the more important side, but for many services the environment at the atmospheric side is also of major importance. The services in which this is the case are those that may produce freezing, crystallization, carbonization, or precipitation on the atmospheric side as a result of the small leakage that is inherent in mechanical seals. These physical phenomena must be avoided lest seal operation can be impaired or the seal damaged by the build up of solids in the region of the seal interface. Freezing is prevented using a dead-ended blanket (API plan 51). An external fluid quench of water, steam, or a gas (API plan 62), is used to prevent crystallization, carbonization, or precipitation. In many instances, it is necessary to incorporate a special sleeve or bushing in the seal flange to ensure the quench fluid circulates into the region under the sealing interface. Operation An all encompassing rule often quoted by seal manufacturers is: Never start up seals dry. With the variations in modem mechanical seal designs, this means: Do not start the pump before ensuring its seal has the means needed for face lubrication. Mechanical Seals HGH I'RESSUIIE AlAAM 9 I r I I I 193 o lOW LEVEL AlARM RElIEf -AlVE PRESSURE INOICATOR HGH PRfSSURE SWITCH lEVEL INDICATOR PUMP SHAFT TANDEM SEAL Fig. 9.40 API plan 52 system for tandem (unpressurized dual) seals. (Courtesy Flexibox International) In the simpler cases, just following normal pump operating practice is sufficient to ensure the seal functions correctly. As the seal becomes more complicated, however, it becomes necessary to include some additional procedures. What is necessary can be determined fairly easily by considering the provisions made to ensure the correct seal environment. When the temperature at the seal is maintained at other than the pumping temperature, there should be means to check the actual temperature and the temperature needs to be verified periodically. The same facility and periodic check is necessary when 194 Mechanical Seals the pressure at the seal is maintained at other than that inside the pump. By doing this, a change in temperature or pressure can be used as an indicator of some deterioration in the pump or seal, thus leading to investigation before seal failure indicates there was a problem. The even more complicated auxiliary systems used with double and tandem seals should be checked for cleanliness and function before being put into service, and once in service, their operation requires periodic verification. In critical services, monitoring equipment is being used to warn of a significant change in seal environment, for example, return liquid temperature in a plan-23 system or high seal leakage. The latter rely on accumulation of leakage in a vessel or a rise in pressure in the vent space of the seal flange. When contemplating this degree of sophistication, it is worthwhile to weigh what has to be monitored automatically against the added complexity of doing so. Often it is better to adopt a slightly simpler approach. And in that simpler approach it is always worthwhile to pay heed to visual observation; instrumentation cannot tell all. Maintenance As a general rule it is better not to open a seal for maintenance unless a change in operation (pressure, temperature, or leakage) or seal wear (some seals have wear indicators) dictates doing so. Once the seal is opened, it is important to carefully inspect the parts to learn whether the deterioration of the seal was due to normal wear and tear or an abnormality (operating condition or component) that could be avoided the next time. As an aid to this activity, the major seal manufacturers have available excellent troubleshooting guides, complete with illustrations of the various types of damage that can be encountered. If examination of the seal parts identifies a correctable problem (e.g., seal environment or component materials), correcting the deficiency should be the next step in returning the seal to service. Restoring the seal to new condition can be handled one of two ways. The plant can have a stock of replacement parts, preferably obtained from the seal manufacturer to ensure continuity of quality, and draw from these to rebuild the seal. Alternatively, the plant can just stock replacement units, sending the entire worn seal to a specialist shop for restoration. Unless the plant maintenance shop is very sophisticated, this approach is necessary for seals such as metal bellows, which must be leak tested with gas to verify bellows integrity. The concept of exchanging complete seal units is entirely consistent with that of cartridge-mounted seals, and explains why the practice is on the increase. When the maintenance practice is to exchange the seal unit, examining the replaced seal for abnormal damage becomes the responsibility of the specialist shop. The plant, however, still needs to maintain a certain awareness of what is normal so any tendency toward premature failure is quickly detected, its cause identified, generally in conjunction with the repair shop, and the problem corrected. Following the lines of the discussion of what pump design does for seals, it is important to pay heed to what pump condition can do to seals. During maintenance, this refers to checking that the pump's rotor is sufficiently straight, that its axis is sufficiently concentric with and square to the surfaces that locate the seal flange, and that the adjacent bearing clearances, radial and axial, are within those for which the seal was designed. Detailed diagrams of the checks that need to be made are invariably included in the seal manufacturers' trouble shooting guides. Acceptance criteria are given on other the seal drawing or in the installation instructions. BIBLIOGRAPHY [9.1] E. Mayer, Mechanical Seals, 5th edition, 1977 Newnes-Butterworths, London, UK. [9.2] API-682, Shaft Sealing Systems for Centrifugal and Rotary Pumps, American Petroleum Institute, Washington, D.C., 1995. [9.3] ANSI B73.1, 1991. [9.4] A. O. Lebeck, Principles and Design of Mechanical Face Seals, John Wiley, New York, 1991 10 Breakdown Seals In the history of centrifugal pump development, breakdown-type seals were employed when the sealing conditions of surface speed, pressure drop, or both exceeded the capability of packed boxes. Their greatest use came with the advent of the high-speed boiler feed pump. At the time of this development, the early 1950s, mechanical seals were not able to demonstrate the dependability necessary for such a critical application. Today the circumstances are different; mechanical seals are an equal contender for such services. Breakdown seals act on the circumference of the shaft or rotor, and are therefore termed radial seals, as are packed boxes. They are distinguished from packed boxes by having a specific clearance between the shaft or rotor and the stationary breakdown device (Fig. 10.1). This arrangement eliminates the heat generated by rubbing in packed boxes, but does, of course, allow greater leakage through the seal. The magnitude of the clearance is a compromise between leakage rate and the need to accommodate rotor runout and minor variations in the rotor's radial position. All conventional breakdown seal installations require an auxilliary system to gather and dispose of the seal leakage. Whether the installation also requires an injection system to introduce liquid from an external source into the seal depends on the nature of the pumped liquid. CONDENSATE INJECTION SEALING Most of the breakdown seals in use today are in boiler feed pumps. The pumped liquid in these cases is at a temperature above its atmospheric boiling point, and so would flash into vapor if allowed to leak through the seal. To avoid this, the seals are injected with cold condensate to cool the leakage. This arrangement is commonly known as "condensate injection sealing." The seals, given their development from packed boxes, are often termed "packless" stuffing boxes. The construction of a pump with condensate injection sealing is illustrated in Fig. 10.1. A labyrinth breakdown bushing is substituted for the conventional packing, and the pump shaft sleeve runs within this bushing with a reasonably small radial clearance. Cold condensate, available at a pressure in excess of the boiler feed pump suction pressure, is introduced centrally in this breakdown bushing. A small portion of the injection water flows inwardly into the pump proper; the remainder flows out into a 195 I. J. Karassik et al., Centrifugal Pumps © Chapman & Hall 1998 196 Breakdown Seals Fig. 10.1 Breakdown seal construction for high-pressure boiler feed pump. collecting chamber that is vented to the atmosphere. From this chamber, the leakage is piped back to the condenser. SOURCE OF SUPPLY Cold condensate (at temperatures from 27-38°C (80 to 100°F)) is available at the condensate pump discharge. In closed cycles (Fig. 10.2) and those open cycles where the feed pump takes its suction directly from the deaerator (Fig. 10.3), the pressure at the condensate pump discharge is higher than feed pump suction pressure. When the feed pump in an open cycle is preceded by a suction booster pump (Fig. 10.4), feed pump suction pressure is generally higher than condensate pump discharge pressure. In these cases, it is necessary to either lower the pressure at the feed pump seals (by bleeding off to the deaerator) or use booster pumps to raise the pressure of the cold condensate. Some installations employ a closed heater between the suction booster and boiler feed pump. Along with a certain penalty in total pumping power, this arrangement dictates the need for condensate injection booster pumps, since the pressure at the seals cannot be lowered appreciably. The water for the injection in all cases should be taken immediately from the condensate pump discharge before it has gone through any closed heaters. It is preferable to use injection water at Breakdown Seals SUCTION PRESSURE: Z50 PSI AT FULL LOAD 337 PSI AT 1/4 LOAD FRICTION LOSSES: 40 PSI AT FULL LOAD 3 PSI AT 114 LOAD TEMPERATURES: 32O"F AT FULL LOAD Z50-F AT 1/4 LOAD '------11 CALIBRATED ORIFICE STATIC HEAD IOPSI I CONDENSER HOTWELL CLOSED HEATERS CONDENSATE INJ£CTION LINE FRICTION LOSS: 5 PSI AT FULL LOAD DISCHARGE PRESSURES' 300 PSI AT FULL LOAD 350 PSI AT 1/4 LOAD Fig. 10.2 Application of injection breakdown seals in a closed feedwater cycle. Pressure distribution indicated for full and one-quarter load. DEAERATING HEATER 316·F, 70 PSIG AT FULL LOAD 23Z"F, 7 PSIG AT 114 LOAD STATIC HEAD 60FT SUCTION PHESSURE: 906 PSIG AT FULL L0401 31 4 PSIG AT 1/4 LOAD CLOSED HEATERS INJECTION PRESSURE· I~~ PSIG AT FULL LOAD 200 PSIG AT 114 LOAD DISCHARGE PRESSURE· CONDENSATE 170 PSIG AT FULL LOAD PUMP ZI5 PSIG AT 1/4 LOAD Fig. 10.3 Application of injection breakdown seals in an open feedwater cycle. 197 198 Breakdown Seals Deaerating Heater 316°F, 70 PSIG at full load 232°F, 7 PSIG at V4 load Antiflash Orifice LiP = 20 PSI 1/ Suction End Bleed-off Balancing Leak-off \.------1~___f/ LiP = 5 PSI Calibrated Orifice - - - LiP=5PSI 1ft 20 j '----./-"'1 -, 15 ft Condenser Hot-well I Closed Heaters -.1-ft- f-_P..."ip_in..."g=-Li_P_=_5_P_S_I_--{ I Allema.v~o \ Condensate Pump Discharge Pressure: 170 PSIG at full load 215 PSIG at V4 load Fig. 10.4 Suction Booster Discharge Pressure 194 PSIG at Full Load 157 PSIG at V4 Load Boiler Feed Pump Suction Pressure: 188 PSIG at full load 151 PSIG at V4 load Bleed-ofts back 10 deaerator tI 0 ,I Injection Booster Pump LiP = 59 PSI Application of injection breakdown seals in an open feedwater cycle with a suction booster pump. Pressure distribution indicated for full and one-quarter load. temperatures below 49°C (l20°F) so as to avoid the slight steaming at the seal covers (steaming takes place if injection temperatures in excess of that figure are used). This steaming is undesirable partly because of the concern it may arouse in the operators and partly because of the possibility of its condensation near the pump bearings. Pumps arranged for condensate injection sealing, moreover, are usually not provided with any other cooling means in that area. If the shaft sleeves rotating within the condensate seal breakdown bushing are not adequately cooled, the heat from inside the pump will travel through the shaft to the pump bearings and may be injurious to the bearing life. In the closed feedwater cycle, all de aeration takes place in the condenser, and therefore the injection water is fully deaerated. Although this is not quite true in the open cycle, an appreciable amount of deaeration takes place in the condenser even though a deaerating heater is provided in the feed cycle. Thus the injection condensate in a modem steam power plant will contain almost no oxygen (0.01 cc per liter or less). As the saturation level at a temperature of 38°C (lOO°F) and atmospheric pressure is Breakdown Seals 199 about 4.7 cc per liter, the oxygen in the injection supply itself has no significance. Moreover, the amount of injection water that enters the pump proper and is not returned to the condenser is very small. Thus no appreciable contamination of the feedwater will take place through the condensate injection sealing. The one exception to this general rule can occur in an open cycle with a suction booster ahead of the feed pump (Fig. 10.4). If both the feed pump and its suction booster have breakdown-type seals, and condensate injection is achieved with a booster pump, the injection pressure available at the booster pump is appreciably higher than its suction pressure. Unless the seal injection flow into the booster pump seals is carefully controlled, the flow of partially deaerated condensate into the feedwater can be high enough to materially raise the oxygen content. The amount of the injection water will depend on (1) the diameter of the seal, (2) the clearance between the shaft sleeve and the pressure breakdown bushing, and (3) the injection pressure. To give some general idea of the values in question, if the sleeve diameter is 125 mm (5 in.) and the diametral clearance 0.225 mm (0.009 in.), the amounts measured in a 3,600-rpm pump will be approximately as follows: 1. 2. 3. Total injection per seal-1.8 to 2.3 m3/hr (8 to 10 gpm) Leakage into the pump interior, per seal-0.4-0.9 m 3/hr (2 to 4 gpm) Return to condenser, per seal-1.4-1.8 m 3/hr (6 to 8 gpm). It is essential that the injection supply be absolutely clear and free of foreign matter. It is, therefore, necessary to install filters or strainers in the injection line to avoid the entrance of fine mill scale or oxide particles into the close clearances between the stationary bushings and the sleeves. Pressure gages should be installed upstream and downstream of these filters to permit the operator to follow the rate at which foreign matter clogs up the filters and to clean these when the pressure drop across them becomes excessive. For overall reliability, the source of injection condensate must be adequate for all likely operating conditions. To ensure this, the following influences need to be taken into account: 1. 2. 3. Variations in the pressure at the pump's seals over the entire range of operating flows (see open cycle and closed cycle) An increase in the pressure at the seals as the pump's running clearances wear. This refers specifically to those clearances located adjacent to the shaft seals (e.g., the balancing device in Fig. 10.5). As these wear, the higher leakage raises the back pressure in the region of the seal. Higher seal injection flows to maintain the same injection pressure (or seal drain temperature) as the seals wear. DRAINS FROM CONDENSATE INJECTION SEALING Two different systems are used to dispose of the drains coming from the collecting chambers. The first utilizes traps that drain directly to the condenser. The second collects the drains in a condensate storage tank into which various other drains are also returned. As this tank is under atmospheric pressure, it must be set at a reasonable elevation below the pump centerline so that the static elevation difference will overcome friction losses in the drain piping. A pump then transfers the condensate drains from the storage tank into the condenser. To our knowledge, no specific difficulties have ever taken place in installations in which the injection sealing condensate is evacuated through traps, except for an isolated case of trap malfunctioning. Proper maintenance of this equipment should hold such occurrences to an absolute minimum. A minor problem may arise if boiler feed pumps are operated during the start-up before condenser vacuum is established. 200 Breakdown Seals FILTERED CONDENSATE INJECTION t STATION AIR SUPPLY STATION AIR SUPPLY I CONTROL DIAPHRAGM VALVE t AIR X-;>-_~_·~lTanf ER SI B~!!.S~~~~ I SENSING LINE __ I r---~ I I I II I' BLEEDOFF TO DEAERATORA OR BF PUMP SUCnON ( IF NO BLEEDOFF IS REQUIRED ) DRAIN BALANCING DEVICE LEAKOFF Fig. 10.5 Pressure control of condensate injection. This operation causes a rise in the back pressure on the seal drains and, unless provision is made to relieve this back pressure, some overflow of injection condensate may take place at the collecting chamber covers. Neither system of evacuation has major advantages over the other, and the choice between the two is dictated primarily by personal preferences. However, if the boiler feed pumps are located at the lowest plant elevation (in some outdoor plants, for instance), it becomes necessary to use traps because there is insufficient elevation difference to drain from the collecting chambers into an open tank. The clearances between the sleeves and the breakdown bushings will increase about 50% in a time approximately equal to the life of the internal wearing parts. With 50% larger clearances, the leakage will double. This factor should be considered when sizing the return drain piping back to the condenser or to the collecting tank if friction losses are to be kept to a minimum in this piping. The collecting chamber at the pump stuffing box is vented to the atmosphere; the only head available to evacuate it is the static head between the pump and the point of return. This head must always be well in excess of the frictional losses (even after the leakage doubles); otherwise the drains will back up and run off at the collecting chamber. The water thrown off the shaft into the ventilated collection chamber will probably reach 75 percent saturation or more before it reaches the drain pipes. Assuming that there is a considerable length of partially full piping between the collecting chamber and the trap in the drain line to the condenser, the oxygen content of the returned condensate can well be assumed to have 100 percent saturation. Although this figure may seem very high, the deaerating capacity of a modem condenser is greatly in excess of average requirements and should be amply capable of handling the oxygen in a saturated return, for it Breakdown Seals 201 makes up 2 percent or less of the normal flow. Its presence, nevertheless, makes it necessary to provide vents in the drain lines to avoid the accumulation of air pockets produced by separation of the entrained air. Without vents there is a risk of erratic drain operation, and some "cyclic" spillover at the seal covers each time a slug of air forms in the drain piping. In installations where this has occurred, a smaller "geyser" would rise from the collecting chamber vents; increasing static head in the collecting chambers would then force the slug of air out through the piping, and the geyser would subside. The installation of vents or breathers eliminated the difficulty entirely. CONTROL OF THE INJECTION To complement the advantages gained from breakdown seals in maintenance and availability, it is desirable to reduce the consumption of condensate for injection to as little as possible. Throttling valves in the seal injection lines are used to achieve this. Generally, a separate throttling valve is installed at each injection point (i.e., two valves per pump). In some early applications of condensate injection sealing, the desire to simplify the installation led to the use of two valves for each group of pumps serving a common turbo-generator unit. Such an arrangement is unable to compensate for differences in pump and seal condition (extent of wear), and is therefore no longer used. Two valves are used because the pressure on the suction and discharge sides will not necessarily be the same. An examination of Fig. 10.1 shows that the inward flow on the suction side has to overcome a pressure exactly equal to the pump suction pressure. On the discharge side, the flow will proceed into the balancing-device relief chamber. The pressure there will exceed the suction pressure by the amount of loss through the calibrated orifice in the balancing relief line, which is used to measure the leakage past the balancing device. This loss may be quite appreciable after the pump has become worn. Control of the injection throttling valves is by one of three systems: manual, pressure, and temperature. Manual Each throttling valve is adjusted manually to give the desired drain conditions. As operating conditions change, it may be necessary to readjust the valves, particularly for pumps operating in closed cycles. The valves also have to be readjusted periodically to compensate for the effects of pump and seal wear. Pressure An automatic pressure controller adjusts the throttling valve to maintain a constant pressure differential between the injection pressure and the pump's internal pressure, thus ensuring a flow of condensate into the pump under all conditions (Fig. 10.5). Pressure control compensates for changes in operating pressures, but injects a constant amount of condensate regardless of changes in condensate or pumped liquid temperature. Further, pressure control is not able to distinguish between a running and a stationary pump. At the suction end, this makes no difference, but at the discharge end, the balancing disk does quite a deal of pumping when the pump is running. This results in the pressure at the seal being below the balancing leakoff chamber pressure, which leads to higher condensate consumption since the control has to be set for the higher pressure, which prevails when the pump is stationary. Temperature Instead of ensuring a certain condensate flow into the pump, temperature control automates manual control by using a temperature controller to adjust the throttling valve to maintain a "safe" seal drain 202 Breakdown Seals FILTERED CONDENSATE INJECTION STATION AIR SUPPLY DIAPHRAGM TROI.L£ I 4 + A!!!_~X SIGNAL STATION AIR SUPPLY !== I\-D- AIR _~_,.....JI"II.,..,-.:tnI VALVE VALVE SIGNAL I I I I ITEMP • I TEMP. jSENSING LINE I'EN SING A fiNE I I I BALANCING DEVICE IL _____ ~~ _ __- i. .~L~E~A~KO~F__~~__~ I I I I I _ ______ -1I DRAIN Fig. 10.6 Temperature control of condensate injection. temperature (Fig. 10.6). With this control, the consumption of condensate is kept to the minimum necessary for all conditions. Accompanying the minimal consumption of condensate, there is a need for additional care in the design of the seal and its injection control system. This is best explained by first examining the nature of flow within a breakdown seal with temperature-controlled injection. Given a normal drain temperature of 60 to 65°C (140 to 150°F), and having injection condensate typically at 27 to 38°C (80 to 100°F), it is reasonable to hypothesize that a small flow of "hot" feedwater from the pump mixes with "cool" injected condensate to give "warm" seal leakage (Fig. 10.7). Field tests have ) TH>TD>Tc QD = QL +Qj Fig. 10.7 Flow within temperature-controlled seal. Breakdown Seals 203 ___ Approximately equal to condensate temperature Injection Pressure, Pi Fig. 10.8 Drain temperature versus injection pressure. confinned this is the case. The existence of a small flow of hot water from the pump has three ramifications: 1. 2. 3. The operating temperature of the shaft sleeve at the inner end of the seal will be higher than at the outer end. Since the labyrinth bushing has cool condensate circulating around it, it will remain cooler than the sleeve, particularly at the inner end. To compensate for this difference in operating temperatures, and hence thermal expansion, it is necessary that the inner end of the seal have a larger "cold" clearance than the outer end. Once the injection pressure is reduced to the point where there is a flow of hot water out of the pump, the drain temperature changes rapidly with only small changes in injection pressure (Fig. 10.8). To avoid flashing in the seal (see later), it is crucial to measure the temperature of the seal leakage proper, not some reservoir that would take too long to register the change in drain temperature, and to have a control system able to respond quickly to small changes in that temperature. Because there is little or no flow of cool condensate into the pump (the control valves have stops to prevent their closing entirely so there will be flow into the pump under some conditions), temperature control aids the warmup process and is critical for turbine-driven pumps, which must operate on turning gear. In the latter case, pressure control would admit large flows of cool condensate into the pump, leading to temperature stratification and consequent casing distortion, with pump seizure the likely result. Although the objective of condensate injection control is to reduce the consumption of condensate, it is of prime importance that the system be designed to avoid the possibility of inadequate injection and consequent flashing in the seals. Should flashing occur, it is likely the seal will be destroyed by rubbing between the shaft sleeve and labyrinth bushing. Compounding that, there is the possibility of shaft failure from overheating in the region of the seal rub. In this connection the control system design needs to pay due attention to the following: . 1. 2. 3. Accurate measurement of the control parameter (Le., pump internal pressure of seal drain temperature). Design pressure drop across the control valve high enough to ensure the valve has control of the injection flow. A pressure drop of 0.35 bar (5 psi) at maximum seal flow (typically two times the flow with "new" clearances) has proven operable. Control loop with minimum hysteresis. 204 Breakdown Seals We must now examine the relationship between the pressure available at the injection of the condensate and the internal pressure over the complete range of operating station loads. For reasons that will become obvious, this relationship is vastly different for open and for closed feedwater cycles. The application of breakdown seals to the two cycles should thus be studied separately. OPEN CYCLE The relationship between the various pressures under consideration is illustrated in Figures 10.3 and 10.4, both of which represent typical installations with condensate injection seals in an open cycle. In the simpler arrangement (Fig. 10.3), the feed pump takes its suction directly from the deaerator. The condensate pump discharges into a deaerating heater through a series of closed heaters. The discharge pressure at the condensate pump rises from 11.1 bar (170 psig) at full load to 14.8 bar (215 psig) at one-quarter load. The static head between the condensate pump and the deaerating heater is 24.4 m (80 ft), or approximately 2.4 bar (35 psi). The friction losses in the piping and through the closed heaters are 3.1 bar (45 psi) at full load and only 0.20 bar (3 psi) at one-quarter load. Thus the pressure immediately ahead of the heater will be 6.2 bar (90 psig) at full load and 12.2 bar (177 psig) at one-quarter load. The condensate control valve located at the entrance to the deaerating heater will vary the admission of condensate in accordance with load requirements, throttling off approximately 1.4 bar (20-psi) pressure at full load and as much as 11.1 bar (170-psi) pressure at one-quarter load. The boiler feed pump centerline is located 18.3 m (60 ft) below the waterlevel in the deaerating heater. The friction losses in the suction piping are 0.20 bar (3 psi) at full load and 0.01 bar (0.2 psi) at one-quarter load. Thus, the suction pressure at the boiler feed pump varies from 6.25 bar (90.6 psig) at full load down to 2.17 bar (31.4 psig) at one-quarter load. The internal pressure on the suction side of the pump varies the same. On the discharge side, the internal pressure will be somewhat higher. In an open feedwater cycle arranged with the feed pump taking its suction directly from the de aerator, the balancing device leakoff is either returned to the deaerator (Fig. 10.3) or directly to the pump suction. Returning the leakoff to the de aerator has a greater effect on the pump internal pressure, and so will be the arrangement considered here. The calibrated orifice in this return line can be assumed to have a loss of 0.35 bar (5 psi) and the return piping itself another 0.35 bar (5-psi) friction loss. Thus the internal pressure on the discharge side will exceed that on the suction side by approximately 0.70 bar (10 psi) and will therefore range from 6.94 bar (100.6 psig) at full load to 2.86 bar (41.4 psig) at one-quarter load. As the condensate pump is located 6.1 m (20 ft) below the boiler feed pump, the injection pressure will range from 10.7 bar (155 psig) at full load to 13.8 bar (200 psig) at one-quarter load if we assume friction losses of approximately 0.40 bar (6 psi) in the injection line. Thus the injection pressure will exceed the internal pressures at all loads. If it is desirable to minimize both the amount of inward flow and of the condensate being returned to the condenser and being repumped, the injection lines may well be provided with control throttling valves. If it is desirable to maintain, let us say, a 0.35 bar (5-psi) differential between the injection pressure and the internal pressure, the amounts of pressure to be throttled will be the following: 1. 2. At the suction side-4.44 (64.4 psi) at full load and 11.63 (168.6 psi) at one-quarter load At the discharge side-3.75 (54.4 psi) at full load and 10.94 (158.6 psi) at one-quarter load. There should be no difficulty in selecting control valves that will maintain the desired pressure differential, and the rather high value of the pressure to be throttled will permit selection of a reasonably small valve for the purpose. Breakdown Seals 205 When the feed pump takes its suction from a booster pump (Fig. 10.4), the relationship between seal and injection pressures becomes more complicated. The available injection pressure is that at the condensate pump discharge: 11.7 bar (170 psig) at full load, and rising to 14.8 bar (215 psig) at one-quarter load. With the deaerator located 10.7 m (35 ft) above the booster pump centerline, deaerator pressure ranging from 4.8 bar (70 psig) at full load to 0.5 bar (7 psig) at one-quarter load, and the suction piping losses 0.20 bar (3 psi) at full load and 0.01 bar (0.2 psi) at one-quarter load, the suction pressure at the booster pump varies from 5.6 bar (81 psig) at full load down to 1.5 bar (21 psig) at one-quarter load. For a booster pump with breakdown type seals, the injection pressure exceeds that at the seals by 5.1 bar (74 psi), at full load and 12.0 bar (174 psi) at one-quarter load after allowing 1.0 bar (15 psi) for head loss in the injection and filter piping. As discussed under source of injection, pressure differentials on this order dictate injection controls to avoid the risk of oxygen contamination of the feedwater. For the conditions described, the suction pressure at the boiler feed pump ranges from 13.0 bar (188 psig) at full load down to 10.4 bar (151 psig) at one-quarter load. Since the suction pressure at full load exceeds the available injection pressure, injection is not available, so some modification is necessary. Two approaches are used: lower the pressure at the seals or increase the available injection pressure. Lowering the pressure at the seals is accomplished by adding a pressure breakdown bushing at the suction end of the pump, then returning the suction end bleed-off and the balancing leakoff to the deaerator (Fig. 10.4). The return line has to include an antiflash orifice sized to ensure the back pressure at the balancing device is at least 0.35 bar (5 psi) above the leakage vapor pressure under all operating conditions. For the installation being used as an example, the pressure drop necessary is 1.4 bar (20 psi), the limiting condition being pump start-up with the deaerator at full load temperature. With this arrangement, the pressures at the seals and the consequent control valve pressure drops are the following Seal Discharge Suction Load Pressure at Seal bar (psig) Valve Pressure Drop bar (psi) Full 7.5 (108) (2.9) 42 Quarter 3.1 (45) (10.3) 150 Full 7.1 (103) (3.2) 47 Quarter 6.8 (98) (10.7) 155 As the balancing device and suction end bleed-off bushing clearances increase with wear, the pressure at the seals will increase by way of the higher pressure drop through the return piping and orifices. As an illustration, consider taking the suction end bleed-off flow as 25 percent of the balancing leakoff flow, an increase of approximately 30 percent in leakage (equivalent to only a 20 percent increase in running clearance) will raise the pressure at the discharge end seal to 10.3 bar (150 psig). With the pump in this condition, available injection pressure will be approximately equal to the pressure at the seal during full load operation. Given that it is generally desirable to not have to restore the balancing device clearance until it is worn to 150 percent of its new value, the system being used as an example is marginal at best. Increasing the injection pressure can be used either as an alternative to lowering the pressure at the seals, or as a means of correcting a marginal design such as the example above. For the first case, the balancing leakoff would be returned to the pump suction, typically with a total pressure drop of 0.35 bar (5 psi), all of it across the calibrated orifice. With the balancing device clearance worn to 150 percent of its new value, the leakoff pressure drop will rise to 1.1 bar (16 psi). At full load, the resultant pressure at the discharge end seal is 14.0 bar (204 psig). Allowing for injection piping and filter losses (1 bar or 15 psi total), 0.35 bar (5 psi) pressure drop across the injection valve, and a 0.35 bar (5 psi) margin of injection over seal pressure, the minimum booster pump pressure rise is 4.1 bar (59 psi), at the flow corresponding to worn seals. 206 Breakdown Seals Evaluating the marginal "lower seal pressure" design for the same worn conditions yields a pressure at the discharge end seal of 15.2 bar (221 psig). This is higher than the pressure with the balancing leakoff returned to suction, and serves to illustrate an important point. When it is necessary to include relatively high pressure drops to avoid flashing in a leakoff system, the effect of higher leakage flows as the pump wears may well negate the advantage sought. For the example used, it would be necessary to reduce the effect of increased leakage (by keeping most the back pressure constant with a regulator or elevated flash tank) if injection booster pumps are to be avoided. If that is not feasible, the simpler approach would be to return the balancing leakoff to suction and resort to booster pumps to increase the injection pressure. CLOSED CYCLE When the breakdown-type seal is applied to a closed feedwater cycle, the conditions prevailing at the discharge (balancing-device) end of the pump are actually more severe than at the suction end (Fig. 10.9). At full load and at some reduced load conditions, the injection pressure, PB, is greater than the RETURN TO SUCTION INJECTION FROM CONDENSATE PUMP Fig. 10.9 Section through injection breakdown seal at the discharge end. KEY: (A) Suction pressure plus pressure drop through calibrated orifice in balancing device leak-off line; (B) discharge pressure of condensate pump, less friction loss through supply piping; (C) essentially same as (B); (D) essentially atmospheric pressure. Breakdown Seals 207 pressure in the balancing-device relief chamber, P A, because of the friction losses between the discharge of the condensate pump and the suction of the boiler feed pump. As the pressure, Po is essentially the same as the pressure at the injection point, it also exceeds the pressure in the balancing-device relief chamber, and flow takes place inwardly from point C to point A as well as outwardly from point C into the collecting chamber, D. As the load is reduced, the friction losses between the condensate pump and the main feed pump decrease approximately with the square of the capacity. Thus at some extremely low pump loads, the boiler feed pump suction pressure may be only 0.10-0.15 bar (lor 2 psi) lower than the condensate pump discharge pressure (neglecting the static elevation difference, which is the same for both suction and injection piping). A typical example of what happens is shown in Fig. 10.2. At full load, there is ample excess pressure in the injection line to produce flow into the pump. When the load is reduced to one-quarter flow, the following situation prevails: 1. At the suction end, the suction pressure becomes 23.2 bar (337 psig) whereas the discharge pressure of the condensate pump (less the static head) is 23.4 bar (340 psig). If the injection flow remains essentially unchanged and the friction losses in the injection piping are still assumed to be 0.35 bar (5 psi), the available injection pressure is reduced to 23.1 bar (335 psig), or 0.14 bar (2 psi) less than the suction pressure. 2. At the discharge end, the pressure in the balancing-device relief chamber is equal to the suction pressure plus the loss through that calibrated orifice in the balancing relief line which is used to measure the leakage past the balancing device. When the pump is new, this loss is approximately 0.35 bar (5 psi), and the pressure in this chamber at full load is 17.6 bar (255 psig). The injection-line pressure is 19.7 bar (285 psig), and a 2.1 bar (3D-psi) differential is available to cause inward flow of injection water. At one-quarter load, the pressure in the relief chamber is 23.6 bar (342 psig), whereas the injection-line pressure is only 23.1 bar (335 psig), or 0.5 bar (7 psi) less than the relief chamber pressure. If the pump is worn and the pressure drop through the calibrated orifice is permitted to go up to 2.4 bar (35 psi), the relief chamber pressure will become 19.7 bar (285 psig), balancing exactly the injection line pressure. At one-quarter load, the relief chamber pressure becomes 25.7 bar (372 psig) whereas the injection pressure is only 23.1 bar (335 psig). Thus no excess pressure exists in a worn pump between the injection pressure and the relief chamber pressure under any load conditions. What actually does take place, then, in the packless stuffing box under these conditions? As the difference between pressures at C and A in Fig. 10.9 diminishes, less and less flow takes place inwardly from point C to point A. Finally, a condition prevails in which the pressure at A slightly exceeds the pressure at C. At that time, a small amount of feedwater flows from point A to point C and mixes with the injection water. The mixture proceeds as before toward the collecting chamber, from which it is returned to the condenser. Because of the breakdown between points A and C and because the pressure differential between them is only a fraction of the pressure differential between points C and D, the amount of this "reverse" flow is relatively small and should not raise the temperature of the mixture appreciably. Thus, even though the reduction of the pressure drop between the condensate pump discharge and the boiler feed pump suction results in a change of flow direction between points C and A, the operation of the breakdown seal remains acceptable. This description of the flow process eliminates the effects of the balancing device on the pressure at point A for the sake of simplicity. Actually, this device develops a pumping action that leaves the pressure at the shaft sleeve near point A some 1.4 to 2.1 bar (20 to 30 psi) below the pressure at the periphery of the relief chamber in pumps running at 3,570 rpm, on the order of 3.5 to 5.2 bar (50 to 75 psi) in 208 Breakdown Seals INJECTION PRESSURE-BALANCING RELIEF CHAMBER PRESSURE, PSI -80 -70 -60 -50 -40 -30 -20 -10 0 PUMP AT ~ ~ IL. C) a: 0 ~ -2 IL. i-4 ""-6 - ",... i""""'" ---- ~ ~ ~ ~ V ~ ~ ,..,.- 3~70 RPM or .....- - ~ rJ.....}- 1--'+ lL ~ r-- PUMP STATIONARY - ! ~ -B "" o 10 20 30 40 50 60 70 80 INJECTION PRESSURE-BALANCING RELIEF CHAMBER PRESSURE, PSI Figo 10.10 Effect of pump rotation on injection flow. high-speed pumps. Figure lD.lD which shows the inward leakage (from points C to A) under varying pressure differences between injection line and the relief chamber, graphically illustrates this condition. Paradoxically, some flow still takes place inwardly, even though the pressure difference is negative, as long as the pump is running. When the pump is idle, of course, the condition disappears. Of course, if a continuous flow of injection water from point C to point A is desired regardless of load, a small booster pump should be installed in the injection line, taking its suction from the condensate pump discharge and raising that pressure by some 3.5 bar (50 psi). It should be noted that no flow takes place through the balancing device when the pump is idle and that the inward pressures at the suction and discharge sides are essentially equal. Thus there should be no problem in maintaining inward sealing flow to a pump kept idle on standby service. The fundamental principle of the condensate injection seals applied so successfully to boiler feed pumps, a pressure breakdown bushing to control leakage, is not restricted to boiler feed pumps. In applications where the leakage can be readily disposed of, a breakdown-type seal often represents a lowmaintenance solution to sealing the shaft. This typically occurs when the pumped liquid is below its atmospheric boiling point and free of large, abrasive solids, thus removing the need for any injection into the seal, which simplifies the installation. Pumps applied to water injection, hydraulic descaling, and hydraulic presses are common examples of such a choice of shaft seal. A further use of breakdown seals is in a form of "sealless" pump, one in which the leakage is returned directly to the pump's suction reservoir (see Chap. 14). Breakdown Seals 209 MECHANICAL MODIFICATIONS The compromise that has to be struck in the design of a breakdown seal is between running clearance and leakage. Make the clearance too small and incidental contact between the sleeve and bushing will result in rapid wear and a commensurate increase in leakage. With a solid bushing, the clearance is that necessary to accommodate minor eccentricity and runout from manufacturing variations, and small Fig. 10.11 Floating seal ring design. 210 Breakdown Seals changes in clearance and alignment during pump operation. One solution advanced to allow smaller effective clearances without the risk of premature wear is the so-called .floating ring seal (Fig. 10.11). The essential feature of this design is to make the seal radially "flexible." This is achieved, in theory, by building up the seal with a series of alternate rings: seal rings having a close clearance over the sleeve but free to "float" radially within the seal housing; spacer rings accurately located in the seal housing and with a large clearance over the sleeve. All the rings are prevented from rotating by some form of pin-and-slot arrangement. In practice, floating ring seals have not functioned as well as the design promised. Although there were, and still are, examples of well-behaved seals, the general experience was poor; the seals typically wore at a higher rate than comparable solid bushings. The principal difficulty appeared to be limited radial flexibility, a result of not achieving sufficient axial force balance on each seal ring to allow ready radial movement. But for isolated installations, floating ring seals are no longer used in boiler feed pumps. With axial face (mechanical) seals demonstrating adequate capability for most services, there is little incentive to refine the design until it works as expected. 11 Bearings ------------~-~-----~--~- ... - ~~~- -.-~~--- - - - - - - Centrifugal pumps require bearings to allow the rotor to tum while maintaining correct alignment between the rotor and the pump's stationary parts under the action of radial and axial forces. Their design, therefore, is as critical as any of the other major pump parts; a pump with unreliable bearings is a continual cause of unnecessary outages and maintenance expense. The provision of adequate bearings is not an easy task. Doing so is the pump designer's responsibility, but some understanding of the process can aid equipment evaluation and trouble shooting, should that be necessary. To start the process, the designer first determines accurately the bearing loads over the pump's expected operating flow range. These data are supplemented with any unusual environmental conditions that could influence the design, for example, high pumping temperature or pumps that are exposed to wind-driven dust or frequent hosing down. Using these data, the designer then adopts a sequence similar to the following to develop the design: 1. Select bearing type and size. 2. Select means of lubrication. 3. Check heat load and dissipation; provide supplementary means of dissipation if necessary. 4. 5. 6. Verify stiffness of bearing housing to avoid both bearing misalignment and resonant vibration. Check the effect of bearing and bearing housing stiffness on the dynamic behavior of the pump's rotor. Select means of sealing the bearing housing. Each of these steps involves the consideration of several factors, all of which are dealt with in the relevant sections of this chapter. BEARING ARRANGEMENTS Most centrifugal pumps are equipped with external oil- or grease-lubricated bearings in a classical twobearing arrangement. The bearing providing radial location is called a line bearing; that providing axial 211 I. J. Karassik et al., Centrifugal Pumps © Chapman & Hall 1998 212 Bearings location, a thrust bearing. To realize the two-bearing arrangement, many designs have the thrust bearing providing both radial and axial location. Others incorporate a radial and thrust bearing in one housing, which is usually designated as the thrust bearing. Overhung pumps, those with cantilever rotors (Fig. 11.1 [aD, have both the line and thrust bearings on one side of the impeller. By convention the bearing nearer the impeller is designated the inboard bearing and that farther away the outboard bearing. Generally, the outboard bearing is the thrust bearing to better balance the total bearing loads. In pumps with the impeller or impellers between the bearings, a simply supported rotor (Fig. 11.1 [bD, convention has the bearing adjacent to the coupling designated the inboard bearing, that at the opposite end of the pump the outboard bearing. Again, usual practice is to have the outboard bearing the thrust bearing to allow an optimum bearing selection (a thrust bearing at the inboard location would be influenced by the shaft size necessary to transmit the pump's torque). Fr -·-- L1 1 ----L2- - Inboard Outboard - Coupling - - - RT (a) Overhung (cantilever) rotor - Outboard I L2 --··l. . >-~-r-- L1 - Inboard I Coupling (b) Between bearings (simply supported) rotor Fig. 11.1 Basic rotor configurations: (a) overhung (cantilever), (b) between bearings (simply supported). Bearings 213 In modem pump designs, the bearings are almost invariably mounted in housings attached directly to the pump casing. Occasionally the bearings for very large vertical and horizontal pumps are mounted in housings attached to the pump's baseplate or foundation. In the case of horizontal pumps, this arrangement is known as "pedestal bearings." In many centrifugal pump configurations, the classical two-bearing arrangement cannot provide sufficient rotor support to maintain internal alignment. This is primarily a consequence of low rotor stiffness, and necessitates a multiple-bearing arrangement, with some of the bearings usually located within the pump proper. These internal bearings pose a special set of problems (see internal bearings). For a given set of imposed loads, radial and axial at the impeller, bearing loads vary significantly with rotor configuration and geometry. To illustrate the point, consider the rotors shown in Fig. 11.1 are subject to a maximum radial load, F" of 2,200 N (500 lb) and an axial thrust, Fa, of 4,400 N (1,000 lb). Applying these loads to two versions of a cantilever rotor and one of a simply supported rotor produces the bearing reactions, RL and Rr , set out in the table. RT-N Rotor LI-mm L2 Cantilever Cantilever Simply supported 254 191 254 RL Radial Axial Total 254 125 254 4,440 5,550 1,110 2,220 3,330 1,110 4,440 4,440 4,440 4,970 5,550 4,580 RL Radial Axial Total 500 750 250 1,000 1,000 1,000 1,118 1,250 1,031 RT-lb Rotor LI-in L2 Cantilever Cantilever Simply supported 10 7.5 10 10 5 10 1,000 1,250 250 Two significant points need to be drawn from these results. First, although the second cantilever rotor is, for the same diameters, notably stiffer than the first (65 percent less deflection; see shafts in Chap. 7), both the bearing reactions are higher, 25 percent at the line bearing, 12 percent at the thrust bearing. For these two-bearing frames to have the same nominal bearing life, the bearings on the stiffer shaft would have to have correspondingly higher basic capacities (see bearing life in this chapter). If rotor geometry is not taken into account when evaluating cantilever bearing frames, the evaluation can be quite misleading. Second, changing to a simply supported rotor results in lower bearing reactions than even the best case cantilever rotor, 75 percent lower at the line bearing and 8 percent lower at the thrust bearing. (The lesser reduction at the thrust bearing is a product of the high axial thrust chosen for this example). Evidently it is easier to achieve high bearing integrity (low bearing loads relative to basic capacity) with a simply supported rotor than with a cantilever rotor. In small, low duty pumps (single stage, 10 to 12-in. discharge), the cost advantage of a simply supported rotor typically does not offset the higher costs of other aspects of a between-bearings pump (heavier, more complex casing, additional shaft seal, and bearing housing). For heavier duty single- and almost all multistage pumps, between bearings is the normal configuration. In some services, however, such as sewage and slurry, the needs of the liquid end design dictate overhung construction regardless of size. Very large pumps, those used for water transfer and pumped storage, are overhung when vertical, the usual arrangement of modem designs, and between bearings when horizontal. 214 Bearings Fig. 11.2 Internal sleeve bearing. BEARING TYPES Centrifugal pumps employ a wide variety of bearing fonns, ranging from simple internal sleeve bearings (Fig. 11.2) in low-cost water pumps to electronically controlled magnetic bearings in sophisticated highenergy pumps. All of the fonns, however, can be classified as one of three types, based on their method of operation: 1. Antifriction or rolling element 2. Plain; either boundary lubricated, hydrodynamic, or hydrostatic 3. Magnetic ANTIFRICTION BEARINGS Relative motion within the bearing is through the rolling action of balls or rollers between an inner and outer race (Fig. 11.3). The tenn "antifriction" derives from the very low coefficient of friction associated with rolling motion as distinct from sliding motion. To function correctly, the rolling elements in antifriction bearings must be kept equally distributed around the bearing. This is achieved with a separator or cage (Fig. 11.3). Although the fundamental motion in antifriction bearings is rolling there is nevertheless some sliding present. First, the rolling elements are subject to dynamic action (acceleration and deceleration) as they pass into and out of the loaded zone of the bearing, or as the rotor's speed is varied during the course of operation. Second, there is defonnation at the points of contact between rolling elements and races, the consequent "imperfect geometry" resulting in local sliding motion. Third, the cage or separator comes into contact with the rolling elements in the course of keeping them in position. To minimize the heat generated at these points of sliding friction, antifriction bearings require lubrication. Bearings 215 , . . . - - - - - - - Outer Ring Raceway r - - - - - - - Outer Ring Land Cage ---_~~ Inner Ring ---1tf);.~=--.) ----jL-_ _ _ _ _ Bore Surface ,...,J...J::::;;;T-=;----- Inner Ring Raceway +---- Inner Ring Land Outer Ring ---:".-c-+- ' - I- -+- - - - 00 Surface Side Faces Figure 11.3 Rolling-element bearing. (Courtesy SKF Industries, Inc.) TYPES AND APPLICATIONS There are many types of antifriction bearings. To make assessment a little easier, it is common to differentiate between "ball" and "roller" bearings. Of these two, ball bearings are the more common in centrifugal pump practice, since they offer an excellent compromise between capability and cost. Roller bearings have greater capability, but are more expensive and so are only used when the higher cost is justified. Most centrifugal pumps are equipped with single-row deep-groove ball, or Conrad, bearings (Fig. 11.4). This configuration can accommodate both radial and axial loads, the latter in either direction, has reasonable speed capability, and can tolerate misalignment up to 0.25 deg. An alternate design with a filling slot in the inner race allows more rolling elements, which increases the radial load capacity by 20 to 40 percent, but reduces thrust capacity and tolerance of misalignment by approximately 70 percent. When used at all, filling slot bearings should be used in an arrangement which allows only radial loads. Some industry specifications preclude their use regardless of loading. For loads beyond the capacity of single row ball bearings, the usual next choice is a double-row arrangement (Fig. 11.5). Although the radial load capacity is approximately 50 percent higher, the maximum speed is lower, a consequence of the greater number of rolling elements within the bearing. Thrust capacity and tolerance of misalignment depend on the detail design of the races. Designs with the ball load paths converging outward (usual) generally have filling slots, hence low thrust capacity and can tolerate only 0.05 deg misalignment. Those bearings with the ball load paths converging inward (less usual) have higher thrust capacity and can tolerate more misalignment, but in no case more than a single-row bearing. These limitations in speed, thrust capacity and misalignment often dictate the choice of another bearing type. If the designer foresees significant misalignment at the bearing (up to 2.5 deg, which in these days when the advantages of relatively stiff shafts are well understood should be the exception), a self-aligning ball bearing is available (Fig. 11.6). The bearing is double row to achieve a radial load capacity of 216 Bearings Figure 11.4 Single-row deep-groove ball bearing. (Courtesy SKF Industries, Inc.) Figure 11.5 Double-row deep-groove ball bearing. (Courtesy SKF Industries, Inc.) Figure 11.6 Self-aligning double-row ball bearing. (Courtesy SKF Industries, Inc.) Figure 11.7 Single-row angular-contact ball bearing. (Courtesy New Departure.) approximately 70 percent of the comparable single-row deep-groove bearing. With a spherical bore in the outer race, the thrust load capacity of self-aligning ball bearings is negligible, and they should be arranged for radial loading only. As the ratio of axial to radial load increases, it becomes necessary to introduce some matching angularity into the ball load paths. Such bearings are tenned angular contact and are available with contact angles ranging from 15 to 40 deg, although for high-speed angles above 30 deg are not recommended. Single-row angular-contact bearings (Fig. 11.7) have approximately the same radial load capacity as comparable deep-groove bearings while offering up to 2.3 times the thrust capacity but in one direction only. Misalignment tolerance is limited to 0.03 deg. Given their unidirectional thrust capacity, singlerow angular-contact bearings are used in centrifugal pumps only when it is certain the applied thrust will always be in one direction, such as it generally is in vertical turbine pumps. Bearings Figure 11.8 Two single-row (duplex) angular-contact bearings mounted back-to-back. (Courtesy New Departure.) Figure 11.9 217 Two single row (duplex) angular-contact bearings mounted face-to-face. (Courtesy SKF Industries, Inc.) Most centrifugal pumps exhibit axial thrust in both directions, the direction generally changing with operating flow or pump condition or both. When the load in either direction requires an angular contact bearing, the usual practice is to use a duplex arrangement of "ground face" or "matched" single-row bearings to provide bidirectional thrust capacity. There are two possible arrangements, usually known as mounts: "back-to-back" (Fig. 11.8) and "face-to-face" (Fig. 11.9). Several aspects of the application of duplex angular-contact bearings are currently quite controversial, and so warrant discussion in detail. 1. Mounting-From strict geometric considerations, duplex angular-contact bearings as applied to most centrifugal pumps should be mounted face-to-face. With the ball load paths converging inward, the bearing assembly offers the lower resistance to moments and so approaches the point support condition assumed in its loading calculations. There is a body of opinion opposing this on the grounds that the higher moment capability of back-to-back mounting contributes to rotor stiffness (which it undoubtedly does in the case of low stiffness shafts but at considerable expense to bearing loading). Ease of assembly and handling favors back-to-back mounting since it is not possible to accidentally dislodge the outer races. Both mountings tend to "pump" lubricant, back to back from the center out, face to face in toward the center. With back-to-back mounting it is therefore ideal if the lubricant is introduced between the bearings, which requires accurately matched spacers for the inner and outer races. In the absence of this complication, it is often necessary to use an oil ring at each side of the assembly to ensure enough lubricant finds its way into the bearings. Face-to-face mounting requires care to ensure an excess of lubricant is not retained within the bearing leading to churning and subsequent overheating. 218 Bearings 2. 3. Preload-In applications involving high unidirectional thrust and pumps with duplex 40 degree angularcontact bearings, there have been instances where skidding between the balls and races in the unloaded bearing has caused premature failure. One remedy advanced to cure this problem has been to mount the bearings with a "light" preload. The difficulty with this requirement is that component tolerances involved in the bearing assembly produce a far wider range of installed bearing preload than was originally intended. If the preload is too high, the additional loading from thermal expansion as the bearing warms up produces loads high enough to cause immediate failure. Making the inner race a slide fit avoids much of this difficulty, but poses the risk of fretting corrosion of the shaft under the bearing. Unless the pump is known to be subject to high thrust in one direction, there is now general agreement that duplex angular-contact bearings should not be preloaded. Contact angle-Past practice has been, and some industry standards (e.g., API 610) have mandated it, to have both bearings of a duplex arrangement equal, the logic being that the assembly cannot be made back to front. In an attempt to overcome the problem that pre loading sought to correct, some bearing manufacturers are offering duplex arrangements in which the nominally unloaded bearing is a 15-deg contact angle. In this way, the bearing assembly offers bidirectional thrust capacity, although of unequal values, with the lower capacity bearing better suited to running unloaded. Field experience suggests the arrangement realizes its claims, the only qualification being that the assembly must be installed in the correct direction. For thrust loads beyond the capacity of a single angular-contact bearing, there has been a practice of using duplex angular-contact bearings mounted in tandem (Fig. 11.10) to provide higher unidirectional capacity. This rather complex arrangement, usually involving three bearings in total for bidirectional thrust capability, is particularly difficult to lubricate and is now rarely used. Modem practice is to employ a single bearing of inherently higher capacity, for example, a tapered roller (see later). Double-row angular-contact bearings (Fig. 11.11) are nominally the equivalent of a duplex pair. Their usual arrangement is with ball load paths converging outward or back-to-back. Basic bearing capacity Figure 11.10 Two single-row (duplex) angular contact bearings mounted in tandem. (Courtesy SKF Industries, Inc.) Figure 11.11 Double-row angular-contact ball bearing. (Courtesy New Departure) Bearings 219 Figure 11.12 Cylindrical roller bearing (without end rings). (Courtesy SKF Industries, Inc.) Figure 11.13 Double-row spherical roller bearing. (Courtesy SKF Industries, Inc.) is approximately 50 percent higher than that of the same size single-row bearing. Thrust capacity, however, is reduced in one direction by the presence of a filling slot, needed to allow bearing assembly. Given this limitation, double-row angular-contact bearings are used only when the thrust loading is low and incidental. Some industry specifications preclude their use regardless of loading. Roller bearings generally have higher basic capacities than ball bearings of equal size. Except for one type, cylindrical or barrel roller, roller bearings have lower speed limits than equal size ball bearings, and in all cases they are more expensive. Cylindrical roller bearings (Fig. 11.12) are intended for high radial loads and high speeds. The standard bearing does not provide any location between the inner and outer race, so it is necessary to positively locate the outer race in the bearing housing. The inner race typically is mounted with an interference fit and located against a shoulder on the shaft. Inner-races with locating rings are available, but in centrifugal pump practice these additional points of sliding friction are usually avoided. Although termed "cylinders," the rolling elements are actually barreled slightly (relieved at each end) to avoid stress concentration at the ends of the rollers. Even with this refinement, allowable misalignment is only 0.08 deg, meaning that shaft stiffness has to be particularly high to ensure the bearing functions as intended. Care is needed in bearing and related component design to avoid premature failure caused by roller skidding in lightly loaded, high-speed bearings. European pump designs employ cylindrical roller bearings quite extensively. As of this writing, the opposite is the case in the United States. For high loads at low to moderate speeds, spherical roller bearings are frequently the only feasible antifriction bearing selection. In centrifugal pump practice, the double-row convex configuration (Fig. 11.13) has been used quite extensively as the line and thrust bearing when the expected axial thrust was 220 Bearings low, and as the line bearing only when high axial thrust was expected. This usage derives from the bearing's geometry; with the axis of the rollers inclined at a small angle from the shaft axis, thrust capacity is low, typically on the order of 25 to 30 percent of radial load capacity. With a spherical bore in the outer race, tolerance of misalignment is high, 1.5 deg being the limit normally quoted. Recent advances in bearing geometry have increased speed capability. Applications at the upper end of published speed limits need care with lubrication (see lubrication in this chapter) to ensure overheating is not a problem. Thrust loads beyond the capacity of angular contact bearings can be accommodated by a spherical roller thrust bearing (Figure 11.14) provided the speed is low. Two roller designs are used: symmetric and asymmetric, the latter offering 50 percent higher bearing capacity. Misalignment tolerance is quoted at 3.0 deg. Radial load capacity is limited, again a function of the bearing's geometry; therefore if the loading includes a high radial component, a separate radial bearing is used. Typical applications of spherical roller thrust bearings have been large vertical wet pit pumps, and large sealed (as distinct from hermetically sealed or "sealless") boiler circulating pumps. Tapered roller bearings accommodate both radial and axial loads. Single-row bearings (Fig. 11.15) typically have thrust capacity on the order of 60 percent of radial load capacity, but this does vary with the design of the bearing (inclination of the roller axes), and is significantly higher in bearings designed for high thrust. Except in the case of thrust bearings subjected to a high unidirectional load, tapered roller bearings must be used in pairs, either separate (Fig. 2.19) or duplex (Fig. 11.16). This is necessary to maintain the bearings in their correct position and to resist the axial reaction that is produced when radial load is applied to one of the bearings. (Note that when the axial reaction is opposed by a higher ~~'~ !f\ ,\------. ..... t~ \. ~ ~".. :1_ .~ I \ ~-~~ J.~ ----..;;;;;;: Figure 11.14 Spherical roller thrust bearing. Figure 11.15 Single row tapered roller bearing. (Courtesy SKF Industries, Inc.) (Courtesy Timken, Inc.) Bearings (a) 221 (b) Figure 11.16 Duplex tapered roller bearings: (a) mounted back-to-back (b) mounted face-to-face. (Courtesy Timken, Inc.) external thrust, only one bearing of the pair has a resultant axial load.) Tapered roller bearings have limited tolerance of misalignment, therefore designs using separate bearings require high-stiffness shafts and accurately aligned housing bores. Such designs also require provision for adjustment to set the bearings at the correct "cold" or "bench" and play to allow for thermal expansion as the assembly warms to operating temperature. In centrifugal pumps, duplex tapered roller bearings are frequently resorted to when the loading and speed exceed the capabilities of duplex angular contact bearings. Of the two arrangements face-to-face is preferable because it more closely approached point support and is therefore less susceptible to extraneous loads from minor misalignment. As with separate bearings, duplex assemblies must have the correct "bench" end play when cold. To reduce the risk of incorrect adjustment, duplex assemblies are generally furnished preset with a precision spacer between the cups or cones depending on the mounting arrangement. As tapered roller bearings are loaded, the taper of the rolling elements results in a small force tending to push the rollers out from between the races. This force is resisted by the cone rib. As the speed of the bearing increased, lubrication at this point of sliding friction becomes critical (see lubrication in this chapter). 222 Bearings ANTIFRICTION BEARING LIFE When correctly installed, operated, and maintained, antifriction bearings ultimately fail by fatigue of their rolling elements and receways. Out of a great deal of testing, the bearing manufacturers collectively have developed standard equations to determine the basic capacity, designated C, for the various bearing types. Because the mode of failure is fatigue, there is inherently some spread in the test results, so the basic capacity has a probability assigned to it. For regular machine applications such as centrifugal pumps, the basic capacity of a bearing is that load at which 90 percent of production will meet or exceed "standard" life. The service life in a particular application is calculated from the ratio of the bearing's basic capacity to the equivalent bearing load, P. To arrive at the equivalent bearing load, the designer first has to determine the actual axial and radial loads the bearing will carry. These loads, designated Fa and Fro respectively, are converted to an equivalent load using the equation P =XFa + YFr where X and Yare factors dependent on the bearing geometry, and in some instances the nature of the loading (i.e., the ratio F alFr). The factors are obtained from the bearing design manual. With the equivalent bearing load, P, and the bearing's basic capacity, C, the designer calculates the bearing life, designated LIO for 10 percent probability of premature failure, using the equation LIO = (c/p)n where the bearing life is in millions of revolutions, and the exponent n is 3 for ball bearings 10/3 for roller bearings reflecting the difference in stress distribution in the two bearing types. Research into bearing fatigue life is a continual process, and as a result some manufacturers include in their design manuals various "life correction" factors. Generally, these take account of actual lubrication conditions, which can both increase and decrease the theoretical life, and the level of impurities in the bearing materials. LUBRICATION OF ANTIFRICTION BEARINGS In the layout of a line of centrifugal pumps, the choice of the method of bearing lubrication is determined by application requirements, cost considerations, and in many instances the requirements of the principal market for the particular pump type. Application requirements is a broad term, encompassing both the functions the lubricant has to perform for the particular bearing type, and the dictates of the service for which the pump is to be used. For example, the application requirements of a low-speed plain bronze lineshaft bushing in a cold-water pump are distinctly different from those of a high-speed antifriction bearing in a high-temperature hydrocarbon pump. For antifriction bearings, the principal functions of the lubricant are to minimize the heat generated at the various points of sliding friction in the bearing, and to provide elastohydrodynamic lubrication at the points of true rolling contact. At the same time the lubricant has to serve as a heat transfer medium, protect the highly finished bearing surfaces from corrosion, and help maintain the bearing housing environment. Bearings 223 Speaking broadly, antifriction bearings are almost exclusively lubricated with either grease or oil, the latter by at least five distinct methods. This derives directly from the need to protect the bearing components from corrosion and abrasive solids. Only in rare instances, hermetically sealed cryogenic pumps for example, is the nature of the pumped liquid such that it can be used to lubricate antifriction bearings. And in those rare instances, the bearings are generally of special materials needed for the service environment. Grease lubrication (Fig. 11.17) offers simple design, low cost, and reliable operation, and is therefore widely used in centrifugal pumps. It is ideally suited to low-speed pumps, used either intermittently and so needing extra protection against bearing corrosion, or in severe service environments, such as mining, where there is a critical need to exclude the atmosphere from the bearing housing. Vertical pumps are often grease lubricated because it is easier to prevent leakage of the lubricant down the shaft (Fig. 11.18). CENTERtNG JACK-SCREW Figure 11.17 Typical mounting of ball bearings in double-suction pump. Pump uses grease lubrication; the vertical jack-screw is for initial centering of the rotor in its wearing rings. Figure 11.18 Ball-bearing construction with seal in vertical pump. Seal guards against escape of grease. 224 Bearings Grease is a suspension of oil in a carrier, usually a metallic soap, and provides lubrication by the moving parts of the bearing becoming coated with oil as they contact the grease. Because there is essentially no flow of lubricant through or around the bearing, heat dissipation is limited, and so the maximum speed at which the bearing can be operated is also limited, generally to some 70 percent of the limit for oil bath lubrication. The negligible circulation of lubricant has a second effect; it is necessary to periodically remove the spent grease from the bearing, replacing it with fresh grease to relubricate the bearing. How frequently this must be done depends on the type of bearing, its size, and the speed at which it is being operated (see antifriction bearing maintenance). The need for relubrication imposes some special requirements on the design of housings for grease lubricated bearings. During relubrication the spent grease must be completely removed from the bearing. For convenience, this is usually done by arranging the housing to allow fresh grease to purge the bearing of spent grease, and providing a means of accommodating or expelling the spent grease. Figure 11.17 shows a housing designed to accommodate spent grease (although it will need to be cleaned out at major overhauls). Expelling spent grease is accomplished with either a normally plugged drain connection or an automatic grease relief valve (Fig. 11.19). Grease is classified by stiffness, dropping point (temperature at which the oil separates from the grease), and carrier compound. The National Lubricating Grease Institute lists nine stiffness grades, 000 to 6, based on tests by ASTM method D217, and there are at least nine generally recognized carrier compounds, each having a particular dropping point and other characteristics such as moisture resistance, oxidation resistance, behavior at high temperature, and so on. The choice of grease for a particular application depends on bearing size, operating speed, operating temperature, and the pump's operating environment, with high ambient humidity or wind-driven dust dictating special care. For antifriction bearings a grease of #2 consistency provides a good balance between oil feeding capability and resistance to churning within the bearing. Larger bearings, those with unsupported grease depths greater than 1.2 in., usually require a grease of #3 consistency to avoid having the grease slump into the bearing. Lithium soap is the most widely used carrier, offering a working temperature range of -29 to 121°C (-20 to +250°F), very good resistance to oxidation, good corrosion protection (with additives), and good water resistance. For bearing service conditions outside the range of lithium soap greases, it is best to consult a lubricant manufacturer. Figure 11.19 Automatic grease relief valve. Bearings 225 LINE BEAR ING HOU5 INC Figure 11.20 Oil bath lubrication with constant-level oiler. Oil lubrication overcomes the speed limitation inherent in grease lubrication, but at the expense of added complexity. Just how much added complexity depends on the precise method of oil lubrication, a choice made on the basis of expected or actual operating conditions. Oil bath (Fig. 11.20) is the simplest of the methods of oil lubrication. Oil is maintained at a level nominally 0.3 to 0.5d above the bottom of the lowest rolling element (where d is the diameter of the rolling element). Lubrication is effected by the passage of the rolling elements thru the oil bath. A constant level oiler (Fig. 11.20) is the usual means of maintaining oil level. In applications where the bottle of a constant level oiler is likely to be broken, the bearing housing is provided with a sight gage to indicate the actual level. Adding a flinger contributes to oil lubrication in one of two ways. In the simpler arrangement, the flinger, usually a "lobed" shape, creates an oil mist within the bearing housing, and so increases the range over which the oil level can vary without impairing lubrication. The more complicated arrangement uses the flinger to increase the rate of oil circulation in the housing beyond that achieved with oil bath lubrication. This is necessary as pump operating speeds or pumping temperatures or both increase. In the usual arrangement (Fig. 11.21) the circular flinger picks up oil from the housing sump and throws it against the housing wall. The oil then drains into feed canals in the housing, which convey the cooled oil to the bearing. As the operating speed of antifriction bearings approaches its upper limit, most of the heat generated by the bearing is a result of the rolling elements churning the lubricant. To avoid overheating under these conditions, it is necessary to provide only just as much oil as the bearing needs for lubrication and heat dissipation. Of the three methods used to do this, oil-ring lubrication is the simplest. In the classical arrangement (Fig. 11.22), the oil level in the bearing housing is set below the bearings. Oil is picked up from the sump by an oil ring, and transferred to the bearing by what is effectively "splash lubrication." An alternative design, necessary for large bearings running at or close to their maximum speed, is to convey oil to the bearing using feed canals as already discussed for flinger lubrication. The second method is pure oil mist lubrication. With this approach, the bearing housing is set up for 226 Bearings Figure 11.21 Flinger lubrication. Bearing bracket integral with housing; bearing housing jacketed for cooling. dry sump operation (Le., no oil is retained in the housing), and oil mist is supplied to the housing from a centralized mist generator (Fig. 11.23). The bearing housing (Fig. 11.24) is designed to ensure the oil mist passes through the bearing, thereby providing lubrication and cooling. Most of the oil mist accumulates in the housing (up to 10 percent can be lost to the atmosphere through vents and seals), where it condenses and is drained out to a collection vessel. Although dependent on an external system, a factor that often reduces reliability, pure oil mist lubrication has yielded a distinct improvement in bearing lives in refinery pumps. In many instances, its use has led to simpler overall installations by allowing high-temperature pumps to operate without cooling water. Purge oil mist is related to pure oil mist lubrication, but only in that it uses mist supplied from a central system. The function of purge oil mist is to exclude the atmosphere from the bearing housing. Lubrication of the bearing is by oil bath, flinger, or oil ring, as already described. The housing differs from the normal arrangement only by the addition of an overflow drain (Fig. 11.25) to remove the condensed mist. Purge oil mist has seen great usage in high-humidity environments, where bearing housings vented to the atmosphere are prone to water contamination of the oil, a circumstance that can lead to a significant reduction in bearing life (see Armstrong et al. [11.1]). Forced circulation is used when the service conditions, load, speed, or heat load from the process require heat dissipation beyond the capacity of pure oil mist. Filtered and cooled oil is supplied to the bearing housing from a small lubricating oil system, then directed to the bearing's rolling elements by drilled ports or spray nozzles (Fig. 11.26). After passing through the bearing, the oil is drained from the housing back to the lubricating oil system. In most cases for centrifugal pumps, the bearing housing is arranged for dry sump operation, since high speed is generally a factor in the application. Bearings Figure 11.22 Oil-ring lubrication. Bearing bracket integral with casing cover; the bearing housing is fan cooled. G Air supply Dr----+--.&. . .---+ ...... .....,..-~ ~ ---- -----t- --- IReservoir~ I I I I _.--~ ..... : Oil mist console I 1______ - - - - - - - - - - - - - - - - - - - MR MR MR MR MR SR MR MR SR MR MR MR MR = Standard mist reclassifier, for light to moderately loaded antifriction bearings. Also used for purge mist applications. SR = Directed mist reclassifier. For heavily loaded antifriction bearings and bearings with pitch line velocities over 10.2 mls (2000 ftlmin). Figure 11.23 Central system for oil-mist lubrication. (Courtesy Bloch) 227 228 Bearings PURE-MIST (DRY SUMP) LABYRINTH SEAL O IL RINGS AND FLINGERS REMOVED MIST-ALL" DRAIN ASSEMBLY ,/ WITH OVERFLOW VENT Figure 11.24 Bearing housing with pure oil mist lubrication. (Courtesy Alemite Division of Stewart Warner Corporation.) PURGE- MIST (WET SUMP) d MIST·ALL" PURGE·M IST ASSEMBLY SPRAY FITTING'.,.J-_ _--. CONSTANT LEVEL OILER MIST·ALL" OIL LEVEL /- DRAIN A$SEMBL Y WITHOUT VENT Figure 11.25 Bearing housing with purge mist. (Courtesy Alemite Division of Stewart Warner Corporation.) Bearings 229 OUTLET FOR WETSUMP (STATIC LEVEL) MUST BE AT THIS LEVEL ON ONE -orr::J.:..:.=.~ . OR BOTH SIDES ~~;1;P" OIL OUTLET FOR DRY SUMP BOTH SIDES Figure 11.26 Forced lubrication of anti-friction bearing. (Courtesy SKF Industries, Inc.) Lubricating oils are rated by viscosity, viscosity index (a measure of the change in viscosity with temperature), pour point (lowest temperature at which the oil will pour), flash point (temperature at which oil gives off flammable vapors), oxidation resistance, and special properties such as extreme pressure capability or foaming resistance imparted by additives. Of these properties, viscosity is the most important. The viscosity required for a particular application depends on the bearing's size and speed, larger bearings running at lower speeds requiring higher viscosities (see Fig. 11.27). Note that the viscosity determined from Fig. 11.27 is that at the oil's operating temperature. This is typically 3 to 5°e (5 to 20°F) above that of the bearing housing surface. Oil viscosity ratings are quoted today for a "standard" temperature, commonly 40 0 e or 104°F, therefore a second chart is required to convert the viscosity at operating temperature to a viscosity rating. Figure 11.28 is one such chart. As noted in Fig. 11.27, the oil viscosity derived from it is the minimum acceptable. Within limits, higher bearing lives can be achieved by using a higher viscosity. The limiting factor is increased heat generated by churning of the more viscous lubricant within the bearing. Generally solvent refined mineral oils are most satisfactory for temperatures up to 82°e (180°F). At higher temperatures the oxidation rate (which doubles for each lOoe (18°F) temperature rise) becomes too high, and if the oil cannot be cooled it is necessarj to resort to synthetic oils. In applications where very low ambient temperatures are likely, it is important to ensure the pour point of the oil is above the minimum temperature. This may require a higher-than-normal viscosity index, or providing some means of warming the oil. For highly loaded bearings operating at high speed, particularly roller-type bearings, specially compounded oils are generally necessary to realize the best results. The bearing manufacturer or a reputable lubricant manufacturer should be consulted in such cases. 230 Bearings 1000 r---~-.-----~-r-----r-~--,..-----",,"----, 4600 (mm2/s (cSt) SUS 500~~--r-----~~--+--~~r----~~~-~2300 i ~ E ....... 200 930 :::> ~ Ul 100 460 ~ .~ > 'fii "c: 0 ~ ~ 50 230 .~ c: :-s :::> ~ en 100 20 ~ E l a. c:( 10 60 Pitch Diameter (mm) ----....J.. ~ dmmm elm • (bearing bore + bearing 0.0.) + 2 III • required lubricant viscosity for adequate lubrication at the operating temperature I and II refer to Examptes I and II, respectively, on page 43 Figure 11.27 Minimum required lubricant viscosity for antifriction bearings. (Courtesy SKF Industries, Inc.) MAINTENANCE OF ANTIFRICTION BEARINGS If properly applied and lubricated, antifriction bearings in centrifugal pumps have long life and are unusually troublefree. Failure can result, however, from the following: (1) use of the wrong type or size for a particular application, (2) faulty mounting because of improper workmanship in manufacture or Bearings 231 ApproXimate Temperature Conversions Degrees Fahrenheit , 5000 3000 2000 " 500 400 300 .!!! .§. II> '" .l< 200 150 100 75 .i 50 40 () 30 0 E ..,..'" II> 0 20 :> 15 &l 140 160 175 190 210 ~~ ""' """ " """"" '" ~""" ~ ~ ~ ...... ~ l '" .~ "", ~ ~ ""l"-" 1000 E 120 I ...~ tOooo ~ 90 50 20000 " "" ""- ,-""" "- ~ ~""IiiiI "" "" "'" "'" ~ 2300 ""'- "- """ ~'" '-'" ""'- IX: ~ i'oo.. ...... f'.. ~ , '-..... """ !oo..'" I".. ~""' ~ "' "'"""" ""-"'" "'" """"'" "'" """ l ' "' ~, gii> ~ ...... !Ioio.' " ...... """'" ~ ~ ""-0,.,""" ..... " I" ......"" """', 470 350 f""'Io.. ~ " ""'";:.... ~N ~~~~ ~ ~ ~ 10 1250 900 .~~ 700 "'~ ~ 1'........ v", " " l"-'" ~. ~ I'"""i tp,:"I\ r,;>.~ ~. Ii(. 6 ~ p", 5 -10 o 10 20 30 40 140 I.:>t... l" ~ ~ L' ~ ~ ~ ~ ~ 8 4 -20 240 190 50 60 70 80 90 "" 100 , ""'" r..... ~~ o c: ()o ~~ .~~ .!l ~ =: .~ ~5 100 '§~ 80 c(OO e:~ 60 " """"...... ""'..... 120 150 Temperature, Degree Celsius NOTE Viscosity classification numbers are aa:ordng to inlernalional Standard ISO 34481975 for oils having a viscosity index of 95. Approximate equivalent SAE viscosity grades are shown in parenthesis. Figure 11.28 Oil viscosity versus temperature chart. (Courtesy SKF Industries, Inc.) during maintenance, (3) improper design of the mounting, (4) improper lubricant or lubricating practice, (5) entry of water, dirt, or grit into the bearing, and (6) mechanical damage to the balls, rollers, or races. Pump designers base their selection of bearing type, size, and lubrication to suit the field or fields of service for which the lines of pumps will be used. Occasionally through a misunderstanding, a pump will be used for conditions or in surroundings not suitable for its bearing design and consequently suffers from short bearing life. The inner race of antifriction bearings must not tum on the shaft; the outer race must not tum in its housing; and the bearing must be in correct alignment. Antifriction bearings are usually pressed or shrunk: on their shafts; if thrust loads are involved, they are further held in axial position on their shafts by shoulders and shaft nuts. If the shaft is undersize, the fit will be too loose, allowing rotation of the inner race on the shaft with resulting damage to the bearing, the shaft, or both. On the other hand, too large a shaft diameter can result in expansion of the inner race, causing insufficient clearances between the balls or rollers and their inner and outer races. Likewise, the mounting must provide sufficient holding 232 Bearings force through proper gripping of the outer race in the housing to prevent the outer race from turning in the housing. This force is generally more of a problem with radial bearings than with combined radial and thrust bearings or straight-thrust bearings because the outer race is clamped between two shoulders in the housing assembly if thrust is involved. In radial bearings, however, the outer race must be able to move axially in its housing if temperature changes cause unequal expansion of the shaft and casing. The fit of the outer race in its housing is therefore in the nature of a push fit. It is also very important for antifriction bearings to be squarely mounted on their shafts and in their housing and to not be cocked. A pump designer has to make sure that the casing will not distort unduly when pressure is applied, as distortion would throw the bearing out of line. Antifriction bearings have close tolerances; pump design and workmanship must meet them. Some pumps incorporate means for adjusting the radial position of the bearing housings (Fig. 11.17) so the rotor can be accurately centered within its running clearances. After replacing the bearings in pumps so built, it is important to check the rotor centering and correct it if necessary. See the pump's instruction manual for details on how to do this. Many failures of antifriction bearings (and other bearings) can be traced to the use of improper lubricants. Guidance on the correct type of lubricant is given under lubrication of antifriction bearings earlier in this chapter. Care should be exercised to prevent water from entering the bearing. If water gets into the housingexcept for small amounts with soda-soap base grease lubricant-the bearing parts are sure to become rusted and hence fail. Too much cooling of the housing has been known to cause condensation of atmospheric moisture inside the housing. In liquid-jacketed bearings, the flow of cooling liquid should be regulated so that the bearing is reasonably warm and the supply cut off when the pump is idle. Dirt or grit allowed into the bearing will naturally cause damage. As grease makes a good seal against dust and dirt, grease lubrication is generally preferred if the pump is to be installed in a dusty location. Mechanical damage to the balls, roller, or races causes early bearing failure. For that reason, proper mounting and dismounting procedures should be followed. RELUBRICATION PERIODS It is not advisable to schedule any fixed time period for adding or renewing the lubricant in an antifriction bearing but to follow instead the specified period set by the machine manufacturer. The time interval for grease lubrication is a function of bearing type, size, operating speed, and operating mode. A large bearing operating continuously at high speed may require additional grease every 2 months, for example; the grease in a smaller bearing running at moderate speed might last for 4 to 6 months; while a very small bearing operated intermittently at low speed would likely need additional grease every 1 to 2 years, and then only to offset possible deterioration of the grease itself. Figure 11.29 shows one bearing manufacturer's recommendation for relubrication interval versus operating speed. This chart is based on a good quality age-resistant grease and a maximum bearing operating temperature of 70°C (l58°F), measured on the outer race. The chart interval should be halved for every 15°C (27°F) increase in operating temperature over 70°C (l58°F), provided the operating temperature is still less than the maximum allowable operating temperature of the grease. In service conditions where the grease is likely to be contaminated with water or dust, the relubrication interval should be reduced. How much it should be reduced can only be determined from experience with the particular service or one very similar. Oil lubricated bearings may require that oil be added periodically to compensate for losses through the housing seals and vent. The bearing housing generally has an oil level gage to indicate the level in the housing. Note that the level should be checked only when the pump is shut down; while it is running, there is quite a lot of oil in circulation within the bearing. The interval between complete oil changes Bearings c 25000 10000 6000 20000 4000 2000 " t° '0 I!? °" .r: ~ ~ ~ ~ ~ a: b 15000 1000 800 600 500 400 15000 a ~ operating hours o_ft ~nnnn 15000 10000 8000 6000 4000 3000 2500 2000 • ft. oft ~~ t"-o...~...;;:..:- .f""'ooo..... ~ r. < . . .; : ~~~ " .~ 1500 1000 ftftM 150 750 l~nn 100 80 500 400 Iftftft 60 50 300 "'::::--.. . . I......:::...... ~~;::: ..... I':i'oo. . . ~ ~ ........... r-....I'-oo.. '-. 300 250 200 ~ftM i'.. -~- I', 1\ 200 150 20 100 15 75 10 50 " ~\ rY \ " f\. ': \ \ .. I\~ " 'F'\ '\ it. ~ ~~W 161 I~ , "" \ I\. '\ ~ ~~ ~ ~ ....:."> " ", ~I\ 1\ \ \ , "- 1'\ ""- I' I'\. 1\ \ ~ \ '- .NU 30 ~. ~ ,,~ rftft 40 233 i .M ~ ~M ... r • ~ ~ ,on , I ,M 2 100 3 456789 2 3 n r/min 456789 1000 10000 2QOOO Scale a: radial bearings Scale b: cylindrical roller bearings, needle roller bearings Scale c: spherical roller bearings. taper roller bearings, Ihrust ball bearings: full complement cylindrical roller bearings (0,21,): crossed cylindrical rolle~ bearings with cage (0,31": cylindrical roller Ihrust bearings, needle roller Ihrust bearings, spherical roller Ihrusl bearings (0.51r) Scale d: bearing bore ciameter Figure 11.29 Relubrication interval for grease lubricated bearings. (Courtesy SKF Industries, Inc.) is largely a function of the operating conditions and the quality of the oil used. With oil bath, flinger, and oil-ring lubrication using conventional mineral oil the normal interval between oil changes is 1 year, provided the operating temperature of the oil is less than 50°C (150°F) and there is negligible contamination. Higher operating temperatures or service conditions leading to contamination dictate more frequent changes, for example, a conventional mineral oil operating at 100°C (220°F) should be changed every 3 months. Changing to a synthetic oil for such service temperatures allows a significant increase in the interval between changes; consult a lubricant manufacturer for specific information. The interval between oil changes for forced circulation systems also depends primarily on operating temperature and contamination, but the assessment is complicated by the effects of cooling, storage, and circulation (see maintenance of oil lubricated sleeve bearings for further discussion). Oil mist lubrication is essentially a "once through" system, therefore the question of oil change intervals does not arise. RELUBRICATING PROCEDURE In relubricating grease-lubricated bearings having housings with drain plugs, the usual practice is to remove the drain plug and force grease through the bearing until new grease starts to come through the 234 Bearings drain opening. The machine should then be allowed to run at least 20 min before replacing the drain plug so that the excess lubricant in the housing can escape. If it is desired to clean antifriction bearings without removing them from the pump, the following procedure from SKF[11.2] may be used. For cleaning bearings without dismounting, hot, light oil at 93 to 116°C (200 to 240°F) may be flushed through the housing while the shaft or spindle is slowly rotated. In cases of badly oxidized grease and oil, hot, aqueous emulsions may be run into the housing, preferably while rotating the bearing, until the bearing is satisfactorily cleaned. The solution must then be drained thoroughly, providing rotation if possible, and the bearing and housing flushed with hot, light oil and again drained before adding new lubricant. In some very difficult cases an intermediate flushing with a mixture of alcohol and light mineral solvent after the emulsion treatment may be useful. If the bearing is to be lubricated with grease, some of the fresh grease may be forced thru the bearing to purge any remaining c.ontamination. This practice cannot be used unless there are drain plugs which can be removed so that the old grease may be forced out. Light transformer oils, spindle oils, or automotive flushing oils are suitable for cleaning bearings, but anything heavier than light motor (SAB 10) is not recommended. An emulsifying solution made with grinding, cutting or floor cleaning compounds, etc., in hot water, has been found effective. Petroleum solvents must be used with the usual precaution associated with fire hazards. Relubrication of oil lubricated bearings is usually just a matter of draining the old oil and adding the correct amount of fresh oil. If the old oil is dirty, the bearing and housing should be cleaned using some approved method, for example, that just given, before the new oil is added. ANTIFRICTION BEARING CONDITION For a long time, temperature was used as a indicator of bearing condition, a high temperature meaning "trouble to come." Provided the measurement is made with a thermometer, and not a "calibrated finger," temperature is a useful indication of the conditions under which the bearing is operating, particularly if the temperature measured is that of the bearing's outer race. In assessing bearing temperature, it is necessary to establish the stable temperature, evident from a series of readings at say 10- to IS-min intervals, then compare that to the prevailing ambient temperature and the allowable lubricant temperature. It is necessary to take account of the ambient temperature because in most installations the bearing's heat load is being dissipated to the surrounding air. If the bearing temperature will not stabilize, the pump must be shut down and the cause of the overheating found and corrected. Typical causes of overheating are lubricant level (or quantity for grease), shaft and housing fits, misalignment, frictional heat from adjacent seals, rubbing contact between the bearings cage, and shaft or housing shoulders; but consult the guides published by bearing manufacturers for detailed trouble shooting information. A higher than "expected" temperature might be the result of a poor initial estimate or an indication of a serious problem in the bearing's installation or operating conditions, and therefore should be carefully investigated to determine the root cause. For most centrifugal pumps, an antifriction bearing temperature (outer race) of 85 to 90°C (85 to 194°F) is the upper limit of "expected." With modem vibration measuring techniques, it is now possible to learn a great deal more amount an antifriction bearing's condition than can be gleaned from temperature measurement. As an antifriction bearing operates, shock pulses are generated by contact between its rolling elements and races. Measuring these shock pulses and comparing them against reference data shows whether the shock pulses being generated are too high, and if they are whether bearing condition (rolling element and race damage) or the nature of the service conditions is the cause. This form of monitoring offers two notable advantages. Bearings 235 First, it allows a poor operating condition to be detected and corrected before it manifests itself as a bearing failure. Second, it allows for the orderly replacement of bearings that are nearing the end of their service life. In both cases, an unscheduled shutdown, with its high risk of associated damage and plant downtime, is avoided. MOUNTING AND DISMOUNTING ANTIFRICTION BEARINGS As the fit between the outer race of an antifriction bearing and its housing classifies as a push fit, the mounting or dismounting of a bearing in its housing offers little problem. Some housing designs make it impossible however, particularly when dismantling, to apply the force that is necessary to pull the bearing out of its housing anywhere except through the balls or rollers. Such a force can easily damage the bearing. It is desirable to mount a bearing on its shaft with the equivalent of a press fit. Actually, the bearing may be pressed on the shaft or shrunk on. Bearings to be shrunk on are first heated in an oil bath or on a induction heater to about 93°C (200°F) and then slipped into place on the shaft, the inner race being tapped lightly with a tube over the shaft if necessary. Oil bath heating involves some fire hazard and the condition of the bath needs to be carefully maintained to avoid the risk of bearing corrosion from acidified oil. Induction heating avoids these problems. If the bearing is pressed on the shaft, the use of an arbor press is desirable (Fig. 11.30). The force should be applied to the inner race through a tubular sleeve or pipe, a ring, or small blocks of equal thickness. If an arbor press is not available, the bearing can be driven onto the shaft by hammering alternately on opposite points on the circumference of a tubular sleeve held against the inner race. Care must be taken to keep the bearing from being cocked, and feeler gages should be used to make sure it is pressed firmly against the shaft shoulder. Bearings to be dismounted from a shaft must usually be forced off, as the use of heat is seldom feasible. The technique followed will depend on the design and the equipment available, but a split f~­ .r .. Pipe on inner race only ~:II-I~'-D" Bearing Shaft Figure 11.30 Two methods of mounting anti-friction bearing on a shaft. 236 Bearings Figure 11.31 Removing anti-friction bearing with an arbor press. washer is usually employed to bear against the inner race or against a shaft sleeve on which the bearing has been pressed. A firm, steady pressure is applied through the split washer by an arbor press or a form of wheel puller (Fig. 11.31). Care must be taken to keep the shaft straight, to avoid damage from cocking. With proper tools the mounting or dismounting of antifriction bearings is no problem. Improper tools usually cause damage. ANTIFRICTION BEARING INSPECTION After a bearing is removed, it should be dismantled and its components carefully examined to determine how it failed. This is particularly important if the bearing has failed prematurely, because a prime objective of the maintenance process in such cases should be to determine the root cause of the failure and correct it. When examined carefully and the observations compared with reference illustrations available from the various bearing manufacturers, it is usually possible to state how the bearing failed. Working from there, the machine condition that provided the circumstances for failure can be identified and corrected. Of course, if the bearing is essentially destroyed in the failure, finding out why it failed is much harder and the problem may persist. Avoiding this is a further justification for monitoring bearing condition using shock pulse measurement, which allows bearing replacement before catastrophic failure and consequent destruction of evidence. PLAIN BEARINGS Plain bearings preceded antifriction bearings, and are nominally simpler because the relative motion is by sliding rather than rolling. Although most centrifugal pumps made today have antifriction bearings, Bearings 237 since they are generally the most cost-effective solution, the small proportion of pumps made with plain bearings spans virtually the entire range of centrifugal pump applications. A better insight into this range is given by considering the factors governing the choice of plain bearings. 1. Economy-In small, low-cost pumps intended to handle clean liquids, a sleeve-type plain bearing (Fig. 11.2), lubricated by the pumped liquid, offers notable economy of construction. 2. Operating environment-When some or all of a pump's bearings have to operate in the pumped liquid, as they do in vertical turbine pumps, hermetically sealed pumps, and horizontal multistage pumps with slender shafts, plain bearings of sleeve design, lubricated by the pumped liquid, offer the most practical solution in nearly all cases. 3. Configuration-Many pump designs require bearings with small radial dimensions to cause the least obstruction to hydraulic passages, for example, the liquid end and lineshaft bearings in vertical wet pit pumps. For these applications, plain sleeve-type bearings offer the smallest radial dimension. 4. Speed-Pumps used for high-pressure services such as boiler feed, hydrocarbon charge, and similar services run at speeds from 3,600 to 10,000 rpm and have relatively large shafts. For all but the smallest pumps, the d.,.N factor for antifriction bearings (mean bearing diameter in mm multiplied by rotative speed in rpm) is too high, thus dictating the use of plain bearings of either sleeve or tilting pad design. 5. Load-In high-pressure multistage pumps and very large pumps, the axial and radial loads imposed on the pump's bearings generally exceed the capability of antifriction bearings, and thus dictate the use of plain bearings, usually of segmental or tilting pad design. 6. Preference-Some pump users prefer plain over antifriction bearings, the rationale being that the former are easier to inspect and maintain and less susceptible to catastrophic failure. Under the influence of such preferences, purchasers either specify sleeve bearings or devise a bearing selection rule that leads to the same result. From these factors it is evident there are wide variations in the design of plain bearings for centrifugal pumps. To bring some order to the discussion, it is useful to classify the various designs. A fundamental distinction for all plain bearings is the mode oflubrication. Three modes are recognized: boundary, mixed film, and fluid film. One way to illustrate the difference between these is to plot the coefficient of friction, f, against the bearing parameter, ZNIP, where Z is the lubricant viscosity in centipoise, N is the rotative speed in rpm, and P is the bearing pressure in psi. Figure 11.32 shows a plot. Boundary lubrication prevails when the film of lubricant between the bearing surfaces is so thin it allows the high points of the surfaces to come into contact. Bearings operating in this mode have the highest coefficient of friction (Fig. 11.32), and are therefore only suitable for very low speed or oscillating motion. At the speeds inherent in centrifugal pumps, the existence of boundary lubrication will result in rapid bearing wear. Mixedfilm is a transition state between boundary and fluid-film lubrication. Many successful plain bearings operate with mixed-film lubrication (e.g., internal bearings in horizontal and vertical pumps), but as Fig. 1l.32 shows, the coefficient of friction, hence the bearing's life, is critically dependent upon the conditions at the bearing. Fluid-film lubrication results in complete separation of the bearing surfaces and yields the lowest coefficient of friction (see Fig. 1l.32). Increasing the film thickness causes the coefficient of friction to rise, a consequence of increasing shear forces in the lubricant, but the rate of change is relatively insensitive to the bearing conditions. Bearings operating with full-fluid-film lubrication theoretically have infinite life. In practice wear does occur, although usually very slowly, as a result of starting and stopping the pump, momentary overloads during operation, and imperfections in the lubrication. In centrifugal pump practice, full-fluid-film lubrication is generally achieved by hydrodynamic action, meaning that relative motion between the bearing surfaces generated the fluid film (Fig. 11.33). Hydrody- 238 Bearings 0.150 .... Mixed c: o n .;:: 1 , LL -.. - - - - Fluid 1 '0 --w---- Boundry' 1-+-----1 E II) 'u ~ o () 0.001 O~----~----~----------------------~ o Bearing Parameter, W Figure 11.32 Coefficient of friction, 'f: versus ZNIP showing various lubrication modes. ~'----~-'-oto-rLoad _ _-'I + ~-M_i OIL FILM MOVEMENT Gap 1J1LJ.:... Oil from pump Figure 11.33 Ordinary cylindrical bearing with oil film formed by pumping action. Figure 11.34 Principle of hydrostatic lubrication. Bearings 239 namic lubrication can be achieved only when the load is within the bearing's capacity, a function of its detail design and the lubricant provided, and there is some minimum relative velocity between the bearing surfaces. The other means of developing full-fluid lubrication is termed hydrostatic. With this approach high-pressure lubricant is supplied to the bearing, and the leakage of that lubricant across the bearing develops the fluid film (Fig. 1l.34). Hydrostatic lubrication is used in large pumps to "lift" the bearings before starting (line bearings in horizontal pumps and thrust bearings in vertical pumps), and it prevails to varying degrees in all of a pump's internal running clearances, whether designed as bearings or not. The detailed design of plain bearings is influenced significantly by the type of lubricant. From the bearing parameter ZNIP, it is evident high viscosities make it easier to achieve fluid-film lubrication. High viscosities are associated with oil, and low viscosities with the pumped liquid, therefore a simple classification of plain bearing design is to consider oil lubrication and pumped liquid lubrication (or product lubrication as it is often called). The following discussion takes that course. OIL-LUBRICATED PLAIN BEARINGS During normal operation, oil-lubricated plain bearings in centrifugal pumps almost invariably operate with hydrodynamic lubrication. In fact the term "hydrodynamic bearings" is frequently used when referring to oil lubricated plain bearings. In plain bearing terminology, line or radial bearings are generally known as journal bearings. They are either sleeve type or tilting pad (sometimes referred to as segmental), with sleeve type the more usual. The design of sleeve bearings varies with speed. Designs for low speed (Fig. 11.35) generally have a split babbitted bushing with a high LID ratio (length of bearing to journal diameter). The bushing bore is cylindrical with two axial oil feed grooves at the split (Fig. 1l.36[aD. Bearings of this basic design are used for journal velocities up to 12 m/sec (40 ft/sec). For higher speeds, the design must give due consideration to the question of heat dissipation (see lubrication) and bearing stability. OIL HOLE COVER SPLIT BEARING WATER BODY SH OIL RING Figure 11.35 Sleeve type journal bearing for low speed applications. High LID ratio; oil ring lubrication; spherically seated for self-aligning capability. 240 Bearings (a) (b) (c) Figure 11.36 Typical sleeve bearing bore, (a) cylindrical with two oil distribution grooves, (b) single-pressure dam, and (c) tri-lobe. Bearings Figure 11.37 241 Sleeve type, babbitted journal bearing for high speed applications. As the speed of any turbomachine is increased, the rotor weight for a given journal size tends to decrease. If the bearing design does not account for this reduced loading, there is a risk the bearing will develop oil whirl, a self-exciting phenomenon that produces a rotating force on the journal at a frequency just below 50 percent of running speed. Oil whirl can produce one of two results. If the rotor is light enough and the damping is low enough, it can be forced to respond to the subsynchronous excitation, and may develop vibration amplitudes equal to the bearing clearance. A more serious problem arises if the rotor has a lateral critical speed (see Chap. 7) close to the oil whirl frequency. Should this be the case and the rotor damping is low, the resulting resonant response can easily develop destructive vibration amplitudes (sufficient to rapidly wear the internal running clearances). Centrifugal pumps, fortunately, are not particularly susceptible to these problems. This relative immunity derives from the magnitude of forces and damping produced within their internal running clearances. In spite of this, the design of sleeve journal bearings for high-speed pumps does incorporate provisions to ensure the bearing loading is high enough to produce stable operation. The principal design refinement for high-speed plain journal bearings is a notably lower LID ratio values on the order of 0.6 being typical, to raise the nominal bearing loading. The bearing itself can be either a split babbitted bushing (Fig. 11.37) or a pair of precision "automotive"-type inserts in a bolted retainer (Fig. 11.38). Automotive-type inserts are matching steel half shells with a thin deposit of babbitt on a copper backing; they offer the advantage of lower parts cost and simple bearing restoration. A variety of bearing bore profiles is employed to further enhance the bearing behavior at high speed. These range from the simple and very effective single pressure dam (Fig. 11.36[bD to mUltiple pressure lobes (Fig. 11.36[cD. Oil groove designs depend on the bearing bore profile. 242 Bearings Figure 11.38 Sleeve type high speed journal bearing with "precision" automotive type insert. Tilting pad journal bearings (Fig. 11.39) offer higher capacity than equivalent sleeve bearings, and have the virtue of being immune to oil whirl. Citing both these advantages, some designers and purchasers advocate their general use in any pump that requires plain journal bearings. In the majority of cases, the added complexity of tilting pad bearings is hard to justify. As noted earlier, the bearing loading in most centrifugal pumps is low, and the capacity of oil whirl to influence the rotor behavior is quite limited. Where their use is warranted is in large pumps, with both horizontal and vertical axes (Fig. 7.11), In these machines, the loading can be high under some operating conditions, and in vertical-axis designs there is a risk of oil whirl influencing the rotor behavior when the pump is running dewatered. A further significant advantage in large machines is the ability to accurately set the bearing clearance, something that is very difficult with a sleeve bearing, which usually has to be split into more than two pieces to facilitate installation. Tilting pad journal bearings are installed with a specific "preload," meaning that the installed clearance between the journal and pad at the pivot point is less than that for which the pads were machined. Without preload, there is a risk of unstable bearing operation under light loading, a result of an unloaded pad tilting the wrong way (leading edge closer to the journal). Plain journal bearings are sensitive to edge loading caused by angular misalignment between the axes Bearings 243 Figure 11.39 Tilting pad journal bearing, conventional. (Courtesy Kingsbury Inc.) of the bearing and shaft. In older low-speed pumps, where quite large shaft deflections were likely, it was common practice to spherically seat the bearing bushing (Fig. 11.35). Such sophistication is generally not necessary in smaller high-speed pumps because the shaft deflection is usually quite low. For these designs a narrow radial location for the bushing with some provision for rocking (Figs. 11.37 and 11.38) has proven adequate and is simpler to produce accurately. In large pumps, the need for self-aligning bearings is still controversial. Many of the more recent designs, however, have resorted to simple pivoted pads in place of self-aligning spherically supported pads. Rotors supported in plain journal bearings must be provided with some form of thrust bearing to locate the rotor axially and to accommodate any axial thrust developed by the pump. One of the following three arrangements is generally employed to achieve this: 1. 2. 3. Babbitted faces on the sleeve type journal bearing acting against shoulders or collars on the pump shaft (Fig. 11.40) A separate antifriction type thrust bearing located in one of the journal bearing housings, usually the outboard housing (Fig. 11.41) A tilting pad thrust bearing incorporated into the bearing housing at one end of the pump, again usually the outboard end (Fig. 11.42). The first arrangement is the simplest design. In modem pumps, its use is limited to low-speed designs with inherently low values of axial thrust, such as large horizontal-axis single-stage double-suction pumps. And even in these cases, there are many purchasers who will insist on a more substantial thrust bearing. An antifriction thrust bearing, the second arrangement, is used in medium-speed (journal velocities up to 12 m/s (40 ft/sec)) pumps with relatively low axial thrust and operating at moderate pumping temperatures. Within these limits the antifriction thrust bearing can meet the usual life requirements and the bearings can be ring-oil lubricated, thereby avoiding the added expense of a separate lubricating oil system. 244 Bearings Figure 11.41 Figure 11.40 Simple babbitted thrust bearing. Anti-friction thrust bearing with sleeve journal bearing. WATER SLINGER BEARING COVER BEARING BRACK INTERNAL RETURN TO OIL RESERVOIR RESERVOIR ADJUSTING SCREW Figure 11.42 Section of Kingsbury thrust bearing. Incorporates sleeve type journal and flood lubricated tilting pad thrust bearing. Bearings 245 For high-speed pumps or when the axial thrust is or can be high (e.g., when the pump is worn), it is now standard practice to employ tilting pad thrust bearings of the Kingsbury (or Michell) type. Fixed thrust bearings such as the "tapered land" design offer a capability between the simple babbitted face and the relatively complex tilting pad bearing, but the precision necessary in their manufacture tends to offset the initial cost advantage. Such designs are therefore rarely used in centrifugal pump practice. TILTING PAD THRUST BEARINGS The Kingsbury version of this design was first developed to meet the need for a high capacity thrust bearing for vertical axis turbines and has, over time, been widely applied to other rotating equipment, including centrifugal pumps. The operating principle is simple. An ordinary cylindrical or sleeve bearing has a running clearance between the bearing shell and the journal. Because of the relation of the curved surfaces and the capillary attraction of the oil particles, a "pumping" action takes place that draws a lubricating oil film into this clearance (Fig. 11.33). If the oil is of correct viscosity, it will resist the breakdown of the film except at excessive loads. To provide a positive and ample supply of cool oil to the bearing, a simple gravity device is ordinarily used, although operation at higher speeds resulting in maximum tendency to heat requires some form of forced feed lubrication. In an ordinary thrust collar subjected to high pressures and high speeds, the parallel surfaces tend to squeeze out the oil film. The metal-to-metal contact that results makes this type of bearing unsuitable for heavy loads. The principle of the Kingsbury bearing can be described as follows: Suppose that a circular collar is cut into little segments and that each block is suitably supported on its underside so that it may rock slightly on the point indicated as the suspension point and yet stay in place. When the shaft begins to rotate, the film of oil tends to be dragged in under the slightly rounded edges of the blocks. As the speed of the shaft increases, this tendency increases, the block adjusting itself slightly by tipping at a greater angle, riding up on the oil film as a sled runner rides up upon meeting the surface resistance of snow underneath (Fig. 11.43). The higher the speed, the greater this tendency for the block to rock forward, permitting an increased "sledding" action, and the greater the tendency to adjust itself to the increasing oil film dragged underneath it. Construction details of a typical Kingsbury bearing can be examined more closely in the sectional assembly shown in Fig. 11.42. The thrust mounting of Kingsbury bearings used in horizontal pumps is arranged to take thrust in both directions. Sometimes both loads are approximately equal; other times there may be a major thrust in one direction and an occasional minor thrust in the opposite direction. In any event, the Kingsbury bearing is provided with thrust shoes on each side to limit the axial motion of the rotor. The number of shoes on each side mayor may not be equal, depending on the application. Conventional tilting pad thrust bearings have symmetrical pads or shoes, meaning that they are supported at their centre. This design allows equal thrust with either direction or rotation. In their usual form, symmetrical tilting pad thrust bearings are pressure fed with oil at a specified rate and the oil "floods" the entire bearing assembly, some of the flow actually passing through the load carrying oil "wedge," most of it removing heat from the adjacent components. For a given loading the heat generated in such a bearing is quite high. To reduce the heat load, and hence the size and expense of the lubricating oil system, the bearing manufacturers have developed more sophisticated designs. The essential features of these are asymmetric shoes or pads (point of support offset away from the leading edge) and the introduction of oil close to or at the shoes' leading edges (Fig. 11.44). Figure 11.45 shows the reduction in oil flow this refinement affords. At the same time, the bearing runs cooler because the cool oil is being directed to where it's most effective. The one disadvantage of asymmetric bearings is that their capacity in reverse rotation is reduced. For high speed uni-directional equipment, this is not deemed a major disadvantage. 246 Bearings SUSPE~SlO~ POtI\lT THRUST LOAD DIR[CTIOI\I OF ROTATION SHAFT THRUST CO L LAR IN MOT ION Figure 11.43 Principle of Kingsbury thrust bearing. Figure 11.44 Kingsbury-type LEG thrust bearing. (Courtesy Kingsbury Inc.) Bearings Feet/sec. 200 100 247 300 Standard thrust bearing LEG thrust bearing 50 70 90 110 Meters/sec. Mean sliding velocity Figure 11.45 Lubricating oil requirements for flood lubricated versus Kingsbury type LEG thrust bearing. (Courtesy Kingsbury Inc.) MATERIALS Tin-based babbitt is the most widely used material for oil-lubricated plain bearings in centrifugal pumps. Although more expensive than lead based babbitt, it offers greater tolerance of boundary lubrication under transient operating conditions, has higher corrosion resistance, is easier to bond to steel, is less prone to segregation, and has better high-temperature properties. Babbitts have relatively low loadcarrying capacity and fatigue strength, and the capabilities decrease with increasing temperature. For lightly loaded journal bearings, these limitations do not pose a significant design problem, but care is needed with highly loaded thrust bearings. Good design practice is to keep local metal temperature below 120°C (250°F). Note that the temperature indicated by temperature detectors will be lower than this because they are measuring a bulk temperature. Bearing journals are finished directly into the shaft when it is of carbon or low alloy steel such as AISI 4140 or 4340. Alloy steels with more than 1 percent chrome and running at over 20 mls (65 ft/s) pose the risk of "wire wool" damage to the bearing, a phenomenon whereby small embedded chromium carbide particles "machine" the joumal to produce fine turnings, hence the term "wire wool," which quickly destroy the bearing. To avoid this, such shafts have the journals hard chrome plated before being ground to size. Thrust collars are hardened and tempered low alloy steel. 248 Bearings FEED LINE PRESSURE RELIEF VALVE SET AT 20 PSI PRESSURE GAUGE TEIiW'ERATURE GAUGE ~~~~-f==~~==T==T~~~~COOLER PRESSURE GAUGE ____ilt.IRVlCE OIL PUMP OIL TANK CHECK VALVE OIL PUMP SUCTION Figure 11.46 Typical forced-feed oil lubrication flow diagram. PLAIN BEARING OIL LUBRICATION A ring oiled bearing is furnished with a soft steel or bronze oil ring that rides on the pump shaft through a slot cut in the middle of the top half of the bearing shell. This ring rotates as the shaft turns and picks up oil from the reservoir in the bearing housing. The oil is wiped off on the top of the pump shaft, flows between the bearing bore and the shaft, and is discharged at the ends of the bearing (see Fig. 11.35 and Fig. 11.40). Lubrication by means of oil rings is fully satisfactory only at relatively low operating speeds. A provision for automatic circulation of the oil-and if necessary, for cooling it-is an essential feature of all higher speed (plain) bearings, especially thrust bearings. In some bearings, the oil circulation is effected by a rotary positive-displacement gear pump directly connected to the outboard end of the pump shaft by means of a flexible coupling (see Fig. 11.42). The oil pump takes the oil from a reservoir, located either in the bearing housing itself or separately on the pump baseplate, and delivers it under pressure through the oil cooler. From the cooler, the oil flows in part to the outboard thrust bearing, from which it flows into the reservoir located in the lower half of the bearing housing. It then overflows by gravity from this reservoir into the main reservoir on the baseplate. This lubricating system is illustrated in Fig. 11.46. General practice supplies the inboard line bearing of this system with oil under pressure through a branch line in the discharge from the oil cooler. The oil from the inboard bearing is returned by gravity through large return lines into the main reservoir. It is essential to provide an adequate pressure drop from all bearings so that the oil will not overflow because of unsatisfactory evacuation. Numerous alternative methods exist for supplying the bearing with forced-feed lubrication. For example, some arrangements use a vertical oil pump driven from the main pump shaft by means of a worm gear (Fig. 11.47). Other bearings employ the Kingsbury "adhesive lubrication" system (Fig. 11.48). In this system, oil from the reservoir beneath the thrust bearing is drawn into a bronze ring (Fig. 11.48[a]), called the "circulator" or "oil pumping ring," which is around the collar. The adhesion of oil to the collar carries the oil around in the groove in the ring (Fig. 11.48[b]). The oil travels with the collar for almost a complete revolution. It then meets a dam in the groove and is pushed by the stream behind it into a port leading to spaces between the two lowest shoes on both sides of the thrust collar. Shaft rotation carries it to the other shoes, and it finally escapes, above the collar, into a passage leading down to a cooler. From the cooler it returns to the reservoir. The oil will circulate equally well with the collar running the other way. When the collar changes direction, the adhesiveness of the oil carries the circulator Bearings Figure 11.47 249 Vertical oil pump driven from main pump shaft by worm gear. with it through a short angle, until the lug at the top of the circulator meets a stop. In either of the two "stop" positions, oil enters the groove in the circulator by the proper port for the direction of rotation and is discharged through the middle port. The Kingsbury "adhesion ring" does not produce sufficient pressure to allow a filter to be included in the oil circuit. Concern over oil cleanliness in high-speed machines and the desire to avoid a separate (8) (b) Figure 11.48 Pumping ring of Kingsbury bearing. 250 Bearings Operation 1. Arotating drive hub fixed to the pump shaft causes pressure ring to rotate by viscous shear forces (VSF). The major VSF occurs between the flanges of the drive hub and sidewall of the pressure ring. 2. Surface velocity of the pressure ring, aided by drive vanes internal to the ring, accelerate sump oil to a velocity which generates a static head (or pressure) when rammed into the pickup tube. This principle of pressure generation is well known from Pitot tube gaging in flowing pipes. 3. Sufficient pressure can easily be generated to force lubricating oil through a conventional filter and orificed inlets to all types of bearings. 4. The pressure ring oil system is not sensitive to variations in lube oil viscosity and therefore works well at all temperatures with a wide range of oil grades. While fluid friction losses increase somewhat with viscosity, the pressure ring velocity also increases. Therefore, the system is self compensating. Figure 11.49 Pitot tube integral oil circulation system. (Patented) oil pump have led to the development of the "pitot tube" oil circulation device (Fig. 11.49). In this device, oil is accelerated to a high velocity by hydroviscous action within the pumping ring. The pitot tube gathers a portion of the high-velocity oil stream, diffuses it to a lower velocity and higher pressure, then passes it to an oil circuit, which includes a micronic filter. Unlike the Kingsbury adhesion ring, the pitot tube circulator is unidirectional. Sometimes the forced-feed lubrication system supplies oil to the driver bearings as well. A typical system combining pump and driver lubrication is shown in Figs. 11.50 and 11.51. If pumps are driven by steam turbines or through gears, it is customary to have the turbine or the gear supply oil to the pump bearings. Such arrangements require reconcilement of the lubricating oil characteristics and of the operating temperatures established by the manufacturers of the individual pieces of equipment. The use of oil rings for line sleeve bearings normally supplied with oil under pressure is optional and not always justified. Their function is basically that of supplying oil to the bearing at the start of the pump operation, supposedly before the forced-feed system has had the time to do so. It should be remembered that sufficient oil is generally retained in the bearings to take care of their needs before forced-feed delivery takes place. If the normal retention of oil in the bearing or the use of oil rings will not afford adequate protection, auxiliary oil pumps are called upon. These may be manually operated gear pumps (Fig. 11.52) intended for use at scheduled intervals when the pump is standing idle. Operation of this auxiliary pump at weekly or bi-weekly intervals is usually sufficient to keep the oil from draining out completely from the bearings or the oil piping. More elaborate lubricating systems incorporate a motor-driven auxiliary oil pump, which is started before the main pump begins operating. The motor starter controls are interlocked in such a manner that Bearings 251 1/2 IN. PT CONNECTION FOR PRESSURE SWITCH TO STOP MOTOR-ORIVEN AUXI~IARY Ol~ PUMP WHEN SERVICE PRESSURE REACHES 32 PSI AND TO START PUMP WHEN PRESSURE DROPS TO 10 PSI RELIEF VAL SET AT 20 o RELIEF VAL\IE--~HI SET AT 30PSI OIL RESERV'OIR·----jAUXILIARY OIL PUMIP--t====~~~~L_~ Figure 11.50 Simple forced-feed system for pump and motor bearings. the main motor cannot be started until the oil pressure in the system reaches a predetennined value. As soon as the oil pump driven from the main pump shaft develops sufficient pressure, the auxiliary pump is shut down by means of a pressure switch. A second pressure switch setting automatically restarts the auxiliary pump on failure of the regular pump to maintain the desired pressure. This arrangement was illustrated in Figs. 11.50 and 11.51. The settings for the pressure switch are indicated in the fonner, and both drawings show the arrangements of oil cooler, oil filter, oil flow indicators, relief valves, and the like. The lubricating oil system illustrated in Figs. 11.50 and 11.51 is the minimum necessary for the functional requirements. Many purchasers today specify more elaborate systems in the search for higher equipment reliability. Specifying API-61O adds approximately 25 percent to the system cost, by requiring that the reservoir and all oil piping be fabricated from austenitic stainless steel. The next increment is to specify API-614 [1l.3], which raises the system cost by a factor of 2.0 to 2.5. As an aid to evaluation, the extra cost comes from the following: 1. 2. 3. 4. Larger reservoir: 8 min retention time at minimum operating level versus 3 min Reservoir and all oil piping fabricated from austenitic stainless steel Duplex full-capacity heat exchangers Dual-pressure system: oil pressure to downstream of the heat exchangers above the maximum available cooling water pressure 5. More elaborate instrumentation 6. Extensive shop testing. Whether the additional expense of more sophisticated lubricating oil systems is warranted is a question only the purchaser can decide. It depends on recent experience with system manufacturers, the capabilities of those installing and maintaining the plant, and the criticality of the equipment being lubricated. PRODUCT LUBRICATED PLAIN BEARINGS The tenn "product lubricated" refers to bearings that are within the pump and therefore lubricated by the pumped liquid or product, or a liquid other than lubricating oil. The usual attraction of such bearings N ~ J A Figure 11.51 Oil piping layout of lubrication system in Fig. 11.50. !It:CTIOH A-A Ib t ,I Ii 711 /./~~~~\TER Bearings Figure 11.52 253 Manually operated auxiliary oil pump for forced-feed system. is a simpler pump. Whether the simpler pump is more reliable depends on the design of the bearings and their means of lubrication and cooling. Of the various centrifugal pump classes (see Chap. 1), vertical turbine or diffuser pumps and vertical wet-pit volute pumps (see Chap. 14) rely exclusively on product-lubricated plain journal bearings. In the past, some of these bearings were drip oil lubricated, but environmental considerations now preclude that, so all modern designs use strictly product-lubricated bearings. Vertical turbine and vertical wet-pit volute pumps have journal bearings in two locations: within the liquid end or bowl assembly to guide the pump's rotor or spaced up the column to guide the pump' s lineshaft. With some limitations imposed by pump design, these journal bearings can be either open or enclosed, meaning the bearings are either exposed to or isolated from the pumped liquid. Because the bearing arrangement is related to pump design and construction, the two options are dealt with in detail in Chapter 14. A wide variety of designs and materials has been advanced for vertical wet pit journal bearings. All have had the objective of providing bearing life at low initial cost. Not all have been successful, usually because the design failed to take into account variations in loading, liquid cleanliness, and realistic bearing material properties. Successful designs have generally met the following guidelines: l. No reliance on internal seals with a high pressure differential (i.e., more than, say, 0.35 bar 5 psi), to exclude solids laden pumped liquid from the bearings 2. Design factor of at least 1.5 on the highest expected loading 3. PV (unit pressure in bar [psi] times journal velocity in m/s (ft/min) no higher than 3.50 (10,000) at maximum design loading 4. Adequate lubrication grooving to allow a high flow of liquid for lubrication and cooling. 254 Bearings Materials and design techniques are improving and will continue to do so. It is therefore quite likely that the above guidelines, particularly that for PV, will eventually be too conservative. Noting that most product lubricated bearings run with mixed film lubrication, a mode in which the coefficient of friction varies widely with bearing conditions (Fig. 11.32), it should be evident that such a decision can only be made on the basis of carefully conducted and validated tests. In the absence of such data, the conservative guidelines will usually prove less expensive in the long term. For pumps handling clean liquids and having open lineshaft construction (Fig. 11.53) bearings of PTFE tape (petro coke flour filled), various reinforced plastics, metal impregnated carbon, or rubber have proven successful. Journal materials are typically that of the shaft, unless the shaft is relatively soft as is the case with austenitic stainless steels. In these cases, the shaft can be ceramic hard coated in the journal areas or furnished with ceramic hard coated sleeves. The usual form of rubber bearing is that known as "cutlass" (Fig. 11.54), which is intended to tolerate some solids and therefore runs with larger than normal clearances. Since the guidance is not as accurate, designers generally choose this material only when there is a risk of solids being present. Figure 11.53 Open lineshaft bearing. Bearings 255 Figure 11.54 Cutlass rubber bearing. (Courtesy Johnson Duramax) When it is known the pumped liquid will contain some solids, and open lineshaft construction is being employed, most pumps are furnished with Cutlass rubber bearings running on 13 chrome or ceramic hard coated journals. The tolerance of these bearings to solids is limited, particularly if the journal surface speed is high. For difficult services, such as primary and secondary steel mill scale pit, or even cooling tower basin in a dusty environment, the pump really has to have enclosed bearings, lineshaft and liquid end, to achieve reasonable service line between overhauls. Enclosed bearings (Fig. 11.55) are typically either leaded bronze or reinforced plastic running on 13 chrome steel journals. When the environment is corrosive to 13 chrome, such as in a sea water application, the duplex stainless steel or Monel shafting typically used provides an adequate journal. Horizontal-axis pumps employ product lubricated bearings in two ways. The first and nominally simpler design has a slender shaft, one whose static deflection exceeds the internal radial running clearances, and therefore needs additional internal bearings to prevent rubbing contact at the running clearances. Pump designs following this principle have evolved using various combinations of metalto-metal bearings, with alloys, hardness, and surface finish all carefully chosen to reduce the rate of adhesive wear and the risk of seizure. Most these bearings have only a low-pressure drop across them, and therefore operate with mixed film lubrication at best. Given this, the life of the bearings, and subsequently the running clearances, is very much determined by conditions that affect the lubrication mode and bearing loading, for example, the frequency of starting and stopping the pump, its operating flow range, the surface finish of the internal bearings, and the pumped liquid properties, particularly viscosity and cleanliness. Recognizing these difficulties, designers have sought better materials. Filled Teflon tape has proven moderately successful in small low-head-per-stage pumps (Fig. 11.56), where speed and loading were within the material's capability. Metal filled carbon has also been employed with some success in this application. And more recently so, too, have polymers such as polyetheretherketone (PEEK). To be really effective, internal bearings in horizontal pumps need to operate with full-film lubrication. This means that the bearings must be proportioned to develop a sufficient liquid film thickness by hydrodynamic action, or be subjected to a pressure differential high enough to achieve the same by hydrostatic action. For bearings spaced along the pump rotor, the latter is generally easier to achieve. In pumps whose impellers are opposed to minimize axial thrust, (see Chap. 5) the usual impeller arrangement has the pump's differential pressure broken down across two internal clearances, each carrying approximately half the total differential. Being at rotor midspan, the center breakdown bushing 2S6 Bearings 1 r- ~ I-l- ~ ~ - -+- ~ ~ ~ ~ --+- ~ ~ ~ ~ r" ~~ ---..J ~ - ~ --+i ' ..::::t=. r-r~ ~ ;..; ~ ~ ~ ~ ~ ~ ~ ~ ~ r--r--r--r--r--- ~ ~ ~~ ~ r" ~ L-~ r- Figure 11.55 Enclosed lineshaft bearing. (Fig. 11.57) is also a very effective internal bearing, operating with hydrostatic lubrication once the pump's differential pressure is high enough. Although these hydrostatic bearings are less sensitive to adverse conditions than the mixed-film lubricated bearings already discussed, their design still needs close attention to the same operating factors if it is to be reliable. None of the internal· bearings spaced along the pump rotor, and therefore dependent on the pumped liquid for lubrication, can tolerate running dry. If such an operating circumstance is thought likely and the desire is to have the pump survive in an operable condition, the pump design must be based on a rotor capable of running dry (see Chap. 7). The second way product-lubricated bearings are employed in centrifugal pumps is at each end of the rotor in place of the usual oil lubricated bearings. Two considerations can tum the design in this direction. The first is hermetically sealed pumps (see Chap. 24), a requirement that is increasing as a consequence of growing environmental concerns. The second, a desire to simplify the pump by eliminating one shaft seal and the bearing lubricating oil system (Fig. 11.58). Product-lubricated main bearings are generally designed for hydrodynamic lubrication, with bearing proportions and surface finish selected to ensure an adequate liquid film with the available lubricant. Material selection has proven critical in the history of these bearings, which suggests the hydrodynamic condition thought to prevail did not always do so. This is not too surprising when it is recognized that the viscosity of the usual lubricant, water, is only N -.l Ul Figure 11.56 Multistage pump with polymer internal bearings. 1';"8 258 Bearings Figure 11.57 Hydrostatic bearing at midspan of opposed impeller multistage pump. Figure 11.58 Horizontal multistage pump with internal product-lubricated main bearings. (Courtesy KSB) Bearings 259 1/100 that of oil, and the bearing will therefore have a significantly lower minimum film thickness than an equivalent oil lubricated bearing. Large low-speed designs have successfully employed various reinforced plastics. Smaller high-speed designs have also had success with plastics, but are today turning to silicon carbide for the bearing and the journal in the search for longer bearing life. The lubrication of product-lubricated bearings is just as critical as that of oil-lubricated bearings, yet it is often not given the same attention, frequently with disastrous results. As a general rule, product lubricated bearings require a "clean" lubricant to yield tolerable bearing service lives. The one exception is the Cutlass rubber bearing, and that is by no means a panacea, being limited at nonnal pump speeds to only low concentrations of solids in the liquid. By definition, the desired lubricant is the pumped liquid, and when the liquid is clean, that is what is done. What constitutes clean varies with bearing design and service conditions. With conventional materials at nonnal speeds, solids concentrations up to 0.5 percent by weight can be tolerated. Resorting to ultrahard materials (e.g., silicon carbide) has raised the allowable solids concentration for nonnal speeds to some 2.5 percent by weight. High-speed bearings require the lubricant filtered to at least 15 !lm, even with the use of ultrahard materials. When the pumped liquid is "dirty," product-lubricated bearings will not survive unless isolated from the pumped liquid and supplied with a clean lubricant. (This excludes vertical multistage pumps and horizontal multistage pumps with slender shafts from such services because the pumped liquid cannot be effectively kept out of the internal bearings; see Chaps. 14 and 7, respectively.) Since the lubricant generally passes from the bearing into the pump, it has to be compatible with the pumped liquid. Clean lubricant can be obtained by taking a stream from the pump discharge and cleaning it using a strainer and a cyclone separator (Fig. 11.59). The virtue of a cyclone separator is that it does not accumulate solids as does a filter. Installing a strainer upstream ensures the separator inlet does not become plugged with an occasional large solid. Such a system must be monitored with a flow switch to shut down the pump on a significant drop in lubricant flow. In a large critical pump, it is desirable to use parallel "Y" strainer with backflush valve From pump discharge Cyclone separator --" 1 Orifice to balance flows CJ Figure 11.59 Product lubrication from pump discharges through cyclone separator. 260 Bearings strainers and cyclones, with a differential pressure switch to sound an alann when there is a high pressure drop. When the pumped liquid cannot be cleaned up with a cyclone separator (low-SG solids or highviscosity liquid), clean lubricant is supplied from a central source. If there are several pumps in one installation, it is often simpler overall to use a central source of clean liquid rather than equipping each pump with its own cleaning system. Regardless of the source of clean liquid, it is crucial to monitor lubricant flow to the bearings. Monitoring pressure, although easier, is not a suitable substitute; should the lubricant path become plugged downstream of the bearing, there will be no flow through the bearing but the pressure upstream will be normal or higher. PLAIN BEARING MAINTENANCE In theory, plain bearings operating with full-film lubrication have infinite life and therefore should not require any maintenance beyond periodic renewal of lubricant and cleaning. The working practice is otherwise; rubbing contact during start-up and incidental overloads combined with occasional lubricant contamination produces some wear in even the most carefully designed and operated bearings. When the operating conditions are less than ideal, for example, high bearing temperatures, high rotor vibration, or poor quality lubricant, plain bearings are just as susceptible to premature failure as antifriction bearings. Plain bearings designed for oil lubrication operate with close to ideal circumstances (full-film lubrication and a clean, viscous lubricant), and therefore require only periodic dismantling and inspection to determine actual clearances and the condition of the working surfaces. As a general rule, a journal bearing should be renewed when its clearance exceeds 150 percent of the original value. If the diametral clearance is not given in the instruction book, it can be approximated on the basis of allowing 0.001 nun per mm (in. per in.) of journal diameter. Tilting pad thrust bearings and the larger sizes of tilting pad journal bearings are adjustable so the working clearance can be reset at each inspection. When to renew or restore the bearing pads is then a matter of allowable wear, and must follow the manufacturer's recommendation. If the working surfaces show signs of abnormal damage, for example, pitting, scoring, bearing metal fatigue, cracking, or corrosion, the precise nature of the damage and its likely cause should be determined. Comparing the damage to reference photographs provided by some of the manufacturers will often allow the root cause to be identified, leaving the maintenance engineer to determine what is producing the root cause. In complex cases, it is often beneficial to retain the services of a specialist familiar with plain bearings and the type of pump involved. Babbitt-lined sleeve-type bearings can be restored by melting out the old babbitt, pouring in a new lining, machining the bore to the required dimensions, then cutting in the oil grooving. When the bearing has a profiled bore, the machining is more complicated and may be beyond the capability of the usual maintenance shop. In these cases, it is better to purchase replacement or exchange reconditioned parts from the manufacturer. Thin wall liners and tilting pads are produced using specialized techniques and should always be replaced with new parts obtained from the manufacturer. Damaged journals or thrust collars can be restored by refinishing provided the resulting undersize is acceptable considering strength, and the availability of undersized bearings or the ability to adjust to maintain clearances with the undersized part. If there is any doubt, consult the manufacturer. When undersized parts are not acceptable, journals can be restored by grinding to a smooth surface, chrome plating, and finish grinding to size. The plating method must avoid hydrogen embrittlement of the shaft, and the maximum thickness in anyone deposit is 0.40 nun (0.015 in.), ground back to 0.25 mm (0.010 in.) before any subsequent deposit. For example, a journal cleaned up at 1.50 nun (0.060 in.) undersize would have to be plated and ground a total of three times. Product-lubricated plain bearings generally do not enjoy operating conditions as good as those of Bearings 261 most oil lubricated bearings. One immediate consequence of this is a higher wear rate and consequently a greater need for maintenance. Since most these bearings are located within the pump, periodic inspection to check clearance and condition is not a simple task. Accordingly, the general practice is to monitor machine condition, typically vibration, and only open the pump when it is obviously worn. The one exception to this is those bearings installed at each end of the rotor in the place of conventional oil lubricated bearings (Fig. 11.58). The principles for when and how to renew product-lubricated bearings follow those already discussed for oil-lubricated bearings. New running clearances vary significantly, however, with materials and it is therefore important to establish what the design values are before assessing bearing condition or renewing clearances. Bearing wear should be examined carefully and documented for future reference. Particular care should be taken with the lineshaft bearings in vertical pumps, since wear patterns can be clues to fundamental structural problems in the pump. Scoring is usually caused by solids in the lubricating liquid, and if found should lead to providing cleaner liquid. Damage with the appearance of scoring can also be caused by running at too high a load or running at too high a temperature. Microscopic examination of the bearing surface and a section through it will often yield more specific information about the cause of failure. Worn bearing elements are almost invariably replaced with new, since the materials used do not lend themselves to designs such as babbitted bushings. In most cases, worn journals must be either replaced or restored to new size, as usually there is little or no capacity to accommodate undersize parts. Chrome plating or hard coating are common means of restoring journals. Plating must follow the rules already given for oil-lubricated bearings. Hard coating should be a relatively tough ceramic, applied by the ultrahigh-velocity oxy fuel process, then finish ground to new size. Coatings applied by lesser processes run a high risk of spalling off in service, an event that destroys the bearing. MAGNETIC BEARINGS Compared to antifriction and plain bearings, the distinguishing feature of magnetic bearings is freedom from contact, either rolling or sliding, within the bearing. This means the bearing no longer requires a lubricant and is relatively immune to its operating environment. These two attributes coincide nicely with two requirements that are emerging in centrifugal pump development, namely the elimination of complex oil lubrication systems and the need for highly reliable bearings in hermetically sealed pumps. Of these two requirements, the latter is likely to have the greater influence because it is associated with rendering hermetically sealed pumps an entirely viable means of eliminating the emissions produced by leakage from conventional seals. The viability comes from freeing the pump from dependence on product lubricated bearings. A third but little publicized need is lower mechanical noise in pumps for military service. Being contactless and not requiring any mechanical auxiliary system, magnetic bearings offer a potential solution to that need. The magnetic bearings now in use are termed "active" and operate as follows: Referring to Fig. 11.60, a journal of magnetic material is surrounded by a number of electromagnets, all designed to attract the journal. At each of the electromagnets, there is also a proximity probe to sense the rotor's position relative to "zero." Signals from each proximity probe are sent to a controller which compares the rotor's position with "zero" and varies the excitation of the electromagnets to position the rotor within tolerance of zero. Typically the bearing system is designed to keep the rotor within 0.025 mm (0.001 in) of zero at the rated load. The power absorbed by the bearing is essentially that required for magnet excitation, and is lower than that required for lubricating-oil systems or absorbed by high-speed liquid-lubricated 262 Bearings Electronic control system Bearing system Bearing stator Power amplifier Reference ~ signal .--_ _ _-, Signal processing Error signal Power amplifier Sensor signal Sensor stator Figure 11.60 Magnetic bearing control system. bearings. The power can be lowered further by accommodating a portion of the load with permanent magnets, and using the electromagnets for fine control, an arrangement known as "permanent magnet biasing." Radial bearings (Fig. 11.61) have four or more poles distributed around the journal, positioned such that the maximum load is shared between poles. Thrust bearings have two poles, one on either side of a magnetic thrust collar. Beyond contactless support, active magnetic bearings have two further advantages. The first is direct measurement of actual bearing loads, a capability afforded by varying magnet excitation to maintain rotor position. Associated with this, and an inherent feature of the controller, is raising an alarm and shutting down the pump if the bearing loads exceed capacity. Following on this, it is possible to program the controller to vary the bearing's stiffness and damping over its working speed range, thereby changing the rotor's dynamic characteristic to avoid resonant conditions. This second advantage is of limited value in centrifugal pumps because the liquid effects in internal clearances generally dominate the rotor's behavior. Depending on the actual pump design, it could be beneficial to pumps required to be capable of running dry. The mechanical construction of an active magnetic bearing (Fig. 11.61) has several notable features. First, the shaft must be magnetic or sleeved with a magnetic journal. Second, when the beining is for a hermetically sealed pump, the journal, electromagnets, and proximity probes must be canned if the pumped liquid is corrosive to the materials used for these components. Third, some form of backup bearing is required to safely bring the rotor to standstill should the magnetic bearing fail, and to support the rotor when it is at rest and the magnetic bearing is off. The backup bearing is normally inactive and is designed with a normal clearance equal to half the magnetic bearing air gap. With the usual air gap at 0.50 mm (0.020 in.), the backup bearing radial clearance is 0.25 mm (0.010 in). This means that should the magnetic bearing fail, the pump's rotor will drop by some 0.25 mm (0.010 in.), a shift that Bearings 263 Control Coil annlng Material Figure 11.61 Section of canned radial magnetic bearing. (Courtesy Avcon) needs to be taken into account in determining the pump's internal clearances to ensure loss of the magnetic bearing does not result in destruction of the internal running clearances. At the time of this writing, magnetic bearings have been incorporated in several designs of hermetically sealed integral motor pumps (Fig. 11.62 shows one such design), and a multistage boiler feed pump. Their use will increase as capability is demonstrated and as cost comes down, the latter reportedly awaiting the development of self-programming digital controllers. The maintenance of magnetic bearings can be likened to that of an electric motor with a variable frequency controller. The bearing parts themselves should not need any maintenance beyond inspection when the pump is opened for some other reason. Frequent "letdowns" or known corrosion or erosion problems with "canned" bearings would be cause to increase the inspection frequency. Existing controller designs have proven reliable to the point where the only built in redundancy is a battery power supply, and therefore should only require periodic cleaning and changing of cards when a malfunction develops. Cleanliness is very important; some of the early installations of magnetic bearings on centrifugal compressors were plagued by poor quality controller enclosures. One fundamental rule to close the discussion: do not work the controller while the pump is running. BEARING HOUSINGS A wide variety of bearing housing configurations is employed for centrifugal pumps, with the choice being influenced by the type of rotor (overhung or between bearings), the type of casing mounting (foot 264 Bearings I PUMP VIll..UTE CASE PUMP IMPELLER 6 i! 3 MOTOR ADAPTOR 4 INBOARD POSITlON SENSOR B 9 5 INBOARD BEARING STATOR 10 7 INBOARD BE ARING ROT [R MOTOR STATOR Ii! IlUTBOARD BEARING ROTOR IlUTBOARD POSITION SENSOR MOTOR ROTOR 13 THRUST BEARING ROTOR ELECTRICAL fEEDTHRDUGH OUTBOARD BEARING STAT[R 14 THRUST BEARING STATOR IS AXIAL POSITiON SENSOR II Figure 11.62 Schematic of canned motor pump with magnetic bearings. (Courtesy BWIIP International) or frame), the casing joint (radially or axially split), access to the shaft seal, the pumping temperature, and the designer's preference based on stiffness and manufacturing considerations. Within the basic bearing housing configurations, there is a further distinction, namely, whether the housing itself is radially or axially split. As a general rule, antifriction bearings are installed in radially split housings, and plain bearings in axially split housings. There are exceptions. Very large antifriction bearings often have axially split housings to facilitate installation; vertical axis plain bearings will be installed in radially split housings unless the size of pieces for dismantling dictates otherwise. In most designs of overhung pumps, both the line and thrust bearings are in a single housing, and the bearings are antifriction. The housing is therefore radially split and is either connected to the pump by a bracket or adaptor (Fig. 11.22), or is part of a frame assembly which has the casing attached to it (Figs. 2.18, 2.20). Since overhung pumps usually have radially split casings, the bracket or adaptor can easily be designed for "full-circle" support, which is inherently stronger than the alternative "half-circle" support. Cutouts in the bracket, with suitable compensating reinforcement, allow access to the shaft seal and ventilation when necessary. Depending on the design of the casing and housing and the pump's intended service, the bracket or adaptor is either integral with the casing (actually the cover); as Fig. 11.22, integral with the housing (Fig. 11.21), or a separate piece. Having the bracket integral with the casing ensures it has the same material properties, which is an important consideration in corrosive services and applications involving very high or very low temperatures. Incorporating the bracket in the housing allows greater flexibility in the configuration and manufacture of the casing cover. A separate adaptor allows the greatest design flexibility and can accommodate any special material requirements. Bearings 265 Against this, there is an additional bolted joint and centering fit involved in maintaining rotor alignment within the casing. Between-bearings pumps can have their casing either axially or radially split and are equipped with either antifriction or plain bearings. As a consequence, they employ a wider variety of bearing housing configurations than pumps with overhung rotors. When the casing is axially split the bearing housings are normally "half-circle" connected to the lower or fixed half of the casing. This is the simplest arrangement for such a casing, and when properly designed has adequate stiffness for the class of pumps that usually employ axially split casings. The bracket connecting the housing and casing can be integral with the casing (Fig. 11.20) or part of the bearing housing (Fig. 11.63), with the choice being based on materials and manufacturing considerations. When abnormal service conditions warrant the added complexity, pumps with axially split casings are equipped with full-circle bearing housing support. A common example is pumps for navy combat vessels, in which full-circle support is necessary to survive high-shock loading. Modem pumps with radially split casings employ bearing housing and connecting bracket arrangements similar to those previously described for overhung pumps. The only justification for half-circle-supported bearing housings was easy access to packed box shaft seals when the bearing housing was axially split for plain bearings. Since packed box seals are rarely used today in radially split between bearings pumps, there is no reason not to employ the inherently stiffer full-circle support. Axially split bearing housings are either bolted to a bracket or adaptor or have an integral bracket, meaning that it is also axially split (Fig. 11.64). The latter arrangement yields a compact design yet provides good access for rotor, bearing, and seal setting when the upper half of the housing is removed. Figure 11.63 Axially split pump with half circle supported bearing housing. Bracket integral with housing. 266 Bearings Figure 11.64 Full circle supported axially split bearing housing. The stiffness and strength of bearings housings and their connection to the pump is a critical but often overlooked requirement. Stiffness has two aspects. First, the bearing housings and their connection to the casing must be stiff enough to transmit the bearing loads to the casing (or foundation in those few instances where pedestal bearings are used) while maintaining alignment of the pump's rotor within the casing. When the bearing housing or adaptor has support built into or attached to it, thus producing a three point-supported pump (Fig. 11.65), the bearing housing and its connection must now withstand portion of the piping load as well. Second, the bearing housing connection must be stiff enough to have its first natural frequency above the highest excitation frequency the pump is likely to produce, which is usually the vane passing frequency. If the bearing housing's natural frequency is close to an even moderately intense excitation frequency, the bearing housing will resonate, producing vibration of high velocity. Although this vibration is generally of very low amplitude, 6 11m (0.00025 in.) or lower, and does not seem to cause any actual damage, the velocities are well above the limits currently deemed acceptable, and can therefore pose an acceptance problem. Beyond being stiff enough to accommodate normal loads, bearing housings need to be strong enough to tolerate some degree of abnormal loading, such as might be imposed by shaft failure or a similar incident. In the petroleum refining industry there have been several major fires caused by a cast-iron bearing bracket fracturing under abnormal loading and allowing gross leakage of a product whose temperature was above the autoignition temperature. Similarly, there have been instances where a running pump was within a fire but not contributing to it until thermal shock from fire extinguishing efforts fractured the cast-iron bearing housing. It is for these two reasons that API-61O now specifies that pumps handling flammable or toxic liquids have steel bearing brackets, housings, and load-carrying bearing covers. Depending on the method of lubrication, bearing housings incorporate various features to retain or Bearings 2 + 267 3 Figure 11.65 "Three-point"-supported pump. direct the lubricant. Housings for grease lubricated bearings have either space to accommodate spent grease as it is purged from the bearing (Fig. 11.17) or means of expelling the spent grease, such as a grease escape valve (Fig. 11.19). With oil bath, flinger, and oil-ring lubrication, the bearing housing has a sump to hold the necessary volume of oil. Some designs for flinger and oil-ring lubrication go a step farther and include channels and associated ports to circulate oil from the sump, thru the bearings and back to the sump (Fig. 11.21). Pure oil mist, oil spray, and force-fed oil lubrication eliminate the need for a sump, and instead have galleries, often with flow control orifices, to supply the oil to the bearing and ports to drain it away for return to the lubrication system (Figs. 11.37 and 11.38). The oil from tilting pad thrust bearings passes to the OD of the thrust collar where it collects in an annulus around the collar, and is expelled through the oil outlet back to the housing's drain system. Bearing design and speed influence the location and form of the oil outlet. With conventional pressure-fed flood lubrication, the oil outlet is in the upper half of the bearing housing, and is usually radial for speeds to 23 mls (4,500 ft/min) (based on the mean collar diameter), tangential for higher speeds (Fig. 11.66). When the oil is brought directly to the thrust shoes, as in Kingsbury's type LEG bearing, there is no need to flood the thrust bearing assembly so the oil outlet is in the lower half of the housing. As these bearings are only used for high-speed applications, the oil outlet is always tangential. Heat dissipation is a fundamental element of bearing housing design. Although the heat load involved is usually quite low, so, too, is the capacity of the housing to dissipate heat, which means that the temperature of the bearings depends on a delicate balance between heat load and dissipating capacity. The sources of heat load for a typical bearing housing are shown in Fig. 11.67. Some discussion of the various sources is warranted. QI,2 The heat generated by the bearings themselves is related to their design and operating conditions. Antifriction bearings, as generally used in centrifugal pumps, generate most of their heat from the action of the bearing rolling elements on the lubricant. The only exception to this is large low-speed bearings whose heat generation is principally a function of bearing load. Plain bearings develop heat by shearing action in the lubricant film. Figure 11.67 shows labyrinth seals adjacent to each of 268 Bearings CONVENTIONAL FLOODED OIL oun.ET LOCATION OIL INLET· OIL INLET" L.E.G. OIL 0UT1.ET LOCATION Figure 11.66 Tilting pad thrust bearing oil outlet arrangements. (Courtesy Kingsbury Inc.) the bearings. Such seals are not contacting and therefore do not develop any heat. The same is not true for so-called "positive" seals such as the lip type. These seals function by contact and can generate significant additional heat when their rubbing speed is high. Q3 Conduction along the shaft is a factor in high-temperature applications. Many designs include a heat dissipating thrower (Fig. 11.22) on the shaft between the pump's liquid end and the bearing frame to draw off some of the heat before it enters the bearing frame. In other instances, the shaft under the sleeve has been coated with a low-thermal-conductivity ceramic to impede heat transfer. This approach works as predicted, but the coatings have proved vulnerable during pump maintenance. Q4 High-temperature applications also raise the possibility of conduction through the bearing bracket or adaptor. With judicious design, such as an air gap between the faces (Fig. 11.22) to form a thermal barrier, the heat load from this source can be minimized. Qs In regions exposed to intense solar radiation, that same radiation can serve as a significant source of heat into the bearing housing. Often, when this is the case, the bearing housing is equipped with a sun shield to reduce the heat load from this source. The means employed to dissipate the bearing housing heat load are: 1. Natural convection-For low-speed applications with lightly loaded bearings at pumping temperatures up to, say, 120°C (250°F), natural convection to the atmosphere is sufficient to keep the bearing cool. Bearings 269 Labyrinth seal .......... Figure 11.67 Heat balance on bearing housing. KEY: QI = line bearing heat input Q2 = thrust bearing heat input Q3 = conduction along shaft Q4 = conduction through bearing bracket Qs = solar radiation Q6 = heat lost to convection, natural or forced Q7 = heat lost to cooling jacket QI + Q2 + Q3 + Q4 + Qs = Q6 + Q7. 2. 3. Forced convection-At higher speeds, such as those of pumps driven by two-pole electric motors, and temperatures above, say, 95°C (200°F), natural convection will not keep the bearings cool. Raising the velocity of the air over the housing by the use of a shaft mounted fan and the appropriate shroud significantly increases the heat load the housing can dissipate. With thorough design, including fins on the housing to increase the surface area, fan-cooled housing can maintain acceptable bearing temperatures for pumping temperatures to 425°C (800°F) with ambient air of 43°C (110°F). Cooling jacket or coil-Adding a cooling jacket around the bearing housing or inserting a cooling coil into the housing sump is an alternative to fan cooling. A jacket around the housing (Fig. 11.21) is most effective when the oil is circulated through the bearings by flingers and internal galleries; it ensures the oil delivered to the bearings is cooled. Limiting the jacket to under the sump is usual when the housing does not include oil circulation galleries. With such an arrangement it is crucial that the oil sump be well agitated by the oil rings or flingers, otherwise the coolest oil will remain at the bottom of the sump where the cooling is being applied. A principle common to all jacket-cooling arrangements is that the cooling be applied to the lubricant, not around the bearing. Experience has shown that the latter, an old practice, keeps the bearing outer race cool but can, by way of differential thermal expansion, lead to loss of internal clearance and consequent bearing failure. Cooling coils are an alternative to a jacket under the sump, and provided the design is correct, are probably a more effective approach, although at the expense of greater complexity. 270 Bearings GREASE '" Figure 11.68 "Taconite" bearing housing seal. 4. Forced-oil circulation-For high speeds, high loads, high pumping temperatures, or various combinations of these, forced-oil circulation is the most effective means of keeping bearings cool. The flow needed depends on the bearing type and the sources of heat. Antifriction bearings operating at high speed but in a cool environment require only a very low flow. The same can be said for plain bearings, although the flow is nominally higher because of the nature of the bearing. When the pumping temperature is high, higher flows are needed to dissipate the additional heat load. The final aspect of bearing housings that needs to be discussed is seals. Often overlooked as a minor detail, the means of sealing bearing housings, both against the ingress of dirt and the like and the egress of lubricant, can be a major factor in the reliability, and consequent availability, of a pump. A fundamental principle in all designs is that there be some form of thrower between the bearing housing and any adjacent pumped liquid seal. If a thrower is not provided or its design is inadequate (e.g., an elastomer that expands during rotation to give a gap between the thrower and the shaft), leakage from the shaft seal can pass practically unimpeded into the bearing housing and so contaminate the lubricant. Many seal designs are employed; only those representing the basic types are discussed here. For pumps installed indoors, a simple labyrinth machined into the bearing cover (Fig. 11.17) is quite adequate. The drain from the labyrinth back to the bearing housing is an important feature of this seal; without it oil will accumulate in the labyrinth and eventually leak out of the housing. Pumps installed in a moderately severe environment or pumps whose axis is vertical often require a "positive" seal, the most common form of which is, the lip seal (Fig. 11.18). Lip seals have finite life, very definite limits on rubbing speed and service temperature, and tend to wear the journal on which they are running. Given these limitations, they obviously cannot be used for all applications. API-61O precludes their use in pumps for refinery service. When effective housing sealing is necessary but is outside the capability of lip seals, a labyrinth plus a thrower offers an effective alternative. The labyrinth is frequently made renewable (Figs. 11.21 and 11.22) to allow for ready restoration in the event of damage, and to allow a nonsparking material where needed. If it is mandatory that the bearing housing be positively sealed from the atmosphere but lip seals cannot be used, one alternative is the magnetically energized face seal (Fig. 9.24). These seals, used extensively in the aircraft industry, offer a very effective, albeit moderately expensive, solution to positive sealing. A second approach, born in the mining industry, is the so-called "taconite" seal. Figure 11.68 Bearings 271 shows a typical design, the essence of which is a grease-filled space between the bearing housing and the atmosphere. Taconite seals have earned a notable reputation in pumps operating under severe conditions on mining and mineral processing sites. BIBLIOGRAPHY [11.1] E. L. Annstrong, W. R. Murphy, and P. S. Wooding. "Evaluation of Water-Accelerated Failure in Oil Lubricated Ball Bearings"; Journal of the ALSE (January 1978): 15-21. [11.2] Bearing Installation and Maintenance Guide, Publication #140-70, SKF USA Inc., King of Prussia, PA, August 1988. [11.3] API-614, Lubrication, Shaft Sealing, and Control Oil Systems for Special-Purpose Applications, American Petroleum Institute, Washington, DC, January 1984 12 Couplings Centrifugal pumps are connected to their drivers through couplings of one sort or another, except for close-coupled units, in which the impeller is mounted on an extension of the driver shaft. Couplings are either rigid or flexible. The choice is determined by the bearing arrangement of the pump and driver combination. Rigid couplings permit neither radial nor axial relative motion between the driving and driven shafts, effectively making them a single shaft. Their use is therefore limited to pump and driver combinations with two or three bearings (Fig. 12.1[a] and [b]). This category includes lineshaft-driven vertically suspended pumps, which are considered two-bearing machines with additional precision aligned guide bearings. A flexible coupling, on the other hand, is a device to transmit torque between the two shafts while allowing for minor misalignment (angular, parallel, or a combination) between their axes of rotation. Contrary to some popular perceptions, flexible couplings are not intended to accommodate gross misalignment between pump and driver. If that is envisaged, the machines should be coupled with a universal drive shaft. In a general sense, misalignment between axes of rotation imposes bending on the shaft and additional loads on the coupled machines' bearings, and therefore has to be kept to a minimum. The purpose of a flexible coupling is to accommodate the minor misalignment that is either impractical to eliminate or occurs during some transient condition encountered in the pump's operation. The necessary accuracy of alignment depends on the coupling type, its installed configuration, and the rotative speed, details that will be dealt with in discussion of the various coupling types. Unless the size of the pump precludes them, pump and driver arrangements with four bearings (Fig. 12.1[c]) are almost invariably equipped with flexible bearings. Depending on their detailed design, three-bearing machines (Fig. 12.1[b]) may be equipped with a flexible coupling allowing only angular misalignment. A flexible coupling must also permit some lateral float of the shafts so that the two shaft ends may move closer together or farther apart under the influence of thermal expansion, hydraulic float, or shifting of the magnetic centers of electric motors, and so move without introducing excessive thrusts on the bearings. This aspect of flexible coupling design will be discussed in greater detail subsequently. 272 I. J. Karassik et al., Centrifugal Pumps © Chapman & Hall 1998 Couplings 273 J C J C Coupling~ (Rigid) (a) Two bearing arrangement: - coupling transmits torque and bending moment - no misalignment. ~ Coupling ) ~L.....----...J~~ (b) Three-bearing arrangement: - coupling transmits torque and radial reaction - angular misalignment only (if necessary). Coupling ) ~L...------'~ ~ --=---I~[p 1 - - - = - - 1 Fig. 12.1 (c) Four-bearing arrangement: - coupling transmits torque only - angular and parallel misalignment. Coupling requirements for various machine bearing arrangements. RIGID COUPLINGS Threaded Couplings In a threaded coupling (Fig. 12.2), the threaded shaft ends are screwed into each end of the coupling and butted together at the center. When torque is applied, the shafts tighten against each other until the friction force on the thread faces equals that produced by the torque. The coupling is relieved at the center to reduce stress concentration, and vented to allow for displacement of lubricant and air as the coupling is assembled. These simple couplings are widely used to connect lineshaft sections in vertically suspended pumps of low to medium torque. For higher torque applications, on the order of 7,000 N-m (62,000 lb. in), the effort necessary to dismantle the couplings after they have been in service usually dictates some other design. Clamp Couplings The clamp coupling (Fig. 12.3) is a typical rigid coupling. It consists basically of a split sleeve provided with bolts so that it can be clamped on the adjoining ends of the two shafts and form a solid 274 Couplings Fig. 12.2 Threaded coupling. connection. Both axial and circular keys are commonly incorporated in the clamp coupling so that the transmission of torque and thrust is not made solely dependent upon the frictional grip. Sliding Sleeve Couplings A sliding sleeve coupling (Fig. 12.4) is made up of a slide fit sleeve that fits over each shaft end and engages a key in each, thereby allowing the transmission of torque. Axial thrust is transmitted via a split ring that locks into a groove in each shaft end, and is kept in place by the sleeve. Once in its correct position, the sleeve is located with two retaining rings, one on each shaft. Sliding sleeve couplings are often used instead of threaded couplings when difficulty of assembly and dismantling is deemed a major issue. Tapered Sleeve Couplings The tapered sleeve coupling (Fig. 12.5) is a classical design employed for high-torque applications where the coupling assembly must be tight and of a diameter not significantly larger than the connected shafts. Each end of the shaft is tapered with a key, usually parallel to the axis, and has a split ring groove just beyond the taper. The coupling has a corresponding taper in each end, and a threaded extension for a coupling nut. The coupling is tightened by drawing each coupling nut against its split ring. Once tightened, each coupling nut is locked to prevent it coming loose during operation. Flanged Couplings Quite a wide variety of pumps employ flanged rigid couplings, which may be just a single coupling (Fig. 7.11) or a double-flanged spacer (Fig. 12.6). All designs transmit torque by way of shear in the fitted coupling bolts or dowel bushings around the bolts (many also rely on friction between the coupling faces to transmit a portion of the torque). Bending is transmitted by tension in the bolts. Smaller sizes employ a premachined rabbet or spigot fit to maintain concentricity. (Because each flange assembly Couplings CLEARANCE BETWEEN HALVES TO AllOW CLAMPING ON SHAFTS Fig. 12.3 Clamp coupling. 275 Split lock ring _ Coupling nut -Coupling Fig. 12.4 Sliding sleeve coupling. Fig. 12.6 276 Fig. 12.5 Tapered sleeve coupling. Double flange coupling (spacer or extension type). Couplings 277 inherently has some eccentricity, double-flanged spacer couplings cannot maintain the same degree of assembled shaft straightness as single-flanged couplings.) Larger sizes generally have plain faces, and are carefully aligned then the bolt holes finished bored to size in situ. Compression Couplings All compression couplings rely solely on friction between the coupling and the connected shafts to transmit torque and axial thrust. This requires that the coupling develop a substantial interference fit with the shafts, and it is the means of developing the fit that distinguishes the various types of compression couplings. For smaller sizes, designs using thread driven tapers have proven successful. In a typical design (Fig. 12.7[a]), the central portion of the coupling is made up of a slotted bushing, bored to fit the two shafts and taper machined on its outside diameter from the center out to both ends. The two couplings halves are finish bored to match this taper. When the coupling halves are drawn together by bolting, the bushing is compressed onto the two shafts, thereby producing the necessary interference fit. (b) (8) Fig. 12.7 Compression couplings; (a) thread driven taper, (b) oil-injection. 278 Couplings As coupling sizes increase, the radial force necessary for torque transmission is hard to achieve with thread driven tapers, so shrink fitting or oil injection mounting is employed. Figure 12.7(b) shows a vertical pump lineshaft coupling design that employs both methods. Each shaft end has a precision finished stepped fit, and the coupling has corresponding stepped bores in each end. Assembly is carried out with the shafting vertical, heating the coupling to shrink it on to the shaft ends. When dismantling is necessary, oil injection is employed to dilate the coupling and push it off the shaft end (the small annulus formed by the stepped fit serving as a hydraulic jack). Oil injection mounting and dismounting involves high pressure oil, on the order of 1,000 to 2,000 bar, (15,000 to 30,000 psig), and significant strain energy, and therefore must be undertaken with due care (see coupling mounting in this chapter). FLEXIBLE COUPLINGS A wide variety of flexible coupling designs are used to connect centrifugal pumps to their drivers. Despite the variations, some order can be brought to the designs by first distinguishing between materials. There are two classes: elastomer couplings, which employ some form of elastomer or polymer element to realize flexibility, and all-metal couplings, arrangements relying on the flexure of or sliding between metal components to achieve flexibility. Within the all-metal class, there is a further distinction. Couplings that rely on flexure are nonlubricated, those that rely on sliding are lubricated. The net result is three fundamental classes of flexible couplings. The designs or types commonly used for centrifugal pumps are tabulated below. Figure 12.8 shows the nominal coverage of each class. Coupling Class Elastomer All-metal, nonlubricated All-metal, lubricated Usual Types Buffer, block, ring, sleeve Disk, diaphragm Spring-grid, gear Choosing the type of flexible coupling most appropriate to a particular application requires consideration of at least the following factors: 1. 2. 3. 4. 5. 6. 7. 8. Torque to be transmitted Rotative speed Attainable alignment Size and weight Operating cycle Type of driver Service environment, i.e. temperature, atmosphere Cost How the commonly used designs relate to these application factors is dealt with in the discussion of each design. Elastomer Couplings The principal advantages of elastomer couplings are freedom from the need for periodic lubrication, and, provided the correct type is chosen, tolerance of quite high misalignment at moderate speeds. Against these advantages, elastomer couplings tend to be larger than equivalent all-metal couplings, Couplings 279 20,000 15,000 ® 10,000 8,000 7,000 6,000 ::2 5,000 a. 4,000 a: I "0 Ql Ql i- O - . , . , ® 3,000 ., • C. m 2,000 CD 1,000 ® 500 100 1,000 10,000 100,000 Torque -# in 100 1,000 Torque- Nm 10,000 1,000,000 10,000,000 100,000 1,000,000 Fig. 12.8 Flexible coupling type coverage. (Based on average rating data-consult manufacturer for specific couplings.) KEY: 1. Elastomer 2. All-metal, non-lubricated (disk and diaphragm) 3. All-metal, lubricated (spring-grid and gear.) because the torque is transmitted through a low strength material, and therefore they are limited in speed and at some point become more expensive, despite the latter's inherently more expensive design. Compounding that, the size and weight of the larger elastomer coupling can pose problems with rotor inertia and overhung weight. Finally, the elastomer itself can be sensitive to the operating environment, thus precluding the use of certain materials or the coupling class in general. Pin and Buffer Couplings A pin and buffer coupling is a flexible coupling with pins attached to one half of the coupling; these projects into the buffers, which are mounted in the half of the coupling on the other shaft (Fig. 12.9). The buffers are made of rubber or other compressible material to provide the necessary flexibility. The driving bolts have an easy sliding fit in the bushings; slight longitudinal variations are therefore taken care of whereas slight errors in angularity are compensated for by the flexibility of the rubber. Because flexibility is achieved with the elastomer in compression, which means the rubber must elongate since it is essentially incompressible, pin and buffer couplings have a low tolerance of misalignment. 280 Couplings Fig. 12.9 Pin and buffer coupling. Fig. 12.10 Lovejoy coupling. Elastomer Block Couplings Closely related to the pin and buffer coupling, elastomer block couplings transmit torque via elastomer blocks in compression between "fingers" located alternately on each half of the coupling. The Lovejoy coupling shown in Fig. 12.10 is a simple form of elastomer block coupling. Being relatively small, this design has only four blocks that are made in the form of a cross. As the size increases it is necessary to use more blocks, and the result is designs such as that shown in Figure 12.11. Elastomer block couplings are torsionally soft, and the larger sizes are available with blocks of various hardnesses to allow the coupling to be "tuned" to avoid torsional resonance, a potential problem when the drive is pulsating. In the same manner as pin and buffer couplings, elastomer block couplings derive their flexibility from displacement of the elastomer, which means they have high radial stiffness and therefore low tolerance of misalignment. Elastomer Ring Couplings By taking an elastomer ring and putting it in compression during assembly, a practice termed "banding," a relatively simple design is produced that transmits torque by further compressing the loaded segments of the ring, relaxing the compression on the unloaded segments. Figure 12.12 shows a typical design, this version using radial bolts to provide the initial ring compression. Radial and angular flexibility is achieved by flexure of the ring, and consequently the design has greater tolerance of misalignment than Couplings Fig. 12.11 Elastomer block flexible coupling. (Courtesy Kop-Flex, Inc.). 281 Fig. 12.12 Elastomer ring coupling. (Courtesy Lovejoy, Inc.) elastomer block couplings. Despite this, it is recommended that the couplings be used in pairs if high parallel misalignment is expected. Elastomer Sleeve Couplings Couplings of this design transmit torque by shear in an elastomer sleeve, an arrangement that offers significantly higher misalignment capacity than elastomer buffer, block, and ring couplings. The most common form of elastomer sleeve coupling (Fig. 12.13) has a split convex section sleeve. This confers the highest torque capacity since the elastomer is acting at a large radius, but does limit the allowable rotative speed. Resorting to a continuous diaphragm (Fig. 12.14[a]) raises the allowable speed, but at the expense of added weight and complexity. Employing a concave section sleeve (Fig. 12.14[b]) is a second means of raising the allowable speed, although in this case, the gain is at the expense of coupling size since the elastomer is acting at a smaller radius. A third approach is to retain the split convex sleeve but make it of a stiffer material, a variation that lowers the coupling's misalignment capacity. For centrifugal pumps, elastomer sleeve couplings are widely used in mining and mineral processing, applications where pump speeds tend to be low, the service environment generally is not injurious to elastomers, and the coupling 's negligible maintenance needs and high misalignment capacity offer significant advantages. All-Metal Couplings Compared to elastomer couplings, all-metal construction offers smaller lighter designs for the same torque, greater ultimate torque capacity, higher allowable rotative speeds, and greater tolerance of adverse service conditions such as high temperature and some forms of atmospheric contamination. None of the all-metal coupling designs has the misalignment capacity of elastomer sleeve couplings, but several have greater tolerance than elastomer buffer, block, and ring couplings. 282 Couplings Fig. 12.13 Sleeve-type clamped elastomer coupling. (Courtesy Dodge Manufacturing Division, Reliance Electric) Flexible Disk Couplings Flexible metal disk couplings (Fig. 12.15) transmit torque by tension in a disk, which is alternately bolted to each side of the coupling. To raise flexibility without overstressing, the disk is generally a laminate of thin disks, often of stainless steel for corrosion resistance. Coupling flexibility is achieved by flexure of the disk. A single disk element has high angular flexibility but is very stiff radially. It is therefore necessary to use a pair of disk elements to accommodate both angular and parallel misalignment. Since parallel misalignment is accommodated by an angular displacement at each disk element, the parallel misalignment capacity of the coupling increases with separation of the disk elements. Because they do not have internal clearances and do not wear during operation, flexible metal disk couplings can be accurately balanced and will maintain their balance, thus making them suitable for very high rotative speeds (see Fig. 12.8). Flexible Metal Diaphragm Couplings Instead of transmitting torque at a constant radius, as a flexible disk coupling does, a flexible diaphragm coupling (Fig. 12.16) transmits torque from one radius to another. Shear stress in the diaphragm at the smaller radius determines the minimum diameter of the diaphragm. To achieve the required degree of flexibility, the diaphragm must have a certain ratio of maximum to minimum diameter, which means that for the same torque a flexible diaphragm coupling has a larger outside diameter than a flexible disk design. As is the case with flexible disk couplings, a single diaphragm element has high angular flexibility and high radial stiffness, meaning that a pair of elements is necessary to accommodate parallel misalignment. Diaphragms are either one piece, profiled, or a laminate of thin plates to provide high flexibility without overstressing. Some designs rely on the high shear stress at the diaphragm's minimum radius to serve as a "shear pin" in the event of pump seizure. Such designs need to ensure the transmission Couplings (a) Continuous diaphragm-type (Courtesy Dodge Manufacturing Division, Reliance Electric) Fig. 12.14 Fig. 12.15 Flexible metal disk coupling. (Courtesy Rexnord) (b) Continuous concave sleeve-type. (Courtesy Falk Corporation) Elastomer sleeve couplings. Fig. 12.16 Flexible metal diaphragm coupling. (Courtesy Bendix Fluid Power Division) 283 284 Couplings unit (diaphragms plus spacer between them) is retained in the event of diaphragm failure. And if the environment is hazardous, the coupling parts need to be nonsparking. Spring-Grid Couplings In a spring-grid coupling (Fig. 12.17) torque is transmitted by bending in a tempered steel spring element acting in slots in each of the coupling halves. The slots are shaped such that the span between the points of contact with the spring in each hub decrease as torque increases, thus increasing the stiffness of the coupling as torque increases. This provides torsional flexibility and a certain capacity for momentary overload. Misalignment is accommodated by a combination of flexure of the spring-grid and movement of the grid within the hub slots. The latter requires that the coupling be lubricated. Because the springgrid is very stiff in bending in one direction, the coupling produces high cyclic forces if subjected to significant misalignment, and therefore should only be used when close alignment can be assured. Gear-Type Couplings A gear-type coupling (Fig. 12.18) transmits torque by the mesh of gear teeth cut on the outside diameter of the hub with internal gear teeth cut into the cover. To allow angular displacement between the hub and cover axes, without tooth interference, the hub teeth are usually barreled and crowned. In the same manner as flexible disk and diaphragm couplings, a single gear mesh or engagement can only accommodate angular misalignment, therefore a pair of meshes is required to accommodate parallel misalignment. Such a coupling is termed "double engagement," and the greater the separation of the meshes, the greater the misalignment capacity. Any misalignment of a gear-type coupling produces sliding in the mesh, which dictates that the coupling be adequately lubricated. Failure to properly lubricate gear-type couplings results in large forces and moments being imposed on the shafts and bearings of the coupled machines, thus significantly increasing the risk of premature, even catastrophic, failure. For low-speed applications, the usual lubricant is grease. At higher speeds, grease tends to separate so oil is used. If interruption of operation for the purpose of relubricating cannot be tolerated, continuously lubricated couplings are used. An example of this is an unspared boiler feed pump or one driven directly from the generator shaft. Figure 12.19 shows a typical arrangement of such a coupling. As a general rule, the maximum allowable misalignment of a gear type coupling is that which produces a peak sliding velocity at the teeth of 1.S to 2.4 mls (S to 8 ft/sec). Velocities beyond this will cause rapid wear regardless of the quality of lubrication. Gear-type couplings can be balanced to operate at high speed, but wear of the teeth eventually allows the covers to move radially, thus putting the coupling out of balance. For this reason, today most high-speed pumps are equipped with flexible disk or diaphragm couplings. The province of gear-type couplings is very high torque severe service applications. Limited End-Float Travel Horizontal sleeve-bearing electric motors are usually not equipped with thrust bearings but rather with babbitted faces or shoulders on the line bearings. The motor rotor, which is allowed to float, will seek the magnetic center, but a rather small force can cause it to move off this center. This movement may sometimes be sufficient to cause the shaft collar to contact the bearing shoulders, causing heat and bearing difficulties. This effect is particularly noticeable in electric motors of ISO kW (200 hp) and more. As all horizontal centrifugal pumps are equipped with thrust bearings, it has become the practice to use "limited endfloat" couplings between pumps and motors in this power range to keep the motor rotor within a restricted location. The motors are built so that the total clearance between shaft collars and bearing shoulders is not less than 12 mm (O.S in). In tum, the flexible couplings are arranged to restrict the end float of the Couplings Fig. 12.17 Spring-grid coupling. (Courtesy Falk Corporation) ~· - -rI I L Fig. 12.18 Fast double engagement gear-type coupling. 285 286 Couplings Fig. 12.19 Continuously lubricated gear-type coupling. COUPUNG SLEEVES MOtOR BURING FACE Fig. 12.20 Limited end-float coupling. Couplings 287 motor rotor to less than 5 mm (0.2 in). To keep the gap open between the shaft collar and the shoulders, one of the following methods is used: 1. 2. For gear or grid couplings-by a "button" at the end of the pump shaft or by a predimensioned plate between the two shaft ends (Fig. 12.20). For flexible-disk or diaphragm couplings-by the stiffness of the flexible disks themselves, which have inherent float-restricting characteristics. Contact between the hubs and the coupling covers prevents excessive movement in the opposite direction in gear or grid couplings. The stiffness of the flexible disks or diaphragms is the restraining force in both directions in these types of couplings. Spacer and Floating-Shaft Couplings Regular flexible couplings are designed to connect driving and driven shafts with a relatively small distance between the shaft ends, and therefore have only limited tolerance of misalignment. In some applications provision has to be made for greater misalignment, or in others the shaft end separation must be significantly greater to allow dismantling of the pump. Such is the case, for example, with endsuction pump designs in which the rotor and bearing assembly is removed by withdrawing it axially toward the driver, an arrangement known as "back pull out." One of the principal objectives of back pull out design is to allow dismantling of the pump without having to disturb either the pump casing or the driver (Figs. 12.21 and 12.22). A second common example is the need to be able to remove the inboard seal of a between bearings pump without having to disturb the pump or its driver (Fig. 12.23). In either case, the distance between the pump and driver shaft ends has to be enough to allow the dismantling. For this purpose, an easily removed spacer or extension of sufficient length is necessary. Beyond providing room for dismantling the pump, an extension or spacer couplings is commonly Fig. 12.21 Spacer (extension) coupling installed on back pull-out pump. Fig. 12.22 Back pull-out assembly (bearing frame, casing cover, seal, and impeller) being removed. A spacer or extension coupling enables the pump to be dismantled without disturbing either the driver or the pump casing. Fig. 12.23 288 Between bearings pump with spacer coupling (spacer removed) to allow dismantling inboard bearing and shaft seal. Couplings 289 Fig. 12.24 Gear-type spacer (extension) coupling. used for pumps handling hot liquids and therefore subject to thermal expansion and possible misalignment. Their purpose in this case is to increase the separation of the flexible elements thereby avoiding the harmful misalignment that would occur within the coupling with minimum separation of the driving and driven shaft ends. Usually they consist of two single-engagement elements connected by a sleeve (Fig. 12.24). Elastomer and spring-grid couplings are also furnished in spacer configurations. Most the elastomer designs have the flexible coupling at one end of the spacer and a rigid coupling at the other end (Fig. 12.25). With this arrangement, misalignment of the flexible coupling results in a force and Fig. 12.25 Elastomer spacer (extension) coupling. (Courtesy Falk Corporation) 290 Couplings Fig. 12.26 Flexible drive shaft. moment at the rigid coupling. Depending on the coupling type and the extent of misalignment, these reactions can be high enough to cause fracture of the rigid coupling. Spacer versions of spring-grid couplings have the coupling in the middle of the spacer, an arrangement that increases the overhung weight and the potential for high reactions on the connected equipment shafts. The floating-shaft coupling consists of two flexible elements connected by a shaft that must be supported on each end by the flexible elements themselves. Different manufacturers use different approaches as required by their basic coupling designs. For instance, each of the two couplings may be of the singleengagement type, may consist of a flexible half-coupling and a rigid half-coupling at each end, or may be completely flexible couplings with some piloting or guiding construction. In the smaller horsepower field (below 19 kW [25 hpJ per 100 rpm), "flexible drive shafts" are commercially available. These use universal joints at each end with a tubular floating shaft and a splined portion to provide for length variation (Fig. 12.26). The floating shaft and flexible drive shaft are frequently used in vertical dry-pit pumps, an application that is discussed with that type of pump. CLUTCH COUPLINGS Regular disk clutches are rarely used to connect a centrifugal pump to its driver for two major reasons. The first is that most clutch designs impose a high additional thrust load on the pump thrust bearing; the second is that very accurate alignment between the clutch parts is necessary, and this is difficult to maintain. The two designs of clutch couplings that are commonly used to connect centrifugal pumps to their drivers are centrifugal and overrunning. A centrifugal clutch coupling (Fig. 12.27) has spring retained shoes that throw out on rotation to transmit torque by friction with the drum. All but the smallest of these couplings have "leading" shoes (friction between the shoe and the drum acts to drive the shoe into the drum) to keep the size and weight of the coupling to a minimum. Overrunning or Sprag type clutch couplings (Fig. 12.28) employ cam-shaped elements, which lock and transmit torque by friction when torque is from the driving to the driven machine, but unlock to allow relative motion should the driven machine tend to overrun the driving. Overrunning couplings of the type shown in Fig. 12.28 require very accurate machine alignment, tend to overheat if run in the overrun mode for extended periods, and require that the whole unit be shut down to replenish or change the oil in the clutch. When these limitations cannot be tolerated, a separate, foot-mounted totally enclosed overrunning type clutch is used (see Fig. 12.29). Couplings 291 Fig. 12.27 Centrifugal clutch coupling. (Courtesy Ameridrives International, Centric Clutch Products-formerly Zurn Industries) Fig. 12.28 Sprag-type clutch coupling. Sprags are kept in contact with members by energizing springs; wedge tight for one direction of drive and release for the other direction. (Courtesy Dana Corporation, Formsprag, Warren, Michigan) 292 Couplings Fig. 12.29 Overrunning-type clutch with separate bearings. (Courtesy Ameridrives Internationl, Marland Clutch Products-formerly Zurn Industries) COUPLINGS FOR DUAL·DRIVE In dual-driven pump installations, it is generally desirable to have one driver idle either to save power or to save wear. Internal combustion engines, however, cannot be allowed to tum over idle and must be disconnected. The ideal type of couplings for such units are those that can be readily disengaged and reengaged. The simplest means of coupling and uncoupling one driver in a dual drive arrangement is to employ a disconnect or "cut-out" type of coupling. Figure 12.30 shows a manually operated, gear type version of such a coupling. The left view shows the coupling in the connected position; the right view, in the disconnected position. It is a quick and simple operation to release the location pins, slide the sleeve into or out of engagement, and thereby connect or disconnect the driving unit and the pump. If time is of extreme importance or if the starting of the standby driver is automatically controlled, Couplings 293 j Fig. 12.30 Fast's gear-type disconnect coupling. the disconnect coupling needs to be servo operated, a complex arrangement needing care in its operation and maintenance. The alternative is to use some form of automatic or "free-wheeling" clutch type coupling. Of these, the simplest is the centrifugal clutch (Fig. 12.27), which is installed with the shoes in the driven half. The centrifugal action of these shoes can be controlled to any predetermined speed, and no shoe engagement takes place until this speed is reached. Above this speed, the coupling automatically picks up the load. Centrifugal clutch type couplings are frequently used for dual driven fire pumps, usually for the engine only, occasionally for both the motor and the engine. A subtle variation of the dual drive arrangement is having a hydraulic power recovery turbine (HPRT) driving a pump in tandem through an electric motor (Fig. 12.31). With the process operating at rated flow, the HPRT produces power and so lowers the electrical energy consumed by the motor. As the process flow drops, the turbine power also drops, and at some point the turbine starts to absorb power. When this condition is reached it is necessary to automatically disconnect the turbine. The device commonly used to do this is a separate foot-mounted overrunning type clutch (Fig. 12.29). An added advantage of the separate foot mounted clutch in these cases is that it allows a positive separation of the alternate driver from the train, thereby permitting safe work on it while the rest of the train remains on-line. Overrunning Clutch I 01 Fig. 12.31 Motor Drive train of typical charge pump with hydraulic power recovery turbine. 294 Couplings MOUNTING COUPLINGS The means employed to mount a coupling hub on its shaft have a significant effect on machine balance, the reliability of the drive, and the ease of subsequent maintenance. In order of increasing sophistication, the following means are in common use: slide fit, taper-lock bushing, shrink fit, taper, and oil injection or keyless. Slide-fit mounting is convenient but is really only suitable for very small couplings. Torque is transmitted by a key; the coupling is located axially with a headless set screw driven against the top of the key. Machine balance is poor, and the clearance fit allows relative motion between the hub and the shaft, which can lead to fretting corrosion. Taper-lock bushings (Fig. 12.32) offer the convenience of slide-fit assembly with the integrity of a tight fit. Torque is transmitted by a key. The assembly is tightened onto the shaft by drawing the taper-lock bushing into the hub with a pair or more of headless set screws; loosened by moving the set screws to an alternate set of holes (see Fig. 12.32). Because the maintenance of machine balance is not good and the coupling hubs are heavier, both a consequence of the bushing, taper-lock mounting is generally limited to low-speed high-torque applications. A high-integrity coupling mounting, capable of maintaining good machine balance, requires an interference fit between the hub and shaft. Three means are employed to achieve this result. The simplest is a cylindrical shrink fit (Fig. 12.33), in which the torque is transmitted by a key, and the coupling hub is a light shrink fit on the shaft. Shrink fits involve the use of heat for assembly and dismantling. This is not always convenient-a refinery pump that has to have its coupling removed in the field, for example-so a tapered mounting (Fig. 12.34) is often used instead. Torque is still transmitted by a key, but the interference is provided by drawing the coupling hub a predetermined distance along the taper. In applications where the presence of a key in the coupling to shaft connection is undesirable (stress concentration, hub size, balance), a keyless mounting employing oil injection is used. The fit may be stepped cylindrical (Fig. 12.7[b]) or tapered (Fig. 12.35). In both cases, torque is transmitted solely by friction between the shaft to coupling. The necessary interference is high, on the order of 0.00125 mm per mm (in per in) of shaft diameter. Cylindrical fits (Fig. 12.7[b]) are assembled by shrink fitting; tapered fits (Fig. 12.35) by oil injection dilation of the hub, then hydraulic advancement to give the required interference. Dismounting is by oil injection for both designs. Successfully mounting and dismounting keyless couplings requires the following: Withdraw bushing Fig. 12.32 Taper-lock bushing mounted coupling hub. Couplings L Fig. 12.33 1. 2. 3. 4. 5. 6. 295 Interference fit (otherwise require secondary device to lock axially) Cylindrical shrink fit mounted coupling hub. Fit surfaces must be a ground finish and free of scratches Tapered fits must have at least 85 percent contact Adequate grooving for oil drainage in the fit region of tapered shafts, particularly if assembly is being done in a cold environment Ensuring the installed fit is correct, by either measuring the diameters before assembling cylindrical fits or measuring hub advancement as tapered fits are assembled Having the correct tooling-measuring apparatus, lifting devices, oil injection pump and connections, hydraulic nuts, and a restraint for dismounting cylindrical fit hubs (the mounted hub has considerable strain energy and moves off the last portion of its fit quite suddenly) Taking safety precautions appropriate for the use of high pressure oil--equipment integrity, joint tightness, venting air before pressurizing. Taper: typically 0.625-0.750 in/ft on dia Fig. 12.34 Taper-mounted coupling hub. 296 Couplings Fig. 12.35 Oil-injection taper mounted coupling hub. (Courtesy Flexibox International) As the speed of the pump increases, so does the need for finer mechanical balance of its coupling. This progresses through four stages. First, certain types are inherently limited in speed because their construction does not achieve fine balance (see discussion of various types in this chapter). Second, the precision of manufacture is raised (higher class number in the United States) to improve the balance of the components. Third, each major component or sub-assembly is dynamically balanced. And fourth, the entire assembly is dynamically balanced. In the oil industry, couplings for high power, high speed pumps are generally purchased to API-671 [12.1]. COUPLING GUARDS Left exposed, the coupling and the adjacent pump and driver shaft extensions pose a significant hazard to the operator when the pump is running. To eliminate this, couplings and the adjacent shaft extensions are enclosed in a metal guard, designed to prevent operators coming into accidental contact with the moving surfaces. The guards are usually made of steel and supported from the pump base or foundation in the absence of a base. Variations include partial mesh construction for visibility (but beware of small parts falling through the mesh and being thrown back out at high velocity); a hinged opening for inspection; heavy duty design (#10 gauge or thicker) to tolerate abuse; nonsparking materials (aluminum, or bronze where there is concern over the potential for aluminum to spark under some circumstances); and sealed construction for continuously lubricated couplings. Couplings 297 COUPLING MAINTENANCE The greatest contribution to coupling life comes from carefully aligning the coupled machines during installation, then periodically checking the alignment during routine maintenance (see Chaps. 28 and 31). Beyond checking alignment, couplings should be periodically inspected for wear of or damage to their flexible elements. Abnormal wear must be investigated and the cause corrected. The usual causes are poor alignment and lack of or incorrect lubrication. Damage, such as cracking of flexible disks or diaphragms, requires careful investigation to ensure there is not an insidious influence, such as an unexpected operating condition or an occasionally corrosive atmosphere, which could lead to sudden failure. The damaged parts should, of course, be replaced. After each inspection, lubricated couplings need to be relubricated. MAGNETIC CLUTCHES, MAGNETIC DRIVES, AND HYDRAULIC COUPLINGS Magnetic clutches, magnetic drives, and hydraulic couplings are not couplings in the strict sense of the word, as their function is to vary the speed of the driven unit rather than to provide merely a connecting device between pump and driver. Magnetic clutches are rarely used to connect a centrifugal pump to its driver because they require accurate alignment and the few installations that have been made have not been very successful. Their maintenance costs are also high. The only advantageous application of this device is in accumulatortank pumping or similar services for which the demand varies over a wide range. It is now the practice either to start and stop the entire pumping unit or, if the cycle is too frequent for that, to allow the pump to operate at reduced capacity during the period of small demand, incorporating a bypass so the capacity will never fall below a safe value if the demand drops too low for proper operation. Both hydraulic couplings and magnetic drives are used in centrifugal pumps if variations in operating conditions warrant the use of variable output speed devices. Although they have approximately the same overall efficiency as slip ring motors with speed control, they have the advantage of easily producing any desired output speed, whereas the regular control for slip ring motors permits adjustment of speed only by steps. A more complete discussion of these devices appears in Chapter 24. BIBLIOGRAPHY [12.1] API-671, 2nd Edition, Special Purpose Couplings, 1990. American Petroleum Institute, Washington, DC. 13 Baseplates and Other Pump Supports For very obvious reasons, it is desirable that pumps and their drivers be removable from their mountings. Consequently, they are usually bolted and doweled to machined surfaces that in tum are firmly connected to the foundations. To simplify the installation of horizontal-shaft units, these machined surfaces are usually part of a common baseplate on which either the pump or the pump and its driver have been prealigned. BEDPLATES The primary function of a pump baseplate is to furnish mounting surfaces for the pump feet that are capable of being rigidly attached to the foundation. Mounting surfaces are also necessary for the feet of the pump driver or drivers or of any independently mounted power transmission device. Although such surfaces could be provided by separate bedplates or by individually planned surfaces, it would be necessary to align these separate surfaces and fasten them to the foundation with the utmost care. Usually this method requires in-place mounting in the field as well as drilling and tapping for the holding-down bolts after all parts have been aligned. To minimize such "field work," coupled horizontal-shaft pumps are usually purchased with a continuous base extending under the pump and its driver (Fig. l3.1); ordinarily, both these units are mounted and aligned at the place of manufacture. As the unit size increases so does the size, weight, and cost of the base required. The cost of a prealigned base for most large units would exceed the cost of the field work necessary to align individual baseplates or soleplates and to mount the component parts. Such bases are therefore used only if appearances require them or if their function as a drip collector justifies the additional cost. Even in fairly small units, the height at which the feet of the pump and the other elements are located may differ considerably. A more rigid and pleasant looking installation can frequently be obtained by using individual bases or soleplates and building up the foundation to various heights under the separate portions of equipment. (Fig. l3.2). When a baseplate is used, whether it be under both the pump and its driver, or separate bases under each piece of equipment, it is a fundamental element of the structural connection that maintains alignment 298 I. J. Karassik et al., Centrifugal Pumps © Chapman & Hall 1998 Baseplates and Other Pump Supports Fig. 13.1 Baseplate under pump and driver, bolted to the foundation. Fig. 13.2 Pump and driver on soleplates with stepped foundation. 299 300 Baseplates and Other Pump Supports MACHINE LOADS INTO PEDESTALS FOUNDATION PROVIDES HIGH BENDING AND TORSIONAL STIFFNESS TO MAINTAIN ALIGNMENT LOADS INTO FOUNDATION VIA PEDESTALS, SIDE BEAMS, FOUNDATION BOLTS 80 GROUT Fig. 13.3 Base supported by "stiff' foundation. between the pump and its driver. Although this is clearly a very important requirement, it is frequently sacrificed to cost, invariably at the expense of machine reliability. Baseplates for horizontal axis pumps fall into two categories, which for this discussion can be termed "supported" and "suspended." The distinction revolves around how the base is connected to and supported by the foundation. Supported bases, the more common category, are bolted and grouted to a "stiff' foundation (Fig. 13.3). Once installed, the function of a supported base is to transmit equipment loads and drive reaction to the foundation. The remainder of the structural connection to maintain alignment, bending, and torsion, is then provided by the foundation. Given these functions, supported bases are designed for 1. Moderate bending stiffness; sufficient for handling as an assembled unit without yielding (taking a permanent set) 2. High pedestal and foundation connection stiffness; sufficient to maintain coupling alignment under the imposed equipment loads (e.g., piping) and the drive reaction. It is important to note that torsional stiffness is not a design requirement because the foundation provides it. This reduces the cost of the baseplate, but increases the installation cost since the baseplate must be carefully leveled after positioning it on the foundation (see installation in Chap. 28). A noteworthy consequence of the deliberate lack of torsional stiffness is that precise shop alignment of the equipment is meaningless; the alignment will change when the unit is moved. Two things are important in the shop alignment of equipment on supported bases. First, the equipment mounting surfaces must be carefully leveled before aligning the equipment to mark out the mounting surfaces for drilling or to make a final check of alignment. Second, the equipment alignment must be accurate enough to allow precise alignment in the field. Suspended bases, the second and less common category, are those that do not rely on a foundation for the bending and torsional stiffness necessary to maintain alignment. They are used in the following circumstances: Baseplates and Other Pump Supports 301 MACHINE LOADS INTO PEDESTALS c BASE BASE PROVIDES HIGH BENDING TO MAINTAIN ALIGNMENT Fig. 13.4 1. a TORSIONAL STIFFNESS Flexibility mounted baseplate. Simplified installation-the unit is prealigned and can be positioned, connected, and started. Any attachment to the foundation is nominal and usually three-point to be self-leveling. 2. Minimize structure-borne noise-The unit is suspended above the foundation on resilient mountings (springs or elastomer pads). 3. Reduce piping loads-The unit is suspended on springs or stilts or free to slide so it can move to accommodate piping expansion. A typical spring-mounted base is shown in Fig. 13.4. Compared to supported bases, the additional design requirements for suspended bases are 1. High bending stiffness-sufficient to maintain pump to driver alignment under equipment weight and imposed loads. 2. High torsional stiffness-sufficient to maintain pump to driver alignment under drive reaction and any torsion from imposed loads. These two additional requirements raise the baseplate cost. Both requirements add weight, although not significantly if well designed, but providing torsional stiffness involves more difficult fabrication. To achieve worthwhile torsional stiffness, the base must either have a closed cross section (undesirable for corrosion resistance) or diagonal bracing. Conventional cross-bracing makes little or no contribution to torsional stiffness, a fact quite evident in Fig. 13.5. Today, baseplates are furnished in fabricated structural steel, fabricated stainless steel, cast iron, and reinforced polymer. Regardless of the material, the principal design criterion is stiffness. Structural or carbon-steel bases generally realize this at minimum cost by a simple arrangement of moderately heavy pieces. In stainless steel, a more expensive material, lighter, more complex shapes are warranted to minimize cost. Cast iron is only half as stiff as steel, so (he sections need to be heavier, with the increase in weight sometimes offset by the ease of producing more complex shapes. Reinforced polymers are an order of magnitude less stiff than steel, which limits their use in structures designed for stiffness. When they are used, the sections and configurations are necessarily quite different to those for metals. The virtue of fabricated baseplates is the flexibility of form allowed to the designer, ranging from a simple inverted channel (Fig. 13.6) to a complex, suspended skid (Fig. 13.7). Structural or straight carbon steel is the usual material since it is available in a wide range of shapes and sections, and is relatively (CI Fig. 13.5 Effect of section and bracing on torsional stiffness; (a) flat plate, (b) cross-bracing, and (C) diagonal bracing. 302 Baseplates and Other Pump Supports Fig. 13.6 Fig. 13.7 Small frame-mounted centrifugal pump on inverted channel base. Offshore water injection pump with pump, driver, and accessories mounted on suspended, three-point supported skid. 303 304 Baseplates and Other Pump Supports SLOPE - rA SECTION 'A-A' DRIP PAN SECTION 'A-A' (ALTERNATE SIDE BEAM) SECTION 'A-A' Fig. 13.8 Base drain arrangements. inexpensive. Austenitic stainless steel is used when corrosion is a concern. Frequently pumps handle liquids that cannot be allowed to fallon or accumulate on the foundation, since they would then pose a problem of corrosion or combustion. In these cases, the base must also serve as a collector of incidental leakage. Two arrangements are in use: drip pan and drain rim. Figure 13.8 shows the essential difference. Drip-pan bases offer an extensive sloping drainage surface but require careful design to ensure structural integrity and are difficult to fabricate. Drain-rim bases are usually easier to design and fabricate. Most designs, however, suffer from the disadvantage of the regions where leakage falls being flat, and thus prone to some leakage accumulation. Bending a "crown" into the top plate overcomes this, although at some additional cost and fabrication effort. Openings in drip pans and the top plate of drain-rim bases must be collared or bossed to avoid leakage through the opening. Cast iron is restricted to small baseplates for standard pumps, where the quantity being produced is sufficient to justify the pattern expense. Since the base is cast, it is relatively easy to produce a rimmed, sloping drainage surface between the equipment mounting pads (Fig. 13.9). Reinforced polymer bases are sometimes used in place of stainless steel when base corrosion is a problem. As with cast iron, this material is only viable when the quantities are high enough to justify the mold cost. Because the shape is molded, a rimmed, sloping drainage surface is easily incorporated in the design. By definition, supported bases must be designed for grouting. If the base is well designed (meaning that its pedestals do not rely on grout for stiffness), the essential functions of grouting are to 1. 2. Ensure intimate contact between the base underside and the foundation. Provide additional lateral restraint. A secondary function is to fill voids in or under the base to prevent the accumulation of liquid or debris or both. At one extreme the base is an open structure designed to be filled with grout (Fig. 13.10); at the other, a closed structure designed for grouting to the underside of a drip pan (Fig. 13.11). Designs with drip pans or deck plates require special features to ensure grout can completely fill the void beneath Baseplates and Other Pump Supports Fig. 13.9 305 Horizontal centrifugal pump and driver on cast-iron baseplate. the plate or pan. If the void is not completely filled, there is a risk liquid will accumulate under the plate, or the plate will "drum" and create unnecessary noise. Figure 13.12 shows the features necessary for grouting under a drip pan. Except for very small units, under, say, 225 kg (500 lb), the base generally includes provision for lifting. In most cases the lift is four point, because rigging to equalize loading becomes complicated with more than a four-point lift. The lifting lugs are positioned for balance. If equipment obstruction is a problem, a spreader must be used for the lift. Since baseplates are designed for stiffness, the volume of welding required in fabricated designs is not high. Weld extent and size combine to give an actual weld volume greater than that required for stiffness. Continuous welding is necessary for all joints. Intermittent welding should not be used because joints so welded are prone to corrosion and subsequent distortion. Weld sizes are those necessary to develop 50 percent of the plate strength. As noted in the introduction to this discussion, the intention of a baseplate is to provide precision surfaces on which to mount and accurately align the equipment. This function can only be realized when the equipment mounting surfaces of the base are machined. When the fabrication involves extensive Fig. 13.10 Grout-filled baseplate. Fig. 13.11 Grouted drip-pan baseplate. 306 Baseplates and Other Pump Supports UNDERPAN STIFFENERS (WITH CLIPPED CORNER, GROUT OPENING@ CENTRE) + + ~i 'L I I I / / ~ , I , -$-rn -$+ I I I c::=:=::J \ !SIN. DIA OPENINGS OFFSET IF NECESSARY FOR ACCESS BENEATH EQUIPMENT COLLARED, 112" HIGH + l I I I I +\ J + I :~ I \ / 1- / 1/2" DIA DRILLED HOLES FOR GROUT VENT MAX SPACING 36" (ci)HIGH POINT IN EACH 'COMPARTMENT' NO COLLAR UNLESS SPECIFIED API-610 REQUIRES AT LEAST 1-19 SQ. I N. OPENI NG I N EACH UNDERPAN 'COMPARTMENT.' NOT ALWAYS PRACTICABLE 10. OPENING BENEATH EQUIPMENT Fig. 13.12 Design features necessary for grouting under a drip pan. welding, it is usual to oven-stress relieve the base before machining. Doing this eliminates the risk of subsequent distortion as residual stress is relieved over time. The separation of the finished machined surfaces normally provides for at least 3 mm (0.12 in.) of shims under the driver. Provided the base is not "sprung" (twisted out of shape) on the machine tool, the machined surfaces in each plane will be coplanar within 0.15 mm per meter (0.002 in. per foot) of separation, a common specification requirement. When deemed necessary by the designer or the purchaser, baseplates are furnished with a number of t:efinements to aid installation and equipment alignment. Typical of these are leveling screws adjacent to the foundation bolts in supported bases and jacking screws on the pedestals of both supported and suspended designs. CENTERLINE SUPPORT For operation at high temperatures, the pump casing must be supported as near to its horizontal centerline as possible to minimize the consequences of thermal expansion of the casing. Failure to do this will result in distortion of the pump if it is three-point supported (Fig. 13.6) and misalignment of the pump to its driver, both of which can ultimately cause significant damage to the pump. Centerline support is generally adopted when the pumping temperature reaches 175°C (350°F). The real criterion, however, is not the temperature, but the thermal expansion as the casing comes up to temperature. Unusually large pumps therefore require centerline support at temperatures below 175°C (350°F). Centerline support complicates baseplate design significantly, because the tall pedestals must be sufficiently stiff to accommodate loads imposed on the pump without any significant change in the alignment of the pump and its driver. This is particularly difficult with single-stage overhung pumps Baseplates and Other Pump Supports 307 Fig. 13.13 Centerline-supported overhung process pump. (Pig. 13.13), which are effectively only 2-point supported. To develop the required stiffness, the pedestals usually must be closed (box section) and directly connected to the side beam of the base. Units with a large amount of accessory equipment around them often require baseplates so large the pedestals cannot be directly connected to the side beams. In these cases, the connection between the pedestals and the side beams must achieve the same stiffness, which is usually done with judiciously designed lateral and longitudinal bracing underneath the drip pan or deck plate. Inadequate stiffness in bases for centerline supported pumps has caused a great of deal of difficulty in the refining industry. So much, in fact, that API-61O [3.1], the usual industry standard for refinery pumps, now includes requirements for combined base and pump stiffness, and specifies a simple means of testing to verify the design. At temperatures significantly above 175°C (350 0 P), say 290 to 315°C (550 to 600 0 P), many designs have added water cooling to the pedestals, the idea being to remove any heat passed to the pedestals by conduction and convection from the adjacent casing. Tests to measure the amount of heat gained by the cooling water show that it is so little as to be of no practical benefit. In the light of this, it is possible to simplify the installation of high-temperature pumps by eliminating water-cooled pedestals. SOLEPLATES Soleplates are cast-iron or steel pads located under the feet of the pump or its driver and embedded into the foundation. The pump or its driver are doweled and bolted to them. Soleplates are customarily used for vertical dry-pit pumps and also for some of the larger horizontal units to save the cost of the large bedplates otherwise required. HORIZONTAL UNITS USING FLEXIBLE PIPE CONNECTIONS The foregoing discussion of bedplates and supports for horizontal shaft units assumed their application to pumps with piping setups that do not impose hydraulic thrusts on the pumps themselves. If flexible 308 Baseplates and Other Pump Supports Fig. 13.14 Vertical-shaft installation of double-suction single-stage pump. Casing is provided with mounting support flange . pipe connections or expansion joints are desirable in the suction or discharge piping of a pump (or in both), however, the pump manufacturer should be so advised for several reasons. First, the pump casing will be required to withstand various stresses caused by the resultant hydraulic thrust load. Although this is rarely a limiting or dangerous factor, it is best that the manufacturer have the opportunity to check the strength of the pump casing. Second, the resulting hydraulic thrust must be transmitted from the pump casing through the casing feet to the bedplate or soleplate and then to the foundation. Usually, horizontal-shaft pumps are merely bolted to their bases or soleplates so that any tendency to displacement is resisted only by the frictional grip of the casing feet on the base and by relatively small dowels. If flexible pipe joints are used, this attachment may not be sufficient to withstand the hydraulic thrust. If high hydraulic thrust loads are to be accommodated, the pump feet must be keyed to the base or supports. Similarly, the bedplate or supporting soleplates must be of a design that will permit transmission of the load to the foundation. (For a more complete discussion of flexible expansion joints, see Chap. 28.) Baseplates and Other Pump Supports Fig. 13.15 309 Large vertical-shaft double-suction single-stage pump. Note: outrigger supports for driver, and tooling for removing and installing front-half casing. (Courtesy Thompsons, Kelly and Lewis Pty. Ltd.) BASES AND SUPPORTS FOR VERTICAL PUMPING EQUIPMENT Vertical-shaft pumps, like horizontal-shaft units, must be firmly supported. Depending on the installation, the unit may be supported at one or several elevations. Vertical units are seldom supported from walls, but even that type of support is sometimes encountered. Occasionally, a nominally horizontal-shaft pump design is arranged with a vertical shaft and a wall used as the supporting foundation. The regular horizontal shaft unit shown in Fig. 13.9 could be used for this purpose without modification, except that the bedplate is attached to a wall. For such installations, it is advisable to lock the pump feet to the bedplate by keys or dowels rather than to rely strictly on the friction between the pump feet and the pads of the bedplate. Of course, it is assumed that careful attention will have been given to the arrangement of the pump bearings to prevent the escape of the lubricant. Installations of double-suction single-stage pumps with the shaft in the vertical position are relatively rare, except in some marine and navy applications and waterworks installations where floor space is at a premium. Hence manufacturers have very few standard pumps of this kind arranged so that a portion of the casing itself forms the support (to be mounted on soleplates). Figure 13.14 shows such a pump, which also has a casing extension to support the driving motor. As the size of the pumps arranged in 310 Baseplates and Other Pump Supports this manner increases, so does the need to pay particular attention to the design of the pump casing, the pump support beneath it, and the motor support above it to ensure the structural stiffness is high enough to maintain alignment and avoid resonant vibration. For large pumps, typically those for waterworks, it is sometimes necessary to provide outriggers (Fig. 13.15) to achieve the required stiffness. A complete discussion of the methods of supporting pumps that are specifically designed for vertical mounting is given in Chapter 14. 14 Special Designs: Vertical Pumps Preceding chapters on centrifugal pumps with horizontal-shaft construction should not obscure the fact that many centrifugal pumps utilize vertical-shafting. Vertical-shaft pumps fall into two separate classifications: (1) dry pit and (2) wet pit. The former operate surrounded by air, whereas the latter are either fully or partially submerged in the liquid handled. Vertical Dry-Pit Pumps Dry-pit pumps with external bearings include most medium and large vertical sewage pumps, most medium and large drainage and irrigation pumps for medium and high head, many large condenser circulating and water supply pumps, many marine pumps, most nuclear reactor primary cooling water circulating pumps, and an increasing number of vertical in-line pumps for petrochemical and refining applications. A related design, hermetically sealed dry-pit pumps with integral motors, and hence internal bearings, is employed for high-pressure circulating services in power generation and hydrocarbon processing (see Chap. 24). Vertical shaft designs are usually justified on the following grounds: 1. 2. 3. 4. Floor space is limited; marine pumps are a particular example. Suction conditions dictate that the pump be mounted at a low level, whereas the installation as a whole requires that the driver be mounted at a high level. Simplified installation and relative immunity to piping loads; afforded by having the driver mounted directly on top of the pump. Pump size; large vertical shaft overhung pumps achieve higher efficiency (no obstruction in the impeller eye) and are more economical to manufacture and install than equivalent horizontal-shaft designs. Many vertical dry-pit pumps are basically horizontal designs with minor modifications (usually in the bearings) to adapt them for vertical-shaft drive (see Chap. 13, Figs. 13.14 and 13.15). The reverse is true of small- and medium-sized sewage pumps; a purely vertical design is the most popular for that 311 I. J. Karassik et al., Centrifugal Pumps © Chapman & Hall 1998 312 Special Designs: Vertical Pumps Fig. 14.1 Small vertical sewage pump with intermediate shafting. Fig. 14.2 Section of pump in Fig. 14.1. service. Most of these sewage pumps have elbow suction nozzles (Figs. 14.1-14.3) because their suction supply is usually taken from a wet well adjacent to the pit in which the pump is installed. The suction elbow usually contains a handhole with a removable cover to provide easy access to the impeller. To dismantle one of these pumps, the stuffing box head must be unbolted from the casing after the intermediate shaft or the motor and motor stand have been removed. The rotor assembly is drawn out upward, complete with the stuffing box head, the bearing housing, and the like. This rotor assembly can then be completely dismantled at a convenient location. Vertical-shaft installations of single-suction pumps with a suction elbow are commonly furnished with either a pedestal or a base elbow (see Fig. 14.1). These may be bolted to soleplates or even grouted in. The grouting arrangement is not too desirable unless there is full assurance that the pedestal or elbow will never be disturbed or that the grouted space is reasonably regular and the grout will separate from the pump without excessive difficulty. Vertical single-suction pumps with bottom suction are commonly used for larger sewage, water supply, or condenser circulating applications. Such pumps are provided with wing feet that are bolted to soleplates grouted in concrete pedestals or piers (Fig. 14.4). Sometimes the wing feet may be grouted Special Designs: Vertical Pumps Fig. 14.3 313 Vertical sewage pump with direct mounted motor. right in the pedestals. These must be suitably arranged to provide proper access to any handholes in the pump and to allow clearance for the elbow section nozzles if these are used. Vertical in-line pumps (Fig. 14.5) are also generally single suction but have an elbow-type suction nozzle to produce a side-suction flange that is in line with the discharge flange. This configuration is used for a variety of applications ranging from household hot water circulating pumps through hydrocarbon processing to medium-size pipeline pumps. Small vertical in-line pumps are supported by the piping; larger sizes have an additional support built into the bottom of the casing. If a vertical pump is applied to condensate service or some other service for which the eye of the impeller must be vented to prevent vapor binding, a pump with a bottom single-inlet impeller is not desirable because it does not permit effective venting. Neither does a vertical pump employing a doublesuction impeller (Fig. 14.6). The most suitable design for such applications incorporates a top singleinlet impeller (Fig. 14.7). If the driver of a vertical dry-pit pump can be located immediately above the pump, it is often 314 Special Designs: Vertical Pumps Fig. 14.4 Fig. 14.5 Vertical bottom-suction volute pumps with lineshaft drive. Close coupled (extended motor shaft) vertical in-line pump. Special Designs: Vertical Pumps Fig. 14.6 Vertical double-suction volute pump with direct mounted motor. Fig. 14.7 315 Section of vertical pump with top single suction impeller. supported on the pump itself (see Fig. 14.3). When the driver is so mounted, there are three common arrangements for the pump and driver shafts: 1. 2. 3. Separate shafts, flexibly coupled-The pump and driver each have their own radial and thrust bearings. Some designs employ a spacer-type coupling and an open-sided driver support (Fig. 14.8) to allow removal of the pumps bearing frame and impeller without disturbing the driver. Separate shafts, rigidly coupled (Fig. 2.16)-Usually the pump rotor is supported by the driver's bearings. When a mechanical shaft seal is used, the coupling is often a spacer type to allow replacement of the seal without having to disturb the driver. Extended driver shaft (Fig. 14.5)-The impeller is mounted directly on the driver shaft and is supported by the driver's bearings. If a mechanical shaft seal is used, the pump must be dismantled to replace it. Although the driving motors are frequently mounted right on top of the pump casing, one important reason for use of the vertical-shaft design is the possibility of locating the motors at an elevation sufficiently above the pumps to prevent their accidental flooding. The pump and its driver may be separated by an appreciable length of shafting, which may require steady bearings between the two units. It is extremely important that these steadying bearings be rigidly supported and maintained in strict 316 Special Designs: Vertical Pumps Fig. 14.8 Separately coupled vertical in-line pump. alignment. The support is generally provided by horizontal structural steel beams tied into the wall structure, although occasionally a similar vertical support is used. For proper operation of the vertical shafting, the deflection of the vertical guide bearings under any operating conditions must be kept within the limits set by the design of the shafting and the operating speed. In small units, a channel located between the walls of the station usually gives adequate support in all directions. Larger units with larger reaction loads on the guide bearings may require two channels or beams with lattice bars. Some installations incorporate reinforced concrete beams in the structure. Naturally, if the design of the building requires the construction of an intermediate floor, this floor can be used to support the guide bearings. The most common shafting connecting a small- or medium-size centrifugal pump with its driver makes use of the universal joint with hollow tubing (Fig. 14.9). The lower section has a universal joint at both ends whereas the upper sections (if more than one is used) have a guide bearing supporting the lower end and a universal joint at the upper end. Such shafting compensates for angular misalignment and, as the lower section incorporates a splined joint, also compensates for any minor discrepancy in length. If speed permits, shaft sections as long as 3.0 m (lOft.) or more can be obtained. Sections longer than 3.0 m (10 ft.) are easily sprung and must be handled carefully. As this shafting does not transmit thrust, both pump and driver must have a thrust bearing. Although a vertical motor may be mounted directly on soleplates grouted into the floor, a separate Special Designs: Vertical Pumps 317 stand is sometimes necessary so that the motor may be raised to provide access to the coupling. Occasionally, removable beams are placed directly across a large opening in the floor to serve as the motor mounting. This method permits easy access to the pumps for servicing and simplifies lowering them into place during the initial installation. A driver supported on a stand above the floor provides access to the flange connection and upper universal joint for bolting purposes and for relubrication. If the driver uses hollow-shaft rather than solid-shaft construction, it must be provided with a head shaft guided by a lower bearing to act in the same capacity. The weight of this shafting (excluding that of the lowest universal joint) is carried on the motor; provided it is not extremely long, the total weight involved is relatively small and a normal thrust motor can be used. When shafting weight is a concern, hollow fiber reinforced polymer (FRP) shafting is an alternative that offers lower weight, albeit at higher cost, than equivalent hollow-steel shafting. Actually, hollow shafting is more expensive than solid shafting. But the basic universal joint is so widely used on automobiles and trucks that it is somewhat of a production item, and the increase in cost it entails over solid shafting is very reasonable. Units requiring more torque in their intermediate shafting than can be carried by the available sizes of universal-joint shafting use solid shafting, either with solid or with flexible couplings. If solid or rigid couplings are used, only one thrust bearing is needed (usually in the driver), and all other bearings are merely guide bearings. This shafting has the disadvantage of requiring very accurate alignment of all bearings, a difficult feat for open shafting employing more than three bearings. Solid vertical shafting using flexible couplings usually consists of several shaft sections (including pump and driver), each having two or possibly three bearings connected by floating shaft sections and a piloted or guided flexible coupling at each end, thus acting in effect like a universal joint (see Fig. 14.4). Naturally each section has to have a thrust bearing to carry the weight of the shaft section. The intermediate shafting for large pumps requiring large shafts is usually of solid construction with solid flanged couplings that are often forged onto the shaft section (Figs. 7.11 and 14.10). The size of the shafting used for an installation is initially determined by the torque to be transmitted. However, if a certain span between bearings is desirable because of existing supports (floors or beams), a shaft larger than that required by the torque may be necessary so that the operating speed will be sufficiently below the critical speed. It is thus general practice to have the first critical speed ("first bending natural frequency" in modem parlance) above the highest operating or runaway speed of the pump. The critical speed of a vertical solid shaft is a direct function of the diameter and an inverse function of the square of the span between bearings. Thus if a shaft is to run at twice the speed of another, it must be twice as large in diameter for the same bearing span, or its permissible bearing span will be reduced to 70 percent of that permissible with the lower speed. Bearings for vertical dry-pit pumps and for intermediate guide purposes are usually antifriction bearings that are grease lubricated to simplify the problem of retaining a lubricant in a housing with a shaft projecting vertically through it. Typical ball steady bearings used as intermediate shaft steady bearings are shown in Fig. 14.11. Larger units, for which antifriction bearings are not available or desirable, use self-oiling babbitt bearings or forced-feed-oiled babbitt bearings with a separate oiling system (Fig. 14.12 and 14.13). Figure 14.13 illustrates a vertical dry-pit pump design with a singlesleeve type line bearing. Th~ pump is connected by a rigid coupling to its motor (not shown in the illustration), which is provided with a line and a thrust bearing. The supports for the guide bearings of vertical shafting connecting a centrifugal pump and its driver must be sufficiently rigid. The radial load is usually assumed to be the same as if the unit were in a horizontal position. With this loading, the deflection of the supports in any direction should not exceed A in the following equation: 318 Special Designs: Vertical Pumps MOTOR MOTOR STANO STEADY BEARING t I PUMP DISCHARGE SUCTION Fig. 14.9 Elevation of vertical pump with tabular lineshaft. where d NCI =the deflection in mm =critical speed of the shafting in rpm. or for US units where d = the deflection in inches. Fig. 14.10 Elevation of vertical pump with solid lineshaft. Motor supports rotating parts. Special Designs: Vertical Pumps Fig. 14.11 319 Ball bearing used for intermediate shaft guide bearings. (Courtesy Seal Master.) This critical speed is usually 125 percent of the pump rotative speed or some value above the possible runaway speed to allow for back flow through the pump. If beams or channels support the bearings, the design of the latter naturally depends on the span between them, the radial force, and the permissible deflection. Small pump installations with short spans usually require a single channel (to which vertically mounted bearings are most easily attached). Larger units with long spans often require fairly widely spaced channels or beams with strengthening lattice work (for which a horizontally mounted bearing resting directly on the beams or on a bridging plate is more convenient). These considerations tend to make vertically mounted bearings preferable for small units and horizontally mounted bearings preferable for large units. Vertical dry-pit centrifugal pumps are structurally similar to horizontal-shaft pumps. It is to be noted, however, that many of the very large single-stage single-suction (usually bottom) volute pumps that are preferred for large storm water pumpage, drainage, irrigation, sewage, and water supply projects have no comparable counterpart among horizontal-shaft units. The basic U-section casing of these pumps, which is structurally weak, often requires the use of heavy ribbing to provide sufficient rigidity. Some high-head pumps of this type have been made in the twin-volute design. The wall separating the two volutes acts as a strengthening rib for the casing, thus making it easier to design a casing strong enough for the pressure involved (see Fig. 2.9). Another approach is to borrow from water turbine practice and employ a stay ring, a set of vanes between the impeller and casing, to act as a strut (Fig. 14.14). When used in a pump, the stay ring is designed as a diffuser (see Chap. 2). As the size of vertical dry-pit pumps increases, a point is reached where it becomes more practical to form the casing as an integral part of the pump's foundation, an arrangement known as a "concrete volute pump." Figure 14.15 shows such a design. The volute shape is produced by either embedding a fabricated steel shell or pouring around conventional concrete form work. Most designs employ a stay 320 Special Designs: Vertical Pumps ; 1-) L- _ f I I .---&.1_ _ -, Fig. 14.12 Fig. 14.13 Self-oiling steady bearing for large vertical shafting. Section of large vertical bottom-suction volute pump with single guide bearing. Special Designs: Vertical Pumps ........ ,... ... . ... , ' , . ····, ... ... .... .. :.,:..': . :" : . :" ', :" ' .' :.::. :":' :":' :.,', " . .... ... .. . .:. ':" .:. :.'" ': .. ':' .': ..:.:.'...:.:: ::. ::.::" ':... :. ... .-: ..-:..-:...:...:.::.. , ..... . . . .... ;: . .'. ',. .': .':" ': ,': . ... ..... . . . .· ...... . . . . ,'. , • " ' , ' 0' • " .' " " .' , .. , ..... '. '. ' ·. .. . .. .. ., ..... .. . . .. ,. .. . ., .. ...... ,': .. ', .' .. '. .... ....... ..........' .. ", ", ", ", " , , ',' , ,'.' ' ' . ' ' . '.' "."' .., ' ,',' ' , ' , ' , ' , -, ' . ' , ' : ", :', ':" :'::'::'a':' "" .:.... . . . .. . ". ':" :" :" ,':' ':',':''':''':':.',.. ':' ........... : ..: ..: .. ", ....... :" :" :''':' :...:.::.:> .... :.' " ", " " " ' ', , ' , ' , ,' " " " .' , ', ' " . Rat"" P"'!9 perlonnance Flow 11 m~. Head Speed -nroe,. 1'>'1;1 ..... ; ......... p.. .... ..... '-.... BOm 4!50rpm ~~=~R1rt~3 ':;~~::;~,;~:;~:;::;::.~;:..,~ "'..., . ,. ....,.....,.....,..."T"". -'"'~~ · :', :" .... . .. ....:', . ·': . : .': :.' . : :: ~.: ;'".: ",". . '" '" '" '" " ,'. ·':'::" ':"-:" ':" ':'" ':': '" ..... ,' .... .. . .., '..'.. ' . .. ' . ' , . ' . ' . .. . .. ' . ' . , ' , , ' . . . . .. . ... ... . . ..... ' ' ..' ....:.:.::: :::':::':.':>.,':::: . .................... : .. ......: . ," ' .: :.:. , :':.::~: :::: :::: :\ :::: :.:::.:. : :~..., 'o!l'c-IR-o>JIg,·, : :: :. '. '. .. .. .. .. .. '. •. '. ' . ' ... •... : ,:', " . '" ". '.: . , • . • • ' • • •• , ' f" " Fig. 14.14 Section of large vertical bottom-suction pump with stay ring. (Courtesy Voith) '. 321 ....-==I LOWER FLOOR . , ' . '. ' j TOP OF 8EAR1NG COUAR . -..;. , ...... OAOUT~ ACCESS8TEP I-~ 'fl PRIMARY CONa:lETE I ....... ---I BOTTOM OF PEDESTAl .- '.: ~' I 1r I .. OIsalAROE i~ , I I· I"@) n , .r-$-J RUNNING CLEARANCE DIAMETERS Impeller to Cover 6.0 mm Impeller to Wear Ri1g 2.2 mm on diameter ; PRIIolARY CONCRETE _1 Fig. 14.15 Section of bottom-suction concrete volute pump. (Courtesy Thompsons, Kelly and Lewis) 322 I ..... Special Designs: Vertical Pumps Fig. 14.16 323 Wearing ring construction with extended skirt for large vertical pumps. ring to support the pump's bearings and its driver. Concrete volute pumps have been used quite extensively for high-flow duties, typically above 15,000 m3/hr (65,000 gpm), such as condenser circulating, water supply and irrigation, where they can offer a more economical installation than conventional dry-pit pumps or large "pull out" wet-pit pumps. Vertical pumps equipped with bottom single-inlet impellers (see Fig. 14.2) have a leakage joint between the wearing ring hub of the impeller and the suction head. When pumps of this type handle gritty water, the grit separates out during periods of shutdown and concentrates at or near this joint. As soon as the pump is started again, this concentration of grit is washed through the leakage joint, causing wear. Large pumps may resort to a ring construction like that shown in Fig. 14.16, in which the stationary ring is extended above the suction head to form a pocket for the grit to be deposited in and from which it can be periodically flushed. A further aspect of large pumps is that they are often started dry or "dewatered" to reduce their starting torque. When this is the intention, the wearing rings are designed to be flushed during start-up so that any incidental contact within the running clearance does not cause damage or seizure (see Chap. 4, Figs. 4.28 and 4.31). These and other refinements are feasible in large but not in small pumps. Vertical Wet-Pit Pumps Vertical pumps intended for submerged operation are manufactured in a great number of designs, depending mainly upon the service for which they are intended. Thus wet-pit centrifugal pumps can be classified in the following manner: 1. Vertical turbine pumps 2. Propeller or modified propeller pumps 324 Special Designs: Vertical Pumps 3. Sewage pumps 4. Volute pumps S. Sump pumps VERTICAL TURBINE PUMPS Vertical turbine pumps were originally developed for pumping water from wells and have been called "deep-well pumps," "turbine-well pumps," and "borehole pumps." As their application to other fields has increased, the name "vertical turbine pumps" has been generally adopted by the manufacturers. (This is not too specific a designation because the term "turbine pump" has been applied in the past to any pump employing a diffuser. There is now a tendency to designate pumps using diffusion vanes as "diffuser pumps" to distinguish them from "volute pumps." As that designation becomes more universal, applying the term "vertical turbine pumps" to the construction formerly called "turbine-well pumps" will become more specific.) The largest fields of application for the vertical turbine pump are pumping from wells for irrigation and other agricultural purposes, for municipal water supply, and for industrial water supplies, processing, circulating, refrigerating, and air conditioning. This type of pump has also been used for brine pumping, mine dewatering, oil field repressuring, and other purposes. These pumps have been made for capacities as low as 2.S or 3.5 m3/hr (10 or 15 gpm) and as high as 6,000 m3/hr (25,000 gpm) or more, and for heads up to 300 m (1,000 ft.). Most applications naturally involve the smaller capacities. The capacity of the pumps used for bored wells is naturally limited by the physical size of the well as well as by the rate at which water can be drawn without lowering its level to a point of insufficient pump submergence. Vertical turbine pumps should be designed with a shaft that can be readily raised or lowered from the top to permit proper adjustment of the position of the impeller in the bowl. An adequate thrust bearing is also necessary to support the vertical shafting, the impeller, and the hydraulic thrust developed when the pump is in service. As the driving mechanism must also have a thrust bearing to support its vertical shaft, it is usually provided with one of adequate size to carry the pump parts as well. For these two reasons, the hollow-shaft motor or gear is more commonly used for vertical turbine pump drive. In addition, these pumps are sometimes made with their own thrust bearings to allow for belt drive or for drive through a flexible coupling by a solid-shaft motor, gear, or turbine. Dual-driven pumps usually employ an angle gear with a vertical motor mounted on its top. The design of vertical pumps illustrates how a centrifugal pump can be specialized to meet a specific application. Figure 14.17 illustrates a turbine design with closed impellers and enclosed line shafting; Fig. 14.18 illustrates another turbine design with closed impellers and open line shafting. The bowl assembly or section consists of the suction case (also called suction head or inlet vane), the impeller or impellers, the discharge bowl, the intermediate bowl or bowls (if more than one stage is involved), the discharge case, the various bearings, the shaft, and miscellaneous parts such as keys, impeller locking devices, and the like. The column pipe assembly consists of the column pipe itself, the shafting above the bowl assembly, the shaft bearings, and the cover pipe or bearing retainers. The pump is suspended from the driving head, which consists of the discharge elbow (for above-ground discharge), the motor or driver support, and either the stuffing box (in open-shaft construction) or the assembly for providing tension on and the introduction of lubricant to the cover pipe. Below-ground discharge is taken from a tee in the column pipe, and the driving head functions principally as a stand for the driver and support for the column pipe. Liquid in a vertical turbine pump is guided into the impeller by the suction case or head. This may SI<><f f"[[l) "'lVE FIIOONG FOLlCI'II'FR ---':~W~~~9tF~~Z\::t---- SHoFl' -------/-+Y TUllE TO<SI()IO SEARING SO< S~ I NG '--_--TOP S>WT lOP SHAFT TL&: LIMO S>WT ~::::;lllllL4~:dlr-- OISOIAAG£ ~ F------SHoFl' CQAJNG -------+-41 ~------ TOP ~ PIP( f-ff-------ENCL05£O l IN[ SlW'T OfARIIIe; 11n-------- ~ ~WG --fml-- If-- - - - - - COLUMN SHAFT TI.&: S>tAf PIPE _CEO TL&: STASI.IZlR iMf'{ll[ll SHAFT 11------- TOP 80M.. COfoOo£C1OA OfARING t - - - - - -- SlJll. RING SPlOGER ""TAIN[R .....T£ 9OWI. "If------IMP£U.£R RI1='------_1NG RING ~------9OWI. SEARING IW'UI.£R BiISHING ~f_----- ~ING CAP I--- \ - - - - -- - SUCTIOII >€AD OfAIIONG ~~wM~e--------SUCTIOII 1t------~<!CToa. HEAD PIPE STRAINER Fig. 14.17 Section of vertical turbine pump with closed impellers and enclosed line shafting (oil lubrication). 325 ;-2\ 1 '\ ~ TOP SHIFT PIU)QNG STUFfIl«i IIOX II£""IHG PII[-U8IICATlNG PlI'£ L / ,--..., - TOP~PIP[ ~ PIP£ COUPI. ING eEAA II«i II[TAlr«A 5 01 I ~ ! SHAF T COUPI.ING I HE I COl.~ \I. I~ t 1'i ~~ r~;::~ ~ II ~ \.D. ~ :~ ". ~I~ ~ SHAFT IlEAAING 8AAQ(£T SOiAFT SLEEVE OPEN LIN£5>W'T II!EAAINC< UMlI Plp£ I MPELLER , , ~ ~ ~~ ~'rs !. ~ ~ ~ SHAFT AIlING CAP = ~ ""'" TOP TOP IIOWL IMP£LLER WE AIliNG RING ~ BEAIIING IMPELLEA 8I/SHING IlEAAING CAP SUCTION MUll 8£AIliHG SUCTION HEAl) sucnON PIP£ 5 a~ i§ Fig. 14.18 Section of vertical turbine with closed impellers and open line shafting (water lubrication). 326 ....... ----~...."""''''i H......\l--~:r-·-- -- ~1..._--- -- """- Fig. 14.19 Section of bowl of vertical turbine pump (closed impellers) for connection to enclosed shafting. 327 328 Special Designs: Vertical Pumps Fig. 14.20 Section of bowl of vertical turbine pump (open impeller) for connection to open line shafting. Special Designs: Vertical Pumps Fig. 14.21 329 Vertical turbine double casing ("can") pump for condensate and hydrocarbon service. be a tapered section (Fig. 14.19 and 14.20) for attachment of a conical strainer or suction pipe, or it may be a bellmouth. Semi open and enclosed impellers are both commonly used. For proper clearances in the various stages, the semiopen impeller requires more care in assembly on the impeller shaft and more accurate field adjustment of the vertical shaft position to obtain the best efficiency. Enclosed impellers are favored over semiopen ones, moreover, because wear on the latter reduces capacity, which cannot be restored unless new impellers are installed. Normal wear on enclosed impellers does not affect impeller vanes, and worn clearances may be restored by replacing wearing rings. The thrust produced by semi open impellers may be as much as 150 percent greater than that by enclosed impellers. Various applications in power generation and hydrocarbon processing involve pumping from vessels in which the liquid level is not high enough to provide the NPSH (net positive suction head) required by a conventional horizontal pump. This difficulty is often aggravated by the need to develop quite a high head to move the liquid into the discharge vessel. Typical applications are condensate pumps, heater drain pumps, and pumps transferring "light" hydrocarbons (propane and lighter). Building a pit alongside the suction vessel to provide additional submergence for a horizontal pump is an expensive solution and is not always practical. An alternative approach, widely used in modem power plants, is to mount a vertical wet-pit pump in a tank: (often called a "can") that is sunk into the floor (Fig. 14.21). The length of the pump has to be such that sufficient NPSH will be available for the first-stage impeller design, and the diameter and length of the tank must allow for proper flow through the annulus between the pump and can and then around the tum into the bellmouth. When the pump length necessary to achieve this poses a problem, the use of a double-suction first stage (Fig. 14.22) allows a shorter but larger 330 Special Designs: Vertical Pumps 1 .Inlet from condenser 2. On-line condensate polishing plant 3. Discharge to heaters and feed pump }<'ig. 14.23 Passout or re-entry type vertical double casing ("can") pump for condensate service. (Courtesy Thompsons, Kelly and Lewis Pty. Ltd.) Fig. 14.22 Section of vertical double casing ("can") pump with double-suction volute type first stage. diameter can. The application of can pumps to difficult services has lead to a number of novel designs. One notable example is the so-called "pass-out" condensate pump (Fig. 14.23), in which the flow leaves the pump at an intermediate stage, passes through an on-line polishing plant, then reenters the pump for the balance of the head addition. A second is the use of low-specific-speed hydraulically balanced tandem impellers (Fig. 14.24) to develop high heads without imposing intolerable loads on the thrust bearing. PROPELLER PUMPS Originally the term "vertical propeller pump" was applied to vertical wet-pit diffuser or turbine pumps with a propeller or axial-flow impellers, usually for installation in an open sump with a relatively short setting (Fig. 14.25 and 14.26). Operating heads exceeding the capacity of a single-stage axial-flow impeller might call for a pump of two or more stages or a single-stage pump with a lower specific speed and a mixed-flow impeller. High enough operating heads might demand a pump with mixed-flow impellers and two or more stages. For lack of a more suitable name, such high-head designs have usually been classified as propeller pumps also. Although vertical turbine pumps and vertical modified propeller pumps are basically the same mechani- ~ ,,, rl ... -,,'" "-'" I' II I I L - r' ~ ~~ I I I I 1 -l., ...,1. _ -If I "1'- -r" - .J -. (j " r. ._ t ." ~ I ~ l, --. ..... I f '" , ;. 1;1= = ~t~~ ~ ! ~u..; .......... ./ ~-===:r,;~~ -. i:4 !l ll· cW I;u ,· , werl-· 11\:" , , ' I! ; I- ~ W iii .- ~, II f------oISCloE .1 if . j .. --. I- ". l~. IIIII :n -;r . -[1: - .. ~- ffi:- ' & " D ~ ''II'' II IIII'1'1 \l\. \ \ \ p~ m Irl ~~ 1""'""" I ~ I ~J5:i:i ~ ~ Fig. 14.24 ~t :11 "" .1 ~v I ~ 11 1 I,' ~ ~! M --, ~ ~ I ~~ ~~! ~~ III ; r..l~ I jllI lJ ~ ~r~' " I 1., ~ ... ~ )}: / k~;/~ Vertical double casing ("can") pump with low specific speed hydraulically balanced tandem impellers. 331 332 Special Designs: Vertical Pumps 1ZZ:I:ZZl2D~-. P-p!hzzzz:zzz:z::o I i Column --- pipe eov.r - pip. Impeller -----,t-~-"'Il ,BearlnQ /Bearinll /80wl ,haft Impelle,-- __ _ Fig. 14.25 " ...-seal Section of vertical propeller pump with below-ground discharge. Fig. 14.26 Vertical propeller pump with belowground discharge. (Courtesy Peerless Pump Co.) cally and even could be of the same specific speed hydraulically, a basic turbine pump design is one that is suitable for a large number of stages, whereas a modified propeller pump is a mechanical design basically intended for a maximum of two or three stages. Most wet-pit drainage, low-head irrigation, and storm-water installations employ conventional propeller or modified propeller pumps. These pumps have also been used for condenser circulating service, but a specialized design dominates this field. As large power plants are usually located in heavily populated areas, they frequently have to use badly contaminated water (both fresh and salt) as a cooling medium. Such water quickly shortens the life of fabricated steel. Cast iron, bronze, or an even more Special Designs: Vertical Pumps 333 corrosion resistant cast metal must therefore be used for the column pipe assembly. This requirement means a very heavy pump if large capacities are involved. To avoid the necessity of lifting this large mass for maintenance of the rotating parts, some designs (one of which is illustrated in Fig. 14.27) are built so that the impeller, diffuser, and shaft assembly can be removed from the top without disturbing the column pipe assembly. These designs are commonly designated as "pull-out" designs. Like vertical-turbine pumps, propeller and modified propeller pumps are made with both open and enclosed line shafting. Open line shafting is used only when it is certain the pumped liquid is free of solids. In condenser circulating applications, the pumped liquid often contains unexpected solids, so many power plant designers specify enclosed line shafting to be sure of satisfactory bearing life. When Fig. 14.27 Section of modified vertical propeller pump with removable bowl and shafting assembly. 334 Special Designs: Vertical Pumps the line shafting is enclosed, lubrication of the bearings is generally with water or a compatible liquid if the pump is handling other than water. (Environmental concerns have all but eliminated drip feed oil or grease lubrication in vertical wet pit pumps handling water.) The lubricating liquid comes from either a separate source or the pump discharge. In the latter case, it is usually necessary to employ a small booster pump to raise the pressure of the lubricant above that adjacent to the bottom bearing, which is close to impeller discharge pressure (Fig. 14.27; see product lubricated bearings in Chap. 11 for details on lubricant filtration and monitoring). Propeller pumps have open propellers. Modified propeller pumps with mixed-flow impellers are made with both open and closed impellers. SEWAGE PUMPS Except for some large vertical propeller pumps that handle dilute sewage (basically storm water contaminated by domestic sewage), vertical wet-pit sewage pumps have a bottom-suction volute design with impellers capable of handling solids and stringy materials with minimum clogging. Two configurations are used: suspended and submersible, with most modem installations being the latter. Suspended pumps (Fig. 14.28) usually employ an impeller without back wearing rings, a seal of some form above the impeller to limit the amount of leakage back to the suction pit, and a guide bearing or bearings separate from and above the shaft seal. Other lower-cost designs incorporate the lower guide bearing in the stuffing box, which means the seal then has to prevent pumped liquid from entering the bearing. Experience has shown this is not an effective design; it almost invariably suffers rapid guide bearing wear. Guide bearings are lubricated with either oil or grease, as in Fig. 14.28, or clear water (see product-lubricated bearings in Chap. 11). With either approach, the lubrication is not as good as that in a conventional sleeve bearing, and therefore the bearings will wear relatively faster. Suspended wet-pit sewage pumps should only be used for services requiring operation for a very limited portion of the day. Submersible sewage pumps (Fig. 14.29) are close-coupled pumps with the motor either dry or liquid filled. In either case, the motor is isolated from the pumped liquid by some form of axial face seal, and so the pump bearings are always well lubricated. It is this feature that affords greater reliability and longer service life than the suspended design, and it has led to the almost exclusive use of submersible pumps for sewage service, where size allows. Liquid end design follows usual nonclogging pump practice for the impeller and casing. Some incorporate a form of grinding or shredding device upstream of the impeller to allow the pump to better handle the tramp material found in sewage. Most installations have the pump on some form of guide rail (Fig. 14.30) to allow removal and reinstallation without having to drain the suction pit (see Chap. 24 for details on the construction of submersible motors). VOLUTE PUMPS Wet-pit volute pumps are used in a wide variety of applications beyond the sewage and sump services dealt with so far in this chapter. Single-suction cantilever pumps (Fig. 14.31) are designed so the rotor has its first critical speed at least 25 percent above the maximum operating speed and does not rely on support from a submerged bearing. With these features, the design is ideally suited to corrosive and erosive applications where neither a suspended nor a submersible pump is suitable. Typical applications range from paint lines to severe sump service to steel-mill primary scale pit. Liquid end construction is either chemical or slurry pump, depending on the nature of the pumped liquid. If the mounting flange is sealed to the top of the Special Designs: Vertical Pumps Fig. 14.28 Section of vertical wet-pit sewage (non-clogging) pump. Fig. 14.29 335 Section of submersible sewage pump. (Courtesy ITT Flyght AB) suction vessel, and an effective vapor seal is made where the shaft passes through the mounting flange, for example, grease injected double labyrinth; this configuration is a practical "sealless" pump. Large single-suction suspended pumps (Fig. 14.32) have been used for low head condensate service, and, with the appropriate liquid end materials, abrasive service in mineral processing and steel mills. The difficulty with the latter application is keeping the pumped liquid out of the submerged bearings; 336 Special Designs: Vertical Pumps Fig. 14.30 Guide rail system for submersible sewage pump. The pump slides down the guide and automatically hooks up to the discharge connection. Normally two guide rails are used to ensure proper hook up. (Courtesy ITT Flyght AB) unless the lubricating water pressure is greater than that adjacent to the bearing and the seal clearance close enough to produce a velocity of at least 2.1 mls (7 ft.), the pumped liquid will get into the bearings and significantly shorten their life. Double-suction suspended pumps (Fig. 14.33) are used extensively in utility, industrial, refinery, and mineral processing services where the NPSHA is low, the liquid contains a low concentration of solids, or the purchaser just wants a single-stage pump because it is simpler. Being double suction, the NPSHR is 63 percent of that for an equivalent single-suction impeller (same capacity, speed, and suction specific speed). With both the impeller guide bearings exposed to impeller suction pressure, keeping the pumped liquid out of the bearings is easier than in a single-suction design. Because the design allows much lower specific speeds than those used in vertical-turbine pumps (at the expense of pump diameter), it is possible to develop in a single stage, heads that would require six or seven stages of vertical-turbine pump. Lineshafts are either open or closed, depending on the cleanliness of the pumped liquid. As these pumps get larger it becomes necessary to resort to more sophisticated lineshaft couplings than the simple threaded coupling (see Chap. 12 for further details). When the head necessary exceeds that attainable with a single-stage volute pump, a common solution is to make the pump multistage by adding the required number of matching vertical-turbine pump stages (Fig. 14.22). The vertical-turbine pump stages have to be a special design because the shaft is larger than normal to accommodate the high first-stage power. This arrangement retains the lower NPSHR Special Designs: Vertical Pumps 337 $ $ := ~ 1= \Vr ~,. ~ '-- , ~ - - i" I "", i== ~ r?;. ..... III ]1 [J + dB! 1+ Fig. 14.31 Section of vertical cantilever pump for abrasive service. (Courtesy Lawrence Pumps, Inc.) inherent in the double-suction first stage, and reduces the total number of stages needed. It is widely used for condensate service and oil pipeline boosting. SUMP PUMPS The term "sump pump" ordinarily conveys the idea of a vertical wet-pit pump that is suspended from a floor plate or sump cover or supported by a foot on the bottom of a well, that is motor-driven and ~ oc Fig. 14.32 S . ~d It o CDOLlJIo .,.".... .1~ ...J • ....-c "'''W'CD nu....... ~,nwl.. ...... J... Section of single suction vertical suspended mixed flow volute pump for solids handling applications. (Ingersoll-Dresser Pumps model QMN; patents pending) ~~U'tJ1D~ "''''lIIl-'''lIld~:~I''''iII ~ ,- . ~ / ~ b-0 Special Designs: Vertical Pumps 339 Fig. 14.33 Section of double suction vertical suspended volute pump. automatically controlled by a float switch, and that is used to remove drains collected in a sump. The term does not indicate a specific construction, for both diffuser and volute designs are used; these may be single-stage or multistage and have open or closed impellers of a wide range of specific speeds. For very small capacities serviced by fractional hp motors, "cellar drainers" can be obtained. These are small and usually single-stage volute pumps with single-suction impellers (either top or bottom suction) supported by a foot on the casing; the motor is supported well above the impeller by some form of a column enclosing the shaft. These drainers are made as complete units, including float, float switch, motor, and strainers (Fig. 14.34). 340 Special Designs: Vertical Pumps Fig. 14.34 Typical cellar-drainer sump pump. Fig. 14.35 Typical duplex sump pump. (Courtesy Sta-Rite Products) (Courtesy Economy Photo) Sump pumps of larger capacity may be vertical propeller or turbine pumps (single stage or multistage) or vertical wet-pit sewage or volute pumps. If solids or other waste materials may be washed into the sump, the vertical wet-pit sewage pump with a nonclogging impeller is preferred. The larger sump pumps are usually standardized but obtainable in any length, with covers of various sizes (on which a float switch may be mounted), and the like. Duplex units, that is, two pumps on a common sump cover Special Designs: Vertical Pumps 341 (sometimes with a manhole for access to the sump) are often used (Fig. 14.35). Such units may operate their pumps in a fixed order, or a mechanical or electrical alternator may be used to equalize their operation. Most sump pumps are intended to run only occasionally, and therefore employ construction that will yield several years "life" when operated intermittently. This low-cost construction will not realize an acceptable service life (in hours) if the pump is run frequently or continuously. When the service involves pumping more than a few minutes a day, and particularly when the liquid contains abrasive solids, the more expensive vertical cantilever construction (Fig. 14.31) will prove less expensive to own. Vertical suspended construction (Fig. 14.28), with clear liquid lubrication to the guide bearings, is le&s expensive than vertical cantilever but does require the provision of clear liquid and will not realize the same service life in severe applications. APPLICATION OF VERTICAL WET-PIT PUMPS Like all pumps, the vertical wet-pit pump has advantages and disadvantages, the' former mostly hydraulic and the latter primarily mechanical. If the impeller (first-stage impeller in multistage pumps) is submerged, there is no priming problem, and the pump can be automatically controlled without fear of its ever running dry. Moreover, the available NPSH is greater (except in closed tanks) and often permits a higher rotative speed for the same service conditions. There are two mechanical advantages. First, with the appropriate arrangement, it is possible to eliminate a liquid shaft seal. Second, the motor or driver can be located at any desired height above flood level. The mechanical disadvantages are the following: (1) possibility of freezing when idle, (2) possibility of damage by floating objects if unit is installed in an open ditch or similar installation, (3) inconvenience of lifting out and dismantling for inspection and repairs, no matter how small, and (4) the relatively short life of the pump bearings unless the water and bearing design are ideal. The vertical wet-pit pump is the best pump available for some applications, not ideal but the most economical for other installations, a poor choice for some, and the least desirable for still others. TYPICAL ARRANGEMENTS OF VERTICAL PUMPS A pump is only part of a pumping system. The hydraulic design of the system external to the pump will affect the overall economy of the installation and can easily have an adverse effect upon the performance of the pump itself. Vertical pumps are particularly susceptible because the small floor space occupied by each unit offers the temptation to reduce the size of the station by placing the units closer together. If the size is reduced, the suction arrangement may not permit the proper flow of water to the pump suction intake. This difficulty is compounded by the pump's hydraulic design, with those of higher specific speed being increasingly sensitive to irregularities in their inlet flow. As many factors are involved in the design of a suction well and the location of a bellmouth and no simple rules or relations can be reliably applied, none is included in this discussion. The physical size of the pumps (whether propeller or volute) rarely affects the design of the suction well, the location of the bellmouth, or the spacing of the units. These are usually controlled by factors governing the proper flow of the water to the bellmouth. Figure 14.36 illustrates an ideal arrangement for a multiple-unit station with dry-pit pumps. It provides an unrestricted flow on the suction side to all the units. Stations using this arrangement for a group of vertical volute pumps often have the suction bellmouths and elbows formed right in the concrete substructure. If dry-pit pumps are installed with vertical bellmouths, adequate clearance must be provided at the back wall and between the units (Fig. 14.37). This arrangement illustrates a common situation in 342 Special Designs: Vertical Pumps ELEVATION Fig. 14.36 Multiple-unit station with vertical dry-pit volute pumps alongside each other in wide suction bay. Fig. 14.37 Multiple-unit station with vertical wet-pit volute pumps at end of conduit. Special Designs: Vertical Pumps TOP VIEW ~~. ;. : I~_ ~! . p".~:.-r. f.~~' ~{.',:1".'-= [(! ~,~\ ~} ~;~ ~~. £- - .- - - --J&~~.~~~(,.,i:.;;:.:; :.: ~} :";i::/:;,.:; :;L;::::';:\'i;:: ~-;-;'~;:;~,,·~.~;;:~~;::t~~_::. ·..;tiXf:;';i /;~:~ :'.-: ;;;;1 , ;',;A~:.~{{;,;~ ;{;.,~:,~;~ '~ 1:~~: . Fig. 14.38 ELEVATION Multiple-unit station of vertical propeller pumps with suction flow from one end of well. Fig. 14.39 Pump installation with good intake design. D = suction bel/mouth diameter. 343 344 Special Designs: Vertical Pumps -$, PARTITION WALL B=2iO(MIN) f MINIMUM to RECOMMENDED Fig. 14.40 Recommended channel and pit design. KEY: A = Minimum submergence above impeller centerline, approximately 1.5 to 2.0D depending on pump cavitation characteristics; B = minimum width of sump or pit; C = minimum depth of sump or pit; D = suction bell diameter (normally same as bowl diameter). Cross-sectional area of sump (B x C) shall not be less than ten times the suction bell area (1CD 2/4). Fig. 14.41 Vertical wet-pit propeller pump with gate valve and flap valve. Fig. 14.42 Vertical wet-pit propeller pump with siphon discharge. 34S 346 Special Designs: Vertical Pumps which the suction is located at the end of a conduit the width of which is less than the length of the suction well. Without a flared section with division walls to guide the distribution of the incoming water to the various units, the flow would be badly disturbed and the operation of the pumps adversely affected. A propeller-pump arrangement that is often troublesome (vertical volute-pump arrangements with suction bellmouths like those in Fig. 14.37 have the same problem) is shown in Fig. 14.38. Unless the width of the suction well provides sufficient area and unless the locations of the bellmouths permit good flow, the demand of the units first in line will disturb the flow in more removed units. Very often installations of this general arrangement require extensive baffling to correct the distribution. Some stations are made with walls that form individual wells for each pump, a channel to supply these wells running lengthwise of the station. Various recommendations have been developed over the years for the dimensioning of intake channels and approaches. If feasible, an intake like that illustrated in Fig. 14.39 will give excellent results. The dimensions for the channel width and spacing are given in terms of the suction bellmouth diameter. Another example of good channel and pit design for vertical turbine pumps is given in Fig. 14.40, which also indicates recommended clearances between the suction bellmouth and the bottom of the pit and between the pump, the pit back wall, and the partition walls. If long discharge lines are involved, valves are required in the piping. Normally, both a gate valve and a check valve are used (Fig. 14.41). The check valve acts to prevent reverse flow, whereas the gate valve functions when the unit is shut down for an extended period. In some installations, the gate valve is omitted, and stop planks or a sluice gate are used. A cone valve that acts both as a check and a stop valve appears in other installations. The high cost of this valve, however, usually restricts its use to installations requiring a flow that is started and stopped gradually to prevent water hammer. A few installations with long discharge lines for single pumps have no valve other than a flap valve at the discharge end. If the unit is stopped, the water in the discharge line flows back through the pump until the pipe is emptied. If the design of an installation or the failure of a check or flap valve to close permits a reverse flow of water through a pump, the pump acts as a water turbine. The torque developed by the pump as a turbine will cause reverse rotation in freely rotating drivers like electric motors. Usually it is not sufficient to cause reverse rotation in internal combustion engines. In motors, the reverse speed that will be attained will depend both on the net head and the runaway speed of the pump acting as a water turbine. The net head is then less than the static head because of friction losses. The runaway speed is dependent on the specific speed of the pump. Higher specific speeds have higher runaway speeds (measured as a percentage of normal speeds). The reverse speed obtainable in an actual installation is usually below the safe operating speed of its component parts, and it is not necessary to use a special design. The use of a siphon discharge eliminates the necessity for valves in the discharge line (Fig. 14.42). The high point of the siphon must be above high-water level on the discharge to break the siphon and prevent backflow of the water when the pump is shut down. When a pump operating on a siphon discharge is started, the usual procedure is to exhaust air from the system by a priming device until the pump is primed. The pump may then be started to help fill the siphon. The connection to the high point of the siphon is also provided with a valved opening so that air can be admitted and the siphon broken when it is desired to stop the unit. It is possible to control the admission of air automatically so that the valve functions if the unit stops for any reason. Although siphons with short legs are relatively simple and troublefree both in design and operation, more care must be taken if they have long legs. Some siphons operate successfully, with legs exceeding 7.6 m (25 ft), but these are primarily limited to circulating systems in power plant installations. The use of a siphon discharge is desirable in drainage installations for pumping over a levee because it provides a lower head than would be obtained if the water were discharged at the top of the levee. 15 Special Designs: Self-Priming Pumps .~--~--- ----- The standard centrifugal pump cannot handle air or vapors. Unless it is located beneath its source of supply, some means must be found of filling both the pump and its suction piping with liquid, that is, to prime it. A demand naturally developed, therefore, for a centrifugal pump able to handle appreciable quantities of air and to reprime itself automatically when located above the water supply. This requirement is especially important in the construction field because pumps may be used to dewater areas into which seepage is slower than the pump can handle. A standard pump will operate until it uncovers the entrance to the suction pipe, get air-bound, and then be unable to reprime itself even after sufficient seepage has accumulated to prevent further air infiltration. A true "self-priming pump" is one that will clear its passages of air if it becomes air-bound and resume delivery of the pumped liquid without outside attention. Therefore, its basic requirement is that the pumped liquid entrain air (in the form of bubbles) so that the air will be removed from its suction side. The air must be allowed to separate from the liquid once the mixture of the two has been discharged by the impeller, and the separated air must be allowed to escape or to be swept out through the pump discharge. A self-priming pump therefore requires an air-separator, which is a large stilling chamber or reservoir provided on its discharge side to effect this separation. Several ways exist of making a centrifugal pump self-priming, the most important being the following: 1. Recirculation from discharge back into suction 2. Recirculation within the discharge and impeller itself. These two basic methods have many variations; only one example of each will be discussed here. RECIRCULATION TO SUCTION A pump made self-priming by this method contains a liquid reservoir either attached to or built in the casing. The first time the pump is to be started, this reservoir is filled. A recirculating port is provided in the reservoir, communicating with the suction side of the impeller. As the pump is started, the impeller 347 I. J. Karassik et al., Centrifugal Pumps © Chapman & Hall 1998 348 Special Designs: Self-Priming Pumps handles whatever liquid comes to it through the recirculating port plus a certain amount of air from the suction line_ This mixture of air and liquid is discharged into the water reservoir where the two elements separate, the air passing out of the pump discharge and the liquid returning to the suction of the impeller through the recirculating port. This operation continues until all the air has been exhausted from the suction line. The vacuum thus produced draws the liquid from the suction supply right up to the impeller. It is essential that the reservoir remain filled with liquid when the pump is brought to a stop. This is accomplished by incorporating either a valve or some form of trap between the suction line and the impeller. A typical self-priming pump operating on this principle is illustrated in Fig. 15.1. The pump housing, B, consists of a conventional volute and an inlet passage. The inlet has a priming passage with a priming valve, C, attached to it. This priming valve is a cylindrical rubber tube. The impeller, A, is of a conventional semi-open design. During priming, the pump body is filled with water. This water is drawn into the pump housing through the priming valve and discharged from the volute back into the pump body. The suction created by the impeller draws air from the inlet passage at the same time that it is drawing water through the priming valve. The air is mixed with the water and discharged into the pump body along with the water. In the pump body, the air bubbles separate from the water, rise to the surface, and pass out through the pump discharge while the priming valve picks up water that is relatively free of air. After the air has been exhausted from the suction piping or hose and water is drawn into the pump, sufficient pressure difference exists between the pump body and the inlet passage to cause the rubber priming valve to collapse. The recirculation thereby being stopped, all the water that goes through the Fig. 15.1 Self-priming pump with valved recirculation to suction. (Courtesy Homelite Corp.) Special Designs: Self-Priming Pumps 349 impeller is discharged from the pump body_ A ball check valve is built into the suction line to maintain the vacuum in the line between operations. RECIRCULATION AT DISCHARGE This form of priming is called "volute priming" or "diffuser priming," depending on the design of the discharge casing. It may be distinguished from the preceding method by the fact that the priming liquid is not returned to the suction of the pump but mixes with the air either within the impeller itself or at its periphery. Its principal advantage, therefore, is that it eliminates the complexity of internal valve mechanisms. A typical "volute priming" self-priming pump is illustrated in Fig. 15.2. An open impeller, A, rotates within a volute casing, B, discharging the pumped liquid through passage C into the sealing reservoir, D. When the pump starts, the trapped liquid carries entrained air bubbles from the suction to the discharge chamber. There, the air separates from the liquid and escapes into the discharge chamber, E. The liquid in the reservoir returns to the impeller through the recirculation port, F, reenters the impeller, and mixing once more with air bubbles is discharged through C. This operation is repeated continuously until all the air has been expelled through E. Once the pump is primed, the uniform pressure distribution established around the impeller prevents further recirculation, and the liquid is discharged into reservoir D both at C and at F. Some sizes of this pump incorporate an externally adjustable recirculation port (Fig. 15.3). The original clearance between the impeller and the casing can be restored, when these parts become worn, by the following steps: Fig. 15.2 Self-priming pump with volute recirculation. Fig. 15.3 Adjustable recirculating port of volute recirculation pump. 350 Special Designs: Self-Priming Pumps Fig. 15.4 Self-priming pump with separate motor drive. Fig. 15.5 Close-coupled self-priming pump. I. Remove cover nut 2. Turn adjusting stem until recirculating port touches impeller 3. Back off adjusting stem I Y2 turns 4. Replace cover nut. Special Designs: Self-Priming Pumps 351 Fig. 15.6 Portable engine driven self-priming pump. This adjustment appreciably extends the usable life of the pump casing. An added advantage of this design is the ability to use impellers of different diameters in the same casing without losing priming capabilities. Such pumps are built with as many combinations of drives as ordinary nonpriming pumps. They are commonly available either with separate drive (Fig. 15.4), close coupled (Fig. 15.5), or engine drive (Fig. 15.6). REGENERATIVE PUMPS One of the "special effect" kinetic pumps, regenerative pumps are self priming provided the casing retains sufficient liquid to effect a seal between the casing and the impeller. These designs have been used alone as self priming pumps when their hydraulic characteristics suited the application, and as a priming impeller acting in series with a conventional centrifugal impeller for other applications. Chapter 16 includes a detailed discussion of regenerative pumps, their characteristics, and typical applications. 16 Special Effect Pumps Within the classification "kinetic pumps" (see Chap. 1), there is a group termed "special effect" pumps. These are pumps in which the means of energy addition is still kinetic, the addition of velocity, but that employ effects other than that of the classical centrifugal pump (see Chap. 2) to do so. At present there are six distinct types of special effect pumps: regenerative, partial emission, induced vortex, viscous drag, impact, and reversible. Regenerative Pumps The name "regenerative pump" describes a unit with a multi blade impeller that develops head or pressure by a principle considerably different from that of a centrifugal pump. These pumps have had a number of other names given to them, for example, "turbulence pumps," "peripheral pumps," "vortex pumps," and "turbine pumps." The term "regenerative," however, best describes the actual pumping principle involved. Principle of operation. Figure 16.1 shows a cross section of a regenerative pump; Fig. 16.2 is an "exploded" photograph of the same unit. The impeller has a multiplicity of radial vanes cut into its rim that rotate within an annular chamber. The liquid enters the pump casing and flows to both sides of the impeller either through a cored passage in the casing or through ports or openings provided for this purpose in the web of the impeller. This design, in effect, makes the pump a double-suction unit and balances the axial hydraulic thrust. At one point of the periphery, there is a separating wall or "stripper" that the impeller passes, in its rotation, with a very narrow clearance. Passages are provided from the suction into the annular chamber surrounding the impeller rim, immediately beyond this dividing wall. The liquid is picked up in the spaces between the impeller vanes and then thrown out again into the annular chamber because of the kinetic energy it gains from the centrifugal force action in the impeller. The kinetic energy is transformed into pressure energy as the liquid slows down in the casing. The manner in which a regenerative pump develops head is illustrated in Fig. 16.3. The liquid enters the casing and flows to both sides of the impeller, twin passages leading the liquid to the impeller blades (Fig. 16.3[a]). Each casing is equipped with a dividing wall (or stripper) through which the impeller 352 I. J. Karassik et al., Centrifugal Pumps © Chapman & Hall 1998 Special Effect Pumps IMPEL L ER KE v RING P",CK ING 353 WAT ER SL INGER Fig. 16.1 Section of a regenerative pump. passes with close clearance, as shown in Fig. 16.3(b) (at A). Just beyond this wall in the direction of rotation, the twin suction passages, which have passed around the sealing wall, come into the impeller chamber (at B). The impeller blade engages the liquid as it comes out of the suction passage, and centrifugal force throws the liquid out to the periphery of the impeller (Fig. 16.3[c]). The liquid leaving the impeller blade has had velocity energy added and leaves the impeller as shown in the vector diagram (Fig. 16.3[d]). The casing passage causes a gradual reduction of velocity with the accompanying increase in potential energy (pressure). The pump has thus generated head. The shape of the space between the impeller vanes imparts a rotating motion to the liquid as it leaves the impeller cavities (Fig. 16.3[e]). As the rotating motion continues in the annular chamber, the liquid is guided back into the "root" of the cavities, proceeding circumferentially around the chamber (Fig. 16.3[f]). The cycle is then repeated, adding energy to the liquid every time it leaves and reenters the impeller. The number of times the process repeats itself may vary from 2 to 50 depending on the head to be developed by the pump. The more times the liquid reenters and is discharged from the impeller, the higher the head. When the liquid finally reaches the discharge side of the separating wall, it flows into the discharge passage and out the discharge nozzle. 354 Special Effect Pumps Fig. 16.2 "Exploded" view of regenerative pump. c d Fig. 16.3 Development of pressure in regenerative pumps. Special Effect Pumps 355 Performance characteristics. The perfonnance of a regenerative pump resembles that of a high specific-speed centrifugal pump in that the head rises very rapidly with a reduction in capacity, as does power consumption. Typical perfonnance characteristics are illustrated in Fig. 16.4. Both pumps follow the same laws of speed variation: (1) the capacity varies directly with the speed, (2) the head varies as the square of the speed, and (3) the power consumption varies as the cube of the speed. The efficiency of regenerative pumps is considerably lower than that of centrifugal pumps. In the past, this disadvantage was offset by their ability to develop much higher heads at low flows, applications that would otherwise have required multistage centrifugal pumps. Typical regenerative applications were for flows less than 25 m3/hr (100 gpm), with heads up to 150 to 180 m (500 or 600 ft), with a few special designs capable of capacities to 45 m3/hr (200 gpm) and heads of 360 to 460 m (1200 to 1500 ft). Today, it is more usual to meet such applications with small, mass-produced vertical multistage centrifugal pumps or single-stage partial-emission (Barske) pumps. For most applications, the fonner offer lower overall cost, being more efficient than regenerative pumps and generally having a longer period between the need to renew clearances. The latter have the virtue of large running clearances and limited sensitivity to increases in the clearances. Because they are designed only for low flows, regenerative pumps have relatively low NPSHR, and therefore NPSH is generally not a concern in their application. For the same reason, however, entrained 240 \ 220 200 \~ 180 t- IIJ IIJ ~1b 160 ~ ~ La.. ~ ci « IIJ :t: .J « t- \~ 140 \ 120 100 o t- 80 60 ... 40 \ \ \ 10 4 I' ~Jf~ ~ o 5 20 CAPACITY, IN GPM ·2 -- 30 40 Fig. 16.4 Typical performance characteristics of a regenerative pump. Shut-off head of 102 m (355 ft), 1,730 rpm, and 4.6 m (15 ft) suction lift· 356 Special Effect Pumps Fig. 16.5 Arrangement of trap in the suction of a regenerative pump. gas is, because relatively small volumes significantly reduce the pumps' capacity. Given this, many rating curves are published for various suction lifts, based on lifting water from a reservoir exposed to the atmosphere. The regenerative pump can handle viscous liquids up to about 48 cSt (250 ssu); when viscosities exceed this value, performance falls off very rapidly, and the pump ceases to be practical. Self-priming features. As long as sufficient liquid remains within the pump to seal the clearance between the impeller and the separating wall in the casing, the impeller cavities will take up all fluid present, whether simple liquid or a mixture of liquid and vapor or air. The regenerative pump will therefore always prime itself-by evacuating the air out of its suction line-provided the installation is arranged to trap sufficient liquid on shut-down. This condition is usually met by building in a trap in the pump suction (Fig. 16.5). In addition, an enlargement is provided in the discharge of the pump to slow down the velocity of the delivered liquid and to permit its separation from any vapor or air. General application. Because the satisfactory operation of a regenerative pump depends on the close clearance between the impeller and the separating wall, or stripper, this pump is not too suitable for handling corrosive liquids or liquids containing abrasive foreign particles. The first may attack the metal at the running clearance joint to a point that the pump will lose a major part of its capacity through internal recirculation. Solid particles of the products of corrosion may also build up on the pump surfaces and cause wear at the running clearances just as grit or other abrasive particles in the liquid would. The regenerative pump should ordinarily be used to handle clean, clear liquids. To prevent the entry of foreign material, a 40-mesh strainer is desirable. Special Effect Pumps 357 The clearance at the dividing wall, moreover, has a greater effect on the effective capacity of this pump than the clearances at the wearing ring of a centrifugal pump. Regenerative pumps thus require more frequent maintenance and renewal of internal clearances. An ample margin over the maximum requirement for pump capacity is recommended. Depending on the pump's construction, clearances can be renewed either by replacement of parts (side-plates, casing heads, and the like) or by changing the thickness of the gaskets that determine the relative location of the casing walls and the impeller itself. Because of the steepness of its head-capacity curve, a regenerative pump operated at excessively low capacities may develop excessive pressures. Consequently, a relief valve is usually arranged in the discharge line to bypass some of the capacity back to the suction line whenever the discharge pressure reaches a predetermined maximum. Partial-Emission Pumps Although not in the strictest sense special effect pumps, partial-emission pumps are sufficiently different in their design and characteristics to warrant distinction from conventional centrifugal pumps. The partial-emission pump was first described by Barske [16.1], and is therefore frequently so called. Because of the shape of the impeller, partial emission pumps are sometimes also called "paddle wheel" pumps. Principle of operation. Figure 16.6 shows the impeller and casing insert of one design of partialemission pump. Energy is added to the liquid in the same manner as in a conventional centrifugal pump. Where the operation differs is in the amount of energy added, and the means of controlling the pump's best efficiency capacity. Because the impeller vane angle is very high, close to or equal to 90 deg, the head developed by partial emission pumps is on the order of 50 percent higher than a low-specific-speed centrifugal pump with the same impeller diameter and running at the same speed. When run at high speeds (up to 25,000 rpm), heads up to 2,100 m (7,000 ft) in a single stage have been achieved in partialemission pumps intended for process and industrial applications. The term "partial emission" derives Fig. 16.6 Impeller and casing insert of one design of partial emission pump. 358 Special Effect Pumps 250 :; J: 200 1~ : m J: 40 j 30 Iii 120 10 Total Head e 50 Q. J:40 8 2.5 130 eU:I 2.0 ::::iE J: 1.5 z m 1.0 z I Q. 011 ~20 I ~ 10 "" 0 i o ."" 10 4~ ~. .~·Tt 20 5 30 2 40 50 Flow-GPM 10 M3/Hr. eo 70 i 15 80 I Q. 0.5 90 20 Fig. 16.7 Typical perfonnance characteristics of a partial-emission pump. from the nature of the radial flow through the impeller. Unlike higher specific speed impellers, in which the radial flow is fairly uniform over the periphery of the impeller, partial emission impellers have radial flow over only part of each passage at the impeller periphery. This is a result of having the ratio of impeller normal flow area to casing throat area much larger than in conventional centrifugal pumps. Experience has shown that for small, low specific speed pumps, these designs achieve higher efficiency. With such an area ratio, the pump's capacity is limited by separation and consequent blockage in the casing throat. As such, a given pump has a range of best efficiency capacities, each corresponding to a particular casing throat area. For manufacturing convenience, the casing throat is usually produced by drilling. Partial emission pumps have open or semiopen (Fig. 16.6) impellers, with relatively large axial clearances between the casing and impeller, which means the pump performance is not greatly affected by wear. PerjormtJ"ce characteristics. With radial or nearly radial impeller vanes, the head characteristic is effectively flat out to best efficiency capacity, dropping steeply beyond where separation in the discharge occurs, whereas the power rises continually with increasing capacity. Impellers of "high solidity" (more vanes of angle less than 90 deg) or other design refinements have constantly rising head characteristics (Fig. 16.7) and generate less noise, an important factor in high-speed designs. Over a speed range of 2: 1, partial emission pumps follow the affinity laws for variations in speed. AppUctJtio". For designs at the low end of conventional centrifugal pump specific speeds, partialemission pumps achieve equal or higher efficiency, and are therefore a good choice for applications requiring high head at low capacities. Direct coupled pumps running at 3,600 rpm (Fig. 16.8) are available for flows to 90 m3/hr (400 gpm) and heads up to 210 m (700 ft). High-speed designs are a viable alternative to multistage centrifugal pumps in services where the pumped liquid sa, viscosity, and lubricity are low, factors that reduce the reliability of multistage designs dependent on the Lomakin effect for rotor stability (see Chap. 7). Motor-gear driven high-speed pumps (Fig. 16.9) are in regular Special Effect Pumps Fig. 16.8 Horizontal 3,600 RPM partial-emission pump. Fig. 16.9 High-speed partial-emission pump. (Courtesy of Sunstrand Fluid Handling Corporation) 359 360 Special Effect Pumps use for flows to 90 m3/hr (400 gpm), at heads up to 1,900 m (6,200 ft). In most applications, high-speed pumps are equipped with inducers to lower the NPSH that must be provided by the system. Induced-Vortex Pumps Known also as "recessed impeller," "free flow," or "torque flow" pumps, induced-vortex pumps employ a means of head generation that makes them particularly useful for pumping liquids laden with solids or moderate percentages of air or entrained gas. Principle of operation. Rather than having the pumped liquid pass through the impeller as it does in a conventional centrifugal pump, an induced-vortex pump has its impeller recessed back out of the flow path, the degree of recess varying from 50 to 100 percent (Fig. 16.10), depending on the intended service. Designs with less than 100 percent impeller recess sometimes have axial rotor adjustment to allow the pump's performance to be "tuned" to a particular service. The recessed impeller imparts head to the pumped liquid by momentum exchange. With the impeller out of the flow path, the pump's ability to pass solids is limited by the size of its casing throat. Performance characteristics. Over the range of specific speeds used for induced-vortex pumps, typically 1,500 to 2,800, their head and power characteristics are similar to equivalent centrifugal pumps (Fig. 16.11). Because the means of head addition is indirect, the head produced for a given size impeller is lower and the power higher, resulting in lower efficiency, usually between 35 and 55 percent. NPSHR tends to be lower than a centrifugal pump of the same capacity, because the rate of energy addition at the impeller inlet is lower. Fig. 16.10 Section of induced-vortex pump. (Courtesy Met-Pro Corp; FYBROC Division) Special Effect Pumps 100 361 100 Io J ~ Recessed v - -- .. '0 . ~ - . .. ~- ..,- - ~ 60 ., ~ , :I: 0 ~ , 40 V ~ ,, 20 o --- -. _. . . .• 0 - ~b / ----a-- '0 ' ~ - --a--0 - 60 -.:J I-- , 100 -0- -. ~ . . - '- 0 ..---a- ,, ~. o 0- Standard 40 --, .. - ~ - - - -0 .-a--- f..--£I .' . - -- . 20 i<>' o 200 300 400 500 600 700 800 Capacity (USGPM) Fig. 16.11 Typical performance characteristic of an induced-vortex pump. Dashed lines show performance of equal size conventional centrifugal pump; note similar head but lower power than induced vortex pump. Application. Induced-vortex pumps are used for pumping liquids carrying large or fibrous solids, or having a moderate concentration of entrained gas. Such services are common in the food and waste water industries. Flows typically range from 25 to 900 m3/hr (100 to 4,000 gpm), with heads to 30 m (100 ft). Viscous Drag Pumps First developed in 1910 by Nikola Tesla, viscous drag or laminated-rotor pumps were intended to effectively handle liquids whose viscosity ranged from 2,000 to 8,000 ssu. Today such applications are generally handled more efficiently by rotary pumps. Principle of operation. The "impeller" of a viscous drag pump is a series of coaxial disks, each with one or more holes in the center, and separated from each other with spacers (Fig. 16.12). Energy is imparted to the pumped liquid by viscous drag between the disks and liquid. The number of disks and their spacing is varied, depending on the viscosity of the pumped liquid to maintain a moderate relative velocity through the impeller, thereby achieving a reasonable efficiency. 362 Special Effect Pumps I t Wearing ring ' " ........... Concentric casing Fig. 16.12 Diagram of viscous drag (Tesla) pump. Configuration shown is end suction with concentric casing. 140 120 100 ~ 0 ~ c:: (I) ·13 80 w == o!S CD ~ 60 a.. ~ CD J: 40 20 o 20 40 60 80 100 120 Flow-% BEP Fig. 16.13 Type performance characteristics of a viscous drag (Tesla) pump. Special Effect Pumps 363 Performance characteristics. Over the usual specific speed range of 700 to 1,000, the head characteristic of viscous drag pumps ranges from flat to continually rising with decreasing flow (Fig. 16.13), whereas the power characteristic rises continually with increasing capacity. Because the energy lost to friction is high, the efficiency is quite low, generally not exceeding 25 percent. Application. With efficiency well below that of rotary pumps, viscous drag pumps are limited to pumping abrasive viscous liquids at elevated temperatures, conditions not suitable for rotary pumps. Because the separation of the impeller disks is relatively close, viscous drag pumps cannot handle solids of any significant size. Known designs produce flows to 230 m3/hr (1,000 gpm) and heads to 90 m (300 ft). Rotating Casing (Pi tot Thbe) Pump Rotating casing pumps, known also as "pitot-tube" or "impact" pumps, are a design that has been in use, to varying degrees, for the past 80 years. In keeping with regenerative and partial-emission pumps, they are a special-effect kinetic pump, intended to develop high heads at low flows. Principle of operation. The principle of operation draws from that of a pitot tube, which when facing directly into an oncoming fluid stream indicates the total head of the stream at that point. In a rotating casing pump (Fig. 16.14), liquid enters the casing along the axis of rotation, and has momentum added as it passes through the enclosed radial vanes of the impeller into the rotating casing. The action of the rotating casing maintains the high velocity of the liquid stream. High-energy liquid is then drawn off through the pitot tube and passed to the pump discharge. The head developed by the pump is equal to the sum of the static pressure created by centrifugal force and the velocity head. Inlet Fig. 16.14 Section of "Roto-Jet" pitot tube pump. (Courtesy EnviroTech PUMPSYSTEMS) 75 50 Wr-;PSH REQUIRED 2800 ~ 2600 2200 .. • :ez l: o t=-i Obtainable Minimum Rcquired Flow for Safc Pump Operation. L with Bypass Orifice (0.156" Dia.)(J.962mm) 1 + - - - 1 - - - - 1 - - - ; 2000 .. ,.... - ~- Iii 1600·.. W ~ 1400 t-= ~ I¥' 1800 ... Q w ~-~V-7''''--+--i1 2400 ::r:: 25 1....----- Iii 1200 1000 800 600 i 400 ./ ~'" 200 .-t - -.........=--t-- - t'">... :">. '" i-' 1m, RP"II i -- DO :'\OT OPERATE BI:.YONDTHIS UKIo J 400 ~r-:-:-:=!:;-:, !1750RP\1 ! o "'-~-~-~-~f4!I'~25~R~r~MJ--t---t---tI-~--t~~~+~~~~~i85~4'~K(='RTI'~=U~-t----1 t.--:~~ nm1 ~I:=-:~ ~ ~ 300 200 n: ::r:: 100 ai ~ o Perfo manCE Base ~ On VIi ater o 100 200 300 400 500 600 FLOW·GPM Fig. 16.15 Performance characteristics of a pitot tube pump. (Courtesy EnviroTech PUMPSYSTEMS) Performance characteristics. Design specific speed is typically within the range 60 to 500. The head characteristic depends on the size of the pitot tube, ranging from continuously rising with decreasing flow to "drooping" (Fig. 16.15). The power characteristic rises continuously with increasing flow. For the range of specific speeds covered, efficiency is good, values on the order of 60 percent having been achieved. NPSHR is typically lower than a centrifugal pump of the same capacity. 364 Special Effect Pumps 365 The hydraulic performance of rotating casing pumps, flows from 1.0-170 m 3/hr (5-750 gpm) and heads to 1,525 (5,000 ft), makes them suitable for the applications also met with regenerative, partial-emission, or small multistage centrifugal pumps. The advantages offered by this design for such applications are wide flow rangeability, no critical internal running clearances, smaller size than multistage centrifugal pumps, and the ability to tolerate running dry. Its disadvantages are erosion when the pumped liquid contains abrasive solids, and a low tolerance of air or entrained gas in the pumped liquid. Variations of the design are used for integral lubricating oil pumps (Fig. 11.49). Application. Reversible Pumps In the same manner as partial-emission pumps, reversible pumps are not strictly special effect pumps, but their design, performance, and application are sufficiently different to warrant inclusion in this chapter. Principle of operation. Head in reversible pumps is developed in the same manner as in conventional centrifugal pumps. To be reversible, however, several compromises have to be made in the pump design; specifically the impeller vanes must be radial, the casing concentric, and the discharge nozzle radial. With this symmetrical construction, the pump performs equally in either direction of rotation. Performance characteristics. Unlike partial-emission pumps, whose impeller design is similar, reversible pumps have a falling head characteristic (Fig. 16.16), a consequence of impeller discharge to casing throat area ratios used in their design. The power characteristic rises with increasing capacity. Efficiency at 30 to 40 percent is lower than a centrifugal pump of equal performance because the design is compromised for reversibility. NPSHR is higher than an equivalent centrifugal pump for the same reason. 140 120 100 cJ< 80 15<ll J: 60 40 20 o 20 40 60 80 100 120 140 Flow-% Fig. 16.16 Type head characteristic of a reversible pump. 160 366 Special Effect Pumps Application. Reversible pumps are applied to low-energy auxiliary services, for example, cooling water circulation through an engine, where it is necessary to have the pumped liquid move in one direction regardless of the driver's direction of rotation. The one known design is specific speed 900, with a capacity of 11.5 m3Jhr (50 gpm) and head of 12.2 m (40 ft) at maximum speed of 2,000 RPM. BIBLIOGRAPHY [16.1] Barske, U.M., and Dr. Ing.; "Development of Some Unconventional Centrifugal Pumps", Proc. Institute of Mechanical Engineers (Britain), Vol. 174 No. 11, 1960. 17 Materials of Construction - - . -.. ~ - - - - - - - Centrifugal pumps are fabricated of almost all the known engineering materials, from simple thermoplastic polymers through metals ranging from cast iron to the various nickel-based alloys to composites and ceramics. The conditions of service and the nature of the pumped liquid finally determine which among this wide range of materials will be the most suitable. A specific choice is based first on past experience with the same liquid or a similar liquid. When past experience is lacking, material properties and known performance must be used. Listings of the materials commonly recommended for various liquids can be readily found in the Standards published by the Hydraulic Institute [1.1], in API-61O [3.1] and in the catalogs and bulletins of pump manufacturers, particularly those who specialize in centrifugal pumps for chemical service, the field that presents the greatest variety of material selection problems. Note, in this connection, that the plant owner is ultimately responsible for the performance of the specified materials, because the precise nature of the pumped liquid is solely under his or her control. It is the pump manufacturer's responsibility to furnish the specified materials (provided, of course, they are mechanically suitable). The principal service conditions that affect the selection of materials are 1. Operating pressure 2. 3. Pumping temperature Head per stage (affects both the peripheral velocity of the impeller and the liquid velocity in the waterways) 4. Corrosiveness of the pumped liquid (can vary markedly with traces of halogens, halides, or compounds of hydrogen) 5. 6. Concentration and abrasiveness of any suspended solids Load factor (fraction of time running) and expected life. In selecting the material for any part of a pump, the material properties to be considered are I. Strength: tensile, impact and endurance or fatigue. 2. Stiffness 367 I. J. Karassik et al., Centrifugal Pumps © Chapman & Hall 1998 368 Materials of Construction 3. Thennal expansion and thennal shock resistance 4. Corrosion resistance, considering the effects of velocity and stress 5. Erosion resistance (both abrasion and cavitation) 6. Feasibility of fabrication into the required component. Table 17.1 gives a qualitative ranking of these properties for the usual pump materials. In developing general guidelines for material selection, we first concentrate on the materials most commonly used for individual parts. Table 17.2 summarizes these materials for the three major parts: casing (plus inner casing where applicable), impeller, and shaft. Table 17.3 lists the specification and chemical composition of the metals commonly used in centrifugal pump construction. CASING MATERIALS The foremost requirement of the material of a centrifugal pump casing is that it be strong enough, given the sections employed in the design, to safely contain the maximum working pressure. Next, the material or combination of materials must be stiff enough to limit distortion of the casing under pressure and imposed nozzle loads to that which will enable the pump to operate as intended. Finally, the material must provide an economical balance between service life (determined by loss of wall thickness due to corrosion or erosion or both) and cost. Injection-molded polymers are viable materials for the casings of small, mass produced pumps for low pressure, 1.0 to 1.4 bar (15 to 20 psig), at ambient temperature. Limited strength, low stiffness, and the cost of molds generally preclude their use above these limits. Cast iron has higher strength and stiffness than polymers, yet is still economical to produce. For these reasons it is the material used for the casings of most centrifugal pumps. Its strength and stiffness are limited, however, which places a practical upper limit on the pressure for which cast iron casings can be built. This limit varies with size, being around 35 bar (500 psig) for small pumps and falling to 10 bar (150 psig) for large pumps. Cast iron has poor resistance to thermal shock, and therefore is generally not used at pumping temperatures above 175°C (350°F), nor for services where the pumped liquid is flammable or toxic. In the latter case, the concern is that should the pump be involved in a fire, attempts to extinguish the fire may quench and fracture the heated casing. Ductile iron offers higher strength, stiffness, and thermal shock resistance than cast iron, with the degree of improvement depending on the grade specified. Many chemical pumps have high-elongation ductile-iron casings to allow their use for flammable or toxic liquids. Larger pumps have ductile iron casings, usually of lower elongation, to increase their pressure rating. Carbon steel is stronger, stiffer, and more ductile than ductile iron. Beyond mechanical properties, carbon steel has the advantage that it can be welded, thus enabling ready repair in the field, something that is not feasible with either iron or ductile iron. Given its mechanical properties, carbon steel is the usual material for medium- and high-pressure casings: in cast form for medium pressure and forged for high pressure. Carbon steel is the standard casing material for pumps handling flammable or toxic liquids in petroleum refining service, a practice related to the material's strength and thermal shock resistance. Because they can be readily repaired by welding, carbon-steel casings are frequently used in mildly erosive mineral processing services. Chrome steels offer higher strength than carbon steel, superior corrosion resistance in some services (e.g., boiler feed) and marginally better erosion resistance. When taking advantage of the higher strength of chrome steels, the casing design must be able to accommodate the higher deflection that will occur - ---"- Above nil ductility transition temperature. Code: L = low, I = intermediate, and H = high. Varies with polymer and extent of reinforcement. H H 13 H H L H I I H I I W H H L H L L - L-W H None L I H H L H H - 13 Chrome Material Steel -"------------ Bronze -----.- l L L L L L L I H L I - Varies with alloy; aluminum and nickel aluminum bronzes have high tensile strength. I L I I L L H I - Hard iron ------- I L L L L L L I L L H -- Ductile iron 2 Strength Tensile Impact Endurance Stiffness Thermal expansion Thermal shock resistance Corrosion resistance Erosion resistance: Abrasion Cavitation Ease of manufacture Iron Ranking of Properties of Usual Pump Materials Property Table 17.1 I H H H I H H I H H 316 H H H H I H H I H I Duplex - - ----- L L None L L L H H L L ----- L-I2 I None L H I H L L I -- Ceramic - Polymer $ g. 1'; ~ ~ ~ ~ 1\ ~ Mineral processing Water injection Petrochemical Hydrocarbon Low pressure Medium pressure High pressure Normal High pressure Abrasive High temperature Corrosive Corrosive Noncorrosive Corrosive Corrosive Corrosive Nonabrasive Abrasive Abrasive Abrasive Fresh Fresh Salt Condition Common Pump Material Combinations Condensate (water) Boiler feed Water Service Table 17.2 316 Hard metal Rubber Duplex Cast iron Alloy 20 Stainless Steel Steel Steel Steel 316 Alloy 20 Polymer Chrome steel Rubber lined Hard metal Hard metal 316 Duplex 317 Alloy 20 Polymer Steel Iron Hard metal Steel 317 317 Duplex Ductile iron Steel Hard metal Chrome steel Chrome steel Gray iron Bronze Steel Steel Monel Steel Steel Chrome steel Chrome steel Alloy steel Chrome steel Chrome steel Chrome steel Duplex Duplex Steel Polymer Bronze Bronze Chrome steel Bronze Chrome steel Chrome steel Cast iron Chrome steel Hard metal Chrome steel Polymer Cast iron Bronze Steel, Iron Iron Chrome steel Steel Steel Steel Steel Chrome steel Shaft Inner casing/liner Impeller Casing to> "g.::s ~ .,~::s ~ 1:;- .iii·~ -.I = ... ~ Carbon Steel Nickel Chromium White Iron Ferritic S.O. Iron Austenitic Cast Iron Grey Cast Iron C Type 2 Fe Bal Bal P C C C LCA WCA C WCB NiHard4 WCB LCA WCA ASTM A352 ASTM A216 2D ASTM A216 BS 4844 0.25 Max 0.25 Max 0.30 Max 2.8 3.2 0.50 Max 0.50 Max 0.50 Max 0.30 Max 0.30 Max 0.20 Max 0.20 Max 0.20 Max 0.50 Max 0.40 Max 0.50 Max 0.30 Max 0.5 Max 8.0 -10.0 Bal Bal Bal Bal V 0.03 Max V 0.03 Max V 0.03 Max Si 1.5 -2.2 0.5 Max 5.5 -7.5 Others Mn 0.2 -0.8 4.0 -6.0 Cu At the discretion of the foundry Mo 0.08 Max 1.5 -2.5 1.5 -2.5 Cr Si 2.5 Max 3.0 Max 18.0 -22.0 13.5 -17.5 Ni 60-40-18 Pressure Not applicable 3.0 Max 3.0 Max C At the discretion of the foundry ASTM A395 Type 2 ASTM A436 Class 40 ASTM A48 Type 1 Class 25 ASTM A48 ASTM A436 Orade No Standard 60-40-18 C C C Class 40 Type I C Class 25 Material Type Prod. Form C=Cast W= Wrought Table 17.3 Standard materials and their chemical composition NOTE: Where the material is in wrought form, the International Standard defined is that relating to bar. This table is supplied for information only and is not to be used for specification purposes. (t) The materials defined here are proprietary alloys. I ~ N Austenitic Stainless Steel Martensiticl Ferritic Stainless Steel C W C C W 3l6L 316L 317 347 XM19 C CB7Cu-l C C CA6NM 316 C CA-15 - - Prod. Form C=Cast W= Wrought CA6NM CB7Cu-l CF-SM CF-3M 316L CG-SM CF-SC XM19 ASTM A4S7 ASTM A747 ASTM A744 ASTM A744 ASTM A276 ASTM A744 ASTM A744 ASTM A479 ---- CA-15 ASTM A217 - - Grade No Standard 0.06 Max 20.0 -23.5 1.5 -3.0 IS.0 -21.0 11.5 -13.5 16.0 -IS.0 10.0 -14.0 18.0 -21.0 3.0 -4.0 17.0 -21.0 9.0 -13.0 9.0 -12.0 2.0 -3.0 IS.0 -21.0 9.0 -12.0 0.08 Max 2.0 -3.0 15.5 -17.5 3.6 -4.6 9.0 -13.0 2.0 -3.0 11.5 -14.0 3.5 -4.5 0.4 -1.0 Mo 11.5 -14.0 Cr 1.0 Max Ni O.OS Max 0.03 Max 0.03 Max O.OS Max 0.07 Max 0.06 Max 0.15 Max C Standard materials and their chemical composition (Continued) Material Type Table 17.3 2.5 -3.2 Cu Bal Bal Bal Bal Bal Bal Bal Bal Bal Fe Mn 4.0 -6.0 Cb SxC -1.0 N 0.10 Max Nb 0.15 -0.35 N 0.2 -0.4 N 0.05 Max Cb 0.1 -0.3 Others V 0.1 -0.3 ~ High Alloy Austenitic Stainless Steel Duplex Stainless Steel C C 254sMo W 255 CN3MN C CD3MWGJN C C CD4MCuN CN7M C 255 Prod. Form C=Cast W= Wrought I Grade CN3MN CK3MCuN ASTM A351 ASTM A351 UNS 32550 ASTM A479 CN7M 6A ASTM A890 ASTM A744 1B ASTM A890 Ferralium 255-3SC (t) No Standard 0.02 Max 0.03 Max 0.07 Max 0.04 Max 0.03 Max 0.04 Max 0.05 Max C Standard materials and their chemical composition (Continued) Material Type Table 17.3 3.0 -4.0 24.0 -26.0 24.0 27.0 19.0 22.0 20.0 -22.0 19.5 -20.5 6.5 -8.5 4.5 6.5 27.5 30.5 23.5 -25.5 17.5 -19.5 6.0 -7.0 6.0 -7.0 2.0 -3.0 2.9 3.9 1.75 -2.25 24.5 -26.5 4.75 -6.00 3 Mo 25 Cr 6 Ni Fe 0.50 -1.00 0.75 Max 3.0 -4.0 1.5 2.5 0.5 -1.0 2.75 -3.25 2.5 Bal Bal Bal Bal Fe Bal Bal Nominal analysis Cu Si 1.00 Max Mn 1.2 Max Si 1.0 Max Mn 1.5 Max Si 1.00 Max Si 1.0 Max Mn 1.0 Max Mn 2.0 Max Si 1.0 Max Mn 1.0 Max N 0.18 N 0.18 -0.24 N 0.18 -0.26 N 0.10 0.25 N 0.2 0.3 N 0.10 -0.25 Others W 0.5 1.0 I ~ W C W 825 CW-2M C276 W K-500 Monel + Co. C Monel C W 625 Hastelloy B C Worthalloy 55 (1) Range given for Ni is total for Ni Nickel Copper Nickel Molybdenum Nickel Chromium Molybdenum Material Type Prod. Form C=Cast W= Wrought Fed'l ASTM A494 ASTM A494 0.35 Max 0.25 Max QQ-N-286 Class A 0.12 Max M-35-1 N-12MV 63.0 -70.0 (1) Bal Bal 1.0 Max 15.0 -17.0 Bal 14.5 -16.5 Hastelloy C-276(t) 0.01 Max 15.0 -17.5 Bal 0.02 Max 15.0 -17.5 CW-2M 2.5 -3.5 19.5 -23.5 38.0 -46.0 0.05 Max Incoloy 825(t) 26.0 -30.0 8.0 -10.0 20.0 -23.0 Min 58.0 0.10 Max 3.0 -5.0 Mo Inconel 625 (t) 22.0 -24.0 Cr Bal Grade Ni 0.12 Max I C (t) ASTM A494 No Standard Table 17.3 Standard materials and their chemical composition (Continued) Bal 26.0 33.0 1.5 -3.0 3.0 -5.0 Cu W 1.0 Max W 3.0 -4.5 Mn 1.0 Max Mn 1.0 Max Co 2.5 Max V 0.20 --0.60 2.0 Max 4.0 -7.0 2.0 Max 3.5 Max Co (1) Al 2.30 -3.15 Al 0.2 Max Ti 0.6 -1.2 Min 22.0 Cb 1.0 3.0 Al 0.40 Max Nb+Ta 3.15 -4.15 5.0 Max 4.0 -6.0 Si 3.0 -5.0 W 1.0 -3.0 W 0.35 --0.85 Si 1.0 Max Si 0.08 Max Ti 0.40 Max Others 10.0 Max Fe Co 2.5 Max V 0.35 Max Co 1.0 Max ~ Titanium -- --- - W C C C Grade 2 C95500 C93700 Leaded Bronze Nickel Aluminium Bronze PB2 C C LG4 C90700 C C83600 Phosphor Bronze Tin Bronze Leaded Gunmetal Prod. Fonn C=Cast W= Wrought -- ASTM B265 ASTM B148 ASTM B548 BS 1400 L - ____ 2 --- C95500 C93700 PB2 C90700 LG4 BS 1400 ASTM B584 C83600 Grade ASTM B-584 No Standard - 0.10 Max C Standard materials and their chemical composition (Continued) Material Type Table 17.3 - - 3.0 -5.5 1.0 Max 0.5 Max 0.5 Max 2.0 Max 1.0 Max Ni - - Cr ------ Mo --- 78.0 Min 78.0 -82.0 Bal 88.0 -90.0 Bal 84.0 -86.0 Cu --- 0.30 Max 3.0 -5.0 0.03 Max Fe - - N 0.03 Max '------- 0 0.25 Max - - '------- H 0.015 Max Mn 3.5 Max - Pb 8.0 -11.0 Zn 0.8 Max Sn 9.0 -11.0 AI 10.0 -11.5 Pb 0.50 Max Zn 0.30 Max Sn 11.0 -13.0 Pb 0.5 Max Pb 2.5 -3.5 Zn 1.5 -3.0 Sn 6.0 -8.0 Sn 10.0 -12.0 Pb 4.0 -6.0 Zn 4.0 -6.0 Sn 4.0 -6.0 Others "----- Ti Bal P 0.15 Max - P 0.15 -0.60 I I I I 376 Materials of Construction at sealing surfaces and locating fits. Chrome steels are weldable, with the 13 chrome, 4 nickel alloy being considered the most weldable, and 5 chrome, 0.5 molybdenum the least. All require preheating before welding, and any structural welds require postweld heat treatment. The choice between a cast or forged casing depends on an assessment of the risk of in-service leakage versus manufacturing cost. In high-temperature applications, repeated heating and cooling of the pump can cause the internal shrinkage inherent in cast casings to develop into minor cracking, thereby allowing an originally pressure-tight casing to leak. For medium-pressure casings, typically 100 bar (1450 psig) at 230°C (450°F), cast casings are normally used because they are economical and can be repaired by welding. At higher pressures, forged casings are deemed the better choice because they eliminate the potential cracking problem. Although forged casings are more expensive to manufacture than cast casings, the difference decreases with increasing pressure, and is generally negligible for pressures beyond 200 bar (3,000 psig). At low temperatures, below what is known as the "nil ductility transition temperature" (which varies with alloy, heat treatment, and section thickness), carbon steel and chrome steels becomes brittle. In these circumstances, austenitic stainless steel, or in some cases alloys of aluminum, both of which do not exhibit a "nil ductility transition temperature," are used. Corrosive liquids pose a problem in that the corrosion resistance of the usual materials is almost the inverse of their strength and stiffness. Reinforced polymers of the appropriate grades offer extremely good corrosion resistance. These materials, however, have relatively low strength and stiffness, and therefore casings made of them have a low pressure rating. Bronze is produced in a wide range of alloys, from leaded gunmetals, which offer moderate resistance to seawater corrosion (depending on temperature and contamination), through phosphor bronze, with good resistance to seawater and mild acids, to nickel aluminum bronze and similar alloys, with excellent resistance to seawater. All the bronzes have higher strength and stiffness than reinforced polymer, but across the range of alloys cited, the mechanical properties vary from below that of cast iron to approaching that of the chrome steels. Because bronze is not used extensively for centrifugal pump casings, most casings produced are designs based on cast iron. As such, their pressure rating will depend on the alloy being used. For leaded gunmetals and phosphor bronze, the pressure rating will be lower. Lined casings afford high corrosion resistance without the expense of having to produce the entire casing of an exotic or impractical material. Two forms of construction are used: a separate lining contained by the casing (Figs. 26.42 & 26.43), or a lining bonded to the casing. Of the usual lining materials, only glass and Teflon® are bonded to the casing. The linings have various properties. Rubber exhibits high resistance to corrosion and erosion, but is limited by temperature. Ceramic is useful for corrosive or erosive services at temperatures above the limit of rubber. Graphite, impregnated to make it impervious, has high corrosion resistance but is soft and cannot tolerate any solids in the pumped liquid. Teflon® is inert in most liquids but too soft to have useful resistance to erosion; its advantage over graphite is simpler casing construction. Glass is inert to all liquids, but prone to microcracking caused by differential thermal expansion at high temperatures, which can lead to corrosion of the substrate. The pressure rating of lined casings is determined by the material of the structural portion of the casing. This is usually cast iron or ductile iron, and so the pressure rating is limited to around 17 bar (250 psig). Austenitic stainless steel covers a wide range of alloys, the most common being type 316 stainless steel (or ASTM A744 CF8M for castings). The corrosion resistance of these alloys depends on the particular alloy and liquid. They all rely on a passive oxide film for corrosion resistance. Localized corrosion will start at damaged areas of this oxide film. An example of how this limits their application is the high risk of corrosion if exposed to stagnant seawater. The chloride ion initiates pitting and the stagnant conditions do not provide enough oxygen to re-establish a continuous oxide film. As a class of materials, austenitic stainless steels have strength and stiffness higher than ductile iron but below steel. Their elastic limit (yield point) is not well defined, which makes components of these alloys prone Materials of Construction 377 to plastic deformation (permanent distortion) if stressed close to their yield point (usually based on 0.2 percent offset). With these mechanical properties, casing designs based on steel must be derated for pressure when produced in austenitic stainless steel. On the other hand, if a casing is required for a particular pressure rating, its effective sections in austenitic stainless steel must be larger than in steel. The so-called "higher alloys," those with high nickel or molydenum contents, have excellent corrosion resistance to a particular liquid, but often poor resistance if one element in the liquid's composition is changed. For the purposes of casing pressure rating, the mechanical properties of the higher alloys are similar to those of austenitic stainless steel. Duplex materials, alloys whose structure is a mixture of two phases, austenite and ferrite, have excellent resistance to corrosion by sea water and napthenic acid, and can be used for liquids containing the latter at temperatures up to 260°C (500°F). Although the corrosion resistance of duplex alloys is not equal to higher-nickel-based alloys for some liquids, they have the advantage of higher strength. Given this, duplex casings can have pressure ratings close to those of chrome steel while achieving significantly higher corrosion resistance. Hard metals for solids-handling pumps range from austenitic manganese steels for dredge pumps (whose casing material must have sufficient ductility to absorb the impact of large solids), through Nihard® for high concentration slurries to high chrome irons for high concentration slurries of a corrosive liquid. Solid casings are constructed entirely of hard metal, generally with replaceable wear plates alongside the impeller (Fig. 2.20). Hard metals have limited strength and low ductility, therefore the attainable casing pressure ratings are low. When the required pressure rating is beyond the limit of hard metal, the casing is constructed by containing a hard-metal liner within a carbon-steel casing. In hydrocarbon catalyst slurry service, similar construction is used to achieve high erosion resistance while maintaining the pressure containment integrity required for flammable services. INNER CASING MATERIALS Axially split single and multistage pumps of the arrangements shown in Figs 2.13 and 5.9, and doublecasing (barrel) pumps (Figs. 3.14 & 3.15) have an inner casing that serves to collect, diffuse, and guide the pumped liquid. Depending on the conditions of service, the inner casing can be a lesser material than the outer casing, the same material, or a higher material. Table 17.2 shows the common combinations of casing and inner casing materials. In corrosive hydrocarbon applications, there is also good experience with duplex, 316, and 317 inner casings in carbon-steel casings. IMPELLER MATERIALS The impeller of a centrifugal pump is a dynamic component, which in operation is subjected to 1. Stresses caused by centrifugal force 2. Bending stresses produced by pressure differentials and fluctuations within the waterways. 3. High liquid velocities 4. Possible cavitation. Drawing on the list of fundamental requirements given at the beginning of this chapter, the materials for impellers must be 378 Materials of Construction 1. 2. 3. 4. 5. Strong enough and stiff enough to withstand the stresses produced by rotation and pressure without fracture or excessive strain At least as corrosion resistant to the pumped liquid as the casing Significantly more resistant to cavitation erosion than the pump casing As resistant to abrasive erosion as the pump casing Possessed of a thermal expansion rate able to maintain the required fit with the shaft at the pumping temperature. Injected molded thermoplastic is used for the impellers of small, mass-produced single- and multistage pumps on water, circulator, and boiler feed service. Cast-iron impellers are used for hydrocarbon service up to peripheral speeds of 45 rn/sec (145 ft/sec) and temperatures of 230°C (450°F). For water service, cast iron is really suitable only for small pumps, up to about 170 m 3Jhr (750 gpm) (typically 4-in. discharge), because in larger pumps the localized cavitation that frequently occurs has enough energy to cause premature impeller erosion. The same risk does not exist in hydrocarbon services because the intensity of cavitation is much lower (see Chap. 19). Bronze is widely used for impellers wherever it is suitable because (1) it is easy to cast in complicated cored shapes, (2) it produces smooth as-cast surfaces, (3) it is easy to machine, (4) it does not rust, and (5) its resistance to cavitation erosion, depending on the alloy used, is 3 to 40 times higher than that of cast iron. Bronze impellers should not be used with cast-iron casings if the pumped liquid is a strong electrolyte, or if the pumped liquid is basic (pH above 7). The coefficient of thermal expansion of bronze is 1.4 times that of carbon steel, therefore the clearance between a bronze impeller and a steel shaft will increase as the pumping temperature increases. At the same time, the impeller hub will expand axially, thereby applying an axial load to whatever is retaining the impeller and producing a corresponding tensile load in the shaft. To avoid these difficulties, bronze is not normally used for pumping temperatures above 120°C (250°F). Most of the bronze alloys used (leaded gunmetal, tin bronze, phosphor bronze, and leaded bronze) have low tensile strength and stiffness, which limits the peripheral speed to which they can be used. The centrifugal stress developed in an impeller and the resulting stretch at the impeller hub can be significant at the higher peripheral speeds of high-head pumps. For example, a 305-mm (12-in.) bronze or iron impeller mounted on a 75-mm (3-in.) shaft and rotating at 3,600 rpm will have its bore stretch by approximately 0.028 mm (0.0011 in.). At a pumping temperature of 120°C (250°F), and assuming the shaft is steel, a bronze impeller will have its bore increased a further 0.036 mm (0.0014 in.), producing a total additional clearance of 0.064 mm (0.0025 in.) between the shaft and the impeller, which is excessive. To avoid the cumulative effect of excessive centrifugal and thermal expansion, the empirical limit on the peripheral speed of the common alloy bronze impellers handling hot liquids is approximately 59 rn/sec (160 ft/sec), or a head of 114 m (375 ft) per stage. Aluminum, aluminum manganese, and nickel aluminum bronzes have high tensile strength (approaching that of 13 chrome steel) and excellent corrosion resistance. Provided the foundry has the necessary expertise, their castability is as good as that of the lower-strength alloys. Aluminum bronzes are used for seawater, in conjunction with a casing of the same alloy, and for high-head services where the lower strength alloys will not withstand the centrifugal stress or the bending stress produced in the shrouds by pressure pulsations within the impeller passages. Steel impellers do not have the corrosion resistance of cast iron but do exhibit better resistance to cavitation erosion. They are used to a limited extent in noncorrosive hydrocarbon services. For small impellers, cast steel costs about the same as 13 chrome, therefore many manufacturers furnish only 13 chrome since it is a superior material. The chrome steel alloys used for impellers are 13 chrome (CA15) or 13 chrome 4 nickel (CA6NM), with the latter generally considered the better in terms of castability and weldability. In hydrocarbon Materials of Construction 379 services where H2S is present, CA6NM is modified to limit the carbon to 0.03 percent so the castings can be tempered to a hardness low enough to avoid stress-corrosion cracking. Chrome steel is necessary for high-purity boiler feed water, and is suitable for all boiler feed waters over a pH range of 4.S to 14.0. Both alloys have proven useful in pumping caustic liquors at temperatures up to 120°C (2S0°F). The nickel bearing alloy CA6NM has the better corrosion resistance, making it a suitable substitute for cast iron in applications where copper-bearing alloys are not acceptable and cast iron will be prone to premature cavitation erosion. Austenitic stainless steel, of which type 316 (CF8M) is the most common, is used for its corrosion and cavitation erosion resistance. These alloys are suitable for impellers that are mounted with a clearance fit on an austenitic stainless steel shaft, such as chemical and some water pumps. They are usually not suitable for impellers in high head multistage pumps at temperatures above 120°C (2S0°F), because differential expansion with the high strength shafting (see Structural requirements later in this chapter) will loosen the interference fit needed to maintain rotor balance. For applications where cavitation erosion cannot be overcome with system or pump design changes, there are now available proprietary austenitic stainless steels whose cavitation erosion resistance is 40 times that of cast iron. These are high manganese alloys, of high strength and toughness, that work harden at the surface in the presence of cavitation. They are available as welding consumables for repairs and castings for new impellers. Chemical pumps whose casings are fiber-reinforced polymer use impellers of the same material. To ensure the integrity of the impeller mounting on the shaft, a metal insert is frequently molded into the impeller, then machined to the required dimensions. The low strength and stiffness of fiber-reinforced polymer limits the head per stage to ISO m (SOO ft). By definition, higher alloy chemical pumps are handling liquids that are strong electrolytes, therefore the impeller, and all the other wetted parts for that matter, are of the same or a similar alloy. Duplex impellers are used in two circumstances: (1) when the pump's casing or inner casing is a duplex alloy or (2) when the pump's casing or inner casing is an austenitic alloy but the pump's temperature or rotative speed or both preclude the use of austenitic impellers due to high-differential thermal expansion or high strain. As already noted, under casings, duplex alloys cannot be used at temperatures above 260°C (SOO°F) because of the risk of embrittlement. Within its limits of temperature and strength, rubber offers outstanding resistance to erosion, therefore the impellers of rubber-lined slurry pumps are also rubber lined whenever the service conditions allow it. These impellers are fabricated by molding a thick rubber lining onto a ductile iron or carbon steel "skeleton." The threaded connection used to mount the impeller on the shaft is machined into the metal skeleton. Rubber lined impellers are limited to pumping temperatures of 6SoC (1S0°F) for natural rubber and lOsoC (22S0F) for synthetic rubbers, and heads per stage of 4S m (1S0 ft). For severe slurry applications (high concentration of solids, sharp or acicular fines, large solids), the hard-metal slurry pumps used have hard metal impellers, usually of Nihard®, sometimes of high-chrome iron when the liquid is corrosive. Hard-metal impellers are also used in rubber-lined slurry pumps when the required head is higher than can be produced with a rubber-lined impeller, or in applications where the combination of materials has demonstrated better erosion resistance than an all-rubber-lined pump. WEARING PARTS Usually a centrifugal pump's wearing parts are its impeller and casing wearing rings, any interstage bushings and sleeves, the balancing device (if used), the shaft sleeves, and the throat bushings. When mechanical seals are used, they also have wearing parts, which are specialized and dealt with in Chapter 380 Materials of Construction Table 17.4 Impeller and Wearing Ring Material Combinations Impeller/casing wearing ring material combination Steel/lron Bronze/bronzea 13 chrome/17 chromeb 316/Stellite on 316U Impeller material Iron L1 L1 L1 Bronze Steel 13 Chr 316 L1 L1 L1 • Generally different alloys to improve galling resistance. b Hardness difference at least 50 BHN unless softer ring 450 BHN or higher. Some manufacturers use different alloys of 13 chrome steel, for example, types 410 and 420, instead of 13 and 17 chrome. , One-surface is fusion hard coated for galling resistance. The alternative is to use increased running clearance. 9. Similarly, the impeller and casing of slurry pumps are wearing parts, and have already been discussed under casing and impeller materials. The purpose of wearing rings and important aspects of their mechanical design are covered in Chapter 4. Of particular note for the selection of materials is the very practical requirement of not putting brittle materials in tension because they are prone to fracture. The choice of materials for wearing rings is determined first by the impeller material, then by the need for the smallest running clearance consistent with good galling resistance. Table 17.4 summarizes the usual wearing ring material combinations and shows which impeller materials they are typically used with. Wearing ring materials always have corrosion resistance at least equal to that of the impeller. Table 17.4 does not extend to the higher alloys. These are almost exclusively used in chemical pumps, many of which have semiopen impellers and therefore do not have wearing rings. In those cases where pumps with closed impellers are used, both the wearing rings are the same material as the impeller, and usually the running clearances are increased to minimize the risk of galling. The practice for duplex impellers follows that for 316 stainless steel. The impeller wearing ring, if used, is duplex, and the casing ring is fusion hard coated duplex. Hard coating has already been mentioned in connection with improving the galling resistance of certain wearing ring material combinations. In this circumstance, only one of the surfaces needs to be hard coated to achieve the desired effect. Fusion hard coating with Stellite or similar materials is the most common method, and is entirely serviceable, provided the coating is applied to low-carbon alloys when high corrosion resistance is needed. In applications involving low concentrations of solids in the pumped liquid, it is often practical to hard coat both the rotating and stationary surfaces of the impeller's running clearances to reduce the wear rate. In these cases, it is preferable to hard coat the impeller hub, thereby avoiding the difficulty of having to safely mount and retain a hard coated impeller ring. The means of coating can be fusion, plasma transfer arc, or high-velocity oxy fuel spray. When spray coating is used it is important to use a high-density coating material (e.g., tungsten carbide) to help ensure a good bond to the substrate. Hard coating is not the only means of improving the abrasion resistance of pump wearing surfaces. Components of hardenable material can have their wearing surfaces fully hardened to a depth of some 0.5 mm (0.020 in.) by induction or laser hardening, thereby providing better wear resistance while retaining the general ductility needed for the component function. Alternatively, some materials can have their abrasion resistance increased by surface conversion, boron diffusion being the most common today (but not for austenitic or duplex materials, which are embrittled by this process), followed by ion implantation, then nitriding. The surface conversion processes in use today produce only a relatively Materials of Construction 381 thin hard region, ranging from 0.01 mm (0.0005 in.) for ion implantation through 0.25 mm (0.010 in.) for nitriding applied to a suitable alloy. Interstage sleeve and bushing materials follow the same practice as wearing rings. Balancing device components, the balancing drum or disk and the matching bushing or head in tandem impeller pumps, or the sleeves and bushings in opposed impeller pumps, are subject to a high pressure drop per unit length and therefore have materials chosen for good resistance to high velocity liquid erosion. At the same time, the running clearance needs to be kept small, so galling resistance is also important. For small, low-pressure multistage pumps, bronze, Ni-resist, or even iron components have proven serviceable. Pumps designed for higher pressures generally use 13 chrome versus 17 chrome components, with the appropriate hardness differences, as a minimum. In applications involving even quite low concentrations of solids, the rate of balancing device wear can be reduced by hard coating the drum, disk, or sleeves. Higher concentrations of abrasive solids require even more elaborate treatment, some designs having resorted to solid tungsten carbide components to achieve a tolerable service life. Corrosive services are usually accommodated by making both the components of the same alloy as the impellers, then hard coating the drum, disk, or sleeves for galling resistance. Shaft sleeves for pumps with packed box seals are bronze, 13 chrome, or hard-coated 316 stainless steel in order of ascending PV rating (pressure times velocity). The sleeves for mechanical seals are generally 316 stainless steel because it is suitable for most applications. In high-temperature service, however, differential thermal expansion is a concern, and the sleeve is the same material as the shaft. Shaft sleeves for pusher-type mechanical seals (see Chap. 9) are more durable (resistant to fretting erosion) if hard coated in the region under the dynamic gasket. Throat bushing materials generally follow those used for wearing rings. When a close clearance is needed to change the pressure at the seal, hard coating the sleeve under the bushing is desirable to enable a close clearance without raising the risk of galling in the clearance. An alternative approach is to use a floating carbon throat bushing. SHAFTS Unless a pump shaft is completely isolated from the pumped liquid, a rare and difficult achievement, corrosion resistance is the first consideration in selecting its material. This is so for two reasons. First, in general, the strength of typical shaft materials decreases with increasing corrosion resistance. Second, corrosion, even at low rates of penetration, has a significant effect on endurance strength, an important factor for a component subject to cyclic bending and torsional stress. Following corrosion resistance, the next consideration is strength, both impact for shock resistance and endurance to avoid failure by fatigue. The final consideration, of particular importance for multistage pumps, is dimensional stability, a property necessary to maintain shaft straightness. Low-carbon steel is suitable for the shaft in pumps handling a wide variety of liquids at low temperatures or in noncritical services (see Table 17.2). When these pumps have a packed box shaft seal, the shaft is usually fitted with shaft sleeves to avoid wear of the shaft. Alloy steels, typically AISI 4140 or 4340, are employed when a higher strength material is needed, or when the service warrants a higher design factor. High-speed boiler-feed pumps and pumps handling mildly corrosive water at ambient temperature or hydrocarbon at 246°C (475°F) and higher, have shafts of 13 percent chrome steel, AISI Type 410. This alloy is resistant to corrosion by high-velocity water, has strength close to that of the alloy steels, and has superior high-temperature strength and stiffness. Provided the material used has been adequately stress relieved, it has good dimensional stability. Type 316 stainless steel is widely used for shafts in chemical pumps. Its strength is similar to lowcarbon steel, and its dimensional stability is poor, two factors that usually preclude its use for larger 382 Materials of Construction pumps, where high strength is necessary, or for multistage pumps. Shafts of the higher austenitic alloys are used only when necessary for their superior corrosion resistance. Most the alloys have mechanical properties similar to type 316 stainless steel. Bronze pumps for seawater service use either bronze or Monel shafts depending on the pump's size and service. The preferred Monel alloy is KSOO, which has strength and stiffness close to that of 13 percent chrome steel. In medium-temperature, corrosive hydrocarbon service, duplex shafts are used with duplex impellers to avoid fit relaxation due to differential thermal expansion. Adequate stress relief is necessary to ensure dimensional stability of duplex shafts at elevated service temperatures. MATERIAL CLASSIFICATION The material classification of a centrifugal pump can be determined by the materials of its three principal components: casing (and inner casing where applicable), impeller, and shaft. This is not to say the materials of the running clearances are unimportant, but they tend to be determined by the impeller material and therefore do not have to be included in the classification. Table 17.2 shows a summary of the common material combinations for the three principal components. API-610 [3.1] includes a detailed tabulation of the material classes commonly used in the oil industry. PUMP FITTINGS During the history of pump development, the expression "pump fittings" has been used rather loosely to mean two entirely separate things. In the water and industrial markets, it refers to the general Table 17.5 Materials for Various Classes of Pump Fittings Standard Fitted All Iron Fitted All Bronze Fitted 109 6 6-A Cast iron Cast iron Bronze Bronze Bronze Bronze Cast iron or bronze Cast iron or bronze Steel Chrome steel or steel Bronze Bronze Bronze Bronze Bronze Bronze Bronze Bronze Bronze or Monel Bronze or Monel Shaft sleeve 14 Bronze Gland 17 Bronze Cast iron Cast iron Cast iron Steel Cast iron Cast iron Cast iron Cast iron Steel Chrome steel or steel Steel or chrome steel Cast iron Chemical; non-corrosive Salt water Part Casing Stuffing box cover Impeller Impeller ring Casing ring Stuffing box ring Diffuser Stage piece Shaft (with sleeve) Shaft (without sleeve) Typical service from Table 17.2 Ref No.' 11 2 8 7 27 5 Fresh water Bronze Bronze I Parts in this list and in Figs. 17.1 through 17.4 are numbered according to the Standards of the Hydraulic Institute [1.1]. This standard gives stationary parts odd numbers and rotating parts even numbers. The standard was first proposed to the Hydraulic Institute by Charles J. Tullo, Chief Engineer, Worthington Corporation. Materials of Construction Fig. 17.1 383 Section of a double-suction, single-stage pump with shaft sleeves. Numbers refer to parts listed in Table 17.5. construction features of the pump, for example, "ball-bearing-fitted pump," or to the combination of materials used in the pump, for example, "all-iron-fitted pump." In the fire protection market (as in the expression "underwriter fittings"), it may refer to various pieces of auxiliary equipment such as valves, gauges, or even tools. Table 17.5 shows the various component materials for the three commonly used "fitting" classifications, and includes a cross reference to the material classifications in Table 17.2. Figures 17.1 through 17.4 illustrate the materials used for particular parts in four different pump types. Beyond the three common pump "fitting" classes detailed in Table 17.4, there are two more worthy of mention. Acid-Resisting Pump An acid-resisting pump is one in which all the parts in direct contact with the pumped liquid are constructed of materials that offer the maximum resistance to its corrosive action. Typically such pumps were produced in silicon iron, a highly corrosion resistant but very brittle material, or acid-resisting bronze. Today, all 316 stainless steel or Alloy 20 construction would be more usual, the choice depending upon the acid and its concentration and temperature. Salt Water Pumps Centrifugal pumps handling salt water may be standard fitted (cast-iron casing with bronze fittings), all iron or all bronze, or with an iron casing and stainless steel fittings. Although thousands of standard 384 Materials of Construction Fig. 17.2 Section of a single-suction, single-stage pump without shaft sleeves. Numbers refer to parts listed in Table 17.5. Fig. 17.3 Section of a two-stage axially split pump. Numbers refer to parts listed in Table 17.5. Materials of Construction 385 Fig. 17.4 Section of an end-suction, single stage pump. Numbers refer to parts listed in Table 17.5. fitted pumps are used for this purpose, such construction is not suitable if the sea water is contaminated (for example, harbour water). Failures are usually caused by galvanic action between the bronze parts and the cast-iron casing, which results in either the loss of the casing or the bronze parts. Failure in the latter mode occurs if the casing wetted surface area is large enough to become an effective cathode once the cast-iron surface is graphitized (see corrosion in this chapter). An all-iron pump discourages galvanic corrosion, but it may occur nevertheless. A certain amount of iron dissolution may take place, leaving graphitized areas that act as cathodes to the uncorroded areas of cast iron. The resulting galvanic action is self-accelerating. To avoid the graphitization (and poor resistance to cavitation erosion) of cast iron, the impellers and other small pump parts may be made of stainless steel. The grade of stainless steel should be at least type 316 (CF8M), and that is suitable only for well-aerated liquid. If the pump is to stand filled with liquid for long periods, austenitic stainless steel containing at least 6 percent molybdenum or all-bronze construction is necessary. MATERIAL PROPERTIES A summary of the qualitative properties of typical pump materials is given in Table 17.1. Structural requirements, and to some degree corrosion and erosion resistance, are dealt with in the discussion of 386 Materials of Construction materials for the major components. The following text addresses corrosion and erosion resistance, thermal expansion, and thermal shock resistance in more detail, then aspects of structural requirements not dealt with in the discussion of components. Corrosion In centrifugal pumps, corrosion differs from general practice in two important respects. First, liquid velocities in pumps are inherently higher than in pipelines or vessels, so corrosion data based on lowvelocity tests may not be applicable to pump parts. Second, some pump parts (e.g., seals and shafts) cannot tolerate appreciable penetration or weight loss without failure, thus when corrosion determines the material selection these parts may have to be made of materials superior to those in the rest of the system. Corrosion can be broadly defined as the deterioration of materials by chemical or electrochemical action. For metals, whose electrons are free to move, the definition can be narrowed to the deterioration of solids by liquid electrolytes. Nonmetals generally do not have free electrons, therefore any deterioration is by chemical action alone. The corrosion of metals is fundamentally galvanic. From Fig. 17.5 the essential requirements are a potential difference between two sites immersed in an electrolyte and connected with an external electric circuit. The potential difference causes metal loss or oxidation at the anode (metal ions go into solution and electrons move into the external circuit) and metal deposition or reduction at the cathode (electrons from the external circuit reduce ions from solution). In pumps, the prevailing high velocities generally wash away metal deposited at the cathode. As in electroplating, the rate of anode consumption or corrosion depends on current density. Current density, in turn, depends on the potential difference and balanced oxidation-reduction reactions. These dependencies lead to means of limiting corrosion. First, the potential difference can be reduced. Second, the oxidation-reducation balance can be kept at a very low level. Two means are available to achieve the latter: cathode polarization, in which the reduction rate limits the balance, and passivation, in which initial oxidation of the anode renders it essentially inactive. A mechanical factor of great consequence to the oxidation-reduction balance is the relative size of anode and cathode; a relatively small anode is susceptible to rapid corrosion. In this connection, materials protected by passivation are vulnerable if the passive film is perforated, because the unprotected region becomes a small anode. Corrosion damage to metals is generally identified by 10 types. While in some cases the whole mechanism is not yet fully understood, these 10 types of corrosion are the products of three basic galvanic cells: unlike electrodes, which is self-explanatory; stress-induced potential differences; and concentration, potential differences created by variations in electrolyte concentration. A brief description of each type follows. For a detailed treatment of this complex subject, see the Corrosion Engineers Reference Book [17.1 J. ANODE (OXIDATION) CORRMO+SION_ M - ELECTROLYTE M+ M+ I __---'c=\=::... . _ +e~ e\ ELECTRICAL CONNECTION CATHODE (REDUCTION) PRODUCT OF CORROSION M++e--M )e- POTENTIAL DIFFERENCE Fig. 17.5 Fundamental corrosion mechanism. Materials of Construction 387 Influence of pH The pH value of a liquid is a quantitative representation of its relative acidity or alkalinity. The value is based on the concentration of H+ (positive hydrogen) ions as opposed to OH- (negative hydroxyl) ions in the solution. It is calculated as follows: 1 pH = log ==0----=---,--H+ concentration The lower the pH, the more acidic the solution. A solution with a pH value of 7.0 is neutral; values above 7.0 indicate alkalinity and values below 7.0, acidity. Because pH values are expressed logarithmically, changes in pH represent more than a direct linear change. For instance, a solution having a pH of 5.0 is 10 times more acidic than one with a pH of 6.0. The pH of a given solution varies somewhat with temperature changes, decreasing rather rapidly up to 150°C (300°F) and remaining fairly constant at higher temperatures. For instance, a solution with a pH of8.5 at21 °C (70°F) will have a pH of about 7.0 at 150°C (300°F) and 6.8 at 260°C (500°F) (Fig. 17.6). How pH affects metal corrosion depends on whether the metal oxide is stable in both acid and alkaline solutions (as it is for noble metals), soluble in acid solutions, or soluble in both acid and alkali solutions. 14 I I 13 12 II w z :::::i <l - ~ ...J <l \ 10 w :::J ...J <l > :I: Q. 9 8 7 \ -- .---, ~ I"" ..... '", ........ .... 1'- u 0 .... <l 4 'I'-... 3 o 50 -------:::-- ~ ....... ........ r-.., "- NEUTRAL ...... ... 6 5 70 DEG F - USUAL LABORATORY / TEMPERATURE r--........ "'u.._ 0 10 N t- ~ .............. r-- -.! I I I ............... - ~ : I I 100 150 200 250 350 350 400 450 500 PUMPING TEMPERATURE, DEG F Fig. 17.6 Effect of temperature on pH values. A laboratory test for low pH usually involves contact with atmosphere, and as a result, the value is about 0.5 high. 388 Materials of Construction Table 17.6 Galvanic Series of Metals Commonly Used in Centrifugal Pumps Corroded end (anodic) Zinc Iron, carbon steel Chrome nickel iron 13 chrome steel (active) 316 & 317 stainless steel (active) Aluminum bronze Brasses Bronzes 13 chrome steel (passive) Copper-nickel alloys 316 & 317 stainless steel (passive) Chrome-nickel alloy 20 Graphite Protected end (cathodic) Metal Corrosion Mechanisms Galvanic: One metal in a multimetal system is preferentially corroded. Corrosion is produced by a classic galvanic cell; a combination of metals far apart in a galvanic series in the presence of a strong electrolyte. The series in Table 17.6 gives an approximate idea, based on the corrosion potentials in seawater, of the interrelation of the metals most commonly used in centrifugal pumps. The active states of 13 chrome steel and types 316 and 317 stainless steel occur in poorly aerated liquids or in oxygen deficient regions. Graphite's nobility is of consequence to cast iron pumps handling seawater or brackish water; once the casing is graphitized, the previously cathodic bronze impeller will be anodic to the casing, thus subject to corrosion. General: Corrosion of all surfaces, with greatest metal loss in regions of high velocity. Occurs when the electrochemical potential of the pumped liquid is sufficient to remove the protective passive film, and is accelerated where high velocity liquid quickly removes the products of corrosion. Selective leaching: Only part of the material is corroded. Prevalent in metals whose structure is a matrix of dissimilar materials (e.g., iron and graphite in cast iron), which in seawater will suffer selective leaching of the iron until the exposed surface is graphite, a process known as graphitization. Materials of Construction 389 Fig. 17.7 Corrosion-erosion damage to an impeller. Corrosion-erosion: Rapid metal loss with the fluted appearance of fine erosion. Process whereby mild general corrosion is accelerated by particles in the pumped liquid or the high liquid velocities inherent in high head per stage designs. Figure 17.7 shows corrosion-erosion damage to an impeller. Crevice: Metal is lost from the surfaces forming the crevice. Caused by a concentration cell in which the liquid in the crevice has a different concentration than the bulk liquid; usually a lower oxygen content leading to reduced passivation. Pitting: Pinpoint penetration of the material, at an accelerated rate within the pits. Initiated at local variations in the metal; accelerated as the pitting becomes deep enough to form concentration cells. Stress corrosion cracking: Parts develop cracks at low nominal levels of tensile stress. The stress may be residual or applied or a combination of both. By a mechanism not yet fully understood, a low concentration of a corrosive element or compound (e.g., chlorine or hydrogen sulphide), in the presence of water, promotes cracking at low tensile stress levels. The cracking is typically transgranular (Fig. 17.8). 390 Materials of Construction Fig. 17.8 Photomicrograph of stress erosion cracking. Corrosion fatigue: Parts subject to cyclic stress quickly fail catastrophically at stress levels below the nonnal endurance limit of the material, a consequence of active corrosion reducing the material's endurance limit. Intergranular: Corrosion at the grain boundaries of austenitic materials. A direct result of the material being "sensitized" by slow cooling from above the austenitizing temperature, with resultant chrome depletion at the grain boundaries (fonnation of chrome carbide; Fig. 17.9). Microbiological: Localized corrosion under microbiological deposits. A fonn of concentration cell in which bacteria, either aerobic or anaerobic, alter the bulk environment within the colony. Beyond the 10 metal corrosion mechanisms just cited above, there is one identified as "corrosion" that appears not to be the result of electrochemical action. Fretting corrosion: results from loss of metal from one or both of a pair of contacting surfaces. Caused by minute, high-frequency movement between the surfaces, it occurs in both wet and dry environments, and in inert gases, which suggests it is not dependent on electrochemical action. Materials of Construction 391 • Fig. 17.9 Photomicrograph of intergranular carbide precipitation. Nonmetallic Corrosion Mechanisms Chemical attack: Softening or swelling of hydrocarbon polymers, caused by the action of the pumped liquid on the polymer's inter and intramolecular bonds. Stress cracking: Cracking caused by the combined effects of tensile stress, either residual or imposed, and a "stress cracking agent," a liquid not normally corrosive to the polymer. As is the case with metals, even quite low concentrations of the stress-cracking agents will promote failure. EROSION Pump components can be eroded by either the action of solids in the liquid, a process termed abrasion, or the action of collapsing vapor bubbles, a process known as cavitation erosion. Abrasion Three mechanisms of abrasion are generally recognized, with each having a distinct effect on the material choice. 1. Cutting or gouging: The solids contact the pump component surfaces at a relatively low angle (Fig. 17.10) and thereby remove material by gouging or cutting the surface. The rate of material loss is related to the 392 Materials of Construction Fig. 17.10 2. 3. Abrasion-cutting or gouging. relative velocity between the particles and the surface, and the size and shape of the particles. Cutting or gouging erosion is the usual mechanism in pumps handling nonsettling slurries. Rubber-lined or hard-metal components are used to achieve the best resistance to cutting or gouging erosion. Hard metal is required for high-concentration slurries or slurries of sharp solids. Impact: Large, high-mass solids impinging on the component surfaces at high angles produce fatigue failure and spalling of the surface. Dredge pumps and pumps handling settling slurries typically suffer impact erosion. To absorb the energy without spalling, their components are made from strong, ductile metals such as high-manganese steel. Grinding: Irregularly shaped particles get between the surfaces of the close running clearances and in the process of passing through remove material by grinding. All pumps handling solids laden liquids are subject to grinding erosion. Cavitation The cause of cavitation and its effect on pump performance are discussed in Chapter 19. Cavitation itself, the formation of vapor bubbles, does not damage pump components. What can cause damage (Fig. 17.11) is the subsequent collapse of the vapor bubbles (but not the noncondensible gases) as they pass into regions of higher pressure. The mechanism is thought to be basically fatigue in nature, a consequence of high pressures and temperatures associated with bubble collapse. Corrosion has been suggested as a contributing factor, but data are lacking. In a pump handling corrosive liquids, however, it is quite conceivable that the erosive action of bubble collapse could aid corrosion, as in corrosion-erosion, and there could be sufficient temperature rise in the region to accelerate the corrosion rate. THERMAL EXPANSION AND SHOCK RESISTANCE Thermal expansion has two consequences on pump components. First, at elevated temperatures, the increase in the component's size can be sufficient to require special provisions to compensate for the Materials of Construction Fig. 17.11 393 Cavitation erosion in the fillet between the hub and vane underside at the suction side of an impeller. expansion, or the component can be distorted, overstressed, or cause damage to a connected component. Provision for up to 13 mm (0.5 in.) of movement in the casings of barrel pumps in hydrocarbon charge service at temperatures of 400 to 425°C (750 to 800 0 P) is a good example. Second, at even quite low temperatures, a large difference in the thermal expansion rate of materials used in an assembly can cause what is termed "differential thermal expansion" to render the assembly unserviceable due to either loosening or tightening of fits. Bronze impellers on a steel shaft is a good example (see impeller materials). Thermal shock resistance is a function of a material's thermal conductivity, thermal expansion, and ductility. Materials of low thermal conductivity and low ductility, ceramics, for example, develop a significant stress gradient when heated rapidly and are therefore prone to fracture. Several of the chrome steel alloys in the fully hardened state have a similar characteristic. Ductile materials will not fracture immediately when subjected to thermal shock, but will suffer low cycle thermal fatigue if the rate of heating is high enough to produce local stresses beyond the material's endurance limit. STRUCTURAL REQUIREMENTS Although the first pass at material selection is almost always based on corrosion and erosion resistance, the structural features of a pump or the manufacture of the part or both may dictate either a compromise in the material selection or a change in the pump configuration or its manufacture. Starting with examples of compromises in material selection, the more usual are 1. Multistage pump shafts: made from one of the duplex alloys or other high strength grades instead of type 316 stainless steel to overcome the low strength and difficulty maintaining straightness inherent in type 316. 2 Impellers: steel, chrome steel, or stainless steel is used instead of iron or bronze because the peripheral speed is too high for both, the pumping temperature is too high for bronze, or the impellers must be mounted with a shrink fit (see impeller materials). 394 Materials of Construction (b) -T (8) T ~ '-O.3T Fig. 17.12 (a) Transition in casting section. (b) Coring of a double-suction impeller hub. 3. Interference fit impeller wearing rings: steel or chrome steel is used instead of iron or similar materials to avoid putting a brittle material in tension with the attendant risk of fracture. 4. Shrink-fit-mounted single suction unbalanced impellers: plain back hubs are used regardless of what has been done to the front hubs, to avoid putting a brittle material in tension and thereby the risk of it spalling. Adequate galling resistance of the back hub running clearance is provided by increasing the clearance. When resistance to abrasive wear is necessary, one of the surface conversion processes is used (see wearing parts). The strength and pressure tightness of metal castings depends a great deal on the relative uniformity of their cross sections, a fact that is at the heart of many discussions between pump designers and foundrymen. The more uniform the cross sections, the stronger the casting, and the lower the risk of internal shrinkage or tearing. Achieving this generally requires a compromise in the form of extra work in the manufacture of the casting. The shape of many of the components of centrifugal pumps is determined first by the hydraulic design and then by the mechanical requirements, and generally the cross sections are not uniform. To avoid· the ill effects of this, the designer resorts to gradual changes in section by either adding material (Fig. 17.12[a]) or removing it by coring (Fig. 17. 12[bD. The double-suction impeller (Fig. 17.12[bD is an interesting case, because for hydrocarbon service the hub must be either cast solid or filled with a bighmelting-point solid. The reason is that during operation, hydrocarbon will accumulate in the cored space, and if the impeller is heated for removal (a practice frequently necessary) there is a risk the hydrocarbon will bum or explode with consequent personnel injury. Finally, examples of changes in pump configuration or manufacturing method, include the following: 1. Pumps with lined casings often have the liner constrained within a radially split casing (Fig. 17.13), which provides the structural strength the liner lacks. Materials of Construction Fig. 17.13 2. 3. 395 Hard metal slurry pump with "solid" casing liner. (Courtesy of Lawrence Pumps, Inc.) The impellers and casings of small, mass-produced pumps for water and industrial service are made by spot welding together stainless steel pressings. This technique is employed because the necessary metal thickness of the components is lower than can be produced by the economical casting techniques. Critical-service single-stage pumps, such as nuclear reactor primary coolant circulating pumps, have casings that are symmetrical and made of wrought material to achieve the highest possible mechanical integrity. A diffuser within the casing achieves the hydraulic function normally carried out by the casing in singlestage pumps. LOAD FACTOR AND SERVICE LIFE It is obvious that a selection of materials to provide the longest possible service life for a temporary installation would be very uneconomical. Thus, standard fitted pumps are frequently used for services in which corrosion or erosion will wear a pump out in a relatively short time, if this pump will no longer be used after the service is performed. The same reasoning applies to installations in which pumps operate an extremely small percentage of the time, providing that contact with the pumped liquid during idle periods does not continue the disintegration process, or else that the pump can be drained and flushed out. Plain common sense dictates that materials be chosen on the basis of optimum economic life, that is, for an initial cost and a cost of part replacement (including the necessary labor) that will yield the lowest overall total investment during the expected life of the equipment. The materials chosen, therefore, may often be neither the cheapest nor the most expensive available. If outstanding reliability is desired, on the other hand, the best materials are none too good, even if a pump is to operate once every 10 years. Although operation ofthe centrifugal pumps on board ships of the U.S. Navy is relatively infrequent 396 Materials of Construction in peacetime, for example, and not constant even in war, the most rigid material specifications are enforced because failure of any part of the equipment may prove fatal. MATERIAL CHOICE AND MATERIALS ENGINEERING PROGRESS Advances in materials engineering of both metals and nonmetals have had a marked effect on the design of centrifugal pumps for pumping chemicals, hydrocarbons, corrosive waters (including boiler-feed water), and slurries. Looking at chemical services first, there has been a gradual evolution of the stainless steels and the so-called "high alloys" to achieve better performance. The range of available metals has been extended to include titanium and zirconium. At the same time, progress has been made with reinforced polymers such that pumps of high corrosion resistance and adequate pressure containment capability are now made of polymer alone. As the quality of crude oil reserves has deteriorated over the past 20 or so years, refiners have been faced with hydrogen sulphide stress corrosion cracking (of parts in tension), and general corrosion caused by naphthenic acid. In 1975 NACE [17.2], published guidelines recommending various limits to the hardness and strength of the commonly used materials to avoid hydrogen stress corrosion cracking. API610 has distilled those recommendations into requirements for refinery pump construction. Resistance to naphthenic acid corrosion is achieved with either one of the duplex alloys, CD4MCu with nitrogen added being typical, or C08M, the cast version of type 317 stainless steel. Duplex alloys are preferred wherever possible because their coefficient of thermal expansion is close to that of steel. When CO 8M is necessary, usually at high temperatures, care is needed in the pump's detail design to compensate for differential thermal expansion where it occurs. The term "corrosive waters" covers boiler feed through seawater and brackish water, the last two being pumped by the oil industry for water injection, a process used in tertiary oil recovery. Boiler-feed water is discussed first. Most of the knowledge on boiler-feed pump materials was developed 50 years ago, and is largely still valid today. The principal development was made in 1944 based on the findings of an investigation conducted by the Boiler Auxiliary Subcommittee of the Prime Movers Committee of the Edison Electric Institute. This investigation was initiated to determine the cause of the rapid pump deterioration being experienced in many high-pressure power plants, a condition that had reached alarming proportions in the early 1940s. Among the findings made by this subcommittee was the fact that steels containing 5 percent chromium or more (today known as chrome steels) were immune to corrosion by any boilerfeed water then known. Table 17.7 is a current general guide to the selection of boiler-feed pump materials. It is more complicated than earlier guides in that it requires careful attention to feed-water condition. Note that 13 percent chrome steel is recommended, with CA-6NM (the 13 chrome, 4 nickel alloy) being the most widely used today. Although 5 percent chrome is sufficient to provide immunity to corrosion-erosion by boiler-feed water, the usual alloy, designated C-5, has poor castability and is difficult to weld. Note, too, that when austenitic stainless steel is recommended, the whole pump is to be of that material to avoid difficulties with differential thermal expansion. Pumping seawater and brackish water at high heads per stage in water-injection service precipitated the development of several duplex (austenitic ferritic) alloys to overcome the problems of corrosion and low strength inherent in the austenitic stainless steels used originally, particularly when subjected to high liquid velocities and the stresses associated with high rotative speeds. The more notable are Ferralium™ 255 (UNS-S32550) and Zeron™ 100 (UNS-J93380). Ferralium 255 castings are not covered by an ASTM specification, but are produced by various foundries in the United States and Europe. Zeron Materials of Construction Table 17.7 Temperature °C (OF) :595 (200) >95 (200) >95 (200) >95 (200) 397 Boiler Feed Pump Materials Conductivity (micromohs/cm) O2 pH (ppm) Materials' ------~ I-I 0-14 4.5-14 6-9 6-14 9-14 1-2 S-1 S-6 C-6 A-8 ~ ~b ~b 0-14 4.5-14 >0.04 0-14 4.5-14 :50.04 0-14 4.5-14 6-9 6-14 9-14 :50.04 ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ :520 ~ ~ ~ ~ ~ :520 ~ >20 ~ ~b ~b ~ ~ ~ ~ ~ ~ ~ ~ ~b , Many chemistries are marginal; avoid selecting less expensive materials when C-6 is indicated. The code for these materials is Code (API-610) 1-1 1-2 S-1 S-6 C-6 A-8 b Casing, impeller All cast iron Cast iron, bronze Cast steel, cast iron Cast steel, 13 chrome All 13 chrome All CF-3M Head less than 120 m (400 ft) per stage. 100 castings are available as ASTM A890 Grade 6A. Manufacturing methods also took an interesting tum in some cases, one instance being impellers produced by electrodischarge machining (EDM) from Ferralium 255 forgings. Process designers have presented slurry pump manufacturers with slurries of a corrosive carrier liquid or at temperatures above the operating limit of rubber or both. The result has been a series of highchrome hard irons, up to 35 percent chrome, with better corrosion resistance than the lower chrome alloys. For those applications where hard metal did not have sufficient corrosion resistance, and the temperature exceeded the limit of rubber, pumps with a ceramic impeller and ceramic-lined casing have been produced. Silicon nitride bonded silicon carbide is one such material that has been used. Materials engineering has made substantial progress over the past 20 years, much of it a direct result of improving the performance of gas turbines. Applicable segments of this work are now gradually being adopted by the pump industry. One worthy example is the use of hard coatings and surface-hardening techniques to increase the wear resistance of running clearance surfaces while retaining the necessary bulk structural properties of the part. This can also lead to simpler pumps. Impellers with hard-coated hubs, as an example, do not require the added complexity of wearing rings. Ceramic antifriction bearings running in the pumped liquid have been used for some time in pumps for cryogenic services such as liquefied natural gas. Similarly, progress is being made in the development 398 Materials of Construction of high-chrome corrosion-resistant antifriction bearings, raising the possibility of one day being able to run such bearings in water and similar liquids. Product-lubricated hydrodynamic bearings, typically of silicon carbide, are now in the proving phase. Much of the current materials engineering effort is being devoted to ceramics. A new generation of these materials based on zirconium holds the promise of ceramics with high strength and toughness, characteristics that will allow their extensive use in tomorrow's centrifugal pumps. BIBLIOGRAPHY [17.1] Corrosion Engineers Reference Book, [2nd Edition, 1980] National Association of Chemical Engineers, Houston, Texas. [17.2] NACE MR-01-75, Sulfide Stress Corrosion Resistant Metallic Material for Oil Field Equipment, 1975, National Association of Chemical Engineers, Houston, Texas. II PUMP PERFORMANCE 18 Heads, Conditions of Service Performance Characteristics, and Specific Speed In selecting the most suitable centrifugal pump for a given application, the most important information to be given the manufacturer is the desired capacity and the head against which the pump will be required to operate while delivering the specified rate of flow. UNITS OF CAPACITY The standard unit of capacity for centrifugal pumps varies with the application of the pump as well as the design standards of the country where the pump is used-gallons per minute in the United States, occasionally imperial gallons per minute in countries of the former British Commonwealth, and cubic meters per hour in countries using the metric system. In the United States, units vary with the pump application as follows: million gallons per day, cubic feet per second, gallons per hour, barrels per day, barrels per hour, pounds per hour, and acre feet per day. Common equivalent variations in the metric system are: liters per second, cubic meters per second, and metric tons (tonnes) per hour. It is a simple matter to convert the various units into gallons per minute (gpm). The equivalents for most units are incorporated in Table 18.1. For a direct conversion chart, see Fig. 18.1. The pump capacity required by an installation should be stated in cubic meters per hour (gallons per minute) at the pumping temperature; any desired or imposed variation in the range of capacities should also be clearly stated. The proper method of specifying required capacity in preparing an inquiry for centrifugal pumps is discussed in some detail in Chapter 27. HEADS Pumping is the addition of kinetic and potential energy to a liquid for the purpose of moving it from one point to another. This energy will cause the liquid to do work, such as flow through a pipe or rise to a higher level. A centrifugal pump transforms mechanical energy from a rotating impeller into the kinetic and potential energy required. Although the centrifugal force developed depends on both the 401 I. J. Karassik et al., Centrifugal Pumps © Chapman & Hall 1998 402 Heads, Conditions of Service Performance Characteristics, and Specific Speed Table IS.1 Capacity Equivalents For conversion chart, see Fig. 18.1 Various units gpm 1 second-foot or cubic foot per second (cfs) 1,000,000 gallons per day (mgd) 1 imperial gallon per minute 1,000,000 imperial gallons per day 1 barrel (42 gal) per day (bbVday) 1 barrel per hour (bbl/hr) 1 acre-foot per day 1,000 pounds per hour (lb/hr) 1 cubic meter per hour (m3/hr) 1 liter per second (lIs) 1 metric ton per hour 1,000,000 liters per day = 1,000 cubic meters per day 448.8 694.4 1.201 834.0 0.0292 0.700 226.3 2.00' 4.403 15.851 4.403' 183.5 IThese equivalents are based on a specific gravity of I for water at 62°F for English units and a specific gravity of I for water at 15°C for metric units. They can be used with little error for cold water of any temperature between 32°F and 80°F. For specific gravity of water at various temperatures, see Fig. 18.6. peripheral speed of the impeller and the density of the fluid, the amount of energy imparted per pound of fluid is independent of the fluid itself. Therefore, for a given machine operating at a certain speed and handling a definite volume, the mechanical energy applied and transferred to the fluid-joules per kilogram of fluid or foot-pounds per pound of fluid-is the same for any fluid, regardless of density. The pump head, or energy in joules per kilogram (foot-pounds per pound), will therefore be expressed in meters (feet). Barring viscosity effects, the head generated by a given pump at a certain speed and capacity will remain constant for all fluids. Thus, it is natural to speak. of heads in centrifugal pumps in terms of meters (feet) of liquid. Before discussing the various head terms involved in pumping systems it should be mentioned that (1) heads can be measured in various units, such as feet of liquid, pounds per square inch of pressure, inches of mercury, and others depending upon the application and the units of measurement of the country; (2) pressures and head readings can be in gage or absolute units; (3) the difference between gage and absolute units is affected by the existing atmospheric pressure and thus by the altitude; and (4) the pressure at any point in a system handling liquids must never be reduced below the vapor pressure of the liquid. Conversion of Pressure to Static Head A column of cold water approximately 10.2 m high will produce a pressure of 1 bar at its base (as will 2.31 ft produce 1 psi). Thus for water at ordinary temperatures, any pressure can be converted to an equivalent head by multiplying by 10.2 for bars to meters or 2.31 for psi to feet. For liquids other than water, the column of liquid equivalent to the basic unit of pressure (1 bar or 1 psi) can be calculated by dividing the constant (l0.2 or 2.31) by the specific gravity of the liquid. Figure 18.2 illustrates the effect that specific gravity has on the height of a column of various liquids for equal pressures. Thus a pump that must handle 1.2 specific gravity brine against 6.90 bar (lOO-psi) net pressure would be designed for a head of 58.8 m (193 ft). If the pump had to handle cold water against the same net pressure, the head would have to be 70.4 m (231 ft), whereas a pump handling Heads. Conditions of Service Performance Characteristics. and Specific Speed CAPACITY ,101 GAllONS (Y S) Pel MlNYTE I!! :> Z 2._ ~ :> Z .. i i ~ 1,_ g '"Z 2 . ~ ~ CJ " :> :> Z z « r!I .. 0 0 « ~ ~ ~ ~ '"z ~ J; J; ~ :> t t "« 3 ~ 3 CAPACITY 'N GAllONS IU S) 'U ..'Nun; Fig. 18.1 Capacity conversions. For more accurate values, calculate from the equivalents shown in Table lS.l. 403 404 Heads. Conditions of Service Performance Characteristics. and Specific Speed GASOLINE (SPECIFIC GRAVITY 0.75) WATER (SPECIFIC GRAVITY 1,0) ---1 BRINE (SPECIFIC GRAVITY 1.2) ---l - - Fig. 18.2 Effect of fluid density on static head. Comparison of the heights of a column of water. brine. and gasoline needed to produce 6.9 bar (100 psig) pressure at datum level. 0.75 specific gravity liquid against the same net 6.90 bar (1oo-psi) pressure would require a head of 96.0 m (308 ft). It is obvious that a pump designed to handle water but applied on brine service would develop a 70.4 m (231-ft) head of brine or 8.28 bar (120-psi) pressure while if it was applied to pump 0.75 specific gravity gasoline it would develop a 70.4 m (231-ft) head of gasoline or only 5.17 bar (75-psi) pressure. The equivalents for the conversion of various pressure and head units other than feet into feet of liquid are indicated in Table 18.2. For quick conversion of pressures and heads into feet of liquid, see Fig. 18.3. Gage and Absolute Units Pressures and their corresponding heads can be expressed either in absolute units or gage units. In the metric system, pressures are gage unless noted, for instance, 6.90 bar is gage pressure, or 11.0 bar (abs) is absolute. The same pressures are expressed as 100 psig or 160 psia, respectively. In gage readings the pressure is given merely in relation to the atmospheric pressure, whereas absolute pressures are gage readings plus the existing atmospheric pressure. In other words, the pressure is referred to an absolute vacuum (Fig. 18.4). To illustrate, assume a person standing part way up a hill, 7.60 m (25 ft) from the bottom. The elevation or level at which he is standing would be his gage basis of measurement. Points below him would be negative (-) gage elevations, and points above him would be positive (+) gage elevations. Thus he would speak of a point 30.5 m (100 ft) up as 30.5 m (100 ft) gage elevation or of one 3.05 m (10 ft) down as 3.05 m (10 ft) below gage level, corresponding to a vacuum in our problem. If he desired Heads, Conditions of Service Performance Characteristics, and Specific Speed 405 Table 18.2 Pressure and Head Equivalents For conversion chart, see Fig. 18.3 2.310 Ib/sq in. 1 in. mercury (32°F) atmosphere2 kilogram/sq cm specific gravity' = = 1.134 ft of 62°F water 1.134 ft of liquid 33.95 ft of liquid = 33.95 ft of 62°F water specific gravity' specific gravity' = 1 metric atmosphere 32.85 specific gravity' 10.01 specific gravity' 1 bar ft of liquid = 2.310 ft of 62°F water 33.51 specific gravity' 10.21 specific gravity' 1 meter ft of liquid = 32.85 ft of 62°F water m of liquid = 10.01 m of 15°C water ft of liquid = 33.51 ft of 62°F water m of liquid = 10.21 m of 15°C water = 3.281 ft 'These equivalents are based on a specific gravity of I for water at 62°F for English units and a specific gravity of I for water at 15°C for metric units. They can be used, with little error, for cold water of any temperature between 32°F and 80°F. For the actual specific gravity of water for temperatures to 220°F, see Fig. 18.6. 2Not used in conjunction with pumps. to express an elevation measured from the bottom of the hill (absolute datum level, corresponding to zero absolute pressure or a perfect vacuum), he would add 7.6 m (25 ft) to his gage reading so that the point 30.5 m (100 ft) above him would be 30.5 + 7.6, or 38.1 m (100 + 25, or 125 ft) above the bottom of the hill (38.1 m or 125 ft absolute elevation), whereas the point 3.05 m (10 ft) below him would be -3.05 + 7.60, or 4.55 m (-10 + 25, or 15 ft) above the bottom of the hill (4.55 mor 15 ft absolute elevation). It is usually feasible to work in terms of gage pressure, but a complicated problem can occasionally be clarified by working entirely in terms of absolute pressure. Effect of Altitude on Atmospheric Pressure For pumps installed at elevations above sea level, it must be remembered that there is a decrease in atmospheric pressure of about 83 mm of mercury per 1,000 m (1 in per 1,000 ft) of elevation. At an elevation of 1,220 m (4,000 ft) therefore, the atmospheric pressure is 101 mm of mercury or about 1.4 m of water (4 in of mercury or about 4.5 ft of water) less than that at sea level, with the result that a centrifugal pump will operate satisfactorily for the same maximum capacities only if the suction lift is 1.4 m (4.5 ft) less than that at sea level. This effect should not, however, lead to the confused notion that the net positive suction head required for a pump changes with elevation above sea level. It does not, but the available atmospheric pressure is reduced. For barometric pressures at various altitudes, see Fig. 18.5. 406 Heads, Conditions of Service Performance Characteristics, and Specific Speed HEAD IN FEET OF COLD WATER 2 3 4 5 6 8 10 20 30 .a 60 80100 200 300 100 100 80 80 60 III ~ SO SO .a 40 30 30 « 20 ~ ~ ~ 0 0 0v", 0V IX ... W 0:" 10 IX __ "'! ~z ......... ~v -~ :1:« ~~ 8 6 5 6 5 4 '" ~. :::>~ 3 :~ Got:) 10 8 v:::> :I~ IX 2 2 % ~ --wZ ... ~v w ~'" "'~ '" IX Got:) :.:0 IX~ :::>:w: 1.0 ~'" ... 0 0.8 :e 1.0 :0 0.8 :IE ...0 '"... "'! IX-- -'" :1:« 4 ~~ w IX 3 IX «w :::>Go :.:0 "'= ot v:::> "'IX v III w ... 0.6 0.5 0.6 0 0.5 ~ 0.4 0.4 ~ 0.3 0.3 0.2 0.2 :I: 0.1 0.1 2 3 4 5 300 HEAD IN FEET OF COlD WATER Fig. 18.3 Pressure and head conversion chart. Values are plotted for 18.7°C (62°F) water but can be used for water between DoC (32°F) and 26.7°C (80°F). For liquids other than cold water, divide the head by the specific gravity (I8.7°C (62°F] water = 1.0) of the liquid at the pumping temperature to get the head in meters (feet). For more accurate values, calculate heads from the head equivalents in Table 18.2 . ANY PRESSURE ABOVE ATMOSPHERIC 1 GAGE PRESSURE ABSOLUTE PRESSUREGAGE PRESSURE + BAROMETRIC PRESSURE VACUUM (A NEGATIVE GAGE PRESSURE) ANY PRESSURE BELOW ATMOSPHERIC BAROMETRIC PRESSllRE ABSOLUTE PRESSURE Fig. 18.4 Graphical illustration of atmospheric, gage, and absolute pressures. 215 .......... so 29 '\. 21 co :> u co ...'"0:I '"'"r u ~ r-.... -<:: 2S '\. 25 .......... ......... ......... ~ 200 - """""= ....... i' 20 "" 2:5 '"'" '" "'"0 co 190 ~ ...... 4 5 • T ...«:> II< '":I ...'" ~ 19 o II< it Q. 21 II 115 ......... .... ; ""- ATMOSPHERIC PRESSURE 22 205 co 24 23 210 ...... TEMPERATURE OF BOILING WATER \.. -~ 27 >- ....... t: '"zr '"r • • 10 ~ 1/ 12 ELEVATION ABOVE SEA LEVEL,IN \p00 FEET Fig. 18.5 Atmospheric pressures for altitudes up to 3,660 m (12,000 ft). 407 408 Heads. Conditions of Service Peiformance Characteristics. and Specific Speed g S IS" 100 20 1099 18 lII. ~ 0.98 16 >= 0.91 14 ~ 0.96 12 I- ~ 095 Cl - ...... ~ .!PfClf'O;C I -i"'::~ry j"ooo. 10 ~ 8 -~ ~ 6 ::l ~ 4 LLJ f ~ ~ POR PRESSURE, 2 I J ...... ~ / 7~/ J l/ ~~V ~,;' ~?o~'~~~ ~ -r"1 I " Of ~~ I'1APORP~ 1 IRES~URE'~ "A 40 60 80 100 120 140 160 TEMPERATURE, DEGREES FAHRFNHEIT 180 200 Fig. 18.6 Specific gravity, temperature. and vapor pressure relations for water. Vapor Pressure The vapor pressure of a liquid at a given temperature is that pressure at which it will flash into vapor if heat is added to the liquid or, conversely, that pressure at which vapor at the given temperature will condense into liquid if heat is subtracted. For homogeneous or single-component liquids, such as water, the vapor pressure has a very definite value at any given temperature, and tables (such as steam tables) are available that give the vapor pressure of such liquids over a wide range of temperatures (see Table 26.1). Certain mixed liquids, however, such as gasoline, are made up of several components, each having its own vapor pressure, and partial vaporization may take place at various pressures and temperatures. In figuring heads for pumps, it is important that pressures expressed in bar (pounds per square inch) or other pressure units be converted into meters (feet) of liquid at the pumping temperature. Care must be taken not to use conversion factors applying to other temperatures for such conversions. For example, the vapor pressure of 100°C (212°F) water is 1.01 bar (abs) or 14.7 psia (standard barometric pressure at sea level). The equivalent head in meters (feet) of water is 10.34 m (33.9 ft) of 15°C (62°F) water. As 100°C (212°F) water has a specific gravity of 0.959 compared to a gravity of 1.0 for 15°C (62°F) water, its equivalent head would be 10.34/0.959, or 10.78 m (33.9/0.959, or 35.1 ft) (Fig. 18.6). Head Terms In its elementary form, "head" denotes the distance at which the free surface of a body of water lies above some datum line; as such, it represents an energy or ability to do work. Energy can also exist as a pressure. Some consider that static head is the sum of the pressure head and the static head of elevation; Heads, Conditions of Service Performance Characteristics, and Specific Speed 409 however, these two factors are generally considered separately. In any pumping system, the liquid must be moved through pipes or conduits that offer certain resistances or, in other words, cause certain frictional losses. This energy dissipation, or head loss, is called a frictional head whereas the energy that has been converted into velocity energy is called velocity head. Thus, static heads, pressure heads, friction heads, and velocity heads may all be encountered in any system. When considering a pump by itself, "head" is a measure of the total energy imparted to the liquid at a certain operating speed and capacity. SYSTEM HEAD The total head of a system against which a pump must operate is made up of the following components: 1. 2. 3. 4. 5. Static head Difference in pressures existing on the liquid Friction head Entrance and exit losses Velocity head. Static Head Static head refers to a difference in elevation. Thus the "total static head" of a system is the difference in elevation between the discharge liquid level and the suction liquid level (Figs. 18.7 to 18.9). The "static discharge head" is the difference in elevation between the discharge liquid level and the centerline of the pump. The "static suction head" is the difference in elevation between the suction liquid level and the centerline of the pump. If the static suction head is a negative value because the suction liquid level is below the pump centerline, it is usually spoken of as a "static suction lift." If either the suction or discharge liquid level is under a pressure other than atmospheric, this pressure is sometimes considered as part of the static head, but it is often considered separately. The latter practice usually permits a clearer picture of the system. If the suction supply is taken from a closed vessel and the liquid level lies above the pump centerline, the difference in elevation of the suction liquid level and the pump centerline is commonly spoken of as "submergence" instead of "static suction head." Friction Head Friction head is the equivalent head, expressed in meters (feet) of the liquid pumped, that is necessary to overcome the friction losses caused by the flow of the liquid through the piping, including all the fittings. The friction head varies with (1) the quantity of flow; (2) the size, type, and condition of the piping and fittings; and (3) the character of the liquid pumped. Entrance and Exit Losses Unless it comes from a main under pressure, such as a city water supply, the suction supply of a pump comes from some form of reservoir or intake chamber. The point of connection of the suction pipe to the wall of the intake chamber or the end of the suction pipe projecting into the intake chamber or reservoir is called the entrance of the suction pipe. The frictional loss at this point is called the "entrance loss." The magnitude of this loss depends on the design of the pipe entrance, a well-designed bellmouth providing the lowest possible loss. Similarly, on the discharge side of the system where the discharge line terminates at some body of liquid, the end of the piping is called the exit. This exit is usually of the same size as the piping, and 410 Heads, Conditions of Service Performance Characteristics, and Specific Speed TOTAL STATIC HEAD STATIC DISCHARGE HEAD STATIC SUCTION HEAD ~ Fig. 18.7 Static heads. System with pump suction and discharge vessels at pressures other than atmospheric. the velocity head of the liquid is entirely lost. The end of the discharge piping is sometimes a long taper so that the velocity can be effectively reduced and the energy recovered. Some engineers consider entrance and exit losses as part of the suction and discharge pipe friction losses. Others prefer to consider them separately to make sure that they are not overlooked. This method has the additional advantage of clearly showing if either or both losses are excessive. Velocity Head Velocity head is the kinetic energy in a liquid at any point, expressed in joules per kilogram (footpounds per pound) of liquid, that is, in meters (feet) of the liquid in question. If the liquid is moving at a given velocity, the velocity head is equivalent to the distance the mass of water would have to fall in order to attain this velocity. Thus velocity head can be calculated by the equation: V2 h=v 2g where hv = the velocity head, in feet V = the liquid velocity, in feet per second g = the acceleration due to gravity, or 9.81 rn/s 2 (32.2 ftls 2). In determining the head existing in a pipe at any point, it is necessary to add the velocity head to the pressure gage reading, for the pressure gage can indicate only the pressure energy, whereas the actual Heads, Conditions of Service Perforrrumce Characteristics, and Specific Speed ----~ TOTAL STATIC HEAD ~-,L STATIC DISCHARGE HEAD STATIC SUCTION HEAD 1 Fig. 18.8 Static heads. Suction and discharge vessels at atmospheric pressure and suction liquid level above pump centerline. TOTAL STATIC HEAD STATIC DISCHARGE HEAD - ST1TIC SUCTION LIFT cQ.l - - --.-- ~. j I...... Fig. 18.9 Static heads. Suction and discharge vessels at atmospheric pressure and suction liquid level below pump centerline. 411 412 Heads, Conditions of Service Performance Characteristics, and Specific Speed head is the sum of the kinetic (velocity) and potential (pressure) energies. Thus, to detennine the actual suction head or discharge head, it is necessary to add the velocity head to the gage reading. If the suction and discharge pressures of a centrifugal pump are taken at points at which the velocities are the same, the velocity head component of each will be the same. The kinetic energy components of both the suction head and the discharge head will also be equal, and the total head can be determined by subtracting the suction gage reading from the discharge gage reading. In high-head pumps, the kinetic energy is relatively small, but in low-head pumps, it is relatively high. Thus failure to consider the velocity head in detennining heads in high-head pumps will not appreciably affect the results. For example, consider a pump handling 34Om3/hr (1,500 gpm) with a 6in. discharge and 8-in. suction. The discharge velocity head is 1.37 m (4.5 ft), whereas the suction velocity head is 0.43 m (1.4 ft). If the suction gage showed 2.62 m (8.6-ft) pressure and the discharge gage showed a 32.17 m (105.5 ft) head, the true total head would be (32.17 + 1.37) less (2.62 + 0.43) or 30.49 m [(105.5 + 4.5) less (8.6 + 1.4), or 100 ft], whereas the difference in gage readings would be 29.55 m (96.9 ft). Thus the error would be 3.1 percent of the total head. Had this been a pump in which the discharge gage reading was 305 m (1,000 ft), the true total head would be 303.2 m (994.5 ft), whereas the difference in gage readings would be 302.3 m (991.4 ft). The error of 0.3 percent is too small to be of any concern. If this were a pump in which the discharge head was 13.87 m (45.5 ft), however, the true total head would be 12.20 m (40 ft), whereas the difference in gage readings would be 11.25 m (36.9 ft), for an error of 7.8 percent. Whether or not the velocity head can be ignored depends on the desired accuracy of head detennination and upon the accuracy of the pressure readings that can be made. For the cited 305 m (I,OOO-ft) head reading, even with an accurate large scale gage it would be impossible for anyone to read the pressure within 3.05 m (10 ft), a basic error of 1 percent. SYSTEM FRICTION CURVE The friction-head loss in a system of pipes, valves, and fittings varies as a function (roughly as the square) of the capacity flow through the system. For the solution of pumping problems, it is often convenient to show the relation between capacity and friction-head loss through the system graphically. The resulting curve is called the "system friction curve," as shown in Fig. 18.10. The detenninations of friction losses are usually rough approximations at best, for the roughness of the pipe is not known. As the friction loss will increase when the pipe tuberculates or otherwise deteriorates with age, it is usual to base the friction loss on constants that have been found from the average of pipe 10 or 15 years old, thus allowing for friction losses in excess of those that will be obtained when the pipe is new. As a result, the pump is generally designed for excess head and delivers overcapacity when installed in a new system or in one that has not suffered from pipe deterioration. (For a complete treatment of friction loss calculations, see Chap. 20). SYSTEM·HEAD CURVE The friction-head losses, pressure differences, and static heads of any system can be graphically related (Fig. 18.11). The resulting curve is called the "system-head curve." For systems with varying static heads or pressure differences, it is possible to construct curves for minimum and maximum static heads or pressure differentials. The capacity that a pump will be able to deliver under varying conditions can be predicted by superimposing such system-head curves on a pump head-capacity curve (see Fig. 27.3). Heads. Conditions of Service Performance Characteristics. and Specific Speed 413 SYSTEM FRICTION CURVE CAPACITY Fig. 18.10 System-friction curve. SYSTEM-HEAD CURVE o c FRICTION LOSSES '" % TOTAL STATIC HEAD CAPACITY Fig. 18.11 System-head curve. Definitions Explanation of the head terms used with centrifugal pumps should be applicable to all installations although one or more elements of the total head are usually not involved (because they have zero 414 Heads. Conditions of Service Performance Characteristics. and Specific Speed values). Except as otherwise noted, the definitions given here are based on the current Standards of the Hydraulic Institute. SUCTION HEAD AND SUCTION LIFT As now defined, the total suction head (h s) is the static head on the pump suction line above the pump centerline minus all friction head losses for the capacity being considered (including entrance loss in the suction piping) plus any pressure (a vacuum being a negative pressure) existing in the suction supply. Rather than express the suction head as a negative value, the term "suction lift" is normally used when the suction head is negative and when the pump takes its suction from an open tank under atmospheric pressure. As the suction lift is a negative suction head measured below atmospheric pressure, the total suction lift (symbol also hs ) is the sum of the static suction lift measured to the pump centerline and the friction head losses as defined above. (It is sometimes advantageous to express both suction and discharge heads in absolute pressure, but usually it is more suitable to measure them above or below atmospheric pressure.) A gage on the suction line to a pump, when corrected to the pump centerline, measures the total suction head above atmospheric pressure minus the velocity head at the point of attachment. As suction lift is a negative suction head, a vacuum gage will indicate the sum of the total suction lift and velocity head at the point of attachment. The three most common suction supply conditions are illustrated in Fig. 18.12. System I involves a suction supply under a pressure other than atmospheric and located above pump centerline; it includes all the components of suction head (h s). If hs is to be expressed as a gage reading and P s is a partial vacuum, the vacuum expressed in feet of liquid would constitute a negative pressure I II rn S I B h. = S - h,s - hi + p. hs=<-Sl-hfs-h j - hs = S + his + hi Fig. 18.12 Suction head determination for three typical examples. KEY: P, = pressure other than atmospheric S = static head hs = suction head hI' = total friction loss from A to B hi = entrance loss at A -hs = suction lift The gage reading at B corrected to pump centerline equals the suction head minus velocity head at B. Heads. Conditions of Service Performance Characteristics. and Specific Speed 415 head and carry a minus (-) sign. If the pressure P s is expressed in absolute pressure values, hs will also be in absolute pressure values. A very common installation, II, involves a suction supply under atmospheric pressure located above the pump centerline. As the suction head (expressed as a gage value) has a P s value of zero, the P s value can be dropped from the formula. System III, the most common installation for pumps handling water, involves a suction supply under atmospheric pressure located below the pump centerline. It is optional whether the suction head is expressed as a negative suction head or in positive values as a suction lift. As the source of supply is below the pump centerline (which is the datum line), S is a negative value. It should be noted that the suction lift formula is the same as that for suction head except that both sides have been multiplied by -1. A gage attached to the pump suction flange, when corrected to the pump centerline, will register a partial vacuum or negative pressure. To determine the suction head, it is therefore necessary to add the velocity head to this negative pressure algebraically, or, if it is desired to work in terms of a vacuum, the velocity head must be subtracted from the vacuum to obtain the suction lift. For example, if the gage attached to the suction of a pump having a 6-in. suction and pumping at a capacity of 227 m3/hr (1,000 gpm) of cold water showed a vacuum of 152 mm (6 in) of mercury (equal to 2.07 m or 6.8 ft of water), the velocity head at the gage attachment would be 0.61 m (2.0 ft) of water, and the suction head would be -2.07 + 0.61, or -1.46 m (-6.8 + 2.0, or -4.8 ft of water), or the suction lift would be 2.07 - 0.61, or 1.46 m (6.8 - 2.0, or 4.8 ft of water). As most centrifugal pump troubles occur on the suction side of the pump, it is a very important part of pump selection to supply complete information on suction conditions, including all operational variations. For some complex problems, it is often necessary to superimpose the variation in total suction head graphically on the suction head limitations of the pump being considered in order to make sure the pump will be suitable. NPSH In the pumping of liquids, the pressure at any point in the suction line must never be reduced to the vapor pressure of the liquid. The available energy that can be utilized to get the liquid through the suction piping and suction waterway of the pump into the impeller is thus the total suction head less the vapor pressure of the liquid at the pumping temperature. The available head-measured at the suction opening of the pump-has been named "net positive suction head." It is usually indicated by its initials, NPSH. A complete discussion of Suction Conditions and of the Limitations on Suction Performance is given in Chapter 19. Specifying Suction Conditions The importance of accurately advising a manufacturer of the actual suction conditions for a centrifugal pump cannot be overemphasized. A pump will be unable to meet its design capacity conditions unless the suction head can provide enough energy to get the liquid into the pump as previously discussed. If a cold nonvolatile liquid is to be handled, it is necessary to know whether there will be suction head or suction lift, and if the latter, what maximum lift can be expected. If the liquid is to be hot or under a pressure corresponding to or near its vapor pressure, the pump must be installed with head on suction, and the available submergence must be indicated. For liquids other than water, information on the pumping temperature and vapor pressure is also necessary. All expected or probable variations in suction conditions should also be specified. 416 Heads, Conditions of Service Performance Characteristics, and Specific Speed I S -13.0 FT 20.4FT S 20.4 FT I n m v Fig. 18.13 Seven installations of duplicate pumps referred to in Table 18.3. Pumps have 8 in discharge and 10 in suction and all operate at 454 m 31hr (2,000 gpm), 24.4 m (80 ft) total head, and 5.6 m (18.4 fl) NPSH. Examples of NPSH Calculations The NPSH calculations of seven different installations, with the same hydraulic conditions (gallons per minute, total head, and NPSH), are shown in Fig. 18.13 and Table 18.3. This illustration and table show the effect on the physical installation of a pump, for various applications, if the same NPSH is to be available at the pump. Installations I and II have the same conditions except for altitude. The reduction in barometric pressure at 1,220 m (4,000 ft) elevation makes it necessary to raise the liquid level 1.46 m (4.8 ft) lower to obtain the same NPSH. Installation III illustrates how a liquid with a high vapor pressure forces a reduction in possible suction lift. In this case the liquid is considerably lighter than water, and, if it had a vapor pressure equal to water at 15°C (60°F), it would have been possible to have a static suction lift of 7.68 m (25.2 ft). The effect of the specific gravity of the liquid on suction conditions is illustrated more clearly in installation IV. Here, because brine has a specific gravity of 1.2, the atmospheric pressure corresponds to only 6.83 m (28.3 ft) of liquid instead of 10.34 m (34.0 ft) as with cold water (in installation I). As a result, in order to obtain the same 5.61 m (18.4 ft) of NPSH, the value of S, the static component of the suction head, can only be -2.38 m (-7.8 ft) instead of -3.96 (-13.0 ft) as with cold water. (Usually in installations handling gasoline and brine, the pumps are located so that the liquid level is above the pump. Many such installations have long suction pipes with considerable friction head loss, so that the same suction conditions indicated here could logically result.) Installation V is similar to many boiler feed pump installations. When the liquid handled is at a temperature corresponding to its boiling point at the suction pressure, the suction head available to overcome friction and provide the required NPSH must be entirely static as Ps - P vp is zero. This is also demonstrated in installation VI, which shows a typical condition encountered in condensate or hotwell pumps. Condensate pumps serving surface condensers are generally located on the floor, just slightly below the liquid level in the hotwell, and pumps of a special design requiring a very low NPSH have to be used. ~ hq = h.t - h vd , in m of liquid hq, pressure gage hVd h.t = H + h., in m of liquid P" bar absolute P, in m of liquid, gage P, in m of liquid, absolute Pvp' bar absolute P vp' m absolute hr,+hb inm S, in m NPSH, in m of liquid = S-(hr• + hi) + P, - Pvp h., in m of liquid, gage = S-(hfs + hi) + P, h... in m of liquid h.g = h. - hv.. in m, gage h.g, pressure gage Liquid Temperature, in deg C Specific gravity Altitude, in m Barometric pressure, bar absolute P" gage 1.014 0 14.2 0.41 5.78 0.61 -2.17 5.6 -2.78 0.31 -3.09 165 mm Hg vacuum 21.6 1.19 20.4 1.46 0.872 0 8.90 0.019 0.19 0.61 -2.50 5.6 -3.11 0.31 -3.42 252 mm Hg vacuum 21.3 1.19 20.1 1.97 1.014 0 10.37 0.019 0.19 0.61 -3.96 5.6 -4.57 0.31 -4.88 358 mm Hg vacuum 19.8 1.19 18.6 1.83 Gasoline 21 0.73 Sea level 1.014 0 III Water 17 1.0 1,220 m 0.872 0 II Water 17 1.0 Sea level 1.014 0 I Table 18.3(a) Head calculations for pumps in Fig. 18.13 (metric units) All suction and discharge heads are as corrected to centerline of pumps. For explanation of head symbols, see Fig. 18.12. 0.31 -3.30 290 mm Hg vacuum 21.1 1.19 19.9 2.34 -2.99 1.014 0 8.63 0.005 0.04 0.61 -2.38 5.6 Brine 0 1.2 Sea level 1.014 0 IV 30.0 1.19 28.8 2.71 0.31 5.31 0.50 bar 5.61 1.014 0 10.8 1.014 10.8 0.61 6.22 5.6 Water 100 0.959 Sea level 1.014 0 V 0.31 -4.44 325 mm Hg vacuum 19.9 1.19 18.7 1.83 -4.13 Water 38 0.995 Sea level 1.014 714 mm Hg vacuum 0.062 -9.74 0.63 0.062 0.64 0.61 6.22 5.6 VI 0.31 0.73 0.069 bar 25.4 1.19 24.2 2.30 1.04 1.014 0 10.7 0.58 6.10 0.61 1.65 5.6 Water 85 0.970 Sea level 1.014 0 VII QO ........ hq =h.t - hVd' in ft of liquid h.tg, pressure gage hVd h.t =H + h .. in ft of liquid p .. psi absolute P" in ft of liquid, gage p .. in ft of liquid, absolute PVP' psi absolute PVP ' in ft of liquid, absolute hr, + hi' in ft S, in ft NPSH, in ft of liquid = S- (h,. + h;) + P, - Pvp h" in ft of liquid, gage = S - (hr. + hi) + P, hv., in ft of liquid hog =h, - hv.. in ft, gage hog, pressure gage Liquid Temperature, in deg F Specific gravity Altitude Barometric pressure, psi absolute p .. gage -10.2 1.0 -15.0 1.0 -16.0 ft 14.1 in. Hg vacuum 65.0 3.9 61.1 26.4 9.9 in. Hg vacuum 69.8 3.9 65.9 28.5 -11.2 ft 12.65 0 29.2 0.275 0.6 2.0 -8.2 18.4 Water 62 1.0 4,000 ft 12.65 0 II 14.7 0 34.0 0.275 0.6 2.0 -13.0 18.4 Water 62 1.0 Sea level 14.7 0 I Table 18.3(b) Head calculations for pumps in Fig. 18.13 (US units) All suction and discharge heads are as corrected to centerline of pumps. For explanation of head symbols, see Fig. 18.12. 1.0 -10.1 ft 6.5 in. Hg vacuum 70.9 3.9 67.0 21.2 -9.1 14.7 0 46.5 6.0 19.0 2.0 -7.1 18.4 Gasoline 70 0.73 Sea level 14.7 0 III 1.0 -10.8 ft 11.4 in. Hg vacuum 69.2 3.9 65.3 33.9 -9.8 14.7 0 28.3 0.Q7 0.1 2.0 -7.8 18.4 Brine 32 1.2 Sea level 14.7 0 IV 98.4 3.9 94.5 39.2 1.0 17.4 ft 7.2 psi 18.4 14.7 0 35.4 14.7 35.4 2.0 20.4 18.4 Water 212 0.959 Sea level 14.7 0 V 1.0 -14.6 ft 12.8 in. Hg vacuum 65.4 3.9 61.5 26.5 -13.6 Water 100 0.995 Sea level 14.7 28.1 in. Hg vacuum 0.9 -32.0 2.2 0.9 2.2 2.0 20.4 18.4 VI 83.4 3.9 79.5 33.4 1.0 2.4 ft 1.o-psi 3.4 14.7 0 35.08.38 20.0 2.0 5.4 18.4 Water 185 0.970 Sea level 14.7 0 VII Heads, Conditions of Service Performance Characteristics, and Specific Speed 419 A comparison of installations V and VII shows how the reduction in temperature below that corresponding to suction pressure affects the required suction conditions. DISCHARGE HEAD The discharge head (h d) of a centrifugal pump is the head measured at the discharge nozzle. It is the algebraic sum of the static head, the friction head losses for the capacity being considered, the exit loss at the end of the discharge line, and the terminal head or pressure. It can be expressed with absolute or gage readings in meters (feet) of liquid. Established practice expresses the discharge and suction heads of a horizontal pump with the pump centerline as datum. Usually, discharge and suction heads of a vertical pump are given with the centerline of the discharge as datum. Both heads can be given with other elevations as datum, but it is then necessary to indicate the datum at which they are measured. This practice is often necessary because the exact elevation of the pump centerline or discharge centerline have not been determined prior to the purchase of a pump. When the reading of a gage at the pump discharge has been corrected to the pump centerline, it will indicate the discharge head minus the velocity head at the point of attachment. TYPICAL DISCHARGE SYSTEMS Some typical discharge systems are illustrated in Fig. 18.14. System I shows a system of pump delivery to an elevated tank in which a pressure other than atmospheric exists; it therefore includes all the components of discharge head. System II is similar to I except that atmospheric pressure exists on the discharge-liquid level (typical of pumps delivering to open reservoirs and elevated tanks). If the discharge head is to be expressed as a gage reading, Pd equals zero and is therefore not shown in the formula. Should it be necessary to express the discharge head in absolute values, the atmospheric pressure expressed in feet of liquid must be added to the discharge head expressed as a gage reading. Although system III illustrates an overhead tank, it applies to all conditions of "overboard discharge." The actual useful static head (the distance from the pump centerline to the discharge-water level) is less than the actual static discharge head, D. It is possible to recover all or part of this difference by incorporating a siphon leg on the discharge. Although systems IVb and V would theoretically be the most efficient, it is often desirable not to use a sealed discharge. One reason is to prevent the possibility of back siphonage when the pump is stopped. In systems IVa and IVb, the effectiveness of the siphon will depend both on the length of the leg and the design of the piping. Design differences can make the recovery vary from 0 to 100 percent. For example, if the pipe in IVa was very large in relation to the capacity, the pipe would not run full and the actual static discharge head would consequently become the distance to the actual water level in the loop of the piping. All systems using a siphon leg must be investigated carefully to see what percentage of recovery can be expected and what loss is to be included in the friction loss (hid)' As the absolute pressure at any point in a siphon must exceed the vapor pressure of the liquid, it is theoretically possible to employ a siphon leg nearly 10.3 m (34 ft) long with airfree cold water at sea level. The water being handled is usually not airfree and a reduction in pressure to below atmospheric causes separation of this air, reducing the effectiveness of the siphon. Water siphons more than 6 m (20 ft) high are rarely encountered. It is even questionable if many of those under 6 m (20 ft) are 100 percent effective. Siphon design must provide for the washing out or removal of entrapped air when operation begins, 420 Heads. Conditions of Service Performance Characteristics. and Specific Speed n I A hd= 0 + hfd + he + Pd m No B llt:j o I rr-T~ 0 I O2 ~~l A I2:b B A Fig. 18.14 Determination of discharge heads for six typical discharge layouts. KEY: Pd = pressure deviation from atmospheric he = exit loss at B litd =friction loss from A to B (including any siphon losses) h.rJ = velocity head at A Heads, Conditions of Service Performance Characteristics, and Specific Speed 421 so that the siphon will be established. Unless the air in the loop can be evacuated, the pump will have to operate during the starting period against a maximum static component DI (!Vb). In some condenser circulating installations, this condition results in a starting head much higher than the normal operating head, and special consideration has to be given to the head-capacity curve of the pump. The same effect can occur in system I if Pd is a negative pressure that is not established until after pumping has commenced (as in a barometric condenser). In systems with variable discharge head, it is usually advantageous to establish the head at various capacities and prepare a graph showing the variation with capacity. When this graph is related to the suction head, the resulting chart will indicate the system head. The proper method of specifying discharge heads in preparing an inquiry for centrifugal pumps is discussed in some detail in Chapter 27. TOTAL HEAD The total head, H, of a centrifugal pump is the energy imparted to the liquid by the pump, that is, the difference between the discharge head and the suction head. As a suction head lift is a negative suction head, the total head is the sum of the discharge head and the suction lift. If the discharge head and the suction head are not determined independently, the total head can be calculated (Fig. 18.15) by determining the algebraic sum of the static head from supply level to discharge level, H sr, plus all friction losses for the capacity being considered, hI' plus the entrance hi, and exit, he> losses plus the terminal pressure, Pd, minus the suction supply pressure, Ps• For complex systems involving both vacuums and pressure, it is often easier to convert all the vacuums and pressures into absolute pressure values of the liquid being handled, expressed in meters (feet). (To convert bar to m of liquid, multiply by 10.21 and divide by the specific gravity of the liquid at the pumping temperature. Similarly, for psi to ft of liquid, multiply by 2.31 and divide by the specific gravity.) As measured by gages attached to the pump suction and discharge openings, the total head is the discharge head (the sum of the discharge gage reading corrected to the pump centerline and the velocity Hst (0-5) B A H = h d - h, e Hit + hf+ hl+h.+ (Pd - PI) Fig. 18.15 Detennination of total head. 422 Heads, Conditions of Service Performance Characteristics, and Specific Speed head at the point of attachment of the discharge gage) minus the suction head (the sum of the suction gage reading corrected to the pump centerline and the velocity head at the point of attachment of the suction gage). As the plus and minus signs of the various elements are easily reversed, and as there are numerous precautions to be considered in taking gage readings, it is advantageous in any test to follow the instructions in the Test Code of the Hydraulic Institute. Outmoded Terminology Total dynamic head, dynamic suction head, dynamic suction lift, and dynamic discharge head are outmoded terms. Total dynamic head referred to what is now called total head; dynamic suction head, dynamic suction lift, and dynamic discharge head were defined as the heads measured by a gage corrected to the pump centerline, and thus did not include the velocity head element. Misunderstandings arose if the size of the pump suction and discharge openings were not specified, resulting in different head values for pumps working under identical conditions if their openings were not the same. Furthermore, in determining the total dynamic head from the dynamic discharge head and dynamic suction head it was necessary to correct for any difference in velocity head. The present method of specifying heads is more satisfactory than the dynamic head method. HEAD TERMS FOR VERTICAL WET-PIT PUMPS Vertical wet-pit pumps can be either the volute or the turbine type, the latter covering both propeller and vertical turbine pumps, which were formerly called deep-well pumps. The special hydraulic and mechanical problems of vertical turbine pumps have caused them to become virtually independent of the regular centrifugal pump field with different practices and terminology. Both volute and propeller wet-pit pumps have been handled primarily by engineers in the regular centrifugal pump field. With these two types, total head is the discharge head measured at the centerline of the discharge nozzle, with velocity head included, plus the static distance to the suction water level. Thus, the loss in the suction bell and further losses of the suction strainer and suction piping, if either is furnished, as well as the losses in the column pipe and elbow in propeller pumps are charged to the pump. The following head terminology is used by the National Association of Vertical Turbine Pump Manufacturers for vertical turbine pump applications. 1. Laboratory head-discharge pressure by gage in feet plus static vertical distance to suction water level in a test setup using the minimum length of column and shafting for a laboratory test. 2. Total head-discharge pressure by gage in feet plus distance to suction water level. (In case of a closed suction, the total head is discharge pressure plus distance to centerline of suction gage minus suction pressure in feet.) 3. Dynamic laboratory head-laboratory head as defined above plus velocity head at the point of the discharge gage attachment. 4. Total dynamic head-total head as defined above plus velocity head at the point of the discharge gage attachment minus the velocity head at the point of the suction gage attachment, in case of a closed suction. (What was formerly called field pumping head in vertical turbine pump terminology is now called total head.) In most vertical turbine pumps, the velocity head is a very small portion of the head developed by the pump, and its omission is of little importance. Heads. Conditions of Service Performance Characteristics. and Specific Speed 423 Pump Characteristic Curves Unlike positive displacement pumps, a centrifugal pump operating at constant speed can deliver any capacity from zero to a maximum value dependent upon the pump size, design, and suction conditions. The total head developed by the pump, the power required to drive it, and the resulting efficiency vary with the capacity. The interrelations of capacity, head, power, and efficiency are called the pump characteristics. These interrelations are best shown graphically, and the resulting graph is called the characteristic curves of the pump. The head, power, and efficiency are usually plotted against capacity at a constant speed, as shown in Fig. 18.16. It is possible for special problems, however, to plot any three components against any fourth component. When variable-speed drivers are used, a fifth component, the operating pump speed expressed in rpm, is involved. Where suction conditions may be critical,the limit of suction-lift-capacity curve or required NPSH-capacity curve is often shown. Many other relationships can be shown on the same graph as required for specialized studies, for example, specific speed plotted against capacity. The curve H-Q in Fig. 8.16, showing the relationship between capacity and total head, is called the head-capacity curve. Pumps are often classified on the basis of the shape of their head-capacity curves as described below. The curve P-Q in Fig. 8.16, showing the relation between power input and pump capacity, is the 180 H-o~HEAb-cJp4cl 160 w 140 w u... z 120 r 100 0 <f w j'c]'~~ 'l..!!! () ,;. Ij,./ ::r ....J <f 10- ~ 0 ~ 40 20 o ~ ~ lI'",'pOINT O~-= ~ ~ MAXIMUM ~ 80 60 ~~ ~ ............. ~ 90 I .K' EF!,CIENC,( 4a ~~;t"~\ ./ ,.,.,- w "\ '- 80 \. "" \, \ I u... w 40 u... 30 10 6 8 10 12 14 16 18 20 22 ]z 20 4 Q. 50 w u I 2 a:: 60 >u \, L a u w 70 \ '\ ~,Q ~ z --a::::r Q. CD 0 CAPACIT Y (a), IN 100 GPM Fig. 18.16 Typical centrifugal pump characteristics. Double-suction, single-stage volute pump with 8 in suction and 6 in discharge at 1,760 rpm. 424 Heads. Conditions of Service Performance Characteristics. and Specific Speed power-capacity curve, but is generally referred to as the power curve, the brake horsepower curve, or the bhp curve. The curve T\-Q in Fig. 18.16, showing the relation between efficiency and capacity, is properly called the efficiency-capacity curve, but is commonly referred to as the efficiency curve. Usually the graph of a pump characteristic is made for a capacity range from zero to the maximum operating capacity of the unit. The scales on the graph for head, efficiency, and brake horsepower (bhp) all have the same zero line at the base of the graph (Fig. 18.16). In some cases, the curve is made for a limited range in capacity. In other cases, to permit clearer presentation, the head, efficiency, and power scales are so selected that their zero lines do not coincide, and sometimes these scales are so enlarged that their full range cannot be shown on the graph. CLASSIFICATION OF HEAD·CAPACITY CURVE SHAPES Pump head-capacity curves are commonly classified as follows: 1. Rising characteristic-or rising head-capacity characteristic, meaning a curve in which the head rises continuously as the capacity is decreased (Fig. 8.17). 2. Drooping characteristic-or drooping head-capacity characteristic, indicating cases in which the headcapacity developed at shutoff is less than that developed at some other capacities. This is also known as a looping curve (Fig. 18.18). 3. Steep characteristic-a rising head-capacity characteristic in which there is a large increase in head between that developed at design capacity and that developed at shutoff. It is sometimes applied to a limited portion of the curve; for example, a pump may have a steep characteristic between 100 per cent and 50 per cent of the design capacity (Fig. 18.19). 4. Flat characteristic-a head-capacity characteristic in which the head varies only slightly with capacity from shutoff to design capacity. The characteristic might also be either drooping or rising. All drooping curves have a portion where the head developed is approximately constant for a range in capacity, called the flat ...:r~ CAPACITY CAPACITY Fig. 18.17 Rising head-capacity curve. Fig. 18.18 Drooping head-capacity curve. Heads. Conditions of Service Performance Characteristics. and Specific Speed 425 o '" III :r CAPACITY Fig. 18.19 5. 6. Steep head-capacity curve. CAPACITY Fig. 18.20 Flat head-capacity curve. portion of the curve. Other curves are sometimes qualified as fiat, either for their full range or for a limited portion of their range (Fig. 18.20). Stable characteristic-a head-capacity characteristic in which only one capacity can be obtained at anyone head. Basically this has to be a rising characteristic (Fig. 18.17 and 18.19). Unstable characteristic-a head-capacity characteristic in which the same head is developed at two or more capacities. (Fig. 18.18 and 18.21). The successful application of any pump depends as much upon the intrinsic characteristics of the system on which it is operated as upon the head-capacity characteristic. Most pumping systems permit the use of pumps with moderately unstable characteristics. CLASSIFICATION OF POWER CURVE SHAPES Power-capacity curves are also classified according to shape. Fig. 18.22 illustrates a pump characteristic with a power curve that flattens out and decreases as the capacity increases beyond the maximum efficiency point. This is called a nonoverloading curve. When the power curve continues to increase with an increase in capacity, as in Fig. 18.23, the pump is said to have an overloading curve. The shape of the power curve varies with the specific speed type. As a result, the power curve may have a very low value at shutoff (see Fig. 18.22 and 18.23), it may have a high value at shutoff (Fig. 18.24), or any value in between. Whereas in Fig. 18.23 the power curve is an overloading curve with a decrease in head and increase in capacity, the power curve in Fig. 18.24 is an overloading curve with an increase in head and decrease in capacity. Pumps with nonoverloading power curves are advantageous because the driver is not overloaded under any operating conditions, but they are not obtainable in all specific speed types of pumps. The actual range of operating conditions encountered in the operation of a pump determines the range in power requirements, and the driver size should be selected for the power to be encountered. 426 Heads, Conditions of Service Performance Characteristics, and Specific Speed CAPACITY Fig. 18.21 .... z ~ 90 a: w a.. 80 I - HEAD_ w () u. ~ ~ 20 -' 10 / J~' I ""n ~ .'\. , , ~ V o 140 120 100 80 60 40 / ::c ~ ~ 0 ~ I o ...- -",vyr--.... '"'««? --- V ---I~ ~ ~ 40 w u. z 30 I -~/r't' / ~70 iL60 w 50 Potentially unstable head-capacity curve . CL :x: III 20 20 40 60 CAPACITY, IN 100 80 100 o G PM Fig. 18.22 Characteristics of a pump with a non-overloading power curve with reduction in head. Heads, Conditions of Service Performance Characteristics, and Specific Speed 90 ~ 70 IZ UJ 60 0:: UJ 50 u c.. .,: 40 zUJ u iL: LL UJ ~ 30 20 z V / ..,.,.., J: ...J « l- 0 ~~ ~ V ~ I-- \ 80 60 ~ 40 ~ I c.. z III 20 o o 40 20 60 CAPACITY, IN 100 Fig. 18.23 \ "\ \ / cS ~20 0 ~/7')- I/j LL 10 ~~('.4P4 1'\ ~,(j 1:j30 ~ 10 v~/ ~ 1j7 UJ u ......... I--""" 40 80 100 80 G PM Characteristics of a pump with an overloading power curve with a reduction in head. ~o IZ ..... ~ 40 -...!:!.f4 D-C w 30 ~ ............ 0 .......... ......... ~ UJ :r ~O ...J ~ I- 0 I- 10 0 r--.... "\ ~rzr....... <:v9'Y IUJ LL ~ ,.G~~ V o V V 10 / V / -<.... ...... ~ K.... 8H V 20 30 CAPACITY. IN 100 "- ~ (J 80 Q. 60 iL: ~ ..... '" ~ 50 0: UJ .,: (J 70 z !!;! (J 50 r-- ~ 40 \\ UJ 90 LL UJ 40 ~ \ 60 30 20 c.. z III 10 0 G PM Fig. 18.24 Characteristics of a pump with an overloading power curve with an increase in head. 427 428 Heads, Conditions of Service Performance Characteristics, and Specific Speed MATHEMATICAL RELATIONS OF HEAD, CAPACITY, POWER, AND EFFICIENCY The useful work done by a pump is the weight of liquid pumped in a period of time multiplied by the head developed by the pump and is generally known as the hydraulic power. It is usually expressed as kilowatts or horsepower and can be calculated from the relations: . specific gravity hydraulIc power, kW = QH 368 where Q = pump capacity in cubic meters per hour (m3/hr) H = total head in meters (m) or . specific gravity hydraulIc power, hp = QH 3960 where Q = pump capacity in gallons per minute (gpm) H = total head in feet (ft) The power required to drive the pump is regularly determined in kilowatts or horsepower and is called the power input to the pump. The ratio of the hydraulic power to the power input is the pump efficiency. The relation between power, capacity, head, and efficiency is therefore: QH specific gravity power, kW = . efficIency 368 or QH specific gravity h power, p = effi· ICIency 39 60 Type Characteristics If the operating conditions of a pump at the design speed, that is, the capacity, head, input power, and efficiency at which the efficiency curve reaches its maximum, are taken as the 100 percent standard of comparison, the head-capacity, power-capacity, and efficiency-capacity curves can all be plotted in terms of the percentage of their respective values at the capacity at maximum efficiency. Such a set of curves represents the type characteristic or 100 percent curve of the pump. Figure 18.25 shows the type characteristic of the pump whose performance is shown in Fig. 18.16. Centrifugal Pump Characteristics Relations A set of relations, known as the affinity laws, allow the performance of a centrifugal pump to be predicted. for a speed other than that for which the pump characteristic is known. These same relations also allow prediction of the performance of a pump if the impeller is reduced in diameter (within a limit dependent upon the impeller design) from the characteristics obtained at the larger diameter. Heads. Conditions of Service Performance Characteristics. and Specific Speed 130 -r-- r--t. 120 c • ~ - 110 W 100 0 A- Q» Zu 4.Z >w uz~ WI&. -I&. ~w a \oJ:) I&. I&. da cw)( XC a ...°c~ 70 60 40 u 30 z w c W A- ~i'l: 80 ~ ...V J V ~ 20 10 ""- ~ ",."". ...- ~ """-' c.... ~ ~t/ ~~ / ~ "~ '1/' 90 ~O r--.... oI o I / I ~ 429 ~/ i\. "~' ,..... ~ \ \ ~ , ~ -_. / 20 40 60 80 120 140 160 PERCENT OF CAPACITY AT MAXIMUM EFFICIENOY Fig. 18.25 Type characteristic, or 100 percent curve. When the speed is changed (1) the capacity for a given point on the pump characteristics varies as the speed; and at the same time; (2) the head varies as the square of the speed; and (3) the brake horsepower varies as the cube of the speed. These relations take the form of equations as follows: Q = Q,(n/n,) H = H,(n/n,)2 P = P,(n/n,? or where n =new speed desired, in revolutions per minute Q = capacity, at desired speed n H =head, at desired speed n for capacity Q P = power, at desired speed nat H and Q n, = a speed, in revolutions per minute, at which the characteristics are known 430 Heads, Conditions of Service Performance Characteristics, and Specific Speed Q. H. p. =a capacity, at speed n. =brake horsepower, at speed n. at H. and Q. =head, at capacity Q. at speed n. For example, a pump is tested at 1,800 rpm and gives the following results: Capacity m3/hr gpm 908 795 681 454 227 0 4,000 3,500 3,000 2,000 1,000 0 Head Power bhp m ft kW 47.9 56.1 61.3 67.4 69.5 70.1 157 184 201 221 228 230 142 138 131 106 80 57 Efficiency decimal 190 185 174 142 107 76 0.83 0.88 0.87 0.78 0.54 0 To obtain the performance of this pump at 1,600 rpm, the first set of values is corrected to 1,600 rpm, as follows: =4,000 (1,600/1,800) =3,556 gpm = 157 (1,600/1,800)2 = 124 ft = 190 (1,600/1,800)3 = 134 bhp Q = 908 (1,600/1,800) = 807 m3/hr H = 47.9 (1,600/1,800)2 = 37.8 m P = 142 (1,600/1,800)3 = 100kW Changing the other sets of values yields the following (Fig. 18.26). Capacity gpm m3/hr 807 706 606 404 202 0 3,556 3,110 2,667 1,777 890 0 Head Power bhp m ft kW 37.8 44.2 48.2 53.4 55.1 55.5 124 145 158 175 181 182 100 97 91 75 56 40 134 130 122 100 75 54 The capacity and head figures for these various points can be calculated on a slide rule with one setting. In this case 1.8 on the C scale would be set over 1.6 on the D scale, and the new capacities would be read on the D scale opposite the 1,800-rpm capacities on the C scale. The new heads would be read on the A scale opposite the 1,800-rpm heads on the B scale. Although it is possible to obtain the cube of a ratio on a slide rule, errors are often made in this step. Except for shutoff (zero capacity) the bhp can be calculated from the new head and capacity (at 1,600 rpm) using the same efficiency as for the corresponding head-capacity at 1,800 rpm. Thus the power for the first point can be calculated as (807 x 37.8)/(368 x 0.83) or 100 kW, and in US units as (3,556 x 124)/(3,960 x 0.83) or 134 bhp. The shutoff horsepower can only be obtained by using the cube of the speed ratio, as both the capacity and the efficiency are zero. These relations for a change in speed can be used safely for speed changes up to 2: 1. 431 Heads, Conditions of Service Performance Characteristics, and Specific Speed 240 HE~D-~APlCITly IAoo IRPJ -r-- r-- - 220 200 I- IU IU ~ HEAD-CAPACITY 1600 180 RPf.f -:-.;.,. ~ 0 ~ IU :J: ..J I r- 140 . . .V V 200 (i~ ~~ 100 ,~ C 180 ~ c)~ lc.lc." 160 ~ V/ 140 120 60 «.,~ c /, V Il. :J: CD 80 ~4. h , '" VI '/ ! J V / V V .......... - ~ V r-.... I-"" "\ ..... "- ,,/ . /V i J l.J' '" ~ .. '" 1\ ,- 1\ 9o ~ - " ,.. ~ I' 7o r'" - 50 a: 0 .,: u Z IU u 3 0 iL ro~ ~ IU ~ 20 ./ I0 ~ ~ o 10 20 30 CA PACITV. IN 100 G P M Fig. 18.26 IZ IU U IU Il. ~~~ ./ 8o 0 1 :?-~~ /~ - I-- _- .. ". oo1J" I ~~ ~ V l'/ V: JI 0 ~~~ 'f ~ It ,.q,O l" j 100 O~ V~ I K ........ 160 120 / -t"-..... ......... J ~ I0 I- , ........ ........ Effects of speed change on pump characteristics. 40 0 432 Heads, Conditions of Service Performance Characteristics, and Specific Speed The diameter of an average impeller can be cut down on a lathe by 20 percent of its original maximum value without adverse effect. Cutting it down to less than 80 percent will generally result in a significant reduction in head and consequently a much lower efficiency. This 20 percent limit is approximate, as some impeller designs can be cut more than this, whereas others cannot be cut more than a small percentage without adverse effect. Any change in diameter will affect the proportions of the impeller, and some variations from the theoretical results should be expected when tested. If an impeller is cut in diameter, it is found that, at the same speed, the characteristics of the pump will have a definite relation to its original characteristics. These relations are (1) the capacity for a given point in the pump characteristic varies as the impeller diameter, and at the same time; (2) the head varies as the square of the impeller diameter; and (3) the horsepower varies as the cube of the impeller diameter. Expressed as equations, these are Q = Q.(D/D.) H =H.(D/D.)2 P = P.(D/D.)3 or where D. = original diameter D = cut-down diameter Q. = capacity with D. impeller Q = corresponding capacity with D impeller H. = head with D. impeller at Q. H = corresponding head with D impeller at Q p. = power with D. impeller at Q. and H. P = power with D impeller at Q and H. Changing only the impeller diameter of a centrifugal pump alters its design slightly, and so the affinity laws do not exactly predict the new performance, the usual case of reducing the impeller diameter producing a greater reduction in head and capacity than predicted. To compensate for this, the theoretical impeller diameter ratio has to be corrected in some way. Fig. 18.27 gives a correction for radial impellers (Ns up to 2,500) in the form of the required diameter ratio versus the theoretical, both expressed as percent of the original diameter. At the same time, the power varies as approximately the cube of the actual impeller diameter ratio, so it doesn't decrease at the same rate as the head and capacity, and consequently pump efficiency tends to decrease as the impeller diameter is reduced. An example will help to clarify all this. Referring back to the tabulation of values of the pump tested at 1,800 rpm (with an impeller diameter of 14.75 in.), if the impeller is reduced to 14.00 in. in diameter, the actual impeller diameter ratio is 0.949, and from Fig. 18.27 the effective ratio for head and capacity will be 0.940 (read from the theoretical axis.) Applying these ratios, the first set of values is corrected as follows: Q = 908 (0.940) = 854 m3/hr = 4,000 (0.940) = 3,760 gpm H = 47.9 (0.940)2 = 42.4 m = 157 (0.940)2 = 139 ft P = 142 (0.949)3 = 121kW = 190 (0.949)3 = 162 bhp The other sets of values yield the following (Fig. 18.28): Heads, Conditions of Service Performance Characteristics, and Specific Speed Capacity gpm m 31hr 854 747 640 427 214 0 3,760 3,290 2,820 1,880 940 0 Head Power bhp m It kW 42.4 49.6 54.2 59.3 61.4 62.0 139 163 178 195 201 203 121 118 111 90 68 48 433 Efficiency decimal 162 158 149 121 91 65 0.82 0.85 0.85 0.76 0.52 0 These relationships are most commonly used to determine the change in speed, the change in diameter of an impeller, or the combination of both that is necessary to produce a head capacity curve passing through a given point. For example, suppose the pump whose characteristics are shown in Fig. 18.26 has to meet the conditions of 681 m3/hr (3,000 gpm) at 54.9 m (180 ft) total head. Since this falls below the head-capacity curve of the 375 mm (14.75 in) impeller at 1,800 rpm, the desired head capacity is obtained by reducing the speed or reducing the diameter of the impeller. If the pump, which is to give 681 m3/hr (3,000 gpm) at 54.9 ft (180 ft) were speeded up, or the impeller diameter increased so that point on the characteristic became 704 m3/hr (3,100 gpm), the head, at the same time, would have become 54.9 (704/681)2 or 58.7 m (192 ft). Similarly, if 727 m3/hr (3,200 gpm) were obtained by a further increase in speed or impeller diameter, the head would be 54.9 (727/ 681)2 or 62.5 m (205 ft). Plotted as shown in Fig. 18.26, these values form a section of a curve (A). This intersects the 1,800 rpm (375 mm or 14.75-in. D2) head-capacity curve at 712 m3/hr (3,135 gpm) and 60.1 m (196 ft), indicating the desired point on that characteristic. To obtain 681 m3/hr (3,000 gpm) and 54.9 m (180 ft), the required speed can be determined by calculation of 1,800 (681/712) or by 1,800 (54.9/60.1)°.5, both of which give 1,722 rpm. 100 a:: wa:: I-W 95 WI:::2:W e(:::2: -e( 0a:: ° w...J ...Je( ...Jz 90 wo..S2 :::2: a:: -0 °LL ~o 5~ 85 Oz wa:: 80 ./ / V ./ 75 ~ V / 80 / V / /' / / / " 85 90 95 100 CALCULATED IMPELLER DIAMETER IN % OF ORIGINAL DIAMETER Fig. 18.27 Correction for theoretical impeller diameter reduction. 434 Heads, Conditions of Service Performance Characteristics, and Specific Speed 1,800 RPM 240 14.75 IMPELLER TOTAL HEAD 220 14.00 t:L: 200 ~ 180 w ::c 160 140 0.9 4.75 EFFICIENCY 200 0.8 180 0.7 160 0.6 ::c I a: 140 0.5 ~ 120 0.4 100 0.3 80 0.2 60 0.1 a. w a. 0 10 20 CAPACITY - 100 GPM 30 >zw U U u::: L1. w 40 Fig. 18.28 Effects of change in impeller diameter on pump characteristics. If no speed change was desired, it would have been necessary to change the impeller diameter. The theoretical impeller diameter ratio is the same as the speed ratio, namely 0.957. From Fig. 18.27 the actual ratio would be 0.965, therefore the impeller diameter would have to be reduced to 375 (0.965) or 362 mm (14.25 in). Had the new driver run at 1,760 rpm, the 375 mm (14.75 in) diameter impeller would have given 696 m 3/hr (3,065 gpm) and 57.3 m (188 ft) head requiring, in addition, a cut in the impeller diameter to 369 mm (14.53 in). In all three cases a new curve that would pass through 681 m31 hr (3,000 gpm) at 54.9 m (180 ft) can be plotted by stepping down a number of the 1,800 rpm and 375 mm (14.75 in) diameter impeller points, the capacities being reduced by the ratio of 681n12, while the corresponding heads are reduced by the ratio of (681nI2)2, and for the speed reduction only the corresponding power is reduced by the ratio of (681n12)3. For reduced impeller diameters, noting the point made earlier in this discussion, the corresponding power is reduced by the cube of the actual impeller diameter ratio. Heads. Conditions of Service Performance Characteristics. and Specific Speed 435 CALCULATIONS OF SPEED AND DIAMETER FOR OFF-THE-CURVE CONDITIONS The process just described in detail is essentially the application of the affinity laws. It is a powerful tool for calculating the speed or impeller diameter or a combination of both that a pump must operate with to meet a head and capacity condition that does not correspond to the performance at the speed and diameter for which test data are available. A simplified approach to its use is illustrated in the following example. Let us assume we are dealing with a known pump performance as given on Fig. 18.29 at a speed of 1,800 rpm. We want to determine the speed at which this pump would have to run so as to deliver 454 ml/hr (2,000 gpm) at a total head of 45.7 m (150 ft). The steps required would be as follows: 1. Since the required condition point is below the known pump performance, select an arbitrary capacity greater than the 454 m3jhr (2,000 gpm), such that it will be located on the parabola defined by the affinity laws: Say, for instance, that Q3 = 568 m 3/hr (2,500 gpm), then, H3 = HI (~:)2 = 45.7 (568/454)2 = 71.5 m (234 ft) 2. Draw the portion of the parabola defining the affinity laws between 454 m 3/hr at 45.7 m and 568 m 3/hr, 71.5 m (2,000 gpm at 150 ft and 2,500 gpm, 234 ft). It can be assumed that this is essentially a straight line. 3. The intersection of this straight line with the head-capacity curve of the pump at 1,800 rpm corresponds to 544 m 3/hr and 65.6 m (2,395 gpm and 215 ft). We can now determine the speed required to meet the desired conditions of 454 m3/hr (2,000 gpm) and 45.7 m (150 ft): n2 = 1,800 (45.7/65.6)°.5 = 1,503 rpm 240 /-- H: 150_(~ggg)2 H-Q 1800 RPM 220 : 234A ft. - intersection --" at ft. .' 215 200 , --: 180 :1800-J150 215 :1503 RPM ,, ::I: ~ , 1L2 for 2000 gpm. 150 ft. 160 • 14O~____~~____~~____~~~____~~ o 1000 2000 3000 4000 Capacity in G.P.M Fig. 18.29 Calculation of speed change. 436 Heads, Conditions of Service Performance Characteristics, and Specific Speed Although the ratio of the capacities could also have been used to calculate the speed, it is easier to read the head values accurately and taking the square root of them halves any errors in reading. A similar process is used to determine the impeller diameter required to meet conditions at the same speed and a reduced impeller diameter. In the example just given, assuming that the original impeller was 375 mm (14.75 in), the new impeller would have to be cut down to a ratio of (45.7/65.6)°.5 or 83.3 percent theoretically. Applying the correction indicated in Fig. 18.27, however, we would cut the diameter to 85.5 percent of its original diameter, or 320 mm (12.6 in). Design Constants The designing of centrifugal pumps is not an exact science because of the many interrelated factors whose combined effect cannot be accurately foreseen and thus must be determined experimentally. The development of centrifugal pumps has been largely a result of the accumulation of data on the performance of both specific designs in service and of experimental designs, the result of research and experiences in other hydraulic fields, and the application of this information to the development of new designs. In analyzing data, centrifugal pump designers use various constants, formulas, and relations, two of which are of interest to users of centrifugal pumps: (1) model pump relations and (2) specific speed. Pumps are analyzed and compared basically at their so-called design conditions; that is, at the head and capacity condition at rated speed at which maximum efficiency is obtained. Thus, for the pump whose characteristics are shown in Fig. 18.16, the design conditions would be 336 m3Jhr (1,480 gpm) and 40.2 m (132 ft) total head at 1,760 rpm. MODEL PUMPS A model pump has the design features of a full-size unit on a smaller scale. To meet the requirements of a strict model, all linear dimensions of the model must be in the same proportion as the corresponding dimensions of the full-size pump. The theoretical relationship of the performance of a model pump can be easily visualized by considering two pumps identically proportioned, with one having twice the linear dimensions of the other. The impeller of the smaller pump will be half the diameter of the larger and will, therefore, have to run at twice the rotative speed of the larger for the same peripheral velocity and equal design head. The areas through the waterways of the smaller pump will be one-half squared or one-quarter the areas of the larger pump. Thus, at equal velocities, the capacity of the smaller pump will be one-quarter that of the larger pump. Therefore, it is apparent that for the same design head the interrelationship of exactly similar pumps would be theoretically: f=~=~=~~ Lb where na "'VQb f = the ratio or factor of the two pumps La and Lb = comparable dimensions of the two pumps na and nb = the rotative speeds of the two pumps Qa and Qb =the capacities of the two pumps at comparable points on their characteristic curves. From dimensional analysis the general equations for the performance of model pumps are: Qb = Q af3(Ilt,/n.,) Hb = Haf2(nb/na)2 Heads, Conditions of Service Performance Characteristics, and Specific Speed 437 The preceding equations are based on the assumption that the two pumps are proportional in every way and that the same relative degree of smoothness is obtained in the two pumps. This is difficult to attain, as the actual smoothness of castings is approximately the same, regardless of size. Thus, the relative internal smoothness of a larger pump is greater than that of a smaller pump. This is reflected in the head losses in the pump waterways; the larger pump should produce a higher head than the smaller pump for points of similar capacity. Inasmuch as part of the liquid pumped leaks through the wearing rings, this loss may not be in exact proportion in both sizes of pumps, thus affecting the net quantity delivered. Part of the power input goes into mechanical losses (bearings and stuffing boxes), that are roughly but not exactly proportional to the pump sizes, resulting in a third discrepancy. Good mechanical design (especially in the production of a commercial line of pumps) precludes making the shaft, casing thickness, or thickness of impeller vanes of two pumps in exact proportion to their size factor. A comparison of the largest and smallest pumps of a closely homologous line of a commercial design, therefore, will show some difference in performance. The magnitude of this difference will depend upon the size factor and the actual physical sizes of the two pumps. Centrifugal pump designers are careful, when making model pumps, to use a size that will be close enough to the full-size pump so that the results of the model will permit a reasonably close prediction of the performance of the full-size pump. Model pumps have been used to prove within a reasonable degree of accuracy the performance of the full-size unit for almost every case involving special large-capacity pumps. SPECIFIC SPEED An analysis of the performance of a projected centrifugal pump would be difficult without the progress achieved in the science of hydrodynamics in the four centuries of its existence. This progress may be directly credited to the almost universal application of model study, which precludes the necessity of experimenting upon full size commercial constructions that are too expensive and least convenient for securing the necessary information. Sir Isaac Newton evolved the theory of dynamical similarity, in 1687, thereby introducing the mathematical background for model investigations. The application of the Newtonian principle of dynamical similarity has since given rise to the wide use of models in hydraulic machinery, as well as in other fields of science, and to an extensive knowledge of the relative performance of models and prototypes. One such application of the principle of model and prototype relationship has enabled engineers to predict the performance of centrifugal pumps on the basis of the behavior of other machines, smaller or larger in size, operating over a wide range of design conditions, but modeled from and similar to each other. The principle of dynamical similarity expresses the fact that two pumps geometrically similar to each other will have similar performance characteristics. In order to afford some basis of comparison among various types of centrifugal machines, it became necessary to evolve a concept which would link the three main factors of these performance characteristics-capacity, head, and rotative speed-into a single term. The term "specific speed" is such a concept. The mathematical analysis used to establish the relationship between the specific speed of a pump and its operating characteristics does not enter the scope of this book. In its basic form, the specific speed is a non-dimensional index number which is numerically equal to the rotative speed at which an exact theoretical model centrifugal machine would have to operate in order to deliver one unit of capacity against one unit of total head. It is mathematically expressed as: -~ Ns - (gH)"3t'4 438 Heads, Conditions of Service Performance Characteristics, and Specific Speed in which: N, = specific speed n = rotative speed Q = capacity H = head (head per stage for a multistage pump) g = gravitational constant, 9.81 m/s2 (32.2 ft/S2) at sea level. In order for this relation to remain dimensionless, when using English units, the rotative speed would have to be expressed in revolutions per second, the capacity in cubic feet per second and the head in foot-pounds per pound or foot. However, since specific speed is used only as an index or type number, certain liberties are permissible in selecting the units used. Thus, the gravitational constant, g, is dropped out of the relation, leaving: The rotative speed is expressed in revolutions per minute. For some time, two units of capacity, gallons per minute and cubic feet per second, were used in the United States to determine specific speed, but the gallons per minute basis has been accepted as standard by the Hydraulic Institute and is now the approved basis. The unit of head is one foot. In countries using the metric system, specific speed is today designated nq and the usual unit for flow in pump design is cubic meters per hour (m3Jhr). The unit for head is one meter (m). The mathematical relationship between values calculated in the two systems of units is The formula for the specific speed of a pump remains unchanged whether a single- or a doublesuction impeller is used. It is customary, therefore, when listing a definite value of specific speed, to mention what type of impeller is in question. Type Specific Speed The type specific speed, by definition, is that operating specific speed that gives the maximum efficiency for a particular pump and is the number that identifies the pump type. It should be noted that this index number is independent of the rotative speed at which the pump is operated, since any change in speed carries with it a change in capacity in a direct proportion and a change in head varying as the square of the speed. The normal range in specific speeds encountered in single-suction impeller designs is from 500 to 15,000. Basically, the lower the specific speed type, the higher the head per stage that can be developed by the pump. Normally, the conditions of service for which a pump is sold are relatively close to the maximum efficiency point, and the specific speed determined from the conditions of service will be a close indication of the pump type. For example, the true type specific speed of the pump whose characteristics are illustrated in Fig. 18.16 is 1,740. This pump would normally be applied for a range of conditions between 295 m3Jhr and 42.7 m (1,300-gpm and l40-ft) total head and 363 m3Jhr and 38.1 m (1,600-gpm and 125-ft) total head. Significance of Type Specific Speed One of the most important applications of the specific speed concept is the fact that all sizes of pumps can be indexed by the rotative speed of their unit capacity-unit head model. Thus, the specific speed Heads, Conditions of Service Performance Characteristics, and Specific Speed 439 concept can be used in such a manner that for homologous designs, the performance of any impeller of the series can be predicted from the knowledge of the performance of any other impeller of the series. Because the physical characteristics and the general outline of impeller profiles are intimately connected to their respective type specific speeds, the value of the latter will immediately describe the approximate impeller shape in question. As an illustration of this statement, Fig. 18.30 represents a few typical impeller outlines tied down to their type specific speeds. The specific speed of a given pump will also definitely be reflected in the shape of the pump characteristic curves, and, whereas some variations in the shape of these curves can be obtained by changes in the design of the impeller and casing waterways, the variation that can be obtained without adversely affecting the pump efficiency is relatively small. Approximate type characteristics for four single-suction impeller types are shown in Figs. 18.31 to 18.34. Figure 18.35 shows the variation of head with the specific speed for shutoff, 25, 50, 75, and 110 percent capacity. Figure 18.36 shows the variation of power with specific speed for the same capacities, while Fig. 18.37 shows the variation of efficiency with specific speed for these same capacities. The values shown in Figs. 18.31 to 18.37 are for more or less normal impeller-casing designs and combinations. Variations in the shape of the curve will be found, depending on the individual design of the pump. The variation in the shape of the type characteristics between a single-suction impeller with shaft through the eye and an overhung single-suction impeller is small, therefore Figs. 18.31-18.37 can be applied to either type. Historical practice for double suction impellers was to design them as two halfcapacity single-suction impellers back-to-back, and so they had a type characteristic approximating that of a single-suction impeller having a specific speed 70.7 percent or l/-{2 of that of a double-suction impeller. Modern practice is to design double-suction impellers for the full capacity, changing only the inlet portion to reflect the different suction arrangement. These designs therefore have efficiency and type characteristics similar to that of single-suction impellers of the same specific speed. Figure 18.30 also indicates the maximum range of efficiencies obtainable from pumps of different specific speeds. Low specific-speed impellers have a lower maximum efficiency than medium-specific-speed impellers because the former have considerably more disk area for a given set of operating conditions and, therefore, a greater loss in disk horsepower. The curve of efficiencies in Fig. 18.30 was compiled from data assembled in the late 1940s. More recent experience gives somewhat different and improved efficiencies, particularly in the range of lower specific speeds. In addition, the curves in Fig. 18.30 do not take into consideration a number of variables, all of which affect the efficiency of a pump to a significant degree. The latest available data on today's commercially attainable efficiencies are provided in two papers published in 1986 and 1987 [18.1, 18.2]. The data published in these two papers are based on certain constraints on the following variables: 1. Single-stage pumps only 2. Finish and dimensional fidelity are comparable to precision cast impellers with a I-percent plus or minus tolerance on all dimensions of the vanes and hydraulic passages. 3. A relative roughness of all hydraulic waterways of the impeller and casing be 0.000020 or better. 4. Standard commercial diametrical clearances of all wearing rings-that is, approximately 0.0015 of the ring diameter. 5. A suction specific speed (see Chap. 19) not exceeding 8,500 for single-suction overhung impellers or 7,500 for single-suction shaft-through-eye or double suction impellers. This corresponds to incipient suction recirculation at about 55 percent of best efficiency point (BEP) for pumps of Ns 500-2,500, rising to about 70 percent for pumps of Ns 2,500-10,000. See Chap. 22 for a method of estimating the incipient suction recirculation capacity. 440 Heads. Conditions of Service Performance Characteristics. and Specific Speed §. 8 II') 0 § ~ ~ 8 ~ ... ~ I \()A ~l9- ~~ r-f!~~ ~ (;\'~ 8 7 )- t ~, / V ~ / ,1G; c..\'+ ...-Vo ~+ ~~~,O -- r-- 00 i ~ ---- --G in;::;.- -- :0: ~ 90 50 ~ a- -- I:':-~ r<' ~ PAl ~~ iP..- 90 80 70 60 ~i;; 50 J § St J 0 0 ~ it 0 0 40 ~ CENTER OF ROTATION Fig. 18.30 Approximate relative impeller shapes and efficiency variations with specific speed. Heads. Conditions of Service Performance Characteristics. and Specific Speed 130 120 >- 100 u.. w 90 Li: ::e :::> ::e x « ::e HEA D-CA PAC I Y 110 u z w u >f- U « a. « u u.. 0 f- z w u a:: w V E FICIENCY V 80 70 f- « 60 50 40 30 /' 20 / a. 10 0 --- .....- V' -V" ........... ~ /J f ) I/:V / I" ./ V ./ / /" """"" BHP V / I V o 10 20 30 40 50 60 70 80 90 100 110 120 PER CENT OF HEAD,EFFICIENCY, AND POWER AT MAXIMUM EFFICIENCY Fig. 18.31 Type characteristics for N, = 600 single-suction impeller. 441 442 Heads. Conditions of Service Performance Characteristics. and Specific Speed 130 120 HEAD-CAPACITY 110 Q ~ 100 ~~ ,.:Z 90 u'" zu "'- Lt.. ULt.. 80 ti ~ 70 G:'" 02 cc'" ~ ::r 2 60 EFFICIENCY / ~ ~ ~ 50 ~~J za: i u.152 ~ '" '" 40 ~ 30 i i / V Ii oV o 20 ~ ~V --... ~ V t::::: ~ .......... ~ V ~V " po. r--. 8HP r' V II 10 T i I 10 20 30 40 50 60 70 80 90 100 110 PER CENT OF CAPACITY AT MAXIMUM EFFICIENCY Fig. 18.32 Type characteristics for N, = 1,550 single-suction impeller. 120 Heads, Conditions of Service Performance Characteristics, and Specific Speed 160 u> z 150 w 140 LA. LA. 130 2 :;) 2 120 U UJ X ~ r-- r-- r---... """""" ............ ~ 110 2 .~ II: LIJ ~ 0 n, 0 z~ ~ u z w U Li: 100 90 60 ~ 40 0 LIJ - 70 50 I % ""0 .-z LIJ 0 cr: LIJ Il. 30 20 10 '" BHPr 80 LA. LIJ HEAD-CAPACITY / I J V V Y ~ "'- ./ ~ ~ -",- .. K [\ EFFICIENCY i ! I( j:t 1/ 10 20 30 40 50 60 70 80 90 100 110 PER CENT OF CAPACITY ATMAXIMUM EFFICIENCY Fig. 18.33 Type characteristics for N, =4,000 single-suction impeller. 120 443 444 Heads, Conditions of Service Peiformance Characteristics, and Specific Speed 300 280 >u 260 z 240 w U ~ ~ w ~ 220 " '" ~ "- 200 ~ ;:) !)( 1\\ 180 ~ c( ... ~ ~ 0 Q. 0 Z C( '\~ V"'" "" ~ " ~/ ~ f' / "" w :r l&.. ...z 0 w a: 160 ~ 140 ) 120 100 80 / 60 u 40 l&.I 20 Q. 100 / 0 C( -. i"- 90 FFICIENCY C( a: w HEAD-CAPACI T Y t1 V 10 j 1/ ~ V 80 ~ r---..... B~ .......... p 70 ~ 60 r----. ~. 50 ~~ t\ 40 30 1/ >- u z l&.I U ~ ~ l&.I ~ ;:) ~ X c ~ ~ ...z 0 l&.I U 20 « ~ 10 20 30 40 50 60 70 80 90 100 li D 120 PER CENT OF CAPACITY AT MAXIMUM EFFICIENCY Fig. 18.34 Type characteristics for N, = 10,000 single-suction impeller. o 445 Heads, Conditions of Service Performance Characteristics, and Specific Speed - 300 . 300 .J. / 2~O >- u z w U IL. IL. W j I 20 0 ! 25 PER CENT CAPACITY ~ I ::> :E b( ! I )( 150 ~ « 14 0 a « 13 0 J: Lo- 12 :E w o z w ~ u V/ I i - ... 10 0 lL..l IL J/ - I i . I) o • 0 0 ... 0 0 ID 0 o 2- ./ V- ~ ./ 150 I , :/ 140 L 130 0 o ~ ~ • 120 I 110 j 100 - 110 PER CENT CAPACITY .....-.,1 ! 80 - V ~ ~ ~. j .-A" ~ ~ ~ io"""" -----75 PER CENT CAPACI!) 0 7 ./ if 200 II' LL 50 PER CENT CAPACITYL a: w / / .l L . / II 0 Il. / I ~ V --, 1/ SHUTOFF I « 250 I I) I) o ~- 0 o ~ 0 2- i 90 r--- r-...... o~ .0 ~ TO i SPECIFIC SPEED, SINGLE-SUCTION TYPE Fig. 18.35 Variation in head values at shutoff, 25, 50, 75, and 110 percent capacity with specific speed. 446 Heads, Conditions of Service Performance Characteristics, and Specific Speed '00 :5 00 100 ~ ~ ./ l/~ L.:~ ~ !<.,o ,;.:~v~ t-~ H so IS 0 ./ , • ,• 110 PER CENT CAPACITY - .... - .- -- ~ ._.- - - 10- 50 PER CENT CAPACITY 10 .. ,. ~to.P\t!,..... .1 1.' pI 0 RCE'L-- .... 1ft .8 .....::: , ..... ....... V ...... ~ ~ i""'" ~ ~ - I 00 10 70 ~ L •.oo ""7 I ~\' 1/ ~-J"O/ " 0 ~ f- ~5, ~ ¥-ENT CAPA,cITY 10 0 I - - , I 00 .o .,~ !,...-o i--'" ~ t- I .. 8o 0 8 0 :o ~ 8 • til . 8o ." :5 o , 0 o • SPECIFIC SPEED, SINGLE -SUCTION TYPES Fig. 18.36 Variation in power values at shutoff, 25, 50, 75, and 110 percent capacity with specific speed. /11 o PER CENT CAPACITY 10 0 • 100 I 0 to 75 PER CENT CAPACI TV I 0 -r- - 50 PER CENT CAPACITY 10 1'--0. 10 0 ""-- .. 0 - - l"- t-- .. •o g • o o 9- o ;. 0 SPECIFlC SPEED, SINGLE - SUCTION Fig. 18.37 TO 10 SO IS PER CENT CiPAclTv 0 I 10 0 t-- ...... 0 )'-. o o ~ ~ o o o :50 10 2 TYPE Variation in efficiency values at shutoff, 25, 50, 75, and 110 percent capacity with specific speed. Heads. Conditions of Service Performance Characteristics. and Specific Speed 447 6. For single stage pumps with a shaft through the eye, the shaft-to-eye diameter ratio is sufficiently low to preclude blockage in the fluid passages of the impeller inlet. 7. The discharge recirculation value is not less than nor more than 80 to 90 percent of the maximum efficiency capacity. 8. A uniform velocity profile of the fluid entering the impeller inlet. This requires an evaluation of the piping or channel flow at the pump inlet to assure that a uniform velocity profile is achieved at the rated flow conditions. 9. Pumped liquid is clear water at 66°C (l50°F) or less. 10. Efficiencies for maximum impeller diameters. Cutdown impellers usually result in a two to three point loss in efficiency. 11. Wet-pit pump efficiencies are based on impellers with no back wearing rings or balancing holes. The results of analyzing the perfonnance of pumps meeting these constraints are shown in Fig. 18.38 for single- and double-suction pumps and in Fig. 18.39 for wet-pit pumps. To use these curves requires some measure of the pump speed. The curve shown in Fig. 18.40 relates speed to capacity, and is based on a n-/Q parameter of approximately 115,000, where n is the rotative speed in rpm and Q is the rated capacity in gpm. In practice, first enter Fig. 18.40 with the maximum efficiency capacity of the pump in question and then read off the standard speed from the ordinate. The capacity of the pump is then corrected by the ratio of the speeds. Next enter Fig. 18.38 or Fig. 18.39, depending on the type of pump, with this capacity and the specific speed detennined from the original pump rating. As an example, consider the following conditions of service for a single stage single suction pump. 1,100 gpm 225 ft. thd 1.750 rpm 1,000 Ns Enter Fig. 18.40 for speed correction. The corrected speed is 3,450 rpm then 3,450 1,750 x 1,100 gpm = 2,200 gpm Enter Fig. 18.38 with I,OOONs and 2,200 gpm to detennine the efficiency as equal to 81.9 percent. The second paper referred to above provided correction factors to be applied to the efficiencies given in Figs. 18.38 and 18.39 when deviations occur from the constraints established for the basic efficiencies: 1. The effect of changing hydraulic surface roughness from 0.000002 per inch of impeller diameter to 0.00001 per inch of impeller diameter is shown in Fig. 18.41. 2. The effect of increasing or decreasing ring clearances from the stated value of 0.0015 ratio of ring clearance to ring diameter is shown in Fig. 18.42. 3. The loss of efficiency associated with an increase in the Suction Specific Speed over the 8,500 and 7,500 values chosen as the basic constraint is shown in Fig. 18.43 for an impeller without a shaft through the eye and in Fig. 18.44 for an impeller with a shaft through the eye and a shaft to impeller diameter ratio of 0.2. 4. Finally, the effect of discharge recirculation values on pump efficiency is illustrated on Fig. 18.45. 448 Heads, Conditions of Service Performance Characteristics, and Specific Speed 96 94 -"~ 92 90 88 86 84 82 ~ 0 z 80 78 76 >- 74 (3 70 ~ 68 () zw u:: w 72 66 64 62 ~ ~ ~ """' " ~ ~ i"""" ~~ ~ ~ ~ ~~ V-'" ~ W 1/ V/ i-""" fHv I.; V L ~ ~ ~rl II 1.1 V-" V-" ~ r/) 'I II //V V )) .... ~ V / If)r/ ~I ' / rr; I{j ~V, Vl V. V J f/j Vj rJ.V '/ 60 58 56 54 52 -- V 1/ V / ~ V 500,000 GPM ~~~ g :888 10,000 GPM 1r'000 5,000 GPM 2,500GPM 1,000 GPM 750 GPM 500 GPM 400 GPM 300 GPM ,..... 200 GPM 100 GPM ~ V j V 50 48 46 500 1,000 2,000 3,000 5,000 10,000 VALUES OF SPECIFIC SPEED Ns = RPM~ H% Fig. 18.38 Efficiency of single stage end suction and double suction centrifugal pumps. Heads, Conditions of Service Performance Characteristics, and Specific Speed ;:.!! 0 z >- <.) z w C3 u::: LL w 96 94 92 90 88 86 84 82 80 78 76 74 72 70 68 66 64 62 60 58 56 54 52 50 48 46 - I 00,000 40,000 20,000 10,000 1,000 GPM i'" t--"", r- t- t--"", - l- I"'" t--,... - 500GPM 400GPM 300GPM r- ~ -~ ~ 1,000 GPM GPM GPM GPM 5,000GPM - 500 449 t--.... 2,000 3,000 5,000 VALUES OF SPECIFIC SPEED Ns= RPM..JGPM H% Fig. 18.39 Bowl efficiency of wet-pit centrifugal pumps. 10,000 200GPM 100GPM § 1 1 100 100 1.5 2 3 2.5 4 5 1,000 9 8 7 6 RPM 1.5 2 3 2.5 9 8 7 6 5 4 10,000 1.5 1.5 2 2.53 2 2.53 4 4 2 2.5 3 ~ ........ ............. 1.5 FLOW-GPM 5 6 7 891 1.5 10,000 ....... 5 6 7 891 ......... ~ 4 ........ 4 Fig. 18.40 Chart for speed correction. 1.5 ....... 2 2.5 3 "" 1.5 ............. 5 6 7891 1,000 5 6 7891 ro...... 2 2.5 3 ="'" ....... 2 2.5 3 4 ~ 2 2.5 3 ........ ...... 2 2.5 3 ........... ~ 1.5 5 6 7 891 1.5 100,000 r--.... 5 6 7 891 r..... 4 5 6 789 1 1.5 2 3 2.5 4 5 1,000 9 8 7 6 RPM 1.5 2 3 2.5 10,000 9 8 7 6 5 4 100 4567891 1,000,000 ......... 4 Heads, Conditions of Service Performance Characteristics, and Specific Speed CJ) 10 9 8 7 I- 6 0a.. 5 z I 4 0 3 >z w u::: u. w \. i\. 2 Z w CJ) «w a: 0 w Cl , ~ 0 1 .9 .8 .7 \ ", \ "- ", .6 .5 .4 451 500 1,000 2,000 3,000 5,000 VALUES OF SPECIFIC SPEED Ns = RPM~ H% Fig. 18.41 Loss of pump efficiency with specific speed for change in relative roughness of waterway surfaces. Relative roughness increased from 0.000002 to 0.00001 per mm (in) of impeller diameter. We repeat that the charts on Figs. 18.38 through 18.45 reflect results obtainable with modern pumps. For the efficiency obtainable from older pumps, it is more prudent to use values from Fig. 18.30. Approximating Specific Speed Type From Impeller Outline Prior to the general adoption of specific speed as a type indicator, the ratio of outside diameter (D 2) to suction eye diameter (D,) or the reciprocal of this relationship, was generally used for that purpose (Fig. 18.46). An approximate relation of the DJD, ratio to N, for single-suction impellers is shown in Fig. 18.47. These values are necessarily approximate, as a true curve would be a fairly wide band. One reason for this can easily be seen if one considers an impeller for a given set of conditions. The velocity of the liquid would have to be approximately the same whether the impeller had no hub or a hub extending into the eye. Thus an impeller with a hub extending into the eye would necessarily have a larger D, for the same capacity and head or the same D 2• Multistage pumps require a large shaft because of the power involved, so that the impellers of such pumps would have relatively large hubs. The impeller would have an abnormally large D, or a smaller DJD, ratio than normal for its specific speed type. This method of identifying the specific speed fails for axial-flow impellers. Axial-flow impellers fall into a 9,000 to 20,000 specific-speed range. Their output and, therefore, their specific speed depends on 452 Heads, Conditions of Service Performance Characteristics, and Specific Speed -10 en en 0 ....J -5 =__ ~ z 0a.. =, 2 X STD. CL. _1.5 0 x STD. CL. STD. CLEARANCE 0.0015 IN/IN 0.5 STD. CL. ~ 5 z <C CJ 10 1,000 2,000 3,000 4,000 SPECIFIC SPEED Fig. 18.42 Variation in pump efficiency with specific speed for various running clearances. the angle and length of the vanes as well as the number of vanes. To predict the characteristics of axialflow impellers, a designer would require very detailed information on the impeller and other pump parts. No simplified guide can be offered for general use for this type of pump. HEAD AND CAPACITY CONSTANTS Two design constants can be used to approximate the performance of a centrifugal pump. One expresses the relation between the impeller peripheral speed and the total head. The second relates the radial discharge velocity from the impeller (and, therefore, the capacity) and the total head. The formulas for these constants are: U2 cp = ...j2gH and: in which: U2 = peripheral velocity, in mls (ft/s) g = gravitational constant 9.81 mls2 (32.2 ft/s2) Heads, Conditions of Service Performance Characteristics, and Specific Speed 12,000 0 w W DC/) 0 11,000 u::: C3 W D- C/) z 0 10,000 t= -3 POINTS 0 :::> C/) u... 0 9,000 -2.5 POINTS C/) w :::> ....J ~ 8,000 7,OOO...L----.,-------.---------r------1,000 2,000 3,000 VALUES OF SPECIFIC SPEED Fig. 18.43 Loss of pump efficiency with specific speed for various suction specific speeds, hdD2 = O. Cm2 = radial discharge velocity, in mls (ft/s) H = total head (per stage), in m (ft). These relationships can be converted into terms of impeller dimensions that can be measured: and QxlO" Q. . . m2 = 3,600Az = 0.36A2 m metnc UnIts C C m2 144Q Q. = 7.48 x 60 x A z = 3.117Az m us . UnIts where Dz =outside diameter of impeller, in mm (in) n = speed, in revolutions per minute Q = capacity, in m3/hr (gpm) A z = circumferential discharge area of impeller, cm 2 (in2) (Fig. 18.46) 453 454 Heads. Conditions of Service Performance Characteristics. and Specific Speed 12,000 o I±l 0- en (,) u::: C3 ~ en 11,000 10,000 z o i= (,) ~ u.. 9,000 o en -3 POINTS w =:l ...J ~ -2.5 POINTS 8,000 -2 POINTS -1 POINT 7,000 6,000...L..----r--------r----------,---1,000 2,000 3,000 VALUES OF SPECIFIC SPEED Fig. 18.44 Loss of pump efficiency with specific speed for various suction specific speeds, hdD2 = 0.2. (In high-speed Francis vanes, mixed-flow, and axial-flow impellers, the effective discharge diameter is not D2 but a geometric mean: ""D~ + h'Y2. When there is little difference between D2 and h2' an arithmetical mean is commonly used. However, for simplicity, constants presented here are calculated on the basis of D 2 , not the effective diameter that most designers would use in calculating their constants.) The equations for the design constants can now be replaced by '" 'f' = 19.1 D2n D2n.. 4> = D 2n = D 2n in US units 229 ....j2gH 1,840 -{ii and K cr . x 1()3 (2gH)0.5 = 84.6 x 1()3 (H)0.5 m metnc umts =0.36A Ker = QQ... (2gH)0.5 = 1.60A2 (H)0.5 m metric umts 2 Q = Q in US units 3.117A2 ....j2gH 25A 2 -{ii Heads, Conditions of Service Performance Characteristics, and Specific Speed 455 10 9 8 7 6 5 4 3 2 en I- z 6 Il.. W (!) z « I DISCH REC = 1.1 BEP CAPACITY DISCH REC = 1.0 BEP CAPACITY 0 0 -1 zw -2 (5 -3 u:: u. w -4 -5 -6 >- DISCH REC = 0.7 BEP CAPACITY 0 DISCH REC = 0.7 BEP CAPACITY -7 -8 -9 -10 500 1,000 2,000 3,000 4,000 SPECIFIC SPEED Fig. 18.45 Variation in pump efficiency with specific speed for various ratios of discharge recirculation to design capacity. RADIAL TYPE MIXED-FLOW TYPE AXIAL-FLOW TYPE AXIS OF ROTATION r';I>. -Z2~ A,o •• Fig. 18.46 Dimensional symbols for impellers and formula for determining discharge area A2• These equations can be further transformed to give head and capacity values directly: H D2n 103<\1 = ( 84.6 X )2. III . . metrIc umts D2n)2. US . H = ( 1,840<\1 III umts 456 Heads, Conditions of Service Performance Characteristics, and Specific Speed SPECIFIC SPEED DOUBLE - SUCTION TYPES -I I 8 7 6 5 o..... ~ ~ *-<1,./ 3 ........ ...... D. -::-.....' r~ V Q O•II o.7 ..... V -L o a ... -- 1/ ./' ..... ..... / .- ~ / / 0.:5 0.4 ./ 0.2 0.15 I": ~ 'u" ~ L4. 0 &/ V (f) 3 ~ ........ ~ o g2· 0.6 0.3 .....~/O 2 1.0 / / / / 0.8 0.7 § g ~ SPECFIC SPEED SINGLE-SUCTION TYPES Fig. 18.47 Variation with specific speed of DJDI ratio, <I> 0.10 0.09 0.08 0.01 and Kcr constants. and Q = 1.60Ka AzeH)o.5 in metric units Q = 25Kcr AzeH)05 in US units Both <I> and Kcr vary with the specific speed type and, to some extent, with the individual impeller and casing design. They are also affected by the physical size of the pump. Figure 18.47 shows a <I>-N, relation and a Kcr-N, relation that are representative for normal pump design. Like the DJDJ-N, curve, these curves show average values; the true values for an individual design will vary somewhat from those shown. Approximating Characteristics From Physical Measurements Generally, a centrifugal pump user who wishes to determine the performance characteristics of a given pump in his possession has a large reservoir of information from which these data can be determined: Heads, Conditions of Service Performance Characteristics, and Specific Speed 1. 2. 3. 457 A copy of the order on which the pump was purchased. The nameplate of the pump. This nameplate generally carries the pump shop serial number, the manufacturer's type designation, and the rated conditions of service, including the operating speed. The pump driver nameplate. If this nameplate is missing, a direct measurement on the driver will give the operating speed. If the pump make and serial number are known, it is a simple matter to get the desired information from the manufacturer. If the make, but not the serial or other identifying number or letter is known, most manufacturers can identify the pump type and impeller design, if given the following: (1) the nozzle sizes, (2) a sketch showing the external appearance and dimensions of the pump, and (3) the major impeller dimensions. It is seldom that a pump is without both pump and driver nameplates and that no record of the purchase is available, leaving the physical presence of the pump itself as the only thing certain. But even in this case it is possible to carry out certain measurements and calculations to obtain the desired information with some degree of accuracy. Two separate phases exist in the problem of estimating the performance of a centrifugal pump when nothing is known except the physical dimensions and proportions. The first phase of the problem is the theoretical aspect, which gives a reasonable approximation of the pump head-capacity curve at any given operating speed and the expected power consumption of the pump. This phase requires the application of the data presented on the preceding pages and in Fig. 18.31-18.37 and 18.46-48 for its solution. The second phase of the problem concerns the practical aspects of the application of the pump to a particular service. Is the physical design of the pump suitable for the power and the speed selected? Is the casing design suitable for the operating pressure? Will the pump operate satisfactorily under the suction conditions contemplated? MAXIMUM SPEED LIMITATION Present-day practice in the United States places a limit on pump speed by limiting the suction specific speed for a given class of service and pump (see Chap. 19). A much earlier approach was to determine the maximum rotative speed of an impeller by limiting the peripheral velocity of its suction eye (D 1) to a certain value, depending on the suction conditions. This velocity can be established exactly, as in the case of the peripheral velocity of the outside impeller diameter: · I' SuctlOn eye ve OClty . . = 19.1Din. X 10310 metnc umts · eye ve Ioelty ' = Din. . SuctlOn 229 10 US umts A reasonable maximum peripheral velocity for the suction eye is shown in Fig. 18.48 for various suction conditions. EXPECTED POWER CONSUMPTION Determining the possible head and capacity of a pump would be of little value if the power required to drive the pump could not be predicted. Data on the preceeding pages show the approximate maximum efficiency for both single- and double-suction pumps that can be obtained with present-day designs. 458 Heads, Conditions of Service Performance Characteristics, and Specific Speed FEET OF SUCTION HEAD AT SEA LEVEL AND 85- F -I' -20 10 o -5 .10 ., 10 ~ 00 >Z .... 0 _u uw 0(1) ...1« .... 10 " 1£11£1 >CL ...I .... C(w «1£1 50 W~ I Z CL_ ii . wllJ CL> IIJ ~Z 40 ./ =>0 " V V 10' ....... ...... ~ .JI ~- -~ Xu C(::> ~(I) 50 I' 10 10 10 I' 40 NET POSITIVE SUCTION HEAD. IN FEET Fig. 18.48 Approximate limit for peripheral velocity of suction eye and required NPSH. How close an existing pump would approach these values would depend on the individual pump. Multistage pumps, with abrupt crossover passages from one stage to the next, should be expected to be less efficient by two to three percentage points. DETERMINATION OF SAFE POWER INPUT The shaft of a centrifugal pump is subject to both bending and torsional stresses. Usually, its smallest diameter is at the coupling and this section is subjected primarily to torsional stress only. Generally, centrifugal pump shafts are designed not to exceed a torsional stress at the coupling of 48 MPa (7,000 psi) for safe maximum continuous loading. Therefore, in predicting pump performance, a check should be made to see if the maximum expected power at the selected speed keeps the torsional stress within the recommended 48 MPa (7,000-psi) limit. If not, the pump is not mechanically safe for operation at the selected speed. The relation between transmitted horsepower, speed, shaft diameter, and permissible torsional stress is given by the formula kW SntP. . . H)6 m metric uruts = 48.6 x h p SntP. US = 321,000 m . uruts Heads. Conditions of Service Performance Characteristics. and Specific Speed where kW hp S n d 459 = power in kilowatts = horsepower = allowable stress, MPa (psi) = rotative speed, rpm =shaft diameter at coupling, mm (in) DETERMINATION OF SAFE OPERATING PRESSURE Detennination of the safe operating pressure of a given pump requires a very detailed study. Some idea of a possible maximum can be obtained by examining the size and drilling of the discharge nozzle flange. This is an indefinite limit, especially in the United States where the "125-lb flange," which is good up to 175-psi hydraulic operating pressure, is generally used for all pressures below that value. Many pump designs using such flanges, however, are not good for operating pressures that high. It is more satisfactory to make a check of safe pressures at the bolting of the casing or casing heads. In actual design studies, maximum safe bolt stresses are calculated with full knowledge of the areas subjected to internal pressures, of the maximum expected hydraulic pressure, and of the forces required to compress joint gaskets. A good approximation can be obtained by limiting the bolting stress at the root of the threads to 35 MPa (5,000 psi); thus, safe working pressure can be computed as follows: swp = A,nb 35 x 10 1 A swp = where swp A, nb A • ill A,nb 5,000. US A ill • • metnc umts . umts = safe working pressure, bar (psig) = root area of bolt, cm2 (in2) = number of bolts = area subjected to hydraulic pressure, cm2 (in2). For purposes of analysis, assume a 20-year-old double-suction, single-stage centrifugal pump with an 8-in. discharge and lO-in. suction, both with 125-lb flanges. Various relevant dimensions (see Fig. 18.46) are given below for the impeller: D2 = 311 mm (12.25 in) DI = 156 mrn (6.12 in) W2 = 52.5 mm (2.06 in) Z2 = 7 S2 = 10 mm (0.38 in) The shaft diameter is 39.6 mm (1.56 in) at the coupling, increasing to a maximum at the impeller. The area of the horizontal split is 1290 cm2 (200 in2). The pump casing is held together by 21 qty 19 mm (0.75 in) studs and bolts. The intended drive is a 60-cycle induction motor. DJDI = 311/156 = 2.0 Referring to Fig. 18.47, a DJD I ratio of 2.0 indicates an impeller type with specific speed Ns if single suction or Ns = 2,400 if double suction. The head and capacity constants are = 1,700 Heads, Conditions of Service Performance Characteristics, and Specific Speed "'=1.06 Kcr = 0.13 Assuming that the pump will be applied to an installation involving a 4.6 m (I5-ft) suction lift at sea level, handling cold water, the NPSH will be, roughly, 5.2 m (17 ft). From Fig. 18.48, it can be established that the maximum safe peripheral velocity at the impeller suction eye is about 15.2 rn/s (50 ft/s). Solving for the rotative speed gives: n = 15.2 x (19.1 x 1()3) = 1 860 156 ' rpm n= 50 x 229 6.125 = 1,860 rpm Therefore, 1,750 rpm will be the maximum possible rotative speed with a 60-cycle motor. The pump head can now be calculated at 1,750 rpm: 311 (1750) ]2 H = [ 84.6 x 1()3(1.06) = 36.8 m H = (12.25 X 1,750)2 = 121 ft 1,840 x 1.06 Using the formula in Fig. 18.46, A 2, the discharge area of the impeller, can be calculated: - (7)10] _ 476 2 A 2-- 52.5 [1t(311) 102 cm = 2.06[1t(12.25) - (7)0.38] = 74.0 in2 The pump capacity is estimated: Q = 1.60(0.13)476(36.8)°·5 = 600 m 3Jhr = 25 (0.13)742(121)°·5 = 2,645 gpm When operated at 1,750 rpm, this pump will deliver 600 m 3/hr (2,645 gpm) against a total head of 36.8 m (121 ft) at its best efficiency point. Its specific speed can be recalculated: N. = 1,750(600)°.5/(36.8)°·75 = 2,865/1.16 = 2,470 (double suction) = 1,750(2,645)°·5/(121)°·75 = 2,470 For an older pump, Fig. 18.30 shows that, for this specific speed and capacity, the maximum efficiency would be somewhat over 85 percent. If 85 percent is used, the power consumption would be power = 600(36.8)1.0/368(0.85) = 71 kW = 2,645(121)1.0/3,960(0.85) = 95 bp Working from these values of capacity, head, efficiency, and horsepower, and using the percentages in Figs. 18.35 to 18.37 (for a single-suction N. of 2,470 x 0.707 = 1,746), the points in Table 18.4 can be obtained. Plotting these points, the approximate curve shown in Fig. 18.49 is obtained. (The actual test curve of the pump has been superimposed on the same graph for comparison.) 461 Heads, Conditions o f Service Performance Characteristics, and Specific Speed Table 18.4 Characteristics Predicted From Impeller Measurements Capacity Head Power Percent 0 25 50 75 100 110 mlfhr gpm Percent m ft Percent kW bhp 0 150 300 450 600 660 0 661 1,322 1,987 2,645 2,915 117 43.0 142 115 110 100 93 42.3 40.5 36.8 34.2 139 133 121 112 54 63 75 88 100 103 38 45 53 62 71 73 51 60 71 84 95 98 0 46 76 94 100 99 150 ~ w 140 w ... --- -- -- -...;; ~ ~ Q c w 1 20 I '"........ .... ,.............. i'-... I- 1 10 0 I100 [fI1'1C1!NCY eo ,. ,. 10 /'" '" ,/ .0 .., / / II: 40 ~ 30 > U e: III 20 10 0 / ,... I o /; / _.... ,,/'" -:;:. -~ ~ V 7- -- -- -,/' V 50 Go " , "~ ItO u 0 0.39 0.65 0.80 0.85 0.84 HEAD- CAPACITY ........ :J: oJ C 11 COI'~5 ACTUAL TUT CUIND I - - -- I"ttEDlCT£O I ----- ~ 150 w - ---- Percent of max. 1.0 IZ Efficiency - ~-- -~- - - - -- - ~- - -- - - -- - v:- -- ... .e:::: ... --:::.. -- ~ - -- ------ 100 ...-:: -- _Mit eo 60 Go :J: 40 GI 20 o 10 IS 20 30 CAMCITY. IN 100 GPM Fig. 18.49 Comparison of characteristics predicted from impeller measurements and actual characteristics determined by test. Dash lines are predicted curves, and solid lines are actual test curves. 462 Heads, Conditions of Service Peiformance Characteristics, and Specific Speed To detennine if the pump shaft is suitable for this application: - 107 kW Safie power -- 48(1750)(39.6)3 48.6 x 106 7,000 x 1,750 X 1.5623 = 145 h 321,000 P The shaft is obviously safe for 1,750-rpm operation. It remains to check the pump for safe operating pressure. The 19 mm (0.75 in) bolts and studs holding the two halves of the casing together have an area of 1.95 cm2 (0.302 in2) at the root of the threads. . 35(1.95)21 X 101 Safe working pressure = 1290 = 11.1 bar 5,000 x 0.302 x 21 _ 159 . 200 pSlg This is approximately 2.6 times the expected shutoff head of 43/10.21 or 4.2 bar (142/2.31 or 62 psi), when operating at 1,750 rpm. The casing will be strong enough for the intended operation. (The actual pump design is good for 12 bar (175-psig) operating pressure.) The foregoing example has demonstrated that it is possible to approximate the perfonnance of centrifugal pumps other than those of the axial-flow impeller type. Nevertheless, this should be used with caution and only in the absence of a more reliable method. Rating Curves and Charts Rating curves and rating charts were originally intended for pump salesmen to use for making pump selections. They are now also common in bulletins and other sales literature. A rating curve for a centrifugal pump of specific design shows in a condensed fonn, the possible range of applications of that pump, either for a range in speed or for a range in impeller diameter. In earlier days, some small centrifugal pumps for belt drive were manufactured in lots for stock sale, and the most efficient operating speed for each installation was obtained by selecting a proper pulley ratio to give the head and capacity condition desired. A curve showing the head, capacity, and brake horsepower for such a pump at a number of speeds, could be utilized for detennining the speed necessary and the power involved, but these rating curves were rarely used. Instead, a table (Table 18.5) was generally more convenient and pennitted showing a number of pump sizes on the same sheet. Before the recent energy crisis a few lines of pumps, notably small motor-driven stock units, were made with several different impeller diameters, of the same or different patterns, that load up various sizes of motors. A rating curve for this type is shown in Fig. 18.50. With such a line of pumps, a pump with a 19 kW (25-hp) motor and an impeller that would approximate the results shown on curve (2) would be furnished if the desired head condition fell anywhere within the zone between the head-capacity curves (2) and (3) in Fig. 18.50. Thus, for some customers' requirements, such as 57 m 3/hr (250 gpm), 61 m (200 ft) total head, the pump supplied would produce more capacity or head than required. When installed, this unit would either give excess capacity or excess pressure, depending upon the system, e 250 -- - - - Size-type hp rpm Size-type hp rpm - -- - 2V2-CF-1 2.2 1,095 ----------- 225 - 2V2-CF-l 1.9 1,055 Size-type hp rpm Size-type hp rpm 200 - - -- - - - - -- - -- 2V2-CF-l 2.7 1,205 3-CF-l 2.9 907 2V2-CF-l 2.4 1,170 3-CF-l 2.6 890 30 - 2V2-CF-1 2.6 1,170 3-CF-1 2.9 870 2V2-CF-1 3.1 1,245 3-CF-1 3.2 927 -----------~--------------- 2V2-CF-l 2.3 1,130 3-CF-l 2.6 850 - 2V2-CF-l 2.0 1,090 3-CF-l 2.25 830 2V2-CF-l 1.6 1,010 25 20 Portion of Pump Rating Chart Size-type hp rpm Size-type hp rpm gpm Table 18.5 -- - -- - -- - 2V2-CF-1 3.6 1,315 3-CF-1 3.6 980 - 2V2-CF-l 3.2 1,280 3-CF-l 3.3 962 2V2-CF-l 2.8 1,240 3-CF-l 3.0 945 35 - - -- -- --- - 2V2-CF-l 4.1 1,385 3-CF-1 4.0 1,035 ---- 2V2-CF-l 3.65 1,345 3-CF-l 3.6 1,015 2V2-CF-l 3.25 1,310 3-CF-l 3.3 1,000 40 Total head, in feet ------- ---- 2V2-CF-l 4.6 1,450 3-CF-1 4.4 1,085 -- - - ----------- 21/2-CF-l 5.1 1,510 3-CF-l 4.9 1,130 2V2-CF-l 4.7 1,470 3-CF-l 4.6 1,113 2V2-CF-l 4.2 1,440 3-CF-l 4.1 1,095 21/2-CF-l 3.75 1,380 3-CF-l 3.6 1,048 2V2-CF-l 4.15 1,410 3-CF-l 4.0 1,065 50 45 21/2-CF-l 5.55 1,585 3-CF-l 5.5 1,205 21/2-CF-l 5.05 1,550 3-CF-l 5.0 1,185 60 2V2-CF-1 5.6 1,565 3-CF-1 5.5 1,175 2V2-CF-1 6.2 1,620 3-CF-l 5.9 1,220 ---~------- 2V2-CF-l 5.1 1,530 3-CF-l 5.0 1,155 2V2-CF-l 4.65 1,500 3-CF-l 4.6 1,140 55 464 Heads. Conditions of Service Performance Characteristics. and Specific Speed unless throttling were employed to increase the frictional head artificially. Today, this practice has essentially disappeared. For pumps which are built-to-order with an impeller pattern and diameter individually selected for the prevalent service condition, a curve showing the range in conditions that can be met by a given impeller design or by several impeller designs for a given speed is used. These are generally complicated in appearance because the efficiency that can be obtained varies with the diameter of the impeller. This variation in efficiency is covered either by isoefficiency curves, as shown in Fig. 18.51 or by figures on the curves of similar points (Q/Qt = -VH/Ht relation) or lines approximating that relation as shown in Fig. 18.52. For their proper use, rating curves must also show the required minimum NPSH shown in Fig. 18.52. A different chart is required for each motor speed for which the particular pump may be offered. For unusual conditions of driver speeds not covered by a curve, the use of standard relations for speed changes permits determining what the pump will do. EFFECT OF SPECIFIC GRAVITY ON PUMP CHARACTERISTICS The only effect that specific gravity of liquids with viscosities equal to water has on the operation of a pump is to vary the power required to drive it. The capacity and head (measured in feet of liquid) are the same as for water and so is the efficiency. The power input for any capacity is that required with cold water multiplied by the specific gravity. EFFECT OF VISCOSITY ON PUMP CHARACTERISTICS Two of the major losses in a centrifugal pump are through fluid friction and disk friction. These losses vary with the viscosity of the liquid so that the head-capacity output, as well as the mechanical input, differ from the values produced when handling water. It is not practical to present here a complete discussion on viscosity as a property of liquids and on the effect of viscosity on flow of liquids. The reader can find such a discussion in textbooks on fluid mechanics. It is necessary, however, to know the three different units that may be encountered describing the viscosity of a specific liquid: 1. Saybolt seconds universal, or ssu 2. Centistokes-defining the kinematic viscosity 3. Centipoises-defining the absolute viscosity. Data for the conversion from one to another of these units and relations between the viscosity and temperature of a number of liquids are given in the Data Section of this book. Considerable experimental testing has been done in determining the effect of liquid viscosity on the performance of different centrifugal pumps. Even with extensive data on the effect of viscosity, it is difficult to predict accurately the performance of a pump when handling a viscous fluid from its performance when handling cold water. The Hydraulic Institute has published the charts shown in Figs. 18.53 and 18.54 which permit approximating the characteristics on uniform liquids (not paper stock, slurries, or the like) of conventional single-stage centrifugal pumps, not of the mixed-flow or axial-flow types, up to about 8 in discharge. These charts can also be used for multistage pumps if the Heads . Conditions of Service Performance Characteristics. and Specific Speed ~ 2~ ...... ~ ,,.. r- Jo-o.I. I- r- <I ~ 2vv ..J <I r r"- JII ,.... - 1 ci J-, r- ~ ,. ""'" l - t-... - 3 L ..... ..... ..... o ..... ""'" r"-po." r-- r" r-.... r"- '" 1"'" "" ~ I'. I""- i'oo.. r-.. '" 5C) ...30 HP MOTOR ..... ..... I""- r-- ..... ~ I-Z5 I-IP MOTOR _ r-ZO HP MOTOR I~ 200 100 CAPACITY. IN GPM Fig. 18.50 Rating curve of 2V2-in motor mounted pump. Pump equipped with different impellers that load up several sizes of motors. I~ ':':-r-~ 250 ~I!-~~-~il I.1:-- ;:1 ! f- . P[RCEHTAQES N 00 / I'-! i'-o h V rr V 1/ r::: r- h 7 f'")I V r.L" ~ ",i . . ~ '! /~.; Vr" I I 50 / I ...... V. . . . .L II J 1 I uFo- "-. 1-. ". "-r .':I) • P- f-I.. r-- ..... ~ .... ",'" V i" 1 " {) I-r:ttil r---~ j : r--1. j ~ Io.i ) : .. K, 1/ 2 ..... r, ~I' V II "" / "~II ~, / V L~ ./ r--.~ 1' ... ~ "./ r-", .iC. V V:' V. . . ~ l.r' t"'S ~ '" '" vv v" i r~ .. l'~ - "" I"v..., ... !~ ....~ I~ ~ 20 CAPACITY, IN 100 G PM Fig. 18.51 Rating curve of 10 in double-suction single-stage pump. Revealing the wide range that can be covered by an impeller of single design by machining it to the proper diameter for a particular service. 465 466 Heads, Conditions of Service Performance Characteristics, and Specific Speed IW W IJ... Z cl I <X f.I '" / w :x: ...J ~ I 5 11 o I I /, / / / ~,() - , ~ I- 250 20 15 10 o 50 Fig. 18.52 - -- - 5 100 ..... 150 CAPACITY, IN GPM .-,.",. ,.",. ,.... ..... 200 Rating curve of 2 in discharge, 3,500-rpm pump. 250 1.00 .90 .eo CIl 0: .70 b .60 Z .50 0 ~ 0 ~ r-F -= I "\..<;; i= (J W 0: 0: 0 .-:: Cif I-- .~ .30 (J ..20 Il"- I t- - r-- .10 .0 10 I~ 20 25 30 40 50 60 10 eo go 100 CAPACITY-GALLONS PER MINUTE (at SEP) Fig. 18.53 Performance correction for viscous liquids. Pump design capacities up to 23 m31hr (100 gpm). (Courtesy Hydraulic Institute) 467 468 Heads, Conditions of Service Performance Characteristics, and Specific Speed 100 0 C/) cr 0 < w J: ~ > U Z I 100 90 Li: 10.. ~ w 70 W 60 cr cr 0 z c 0 > I I I -r--. i'-.- - K ......... I"'-- ....... '(' I ~9 \ \ ~ f- 1'\ 50 I I I U \ \ I 30 i ~ "(,~ \'\ 1\ ;~ b~ '4 t.t,. \ '\ \ \ "- '-O.8.Q. -O.8.Q. ' -I.O.Q. 1'-12'Q. r-..... I I 't--c 20 ~ I' I U t: 40 ~ u " I 70 Z w 0 u 80 U ;:::::.. ely T~ ~ ~ 80 60 U ~ ~~ 90 ,~~ ~ \~ ~ b~ ~'~ ~ 1\\ 1\ 1\1\ ,~ 1\ \ \ CENTISTOKE'S ,\ ~ 1\\ \\ 1\ \ \1\ 1\ \ \ i\ \\ \ '\ \ 1\\\ \ 1\ 1\\ \ 1\1\ \ '\ l\\r\\ 1\ v-:: ~ 1\ \' ~\\ \ I~ \ 1\:\ \~~~ [\; ~ ~ ~ ~ \ \ \ \ 1\ \~Ps;.- ~ ~ ~ ~ ~ \ \\ \ ~ ~~ ~flI~ ~ ~ ~ \ 3 \ \ ~ ?(\ \[\ \ v ~ v- I--': v I-- ~ ~ ~~~ ~ 1\ \ \ &00 400 300 200 Irsso 40 ~ v- ~I-:;....- \ ~~ .W W ~ Z a 4( W J: ~ ;::;:. ~ ~ ~ ~~~ &00 400 300 200 \ 1\f\1: 1\ 1\ \ \ ~ ~~ V t::Y !830 ~ ~ 188 I' VISC~I"?, - s~u L5 2 \ _\ 1\ \ 1\ \ \ \\ \\ 1\ \ \ 1\ 1\ 1\\r\\ 1\\ 1\ 1\ l\ 1\ 1\1\1"\I I\l\\ \\ l\\' \\ 1\ 1\ \ \\ 1\ \ 20 \\ \ '\ \\ \ \\ ./"':: ~~ ~~ ~ t:/:: ~ ~ tx v~ \ \ .\ 1\\ ~ ~ ~ ~ ~ ~ 11\ \ \ CI!~,:< ~ ~I( p~\ ~~ oc Ibo & ~ I 0 .]" \ 5 II 7 II 1110 CAPACITY 15 20 30 IN 100 GPM Fig. 18.54 Perfonnance correction for viscous liquids. Pump design capacities above 23 mllhr (100 gpm). (Courtesy Hydraulic Institute) \ \~ ~ ~, "\ """' 40 50 110 1011011000 Heads, Conditions of Service Performance Characteristics, and Specific Speed 469 correction factors are selected on the basis of the head per stage, and provided the losses (which result in heating the liquid) do not cause sufficient increase in the temperature to change the viscosity of the liquid appreciably. The correction factors in Fig. 18.54 are selected for the head (per stage) and capacity at which the pump gives maximum efficiency on cold water. For example, a pump whose maximum efficiency capacity (1.0 x Qn) was 170 m3jhr (750 gpm) at a 30.5 m (100 ft) total head on water would, on a 1,000-ssu viscosity liquid, have the following characteristics: (1) A reduction of capacity to 95 per cent of its corresponding water capacity, (2) a reduction in the head produced at these reduced capacities to 96, 94, 92, and 89 per cent of the cold water heads at 60, 80, 100, and 120 per cent of normal capacity respectively, and (3) a reduction in the efficiency to 63.5 per cent of that produced on water for the corresponding capacities. The power required to drive is determined by calculating by the formula: kW = QH x specific gravity . 36811 . . m metnc umts . h _ QH x specific gravity. US P3,96Ort m umts in which Q = capacity, m3jhr or gpm (corrected for viscosity) H =total head, m or ft (corrected for viscosity) 11 =efficiency (corrected for viscosity). Applying these corrective factors to a pump whose cold water characteristics are identified in Fig. 18.55 by 32 ssu, the approximate performance for 100-,400-, 1,000-,2,000- and 4,000-ssu liquids have been developed, the values for bhp being calculated on basis of 1.0 specific gravity. Whereas the pump produced a maximum efficiency of 76 percent when pumping 100 m3jhr (440 gpm) of cold water against a 40.2 m (l32-ft) total head, it would be expected to produce a maximum efficiency of only 19.7 percent when pumping 73 m3/hr (321 gpm) of a 4,000-ssu liquid against a 31.2 m (102 ft) total head. In applying regular cold-water pumps for use in pumping viscous liquids, care must be taken to make sure that the shaft design is strong enough for the required power, which may be considerably in excess of the cold-water brake horsepower, even though the specific gravity of the liquid may be less than that of water. EFFECT OF AIR OR GASES IN THE LIQUID ON PUMP CHARACTERISTICS If as little as 1 percent by volume of air or gases is present in the liquid pumped, the head-capacity curve is affected very significantly, as illustrated in Fig. 18.56. As this percentage increases, the unfavorable effect becomes even more drastic, until at 6 percent by volume for the pump illustrated in Fig. 18.56, we reach a condition when the pump almost ceases to perform satisfactorily. The presence of air or gases creates a fairly complex phenomenon and, at this moment, cannot be described by an exact mathematical relation that could be applied indiscriminately to any given pump. Figure 18.57 illustrates another test of the effect of air content on the performance of a pump. The deterioration in this case appears to be less severe than in the case of the pump illustrated in Fig. 18.56. The reason for the difference is that a large number of variables in the geometric configuration of the impeller and of the casing playa major role in the extent of the deterioration. But the exact relationship between design and performance still remains an unknown. 470 Heads, Conditions of Service Peiformance Characteristics, and Specific Speed 180 160 0 CI ILl l: ..J 140 CI I- 0 lIILl ILl 12 0 10 0 LL 80 60 0 80 70 60 EFFICIENCY I- Z ILl 50 () Q: ILl Q. ~ 40 () Z / / .... 5 "v ILl v 30 (3 ~ 20 j -- I +++-+-+-+-+-+-+-+-+-r-r-r-r-r-~.~OOOSSU~-r~~~+ l--, I V o ~4 0 BHP >- -- Q: C) ~ 30 -- Q. l: CD 2000 SSU , ,J..06 SUr,v . 'SU 400 SSSU- 20 'O~2 S~ 0 o 100 200 300 400 500 600 CAPACITY, IN GPM Fig. 1S.55 Predicted characteristics for a centrifugal pump for liquids of various viscosities. I&. ILl Heads, Conditions of Service Performance Characteristics, and Specific Speed "- 100 90 IW w u. 80 ci « w 70 :x: ...J ~ 60 0 l- SO 6% 250 750 500 1,000 CAPACITY, GPM Fig. 18.56 25 Effect of entrained air on the head-capacity curve of a centrifugal pump. (Courtesy Chemical Processing, June 1987.) ,, O%AIR M ....... 20 r-.... " r\ 10%AIR '" "- \. \ ~ ~ 15 ", , \ , l \ \ , \ \ 10 9 Fig. 18.57 11 13 M3/H x 1,000 Another example of the effect of entrained air on centrifugal pump performance. (Courtesy Sulzer) 471 472 Heads, Conditions of Service Performance Characteristics, and Specific Speed BmLIOGRAPHY [18.1] E. P. Sabini and W. H. Fraser. ''The Effect of Specific Speed on the Efficiency of Single Stage Centrifugal Pumps." Proceedings of the Third International Pump Symposium, Houston, Texas, May 1986. [18.2] E. P. Sabini and W. H. Fraser. ''The Effect of Design Features on Centrifugal Pump Efficiency." Proceedings of the Fourth International Pump Symposium, Houston, Texas, May 1987. 19 Suction Conditions and Limitations on Suction Performance Every piece of machinery is preordained to have its Achilles' heel. That of the centrifugal pump can generally be found in its suction. This fact must have been discovered quite early in the commercial application of centrifugal pumps and, probably, accepted as an inescapable penalty exacted in return for the advantages that were made available by this newer means of raising water to a desired location at a reasonable cost. And because most centrifugal pump troubles occur on the suction side of the pump, it is imperative to understand how to relate the suction capability of a centrifugal pump to the suction characteristics of the system in which it will operate. Most difficulties at the suction of centrifugal pumps have as their root cause the phenomenon known as cavitation: the process whereby the pressure at some point in a pump or turbine falls below the liquid's vapor pressure thus allowing local vaporization. The resulting vapor can have two effects: a) its extent can be sufficient to obstruct the machine's waterways leading to a deterioration of hydraulic performance, or b) the subsequent collapse of the vapor as it moves into regions of higher pressure can produce noise and erosion of the waterway surfaces in the vicinity of the collapsing vapor. Recognizing this, it is therefore important in the pumping of liquids to ensure there is always sufficient energy available at the pump suction to move the liquid from the pump suction nozzle into the impeller without vaporization to the extent that pump performance deteriorates noticeably or pump parts are damaged prematurely. Pump performance is normally presented in the form of curves, such as in Fig. 18.16, showing head and power versus capacity at fixed speed. The head a pump will produce and the power it will absorb at various capacities are two of its three fundamental performance characteristics. The third is the net positive suction head (NPSH) required. This is the energy in meters or feet required at the pump suction over and above the vapor pressure of the liquid to permit the pump to run without undue deterioration of performance or expected life. As simple as this definition seems, the practical application of it is actually quite complicated, with the pumped liquid, impeller energy level, and impeller material having a profound effect on which of these two criteria determine the NPSH required; see Definition of NPSH required later in this chapter. Considering deterioration of performance first, changes in available NPSH do not affect pump performance materially, as long as it remains above the value of required NPSH. The characteristics labeled 473 I. J. Karassik et al., Centrifugal Pumps © Chapman & Hall 1998 474 Suction Conditions and Limitations on Suction Performance J: (J) a. z ~ ou:: UJ tt HE~. ___ ·~·! I • AMPLE NPSH ~L---AVAILABLE 1 '~IN~UFFICIENT N~SH ~r-----:i~::lA~V~A~'LA~B~LE~N;P;S:H~=~R:E:Q~U~/t---~~~____ ~ J: INSUFFICIENT NPSH NPSH= REQUIRED RED NPSH REQUIRED CAPACITY Fig. 19.1 Effect of cavitation on pump performance. "Ample NPSH" in Fig. 19.1 show such performance. Lowering the available NPSH to the required value causes cavitation sufficient to degrade performance and the pump "works in the break" (Fig. 19.1). Running in this condition, a decrease in system head will produce only a small increase in flow, to the point where the available NPSH is "insufficient" and the head developed "breaks down". At this condition, lowering the system head further produces no increase in capacity. In the early days of pump application, the term NPSH was not used frequently, and the suction characteristics of centrifugal pumps were generally expressed in terms of "suction lift" and "suction head," as defined in Chapter 18. NET POSITIVE SUCTION HEAD The use of "permissible suction lift" or of "required suction head" has very definite shortcomings. First, it can only be applied to water, since it refers to the energy of barometric pressure expressed in feet of water. Second, changes in barometric pressure, whether caused by differences in elevation above sea level or by climatic conditions, affect the value of these two terms. Finally, changes in pumping temperature affect these values as well, since they affect the vapor pressure of the liquid. For this reason, all references to suction conditions today are made in terms of NPSH (net positive suction head above the liquid vapor pressure). Both suction head and vapor pressure should be expressed in meters (feet) of liquid being handled, and must both be expressed either in gage or absolute pressure units. A pump handling 17°C (62°F) water (vapor pressure of 0.18 m [0.6 ft]) at sea level, with a total suction lift of 0 m (ft), has an NPSH of 10.34 - 0.18 or 10.16 m (33.9-0.6, or 33.3 ft), whereas one operating with a 4.6 m (15-ft) total suction lift has an NPSH of 10.34 - 0.18 - 4.6, or 5.56 m (33.9-0.6-15, or 18.3 ft). A pump operating on suction lift will handle a certain maximum capacity of cold water without Suction Conditions and Limitations on Suction Performance 475 hj=3FT 1 ! 15 FT ATMOSPHERIC j PRESSURE water, BO°F PVP = 0.5 PSIA (a) AT SEA LEVEL NPSHA = (14.7 - 0.5) x 2.31 -15 _ 3 1.0 = 32.B - 15 - 3 = 14.B FT (b) AT 5,000 FT ABOVE SEA LEVEL NPSHA = (12.2 - 0.5) x 2.31 -15 _ 3 1.0 = 27 - 15 - 3 = 9.0 FT Fig. 19.2 NPSHA for suction lift at sea level and at 1,525 m (5,000 ft) above sea level. cavitation. The NPSH or amount of energy available at the suction nozzle of such a pump is the atmospheric pressure minus the sum of the suction lift (including friction) and the vapor pressure of the water. To handle this same capacity with any other liquid, the same amount of energy must be available at the suction nozzle. Thus, for a liquid at its boiling point (in other words, under a pressure equivalent to the vapor pressure corresponding to its temperature), this energy has to exist entirely as a positive head. If the liquid is below its boiling point, the suction head required is reduced by the difference between the pressure existing in the liquid and the vapor pressure corresponding to the temperature. It is necessary to differentiate between available NPSH and required NPSH. The former, which is a characteristic of the system in which a centrifugal pump works, represents the difference between the existing absolute suction head and the vapor pressure at the prevailing temperature. The required NPSH, which is a function of the pump design, represents the minimum required margin between the suction head and the vapor pressure. Figures 19.2, 19.3, and 19.4 illustrate the manner in which available NPSH at a given capacity should be calculated for a typical installation with a suction lift, for a pump taking its suction from a tank, and for a pump handling a liquid at the boiling point, respectively. Both the available and required NPSH vary with capacity (Fig. 19.5). With a given static pressure or elevation difference at the suction side of a centrifugal pump, the available NPSH is reduced with increasing capacities by the friction losses in the suction piping. On the other hand, the required NPSH, being a function of the velocities in the pump suction passages and at the inlet of the impeller, increases basically as the square of the capacity. 476 Suction Conditions and Limitations on Suction Performance WATER 80°F PV=0.5 PSIA r 10 FT 1 =4FT NPSHA = (14.7 + 5 - 0.5) x 2.31 + 10 _ 4 1.0 = 44.3 + 10 - 4 = 50.3 FT Fig. 19.3 NPSHA for pressurized suction. N-BUTANE PV = 52.2 ____ PSIA""""'SPGR = 0.56 r 10 FT 1 NPSHA = (37.5 + 14.7 - 52.2) x 2.31 + 10 _ 2 1.0 =0+ 10-2=8 FT Fig. 19.4 NPSHA for liquid at boiling point. A great many factors, for example, eye diameter, suction area of the impeller, shape and number of impeller vanes, area between these vanes, shaft and impeller hub diameter, impeller specific speed, the shape of the suction passages, all enter in some form or another into the determination of the required NPSH. Different designers may use different methods to produce an impeller that will perform satisfactorily with a specific value of required NPSH. As a result, it is not recommended that users attempt to Suction Conditions and Limitations on Suction Performance 477 T z ~ B NPSH = Z + (Ps - Pvp ) - (hfs + ALL UNITS IN FEET h/~ CAPACITY Fig.19.5 Available and required NPSH. estimate required NPSH from the knowledge of just one or two of these factors. Instead, they should base their selections on the data provided by the manufacturers. HISTORICAL BACKGROUND In the early days of centrifugal pumps, limitations on permissible suction lifts were imposed by the manufacturers on strictly empirical grounds. Because the understanding of the phenomenon of cavitation was imperfect, these limitations were sometimes overconservative and sometimes quite optimistic. However, the commercial pressures of a very severe competitive situation seem to have outweighed sound engineering judgment much too often in the 1920s. The attendant difficulties could not have failed to Suction Conditions and Limitations on Suction Performance 478 stimulate a considerable amount of head-scratching by centrifugal pump designers. The thinking of the designers must have been heavily influenced by the experience of water turbine builders. In 1922, at the Hydroelectric Conference held at Philadelphia, H. B. Taylor and L. F. Moody first presented the concept of a parameter, Sigma, to facilitate the description of the conditions under which cavitation occurs. Sigma was defined as . Sigma = (J NPSH =H where H is total head. At about the same time, Dr. Thoma was developing the same concept in Germany and, therefore, "Sigma" has since then been known to centrifugal pump designers as the ThomaMoody parameter. Means were now available to relate the operating conditions of a centrifugal pump-its capacity, head, and rotating speed-to the minimum net positive suction head required for satisfactory operation. But commercial pressures seem to have again outweighed sound engineering judgment much too often in the 1920s. The number of companies manufacturing centrifugal pumps proliferated without there necessarily being a corresponding increase of knowledgeable and experienced designers. Spurred on by the advantage of offering a higher operating speed than the competition or of guaranteeing satisfactory operation with higher suction lifts, some companies made installations that had disastrously expensive consequences for user and manufacturer alike. As field difficulties continued to occur, it became evident that some official guidelines were necessary. An organization for the discussion and solution of technical problems in the realm of pumping machinery had been formed some years before by the older, larger, and most reputable pump manufacturers under the name of the Hydraulic Institute. Standards had been developed and published by this institute to codify sound practices, including testing and guarantee practices. At this point, the Hydraulic Institute (HI) appointed a committee to investigate centrifugal pump suction problems. The committee proceeded to collect information on centrifugal pump installations in which cavitation troubles had been experienced as well as on satisfactory installations. It was found that to avoid difficulties for any given total head and suction lift conditions, the specific speed of the pump should be kept below a certain value. The conclusions of the committee were published in October 1932 in the Hydraulic Institute Standards in the form of charts that became commonly known among centrifugal pump engineers and users as "specific speed limit charts." As experience was accumulated on better design than described in these first charts of 1932, revised charts were prepared and published by the Hydraulic Institute. Ultimately, charts were provided for several varieties of pump design as follows: Double-suction pumps 2. Single-suction pumps with shaft through the eye of the impeller 3. Single-suction overhung impeller pump 4. Single-suction mixed and axial flow pumps 5. Single-suction hot water pumps 6. Double-suction hot water pumps 7. Condensate pumps with shaft through the eye of the impeller. 1. Figure 19.6 illustrates one such chart, giving specific speed limits for single-suction overhung impeller type pumps, such as the ANSI pumps. For the record, it is important to remember that these charts were strictly empirical. They did not Suction Conditions and Limitations on Suction Performance o 0 o !D 0 It) o a 0 a<t 0 a ,.., a 4,000 ~ x~~ ~ J" ~ 3,500 ~t~~ I? ;$' 11~ 3,000 ..J ..J !oJ 2 " ~ I C> Z I ~ ::I: 0:: o z a ~ ~~ ~{ I 1,500 (/') I a u. o I W ~ ..., V V 't?.,'4. "v ,,0 I/~ V 1/ V JL" etl i:: 1/ ,,~ ~I " 4.1 ~ V ~/ I? ~ I ,,0 V 4. ~ V ~ " u ~I ., ...,...." let u" ,,0 ~ ~ I- --:~L ....1 t1 " ~ t , --~ I--- -; ~ "v II §I- ~I ~ ,,~ Co; VII C> Z 0:: (\j -oJ ~ -oJ ' ~ 1/ ~ o (/') I ~ t- !oJ d. ~ r- ~ 2,000 !oJ ..J ° ~~ " v.,r" 2,500 I ~ (/') I a 0 ,.., f-_J... ~ ,,~/ ~ d. 0 V A 2 d. 0:: !oJ 0000 a a 00'1 (I) ""!D 10 It) (\j 479 V V I II 1,000 V u. oW 900 0.. (/') 800 700a a a !Dill a aV a 0 If') 0 a (\j a III 0000 a 00'1 CI) ""!D a It) a V a If') a (\j TOTAL HEAD,IN FEET(FIRST STAGE) Fig. 19.6 Specific speed limit chart formerly recommended by the Hydraulic Institute. Circa 1960; for single-stage. overhung-impeller pumps indicate that pumps built for the limit allowed were necessarily the best design, nor that pumps built to lower limits were not more economical in certain cases, nor finally that pumps could not be designed and built for higher limits. All that these charts were intended to indicate was that for a given set of head, capacity and suction conditions, a certain maximum rotative speed should give assurance that the pump would be capable of giving satisfactory service. 480 Suction Conditions and Limitations on Suction Performance It must be realized that pumps built for the allowed limit are not necessarily the best design for the intended service and that a lower specific speed type might be more economical. It must also be realized that the individual pump design limits its application for both maximum head and for suction condition limitations. For example, using the HI charts, the maximum recommended specific speed for a doublesuction, single-stage pump would have been 1,990 for a 61 m (200 ft) total head and a 4.6 m (15 ft) suction lift. It does not follow that all double-suction, single-stage pumps of 1,990 specific speed type are suitable for operation at speeds which will cause them to develop a 61 m (200 ft) total head (at maximum efficiency); nor that the pump, if suitable for operation at a 61 m (200 ft) total head, is suitable for operation with a 4.6 m (15 ft) suction lift; nor that a pump of this type operating against a 61 m (200 ft) total head would on test be found capable of operating on only a 4.6 m (15 ft) maximum suction lift. These charts were intended to indicate only the maximum rotative speed for which experience had shown a centrifugal pump could be designed with assurance of reasonable and proper operation for the combination of operating conditions. Nothing in these charts suggested that the specific speed indicated corresponds to the point of maximum efficiency. However, pumps are normally applied for conditions near their maximum efficiency points. Thus, even though the service conditions do not correspond exactly with the design conditions, the specific speed value is generally sufficiently close to the specific speed of the design condition. SUCTION SPECIFIC SPEED The application of the specific speed limit charts as they were originally developed, however, had a very important shortcoming: the fact that satisfactory suction conditions were tied directly to the total head developed by the pump. The perceived flaw was that the performance of an impeller from the point of view of cavitation cannot be affected too significantly by conditions existing at its discharge periphery, which, however, are the prime factors in determining the total head that the impeller will develop. This statement must be qualified to some extent: as the specific speed, Ns, increases, the loading of the suction region of the impeller vanes extends far enough along the vanes to influence the total head and the power consumption. Expressed in another way, we can say that as the dynamic portion of the total head increases, the nature of the flow around the whole vane assumes a greater importance in both the net positive suction head required and in the total head produced by the impeller. This was recognized much later than the time when the suction specific speed concept was developed, when the onset of internal recirculation at the discharge of the impeller was found to trigger off that of internal recirculation at the suction in the case of higher specific speed pumps (see Chap. 22 for a detailed discussion of this phenomenon). Returning to the perceived flaw, the argument was that, if an impeller exhibits certain suction characteristics, cutting down its diameter within reasonable limits and thus, reducing its head, should have no influence on its suction capabilities. At the same time, since the total head is changed, a strict interpretation of the specific speed limits charts would indicate that, unless the suction lift were to be commensurately altered, the maximum permissible specific speed must be changed. Likewise, to maintain a fixed value for the Thoma-Moody parameter, a reduction in head by cutting the impeller diameter should be followed by a proportionate reduction in the net positive suction head. This inconsistency was finally resolved in 1937 by the development of the suction specific speed concept. It is essentially an index number descriptive of the suction characteristics of a given impeller. It is defined as: n(1J.5 S = NPSH o.75 Suction Conditions and Limitations on Suction Performance where S 481 =suction specific speed n =rotative speed, RPM Q = flow per impeller eye, gpm (total flow for single suction impellers; one-half of the total flow for double suction impellers) NPSH = required net positive suction head, ft. As with specific speed, countries using the metric system assign a different designation to suction specific speed, namely nqn and express Q in m3/hr, NPSH in m. The mathematical relation between values calculated in the two systems of units is If one refers to the papers in question,! it will be seen that the specific speed index number can be derived by considerations of the laws of similarity and by means of dimensional analysis. The fact is that the steps which led the authors to the solution were much simpler and involved no complex considerations. We had developed reasonable evidence of the fact that cr, the Thoma-Moody parameter, appeared to be a function of the specific speed, but the head seemed to refuse stubbornly to disappear from the relationship. However, we knew that, at least for a certain range of specific speeds, conditions at the impeller discharge could not be affecting suction conditions. We suddenly saw that all that was required was a mere algebraic manipulation. If instead of trying to relate Sigma to the specific speed, we looked for a relation between the specific speed and the 3/4 power of Sigma, the total head disappeared very conveniently from the relation. To say that this concept was received with unanimous approval would be an exaggeration. In keeping with any suggestion for a major change from the status quo, there immediately developed a substantial controversy over the validity of the concept. Fortunately, the controversy was short-lived and the suction specific speed was soon accepted at the most convenient parameter for describing the suction capabilities of centrifugal pumps. The Hydraulic Institute specific speed limit charts have been revised several times since they were first adopted as a guideline for centrifugal pump suction conditions. Unfortunately, for a long time they continued to be based on the erroneous concept that the total head developed by the pump plays a part in determining the maximum permissible rotative speed for a given set of suction conditions, despite the recognition of the concept of suction specific speed in the Hydraulic Institute Standards. Finally, in 1983, the 14th edition of the Hydraulic Institute Standards incorporated charts that had been significantly revised. They are now based on a suction specific speed of 8,500 throughout, that is, for both sing1e- and double-suction impellers. Thus, the total head factor has finally been eliminated from these charts. In addition, the recommended values are now expressed in terms of NPSH instead of suction lifts or suction heads, significantly simplifying their use (see Figs. 19.7 and 19.8). A final note of caution is necessary. The published Hydraulic Institute Standards suction limitation charts should be considered as guidelines, in that they represent conditions that have shown satisfactory operation. As such, they are conservative in certain cases, and a manufacturer may sometimes guarantee performance at suction specific speeds higher than these Hydraulic Institute ratings, because the manufacturer has evidence of successful operation at such ratings. In such a case, the user needs to consider the reputation of the manufacturer and/or any previous experience with him. If this reputation and experience t"Some Notes on a New Method of Representing Cavitation Results" by Dr. O. F. Wislicenus, R. M. Watson, and I. 1. Karassik, presented at the Hydraulic Institute Meeting in New York, December 6, 1937; and "Cavitation Characteristics of Centrifugal Pumps Described by Similarity Considerations" by O. F. Wislicenus, R. M. Wilson, and I. 1. Karassik, presented at the Spring Meeting of the ASME at Los Angeles, California, March 23-25, 1938 (ASME Transactions for January 1939). 482 Suction Conditions and Limitations on Suction Performance Capacity - m3lh 6 4 8 10" 2 , ii' 4 iii 8 4 2 8 10' 8 8 10' 6 4 2 it' , 8 10" iii i l00~.-..-.. -. . -.. .~.;.. -.. ~ .. ,~ . .-.. ~ < ..-..~ :..~ .; ~ .. ;~.;~.<~.,...-..- .-.. -...~,--~~~~~~----~~~~~~~~~~~~~~~~ 80 20 80 . · ··, il TU•1• 20 Gi at ~ en CL ,:::::::::::::t::::::::t:~:::i: : ::~:::~:: l::~ ::~ : .:'l':::~~:: ~:: 1:: 1:+:1 : :::::::::::::~::::::::~: ~: : :~::::~:::~:: j::~: +: ... .... , 6 4 .~ ..... ! ... ': .. ,t··!··!· ':- ,! .............. !........ ~ ..... ~" .. ~ ... ~ .. !. ,!. '? ' 2 ··;r·:r]:!!: ~~~t 4 ... r 2 II , •• •• : •• : •.! . : . 8 10 8 ~ 10 Z . - :' .~ ·~··~··~·t, .8 .8 .4 1 10" 8 4 2 8 10' .. 2 8 8 10' 4 2 8 8 10" 4 2 II 8 10" capacity U.S. GPM Fig_ 19.7 Hydraulic Institute recommended maximum operating speeds for single-suction pumps. (Courtesy of the Hydraulic Institute) . 6 8 10" 2 Iii 8 4 , 8 10" I 2 I, 8 4 2 8 11),' ii' .. 8 8 10" i i 100 80 20 80 40 10 8 20 II Gi at ~ en CL Z 4 ···1· 10 ---- --- _. __ ........ ................... ;r- .. ............... . . 8 6 ··::::::::I::::.::.I .. :.:i:...l . 4 ,.~ . t·l: i:I: NPSHA va Capacity for speeds shown at eonatant S = 8500. For use wtth double suctlon pumps. 2 ········.. ····1········, .. ·· ., ....,...1-___"_=_::._85:00:'-'-(,6~/=-:-P_::)H7._6~:=·7=6_ .,.....,.... ..,-! I ~~~~~~~~~~~~~~~~~--~~~~~~~----~~~~~~ 10" 2 4 8 8 10> 2 4 8 8 104 2 4 8 8 10" 2 4 8 8 10" capacity U.S. GPM (total pump capacity) Fig. 19.8 Hydraulic Institute recommended maximum operating speeds for double-suction pumps. (Courtesy of the Hydraulic Institute) 2 .8 .8 .4 Suction Conditions and Limitations on Suction Performance 483 are favorable, the user should have no concern, with but one qualification, over accepting these recommendations. The one qualification is consideration of the effect of designing a pump for low values of NPSH required on the permissible operating range of this pump (see Chap. 22). EFFECT OF LIQUID CHARACTERISTICS ON PUMP SUCTION PERFORMANCE OR NPSH As has been stated, cavitation occurs when the absolute pressure within an impeller falls below the vapor pressure of the liquid and bubbles of vapor are formed; these bubbles collapse further within the impeller when they reach a region of higher pressure. The minimum required NPSH for a given capacity and at a given pump speed is defined as that difference between the absolute suction head and the vapor pressure of the liquid pumped at the pumping temperature that is necessary to prevent cavitation. The fact that a pump is cavitating manifests itself by one or more of the following signs: noise, vibration, drop in the head-capacity and efficiency curves, and, with time, damage to the impeller by pitting and erosion. All of these signs are obviously inexact and it became necessary for pump engineers to agree on certain ground rules to establish some uniformity in the detection of cavitation. The minimum NPSH required is determined by a test in which the total head is measured at a given speed and capacity, with varying NPSH available conditions. Preferably this test is conducted in a closed loop such as is described on Fig. 19.9. The pump takes its suction from a closed vessel in which the pressure level can be adjusted or varied by the gas pressure over the liquid level, by the temperature of the liquid, or by a combination of these two variables. This variation in pressure level, in tum, controls the available NPSH. Results of such a test, plotted against NPSH appear in a form similar to that in Fig. 19.10. At the higher values of NPSH, the values of head remain substantially constant. As the NPSH is reduced, a point is finally reached where the curves break, showing the impairment of pump performance caused by cavitation. The exact value of NPSH where cavitation starts is, as mentioned before, difficult to Gas Pressure Suction Vessel Flow Distributor Heating or Cooling Coil Suction • Fig. 19.9 Pressure and/or temperature control NPSH test with closed loop. (Courtesy of the Hydraulic Institute) 484 Suction Conditions and Limitations on Suction Performance a l :=: t H = 3 PERCENT OF H1 !( HEAD AT CAPACITY Q AND AT SPEED N 0 II: :f!! HSo NET POSITIVE SUCTION HEAD Fig. 19.10 Detennination of required NPSH as presently defined by the Hydraulic Institute. Pressure Gauge Dampening Valve Thermometer Dampening Device Control Valve for Throttling Suction Flow Meter if Located in Suction Constant Level Pump on ,-, f1, Test traightening t~ Vanes Booster Pump may be Installed if additional suction pressure Is required Retum to sump Dlactwge nl~====~ , Discharge Control Valve, or '. - - • Adjustable Spring Loaded Back Pressure Valve or Ac:f)UStable Choke Valve Heat exchanger, if required -r-------I - Note: Position of these devices may be reversed in some set ups. Fig. 19.11 Suppression type NPSH test with constant level sump. (Courtesy of the Hydraulic Institute) Suction Conditions and Limitations on Suction Performance 485 pinpoint. To overcome this difficulty, engineers have generally agreed that a drop of 3 percent in the head developed is taken as evidence that cavitation is taking place. For that particular speed and the capacity being tested, the NPSH that produces a 3 percent drop in head is stated to be the minimum required NPSH. The Hydraulic Institute Standards for centrifugal pump testing [19.1] permits two simpler forms of cavitation tests. In the first arrangement (Fig. 19.11), the pump takes its suction from a constant level sump through a throttle valve, which is followed by a section of pipe containing a screen and straightening vanes. The operation of the throttle valve is used to vary the available NPSH and is therefore often termed a "suppression test." In the second arrangement (Fig. 19.12), the pump takes its suction from a relatively deep sump in which the level can be varied to establish the desired available NPSH. Generally, a "new" pump, that is a brand new design that has not been manufactured before, is always NPSH tested by the "closed loop" method. If one is dealing with pumps that have been manufactured before, considerable expense can be saved by using one or the other of the two alternate test methods. There is a risk, however, that the required NPSH determined by either of these alternate methods will be higher than that from a "closed loop" test. If the liquid pumped on test contains dissolved air or gas, some of this will come out of solution at the lower pressure in the suction line and can cause a drop in head similar to that caused by cavitation (but is actually caused by pumping a two-phase flow (see air entrainment in Chap. 18). In discussing the various NPSH test methods, the Hydraulic Institute Standards draws attention to this possibility and its effect. The risk of inaccurate results rises with decreasing NPSHR, and it is therefore better to test by the "closed loop" method in all cases where the NPSHR is below 4.5 m (15 ft). NPSH tests of centrifugal pumps are normally carried out on cold water and both the Hydraulic Institute Standards curves and pump manufacturers' rating curves indicate NPSH requirements on cold water. Thus, it might be assumed that the NPSH required by a centrifugal pump for satisfactory operation PUMP SUCTION FLANGe~ It IMPELLER EYE ~1It""-"ffi---.ffi-_1 -ttt--.fiIor-----r 10 ft. min. (3 m) o .. DIAMETER OF PIPE ~ Fig. 19.12 Suction line for static lift test. (Courtesy of the Hydraulic Institute) 486 Suction Conditions and Limitations on Suction Performance NPSH Requirement by Test, at Design Flow and 3 Percent Drop in Head Table 19.1 Temperature Fluid °C COF) Water 21.1 121.1 148.9 1.67 12.8 32.2 29.4 48.9 ( 70) (250) (300) ( 35) ( 55) ( 90) ( 85) (120) Butane Freon-ll NPSH, min. accuracy (± 0.5 ft) 0.15 m (m) (ft) 3.75 3.35 2.62 2.99 2.68 1.07 3.11 2.56 12.3 11.0 8.6 9.8 8.8 3.5 10.2 8.4 ~NPSH m ft 0.0 0.4 1.13 0.76 1.07 2.68 0.64 1.19 0.0 1.3 3.7 2.5 3.5 8.8 2.1 3.9 = 1.600 = 3,585 rpm. Pump Ns N is independent of the liquid vapor pressure at the pumping temperature. This is actually not true. It is merely an oversimplification used to illustrate the definition that NPSH is a measurement of the energy in the liquid at the pump suction over the datum line of its vapor pressure. At the same time, both laboratory and field tests run on pumps handling a wide variety of liquids and over a range of temperatures have always shown that the NPSH required for a given capacity and with a given pump apparently vary appreciably. For example, the required NPSH when handling some hydrocarbons is frequently much less than that required when the pump handles cold water. Even when pumping water, there is definite evidence that required NPSH decreases when the water temperature increases. For example, Table 19.1 illustrates test results of a pump at 3,585 rpm, specific speed of 1,600, and handling different liquids at several different temperatures. It became evident quite a number of years ago that the reduction in the required NPSH must be a function of the vapor pressure and of the characteristics of the liquid handled by the pump. In general, it can be proved that the factors affecting the required NPSH are, at least, the following three: 1. The ratio of the specific volume of the vapor to that of the liquid at the pumping temperature 2. The homogeneity of the liquid 3. The effect of subcooling derived by any partial flashing of the liquid in question. Because in the case of hydrocarbons this reduction in NPSH could play a most important role in the relative costs of a refinery installation, most efforts were directed at understanding the phenomena involved in connection with hydrocarbons. Thus, it was felt that rules could be developed to predict the effect of liquid characteristics on the required NPSH to take advantage of this phenomenon without the risk of overoptimistic assumptions. Such rules have been developed by the members of the Hydraulic Institute and incorporated in its standards. We shall examine these rules, but before doing this, let us consider the effect of temperature on the required NPSH for water, because this may help us better understand the effect of other liquids. Suction Conditions and Limitations on Suction Peiformance 487 PERFORMANCE ON WATER AT VARYING TEMPERATURES It has been noted for some time that pumps handling hot water seem to require less NPSH than shown by cold water tests. The theory underlying this effect is fairly simple and need not be discussed in detail here. It is based on the fact that mild and partial cavitation can take place in a pump without causing extremely unfavorable effects. The degree of interference with the proper operation of the pump caused by such minor cavitation will bear a definite relation to the temperature of the liquid handled by the pump. Remember that when we say that a pump is cavitating we mean that somewhere within the confines of the pump, the pressure will have fallen below the vapor pressure of the liquid at the prevailing temperature. Thus, a small portion of the liquid handled by the pump will vaporize and this vapor will occupy considerably more space within the impeller than the equivalent mass ofliquid before vaporization. If the pump is handling water at normal temperatures, the volume of a bubble of steam is tremendously larger than the volume of the original quantity of the water. For instance, at 4.4°e (40°F), 0.45 kg (1 lb) of water occupies 0.0004 m3 (0.016 fe), while steam at the same temperature occupies 69.2 m 3 (2441 ft 3). The ratio of the two volumes is 152,500. The rapidity with which this ratio diminishes as water temperature increases is illustrated in Fig. 19.13, which presents a plot of the ratio of the volume of steam to the volume of the equivalent mass of water for temperatures between lOoe (50°F) and 374.1 °e 100,000 10,000 1000 l '\~ a: w \ \. ~ !;t 3: .J 0 100 > -- ::i: « w IrJ) .J 0 10 RATIO OF STEAM TO WATER > '"'" ""~ \ TEMPERATURE IN OF 100 200 300 400 500 600 Fig. 19.13 Ratio of steam to water volumes versus temperature. 488 Suction Conditions and Limitations on Suction Performance (705.4°F) (the critical temperature of water at which steam occupies the same volume as water). At lOO°C (212°F), 0.45 kg (lib) of water occupies 0.00047 m3 (0.0167 ft 3) and 0.45kg (lib) of steam 0.76 m3 (26.S1 ft3), so that the ratio of volumes is only 1,605-almost 100 times less than at lOoC (50°F). Thus, the higher the temperature of the water, the more NPSH reduction can be permitted for the same degree of effect on the pump performance. There is another important thermodynamic factor that affects the relative cavitation characteristics of a liquid-the difference in the effect of subcooling caused by any flashing of the liquid. The reduction in the vapor pressure corresponding to a given change in temperature of the liquid varies for different liquids as well as for different temperatures of the same liquid. Consider, for instance, what happens with water at 204.4°C (400°F) and at 26.7°C (SO°F), respectively. The vapor pressure of 204.4°C (400°F) water is 17.03 bar abs (247 psia). A 0.56°C (1°F) degree drop in temperature to 203.SoC (399°F) will reduce the vapor pressure to 16.S4 bar abs (244.2 psia), a reduction of 0.19 bar (2.S psi) or 2.3 m (7.5 ft). This, then, is equivalent to instantaneously increasing the available NPSH by these same 2.3 m (7.5 ft). On the other hand, the vapor pressure of water at 26.7°C (SO°F) is 0.035 bar abs (0.507 psia). With the same 0.56°C (1°F) drop, at 26.1 °C (79°F) the vapor pressure is 0.034 bar abs (0.490 psia), a difference now of only 0.001 bar (0.017 psi) or 0.01 m (0.04 ft), a completely insignificant contribution to the available NPSH. Meanwhile, since the available NPSH is calculated based on the liquid temperature measured at the pump suction (before any flashing and subcooling will have taken place), the apparent result is that there is a reduction in NPSH required rather than an increase in NPSH available and that this reduction is greater for water at 204.4 °C (400°F) than at 26.7°C (SO°F). NPSH FOR PUMPS HANDLING HYDROCARBONS Pump applications for hydrocarbon processes frequently impose restrictive limitations to the available NPSH. On the other hand, it was found that variations between the required NPSH when handling hydrocarbons and that in cold water service were generally in a favorable direction. These two circumstances led both pump designers and designers of refineries to direct their efforts at understanding the phenomena involved and at establishing rules that could be applied to predict the effect of any special liquid characteristics on the required NPSH of any centrifugal pump. At first it was thought that these variations were only apparent and that if "true vapor pressures" or "bubble point" pressures were to be used in the calculations of test NPSH, the discrepancies would disappear and complete correlation with water test cavitation data would exist. Corrections for NPSH with hydrocarbons were nevertheless used, as a matter of policy rather than based on accepted theoretical deductions. It was believed that a reduced NPSH could be justified for the following reasons: 1. 2. Oil companies' specifications generally called for a maximum capacity and head at a minimum NPSH. In practice, it was unlikely that these two requirements would be imposed simultaneously. In fact, some of the field conditions are self-regulating-for instance, low capacity occurs at low NPSH, as a result of a reduced flow in the system. Under these conditions, even if the pump capacity falls off, available NPSH is increased and equilibrium is eventually attained. The effect of cavitation with hydrocarbons was noted to be not as severe as with water, that is, the headcapacity curve does not break: off suddenly for two reasons: (a) only the lighter fractions will boil first and (b) the specific volume of hydrocarbon vapors is very small in comparison with that of water vapor. Obviously, these facts do not tell the whole story, as many other factors affect the behavior of a pump handling hydrocarbons with low NPSH. Thus, attempts to arrive at a more reasoned understanding continued while some interim correction factors of an approximate nature were being used. Suction Conditions and Limitations on Suction Performance 489 These efforts centered in the accumulation and comparison of many tests, using a variety of pumps and handling many different hydrocarbons. These tests, in turn, helped generate a variety of correction curves for NPSH. Some of these charts occasionally led to rather impractical conclusions and additional rules were then introduced to avoid this situation. In 1951, the Hydraulic Institute Standards incorporated a conversion chart for hydrocarbons which has since been updated. It provided an estimate of the NPSH required by a centrifugal pump handling hydrocarbons of various gravities and vapor pressures in percentages of that required by the same pump when handling cold water. These curves were derived from an accumulation of experimental data and did not pretend to be arrived at by analytical means. The latest revised correction chart is incorporated in the 1983 edition of the Hydraulic Institute Standards (see Fig. 19.14). To use this chart, enter at the bottom with the pumping temperature in degrees Fahrenheit and proceed vertically upward to the vapor pressure in psia. From this point follow along or parallel to the sloping lines to the right side of the chart, where the NPSH reductions in feet of liquid can be read on the scale provided. If this value is greater than one-half of the NPSH required on cold water, deduct one-half of the cold water NPSH to obtain corrected NPSH required. If the value read on the chart is less than one-half of the cold water NPSH, deduct this chart value from the cold water NPSH to obtain corrected NPSH required. Because of the absence of available data demonstrating NPSH reductions greater than 3m (10 ft), the chart has been limited to that extent and extrapolation beyond that limit is not recommended. In addition, warnings are included in the Hydraulic Institute Standards regarding the effect of entrained air or gases. This circumstance can cause serious deterioration of the head-capacity curve, of the efficiency and of the suction capabilities even when relatively small percentages of air or gas are present (see Chap. 18). The fact remains that there is insufficient correlation at this moment among the many tests cited in the technical literature. It appears rather probable that the very characteristics of a pump-that is, its specific speed and its actual design-play some role in the actual reduction in NPSH right along with the characteristics of the hydrocarbon. This role may be minor, but it probably does exist. A more exhaustive analysis of the phenomena that take place in a pump handling hydrocarbons is beyond the scope of this discussion. As a matter of fact, such an analysis would at best be open to argument, because several somewhat conflicting interpretations still exist with respect to what actually takes place. Whether a more rigorous theoretical derivation of NPSH reduction is ever developed is really immaterial. The important fact remains that as further experience is gained and more and more experimental data are accumulated, the validity of correction charts will be even greater. At the same time, we would like to incorporate here a word of caution: it is probably best to use this correction factor as an additional safety factor rather than as a license to reduce the available NPSH. This is a personal opinion, but one we share with a number of rotating machinery specialists of some of the major petroleum and petrochemical companies, and one that is reflected in the refinery pump specification API-61O [3.1]. NPSH REQUIRED FOR CRYOGENIC PUMPS It has been frequently claimed by users that the required NPSH curve of cryogenic pumps has a marked increase as the capacity falls to some 20 or 30 percent of design conditions. The question involves us with some ambiguity introduced by our semantics. If we consider this statement strictly on its literal interpretation, the answer is, no, a pump handling cryogenic liquids does not require any greater NPSH at reduced capacities than would be the case if the pump were to handle water. But if we instead word the question, Should a pump handling cryogenic liquids be provided appreciably more available NPSH 490 Suction Conditions and Limitations on Suction Performance J!! I/) a.. 6000 1000 600 400 -----.. . -... -1- Temperature OC o ·10 20 40 60 80 200 100 i i ' : : -~.-..-....I..------ -.-..~. ::=j!..~-·-t--:--Ir "-r ! •••.. , .•- i f -......-+-It- I i -,'-+-+-+-+- 200 i 1000 i I ; 100 600 400 80 10 3.0 8 2.4 8 5 1.8 1.5 4 1.2 3 0.9 2 0.6 80 40 1.5 0.45 200 c:: o ".1:1 () ::J "t:J ! a: J: en a.. z 1.0 0.3 20 100 0.5 0.15 10 60 8 40 8 ..-...k~-+-+-++ 4 . -+-+-+ ~ 20 / ! I , ! : : I i j ··.... -r--r·-!-+--++ 2 I ; I 10 o .! I I I !, 50 100 150 200 300 400 Temperature OF Fig. 19.14 NPSHR reductions for pumps handling hydrocarbons and high-temperature water. (Courtesy of the Hydraulic Institute) than it would require when handling water, if the pump is expected to operate at reduced flows?-the answer is an unequivocal yes. The problem of semantics arises from our accepted definition of NPSH, be it required or available. The only practical means to define NPSH is to refer to conditions prevailing at the pump suction flange, corrected to the pump centerline (assuming for the sake of simplifying this explanation that we are Suction Conditions and Limitations on Suction Performance 491 dealing with a horizontal pump). The energy at that location less the vapor pressure of the liquid, expressed in foot-pounds per pound or feet, is defined as the NPSH available, whereas the NPSH required by the pump at a given speed and for a given capacity is defined as the NPSH available when the total head of the pump is reduced by exactly 3 percent. The observed facts are strictly apparent and not real. What one sees in a test for NPSH of a cryogenic pump is an error in measuring the NPSH available and not an increase in NPSH required. One does not measure the NPSH required, one measures the available NPSH and then determines the required NPSH by observing the test values and calling that NPSH available at which a 3 percent drop in head occurs the required NPSH. The available NPSH is stated to be equal to the energy over and above the vapor pressure at the pumping temperature at the pump suction flange. In most cases, the fact that the vapor pressure at the impeller inlet differs to some extent from the vapor pressure at the suction flange can be neglected because this difference is negligible. But in the case of cryogenic pumps this difference can become so large under certain conditions that the effect is quite dramatic. At or near the best efficiency point, this cannot introduce any significant error, since the temperature rise in the pump is negligible and the flow past the wearing ring of the first stage is but a diminutive fraction of the flow into the pump. Thus, the temperature at the eye of the impeller does not change appreciably from the temperature at the suction flange and the assumed vapor pressure is essentially correct. As the capacity is reduced, the temperature rise increases while the leakage flow increases as a percentage of the suction flow. Of course, the calculated temperature rise takes place as the liquid passes through the impeller and casing passages. But some of the liquid from the impeller discharge passes back through the running clearances, where its temperature rises still farther, and mixes with the incoming flow at the impeller suction. The net effect is that the temperature at the eye of the impeller is no longer the same as at the suction flange, nor, of course, is the vapor pressure. The effect of the temperature rise in cryogenic pumps at reduced flows is frequently discussed under the subject of recommended minimum flows, since it generally dictates the setting of the minimum flow for this type of service. Consider, for instance, the effect of an increase in liquid temperature of 0.56°C (lOP) on the vapor pressure of water at 26.7°C (SOOP) and, say, of methane at the usual pumping temperature of -151°C (-240°F). Por water, Temperature 26.7°C (80°F) 27.2°C (81°F) ~T = 0.56°C WF) Vapor pressure 0.035 bar abs (0.507 psia) 0.036 bar abs (0.526 psia) Difference = 0.001 bar (0.019 psi) or 0.012 m (0.04 ft) whereas for methane, Temperature -151°C (-240°F) -140°C (-220°F) ~T = 11 °C (20°F) ~T = 0.56°C (1°F) Vapor pressure 2.28 bar abs (33 psia) 4.41 bar abs (64 psia) Difference = 2.13 bar (31 psi) Difference = 0.107 bar (1.55 psi) or, at SG of 0.4 = 2.7 m (8.9 ft) In other words, an increase in temperature of 0.56°C (1°P) increases the vapor pressure of 26.7°C (SOOP) water by 0.012 m (0.04 ft) and that of -151°C (-2400P) methane by 2.7 m (S.9 ft). 492 Suction Conditions and Limitations on Suction Peiformance If we were to imagine that at some low flow the effect described raises the liquid temperature at the eye of the impeller by 0.28°C (0.5°P) over that at the suction flange, the result is to increase the vapor pressure by a negligible amount if the liquid is 26.7°C (80 0P) water, but by as much as almost 1.4 m (4.5 ft) if it is methane at -151°C (-2400P). This increase in vapor pressure is not normally taken into account when running the NPSH test, and therefore the real NPSH available is 1.4 m (4.5 ft) less than the apparent NPSH available, if we use the temperature rise we have assumed. Since by definition the NPSH required is that NPSH available that will not cause a drop in total head of over 3 percent, it appears that the NPSH required has gone up. But it has not, actually. EFFECT OF SUCTION CONDITIONS ON PUMP CHARACTERISTICS The suction limitation of centrifugal pumps is determined by the fact that the impeller cannot impart energy to the liquid until the liquid is in the impeller between the vanes. Thus, the energy necessary to overcome the frictional losses up to the entrance of the suction vane ends of the impeller and the energy necessary to create the velocity required at this point have to come from some outside source. Furthermore, sufficient additional energy must be available in excess of these and other requirements so that the absolute pressure at all points is above the vapor pressure of the liquid, to prevent its flashing into vapor. Figure 18.16 shows the characteristics of a 6-in. pump. If it is operated in a system in which the available external energy on the suction side could only force 320 m3/hr (1,400 gpm) into the impeller, and if the total head of the system with this capacity is 30 m (100 ft), the pump will work to pump over 430 m3/hr (1,900 gpm) against this head. As there is insufficient suction head to get more than 320 m3/hr (1,400 gpm) into the impeller, however, the pressure at that point would be reduced below the vapor pressure of the liquid and part of the liquid would flash into vapor. If there is not sufficient available NPSH to permit a pump to develop its normal characteristics, cavitation will result and the pump will "work in the break." Thus, the characteristics of a centrifugal pump will vary with the available NPSH. Por the specific pump shown in Fig. 19.15, the characteristics in solid lines are for 0 suction lift (9.8 m [32 ft] NPSH) whereas with a 6.1 m (20 ft) suction lift (3.7 m [12 ft] NPSH approximately) the pump follows the 0 suction lift characteristics out to 1,500 gpm when cavitation starts, evidenced by the pump producing less head. Some increase in capacity results with further reduction in head until 420 m3/hr (1,850 gpm) is reached, when further reduction in head causes no increase in capacity. Thus the pump characteristics with a 6.1 m (20 ft) suction lift would be shown by the solid lines out to 340 m3/hr (1,500 gpm) capacity, and then by the broken line. The pump illustrated in Fig. 19.15 is of a fairly low specific speed type. In higher specific speed types, such as the high-speed, Francis screw vane and mixed-flow impeller designs, the operation at reduced NPSH also reduces the head developed at or near shut-off. With high-specific-speed types this reduction in head is even more pronounced. Unlike the low-specific-speed types, the higher-specificspeed types may deliver (with reduced NPSH), with lower total heads, up to a maximum capacity, and then, as the total head is further reduced, the capacity may be reduced below this maximum, reversing the head-capacity curve on itself. Usually cavitation is to be avoided. However, one type of pump, the condensate pump operating on nonthrottled systems, is especially designed for such operation. Figure 19.16 shows the normal headcapacity curve, with sufficient NPSH to prevent cavitation, and the system head-capacity curve; Pig. 19.17 shows the layout of the system on the suction side. If the amount of steam being condensed is equivalent to 11.8 m3/hr (52 gpm), the level in the hotwell will be that which gives 0.31 m (12 in) NPSH at the suction nozzle, so that the pump is operating in the break at 11.8 m3/hr (52 gpm) capacity and a 16.5 m (54 ft) total head, as dictated by the system head curve. If the amount of steam increases to equal 16.1 m3/hr (71 gpm), the liquid level in the hotwell will build up until it is 0.46 m (18 in) plus Suction Conditions and Limitations on Suction Performance 100 200 ... 90 180 z w u a: w Q. 20 10 o 8 4 12 16 20 24 28 CAPACITY, IN 100 GPM Fig. 19.15 A typical group of curves for a pump operating under varying suction conditions. 100 90 ... 80 ~ 60 W 1&.1 ..... 70 0 cI w 50 % ... ..J cI ....0 N 40 >... r- ~ >... • N- >30 r---i---+--+--f---+t ~ r - U ~ !:;a: f ~ cI t--~­ 20 I----lf----t--+--+-_t_ ucI r - .... u I I .... W % t--~--1&.1 00 10 r-~~-+--+-~--+_c1 W o % ' % I o 20 40 60 80 100 CAPACITY. IN GPM Fig. 19.16 Characteristics of a condensate pump operating on a submergence-controlled system. 493 494 Suction Conditions and Limitations on Suction Performance SURFACE CONDENSER WATERlEVEl~~~~ __~ __ ~_~I __~~=t__-.~~~ - -r +--- HOTWEll SUCTION.LINE LOSSES NE\ PoSITIVE SUCTION HEAD ~--,-_L Fig. 19.17 Typical installation of submergence-controlled condensate pump. the friction losses above the pump centerline, and the pump will be delivering 16.1 m3/hr (71 gpm) against a 17.7 m (58 ft) total head (the intersection of the head-capacity [0.46 m or 18 in] and the system-head curve). A regular impeller design on such service would be noisy and would show evidence of cavitation by damage to the vanes after a short time. For hotwell or condensate service, special impeller designs have been developed with larger suction areas (to operate on low NPSH) and with special suction vanes to give quiet operation and long life even though cavitating all the time they are in operation. In handling liquids containing dissolved gases, the pressure reduction on the suction side of the impeller vanes can be sufficient to allow the gases to be liberated and so the pump is actually handling a gas-and-liquid mixture. If the amount of gas liberated is not excessive, the only effect may be a reduction in capacity output and efficiency. This separation of gas from liquid is often mistaken for cavitation; it is not. If both cavitation and gas separation occur in a pump, the cushioning effect of the gas often quiets the cavitation noise. The cushioning effect has sometimes been used to quiet noisy cavitating pumps by bleeding air into the suction. Although it serves as a temporary expedient, the most economical solution should be replacement of the impeller by a design suitable for the suction conditions or a redesign of the pumping system so that the pump has sufficient NPSH to operate on its normal characteristics. WHEN SUCTION CONDITIONS ARE INADEQUATE When a system offers insufficient NPSH available for an optimum pump selection, there are several ways to deal with the problem. Basically, to correct the situation we can either find means to increase Suction Conditions and Limitations on Suction Performance 495 the NPSH available, means to reduce the NPSH required, or combine both approaches. Under the first category, we can 1. Raise the liquid level. 2. Lower the pump. 3. Reduce the friction losses in the suction piping. 4. Use a booster pump. 5. Subcool the liquid. To reduce the NPSH required, we can 6. Use slower speeds. 7. Use a double-suction impeller. 8. Use a larger impeller eye area. 9. Use an oversize pump. 10. Use an inducer ahead of a conventional impeller. 11. Use several smaller pumps in parallel. Each of these methods presents some advantages and some disadvantages and we shall examine and evaluate these methods individually. 1. Raise the liquid level-At first glance, this appears to be the simplest solution unless it is impractical because (a) the liquid level is fixed as in the case of a river, a pond, or a lake; (b) the amount by which the level must be raised is completely impractical; or (c) the cost of raising a tank or a fractionating tower is excessive. But frequently it will be found that only a few extra feet may permit the selection of a much less expensive or much more efficient pump and the resultant savings in first cost, energy, or maintenance will far outweigh the additional costs incurred by raising the source of the liquid. 2. Lower the pump-Just as in the case of raising the liquid level, the cost of lowering the pump may not be as prohibitive as one might imagine from past experience, since it may permit the selection of a higher speed, less costly and more efficient pump. An alternate approach may be to use a vertical pump with the impeller located below ground level. The penalty for this solution lies in the fact that the pump bearings may have to be lubricated by the liquid pumped. Although successful bearing designs and materials have been developed for this purpose, it should be well understood that the pump life cannot compare with the life obtainable from external bearings either grease or oil lubricated. Thus, one should expect more frequent scheduled overhauls with this solution. 3. Reduce piping friction losses-This is recommended under any circumstances and the cost of doing so will be easily repaid by both improved suction conditions and savings in energy. 4. Use a booster pump-This solution is particularly effective in the case of pumps intended for high-pressure service, where the resulting permissible higher speeds will yield great savings in first costs of the main pump, higher efficiencies, and frequently a lesser number of stages, which in itself leads to greater reliability. The booster pump can be selected as a low-speed, low-head pump of single-stage design. 5. Subcool the liquid-This approach increases the available NPSH by reducing the vapor pressure of the liquid pumped. It is most readily accomplished by injecting liquid taken somewhere from the stream where it is available at a colder temperature. In many cases, particularly at higher pumping temperatures, the amount of injected cold liquid is very small. As an example, if we are pumping water at 163°C (325°F), the injection of only 4 percent of 79°C (175°F) water will subcool our stream to the point that the available NPSH will have been increased by 6.1 m (20 ft) (see Figs. 19.18, 19.19, and 19.20). 496 Suction Conditions and Limitations on Suction Performance Q = INJECTION FLOW T2 =TEMP CONTROL VALVE 0= TOTAL FLOW T3 =TEMP T3 = Fig. 19.18 0 wz (0- Q) T1 + QT2 o Sub-cooling pumped liquid. v 50 ~o 45 a:wC/) offl lift: ZW _0 :x:W 40 .~ 35 ~ 1~V ~ 'r>~«7-V / 1~ V V L~~ C/)a: 30 a.:::J Z!;( C/)a: 25 :::Jw ....I a. a.;:E 20 a: w :::JI- 15 C/)w W:x: ~I- I-;:E Uo ~a: u..u.. W 10 5 V / / / / / . . .V / /' l-<U~ ~~ V .....V ~ ~ ~V ~ V ~ ~ ~ ::::::: ~ ~ ~ ~ I""" ~~, ==== ~ E::::: -- V 220 ::::::~ 240 ~ ~~ ~ j ; fI'" 6° / .:;,.- T 4° ..,..". ~ 2° ". rr V L L - V ~ ~~ ,,/ ~ ~ , I 260 280 300 TEMPERATURE IN OF 320 340 350 Fig. 19.19 Effect of sub-cooling on available NPSH with water. 6. Use slower speeds-Once a reasonable value of suction specific speed has been selected, it becomes obvious that the lower the pump speed, the lower will be the required NPSH. The problem, however, is that a lower speed pump will be more expensive and less efficient than a higher speed pump selected for the same conditions of service. Thus, lowering the pump speed will seldom prove to be the most economical solution. Suction Conditions and Limitations on Suction Peiformance 497 20 z 18 0 Cii en w 16 1I:u. n. WO 14 Wz 12 0 oz II: 0 =>- 1----+-+--b'-7~~A-r-~~~r*~""""~~r__::74 0.07 ~G 10 0.06 II:=> wen 8 ~+-4,~~~~~~~~~~~~~~ 6 ~~~~~~~~~~~~~~~~~~T-=t~0.~ ~~ 4 ~~~~~~::::::r1t:~=r-1'""1:JO.03 => en w II: 2 n.n. ::!:::!: w=> I-n. (!) !:i ~~§~::;~~~Ftf=-t'=::::=r-::::f~ 0.02 0 Fig. 19.20 7. 0.05 Effect of cold water injection. Use a double-suction impeller-Particularly for larger capacities, whenever a double-suction impeller is available for the desired conditions of service, this presents the most desirable solution. It is based on the following considerations: First, if we select the same suitable S value for both single and double suction impellers such that where SUbscript I refers to a single-suction impeller and subscript 2 refers to a double-suction impeller. Since We can assume first that (a) in which case NPSHR 2 = O.63NPSHR h or that NPSHR 2 = NPSHR 1 (b) in which case n2 = 1.414 nl' Keeping the pump speed the same in both cases, as in equation (a), we can reduce the required NPSH by 27 percent if we use a double-suction impeller. Alternatively, with a given required NPSH, as shown in equation (b), we can operate a double-suction pump at 41 percent higher speed (see Figs. 19.21 and 19.22). 8. Use a larger impeller eye area (Fig. 19.23)-This solution reduces the required NPSH by reducing the entrance velocities into the impeller. These lower velocities may have little effect on pump performance at or near its best efficiency point. But when such pumps run at part capacity, this practice can lead to noisy operation, hydraulic surges, and premature wear. This problem will be discussed in greater detail in Chapter 22. At this point, suffice it to say that it is a dangerous procedure and should be avoided if possible. 498 Suction Conditions and Limitations on Suction Performance 14 a:W ...J ...J W 12 10 Q..(f) ~a: OW wti:i 9:2: wO 8 (f)a: ...J~ al w =>w 6 011. 0 11. 0 4 ~ / 2 ~ V / V V ..L V l/ ~ I 2 4 ~ ASSUME: S= CONSTANT RPM = CONSTANT Q= CONSTANT ...-~ o V ./ ~ ..L V ,;' 6 8 10 12 14 I 16 I I I 18 20 Hs OF SINGLE SUCTION IMPELLER, FEET OR METERS Fig. 19.21 Required NPSH of double-suction impeller versus single suction impeller. 9. Use an oversize pump-Because the NPSH required by a pump decreases as the capacity is decreased, a larger pump than would otherwise be applied to the service is occasionally selected. This practice is risky and can lead to undesirable results. At best, the penalty is the choice of a more expensive pump that operates at a lower efficiency than might otherwise have been obtained (see Fig. 19.24). At worst, the operation at a lower percentage of the best efficiency flow can lead to exactly the same problems as the use of excessively enlarged impeller eye areas. 10. Use an Inducer-An inducer is a low head axial type impeller with few blades which is located in front of a conventional impeller (Fig. 4.17). By design, it requires considerably less NPSH than a conventional impeller, so it can be used to reduce the NPSH requirements of a pump (Fig. 19.25) or to let it operate at higher speeds with a given NPSH. The inducer is a very adequate solution for many situations but must be applied with care, as the permissible operating range of pumps with inducers is generally narrower than with conventional impellers. 11. Use several smaller pumps in parallel-Obviously, smaller capacity pumps at the same speed require less NPSH. Although this appears to be a costly solution, this is not necessarily so. In many cases, three halfcapacity pumps of which one is a spare are no more expensive than one full-capacity pump plus its spare. As a matter of fact, in many cases, two half-capacity pumps may be installed without a spare, since partload can still be carried if one pump is temporarily out of service. In addition, if the demand varies widely, operating a single pump during light load conditions will conserve energy, as we shall see in Chapter 21. DEFINITION OF NPSH REQUIRED The traditional definition of required NPSH for centrifugal pumps is that value at which the total head developed by the pump has deteriorated by exactly 3 percent. This value is often designated NPSH 3• Simplicity of testing (within reason) lead to the use of deterioration in performance as the indicator of Suction Conditions and Limitations on Suction Performance 2600 ASSUME: S=CONSTANI Hs = CONSTANT Q=CONSTANT 2400 J I 2200 2000 J II: w ...J ...J ) 1800 W a.. / )' ~ uj ci 1600 II: 0 u. :::ii: a.. 1400 II: J 1200 1000 800 / / I / 499 '/ V / V V " V )~ )' 600 800 1000 1200 1400 1600 1800 RPM FOR S.S. IMPELLER Fig. 19.22 Allowable speed of double-suction impeller versus single-suction impeller. cavitation, and a deviation well beyond the accuracy of measuring total head (generally about 1 percent) to the measure of 3 percent. In the 1960's, as the heads and capacities of pumps staged a spectacular climb upward, there developed a growing number of field problems with severe cavitation erosion, even when the available NPSH exceeded the required NPSH by a generally acceptable margin. As a result of these problems, pump users started asking themselves and the pump manufacturers whether the traditional definition of 3 percent head drop needed to be reexamined. The initial approach, driven by intuition, was to say that the extent of cavitation allowed by 3 percent head drop is evidently so great it causes erosion in some circumstances, so the solution is to base the required NPSH on less cavitation, hence a lower head drop. From this came the suggestions of NPSH required based on 1 percent and 0 percent head drop. Defining NPSH required as that at which the total head has deteriorated by 1 percent suffers the limitation that the deviation is equal to the accuracy of measuring the parameter whose deviation is being sought. In other words, the deviation necessary to 500 Suction Conditions and Limitations on Suction Performance Fig. 19.23 Enlarging impeller eye area to reduce required NPSH. CAPACITY IN M3 HR. 25 50 75 100 125 100 300 IUJ UJ U. V 250 75 lUi t;; ..J 150 50 z I ~ 0 I- 100 25 I ~ r-- "" / L ...... ~ '" 70 ~ o ~ B -- r-.... r-..... 60 A = DESIRED O,H. B = BEST EFF. O.H. 30 J - I( ~ ~ ./ ~ 8 / I{ 160 240 320 IUJ rn cc 6 20 ~ w ~ 4 ~ 80 tl:: UJ 50 / o A JIf' :IE CI J: ~~ (J) ~ 200 c:( UJ / -r---. l"oo" ~ 80 ~ en 10 ~ 2 400 480 560 CAPACITY IN GPM Fig. 19.24 Effect of oversizing a pump. 640 o Suction Conditions and Limitations on Suction Performance a> 2 (/) ..... <D a> E 0 0 <0 0 0 C\J <Do ::M 3,550 rpm , \ \ \ ~ 5.90 in. 1, -.:t -.:t "C C1l Dia., in. 6.50 in. 6.20 in. 0 0 5.60 in. 5.30 in. a> 2 C1l ~ 0 <X> 0 C\J 501 0 C\J 0 <0 ll') (/) ..... .i!l <D E <0 ll') -.:t 0 ------o _ ll') 6.50 in. __-:::::::::~:: 5.30 in. ,~~~~;;;==~~====~:~5.90 in. w, bhp 100 50 o Fig. 19.25 , 10 150 M C\J o o "C .0" :::c CI) a: z <D a.. 200 gpm , 20 30 Capacity 40 m3/hr. Performance of pump with and without inducer. define NPSH required cannot be separated from the inherent variations in the measured pump head. Zero percent head drop has no meaning in a definition based on deviation of a measured parameter, and therefore is not a valid definition. From the point of view of achieving rated performance, it is important in applying the pump to know the NPSH needed to ensure it produces 100 percent head. This is one purpose of the NPSH margin, but that value will be a conservative estimate from test data not an attempt to discern just where the head starts to deviate from 100 percent. These problems with lowering the defining head drop were compounded by experience that showed some pumps were suffering severe cavitation erosion even when operating with NPSH well above that at which there was any discernible deterioration in the total head (Fig. 19.26). This pointed to the need to adopt another means of investigating the development of cavitation in these pumps. Flow visualization, the technique used to verify the cavitation performance of model hydro-turbines and pump-turbines, filled this role. Research by many investigators, [19.2], [19.3], [19.4], [19.5], [19.6] established that the principal factors leading to rapid erosion despite high NPSH margins were the following: • Impeller energy level, which is related to the inlet peripheral velocity, VI' Generally impellers with VI of 30 m/s (100 ft/s) and higher are considered "high energy". Specific speed does have an effect, however, and at high specific speeds the defining limit falls to 25 m/s (80 ft/s). S02 Suction Conditions and Limitations on Suction Performance Fig. 19.26 Effect of erosion, noise, and pressure pulsations as available NPSH is decreased. (Reprinted with pennission from Oil & Gas Journal, Nov. 19, 1984) • Operating capacity as a fraction of impeller shockless capacity(l). • Intensity of cavitation associated with suction recirculation, which generally increases with suction specific speed, S (see chapter 22), but varies for any given S with the detail design of the impeller inlet, particularly its vane geometry. • Nature and temperature of the pumped liquid, with pure liquids of high specific gravity, e.g. water and water solutions, being the most aggressive, mixtures of low specific gravity, e.g. light hydrocarbons, the least. • Strength and resilience of the impeller material, with high strength and high resilience lowering the erosion rate. One suggestion that arose out of flow visualization research was to redefine required NPSH as that at the inception of caviation (Fig. 19.27). This was a philosophically "pure" concept, but one that quickly ran afoul of practicality when it was realized that the 90 percent or more of the pumps currently giving good service would need a significant increase in NPSH to satisfy this new definition. Following that short flirtation with a radical definition, the needs of the pump user began to prevail. These reduce to two simple questions: 1. How much NPSH should be provided to ensure the pump develops essentially rated total head? 2. How much NPSH should be provided, what materials should be used, and what precautions must be applied in operation to obtain a reasonable life for the component parts of the pump? In current application practice, the answers to these questions depend primarily on the energy level of the impeller (first stage impeller of multistage pumps). The impeller categories used and the corresponding application practice are: High energy impellers (VI ~ 25-30 m/s (80-100 ft/s); see earlier discussion). The design or a model (I) Capacity at which the liquid flow angle equals the impeller vane angle at the eye periphery; usually above pump BEP by 10 percent or more depending on the design. Suction Conditions and Limitations on Suction Performance ., 1_ POTENTIAL .... EROSION / NPSHd 1 NPSH 1 NPSHR (2) .... iI 1 I, NPSHA ., " , 503 + -I • '" . """-- ' ~ __ • / ' 1/ 1 MARGIN 1 '_~_--,-+_ ...... ----,,,,. (1)-~--~ (1) Typical test characteristic (2) Rise in characteristic observed in some tests 1 1 BEP MAX FLOW Fig. 19.27 Desired relationship between available NPSH, operating flow range. NPS~, and NPSH3 over a pump's of it is verified by flow visualization to ensure cavitation develops uniformly, and to establish the NPSH at 3 percent head drop, NPSH3, and at what NPSH the impeller is likely to suffer damage at a rate compatible with desired impeller life. This value, which is designated NPS~, corresponds in most practical cases to vapor cavities 10 mm (0.4 in) long. Production tests of the design or others factored from it are by 3 percent head drop. Such impellers are applied with the available NPSH above NPS~ over the expected operating flow range (Fig. 19.27). The margin over NPSH 3 for well designed impellers ranges from 100 to 200 percent. In applications subject to transient conditions that can lower the available NPSH substantially, such as boiler feed, it is necessary to check that this margin is sufficient to prevent the pump from flashing during the transient (see chapter 26). Medium and low energy impellers. Pumps that fall into this category-more than 90 percent of applications-are applied with various margins over NPSH3• The magnitude of the margin is sufficient to: a) ensure the pump develops essentially rated total head, and b) from experience, avoid serious cavitation erosion in impellers of moderate suction specific speed (see Chapter 22 for a detailed discussion of the effect of suction specific speed on impeller erosion). Table 19.2 summarizes typical margins for both categories of impellers. These margins assume impellers of adequate materials (see Chapter 17). The lower margin value for each application corresponds to low energy impellers, those whose inlet peripheral velocity, VI. is 15 m/s (50 ft/s) or lower. In assessing past experience against these margins, it is important to recognize that many, if not in fact most, centrifugal pumps normally operate with a greater NPSH margin than that given by the difference between the NPSH available from the data sheet and NPSH3 for the pump. The additional 504 Suction Conditions and Limitations on Suction Performance Table 19.2 Typical NPSH Margins Application Cold water Hydrocarbon Boiler feed-small High energy NPSH Margin (% of NPSH3) 35-50(1·2) 10(1) 50(3) 100-200 Notes: 1. 1 m (3 ft) minimum 2. Varies with pump size 3. Pumps to 1,850 kW (2,500 HP) at 3,600 RPM margin generally comes from conservatism in plant design by using an abnonnally low liquid level, an abnonnally high liquid temperature if the suction vessel is not saturated, an abnonnally high suction line friction loss, or a combination of all three. This is not always a conservative approach since it can lead to a pump that operates poorly all the time rather than cavitating on the few occasions extreme suction conditions are encountered (see Chapter 22). If we, pump users and manufacturers alike, are to refine the application of centrifugal pumps in tenns of cavitation, it is important that the data used are accurate. This means the stated NPSH available should be that under nonnal conditions with the minimum under extreme conditions given for additional infonnation. Doolin [19.7] has proposed a general approach to the question of impeller life. By this method, a series of factors is applied to detennine the relative life of a given impeller in various applications. The factors considered are: • • • • • • • • Actual margin over NPSH3 Thermodynamic properties of the pumped liquid Corrosiveness of the pumped liquid Impeller material Operating speed Off-design operation Suction specific speed Pump duty cycle The NPSH margin is assumed in all cases to be sufficient to allow the pump to produce rated head. And all the factors assume the suction piping is able to deliver unifonn. swirl-free flow to the impeller (see Chapter 28). With a "base" impeller life and a "standard" value of NPSH required, this method can be used to determine the NPSH that should be made available to ensure the pump impeller achieves its desired life in any given service. Because the calculation is relative, the "standard" NPSH required can be whatever is convenient. which today is NPSH3• The difficulty with this approach is detennining the value of the various "life" coefficients. At the present state of the art, we have only meager data on the effect of the numerous factors known to affect impeller life, and are hampered in improving those data by the difficulty of carrying out qualified erosion rate tests. The saving grace is that reasonable data are available for the effect of water, both cold and hot. on various materials. Since water has a very high potential for causing Suction Conditions and Limitations on Suction Performance 505 cavitation erosion, the data that are available allow adequate designs for those services. The lack of data for other liquids may mean that today's applications involving these liquids are overly conservative, but that is both a safe approach and an opportunity for the future. Taking account of where we are today and noting the progress being made in cavitation research, the future holds the possibility of being able to state the required NPSH in terms of a given life, what we might term NPSHLxo with the value "x" being selected at the design stage taking account of the cost of impeller replacement versus the cost of providing various amounts of NPSH. In this connection, Vlaming [19.4] has already proposed 40,000 hours impeller life as a standard and presented means to estimate the NPSH that must be provided to achieve it. More recently pump manufacturers, [19.8], [19.9], have reported the development of computer models able to estimate impeller life and the probability that the estimated life will be achieved. These computer models are based on correlations of cavitation intensity and impeller erosion rate. Cavitation intensity is, in tum, derived from bubble length and cavitation noise measurement. Although these models are not yet in wide use, and don't take into account all the factors involved in the complex phenomenon of cavitation, they do represent a notable step toward being able to assess impeller life in terms of cavitation erosion in the same way we now treat other components of turbomachines such as bearings and shafts. BIBLIOGRAPHY [19.1] ANSI/HI 1.6, 1994, Centrifugal Pump Test, Hydraulic Institute, Parsippany, NJ, USA. [19.2] Robert R. Ross, Theoretical Predictions of Net Positive Suction Head Required (NPSHR) for Cavitation Free Operation of Centrifugal Pumps, United Centrifugal Pumps, San Jose, USA. [or similar paper by Johnson that preceded this]. [19.3] E. Grist, Net Positive Suction Head Requirements for Avoidance of Unacceptable Cavitation Erosion in Centrifugal Pumps, I. Mech. E Paper C163n4, London, 1974. [19.4] D.J. Vlaming, A Methodfor Estimating the Net Positive Suction Head Required by Centrifugal Pumps, ASME Paper No. 81-WA/FE-32, 1981. [19.5] P. Cooper and F. Antunes, Cavitation Damage in Boiler Feed Pumps, Symposium Proceedings: Power Plant Pumps-The State of the Art, EPRI CS-3158, July 1983, pp. 2-24 to 2-49. [19.6] B. Schiavello, Visual Study of Cavitation-An Engineering Tool to Improve Pump Reliability, EPRllst International Conference on Improved Coal Fired Power Plants, Palo Alto, California, November 19-21, 1986. [19.7] J.H. Doolin, Judge Relative Cavitation Peril with Aid of These 8 Factors, Power Magazine, pp. 77-80, October 1986. [19.8] J.F. Gulich and S. Pace, Quantitative Prediction of Cavitation Erosion in Centrifugal Pumps, Proc. of the 13th IAHR Symposium on Progress in Technology, Montreal, Canada, September 1986, Paper #42. [19.9] B. Schiavello and M.R. Prescott, Field Cases Due to Various Cavitation Damage Mechanisms: Analysis and Solutions, Porch. EPROM Symposium: Power Plant Pumps, June 1991, Tampa, Florida. 20 System-Head Curves A centrifugal pump must be suitable for operation with the system in which it is used. To select a suitable pump, the characteristics of the system must be considered. It is usually easy to determine the characteristics of the system, but, occasionally, a complicated system that requires analysis of each of its parts is encountered. It is not possible to provide a detailed analysis of every type of problem that may be encountered when using centrifugal pumps. However, the following discussion of a few typical examples will acquaint the reader with the general method of solving such problems. The total operating head for a given capacity through a system is the algebraic sum of the static head from supply level to discharge level (Hst ); the terminal pressure minus the suction pressure (P rIPs); all friction losses at this capacity (hI); and the entrance and exit losses (h j and he). These values are expressed in meters (feet) of the liquid being handled (see Fig. 18.15). Ideally, the simplest system would have only one static head. In an actual system, there would also be some friction losses. If there is no static head component and no difference in pressure on the suction and discharge liquid levels (Fig. 20.1), the head would be entirely frictional. CAUSES OF FRICTION The characteristics of the flow of liquid in a pipe vary with the velocity. When the velocity is very low, the flow is laminar. Under these conditions, the effect is that of concentric cylinders of the liquid shearing past each other in an orderly fashion. The greatest velocity is at the center of the pipe; the velocity falls to zero at the pipe walls. With water, laminar flow occurs when the average velocity is very low. As a result, laminar flow with water is rarely encountered in normal applications. As the average velocity of the liquid is increased, the flow becomes turbulent. Under turbulent flow conditions, the axial velocity measured across the pipe diameter is more uniform than in laminar flow; the flow is laminar in an area adjacent to the pipe walls. The average velocity at which the flow changes from laminar to turbulent is not absolute; there is a critical range in which the character of the flow may be of either type. The flow of any liquid is accompanied by two types of friction: internal friction caused by the rubbing of the fluid particles against one another and external friction caused by the rubbing of the fluid particles 506 I. J. Karassik et al., Centrifugal Pumps © Chapman & Hall 1998 System-Head Curves DISCHARGE PIPING ONE a-IN. CHECK VALVE ONE a-IN. GATE VALVE ONE 8- x 12-IN. INCREASER 3,000 FT OF 12-IN. PIPE TWO 12-IN. LONG RADIUS ELBOWS THREE 12-IN. 45 DEG ELBOWS SUCTION PIPING ONE 10- xI2-IN. REDUCER ONE 12-IN. LONG RADIUS ELBOW 20 FT TOTAL OF 12-IN. PIPE Fig. 20.1 507 Simple pumping system with head that is entirely friction. against the pipe walls or against the static layer of liquid adhering to the walls. Energy must be expended to overcome this friction. If the flow is turbulent, the friction developed is partly dependent on the roughness of the walls. Because the interior surfaces of pipes of the same material are practically the same irrespective of diameter, small pipes are relatively rougher than large ones. Thus, for equal velocities, the larger the pipe, the smaller will be the friction loss. The roughness of the pipe wall also depends on the material from which the pipe is made and, after the pipe has been in service, on any change that occurs at the inner surface. Numerous pipe friction experiments and studies have been made, and a great number of tables and charts are available. The Williams and Hazen tables are one of the earlier standards for water and have been found particularly reliable for cast-iron pipes of 3-in. or larger diameter. These tables are based on an empirical formula that can be modified to the following form: hi = 10.45 (QIC)L852(L/(N 87 where hi =loss in head for length L, in feet of water Q = flow, in gallons per minute d =inside diameter of the pipe, in inches C =coefficient of pipe smoothness L = length of pipe, in feet The coefficient C is an index of the smoothness of the interior pipe surface (the smoother the pipe interior, the higher the C value), and the selection of the proper value of this coefficient will determine the accuracy of the friction head loss calculated for any problem. For new unlined cast-iron pipe, a C of 130 is the common value, but some new pipes in which the friction head losses indicate C values of 140 or higher have been encountered. Pipes coated on the interior to give a smoother surface naturally have a higher C value. There are also records of pipes made of rolled metal and very smooth cement that have C values of 145 to 150 or higher. 50S System-Head Curves Most pipes deteriorate with age, and thus the C value becomes lower. This decrease in C value or increase in friction head loss depends upon the material of the pipe, the pipe coating used (if any), and the character of the water. Therefore, any C value selected for an old pipe represents a pure guess. When it is necessary to ascertain friction head losses in such pipe, a test should be made, if possible, to find the friction loss at some known capacity so that the coefficient can be approximated. If such a test cannot be made, some guide to indicate the average C change with age is desirable. Figure 20.2 shows in chart form the coefficients that might be expected for cast-iron pipes handling soft, clear, unfiltered water. Pipes carrying water that has been filtered but not chemically treated have been found to deteriorate less rapidly than pipes handling unfiltered water. Chemically treated waters have sometimes been found to produce more corrosion in the pipe than untreated water. Brackish water usually results in increased tuberculation. Some moderately hard waters have been found to cause a slow rate of deterioration. On the other hand, they are also capable of depositing calcium carbonate on the interior of the pipe, thus both reducing its size and increasing its roughness. Smooth cement and cement-lined pipes have been found to maintain a high C value for many years. 140 I 'NEW' 130 I 30 II: S'YEARS 120 \) ...: Z .... 2 ~ ~ ....0 liD 100 - Z .... N c( :J: ./ • Z c( <II :E !! ,J 90 0 80 ~ ~ i 70 ,/' V ~ ~ ./ / / 60 3 Zo Qo ~- 10 yEARS ..,..",.. ~ u , ~ i""" 4 ~ ".,..,.. ~..J I 00 ~ ~ ~ ,/ ,r ", ~ 8 10 1.2 ~Z a. .... 1.4 ell:' Z -en Z .... ".,. "". i-"" l JA~ )9- Q\) ~c( ~ 'liAR"!. """" ~~ ~ i"'""" - :J: -:;, :E~ 1I:c( 1.6 1.8 ~> ~\) II:~ Oz ....... .... 11: 2.0 ..J .... c(~ u~ enO 60 6 1.0 II: ~'ARS ~ , 5 ....:;, --.-- io"""" ~ ...i o.... YEiRS J 25 yEARS .",... ~ V ~ I""'" "" / V u~ I 10 26 yJARS """". . 00 ... -, I 20 12 14 16 1.20 24 3036 4248 2.5 60 INSIDE DIAMETER OF PIPE. IN INCHES Fig.20.2 Change in Williams and Hazen coefficient C with years of service, for cast-iron pipes handling soft, clear unfiltered water. System-Head Curves 509 All these possibilities make it difficult to select, with any assurance of accuracy, the proper coefficient, so that any guide should be used with reservations. In important studies it is often possible to locate a similar installation and use the head losses obtained on that installation as a guide. ESTIMATING FRICTION LOSS When selecting pumping machinery, it is particularly desirable to consider the friction head loss that may occur when the installation is new, as well as that which may result some years after it has been in service. Most charts and tables based on the Williams and Hazen formula have been made for a C value of 100, which is approximately the value expected for pipe that is 15 years old. A C value of 100 is commonly used as a design value; no calculation is made to determine the friction when the installation is new. This practice tends to distort the problem of compensating for friction losses, and may result in trouble when centrifugal pumps are used. For example, in a new installation in which most of the pumping head is friction, the actual friction head would be lower than that allowed for in the selection of the pump. As a result, the pump would deliver more capacity at some reduced head that would equal the system head. The increased capacity would depend on the pump characteristics and the increase in system head with capacity, but might be 15 to 25 percent more than the capacity for which the pump was selected. Operation at this increased capacity might cause the pump to require more power, thus overloading the driver. If the installation was such that the available net positive suction head (NPSH) at the design capacity exceeded only slightly the NPSH required by the pump for this capacity, the resulting increase in pump capacity with the lower operating head would result in cavitation. Table 20.1 shows pipe friction losses for 3-in. to 24-in. inside diameter pipes based on the Williams and Hazen formula with C of 100. The usual values of C for new pipe are: Smooth, unlined cast iron Asphalted cast iron Cement asbestos Very smooth cement or cement-lined cast iron Ordinary cement Drawn steel or wrought iron Riveted steel 130 140 130-140 130-140 110-120 130-140 90-110 Conversion factors for changing friction values based on C = 100 to other values are indicated on the right-hand side of Fig. 20.2. For example, with a flow of 700 gpm through a 6-in. pipe, the friction head loss is 6.23 ft per 100 ft of pipe with C = 100. For C = 130, the conversion factor is 0.613; therefore, the friction head loss will be 6.23 x 0.613 or 3.83 ft per 100 ft of pipe. Steel and wrought-iron pipes are used extensively in sizes up to 8 in. and larger with cold water. In drainage and irrigation work, steel pipe is used almost exclusively with larger sizes fabricated of steel plate. Cast-iron pipe is now seldom used for water lines in sizes less than 3 in. Most long water lines are cast iron, although plastic is growing in popUlarity for smaller diameter lines. Cement asbestos is not used in new lines today. Steel pipe is made with the same outside diameter for a number of different weights or wall thicknesses. Therefore, the inside diameter will not be the same as the nominal diameter, and the friction losses for a given capacity must be corrected for such differences. With steel and wrought-iron pipe, it is more difficult to predict the change in friction head that will result when the pipe becomes older than it is to predict the changes in cast-iron pipes. In some situations, the pipe decreases in area due to tuberculation, while in other situations the pipe corrodes and the film is washed ... ~ u. 300 350 400 450 500 550 600 650 700 750 800 900 1,000 1,100 1,200 100 125 150 175 200 225 250 275 90 50 60 70 80 40 30 gpm f 0.99 1.13 1.28 1.42 1.56 1.70 1.84 1.99 2.13 2.27 2.55 2.83 3.12 3.40 0.059 0.076 0.094 0.114 0.136 0.160 0.186 0.214 0.242 0.273 0.339 0.412 0.492 0.578 12-in. ID pipe VI f 0.94 1.04 1.15 1.25 1.36 1.46 1.56 1.67 1.88 2.08 2.29 2.50 0.044 0.054 0.064 0.076 0.088 0.100 0.114 0.129 0.160 0.195 0.232 0.273 14-in. ID pipe v f 13.6 15.9 18.2 37.9 50.4 64.6 0.82 0.98 1.14 1.31 1.47 1.63 2.04 2.47 2.86 3.27 3.68 4.08 4.50 5-in. v 4.90 5.72 6.54 7.36 8.18 8.99 9.81 10.6 11.4 12.3 ID pipe 13.1 14.7 0.034 16.3 0.041 18.0 0.048 9.34 12.4 15.9 19.8 24.1 28.7 33.7 39.1 44.9 0.131 0.224 0.338 0.475 0.631 0.808 1.01 1.22 1.85 2.59 3.44 4.41 5.48 6.67 7.96 0.77 1.02 1.28 1.53 1.79 2.04 2.30 2.55 3.19 3.83 4.47 5.10 5.74 6.38 7.02 0.534 0.910 1.38 1.92 2.56 3.28 4.08 4.96 7.50 10.5 14.0 17.9 22.3 27.1 32.3 1.36 1.81 2.27 2.72 3.18 3.63 4.08 4.54 5.68 6.81 7.95 9.08 10.2 11.3 12.5 f ID pipe v ID pipe 4-in. f 3-in. v 7.65 8.93 10.2 11.5 12.8 16-in. ID pipe 14.0 15.3 0.96 .039 18-in. ID pipe 16.6 1.04 .046 1.12 .052 17.9 1.20 .060 0.95 0.034 1.01 0.038 20-in. 1.28 .067 1.44 .084 1.13 0.047 1.60 .102 1.26 0.057 1.02 1.76 .121 1.39 0.068 1.12 1.51 0.080 1.23 1.92 .143 v 3.13 4.20 5.38 6.68 8.12 9.69 11.4 13.2 15.1 17.2 19.4 24.1 29.3 35.0 0.114 0.160 0.213 0.273 0.339 0.412 0.623 0.874 1.16 1.49 1.85 2.25 2.68 ID pipe f 1.30 1.73 2.21 2.75 3.34 3.99 4.68 5.43 6.23 7.08 7.98 9.92 12.1 14.4 16.9 0.088 0.112 0.139 0.170 0.256 0.360 0.478 0.613 0.762 0.926 1.11 0.79 0.91 1.02 1.14 1.42 1.70 1.99 2.27 2.55 2.84 3.12 3.41 3.97 4.54 5.10 5.68 6.24 6.81 7.38 7.94 8.51 9.08 10.2 11.4 12.5 13.6 ID pipe f 6-in. v 0.320 0.425 0.545 0.678 0.823 0.982 1.15 1.34 1.53 1.74 1.97 2.44 2.97 3.55 4.17 0.089 0.118 0.151 0.188 0.228 0.272 0.96 1.12 1.28 1.44 1.60 1.76 1.91 2.23 2.55 2.87 3.19 3.51 3.82 4.15 4.47 4.78 5.10 5.74 6.38 7.02 7.66 ID pipe f 8-in. v f 1.23 1.43 1.63 1.84 2.04 2.24 2.45 2.65 2.86 3.06 3.26 3.67 4.08 4.50 4.90 1.02 1.12 0.108 0.144 0.184 0.228 0.278 0.331 0.389 0.452 0.518 0.589 0.666 0.825 1.00 1.20 1.41 0.077 0.092 IO-in. ID pipe v Table 20.1 Velocity and Friction Head Loss in Old Piping Friction values apply to cast-iron pipes after 15 years service handling average water. Based on Williams and Hazen's formula with C = 100 . 300 350 400 450 500 550 600 650 700 750 800 900 1,000 1,100 1,200 100 125 150 175 200 225 250 275 90 50 60 70 80 40 30 gpm ........ III 12-in. 3.69 3.97 4.25 4.54 5.11 5.67 7.09 8.51 9.93 11.3 12.8 14.2 15.6 17.0 18.4 19.9 ID pipe 0.671 0.770 0.875 0.985 1.22 1.49 2.25 3.16 4.20 5.38 6.68 8.13 9.70 11.4 13.2 15.2 14-in. 2.71 2.92 3.12 3.33 3.75 4.17 5.21 6.25 7.29 8.33 9.38 lOA 11.5 12.5 13.6 14.6 15.6 16.7 18.8 Continued ID pipe 0.316 0.363 00413 00465 0.578 0.703 1.06 1.49 1.98 2.54 3.15 3.83 4.58 5.38 6.24 7.16 8.13 9.16 11.4 16-in. 2.08 2.24 2.40 2.55 2.87 3.19 3.99 4.78 5.59 6.39 7.18 7.98 8.78 9.68 lOA 11.2 12.0 12.8 1404 16.0 17.6 19.2 ID pipe 0.165 0.190 0.215 0.243 0.302 0.367 0.555 0.778 1.04 1.33 1.65 2.00 2.39 2.81 3.26 3.74 4.24 4.79 5.95 7.24 8.63 10.1 ·Velocity, in feet per second. lfriction head loss, in feet of water per 100ft of pipe. 1,300 1,400 1,500 1,600 1,800 2,000 2,500 3,000 3,500 4,000 4,500 5,000 5,500 6,000 6,500 7,000 7,500 8,000 9,000 10,000 11,000 12,000 13,000 14,000 15,000 16,000 18,000 20,000 25,000 Table 20.1 18-in. 1.64 1.76 1.89 2.02 2.27 2.52 3.15 3.78 4.41 5.04 5.67 6.30 6.93 7.56 8.19 8.82 9045 10.1 11.3 12.6 13.9 15.1 1604 17.6 18.9 ID pipe 0.093 0.107 0.121 0.137 0.170 0.207 0.312 00438 0.583 0.746 0.928 1.13 1.35 1.58 1.83 2.11 2.39 2.69 3.39 4.07 4.86 5.71 6.62 7.59 8.63 20-in. 1.33 1.43 1.53 1.63 1.84 2.04 2.55 3.06 3.57 4.08 4.59 5.10 5.61 6.12 6.73 7.15 7.66 8.17 9.18 10.2 11.2 12.3 13.3 14.3 15.3 16.3 1804 ID pipe 0.056 0.064 0.073 0.082 0.102 0.124 0.187 0.262 0.349 0.447 0.555 0.675 0.806 0.947 1.10 1.26 1.43 1.61 2.01 2.44 2.91 3042 3.96 4.54 5.27 5.82 7.24 6-in. ID pipe 24-in. ID pipe 14.8 19.6 15.9 22.5 1.06 0.030 17.0 25.5 1.13 0.034 18.2 28.8 1.28 0.042 1.42 0.051 1.77 0.077 2.13 0.108 2.48 0.143 2.83 0.184 3.19 0.228 3.54 0.278 3.90 0.332 4.25 0.390 4.61 00452 4.96 0.518 5.32 0.589 5.66 0.664 6.38 0.825 7.09 1.00 7.80 1.20 8.51 1.41 9.12 1.63 9.93 1.87 10.6 2.13 11.3 2040 12.8 2.98 14.2 3.62 17.7 5048 8-in. ID pipe 8.30 4.83 8.93 5.54 9.55 6.30 10.2 7.10 11.5 8.83 12.8 10.7 16.0 16.2 19.1 22.8 lO-in. 5.31 5.72 6.12 6.53 7.35 8.17 10.2 12.3 14.3 16.3 1804 ID pipe 1.63 1.87 2.13 2.39 2.98 3.62 5048 7.67 10.2 13.1 16.3 1,300 1,400 1,500 1,600 1,800 2,000 2,500 3,000 3,500 4,000 4,500 5,000 5,500 6,000 6,500 7,000 7,500 8,000 9,000 10,000 11,000 12,000 13,000 14,000 15,000 16,000 18,000 20,000 25,000 512 System-Head Curves away. With smaller steel piping, it is best to consider what the friction head will probably be when the pipe is new and to make allowance for an increase in the loss based on local conditions. If a basis of comparison is not available, an increase in friction of 25 percent with age would be a reasonable allowance. A general solution for the head loss caused by incompressible flow in piping is given by the DarcyWeisbach equation [20.1] where: hI ht =head loss caused by friction, =j(UD)(V'l!2g) in meters (feet) of liquid L = length of straight pipe run, in meters (feet) D = inside diameter of the pipe, in meters (feet) V = average liquid velocity, in m/s (ft/s) g = acceleration due to gravity; 9.S1 m/s2 (32.2 ft/s 2) 1 =friction factor The value of the friction factor, f, depends on the relative roughness of the pipe, kID, and the Reynolds number Re = VDlv where: k = pipe roughness, in m (ft) v = kinematic viscosity, in m2/s (ft2/s) For laminar flow, Re < 2,320, the value of / is independent of the relative roughness of the pipe bore, and is given by the Hagen-Poiseuille equation 1 = 64IR e The flow in most pumping applications is turbulent with Re > 2,320, for which the value of/is determined from the Prandtl-Colebrook equation 1/"1 = -2log (2.51/R;.JI + kI3.71D) For the limiting case of hydraulically "rough" piping, R.(k/D) > 1,300, the value of/can be determined from the simpler Nikuradse equation INI = 1.14 - 2log(klD) Typical values of k are: k Pipe material and lorm Smooth; plastic, glass, copper, brass; drawn, extruded, ground finish Cast iron, cement lined Cast iron, asphalt lined Cast iron, unlined, new Cast iron, encrusted Seamless steel, new Welded steel, new Galvanized steel Welded steel, corroded Concrete, new, rendered Heavily encrusted, timber, masonry mm up to 0.002 in SOJ1in 0.025 0.10-0.15 0.15-0.25 1.5-3.0 up to 0.05 0.05-0.10 up to 0.15 0.15-0.20 0.20-0.S0 0.5-2.0 0.001 0.004-0.006 0.006-0.010 0.060-0.120 up to 0.002 0.002-0.004 up to 0.006 O.OO6-O.00S 0.OOS-O.030 0.20-0.S0 System-Head Curves 513 To allow estimates of piping friction loss without having to repeatedly solve the Prandtl-Colbrook equation, charts or tables are often used. Table 20.2(a) [20.2] gives friction losses in metric units for liquids of v = 1.236 mm 2/s (pure fresh water at 12°C or 54°F) and k = 0.10 mm. Friction losses in pipes with k other than 0.10 mm, are determined by applying the correction factor from Table 20.2(b). Table 20.2(c), drawn from data published by the Hydraulic Institute [20.3], shows friction losses in US units for liquids of v = 1.130 mm2/s (l2.16xlO-6 ft 2/s; equal to pure fresh water at 60°F) and k = 0.05 mm (0.002 in or 0.00015 ft). I~.5 2 I , 3 5 6 flowa,ele 0 Flowrate 0 In m'lh 20 3O~ & 10 eo 100 60 200 In 60 50 40 JO . 600 800 1000 _I I " 2o dl I § 0.& ;;; 0.6 0.5 Co :t ".,. 10 ~ ~ & I'll " ~ l' 's 5 S < $ 3 r{ 1 111 V ... 2 ''/s !! i "'·,6 r---. ... ~s . co c E I 00 "' ~IL < 27- 50000 $ y..... 6 5 Co 20 000 50 50 <0 & c, '0 10000 10 ~ 0 3 5000 ...... ::; "!O m' /h - - t! 0 Qj In 2000 JOOO I ~.~ l'. . JOO 0.1 ~ 0.2 ~s 11 04 Il' II 0.6 0oS IS; I V ... ... 0' oa "!- ... 004 001 001 l- ~ f' 0.02 'll -..... 001 0.5 3 < 5 6 &10 Flowrale 203040 a In m )/h - 60 eo 100 200 JOO 2000 JOOO 5000 FlowratftO inm'/h _ _ 600 1001000 Table 20.2(a) Head loss, hI' per 100 m of straight pipe. (Based on Prandtl-Colebrook equation with k = 0.1 mm, turbulent flow, and v (pure fresh water at 12°C). 10000 20000 = 1.2136 mm2/s ~ ..., ~ O.OS ~ J. ~ 0.2 0,06 0.02 i ~ 0.0& o,00. 8 0.3 0-' Q06 0.os !! E .' = 0 I 'J 0,1 00& ~ 1.,/ 11$ I l', 'tl '0 ;: '"c II' " 11, 0,4 !2 "-s ~ I . E 8. 'c, 0&,01 514 System-Head Curves 2.1 U 'r-... r--..r-... 2.6 I" ' 2.4 ......... r-.... 2.2 2.0 i"-. ........ ......... ~ .......... 1.8 t"-. (; U ~ c: I""- ~ f'.. r... ~~ 1.& " I'r-- , . . . r- 2.6 '-!,I 2.4 "~~ r-- r-- ~..~ i'"- r-!-.: I ...... ~ r- r- "'1- l"'- I"'- I'-~ r- I.' " • 0.25 mm II .'0.1 1.0 U ~ c: .~ U 1.4 1.2 ~ (; I.) 1.2 ~~ 1.0 k • 0.05 mm 0.1 o• I.e (; 1.4 o 2.2 2.0 r--r-- U (; r- 1"-1'- "'", .~ I.) r--t---., 0.' 1-":0.01 mm_ ,... o" 25 • ~ , ml, y! 1 m~' y. 1m" j 2 ;0 iO 85 D.gs eo I 0.s )() 200 400 Soo! 00 nominal pipe diameter in mm. 100 15() 8)0 1100 mm 2t,a .6 Table 20.2(b) Correction factors for roughness k ± 0.1 mm. For k = 0.05 to 3.0 mm the differences between the correction factors due to flow velocity can be neglected, therefore average values are shown. However, for k = O.OJ mm the effect of flow velocity must be taken into consideration. ... III III 0.10 0.13 0.23 0.34 0.48 0.63 0.82 1.00 1.24 1.82 2.55 3.40 4.35 5.44 6.59 1.01 1.26 1.51 1.76 2.01 2.27 2.52 3.15 3.78 4.40 5.04 5.66 6.29 0.12 0.18 0.25 0.34 0.43 0.54 0.65 1.00 1.39 1.90 2.40 2.98 3.68 2.83 4.88 7.12 15.0 25.6 0.11 0.39 0.82 1.37 2.08 5-in. pipe (5.047-in. 10) 1.12 0.11 1.28 0.15 1.44 0.18 0.22 1.60 2.00 0.33 2.40 0.47 2.80 0.62 3.20 0.80 0.97 3.60 4.00 1.19 0.81 0.97 1.30 1.62 1.94 2.27 2.59 2.91 3.24 4.05 4.86 5.66 6.48 7.30 8.10 25 30 40 50 60 70 80 90 100 125 150 175 200 225 250 4-in. pipe (4.026-in 10) f I-in. pipe (1.049-in. 10) v (3V2-in. pipe (3.548-in. 10) f 2.23 2.97 3.71 5.56 7.41 v 6 8 10 15 20 h/ 2 3 4 5 VI 0.37 0.74 1.11 1.49 1.86 gpm f 10.3 14.4 0.76 1.29 1.95 4.06 6.80 0.10 0.21 0.36 0.54 1.11 1.39 1.66 1.94 2.22 2.50 2.77 0.09 0.13 0.18 0.24 0.31 0.38 0.47 6-in. pipe (6.065-in. 10) 5.35 6.43 1.28 1.72 2.14 3.21 4.28 0.43 0.64 0.86 1.07 1V4-in. pipe (1.380-in. 10) v v f 1.44 1.60 0.10 0.12 8-in. pipe (7.981-in.lO) 4.70 6.60 11.2 16.6 0.35 0.61 0.90 1.87 3.12 0.95 1.26 1.57 2.36 3.15 3.94 4.72 6.30 7.87 0.10 0.17 0.26 0.47 0.63 0.79 1V2-in. pipe (1.61O-in 10) Table 20.2(c) Velocity and Friction Head Loss in New Piping Friction values apply to Schedule 40 (standard weight) steel pipe carrying water. f 2.38 2.86 3.82 4.77 5.72 6.68 7.62 8.60 9.56 0.57 0.76 0.96 1.43 1.91 1.39 1.92 3.35 5.00 7.00 9.40 11.9 14.7 18.7 0.10 0.17 0.26 0.54 0.92 2-in. pipe (2.067-in. 10) v f 1.67 2.00 2.68 3.34 4.02 4.68 5.35 6.02 6.70 8.37 10.0 11.7 0.67 1.00 1.34 0.58 0.81 1.36 2.06 2.85 3.80 4.95 6.05 7.47 11.1 15.4 20.8 0.11 0.23 0.38 2Y2-in. pipe (2.469-in. 10) v f 1.08 1.30 1.73 2.16 2.60 3.03 3.46 3.89 4.34 5.41 6.50 7.58 8.66 9.75 10.8 0.87 0.20 0.28 0.47 0.72 0.99 1.33 1.72 2.13 2.58 3.90 5.44 7.30 9.18 11.6 14.0 0.13 3-in pipe (3.068-in. 10) v 25 30 40 50 60 70 80 90 100 125 150 175 200 225 250 6 8 10 15 20 2 3 4 5 gpm !Jl ... 0\ 4-in. pipe (4.026-in. ID) 6.92 4.35 7.55 5.04 8.80 6.85 10.1 8.67 11.3 10.9 12.6 13.3 13.9 16.0 19.1 15.1 5-in. pipe (5.047-in. ID) 4.40 1.43 4.80 1.65 5.60 2.21 6.40 2.89 7.20 3.56 8.00 4.36 8.80 5.17 6.16 9.60 10.4 7.22 11.2 8.29 12.0 9.40 12.8 10.3 13.0 14.4 15.8 16.0 19.0 17.6 'Velocity, in feet per second. 2Priction head loss, in feet of water per 1()() ft of pipe. 275 300 350 400 450 500 550 600 650 700 750 800 900 1,000 1,100 1,200 1,300 1,400 1,500 1,600 1,800 2,000 2,500 3,000 3,500 4,000 4,500 5,000 5,500 6,000 Continued 3Y2-in. pipe (3.548-in. ID) 8.91 7.90 9.72 9.30 11.3 12.2 13.0 15.9 14.6 20.0 Table 20.2(c) 6-in. pipe (6.065-in. ID) 3.05 0.56 3.32 0.66 3.88 0.88 4.44 1.12 4.99 1.40 5.54 1.72 2.06 6.10 6.65 2.42 7.20 2.78 7.75 3.25 8.31 3.63 8.87 4.11 9.96 5.12 11.1 6.17 12.2 7.45 8.73 13.3 14.4 10.2 15.5 11.9 16.7 13.2 17.8 15.0 20.0 18.5 8-in. pipe (7.981-in. ID) 1.76 0.15 1.92 0.17 2.24 0.23 2.56 0.29 2.88 0.37 3.20 0.45 3.52 0.55 3.84 0.63 4.16 0.73 4.47 0.85 4.80 0.97 1.11 5.11 5.75 1.33 6.40 1.64 7.04 1.98 7.67 2.36 8.31 2.71 8.95 3.10 9.60 3.49 10.2 3.92 11.5 4.99 12.8 5.96 16.0 9.00 19.2 12.5 22.4 16.6 1.62 1.82 2.03 2.23 2.44 2.64 2.84 3.04 3.25 3.65 4.06 4.46 4.87 5.27 5.68 6.09 6.49 7.30 8.11 10.2 12.2 14.2 16.2 18.3 20.3 22.3 24.4 0.10 0.12 0.15 0.18 0.21 0.24 0.28 0.31 0.35 0.44 0.55 0.64 0.75 0.88 1.02 1.18 1.31 1.60 1.97 2.95 4.15 5.60 6.90 8.80 10.8 13.0 15.3 lO-in. pipe (1O.020-in. ID) 3-in. pipe (3.068-in. ID) 11.9 16.9 13.0 19.6 275 300 350 400 450 500 550 600 650 700 750 800 900 1,000 1,100 1,200 1,300 1,400 1,500 1,600 1,800 2,000 2,500 3,000 3,500 4,000 4,500 5,000 5,500 6,000 System-Head Curves 517 FRICTION LOSS IN VALVES AND FITTINGS When liquid flows through valves, elbows, tees, and other fittings, there will be a frictional loss_ Irrespective of the pipe size, these losses in fittings and valves can be expressed as percentages of the velocity head and may be calculated by the formula: where hI = head loss, in meters (feet) of liquid K = constant (depending on the fitting design) V = nominal liquid velocity, in mls (ft/s) g = acceleration due to gravity; 9.81 mls 2 (32.2 ft/s 2) Values of K for common fittings, valves, and other resistances to flow have been determined experimentally. Type of resistance Globe valve Angle valve Fully open swing check valve Close return bend Standard tee acting as elbow Standard elbow Long-sweep elbow 45-deg elbow Fully open gate valve K value 10 5 1.5-2.5 2.2 1.8 0.9 0.6 0.4 0.2 The K values for various types of entrances are shown in Fig. 20.3. The K values for sudden enlargements and sudden contractions are shown in Figs. 20.4 and 20.5. There is such a wide variation in the design of check valves that it is impossible to give any general values of K. In the swing-type valve, the disk is opened by the force of the flowing liquid. Thus, at low velocities when the disk is not fully open, the flow is throttled and the loss measured in terms of the velocity head is greater than at higher velocities. Very few data have been published on the loss in swing check valves. One manufacturer provides a chart for equivalent length of pipe that gives values of K 2.0, approximately, for valves of 3-in. to 24-in. size. Assumptions of a K value of 2.5 for I-in. valves, 2.0 for 2-in. valves and 1.5 for lO-in. and larger valves should give reasonable friction head allowances. A check valve using a disk hinged slightly above its center has become quite popular. Published data on two sizes of this type of valve indicate a K value of about 0.3 at all velocities. Fully open butterfly valves should have K values in this range. In many municipal or other important installations of large or fairly large size, a combined check and stop valve design made on the principle of the plug cock, with the plug rotated by an external mechanism, is used. This special valve has a straight full-size passage when fully open, and should have a loss no greater than a section of pipe of the same length. A flap valve is a form of a check valve used on the end of a pipe. The flap is quite light in most designs. Some special designs with the flap partially counterweighted have also been made. Flap valves have very low losses even at low velocities when the disk is not raised very high by the flow. In most designs, a loss of 0.06 m (0.2 ft) of water irrespective of velocity should be ample allowance. The exit loss equal to the velocity head at the valve must also be added. Losses in multiported check and foot = 518 System-Head Curves PLAIN END PIPE PROJECTING THROUGH WALL OR VERTICALLY INTO BODY OF WATER WITH ADEQUATE SUBMERGENCE AND CLEARANCE K=O.B PLAIN END PIPE FLUSH WITH WALL K=0.5 BELL MOUTH PIPE FLUSH WITH WALL K= 0.1 (well rounded) TO 0.25 (slighlly rounded) BELL MOUTH PIPE SUSPENDED IN BODY OF WATER, WITH ADEQUATE SUBMERGENCE AND CLEARANCE K=0.2(well rounded) TO 0.5(slighlly rounded) Fig.20.3 Various types of piping connections and their K values. valves vary too widely to make any assumption. This type of construction is now rarely used so that it is likely to be encountered only in existing installations in which the loss can be detennined by test. While designs of foot valves with strainers vary widely, a K value of 5 to 15 might be expected. The value of K varies with the design of any valve or fitting and, in the case of elbows in which part of the loss is due to the bend and part due to the length of pipe involved, the value of K varies with the smoothness of the walls. Thus, calculated friction values are approximations, not definite values. The approximate value of velocity head for any capacity in any size pipe up to NO 600 (24 in) pipe can be quicldy obtained (Fig. 20.6). This value when multiplied by the appropriate K value gives the head loss in the fitting. For example, with a flow of 340 m3Jhr (1,500 gpm) through NO 250 (10 in) pipe, the velocity will be 1.86 mls (6.1 ft/s) for which the corresponding velocity head is 0.18 (0.58 ft). The loss in any valve, fitting or other resistance can be expressed as the loss in a length of pipe of the same size as the fitting. The total friction loss involved can be detennined for the total length of System-Head Curves -"" 1.0 0.9 0.8 0.7 0.6 :.c I '" '\1\ 0.4 \ 0.3 1\ \ 0.2 \.. '\ 0.1 0 o 0.1 0.2 0.3 0.4 0.5 I ~= ~I : v- 1\ 0.5 I '" i'-.. 0.6 0.7 0.8 0.9 1.0 dID Fig. 20.4 Head loss in sudden enlargement of pipe. Based on assumption that the difference in velocity head is lost. 0.4 "" ~, ~ ~ "'" """...... 0.3 0.2 '\. ~ 1\ \ 0.1 !\, 1\ o \ o 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 diD Fig. 20.5 Head loss in sudden contraction of pipe. Average of data obtained from various sources. 1.0 519 S20 System-Head Curves 25 !O,ooo 20 20,000 15 10,000 8,000 20 6 5 15 3 6,000 5,000 4.000 ----- --- 2 3,000 I~ 2,000 8 ~OOO 800 (/) '"~6 ~ 5 ~5 ~ ...J4 '"'" 3t 4 ~ 0 It: 3 3 ct ~ ct :::E ct 2 ~ ...J Z ~ ci '" I&J 2t (/)2 ct ~ 0 '" !ill :::E 100 Q.. 80 C!) 60 50 ~ 40 >= 30 1.5 I.l. • ~ ~ (3 ct 20 Q.. ct u (/) It 10 8 1.0 08 0.5 0 5 8 '" 4 (/) '" '"'" 3 ~ ~ !:: u :J 0 ~ :!l 0.10 Ci ~ Z 0.08: 2 9 ~ 0 0.15 ~ ~ 2 :::> ~ 0.2 It: Q.. OA 0.3 1.5 ~ 0.06~ 0.05_ U 0.040 ...J '" 0.03> 0.02 1.0 C9 Q8 I t o.s 3 2 t 1.0 o.a 6 5 4 0 Z t --z 200 ~ ~ ~ '"~ '" u ~ (/) -_ 300 (/) ~ --_ 600 500 400 6 4 o.a 0.7 Q6 OS 0.5 0.4 o.s 05 Q.3 0.5 0.01 Fig.20.6 Velocity of liquids in pipes. piping, plus the equivalent lengths of all the valves, fittings, and other resistances. Using the K value of the fitting, the resistance of any fitting expressed in equivalent length of pipe can be approximated from the chart in Fig. 20.7. For example, the loss in a fully open ND 250 (10 in) gate valve (K = 0.2) would be approximately the same as the loss in 1.8 m (6 ft) ofND 250 (10 in) pipe. It must be remembered that any such conversion may result in a somewhat different value for the head loss in any fitting when compared with the value obtained by the velocity head method. The magnitude of the difference depends System-Head Curves ilQIE ~~, 1,500 10 8 6 ~E IIlLVE . 521 48 -IQOO 42 800 36 - 600 500 30 400 5 24 300 4 20 3 - 200 18 150 16 14 100 12 80 - 60 2 0 ~TANI2ARD U;~ .. ~ ~ 1.0 15 ~ W ~ 0.5 0.4 0.3 . iWo1TT Fm,AL THOIiLlr / / 0.2 0.15 / THROUGH TEE 0.10 ~/ ~ / / / / / / / / / / / (/) / I&J 8 6 6 5 5 4 4 (/) 5 ~~ 3 ~ W ~ 21 ....J 2 4 it: 2 W 1.5 i 8Z 1.0 w li; I&J" 0.4 ~ 0.15 3 LL. 0 a:: 2 It It 1.0 ~ ~ • ~ 1.5 -- 1.0 0.8 0.7 t 0.6 i- 0.5 Fig. 20.7 Friction losses in fittings expressed in equivalent lengths of straight pipe. ~ w 2 ~ (i5 ~ ~ II) 0.6 0.5 0.3 it: ~ 3t 3 0.8 &J' Q. I&J ~ ~ X <.> ~ ~ 76 0.2 STRAIGHT FLOW 0 X / / e/!Z ~ 45-DEGREE ELBOW Ii it: ~ 0.. ....J LATERAL ~ LL. ::;) 0.6 LL. 20 10 10 ~ I&J I&J (!) 4 0.8 JZ-~~ 8 30 0.. ELBOW ~ 40 Z ~ ___ STAN~DruS ~Y.£.~ i= tG: 0 t- 1.5 ~ 50 Z AS ELBOW ~ (!) 522 System-Head Curves on the Williams and Hazen C value or equivalent used in detennining the friction head loss per unit length of pipe. There is very little loss in taper reducers because a liquid can be accelerated with little loss. For long reducers there will be a greater loss because of length. In such cases, determine the loss as for a pipe with a diameter equal to the average diameter of the reducer. There is greater friction loss in increasers. A taper increaser up to about a 15-deg included angle [Fig. 20.4, (D - dJ/L equals 0.266 or less) will result in the water following the taper. A taper with over 60-deg included angle (Fig. 20.4, [D - dJ/L equals 1.15 or more) will have about the same loss as that which would be determined for a sudden expansion. For tapers between 15-deg and 60-deg included angle, calculate the loss as one-half the loss determined for a sudden expansion. This subject of losses in fittings has been discussed primarily for systems handling water. In general, these methods of determining the head loss through fittings apply as well to systems handling other noncompressible liquids. DETERMINING FRICTION HEAD Using frictional values for C = 100 for the pipe and figuring the losses in fittings and valves in the Ktimes velocity-head basis, the head for the system shown in Fig. 20.1 for a flow of 454 ms3fhr (2,000 gpm) would be determined as follows: Entrance loss (12 in bell not well rounded)-K = 0.5 ND 300 12-in. long radius elbow-K = 0.2 6.1m (20 ft) of ND 300 (12 in) pipe (at 1.49 ft loss per 100 ft of pipe) ND 250 x 300 (10 in x 12-in) reducer ND 200 (8 in) gate valve-K = 0.2 ND 200 (8 in) swing check valve-K = 1.8 ND 200 x 300 (8 in x 12 in) increaser-K = 0.30 915 m (3,()()() ft) of ND 300 (12 in) pipe (at 1.49 ft loss per 100 ft of pipe) Two ND 300 (12 in) long-radius elbows-K = 0.2 Three 45-deg elbows-K = 0.2 Exit loss (ND 300 [12 in] pipe-1 velocity head) Total losses 0.08m 0.03 0.09 0.03 0.16 1.39 0.23 13.63 0.06 0.09 0.15 15.94m (0.25 ft) (0.10) (0.30) (0.10) (0.51) (4.56) (0.76) (44.70) (0.20) (0.30) (0.50) (52.28 ft say, 52.3 ft) Of this 15.9 m (52.3 ft) loss, 13.7 m (45 ft) is loss in the pipe and will vary according to the C value of the pipe. The remaining 2.2 m (7.3 ft) is the allowance for loss in valves and fittings and will vary only slightly with the age of the pipe. By computing the values for various other capacities, we would be able to graph the relation of the system head to the capacity (Fig. 20.8). Without further analysis it appears that for a flow of 454 m3/hr (2,000 gpm), a good selection would be a pump with the same characteristics as that in Fig. 20.8. If the pipe were new, there would have been less friction loss. If the condition of the pipe was such that C = 130, the pipe friction loss would be 61.5 percent of the friction loss when C =100. For example, at 454 m3/hr (2,000 gpm) the pipe friction loss would have been 45 times 0.615 or 8.44 m (27.7 ft). The total friction head, including friction losses in the fittings, would be 8.44 m plus 2.23 or 10.67 m (27.7 ft. plus 7.3 or 35.0 ft). The resulting system-head curve labeled C = 130 is shown in Fig. 20.8. System-Head Curves 7 SYSTEM HEAp C'= 100 r--I-. ~ 60 w HEAD-CAPACITY 1.L SYSTEM I HEAD C= rio f""". z "'- ""'- / / «w / :c -1 ~ 40 ~ 70 ~ w u 60 30 0: / ~ 50 >-'" z u ~ CI.. 30 :c m u ii: 20 LL W 10 0 Fig. 20.8 20 40 / V 0 50 80 523 .L V 1 o/ oVo / ,... "....- 5 / / L V ...- J.- /' ~. -/ ~ SYSTEM HEAD c= 130 .i. / / / E~FICiENCY SYSTEM HEAD C= 120 -:-..... l\. ~ ~ I-- ...--:- BHP 15 10 20 CAPACITY, IN 100 GPM 25 30 System head for installation shown in Fig. 20.1 for various roughness factors using an 8-in. pump. Thus, the pump delivers a greater amount of liquid (527m 3/hr [2,320 gpm]) with less head (14.0 m [46ft] total head) and less efficiency (82.5 percent). If it was known that the water would cause a very slow increase in friction with increasing age of pipe (reaching a value of C = 110 in 15 years or longer) or if power costs were so high that the friction was to be kept low by periodic cleaning of the pipe, then it would be advisable to select the pump for a lower head. Using the system head for C = 110 as the maximum to be encountered and at which 454 m3/hr (2,000 gpm) capacity is desired, the pump would have to be selected for 13.7 m (45 ft) total head. If the same pump was used with a smaller impeller for 454 m3/hr (2,000 gpm), a 13.7 m (45 ft) head would yield an initial efficiency of 82.5 percent for the system when the piping had a C value of 130, and would reach an efficiency of about 84.5 percent when the C value had fallen to 110. If it was desired to obtain greater economy over the entire operating range, a larger pump would have to be used. The larger pump would have a IO-in. discharge and a ND 250 (10 in) gate valve. AND 250 (10 in) check valve could be used with smaller friction losses. A graph of the relation of the system head to the capacity for this system is shown in Fig. 20.9. In circulating pumps for surface condensers the head is composed entirely, or almost entirely, of friction losses. These systems are generally complicated because of the need for less water in winter, when the water temperature is low, than in summer when the water temperature is high. Generally, two pumps of equal capacity are used. Both are run during the summer to give the required large capacity and one is run in winter, when less capacity is needed. In this installation, the head would be made up of losses through the piping and fittings carrying the capacity handled by each pump and losses through the piping, fittings, and condenser that carry the combined flow. Thus, the system-head curve for the operation of one pump would not be the same as the system-head curve for the operation of both pumps. The losses for the individual pumps are shown by curve PI in Fig. 20.10. If both pumps are running, twice the capacity flow through the condenser yields the same loss in the individual piping for each t;J 50 W u. ~ ;j 40 80 - - HEAD - CAPACITY / <I ~ 60 W U Q: W I- f2 50 a. CL u III )-'"40 Z W Q u. ~ 30 % 20 ~ 30 20 10 o 10 L / I V Fig. 20.9 / - V- - 5 ~ V /" W r 70 ~ r- r-- / -S L l! 7 V r-.... // :/7" ~ r-... IL / // EFFICIENCY V I--I-- ~ SYSTEM HEAD C= 110 /~ I ) I I SYSTEM HEAD C = 120 } I I I SYSTEM HEAD C=130 ~ -- "I-- BHP 25 10 15 20 CAPACITY, IN 100 GPM "'\ ~ 30 System head for installation shown in Fig. 20.1 using a 10 in pump. Performance is improved. 40 III ~a. CO~OEN~ER~ I o:t ...J::l PUMP ~() 30 + u.a. ON W I - liC,'I- .():-PUMP T 1-1-/ <1- ~~ Q:~ c, .... IW W u.. ~ / 20 0 <I W I / 10 / " 10 'I V ,v / / V V / '/ / / '/ / / ~ / ,.~ ~ ~, 1- - -- V ",--- ~'I,- I-- 20 30 40 FLOW, IN 100 GPM Fig. 20.10 Typical condenser installation with two pumps in parallel showing operating conditions for one- and two-pump operation. KEY: SI = System head-one pump running (C + PI) S2 = System head-two pumps running (C + P2) C = Friction losses in condenser and common piping PI = Friction losses in individual pump piping-one pump running P2 = Friction losses in individual pump piping-two pumps running. 524 System-Head Curves 525 pump. This is shown by curve P 2• The loss in the condenser and in the piping and fittings in which the flow is the same is shown in curve C. At any capacity, the system head with one pump running (SI) is the head shown in curve PI plus that shown in curve C. With two pumps running (S2), it is the head shown in curve P 2 plus that shown in curve C. If the loss in the individual piping is low, curves SI and S2 are so close that only S2 is constructed and the discrepancy between SI and S2 is ignored. The system illustrated in Fig. 20.lO indicates no static head, and is based on the assumption that the full siphon head is recovered. Although siphons up to 7.6 m (25 ft) or more are feasible, full recovery is rarely obtained. Also, in this system, unless the piping and condenser waterways are primed before the pumps are started, the pumps will have to fill the piping and condenser before the siphon can be established. Thus, in the starting cycle, a static head equal to the siphon leg will be encountered just before the siphon is established. The maximum starting head can be determined by adding the siphon leg as a static component to curves SI and S2. It is often impossible to obtain a pump that will deliver sufficient capacity to establish the siphon without impairing the results obtained when the siphon has been established. Modem practice is to provide priming equipment, so that the siphon loop can be evacuated, and the siphon established without the necessity of a high starting head. It is desirable that good efficiency be obtained when two pumps are running as well as when one pump is running. The system head when both pumps are running can be plotted against the capacity handled by each pump (Figs. 20.11 and 20.12). The problem is to select a pump for this installation that will give good efficiency at 363 m3/hr (1,600 gpm) and 7.6 m (25 ft) head as well as at 477 m3/hr (2,lOO gpm) and 3.5 m (18 ft) head resulting from the intersection of the pump head-capacity curve and the system curve SI. This generally requires the use of a larger pump than would be used if the pump were selected only for the 363 m3/hr (1,600 gpm) 7.6 m (25 ft) head condition. The selection of a pump with 82 percent efficiency at both operating conditions is ideal (Fig. 20.11). If a smaller pump had been 1'000.. HEAD - CAPACI TY -~r-.~ I / 10 o 1 / / """" V 10"'" ~Q ~~, 4,,~+r ~%~ ......... j"-..... r--...... V- / EFFICIENCY V .......... ~ // / 5 10 ......... " \ .. ~ ..~l"'· , '- ~.....~-. ~7- ,oJ ~. >. ~ ~ r- 8HP ~I V - 15 zo CAPIlCITY. IN 100 GPM Fig. 20.11 Ideal pump selection for the system shown in Fig. 20.10 if one- and two-pump operation are equally important. S26 System-Head Curves ...or 70 HI AO-C ~PACITY ~ to II: ~ 50 ,: u z / 40 III ~ S J 10 IlL. 20 '"'""'-t: ".- 10 i I 0 / I( ""'" // V 10 10 / V ~EFFICIENCY ,,~, ~~~ ~~ ....... / / / ....... ~, -- ./ ~ I~P 7 5 10 15 ""'r- "tP- .~ r/],'f,; ~t ~,?,~ " 20 25 CAPlCITY. IN 100 GPM Fig.20.12 Results of smaller pump for installation in the system in Fig. 20.10. This pump shows poor efficiency with single-pump operation. 200 r-- 90 ~ 80 :::: IL. ~ 70 z 150 z EFFICIE . ~ 60 ~ ~ 0.. 50 >40 u z w ~ 100 ..J / <I: ~ 0 30 ~ <.> l::: 50 20 0.. :J: 10 m I.&J o -- - J ". I"'" I / /v / V ~ r-... ....... .... / --- ~ --V / 10 -15 V 1 138 F T PUMP r--.... :::=: :::::. ~ 138 1FT STATIC HEAD ., , -. HEA D-clpAclTY ..- - ~ ~+.... i"'t --:----..,... ';YSTEM HEAD C=IOO r-... I : ....... ~SYSTEM HEJ\D C=130 1--- BHP o LosSES I--- C= ,00 f~~ ~ - 20 25 CAPACITY. IN 100 G PM Fig. 20.13 Characteristics of pump whose total head is mostly static. Error in calculating friction element or change in friction with age has little effect on selection. System-Head Curves 527 selected, more actual capacity would have been obtained with one pump operating but only 74.5 percent pump efficiency would have been obtained (Fig. 20.12). If, in this installation, both pumps were normally operated all the time and two units had been installed instead of one larger unit (in order to permit operation at reduced capacity if one unit is out of service), the selection shown in Fig. 20.12 would have been preferable to that shown in Fig. 20.11 because the efficiency at 363 m3jhr (1,600 gpm) and a 7.6 m (25 ft) head is greater and the first cost would be lower. When there is a static head, or its equivalent in pressure, or both, included in the head, the system head is the sum of these components plus the friction head. Thus, for the system in Fig. 20.13, the friction head losses have been determined in curve form and added to the static head, giving the system head indicated. If the pipe had been new and had a coefficient of C = 130, very little increase in capacity would have resulted. Consequently, the possible error in determining the friction loss becomes less important as the percentage of the friction head in the total operating head is reduced. EFFECT OF VARIABLE STATIC HEAD At a constant speed, the head developed by a centrifugal pump varies with the capacity delivered by the pump. Thus, if a pump is to be used in a system in which there is a variation in static head, the capacity delivered through the system will also vary. The purchaser of a pump for such an installation, will often calculate the friction at rated capacity, add it to the average static head, and state the sum as the design head. In addition, he will add the same friction head to the maximum and minimum static heads and give the resulting heads as the maximum and minimum operating heads that the pump will encounter. Thus, the change in friction with change in capacity is neglected, and the manufacturer is handicapped in selecting a suitable pump. For example, in the installation shown in Fig. 20.14 some purchasers would specify that the pump had to operate over a head range of 19.8 to 29.0 m (65 to 95 ft), giving a rated capacity of 56.8 m3/hr (250 gpm) at 24.4 m (80 ft) head. The pump in Fig. 20.14 would appear to be unsatisfactory, although it will actually deliver 79 percent rated capacity at the maximum static head and 115 percent rated capacity at the minimum static head. It is often good to know what capacity will be delivered by a pump operating on a system in terms of static head (Fig. 20.14). For any capacity, the static head will be the total head of the pump minus the friction loss at that capacity. This can be graphed (Fig. 20.14) to show, for example, that the flow to the tank will be 55.4 m3/hr (244 gpm) when the static head is 17.4 m (57 ft). DETERMINING PUMP DELIVERY If a plant or community is located at some distance from its source of water supply, the demand for water very often increases over a period of time. It ultimately becomes uneconomical to continue to use the existing pipe line because of the frictional head loss with increased capacity. If the original line is in good condition, the usual solution is to install a second line, in parallel with the existing line that will allow economical pumpage of the desired increased rated capacity. If two pipes are operating in parallel, the friction head loss in each branch must be the same. The proper approach to this problem is to plot the relation of capacity to friction head loss for each line and then to determine the relation of combined capacity to friction head loss for the two by adding together the capacity of each line, when the head losses are the same, at a number of points. For example, Fig. 20.15 shows the head loss for a ND 250 (10 in) line and the head loss for a paralleling ND 300 (12 in) line in the form of a graph. With 6.1 m (20 ft) friction head loss, the ND 250 (10 in) line will have a flow of 227 m3/hr (1,000 gpm), whereas the ND 300 (12 in) line will have a flow of 367 m3/hr (1,615 gpm). Thus, 227 plus 367 or 594 528 System-Head Curves 100 90 -----.--~I"""--- - ~ 60 f- -;c-- -..,..- 20 10 ~ LL~ Illj~ ~~~~ 't'>~ " ,'" ·s~~,-.O S 1 0 ~"'i ~'t'>~ ~\C l~ ___ ~<;,"'ie _ V----~ :'\~~ ~ "'i~"'i\C ~ ~~O "AAO ~"'iS " V 1'" "-, -- 't'>~~ I 150 / "- ~ '\. ~~\C.~~ V V 100 "'i <;,"'i ~~~ LL~O::!; V 50 ~ ~ -- tl~ Illilt: P~P .((.~Clry _I.~_ Iw z 50 ,-- o<I: 40 - i TANK w u.. 30 ------::;:::> ---[-tlf,.4D 70 w j -.§ T4TtC 80 :I: ~ ~r.Q TOTAL HEAD-CAPACITY I 250 200 300 CAPACITY, IN GPM Fig. 20.14 Characteristics of pump installation with a variable static head. Friction head variation with capacity must be considered in the selection. 30 It: w 25 II ~ « ~ LL 0 I- w 20 / W lL ~ vi (/) ..J 0 « :r z 10 9 I- U a:: LL 5 / / / / V/ 15 0 w / I (12-'N PIPE LIN! -f I 10-IN plPE LINE II ~V 5 V / ~ 10- AND 12-IN PIPE LINES IN PARALLEL / / 10 / 15 20 25 30 35 CAPACITY, IN 100 GPM Fig. 20.15 Relationship of capacity to friction head for two pipe lines in parallel. 40 System-Head Curves 529 m3/hr (1,000 plus 1,615 or 2,615 gpm) will be the combined flow of the two lines with 6.1 m (20 ft) head loss. The capacity for the two lines in parallel for equal head losses can be determined for a number of points and a curve showing combined capacity against head loss can be drawn (Fig. 20.15). In some systems, such as in a water works distribution system, it is desirable to maintain a nearly constant pressure although the demand varies. To maintain an exactly constant pressure, it would be necessary to vary the speed of the pump or pumps; but, in most systems, it is rarely necessary to maintain the pressure exactly and some variation can be allowed. Most electric-motor-driven pumps that maintain nearly constant pressure are, therefore, driven by constant-speed motors. Thus, the pressure will depend on the head developed by the pump or pumps operating in parallel at the demand capacity. To produce a reasonably constant pressure for the full range of demand, it is desirable to select pumps having headcapacity curves that have a shutoff head of 10 to 20 percent more than the head at design capacity. Installations of divided flow or branch lines, in which the flow is controlled only to prevent overflowing of a tank or reservoir, usually involve two or possibly three branches. In an installation that has two tanks at different elevations (Fig. 20.16), it is obvious that flow will not reach tank A unless the friction head loss in the ND 100 (4 in) line from point C to tank B exceeds 3.05 m (10 ft), which is the difference in static head for the two inlets. Considering the branch from point C to tank B, the system head has no static component and will be frictional head only. This may be calculated (curve B, Fig. 20.17). The system head for the branch from point C to tank A, has a 3.05 m (10 ft) static component and a friction component caused by the friction in 152 m (500 ft) of ND 100 (4 in). pipe (curve A, Fig. 20.17). The capacities for the two branches for equal system heads up to point C can be added together to give the system head of the two branches as a unit (curve A + B, Fig. 20.17). As the friction loss in the piping from the supply to point C is the same for both branches, there would be no difficulty in establishing the friction head curve (curve D, Fig. 20.17). Point C is 15.2 m (50 ft) above the suction supply, therefore the system head for the common system up to point C will be the friction head plus 15.2 m (50 ft). By ,500 FT OF 4-1N. PIPE 1--,-::::::-- ~.- TANK 10FT A ".c ~ .. 1.000 FT OF 4-IN. PIPE TANK B 50FT ( Fig. 20.16 Pumping system involving two tanks at different elevations. 530 System-Head Curves 130 8s ~8+D+50 120 1 110 PUMP H ADCAPACITY 100 90 I- ILl ILl LL. ~ 0 <t ILl :I: 70 60 50 / -- ~~ V j / V/ V V /QJ V / J LV 40 30 V ~ 20 10 ~ - ~ !J'/ )V 80 A =A+D+50 ~ ---V ,., ~ ~ -- ..-"V V 2 (1+8)1 = '" / / f-- s 'IA+8l+D+ 50 / "-.. "\ f\ ~ I ,~Y V / / r--.... / V V V ". V ...... ~ ,/' ./' 3 4 5 CAPACITY, IN 100 GPM Fig.20.17 System head-capacity curves for installation in Fig. 20.16. adding this value to the head values on curve (A + B), we derive the system-head curve for the entire system as shown in curve (A + B), (Fig. 20.17). If the pump used for this service had the head-capacity curve shown in Fig. 20.17, the resulting total flow would be 81.3 m3Jhr (358 gpm). This capacity would require a head at C of 9.45m (31 ft), as shown by projecting a line from the intersection of curve (A + B), and the pump head-capacity curve to curve (A + B). By projecting lines to curve A and to curve B from this point, we see that 43.8 m3/hr (193 gpm) would be going to tank A and 37.5 m3/hr (165 gpm) to tank B. If the two branches to the tanks are each equipped with a valve actuated by a control that closes the valve when the tanks become full, at times there would be flow to only one of the tanks. The flow to tank A only can be determined by constructing its system head curve As (by adding head values on curves A and D plus the 15.2 m [50 ft] static head) and determining the point at which curve A, intersects the pump head-capacity curve. In the same way, a curve showing the extent of flow to tank B if the branch to tank A is shut off can be constructed (curve Bs). If a pump that developed 18.8 m (61.5 ft), or less, total head at 20.4 (90 gpm) capacity had been used, the entire flow would have gone to tank B. In many cases, especially those involving two or more pumps each with its own piping, valves, and fittings discharging into a common discharge line, the solution of a problem can be simplified by determining the head each pump will produce for its range of capacity up to the point in the system at System-Head Curves Fig. 20.18 531 Pumping system involving two pumps that have considerable individual piping discharging into a common line. which their pipes join. A system involving two pumps with separate piping discharging into a common line is shown diagrammatically in Fig. 20.18. The usual head capacity of pump No.1 (Fig. 20.l8) is graphed in Fig. 20.l9. The friction loss from suction supply to point C is plotted (curve hf) and the system head (curve hf + S) for pump No.1 from the suction supply to point C is thus determined. By subtracting the values on curve hf + S from those on the pump head-capacity curve (H-Q), we derive curve Hc-Q. Curve Hc-Q indicates the head that will be produced by pump No.1 at point C as a function of the capacity being delivered. 70 - 50 '"z -lO • '"% 20 pu~p ~EAo-tAPAcrrv ""- ....... ~ HC_Q -~ .......... ~ ~~ 10 ..- '" ..- ~ i""" ~~ 10 ~ ~ ~ ..- "- r--.... - -15 IH-Q) ' hf t S I&. t:J ..... f"o I'-. 60 ~ 40 He· H-(hr +$) --- ,.",. ~ '" "' ~ ~V 20 \ 25 '" ~c:, ~O 0' 90\~~ O\~~ \ CAPACIT Y, IN 100 GPM Fig.20.19 System head-capacity curves for installation in Fig. 20.18. C C_ 532 System-Head Curves TYPES OF PUMPING SYSTEMS Pumping systems are of two types-throttled and unthrottled. In a throttled system, the capacity is detennined primarily by the demand, and the flow is controlled by throttling the excess head developed by the pump or pumps. In some systems, boiler feed pumps for example, a throttle valve located in the discharge line controls the flow. In others, such as city water-supply systems without a standpipe or reservoir "floating" on the distribution mains, the consumers of the water control pump discharge as they open or close valves. For an unthrottled system in which pumps discharge into a standpipe or a reservoir, the flow depends on the head developed by the pumps and on the characteristics of the system. THROTTLED SYSTEMS In a throttled system, such as a boiler feed pump installation (Fig. 20.20), the flow is controlled by the throttle valve, which is usually positioned automatically by the feedwater regulator (valve A. Fig. 20.20). Fig. 20.21 shows the boiler feed system-head curves superimposed on the head-capacity curve of the pump. Curve C-B represents the boiler pressure plus the static elevation. Although slight changes take place in the boiler pressure with changes in load, for the sake of simplicity we shall assume the boiler pressure to be constant. When water is supplied to the boiler, the pump operates against a pressure that increases with flow because of the friction head losses in the piping, fittings, and valves in the line. With throttle valve A wide open, the system-head curve will be curve C-D (Fig. 20.21). The point at which this curve crosses the pump head-capacity curve (L) is the rated head and capacity of the pump. If valve A is partially closed, the friction head increases, and the system-head curve may rise to position C-E. Further closing of valve A would produce other system-head curves such as C-F or C-G. If valve A is closed entirely, the pump pressure would go to shutoff (point 1). Thus, the system-head curve can be varied by opening and closing the throttle valve so that a family of curves is produced. These curves intersect the head-capacity curve at various points between the fully closed position (1) and the fully open position (D). To supply the boiler with a quantity of water, Q. the throttle valve is adjusted until the system-head THROTTLING DEVICE "A" ~ BOILER ~PUMP Fig. 20.20 Boiler feed pump installation. A typical throttled system. ~ System-Head Curves 533 o « w :I: CAPACITY Fig. 20.21 Boiler feed installation system-head curves superimposed on the feed pump head-capacity curve. curve becomes C-F (Fig. 20.21). This curve crosses the head-capacity curve at K and the head against which the pump operates is represented by the vertical distance H. The actual head required to deliver quantity Q to the boiler on the normal curve C-D is represented by HI. As the pump develops a head H at capacity Q, valve A will have to throttle an excess-head equal to H minus HI (distance h, Fig. 20.21). When a single pump operates on such a system, the shape of the pump head-capacity curve does not matter. The two pumps whose characteristics are shown in Figs. 20.22 and 20.23 could be used alone on a throttled system. If the cost of power were high, the pump shown in Fig. 20.22 would be preferred because the power it requires at part capacities is slightly lower in this particular case. It is not to be inferred that a pump with a flatter head-capacity curve will always have lower power requirements at part capacities. Lower power requirements depend on many factors: individual impeller and casing designs, ratio of design point to point of maximum efficiency, and the like. A pump with a steeper headcapacity curve has the advantage in a single-pump throttled system because it is less sensitive-the throttling valve must be moved through a greater distance as more head is throttled off. Despite having a drooping head-capacity curve, the pump characterized by Fig. 20.22 could be used on a single-pump throttled system with general assurance of satisfactory operation provided the difference between the pump head-capacity and unthrottled system head-capacity curves is greatest at zero flow. With this provision satisfied, the operating point will always be determined by the throttled system head. In rare cases, surging has resulted in single-pump throttled systems with pumps having drooping head- S34 System-Head Curves 240 220 200 90 80 ...z III u IE III A. 70 60 50 ,.: 40 200 ~ III ..ii 100 0 ......Q III ... ... 160 ~ 140 ~ 120 '.J..~/ ~~~'7 -' 100 0 t- 80 30 60 20 40 10 20 0 .......... % ~ - 180 III III III - H~"D-C"PACln / V r1 V I ~/ / ...- ...10 ~ ....... - "" - ~ 20 30 CAPACITY. IN 100 GPM 40 Fig. 20.22 Slightly drooping head-capacity curve. capacity curves and, even less frequently, with pumps having stable (constantly rising) head-capacity curves. Such problems are usually caused by either high control valve sensitivity or an undetected discontinuity in the pump head-capacity curve. Installations of two or more pumps operating in parallel involve piping and fitting losses for each pump as well as for common piping (Fig. 20.24). Instead of the true pump head-capacity characteristics, a bead-capacity characteristic measured from B to C should be used in the analysis. In throttled systems in general, and particularly in high-head systems such as boiler feed installations, the losses in the individual pump piping are such a small percentage of the total head, that their effect is not noticeable on a curve drawn to reasonable scale. Two pumps designed for 795 m 3/hr (3,500 gpm), 60.1 m (197 ft) total head are shown in Figs. 20.22 and 20.23. They have differently shaped head-capacity curves. The effect of the difference in losses in the individual pump piping in each pump will be ignored in this discussion. The individual head-capacity characteristics for each pump are shown in Fig. 20.25 as A and B. Their combined characteristics are labeled C. Curve C is obtained by adding together the capacities of the individual pumps at the same head. For example, at 64.0 m (210 ft) total head, pump A will handle 670 m 3/hr (2,950 gpm) and pump B will handle 709 m3/hr (3,120 gpm); thus they will produce 1,379 m 3/hr (6,070 gpm) together at 64.0 m (210 ft) total head. If these pumps were installed in a water works plant delivering water into a direct distribution system, in which the desired main pressure corresponds to a total head of 60.1 m (197 ft), and the demand was 1,363 m 3/hr (6,000 gpm), the two pumps in parallel would produce 64.3 m (211 ft) total head and the System-Head Curves - 260 240 ~~-4DI"C-4 ~~~ 220 """'"" 200 90 I- 180 80 LI- 160 IZ 70 0C( 140 U 60 J: 120 Q.. 50 W a::: w u z !!! ~ 100 LILIW w 40 C( I- 0 0 #'7 ~" ~~V / / I- 80 30 60 20 40 10 20 o ......... ~ " ~ ~ 100 Q.. J: CD r,.4y V ~ ..J ~ 200 w w / / V / ,-V 6~ --- --- / 10 20 30 CAPACITY, IN 100 GPM 40 Fig. 20.23 Stable head-capacity curve. - SUCTION - B C DISCHARGE lpuMP GATE NQ2\ VALVES~ Fig. 20.24 Simplified piping hookup for two centrifugal pumps operating in parallel. 535 536 System-Head Curves 210 250 ...... ~ II. Z Q 240 230 220 ... 210 ~ ~ 200 c % 0 ~ """-- -~ • "'" "- V' A -..... C "- y ~ .......... ~ ~ 110 110 \ \ -..... '" '"" ~, \., 'i 110 o 10 20 50 40 eo 10 10 CAPACITY. IN 100 GPM Fig. 20.25 Individual and combined head-capacity characteristics of pumps in Figs. 20.22 and 20.23. main pressure would be 64.3 m minus 60.1 or 4.2 m (0.41 bar) (211 minus 197 or 14 ft [6.06 psi]) greater than desired. Of the 1,363 m3Jhr (6,000 gpm), 659 m 3Jhr (2,900 gpm) would be delivered by pump A and 704 m 3Jhr (3,100 gpm) by pump B. If the demand were reduced to 1,136 m3Jhr (5,000 gpm), the main pressure would be somewhat higher. The pumps would be working against 67.4 m (221 ft) total head with pump A delivering 516 m 3Jhr (2,270 gpm) and pump B delivering 620 m3Jhr (2,730 gpm). If the demand were reduced further to 682 m3Jhr (3,000 gpm), the division of pumping capacity would be 114 m 3Jhr (500 gpm) by pump A and 568 m3Jhr (2,500 gpm) by pump B. Finally, should the demand fall to 597 m 3Jhr (2,630 gpm), pump B would be delivering all the water while pump A would be delivering none. Thus, at 597 m3Jhr (2,630 gpm) or less demand, pump A would be backed off the line by pump B and would be operating at shutoff-a dangerous situation even for a short duration. If pump A had been operating alone on a demand of 597 m3/hr (2,630 gpm) or less and pump B were started, pump B would pick up the entire load and back pump A off the line. If pump B had been operating alone at a demand of 597 m3Jhr (2,630 gpm) or less, and pump A were started, pump A would be unable to deliver any water to the system. If these pumps were operated in a system in which the change in demand was relatively slow and in which units were cut out when the demand fell to the rated capacity with one less unit in service, they should never be allowed to operate in parallel below 795 m 3Jhr (3,500 gpm). For demands less than 795 m3/hr (3,500 gpm), either pump A or B would be operated alone. In such a carefully supervised situation, the two pumps could be operated successfully in parallel on the throttled type of system. It should be noted that at 1,136 m%r (5,000 gpm) combined flow, pump A with 516 m3Jhr (2,270 gpm) flow has 76.8 percent efficiency, requiring 123kW (165 hp) and pump B delivering 620 m 3Jhr (2,730 gpm) flow has 82.3 percent efficiency, requiring 138 kW (185 hp), a total of 261 kW (350 hp) for the two pumps. If both pumps were the same as pump A, a flow of 1,136 m 3Jhr (5,000 gpm) would have meant 568 m3Jhr (2,500 gpm) per pump with 129 kW (173 bhp) per pump, or 258 kW (346 bhp) total. If both pumps were the same as pump B, the power would have System-Head Curves 537 been 133 kW (178 bhp) each or 266 kW (356 bhp) total. The use oftwo pumps that have equal capacities does not necessarily result in power economy. Difficulties may be encountered on throttled systems with parallel operation of similar pumps if the pumps have even moderately drooping head-capacity characteristics (Fig. 20.22). Figure 20.26 shows, with an exaggerated head scale, the theoretical head-capacity curve of one such pump and of two such pumps in parallel. Let us assume that the friction losses in the individual pump piping are relatively small and that they may be ignored. If the demand was 397 m3/hr (1,750 gpm) with one pump operating alone, the pump would operate against 68.0 m (226 ft) total head and exert a discharge pressure corresponding to that against the check valve of the second pump. This discharge pressure is greater than the shutoff head developed by the second pump. If the second pump were started, it would come up to speed against shutoff and would be unable to establish any flow because the pressure on the discharge side of the check valve would have been greater than the pump could develop at shutoff. In some installations with two pumps (Fig. 20.26), various methods are used when it is desired to start the second pump with the first operating on the top of the curve. One, possibly the most common, is to throttle a little on the gate valve of the pump that is running so that the net head (B to C, Fig. 20.24) is less than the shutoff head of the second pump. This, and other techniques, generally require very experienced manipulation and careful timing. With the pumps in Fig. 20.26, it is possible to obtain unequal capacities at certain flows even if they are hydraulically duplicates and operating at the same speed. For example, with a demand of 507 m3/hr (2,230 gpm), one pump could be delivering 114 m3/hr (500 gpm) and the other 393 m3/hr (1,730 gpm). Actually, it is inadvisable to run two pumps, such as shown in Figs. 20.22 and 20.26, in parallel for capacities at which the developed head exceeds the shutoff head, in this case below 475 m3/hr (2,100 gpm). First, although the two pumps and their drivers are apparently duplicates, there will be minor differences in the operating characteristics. This will cause unequal distribution of the capacity and, sometimes, backing one off the line. Second, a motor-driven pump operating under apparently stable conditions may have minor speed variations as well as minor variations in hydraulic 240 ..... LLJ LLJ lL. ~ 0 230 220 -- ........... ""- 210 -l eX ..... 0 ..... ~~ :0, -r-- -- ~e-4 ....... ~c ~4r-. ~~u.." ~0;. eX LLJ :I: J.S.: 200 ). ~s j\/ I'- ~ 190 ~..o 180 u 10 20 30 40 50 60 70 CAPACITY, IN 100 GPM Fig. 20.26 Individual and combined head-capacity characteristics of two pumps with slightly drooping headcapacity curves. 538 System-Head Curves perfonnance that can result in unequal sharing of the load between the two pumps. This could result in one pump operating at shutoff. Thus, for pumps to operate satisfactorily in parallel in a throttled system, it is desirable (1) that they have stable (steadily rising to shutoff) head-capacity curves and (2) that over the operating head range, the pumps have approximately the same percentage reduction in capacity, or at least deliver some capacity. As previously mentioned, the increase in head from design capacity to shutoff should not be too high, otherwise excessive pressure is developed at part-capacity flows. In a system in which it is desired to maintain a constant minimum pressure at the pumping plant despite varying demand, the design heads and shutoff heads of all the units are usually the same, or approximately so. Thus, if flows are less than the units in service will produce at rated head, the capacity delivered by each pump will be about the same proportion of the rated capacity. For example, if a 568 m3Jhr (2,5OO-gpm) pump (pump A) and a 1,136 m3Jhr (5,OOO-gpm) pump (pump B) operate in parallel (Fig. 20.27), and the demand is 1,249 m 3Jhr (5,500 gpm), the head developed by the two pumps would be 64.3 m (211 ft) (6.4 m [21 ft] above that desired). The capacity delivered by pump A would be 409 m3Jhr (1,800 gpm) or 72 percent of rated capacity, whereas that delivered by pump B would be 840 m3Jhr (3,700 gpm) or 74 percent of rated capacity. Usually, two or more pumps with stable head-capacity characteristics, and equal or nearly equal shutoff heads when operating in parallel in a throttled system, will share the load about equally down to a system capacity much below the capacity at which one or more pumps would be taken out of service. When purchasing a new pump or pumps that are to be placed in parallel to existing units, the purchaser should supply the vendor with the head-capacity characteristics of the existing pumps and infonnation on the operating pressure, to enable the vendor to select a new pump with suitable characteristics. Some throttled systems utilize a long transmission line between the pumping station and the point at which a minimum pressure is to be maintained. In such cases, the reduction in pipe friction in the line when the flow is reduced will cause increased pressure. If this increased pressure is objectionable, I- w 250 w "- 225 ~ 0200 ex ~ 175 '" --r---.::: " ........... ~~CAPACI '\. HEAD-CAPAf).~Y ;'UMP A 10 20 DESIRE ;> ....... ~ H",AD " "' HEAD-CAP~~ ITY PUMP B 150 o "'- ~ Y. BOTH PUMPS 30 40 50 60 70 80 90 100 CAPACITY. IN 100 GPM Fig. 20.27 Head produced by two pumps operating in parallel. System-Head Curves 539 possible solutions are (1) maintaining constant pressure by throttling the excess head with some form of valve, (2) varying the speed of the pumps so that the required head is developed at the capacity demand, (3) using one or more booster pumps in series with the pumps operating in parallel so that the head developed by the pumps in service can be increased in steps as the capacity demand increases, or (4) installing a number of pumps so that small increments of capacity can be obtained. The proper solution is usually the one that is economically best and therefore depends, in part, on the cost of power as well as on the cost of personnel necessary for the operation of the system. UNTHROTTLED SYSTEMS For a system in which the flow is not throttled, and in which the capacity is such that the head developed by the pumping system equals the head necessary to deliver the capacity through the system, it is not necessary for pumps to have similar characteristics to be operated in parallel. When buying additional pumps to operate in such a system, many purchasers make the mistake of requiring the additional pumps to have characteristics exactly similar to those of their existing units-this is not necessary. A system is shown diagrammatically in Fig. 20.28. The system head beyond point C (Fig. 20.28) is indicated in Fig. 20.33. The desired pumpage rate is from 568 to 1136 m3/hr (2,500 to 5,000 gpm). Four pumps that are dissimilar (Figs. 20.29 to 20.32), may be operated in parallel on this system, since the maximum head against which they will operate is 48.8 m (160 ft). The head-capacity curves plotted in Fig. 20.33 have individual piping and fitting losses deducted. For unthrottled systems, the most economical pump operation is obtained when there is little variation in the system head as the capacity changes. In many installations, the friction head is so large a part of the total head at maximum capacity that pumps designed for specific capacities and heads are better in the long run than pumps in parallel. Pumps in parallel would operate at poor efficiency at heads other than the desired head. For example, in an installation in which a flow of 1,420 to 2,360 m3/hr (6,250 to 10,400 gpm) is wanted (Fig. 20.34), three separate pumps designed for 1,420 m3/hr (6,250 gpm) at 42.4 m (139 ft) head, 1,890 m3/hr (8,330 gpm) at 50.6 m (166 ft) head, and 2,362 m3/hr (10,400 gpm) at 61.0 m (200 ft) head might be the proper solution. In other cases in which the head is practically all friction, the solution might be a full-capacity pump driven by a two- or three-speed motor. The characteristics of a pump driven by a two-speed (1,200 and 900 rpm) motor operating against a system head that is entirely friction is shown in Fig. 20.35. When operated at 900 rpm, the capacity would be approximately three-fourths as much and the pump efficiency would remain almost the same. If pumps are driven by multispeed motors, the capacities that can be obtained at lower speeds depend on the speeds available STATIC HEAD PUMPS Fig. 20.28 I System involving four pumps with individual piping but with a common transmission line. 540 System-Head Curves 200 - --. I\oJ ~ - PUMP HEAD-CAPACITY -...:::: t:"'-- ~ ~ ..... PUMP HEAD-CAPACITY LESS ........... FRICTION LOSSES TO POINT C 150 ~ ....... ci <[ .....;: \oJ J: ci 100 I- oI50 FRICTION LOSSES TO PO INT C o I 10 5 25 20 15 CAPACITY, IN 100 GPM Fig. 20.29 Characteristics of pump no. 1 in Fig. 20.28. 200 ~ ~ ::::::::: ~ PU~P Ht AO-ICAP~CITY ........... I- ~ I'- ~ PUMP HEAD-CAPAC ITY LESS ~ FRIC T ION LOSSES TO POINT C 150 z cl <l \oJ J: ..J ~ '~~ ~~ 100 ~ ~ 50 FRICTION LOSSES TO POINT C I 2 3 4 5 6 7 8 9 10 II CAPAC ITY, IN 100 GPM Fig. 20.30 Characteristics of pump no. 2 in Fig. 20.28. 12 13 System-Head Curves 541 200 ..... w w 150 LL 1",\t\ PUMP HEAD-CAPAC ITY L ESS FRIC TI ON LOSSES TO POINT C a <l w ...J <l I PUMP HEAD - CAPAC IT Y ~~ Z J: I R ~ r--... I-"-'" \\ 100 \ ..... 0 ..... so FRICTION1 LOSISES TO ~ O I NTI C 5 10 H---r 25 20 15 CAPACITY. IN 100 GPM Fig. 20.31 Characteristics of pump no. 3 in Fig. 20.28. 200 r::::::: f=::::: t--...... ........... ..... w w 150 LL PU~ P HE1AD - CAPACITY r':: ~ PUMP HEAD- CAPACIT Y LESS ~ FR ICTION LOSSES TO POINT C ~ ~ "- ,«0 w ........ ~'~ J: ...J <l ..... 100 0 ..... 50 F~ICT I 9N L9SSE~ TO FOIN! C I i 2 4 5 CAPACITY, IN100 GPM Fig. 20.32 Characteristics of pump no. 4 in Fig. 20.28. 6 7 542 System-Head Curves 200~-+--+--+--4--4--~--~~--+--+--+--4--4-~~~~ O~~ o __~__~~__~-=~~__~__~~~-L__~~__~__~~ 10 20 30 40 50 CAPACITY, IN 100 GPM 60 70 Fig. 20.33 Combined characteristics of pumps in system in Fig. 20.28. Based on head developed at beginning of common line. 250 t- ':I" ~ ..... ..,.., ... 200 ......... I- . .. ~ 0 ..,:t ........... - ..J l- e I- I'-. V -'" ISO 100 I--V / "- >< V" oS) ~ 'fa / //'.." ~ ~~~.6(;k ""1. i! 1-~ "" '~ c.,.~ &'" /~ ".0 :90 ~G'c'~~ "'~~-,,"1. -'9,z ~."p;.~ ~ ~ '>;. ".0 ~ 110 120 '0 so o 10 20 30 40 50 60 70 80 90 100 130 CAPACITY, IN 100 GPM Fig. 20.34 System characteristics for head that has a large frictional component. Different size pumps designed for different heads are required. System-Head Curves ....LL.~IOO z90 0 or 80 ..J 70 0 60 .... % or ~ ~ 100 CL z 80 .... U 60 CL % m ~ 40 20 0 IZ: .... ,: u z .... Q LL. LL. &oJ ~~-C4P4C'TY ~~~ ~- ~.~ K 1.200 RPM ~~ 00 ~v (}«-'1 ~¥ pc f""'.. ........... ~ 40 «-If ~~ -L,,<c.<c. j /L 30 I: ,II 7' L ~ j~-~-I-- ,V ~~ I-- V .". P' 2 ~ """ /' -... / r;. ~"'- i)K. ,<<t'Z+v 90'ORi5ii 10 ~ 4;.~ "'£40_ 50 ~P4C'T 20 543 / I!'- 3 ./ ~..... BHP " ,£- V1.200 RPM " " ~...... BHP 9)0 RPM 4 6 CAPACITY, IN 100 GPM Fig. 20.35 System characteristics of an installation that is all friction. Efficient operation of a pump can be obtained by part-speed operation. so that it is not always possible to obtain the exact capacities desired. To obtain exact capacities, a variable speed driver would have to be used. Frequently, one or more booster pumps are installed, either in the suction line to the main pumps or in the common discharge line to increase the capacity of existing stations. If conditions in the system illustrated in Figs. 20.28-20.33 should change so that the maximum demand at times is 1,340 m3/hr (5,900 gpm), one solution would be to have all four pumps discharge into a 1,340 m3/hr (5,900 gpm) booster pump that has a total head of 9.2 m (30 ft). Booster pumps are particularly practical when an increase in head would cause considerable reduction in capacity of the main pumps. Although the foregoing examples have described systems handling water, the basic principles apply to systems handling other liquids as well. There are sometimes certain limitations when liquids other than water are used. In systems handling volatile liquids minimum pressures must be maintained at every point. These requirements must be checked when analyzing the system. Pumps with high-specific-speed impeller designs have steeper head-capacity curves than pumps with low-specific-speed designs. Thus, in systems involving low heads for which a high-specific-speed type of pump will be used, a greater variation in percentage of total head can be met efficiently than in systems involving high heads for which a low-specific-speed pump must be used. Occasionally, some low-head systems will require the use of a low-specific-speed type of pump to accomplish the desired operation. There are a few systems in which there is a wide variation in head range with no need for a fixed capacity to be delivered at any specific head. Such a system is met in dewatering a flooded mine. This is an unusual application of a centrifugal pump because the total head against which the pump must work varies from approximately zero to a high maximum that occurs when the mine is almost clear of water. A mine-dewatering pump should be designed not for a single point of head and capacity, 544 System-Head Curves lZPUM'ING EL ~Mt:NTS 2 PUMPING t: _EWENrs IN 'UALLEL CAPACITY. IN 100 GPM Fig. 20.36 Characteristics of series-parallel type of mine dewatering pump. but for the greatest possible capacity at all heads within the capacity of the motor. For installations involving final heads for which multistage pumps are required, the best possible design is a parallelseries unit (Fig. 20.36). With this unit the dewatering takes place almost twice as fast at the beginning than it would if the various stages were arranged to pump only in series, but the power expenditure is the same. BIBLIOGRAPHY [20.1] Lewis F. Moody, Friction Factors for Pipe Flow, Transactions of ASME, November, 1944. [20.2] SIHI Group, Basic Principles for the Design of Centrifugal Pump Installations, 1980, SIHI-HALBERG, Ludwigshafen, Germany. [20.3] Engineering Data Book, 2nd Edition, 1990, Hydraulic Institute, Parsippany, NJ, USA. II PUMP PERFORMANCE 21 Centrifugal Pumps and Energy Conservation ~~--~-~ ~--~----------- ---- The high cost of energy and the scarcity of fuels have become a hard fact of life, making it imperative to examine all energy-consuming processes with a view to improving their overall efficiency. And since every industrial process that underlies our modern civilization involves the transfer of liquids from one level of pressure or static energy to another, pumps have become an essential part of all industrial processes, and in turn, major consumers of energy themselves. It thus becomes even more important to avoid waste whenever possible and to examine both the selection and operation of our pumps to see whether we can effect significant savings in energy consumption. Pump Efficiency All things being equal, it is natural that the user of centrifugal pumps will look with greater favor on pumps with higher efficiencies and will favor pumps offerings that might exceed others by as little as 0.5 or 1 point of efficiency. But all things are not always equal, and these small differences in guaranteed efficiencies may have been obtained at the expense of reliability, either by using smaller running clearances or a higher head coefficient impeller, or some other feature or configuration that does improve efficiency, but may at the same time reflect unfavorably on pump reliability. If we are dealing with a multistage pump, we can increase the efficiency by selecting a higherspecific-speed design. This requires a lower head per stage, hence more stages, and a longer shaft span. In turn, this leads to a larger shaft deflection and-unless we choose to be counterproductive and use larger clearances-to a reduced reliability. Effect of Specific Speed This does not mean to imply that improvements in efficiency based on the proper selection of pump design should be neglected. Thus, we must still consider all the factors that can affect the power consumption of a centrifugal pump. One of the parameters that is affected by the specific speed is the maximum efficiency obtainable from pump impellers of different specific speeds and different sizes, as 545 I. J. Karassik et al., Centrifugal Pumps © Chapman & Hall 1998 546 Centrifugal Pumps and Energy Conservation Table 21.1 Selections for 454 m 3Jhr (2,000 gpm) and 122 m (400 ft) Solution Number of stages Speed (rpm) Specific speed Chart efficiency (%) kW (bhp) 1 2 1 2 3,550 3,550 1,775 2,985 0.830 0.855 181 (243) 176 (236) illustrated in Fig. 18.30. The specific speeds to be used in connection with these curves must correspond to the maximum impeller diameter. Some reduction in efficiency will generally accompany the cutting down of the impeller or impellers. Theoretically, one should always try to use specific speeds in the region of 2,500 to obtain a pump with the highest possible efficiency for its capacity and head. This is frequently impractical, especially for small standard-size pumps. Consider, for instance, the case of a pump to be designed for 22.7 m 3/hr (100 gpm) and a 61.0 m (200 ft) head. At 3,560 rpm, the specific speed will be 669 and the efficiency can be expected to be 53 percent (see Fig. 18.30). If we were to design this pump for a specific speed of 2,500, we could probably reach an efficiency of 70 percent, but the pump would have to run at 13,300 rpm. This would require the use of a gear (dropping the overall efficiency to about 65 percent) and a rather special and expensive type of pump. Let us consider some typical examples (see Table 21.1) where two alternative selections are examined. It has been assumed that the design point corresponds to the best efficiency point of the pump selected. The difference between solutions 1 and 2 appears to be significant enough to warrant consideration of a two-stage pump, which saves 5 kW (7 hp), equivalent to an annual saving of $2,190 to $2,930 when evaluated to $0.050 to 0.067 per kW/hr. Against these savings, one must weigh a number of counterbalancing factors. Among these are (1) the higher initial cost of the two-stage pump and (2) the fact that a two-stage design precludes the use of a simpler overhung, end-suction pump with a single shaft seal. It may still be that the higher-specific-speed pumps will show sufficient savings to justify their selection. But are these savings really there? The answer to this question depends entirely on the expected operating capacity range of these pumps. The shape of the power consumption curve varies considerably with the specific speed of the pump in question, as illustrated in Fig. 18.36. Before we can decide which of the possible solutions is best from the point of view of energy consumption, we must examine the power consumption not only at the design point but also over the entire range of capacities the pump will encounter. Let us, for instance, expand our analysis of the case examined in Table 21.1. In addition to the bhp at the 100 percent design capacity, we shall compare the power consumption of the single-and twoTable 21.2 Comparison of Power Consumption at Part Loads for Selections for 454 m3Jhr (2000 gpm) and 122 m (400 ft) Solution Specific speed 1 1 1 2 2 2 1,775 1,775 1,775 2,985 2,985 2,985 Percentage of design flow 100% 75 50 100 75 50 Power as percentage of design (hp) 100% 89 76 100 95 86 kW (bhp) 181 161 138 176 167 152 (243) (216) (185) (236) (224) (203) Gain or loss compared to solution 1 Base Base Base 5kW gain (6kW loss) (13kW loss) Centrifugal Pumps and Energy Conservation 547 Table 21.3 Comparison of One- and Two-Stage Pump Selections in Tenns of Yearly Operation at Various Loads (Conditions: 454 m 3Jhr [2000 gpm], 122 m [400 ft]) Advantage in kWhr Operating time Capacity in percentage of design flow 100% 75 50 Total In % In hrs One-stage pump 30 60 10 100 2,628 5,256 876 8,760 31,536 11,388 42,924 Two-stage pump 13,140 13,140 Net savings in favor of one-stage pump = 29,784 kWhr. stage pumps at 75 percent and 50 percent flow (see Table 21.2). Instead of saving energy at all flows, the two-stage pump uses 6kW (8 hp) more at 75 percent flow and 13 kW (18 hp) more at 50 percent. To establish the real energy balance between the two solutions, we need to predict the subdivision of operating hours at various loads. If we assume that this subdivision will correspond to that shown in Table 21.3, we find that the most efficient pump is not the best selection and that the single-stage pump will save 29,784 kWhr yearly over the two-stage pump. Obviously, the final answer will always depend on the load factor that will prevail in a given installation. WHERE CAN WE SEARC