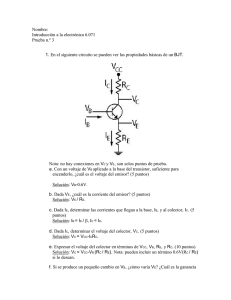
Unidad 2 Transistores Bipolares BJT El transistor es un dispositivo semiconductor capaz de amplificar señales de radio y Televisión. Gracias al transistor se han logrado muchos otros inventos, incluyendo el circuito integrado (CI), pequeño dispositivo que contiene miles de transistores. La palabra bipolar es una abreviatura de “dos polaridades “. 2.1 Estructura La figura 2.1 muestra la estructura de un transistor, el transistor tiene dos uniones, es similar a dos diodos. El emisor y base forman el diodo emisor, el colector y la base forman el diodo colector. 2.2 Polarización En la figura 2.2 se ve un transistor con polarización. La fuente de la izquierda polariza directamente al diodo emisor, y la fuente de la derecha polariza inversamente el diodo colector. 2.3Corrientes en un Transistor Relación entre las tres corrientes del transistor 𝐼𝐸 = 𝐼𝐶 +𝐼𝐵 La corriente de la base es mucho menor que la corriente de colector, en muy buena aproximación, la corriente del colector es igual a la corriente del emisor. La ganancia de corriente 𝛽𝐶𝑑 de un transistor, se expresa β𝑐𝑑= 𝐼𝐶 𝐼𝐵 Para transistores de baja potencia, la ganancia generalmente fluctúa entre 100 y 300, esto significa que el 95% o más de los electrones del emisor pasan hacia el colector. 𝐼𝐶 =β𝑐𝑑 𝐼𝐵 2.4 Conexión emisor común (EC) En la figura 2.4 el lado común de cada fuente de voltaje está conectado al emisor. Debido a esto, el circuito se conoce como conexión emisor común. El circuito de la base controla al circuito del colector. Usando diferentes valores de VBB y/o 𝑅𝐵 , se puede controlar la corriente de la base. 2.5 Curva de la base Es como la gráfica de un diodo rectificador ordinario, porque estamos hablando acerca de la corriente y el voltaje del diodo emisor, esto significa que podemos usar cualquiera de las tres aproximaciones de un diodo analizadas con anterioridad. Para calcular la𝐼𝐵 en una conexión EC se aplica la ley de Ohm 𝐼𝐵 = 𝑉𝐵𝐵−𝑉𝐵𝐸 𝑅𝐵 VCE= VC-VE VCB= VC-VB VBE= VB-VE 2.6 Curvas del Colector En un circuito EC como el de la figura 2.4.Se puede variar V BB o VCC para establecer diferentes voltajes y corrientes. Midiendo IC y VCE se obtienen los datos para graficar la curva del colector fig 2.6. La curva muestra lo siguiente: Cuando VCE es cero, el diodo colector no tiene polarización inversa. Para VCE cero y aproximadamente IV, la corriente del colector se eleva rápidamente y luego se mantiene casi constante. Esto está ligado con la idea de la polarización inversa de diodo colector. Se requieren cerca de 0.7v inversamente el diodo colector. para polarizar El Voltaje y Potencia del transistor son: 𝑉𝐶𝐸 = 𝑉𝐶𝐶 -𝐼𝐶 𝑅𝐶 𝑃𝐷 =𝑉𝐶𝐸 𝐼𝐶 𝑃𝐷 (máx)=Potencia máxima Tres regiones de Operación La curva de la figura 2.6 exhibe tres regiones de operación del transistor. Primero tenemos la región central. Ésta región representa la operación normal del transistor .En el diodo emisor está polarizado directamente y el diodo colector tiene polaridad inversa. En ésta región los cambios en el voltaje del colector no tiene efecto sobre la corriente del colector. A esta región se le da el nombre de región activa. Otra de las regiones de operación es la región de rompimiento. El transistor nunca debe de operar en ella, ya que se puede destruir o degradar. La parte ascendente de la curva donde VCE está entre 0 y aproximadamente 1V se llama región de saturación o región óhmica. En esta región, el diodo colector no está polarizado inversamente. Más curvas Si se miden IC y VCE para otros valores de IB se pueden trazar un conjunto de curvas como lo muestra la figura 2.7. 2.7 Aproximaciones para el transistor Transistor Ideal Si se pudiera construir un transistor ideal o perfecto, tendría las curvas del colector como las de la figura 2.8. En primer lugar no habría región de rompimiento. En segundo lugar, no existiría una corriente de corte de colector. En tercer lugar, no habría región de saturación. La figura 2.9 resume lo dicho en el párrafo anterior. Segunda aproximación En la segunda aproximación se incluyen los 0.7volts de la barrera de potencial del diodo base-emisor en el cálculo de la corriente de la base. En la figura 2.10 se resume la segunda aproximación para un transistor. Tercera aproximación Se utiliza únicamente cuando se está trabajando en el diseño de circuitos. Lo que hay que saber acerca de la tercera aproximación son dos cosas. El diodo emisor tiene una resistencia de estructura que produce un voltaje que tiene que sumarse a 0.7v para obtener el voltaje total entre las terminales base-emisor. Segunda, el diodo colector tiene una resistencia de estructura en la que aparecen unas décimas de volt. Este voltaje no será perceptible a menos que el transistor esté operando en la región de saturación. Así, en vez de que el voltímetro marcase cero, podría indicar de 0.1 a 0.2v en transistores de baja potencia. En la figura 2.11 se resume la tercera aproximación para un transistor. Hoja de datos Cuando se leen las hojas de datos de un transistor, se debe comenzar por las especificaciones máximas ya que son los límites para las corrientes, voltajes y otras cantidades del transistor. Especificaciones de rompimiento VCB 60V VCEO 40V VEB 2N3904 Voltajes inversos de rompimiento VCEO=Voltaje colector emisor con la base abierta. 6V Basta con acercarse a las especificaciones máximas para acortar la vida de algunos dispositivos. Corriente y potencia máximas 2N3904 IC= 200 mA cd PD= 250 mW (para TA=60° c) PD=350 mW (para TA= 25° c) Factores de ajuste El factor de ajuste indica cuanto hay que reducir la especificación de potencia de un dispositivo. Por ejemplo el factor de ajuste de un 2N3904 está dado como 2.8 mW/°C. Esto significa que hay que reducir la especificación de potencia de 300 mW en 2.8mW por cada grado Celsius que esté por encima de los 25°C. Disipadores de calor Una manera de aumentar la especificación de potencia de un transistor consiste en deshacerse con mayor rapidez del calor interno. Éste es el propósito de un disipador de calor. Fig.2.12.-Tipos de encapsulados con disipador de calor Ganancia de corriente En otro sistema de análisis llamado parámetros h, se usa h FE en vez de βcd como símbolo para la ganancia de corriente. βcd=hFE La hoja de datos de un 2N3904 lista los valores de hFE como sigue: IC, mA 0.1 1 10 50 100 Min hFE 40 70 100 60 30 Máx hFE ----------300 ----------- La hoja de datos contiene solamente la ganancia mínima de corriente para corrientes distintas de 10mA, ya que los valores mínimos representan el peor de los casos. Alfa para cd El valor alfa para cd de un transistor indica que tan iguales son las corrientes I E e IC; se define como: 𝐼𝐶 αcd=𝐼𝐸 Ejemplo si en un transistor, se mide una IC=8mA y una IE=8.2mA entonces 8𝑚𝐴 αcd=8.2𝑚𝐴=0.97 Casi todos los transistores tienen valores mayores que 0.95 Lo que significa que la IC es el 98% de la corriente del emisor. Relación entre Alfa y Beta Se tiene que ….1 IE=IC+IB Dividiendo ambos lados de la ecuación 1 entre IC se obtiene 𝐼𝐸 𝐼𝐵 =1+𝐼𝐶 𝐼𝐶 Si αcd= 𝐼𝐶 𝐼𝐸 entonces βcd= 1 𝐼𝐶 𝐼𝐵 1 =1+𝛽𝑐𝑑 𝛼𝑐𝑑 Re arreglando y despejando βcd se tiene 1 1 = 𝛼𝑐𝑑 -1 𝛽𝑐𝑑 1 Ejemplo si αcd =0.97 = 1−𝛼𝑐𝑑 𝛽𝑐𝑑 𝛼𝑐𝑑 βcd= 𝛼𝑐𝑑 1−𝛼𝑐𝑑 0.97 βcd =1−0.97=32.33 Una fórmula para αcd en términos de βcd αcd = 𝛽𝑐𝑑 𝛽𝑐𝑑+1 Ejemplo si βcd = 150 150 α=150+1=0.993 Variaciones en la ganancia de corriente de un transistor.Las variaciones de la ganancia de un transistor varían por tres factores. 1-Por construcción, tiene una variación de 3:1 cuando se cambia de un transistor a otro del mismo tipo. Ejemplo: el 2N3904 tiene una hFE mínima de 100 y una hFE máxima de 300 para un IC de 10mA. Cuando se producen estos transistores en serie algunos transistores tendrán una ganancia de 100, mientras que otros tendrán una ganancia de 300. 2-La ganancia depende del valor de la corriente del colector. Ver tabla de ganancias para el transistor 2N3904 dada anteriormente. 3-Debido a la temperatura de la unión (figura 2.13) 2.8 Línea de carga Una línea de carga es una recta trazada sobre las curvas del colector, para mostrar todos y cada uno de los puntos de operación posibles de un transistor, figura 2.14. Punto de Saturación El punto de saturación indica la máxima corriente del colector que es posible alcanzar en el circuito. El procedimiento para hallar la corriente de saturación es el siguiente: 1-Ponga en corto las terminales del colector-emisor. 2-Halle la corriente del colector IC (sat)= 𝑉𝐶𝐶 𝑅𝐶 Punto de Corte El punto de corte es el punto en que la línea de carga intersecta la región de corte de las curvas del colector. El punto de corte indica el máximo voltaje colector-emisor que es posible alcanzar en el circuito. El proceso para hallar el VCE de corte es el siguiente; 1-Abra las terminales colector-emisor. 2-Calcule el voltaje colector-emisor. VCE(corte)= VCC Punto de operación Q Q= Quiet point. (Quieto callado o en reposo) Son los valores de IC y VCE a los que trabaja un transistor. Ejemplo: Por lo tanto si la ganancia es β = 100 encontrar el punto Q. Sabemos que la ganancia de corriente varía con los cambios de temperatura., por construcción, por cambios en IC. Si la βcd =50 Iβ = 𝑉𝐵𝐵−𝑉𝐵𝐸 𝑅𝐵 IC= 𝛽𝑐𝑑 𝐼𝐵 VCE=𝑉𝐶𝐶 − 𝐼𝐶 𝑅𝐶 Si la βcd = 150 2.9Cómo reconocer la saturación Para saber si un transistor está operando en la región de saturación o en la región activa, se puede utilizar el siguiente método para analizar un circuito nuevo. Conocido como reducción a lo absurdo éste indica con rapidez la región de operación. 1-Supóngase que la región es la activa. 2-Efectúense los cálculos. 3-Si surge una respuesta absurda, la suposición era falsa. Ejemplo: Otro método Se comienza calculando la corriente de saturación del colector. Éste es el valor máximo posible que la IC puede alcanzar en el circuito. Más allá de éste valor, el transistor entra en saturación. IC(sat)= 𝑉𝐶𝐶 𝑅𝐶 Entonces si IC > IC (sat), el transistor debe estar saturado. Ejemplo: circuito figura anterior En la región de saturación no se le obtiene toda la ganancia que da el transistor. En una hoja de datos cuando se da la ganancia de corriente, casi siempre es para la región activa (ganancia mínima del transistor). La ganancia de corriente saturada se puede calcular como sigue: βcd(sat)= 𝐼𝑐(𝑠𝑎𝑡) 𝐼𝐵 Βcd = ?. Ejemplo: circuito figura anterior. Saturación dura Cuando un transistor está saturado, la corriente del colector es máxima, no hay nada que se pueda hacer para aumentarla. Si se desea que un transistor opere en la región de saturación, se elige a menudo una resistencia de la base que produzca una ganancia de corriente en saturación igual a 10. A esto se le llama saturación dura, porque es una corriente de la base más que suficiente para saturar al transistor, sin que le afecten los cambios en la ganancia. βcd(sat dura) = 𝐼𝐶(𝑠𝑎𝑡) 𝐼𝐵 = 10 βcd en el peor de los casos es de 36 Saturación suave Se refiere a cualquier diseño que apenas ponga en saturación al transistor. 𝐼𝛽 = 𝐼𝐶(𝑠𝑎𝑡) 𝛽𝑐𝑑(𝑔𝑎𝑛𝑎𝑛𝑐𝑖𝑎 𝑑𝑒𝑙 𝑡𝑟𝑎𝑛𝑠𝑖𝑠𝑡𝑜𝑟 𝑑𝑒 𝑙𝑎 ℎ𝑜𝑗𝑎 𝑑𝑒 𝑑𝑎𝑡𝑜𝑠) Ejemplo: circuito figura anterior. 2.10 El transistor como conmutador La polarización de la base es útil en los circuitos digitales ya que por lo general estos circuitos se diseñan para operar en saturación y en corte. Por esto, tienen un voltaje de salida bajo o alto, es decir no se emplea ningún punto Q que no sea el de corte o el de saturación. VCE(sat)= 0.2V ICEO= 70nA Idealmente el voltaje de salida debe ser 0 y 5v. Realmente se debe de tomar en cuenta VCE(sat)=0.2 ICEO= 70nA 2.11 Polarización del emisor En circuitos amplificadores se requieren circuitos cuyos puntos Q sean inmunes a los cambios en la ganancia de corriente. Esto hace necesario un nuevo diseño llamado polarización del emisor. Cuando la ganancia de corriente cambia de 50 a 150 el punto Q es casi inamovible. El voltaje del emisor está dado por 𝑉𝐸 = 𝑉𝐵𝐵 − 𝑉𝐵𝐸 Cómo hallar el punto Q La corriente del emisor es: 𝑉𝐸 𝐼𝐸 =𝑅𝐸 En una buena aproximación IC ≅IE El voltaje entre colector y tierra será: 𝑉𝐶 =𝑉𝐶𝐶 − 𝐼𝐸 𝑅𝐶 El voltaje colector emisor es: 𝑉𝐶𝐸 = 𝑉𝐶 − 𝑉𝐸 Con VCE e IC obtenemos las coordenadas del punto Q. El circuito es inmune a los cambios de la ganancia del transistor. Los cálculos del punto Q para la polarización del emisor, en ningún momento hubo necesidad de utilizar la ganancia de corriente, por lo tanto su valor exacto ya no es importante. En un circuito con polarización del emisor el punto Q es casi inamovible por lo siguiente. Todo el voltaje VBB de la fuente menos 0.7V aparece en el resistor del emisor estableciendo una corriente fija en el emisor aun cuando la temperatura cambie a los transistores se reemplacen etc. La ganancia de corriente sigue siendo inestable, y esto hace que la corriente de la base cambie, esto ya no tiene nada que ver con la corriente del colector ya que es aproximadamente igual a la corriente del emisor, por lo tanto su valor se mantiene fijo. La ganancia de corriente tiene un efecto muy pequeño sobre la corriente del colector. El valor exacto de ese efecto se halla como se indica a continuación: 𝐼𝐸 =𝐼𝐶 + 𝐼𝛽 𝐼𝐶 𝐼𝐸 =𝐼𝐶 +𝛽𝑐𝑑 𝛽𝑐𝑑 𝐼𝐶 = 𝛽𝑐𝑑+1 𝐼𝐸 𝛽𝑐𝑑 𝛽𝑐𝑑+1 Es el factor de corrección y es un indicador de cuanto difiere IC de IE . Se necesita una ganancia de corriente de apenas 20 para tener errores de más del 5%. Línea de carga Teniendo en cuenta que el voltaje del emisor está fijo 𝐼𝐶(𝑠𝑎𝑡) = 𝑉𝑐𝑐−𝑉𝐸 𝑅𝑐 𝑉𝑐𝐸(𝑐𝑜𝑟𝑡𝑒) = 𝑉𝑐𝑐 − 𝑉𝐸 Ejemplo: Trazar la línea de carga y encontrar el punto Q. 1-Ignorar el factor de corrección. 2-Con factor de corrección- como afectan los cambios de ganancia el punto Q Para β = 100 3-Para β = 50 4-Para β = 150 2.12Polarización por divisor de voltaje El circuito de polarización por divisor de voltaje está basado en el prototipo de la polarización del emisor. El divisor de voltaje A veces, el voltaje de una fuente de potencia es demasiado grande para aplicarse directamente a la base. La forma más sencilla de reducir el voltaje consiste en insertar un divisor de voltaje como se muestra en la figura 2.16. EL voltaje en R2 es V2 por lo tanto el VB=V2 Algunos sistemas electrónicos disponen únicamente de un voltaje de fuente de potencia. En tal caso, el circuito ha de diseñarse como se ve en la figura 2.17. 2.13 Análisis de la PDV Lo que estudiaremos permite errores de 5% o menos. El proceso principia hallando el voltaje de la base. Para esto, hay que hacer una suposición: la corriente de la base es tan pequeña que no tiene ningún efecto sobre el divisor de voltaje. La corriente en el divisor de voltaje es: 𝑉𝐶𝐶 I= 𝑅1+𝑅2 Para considerar la corriente de la base como pequeña, esta debe ser por lo menos 20 veces menor que la corriente del divisor de voltaje. Esto limita el error de cálculo a un 5%, la corriente de la base debe ser menor que: 𝐼 𝐼𝐵 =20 Si esta condición se satisface, se puede calcular el voltaje como sigue: VB= IB2 Voltaje y corriente del emisor VE= VB-VBE 𝑉𝐸 Y la IE= 𝑅𝐸 Voltaje del colector y voltaje colector-emisor VC= 𝑉𝐶𝐶 − 𝐼𝐶 𝑅 VC E= 𝑉𝐶 − 𝑉𝐸 Verificando la suposición Comprobar que la corriente de la base sea 20 veces menor que la corriente del divisor de voltaje. Supóngase que la ganancia del transistor fluctúe entre 36 y 300. En el peor caso corresponde al valor mínimo de la ganancia de corriente ya que esto produciría la corriente de la base máxima. 𝐼𝐸 IB=𝐵𝑐𝑑 𝑚í𝑛 En la PDV El punto Q es inmune a los cambios de la ganancia del transistor, si la corriente de la base no tiene ningún efecto sobre el voltaje de la base. 2.14 Línea de carga y punto Q para la PDV Puntos de saturación y corte Para hallar la corriente de saturación, imagine un corto entre el colector y emisor, el voltaje en la RC será: VRC=Vcc-VE IC(sat)= 𝑉𝑅𝐶 𝑅𝐶 Para hallar el punto de corte, imaginemos un circuito abierto entre el colector y el emisor por lo tanto: VCE(corte)= VCC-VE El punto Q (Ic, VCE) El punto Q es prácticamente inmune a los cambios en la ganancia de corriente. Una forma de mover el punto Q sobre la línea de carga consiste en variar la resistencia del emisor. La figura 2.18 nos muestra la línea de carga y el punto Q para la PDV. Ejemplo: Trazar la línea de carga y el punto Q del ejemplo anterior. Trazar el punto Q si se cambia la RE (Grande)-(pequeña). 2.15.- Polarización del emisor con dos fuentes. Algunos equipos electrónicos tienen una fuente de potencia que producen voltajes positivos y negativos de fuente. En la figura 2.19 se muestra un circuito transistorizado con dos fuentes de potencia +10v y -2v. La fuente negativa polariza directamente el diodo emisor. La fuente positiva polariza inversamente al diodo colector. Análisis.Cuando este tipo de circuitos está diseñado correctamente, la corriente de la base será lo bastante pequeña para ser ignorada, por lo tanto el voltaje de la base se supondrá que es de 0v. El voltaje en el diodo emisor es de 0.7v. El resistor de nuevo desempeña el papel clave de establecer la corriente del emisor. 𝑉𝑅𝐸 = 𝑉𝐸 − 𝑉𝐸𝐸 La corriente del emisor será: 𝐼𝐸 = 𝑉𝑅𝐸 𝑅𝐸 El voltaje del colector es: 𝑉𝑐 = 𝑉𝑐𝑐 − 𝐼𝑐 𝑅𝑐 Y el voltaje colector emisor será: 𝑉𝐶𝐸 = 𝑉𝑐 − 𝑉𝐸 Ejemplo: Encuentre el voltaje colector-emisor del circuito siguiente. 𝑉𝑅𝐸 = −0.7 − (−2) 𝑉𝑅𝐸 = 1.3𝑉 𝐼𝐸 = 1.3 = 1.625𝑚𝐴 0.8 𝑉𝑐 = 12 − (1.625)(5) = 3.875𝑣 𝑉𝐶𝐸 = 3.875 − (−0.7) 𝑉𝐶𝐸 = 4.575𝑣 Análisis más exacto La polarización del emisor con dos fuentes requiere que la corriente de la base sea pequeña. ¿Qué tan pequeña debe ser la corriente de la base para que el punto Q sea inmune a los cambios en la ganancia de corriente? Para responder a esta pregunta se supondrá que la ganancia de corriente puede fluctuar entre 36 y 300. Idealmente el voltaje de la base debe ser 0V. En tal caso, el voltaje en el resistor del emisor tiene un valor constante que no se ve afectado por los cambios en la ganancia de corriente. En realidad, la corriente de la base es mayor, que cero, el voltaje en la base es ligeramente negativo. Supóngase que se puede tolerar un voltaje de la base hasta de -0.1V. Entonces el voltaje de la base podrá variar de 0 a -0.1V.Por lo tanto en el peor de los casos, el voltaje de la base puede ser -0.1V, y el voltaje del emisor puede ser hasta de -0.8V. Ejemplo: de la figura del ejemplo anterior calcula el V CE considerando la caída de voltaje de la RB. VRE= -0.8-(-2V)=1.2V 1.2 IE= 0.8= 1.5 mA VC=12-(1.5)(5)=4.5V VCE=4.5-(-0.8)=5.3V En éste punto, se debe verificar la suposición de que el voltaje de la base es de -0.1v. En el peor de los casos: 𝐼𝐸 1.5 IB=𝐵𝑐𝑑(𝑚í𝑛)= 36 = 41.666µA VB= (41.666µA)(2kΩ )= -0.0833v Este voltaje de la base es menor que el límite de -0.1v. En un diseño rápido 𝑅𝐵 < 0.01𝛽𝑐𝑑 𝑅𝐸 2.16.- Transistores PNP 𝐼𝐸 = 𝐼𝑐 + 𝐼𝐵 𝛽𝑐𝑑 = 𝐼𝑐 𝐼𝐵 La figura 2.23 muestra la polarización por divisor de voltaje de un transistor PNP con fuente de voltaje negativa. 𝑅1 = 10𝑘Ω 𝑅2 = 3𝑘Ω 𝑅𝑐 = 4𝑘Ω 𝑅𝐸 = 1𝑘Ω Fuente positiva de potencia Las fuentes positivas de potencia son mucho más comunes que las fuentes de potencia negativas. Por esto, se ven a menudo transistores PNP dibujados cara abajo, como se muestra en la figura 2.24. 𝑉𝐶𝐸(𝑐𝑜𝑟𝑡𝑒) = 𝑉𝐶 − 𝑉𝐸 𝑉𝐶𝐸(𝑐𝑜𝑟𝑡𝑒) = −(𝑉𝐸𝐸 − 𝑉𝑅𝐸 ) 𝐼𝐶(𝑠𝑎𝑡) = 𝑉𝐸 𝑉𝐸𝐸 − 𝑉𝑅𝐸 = 𝑅𝑐 𝑅𝑐 Si la corriente de la base es tan pequeña, puede ser ignorada, la corriente del divisor de voltaje puede calcularse así: 𝐼= 𝑉𝐸𝐸 𝑅1 + 𝑅2 Siguiendo la regla de 20:1, la corriente de base deberá ser menor que: 𝐼𝐵 = 𝐼 20 El voltaje 𝑉2 = 𝐼𝑅2 𝑉𝑅𝐸 = 𝑉2 − 0.7 𝐼𝐸 = 𝑉𝑅𝐸 𝑅𝐸 𝑉𝑐 = 𝐼𝐸 𝑅𝑐 𝑉𝐸 = 𝑉𝐸𝐸 − 𝑉𝑅𝐸 𝑉𝐶𝐸 = 𝑉𝑐 − 𝑉𝐸 Se debe comprobar la suposición de que la corriente de la base es pequeña 20:1: 𝐼= 𝐼𝐸 𝛽𝑐𝑑(minimo) UNIDAD NÚMERO 3 “TRANSISTORES DE EFECTO DE CAMPO (FET)” 3.1.- El JFET. El primer tipo de FET (Fieel Effect Transistor) que estudiaremos es el JFET de unión. La figura 3.1 muestra la construcción y estructura de un JFET canal n. Continuación en siguiente página Una analogía muy grande existe entre el transistor bipolar y el JFET. Una analogía se define como una semejanza en algunos aspectos entre cosas que difieren en otros aspectos, una analogía a notar es las tres regiones: Bipolar JFET Emisor Fuente Base Compuerta Colector Dren 3.2. Polarización del JFET La figura 3.2 presenta la forma normal de polarizar un JFET. Corriente de compuerta En un JFET siempre polarizamos en inversa el diodo compuerta fuente. Debido a la polarización inversa Ia≈0, idealmente: Ia=0 Si un dispositivo no tiene corriente de entrada, significa que el dispositivo tiene una resistencia de entrada infinita, por ejemplo, si VGG= 4v y la Ia=0, la resistencia de entrada es: 4 𝑅𝐺 = 0 = ∞ Por lo tanto RG es de cientos de MΩ. Efecto de campo El término efecto de campo se relaciona con las capas de empobrecimiento alrededor de cada región P como se observa en la figura 3.3. La recomendación de los electrones libres y huecos crea las capas de empobrecimiento mostradas por el área sombreada de la figura 3.3. Cuando los electrones fluyen desde la fuente hacia el dren, deben pasar a través del estrecho canal n entre las dos capas de empobrecimiento. Cuanto más negativo es el voltaje de compuerta, más estrecho será el canal n. El JFET actúa como un dispositivo controlado por voltaje. Los cambios en V GS determinan cuenta corriente puede circular desde la fuente al dren. En un JFET la corriente del dren: ID=Is Un amplificador JFET tiene mucha menor ganancia de voltaje que un amplificador BJT. Símbolo esquemático: 3.3. Curvas del dren Fig.3.5.- Polarización normal del JFET. Fig.3.6.- Polarización del JFET con voltaje de compuerta nula Corriente de dren máxima La corriente de dren máxima que sale de un JFET ocurre cuando el voltaje de la compuerta fuente es cero como se observa en la figura 3.6. VGS=0 Semejante a un transistor bipolar, un JFET actúa como una fuente de corriente cuando está operando a lo largo de la sección casi horizontal de la curva del dren, con un valor I DSS, como se muestra en la figura 3.7. Fig.3.7.- Curva del Dren con la compuerta en corto Al voltaje Vp se le denomina voltaje de estrangulamiento y al voltaje máximo VDS(max) se llama voltaje de rompimiento. La IDSS es la corriente Dren fuente con la compuerta en corto y es la corriente máxima que un JFET puede conducir. Todas las hojas de datos de los JFET listan el valor de IDSS MPF102 IDSS 6mA Corte y estrangulamiento de la compuerta La figura 3.8 muestra un conjunto de curvas de dren para un JFET con una I DSS de 12mA, el voltaje de estrangulamiento es de 4v y el voltaje de rompimiento es de 35v. Fig.3.8.- Curvas del Dren de un JFET Para VGS= -4V la corriente ID es casi cero, a este voltaje se le denomina voltaje de corte compuerta fuente VGS (OFF)“el cual es un dato”. Se puede observar que VGS (OFF) = -Vp, esto se cumple para todos los JFET´S. Región Óhmica La parte casi vertical de la curva del dren se llama región óhmica. Cuando un JFET funciona en la región óhmica, actúa como un resistor pequeño con un valor aproximado de: 𝑅𝐷𝑆 = 𝑉𝑝 𝐼𝐷𝑆𝑆 Ejemplo: ¿Cuál es la resistencia del dren para un JFET con una IDSS de 12mA y Vp= 4v. 4 𝑅𝐷𝑆 = 12=333.33Ω 3.4. Curva de transconductancia. La curva de transconductancia de un JFET es una gráfica de la ID contra VGS (figura 3.4). Fig.3.9.- Curva de transconductancia de un JFET Todos los JFET tienen una curva de transconductancia que es la gráfica de la siguiente ecuación: 𝐼𝐷 = 𝐼𝐷𝑆𝑆 (1 − 𝑉𝐺𝑆 𝑉𝐺𝑆(𝑂𝐹𝐹) )2 Con la ecuación anterior podemos calcular la corriente del dren (Aproximado) una vez dada la corriente máxima de dren, el voltaje VGS (OFF) y el voltaje de compuerta. Podemos ver que la curva es no lineal, la forma de la gráfica es parabólica. ID=KIDSS , donde K= (1 − 𝑉𝐺𝑆 𝑉𝐺𝑆(𝑂𝐹𝐹) )2 3.5. Aproximaciones del JFET. El JFET MPF102 tiene una IDSS máxima de 20mA y una IDSS mínima de 2mA, es decir, una dispersión de 10:1. Con una dispersión como esta, la única solución adecuada es la de utilizar aproximaciones razonables. JFET ideal Las características del JFET ideal son: 1.- No hay región de rompimiento. 2.- Las curvas del dren se sobreponen en la región óhmica. 3.- Las curvas del dren en la región activa son horizontales. La figura 3.10 se observan las curvas del dren de un JFET ideal y una línea de carga. Fig.3.10.- Curvas del dren de un JFET ideal y línea de carga Cuando el JFET funciona en la región activa, se utiliza el modelo fuente de corriente (fig 3.11), es decir, cuando VDS es mayor que Vp, el JFET actuará como una fuente de corriente para cualquier voltaje de compuerta. Fig.3.11.- Modelo fuente de corriente *Nota: Si VDS > Vp se utiliza el modelo fuente de corriente. El modelo óhmico (fig 3.12) es válido cuando el JFET funciona en la parte casi vertical de las curvas del dren. El JFET actúa como una resistencia de valor R DS. Fig.3.12.- Modelo óhmico 𝑉𝑝 𝑅𝐷𝑆 = 𝐼 𝐷𝑆𝑆 Voltaje de estrangulamiento para cualquier valor de VGS. El voltaje de estrangulamiento de la figura 3.10 separa la región óhmica de la región actica cuando VGS es nulo. Cuando VGS no es igual a cero, podemos utilizar el voltaje de estrangulamiento proporcional como nuestra guía. Este voltaje es la frontera entre la región óhmica y la región de fuente de corriente para cualquier valor de V GS. Esta cantidad está dada por: VP´= ID RDS Vp´ Voltaje de estrangulamiento proporcional. En la figura 3.13 se ve la región óhmica de un JFET ideal. Fig.3.13.- Voltaje de estrangulamiento proporcional Mediante geometría, podemos ver la relación de proporcionalidad entre el punto de coordenadas (IDSS, Vp) con cualquier otro punto en esta región. 𝑉𝑝´ 𝐼𝐷 =𝐼 𝑉𝑝 𝐷𝑆𝑆 Por lo tanto 𝑅𝐷𝑆 = 𝑉𝑝´ 𝐼𝐷 Tenemos que 𝑅𝐷𝑆 = 𝑉𝑝 𝐼𝐷𝑆𝑆 Despejando nos queda 𝑉𝑝´ = 𝐼𝐷 𝑅𝐷𝑆 Reducción a lo absurdo Cuando no está seguro de la región en que funciona un transistor, suponemos un funcionamiento en la región activa, si los cálculos producen un resultado absurdo, entonces sabremos que el transistor no puede funcionar en la región supuesta. 3.6. El MOSFET El MOSFET o FET de semiconductor de metal-+oxido, a diferencia del JFET la compuerta está aislada eléctricamente del canal, Al MOSFET frecuentemente se le llama IGFET que quiere decir FET de compuerta asilada (Insulated- Gate FET). Hay dos tipos de MOSFET; el MOSFET en modo de empobrecimiento y el MOSFET en modo de enriquecimiento. 3.7. MOSFET en modo de empobrecimiento En la figura 3.14 se observa un MOSFET en modo de empobrecimiento de canal n. Los electrones libres pueden circular desde la fuente hacia el dren a través del material n. Fig.3.14.- MOSFET en modo de empobrecimiento canal n En un MOSFET una delgada capa de dióxido de silicio (SiO2) se deposita en el lado izquierdo del canal. El dióxido de silicio es semejante al vidrio, por lo tanto es un aislante. Polarización del MOSFET en modo de empobrecimiento En la figura 3.15 se ven los modos de polarización de la compuerta. El voltaje en la compuerta controla el ancho del canal. Para el análisis de un circuito con JFET se procede como sigue: 1.- Se supone la región de fuente de corriente. 2.- Se llevan a cabo los cálculos. 3.- Si surge una respuesta absurda, la suposición es falsa. 4.- Se cambia al modelo óhmico. *Ejemplo: En la siguiente se tiene un JFET canal N que tiene una I DSS DE 20 mA y un VGS (OFF)= -5v. Encontrar el voltaje VDS cuando VGS = -1 VDS>Vp se utiliza modelo fuente de corriente VDS=VDD-IDRD =12 - 4.5 =7.5 Por lo tanto si VDS>Vp, entonces7.5 > 6, la suposición acerca de la fuente de corriente es correcta. *Ahora, si RD se cambia por una de 1.2kΩ y VGS=0, VDS=2. VDS=12-15mA x 1.2 kΩ VDS= -6 respuesta absurda, por lo tanto el JFET trabaja en la región óhmica. Rds= 𝑉𝑝 𝐼𝐷𝑆𝑆 6 = 15𝑚𝐴 Rds= 400Ω a) Voltaje de compuerta negativo b) Voltaje de compuerta positivo Fig.3.15.- Polarización del MOSFET en modo de empobrecimiento Cuando el voltaje de compuerta es lo suficientemente negativo, la corriente del dren se interrumpe. El funcionamiento de un MOSFET en modo empobrecimiento es similar al del JFET cuando VGS es negativo. Si se aplica un voltaje positivo a la compuerta, se incrementa el número de electrones libres que circulan a través del canal. Cuanto más positivo sea el voltaje de compuerta, mayor será la conducción desde la fuente hacia el dren. Gráficas La figura 3.16 muestra las curvas características del dren de un MOSFET en modo de empobrecimiento. Cuando VGS está entre VGS (OFF) y cero, tenemos el funcionamiento en modo de empobrecimiento. VGS mayor que cero proporciona funcionamiento en modo de enriquecimiento. Fig.3.16.- Curvas del dren del MOSFET en modo de empobrecimiento Fig.3.17.- Curvas de transconductancia Para encontrar la corriente ID y voltaje VDS en un circuito con MOSFET, se utilizan las mismas fórmulas y circuitos equivalentes que se utilizan para el JFET. Ejemplo: IDSS=13mA VGS (OFF)= -4v RDS= 𝑉𝑝 𝐼𝐷𝑆𝑆 Vp´=ID RDS Fig.3.18.- Símbolo esquemático 3.8. MOSFET EN MODO DE ENRIQUECIMIENTO Fig.3.19.- Estructura del MOSFET en modo de enriquecimiento Polarización La figura 3.20 muestra la polarización normal de un MOSFET en modo de enriquecimiento. El MOSFET está normalmente apagado cuando el voltaje de compuerta es cero. Fig.3.20.- Polarización del MOSFET en modo de enriquecimiento Cuando el voltaje de la compuerta es lo suficientemente positivo, atrae electrones libres dentro de la región P. Los electrones libres se recombinan con los huecos cercanos al dióxido de silicio. Cuando el voltaje de la compuerta es lo suficientemente positivo todos los huecos que tocan el dióxido de silicio se llenan y los electrones libres comienzan a circular desde la fuente hacia el dren. El efecto es idéntico al de crear una delgada capa de material tipo n próxima al dióxido de silicio llamada capa de inversión tipo n. El VGS mínimo que crea la capa de inversión de tipo n se llama voltaje de umbral VGS (th) en ingles threshold voltaje. Cuando VGS es menor que VGS (th), corriente del dren es nula. Pero cuando VGS es mayor que VGS (th), la corriente del dren es grande. Fig.3.21.- Curvas del dren La corriente del dren está dada por: 𝑉𝐺𝑆 −𝑉𝐺𝑆(𝑡ℎ) ID=KID(ON), donde K=( )2 𝑉𝐺𝑆(𝑂𝑁)−𝑉 𝐺𝑆(𝑡ℎ) Fig.3.22.- Curvas de transconductancia Los datos de un MOSFET en modo de enriquecimiento son ID (ON) y el voltaje, VGS (ON), VGS (th). Fig.3.23.- Símbolo esquemático del MOSFET m. de enr. Canal n Fig.3.24.- Símbolo esquemático del MOSFET m. de enr. Canal P. La capa de asilamiento de dióxido de silicio es tan delgada, se puede destruir fácilmente con un voltaje de compuerta fuente mayor que VGS (max). Por ejemplo el 2N3796 tiene un VGS (max) de ±30v a voltajes mayores de 30v la capa de aislamiento se destruye. Circuitos equivalentes del MOSFET en modo de enriquecimiento Fig.3.25.- Curvas ideales del dren del MOSFET en modo de enriquecimiento Vk´=ID RDS Vk´= Voltaje de rodilla proporcional La razón de no utilizar Vp´ es que el MOSFAT en modo de enriquecimiento no tiene voltaje de estrangulamiento donde las capas de empobrecimiento se juntan. El proceso para decidir qué modelo se usa es el siguiente: 1.- Calcule Vk´. 2.- Si VDS > Vk´ use el circuito equivalente de fuente de corriente. 3.- Si VDS < Vk´ use el circuito equivalente óhmico. Fuente de corriente Óhmico Fig.3.26.- Circuitos equivalentes ideales del MOSFET modo de enriquecimiento *Ejemplo: Se tiene el siguiente circuito, calcular el voltaje dren fuente. ID (ON)= 8mA VGS (th)= 2v VGS (ON)= 5v VDS (ON)= 2.4v Si VGS=4V 1.- VDS= ID=( 𝑉𝐺𝑆 −𝑉𝐺𝑆(𝑇𝐻) 𝑉𝐺𝑆(𝑂𝑁) −𝑉𝐺𝑆(𝑇𝐻) 10- (ID*RD) 2 ) ∗ 𝐼𝐷(𝑂𝑁) VDS=10 – (3.55 x 5) 4−2 ID=(5−2)2 ∗ 8𝑚𝐴 = 3.55𝑚𝐴 =-7.75 absurdo 2.- VDS < o > Vk´ Vk´= (3.55 x 10−3) (0.3 x 103 ) 𝑉𝐷𝑆(𝑂𝑁) RDS= 𝐼 𝐷(𝑂𝑁) 2.4 = 8𝑚𝐴 = 300Ω Vk´=1.065v También VDS < Vk´ por lo tanto se utiliza el modelo óhmico. 4.- AMPLIFICACIÓN 4.1. Capacitor de acoplamiento. Los capacitores de acoplamiento se emplean para acoplar o transmitir señales de C.A. de un circuito a otro. (Figura 4.1) 1 Xc=2 π𝑓𝑐 Un capacitor se comporta como un corto para c.a. a frecuencias altas, y como un circuito abierto para c.d. a frecuencias bajas. Un capacitor de acoplamiento transmite un voltaje de c.a. de un nodo (o punto) a otro. I= 𝑉𝐺 𝑅 Dónde: R=RG + RL Fig.4.1.- Capacitor de acoplamiento Un capacitor de acoplamiento, debe comportase como un cortocircuito para c.a. a la frecuencia más baja que pueda tener el generador. La reactancia debe ser por lo menos 10 veces menor que la resistencia total en serie con el capacitor. Xc < 10R donde R=RG + RL Frecuencia crítica Frecuencia crítica es la frecuencia a la cual la reactancia del capacitor es igual a la resistencia total. Xc=R A la frecuencia crítica la corriente rms, disminuye al 70.7% de su valor. 1 Xc=2 π𝑓𝑐 1 f=2 π𝑅𝐶 Por lo tanto 1 2 π𝑓𝑐 =𝑅 y despejando a f tenemos lo siguiente: 1 Por lo tanto la frecuencia crítica es: fc= 2 π𝑅𝐶 Un capacitor se comporta como un cortocircuito a frecuencias altas. Altas frecuencias significa 10 veces la frecuencia crítica, el límite de la alta frecuencia es fh>10fc. *Ejemplo: Si el generador tiene una frecuencia de 60Hz, el capacitor trabajará como un cortocircuito. 4.2. Capacitor de paso Se conecta en paralelo con un resistor (figura 4.2), si la frecuencia es lo suficientemente elevada, el capacitor actúa como un cortocircuito. En consecuencia la corriente alterna fluirá por el capacitor en vez de por la resistencia RL. Fig.4.2.- Capacitor de paso ¿Cuándo se tiene una frecuencia alta? La frecuencia crítica está dada por la misma fórmula vista para el capacitor de acoplamiento: 1 fc=2 π𝑅𝐶 La resistencia de Thevenin que ve el capacitor es: 𝑅 𝑅 R=𝑅 𝐺+𝑅𝐿 es decir R=RG ll RL 𝐺 𝐿 El límite de alta frecuencia es: fh=10fc Si la frecuencia es igual o mayor que este valor, el capacitor de paso actúa como un cortocircuito y el nodo A está aterrizado para señales de C.A. En otras palabras, el punto A es una tierra para C.A. como se muestra en la figura 4.3. Fig.4.3.- Circuito equivalente de Thevenin de la figura 4.2 *Ejemplo: Calcule el límite de alta frecuencia para la figura siguiente. 4.3. Amplificador transistorizado En la figura 4.4 se muestra un amplificador transistorizado. C1 acopla la señal del generador a la base, C2 acopla la señal amplificada al resistor de carga y CE es un capacitor de paso del nodo del emisor a tierra. Fig.4.4.- Amplificador transistorizado Aplicando el teorema de superposición, el análisis del circuito se hace en dos partes: un análisis para c.d. y un análisis para c.a. Análisis para CD El proceso para el análisis de cd de la figura 4.4 es el siguiente: 1.- Reducir a cero la fuente de c.a. 2.- Abrir todos los capacitores. 3.- Analizar el circuito resultante. Fig.4.5.- Circuito equivalente para c.d. *Ejemplo: Si R1=10, R2=2, Vcc=15v, VG=2mV, RG=300Ω, Rc=4kΩ, RE=1KΩ, RL=8kΩ, mientras que C1, C2 y C3 tienen la capacidad para comportarse como un corto circuito para c.a. y circuito abierto para c.d. El circuito equivalente para c.d. es: VB=2.5v VE=1.8v IE=1.8mA Vc=7.8v VCE=Vc – VE= 6 Análisis para CA El proceso para analizar el circuito de la figura 4.4 es: 4.- En el circuito original reducir a cero todas las fuentes de c.d. 5.- Poner en corto todos los capacitores. 6.- Analizar el circuito equivalente para c.a. Fig.4.5.- Circuito equivalente para c.a. 4.4. Operación con señales pequeñas En l figura 4.6 se incluye la gráfica de corriente en función del voltaje del diodo emisor. Fig.4.6.- Voltaje de c.a. aplicado al diodo base-emisor y la respectiva corriente del emisor Q es el punto de operación para c.d. Si se le añade un voltaje de c.a. al voltaje de c.d, el punto de operación instantáneo o real se aleja del punto estable Q.La razón por la cual la corriente de c.a. del emisor no es una réplica exacta del voltaje de c.a. de la base, es la curvatura de la gráfica del diodo emisor. El semiciclo positivo de la corriente de c.a. del emisor se estira, mientras que el semiciclo negativo se comprime, a esto se le da el nombre de distorsión. Una forma de reducir la distorsión consiste en mantener en un valor pequeño el voltaje de c.a. de la base. Si se reduce el valor pico del voltaje de la base, se reduce el desplazamiento del punto instantáneo de operación. Cuanto menor sea esta fluctuación, menor será la concavidad de la gráfica. Si la señal es lo suficientemente pequeña, la gráfica será lineal, es decir, los cambios en la corriente de c.a. del emisor son directamente proporcionales a los cambios en el voltaje de c.a. de la base ya que la gráfica parece lineal. ¿Qué tan pequeña debe ser la señal? La señal de c.a. es pequeña si el valor pico a pico de la corriente de c.a. del emisor es menor que el 10% de la corriente de c.d. del emisor. Con esta regla la distorsión no queda totalmente eliminada, pero la reduce a un nivel aceptablemente pequeño. *Ejemplo: (del libro) un amplificador tiene una corriente de c.d. del emisor igual a 10mA. Si se está operando como un amplificador para señales pequeñas. El valor pico a pico de la corriente de c.a. del emisor tiene que ser menor que 1mA. Si satisface esta condición, la operación si es de señal pequeña, el arco de la curva es muy pequeño que casi es una línea recta. 4.5. Resistencia del diodo emisor Resistencia para c.d. 𝑉 Rcd= 𝐼 donde V e I representan el voltaje y la corriente de cd. *Ejemplo: En la figura 4.7 el diodo del emisor tiene un punto Q cuyo voltaje de c.d. es de 0.7v (0.5 dato del libro) y cuya corriente de cd es de 1mA (0.9mA dato del libro). Por lo tanto, la resistencia del diodo emisor es de: 0.7𝑣 Rcd= 1𝑚𝐴 = 700Ω Resistencia para c.a. En un resistor lineal, como un resistor de carbono la resistencia de c.a. es la misma que para c.d. En dispositivos no lineales tales como los diodos o los transistores, la resistencia para c.a. es distinta de la resistencia para c.d. Δ𝑉𝐵𝐸 Rca= Δ𝐼𝐸 donde Δ es "el cambio en " son los valores pico a pico.