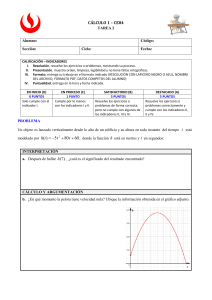
GUÍA DEL PARTICIPANTE Ciclo: Avanzado Grado de estudios: 4° de Avanzado Nombre del Área Curricular: Matemática Temática: 1. Presentación del área: El área de matemática promueve experiencias significativas para que los estudiantes construyan sus aprendizajes, en forma individual y en cooperación con otros. 2. Propósito: Brindar al estudiante oportunidades de aprendizaje para que sea capaz de valorar y utilizar el aporte de la matemática en la comprensión de su entorno físico, social y cultural, y en la identificación y resolución de problemas relacionados con su contexto real. El área de matemática se organiza en tres componentes: Sistema numérico y funciones Geometría y medida Estadística y probabilidad 3. 1. Secuencia temática: Sesiones de aprendizaje Aprendizajes a lograr Contenidos 1.-Resuelvo problemas 2. sobre sistema de ecuaciones con dos variables en R. Resuelve problemas relacionados con la realidad, utilizando sistemas de ecuaciones con dos variables en R. Sistemas de Ecuaciones - Nociones Previas - Métodos de Resolución: Reducción. Gráfico. 3. 2.- Identifico funciones Identifica gráfica y matemáticamente funciones lineales como modelo para el análisis de diversos fenómenos y situaciones de la realidad. Resuelve problemas vinculados con la realidad que involucran funciones lineales. 3.- Identifico funciones4. Identifica gráfica y cuadráticas en matemáticamente funciones situaciones de la vida cuadráticas como modelo real. para el análisis de diversos fenómenos y situaciones de la realidad. lineales en situaciones de la vida real. Indicador de logro (actividades evaluadas) Resuelve problemas de contexto real sobre sistemas de ecuaciones con dos variables en R mediante diversos procesos de resolución. Función Lineal. - Denominación. - Representación. Identifica funciones lineales en situaciones de la vida cotidiana desde el enfoque matemático. Función Cuadrática: - Forma General - Grafica Identifica funciones cuadráticas en situaciones de la vida cotidiana desde el enfoque matemático. Resuelve problemas vinculados con la realidad que involucran funciones cuadráticas. 4.-Resuelvo problemas utilizando razones trigonométricas. Resuelve problemas vinculados con la realidad que involucran razones trigonométricas. Razones Trigonométricas. - Definiciones. - Características. - Problemas diversos. Resuelve problemas de la vida cotidiana sobre razones trigonométricas mediante diversas estrategias. 5.Identifico graficas sobre funciones trigonométricas Seno y Coseno. Emplea funciones trigonométricas en diversas situaciones. Examina funciones trigonométricas en situaciones matemáticas diversas. 6.- Analizo la función Exponencial Relaciona las funciones exponenciales con situaciones de la vida real. Funciones Trigonométricas: - Nociones Previas. - Definiciones. - Grafica - Aplicaciones. Funciones Exponenciales: - Definición - Casos de función exponencial - Gráfica. 7.- Analizo la función logarítmica. Relaciona las funciones logarítmicas con situaciones de la vida real. Función Logarítmica: - Definición - Casos de función exponencial - Gráfica. Resuelve problemas sobre función logarítmica en situaciones de la vida real. 8.- Exploro el patrón de las sucesiones numéricas e identifico su formación. Explora y establece una conjetura sobre el patrón en una sucesión numérica. Determina la regla de formación de las sucesiones. Sucesiones Numéricas: - Definición - Regla de formación de las sucesiones. Identifica patrones de sucesiones numéricas mediante una variedad de ejercicios. 9.Identifico los ángulos diedros y poliedros. Identifica y gráficamente diedros. representa ángulos 10.- Aplico nociones de sólidos geométricos Aplica nociones definición y elementos de poliedros en diferentes objetos de la vida cotidiana. 5. 11.-Aplico propiedades6. Resuelve problemas sobre de áreas de cuerpos áreas de poliedros regulares. geométricos. 7. 12.-Aplico propiedades8. Resuelve problemas sobre de volúmenes poliedros. de 13.-Resuelvo problemas de áreas y volúmenes de cuerpos redondos. volúmenes de pirámides. prismas y Resuelve problemas de contexto real, lúdico y matemático que involucran el cálculo y relaciones entre Ángulos Diedros. Ángulos Poliedros Solidos Geométricos: - Prisma - Pirámide Poliedros: - Poliedros Regulares. - Teorema de Euler. - Situaciones problemáticas Volúmenes de Poliedros: - Volumen de un Prisma. - Volumen de una Pirámide. Áreas – Volúmenes de Cuerpos Redondos: - Cono - Cilindro Resuelve problemas sobre función exponencial en situaciones de la vida real. Compara ángulos diedros y poliedros en diversas situaciones matemáticas. Identifica poliedros en su vida cotidiana. Determina el área y diferentes elementos de poliedros regulares en situaciones diversas. Determina volúmenes de prismas y pirámides en situaciones diversas. Resuelve problemas de contexto real sobre áreas y volúmenes de cuerpos redondos. áreas y volúmenes cuerpos de revolución. de 14.- Identifico la teoría de probabilidades. Realiza experimentos aleatorios, determina su espacio muestral y caracteriza un suceso o evento como parte del mismo. 15.- Diferencio dos términos importantes: posibilidad y probabilidad. Discrimina y utiliza en forma conveniente los términos ” Posibilidad” y “probabilidad”. 16.Analizo la ocurrencia probable de un suceso. Aplica nociones de probabilidad y de sucesos independientes en diferentes situaciones. 1. 17.-Aplico la Formula conjeturas acerca de probabilidad en los resultados de diferentes contextos. experimentos sencillos, utilizando el concepto de probabilidad de un suceso. 1. 18.Resuelvo problemas de probabilidades utilizando diagrama de árbol. 4. Resuelve y formula problemas que implican el cálculo de probabilidades de sucesos compuestos sencillos, utilizando métodos como listas organizadas y diagramas de árbol, entre otros. - Esfera Probabilidades: - Muestra. - Espacio Muestral. - Sucesos Posibles. - Sucesos Probables. Identifica sucesos deterministas y probabilísticos en diferentes situaciones presentadas en la vida real. Probabilidad: - Sucesos Probables. - Sucesos Independientes Diferencia los términos posibilidad y probabilidad mediante la experimentación en situaciones diversas. Utiliza la probabilidad en sucesos independientes de situaciones cotidianas. Probabilidad: - Espacios Muéstrales. - Sucesos Dependientes. Resuelve situaciones problemáticas sobre experimentos probabilísticos usando diferentes estrategias. Probabilidad: - Teoría del azar. - Diagrama del Árbol. - Sucesos Dependientes. Resuelve problemas de probabilidades utilizando diversas estrategias. Posibilidad probabilidad y Metodología El desarrollo del área parte de reconocer que los estudiantes han construido saberes matemáticos, tales como estrategias de cálculo y medición, interactuando con las personas y las cosas, por lo que su experiencia constituye el punto de partida para la construcción de nuevos conocimientos matemáticos y una mejor actitud hacia el área. El proceso de resolución de problemas es de suma importancia por su carácter integrador, resolver problemas implica necesariamente razonar y comunicarse, así como también permite interconectar ideas matemáticas y representarlas. Se aprende a matematizar, con ello aumentan su confianza, tornándose más perseverantes y creativos y mejorando su espíritu investigador. Las sesiones de aprendizaje desarrolladas presentan la siguiente secuencia: Se inicia con situaciones básicas matemáticas (juegos lógicos, lecturas, historias matemáticas, etc.). Se presentan actividades para identificar los conocimientos previos de los estudiantes reconociendo el carácter integrador de las matemáticas. Se organiza la información, los estudiantes interpretan definiciones, principios y términos matemáticos. Identifican en forma paulatina procesos de resolución y no simple soluciones. Describen las pasos de procedimientos matemáticos. Realizan diversas actividades, las cuales presentan resolución y comentario pedagógico para su contrastación. Se presenta ideas fuerza para consolidar el aprendizaje desarrollado. Se Busca pensar matemáticamente, resolviendo problemas, generando la argumentación matemática y representando situaciones problemáticas mediante símbolos matemáticos. Se utilizan estrategias como: Métodos de ensayo y error: Consiste en elegir soluciones u operaciones al azar y aplicar las condiciones del problema a esos resultados u operaciones hasta encontrar el objetivo o comprobar que eso no es posible. Hacer una figura, un esquema, un diagrama, una tabla: En otros problemas se puede llegar fácilmente a la solución si se realiza un dibujo, esquema o diagrama; es decir, si se halla la representación adecuada. Buscar regularidades o un patrón: Esta estrategia empieza por considerar algunos casos particulares o iniciales y, a partir de ellos, buscar una solución general que sirva para todos los casos. Imaginar el problema resuelto: En los problemas de construcciones geométricas es muy útil suponer el problema resuelto. Para ello se traza una figura aproximada a la que se desea. De las relaciones observadas en esta figura se debe desprender el procedimiento para resolver el problema. Utilizar el álgebra para expresar relaciones: Se relaciona algebraicamente los datos con las condiciones del problema. En la resolución de problemas se sugiere los siguientes pasos: 1. Comprender el problema. 2. Elaborar un plan. 3. Ejecutar el plan. 4. Hacer la verificación. 5. Evaluación de aprendizajes Realizan una evaluación de proceso, donde se aplican procedimientos desarrollados en la sesión de aprendizaje, teniendo como objetivo fundamental conocer el grado de asimilación o incorporación del aprendizaje previsto en los estudiantes. Además, se presenta un cuestionario de evaluación, adecuado a los intereses de los estudiantes. Sirve con instrumento de medición de los indicadores propuestos y permite la toma de decisiones. El tutor virtual llevará un registro de los todos procesos seguidos en las actividades que realicen los estudiantes.