1
Identificación de sistemas
Usccachi valencia Darwin darius
Apaestegui centurión Fabricio
Facultad de Ingeniería Electrónica y Eléctrica - UNMSM
Resumen– En el siguiente informe se pone en práctica la
familiarización con las principales técnicas de
identificación experimental para poder encontrar una
función
matemática
que
permita
establecer
posteriormente la ley de control.
Abstract– In the following report, familiarization with the
main experimental identification techniques is put into
practice in order to find a mathematical function that
allows the control law to be applied.
𝐺(𝑠) =
𝑘
∙∙∙ (1)
𝜏𝑠 + 1
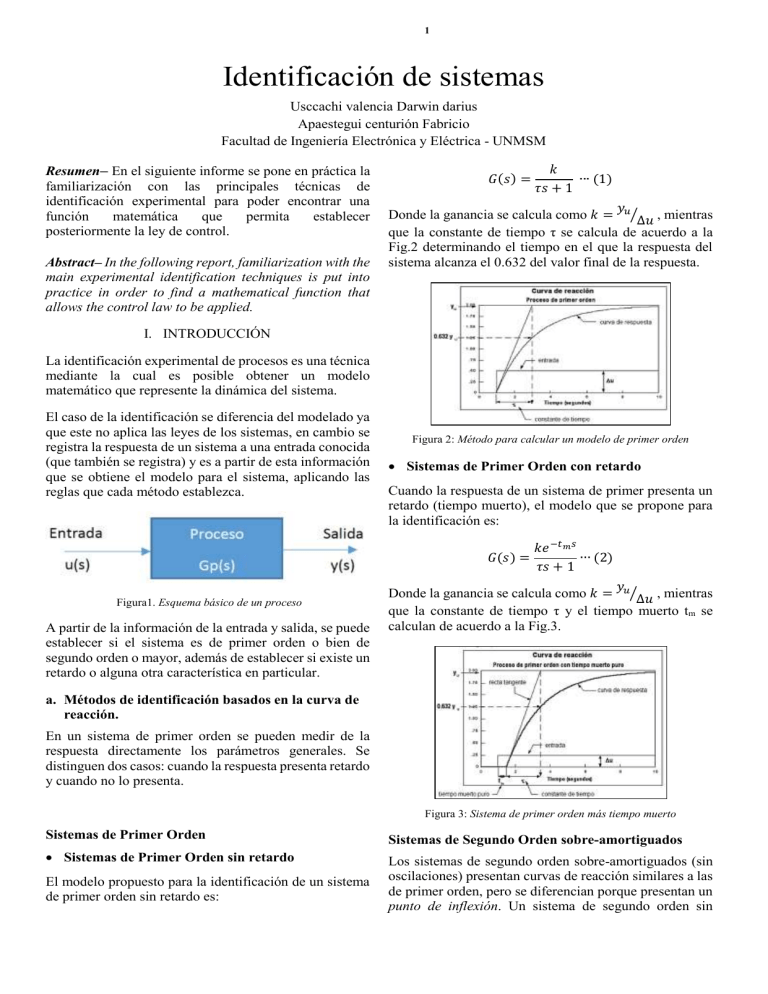
𝑦
Donde la ganancia se calcula como 𝑘 = 𝑢⁄∆𝑢 , mientras
que la constante de tiempo τ se calcula de acuerdo a la
Fig.2 determinando el tiempo en el que la respuesta del
sistema alcanza el 0.632 del valor final de la respuesta.
I. INTRODUCCIÓN
La identificación experimental de procesos es una técnica
mediante la cual es posible obtener un modelo
matemático que represente la dinámica del sistema.
El caso de la identificación se diferencia del modelado ya
que este no aplica las leyes de los sistemas, en cambio se
registra la respuesta de un sistema a una entrada conocida
(que también se registra) y es a partir de esta información
que se obtiene el modelo para el sistema, aplicando las
reglas que cada método establezca.
Figura 2: Método para calcular un modelo de primer orden
Sistemas de Primer Orden con retardo
Cuando la respuesta de un sistema de primer presenta un
retardo (tiempo muerto), el modelo que se propone para
la identificación es:
𝑘𝑒 −𝑡𝑚 𝑠
𝐺(𝑠) =
∙∙∙ (2)
𝜏𝑠 + 1
Figura1. Esquema básico de un proceso
A partir de la información de la entrada y salida, se puede
establecer si el sistema es de primer orden o bien de
segundo orden o mayor, además de establecer si existe un
retardo o alguna otra característica en particular.
𝑦
Donde la ganancia se calcula como 𝑘 = 𝑢⁄∆𝑢 , mientras
que la constante de tiempo τ y el tiempo muerto tm se
calculan de acuerdo a la Fig.3.
a. Métodos de identificación basados en la curva de
reacción.
En un sistema de primer orden se pueden medir de la
respuesta directamente los parámetros generales. Se
distinguen dos casos: cuando la respuesta presenta retardo
y cuando no lo presenta.
Figura 3: Sistema de primer orden más tiempo muerto
Sistemas de Primer Orden
Sistemas de Primer Orden sin retardo
El modelo propuesto para la identificación de un sistema
de primer orden sin retardo es:
Sistemas de Segundo Orden sobre-amortiguados
Los sistemas de segundo orden sobre-amortiguados (sin
oscilaciones) presentan curvas de reacción similares a las
de primer orden, pero se diferencian porque presentan un
punto de inflexión. Un sistema de segundo orden sin
2
oscilaciones se ajusta a un modelo, G(s), de primer orden
con tiempo muerto:
𝐺(𝑠) =
= 𝟏.𝟓(𝒕𝟔𝟑 − 𝒕𝟐𝟖) y el tiempo muerto: 𝒕𝒎 = 𝒕𝟔𝟑 − 𝝉 =
𝟏.𝟓𝒕𝟐𝟖 − 𝟎.𝟓𝒕𝟔𝟑.
𝑘𝑒 −𝑡𝑚𝑠
∙∙∙ (3)
𝜏𝑠 + 1
Donde el cálculo de los parámetros 𝒌, 𝒕𝒎 y 𝝉 variará
según el método de identificación escogido. Los métodos
a desarrollar son el Método de la tangente Modificada de
Miller y el Método de los dos puntos de Smith.
Método de la tangente de Ziegler y Nichols
Consiste en trazar una recta tangente en el punto de
máxima pendiente de la respuesta del sistema (Fig. 4). A
partir de esto, la constante de tiempo τ y el tiempo muerto
tm se calculan de acuerdo a la Figura 4, mientras que la
𝑦
ganancia se calcula: 𝑘 = 𝑢⁄∆𝑢
Figura 6: Método de Smith
La respuesta del modelo y del sistema coincidirá como
mínimo en los dos puntos de referencia.
Sistemas de Segundo Orden sub amortiguados
En un sistema de segundo orden sub amortiguado se
pueden medir de la respuesta directamente los parámetros
generales (su ganancia 𝒌, su factor de amortiguamiento 𝜉
y su frecuencia natural 𝜔𝑛). Por lo que se puede ajustar al
siguiente modelo:
𝐺(𝑠) =
𝑘𝜔𝑛2
∙∙∙ (4)
𝑠 2 + 2ξ𝜔𝑛 𝑠 + 𝜔𝑛2
Figura 4: Método de Ziegler y Nichols
Método de la tangente Modificada de Miller
Consiste en trazar una recta tangente en el punto de
máxima pendiente de la respuesta del sistema y luego
determinar el punto tiempo en el 0.632 del valor final de
la respuesta (Fig. 5). A partir de esto, la constante de
tiempo τ y el tiempo muerto tm se calculan de acuerdo a
la Figura 1, mientras que la ganancia se calcula: 𝑘 =
𝑦𝑢
⁄∆𝑢
Figura 7. Respuesta de un sistema de segundo orden
subamortiguado.
ξπ
𝑡𝑝 =
−
𝜋
2
, 𝑀𝑝 = 𝑒 √1−ξ ,
𝜔𝑑
𝜔𝑑 = 𝜔𝑛 √1 − ξ2 ∙∙∙ (5)
De las ecuaciones anteriores podemos obtener el factor de
amortiguamiento 𝜉 y la frecuencia natural 𝜔𝑛. La
ganancia lo obtendremos de la misma manera que en los
métodos anteriores.
Figura 5: Método de Miller
Método de los dos puntos de Smith
Consiste en tomar dos puntos que corresponde a valores
específicos de la respuesta (28.3% y 63.2%) (Fig.6). A
partir de estos tiempos (𝒕𝟐𝟖 y 𝒕𝟔𝟑) se calculan los
parámetros del modelo, de la siguiente manera: La
𝒚
ganancia: 𝒌 = 𝒖⁄∆𝒖, la constante de tiempo:
𝝉
II. MATERIALES Y MÉTODOS
A. Equipos, materiales y herramientas utilizados
Software MATLAB-SIMULINK 2017
Proteus 8 Professional
3
B. PROCEDIMIENTO Y RESULTADOS
Se adjunta los archivos Sistema1.pdsprj, Sistema2.pdsprj
y proteus2matlab.m. Los 2 primeros archivos deberán ser
ejecutados con el programa Proteus. Cado uno contiene
un sistema diferente a identificar. El archivo
proteus2matlab.m debe ser guardado en el directorio de
MATLAB®. Este archivo es una función que acondiciona
y obtiene a partir de los datos exportados de Proteus.
“Sistema1.dat” en la carpeta que se tiene como
directorio MATLAB®.
Parte I: Métodos basados en la curva de reacción
En esta parte identificaremos un modelo para 2 sistemas
implementados en Proteus, aplicando los métodos
basados en la curva de reacción usando Matlab.
Figura 10. Ilustración del punto v.
i. Ejecute el Ejecute el programa Proteus y abra el
archivo Sistema1.pdsprj. Este archivo contiene un
bloque denominado Sistema1.
vi. En MATLAB®, ejecute la función “proteus2matlab”,
utilizando la siguiente sintaxis:
>> [Tiempo, Vin, Vout]=proteus2matlab('Sistema1.dat');
Lo cual creará en el Workspace los vectores Tiempo, Vin
y Vout obtenidos a partir del archivo exportado en el
punto v.
Figura 8. Diagrama del Sistema1
ii. La respuesta del sistema lo podemos observar en el
visor de ‘Analogue Analysis’, tal como se muestra en
la siguiente figura.
Figura 11. Vectores tiempo Vin y Vout
vii. Grafique los vectores Vin y Vout vs el vector Tiempo.
Verifique que sea la misma respuesta obtenida en
Proteus.
Figura 9. Respuesta temporal del sistema 1 (Proteus).
iii. Indique de que orden es el sistema a analizar.
-ESTE ES UN SISTEMA DE PRIMER ORDEN SIN
RETARDO.
iv. Elija el método basado en la de Curva de Reacción,
más adecuado según su criterio, para identificar un
modelo G(s).
-SE USARÁ LA QUE ES PROPUESTA EN LA
PRESENTE GUIA.
v. Para un mejor análisis y poder comparar la respuesta
del modelo hallado con la respuesta del sistema, se
utilizará el software MATLAB®. Para ello, exporte
los datos haciendo clic en la opción Graph →Export
Graph Data (Fig.10). Guarde el archivo con el nombre
Figura 12. Grafica de proteus.
4
Figura 12. Grafica de MATLAB.
Como vemos las 2 figuras son similares.
viii. Utilice Matlab para hallar un modelo según el método
elegido en el punto iv. (Cree un script que obtengan
los parámetros necesarios)
Obtención de parámetros:
Figura 13. Respuesta escalón mediante función de transferencia.
xi. Presente en una sola gráfica, tanto la respuesta
temporal obtenida en el punto anterior como la
respuesta importada desde Proteus.
-El voltaje de entrada es : 5
-El voltaje de salida máxima es : 5.0000
-La ganancia es =1.0000
-La ganancia tao es:0.2175.
ix. Defina la función de transferencia, G(s), del modelo
obtenido en el paso previo.
Figura 14. Graficando el enunciado XI.
xii. A partir del punto anterior, considera que es aceptable
x. Obtenga su respuesta temporal ante una entrada
escalón.
la respuesta del modelo obtenido G(s). Justifique su
respuesta. (Puede utilizar algunos índices de
desempeño como la suma del error cuadrático)
5
Figura 17. Respuesta temporal del Sistema2.
xv. Repita los pasos del iii al xii.( Además de seleccionar
alguno de los métodos presentados, investigue de otro
método de identificación y también aplíquelo)
Indique de que orden es el sistema a analizar.
-ESTE SISTEMA ES DE
SOBREAMORTIGUADO
SEGUNDO
ORDEN
Elija el método basado en la de Curva de Reacción,
más adecuado según su criterio, para identificar un
modelo G(s).
- El código usado para la primera parte, lo volveremos a
usar, pero con ciertos
cambios. El método a utilizar es el de los 2 puntos de
Smith.
Para un mejor análisis y poder comparar la respuesta
del modelo hallado con la respuesta del sistema, se
utilizará el software MATLAB®. Para ello, exporte
los datos haciendo clic en la opción Graph →Export
Graph Data (Fig.10). Guarde el archivo con el nombre
“Sistema1.dat” en la carpeta que se tiene como
directorio MATLAB®.
Figura 15. Al acercarnos ala figura vemos que el error es mínimo.
Rojo.-grafica mediante identificación
Azul.-grafica mediante función transferencia.
xiii. Ejecute el programa Proteus y abra el archivo
Sistema2.pdsprj. Este archivo contiene un bloque
denominado Sistema2.
Figura 18. Ilustración del punto v.
xvi. En MATLAB®, ejecute la función “proteus2matlab”,
utilizando la siguiente sintaxis:
>> [Tiempo, Vin, Vout]=proteus2matlab('Sistema2.dat');
Figura 16. Diagrama del sistema 2.
Lo cual creará en el Workspace los vectores Tiempo, Vin
y Vout obtenidos a partir del archivo exportado en el
punto v.
xiv. La respuesta del sistema lo podemos observar en el
visor de ‘Analogue Analysis’, tal como se muestra en
la siguiente figura.
Figura 19. Vectores tiempo Vin y Vout
xvii. Grafique los vectores Vin y Vout vs el vector Tiempo.
Verifique que sea la misma respuesta obtenida en
Proteus.
6
Figura 20. Grafica de proteus.
xix. Defina la función de transferencia, G(s), del modelo
obtenido en el paso previo.
Figura 21. Grafica de MATLAB.
Como vemos las 2 figuras son similares.
xx. Obtenga su respuesta temporal ante una entrada
escalón.
xviii. Utilice Matlab para hallar un modelo según el método
elegido en el punto iv. (Cree un script que obtengan
los parámetros necesarios)
Obtención de parámetros:
-El voltaje de entrada es :5.
-El voltaje de salida máxima es:5.0042
-La ganancia es :1.0008.
-La ganancia tao es :0.6095.
-El tiempo muerto es : 0.1826
-La suma de error cuadratico es :313.1712
Figura 22. Respuesta escalón mediante función de transferencia.
xxi. Presente en una sola gráfica, tanto la respuesta
temporal obtenida en el punto anterior como la
respuesta importada desde Proteus.
7
Figura 24. Al acercarnos ala figura vemos que el error es notoria por
eso nos salió muy grande el error
Rojo.-grafica mediante identificación
Azul.-grafica mediante función transferencia.
Parte II: Identificación de un sistema físico
i. Implemente el circuito presentado en la siguiente
figura.
Figura 23. Graficando el enunciado XI.
xxii. A partir del punto anterior, considera que es aceptable
la respuesta del modelo obtenido G(s). Justifique su
respuesta. (Puede utilizar algunos índices de
desempeño como la suma del error cuadrático)
Figura 25. Diagrama del circuito a implementar.
Figura 26. Circuito implementado
ii. Conecte una señal de entrada adecuada que permita
observar la curva de reacción de sistema.
8
K = 1.2910
Sobre impulso:
Mp = 1.4552
Factor de amortiguamiento:
Facmorti = 0.1186
Tiempo pico:
Tpo = 7.0000e-04
Frecuencia natural amortiguada:
Wd = 4.4880e+03
Frecuencia natural:
Figura 27.Reaccion del sistema antes una seña cuadrada con vpp 1v.
iii. Utilizando uno de los métodos de identificación
presentados, el más adecuado según su criterio,
obtenga un modelo para el circuito implementado.
Compare este modelo con el obtenido en su informe
previo.
Wn = 4.5199e+03
Hallando el modelo:
Modelo de respuesta
Hs=tf([Wn^2],[1 2*Facmorti*Wn Wn^2])
Hs =
Utilizaremos un método de identificación para obtener
un modelo para el circuito de la figura25.
Con los parámetros de este método y utilizando el
software de Matlab bosquearemos este método.
Primero calculamos el k ,wn y el factor de
amortiguamiento para poder hallar Hs
Hallando la ganancia_
K=max(VOUT)/max(VIN)
Hallando el sobreimpulso:
Mp=max(VOUT)-max(VIN)
Hallando el factor de amortiguamiento:
Facmorti=log(Mp)/sqrt((log(Mp))^2+pi^2)
Hallando el tiempo pico(Tp):
Tp=TIEMPO(find(VOUT==max(VOUT)),1)
Hallando Wd a partir Tp:
Wd=pi/Tp
Hallando Wn con los datos obtenidos:
Wn=Wd/sqrt(1-Facmorti^2)
Datos Obtenidos:
Ganancia:
2.043e07
----------------------s^2 + 1072 s + 2.043e07
Para compararlo con la respuesta obtenida en el
informe previo utilizamos el siguiente script:
Hallando el H:
NUM=[11];
DEN=[475.2*10^-9 1.596*10^-3 12];
H=tf(NUM,DEN)
figure(2)
step(5*H,'b')
Para Hs.
A=VOUT(length(VOUT)-1,1);
figure(3)
step(A*Hs,TIEMPO,'k')
Comparando las respuesta:
figure(4)
hold on
step(5*H,'b')
step(A*Hs,TIEMPO,'k')
9
Como estaremos trabajando en el dominio del tiempo,
escogeremos esa opción donde se nos indica con la
flecha de color roja, a lo que se nos abrirá la siguiente
ventana:
Figura 28. Comparación de las respuestas obtenidas anteriormente
Ahora compararemos tres respuestas, la obtenida por
el circuito simulado, por un método de identificación
y por el informe previo.
Figura 31. Importación de datos
En esta ventana importamos los datos de vin y vout
necesarios para los cálculos respectivos de una
identificación de sistemas.
Figura 29. Comparación de las respuestas obtenidas anteriormente
En la siguiente imagen observamos ambos datos ya
importados:
iv. Investigue de otro método de identificación y
aplíquelo.
Una forma distinta para poder identificar un sistema es
utilizando la función systemIdentification.
Al llamar la función systemIdentification en la ventana
de comando se nos abrirá la siguiente ventana, cabe
resaltar para un correcto uso de systemIdentification
debemos haber exportado los datos proporciones por
la simulación en Proteus, estamos hablando de los
vectores vin y vout.
Figura 32. Datos importados
En la opción de Operations seleccionamos Select
Range, luego se selecciona un rango que nos ayudará
como muestra para la identificación del sistema.
Figura 30. systemIdentification
Figura 33. Selección de rango
10
Como observamos en la figura 39 ya tenemos un
nuevo dato importado con el nombre de MUESTRA,
este dato debemos cargarlo al Working Data y
Validation Data.
Y su respuesta ante una entrada escalón es la siguiente:
Figura 34. Carga de datos al Working Data y Validation Data
En la opción de estimación seleccionamos Process
Models:
Figura 36. Respuesta ante una entrada escalón
III. CONCLUSIONES Y RECOMENDACIONES
Existen distintas formas de identificar un sistema,
todos con métodos distintos y cada una tratando de
asemejarse a lo deseado.
De la misma forma como existen métodos
matemáticos para la identificación, MATLAB no
proporciona una herramienta muy útil para nuestros
fines.
Pese a la gran diversidad de formas para identificar
sistemas siempre se obtendrá un margen de error.
Conocer las características de los sistemas es muy
importante para facilitar el uso del método correcto.
Figura 35. Process Model
Observamos en la figura 40 el modelo estimado y es
muy similar al planteado con el método de Smith.
Al exportar la estimación “Hest” a nuestro workspace
tenemos lo siguiente, la función transferencia de la
estimación realizada.
>> Hest=tf(Est)
Hest =
From input "u1" to output "y1":
0.916
exp(-0.061*s) * ------------------------------0.1996 s^2 + 1.363 s + 1
Name: Est
Continuos-time transfer function.
REFERENCIAS
[1]. Ingeniería de Control Moderna-Katsuhik Ogata 5ta
edición.
[2]. Documentación
de
(https://es.mathworks.com/help/matlab/)
Matlab
[3]. Material proporcionado en la clase de teoría (PPT)
11