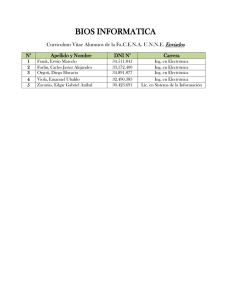
- Ninguna Categoria
Problemas Resueltos de Transferencia de Calor - Ingeniería
Anuncio
Universidad Técnica de Oruro
Facultad Nacional de Ingeniería
Ingeniería Mecánica-Electromecánica
100
PROBLEMAS RESUELTOS
DE TRANSFERENCIA DE
CALOR
1 i T g 1 T
q
i
q q q k
Q.z
d
Q.z dz
dz
Q.r
Q.
d
Q.r dr
dr
d
Q. d
d ( r )
POR:
Univ. ERWIN A. CHOQUE CONDE
Octubre-2007
ORURO BOLIVIA
INDICE
PROBLEMAS RESUELTOS
Transferencia de calor en régimen permanente………………………………….…….…….…….2
Sistemas con generación interna……………………………………………………….….…………14
Espesor técnico económico……………………………………………………………………………31
Aletas…………………………………………………………………………………………….…………40
Flujo bidimensional…………………………………………………………………….……….………..52
Conducción en régimen transitorio………………………………………………………….………..55
Convección………………………………………………………………………………………..……….62
Intercambiadores………………………………………………………………………………..….…….70
Radiación…………………………………………………………………………….………………..……86
ANEXOS
Anexo A. FORMULARIO………………………………………………………….…103
Anexo B. TABLAS Y GRAFICAS
B.-1
TABLA 1. ……………………….……………….………………. 106
B.-2
GRAFICA 1. PARA PLACAS…………………….………….….107
B.-3
GRAFICA 2. PARA CILINDROS………………….…………….108
B.-4
GRAFICA 3. PARA ESFERAS…………………………………..109
Anexo C. PROPIEDADES DE LOS MATERIALES……………………...………..110
Anexo D. UNIDADES Y TABLAS DE CONVERSIÓN Y EQUIVALENCIA……..138
Anexo E. BIBLIOGRAFÍA:……………………………………………………………156
Univ. Erwin Choque Conde
Página 1
PROBLEMAS DE TRANSFERENCIA DE CALOR
Transferencia de calor en régimen permanente
1. Se determina que el flujo de calor a través de una tabla de madera de 50[ mm ] de espesor es de 40[
W / m 2 ] cuyas temperaturas sobre la superficie interna y externa son 40 y 20ºC respectivamente ¿Cuál
es la conductividad térmica de la madera?
Qa 40
T2 40C
DATOS:
T1
W
m
T2
T1 20C
Q
km
L
2
L1 50mm
Qa L1
k m 0.1
T2 T1
W
m C
2. Compare las velocidades de transferencia de calor a través de una muestra de madera de pino blanco
cuando la transferencia es transversal a la fibra y cuando es paralela a la fibra. La conductividad
térmica para el primer caso es 0.15 W / m º C y para el segundo caso 0.35 W / m º C .
SOLUCIÓN Para:
T 1C
Pino transversal
k t 0.15
Pino paralelo
k p 0.35
W
m C
W
m C
Qt k t T
J
Qt 0.15
m s
Qp k p T
J
Qp 0.35
m s
Existe mayor transferencia de calor con el pino de fibra en paralelo
3. Un chip cuadrado isotérmico tiene un ancho w=5[ mm ] de lado y esta montado en un sustrato de
modo que sus superficie lateral e inferior están bien aisladas, mientras que la superficie frontal se
expone a la corriente de un fluido refrigerante a 15ºC. A partir de consideraciones de confiabilidad,
la temperatura del chip no debe exceder de 85ºC. Si el fluido refrigerante es aire y el coeficiente de
2
convección correspondiente es h=200 W / m º C a) ¿Cuál es la potencia máxima admisible del
chip? b) Calcule y elabore una gráfica de la potencia admisible como función de h para el rango
W / m2 º C .
200<h<2000
h
DATOS:
T
w 5mm
circuitos
T1 85C
T 15C
T1
w
h 200
w
W
2
m C
SOLUCIÓN a)
El área de transferencia
Qadm A w h T1 T
La potencia máxima admisible
b)
Aw 2.5 10
Aw w w
Qad ( h) Aw h T1 T
h 200
ºC
W
2
m C
300
5
m
2
Qadm 0.35 W
W
2
m C
2000
W
2
m C
4
W
3
Qad ( h) 2
1
0
0
110
3
210
3
h
W/m2
Univ. Erwin Choque Conde
Página 2
4. Un fluido refrigerante de una unidad de refrigeración construida de acero (k=40 W / mº C ) con
diámetro externo de 1.5 m espesor de ¼¨ y 2 m de altura, debe ser mantenido a una temperatura
constante de -16ºC El tanque esta localizado en un ambiente de aire acondicionado a 22ºC y esta
aislado con 2´´ de poliestireno (k=0.026 W / mº C ) cuya temperatura externa debe ser mantenida
constante e igual a 21ºC. El operador a notado que hubo un aumento de temperatura en el ambiente,
debido a un defecto del termostato del aire acondicionado, ocasionando una variación de 10ºC en la
temperatura de la superficie externa del aislamiento térmico Calcule: a) La razón de variación de T.C.
a través del tanque b) El espesor del aislante para las nuevas condiciones ambientales.
De
eais
et
DATOS:
k 40
Tw2
Ti
Ti 16 C
W
m C
Tw1 21C
De 1.5m
1
et in
4
Tw1
Lt
eais 2in
k ais 0.026
Lt 2m
Di De 2 et
El diámetro interno del tubo
W
m C
Tw2 31C
Di 1.4873 m
Se desprecia el espesor del tubo
El área media logarítmica del aislante
Am1
Q1ais
2 Lt eais
ln 1
De
Am1 k ais
eais
Am1 9.74048 m
2 eais
Tw1 Ti
2
Q1ais 184.4555 W
El calor para las nuevas condiciones
Q2ais
Q%
Am1 k ais
eais
Tw2 Ti
Q2ais 234.30834 W
Q2ais Q1ais
Q% 27.02703 %
Q1ais
b) El espesor del aislante requerido
Q1ais
Am k ais
en
Tw2 Ti
2 Lt k ais
ln 1
2 Lt k ais Tw2 Ti
De
Q1ais
en
e
1
2
Univ. Erwin Choque Conde
2 en
De
Tw2 Ti
Am
2 Lt en
ln 1
2 en
De
en 6.51109 cm
Página 3
5. Se conecta un resistor eléctrico a una batería, como se muestra en el esquema. Después de una
breve fluctuación transitoria, la resistencia toma una temperatura de estado estable casi uniforme
de 95 ºC, mientras que la batería y los alambres de conexión permanecen a la temperatura
ambiente de 25ºC No tome en cuenta la resistencia térmica eléctrica de los alambres de conexión.
a) Si se disipa energía eléctrica de manera uniforme dentro del resistor, que es un cilindro de
diámetro D=60 mm y longitud Lr=25 mm. a) Cuál es la velocidad de generación de calor
volumétrica g W / m 3 b) Sin tener en cuenta la radiación del resistor. ¿Cuál es el coeficiente de
convección que debería tener para evacuar todo el calor?
DATOS:
I=6A
V1 24V
I1 6 A
aire
+
h
Dr 60mm
Tw 95C
T
V=24V
-
Lr 25mm
T 25C
resistor
La velocidad de transferencia de calor
Qtr V1 I 1
El volumen de la resistencia
Vcil
4
2
Dr Lr
Qtr 144 W
El área de T.C. por convección
Vcil 7.06858 10
5
m
3
Atr Dr Lr
Dr
2
2
Atr 0.01037 m
2
La generación volumétrica
Qtr
6 W
gvol
gvol 2.03718 10
3
Vcil
m
El coeficiente de convección
Qtr
W
htr
htr 198.42694
2
Atr Tw T
m C
6. Se requiere calcular la pérdida de calor de un hombre en un ambiente donde la temperatura de la pared
es 27ºC y del ambiente es de 20ºC si el ser humano tiene una temperatura superficial de 32ºC y un
coeficiente de transferencia de calor por convección entre el hombre y el ambiente y emisividad de 3
W / m 2 º C y =0.9 respectivamente, se sabe que un ser humano normal tiene una superficie corporal de
1.5m2, despreciar la resistencia térmica de la ropa. Calcular también la energía perdida en 24hr.
Tw ( 27 273 )K
hh 3
T ( 20 273 )K
5.67 10
Ah 1.5m
8
W
2
4
2
Qh 54 W
Qr Ah Th Tw
4
Qr 42.37919 W
Qtot Qh Qr
Qtot 96.37919 W
E Qtot t d
E 1.98891 10 cal
Univ. Erwin Choque Conde
td 24hr
m K
Qh Ah hh Th T
4
2
m K
0.9
Th ( 32 273 )K
W
6
Página 4
7. Una sonda interplanetaria esférica de 0.5 m de diámetro contiene dispositivos electrónicos que
disipan 150 W la superficie de la sonda tiene una emisividad de 0.2 y la sonda no recibe radiación
de otras superficies como por ejemplo del Sol. a) ¿Cuál es la temperatura de la sonda si la del
ambiente es de 25ºC? b) Si en la superficie exterior de la sonda varia la emisividad en el rango de
0.2 0.9 graficar la temperatura de la sonda en función de la emisividad.
DATOS:
8
W
Dso 0.5m
5.67 10
T ( 273 25 )K
Qsonda 150 W
2
m K
Dso
As 4
2
El área de la sonda
1 0.2
4
2
As 0.7854 m
2
1
Qsonda 1 As Tw T
4
4
Qsonda
4
Tw
T
1 As
La variación de la temperatura
4
Tw 396.54913 K
1
Qsonda
4
Tw ( )
T
As
4
0.2 0.22 0.9
400
380
Tw( ) 360
340
320
0.2
0.4
0.6
0.8
1
8. Se quiere diseñar un calentador de 10[ KW ] usando alambre de Ni - Cr (Nicrom). La temperatura
máxima de la superficie del Nicrom será 1650 ºK y la temperatura mínima del aire circundante es
370K. La resistividad del Nicrom es 110 * cm y la energía para el calentador está disponible a
12 voltios. a) ¿Qué diámetro de alambre se requiere si el calentador usa un solo trozo de 0.6 m de
longitud? b) ¿Qué longitud de alambre debería tener para un calibre de 14 (BWG 14. d = 0.083
p lg) c) Qué coeficiente de convección debería tener el ambiente para evacuar todo el calor en
ambos casos.
DATOS:
3
Ncal 10 10 W
aire
V=12V
D
L
1650K
h
Tn 1650 K
TO
NICROM
To 370 K
110 10
6
cm
Vn 12V
Univ. Erwin Choque Conde
Página 5
2
Vn
Ncal Vn I
Rn
La potencia
L
2
4 L
da 0.76392 cm
2
Vn db
2
Lb
4 Ncal
db 0.083 in
Lb 4.56965 cm
Ncal
ha
La da Tn To
ha 542.5542
Ncal
hb
Lb db Tn To
hb 25813.38996
c)
Vn
2
b)
2
Vn d
Ncal 4 La
da
La 0.6 m
a)
2
Vn At
W
2
m K
W
2
m K
9. Dos ambientes A y B de grandes dimensiones están separadas por una pared de ladrillo k=1.2
W / mº C de 12 cm de espesor y de emisividad superficial de 0.78 la temperatura externa del
ladrillo en el ambiente B es de 120ºC y la temperatura del aire y sus alrededores del mismo
ambiente es de 30ºC la transferencia de calor por convección libre del ambiente B es de 20
W / m 2 º C encontrar la temperatura de la superficie interna del ladrillo en el ambiente A.
DATOS:
A
L 0.12m
k 1.2
TB ( 273 120 )K
B
m K
0.78
TB ( 273 30 )K
Q
W
T
hB
hB 20
W
2
m K
TA
5.67 10
TB
W
2
m K
L
SOLUCIÓN:
8
4
Por balance de energía
Calor por Conducción =Calor por Convección + Calor por Radiación
k
k
L
A
L
TA TB A hB TB TB A TB TB
4
TA TB hB TB TB TB TB
4
4
4
h T T T 4 T 4 L
B B
B
B
B
TA
TB
k
TA 641.22126 K
Univ. Erwin Choque Conde
TA 368 C
Página 6
10. Una casa tiene una pared compuesta de madera (Lm=10 mm , k=0.109 W / m º C ), aislante de
fibra de vidrio (Lf=100 mm , k=0.035 W / m º C ) y tablero de yeso (Ly=20 mm , k=0.814 W / m º C
), como se indica en el esquema. En un día frió de invierno los coeficientes de transferencia de
2
2
calor por convección son hi=60 W / m º C y he=30 W / m º C el área total de la superficie es de
2
350 m si el aire interior se mantiene a 20ºC a) Determine una expresión simbólica para la
resistencia térmica total de la pared, incluyendo los efectos de convección interior y exterior para
las condiciones establecidas. b) Determine la expresión para la perdida de calor a través de la
pared. c) Grafique la potencia disipada en función del tiempo. d) Calcule la energía calorífica
transmitida del interior al exterior para un día. Si las condiciones mas realistas en las que el aire
exterior se caracteriza por una temperatura que varia con el día (tiempo), de la forma:
2 *
Si t hr y T K
Te ( K ) 255 5 * sen (
t)
0 t 12 h
24
2 *
Te ( K ) 273 11 * sen (
t ) 12 t 24 h Si t hr y T K
24
DATOS:
madera
Atrf 350 m
Ti ( 273 20 )K
fibra de vidrio
yeso
Madera
Te
hi
ho
Ti
hi 60
2
k m 0.109
W
m K
he 30
W
2
m K
W
2
m K
Lm 10mm
Fibra de vidrio
k f 0.035
W
m K
Lf 100 mm
Yeso
10mm
20mm
100mm
k y 0.814
a)
R
Lm
Lf
Ly
1
1
hi Atrf k m Atrf k f Atrf k y Atrf he Atrf
b) La transferencia de calor
ñ
Qma ( t1)
1
hi Atrf
Qtar ( t2)
Lm
k m Atrf
Lf
k f Atrf
R 0.00864
K
W
t1 0hr 0.1hr 12hr
2
t2 K
24 hr
t2 12hr 13hr 24hr
Ttar ( t2) 273 K 11 sin
ñ
Ti Tma ( t1)
Ly 20mm
2
t1 K
24 hr
Tma ( t1) 273 K 5 sin
ñ
W
m K
Ly
k y Atrf
1
he Atrf
Ti Ttar ( t2)
1
hi Atrf
Lm
k m Atrf
Univ. Erwin Choque Conde
Lf
k f Atrf
Ly
k y Atrf
1
he Atrf
Página 7
c) ñ
ñ
Tma ( t1)
280
410
3
275
3.510
3
310
3
2.510
3
210
3
1.510
3
Qma ( t1)
270
Ttar ( t2)
Qtar ( t2)
265
260
410
0
4
810
4
d
E
dt
4
810
t1 t2
d) Energía diaria que pierde
Q
4
410
0
t1 t2
ñ
E1
12hr
E2
24hr
7
E1 8.40996 10 J
Qma ( t1) dt1
0hr
ñ
Ti
Tma ( t2)
R
dt2
8
E2 1.15936 10 J
12hr
8
ET 2.00036 10 J
ET E1 E2
11. Por un tubo de material (AISI 304) de 2” de diámetro interior y ½” de espesor, circula vapor a 5 Bar
2
y esta expuesto al medio ambiente de 30ºC con un coeficiente de convección de 10 W / m º C ,
calcular el flujo de color por la tubería por metro de longitud.
DATOS:
L
Del material (AISI 304)
di
k 16.6
de
h 10
h
Tsat
Q
T
R cond
Tsat Tsat T
Q
Rcond Rconv
m C
W
R conv
de di 2 et
T 30C
de 0.0762 m
Tsat 151.86 C
L 1m
et
1
Ae h
2
Área interna del tubo
Ai di L
Ai 0.15959 m
Área externa del tubo
Ae de L
Ae 0.23939 m
El área media logarítmica del tubo
Am
Q
Ae Ai
2
Am 0.1968 m
Ae
ln
Ai
2
Tsat T
et
Am k
Univ. Erwin Choque Conde
et 0.5in
Tsat T
Am k
El calor transmitido
di 2in
2
m C
T
Tsat
W
1
Q 289.03011 W
Ae h
Página 8
12. Una mezcla química se almacena en un contenedor esférico (k=50 W / m º C ) cuyo radio exterior
es de 208 mm y un espesor de 20 mm . En la pared interna de la esfera la temperatura se
mantiene constante a 150ºC. Calcular la transferencia de calor si este esta expuesto al medio
2
ambiente de 15ºC y un h=12.25 W / m º C . Se propone cubrir con una capa de aislante “lana de
vidrio” de espesor 10 mm para reducir las perdidas de calor; en que porcentaje disminuye la T.C.
con el aislante.
DATOS:
k 50
m C
T 15C
re 0.208 m
h
re
Tsat 150 C
W
k ais 0.04
et 20mm
h
T
ri re et
et
W
h 12.25
eais 10mm
Reais Riais eais
eais
m C
ri 0.188 m
Riais re
Tsat
W
2
2
m C
Reais 0.218 m
Ai 0.44415 m
2
El área interna de la esfera
Ai 4 ri
El área externa de la esfera
ó interna del aislante
Ae 4 re
El área externa del aislante
Aeais 4 Reais
El área media cuadrática de la esfera
Am 4 ri re
Am 0.4914 m
El área media cuadrática del aislante
Amais 4 re Reais
Amais 0.56981 m
2
Ae 0.54367 m
2
2
Aeais 0.5972 m
2
2
2
a) Esfera sin aislante
Q
T
R cond
R conv
Tsat T
Q1
et
Am k
Q1 894.2487 W
1
Ae h
b) Esfera con aislante
Q
Tsat
T
R cond
Q2
R cond aisl
R conv
Tsat T
et
Am k
%Q
eais
Amais k ais
Q1 Q2
Q1
Univ. Erwin Choque Conde
1
Aeais h
Q2 234.27394 W
%Q 73.80215 %
Página 9
13. Dos varillas de cobre largas de diámetro D=10 mm , L=70 mm cada una, se sueldan juntas
extremo con extremo; la soldadura tiene un punto de fusión de 650°C. Las varillas están en aire a
2
25°C con un coeficiente de convección de10 W / m º C . ¿Cuál es la potencia mínima de entrada
necesaria para efectuar la soldadura?
DATOS:
h
dv 10mm
T
Tf 650 C
Tf
D
Lv 70mm
ha 10
Ta 25C
2
m C
L
L
W
Qh 2 dv Lv ha Tf Ta
Qh 27.48894 W
14. Las temperaturas de la superficie interior y exterior de una pared plana de 0.60 m de espesor se
mantienen constantes a 773 K y 323 K, respectivamente. El material de la pared tiene
conductividad calorífica que varía linealmente con la temperatura, de acuerdo con la expresión k =
0.116[0.454 + 0.002T] W / m º C . Determinar: a) La transferencia de calor b) Demuestre que a la
transferencia de calor será el mismo cuando la conductividad térmica es calculada a la temperatura
media aritmética de la pared. c) Grafique la distribución de temperatura y la conductividad térmica
en función de la distancia.
DATOS:
X[m]
Qtra
T2=323K
2
etr 0.6 m
At 1m
T1 773 K
T2 323 K
k1 0.116 ( 0.454 0.002 T )
K=o*(p+q*T)
o 0.116
T1=773K
At
T[K]
q 0.002
W
m K
W
m K
p 0.454
1
K
k 1(T ) o(p qT )
a)
e
T2
tr Q
tra
d
x
o ( p q T ) dT
At
T1
d
Qtra k A T
dx
0
Qtra
At
etr o p ( T1 T2)
q
2
o At
q
2
2
Qtra
p ( T1 T2) T1 T2
2
etr
b)
Tm
T1 T2
k 1m o p q Tm
Qtra1
etr
Univ. Erwin Choque Conde
2
2
Qtra 134.85 W
Tm 548 K
2
k 1m At
T1 T2
( T1 T2)
k 1m 0.1798
W
m K
Qtra1 134.85 W
Página 10
c) La distribución de temperatura y la conductividad
At o
Qtra
x (T )
p ( T1 T )
q
2
T1 T
2
2
T 773 K 323 K 323 K
0.6
x ( T ) 0.4
k 1( T )
0.2
0
300
400
500
600
700
800
T
15. Algunas secciones de una tubería que transporta combustóleo están soportadas por barras de
acero (k=61 W / m º C ) de 0.005 m 2 de sección transversal. En general la distribución de
temperatura a lo largo de las barras es de la forma: T ( x) 100 150 x 10 * x 2 donde T esta en
grados Celsius y “x” en metros. Calcule el calor que pierde de la tubería a través de cada barra.
k 61
W
m C
Ai 0.005 m
Tx 100 150 x 10 x
d
dx
Tx ( 150 20 x )
2
2
C
m
d
Tx k Ai ( 150 20 x )
dx
Q k Ai
C
m
Q k Ai ( 150 20 x )
Para el flujo máximo
x 0
Q 45.75 W
16. Un cono truncado solidó tiene una sección transversal circular, y su diámetro esta relacionado con
la coordenada axial mediante una expresión de la forma de D a * x 3 / 2 donde a 1. m 1 / 2 la
superficie lateral esta bien aislada, mientras que la base pequeña se encuentra en x1=0.0075 m y
tiene una temperatura de 100ºC y la base mayor se encuentra a x2=0.225 m y una temperatura
de 20ºC. a) Hallar el flujo de calor b) Derive una expresión para la distribución de temperatura T(x)
c) graficar la distribución de temperatura, si el cono es de aluminio (k=240 W / m º C ).
DATOS:
D a * x3/ 2
x1 0.0075 m
D/2
a 1 m
1
2
T1 100 C
Q
T1
x2 0.225 m
X
T2 20C
k 240
W
m C
T2
Incógnitas
x1
x2
Univ. Erwin Choque Conde
a)
T (x)
b)
Q
Página 11
La ecuación de conducción
a)
Q
T
Q k * A( x ) *
x
...1 )
4*Q
* x k * T
2
* x3
* a
4*Q
( 2) * a 2 * x 2
x2
x1
4*Q
3
* a * x 2
2
* x k * T
... 2)
k * (T ) TT 12
* a 2 * k * (T2 T 1)
Q
1
1
2*( 2 2 )
x 2 x1
b)
* x k * T
( x)
4*Q
* D 2 * x k * T
A
2*Q 1
1
( 2 2 ) k * (T2 T 1)
2
* a x 2 x1
Q
2
2
a k
T2 T1
1
x2
2
1
x1
Q 1.69835 W
2
De la ecuación 2
4*Q
* x k * T
2
* x3
* a
4*Q
( 2) * a 2 * x 2
x
x1
k * (T ) TT 1
2*Q 1
1
( 2 2 ) k * (T T 1)
2
*a x
x1
T ( x ) T1
c)
1 1
2
2
2
k a x
x1
2 Q
x 0.0075 m 0.01m 0.225 m
100
80
60
T( x )
40
20
0
0
0.1
0.2
0.3
x
17. Hallar la distribución de temperatura, el flujo de calor y el área media de una esfera hueca de radio interno
R1 y externo R2, cuyas temperaturas interna y externa son T1 y T2 respectivamente.
1 i T g 1 T
q
q i q q k
1 2 T
x
0
x 2 x x
Univ. Erwin Choque Conde
r
2
T
0 * x
x
Página 12
T( r )
C1
T
2 x
r
x
C1
C 2 T1
r R1
R1
T( r )
rR2
T( r )
C1
C2 T 2
R2
C1
C2
r
(T 1 T 2) * R1 * R 2
( R1 R 2)
C1
C 2 T1
(T 1 T 2) * R 2
( R1 R 2)
La distribución de temperatura es:
T( r )
(T 1 T 2) * R1 * R 2 (T 1 T 2) * R 2
T1
r * ( R 2 R1)
( R1 R 2)
El calor transferido es:
Q k * A(r ) *
T
r
rR2
Q 4 * * k * R1 * R 2 *
k * 4 * * r 2 * (
(T 1 T 2)
( R 2 R1)
El área media es:
Am
rR2
W
R2 R1
(T 1 T 2) * R1 * R 2
)
r 2 * ( R 2 R1)
1
A (r )
dr
R2 R1
R2
1
4 r
2
dr
R1 R2
1 1
4 R2 R1
1
4 R1 R2
R1
18. En el cubo interior de10 cm de lado de plastoform con un espesor de 10 cm se introduce trozos
de hielo con una masa total de 1 kg , después de 45 min , se pudo observar que una parte del
hielo se fusiona y se extrae un volumen de agua de 30ml.¿Calcular la conductividad térmica del
aislante (plastoform) y el coeficiente de T.C. por convección externo del cubo, considerando que la
temperatura en la superficie exterior se mantiene a una temperatura de 13ºC.
w
DATOS:
Two ( 13 273.15 )K
wo 10cm
w
Toi 273.15 K
eo 10cm
Lo wo 2 eo
w
Lo 0.3 m
6
m
3
T ( 15 273.15 )K
La masa del hielo convertido en agua
Ax
Tx
mo h2o Vh2o
mo 0.03 kg
El calor transmitido por el aislante al hielo
mo Lfo
Qo
Qo 3.7216 W
tf
El área variable respecto a la coordenada "x"
Two
Wo
3
cal
Lfo 80000
kg
tf 45min
Vh2o 30 10
kg
m
mh 1kg
L
h2o 1000
Lo
Toi
eo
Univ. Erwin Choque Conde
X
Lo wo
Ax wo
x
eo
2
Página 13
Para el área media se tiene la siguiente formula
eo
Am
eo
1
dx
1
Ax
Lo wo Lo
A dx
x
El área total de transferencia
AmT 6 Am
El calor por conducción
Q k o Am
Am 0.06 m
2
AmT 0.36 m
2
Tw To
eo
Qo eo
La conductividad del aislante
ko
El coeficiente de convección
Qo
hc
6 Lo Lo T Two
Univ. Erwin Choque Conde
Am Lo wo Lo
AmT Two Toi
k o 0.07952
hc 3.44593
W
m K
W
2
m K
Página 14
SISTEMAS CON GENERACION INTERNA
19. Deduzca la ecuación general de la conducción para un cilindro hueco y a partir de ella deducir las
ecuaciones de FOURRIER, POISSON, LA PLACE.
Q.z
d
Q.z dz
dz
Q.r
Q.
d
Q.r dr
dr
d
Q. d
d ( r )
Por balance de energía
Eentra Egenerado Esale Ealmacenado
.... a)
Eentra Qr Q Qz
Esale Qr
d
d
d
Qr dr Q
Q d Qz Qz dz
dr
d
(
r
)
d
z
d
d
d
Eentra Esale Qr dr
Q d Qz dz
d( r )
dz
d r
De la ecuación de Fourier
Q k A
... b)
dT
dx
dT
dT
Qr k r ( dz d ( r ) )
k r r dz d
dr
dr
dT
d
d
Qr k r r dz d
dr
dr
dr
dT
dT
Q k ( dr dz )
k dz dr
d
d
d
d
k dz dr dT
Q
d
d( r )
d( r )
dT
dT
Qz k z ( dr d ( r ) )
k z r dr d
dr
dz
dT
d
d
Qz k z r dr d
dz
dz
dz
Univ. Erwin Choque Conde
Página 15
Reemplazamos estas ecuaciones en la ecuación b)
dT
dT
dT
d
d
d
Eentra Esale k r r
( dz d ) dr
k
dz dr d k z
dr d dz
dr
d
dz
dr
d
dz
Egenerado g d V g dr d ( r ) g r dr d dz
.... c)
.... d)
Ealmacenado m Cp T V Cp T ( r dr d dz ) Cp
dT
.... e)
d
Las ecuaciones c),d) y e) reemplazamos en la ecuación a) y dividiendo entre ( r k dr d dz )
k kr kz k
1 d dT
r
r d r dr
1 d dT d dT g Cp dT
d
r 2 d d d z dz k
Entonces la ecuación general de la conducción para flujo cilíndrico es:
1 d dT
r
r d r dr
2
2
1 d T d T g Cp dT
2
k
d
r 2 d 2
dz
La ecuación de difusión de Fourier:
g 0
d
0
dT
d
0
2
2
2
2
1 d dT
r
r d r dr
1 d T d T g 0
2
k
r 2 d 2
dz
1 d dT
r
r d r dr
1 d T d T 0
2
r 2 d 2
dz
La ecuación de La place:
g 0
2
1 d T d T Cp dT
2
d
r 2 d 2
dz
La ecuación de Poissón:
dT
2
1 d dT
r
r d r dr
20. Una pared plana de 10 cm de espesor (K=19 W / m º C ) genera calor en su interior a la rapidez de
3
0.41 MW / m . La superficie interna de la pared esta perfectamente aislado y la superficie externa
se expone a un ambiente a 89ºC. El coeficiente de convección entre la pared y el ambiente es de
2
570 W / m º C calcule la distribución de temperatura, y la temperatura máxima.
DATOS
L 10cm
g 0.41 10
6 W
3
m
Q=0
k 19
T
h
W
m C
T 89C
W
h 570
2
m C
Incógnita
T (x)
g
k
Condiciones
- régimen permanente
- coordenadas rectangulares i=0 , q=x
- con generación de energía
L
Univ. Erwin Choque Conde
Página 16
SOLUCIÓN:
1 i T g 1 T
q
q i q q k
1 0 T g
x
0
x 0 x x k
T
x
g
x
k
T
g
x k x
g
T x C1 x
k
T( X )
T g
0
x x k
T
x
g
g
x C1
k
T k x C1x
g 2
x C1 * x C 2
2*k
........ 1)
Por la condición de frontera de segunda clase
T ( x)
x
( x 0)
f1 0
g
x C1 0
k
C1 0
Por la condición de frontera de tercera clase
Calor generado = Calor por convección
Q g Qh
g * V h * A * (T ( x)
X L
T )
g * A * L h * A * (
g 2
L C 2 T )
2*k
g * L g * L2
C2
T
h
2*k
Se reemplaza en la ecuación 1
T( X )
g 2 g * L g * L2
x
T
2*k
h
2*k
T( X )
g
g*L
* L2 x 2
T
2*k
h
La temperatura máxima es cuando x=0
T( X )
X 0
g
g*L
* L2 0 2
T
2*k
h
g
2 g L
Tx0
L
T
2 k
h
Univ. Erwin Choque Conde
Tx0 268.82456 C
Página 17
21. Una varilla larga de acero inoxidable de 20 mm *20 mm de sección transversal cuadrado, esta
aislado en tres de sus lados y se mantiene a una temperatura de 400ºC en el lado restante.
Determínese la temperatura máxima en la varilla cuando esta conduciendo una corriente de 1000
Amperios. La conductividad térmica y eléctrica del acero inoxidable se puede suponer que es de
1
46 W / m º C y 1.5E4 cm y se puede despreciar el flujo de calor en la varilla.
DATOS:
a 20mm
W
k t 46
m C
I
a
a
I 1000 A
1
4
k e 1.5 10
Tw 400 C
cm
L 1m
Condiciones
- régimen permanente
- coordenadas rectangulares i=0 , q=x
- con generación de energía
L
TW
C
Tmax( º )
Incógnita:
SOLUCIÓN:
2
At 0.0004 m
At a a
El área transversal
1
R
La resistencia
L
R 0.00167
k e At
2
G I R
El calor generado
G 1666.66667 W
El calor generado por unidad de volumen
g
G
g
V
De la Ecuación
G
6 W
g 4.16667 10
At L
general de la conducción
1 i T g 1 T
q
q i q q k
3
m
T g
0
x x ke
T( X )
g
x 2 C1 * x C 2
2 * kt
........ 1)
Por la condición de frontera de segunda clase
T ( x)
x
( x 0)
f1 0
g
x C1 0
kt
C1 0
Por condición de frontera de primera clase
T( X )
X a
Tw
g
a2 C2
2 * kt
En la ecuación 1)
T( x )
g
2 k t
2
a x
420
Tw
2
C2
g
a 2 Tw
2 * kt
x 0m 0.001 m 0.02 m
La temperatura máxima es cuando x=0 :
415
g
2
Tmax
a Tw
2 k t
T( x ) 410
Tmax 418.11594 C
405
400
0
0.01
0.02
x
Univ. Erwin Choque Conde
Página 18
22. Una pared plana de dos materiales, A y B, la pared del material A tiene una generación de calor
3
uniforme g=2.1E6 W / m kA=65 W / m º C y un espesor LA=50 mm . El material B de la pared
no tiene generación y su kB=150 W / m º C y el espesor LB=20 mm . La superficie interior del
material A esta bien aislada mientras que la superficie exterior del material B se enfría con un flujo
2
de agua con T 30º C y h=5000. W / m º C . a) Dibuje la distribución de temperatura que existe
en el compuesto bajo condiciones de estado estable, b) Determinar la temperatura To de la
superficie aislada c) Calcule la temperatura T2 de la superficie enfriada.
T
1
DATOS:
T
2
6 W
g 2.1 10
KA
3
m
KB
KA 65
T
g
LB 20mm
W
m C
T 30C
LA 50mm
W
KB 150
m C
h
Q=0
2
A 1m
h 5000
W
2
m C
Incógnitas:
k
LA
a) T(x)
b) To
c) T2
LB
Condiciones
- régimen permanente
- coordenadas rectangulares i=0 , q=x
- con generación de energía
SOLUCION:
De la Ecuación
T( X )
general de la conducción en la pared plana se tiene
g
x 2 C1 * x C 2
2* KA
Por la condición de frontera de segunda clase
T ( x)
x
( x 0)
f1 0
g
x C1 0
KA
C1 0
Por condición de frontera de primera clase
T( X )
X a
T1
g
2
LA C 2
2* KA
C2
g
2
L A T1
2* KA
El volumen de la placa generada
Vvol LA A
Balance de energía
3
Vvol 0.05 m
Qg Qk Qh
g Vvol A h T2 T
g Vvol
KB A
LB
T2 T1
Univ. Erwin Choque Conde
T2
T1
g LA
h
T
g LA LB
KB
T2
T2 51 C
T1 65 C
Página 19
g 2
2
TA( x1 )
L
x1 T1
2 KA A
g LA
TB( x2 ) T1
x2 LA
KB
x1 0mm0.1mm 50mm
x2 50mm55mm 70mm
150
100
TA( x1 )
TB( x2 )
50
0
0.02
0.04
0.06
x1 x2
La temperatura máxima
TA( x1 ) 105.38462 C
x1 0
23. Graficar la distribución de temperaturas donde en una placa formada de un material de
conductividad 30 W / m º C de 20 mm de espesor, en el que se genera calor a una rapidez de
3
5*E7 W / m . La placa esta refrigerada por ambos lados con agua en un lado a 60ºC y en el otro a
2
2
90ºC con un coeficiente de traspaso de calor de 8500 W / m º C y 7900 W / m º C en uno y otro
lado respectivamente. Calcule también la temperatura máxima y su posición.
DATOS:
k p 30
T 1
h2
W
T2 90C
m C
Lp 20mm
T1
g p 5 10
3
m
T 2
T1 60C
d
2
dx
x
2
T
gp
kp
W
2
m C
7 W
T2
h1
h1 8500
h2 7900
W
2
m C
0
Lp
La solución general es:
g p
d
T
x C1
kp
dx
Univ. Erwin Choque Conde
T
g p
2
x C1 x C2
2 k p
Página 20
Por condiciones de frontera de primera clase:
d T h1 T T( x )
1
dx
x 0
k p
k p C1 h1 T1 C2
x Lp
g L 2
g p Lp
p
k p 2 k C1 h1 2 k C1 Lp C2 T2
p
p
d
k p T h1 T( x ) T2
dx
g p Lp
C1
T1 T2
2 k p
k p
C2
k p C1
T( x )
h1
h1
g p x
2 k p
kp
h2
2
g p Lp
h2
Lp
T1
C1 17927.97457
C
m
C2 123.2752 C
2
C1 x C2
x 0mm1mm 20mm
220
200
180
T( x )
160
140
120
0
0.01
0.02
x
g
d
T
x C1 0
k
dx
x
C1 k p
gp
x 0.01076 m
T( x ) 219.69889 C
Univ. Erwin Choque Conde
Página 21
24. Un alambre de cobre de 1 mm de diámetro esta uniformemente aislado con un material plástico
de forma que el diámetro externo del conductor aislado es de 3 mm el conductor esta expuesto a
un ambiente de 38ºC. El coeficiente de transmisión de calor desde la superficie exterior del plástico
2
a los alrededores es de 8.5 W / m º C a) Cuál es la máxima corriente que en régimen estacionario
puede conducir este alambre sin que sobrepase en ninguna parte del plástico el limiten de
operación que es de 93ºC? las conductividades caloríficas y eléctricas se suponen constantes para
1
el cobre y son 377 W / m º C y 5.7E5 cm respectivamente, para el plástico kp=0.35 W / m º C
b) Cual es el flujo de calor c) Grafique la distribución de temperatura.
DATOS:
Q
d 1mm
Lcu 1m
D 3mm
Kcu
eais
T 38C
kais
Tw1
T2
h 8.5
W
T
k ais 0.35
Tw1 93C
k cu 377
d=1mm
W
m C
W
m C
5
cu 5.7 10
D=3mm
2
eais 0.001 m
2
m C
h
D d
1
cm
Condiciones
- régimen permanente
- coordenadas cilíndricas i=1 , q=r
- con generación de energía
El área transversal
Atcu
4
d
2
Atcu 7.85398 10
7
2
m
El área de transferencia de calor por convección
Ae D Lcu
2
Ae 0.00942 m
El área media logarítmica del aislante
Amais
Lcu ( D d )
D
ln
d
2
Amais 0.00572 m
De la ecuación general de la conducción
1 i T g 1 T
q
q i q q k
Para nuestras condiciones
1 1 T g
r
0
r1 r r k
Univ. Erwin Choque Conde
2
g r
Tr
C1 ln ( r ) C2
4 k
Página 22
Por las condiciones de frontera
T (r )
r
( r 0)
0
g * 0 C1
2*k
0
C1 0
Qgeneracio Qconduccion Qconveccion
Balance energético
De la siguiente relación
T (r ) ( r d / 2) T 2
g * (d / 2) 2
C2
4*k
C2
g d
8 k
2
T2
La distribución de temperatura
g d
2
Tr
r T2
4 k cu 2
Qconduccion Qconveccion
2
k ais Amais
eais
T2
0 r
Tw1 T2 Ae h T2 T
d
2
k ais Amais Tw1 h Ae T eais
T2 90.88355 C
h Ae eais k ais Amais
Qgeneracion Qconduccion
2
g Vvol I R h Ae T2 Tw1
I
h Ae cu Atcu T2 T
Lcu
I 13.772 A
La generación interna es:
g
I
2
cu Atcu
6 W
g 5.39412 10
2
3
m
a) Calor transferido
Qk
k ais Amais
eais
Tw1 T2
Qh Ae h T2 T
Qk 4.23653 W
Qh 4.23653 W
Qg g Atcu Lcu
Qg 4.23653 W
b) La distribución de temperatura
d
g
2
T1 ( r1 )
r1 Tw1
4 k cu 2
2
El área media variable
Univ. Erwin Choque Conde
Am
r1 0mm0.1mm 0.5mm
2 Lcu
2 r
ln
d
r
d
2
Página 23
g Atcu
2 r2
T2 ( r2 ) Tw1
ln
2 k ais d
r2 0.5mm0.6 mm 1.5mm
94
93
T1( r1)
T2( r2)
92
91
90
0
510
4
110
3
1.510
3
r1 r2
25. Considere un tubo solidó largo, aislado en radio externo r2 y enfriado en el radio interior r1 con
3
generación uniforme de calor g W / m dentro del solidó de k W / m º C . a) Encontrar la distribución
de temperatura b) T máximo c) La rapidez de transferencia de calor por unidad de longitud del tubo.
Si por el interior circula agua a T y “h”.
DATOS
R ( m)
g
W
3
m
r ( m)
k
m C
W
Incógnitas
T2
ai
sl
an
te
h
Q
ro
R
a)
T (x)
b)
T max=T2
c)
T1
d)
Q
Condiciones
- régimen permanente
- coordenadas cilíndricas i=1 , q=r
- con generación de energía
T
T1
De la Ecuación
general de la conducción para pared cilíndrica
1 i T g 1 T
q
q i q q k
1 1 T g
r
0
r 1 r r k
r
T
g *r2
C1
r
2k
2
g r
Tr
C1 ln ( r ) C2
4 k
.......1 )
Por la condición de frontera de segunda clase
T (r )
r
g * R C1
0
( r R ) f 1
R
2k
Univ. Erwin Choque Conde
C1
g R
2
2 k
Página 24
Por la condición de frontera de tercera clase
Calor generado = calor por convección
Q g Qh
g *V h * A * (T (r ) r ro T )
g * ( R 2 r02 ) * L h * 2 * r0 L * (
C2
g
gR 2
2
r0
* ln(r0 ) C 2 T )
4*k
2k
g ( R 2 r02 )
g
gR 2
2
r0
* ln(r0 ) T
2 * h * r0
4*k
2k
En ecuación 1
T (r )
a)
g ( R 2 r02 )
gr 2 gR 2
g
gR 2
2
* ln(r )
r0
* ln(r0 ) T
4k
2k
2 * h * r0
4*k
2k
T (r )
g ( R 2 r02 )
gR 2
r
g
2
* ln( )
(r0 r 2 ) T
2k
r0
2 * h * r0
4*k
b)
T 2 r R T max
c)
T 1 r r0
d)
g ( R 2 r02 )
gR 2
R
g
2
* ln( )
(r0 R 2 ) T
2k
r0
2 * h * r0
4*k
r0
g ( R 2 r02 )
g ( R 2 r02 )
gR 2
g
2
2
* ln( )
(r0 r0 ) T
T
2k
r0
2 * h * r0
4*k
2 * h * r0
Qh hA1 * (T 1 T ) h * 2 * * r0 * L * (T 1 T )
Qh
g ( R 2 r02 )
L
´
o
´
Qg
g ( R 2 r02 )
L
o
Qk
g ( R 2 r02 )
L
26. Un recipiente a presión de un reactor nuclear se puede trazar en forma aproximada como una gran
placa de espesor L, la superficie interior de la placa en x=0 esta aislada, la superficie exterior en
x=L se mantiene a una temperatura uniforme T2; el calentamiento de la placa por rayos gama se
puede representar por un termino de generación de la forma de g ( x) g 0 * e J *x donde g0 y J son
constantes y “x” se mide desde la superficie aislada interior. Encontrar: a) Distribución de la
temperatura T(x), b) temperatura de la superficie aislada c) Determinar el flujo de calor en x=L.
DATOS:
g0
T1
J
T2
L
Incógnitas
Q=0
T2
g ( x ) g0 * e J * x
L
Univ. Erwin Choque Conde
X
a)
T (x)
b)
T1
c)
Q
Condiciones
- régimen permanente
- coordenadas rectangulares i=0 , q=x
- con generación de energía
Página 25
1 i T g 1 T
q
q i q q k
J *x
g0 * e
T
x ke
x
g 0 * e J *x
T ( k * J C1)x
T g
0
x x k
J *x
T g 0 * e
C1
k*J
x
T( x )
g 0 * e J *x
C1 * x C 2
k*J2
... 1)
Para calcular C1 y C2 aplicamos condiciones de frontera
Por la condición de frontera de segunda clase
T ( x)
x
( x 0) f 1 0
g 0 * e J *0
C1 0
k*J
C1
g0
k*J
Por condición de frontera de primera clase
T( X )
X L
T2
g 0 * e J *L
C1 * L C 2
k*J2
C 2 T2
g 0 * e J *L
g
0 *L
2
k*J
k*J
En la ecuación 1
T( x )
T( x )
b)
T( x )
c)
g 0 * e J *x
g0
g 0 * e J *L
g
*
x
T
0 *L
2
2
2
k*J
k*J
k*J
k*J
g 0 * e J *L
g *L
1 e J *( L x ) 0
1
2
k * J
k*J
x
T2
L
Temperatura máxima
x o
g 0 * e J *L
g *L
1 e J *( L 0) 0
1
2
k * J
k*J
g0
g *L
0
T2
e J *L 1 0
T2
2
L
k*J
k*J
El flujo de calor
Q k * A *
T
x
Q g0
1 e J *L
A J
xL
g
g
k * A * ( 0 e J *x 0
J *k
J *k
xL
g
g
k * A * ( 0 e J *L 0
J *k
J *k
Univ. Erwin Choque Conde
Página 26
27. Se genera calor en el interior de una partícula esférica de catalizador debido a una reacción
química. La partícula, de 8 mm de diámetro, tiene conductividad térmica igual a 0.003
cal / cm * s * K , y tiene temperatura superficial de 300 °C. La generación de calor decrece
linealmente hacia el centro de la partícula debido al decrecimiento en la cantidad de material que
reacciona (mayor camino de difusión). La generación está dada por g 67.5 *
r cal
Suponga
R cm 3
que la generación de calor se balancea exactamente con las pérdidas convectivas en la superficie.
Determine la distribución de temperaturas y la temperatura máxima. El catalizador tiende a perder
actividad por encima de los 700 °C; ¿Excede esta temperatura?
DATOS:
k pr 0.003
T2
R
cal
cm s C
d pr
d pr 8mm
R
Twe 300 C
M 67.5
cal
3
cm s
Incógnitas
g=67.5R/r[cal/m3]
R 0.004 m
2
T (x)
Condiciones
- régimen permanente
- coordenadas esféricas i=2, q=r
- con generación de energía
1 i T g 1 T
q
q i q q k
T( x )
M *r3
C1
C2
12 * R * k pr
r
Por condiciones de frontera
T ( x)
x
T( X )
T( r )
( r 0)
r R
0
Twe
M
12 R k pr
3
R r
3
C1 0
C2
Twe
M R
3
12 R k pr
Twe
r 0mm0.6 mm 4mm
La temperatura máxima está en el centro de
la esfera
600
500
3
M R
Tmax
Twe
12 R k pr
T( r)
400
Tmax 600 C
300
0
3
210
410
3
Tmax 700 C
r
Univ. Erwin Choque Conde
Página 27
28. Encontrar la distribución de temperatura y el flujo de calor en estado estable de una esfera hueca
de radio interior “a” y de radio exterior “b” cuya conductividad térmica es constante “k” y en la que
2
W / m3 a la superficie limite en r=a se mantiene a una
se genera calor a una tasa de g c * r
temperatura uniforme Ta. La superficie en r=b disipa calor por convección (cuyo coeficiente es h)
,hacia el medio de temperatura T .
DATOS:
Q
b
C
a
a
b
Ta
Incógnitas
Ta
a)
T
h
g ( x ) g 0 * e J *x
b)
h
T
T (x)
Q
Condiciones
- régimen permanente
- coordenadas esféricas i=2, q=r
- con generación de energía
1 i T g 1 T
q
q i q q k
1 2 T
C *r2
r
k
r 2 r r
C *r4
2 T
r
r k r
T
C *r5
r2
C1
r
5*k
T
C * r 3 C1
2
r
5*k
r
C * r 3 C1
T
5 * k r 2 r
Tr
C *r4
C1
2*
C2
20 * k
r
.......... 1)
Por condición de frontera de primera clase
T( r )
C * a 4 2 * C1
T1
C2
ra
20k
a
C * a 4 2 * C1
C2
T1
20k
a
...... 2)
Realizamos balance térmico en r=b
Q
por.conduccion
r b
Q
sale. por
r b
conveccion
C b 3 C1
C b 4
C1
k
h
2
C2 T
5 k
2
b
20 k
b
3
b C
De ecuaciones 1 y 2
C1
5 h
C
20 k
2
a
T
)
h * (Tr
T )
r b
x r b
C b 3 C1 C b 4
C1
C2
2
T
h 5 K
2
20 k
b
b
k
4
4
2
k
b a
k *(
....3 )
T1 T
....4 )
b
h b
2
La distribución de temperatura será:
Tr
C *r4
C1
2*
C2
20 * k
r
Univ. Erwin Choque Conde
Página 28
29. Determinar el radio critico de aislamiento de una esfera hueca (conductividad k) de radio exterior r=b
y interior r=a si el coeficiente de convección exterior es de h y la temperatura en r=b es T1y la del
medio ambiente es de T
DATOS
El área media cuadrática del aislante
Amais Ae Ai 4 ri re
T
T2
re=Rcrit
El área externa
Ae 4 re
ri
h
T
Q
r
k ais Amais
T
1
Ae h
Q
re ri
k ais 4 ri re
T2 T
Rt 0 Rais Rh
4 k ais T
1
re ri
2
ri re
4 re h
2
k ais
h re
2
Por el teorema de Máximos y Mínimos
4 k ais T
k ais
re ri re ri ri
d
0
Q
2
re ri
k ais
2 2
3
d re
re ri
h re
ri re
2
h re
1 2
k ais
h re
k ais
rcrit re 2
h
0
30. Se desea aislar térmicamente un tubo por el que circula vapor de agua saturado, con el objeto de
evitar en lo posible pérdidas de calor y condensaciones. El material aislante tiene conductividad
calorífica k=0.41 kJ / hr * m º C . y la temperatura de los alrededores permanece constante e igual
a 293 K . Si el coeficiente de transmisión de calor externo para todo el tubo aislado puede
suponerse independiente del diámetro externo del mismo. a) Es posible que en algún momento el
incremento de espesor del aislante aumente las pérdidas de calor b) Grafique el flujo de calor en
función del espesor del aislante c) Calcule el radio critico de aislamiento d) El caudal de calor
máximo perdido con el espesor crítico. Haga un gráfico de espesor contra flujo de calor. Datos:
Tvap H2O = 393 K. Diámetro externo del tubo 0.01 m coeficiente externo h=41.87
kJ / hr * m º CDesprecie la resistencia de la pared del tubo.
2
d e 0.001 m
Lw 1m
de
re
2
T1 20C
3
h 41.87 10
J
2
hr m C
J
3
Tsat 120 C
k as 0.41 10
re 0.0005 m
hr m C
a) El espesor del aislante define el flujo de calor como también su conductividad y el coeficiente
de T.C. por convección
El área media logarítmica de aislamiento (para un cilindro)
Amais
2 L rais re
rais
re
ln
Univ. Erwin Choque Conde
Página 29
El área externa para la transferencia de calor por convección
Ae 2 L rais
T
Q
El flujo de calor
r
k as Amais
b)
Tsat
Q rais
T1 2 Lw k as h rais
1
Ae h
rais 0m 0.001 m 0.04 m
rais
h rais ln
k as
re
20
15
Q rais
10
5
0
0.01
0.02
0.03
0.04
rais
c) El radio crítico de aislamiento
rcrit
k as
rcrit 0.00979 m
h
d) El calor máximo
Qmax
Tsat
Univ. Erwin Choque Conde
T1 2 L k as h rcrit
rcrit
h rcrit ln
k as
re
Qmax 18.00334 W
Página 30
ESPESOR ÓPTIMO TÉCNICO ECONÓMICO DE AISLAMIENTO
31. Para demostrar la conveniencia de aislar las conducciones de vapor, se hizo circular vapor por un
tubo desnudo de 1´´ y 1 metro de longitud, y posteriormente por el mismo recubierto de una capa
de aislante de 20 mm de espesor, obteniéndose los datos siguientes:
Tubo desnudo
Tubo aislado
Peso del condensado
160 g / hr
43.8 g / hr
Presión de vapor (Sobre presión)
63.5 mmHg
63.5 mmHg
Temperatura de la superficie del tubo
Temperatura de la superficie del aislante
Temperatura del aire
Calor latente de condensación
102ºC
--37.5ºC
2251.7 kJ / kg
99%
102ºC
39ºC
30.5ºC
2251.7 kJ / kg
99%
Titulo del vapor
Determínese:
a) El porcentaje de ahorro de calor obtenido con el aislante.
b) El coeficiente de convección del tubo desnudo
c) El coeficiente de convección para el tuvo aislado
La conductividad térmica del aislante.
a)
kg
md 0.160
hr
kg
ma 0.0438
hr
d 1in
Tw 102 C
Tw1 39C
Lt 1m
Td 37.5C
Ta 30.5C
eais 20mm
Xv 0.99
h fg 2251.7 10
3 J
kg
Para el tubo desnudo
Qdes md h fg Xv
Qdes 99.0748 W
Para el tubo aislado
Qais ma h fg Xv
Qais 27.1217 W
Q%
Qdes Qais
Q% 72.625 %
Qdes
b)
Qdes h des Ades T
h des
Qais h des Ades T
h ais
Qdes
d Lt Tw Td
c)
d)
T
Qais k Am
a ais
k ais
Qais eais
Am Tw Tw1
Univ. Erwin Choque Conde
Am
Qais
d 2 eais Lt Tw1 Ta
2 eais Lt
ln 1 2
h des 19.2495
2
m C
W
2
m C
2
Am 0.1329 m
eais
d
h ais 15.53
W
k ais 0.0648
W
m C
Página 31
32. Para efectuar un determinado aislamiento térmico pueden emplearse dos tipos de aislante ambos
2
disponibles en planchas de 2 cm de espesor. El aislante A cuesta 26 Sus / m y su conductividad
térmica es de 0.04 W / m º C , el aislamiento B cuesta 40 Bs / m
2
y su conductividad térmica es
k=0.03 W / m º C se supone que la temperatura en ambas caras será de 500ºC y 40ºC y los dos
materiales son capaces de resistir estas temperaturas. Bajo esta hipótesis determinar a) El
espesor optimo técnico económico del aislante a) A b) B c) El aislante mas conveniente. Se
supone en todos los casos un año laboral de 340 días al año de 24 horas día, el combustible
cuesta 3.9Bs el millón de kilojulios. El aislante se cambiara cada 15 años para ambos casos.
DATOS:
eais 0.02m
A 1m
T1 500 C
T2 50C
2
Incógnitas:
etecA
a)
etecB
b)
Aislante más económico
c)
T
Q k ais Aais
n eais
a) SOLUCION:
Para el aislante A)
Costo fijo
n Cua A
CfA
a
n 26 1
15
ño
Bs
1.733 n
a
Costo variable
3.9Bs
CvA Q E k A AA
0.04
1 m
n eA
m s C
n 0.02 m
6
10 kJ
ño
T
CvA
2 500 C 40C
J
ño
3600 s 24h 340 dia
1h dia a
Bs
105.401
a
nB
El costo total será:
CTA 1.733 n A
CTA CfA CvA
105.401
d
CTA 0
1.7333 0
2
dn
nA
ño
Bs
105.401
nA
a
n A 7.798
etecA n A eais 8 0.02 0.16 m
nA 8
b) Para el aislante B)
Costo fijo
CfB
n Cub A
a
n 40 1
15
2.666 n
ño
Bs
a
Costo variable
3.9Bs
CvB Q E k B AB
0.03
1 m
n eB
m s C
n 0.02 m
6
10 kJ
ño
T
CvB
79.05
nB
J
2 500 C 40C
ño
3600 s 24h 340 dia
1h dia a
Bs
a
Univ. Erwin Choque Conde
Página 32
El costo total será:
CTB 2.66 n B
CTB CfB CvB
79.05
d
CTB 0
2.666 0
2
dn
nB
a
nB
n B 5.4449
CTA 1.733 8
c) El costo total será:
ño
Bs
79.05
CTB 2.66 5
etecB n B eais 5 0.02 0.1m
105.401
ño
Bs
CTA 27.039
8
79.05
a
ño
Bs
CTB 29.11
5
a
El aislante mas económico es "A" CTA=27.039Bs/año
33. El aislamiento térmico de un horno cúbico de dimensiones exteriores de 1*1*1 m deberá ser
construido utilizando placas de 1” se espesor de aislante, lana de vidrio k=0.04 W / m º C , cuyo
2
precio es de 8.7 Sus / m , el costo de mano de obra es de 1 Sus / m
2
y mantenimiento es de 0.3
Sus / m . Las temperaturas de trabajo están fijadas en 400ºC y 50ºC en la cara interna y externa
2
respectivamente. El aislante tiene una vida útil de 5 años para un trabajo de 24 horas al día y 300
días al año. El horno es calentando eléctricamente cuyo costo es de 0.059 $us / kWh . ¿Cuál es el
numero de capas de aislante que UD. Colocaría?
w 1m
50ºC
Tw1 400 C
eaisl 1in
400ºC
k lvid 0.04
Cu 8.7
Sus
2
m
aislante
Sus
Cmo 1
W
m C
Tw2 50C
ños
a 5a
hr
24
dia
ño
dia
300
a
2
m
Cm 0.3
1'’
Sus
0.059
Sus
kW hr
2
m
n
El área total de transferencia
Atr 6 w
2
2
Atr 6 m
El costo total unitario
CuT 10
CuT Cu Cmo Cm
2
m
El costo fijo
Cf
Sus
n CuT Atr
Cf 12 n
a
ño
Sus
a
El calor transferido
Q
Atr k lvid
n eaisl
Tw1 Tw2
El costo variable
Cv Q E
Univ. Erwin Choque Conde
Q
3307.08
n
W
ño
ño
3307.08 W 0.059 Sus
hr 300 dia
58.5354 Sus
Cv
24
n
kW hr
1dia 1a
n
a
Página 33
El costo total
CT
CT Cv Cf
58.5354
n
ño
Sus
12 n
a
El número de capas optimo
d
CT 0
dn
El costo total será
58.5354
n
n 2.2086
12
58.5354
CT
12 n
n
n 2
capas
ño
Sus
CT 53.2677
a
El área el espesor técnico económico
eopt n eaisl
eopt 0.0508 m
34. Calcular el calor trasferido a través de una pared de un horno de 9´´, cuya temperatura interna y
externa de las paredes son 980ºC y 198ºC respectivamente. La pared tiene una conductividad de
0.667 W / m º C . Se adiciona a la pared externa 0.3”de un aislante k=0.04 W / m º C que reduce la
perdida de calor en un 20%. Si el costo del aislante es de 1.37$us/pie cuadrado instalado. Que
tiempo será necesario para pagar el aislamiento. Tomar una operación del horno de 24 horas al día
y 175 días al año, el costo de la energía es de 0.23$us el millón de kJ.
DATOS:
2
Aais 1m
L 9in
T1 980 C
k pared 0.667
T2 198 C
W
m C
%perd 20%
CU 1.37
CALCULAR:
Sus
2
ft
a) (tiempo para pagar)
El calor sin aislante es :
Q1 k pared Aais
T1 T2
Q1 2281.6885 W
L
El calor con aislante es :
Q2 0.8 Q1
El costo fijo es:
Costo variable
CU Aais
Cf
a
14.74655 1
a
Q2 1825.3508 W
a
CV Qaurrado Q1 Q2 456.337
CV 456.337
a
W
ño
175 dia
0.23Sus 3600 s 24hr
1hr dia a
s
6
10 kJ
J
ño
Sus
14.74655
ño
Sus
1.5869
a
Para calcular el tiempo a pagar:
ños
CF CV
Entonces
Univ. Erwin Choque Conde
14.74655
a
1.5868
a
14.74655
1.5869
9.292 a
Página 34
35. Calcular el espesor más económico para aislar una tubería de 200. mm de diámetro interior y
36.5 mm de espesor, que conduce vapor a 300ºC, empleando aislante de amianto (k=0.053
W / mº C ), el material aislante estará protegido con chapa de aluminio de 0.6 mm de espesor y
el conducto esta en un ambiente a una temperatura promedio de 20ºC. A continuación se
muestran los costos estimados para la instalación del aislante:
Espesor del aislante
mm
Costo del material
aislante
Costo del aluminio
Costo de mano de obra
50
60
75
90
100
2274
2762
3249
4383
5460
1035
1107
1179
1269
1360
1380
1476
1572
1692
1810
$ / m
$ / m
$ / m
El costo de la producción de vapor es de 1.5 $ por cada 4118 kJ y el ciclo de trabajo es de 7920
horas / año . Se estima que los coeficientes del lado del vapor y en la superficie exterior estarán en el
2
orden de los 349 y 11.63 W / m º C respectivamente. La vida útil del aislante es aproximadamente 5
años.
DATOS:
k a 0.053
d t 200 mm
et 36.5mm
W
h 1 349
m C
T1 300 C
a 5.yr
2
m C
h 2 11.63
T2 20C
El calor:
W
W
Lt 1m
2
m C
T1 T2
Q
1
h 1 Ain
eais
k ais Am
1
h 2 Aex
2
Ain 0.1436 m
El área interna del tubo
Ain L d t
El área interna del aislante
Ainais Lt d t 2 et
El área externa del aislante
Aex L d t 2 et 2 eais
El área media del aislante
Am
2
Ainais 0.8577 m
2 L eais
ln 1
El flujo de calor:
d t 2 et
2 eais
T1 T2
Q
1
h1 L dt
eais
k ais1 ( 2 L )
ln 1
1
h L d 2 e 2 e
d t 2 et
t
2
t
ais
2 eais
El costo variable
E
Cv Q E
El costo fijo
Cf
Univ. Erwin Choque Conde
1J
1.5Sus
1s
4118 10 J
3
3600 s 7920 hr
1hr
yr
E 10.3856
Sus
yr
Cu Ainais
a
Página 35
a) Para el espesor de:
Cmat 2274
eais 50mm
m
Cal 1035
Sus
m
Cu Ainais
a
Cmh 1380
Cu 4689
Cu Cmat Cal Cmh
ño
Sus
Cf 804.3087
a
El costo unitario
Cf
Sus
Sus
m
Sus
m
T1 T2
Q50
1
h1 L dt
eais
k ais L ( 2 L )
ln 1
Q50 260.62 W
Cv Q50 ( 10.3856 )
eais(mm)
Cv 2706.695
1
d t 2 et
h 2 L d t 2 et 2 eais
2 eais
ño
Sus
a
Cu(Sus/m)
Cf(Sus/año) Q(W)
Cv(Sus/año) Ct(Sus/año)
50
4689
804,3087 260.62
2706,69 3510,9987
60
5345
916,833
207
2150,866
3067,699
75
6000
1029,18
151,6348 1574,8185 2603,9985
90
7344
1259,72
115,4 1198,5013 2458,2213
100
8630
1480,312
98,031 1018,1176 2498,4296
El espesor más económico es el aislante que tiene como espesor de 90mm
36. En una instalación de compresión de una industria 3000 kg / hr de vapor saturado a 10 Bar
(Tsat=179ºC) circula por un tubo de acero k=40 W / m º C de 2” de diámetro externo y 0.2” de
espesor y tiene una longitud de 72 m . El aislamiento de la línea de vapor debido a las
condiciones del local es sustituido anualmente. Se sabe que la instalación trabaja 5000 horas por
año y la temperatura externa del aislante debe ser mantenida a 30ºC tomando la previsión del
cambio de aislante en el momento, se tiene en existencia en el mercado solamente dos tipos de
aislante : a) Lana de vidrio en capas de 3” de espesor y 80 cm de longitud k=0.04 W / m º C y un
costo de 10 Sus la capa b) Lana mineral en capas de 2” de espesor y 90 cm de longitud,
k=0.025 W / m º C y un costo de 13 Sus la capa. El costo de energía es 1kJ=0.001672$us
calcular: El aislante mas adecuado y el numero de capas a ser comprado Nota: las capas de
aislante tienen un ancho requerido para envolver el tubo.
a 1.a
eais
DATOS:
ño
k tub 40
Ltub 72m
W
m C
etub 0.2in
d e 2in
etub
d i d e 2 etub
d i 0.0406 m
El área media logarítmica del tubo
Amed
Ltub d e d i
de
di
2
Amed 10.2989 m
ln
Univ. Erwin Choque Conde
Página 36
Aislante A)
k aislA 0.04
W
Área media logarítmica del aislante
m C
eaislA 3in
CuA 10
Amaisl
Sus
2 n Ltub eaisl
ln 1
2
m
Aislante B)
2
m
2 n eais
de
El área enésima del aislante
W
k aislB 0.025
2
An Ltub d e 2 eaisl ( n 1 )
m C
m
eaislB 2in
CuB 13
Sus
2
m
La transferencia de calor es:
T
Q
etub
Amed k tub
n eais
Amaisl k aisl
T
W
2 n eais
ln 1
Amed k tub
2 Ltub k aisl
de
etub
1
Costo variable
ño
ño
Sus
J
0.001672 Sus 3600 s 5000 h
Cv Q
1 h 1 a Q 30.096
1 kJ
s
a
PARA EL AISLANTE A)
QA
T1 T2
etub
Amed k tub
1
2 Ltub k aislA
ln 1
2 n A eaisA
de
179 30
1.2331 10
5
0.05526 ln ( 1 3 n )
El costo variable para el aislante A)
CvA
CfA
179 30
1.2331 10
CuA A ( n )
a
5
30.096
0.05526 ln ( 1 3 n )
10 Ltub
1
4484.304
1.2331 10
5
0.05526 ln ( 1 3 n )
a
d e 2 eaislA ( n 1 ) 2261.94671 [ 0.0508 0.1524 ( n 1 ) ]
n Q(W)
Cv(Sus/año)
1
1944,68843
58527,343
2
1385,48812
41697,6504
3
1170,89409
35239,2285
4
1051,13576
31634,9819
ño
Sus
a
Cf(Sus/año) Cfac(Sus/año) CT(Sus/año)
114,906892
114,906892 58642,2499
459,627569
574,534462 42272,1848
804,348247
1378,88271 36618,1112
1149,06892
2527,95163 34162,9335
5
972,42247
29266,027 1493,7896
4021,7412
33287,768
6
7
915,671965
872,246162
27558,0635 1838,51028
26251,1205 2183,23095
5860,25151
8043,48247
33418,315
34294,6029
Univ. Erwin Choque Conde
ño
Sus
Página 37
PARA EL AISLANTE B)
QB
T1 T2
etub
Amed k tub
1
2 Ltub k aislB
ln 1
2 n A eaisB
de
179 30
1.2331 10
5
0.08842 ln ( 1 3 n )
El costo variable para el aislante B)
CvB
CfB
179 30
1.2331 10
CuB A ( n )
a
5
30.096
0.08842 ln ( 1 3 n )
13 Ltub
1
1.2331 10
5
4484.304
ño
Sus
0.08842 ln ( 1 3 n )
a
ño
Sus
d e 2 eaislB ( n 1 ) 2940.53072 [ 0.0508 0.1016 ( n 1 ) ]
a
n Q(W)
Cv(Sus/año) Cf(Sus/año) Cfac(Sus/año) CT(Sus/año)
1
1215,44865 36580,1424 149,378961
149,378961 36729,5214
2
865,928135 26060,9732 448,136882
597,515842
26658,489
3
731,802294 22024,3218 746,894803
1344,41065 23368,7325
4
656,951564 19771,6143 1045,65272
2390,06337 22161,6776
5
607,7549
18290,99 1344,411
3734,474
22025,47
6
7
572,285352
545,143947
17223,5 1643,16857
16406,6522 1941,92649
5377,64258
7319,56907
22601,1425
23726,2213
El aislante mas económico es B) lana mineral con 5 capas
37. Un horno semiesférico esta construido con ladrillo refractario cuyo radio externo es 0.5m se aísla
con un material k=0.04 W / m º C de 2.54 cm de espesor cuyo costo unitario es de 4200.
Sus / m Hallar el espesor optimo técnico económico si el horno es calentado eléctricamente
2
con un costo de 0.68 $us / kWh el aislamiento tiene un tiempo de vida de 5 años, el trabajo del
horno es de 24 horas al día y 300 días al año, la temperatura externa del ladrillo es 400ºC y la
externa del aislante tiene que ser tal que no sea un peligro para los trabajadores.
r0 0.5m
k ais 0.04
eais 2.54 cm
W
m C
Cu 4200
2
m
T1 400 C
T2 50C
Sus
No es peligroso
El área interna del aislante
El área enésima de una semiesfera
A1 2 r0
2
A2 2 r0 eais
2
A3 2 r0 2eais
Aiais 2 ro n eais
2
Univ. Erwin Choque Conde
2
2
m
El área media cuadrática del aislante
.
An 2 r0 ( n 1 )eais
2
2
Aiais
m 2 ro
El área externa del aislante
2
Amaisl Aiais Aeais 2 ro n ro eais
2
Página 38
Q
T
n eais
T1 T2 2 k ais ro2 n ro eais
k ais Amaisl
87.96459
n eais
ño
k W hr 0.68Sus 24hr 300 dia
Cv Q
4.896 Q
k hr k W hr dia a
Cf
Cu A ( n )
a
Cu
a
9.84252
n
0.5
W
ño
Sus
a
2
2 r0 ( n 1 ) eais 5277.87566 [ 0.5 ( n 1 ) 0.0254 ]
2
n Q(W )
Cv(Sus/año) Cf(Sus/año) Cfac(Sus/año) CT(Sus/año)
1
909,775531
4454,261 1319,46892
1319,46892 5773,72992
2
476,87891
2334,7992
1456,932
2776,4009
5111,2001
3
4
332,58004
260,430604
1628,31188 1601,2053
1275,06824 1752,28871
4377,60624
6129,89495
6005,91812
7404,96319
El espesor óptimo es:
eopt n eais 2 0.0254 0.0508 m
Univ. Erwin Choque Conde
Página 39
SUPERFICIES ALETADAS
38. Un horno semiesférico esta construido con ladrillo refractario cuyo radio externo es 0.5m se aísla
2
con un material k=0.04 W / m º C de 2.54 cm de espesor cuyo costo unitario es de 4200. Sus / m
Hallar el espesor optimo técnico económico si el horno es calentado eléctricamente con un costo de
0.68 $us / kWh el aislamiento tiene un tiempo de vida de 5 años, el trabajo del horno es de 24
horas al día y 300 días al año, la temperatura externa del ladrillo es 400ºC y la externa del aislante
tiene que ser tal que no sea un peligro para los trabajadores.
DATOS:
Tw 340 K
n 8
T
L 40mm
T 300 K
W
h amb 8
2
m K
t 0.4mm
h
H 3mm
k 175
W
m K
CALCULAR:
Q (W)?
El área transversal
Perímetro de la aleta
P 2 ( H t )
La relación "m":
m1
t
Lc L
2
1
m1 16.095
m
k At
m
Lc 0.0402 m
El área de cada aleta es:
El rendimiento de la aleta
6 2
Longitud corregida:
h amb P
tanh m1 Lc
At 1.2 10
At t H
P 0.0068 m
Aal 2.732 10
Aal 2 H Lc 2 L t
0.8804
4 2
m
m1 Lc
El calor para cada aleta
Qalt Aal h amb Tw T
El calor para el total de las aletas
Qtalt n Qalt
Qtalt 0.6158 W
Qalt 0.077 W
39. De una pared sobre sale una varilla de cobre larga y delgada de k=200 W / m º C y diámetro de 0.5
p lg. El extremo de la varilla que esta en contacto con la pared se mantiene a 358ºC. La
superficie lateral disipa calor por convección al aire que se encuentra a 25ºC cuyo coeficiente de
2
transferencia de calor es 15 W / m º C determinar a) Distribución de temperatura b) La tasa de
flujo de calor que disipa desde la varilla hacia el aire que rodea. c) Que largo deben tener las
DATOS:
varillas para suponer longitud infinita.
T
L
h
k 200
D
T1
W
m C
D 0.5in
h 15
T1 358 C
T1 25C
W
2
m C
Univ. Erwin Choque Conde
Página 40
Perímetro de la aleta
P D
El área transversal
At
4
D
2
h P
ma
La constante m
P 0.0399 m
k At
At 1.2668 10
4 2
m
1
ma 4.8603
m
El modelo matemático de la distribución de temperatura en una aleta
d
2
2
2
( x ) ma ( x ) 0
( x ) T( x ) T1
dx
Una de las soluciones es:
( x ) T( x ) T1 C1 e
ma x
C2 e
ma x
T( x ) C1 e
ma x
C2 e
ma x
T1
Por condición de frontera
T( X )
X 0
T1 C1 * e 0*ma C 2 * e 0*ma T1 C1 C 2 T1
Por otra condición (varilla larga)
x
T( X )
X
T ( ) T1
T C1 * e *ma C 2 * e *ma T1
C1 e
ma
C2
e
ma
0
C1 0
C2 T1 T1
a) La distribución de temperatura
T( x ) T1 T1 e
ma x
T1
x 0m 0.1m 2m
400
300
T( x ) 200
100
0
0
0.5
1
1.5
2
x
b)
c)
Q
h P k At T1 T1
tanh ma Lc 0.99
Univ. Erwin Choque Conde
Q 41.0044 W
L
tanh ( 0.99 )
ma
1
L 0.5445 m
Página 41
40. Una barra de acero hexagonal k=40 W / m º C es de 3 cm de lado y 23 cm de longitud esta
siendo probado para futuras aplicaciones como aleta. La base de la barra de acero se mantiene a
90ºC El otro extremo esta completamente aislado. Aire se hace circular perpendicularmente al eje
de la barra a una velocidad de 5 m / s a una temperatura de 27ºC con un coeficiente de
convección de 20 W / m º C . El calor específico del acero es de 0.56 kJ / kg º C calcular: a) La
distribución de temperatura b) La eficiencia de la barra y c) El flujo de calor a través de las
paredes laterales de la barra.
2
DATOS:
h
k 40
T
W
T 27 C
W
h 20
2
m C
m C
a 3cm
L 23cm
Tw 90C
L
a
El perímetro de la aleta
El área transversal es:
at
mh
a)
b)
3
2
2
a 3
P 6 a
2
a t 0.0023 m
P 0.18 m
El área de la aleta
h P
k at
1
mh 6.204
m
tanh L mh
2
Aal 0.0414 m
Aal P L
0.6244
L mh
Qdis Aal h Tw T
Qdis 32.5735 W
41. En un proceso químico la transferencia calorífica de una superficie al agua se aumenta mediante
cierto numero de aletas finas de aluminio k=204 W / m º C cada uno con espesor de 2 mm y una
longitud de 50 mm se cubre a la aleta metálica con una capa de plástico k=0.5 W / m º C de 0.1
mm de espesor, para impedir la ionización del agua los extremos de las aletas están encajados
en una superficie aislada la temperatura de la base en la aleta es de 80ºC, la temperatura media
del agua es de 20ºC y un coeficiente de transferencia de calor entre el agua y el revestimiento de
2
plástico es de 0.2 W / m º C . Determinar a) La distribución de temperatura en la aleta b) La
temperatura en la extremidad de la aleta c) La eficiencia de la aleta d) El calor de transferencia.
DATOS:
k 204
W
m C
t 2mm
Univ. Erwin Choque Conde
H 1m
Tw 80C
T 20C
L 50mm
k is 0.5
eis 0.1mm
W
m C
h am 0.2 10
3 W
2
m C
Página 42
Aplicamos la analogía eléctrica
1
eais
hT
k ais
1
h mod
h am
1
eis
k is
Equivalencia
h mod 192.30769
1
W
2
m C
h am
El área transversal de la aleta
2
Atra 0.002 m
Atra H t
Perímetro de la aleta
Pv 2 ( t H )
Pv 2.004 m
La constante
mv
h mod Pv
k Atra
1
mv 30.7339
m
Modelo matemático de la distribución de temperatura en una aleta
d
2
2
2
( x ) mv ( x ) 0
( x ) T( x ) T1
dx
Una de las soluciones es:
( x ) T( x ) T C1 e
mv x
C2 e
Por condición de frontera
mv x
T( X )
T( x ) C1 e
X 0
Tw
mv x
C2 e
mv x
T
C1 C2 Tw T
Por otra condición (extremo adiabático)
T
x
X L
0
C1 C2 e
2 m v L
Tw T
C2
e
e
T( x ) C1 e
mv ( x )
C2 e
mv x
2 m v L
T
C2 57.3469 C
1
Tw T
C1
a) La distribución de temperatura
2 m v L
e
2 m v L
1
C1 2.6531 C
x 0m 0.005 m 0.05 m
80
70
T( x ) 60
50
40
0
0.02
0.04
0.06
x
b)
x L
c)
v
d)
Qvr
T( x ) 44.6696 C
tanh mv L
mv L
v 0.5932
h mod Pv k Atra Tw T tan mv L
Univ. Erwin Choque Conde
4
Qvr 2.2053 10 W
Página 43
42. Una varilla de diámetro D=25 mm y conductividad térmica k=60 W / m º C sobresale
normalmente de la pared de un horno que esta a 200ºC y esta cubierta de un aislante de espesor
200 mm . La varilla esta soldada a la pared del horno y se usa como soporte para cargar cables
de instrumentación. Para evitar que se dañen los cables, la temperatura de la varilla en la
superficie expuesta, To debe mantenerse por debajo de un limite de operación especifico
Tmax=100ºC. La temperatura del aire ambiental es 25ºC, y el coeficiente de convección es h=15
W / m 2 º C . a) Derive la expresión de temperatura. b) Calcular el flujo de calor.
DATOS:
T1
aislante
Dv 25mm
hr
T2w
k v 60
T1w
Kv
T2w 100 C
T1 25C
W
m C
h r 15
T1w 200 C
W
2
m C
Lv 0.3m
Laisl 200 mm
Lais
Lv
El área transversal de la varilla
2
Atv
Dv
4
Atv 4.9087 10
4 2
m
El calor transferido por conducción de la varilla será:
Atv k v
Qkv
T1w T2w
Laisl
Perímetro de la aleta
Pv Dv
Qkv 14.7262 W
Pv 0.0785 m
La constante
mr
h r Pv
1
mr 6.3246
m
k v Atv
Modelo matemático de la distribución de temperatura en una aleta
d
2
2
2
( x ) mr ( x ) 0
( x ) T( x ) T1
dx
Una de las soluciones es:
( x ) T( x ) T1 C1 e
Por condición de frontera
T( X )
X 0
mr x
C2 e
T2 w
mr x
C1 e
mr Laisl
T( x ) C1 e
C2 e
mr Laisl
mr x
C2 e
mr x
T1
T2w T1
Por otra condición (extremo adiabático)
T
x
X Lv
0
Univ. Erwin Choque Conde
C1 0
C2 T2w T1 e
mr Laisl
Página 44
a) La distribución de temperatura será:
Qkv
T1 x1 T1w
x
k v Atv 1
T2w T1 e
T2 x2
x1 0m 0.1mm 0.2m
m r Laisl x2
T1
x2 0.2m 0.21m 0.7 m
200
150
100
T2x2
T1 x1
50
0
0
0.2
0.4
0.6
0.8
x1 x2
b) El calor transferido por la aleta
Qah
h r Pv k v Atv T2w T1 tanh mr Lv
Qah 13.356 W
43. Un tubo de acero k=45. W / m º C de 2” de diámetro exterior mediante la superficie de la pared
exterior a 100ºC se propone aumentar la rapidez de transferencia de calor por medio de la adición
de 12 aletas longitudinales de 2.5 mm de espesor y 20 mm de longitud a la superficie exterior
del tubo. El aire circundante se encuentra a 25ºC y el coeficiente de transferencia de de calor es de
2
25 W / m º C calcular el incremento de calor.
DATOS:
k a 45
L
m C
La 20mm
d e 2in
h
t
ta 2.5mm
W
T
T1 25C
W
h a 25
2
m C
Tw 100 C
Na 12
Ha 1m
2
Atra 0.1596 m
El área de transferencia de
calor sin aletas
Atra d e Ha
El calor transferido sin aletas
Qsa Atra h a Tw T1
Longitud corregida
ta
Lce La
2
Lce 0.0213 m
El área de las aletas
Aa Na 2 Ha Lce
Aa 0.51 m
Univ. Erwin Choque Conde
Qsa 299.2367 W
2
Página 45
2
El área libre de aletas
Ala d e Ha Na ta Ha
Ala 0.1296 m
El área total
ATa Aa Ala
ATa 0.6396 m
El área transversal de la aleta
At1 Ha t a
At1 0.0025 m
El perímetro de la aleta
Pa 2 Ha ta
La relación
mal
El rendimiento de la aleta
a
2
2
Pa 2.005 m
h a Pa
1
mal 21.1082
m
k a At1
tanh mal Lce
mal Lce
Aa
'a 1
1 a
ATa
El rendimiento al área ponderada
a 0.9379
'a 0.9505
El calor transferido por las aletas
Qa a Aa h a Tw T1
El calor transferido por la superficie
libre de aletas
QLa Ala h a Tw T1
El calor transferido total
QTT Qa QLa
Qa 896.8913 W
QLa 242.9867 W
QTT 1139.878 W
Otro método para el calor transferido
QaT 'a ATa h a Tw T1
%Q
QaT Qsa
QaT 1139.878 W
%Q 280.92854 %
Qsa
44. A la superficie exterior de un tubo de 32 mm de diámetro exterior se fijan aletas longitudinales de
sección transversal rectangular. El tubo y las aletas tienen una conductividad de 200 W / m º C las
aletas tienen un espesor de 3 mm y 6.6 mm de longitud. La relación de superficie de aletas a la
superficie total de transferencia de calor es del 70% los coeficientes de transferencia de calor de
2
2
los fluidos interior y exterior son hi=49 W / m º C y he=4.9 W / m º C . Determinar el flujo de calor
por metro de longitud de tubo cuando la diferencia de temperatura entre los fluidos interior y
exterior es de 90ºC (Despreciar la resistencia del tubo).
t
L
T 90C
Lf 6.6 mm
d 32mm
Aa
k f 200
H
W
m C
t f 3mm
AT
0.7
h i 49
h e 4.9
W
2
m C
Hf 1m
W
2
m C
Longitud corregida
tf
Lc Lf
2
Univ. Erwin Choque Conde
Lc 0.0081 m
Página 46
El área de las aletas
Aa N 2 H Lc
t
L
El área libre de aletas
Ala d Hf N t f Hf
El área total
hi
Aa
AT Aa Ala
0.7
he
El número de aletas
0.7 d Hf
N
2 0.3 Lc Hf 0.7 t f Hf
N 10
El área interna
N 10.1109
2
Ala d Hf N t f Hf
Ala 0.0705 m
Aa N 2 Hf Lc
Aa 0.162 m
2
Ai 0.1005 m
Ai d Hf
2
El área total
2
AT 0.2325 m
AT Aa Ala
El perímetro de la aleta
Pf 2 Hf t f
El área transversal de la aleta
Atf Hf t f
La relación
mf
El rendimiento de la aleta
f
Qf
h i Ai
2
Atf 0.003 m
1
mf 4.0475
m
k f Atf
tanh mf Lc
f 0.9996
mf Lc
'f 1
T
1
Pf 2.006 m
h e Pf
El rendimiento referido al área global externa
El calor transferido
Aa
AT
1 f
'f 0.9998
Qf 83.2658 W
1
'f AT h e
45. Se considera un tubo calefactor de 2” de diámetro interior y 1/8” de espesor donde circula agua por el
interior y el tubo es de cobre k=380 W / m º C se propone aumentar la transferencia de calor entre el
agua y el medio ambiente (Ti-Te=100ºC) para el cual se propone aumentar aletas de cobre en el tubo
solo en el interior, solo en el exterior, en ambos lados. Las aletas son longitudinales y rectangulares de
1.27 mm de espesor, 10 mm de longitud y espaciados 12.7 mm entre centros. ¿Cuál es el
porcentaje de aumento de transferencia de calor que se puede lograr poniendo en la tubería con aletas
en a) Lado del agua b) Lado de aire c) Ambos lados de la tubería?. Se pueden tomar los coeficientes
2
del lado del aire y del agua a 11.39 y 255.15 W / m º C respectivamente.
DATOS:
d i 2in
et
1
8
in
d e d i 2 et
Univ. Erwin Choque Conde
t 1.27 mm
La aleta
Longitud corregida
L 10mm
H 1m
d e 0.0571 m
t
Lc L
2
Lc 0.0106 m
Perímetro de la aleta
Página 47
S 12.7 mm
k 380
P 2 ( H t )
T 100 C
W
El área transversal
m C
W
h ag 255.15
P 2.0025 m
h air 11.39
2
m C
W
2
At 0.00127 m
At t H
2
m C
El área interna y externa sin aletas
2
Ai d i H
Ai 0.1596 m
Ae d e H
Ae 0.1795 m
2
El calor transferido sin aletas
T
Qsa
1
h ag Ai
Qsa 194.7195 W
1
h air Ae
a) Aletas en el interior del tubo (agua)
Para el número de aletas en el interior
n i S d i
di
ni
n i 12.5664
n i 13
S
t
hi
Área de las aletas interiores:
Aai n i 2 H Lc
he
L
2
Aai 0.2765 m
Área libre de aletas interior
2
ALai 0.1431 m
ALai d i H n i t H
El área total de transferencia de calor interno
Ati Aai ALai
Entonces la constante:
mi
La eficiencia de la aleta interior:
i
Qai
S
n e S d e
n e 14.1372
i 0.9619
'i 0.9749
T
1
Qai 200.5686 W
1
h air Ae
t
L
n e 14
Área de las aletas exteriores
Aae n e 2 H Lc
tanh mi Lc
'i Ati h ag
b) Aletas en el exterior del tubo (aire)
ne
1
mi 32.5383
m
k At
El calor transferido con aletas internas
de
h ag P
mi Lc
Aai
'i 1
1 i
Ati
Eficiencia ponderada al área interior
Para # aletas en el exterior
2
Ati 0.4196 m
hi
2
Aae 0.2978 m
he
Área libre de aletas "exterior"
ALae d e H n e t H
Univ. Erwin Choque Conde
2
ALae 0.1618 m
Página 48
El área total de transferencia de
calor externo
Ate Aae ALae
Entonces la constante ¨m¨ en las aletas
exteriores
me
La eficiencia de la aleta exterior
e
2
Ate 0.4595 m
h air P
1
me 6.8748
m
k At
tanh me Lc
me Lc
Aae
'e 1
1 e
Ate
Eficiencia ponderada al área exterior
El calor transferido con aletas externas
e 0.9982
'e 0.9988
1
Qae 463.3276 W
T
Qae
1
Ai h ag
'e Ate h air
c) El calor transferido con aletas internas y externas
T
Qaie
t
L
1
'i Ati h ag
t
1
'e Ate h air
Qaie 497.8759 W
hi
L
he
a)
b)
c)
Q i
Q e
Q ie
Qai Qsa
Q i 3.0039 %
Qsa
Qae Qsa
Qsa
Qaie Qsa
Qsa
Q e 137.9462 %
Q ie 155.6888 %
46. Un calentador de aire consiste en un tubo de acero (20 W / m º C ), con radios interno y externo
r1=13 mm y r2=16 mm , respectivamente y ocho aletas longitudinales fabricadas integralmente,
cada una de espesor t =3 mm . Las aletas se extienden a un tubo concéntrico, que tiene radio
r3=40 mm y aislado en la superficie externa. Agua a temperatura Ti =90ºC fluye a través del
tubo interno, mientras que aire T0 =25ºC fluye a través de la región anular formada por el tubo
concéntrico más grande. a) Si hi=5000 y ho=200 ¿Cuál es la transferencia de calor por unidad de
longitud?
DATOS:
k n 20
W
m C
r1 13mm
r2 16 mm
r2
Ti
r3
r1
hi
T 0
ho
Ti 90C
To 25C
hi 5000
ho 200
Univ. Erwin Choque Conde
W
2
m C
Hi 1m
n 8
2
m C
r3 40mm
t 3mm
W
Ln r3 r2
Ln 0.024 m
Página 49
2
Ai 0.0817 m
Ai 2 r1 Hi
El área interna
Am
El área media del tubo
2 Hi ( r2 r1 )
2
Am 0.0908 m
r2
ln
r1
El perímetro de la aleta
Pn 2 ( Hi t )
Pn 2.006 m
El área transversal de la aleta
At Hi t
At 0.003 m
El área de la aleta
An 2 n Hi Ln
An 0.384 m
El área libre de la aleta
ALa 2 r2 Hi n t Hi
ALa 0.0765 m
El área total de transferencia de
calor
Atn An ALa
Atn 0.4605 m
mn
Entonces la constante "m" en las aletas
exteriores
al
La eficiencia de la aleta
2
2
2
2
ho P n
1
mn 81.772
m
k nAt
tanh mn Ln
al 0.4898
mn Ln
An
'al 1
1 al
Eficiencia al área ponderada
Atn
Ti To
El calor transferido con aletas externas
Qa
1
r2 r1
1
Ai hi
Am k n
'al Atn ho
'al 0.5746
Qa 2826.601 W
47. Se calienta agua sumergiendo tubos de cobre con pared delgada de 50 mm de diámetro en un
tanque y haciendo pasar gases calientes de combustión (Tg=750K) a través de los tubos. Para
reforzar la transferencia de calor al agua, se insertan en cada tubo cuatro aletas rectas de sección
transversal uniforme, para formar una cruz. Las aletas tienen un espesor de 5 mm y también
están fabricadas de cobre (k=400 W / m º C ). Si la temperatura de la superficie de tubo es
2
Ts=350K y el coeficiente de convección del lado del gas es hg=30 W / m º C , ¿Cuál es la
transferencia de calor al agua por metro de longitud del tubo?
hg
Ts
DATOS:
Tg
Dg 50mm
Tg 750 K
t
t g 5mm
H
k t 400
W
Hg 1m
Ts 350 K
h g 30
W
2
m K
m K
La longitud de la aleta
Lg
D
Univ. Erwin Choque Conde
Dg tg
2
Lg 0.0225 m
Página 50
2
ALa 0.1371 m
Área libre de aletas
ALa Dg Hg 4 t g Hg
El calor transferido del área
libre de aletas
Qla ALa h g Tg Ts
Qla 1644.9556 W
Área de las aletas
Aag 4 2 Hg Lg
Aag 0.18 m
El perímetro de la aleta
Pal 2 Hg t g
El área transversal de la aleta
Aat t g Hg
Entonces la constante m
mg
La eficiencia de la aleta
g
El calor transferido por las aletas
Qal g Aag h g Tg Ts
Otro método
2
Pal 2.01 m
2
Aat 0.005 m
h g Pal
1
mg 5.4909
m
k t Aat
tanh mg Lg
g 99.4943 %
mg Lg
Qal1 4 h g Pal k t Aat tanh mg Lg Tg Ts
El calor total será:
Univ. Erwin Choque Conde
Qt Qla Qal1
Qal 2149.077 W
Qal1 2159.8224 W
Qt 3804.778 W
Página 51
FLUJO BIDIMENSIONAL
48. Un conducto hueco de sección transversal cuadrada de dimensiones internas de 10*10 cm esta
construido con ladrillo de k=0.21 W / m º C con un espesor de 10 cm . En condiciones de equilibrio
la temperatura interna y externa es de 300ºC y 30ºC respectivamente. Estimar la perdida de calor a
través del conducto.
DATOS:
Tw1 300 C
Tw2 30C
30ºC
300ºC
10cm
W
k L 0.21
2
m C
x 5cm
1
x y
En el nodo 1
2
30 300 2 T2 4 T1 0
En el nodo 2
5cm
3
T1 30 T1 T3 4 T2 0
En el nodo 3
10cm
2 30 2 T2 4 T3 0
La solución de las tres ecuaciones es:
T1 153.75 C
T2 142.5 C
El calor que entra en la pared
T3 86.25 C
Tw1 T1
Tw1 T2
2
W
QZe 387.45
m
QZe 8k L
El calor que sale de la pared
T1 Tw2
T2 Tw2 T3 Tw2
2
QZs 8k L
W
QZs 387.45
m
49. Hallar el flujo de calor de una chimenea cuyo interior fluye gases de combustión de tal manera que
en el interior tiene 371ºC y la superficie exterior esta a 38ºC las dimensiones de la chimenea es de
60*30 cm y el espesor es de 30 cm esta construido de ladrillo de conductividad k=1.2 W / m º C .
DATOS:
2
W
T1w 371 C
k c 1.2
T2w 38C
y 15cm
m C
38ºC
371ºC
30cm
Q
1
2
5
6
5
4
Univ. Erwin Choque Conde
T
n
3
Q
Z
A x y
El área
15cm
60cm
k A x
(k T )
n
Página 52
Analizando en el nodo 1
Resolviendo estas ecuaciones se tiene:
2 T2 38 371 4 T1 0
T1 190.69 C
Analizando en el nodo 2
T1 371 38 T3 4 T2 0
T2 176.88 C
Analizando en el nodo 3
T2 T4 2 38 4 T3 0
T3 107.84 C
T4 178.48 C
Analizando en el nodo 4
T3 T5 371 38 4 T4 0
T5 197.06 C
Analizando en el nodo 5
T4 T6 371 38 4 T5 0
T6 200.72 C
Analizando en el nodo 6
2 T5 371 38 4 T6 0
El calor que entra al conducto
T1w T6
T1w T1
T1w T2 T1w T4 T1w T5
2
2
W
QZi 3532.2
m
QZi 4k c
El calor que sale del conducto
T6 T2w
T1 T2w
T2 T2w 2 T3 T2w T4 T2w T5 T2w
2
2
QZe 4k c
W
QZe 3531.864
m
50. Una chimenea de sección cuadrada de 20 cm *20 cm esta construida con ladrillo k=0.81 W / m º C
de 10 cm de espesor, los gases de la chimenea mantiene la temperatura interior de la chimenea a
280ºC el exterior esta compuesto a un ambiente cuya temperatura es de 23ºC y un coeficiente de
2
convección de 10 W / m º C . Encontrar el flujo de calor a través de la chimenea.
DATOS:
w 10cm
T
2
k 0.81
280ºC
1
2
3
4
h
W
m C
Tw1 280 C
5
T 23C
6
h 10
W
2
m C
7
Nodo 1
2 T2 280 T4 4 T1 0
Nodo 2
T1 T5 T3 280 4 T2 0
Nodo 3
2 T6 2 T2 4 T3 0
Nodo 4
2 T1 2 T5
2 h w
k
h w
T 2
2 T4 0
k
Univ. Erwin Choque Conde
Nodo 5
2 T2 T4 T6
2 h w
T 2
h w
k
k
2 T5 0
Nodo 6
2 T3 T5 T7
2 h w
k
T 2
h w
k
2 T6 0
Nodo 7
T6 T6
2 h w
k
T 2
h w
k
1 T7 0
Página 53
Resolviendo estas ecuaciones
T1 172.702 C
T2 161.566 C
T3 112.0 C
T4 87.497 C
T5 81.919 C
T6 62.345 C
T7 40.607 C
El calor que entra en la pared
Tw1 T1
Tw1 T2
2
W
QeZ 139.38723
m
QeZ k
El calor que sale de la pared
T1 T4
T2 T5 T3 T6
2
QsZ k
W
QsZ 139.24265
m
51. Determine el flujo de calor por unidad de profundidad en el segmento circular de la figura siguiente.
Supóngase que la conductividad térmica del material es de 0.7 W / m º C . Una de las superficies es
isotérmica y las otras se encuentran a 100ºC y 25ºC.
DATOS:
k 0.7
W
r1 50cm
m C
r2 54cm
T2 100 C
Lw 1m
T1 25C
Por balance de energía
Eentra Egenerada Esale Ealmacenada
Condiciones
Eentra Q
Esale Q
Egenerada 0
d
Q d
d
d
Q d m Cp T
d
Q Q
Ealmacenada m Cp T
T
dT
r
d
r1
V r Lw r1 d
dT
dT
Q k A
k r Lw
dx
r1 d
m V
dT
dT
dT
d
k r Lw
d V Cp d r Lw r1 d Cp d
r1
d
d
1 d d
dT
k T Cp
2 d d
d
r1
Para estado estable
Su solución
d d
k T 0
d d
T
( T2 T1)
Q k A
C1
T
C2
k
dT
T2
dT
r1 d
k
Univ. Erwin Choque Conde
Por condiciones de frontera
d
( r1 r2 ) Lw
r1
( T1 T2)
C2 T1
C1
k
( T2 T1)
( T2 T1)
Q k
( r1 r2 ) Lw
r1
( T1 T2)
Q 1.3369 W
Página 54
CONDUCCIÓN EN RÉGIMEN TRANSITORIO
52. Se tiene una placa de 10 cm de espesor a una temperatura uniforme de 20ºC que se introduce en un
medio a 100ºC adquiriendo instantáneamente esta temperatura. Determinar mediante técnicas
numéricas el tiempo necesario para qué el plano medio den la pieza alcance una temperatura de
60ºC.
T
DATOS:
T1
T1
10cm
2
T2 100 C
T2
dX
X
T1 20C
6 10
T 60C
dX
2
6 m
s
En la ecuación general de la conducción para coordenadas rectangulares y sin generación
d
2
dx
2
T
d T
d
1
Ta 2T Tb
2
X
2
dx
2
T
d
T
d
T1 T
X
d
1
2
Ta 2T Tb
X
2
T
T1 Ta Tb
dT
T1 T
T1
2
1
2
X
d
0
ln
2
T2 T1 X 2
T2 T
X
2
2
ln
T2 T1
T2 T
144.40566 s
53. Se hace pasar repentinamente una corriente eléctrica de 5 amperios por un conductor eléctrico de
cobre de 1 mm de diámetro con una temperatura ambiente de 25ºC. Calcule la temperatura de la
superficie del conductor a los 40 s suponiendo que el coeficiente de transferencia de calor es de
25 W / m º C . Las propiedades del conductor son: k=386 W / m º C , c=383 J / kg º C y =8950
2
kg / m
3
e
=1.8E-8 * m .
DATOS:
T
I 5A
h
T
d
I=5A
L
h
Bi
d 1mm
Cp 383
T 25C
8950
t 40s
El número de Biot
d
k 386
h 25
Bi 3.23834 10
5
J
kg C
kg
3
m
W
e 1.8 10
2
m C
2
W
m C
8
m
Bi 0.1
k
Balance de energía en el volumen de control
Eentra Egenerado Esale Ealmacenado
dT
0 g V A h T T m Cp
dt
g V h A V Cp
Univ. Erwin Choque Conde
dT
dt
d
dt
h A
V Cp
T T
g
Cp
0
d
dt
dT
dt
....1 )
Página 55
La solución general
h A
g C1 e
Cp V
La solución particular
t
p C2 C3 t
La solución total
h A
T g p C1 e
Cp V
t
C2 C3 t
Por condiciones de frontera
C2
C3 0
( o ) 0
g V
h A
h A
g V
g V
T T
e
h A
h A
C1
Cp V
t
g V
h A
g V
h A
h A
t
Cp V
1 e
La generación de energía por unidad de volumen
V
A
2
I e
g
d 2
4
2
4
2
d L
d h
d
4
5 W
g 7.29513 10
3
m
g d
T T
4 h
4 h
t
Cp d
1 e
T 30.02396 C
54. Una esfera de aluminio k=239 W / m º C Cp=902 J / kg º C y =2700 kg / m
3
con un peso de 6
kg y una temperatura inicial de 250ºC, se sumerge bruscamente en un fluido a 25ºC. El
2
coeficiente de transferencia de calor por convección es 49 W / m º C . Estime el tiempo requerido
para enfriar el aluminio a 85ºC
DATOS:
2700
kg
3
h e 49
m
r
h
k e 239
T 25C
Cp 902
Tf 85C
Ve
me
2
m C
me 6 kg
T
Ti 250 C
El volumen de la esfera
W
W
m C
J
kg C
El radio de la esfera
3
3
Ve 0.00222 m
r
3 Ve
4
r 0.08095 m
Analizamos el número de Biot
Bi
h e r
ke
Bi 0.1
Bi 0.0166
Entonces se aplica el método de
resistencia despreciable
Univ. Erwin Choque Conde
La longitud característica para una esfera
r
Lc
3
Lc 0.02698 m
Página 56
Entonces el número de Biot será:
Bi
h e Lc
Bi 0.00553
ke
La difusividad térmica es:
El número de Fourrier
2
ke
9.81358 10
Cp
5m
Fo
s
Lc
2
La variación de la temperatura en función del tiempo
Tf T
e
Bi Fo
Ti T
El tiempo que tardará en llegar a la temperatura "Tf" es:
Lc
2
Bi
Tf T
Ti T
ln
1772.70783 s
55. Un alambre de diámetro D=1 mm se sumerge en un baño de aceite de temperatura 25ºC. El
alambre tiene una resistencia eléctrica por unidad de longitud de R=0.01 / m. Si fluye una
2
corriente de I=100 Amperios por el alambre y el coeficiente de convección es h=500 W / m º C
¿Cuál es la temperatura de estado estable del alambre? Del tiempo que se aplica la corriente,
¿Cuánto tiempo tarda el alambre en alcanzar una temperatura que esta a 1ºC de distancia del
3
valor de estado estable? Las propiedades del alambre son c=500 J / kg º C y =8000 kg / m
k=20 W / m º C
Datos:
T.8
RL 0.01
d 1mm
h
I
d
h 500
W
k 20
T 25C
m
I 100 A
2
m C
Rl
cp 500
W
8000
J
kg
3
m
kg C
m C
Analizamos el número de Biot:
Bi h
(d )
Bi 0.00625
4k
Por balance térmico
0.00625 0.1
2
2
d h T T I RL
I RL
T T
d h
T 88.66198 C
Sin considerar la transferencia de calor por radiación y cambio de temperatura en el alambre
Egenerado Esale Ealmacenado
dT
2
I RL d h T T cp At
d
2
dT
d
I RL
d 2
cp
4
4 h
T T
cp d
2
I RL
d cp T T d h
ln
4 h
2
I RL
Ti T
d h
Univ. Erwin Choque Conde
T T 1C
T 87.66198 C
Ti 25C
2
I RL
T T
d h
2
4 h
e
d cp
I RL
Ti T
d h
8.30717 s
Página 57
2
56. Una esfera de vidrio de cuarzo tiene una difusividad térmica de 9.5E-7 m / s un diámetro de 2.5
cm y una conductividad térmica de 1.52 W / mº C . La esfera esta inicialmente a una temperatura
de 25ºC y se somete de repente a un medio de convección a 200ºC. El coeficiente de transferencia
2
de calor por convección es de 10 W / m º C . Calcule las temperaturas en el centro y en un radio
de 6.4 mm después de 4 min
DATOS:
9.5 10
r
h
2
7 m
s
d 2.5cm
W
k 1.52
m C
T
4min
T 200 C
r 0.0125 m
Bi
Entonces el número de Biot será:
h r
k
2
Bi 0.08224
k
Entonces se aplica el método de
resistencia despreciable
El número de Fourier
Fo
Bi 0.02741
d
r
Bi 0.1
h Lc
2
m C
T0 25C
La longitud característica para una esfera
r
Lc
Lc 0.00417 m
3
Bi
W
h 10
Lc
Fo 13.1328
2
La variación de la temperatura en función del tiempo
Tf T
e
Bi Fo
Tf T0 T e
Bi Fo
T
Ti T
La temperatura será constante en toda la esfera por Bi<0.1
Tf 77.90664 C
57. Se desea evaluar un tratamiento térmico para un material especial, para tal fin se tiene una esfera
de 5 mm de radio en un horno a 400ºC. Repentinamente se extrae la esfera y se somete a dos
procesos de enfriamiento :
Si se enfría en aire a 20ºC por un período “ta” hasta que el centro alcanza una
temperatura critica de 335ºC. En este caso, el coeficiente de transferencia de calor es
2
igual a 10 W / m º C .
Después de que la esfera logra esta temperatura critica, se enfría en agua a 20º con un
2
coeficiente de transferencia de calor igual a 2000 W / m º C hasta que su centro
alcanza 50ºC. Las propiedades del material son : k=20 W / m º C , c=1000 J / kg º C y
3
=3000 kg / m
a) Calcule el tiempo que debe permanecer la esfera en el aire.
b) Calcule el tiempo que debe permanecer la esfera en el agua.
DATOS:
T1
Tf
r
ha
T
k
Tf2
r 5mm
hb
T1 400 C
T 20C
ta
Univ. Erwin Choque Conde
tb
Tf 335 C
h a 10
k 20
W
h b 6000
2
m C
W
2
m C
W
m C
2
6.66 10
Tf2 50C
6 m
s
Página 58
La longitud característica
r
Lc
3
Lc 0.00167 m
El número de Biot
h a Lc
Bi c
Bi c 0.00083
k
Tf T
e
T1 T
Bi c 0.1
Bi Fo
Fo
a
Lc
a
Lc
2
Bi c
Tf T
T1 T
ln
a 93.8932 s
2
Para el segundo proceso
h b Lc
Bi c
Bi c 0.5
k
Bi c 0.1
El número de Biot definido ahora:
hb r
Bi
k
Bi 1.5
En tablas 5.1 de "transferencia de calor de Incropera
" ver anexo
1 1.1656
C1 1.1441
Fo
1
1
2
1 Tf2 T
C1 Tf T
ln
b Fo
r
Fo 1.82979
2
b 6.86858 s
58. Un ladrillo de 9*4.5*2.5 p lg (k=0.8 W / m º C , =5.11*E-7 m / s inicialmente a 21ºC se suspende
verticalmente en un horno grande donde el aire del ambiente se encuentra a 150ºC. Hallar las
temperaturas en los siguientes puntos al finalizar una hora a) Centro del ladrillo b) Cualquier
esquina del ladrillo c) En el centro de la cara 9*4.5 p lg. Para un coeficiente de convección de
2
2
6.188 W / m º C en todas sus caras.
DATOS:
Z
h
T
2*L3
2*L1
X
2*L2
Univ. Erwin Choque Conde
Y
L1
4.5in
L2
2.5in
L3
9in
2
2
2
Ti 21C
Tw 150 C
W
h 6.188
2
m C
L1 0.05715 m
L2 0.03175 m
L3 0.1143 m
k 0.8
W
m C
5.11 10
2
7 m
s
1hr
Página 59
Para la coordenada x
Para graficas ver Anexos (Graficas
en adelante)
El número de Biot
Bi x
h L1
k
El número de Fourier
Bi x 0.44206
Fo x
L1
Bi x
1
De graficas
2.26216
Yxo
Fo x 0.56324
2
1
T( 0 ) Tw
Ti Tw
Yxo 0.85
Para la coordenada y
Bi y
Fo y
De graficas
h L2
Bi y 0.24559
k
L2
Bi y
1
4.07189
Yyo
Fo y 1.82489
2
Para la coordenada z
Bi z
Fo z
h L3
Yyo 0.7
Ti Tw
De graficas
Bi z 0.88411
k
T( 0 ) Tw
Bi z
1
1.13108
Yzo
Fo z 0.14081
2
L3
a) La temperatura en el centro del ladrillo
T( 0 0 0 ) Tw
T( 0 ) Tw
Ti Tw
Yzo 0.9
Yxo Yyo Yzo
Ti Tw
T( 0 0 0 ) Yxo Yyo Yzo Ti Tw Tw
T( 0 0 0 ) 80.9205 C
b) La temperatura en cualquier esquina
T( L1 L2 L3 ) Tw
Ti Tw
Para
Yx( L1 )
Bi x
1
x
Para
Yy( L2 )
Bi y
x
Para
Yz( L3 )
Bi z
1
L1
YxL1 0.83
Yx( L1 ) Yxo YxL1
YyL2 0.86
Yy( L2 ) Yyo YyL2
YzL3 0.67
Yz( L3 ) Yzo YzL3
Yx( L1 ) 0.7055
4.07189
L2
1
L2
1
x
2.26216
L1
1
Yx( L1 ) Yy( L2 ) Yz( L3 )
Yy( L2 ) 0.602
1.13108
L3
L3
1
T( L1 L2 L3 ) Yx( L1 ) Yy( L2 ) Yz( L3 ) Ti Tw Tw
Yz( L3 ) 0.603
T( L1 L2 L3 ) 116.96301 C
c) La temperatura en el centro de la cara 9*4.5in
T( 0 L2 0 ) Tw
Ti Tw
Yxo 0.85
Yy( L2 ) 0.602
Yxo Yy( L2 ) Yzo
Yzo 0.9
T( xo L2 zo ) Yxo Yy( L2 ) Yzo Ti Tw Tw
Univ. Erwin Choque Conde
T( 0 L2 0 ) 90.59163 C
Página 60
59. Se tiene un cilindro de longitud 100 mm y de diámetro de 80 mm con una densidad de 7900
kg / m con un coeficiente de conductividad 17 W / mº C y una capacidad especifica de 520
J / kg º C y un coeficiente de convección h=450 W / m º C la temperatura inicial del cilindro es
3
2
de 300ºC y del medio ambiente es de 20ºC a) Desarrollar la temperatura en el medio del cilindro
pasado 3.min. b) a 50 mm del punto medio (axial) c) a 20 mm del punto medio (radial) d) a 40
mm y 50 mm del centro.
DATOS:
Lo
x
100 mm
Lo 0.05 m
D
r
r 0.04 m
2
2
D 80mm
h
T
k 17
W
m C
2*L
Cp 520
r
h 450
7900
J
kg C
3min
W
2
T 20C
Ti 300 C
La longitud característica para un cilindro
r
Lc
Lc 0.01429 m
r
2
Lo
Lc h
El número de Biot
Bi
k
3
m
m C
D
kg
T( r x )
Bi 0.37815
La difusividad térmica del cilindro es:
k
4.13827 10
Cp
a) T( 0 0 3min )
T( 0 0 3min ) T
Fo
Para una placa
Lp
Fo
Bi c
Lc
h Lc
Bi c
k
1
Bi p
2
h Lp
Bi p
k
1
Bi p
x
YoCilind 0.465
1.51111
YoPlaca 0.85
Fo 1.19182
2
T( 0 0 3min ) YoCilind YoPlaca Ti T T
b) Para T( 0 40mm3min )
T( 0 L 3min ) T
Grafica 1
para Placas
0.94444
Fo 0.46556
2
Lo
Lp
s
YoCilind YoPlaca
Ti T
Para el cilindro
Lc r
2
6 m
1
Lo
Lo
Ti T
YoCilind YL.Placa
1.51111
1
Yx( Lo ) 0.555
YL.Placa YoPlaca Yx Lo
Univ. Erwin Choque Conde
T( 0 0 3min ) 174.7 C
YL.Placa 0.47175
Página 61
T( 0 L 3min ) YoCilind YL.Placa Ti T T 0.65 0.47175 Ti T T
T( 0 L 3min ) 105.85 C
c) T( 20 0 3min )
T( 20 0 3min ) T
Ti T
Grafica 2
para cilindros
Bi c
1
x
Yro.Cilind Yo.Placa
0.94444
r
ro
0.5
Yr ro 0.88
Yro.Cilind YoCilind Yr ( r ) Yro.Cilind 0.4092
T( 20 0 3min ) Yro.Cilind Yo.Placa Ti T T
T( 20 0 3min ) 156.136 C
d) T( 20 50 3min )
T( 20 50 3min ) T
Ti T
Grafica 2
para cilindros
Bi c
1
x
ro
ro
YrCilind YL.Placa
0.94444
Grafica 1
para Placas
x
1
Lo
Lo
1
YrCilind YoCilind Yr ( r )
Bi p
Yr ro 0.88
Yro.Cilind 0.4092
1.51111
Yx( Lo ) 0.55
1
YL.Placa YoPlaca Yx Lo
YL.Placa 0.4675
T( 20 50 3min ) YrCilind YL.Placa Ti T T
T( 20 50 3min ) 76.43 C
Univ. Erwin Choque Conde
Página 62
CONVECCION
60. Un tubo metálico de 3 cm de diámetro externo que se encuentra a 160ºC se recubre con un
aislante de conductividad de 0.42 W / m º C si la temperatura del medio ambiente es de 20ºC,
Calcule la cantidad de calor perdida por metro de tubo para un espesor de aislante de 2 cm .
Propiedades del aire =1.17 kg / m
3
, Cp =1.006 kJ / kg º C =1.983E-5 kg / m * s, k=0.02624
W / mº C , Pr=0.708. Las constantes exponenciales para el numero de Nusselds son flujo laminar
C=0.47 y n=1/4 y para flujo turbulento es C=0.1 y n=1/3
DATOS:
Para el coeficiente de convección
k ais 0.42
Dc
e ais
eais 2cm
d 3cm
aislante
h
d
W
H 1m
m K
Tw ( 160 273 )K
160ºC
3
m
cp air 1006
J
kg K
air 1.983 10
T ( 20 273 )K
20ºC
kg
air 1.17
g 9.81
5 kg
m s
m
2
s
k air 0.02624
W
m K
pr air 0.708
1
0.00341
T
T Tw T
T 140 K
Dc d 2 eais
Dc 0.07 m
1
K
Lc Dc
El número de Grassofft
2
Gr
3
air Dc g T
air
2
Gr 5.59693 10
El área externa del aislante
2
Gr pr air 3.96263 10
Gr 10
Como
El área media logarítmica del aislante
Ae 0.21991 m
Ae Dc H
9
6
Am
H ( Dc d )
Dc
2
Am 0.14831 m
ln
d
6
Entonces es flujo laminar
1
Nu 0.47 Gr pr air
h
Nu k air
Lc
4
Nu 20.96977
h 7.86067
W
2
m K
El calor transferido es:
Q
eais
W
2
m K
T
Am k ais
Univ. Erwin Choque Conde
h 7.86067
Q 155.63145 W
1
Ae h
Página 63
61. Aire caliente con un flujo másico de 0.05 kg / s por un conducto metálico de espesor despreciable
no aislado de diámetro interno de 0.15m que atraviesa la sala de una casa que tiene una longitud
de 5m. El aire caliente entra a 103ºC y después de atravesar la sala el are sale a 77ºC se sabe
que el coeficiente de convección externa del medio ambiente que se encuentra a 0ºC es 6
W / m º C Calcule la temperatura de la superficie del conducto. Las propiedades del aire caliente
son: d=0.995 kg / m , =208.*10-3 N * s / m , k=0.03 W / m º C y Pr=0.7
2
3
2
w 0.05
T
W=0.05kg/s
Tc1
s
d 0.15 m
h
Tw
kg
d
Tc2
Tc1 103 C
L
Tc2 77 C
La temperatura media del fluido
Tm
Tc1 Tc2
2
Re
Numero de Reynolds
4 w
kg
3
m
208. 10
7 N s
2
m
k 0.03
W
m C
Pr 0.7
W
he 6
Tm 90 C
0.995
2
m C
T 0C
Re 20404.47988
d
1
Nu 0.027 Re
Numero de Nusself
El Coeficiente de convección interno
hi
0.8
Pr
3
Nu k
Nu 67.22181
h i 13.44436
d
Qhi Qhe
Balance de energía
A h i Tm Tw A h e Tw T
h i Tm
Tw
he hi
W
2
m C
Tw 62.22845 C
62. Agua a 100ºC fluye a través de una tubería horizontal de acero de 2” Nº40 (De=2.07” y Di=1.94” y k=0.145
W / mº C ) la cual se expone al aire atmosférico a 25ºC. la velocidad del agua es 25 cm / s . Calcule el
calor perdido de la tubería por metro lineal Tomar la ecuación para convección libre Nu C(Gr * Pr)
donde para el flujo turbulento c=0.47 y n=1/4 y para el flujo laminar C=0.1 n=1/3 Las propiedades del agua
3
2
tomar =998 kg / m , =2.945E-7 m / s , k=0.68 W / m º C ,cp=4.22 kJ / kg º C para el aire =1.17
n
kg / m , =1.57E-5 m / s, k=0.026 W / mº C , Cp=1.01 kJ / kg º C B=3.3E-3 1 / K
3
2
DATOS:
T1 ( 100 273 )K
De 2.07 in
Di 1.94 in
Propiedades del aire
Cpair 1.01 10
3
T2 ( 25 273 )K
cm
v 25
s
Propiedades del agua
J
kg K
Univ. Erwin Choque Conde
Cpag 4.22 10
3
J
kg K
Página 64
2
5 m
air 1.57 10
s
ag 2.94 10
W
k aire 0.026
aire 1.17
m K
3
m
3.33 10
s
m K
kg
ag 998
3 1
W
k ag 0.68
kg
2
7 m
3
m
K
La temperatura media de la pared
Tw
T1 T2
Tw 335.5 K
2
Xe De
El coeficiente de T.C. por convección externo (del aire)
3
Gra
2
g Xe aire Tw T2
Gra 722366.15538328
aire air
2
aire air Cpair
Prair
Prair 0.71357
k aire
Gra Prair 5.15455 10
Nu air C Gra Prair
h aire
5
< 1*E+9
Flujo laminar
C 0.1
n
n
Nu air 8.01796
k aire Nu air
h aire 3.96491
Xe
1
3
W
2
m K
El coeficiente de T.C. por convección interno (del agua)
v Di
Rea
Rea 41901.36054
ag
Prag
ag ag Cpag
k ag
Nu ag 0.027 Rea
h ag
Flujo turbulento
Prag 1.82088
1
0.8
Prag
k ag Nu ag
3
1
Nu ag 164.40186
h ag 2268.71635
Di
W
2
m K
La transferencia de calor es:
Qt
T1 T2
1
De h aire
1
W
Qt 49.02742
m
Di h ag
Univ. Erwin Choque Conde
Página 65
63. Un cubo de plata de 10 cm de lado se encuentra a 150ºC (emisividad 0.025) colgado en una
habitación a 25ºC si la temperatura se mantiene constante mediante una corriente eléctrica,
calcúlese: a) La potencia que habrá que suministrarle en vatios b) El porcentaje de calor perdido
debido a la radiación. Para el coeficiente de convección tomar : Plano o cilindro vertical
0.25
0.25
h 1.42T / L W / m 2 º C ; Placa caliente hacia arriba h 1.32T / L W / m 2 º C ; Placa
caliente hacia abajo h 0.61T / L
0.2
W / m º C
2
DATOS:
5.67 10
w 10cm
Tw 423 K
W
2
m K
4
0.025
T 298 K
T
150ºC
8
T Tw T
T 125 K
h
El área en un plano
2
Ap 0.01 m
Ap w w
Para la placa vertical
125
h v 1.42
0.01
0.25
W
h v 15.01467
2
m K
Qv h v Ap T
W
2
m K
Qv 18.76834 W
Para la placa superior
125
h s 1.32
0.01
0.25
W
2
m K
Qs h s Ap T
Para la placa inferior
h a 0.61
0.01
125
h s 13.9573
W
h a 4.0245
2
m K
Qa h a Ap T
El calor total transferido por convección
Qh 4 Qv Qs Qa
El calor por radiación
Qr 6 Ap Tw T
4
4
2
m K
Qs 17.44663 W
0.2
W
W
2
m K
Qa 5.03062 W
Qh 97.55061 W
Qr 2.05221 W
a) La potencia que suministra el cubo
N Qh Qr
b)
%P
Qr
N
Univ. Erwin Choque Conde
N 99.60282 W
%P 2.06039 %
Página 66
64. Se desea colocar un tubo de acero de 1.5 in de diámetro interior y espesor 0.2 in con superficie
exterior a 200ºC en aire a 20º. Se propone agregar aislante de 85% de magnesio (k=0.065
W / mº C ) para reducir las perdidas de calor en un 60% ¿Cuál debe ser el espesor del aislante
necesario? Se ha determinado que el coeficiente de convección varia de acuerdo con
h 4.6 * D 1 / 4 W / m 2 º C , donde D es el diámetro externo del aislante en metros.
DATOS:
Te
et
di
eais
de
dea
d i 1.5in
Te 200 C
k ais 0.065
et 0.2in
Lt 1m
x% 60%
W
m C
T 20C
El diámetro externo del tubo
d e d i 2 et
d e 0.04826 m
El área externa de transferencia
de calor del tubo
At d e Lt
At 0.15161 m
2
1
4
m 4 C
W
El coeficiente de convección
del tubo y el medio
h 1 4.6 d e
El calor disipado sin aislante
Q1 At h 1 Te T
Por condición del problema
con el aislante
El diámetro externo del
aislante
Q2 ( 1 x% ) Q1
7
W
h 1 9.81434
Q1 267.83708 W
Q2 107.13483 W
2
m C
d ea d e 2 eais
Am
El área media logarítmica
del aislante
d ea Lt d e Lt
d ea Lt
d e Lt
ln
2 eais Lt
ln 1
2 eais
de
El coeficiente de T.C. por convección del aislante y el medio
1
4
h 2. 4.6 d ea
1
4
1
4.6 d ea
4.6 d e 2 eais
4
El área de transferencia de calor por convección al medio
Ae d ea Lt d e 2 eais Lt
La transferencia de calor con el aislante
Q2
Te T
eais
k ais Am
Te T
1
h 2 Ae
1
k ais 2 Lt
ln 1
2 eais
de
1
1
4.6 d e 2 eais
4
d e 2 eais Lt
200 20
107.13483
3
2 eais
1
1
4
ln 1
0.04826 2 eais
0.065 ( 2 1 )
0.04826 4.6 1
Resolviendo esta última ecuación encontramos el espesor del aislante
eais 0.02356 m 23.56 mm
Univ. Erwin Choque Conde
Página 67
65. Un huevo ordinario puede comportarse como una esfera de 5.5 cm de diámetro. El huevo se encuentra
inicialmente en el agua hirviendo a 87ºC y se saca al medio ambiente a 15ºC tomando las propiedades
3
del huevo como la del agua ( =2700 kg / m , Cp=3.32 kJ / kg º C ) determine: a) El coeficiente de
convección al medio ambiente b) Graficar la variación de temperatura respecto al tiempo en la superficie
exterior, a 1 cm , a 2 cm de profundidad y en el centro del huevo c) Determine la temperatura después
de transcurrir un tiempo de 50 minutos en la superficie exterior a 1 cm , 2 cm y en el centro del huevo.
Datos del huevo
T
Ti
d 5.5cm
Diámetro promedio del huevo
Ti 87 C
Temperatura inicial del huevo
T 15C
Temperatura del ambiente
T 7.2
T Ti T
kg
2700
3
m
h
Cp 3.32 10
3
J
kg C
La temperatura promedio
Tprom
Ti T
Tprom 5.1
2
Este método utiliza las ecuaciones del texto T.C. Incropera ecuaciones 5.1
1
0.03085
Tprom 273.15 C
Propiedades del aire a temperatura promedio
kg
1.127
Pr 0.7049
3
m
a 17.29 10
2
6 m
Kaire 0.0273
a 24.572 10
s
W
m C
2
6 m
s
El número de Rayleigh
Rad
g ( T ) d
3
Rad 8.53312 10
a a
Para el número de Nusself
5
1
0.589 Rad
Nu 2
4
4
1
16
0.469
P
r
9
Nu 15.80244
9
El coeficiente de convección
h
Nu Kaire
d
Univ. Erwin Choque Conde
h 7.84376
W
2
m C
Página 68
Análisis del número de Biot
Propiedades del huevo (agua)
W
Khuevo 0.58
h 1.554 10
m C
2
7 m
r
s
La longitud característica de una esfera es:
r
Lc
Lc 0.00917 m
3
h Lc
El número de Biot
Bi
Khuevo
d
2
r 0.0275 m
Bi 0.12397
Como Biot es mayor a 0.1 entonces la incidencia de la conducción y convección tiene
importancia simultánea
0.1 Bi 1.74 40
El nuevo Biot será:
Bi
h r
Bi 0.3719
Khuevo
Con Bi entonces de tabla 5.1 de transferencia de calor "Incropera" o (tabla1 en anexo) para una Esfera:
Cx 1.049336
1 0.99208
o
0 1 1 T( 0. ) T
Fo
ln
ln
2 Cx
1 2 Cx Ti T
1
El número de Fourier
1
Fo
r
.........1
.........2
2
2
1 h
De las ecuaciones 1 y 2
T0. T Cx Ti T e
r
2
La distribución de temperatura en el centro del huevo
2
1 h
T0( ) T Cx Ti T e
r
2
0s 300 s 10000 s
La distribución de temperatura en la cascara de huevo:
Para
0 ( )
rx r
rx
rn
r
La relación:
T0( ) T
rn 1
0 ( )
Tr( ) T Ti T
sin 1 rn
1 rn
Ti T
La distribución de temperatura a 1cm de profundidad
Para
rx r 1cm
0 ( )
Tr1( ) T Ti T
sin 1 rn1
1 rn1
Univ. Erwin Choque Conde
rx
rn1
r
La relación:
rn1 0.63636
Página 69
La distribución de temperatura a 2cm de profundidad
rx r 2cm
Para
0 ( )
Tr2( ) T Ti T
sin 1 rn2
1 rn2
ºC]
rx
rn2
r
La relación:
rn2 0.27273
ón de temperatura
distribuci
10
8
Temperatura[
T0( )
Tr2 ( )
Tr1 ( ) 6
Tr ( )
4
2
0
210
3
410
3
610
3
810
3
110
4
Tiempo[seg.]
Univ. Erwin Choque Conde
Página 70
INTERCAMBIADORES
66. Una corriente de aire fluye a razón de 0.11 kg / s a través de un canal de 1 cm de ancho y 0.5
m de altura que forma parte de un intercambiador de calor tipo placa. El canal tiene 0.8 m de
longitud y sus paredes están a 327ºC. Si la presión del aire es de 1atm y la temperatura media de
entrada y salida de la masa del aire es de 127ºC, determinar el calor transferido al aire.
DATOS:
kg
b 1cm
wa 0.11
h 0.5m
Tw 327 C
Lp 0.8m
T 127 C
s
Propiedades del aire a 227ºC
h
kg
1.4128
3
1.316 10
m
2
5 m
2
9.49 10
b
6 m
k 0.02227
SOLUCION:
s
Pr 0.722
s
W
m C
El diámetro equivalente
Af
h b
Deq 4 Rhid 4
4
P
2 ( h b)
h b
Deq 2
hb
El área transversal
At b h
La velocidad del aire
v
Re
El numero de Reynolds
Deq 0.01961 m
2
At 0.005 m
wa
v 15.57191
At
v Deq
m
s
Re 32174.04064
>2000 flujo turbulento
1
Nu 0.027 Re
0.8
Pr
3
Nu 97.77188
h 1a
El coeficiente de convección
Nu k
Deq
h 1a 111.04637
El calor transferido
Qt 2 h Lp b Lp h 1a Tw T
Univ. Erwin Choque Conde
W
2
m C
Qt 18122.76793 W
Página 71
67. Un intercambiador de calor constituido por una serie de tubos concéntricos de acero se emplean para
enfriar en cada tubo 500 kg / hr de una sustancia cuyo calor específico es 1.881 kJ / kg º C ,
utilizando agua como refrigerante. El agua entra por el interior de los tubos a 15ºC con un caudal en
cada tubo de 450 kg / hr en contracorriente con la sustancia que entra a 95ºC. Los tubos internos
tienen un diámetro interno de 3 cm y un espesor de 3 mm , En las condiciones de operación se a
2
determinado los coeficientes de convección siendo el interno hi=2674 W / m º C y el externo he=1744
W / m º C. Determinar la temperatura de salida de cada uno de los fluidos si la longitud de los tubos
2
es de 4 m y el calor específico del agua igual a 4.18 kJ / kg º C .
DATOS:
wc 500
Tc2
hr
J
3
Cp c 1.881 10
Wc
Wf
Tf1
kg
kg C
Tf2
Tc1 95C
Agua fría
Tc1
kg
d i 3cm
L 4m
wf 450
et 3mm
Ai L d i
Cp f 4.18 10
d e d i 2 et
Ae L d e
Tf1 15C
W
h i 2674
h e 1744
2
m C
hr
3
J
kg C
W
2
m C
El coeficiente global de transferencia de calor
1
Ui
1
hi
T log
Ai
( Tc1 Tf2) ( Tc2 Tf1)
ln
Tc1 Tf2
Tc2 Tf1
h e Ae
Balance de energías
QT QP QG
De la siguiente relación:
QG QP
Tc1 Tc2
Tf2 Tf1
Cp f wf ( Tf2 Tf1) Cp c wc ( Tc1 Tc2 )
Cp f wf
Cp c wc
R
R
Cp f wf
R 2
Cp c wc
( Tc1 Tc2) R ( Tf2 Tf1)
De la siguiente relación:
QP QT
( Tf2 Tf1) Cp f wf Ui Ai T log Ui Ai
( Tc1 Tf2) ( Tc2 Tf1)
ln
Tc1 Tf2
Tc2 Tf1
Ui Ai
Ui Ai Tc1 Tc2
Ui Ai
( Tc1 Tf2) ( Tc2 Tf1)
1
( R 1)
Tf2 Tf1
Tc2 Tf1 Cp f wf
Cp f wf Tf2 Tf1
Cp f wf
ln
Tc1 Tf2
Univ. Erwin Choque Conde
Página 72
Ui Ai
Tc1 Tf2
Tc2 Tf1
e
Cpf wf
Ui Ai
( R 1)
( Tc1 Tf2) ( Tc2 Tf1) e
Ui Ai
Ui Ai
( R 1)
Tc1 Tc1 Tc2 Tf1 Tc2 e Cpf wf
R
Tf1 e
Cpf wf
Ui Ai
( R 1)
Cpf wf
R Tf1 e
1 Tc1 ( R 1 )
Tc2
Ui Ai
R e
Tf2 Tf1
Cpf wf
( R 1)
( R 1)
Tc2 36.82518 C
( R 1)
1
Tc1 Tc2
Tf2 44.08741 C
R
( Tc1 Tf2) ( Tc2 Tf1)
T log
Cpf wf
T log 34.33982 C
Tc1 Tf2
ln
Tc2 Tf1
El calor Ganado, Perdido y Transferido es:
QG wf Cp f ( Tf2 Tf1)
QP wc Cp c ( Tc2 Tc1 )
QT Ui Ai T log
QG 15198.17289 W
QP 15198.17289 W
QT 15198.17289 W
68. Se va diseñar un intercambiador de calor de tubo y coraza para enfriar 1.512 kg / s de aceite
(Cp=2093 kJ / kg º C ) desde 65ºC hasta 42ºC utilizando 1.008 kg / s de agua (Cp=4.187
kJ / kg º C ) que entra a una temperatura de
2
26ºC se considera que el coeficiente global de
transferencia de calor es 681.6 W / m º C . Utilizando el método de eficiencia o NUT, determinar la
superficie de calefacción requerida si el Número de Unidades de Transferencia es igual a 1.7
wc 1.512
wf 1.08
kg
s
kg
s
J
Cp c 2093
kg C
Cp f 4187
kg C
Nut 1.7
J
U 681.6
Cp 3164.616
Cg wf Cp f
Cg 4521.96
La Superficie de calefacción
requerida
Univ. Erwin Choque Conde
W
C
W
C
Cmin Cp
A
2
m C
Cp wc Cp c
Entonces Cmin es:
W
Nut Cmin
U
Cmin 3164.616
W
C
2
A 7.89297 m
Página 73
69. Determinar la superficie de calefacción y el número de sección de un intercambiador de doble tubo
3
que trabajan con las siguientes características. Agua caliente ( =976 kg / m , =0.403E-6
m / s, k=0.67 W / mº C , cp=4.19 kJ / kg º C se mueve por un tubo interior de acero k=45
2
W / mº C cuyo diámetro interior es de 32mm y exterior 35mm y su temperatura de entrada es de
3
2
95ºC y un gasto de 2130 kg / hr . El agua que se calienta ( =996 kg / m , =0.805E-6 m / s,
k=0.617 W / m º C , cp=4.19 kJ / kg º C tiene un gasto de 3200 kg / hr se mueve a contracorriente
por el canal anular y se calienta desde 15ºC hasta 45ºC El diámetro interior del tubo exterior es de
48 mm . La longitud de una sección del intercambiador es de 1.9 m .
d e 35mm
Tf2
DATOS:
Wf
Wc
Tc1
d i 32mm
Tc2
k t 45
W
m C
Di 48mm
Tf1
L 1.9m
Propiedades del agua fría
f 996
Propiedades del agua caliente
kg
c 976
3
m
2
6 m
c 0.403 10
s
W
k c 0.67
m C
3
Cp f 4.19 10
wf 3200
3
m
f 0.805 10
k f 0.618
kg
J
m C
J
3
kg C
wc 2130
hr
s
W
Cp c 4.18 10
kg
Tf1 15C
2
6 m
kg C
kg
hr
Tc1 95C
Tf2 45C
El calor ganado por el agua fría es:
QG wf Cp f ( Tf2 Tf1)
5
QG 1.11733 10 W
QT QG
El balance de energía
QG QP wc Cp c ( Tc1 Tc2 )
Tc2 Tc1
QG
Tc2 49.82175 C
wc Cp c
La temperatura media logarítmica es:
T log
( Tc1 Tf2) ( Tc2 Tf1)
Tc1 Tf2
ln
Tc2 Tf1
T log 41.95427 C
Calculamos el coeficiente de convección en el tubo interior (agua caliente)
El área transversal interno
2
2
Ati 0.0008 m
Ati
d
4 i
La velocidad en el fluido caliente
Univ. Erwin Choque Conde
vi
wc
Ati c
vi 0.754
m
s
Página 74
vi d i
Rei
El número de Reynolds
Pri
El número de Prandtl
Rei 59852.512
c
c Cp c c
Flujo turbulento
Pri 2.4539
kc
1
Nu i 0.027 Rei
El número de Nusself
0.8
Pri
hi
El coeficiente de convección interno
3
Nu i 241.53595
Nu i k c
h i 5057.15898
di
Calculamos el coeficiente de convección en la sección anular (fluido frío)
W
2
m C
El área transversal (sección anular)
2
2
2
Ate 0.00085 m
Ate
Di d e
4
ve
La velocidad en la sección anular
wf
ve 1.0531
Ate f
2
Deq
El diámetro equivalente para una sección anular
Ree
El número de Reynolds
Pre
El número de Prandtl
ve Deq
Di d e
f Cp f f
s
2
de
Ree 40330.567
f
m
Flujo turbulento
Pre 5.43602
kf
1
Nu e 0.027 Ree
El número de Nusself
0.8
Pre
3
he
El coeficiente de convección externo
El coeficiente global de T.C. referido al área interna:
Ui
hi
Nu e k f
Deq
h e 4602.56461
W
2
m C
W
Ui 2522.79028
2
m C
1
1
Nu e 229.59627
di
h e d e
El área de transferencia de calor:
Ai
QT
Ui T log
2
Ai 1.05566 m
El número de secciones es:
n
Ai
d i L
n 5.52678
El número de secciones debe ser
Univ. Erwin Choque Conde
n 6
Página 75
70. Un intercambiador de doble tubo se utiliza para enfriar aceite de transformadores utilizando agua
como refrigerante. El aceite por la tubería interna cuya relación de diámetros es de 14/12 mm a
la velocidad de 4 m / s y una temperatura de entrada de 100ºC0. El agua se mueve en
contracorriente por la sección anular a la velocidad de 2.5 m / s y su temperatura de entrada es
de 20ºC el diámetro interno de la tubería externa es de 22 mm . Determinar la longitud total del
intercambiador para que el aceite tenga una temperatura de salida de 60ºC. Propiedades del
3
2
aceite: =852 kg / m , =0.375E-4 m / s , k=0.138 W / m º C , Pr=490, cp=2.131 kJ / kg º C ,
agua:
=996 kg / m , =0.805E-6 m / s, k=0.618 W / mº C , Pr=5.42, cp=4.18 kJ / kg º C .
3
DATOS:
2
d i 12mm
Di 22mm
Aceite (fluido caliente)
Agua (fluido frio)
Tc1 100 C
Tc2 60C
ac 852
Tf1 20C
ag 996
3
ac 3.75 10
k ac 0.138
kg
3
m
kg
m
ag 0.805 10
2
5 m
s
m C
2
6 m
m C
J
3
Cp ag 4.19 10
J
3
kg C
vag 2.5
m
s
W
k ag 0.618
W
Cp ac 2.13 10
vac 4
d e 14mm
kg C
m
s
s
El coeficiente de T.C. por convección flujo interno (aceite)
Rei
Pri
vac d i
Rei 1280
ac
ac ac Cp ac
Flujo laminar
Pri 493.1413
k ac
1
di
Nu i 1.86 Rei Pri
Lt
hi
1
3
Nu i k ac
Nu i 36.52867 Lt
1
h i 420.0797 Lt
di
3
3
W
5
m 3 C
El coeficiente de T.C. por convección flujo externo (agua)
El diámetro equivalente
2
Deq
Ree
Di d e
2
de
vag Deq
ag
Univ. Erwin Choque Conde
Deq 0.02057 ( m)
Ree 63886.42413
Flujo turbulento
Página 76
ag ag Cp ag
Prag
Prag 5.43602
k ag
1
Nu e 0.027 Ree
he
0.8
Prag
3
Nu e k ag
Nu e 331.72959
h e 9965.70989
W
2
m C
Deq
2
wac vac ac d i
4
El flujo másico del aceite
wac 0.38544
kg
s
El calor perdido (Aceite)
Qp wac Cp ac Tc1 Tc2
El flujo másico del agua
2
2
wag vag ag Di d e
4
wag 0.56322
La temperatura de salida del agua
Qp
Tf2
Tf1
wag Cp ag
Tf2 33.9154 C
La temperatura media logarítmica
T log
1
1
hi
di
d i Lt T log
Tc1 Tf2 Tc2 Tf1
Qg Qp QT Ui Ai T log
32839.1233
Qp 32839.1233 W
s
T log 51.95553 C
Tc1 Tf2
ln
Tc2 Tf1
1.95868 Lt
32839.1233
1
Lt
h e d e
3
420.0797
La solución es:
kg
12
14 9965.709
El coeficiente de T.C. interno es:
Lt 254.3015 m
1
h i 420.0797 Lt
3
W
5
m 3 C
h i 66.30537
W
2
m C
71. Para calentar acido acético (cp=2.09 kJ / kg º C ) desde 20ºC hasta 60ºC se hace pasar por el
intercambiador 1-2 circulando por el exterior agua que entra a 95ºC y sale a 80ºC el coeficiente
2
global de T.C. referido al área interna de los tubos es de 407 W / m º C , el flujo de masa del acido
acético a través de cada tubo es de 200 kg / hr determinar la longitud de los tubos si su diámetro
interno es de 1 cm Tomar como factor de corrección de temperatura 0.95
DATOS:
Tf2
El ácido acético circula por la coraza:
Tc2
Tc1
Cp f 2.09 10
Wc
Tf1
Wf
Tf1 20C
Tf2 60C
Univ. Erwin Choque Conde
3
J
kg C
wf 200
Ui 407
kg
hr
W
2
m C
Página 77
El agua circula por los tubos
Tc1 95C
d i 1cm
Tc2 80C
Fc 0.95
El calor ganado es:
QG Cp f wf ( Tf2 Tf1)
QG 4644.44444 W
QT QG
La temperatura media logarítmica
T log
( Tc1 Tf2) ( Tc2 Tf1)
T log 46.38249 C
Tc1 Tf2
ln
Tc2 Tf1
El calor transferido será:
QT Ui Ai Fc T log Ui d i L Fc T log
L
QT
Ui d i Fc T log
L 8.2435 m
72. Se dispone un intercambiador 1-1 construido a contracorriente de 120 tubos de ¾ pulgadas
(di=20.8mm de=26.6mm) de 6 m de longitud se desea calentar 4000 kg / hr de aceite Cp=2.98
kJ / kg º C ha=250. W / m 2 º C de 30ºC a 180ºC que circula por la coraza, se utiliza gases de
2
3
combustión Cp=1.03 kJ / kg º C hg=6. W / m º C , =0.598 kg / m que sale de un horno a
3
300ºC con un flujo de 4500. m / hr que circula por el interior de los tubos ¿indique si es posible
aprovechar el intercambiador disponible?
QT < ó > Qg=Qp
Propiedades del aceite
Propiedades de los gases
kg
ma 4000
hr
Cp g 1.03 10
Cp a 2.98 10
h a 250
3
d i 20.8 mm
J
kg C
d e 26.6 mm
J
kg C
h g 61
W
2
L 6m
m C
Tc1 300 C
m
Gg 45000
hr
tf1 30C
g 0.598
tf2 180 C
El calor ganado por el aceite:
Qg ma Cp a tf2 tf1
W
3
2
m C
3
N 120
kg
3
m
5
Qg 4.96667 10 W
El flujo másico de los gases
mg g Gg
Qp Qg
La ecuación del calor perdido es:
Qp mg CP g Tc1 Tc2
Univ. Erwin Choque Conde
Qp
Tc2 Tc1
mg Cp g
Tc2 235.49155 C
Página 78
Para la diferencia logarítmica de temperatura en un intercambiador 1-1 a contracorriente
Tc1 tf2 Tc2 tf1
T log
T log 158.93188 C
Tc1 tf2
ln
Tc2 tf1
El coeficiente global de transferencia de calor
Uai
ha
Ai N L d i
W
Uai 59.45681
2
m C
1
1
El área interior
di
2
Ai 47.04849 m
hg de
El calor transferido
5
QT 4.44589 10 W
QT Uai Ai T log
QT Qg
No es posible aprovechar
73. Se desea construir una batería de 50 duchas en el internado de la FNI se considera que cada
ducha debe suministrar 100 ltrs / hr Una manera de lograr este objetivo es calentar agua
potable de suministro desde 10ºC hasta 90ºC en un intercambiador 1-2 donde el agua circula
por los tubos del intercambiador de calor 1-2 mientras en la coraza se condensa a 1 atm vapor
2
de agua saturado residual y saliendo como agua liquida a 100ºC si U=1500 W / m º C
encuéntrese a) La cantidad de vapor de agua necesario en kg / hr b) El área del
intercambiador necesario.
DATOS:
N 50
q1 100
Tf2
Tf1
3
Lit 0.001 m
Tc2
Wf
Wc Tc1
985
Propiedades del agua a 50ºC
kg
3
wf q1
W
U 1500
2
m C
hr
Tf1 10C
Tc1 100 C
Tf2 90C
Tc2 100 C
Cp 4.18 10
m
El flujo másico del agua
Lit
wf 0.02736
J
3
kg C
kg
s
El calor ganado por el agua
Qg wf Cp ( Tf2 Tf1)
Para el calor ganado
Qp wg h fg
Qg 9149.55556 W
QP Qg
QT Qg
De tablas de vapor saturado
3 J
Calor latente de evaporación a (1atm)
h fg 2257 10
kg
a) El flujo másico del vapor de agua residual
wg
QP
wg 0.00405
h fg
kg
s
b) El área de calefacción
Para el factor de corrección de temperatura Fc=1
T log1
( Tc1 Tf2) ( Tc2 Tf1)
ln
Tc1 Tf2
Tc2 Tf1
Fc 1
T log1 36.40957 C
El área
A
QT
U Fc T log1
2
A 0.16753 m
Univ. Erwin Choque Conde
Página 79
74. Se desea calentar 250 kg / hr de agua de 50ºC a 90ºC con aceite para motores (cp=2 kJ / kg º C
). Para este proceso se dispone aceite a 180ºC con un flujo de masa de 250 kg / hr se dispone de
dos intercambiadores de calor de doble tubo.
2
2
Cambiador 1: U=570 W / m º C A=0.5 m
Cambiador 2: U=370 W / m º C A=1. m
¿Que intercambiador de calor seleccionaría?
2
wh2o 250
DATOS:
U1 570
U2 370
2
W
2
A1 0.5m
2
m C
W
2
m C
hr
Tf1 50C
Tf2 90C
A2 1.m
2
kg
Cp h2o 4.18 10
J
3
kg C
Tc1 180 C
kg
wac 250
hr3 J
Cp ac 2 10
kg C
SOLUCION:
De la relación siguiente:
Qg Qp Qt
El calor ganado por el agua
Qh2o wh2o Cp h2o Tf2 Tf1
Qh2o
Tc2 Tc1
wac Cp ac
Qh2o 11611.11111 W
Tc2 96.4 C
La temperatura media logarítmica será constante también
T log
Tc1 Tf2 Tc2 Tf1
Tc1 Tf2
ln
Tc2 Tf1
T log 65.81031 C
Intercambiador 1
QI U1 A1 T log
QI 18755.93733 W
Intercambiador 2
Q2 U2 A2 T log
Q2 24349.81338 W
Puede utilizarse cualquier intercambiador, porque los dos intercambiadores tienen potencias
mayores al calor latente del agua. Recomendable el intercambiador 2.
Univ. Erwin Choque Conde
Página 80
75. Determinar el área de superficie de calefacción y el numero de secciones de 6 m de longitud ,
necesaria para un intercambiador de doble tubo concéntrico de 2” (Di=52.5 mm y De=60.45 mm
) y ¼” (di=35 mm y de=42.16 mm ) para enfriar 2.5 kg / s de una solución de alcohol etílico (
cp=2.54 kJ / kg º C Pr=61.5 ) de 70 a
40ºC, utilizando a contracorriente agua ( =1.006E-6 m / s, k=0.597 W / m º C , =1000 kg / m
=6.26E-3 kg / m * s , k=0.259 W / m º C , =1091.1 kg / m
3
2
3
cp=4.18 kJ / kg º C Pr=7.02 ) disponible a 10ºC y con un flujo de 1.9 kg / s se considerar para
cada fluido un factor de obstrucción de 0.001
DATOS:
Tf2
2
Wf
RDLa 0.001
Wc
Tc1
m C
W
Tc2
De 60.4 mm
L 6m
Di 52.5 mm
d i 35mm
Tf1
d e 42.16 mm
Propiedades del alcohol etílico
kg
ma 2.5
s
Propiedades del agua
kg
mh 1.9
s
Tc1 70C
Tf1 10C
Tc2 40C
Cp a 2.54 10
a 6.26 10
a 1091.1
Cp h 4.18 10
J
3
h 1.006 10
3 kg
m s
h 1000.
kg
k h 0.597
W
m C
QP ma Cp a Tc1 Tc2
di
4
2
kg C
2
6 m
s
kg
3
W
m C
Prh 7.02
5
QP 1.905 10 W
QP
Tf2 Tf1
Tf2 33.9864 C
mh Cp h
El área de flujo en la tubería interna
J
m
3
Pra 61.5
El calor perdido (alcohol etílico)
Afi
3
kg C
m
k a 0.259
RDLh RDLa
2
Afi 0.00096 m
El área de flujo en la sección anular
Afe
4
Di d e
2
2
2
Afe 0.00077 m
El alcohol circula por los tubos por su menor flujo
Afe Afi
El coeficiente de convección en los tubos (alcohol)
Como
Rei
ma d i
Afi a
Univ. Erwin Choque Conde
Rei 14528.06418
Flujo turbulento
Página 81
1
Nu i 0.027 Rei
hi
0.8
Pra
Nu i k a
3
Nu i 227.73075
h i 1685.20752
di
W
2
m C
El coeficiente de convección externo (agua)
2
Deq
El diámetro equivalente
Ree
2
Deq 0.02322 m
de
mh
Gh
Afe
La masa, velocidad del agua
Gh Deq
Di d e
Gh 2471.59143
Ree 57038.11135
h h
kg
2
m s
Flujo turbulento
1
Nu e 0.027 Ree
0.8
Prh
3
Nu e k h
he
Nu e 329.9197
h e 9965.70989
Deq
W
2
m C
El coeficiente global limpio de TC referida al área interna:
ULi
1
1
hi
W
ULi 1446.65233
2
m C
di
h e d e
El coeficiente global de diseño
1
Di
UDi
1
ULi
Coeficiente de obstrucción total
RD RDLa RDLa
RD
1
1
ULi
T log
W
UDi 371.5744
2
m C
RD
Tc1 Tf2 Tc2 Tf1
T log 32.91529 C
Tc1 Tf2
ln
Tc2 Tf1
QL UDi Ai T log
El área de calefacción es:
Ai
QP
UDi T log
Univ. Erwin Choque Conde
El número de tubos
2
Ai 15.57584 m
n
Ai
d i L
n 23.60926
n 24
Página 82
76. Tras un largo tiempo se verifico el estado de cierto enfriador de paso simple a contracorriente de aceite
para determinar si la formación de incrustación ha deteriorado su rendimiento. Durante la prueba una
corriente de aceite SAE-50 que fluye a razón de 2 kg / s se enfría de 149ºC a 107ºC por medio de agua
que entra a razón de 1.0 kg / s y 27ºC el intercambiador o enfriador tiene una superficie de de calefacción
2
2
de 3.33 m y el coeficiente global de transferencia de calor es de 930 W / m º C y su factor de
obstrucción admisible es de 0.0002 verificar si el equipo requiere mantenimiento o no.
DATOS:
Fluido caliente (Aceite)
kg
wc 2
s
Fluido frío (agua)
wf 1
Tc1 147 C
kg
Cp f 4.186 10
s
3
Tf1 27 C
Tc2 107 C
UL 930
2
Ac 3.33 m
Cp c 2.19 10
3
J
kg C
2
W
Radm 0.0002
2
m C
W
m C
J
kg C
El calor perdido por el aceite
Qpa wc Cp c Tc1 Tc2
Qpa
Tf2
Tf1
wf Cp f
T log
5
Qpa 1.752 10 W
Tf2 68.8538 C
Tc1 Tf2 Tc2 Tf1
T log 79.06948 C
Tc1 Tf2
ln
Tc2 Tf1
El coeficiente global de diseño es:
Qpa
UD
Ac T log
El factor de obstrucción calculado:
Rcalc
UL UD
UL UD
2
Rcalc 0.00043
Rcalc Radm
Univ. Erwin Choque Conde
W
UD 665.39723
2
m C
m C
W
Requiere mantenimiento
Página 83
77. En una industria química, orto-oxileno producido deberá ser enfriado de 80ºC a 44ºC, atizando un
2
intercambiador multitubular 1-1 el orto-oxileno con velocidad de masa de 1230000. kg / m * h
circula por el interior de los tubos de 1” de diámetro interior y 1/8” de espesor de 6 m de longitud
3
útil. El fluido refrigerante a ser utilizado es agua residual, con 47.8 m / h y 15ºC y opera en
contracorriente. El coeficiente global de transferencia de calor puede ser admitido como 550
W / m 2 º C y la diferencia media logarítmica de temperaturas a lo largo del intercambiador puede
ser considerado estimativamente en 36.5ºC Calcular: a) La temperatura de salida del agua y b) El
número de tubos a ser utilizados. Datos: Calores específicos Agua 4.19 kJ / kg º C y el orto-
oxileno 1.8 kJ / kg º C
DATOS:
Tf2
d i 1in
Lt 6 m
Wf
Wc
Tc1
t
Tc2
1
8
in
de di 2 t
UAd 550
Tf1
Fluido orto-oxileno
Tc1 80C
Agua residual
Tc2 44C
3
Cp ox 1.8 10
2
m C
3
wag 5.8
Gox 5230000.
W
kg
m
hr
Cp a 4.18 10
2
m hr
a 1000
J
kg C
3
J
kg C
kg
3
m
Tf1 15C
El área del tubo interior:
Ai
4
di
2
2
Ai 0.00051 m
El flujo másico del orto-oxileno
El flujo másico del agua residual
kg
mox 0.73613
mox Gox Ai
s
El calor perdido por el orto-oxileno
QP mox Cp ox Tc1 Tc2
a) La temperatura a la salida es:
QP 47701.44208 W
QP
Tf2
Tf1
Tf2 22.0832 C
Cp a mag
Tc1 Tf2 Tc2 Tf1
T log
Tc1 Tf2
ln
Tc2 Tf1
b) El número de tubos
At
n
Univ. Erwin Choque Conde
kg
mag 1.61111
s
mag wag a
T log 41.8047 C
QP
2
UAd T log
At 2.07464 m
At
d i Lt
n 4.3332
n 5
Página 84
78. En un sistema de potencia de Rankine, salen 1.5 kg / s de la turbina como vapor saturado a 0.5 Bar . El vapor se
condensa a liquido saturado al hacerlo pasar sobre los tubos de un intercambiador de coraza y tubos, mientras que
pasa agua liquida con una temperatura de entrada T1=280K por los tubos .El condensador contiene 100 tubos de pared
delgada, cada uno de 10 mm de diámetro y el flujo másico total de agua por los tubos es 15 kg / s el coeficiente
promedio de convección asociado con la condensación sobre la superficie externa de los tubos se puede aproximar
como ho=5000
=700*10-6
a.
b.
W / m º CValor apropiados de las propiedades para el agua liquida son : c=4.178 kJ / kg º C
2
kg / s * m, k=0.628 W / mº C y Pr=4.6
¿Cuál es la temperatura de salida del agua?
¿Cual es la longitud requerida del tubo (por tubo)?
kg
mv 1.5
s
Turbina
kg
ma 15
s
Condesador
T1
Agua
Tf1 280 K
T2
6 J
Vapor de
la caldera
Liquido saturado
a la bomba
J
Cp 4187
k 0.628
kg K
h o 5000
Tc1 355 K
700 10
h fg 2.304 10
6 kg
W
kg
2
m K
Rt 0.0003
W
2
m K
d 10mm
W
n 100
m K
Tc2 Tc1
Pr 4.6
La energía por condensación del vapor es transferida al agua
m s
Qhf Qh2O
mv h fg ma Cp Tf1 Tf2
Qh mv h fg
mv h fg
Tf2 Tf1
ma Cp
Tf2 335.02747 K
Qh 3.456 10 W
6
El coeficiente de convección en el tubo es:
ma
n
Rei
d
4
Rei 27283.70453
Flujo turbulento
1
Nu 0.027 Rei
ha
0.8
Pr
Nu k
3
Nu 158.85676
h a 9976.20478
d
W
2
m K
El coeficiente Global de T.C. (Limpio)
U
T log
1
1
ha
1
Tc1 Tf2
Tc2 Tf1
ln
ho
U 3330.68522
Tc1 Tf2 Tc2 Tf1
T log 41.58886 K
W
2
m K
b) La longitud del tubo
At
Qh
U T log
Univ. Erwin Choque Conde
2
At 24.94958 m
At
Lt
d n
Lt 7.9417 m
Página 85
RADIACIÓN
79. Cual es la temperatura del sol si su máxima energía monocromática tiene una longitud de onda de 0.25
micrones?
max 0.25 10
DATOS:
C1
Tmax
max
6
C1 0.002898 K m
m
Tmax 11592 K
80. Un tubo de acero base de 2´´ de diámetro exterior lleva vapor a 200ºC a través de un ambiente de 5
m de largo que se encuentra a 20ºC ¿Qué disminución o aumento existe en la perdida de calor si el
tuvo se cubre con una pintura de aluminio?
DATOS:
d 2in
5.67 10
L1 5m
8
W
2
m K
Tw 473.15 K
Constante de Stefan -Boltzman
4
El área de transferencia de calor
T1 ( 20 273.15 )K
At d L1
La emisividad para el acero
1 0.16
Qrad1 At 1 Tw T1
4
4
La emisividad de la pintura de aluminio
Qrad2 At 2 Tw T1
4
2
At 0.79796 m
4
Qrad1 309.35018 W
2 0.35
Qrad2 676.70352 W
Existirá un aumento de transferencia de calor
Q
Qrad2
Q 218.75 %
Qrad1
81. Un tuvo horizontal de 6 m de largo y 123.5 cm de diámetro se mantiene a una temperatura de
2
150ºC en una habitación amplia en el que el aire esta a 20ºC y 8. W / m º C Las paredes de la
habitación están a 38ºC. Suponga que la emisividad del tubo es de 0.76 ¿Cuanto de calor se pierde
por el tubo tanto por convección como por radiación?
T
Tw
h
DATOS:
5.67 10
L 6m
L
W
2
m K
D 123.5 cm
D
8
4
W
h 8
2
T1 ( 150 273 )K
m K
T ( 20 273 )K
Tw ( 38 273 )K
0.76
2
At 23.2792 m
El área de transferencia
At D L
El calor por radiación
Qr At ( T1) Tw
El calor por convección
Qh At h T1 T
El calor total de transferencia de calor
Qtot Qr Qh
Univ. Erwin Choque Conde
4
4
Qr 22731.95624 W
Qh 24210.36963 W
Qtot 46942.32586 W
Página 86
82. Considere un cuerpo negro de masa “m”, calor específico “c” y área “A” a una temperatura uniforme
“To”, que se deja caer en un recipiente muy grande cuyas paredes se encuentran a una temperatura
de 0K. Si el recipiente esta en vacio, determine la temperatura del cuerpo como función del tiempo.
Balance de energía
1
Eentra Egenerado Esale Ealmacenda
Condiciones:
Eentra 0
A T0 T1
Esale A T0 T1
4
Egenerada 0
4
4
4
dT
Ealm m Cp
dt
dT
m Cp dt
T
t
m Cp
d T A d t
4
0
T
T
m Cp
1
To
3
3
A t
T
1
3
o
m Cp
T To
3 3
3 To T
3
3
m Cp 3 A T 3 t
o
m Cp To
T
A t
83. Una noche despejada se deja en un espacio abierto una bandeja de 30 cm *60 cm con una altura
de 4 cm de agua a 10ºC. La bandeja se encuentra perfectamente aislada del exterior, y podemos
suponer nula la transmisión de calor desde el agua al aire. Calcúlese el tiempo necesario para que
la temperatura del agua desciende hasta 0ºC, si el ambiente se encuentra a 10ºC, la emisividad del
agua es 0.95, y se supone que la bóveda celeste a cero absoluto.
Tbob
a 30cm
b 60cm
Qr
kg
h2o 1000
3
m
c 4cm
c
Tw1
Cp h2o 4.18 10
Tw1 ( 10 273 )K
a
Tf ( 0 273 )K
T 10C
b
5.67 10
8
J
3
kg K
W
2
m K
Tbob 0K
4
0.95
El área de transferencia
La masa del agua es:
mh2o h2o ( a b c)
La temperatura media
mh2o 7.2 kg
Tm
Tw1 Tf
La potencia transmitida al medio es:
2
Tm 278 K
Qrad At Tm Tbob
La energía necesaria para enfriar el agua
La potencia es energía por unidad de tiempo
Univ. Erwin Choque Conde
2
At 0.18 m
At a b
4
4
Qrad 57.91064 W
Eh2o mh2o Cp h2o Tw1 Tf
Qrad
Eh2o
t
t
Eh2o
Qrad
5
Eh2o 3.0096 10 J
t 5196.97258 s
Página 87
84. Considere un recipiente aislado térmicamente que contiene una pequeña cantidad de agua. Si
la superficie libre del agua queda expuesta al aire libre durante una noche despejada y la
temperatura ambiente es de 40°C, calcule la temperatura de equilibrio que alcanza el agua en
el recipiente. Suponga que el coeficiente de transferencia de calor en la superficie del agua
2
es igual a 5 W / m º C , que la temperatura efectiva del espacio es del orden de 0 K y que
tanto el agua como el espacio se comportan como cuerpos negros.
DATOS:
Balance de energía
Tesp 0K
W
h 5
2
m K
Eentra Egenerado Esale Ealmacenda
T ( 40 273 )K
1
Condiciones:
Eentra Qconv.
Egenerada 0
Esale Qradiacion
Ealm 0
Qconv. Qradiacion 0
h A T Tw A Tw Tesp
4
4
Tw h Tw h T
4
5.67 10
8
4
Tw 5 Tw 5 ( 40 273 )
Tw 260.6548 K
La solución es:
QA h T Tw
Calor por convección
W
QA 261.726
2
m
85. Encontrar el factor de emisividad de dos cilindros concéntricos infinitos de diámetros 10 y 20 cm
respectivamente, cuyas emisividades y temperatura son: 1 0.8 y T1=800ºC y del cilindro
externo 2 0.2 y T2=80ºC, utilizando las ecuaciones: qi Ri
R
i
( R F ) y
j
i j
iTi ri ( R j Fi j ) donde i 1,2,3....N y la sumatoria varia desde j=1 hasta N. Resolver
4
este mismo problema utilizando la analogía eléctrica.
Los factores de forma
N
q i Ri
Rj Fij
4
Ri i Ti ri
j 1
i 1
Cuerpo 1
N
Rj Fij
j 1
F11 0
F21
j=1a2
A1
A2
F12 1
F22 1
A1
A2
2
q 1 R1
Rj Fij R1 R1 F11 R2 F12 R1 R2
j 1
4
2
R1 1 T1 r1
4
4
Rj Fij 1 T1 r1R1 F11 R2 F12 1 T1 r1R2
j 1
i 2
Cuerpo 2
j=1a2
2
q 2 R2
A1
A1
Rj Fij R2 R1 F21 R2 F22 R2 R1 A2 R2 1 A2
j 1
4
R2 2 T2 r2
2
A1
4
4
Rj Fij 2 T2 r2R1 F12 R2 F22 1 T1 r1R1 R2 1 A2
j 1
Univ. Erwin Choque Conde
Página 88
Ordenando y considerando
(r=1-ε)
R1 R2 1 1 1 T1
4
.... a)
A1
1 2 R2 R2 1 2 1 A
4
1 1 T2
2
.... b)
Con estas ecuaciones a) y b) encontramos R1 y R2
Q1
q1
q2
A1
Q2
A2
b) Resolviendo por analogía eléctrica
T1 T2
4
Q12
1 1
A1 1
1
A1 F12
A1 T1 T2
4
Q12
4
A1 T1 T2
4
1 2
A2 2
1
1
1 1
A1
A2
4
1
2
1
4
A F F T 4 T 4
1
12 1
2
1
1
1
1
A2 2
A1
Entonces el factor de emisividad entre los cuerpos 1 y 2
F
1
A1 1
1
1
1 A2 2
86. Dos placas cuadradas de 0.5 m x0.5 m de lado, están colocados en forma con un borde común.
La placa horizontal esta perfectamente aislado. La placa vertical tiene una temperatura de 727[ºC] y
una emisividad de 0.6 Las placas se encuentran en un ambiente amplio cuya temperatura es 27[ºC]
y su factos de forma de la placa superior a la aislada es 0.25 Calcular: a) La temperatura de la
placa aislada. b) El calor perdido por la placa vertical.
DATOS:
w 0.5m
5.67 10
T1 ( 727 273 )K
T3
8
W
2
m K
4
1 0.6
T3 ( 27 273 )K
F12 0.2
El área
T1
1
T2
2
A1 w w
A1 0.25 m
A2 A1
A2 0.25 m
2
F11 0
F13 1 F12 F11
F22 0
F21 F12
F23 1 F22 F21
Univ. Erwin Choque Conde
F13 0.8
F12 0.2
F23 0.8
Página 89
1 1
4
T 3
2.66667
A1 1
1 3
1
1
20
A1 F12
1
4
2
m
1
5
A2 F23
2
1
5
1
m
A1 F13
T1
1
A1 F13
2
m
0
A3 3
1
2
m
1
A2 F23
1 1
A1 1
Req
A1 F12
Q=0
1
1
1
A1 F12 A2 F23 A1 F13
1 1
1
A1 1
1
A1 F12
1 2
1
A2 F23
1
A1 F13
A2 2
4
T 2
1
Req 6.83333
4
T 3
Q13
Rc
5
4
T1
4
T1 T3
4
2
m
Q13 8230.35073 W
Req
1 1
4
Ra T1 Q13
A1 1
4
Ra
Q13
5
2.666
Rb
20
4
1 1
A1 1
4
T 2
Ra 34752.39805
W
2
m
4
T1
T1 Ra
Rc T3
T 3
Req=6.83
4
1
A1 F12
Rc
2
m
Ra Rc
Qabc
W
Rc 459.27
1
Qabc 1371.72512 W
A2 F23
5
Q ac
Ra
5
Q abc
Qabc
Ra Rb
1
1
Rb Ra Qabc
A1 F12
A1 F12
2.666
Rb 7317.89561
Rb 4
20
T 2
4
T2
W
2
m
Rb
T2 599.37799 K
87. Dos placas paralelas de 90*60 cm están separados por una distancia de 60 cm . Uno de los planos se
mantiene a 550ºC y una emisividad de 0.6. El otro plano esta aislado, los planos se encuentran en una
habitación grande que se mantiene a 10ºC. Calcule la temperatura del plano aislado y la energía perdida
por el plano caliente.
DATOS:
90cm
a 90cm
60cm
T1
1
60cm
T3
b 60cm
T1 ( 550 273 )K
c 60cm
1 0.6
T3 ( 10 273 )K
F12 0.25
5.67 10
7
W
2
m K
T2
Univ. Erwin Choque Conde
Página 90
El área
4
T1
2
A1 a b
A1 0.54 m
A2 A1
A2 0.54 m
2
F11 0
F13 1 F12 F11
1 1
F22 0
A1 1
F21 F12
F23 1 F22 F21
1
A1 F13
1 3
A3 3
1
A1 F12
1 1
0
T 3
1
1
A2 F23
7.40741
A2 2
T 2
1
A1 F12
T1
Q13
1 1
A1 1
1
A1 F13
A1 1
1
A2 F23
1
A1 F13
3
Q13 79905.97195 K W
1 1
4
Ra T1 Q13
A1 1
5
3 W
Ra 1.61476 10 K
T 3
Rc T3
T 2
3 W
4
Rc 3636.87857 K
2
Ra Rc
Qabc
1
A1 F12
Qabc
Ra Rb
1
1
Qabc 15981.19439
T2
3
3
1
Rb Ra Qabc
A1 F12
3 W
Rb 43096.61781 K
4
m kg K
s
A2 F23
A1 F12
Univ. Erwin Choque Conde
2
m
1
A2 F23
2
m
Rc
4
4
T1 Ra
1 1
Qabc
Rb
4
Req
1
Qac
A1 F12
4
T1 T3
4
Q13
2
m
2
m
1
2.46914
1
Req 3.20988
4
1
1
1
1
A1 F12 A2 F23 A1 F13
A1 1
4
2
m
A2 F23
2
m
1 1
Req
1
1
2.46914
A1 F13
2
Q=0
1 2
F23 0.75
1
m
A1 F12
F12 0.25
1
1.23457
A1 1
4
Ra
F13 0.75
2
m
Rb
T2 525.06737 K
Página 91
88. Dos cilindros concéntricos abiertos en sus extremos cuyas características son: Del cilindro interior
D1=12 cm T1=620ºC y 1 0.59 el cilindro exterior que se encuentra aislado externamente
D2=22 cm T2=200ºC 2 0.47 los cilindros tiene una longitud de 25 cm los factores de forma
son F21 0.45 y F22 0.29 . Si los cilindros se encuentran en un ambiente grande cuya
temperatura es de 30ºC encontrar el flujo de calor entre los cilindros.
DATOS:
T1 ( 620 273 )K
T3
d 1 12cm
T2 ( 200 273 )K
1 0.59
d 2 22cm
1
T1
d1
L
2 T2
d2
2 0.47
F21 0.45
L 25cm
F22 0.29
5.67 10
8
W
2
m K
4
2
A1 L d 1
A1 0.09425 m
A2 L d 2
A2 0.17279 m
4
T1
1 1
2
Para los factores de forma
A1 1
POR PROPIEDAD DE SUMATORIA
1
F11 F12 F13 1
A2 F23
F21 F22 F23 1
4
T 3
F31 F32 F33 1
1
A1 F12
1 3
A3 3
POR PROPIEDAD DE RECIPROSIDAD
0
A1 F12 A2 F21
1
A1 F13
F12
1 2
F21
F12 0.825
F13 1 F11 F12
F13 0.175
4
F23 1 F21 F22
F23 0.26
1
4
T1
T1
A1
A2 2
T 2
4
A2
F11 0
Req
1 1
A1 1
A2 F21
1
A1 F13
1
A1 F13
1
A2 F23
1
A2 F23
1
1
2
A2 F21
A2 2
4
T 2
Reqiv
Req 25.03311
1
2
m
4
T 2
Univ. Erwin Choque Conde
T1 T2
4
Q12
Req
4
Q12 1326.99648 W
Página 92
89. Un cono truncado con fondo abierto de 15 cm de Diámetro superior, 30 cm de diámetro inferior y
20 cm de altura, tiene una temperatura uniforme de 1000K en su superficie superior, mientras que
en la superficie lateral esta perfectamente aislada .Las emisividades de las superficies superior y
lateral son 0.72 y 0.32 respectivamente. Tomar el factor de forma de las superficies superior al
lateral como 0.92 Determinar la cantidad de calor que se irradia hacia un ambiente amplio a 20ºC a
través del fondo abierto y la temperatura de la superficie lateral en condiciones estacionarias.
DATOS:
d 15cm
d
2
T2
T2 1000 K
D 30cm
H 20cm
T3 ( 20 273 )K
2 0.72
El área
2
F21 0.92
1 0.32
5.67 10
8
W
2
m K
H
A2
4
1
T1
2
d
4
2
A2 0.01767 m
2
ñ
D
D d H2
2
A1
T3
2
F12
4
T 2
ñ 0.2136 m
2
A1 0.15099 m
ñ ( D d )
A2
F21
A1
F12 0.10768
F11 0.15
1 2
F13 1 F12 F11
A2 2
F22 0
F23 1 F22 F21
1
A1 F12
A1 1
4
T1
A2 F23
A2 2
1
22.00661
1
61.50916
A1 F12
8.92224
A1 F13
2
m
1
A1 F13
A3 3
1 2
Q=0
1
F23 0.08
1 1
1
1 3
F13 0.74232
1
707.3553
A2 F23
2
2
m
1
m
1
1
2
m
1
1
1
1 2
A1 F12 A1 F13 A2 F23
Req
0
A2 2
4
T 3
T 2
Req 86.06019
4
Q23
4
T2 T3
Req
4
1
A1 F12
1
1
A1 F13
1
A2 F23
2
m
Q23 653.98555 W
R e q iv
4
Q23
T 3
4
T2 Rb
1 2
A2 2
1 2
4
Rb T2 Q23
A2 2
Rb 42307.99545
W
2
m
Univ. Erwin Choque Conde
Página 93
4
T 2
Rc T3
4
Rc 417.88188
W
2
m
1 2
Rb Rc
Qbac
A2 2
1
A1 F12
Qbac 594.7648 W
1
A1 F13
1
Rb
A1 F12
1
Ra
Qabc
A2 F23
Qac
Rc
1
4
T1
A1 F12
Ra 5724.51434
1
4
A1 F13
4
1
Ra Rb Qbac
A1 F12
Rb Ra
Qbac
T2
W
2
m
Ra
T2 563.68814 K
T 3
90. Un horno de cocción de pintura consiste en un ducto triangular largo en el que una superficie caliente
se mantiene a 1200K y la otra superficie esta aislada. Paneles pintados que se mantiene a 500K ocupan
una tercera superficie. El triangulo es de ancho 1 m por lado y la superficie caliente y aislada tiene
emisividad de 0.8 y la emisividad delos paneles es de 0.4 Durante la operación en este horno es de
estado estable. ¿a que rapidez se debe proporcionar energía al lado caliente por unidad de longitud del
ducto para mantener su temperatura a 1200K? ¿Cuál es la temperatura de la superficie aislada?
T1 1200 K
T1
1
T2
2
5.67 10
T3 500 K
W
2
m K
1 0.8
4
2 0.8
3 0.4
F12 0.5
T3
8
F31 0.5
F13 0.5
3
2
A 1m
La resistencia equivalente entre la superficie 1 y 3
1 1 1
A F13 A F31 A F12
1 1
1 3
Req
A 1
1
1
1
A 3
A F12
Q13
a)
4
T1 T3
4
A F13
4
R3
1 3
A 3
1 1
A 1
A F12
b)
1
2
m
5 W
Q13
Q13 T3
R1 1.08327 10
2
m
4
R3 51929.99757
W
2
m
1
1
A F12
R2 R1
Q13
A F13
1
1
A F31 A F13
R2 T2
Req 3.08333
Q13 36982.49838 W
Req
R1 T1
4
R2 71344.99703
W
2
m
1
R2
T2
Univ. Erwin Choque Conde
4
T2 1059.11987 K
Página 94
91. Un horno largo que se usa para los procesos de recosido de acero tiene una sección transversal
cuadrada de 3*3 m con paredes laterales a 1427 ºC y el techo a 1127ºC ¿Cuánto de calor se
transfiere por radiación al suelo del horno cuando esta a 327ºC las emisividades de todas las
paredes del horno es 0.5 factor de forma entre dos placas largas del mismo ancho “a” y separadas
a una distancia “c” está dado por F12 1 c / a
T1 1
3m
2 1/ 2
(c / a ) .
DATOS:
T1 ( 1127 273 )K
T2 ( 1427 273 )K
T3 ( 327 273 )K
T2
1 0.5
2
3m
a 3m
2 1
3 2
b 1m
c 3m
El área
A1 a b
T3 3
2
A1 3 m
A3 A1
2
A2 6 m
A2 2 a b
4
T1
F12 1
1 1
A1 1
c
2
0.5
a
F12 0.41421
F21
R1
1
A1 F12
4
T 2
A1 F13
1 2
A2 2
F31
1
A2 F23
A2
A1
A3
F12
F23
1 3
A3 * 3
A3
A2
a
F33 0
F21 0.20711
F13
F13 0.58579
F31 0.58579
F32 1 F31 F33
R3
c
F11 0
F13 1 F11 F12
1
R2
A1
F32
F32 0.41421
F23 0.20711
F22 1 F21 F23
F22 0.58579
4
T 3
Nodo R1
4
T1 R1
1 1
A1 1
R2 R1
1
A1 F12
R3 R1
1
0
A1 F13
6 R1 1.24264 R2 1.75736 R3 6.53456 10
Nodo R2
4
T2 R2
1 2
A2 2
R1 R2
1
A1 F12
R3 R2
1
5
0
A2 F23
1.24264 R1 8.48528 R2 1.24264 R3 2.84138 10
Univ. Erwin Choque Conde
6
Página 95
Nodo R3
4
T3 R3
1 3
A3 3
R2 R3
1
A2 F23
R1 R3
1
0
A1 F13
1.75736 R1 1.24264 R2 6 R3 22044.96
R1 232215.9069
W
2
m
R2 390121.9584
W
2
m
R3 145137.1894
W
2
m
Q13
R1 R3
Q13 153028.595152 W
1
A1 F13
92. Se utiliza un termómetro de mercurio para medir la temperatura del aire en un recipiente metálico
muy grande. Se registra una temperatura de 20ºC, se sabe que las paredes del recipiente se
encuentra a 5ºC el coeficiente de transferencia de calor entre el termómetro y el aire es 8.3
[W/m2ºC] y la emisividad del termómetro es 0.9. Calcule la temperatura efectiva del aire en el
recipiente.
T1 ( 20 273 )K
0.9
Tw ( 5 273 )K
Qh
h 8.3
Qr
W
2
m K
Tp=5ºC
T1=20ºC
5.67 10
8
W
2
m K
Balance de energía en el volumen de control
Eentra Egenerado Esale Ealmacenado
4
codiciones
Eentra 0
Egenerado 0
Ealmacenado 0
Esale Qradiacion Qconveccion
A T1 Tw
4
4
A h T1 T 0
4
4
T T1
T1 Tw
h
T 301.59046 K
93. Determine el factor de forma entre dos superficies concéntricas de radio interior y exterior r y R
respectivamente
F11 0
F11 F12 1
A1 F12 A2 F21
F21
F21 F22 1
Univ. Erwin Choque Conde
A1
A2
F12 1
F12
4 r
2
4 R
F22 1
R
r
2
R
r
2
2
Página 96
94. Dentro de una esfera de radio R se encuentra pegado radialmente a su superficie interior, dos
pequeñas superficies semiesferas de A1 y A2 respectivamente A1 se encuentran a 30º y A2 a 150º
de la horizontal. Encontrar el factor de forma F12 .
A2
A1
1
A1
1
F12
A1
F12
150
30
R
F12
1
A1
1
4 R
2
d A1 d A2
F12
1
A1
cos ( 1 ) cos ( 2 )
r
cos ( )
4 R
2
( 2 R cos ( ) )
A2
2
d A1
d A1 d A2
2
2
d A1 d A2
A1 A2
4 R
2
95. Determinar el flujo de calor desde un elemento de superficie circular de radio r=0.5cm cuya
temperatura es de 700C hasta un disco circular R=10cm y una temperatura de 100ºC paralelos entre
si cuyos centros están a una misma línea vertical situados a una distancia de 20cm ambos cuerpos
son negros.
100ºC
2
R
F12
1
A1
F12
1
A1
L
1
r
700ºC
F12
R
cos ( 1 ) cos ( 2 )
r
1
(L)
2
2
d A1 d A2
d A1 d A2
A1 A2
A1 L
2
2
L
T2 ( 100 273 )K
T1 ( 700 273 )K
L 20cm
R 10cm
5.67 10
8
2
m K
r 0.5cm
El área de los discos es:
W
A1 r
2
A2 R
A1 7.85398 10
2
R
F12
L
A1
A2
m
2
2
F12
F12 0.25
F21 0.00063
El factor de emisividad es
F 1
El calor transmitido de
la placa inferior ala superior
Q12 A1 F12 F T1 T2
Univ. Erwin Choque Conde
5 2
A2 0.03142 m
Los factores de forma:
F21
4
4
4
Q12 0.9763 W
Página 97
96. Un horno hemisférico (semiesférico) de diámetro D que se considera como cuerpo 2 intercambia
energía con un disco de diámetro D/2, colocado en el centro del piso, que se considera cuerpo 1,
estando el horno y el piso externamente aislado. Determinar los factores de forma F11 , F12 , F21 y F22
2
A2 2
D
D
D
A1
4 2
16
A1
2
2
1
Propiedades de la sumatoria
F11 F12 1
F12 F22 1
Por propiedad de reciprocidad
1
F22 1 F21 1
8
D
A2
.....2
De ecuación 2
A1 F12 A2 F21
F12
....1
F12 1
De ecuación 1
A1
2
2 D
F11 0
D/2
D
F21
2
16
16
16
D 2
2
F22
1
7
8
8
97. El receptor central de una planta de energía solar tiene forma de cilindro de 4 m de diámetro 13 m
de altura. El cilindro esta colgando en lo alto de una torre donde recibe la radiación solar reflejadas
por varias hileras de espejos situados al nivel del suelo. Si la temperatura de operación de la
superficie del cilindro es 427ºC calcule la perdida de calor cuando no sopla el viento y el aire esta a
27ºC. Exprese su resultado en forma de porcentaje de la radiación solar total que incide sobre el
cilindro si esta es de 20MW.
DATOS:
Tw
H
T
Qh
h
D 7m
Tw 427 C
H 13m
T 27 C
T Tw T
T 400 C
6
Qr 20 10 W
Qr
D
El coeficiente de convección para un cilindro vertical
1
h v 1.42
4
W
D 7 5
m 4 C 4
T
Univ. Erwin Choque Conde
h v 3.90417
W
2
m C
Página 98
El coeficiente de convección para un plano horizontal
1
4
T W
h H 1.32
D 7 5
m 4 C 4
El área vertical
h H 3.62923
W
2
m C
2
Av 285.88493 m
Av D H
El área horizontal (área circular)
AH
D
2
2
AH 38.48451 m
4
El calor perdido por el cilindro receptor
Qh 2 h H AH Tw T h v Av Tw T
5
Qh 5.58193 10 W
La perdida de calor por convección es:
X1%
Qh
Qr
X1% 2.79096 %
98. Un colector solar plano tiene una superficie con una emisividad 0.1 y un coeficiente de absorción
solar de 0.95, la temperatura de su superficie alcanza a 120ºC cuando la radiación solar es de 750
W / m 2 la temperatura del firmamento efectiva es de -10ºC, la temperatura del aire del medio
ambienté es de 30ºC. Asumir que el coeficiente de convección de la placa es
h 0.22 * (Tw Tamb)1 / 3 Calcular el calor efectivo que el colector aprovecha por superficie de
T1 ( 10 273 )K
calefacción.
Qr
G
T ( 30 273 )K
Tw ( 120 273 )K
Gr 750
0.95
W
2
5.67 10
8
W
2
m K
m
4
0.1
El coeficiente de T.C. por convección
1
h w 0.22 Tw T
Por la conservación de la energía
Eentra Egenerada Esale Ealmacenada
3
4
m2 K 3
W
h w 0.98591
W
2
m K
Egenerada 0
Ealmacenada Eentra Esale Qiradiacion Qradiacion Qconveccion
Ealmacenada Gr Tw T1
Ealmacenada 515.64047
4
4
h w Tw T
W
2
m
Univ. Erwin Choque Conde
Página 99
99. Un fluido criogénico se transporta por una tubería de 20 mm de diámetro, su superficie exterior
tiene una emisividad de 0.02 y 77ºK se coloca una tubería externamente y en forma concéntrica de
50 mm de diámetro interior y una emisividad de 0.05 y 300ºK, el espacio entre las superficies es
vació absoluto. Calcular el calor perdido (o ganado) por el fluido criogénico y en cuanto disminuiría
(o aumentaría) este calor si se coloca una placa cilíndrica de protección contra la radiación de 35
mm de diámetro y emisividad de 0.02 para ambos lados.
DATOS:
d2
d1
d2
d1
d3
1 0.02
2 0.05
T1 77 K
T2 300 K
d1 20mm
d2 50mm
3 0.02
Lt 1m
d3 d1
( d2 d1 )
2
5.67 10
d3 35 mm
a)
q1
4
T1 T2
1 1
A1 1
1
A1 F12
A2 2
4
1 1
d1 Lt 1
4
T1 T2
1 2
T1 T2
q1
4
1 1
d1 Lt 1
8
W
2
m K
F12 1
F32 1
F13 1
F13 1
4
4
1
Lt d1 F12
1 2
d2 Lt 2
4
1
Lt d1 F12
q 1 0.49881 W
1 2
d2 Lt 2
b)
Rtot
q2
1 1
A1 1
A1 F13
2
1 3
A3 3
1
A3 F32
4
T1 T2
1 1
Lt d1 1
x%
1
q2 q1
q1
1
Lt d1 F13
2
4
1 2
A2 2
1 3
Lt d3 3
1
Lt d3 F32
1 2
q 2 0.25165 W
Lt d2 2
x% 49.54955 %
Univ. Erwin Choque Conde
Página 100
incide sobre un colector solar plano que se utiliza para calentar
agua .El área del colector es de 3 m y 90 % de la radiación solar pasa a través de la cubierta de
Un flujo solar de 700 W / m
100.
2
2
vidrio y es absorbida por la placa de absorción. El colector refleja el 10% restante. Fluye agua por
la tubería en la parte posterior de la placa de absorción, y se calienta de una temperatura de Ti a
una temperatura de salida Tf. La cubierta de vidrio que opera a 30ºC tiene una emisividad de 0.94
y experimenta un intercambio de radiación con el espacio abierto a -10ºC. El coeficiente de
2
convección entre la cubierta de vidrio y el aire ambiente a 25ºC es de 10 W / m º C
a) Lleve a cabo un balance de energía general sobre el colector para obtener una
expresión de la rapidez a la que se colecta calor útil por unidad de área del colector, “Q”.
Determine el valor de Q.
b) Calcule la elevación de temperatura del agua (Ti-Tf) si el flujo es 0.01 kg / s . Suponga
que el calor específico del agua es 4.179 kJ / kg º C .
c) La eficiencia del colector se define como la razón del calor útil colectado a la rapidez con
que incide la energía solar sobre el colector. ¿Cuál es el valor del rendimiento?
0.94
0.9
2
Ac 3m
h
Gr
Qr
Tw ( 30 273 )K
T
T1 ( 10 273 )K
Tcp
T ( 25 273 )K
h c 10
W
2
m K
5.67 10
8
W
2
m K
m=0.01kg/s
T1
G 700
T2
4
W
2
m
Cp 4.179 10
a)
Balance de energía
3
J
kg K
kg
mc 0.01
s
Eentra Egenerado Esale Ealmacenado
Qirradiacion Qradiacion Qconveccion Qagua 0
Qagua Ac G Ac Tw T1
4
4
Ac h c Tw T
Qagua 1157.25961 W
b)
Qagua mc Cp Ti Tf
c)
Qagua
G Ac
Univ. Erwin Choque Conde
T fi
Qagua
mc Cp
T fi 27.69226 K
55.1076 %
Página 101
ANEXOS
Univ. Erwin Choque Conde
Página 102
Anexo A. FORMULARIO
Ecuación de Furrier
1 i T 1 T
q
q i q q
1.- MECANISMOS DE TRANSFERENCIA
T
Q A* k *
L
;
Q A * h * T
Ecuación de Poisson
Q A * * * (T1 T 2 )
4
QW : Flujo de Calor
W
k
: Coeficiente de conductividad
mK
W
h 2 : Coeficiente de convección
m K
W
5.67 E 8 2 4 : Constante de Boltzman
m K
: Emisividad del material
T K : Diferencia de temperatura
Analogía eléctrica
Q
T
RTC
Resistencia por conducción
Rk
L
A*k
Resistencia por convección
Rk
1 i T g
q
0
q i q q k
4
Ecuación de La Place
i0
i 1
i2
q: coordenada generalizada
W
g 3 : Generación de energía por unidad de
m
volumen
m2
Difusividad de Térmica
s
Condiciones de frontera
- Condición de frontera de primera clase
(Cuando se conoce la temperatura de pared)
1
A*h
T ( x)
El área media logarítmica (Cilindros)
ALn
Ae Ai
lnAe / Ai
T ( x )
x
Ae * Ai 4 * * D * d
2.- DISTRIBUCIÓN DE TEMPERATURA
Ecuación general de la conducción
g 1 T
k
1 i T g 1 T
q
q i q q k
2T
Univ. Erwin Choque Conde
T1
( x 0 )
f1
- Condición de frontera de tercera clase
(Cuando se conoce la temperatura del medio
ambiente)
Balance térmico en x=0
Qh Qk hT T( x ) k
Univ. ERWIN CHOQUE CONDE
MEC-2251
( x x1)
- Condición de frontera de segunda clase
(Cuando se conoce el flujo de calor)
El área media cuadrática (esferas)
Ac
1 i T
q
0
q i q q
q x Cord Re ct.
q r Cord Cilindriaca.
q r Cord Esferica.
FORMULARIO
T
x
FNI
MEC
x 0
16-4-07
1-3
Página 103
3.- ESPESOR TÉCNICO ECONÓMICO
5.- ALETAS
$us
CV Q * E * t
: Costo variable
año
CU * A( n ) $us
CF
año : Costo fijo
a
$us
CU 2 : Costo unitario
m
$us
CT C F CU
costo total
año
Distribución de temperatura en una aleta
d 2 ( x)
m 2 * ( x) 0
dx 2
( x) T ( x) T C1* e mx C 2 * e mx
Calor transferido con aletas longitudinales de
sección constante
a) Aletas largas
Qa h * P * k * A * (To T)
b) Aletas de longitud finita extremo aislado
Qa h * P * k * A * (To T) * tagh(mL)
Área enésima de un cilindro
A( n ) * L * ( D 2 * ( n 1) * e ais )
c) Aletas de longitud finita en cuyo extremo
existe convección
A( n ) 2 * r * L * ( r ( n 1) * e ais )
Qa Aa * h * * T
área media enésima del aislante para un cilindro
Amaisl
2 * * n * L * e ais
2 * n * e ais
ln 1
de
QLa ALa * h * T
Flujo total de superficies aleteadas
Q QLa Qa
A( n ) 4 * * D 2 * ( n 1) * eais
2
Rendimiento de la aleta
A( n ) 16 * * r ( n 1) * eais
2
área media enésima del aislante para una esfera
A( n ) 4 * * re * re n * eais
4.- CONDUCCIÓN EN RÉGIMEN TRANSITORIO
Ti T
e Bi*Fo
;
k
* Cp
h * Lc
# De Biot
Bi
k
Metodo de resist despresiable
Bi 0.1
Bi 0.1 40
Bi 40
*
Fo
numero de Furrier
2
Lc
V
Longitud característica Lc
A
Para una placa
Lc L
r
Para un cilindro Lc
2r/L
Para una esfera
Lc r / 3
s Tiempo de enfriamiento o calentamiento
Univ. Erwin Choque Conde
tgh(m * Lc )
m * Lc
Calor transferido en la superficie libre de aletas
Área enésima de una esfera
T f T
,
tgh(m * Lc )
m * Lc
; m
h* p
k * Atrans
Para aletas longitudinales en un tubo de sección
constante
L
m Longitud de la aleta
m Longitud equivalente de la
Lc L t / 2
aleta
t
m Espesor de la aleta
Área de la aleta
H * ( * d t * n) m Área libre de
Aa n * 2 * H * Lc m 2
ALa
2
aletas
p 2 * (H t)
m Perímetro de la aleta
Atrans H * t m
Área transversal de la aleta
H m Longitud del tubo.
2
Por analogía eléctrica
Calor transferido por toda la aleta
Q
T
1
AT * h * ,
Rendimiento al área ponderada
, 1
ATOT Aa ALa m 2
Aa
(1 )
ATOT
Área total
Página 104
W
hi 2 Coeficiente de convección interna del tubo
m k
W
he 2 Coeficiente de convección externa del tubo
m k
6.- CONVECCION
Nu * k Nu * k
h
Lc
Deq
Nu C * (Gr * Pr)n * K
Nu C * Rem Pr n * K
e (m) espesor del tubo
Si:
Gr * Pr E 9 Flujo laminar
Gr * Pr E 9 Flujo turbulento
Para flujo turbulento
Nu 0.027 * Re * Pr
0 .8
1/ 3
w
0.14
Para flujo laminar
di
Nu 1.86 * (Re* Pr* ) 0.3
L w
Re
v * Deq
0.14
Caliente
Tf 1 , Tf 2 K temperatura inicial, final del fluido Frió
Factor de obstrucción en un intercambiador
- coeficiente global limpio (sin incrustación)
* v * Deq
1
1
1
,
UiL hi hei
El diámetro equivalente:
Deq 4 *
Area de flujo
perimetro mojado
W
k Coeficiente de conducción del tubo
mk
J
Cp
Calor especifico
kgK
kg
w * Atran * v
s Flujo másico
Ft: factor de corrección de temperatura de( Tlog cc )
Tc1 , Tc 2 K temperatura inicial, final del fluido
-
T .C.
El diámetro equivalente de una sección anular
de 2 di 2
di
2
3
* Lc * g * * T
Gr
Numero de Grashoft
2
Cp *
Numero de Prandtl
Pr
k
Deq
hei
he * Ae
Ai
coeficiente global de diseño (con incrustación)
1
1
1
Rdi Rde
U iD hi hei
Q U iL * Ai * Ft * Tlog
Rdi, Rde
Factor de obstrucción interno, externo
8.- RADIACIÓN
Q A * Fe * F12 * * T14 T 2 4
Para el factor de forma
7.- INTERCAMBIADOR
Fij
Q Ui * Ai * Tlog Ue * Ae * Tlog
1
cos(i ) * cos(j ) * dAi * dAj
Ai Ai Aj
*r2
Propiedades del factor de forma:
- propiedad de reciprocidad
Q w * Cp * T
Ai * Fij Aj * Fji
Q U * A * Ft * Tlog
-
1
W
Ui
1 e Ai
1 Ai m 2 k
hi k Amt he Ae
N
Fij 1
j 1
Ui : coeficiente global referido al área interna
Diferencia logarítmica de temperatura a contra
corriente
Tlog
Tc1 Tf 2 Tc 2 Tf 1
Tc1 Tf 2
ln
Tc 2 Tf 1
propiedad de sumatoria
K
En método de analogía eléctrica:
- Resistencia superficial y de forma
1 i
Ai * i
,
1
Aj * Fji
m Área interna
Ae m Área externa
Ai
2
2
Univ. Erwin Choque Conde
Página 105
Anexo B. TABLAS Y GRAFICAS
B.-a.
TABLA 1. PARA INCROPERA 5.1)
Univ. Erwin Choque Conde
Página 106
B.-b.
GRAFICA 1. PARA PARED PLANA
Univ. Erwin Choque Conde
Página 107
B.-c.
GRAFICA 2. PARA CILINDRO INFINITO
Univ. Erwin Choque Conde
Página 108
B.-d.
GRAFICA 3. PARA ESFERAS
Univ. Erwin Choque Conde
Página 109
Anexo C.
P R O P IE D AD E S DE LO S M ATE R IALE S
Univ. Erwin Choque Conde
Página 110
2.- E M IS IV ID A D E S N O R M A L E S
METALES
Estado superficie Temperatura
(°C)
Emisividad
NO METALES
Estado superficie Temperatura
(°C)
Aluminio
placa pulida
25
0,040
Amianto
en cartón
Aluminio
placa pulida
200-600
0,038-0,06
Amianto
en papel
Aluminio
oxidado
100-500
0,20-0,33
Ladrillo
magnesita refractar
Aluminio
placa mate
25
0,070
Ladrillo
rojo, rugoso
Antimonio
pulido
37-260
0,28-0,31
Ladrillo
Latón
oxidado
200-500
0,600
Ladrillo
Latón
pulido
20-300
0,05-0,032
Carbón,
filamento
Latón
placa usada
50-350
0,220
Carbón,
carbonilla bujías
Latón
mate
50
0,202
Carbón,
Cromo
pulido
37-1100
0,058
Cobre
negro oxidado
37
0,780
Cobre
ligeramente mate
Cobre
pulido
Cobre
pulido electrolítico
Oro
no pulido
Oro
pulido
Hierro
oxidado
Hierro
esmerilado
Hierro
Emisividad
37
0,960
37
0,930
1000
0,380
20
0,930
gris, satinado
1100
0,750
sílice
540
0,800
1050-1400
0,526
95-270
0,953
negro de humo
20
0,930
Cerámica
alfarería, satinado
20
0,900
Cerámica
porcelana
22
0,920
Cerámica
refractaria, negra
93
0,940
Arcilla
caldeada
70
91
37
0,94
25
0,037
37-260
0,04-0,05
80
0,018
Hormigón
rugoso
20
0,470
Vidrio
liso
37-260
0,020
Vidrio
Pyrex, plomo, sosa
22
0,940
260-530
0,95-0,85
100
0,740
Hielo
20
0,240
Hielo
liso
0
0,966
rugoso
0
0,985
pulido
425-1025
0,14-0,38
Mármol
grano fino pulido
22
0,93
Hierro
pulido electrolítico
175-225
Hierro
todo oxidado
Hierro
laminado
Fundición
mecanizada
Fundición
0,052-0,064 Mica
37
0,75
Mampostería
emplastecida
0
0,930
0,87-0,95
Papel
ordinario
20
0,8-0,9
0,44
Papel
amianto
20
0,950
0,64-0,78
Papel
alquitranado
20
0,910
200
0,63
Papel
ordinario
95
0,920
23
0,280
Yeso blanco
rugosa
20
0,930
pulido
130-260
0,08-0,056
Porcelana
vidriada
20
0,930
pulido
37-260
0,07-0,13
Cuarzo fundido
rugoso
20
0,930
Magnesio
oxidado
275-825
0,55-0,2
Goma blanda
gris
25
0,860
Molibdeno
para filamentos
700-2600
0,10-0,20
Goma dura
negra rugosa
25
0,950
Molibdeno
Monel
Níquel
Níquel
Níquel
Platino
Platino
Platino
Platino
Plata
Plata
Acero
Estaño
Estaño
Tungsteno
Tungsteno
Cinc
Cinc
pulido
pulido
oxidado a 600ºC
pulido
electrolítico
electrolítico
placa pulida
oxidado a 600ºC
filamento
pulida, pura
pulida
pulido
brillante
pulido
para filamentos
filamento envejeci
oxidado
pulido
150-480
37
260-540
100-260
37-260
260-540
260-540
260-540
26-1225
225-625
37-370
23
225-265
37-370
3300
25-3300
20
225-325
0,02-0,05
0,170
0,37-0,48
0,045-0,07
0,04-0,06
0,06-0,1
0,06-0,1
0,07-0,11
0,04-0,19
0,02-0,03
0,02-0,03
0,160
0,02-0,03
0,070
0,390
0,03-0,35
0,250
0,05-0,06
Madera de haya
Madera de encina
Tierra
PINTURAS
Aluminio
Aluminio
Aluminio pintado
Aluminio
Aluminio
Laca
Laca
Aceite
Aceite pintura
Baquelita
Esmalte
Esmalte
Pintura al aceite
Imprimación minio
láminas
láminas
25
25
37
0,935
0,885
0,950
100
20
150-300
100
100
100
80
20
100
80
20
25
1-200
20-1100
0,300
0,390
0,350
0,520
0,300
0,925
0,970
0,89-0,97
0,92-0,96
0,935
0,900
0,876
0,885
0,930
20
0,69
925-1100
22
oxidada a 600ºC
200-600
Plomo
oxidado a 200ºC
Plomo
oxidado gris
Plomo
Magnesio
Univ. Erwin Choque Conde
bronce de
esmaltado rugoso
calentado a 325ºC
Al 10%, laca 22%
Al 26%, laca 27%
blanca
negra mate
pintura
todos los colores
esmaltada
blanco rugoso
negro brillante
Página 111
3.- A B S O R T IV ID A D S O L A R D E S U P E R F IC IE S
METALES
Estado superficial
Absortividad
METALES
Estado superficial
Absortividad
Aluminio
pulido
0,10
Magnesio
pulido
0,19
Aluminio
anodizado
0,14
Magnesio
oxidado
0,55-0,2
Aluminio
en placas
0,15
Níquel
muy pulido
0,15
Bronce
pulido
0,3-0,5
Níquel
pulido
0,36
Bronce
mate
0,4-0,65
Níquel
oxidado
0,79
Cromo
electroplateado
0,41
Platino
brillante
0,31
Cobre
muy pulido
0,18
Plata
muy pulida
0,07
Cobre
decapado
0,25
Plata
pulida
0,13
Cobre
decolorada por exposición
0,64
Acero inoxidable
pulido
0,33
0,21
Acero inoxidable
decapado
0,52
Oro
Hierro
galvanizado pulido
0,34
Tungsteno
muy pulido
0,37
Hierro
galvanizado nuevo
0,64
Cinc
muy pulido
0,34
Hierro
mate, oxidado
0,96
Cinc
pulido
0,55
NO METALES
NO METALES
Asfalto pavimento
0,85
Hormigón
descolorido
0,65
Asfalto pavimento
libre de polvo
0,93
Hormigón
marrón
0,85
Asfalto pavimento
nuevo
0,93
Hormigón
sucio, oscuro
0,71
Ladrillo
barnizado blanco
0,26
Granito
Ladrillo
arcilla, barnizado crema
0,36
Grasa
0,75-0,80
Ladrillo
rojo
0,70
Grava
0,29
Ladrillo rojo
satinado oscuro
0,77
Oxido de magnesio
Mármol
sin pulir
0,47
Pintura aceite
plomo blanco
Mármol
blanco
0,44
Pintura aceite
crema clara
0,30
Mármol
con fisuras
0,60
Pintura aceite
verde claro
0,50
Papel aglomerado
0,25
Pintura aluminio
Papel blanco
0,28
Pintura aceite
Arena
0,76
Pintura aceite negra sobre hierro galvanizado
Serrín de madera
0,15
0,24-0,26
0,55
gris claro
0,75
gris plateado
0,79
Pizarra
gris azulado
0,85
Hollín, carbón
0,95 Pizarra
gris verdoso
0,88
Oxido de cinc
0,15 Pizarra
gris oscuro
0,90
Nieve
0,75 Pizarra
0,45
limpia
Univ. Erwin Choque Conde
0,2-0,35
Página 112
4.- P R O P IE D A D E S T E R M IC A S D E A L G U N O S E L E M E N T O S M E T A L IC O S
Conductividad térmica "k" (W/mºK), a la temperatura de:
K g/m 3
Propiedades a 20ºC
6
x 10 T.fusión
k
2
°K
kJ/KgºC W /m .ºK m /seg
cp
ELEMENTO
200°K
273°K
400°K
600°K
800°K 1000°K 1200°K
Aluminio
237,0
236,0
240,0
232,0
220,0
2702
896
236,0
97,5
933
Antimonio
30,2
25,5
21,2
18,2
16,8
6684
208
24,6
17,7
904
Berilio
301,0
218,0
161,0
126,0
107,0
1850
1750
205,0
63,3
1550
Bismuto
9,7
8,2
9780
124
7,9
6,5
545
Boro
52,5
31,7
18,7
2500
1047
28,6
10,9
2573
Cadmio
99,3
97,5
94,7
8650
231
97,0
48,5
594
Cesio
36,8
36,1
1873
230
36,0
83,6
302
Cromo
111,0
94,8
87,3
7160
440
91,4
29,0
2118
Cobalto
122,0
104,0
84,8
8862
389
100,0
29,0
1765
Cobre
413,0
401,0
392,0
383,0
371,0
357,0
342,0
8933
383
399,0
116,6
1356
Germanio
96,8
66,7
43,2
27,3
19,8
17,4
17,4
5360
61,6
Oro
327,0
318,0
312,0
304,0
292,0
278,0
262,0
19300
129
Hafnio
24,4
23,3
22,3
21,3
20,8
20,7
20,9
13280
23,1
2495
Indio
89,7
83,7
74,5
7300
82,2
430
Iridio
153,0
148,0
144,0
138,0
132,0
126,0
120,0
22500
134
147,0
48,8
2716
Hierro
94,0
83,5
69,4
54,7
43,3
32,6
28,2
7870
452
81,1
22,8
1810
Plomo
36,6
35,5
33,8
31,2
11340
129
35,3
24,1
601
11,3
80,5
8,1
71,3
89,0
6,3
65,3
73,0
5,2
62,4
1211
316,0
126,9
1336
Litio
88,1
79,2
72,1
Magnesio
159,0
157,0
153,0
Manganeso
7,2
7,7
Mercurio
28,9
Molibdeno
143,0
139,0
134,0
126,0
118,0
112,0
105,0
10240
251
138,0
53,7
2883
Níquel
106,0
94,0
80,1
65,5
67,4
71,8
76,1
8900
446
91,0
22,9
1726
Niobio
52,6
53,3
55,2
58,2
61,3
64,4
67,5
8570
270
53,6
23,2
2741
Paladio
75,5
75,5
75,5
75,5
75,5
75,5
12020
247
75,5
25,4
1825
Platino
72,4
71,5
71,6
73,0
75,5
78,6
21450
133
71,4
25,0
2042
Potasio
104,0
104,0
52,0
860
741
103,0
161,6
337
149,0
146,0
534
3391
77,4
42,7
454
1740
1017
156,0
88,2
923
7290
486
7,8
2,2
1517
13546
82,6
234
Renio
51,0
48,6
46,1
44,2
44,1
44,6
45,7
21100
137
48,1
16,6
3453
Rodio
154,0
151,0
146,0
136,0
127,0
121,0
115,0
12450
248
150,0
48,6
2233
Rubidio
58,9
58,3
1530
348
58,2
109,3
312
Silicio
264,0
168,0
98,9
61,9
42,2
31,2
25,7
2330
703
153,0
93,4
1685
Plata
403,0
428,0
420,0
405,0
389,0
374,0
358,0
10500
234
427,0
173,8
1234
Sodio
138,0
135,0
971
1206
133,0
113,6
371
Tántalo
57,5
57,4
57,8
58,6
59,4
60,2
61,0
16600
138
57,5
25,1
3269
Estaño
73,3
68,2
62,2
5750
227
67,0
51,3
505
Titanio
24,5
22,4
20,4
19,4
19,7
20,7
22,0
4500
611
22,0
8,0
1953
Tungsteno
197,0
182,0
162,0
139,0
128,0
121,0
115,0
19300
134
179,0
69,2
3653
Uranio
25,1
27,0
29,6
34,0
38,8
43,9
49,0
19070
113
27,4
12,7
1407
Vanadio
31,5
31,3
32,1
34,2
36,3
38,6
41,2
6100
502
31,4
10,3
2192
Cinc
123,0
122,0
116,0
105,0
7140
385
121,0
44,0
693
Circonio
25,2
23,2
21,6
20,7
21,6
23,7
25,7
6570
272
22,8
12,8
2125
Univ. Erwin Choque Conde
Página 113
5.- P R O P IE D A D E S T E R M IC A S D E A L G U N A S A L E A C IO N E S
Conductividad térm ica en (W /m ºC )
Densidad Calor Conduct. Difusividad
x 105
a la tem peratu ra en ºC:
especif
k
2
Kg/m3 J/kgºK W/mºK m /seg
-100 0ºC 100 200 300 400 600 800 1000
Duraluminio
94-96% Al; 3-5% Cu
2787
833
164
6,680
126 159 182 194
Siluminio
87% Al; 1,33% Si
2659
871
164
7,100
119 137 144 152 161
Alusil
80% Al; 20% Si
2627
854
161
7,172
144 157 168 175 178
Al-Mg-Si
97% Al; 1% Mg; 1% Si
2707
8922
177
7,311
175 189 204
Bronce de alumini 95% Cu; 5% Al
8666
410
83
2,330
Bronce
75% Cu; 25% Sn
8666
343
26
0,860
Latón rojo
85% Cu; 9% Sn; 6% Zn
8714
385
61
1,804
71
5
9
Latón
70% Cu; 30% Zn
8522
385
111
3,412
88
128 144 147
Plata alemana
62% Cu; 15% Ni; 22% Zn
8618
394
24,9
0,733
19,2
147
3
40
45 48
Constantán
60% Cu; 40% Ni
8922
410
22,7
0,612
21
21
26
2
Fundición
4% C
7272
420
52
1,702
Acero al carbono 0,5% C
7833
465
54
1,474
52
5 48 45 42 35 31 29
54 42 40 36 33 29 28
1% C
7801
473
43
1,172
43
33 36 35 33 31 28 28
1,5% C
7753
486
36
0,970
36
Acero al cromo
1% Cr
7865
460
61
1,665
55
66 52 47 42 36 33 33
5% Cr
7833
460
40
1,110
38
42 36 36 33 29 29 29
20% Cr
7689
460
40
1,11
22
20 22 22 24 24 26 29
2
Acero al níquel
10% Ni
7945
460
26
0,720
20% Ni
7993
460
19
0,526
40% Ni
8169
460
10
0,279
60% Ni
8378
460
19
0,493
80% Ni
8618
0,46
35
0,872
Invar 36% Ni
8,137
460
10,7
0,286
Acero al Cr-Ni
15% Cr; 10% Ni
7865
460
19
0,526
15% Cr; 40% Ni
8073
460
11,6
0,305
18% Cr; 8% Ni
7817
460
16,3
0,444
17
1 17 19 19 22 27 31
6
20% Cr; 15% Ni
7833
460
15,1
0,415
25% Cr; 20% Ni
7865
460
12,8
0,361
80% Cr; 15% Ni
8522
460
17
0,444
Acero al mangane 1% Mn
7865
460
50
1,388
5% Mn
7849
460
22
0,637
Acero al silicio
1% Si
7769
460
42
1,164
5% Si
7417
460
19
0,555
P ro p ie d a d e s a 2 0 ºC
A leacion e s
C o m p o sic ió n
Acero al tungsteno 1% W
5% W
10% W
Ni-Cr
90% Ni; 10% Cr
80% Ni; 20% Cr
Mg-Al; electrol. Mg; 7 % Al; 1,5% Zn;
Univ. Erwin Choque Conde
7913
8073
8314
8666
8314
1810
448
435
419
444
444
1000
66
54
48
17
12,6
66
1,858
1,525
1,391
0,444
0,343
3,605
19
1 21 23 25
71 16 17 18 23
14
25 74 83
62
2
Página 114
6.- P R O P IE D A D E S T E R M IC A S D E A L G U N O S M A T E R IA L E S D E
C O N S T R U C C IO N Y A IS L A N T E S
MATERIAL
Amianto
Asfalto
Baquelita
Ladrillo común
Ladrillo de carborundum (50% SiC
Ladrillo de carborundum
Ladrillo de magnesita (50% MgO)
Ladrillo de mampostería
Ladrillo de sílice (95% SiO2)
Ladrillo de circonio (62% ZrO2)
Ladrillo al cromo
Arcilla refractaria, cocida a 1330º
Arcilla refractaria, cocida a 1450º
Cartón
Cemento (duro)
Arcilla (48,7% humedad)
Carbón, (antracita)
Hormigón (seco)
Corcho (tableros)
Corcho (expandido)
Tierra de diatomeas
Tierra arcillosa (28% humedad)
Tierra arenosa (8% humedad)
Fibra de vidrio
Vidrio, (ventanas)
Vidrio, (lana de)
Granito
Hielo (0°C)
Linóleo
Mica
Corteza de pino
Yeso
Plexiglás
Madera (chapa)
Poliestireno
Goma dura (ebonita)
Goma esponjosa
Arena seca
Arena húmeda
Serrín
Madera de roble
Madera (Pino, abeto, abeto rojo)
Láminas de fibra de madera
Univ. Erwin Choque Conde
T em p eratu ra
D en sid ad
C a lo r e s p e c ífic o
cp
C o n d . té rm ic a
k
ºC
kg
m3
Joules
kgºK
W
mºK
x 10 5
m2
seg
816
0 ,1 1 3
0 ,0 3 6
20
383
2 0 -5 5
2120
20
20
20
600
1400
20
200
650
1200
20
20
20
200
550
900
500
800
1100
500
800
1100
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
20
1270
1800
2200
0 ,7 4 -0 ,7 6
840
2000
1,13
1700
1900
3600
3000
837
0,84
2000
0,96
2300
0,96
1545
1370
500
120
120
466
1500
1500
220
2800
100
200
2750
913
535
2900
342
1800
1180
590
1050
1150
224
1640
215
609-801
416-421
200
D ifu siv . térm ic a
880
1260
837
1880
879
800
670
1830
2009
2390
2720
0,233
0,38-0,52
5,820
18,5
11,1
2,680
3,81
2,77
1,9
0,658
1,070
2,440
2,32
2,47
1,99
1,04
1,07
1,09
1,28
1,37
1,4
0,14-0,35
1,047
1,260
0,238
0,128
0,042
0,036
0,126
1,510
1,050
0,035
0,810
0,036
0,040
3,000
2,220
0,081
0,523
0,080
0,814
0,195
0,109
0,157
0,163
0,055
0,582
1,130
0,071
0,17-0,21
0,150
0,047
0,028-0,034
0,046
0,092
0,098
0,079
0,054
0,04
0,101
0,013-0,015
0,049
0,015-0,044
0,031
0,034
0,028
0,124
0,006
0,011-0,012
0,012
Página 115
7.- P R O P IE D A D E S T E R M IC A S D E A L G U N O S A C E IT E S Y G L IC E R IN A S
A C E IT E D E M O TO R SIN U SA R
Temperatura
ºC
D en sid a d
(K g/m 3 )
C a lo r
e sp ec ífic o c p
J /K g ºC
C o n d u c tiv .
térm ica "k "
W /m ºC
D if. térm ica
. 1 0 10
(m 2 /s e g )
V isc. d in ám .
. 1 0 3
(N .seg/m 2 )
V isc. cinem .
. 1 0 6
(m 2 /s e g )
Nº de Prandt
Pr
0
20
40
60
80
100
120
140
160
899,1
888,2
876,1
864
852
840
829
816,9
805,9
1796
1880
1964
2047
2131
2219
2307
2395
2483
0,147
0,145
0,144
0,14
0,138
0,137
0,135
0,133
0,132
911
872
834
800
769
738
710
686
663
3848
799
210
72,5
32
17,1
10,3
6,54
4,51
4280
900
240
83,9
37,5
20,3
12,4
8
5,6
47100
10400
2870
1050
490
276
175
116
84
(
g
2
1 0 -10 )
8475
A C E IT E D E T R A N SFO R M A D O R E S
Temperatura
ºC
D en sid a d
(K g/m 3 )
C a lo r
e sp ec ífic o c p
J /K g ºC
C o n d u c tiv .
térm ica "k "
W /m ºC
D if. térm ica
. 1 0 10
(m 2 /s e g )
V isc. d in ám .
. 1 0 3
(N .seg/m 2 )
-50
-40
-30
-20
-10
0
10
20
30
40
922
916
910
904
898
891
885
879
873
867
1,7
1,68
1,65
1,62
1,6
1,62
1,65
1,71
1,78
1,83
0,116
0,116
0,115
0,114
0,113
0,112
0,111
0,111
0,11
0,109
742
750
764
778
788
778
763
736
707
688
29320
3866
1183
365,6
108,1
55,24
33,45
21,1
13,44
9,364
V isc. cinem .
. 1 0 6
(m 2 /s e g )
31800
4220
1300
404
120
67,5
37,8
24
15,4
10,8
Nº de Prandt
Pr
428600
56300
17000
5200
1530
867
495
326
218
157
G L IC ER IN A C 3 H 5 (O H ) 3
T em p eratu ra
ºC
D en sid a d
(K g/m 3 )
0
10
20
30
40
50
1276
1270
1264
1258
1252
1245
V isc. cin em át.
C a lo r
e sp ec ífic o c p
. 1 0 4
(m 2 /s e g )
J /K g ºC
2261
2319
2386
2445
2512
2583
83,1
30
11,8
5
2,2
1,5
C o n d u c ti v i d a
térm ica "k "
W /m ºC
D if. térm ica
. 1 0 7
(m 2 /s e g )
N º d e P ra n d t
Pr
0,282
0,284
0,286
0,286
0,286
0,287
0,983
0,965
0,947
0,929
0,914
0,893
84700
31000
12500
5380
2450
1630
(ºK
0,0005
E T IL E N O G L IC O L C2 H 4 (O H 2 )
T em p eratu r
ºC
D en sid a d
(K g/m 3 )
0
20
40
60
80
100
1130,75
1116,65
1101,43
1087,66
1077,56
1058,5
Univ. Erwin Choque Conde
C a lo r
V isc. cin em át.
e sp ec ífic o c p
. 1 0 6
J /K g ºC
(m 2 /s e g )
2294
2382
2474
2562
2650
2742
57,53
19,18
8,69
4,75
2,98
2,03
C o n d u c ti v i d a
térm ica "k "
W /m ºC
D if. térm ica
. 1 0 7
(m 2 /s e g )
N º d e P ra n d t
Pr
0,242
0,249
0,256
0,26
0,261
0,263
0,934
0,939
0,939
0,932
0,921
0,908
615
204
93
51
32,4
22,4
(ºK
0,00065
Página 116
8.- P R O P IE D A D E S T E R M IC A S D E A L G U N O S M E T A L E S L IQ U ID O S
M E R C U R IO .- P u n to d e fu s ió n : -38,9ºC ; P u n to d e e b u llició n : 3 57ºC
Temper. ºC
0
20
50
100
150
200
250
315,7
D en sid a d
(K g/m 3 )
C o e fic ie n te
C a lo r
C o n d u c tiv .
d ila ta c . té rm . e sp ec ífic o c p térm ica "k "
W /m ºC
J /K g ºC
.1 03
D if. térm ica
. 1 0 7
(m 2 /s e g )
140,3
139,4
138,6
137,3
136,5
157
135,7
134
42,99
46,06
50,22
57,16
63,54
69,08
74,06
81,5
13628
13579
13506
13385
13264
13145
13026
12847
18,2
8,2
8,69
9,4
10,51
11,49
12,34
13,07
14,02
V isc. d in ám . V isc. cinem .
. 1 0 4
. 1 0 6
(m 2 /s e g )
(N .seg/m 2 )
16,9
15,48
14,05
12,42
11,31
10,54
9,96
8,65
0,124
0,114
0,104
0,0928
0,0853
0,0802
0,0765
0,0673
(
g
2
Nº Prandtl
0,0288
0,0249
0,0207
0,0162
0,0134
0,0116
0,0103
0,0083
1 0 -10 )
13,73
S O D IO .- P u n to d e fu sió n : 97,8ºC; P u n to d e eb u llición : 88 3 ºC
D en sid a d
(K g/m 3 )
T(ºC)
94,0
205,0
315,6
371,0
426,7
538,0
650,0
705,0
760,0
C o e fic ie n te
C a lo r
C o n d u c tiv .
d ila ta c . té rm . esp ec ífic o c p térm ica "k "
3
.1 0
J /K g ºC
W /m ºC
929
902
878,5
860
852,8
820,0
790
778
767,5
0,27
0,36
1382
1340
1304
1298
1277
1264
1261
1256
1270
86,30
80,30
75,78
72,40
69,39
64,37
60,56
59,70
56,58
D if. térm ica
. 1 0 5
(m 2 /s e g )
6,71
6,71
6,65
6,45
6,41
6,21
6,11
6,19
5,83
V isc. d in ám . V isc. cinem .
. 1 0 4
. 1 0 7
2
2
(m
/s e g )
(N .seg/m )
6,99
4,32
3,29
2,83
2,52
2,31
1,96
1,79
1,72
7,31
4,60
3,77
3,16
2,97
2,82
2,50
2,26
2,25
(
Pr
0,0110
0,0072
0,0057
0,0051
0,0046
0,0040
0,0041
0,0038
0,0385
B IS M U T O .- P u n to e fu sió n : 271ºC ; P u n t o d e eb u llició n : 1 4 77 ºC
d
C o e fic ie n te
C a lo r
C o n d u c tiv . D if. térm ica V isc. d in ám . V isc. cinem .
D en sid a d
T(ºC)
316
427
811
922
1033
(K g/m 3 )
d ila ta c . té rm . e sp ec ífic o c p térm ica "k "
.1 03
W /m ºC
J /K g ºC
10011
9867
9739
9611
9467
P L O M O .Temperatur
ºC
371
425
525
625
704
0,117
0,122
0,126
P u n to d e
fu s
D en sid a d
(K g/m 3 )
10540
10470
10350
10230
10140
Univ. Erwin Choque Conde
144,5
149,5
154,5
159,5
164,5
16,44
15,58
15,58
15,58
15,58
. 1 0 5
(m 2 /s e g )
. 1 0 4
(N .seg/m 2 )
. 1 0 7
(m 2 /s e g )
1,14
1,06
1,03
1,01
1,01
1,622
1,339
1,101
0,923
0,789
1,57
1,35
1,08
0,903
0,813
ión : 32 7 ºC ; P u n to d e e b u llició n : 737 ºC
V isc. d in ám ica V1 isc. cin em át. C o n d u c ti v i d a D ifu s . térm ic a
C a lo r
e sp ec ífic o c p
J /K g ºC
. 1 0 4
(N .seg/m 2 )
. 1 0 6
(m 2 /s e g )
térm ica "k "
W /m ºC
159
156
155
155
155
2,4
2,11
1,72
1,49
1,37
0,0230
0,0202
0,0166
0,0146
0,0140
16,1
17,5
19,0
20,4
21,9
. 1 0 6
(m 2 /s e g )
9,61
9,48
g
10 -9 )
4,96
16,7
(
Pr
0,014
0,013
0,011
0,009
0,008
2
g
2
1 0 -9 )
46,5
65,6
106
N º d e P ra n d t
Pr
0,024
0,019
0,014
0,011
0,009
Página 117
L IT IO .- P u n to d e fu sió n: 1 7 9ºC ; P u n to d e
llició n : 1 31 7ºC
eb
u
V
isc.
d
in
ám
ica
V isc. cin em át. C o n d u c ti v i d a D ifu s . térm ic a
C a lo r
Temperatur
D en sid a d
e sp ec ífic o c p
térm ica "k "
. 1 0 4
3
. 1 0 6
. 1 0 6
(K
g/m
)
2
2
ºC
2
(m
/s
e
g
)
(m
/s e g )
W
/m
ºC
J /K g ºC
(N .seg/m )
204,4
315,6
426,7
537,8
509,2
498,8
489,1
476,3
4365
4270
4211
4171
5,416
4,465
3,927
3,473
1,1098
0,8982
0,8053
0,7304
46,37
43,08
38,24
30,45
20,96
20,32
18,65
15,4
N º d e P ra n d t
Pr
0,051
0,043
0,0432
0,0476
P O T A S IO .- P u n to d e fu sió n : 6 3,9ºC ; P u n to d e eb u llició n : 7 6 0 ºC
Temperatur
ºC
D en sid a d
(K g/m 3 )
C a lo r
e sp ec ífic o c p
J /K g ºC
426,7
537,8
648,9
760
741,7
714,4
690,3
667,7
766
762
766
783
V isc. d in ám ica V isc. cin em át.
. 1 0 4
. 1 0 6
(m 2 /s e g )
(N .seg/m 2 )
2,108
1,711
1,463
1,331
0,2839
0,24
0,2116
0,1987
C o n d u c ti v i d a D ifu s . térm ic a
térm ica "k "
. 1 0 6
(m 2 /s e g )
W /m ºC
39,45
36,51
33,74
31,15
69,74
67,39
64,1
59,86
N º d e P ra n d t
Pr
0,0041
0,0036
0,0033
0,0033
N a -K , 56 % N a, 44 % K .- P u n to d e fu sió n : -11ºC ; P u n to d e e b u llició n : 7 8 4ºC
Temperatur
ºC
D en sid a d
(K g/m 3 )
C a lo r
e sp ec ífic o c p
J /K g ºC
93,3
204,4
315,6
426,7
537,8
648,9
889,8
865,6
838,3
814,2
788,4
759,5
1130
1089
1068
1051
1047
1051
Univ. Erwin Choque Conde
V isc. d in ám ica V isc. cin em át.
. 1 0 4
. 1 0 6
(m 2 /s e g )
(N .seg/m 2 )
5,622
3,803
2,935
2,15
2,026
1,695
0,6347
0,4414
0,3515
0,2652
0,2581
0,224
C o n d u c ti v i d a
térm ica "k "
W /m ºC
D ifu s . térm ic a
. 1 0 6
(m 2 /s e g )
N º d e P ra n d t
Pr
25,78
26,47
27,17
27,68
27,68
27,68
27,76
28,23
30,5
32,52
33,71
34,86
0,0246
0,0155
0,0115
0,0081
0,0076
0,0064
Página 118
9.- P R O P IE D A D E S T E R M IC A S D E L IQ U ID O S S A T U R A D O S
F R E O N 12
D if. térm ica
. 1 0 6
(m 2 /s e g )
V isc. d in ám .
. 1 0 6
N .seg/m 2
V isc. cinem .
. 1 0 6
(m 2 /s e g )
N º d e P ra n d t
Pr
5,01
5,14
5,26
5,39
5,50
5,57
5,60
5,60
5,60
5,55
5,45
4,796
4,238
3,770
3,433
3,158
2,990
2,769
2,633
2,512
2,401
2,310
0,310
0,279
0,253
0,235
0,221
0,214
0,203
0,198
0,194
0,191
0,190
6,2
5,4
4,8
4,4
4,0
3,8
3,6
3,5
3,5
3,5
3,5
T em p eratu r
ºC
D en sid a d
(K g/m 3 )
C a lo r
e sp ec ífic o c p
J /K g ºC
C o n d u c tiv .
térm ica "k "
W /m ºC
-50
-40
-30
-20
-10
0
10
20
30
40
50
1547
1519
1490
1461
1429
1397
1364
1330
1295
1257
1216
875
884,7
895,6
907,3
920,3
934,5
949,6
965,9
983,5
1001,9
1021,6
0,067
0,069
0,069
0,071
0,073
0,073
0,073
0,073
0,071
0,069
0,067
T em p eratu r
ºC
D en sid a d
(K g/m 3 )
C a lo r
e sp ec ífic o c p
J /K g ºC
C o n d u c tiv .
térm ica "k "
W /m ºC
D if. térm ica
. 1 0 6
(m 2 /s e g )
V isc. d in ám .
. 1 0 6
N .seg/m 2
V isc. cinem .
. 1 0 6
(m 2 /s e g )
N º d e P ra n d t
Pr
-50
-40
-30
-20
-10
0
10
20
30
40
50
703,7
691,7
679,3
666,7
653,6
640,1
626,2
611,8
596,4
581,0
564,3
4463
4467
4476
4509
4564
4635
4714
4798
4890
4999
5116
0,547
0,547
0,549
0,547
0,543
0,540
0,531
0,521
0,507
0,493
0,476
17,42
17,75
18,01
18,19
18,25
18,19
18,01
17,75
17,42
17,01
16,54
3,061
2,808
2,629
2,540
2,471
2,388
2,304
2,195
2,081
1,975
1,862
0,435
0,406
0,387
0,381
0,378
0,373
0,368
0,359
0,349
0,340
0,330
2,60
2,28
2,15
2,09
2,07
2,05
2,04
2,02
2,01
2,00
1,99
V isc. d in ám .
. 1 0 6
N .seg/m 2
V isc. cinem .
. 1 0 6
(m 2 /s e g )
N º d e P ra n d t
Pr
1794
1004
653,0
470,0
353,7
281,0
233,0
198,2
171,5
153,5
129,0
126,0
116,0
107,5
101,4
94,1
1,789
1,006
0,658
0,478
0,364
0,294
0,247
0,214
0,189
0,173
0,160
0,150
0,143
0,137
0,135
0,132
13,7
7,02
4,34
3,02
2,22
1,75
1,45
1,24
1,10
1,00
0,94
0,89
0,87
0,87
0,92
1,02
g
2
. 1 0 -10
26,84
A M O N IA CO
g
2
. 1 0 -10
18,64
AGUA
T em p eratu r
ºC
D en sid a d
(K g/m 3 )
C a lo r
e sp ec ífic o c p
J /K g ºC
C o n d u c tiv .
térm ica "k "
W /m ºC
D if. térm ica
. 1 0 6
(m 2 /s e g )
0
20
40
60
80
100
120
140
160
180
200
220
240
260
280
300
999,9
998,2
992,3
983,2
971,8
958,4
943,1
926,1
907,6
887,0
864,8
840,5
812,2
784,0
750,8
712,5
4226
4182
4178
4181
4194
4211
4245
4279
4338
4413
4501
4606
4752
4944
5204
6594
0,558
0,597
0,633
0,658
0,673
0,682
0,685
0,687
0,682
0,678
0,665
0,656
0,639
0,614
0,583
0,543
0,131
0,143
0,151
0,155
0,165
0,169
0,171
0,172
0,173
0,172
0,170
0,168
0,164
0,157
0,150
0,132
Univ. Erwin Choque Conde
g
2
. 1 0 -9
2,035
8,833
22,75
46,68
85,09
517,2
1766
Página 119
D IO X ID O D E CA R BO N O CO 2
T em p eratu r
ºC
D en sid a d
(K g/m 3 )
-50
-40
-30
-20
-10
0
10
20
30
1156,3
1117,8
1076,8
1032,4
983,4
927,0
860,0
772,6
597,8
C a lo r
V isc. cin em át.
e sp ec ífic o c p
. 1 0 6
J /K g ºC
(m 2 /s e g )
1840
1880
1970
2050
2180
2470
3140
5000
36400
0,119
0,118
0,117
0,115
0,13
0,108
0,101
0,091
0,08
C o n d u c ti v i d a
térm ica "k "
W /m ºC
D if. térm ica
. 1 0 7
(m 2 /s e g )
N º d e P ra n d t
Pr
0,085
0,1011
0,1116
0,1151
0,1099
0,1045
0,0971
0,0872
0,0703
0,4021
0,481
0,5272
0,5445
0,5133
0,4578
0,3608
0,2219
0,0279
2,96
2,46
2,22
2,12
2,2
2,38
2,8
4,1
28,7
(ºK
0,014
D IO X ID O D E A Z U FR E SO 2
T em p eratu r
ºC
D en sid a d
(K g/m 3 )
-50
-40
-30
-20
-10
0
10
20
30
40
50
1560,8
1536,8
1520,64
1488,6
1463,6
1438,46
1412,5
1386,4
1359,33
1329,22
1299,1
V isc. cin em át.
C a lo r
e sp ec ífic o c p
. 1 0 6
(m 2 /s e g )
J /K g ºC
1359,5
1360,7
1361,6
1362,4
1362,8
1363,6
1364,5
1365,3
1366,2
1367,4
1368,3
0,484
0,424
0,371
0,324
0,288
0,257
0,232
0,21
0,19
0,173
0,162
C o n d u c ti v i d a
térm ica "k "
W /m ºC
D if. térm ica
. 1 0 7
(m 2 /s e g )
N º d e P ra n d t
Pr
0,242
0,235
0,23
0,225
0,218
0,211
0,204
0,199
0,192
0,185
0,177
1,141
1,13
1,117
1,107
1,097
1,081
1,066
1,05
1,035
1,019
0,999
4,24
3,74
3,31
2,93
2,62
2,38
2,18
2
1,83
1,7
1,61
(ºK
0,00194
SO L U C IO N E U T E CT IC A CL O RU R O CALC IC O C l 2 C a 29,9%
T em p eratu r
ºC
D en sid a d
(K g/m 3 )
C a lo r
e sp ec ífic o c p
J /K g ºC
V isc. cin em át.
. 1 0 6
(m 2 /s e g )
C o n d u c ti v i d a
térm ica "k "
W /m ºC
D if. térm ica
. 17 0
(m 2 /s e g )
N º d e P ra n d t
Pr
-50
-40
-30
-20
-10
0
10
20
30
40
50
1319,8
1314,9
1310,2
1305,5
1300,7
1296,1
1291,4
1286,6
1281,9
1277,2
1272,5
2608
2635,6
2661,1
2688
2713
2738
2763
2788
2814
2839
2868
36,35
24,97
17,18
11,04
6,96
4,39
3,35
2,72
2,27
1,92
1,65
0,402
0,415
0,429
0,445
0,459
0,472
0,485
0,498
0,511
0,525
0,535
1,166
1,200
1,234
1,267
1,300
1,332
1,363
1,394
1,419
1,445
1,468
312
208
139
87,1
53,6
33
24,6
19,6
16
13,3
11,3
Univ. Erwin Choque Conde
(ºK
Página 120
10.- P R O P IE D A D E S T E R M IC A S D E A L G U N O S G A S E S Y V A P O R E S
V A PO R D E AG U A R E C A L E N T A D O
T em p eratu r
ºK
D en sid a d
(K g/m 3 )
C a lo r
e sp ec ífic o c p
k J/K gºC
V isc. d in ám .
. 1 0 6
(K g/m .seg )
V isc. cinem .
. 1 0 6
(m 2 /s e g )
C o n d u c tiv .
térm ica "k "
W /m ºC
D if. térm ica
. 1 0 4
(m 2 /s e g )
N º d e P ra n d t
Pr
380
0,5863
2,0600
12,71
21,6
0,0246
0,204
1,060
400
450
0,5542
0,4902
2,0140
1,9800
13,44
15,25
24,2
31,1
0,0261
0,0299
0,234
0,307
1,040
1,010
500
550
0,4405
0,4005
1,9850
1,9970
17,04
18,84
38,6
47,0
0,0339
0,0379
0,387
0,475
0,996
0,991
600
650
0,3652
0,3380
2,0260
2,0560
20,67
22,47
56,6
64,4
0,0422
0,0464
0,573
0,666
0,986
0,995
700
750
0,3140
0,2931
2,0850
2,1190
24,26
26,04
77,2
88,8
0,0505
0,0549
0,772
0,883
1,000
1,005
800
850
0,2739
0,2579
2,1520
2,1860
27,86
29,69
102,0
115,2
0,0592
0,0637
1,001
1,130
1,010
1,019
D en sid a d
(K g/m 3 )
C a lo r
e sp ec ífic o c p
k J/K gºC
V isc. d in ám .
. 1 0 7
(K g/m .seg )
C o n d u c tiv .
térm ica "k "
W /m ºC
D if. térm ica
. 1 0 4
(m 2 /s e g )
N º d e P ra n d t
Pr
5,2
5,2
5,2
5,2
5,2
5,2
5,2
5,2
5,2
5,2
5,2
8,4
50,2
125,5
156,6
181,7
230,5
275,0
311,3
347,5
381,7
413,6
H E L IO
T em p eratu r
ºK
3
33
144
200
255
366
477
589
700
800
900
1,4657
3,3799
0,2435
0,1906
0,1328
0,10204
0,08282
0,07032
0,06023
0,05286
V isc. cinem .
. 1 0 6
(m 2 /s e g )
0,0106
3,42
37,11
64,38
95,5
173,6
269,3
375,8
494,2
634,1
781,3
0,0353
0,0928
0,1177
0,1357
0,1691
0,197
0,225
0,251
0,275
0,298
0,04625
0,5275
0,9288
1,3675
2,449
3,716
5,215
6,661
8,774
10,834
0,74
0,7
0,694
0,7
0,71
0,72
0,72
0,72
0,72
0,72
N IT R O G E N O
Temperatur
ºK
D en sid a d
(K g/m 3 )
100
200
300
400
500
600
700
800
900
1000
1100
1200
3,4808
1,7108
1,1421
0,8538
0,6824
0,5687
0,4934
0,4277
0,3796
0,3412
0,3108
0,2851
Univ. Erwin Choque Conde
C a lo r
e sp ec ífic o c p
k J/K gºC
1,0722
1,0429
1,0408
1,0459
1,0555
1,0756
1,0969
1,1225
1,1464
1,1677
1,1857
1,2037
V isc. d in ám .
. 1 0 6
(K g/m .seg )
V isc. cinem .
. 1 0 6
(m 2 /s e g )
C o n d u c tiv .
térm ica "k "
W /m ºC
D if. térm ica
. 1 0 4
(m 2 /s e g )
Nº de Prandt
Pr
6,86
12,95
17,84
21,98
25,70
29,11
32,13
34,84
37,49
40,00
42,28
44,50
1,97
7,57
15,63
25,74
37,66
51,19
65,13
81,46
91,06
117,20
136,00
156,10
0,00945
0,01824
0,02620
0,03335
0,03984
0,04580
0,05123
0,05609
0,06070
0,06475
0,06850
0,07184
0,0253
0,1022
0,2204
0,3734
0,5530
0,7486
0,9466
1,1685
1,3946
1,6250
1,8591
2,0932
0,786
0,747
0,713
0,691
0,684
0,686
0,691
0,700
0,711
0,724
0,736
0,748
Página 121
A M O N IA CO
Temperatur
ºK
D en sid a d
(K g/m 3 )
220
273
323
373
423
473
0,9304
0,7929
0,6487
0,5590
0,4934
0,4405
V isc. d in ám .
. 1 0 6
(K g/m .seg )
V isc. cinem .
. 1 0 6
(m 2 /s e g )
C o n d u c tiv .
térm ica "k "
W /m ºC
D if. térm ica
. 1 0 4
(m 2 /s e g )
Nº de Prandt
Pr
2,1980
2,1770
2,1770
2,2360
2,3150
2,3950
7,25
9,35
11,04
12,89
14,67
16,49
7,60
11,80
17,00
23,00
29,70
37,40
0,01710
0,02200
0,02700
0,03270
0,03910
0,04670
0,2054
0,1308
0,1920
0,2619
0,3432
0,4421
0,930
0,900
0,880
0,870
0,870
0,840
V isc. cinem .
. 1 0 6
(m 2 /s e g )
C o n d u c tiv .
térm ica "k "
W /m ºC
D if. térm ica
. 1 0 4
(m 2 /s e g )
Nº de Prandt
Pr
1,92
4,34
7,49
10,53
16,84
20,76
25,90
31,71
37,90
44,34
51,34
58,51
66,25
73,91
82,29
90,75
99,30
108,20
117,80
138,60
159,10
182,10
205,50
229,10
254,50
280,50
308,10
338,50
369,00
399,60
432,60
464,00
504,00
543,50
0,0092
0,0137
0,0181
0,0223
0,0262
0,0300
0,0336
0,0371
0,0404
0,0436
0,0466
0,0495
0,0523
0,0551
0,0578
0,0603
0,0628
0,0653
0,0675
0,0732
0,0782
0,0837
0,0891
0,0946
0,1000
0,1050
0,1110
0,1170
0,1240
0,1310
0,1390
0,1490
0,1610
0,1750
0,0250
0,0575
0,1017
0,1316
0,2216
0,2983
0,3760
0,4222
0,5564
0,6532
0,7512
0,8578
0,9672
1,0774
1,1981
1,3097
1,4271
1,5510
1,6779
1,9690
2,2510
2,5830
2,9200
3,2620
3,6090
3,9770
4,3790
4,8110
5,2600
5,7150
6,1200
6,5400
7,0200
7,4410
0,770
0,753
0,739
0,722
0,708
0,697
0,689
0,683
0,680
0,680
0,680
0,682
0,684
0,686
0,689
0,692
0,696
0,699
0,702
0,704
0,707
0,705
0,705
0,705
0,705
0,705
0,704
0,704
0,702
0,700
0,707
0,710
0,718
0,730
C a lo r
e sp ec ífic o c p
k J/K gºC
A IR E
Temperatur
ºK
D en sid a d
(K g/m 3 )
C a lo r
e sp ec ífic o c p
k J/K gºC
V isc. d in ám .
. 1 0 5
(K g/m .seg )
100
150
200
250
300
350
400
450
500
550
600
650
700
750
800
850
900
950
1000
1100
1200
1300
1400
1500
1600
1700
1800
1900
2000
2100
2200
2300
2400
2500
3,6010
2,3675
1,7684
1,4128
1,1774
0,9980
0,8826
0,7833
0,7048
0,6423
0,5879
0,5430
0,5030
0,4709
0,4405
0,4149
0,3925
0,3716
0,3524
0,3204
0,2947
0,2707
0,2515
0,2355
0,2211
0,2082
0,1970
0,1858
0,1762
0,1682
0,1602
0,1538
0,1458
0,1394
1,027
1,010
1,006
1,005
1,006
1,009
1,014
1,021
1,030
1,039
1,055
1,063
1,075
1,086
1,098
1,109
1,121
1,132
1,142
1,160
1,179
1,197
1,214
1,230
1,248
1,267
1,287
1,309
1,338
1,372
1,419
1,482
1,574
1,688
0,692
1,028
1,329
1,488
1,983
2,075
2,286
2,484
2,671
2,848
3,018
3,177
3,332
3,481
3,625
3,765
3,899
4,023
4,152
4,440
4,690
4,930
5,170
5,400
5,630
5,850
6,070
6,290
6,500
6,720
6,930
7,140
7,350
7,570
Univ. Erwin Choque Conde
Página 122
M O NO X ID O D E C A R B O N O
Temperatur
ºK
D en sid a d
(K g/m 3 )
C a lo r
e sp ec ífic o c p
k J/K gºC
V isc. d in ám .
. 1 0 6
(K g/m .seg )
V isc. cinem .
. 1 0 6
(m 2 /s e g )
C o n d u c tiv .
térm ica "k "
W /m ºC
D if. térm ica
. 1 0 4
(m 2 /s e g )
Nº de Prandt
Pr
220
250
300
350
400
450
500
550
600
1,5536
1,3649
1,1388
0,9742
0,8536
0,7585
0,6822
0,6202
0,5685
1,0429
1,0425
1,0421
1,0434
1,0484
1,0551
1,0635
1,0756
1,0877
13,83
15,40
17,84
20,09
22,19
24,18
26,06
27,89
29,60
8,90
11,28
15,67
20,62
25,99
31,88
38,19
44,97
52,06
0,01900
0,02144
0,02525
0,02883
0,03226
0,04360
0,03863
0,04162
0,04446
0,1176
0,1506
0,2128
0,2836
0,3605
0,4439
0,5324
0,6240
0,7190
0,758
0,750
0,737
0,728
0,722
0,718
0,718
0,721
0,724
C a lo r
e sp ec ífic o c p
k J/K gºC
V isc. d in ám .
. 1 0 6
(K g/m .seg )
D if. térm ica
. 1 0 4
(m 2 /s e g )
Nº de Prandt
Pr
10,84
10,501
11,229
12,602
13,54
14,059
14,314
14,436
14,491
14,499
14,507
14,532
14,537
14,574
14,675
14,821
14,968
15,165
15,366
15,575
15,638
1,606
2,516
4,212
5,595
6,813
7,919
8,963
9,954
10,864
11,779
12,636
13,475
14,285
15,89
17,40
18,78
20,16
21,46
22,75
24,08
24,44
0,0228
0,0362
0,0665
0,0981
0,1282
0,1561
0,182
0,206
0,228
0,251
0,272
0,292
0,315
0,351
0,384
0,412
0,440
0,464
0,488
0,512
0,519
0,0249
0,0676
0,2408
0,475
0,772
1,13
1,554
2,031
2,568
1,164
3,817
4,516
5,306
6,903
8,563
10,217
11,997
13,726
15,484
17,394
18,013
0,759
0,721
0,712
0,718
0,719
0,713
0,706
0,697
0,69
0,682
0,675
0,668
0,664
0,659
0,664
0,676
0,686
0,703
0,715
0,733
0,736
H ID R O G E N O
Temperatur
ºK
30
50
100
150
200
250
300
350
400
450
500
550
600
700
800
900
1000
1100
1200
1300
1333
D en sid a d
(K g/m 3 )
0,84722
0,50955
0,24572
0,16371
0,12270
0,09819
0,08185
0,07016
0,06135
0,05462
0,04918
0,04469
0,04085
0,03492
0,03060
0,02723
0,02451
0,02227
0,02050
0,01890
0,01842
V isc. cinem .
. 1 0 6
(m 2 /s e g )
1,895
4,88
17,14
34,18
55,53
80,64
109,5
141,9
177,1
215,6
257,0
301,6
349,7
455,1
569
690
822
965
1107
1273
1328
C o n d u c tiv .
térm ica "k "
W /m ºC
O X IG E N O
Temperatur
ºK
D en sid a d
(K g/m 3 )
100
150
200
250
300
350
400
450
500
550
600
3,9918
2,6190
1,9559
1,5618
1,3007
1,1133
0,9755
0,8652
0,7801
0,7096
0,6504
Univ. Erwin Choque Conde
C a lo r
e sp ec ífic o c p
k J/K gºC
0,9479
0,9178
0,9131
0,9157
0,9203
0,9291
0,9420
0,9567
0,9722
0,9881
1,0044
V isc. d in ám .
. 1 0 6
(K g/m .seg )
V isc. cinem .
. 1 0 6
(m 2 /s e g )
C o n d u c tiv .
térm ica "k "
W /m ºC
D if. térm ica
. 1 0 4
(m 2 /s e g )
Nº de Prandt
Pr
7,77
11,49
14,85
17,87
20,63
23,16
25,54
27,77
29,91
31,97
33,92
1,95
4,39
7,59
11,45
15,86
20,80
26,18
31,99
38,34
45,05
52,15
0,00903
0,01367
0,01824
0,02259
0,02676
0,03070
0,03461
0,03828
0,04173
0,04517
0,04832
0,0239
0,0569
0,1021
0,1579
0,2235
0,2968
0,3768
0,4609
0,5502
0,6441
0,7399
0,815
0,773
0,745
0,725
0,709
0,702
0,695
0,694
0,697
0,700
0,704
Página 123
D IO X ID O D E CA R BO N O , CO 2
Temp. ºK
220
250
300
350
400
450
500
550
600
D en sid a d
(K g/m 3 )
C a lo r
e sp ec ífic o c p
k J/K gºC
V isc. d in ám .
. 1 0 6
(K g/m .seg )
V isc. cinem .
. 1 0 6
(m 2 /s e g )
C o n d u c tiv .
térm ica "k "
W /m ºC
D if. térm ica
. 1 0 5
(m 2 /s e g )
2,4733
2,1657
1,7973
1,5362
1,3424
1,1918
1,0732
0,9739
0,8938
0,783
0,804
0,871
0,900
0,942
0,980
1,013
1,047
1,076
11,105
12,59
14,958
17,205
19,32
21,34
23,26
25,08
26,83
4,49
5,81
8,32
11,19
14,39
17,90
21,67
25,74
30,02
0,010805
0,012884
0,016572
0,02047
0,02461
0,02897
0,03352
0,03821
0,04311
0,0592
0,07401
0,10588
0,14808
0,19463
0,24813
0,3084
0,375
0,4483
Nº de Prandtl
0,818
0,793
0,770
0,755
0,738
0,721
0,702
0,685
0,668
V A PO R D E AG U A H U M E D O
Temperatura
ºC
0
5
10
15
20
25
30
40
60
80
100
125
150
200
250
300
Densidad
Kg/m3
Líquido
1000
1000
1000
999
998
997
996
992
983
972
958
939
917
865
799
712
Univ. Erwin Choque Conde
Vapor
0,0049
0,0068
0,0094
0,0128
0,0173
0,0230
0,0304
0,0512
0,130
0,293
0,598
1,30
2,55
7,86
19,98
46,19
Calor específico
kJ/Kg.ºC
Líquido
4,21
4,20
4,19
4,19
4,18
4,18
4,18
4,18
4,19
4,20
4,22
4,26
4,32
4,51
4,87
5,65
Vapor
1,86
1,86
1,86
1,87
1,87
1,88
1,88
1,89
1,91
1,95
2,01
2,12
2,29
2,91
3,94
6,18
Conductividad térmic
W/m.ºC
Líquido
0,569
0,578
0,587
0,595
0,603
0,611
0,618
0,632
0,653
0,670
0,681
0,687
0,687
0,665
0,616
0,541
Vapor
0,0163
0,0167
0,0171
0,0175
0,0179
0,0183
0,0187
0,0195
0,0212
0,0229
0,0248
0,0273
0,0300
0,0375
0,0495
0,0720
Viscosidad dinámica
3
.10 (Kg/m.seg
Número de Prandtl
Líquido
1,75
1,50
1,30
1,14
1,00
0,89
0,80
0,59
0,46
0,351
0,279
0,220
0,181
0,134
0,107
0,085
Líquido
13,00
10,90
9,29
7,99
6,95
6,09
5,39
3,89
2,97
2,20
1,73
1,36
1,14
0,91
0,85
0,89
Vapor
0,0085
0,0087
0,0088
0,0090
0,0092
0,0094
0,0095
0,0100
0,0106
0,0113
0,1120
0,0130
0,0139
0,0157
0,0175
0,0198
Pr
Vapor
0,97
0,96
0,96
0,96
0,96
0,96
0,96
0,95
0,95
0,96
0,97
1,01
1,07
1,22
1,39
1,70
Página 124
C O N STA N TE S T E RM O D IN AM IC A S D E L CO 2 H U M E D O
Presión
Temperatura
ºC
Atmósferas
Bars
-50
-45
-40
-35
-30
-25
-20
-15
-10
-5
0
5
10
15
20
25
30
35
6,97
8,49
10,25
12,26
14,55
17,14
20,06
23,34
26,99
30,51
35,54
40,50
45,95
51,93
58,46
65,59
73,34
74,96
6,83
8,32
10,05
12,02
14,27
16,81
19,67
22,79
26,47
30,45
34,85
39,71
45,06
50,92
57,33
64,32
71,92
73,51
v'
dm3 /Kg
Líquido
i'
Kcal/Kg
s'
Kcal/Kg.ºC
v"
dm3 /Kg
0,867
0,881
0,897
0,913
0,931
0,950
0,971
0,994
1,019
1,048
1,081
1,120
1,166
1,223
1,297
1,409
1,680
2,156
75,00
77,30
79,59
81,80
84,19
86,53
88,93
91,44
94,09
96,91
100,00
103,10
106,50
110,10
114,00
118,80
125,90
133,50
0,9020
0,9120
0,9218
0,9314
0,9408
0,9501
0,9594
0,9690
0,9787
0,9890
1,0000
1,0103
1,0218
1,0340
1,0468
1,0628
1,0854
1,1098
55,407
45,809
38,164
32,008
27,001
22,885
19,466
16,609
14,194
12,141
10,383
8,850
7,519
6,323
5,269
4,232
2,979
2,156
Vapor satur ado seco
r
i"
Kcal/Kg
Kcal/Kg
80,56
78,59
76,58
74,51
72,37
70,14
67,79
65,26
62,51
59,5
56,13
52,35
48,09
43,07
37,1
28,53
15,05
0
155,57
155,89
156,17
156,39
156,56
156,67
156,78
156,70
156,60
156,41
156,13
155,45
154,59
153,17
151,10
147,33
140,95
133,50
s"
Kcal/Kg.ºC
1,2631
1,2563
1,2503
1,2443
1,2385
1,2328
1,2272
1,2218
1,2163
1,2109
1,2055
1,1985
1,1917
1,1836
1,1734
1,1585
1,1351
1,1098
C O N STA N TE S T E RM O D IN AM IC A S D E L SO 2 H U M E D O
Temp.
(ºC)
-30
-25
-20
-15
-10
-5
0
5
10
15
20
25
30
35
40
45
50
55
60
Presión
Atmósferas
Bars
14,55
17,14
20,06
23,34
26,99
30,51
35,54
40,50
45,95
51,93
58,46
65,59
73,34
74,96
6,427
7,447
8,583
9,848
11,25
Univ. Erwin Choque Conde
14,27
16,81
19,67
22,79
26,47
30,45
34,85
39,71
45,06
50,92
57,33
64,32
71,92
73,51
6,303
7,303
8,417
9,657
11,030
v'
dm3 /Kg
Líquido
i'
Kcal/Kg
s'
Kcal/Kg.ºC
v"
dm3 /Kg
0,931
0,950
0,971
0,994
1,019
1,048
1,081
1,120
1,166
1,223
1,297
1,409
1,680
2,156
0,7536
0,7622
0,7712
0,7808
0,7909
84,19
86,53
88,93
91,44
94,09
96,91
100,00
103,10
106,50
110,10
114,00
118,80
125,90
133,50
112,83
114,41
116,01
117,64
119,23
0,9408
0,9501
0,9594
0,9690
0,9787
0,9890
1,0000
1,0103
1,0218
1,0340
1,0468
1,0628
1,0854
1,1098
1,0434
1,0486
1,0534
1,0584
1,0631
27,001
22,885
19,466
16,609
14,194
12,141
10,383
8,850
7,519
6,323
5,269
4,232
2,979
2,156
58,8
51,1
44,6
39,1
34,4
Vapor satur ado seco
r
i"
Kcal/Kg
Kcal/Kg
72,37
70,14
67,79
65,26
62,51
59,5
56,13
52,35
48,09
43,07
37,1
28,53
15,05
0
82,09
80,91
79,71
78,45
77,21
156,56
156,67
156,78
156,70
156,60
156,41
156,13
155,45
154,59
153,17
151,10
147,33
140,95
133,50
194,92
195,32
195,72
196,09
196,44
s"
Kcal/Kg.ºC
1,2385
1,2328
1,2272
1,2218
1,2163
1,2109
1,2055
1,1985
1,1917
1,1835
1,1734
1,1585
1,1351
1,1098
1,3057
1,3029
1,3001
1,2974
1,2949
Página 125
C O N STA N TE S T E RM O D IN AM IC A S D E L N H 3 H U M E D O
Temperat. Presión
ºC
Atm.abs.
-52
0,3697
-50
0,4168
-48
0,4686
-46
0,5256
-44
0,5552
-42
0,6568
-40
0,7318
-38
0,5137
-36
0,9028
-34
0,9999
-32
1,1052
-30
1,219
-28
1,342
-26
1,475
-24
1,619
-22
1,774
-20
1,940
-18
2,117
-16
2,309
-14
2,514
-12
2,732
-10
2,966
-8
3,216
-6
3,481
-4
3,761
-2
4,060
0
4,379
2
4,716
4
5,073
6
5,450
8
5,849
10
6,271
12
6,715
14
7,183
16
7,677
18
8,196
20
8,741
22
9,314
24
9,915
26
10,544
28
11,204
30
11,895
32
12,617
34
13,374
36
14,165
38
14,990
40
15,850
42
16,747
44
17,682
46
18,658
48
19,673
50
20,727
v'
(dm 3 /K g)
0,001420
0,001425
0,001429
0,001434
0,001439
0,001444
0,001449
0,001455
0,001460
0,001465
0,001470
0,001476
0,001481
0,001487
0,001492
0,001498
0,001504
0,001510
0,001516
0,001522
0,001528
0,001534
0,001540
0,001546
0,001553
0,001555
0,001566
0,001573
0,001580
0,001587
0,001594
0,001601
0,001608
0,001616
0,001623
0,001631
0,001639
0,001647
0,001655
0,001663
0,001671
0,001680
0,001689
0,001698
0,001707
0,001716
0,001726
0,001735
0,001745
0,001756
0,001766
0,001777
Univ. Erwin Choque Conde
v"
(m 3 /K g )
2,933
2,623
2,351
2,112
1,901
1,715
1,550
1,404
1,274
1,159
1,055
0,963
0,8799
0,5056
0,7386
0,6782
0,6235
0,5742
0,5295
0,4889
0,4520
0,4185
0,3873
0,3599
0,3344
0,3110
0,2897
0,2700
0,2553
0,2353
0,2200
0,2058
0,1927
0,1806
0,1694
0,1591
0,1494
0,1405
0,1322
0,1245
0,1174
0,1107
0,1045
0,0986
0,0932
0,0881
0,0833
0,0788
0,0746
0,0707
0,0670
0,0635
'
"
i'
i"
r
(K g/m 3 )
(K g/m 3 )
(K c a l/K g )
(K c a l/K g )
(K c a l/K g )
704,4
702,0
699,6
697,2
694,8
692,4
690,0
687,5
685,1
682,6
680,1
671,7
675,2
672,6
670,1
667,6
665,0
662,4
659,8
657,2
654,6
652,0
649,3
646,7
644,0
641,3
638,6
635,8
633,1
630,3
677,5
624,7
621,8
619,0
616,1
613,2
610,3
607,3
604,3
601,3
598,3
595,2
592,1
589,0
585,9
582,7
579,5
576,2
572,9
569,6
566,3
552,9
0,3409
0,3812
0,425
0,473
0,526
0,583
0,045
0,712
0,765
0,663
0,948
1,038
1,136
1,242
1,354
1,474
1,604
1,742
1,889
2,046
2,213
2,390
2,579
2,779
2,991
3,216
3,452
3,703
3,969
4,250
4,546
4,859
5,189
5,537
5,904
6,289
6,694
7,119
7,564
8,031
8,521
9,034
9,573
10,138
10,731
11,353
12,005
12,689
13,404
14,153
14,936
15,756
44,2
46,2
48,4
50,4
52,5
54,6
56,8
58,9
61,0
63,1
65,3
67,4
69,6
71,7
73,9
76,0
78,2
80,3
82,5
84,7
86,9
89,0
91,2
93,4
95,6
97,8
100,0
102,2
104,4
106,6
108,9
111,1
113,4
115,6
117,9
120,1
122,4
124,7
126,9
129,2
131,5
133,8
136,2
138,5
140,8
143,1
145,5
147,9
150,3
152,6
155,0
157,4
383,3
384,1
384,9
385,7
386,5
387,3
388,1
388,9
389,6
390,4
391,2
391,9
392,7
393,4
394,1
394,8
395,5
396,1
396,8
397,4
398,1
398,7
399,3
399,9
400,4
401,0
401,5
402,0
402,5
403,0
403,5
403,9
404,4
404,8
405,2
405,6
405,9
406,3
406,6
406,9
407,2
407,4
407,7
407,9
408,0
408,2
408,4
408,5
408,6
408,6
408,7
408,7
339,1
337,9
336,5
335,3
334,0
332,7
331,3
330,0
328,6
327,3
325,9
324,5
323,1
321,7
320,2
318,8
317,3
315,8
314,3
312,7
311,2
309,7
308,1
306,5
304,8
303,2
301,5
299,8
298,1
296,4
294,6
292,8
291,0
289,2
287,3
285,5
283,5
281,6
279,7
277,7
275,7
273,6
271,5
269,4
267,2
265,1
262,9
260,6
258,3
256,0
253,7
251,3
s'
s"
(K c a l/K g ºC ) (K c a l/K g ºC )
0,7741
0,7832
0,7931
0,8021
0,8112
0,8203
0,8295
0,8385
0,8475
0,8565
0,8654
0,8742
0,8830
0,8917
0,9003
0,9089
0,5174
0,9259
0,9343
0,9427
0,9511
0,9553
0,9675
0,9757
0,9839
0,9920
1,0000
1,0080
1,0160
1,0240
1,0319
1,0397
1,0475
1,0553
1,0631
1,0709
1,0785
1,0862
1,0938
1,1014
1,1050
1,1165
1,1241
1,1315
1,1390
1,1464
1,1538
1,1612
1,1686
1,1759
1,1832
1,1904
2,3078
2,2978
2,2880
2,2692
2,2692
2,2600
2,2510
2,2421
2,2336
2,2252
2,2170
2,2090
2,2011
2,1934
2,1858
2,1784
2,1710
2,1638
2,1567
2,1498
2,1430
2,1362
2,1296
2,1231
2,1167
2,1103
2,1041
2,0979
2,0919
2,0859
2,0799
2,0741
2,0683
2,0626
2,0570
2,0514
2,0459
2,0405
2,0351
2,0297
2,0243
2,0191
2,0139
2,0087
2,0035
1,9981
1,9933
1,9882
1,9832
1,9781
1,9731
1,9681
Página 126
C O N STA N TE S T E RM O D IN AM IC A S D E L V A PO R D E M E R C U R IO
p
Atm
0,0010
0,0015
0,002
0,003
0,004
0,006
0,008
0,010
0,015
0,02
0,03
0,04
0,05
0,06
0,08
0,10
0,12
0,14
0,16
0,18
0,20
0,25
0,30
0,35
0,40
0,50
0,60
0,70
0,80
0,9
1,0
1,2
1,4
1,6
1,8
2,0
2,2
2,4
2,6
2,8
3,0
3,5
4,0
4,5
5,0
5,5
6,0
6,5
7,0
8,0
9,0
10
12
14
16
18
20
25
30
35
40
45
50
T
°C
119,5
128,0
134,6
144,1
151,2
161,5
168,9
175,0
186,6
195,0
207,6
216,9
224,5
230,9
241,0
249,6
256,7
262,7
268,0
272,9
277,3
286,7
294,4
301,7
308,0
318,8
328,0
335,9
342,7
349,7
355,0
365,3
374,0
381,9
389,3
395,8
401,7
407,4
412,5
417,5
422,4
432,8
442,4
451,0
458,9
466,3
472,8
479,1
485,1
496,3
506,3
515,5
532,3
546,7
559,8
571,4
582,4
606,5
627,1
645,5
661,8
677,0
690,9
v´
m /Kg
0,0000752
0,0000753
0,0000754
0,0000755
0,0000756
0,0000758
0,0000759
0,0000760
0,0000761
0,0000762
0,0000764
0,0000765
0,0000766
0,0000767
0,0000769
0,0000770
0,0000771
0,0000772
0,0000772
0,0000773
0,0000774
0,0000775
0,0000776
0,0000777
0,0000778
0,0000780
0,0000781
0,0000782
0,0000783
0,0000784
0,0000785
0,0000787
0,0000788
0,0000789
0,0000790
0,0000791
0,0000792
0,0000793
0,0000794
0,0000794
0,0000795
0,0000797
0,0000798
0,0000799
0,0000801
0,0000802
0,0000803
0,0000804
0,0000805
0,0000806
0,0000808
0,0000809
0,0000812
0,0000814
0,0000816
0,0000818
0,0000819
0,0000823
0,0000827
0,0000830
0,0000832
0,0000835
0,0000837
3
Univ. Erwin Choque Conde
v”
m /Kg
165,9
113
56,16
58,78
44,84
30,62
23,35
18,94
12,95
9,893
6,772
5,178
4,206
3,550
2,716
2,209
1,866
1,618
1,430
1,282
1,163
0,9464
0,7995
0,6941
0,6140
0,5003
0,4234
0,3677
0,3253
0,2922
0,2655
0,2245
0,1553
0,1730
0,1555
0,1414
0,1296
0,1196
0,1114
0,1043
0,09798
0,08524
0,07555
0,06801
0,06187
0,05682
0,05254
0,04891
0,04578
0,04065
0,03660
0,03333
0,02837
0,02475
0,02200
0,01983
0,01808
0,01487
0,01268
0,01109
0,00988
0,00892
0,00815
3
´
3
Kg/m
13298
13250
13263
13245
13228
13193
13175
13158
13141
13123
13089
13072
13055
13038
13004
12987
12970
12953
12953
12937
12920
12903
12887
12870
12853
12821
12804
12768
12771
12755
12739
12706
12690
12674
12658
12642
12626
12610
12594
12584
12579
12547
12531
12516
12484
12469
12453
12433
12422
12407
12376
12361
12315
12285
12255
12225
12210
12151
12092
12048
12019
11976
11947
´´
i’
i”
r
s´
s”
3
Kcal/Kg Kcal/Kg Kcal/Kg Kcal/Kg°C Kcal/Kg°C
Kg/m
0,006028
3,96
76,22
72,26
0,0119
0,1959
0,00555
4,23
76,94
72,21
0,0126
0,1926
0,01161
4,45
76,61
72,16
0,0132
0,1902
0,01701
4,76
76,86
72,10
0,0139
0,1867
0,02230
4,98
77,03
72,05
0,0145
0,1843
0,03266
5,34
77,32
71,98
0,0152
0,1808
0,04253
5,58
77,52
71,94
0,0158
0,1785
0,05250
5,79
77,69
72,90
0,0163
0,1767
0,07722
6,16
77,98
71,82
0,0171
0,1733
0,1011
6,44
78,20
71,76
0,0178
0,1711
0,1477
6,55
75,53
71,68
0,0186
0,1677
0,1931
7,16
78,78
71,62
0,0193
0,1654
0,2378
7,41
78,98
71,57
0,0198
0,1636
0,2817
7,63
79,16
71,53
0,0202
0,1621
0,3682
7,98
79,44
71,46
0,0208
0,1598
0,4527
8,25
79,66
71,41
0,0213
0,1580
0,5359
8,48
79,84
71,36
0,0218
0,1565
0,6181
8,68
80,00
71,32
0,0222
0,1553
0,6993
8,86
80,14
71,28
0,0225
0,1542
0,7800
9,02
80,27
71,25
0,0228
0,1533
0,8599
9,16
80,38
71,22
0,0231
0,1525
1,057
9,46
80,62
71,16
0,0236
0,1507
1,251
9,73
80,84
71,11
0,0241
0,1494
1,441
9,96
81,02
71,06
0,0245
0,1481
1,629
10,18
81,19
71,01
0,0249
0,1471
1,999
10,55
81,49
70,94
0,0255
0,1453
2,362
10,86
81,74
70,68
0,0260
0,1439
2,720
11,12
81,94
70,82
0,0265
0,1428
3,074
11,34
82,01
70,77
0,0269
0,1418
3,422
11,56
82,29
70,73
0,0272
0,1408
3,767
11,76
82,45
70,69
0,0275
0,1400
4,446
12,11
82,63
70,62
0,0280
0,1386
5,120
12,38
82,94
70,56
0,0285
0,1375
5,780
12,64
83,14
70,50
0,0290
0,1366
6,431
12,90
83,35
70,45
0,0294
0,1357
7,072
13,11
83,51
70,40
0,0297
0,1349
7,716
13,32
83,68
70,36
0,0300
0,1342
8,347
13,54
83,86
70,32
0,0303
0,1335
8,977
13,70
83,98
70,28
0,0305
0,1329
9,588
13,87
84,11
70,24
0,0307
0,1324
10,21
14,04
84,25
70,21
0,0309
0,1320
11,73
14,40
84,53
70,13
0,0315
0,1308
13,23
14,74
84,80
70,06
0,0319
0,1298
14,70
15,03
85,02
69,99
0,0323
0,1289
16,16
15,30
85,23
69,93
0,0327
0,1282
17,56
15,56
85,43
69,87
0,0331
0,1760
19,03
15,78
85,59
69,81
0,0334
0,1270
20,45
15,99
85,75
69,76
0,0337
0,1260
21,84
16,20
85,91
69,71
0,0339
0,1258
24,60
16,59
86,20
69,61
0,0344
0,1249
27,32
16,94
86,47
69,53
0,0349
0,1241
30,00
17,25
86,70
69,45
0,0353
0,1234
35,25
17,85
87,15
69,30
0,0360
0,1220
40,40
18,35
87,51
69,16
0,0366
0,1210
45,46
18,81
87,84
69,03
0,0372
0,1201
50,43
19,23
88,14
68,91
0,0377
0,1193
55,31
19,62
88,42
68,80
0,0381
0,1185
67,25
20,46
89,00
68,54
0,0391
0,1170
78,86
21,18
89,48
68,30
0,0399
0,1158
90,17
21,83
89,91
68,08
0,0406
0,1147
101,2
22,41
90,28
67,87
0,0412
0,1138
112,1
22,95
90,62
67,67
0,0418
0,1130
122,7
23,44
90,91
67,47
0,0423
0,1123
Página 127
1 1.- C A L O R E S P E C ÍF IC O M E D I O D E L V A P O R D E A G U A R E C A L E N T A D O
T e m p eratu r a d e recale n ta m ien to e n ºC
p
0 ,5
Ts
8 0 ,9
160
180
200
220
240
260
280
300
320
340
360
380
400
0 ,4 7 0 0 ,4 7 0
0 ,4 6 9
0 ,4 6 9
0 ,4 6 9
0 ,4 6 9
0 ,4 7 0
0 ,4 7 0
0 ,4 7 1
0 ,4 7 2
0 ,4 7 3
0 ,4 7 5
0 ,4 7 6
0 ,4 7 8 0 ,4 7 6
0 ,4 7 5
0 ,4 7 5
0 ,4 7 4
0 ,4 7 4
0 ,4 7 4
0 ,4 7 4
0 ,4 7 5
0 ,4 7 6
0 ,4 7 7
0 ,4 7 8
0 ,4 8 0
460
480
500
520
540
550
1
9 9 ,1
2
1 1 9 ,6 0 , 4 9 1 0 , 4 8 8 0 , 4 8 6 0 , 4 8 5 0 , 4 8 4 0 , 4 8 3 0 , 4 8 2 0 , 4 8 2 0 , 4 8 2 0 , 4 8 2 0 , 4 8 3 0 , 4 8 3 0 , 4 8 4
4
1 4 2 ,9 0 , 5 2 1 0 , 5 1 5 0 , 5 0 9 0 , 5 0 5 0 , 5 0 1 0 , 4 9 9 0 , 4 9 7 0 , 4 9 6 0 , 4 9 5 0 , 4 9 4 0 , 4 9 4 0 , 4 9 4 0 , 4 9 4 0 , 4 9 4
6
1 5 8 ,1
0 ,5 4 4
0 ,5 3 4
0 ,5 2 6
0 ,5 1 9
0 ,5 1 4
0 ,5 1 0
0 ,5 0 8
0 ,5 0 5
0 ,5 0 4
0 ,5 0 4
0 ,5 0 3
0 ,5 0 3
0 ,5 0 3
0 ,5 0 3
8
1 6 9 ,4
0 ,5 7 6
0 ,5 6 1
0 ,5 4 8
0 ,5 3 8
0 ,5 3 0
0 ,5 2 5
0 ,5 2 1
0 ,5 1 7
0 ,5 1 5
0 ,5 1 4
0 ,5 1 2
0 ,5 1 1
0 ,5 1 1
0 ,5 1 1
10
1 7 9 ,0
0 ,5 9 0
0 ,5 7 2
0 ,5 5 8
0 ,5 4 8
0 ,5 4 0
0 ,5 3 4
0 ,5 3 0
0 ,5 2 0
0 ,5 2 4
0 ,5 2 2
0 ,5 2 1
0 ,5 2 1
0 ,5 2 1
12
1 8 7 ,1
0 ,6 2 3
0 ,5 9 9
0 ,5 8 0
0 ,5 6 7
0 ,5 5 6
0 ,5 4 8
0 ,5 4 3
0 ,5 3 8
0 ,5 3 5
0 ,5 3 3
0 ,5 3 1
0 ,5 3 1
0 ,5 2 9
14
1 9 4 ,1
0 ,6 6 0
0 ,6 2 9
0 ,6 0 5
0 ,5 8 8
0 ,5 7 5
0 ,5 6 5
0 ,5 5 8
0 ,5 5 3
0 ,5 4 8
0 ,5 4 5
0 ,5 4 2
0 ,5 4 0
0 ,5 3 6
16
2 0 0 ,4
0 ,6 6 1
0 ,6 3 1
0 ,6 1 0
0 ,5 9 4
0 ,5 8 2
0 ,5 7 2
0 ,5 6 5
0 ,5 6 0
0 ,5 5 6
0 ,5 5 2
0 ,5 4 8
0 ,5 4 3
18
2 0 6 ,1
0 ,6 9 7
0 ,6 6 0
0 ,6 3 4
0 ,6 1 5
0 ,6 0 0
0 ,5 8 9
0 ,5 8 0
0 ,5 7 4
0 ,5 6 8
0 ,5 6 2
0 ,5 5 6
0 ,5 5 2
20
2 1 1 ,4
0 ,7 3 8
0 ,6 9 4
0 ,6 6 0
0 ,6 3 7
0 ,6 1 9
0 ,6 0 6
0 ,5 9 6
0 ,5 8 7
0 ,5 8 0
0 ,5 7 3
0 ,5 6 5
0 ,5 5 9
22
2 1 6 ,2
0 ,8 1 0
0 ,7 2 2
0 ,6 8 4
0 ,6 5 8
0 ,6 3 7
0 ,6 2 1
0 ,6 0 8
0 ,5 9 7
0 ,5 8 7
0 ,5 7 9
0 ,5 7 2
0 ,5 6 7
24
2 2 0 ,8
0 ,7 4 6
0 ,7 0 5
0 ,6 7 6
0 ,6 5 3
0 ,6 3 4
0 ,6 1 9
0 ,6 0 7
0 ,5 9 7
0 ,5 8 8
0 ,5 8 0
0 ,5 7 4
26
2 2 5 ,0
0 ,7 5 2
0 ,7 2 2
0 ,6 9 2
0 ,6 6 7
0 ,6 4 7
0 ,6 3 1
0 ,6 1 8
0 ,6 0 6
0 ,5 9 6
0 ,5 8 8
0 ,5 8 1
28
2 2 9 ,0
0 ,7 7 2
0 ,7 4 2
0 ,7 1 2
0 ,6 8 5
0 ,6 6 3
0 ,6 4 4
0 ,6 3 0
0 ,6 1 7
0 ,6 0 6
0 ,5 9 7
0 ,5 8 9
30
2 3 2 ,8
0 ,7 6 0
0 ,7 3 0
0 ,7 0 2
0 ,6 7 8
0 ,6 5 7
0 ,6 4 1
0 ,6 2 7
0 ,6 1 6
0 ,6 0 7
0 ,5 9 9
0 ,5 9 4
0 ,5 9 0
0 ,5 8 6
0 ,5 8 2
0 ,5 7 9
0 ,5 7 8
35
2 4 1 ,4
0 ,7 9 7
0 ,7 6 7
0 ,7 3 7
0 ,7 0 9
0 ,6 8 6
0 ,6 6 7
0 ,6 5 1
0 ,6 3 7
40
2 4 9 ,2
0 ,8 3 8
0 ,8 0 7
0 ,7 7 6
0 ,7 4 5
0 ,7 1 8
0 ,6 9 5
0 ,6 7 6
0 ,6 6 0
0 ,6 2 5
0 ,6 1 6
0 ,6 1 0
0 ,6 0 5
0 ,6 0 0
0 ,5 9 6
0 ,5 9 2
0 ,5 9 0
0 ,6 4 7
0 ,6 3 5
0 ,6 2 8
0 ,6 2 2
0 ,6 1 6
0 ,6 1 1
0 ,6 0 6
45
2 5 6 ,3
0 ,8 7 8
0 ,8 4 6
0 ,8 1 4
0 ,7 8 2
0 ,7 5 2
0 ,7 2 5
0 ,7 0 3
0 ,6 0 3
0 ,6 8 4
0 ,6 6 8
0 ,6 5 5
0 ,6 4 6
0 ,6 3 8
0 ,6 3 1
0 ,6 2 5
0 ,6 2 0
50
2 6 2 ,7
0 ,8 8 6
0 ,8 5 3
0 ,8 2 0
0 ,7 8 7
0 ,7 5 6
0 ,6 1 7
0 ,7 3 1
0 ,7 0 9
0 ,6 9 0
0 ,6 7 5
0 ,6 6 5
0 ,6 5 5
0 ,6 4 7
0 ,6 4 0
0 ,6 3 4
60
2 7 4 ,3
0 ,9 6 1
0 ,9 2 6
0 ,8 9 1
0 ,8 5 6
0 ,6 3 1
0 ,8 2 0
0 ,7 8 8
0 ,7 6 0
0 ,7 3 7
0 ,7 1 7
0 ,7 0 2
0 ,6 9 0
0 ,6 7 9
0 ,6 7 0
0 ,6 6 2
70
2 8 4 ,5
0 ,9 8 8
0 ,9 5 8
0 ,6 5 8
0 ,9 2 8
0 ,8 8 7
0 ,8 4 9
0 ,8 1 4
0 ,7 8 5
0 ,7 6 0
0 ,7 4 1
0 ,7 2 6
0 ,7 1 2
0 ,7 0 1
0 ,6 9 0
0 ,6 8 6
80
2 9 3 ,6
1 ,0 8 6
90
3 0 1 ,9
1 ,0 4 4
1 ,0 0 2
0 ,9 6 0
0 ,9 1 3
0 ,8 7 2
0 ,8 3 8
0 ,8 0 6
0 ,7 8 3
0 ,7 6 4
0 ,7 4 8
0 ,7 3 3
0 ,7 2 0
0 , 7 l4
1 ,1 3 8
1 ,0 8 8
1 ,0 3 8
0 ,9 8 8
0 ,9 3 9
0 ,8 9 5
0 ,8 5 9
0 ,8 2 8
0 ,8 0 5
0 ,7 8 5
0 ,7 6 8
0 ,7 5 3
0 ,7 4 6
100
120
3 0 9 ,5
1 ,1 3 1
1 ,1 1 7
1 ,0 6 1
1 ,0 0 4
0 ,9 5 4
0 , 9 l2
0 ,8 7 5
0 ,8 4 8
0 ,8 2 4
0 ,8 0 3
0 ,7 8 6
0 ,7 7 8
3 2 3 ,1
1 ,2 9 5
1 ,2 8 1
1 ,2 3 0
1 ,1 5 7
1 ,0 9 4
1 ,0 2 9
0 ,9 8 0
0 ,9 4 2
0 ,9 0 9
0 ,8 8 1
0 ,8 5 7
140
0 ,8 4 6
3 3 5 ,l
1 ,4 2 5
1 ,4 2 5
1 ,3 3 7
1 ,2 4 8
1 ,1 7 4
1 ,1 0 2
1 ,0 4 8
I,0 0 5
0 ,9 6 8
0 ,9 3 7
0 ,9 2 3
160
3 4 5 ,7
1 ,6 6 7
1 ,6 6 7
1 ,5 6 3
1 ,4 4 6
1 ,3 4 1
1 ,2 5 0
1 ,1 7 9
1 ,1 2 0
1 ,0 7 2
1 ,0 3 1
1 ,0 1 2
200
3 6 4 ,1
2 ,7 4 7
2 ,3 5 0
2 ,0 7 0
1 ,8 6 1
1 ,6 8 7
1 ,5 5 1
l, 4 4 4
l, 3 5 8
1 ,2 8 6
1 ,2 5 5
Univ. Erwin Choque Conde
420
440
Página 128
1 2.- C O N S T A N T E S T E R M O D IN A M IC A S D E L V A P O R D E A G U A H U M E D O
Presión sat Temp. sat.
Volumen
Volumen
Entalpía
Entalpía
bars
ºC
v' (d m 3 /K g )
v" (d m 3 /K g )
i'(k J/K g )
i''(k J/K g )
0,0061
0,0061
0,0070
0,0081
0,0094
0,0100
0,0107
0,0123
0,0140
0,0160
0,0182
0,0206
0,0234
0,0250
0,0264
0,0298
0,0336
0,0378
0,0424
0,0475
0,0500
0,0532
0,0594
0,0662
0,0737
0,0750
0,0819
0,0910
0,1000
0,1008
0,1116
0,1233
0,1361
0,1500
0,1651
0,1815
0,1992
0,2000
0,2184
0,2391
0,2500
0,2615
0,2856
0,3000
0,3116
0,3396
0,3500
0,3696
0,4000
0,4019
0,4365
0,4736
0,5000
0,5133
0,5573
0,6000
0,00
1,00
2,00
4,00
6,00
7,00
8,00
10,00
12,00
14,00
16,00
18,00
20,00
21,00
22,00
24,00
26,00
28,00
30,00
32,00
33,00
34,00
36,00
38,00
40,00
40,32
42,00
44,00
45,83
46,00
48,00
50,00
52,00
54,00
56,00
58,00
60,00
60,09
62,00
64,00
65,00
66,00
68,00
69,13
70,00
72,00
72,71
74,00
75,89
76,00
78,00
80,00
81,35
82,00
84,00
85,95
1,0002
1,0002
1,0001
1,0001
1,0001
1,0001
1,0002
1,0003
1,0006
1,0008
1,0011
1,0014
1,0018
1,0021
1,0023
1,0028
1,0033
1,0038
1,0044
1,0050
1,0053
1,0057
1,0064
1,0071
1,0079
1,0080
1,0087
1,0095
1,0103
1,0103
1,0112
1,0121
1,0130
1,0140
1,0150
1,0160
1,0170
1,0171
1,0182
1,0193
1,0199
1,0205
1,0216
1,0223
1,0228
1,0240
1,0244
1,0252
1,0264
1,0264
1,0277
1,0290
1,0299
1,0303
1,0317
1,0331
206288,00
206146,00
179907,00
157258,00
137768,00
129205,00
120956,00
106422,00
93829,00
82894,00
73380,00
65084,00
57836,00
54260,00
51491,00
45925,00
41034,00
36727,00
32929,00
29573,00
28196,00
26601,00
23967,00
21628,00
19546,00
19239,00
17691,00
16035,00
14673,00
14556,00
13232,00
12045,00
10979,00
10021,00
9157,80
8379,90
7677,60
7648,40
7042,80
6468,20
6203,20
5947,30
5474,70
5228,10
5045,30
4654,70
4524,60
4299,10
3992,40
3974,80
3678,80
3408,30
3239,40
3160,90
2934,30
2731,20
0,0
0,0
8,4
16,8
25,2
29,3
33,6
42,0
50,4
58,8
67,1
75,5
53,4
88,4
92,2
100,6
109,0
117,3
125,7
134,0
137,8
142,4
150,7
159,1
167,4
168,8
175,8
184,2
191,8
192,5
200,9
209,3
217,6
226,0
234,3
242,7
251,1
251,5
259,5
267,8
272,0
276,2
284,6
289,3
293,0
301,4
304,3
309,7
317,6
318,1
326,5
334,9
340,6
343,3
351,7
359,9
2500,8
2500,8
2496,0
2508,1
2511,8
2513,6
2515,5
2519,2
2522,9
2526,5
2530,3
2533,9
2537,6
2539,5
2541,2
2544,8
2548,5
2552,1
2555,7
2559,3
2560,9
2562,9
2566,5
2570,1
2573,7
2574,2
2577,2
2580,8
2584,1
2584,3
2587,9
2591,4
2595,0
2598,5
2602,0
2605,5
2609,0
2609,1
2612,5
2615,9
2617,6
2619,4
2622,8
2624,8
2626,3
2629,7
2630,9
2633,1
2636,3
2636,5
2639,8
2643,2
2645,4
2646,5
2649,9
2653,1
Univ. Erwin Choque Conde
Entalpía
Entropía
Entropía
Entropía
r { l- v } (k J/K g) s' (k J/K g.ºK ) s''(k J/K g .ºK ) s(k J/K g.ºK )
2500,8
2500,8
2487,6
2491,3
2486,6
2484,3
2481,9
2477,2
2472,5
2467,8
2463,1
2458,4
2453,7
2451,1
2449,0
2444,2
2439,5
2434,8
2430,0
2425,3
2423,1
2420,5
2415,8
2411,0
2406,2
2405,5
2401,4
2396,6
2392,2
2391,8
2387,0
2382,2
2377,3
2372,5
2367,7
2362,8
2357,9
2357,7
2353,0
2318,1
2345,7
2343,2
2338,2
2335,4
2333,3
2328,3
2326,5
2323,3
2318,6
2318,3
2313,3
2308,3
2304,9
2303,2
2298,1
2293,2
0,000
0,000
0,031
0,061
0,091
0,106
0,121
0,151
0,180
0,210
0,239
0,268
0,296
0,312
0,325
0,353
0,381
0,409
0,436
0,164
0,476
0,491
0,518
0,545
0,572
0,576
0,599
0,625
0,649
0,651
0,678
0,704
0,729
0,755
0,780
0,806
0,831
0,832
0,856
0,881
0,893
0,906
0,930
0,944
0,955
0,979
0,988
1,003
1,026
1,027
1,051
1,075
1,091
1,099
1,123
1,145
9,155
9,155
9,102
9,050
8,999
8,974
8,949
8,900
8,851
8,804
8,757
8,711
8,666
8,642
8,622
8,579
8,536
8,494
8,452
8,412
8,394
8,372
8,333
8,294
8,256
8,250
8,219
8,182
8,149
8,146
8,110
8,075
8,041
8,007
7,974
7,941
7,909
7,907
7,877
7,845
7,830
7,815
7,784
7,767
7,754
7,725
7,715
7,696
7,669
7,667
7,639
7,611
7,593
7,584
7,557
7,531
9,155
9,155
9,071
8,989
8,908
8,868
8,828
8,749
8,671
8,594
8,518
8,444
8,370
8,330
8,297
8,226
8,155
8,085
8,016
7,948
7,918
7,881
7,814
7,749
7,684
7,674
7,620
7,557
7,499
7,494
7,433
7,372
7,312
7,252
7,193
7,135
7,078
7,075
7,021
6,965
6,937
6,909
6,854
6,823
6,800
6,746
6,727
6,693
6,643
6,640
6,588
6,536
6,502
6,485
6,435
6,386
Página 129
C O N ST A N T E S T E R M O D IN A M IC A S D E L V A P O R D E A G U A H U M E D O (C on tinuación )
P re sió n sa t. T em p . sat.
V o lu m en
V o lu m en
E n ta lp ía
E n ta lp ía
bars
ºC
v' (d m 3 /K g )
v" (d m 3 /K g )
i'(k J/K g )
i''(k J/K g )
0,6011
0,6495
0,7000
0,7011
0,7561
0,8000
0,8146
0,8769
0,9000
0,9430
1,0000
1,0132
1,2000
1,2080
1,4000
1,4326
1,6000
1,6905
1,8000
1,9853
2,0000
2,2000
2,3209
2,4000
2,6000
2,7012
2,8000
3,0000
3,1305
3,5000
3,6136
4,0000
4,1549
4,5000
4,7597
5,0000
5,4331
5,5000
6,0000
6,1805
6,5000
7,0000
7,0076
7,5000
7,9203
8,0000
8,5000
8,9247
9,0000
9,5000
10,0271
10,5000
86,00
88,00
89,96
90,00
92,00
93,51
94,00
96,00
96,71
98,00
99,63
100,00
104,81
105,00
109,32
110,00
113,32
115,00
116,93
120,00
120,23
123,27
125,00
126,09
128,73
130,00
131,21
133,54
135,00
138,88
140,00
143,63
145,00
147,92
150,00
151,85
155,00
155,47
158,84
160,00
161,99
164,96
165,00
167,76
170,00
170,41
172,94
175,00
175,36
177,67
180,00
182,01
1,0331
1,0345
1,0359
1,0359
1,0374
1,0385
1,0388
1,0404
1,0409
1,0419
1,0432
1,0435
1,0472
1,0474
1,0509
1,0515
1,0543
1,0558
1,0575
1,0603
1,0605
1,0633
1,0649
1,0659
1,0685
1,0697
1,0709
1,0732
1,0747
1,0786
1,0798
1,0836
1,0851
1,0883
1,0906
1,0926
1,0962
1,0967
1,1007
1,1021
1,1045
1,1080
1,1081
1,1115
1,1144
1,1149
1,1181
1,1208
1,1213
1,1243
1,1275
1,1302
2726,60
2536,00
2364,30
2360,90
2199,90
2086,80
2051,80
1915,20
1869,10
1789,30
1693,70
1673,00
1428,20
1419,40
1236,50
1210,10
1091,30
1036,50
977,39
891,71
885,59
809,99
770,43
746,60
692,66
668,32
646,19
605,72
582,00
524,14
508,66
462,35
446,12
413,86
392,57
374,77
346,65
342,57
315,56
306,85
292,57
272,76
272,48
255,50
242,62
240,32
226,88
216,60
214,87
204,09
193,85
185,51
360,1
368,5
376,8
376,9
385,4
391,7
393,8
402,2
405,2
410,6
417,5
419,1
439,4
440,2
458,4
461,3
475,4
482,5
490,7
503,7
504,7
517,6
525,0
529,6
540,9
546,3
551,5
561,4
567,7
584,3
589,1
604,7
610,6
623,2
632,2
640,1
653,8
655,8
670,4
675,5
684,1
697,1
697,3
709,3
719,1
720,9
732,0
741,1
742,6
752,8
763,1
772,0
2653,2
2656,5
2659,7
2659,7
2663,0
2665,4
2666,2
2669,4
2670,6
2672,6
2675,2
2675,8
2683,3
2683,6
2690,3
2691,3
2696,4
2698,9
2701,8
2706,3
2706,6
2711,0
2713,5
2715,0
2718,7
2720,5
2722,2
2725,4
2727,3
2732,5
2733,9
2738,6
2740,4
2744,0
2746,5
2748,7
2752,5
2735,0
2756,8
2758,1
2760,3
2763,5
2763,5
2766,4
2768,7
2769,1
2771,5
2773,5
2773,8
2776,0
2778,0
2779,8
Univ. Erwin Choque Conde
E n ta lp ía
E n tropía
E n tropía
E n tropía
r { l- v } (k J/K g) s' (k J/K g.ºK ) s''(k J/K g .ºK ) s(k J/K g.ºK )
2293,0
2287,9
2282,9
2282,8
2277,6
2273,7
2272,4
2267,2
2265,4
2262,0
2257,7
2256,7
2244,0
2243,5
2231,9
2230,0
2221,0
2216,4
2211,1
2202,5
2201,9
2193,4
2188,5
2185,4
7177,8
2174,2
2170,7
2163,9
2159,7
2148,2
2144,8
2133,9
2129,8
2120,8
2114,4
2108,6
2098,7
2097,2
2086,4
2082,7
2076,2
2066,4
2066,3
2057,1
2049,6
2048,2
2039,5
2032,4
2031,2
2023,2
2014,9
2007,8
1,146
1,169
1,192
1,192
1,216
1,233
1,239
1,262
1,270
1,284
1,303
1,308
1,361
1,363
1,411
1,419
1,455
1,473
1,494
1,528
1,530
1,563
1,581
1,593
1,621
1,634
1,647
1,672
1,687
1,727
1,739
1,776
1,791
1,820
1,842
1,860
1,892
1,897
1,931
1,942
1,962
1,992
1,992
2,020
2,042
2,046
2,070
2,091
2,094
2,117
2,139
2,159
7,531
7,504
7,478
7,478
7,453
7,434
7,428
7,403
7,394
7,379
7,359
7,355
7,298
7,296
7,246
7,239
7,202
7,183
7,163
7,130
7,127
7,096
7,078
7,067
7,040
7,027
7,015
6,992
6,978
6,941
6,930
6,897
6,884
6,857
6,838
6,822
6,794
6,790
6,761
6,751
6,734
6,709
6,708
6,685
6,667
6,663
6,643
6,626
6,623
6,604
6,586
6,570
6,385
6,335
6,287
6,286
6,237
6,201
6,189
6,142
6,125
6,095
6,056
6,048
5,937
5,933
5,835
5,820
5,747
5,710
5,668
5,602
5,597
5,533
5,497
5,474
5,419
5,393
5,368
5,321
5,291
5,214
5,191
5,120
5,093
5,037
4,997
4,962
4,902
4,893
4,830
4,808
4,772
4,717
4,716
4,665
4,625
4,617
4,573
4,535
4,529
4,487
4,446
4,411
Página 130
C O N ST A N T E S T E R M O D IN A M IC A S D E L V A P O R D E A G U A H U M E D O (C on tinuación )
P re sió n sa t. T em p . sat.
E n ta lp ía
E n ta lp ía
ºC
V o lu m en
v' (d m 3 /K g )
V o lu m en
bars
v" (d m 3 /K g )
i'(k J/K g )
i''(k J/K g )
E n ta lp ía
r { l- v } (k J/K g)
11,0000
11,5000
12,0000
12,5000
13,0000
13,5000
14,0000
14,5000
15,0000
15,5510
16,0000
17,0000
17,2450
18,0000
19,0000
19,0800
20,0000
21,0000
21,0630
22,0000
23,0000
23,2010
24,0000
25,0000
25,5040
27,5000
27,9790
30,0000
30,6350
32,5000
33,4800
35,0000
36,5240
37,5000
39,7760
40,0000
42,5000
43,2450
45,0000
46,9400
47,5000
50,0000
50,8720
55,0000
55,0510
59,4870
60,0000
64,1920
65,0000
69,1750
70,0000
74,4490
75,0000
80,0000
85,0000
85,9170
184,06
186,04
187,96
189,81
191,60
193,34
195,04
196,68
198,28
200,00
201,37
204,30
205,00
207,10
209,79
210,00
212,37
214,85
215,00
217,24
219,55
220,00
221,78
223,94
225,00
229,06
230,00
233,84
235,00
238,32
240,00
242,54
245,00
246,54
250,00
250,33
253,95
255,00
257,41
260,00
260,73
263,92
265,00
269,94
270,00
275,00
275,56
280,00
280,83
285,00
285,80
290,00
290,51
294,98
299,24
300,00
1,1331
1,1359
1,1386
1,1412
1,1438
1,1464
1,1400
1,1514
1,1539
1,1565
1,1586
1,1633
1,1644
1,1678
1,1722
1,1726
1,1766
1,1809
1,1812
1,1851
1,1892
1,1900
1,1932
1,1972
1,1992
1,2069
1,2087
1,2163
1,2187
1,2256
1,2291
1,2345
1,2399
1,2433
1,2512
1,2520
1,2606
1,2631
1,2690
1,2755
1,2774
1,2857
1,2886
1,3021
1,3023
1,3168
1,3185
1,3321
1,3347
1,3483
1,3510
1,3655
1,3673
1,3838
1,4005
1,4036
177,44
170,05
163,25
156,98
151,17
145,79
140,77
136,08
131,70
127,29
123,73
116,66
115,05
110,36
104,69
104,27
99,57
94,93
94,65
90,69
86,80
86,06
83,23
19,94
78,31
72,71
71,47
66,65
65,27
61,49
59,67
57,05
54,62
53,17
50,06
49,77
46,75
45,91
44,05
42,15
41,63
39,44
38,72
35,60
35,63
32,74
32,44
30,13
29,72
27,74
27,37
25,54
25,32
23,52
21,92
21,64
781,1
789,9
798,4
806,7
814,7
822,2
830,0
837,4
844,6
852,4
858,5
871,8
875,0
884,5
896,8
897,7
908,6
919,9
920,6
930,9
941,6
943,7
951,9
961,9
966,9
985,9
990,3
1008,3
1013,8
1029,6
1037,6
1049,8
1061,6
1069,0
1085,8
1087,4
1105,1
1110,2
1122,1
1134,9
1138,9
1154,5
1159,9
1184,9
1185,2
1210,8
1213,7
1236,8
1241,1
1263,1
1267,4
1289,9
1292,6
1317,0
1340,6
1344,9
2781,5
2783,1
2784,6
2786,0
2787,3
2788,5
2789,7
2790,8
2791,8
2792,8
2793,6
2795,2
2795,6
2796,6
2797,8
2797,9
2798,9
2799,8
2799,8
2800,6
2801,3
2801,4
2801,9
2802,3
2802,5
2803,1
2803,2
2803,4
2803,4
2803,2
2803,1
2802,7
2802,2
2801,9
2800,9
2800,8
2799,4
2799,0
2797,8
2796,4
2796,0
2794,0
2793,3
2789,5
2789,4
2784,9
2784,3
2779,6
2788,6
2773,4
2772,3
2766,3
2765,6
2758,3
2750,7
2749,2
2000,4
1993,2
1986,2
1979,3
1972,6
1966,0
1959,6
1953,4
1917,1
1940,4
1935,1
1923,4
1920,6
1912,1
1901,1
1900,2
1890,4
1879,9
1879,3
1869,7
1859,7
1857,8
1850,0
1840,4
1835,6
1817,2
1812,9
1795,0
1789,5
1773,7
1765,5
1753,0
1740,7
1732,9
1715,1
1713,4
1694,3
1688,7
1675,7
1661,5
1657,4
1639,5
1633,3
1604,6
1604,2
1574,0
1570,6
1542,5
1537,5
1510,3
1540,9
1476,4
1472,9
1441,3
1410,1
1404,3
Univ. Erwin Choque Conde
E n tropía
E n tropía
E n tropía
s' (k J/K g.ºK ) s''(k J/K g .ºK ) s(k J/K g.ºK )
2,179
2,198
2,216
2,234
2,251
2,268
2,284
2,299
2,314
2,331
2,344
2,371
2,378
2,398
2,423
2,425
2,447
2,470
2,471
2,492
2,514
2,518
2,534
2,554
2,564
2,602
2,610
2,645
2,656
2,687
2,702
2,725
2,748
2,762
2,793
2,797
2,830
2,839
2,861
2,885
2,892
2,921
2,931
2,976
2,976
3,022
3,027
3,068
3,076
3,114
3,122
3,161
3,166
3,207
3,248
3,255
6,554
6,538
6,523
6,508
6,495
6,482
6,469
6,457
6,445
6,431
6,422
6,400
6,394
6,379
6,359
6,358
6,340
6,322
6,321
6,305
6,288
6,285
6,272
6,257
6,249
6,220
6,213
6,186
6,178
6,154
6,142
6,125
6,107
6,096
6,072
6,070
6,044
6,032
6,020
6,001
5,996
5,973
5,966
5,930
5,930
5,894
5,890
5,857
5,851
5,820
5,814
5,783
5,779
5,744
5,711
5,105
4,375
4,340
4,307
4,274
4,244
4,214
4,186
4,158
4,130
4,101
4,078
4,028
4,017
3,981
3,936
3,933
3,893
3,852
3,850
3,813
3,775
3,767
3,738
3,702
3,685
3,618
3,603
3,541
3,522
3,468
3,440
3,399
3,359
3,335
3,278
3,273
3,214
3,197
3,158
3,116
3,104
3,053
3,035
2,955
2,954
2,872
2,862
2,789
2,775
2,706
2,692
2,622
2,613
2,537
2,463
2,450
Página 131
C O N ST A N T E S T E R M O D IN A M IC A S D E L V A P O R D E A G U A H U M E D O (C on tinuación )
P re sió n sa t. T em p . sat.
E n ta lp ía
ºC
v' (d m 3 /K g )
V o lu m en
v" (d m 3 /K g )
E n ta lp ía
bars
V o lu m en
i'(k J/K g )
i''(k J/K g )
E n ta lp ía
r { l- v } (k J/K g)
90,0000
92,1400
95,0000
98,7000
100,0000
105,6100
110,0000
112,9000
120,0000
120,5700
128,6500
130,0000
137,1400
140,0000
146,0000
150,0000
155,4800
160,0000
165,3700
170,0000
175,7700
180,0000
186,7400
190,0000
198,3000
200,0000
210,0000
220,0000
303,31
305,00
307,22
310,00
310,96
315,00
318,04
320,00
324,64
325,00
330,00
330,81
335,00
336,63
340,00
342,12
345,00
347,32
350,00
352,26
355,00
356,96
360,00
361,44
365,00
365,71
369,79
373,71
1,4174
1,4247
1,4346
1,4475
1,4521
1,4722
1,4883
1,4992
1,5266
1,5289
1,5620
1,5678
1,5990
1,6115
1,6390
1,6580
1,6860
1,7100
1,7410
1,7690
1,8070
1,8380
1,8940
1,9230
2,0160
2,0390
2,2130
2,6900
20,48
19,92
19,19
18,32
18,02
16,83
15,98
15,45
14,26
14,17
12,97
12,78
11,84
11,49
10,78
10,35
9,77
9,32
8,81
8,38
7,87
7,51
6,94
6,67
5,99
5,85
4,98
3,68
1363,5
1373,2
1385,9
1402,1
1407,7
1431,7
1450,1
1462,2
1491,2
1493,5
1526,0
1531,4
1559,7
1571,0
1594,8
1610,1
1631,8
1649,7
1671,2
1690,0
1713,9
1731,8
1761,5
1776,5
1817,5
1826,6
1888,5
2007,9
2742,5
2738,9
2733,9
2727,2
2724,8
2714,1
2705,5
2699,6
2684,7
2683,5
2665,5
2662,3
2645,2
2638,0
2622,0
2611,3
2595,4
2581,6
2564,2
2548,3
2527,0
2510,4
2481,1
2465,7
2420,9
2410,5
2335,6
2178,0
1379,0
1365,8
1348,0
1325,2
1317,1
1282,4
1255,4
1237,5
1193,5
1190,0
1139,5
1131,0
1085,5
1067,0
1027,2
1001,1
963,6
931,9
893,0
858,4
813,1
778,6
719,6
689,2
603,4
583,9
447,1
170,1
Univ. Erwin Choque Conde
E n tropía
E n tropía
E n tropía
s' (k J/K g.ºK ) s''(k J/K g .ºK ) s(k J/K g.ºK )
3,286
3,302
3,324
3,351
3,360
3,400
3,430
3,449
3,496
3,500
3,552
3,561
3,605
3,623
3,661
3,685
3,718
3,746
3,779
3,808
3,844
3,872
3,916
3,941
4,001
4,014
4,108
4,289
5,679
5,665
5,647
5,623
5,615
5,580
5,553
5,535
5,493
5,489
5,441
5,433
5,390
5,373
5,366
5,312
5,277
5,248
5,212
5,181
5,138
5,108
5,053
5,027
4,946
4,928
4,803
4,552
2,392
2,362
2,323
2,272
2,255
2,180
2,123
2,086
1,997
1,989
1,889
1,873
1,785
1,750
1,675
1,627
1,559
1,502
1,433
1,372
1,294
1,236
1,136
1,086
0,945
0,914
0,695
0,263
Página 132
13.- C O N S T A N T E S T E R M O D IN A M IC A S D E L V A P O R D E A G U A
RECALENTADO
v = v o lu m e n e sp e cífico e n (d m 3 /K g )
i = e n ta lp ía e sp e c ífic a e n (k J/K g )
s = e n tro p ía e sp e c ífic a e n (k J/K g ºK )
T(ºC)
0
50
100
p(bar)=0,01 ; Ts= 6,98°C
v)
1,0002 1 4 9 0 9 7 1 7 2 1 9 2
i)
0
2595
2689
s)
0
9,241 9,512
p(bar)=0,1 ; Ts= 45,83°C
v)
1,0002 14870 17198
i)
0
2592
2688
s)
0
8,173 8,447
p(bar)=0,5 ; Ts= 81,35°C
v)
1,0002 1,0121 3420
i)
0
209,3
2683
s)
0
0,703 7,694
p(bar)=1 ; Ts= 99,63°
v)
1,0001 1,0121 1696
i)
0,1
209,3
2676
s)
0
0,703
7,36
p(bar)=1,5 ; Ts= 114,4°C
v)
1,0001 1,012 1,0434
i)
0,1
209,4 419,2
s)
0
0,703 1,307
p(bar)=2,0 ; Ts= 120,23°C
v)
1,0001 1,012 1,0434
i)
0,2
209,4 419,3
s)
0
0,703 1,307
p(bar)=2,5 ; Ts= 127,40°C
v)
1,0001 1,012 1,0433
i)
0,2
209,5 419,3
s)
0
0,703 1,307
p(bar)=3,0 ; Ts= 133,54°C
v)
1
1,012 1,0433
i)
0,3
209,5 419,4
s)
0
0,703 1,307
p(bar)=4,0 ; Ts= 143,63°C
v)
1
1,0119 1,0433
i)
0,4
209,6 419,4
s)
0
0,703 1,307
p(bar)=5,0 ; Ts= 151,85°C
v)
0,9999 1,0119 1,0432
i)
0,5
209,7 419,4
s)
0
0,703 1,307
p(bar)=6,0 ; Ts= 158,84°C
v)
0,9999 1,0118 1,0432
i)
0,6
209,8 419,4
s)
0
0,703 1,306
p(bar)=7,0 ; Ts= 164,96°C
v)
0,999 1,0118 1,0431
i)
0,7
209,9 419,5
s)
0
0,703 1,306
p(bar)=8,0 ; Ts= 170,41°C
v)
0,9998 1,0118 1,0431
i)
0,8
209,9 419,6
s)
0
0,703 1,306
Univ. Erwin Choque Conde
150
200
250
300
350
400
450
500
550
195277
218357
241436
264514
287591
310661
333737
356813
2784
9,751
2880
9,966
2978
3077
3178
10,163 10,344 10,512
3280
10,67
3384
10,819
3489
10,96
19514
2783
8,688
21826
2880
8,903
24136
2977
9,1
26446
3077
9,281
28755
3177
9,449
31063
3280
9,607
33371
3384
9,756
35679 37988 40296 42603 44911
3489
3597
3706
3816
3929
9,897 10,032 10,16 10,284 10,402
3890
2780
7,94
4356
2878
8,158
4821
2976
8,355
5284
3076
8,537
5747
3177
8,705
6209
3279
8,864
6672
3383
9,013
7134
3489
9,154
7596
3596
9,289
8058
3705
9,417
8519
3816
9,541
8981
3929
9,659
1937
2777
7,614
2173
2876
7,834
2406
2975
8,033
2639
3075
8,215
2871
3176
8,384
3103
3278
8,543
3334
3382
8,692
3565
3488
8,834
3797
3596
8,968
4028
3705
9,097
4259
3816
9,22
4490
3928
9,339
1286
2773
7,42
1445
2873
7,643
1601
2973
7,843
1757
3073
8,027
1912
3175
8,196
2067
3277
8,355
2222
3382
8,504
2376
3488
8,646
2530
3595
8,781
2685
3704
8,909
2839
3815
9,033
2993
3928
9,152
960,2
2770
7,28
1081
2871
7,507
1199
2971
7,708
1316
3072
7,892
1433
3174
8,062
1549
3277
8,221
1665
3381
8,371
1781
3487
8,513
1897
3595
8,648
2013
3704
8,776
2129
3815
8,9
2244
3928
9,019
764,7
2766
7,17
862,3
2869
7,4
957,5
2970
7,603
1052
3071
7,788
1145
3173
7,958
1239
3276
8,117
1332
3380
8,267
1424
3487
8,409
1517
3594
8,544
1610
3704
8,673
1703
3815
8,797
1795
3927
8,916
634,2
2762
7,078
716,6
2806
7,312
796,5
2968
7,517
875,4
3070
7,702
953,4
3172
7,873
1031
3275
8,032
1109
3380
8,182
1187
3486
8,324
1264
3594
8,46
1341
3703
8,589
1419
3814
8,712
1496
3927
8,831
471
2753
6,929
534,5
2862
7,172
595,3
2965
7,379
654,9
3067
7,566
713,9
3170
7,738
772,5
3274
7,898
831,1
3378
8,048
889,3
3485
8,326
947,4
3593
8,326
1005
3703
8,455
1063
3814
8,579
1121
3927
8,698
1,0905
632,2
1,842
425,2
2857
7,06
474,5
2962
7,271
522,6
3065
7,46
570,1
3168
7,633
617,2
3272
7,793
664,1
3377
7,944
710,8
3484
8,087
757,5
3592
8,222
804
3702
8,351
850,4
3813
8,475
896,9
3926
8,595
1,0905
632,2
1,841
352,2
2851
6,968
394
2958
7,182
434,4
3062
7,373
474,3
3166
7,546
513,6
3270
7,707
552,8
3376
7,858
591,9
3483
8,001
630,8
3591
8,131
669,7
3701
8,267
708,4
3812
8,391
747,1
3925
8,51
1,0904
632,3
1,841
300,1
2846
6,888
336,4
2955
7,106
371,4
3060
7,298
405,8
3164
7,473
439,7
3269
7,634
473,4
3374
7,786
503,9
3482
7,929
540,4
3590
8,065
573,7
3700
8,195
607
3812
8,319
640,7
3925
8,438
1,0903
632,3
1,841
261
2840
6,817
293,3
2951
7,04
324,2
3057
7,233
354,4
3162
7,409
384,2
3267
7,571
413,8
3373
7,723
443,2
3481
7,866
472,5
3589
8,003
501,8
3699
8,132
530,9
381l
8,257
560
3924
8,376
379889
600
402965
650
700
426041
449117
3597
3706
3816
3929
11,094 11,223 11,346 11,465
Página 133
C O N STA N TE S T E RM O D IN AM IC A S D E L V A PO R D E A G U A R E C A L E N T A D O
C o n tin u a ció n
T(ºC)
0
50
100
p(bar)=9,0 ; Ts= 175,36°C
v)
0,9997 1,0117 1,043
i)
0,9
210
419,7
s)
0
0,703 1,306
p(bar)=10 ; Ts= 179,9°C
v)
0,9997 1,0117 1,043
i)
1
210,1 419,7
s)
0
0,703 1,306
p(bar) = 11,0 ; Ts= 184,06 ºC
v)
0,9996 1,0116 1,0429
i)
1,1
210,2 419,8
s)
0
0,703 1,306
p(bar) = 12,0 ; Ts= 187,96 ºC
v)
0,9996 1,0116 1,0429
i)
1,2
210,3 419,9
s)
0
0,703 1,306
p(bar) = 13,0 ; Ts= 191,60 ºC
v)
0,9995 1,0115 1,0428
i)
1,3
210,4
420
s)
0
0,703 1,306
p(bar) = 14,0 ; Ts= 195,04 ºC
v)
0,9995 1,0115 1,0428
i)
1,4
210,5
420
s)
0
0,7031 1,3061
p(bar) = 15,0 ; Ts= 198,28 ºC
v)
0,9994 1,0114 1,0427
i)
1,5
210,5 420,1
s)
0
0,703 1,306
p(bar) = 16,0 ; Ts= 201,37 ºC
v)
0,9994 1,0114 1,0426
i)
1,6
210,6 420,2
s)
0
0,703 1,306
p(bar) = 17,0 ; Ts= 204,30 ºC
v)
0,9993 1,0114 1,0114
i)
1,7
210,7 420,3
s)
0
0,703 1,306
p(bar) = 18,0 ; Ts= 207,10 ºC
v)
0,9993 1,0113 1,0425
i)
1,8
210,8 420,3
s)
0
0,703 1,306
p(bar) = 19,0 ; Ts= 209,79 ºC
v)
0,9992 1,0113 1,0425
i)
1,9
210,9 420,4
s)
0
0,703 1,305
p(bar) = 20,0 ; Ts= 212,37 ºC
v)
0,9992 1,0112 1,0424
i)
2
211
420,5
s)
0
0,703 1,305
p(bar) = 22,0 ; Ts= 217,24 ºC
v)
0,9991 1,0111 1,0423
i)
2,2
211,1 420,6
s)
0
0,703 1,305
p(bar) = 24,0 ; Ts= 221,78 ºC
v)
0,999 1,011 1,0422
i)
2,4
211,3 420,8
s)
0
0,703 l,305
Univ. Erwin Choque Conde
150
200
250
300
350
400
450
500
550
600
650
700
1,0903
632,4
1,841
230,5
2835
6,753
259,7
2948
6,98
287,4
3055
7,176
314,4
3160
7,352
341
3266
7,515
367,4
3372
7,667
393,7
3480
7,811
419,8
3588
7,948
445,8
3699
8,077
471,7
3810
8,202
497,6
3924
8,321
1,0902
632,5
1,841
206,1
2829
6,695
232,8
2944
6,926
258
3052
7,124
282,5
3158
7,301
306,5
3264
7,464
330,3
3370
7,617
354
3478
7,761
377,6
3587
7,898
401
3698
8,028
424,4
3810
8,153
447,7
3923
8,272
1,0901
632,5
1,841
186,1
2823
6,64
210,8
2940
6,877
233,9
3050
7,076
256,3
3156
7,255
278,2
3262
7,419
300
3369
7,572
321,6
3477
7,716
343
3587
7,853
364,4
3697
7,983
385,7
3809
8,108
406,9
3922
8,228
1,0901
632,6
1,841
169,4
2817
6,59
192,4
2937
6,831
213,9
3047
7,033
234,5
3154
7,212
254,7
3261
7,377
274,7
3368
7,53
294,5
3476
7,675
314,2
3586
7,812
333,8
3696
7,943
353,4
3808
8,067
372,9
3922
8,187
1,09
632,7
1,841
155,2
2810
6,542
176,9
2933
6,788
196,9
3044
5,992
216,1
3152
7,173
234,8
3259
7,338
253,3
3366
7,492
271,7
3475
7,637
289,9
3585
7,774
308,8
3695
7,905
326,1
3808
8,03
344,1
3921
8,15
1,0899
632,7
1,841
143
2803
6,496
163,6
2929
6,749
182,3
3042
6,955
200,3
3150
7,137
217,7
3257
7,302
235,1
3365
7,456
252,1
3474
7,602
269
3584
7,739
285,9
3695
7,87
302,7
3807
7,995
319,4
3921
8,115
1,0899
632,8
1,84
132,4
2796
6,452
152
2925
6,711
169,7
3039
6,919
186,5
3148
7,102
202,9
3256
7,268
219,1
3364
7,423
235,1
3473
7,569
250,9
3583
7,707
266,7
3694
7,838
282,4
3806
7,963
298
3920
8,03
1,0898 1,1565
632,8 852,4
1,84
2,331
141,9
2921
6,675
158,6
3036
6,886
174,6
3546
7,07
190
3254
7,237
205,2
3362
7,392
220,2
3472
7,538
235,1
3582
7,676
249,9
3693
7,807
264,6
3805
7,932
279,3
3919
8,053
1,0898 1,0426
632,9 852,4
1,84
2,33
133
2917
6,641
148,9
3033
6,854
164
3144
7,04
178,5
3252
7,207
192,9
3361
7,362
207,1
3471
7,509
221,1
3581
7,647
235,1
3692
7,778
249
3805
7,904
262,8
3919
8,024
1,087
633
1,00
1,1563
852,5
0,84
125
2913
2,33
140,2
3031
6,609
154,6
3142
6,824
168,4
3251
7,011
182
3360
7,179
195,4
3470
7,335
208,7
3580
7,000
221,9
3691
482
235
3804
7,62
248,1
3918
7,751
1,0896 1,1562
633
852,8
1,84
2,33
117,9
2909
6,578
132,5
3028
6,795
146,1
3140
6,983
159,3
3249
7,152
172,2
3358
7,308
185
3468
7,456
197,6
3579
7,594
210,1
3691
7,726
222,6
3803
7,851
235
3918
7,972
1,0896 1,1561
633,1 852,6
1,84
2,33
111,5
2904
6,547
125,5
3025
6,768
138,6
3138
6,957
151,1
3248
7,126
163,4
3357
7,283
175,6
3467
7,431
187,6
3578
7,57
199,S
3690
7,701
211,4
3803
7,827
223,2
3917
7,948
1,0894 1,1559
633,2 852,6
l,840
2,33
100,4
2896
6,49
113,4
3019
6,716
125,5
3134
6,908
137
3244
7,079
148,3
3354
7,236
159,4
3465
7,385
170,3
3576
7,524
181,2
3688
7,656
192
3801
7,782
202,8
3916
7,903
1,0893 1,1557
635,3 852,7
1,84
2,329
91,13
2887
6437
103,3
3014
6,669
114,5
3130
6,863
125,2
3241
7,035
135,6
3352
7,194
145,8
3463
7,342
155,9
3574
7,482
165,9
3687
7,615
175,9
3800
7,741
185,7
3915
7,862
Página 134
C O N STA N TE S T E RM O D IN AM IC A S D E L V A PO R D E A G U A R E C A L E N T A D O
C o n tin u a ció n
T ºC
0
50
100
p(bar) = 26,0 ; Ts= 226,00 ºC
v)
0,9988 l,0110 1,0421
i)
2,6
211,5 420,9
s)
0
0,702 l,305
p(bar) = 28,0 ; Ts= 230,00 ºC
v)
0,9987 1,0109 1,042
i)
2,8
211,7 421,1
s)
0
0,702 1,305
p(bar) = 30,0 ; Ts= 233,84 ºC
v)
0,9986 1,0108 1,0419
i)
3
211,8 421,2
s)
0
0,702 1,305
p(bar)= 32 ; Ts= 237,4ºC
v)
0,9985 1,0107 1,0418
i)
3,2
212
421,4
s)
0
0,702 1,305
p(bar)= 34 ; Ts= 240,9ºC
v)
0,9984 1,0106 1,0417
i)
3,4
212,2 421,5
s)
0
0,702 1,304
p(bar)= 36 ; Ts= 244,2ºC
v)
0,9983 l,0105 1,0416
i)
3,6
212,3 421,7
s)
0
0,702 1,304
p(bar)= 38 ; Ts= 247,3ºC
v)
0,9982 1,0104 1,0415
i)
3,8
212,5 421,8
s)
0
0,702 1,304
p(bar)= 40 ; Ts= 250,33ºC
v)
0,9981 1,0103 1,0414
i)
4
212,7
422
s)
0
0,702 1,304
p(bar)= 44 ; Ts= 256,0ºC
v)
0,9979 1,0102 1,0412
i)
4,4
213
422,3
s)
0
0,702 1,304
p(bar)= 48 ; Ts= 261,4ºC
v)
0,9977 1,01
1,041
i)
4,8
213,4 422,6
s)
0
0,701 1,303
p(bar)= 52 ; Ts= 266,4ºC
v)
0,9975 1,0098 1,0408
i)
5,2
213,7 422,9
s)
0
0,701 1,303
p(bar)= 56 ; Ts= 271,1ºC
v)
0,9973 1,0096 1,0406
i)
5,6
214,1 423,2
s)
0
0,701 1,303
p(bar)= 60 ; Ts= 275,56ºC
v)
0,9971 1,0095 1,0404
i)
6
214,4 423,5
s)
0
0,701 1,302
p(bar)= 64 ; Ts= 279,8ºC
v)
0,9969 1,0093 1,0402
i)
6,5
214,8 423,8
s)
0
0,701 1,302
Univ. Erwin Choque Conde
150
200
250
300
350
400
450
500
550
600
650
700
l,0892 1,1555
633,5 852,8
1,839 2,329
33,26
2877
5,385
94,82
3008
6,624
105,3
3125
6,821
115,2
3238
6,994
124,9
3349
7,154
134,4
3461
7,303
143,8
3573
7,443
153
3685
7,576
162,2
3799
7,703
171,3
3913
7,824
1,0891 1,1553
633,6 852,9
1,839 2,329
76,49
2868
6,336
87,5
3002
6,581
97,38
3121
6,781
106,7
3234
6,956
115,7
3346
7,117
124,6
3458
7,267
133,3
3571
7,408
142
3683
7,541
150,5
3797
7,667
159
3912
7,689
1,0889 1,1551
633,7 852,9
1,839 2,328
70,61
2858
6,289
81,15
2995
6,541
90,51
3117
6,744
99,28
3231
6,921
107,8
3343
7,082
116,1
3456
7,233
124,3
3569
7,374
132,4
3682
7,507
140,4
3796
7,634
148,3
3911
7,756
1,0888 1,1549
633,8
853
1,839 2,328
75,43
2847
5,243
78,59
2989
6,503
84,49
3112
6,709
92,8
3227
6,887
100,8
3341
7,05
108,7
3454
7,201
116,41
3567
7,343
124
3680
7,476
131,5
3794
7,603
139
3910
7,725
1,0887 1,1547
634
853,1
1,838 2,328
60,84
2836
6,198
70,67
2983
6,466
79,18
3108
6,675
87,08
3224
6,855
94,69
3328
7,019
102,1
3451
7,171
109,4
3565
7,313
116,6
3679
7,447
123,7
3793
7,574
130,7
3909
7,696
1,0885 1,1545
634,1 853,2
1,838 2,327
56,73
2825
6,154
66,3
2976
6,431
74,46
3103
6,644
81,99
3221
6,825
89,23
3335
6,99
96,27
3449
7,142
103,2
3563
7,285
110,1
3677
7,419
116,7
3792
7,547
123,4
3907
7,669
1,0884 1,1543
634,2 853,3
1,838 2,327
53,03
2813
6,11
62,37
2970
6,397
70,23
3099
6,613
77,44
3217
6,796
81,35
3332
6,962
91,05
3447
7,115
97,61
3561
7,258
104,1
3675
7,393
110,5
3790
7,521
116,8
3906
7,643
1,0883 1,1541 1,2511 58,84
634,3 853,4 1085,8 2963
1,838 2,327 2,793 6,364
66,42
3094
6,584
73,34
3214
6,769
79,95
3330
6,935
86,35
3445
7,089
92,61
3559
7,233
98,77
3674
7,368
104,9
3789
7,496
110,9
3905
7,618
1,0881 1,1537 1,2503 52,71
634,6 853,6 1085,8 2949
1,837 2,326 2,792 6,301
59,84
3085
6,528
66,26
3207
6,717
72,35
3324
6,886
78,24
3440
7,04
83,98
3555
7,185
89,61
3671
7,321
95,18
3786
7,449
100,7
3902
7,572
1,0878 1,1533 1,2496
634,8 853,7 1085,7
1,837 2,326 2,791
47,58
2935
6,241
54,34
3075
6,476
60,36
3199
6,669
66,02
3319
6,84
71,47
3435
6,996
76,78
3552
7,141
81,98
3667
7,278
87,11
3783
7,407
92,18
3900
7,53
1,0876 1,1529 1,2489 43,22
635,1 853,9 1085,7 2919
1,836 2,325
2,79
6,183
49,68
3065
6,427
55,35
3192
6,624
60,66
3313
6,797
65,75
3431
6,954
70,69
3548
7,101
75,52
3664
7,238
80,28
3780
7,368
84,98
3898
7,491
1,0873 1,1525 1,2481 39,45
635,3 854,1 1085,7 2904
1,836 2,324 2,789 6,126
45,68
3055
6,38
51,06
3185
6,581
56,07
3307
6,757
60,84
3426
6,916
65,47
3544
7,063
69,98
3661
7,201
74,43
3778
7,331
78,81
3895
7,455
1,0871 1,1522 1,2474 36,16
635,6 854,2 1085,7 2887
1,836 2,124 2,788 6,071
42,2
3045
6,336
47,34
3177
6,541
52,08
3301
6,719
56,59
3421
6,879
60,94
3540
7,028
65,19
3657
7,166
69,35
3775
7,297
73,47
3893
7,421
1,0869 1,1518 1,2467 33,25
635,8 854,4 1085,7 2869
1,835 2,323 2,788 6,016
39,16
3034
6,293
44,08
3170
6,502
48,6
3296
6,683
52,87
3417
6,845
56,98
3536
6,995
60,99
3654
7,134
64,92
3772
7,265
68,79
3890
7,39
Página 135
C O N STA N TE S T E RM O D IN AM IC A S D E L V A PO R D E A G U A R E C A L E N T A D O
C o n tin u a ció n
TºC
0
50
100
p(bar)= 68 ; Ts= 283,8ºC
v)
0,9967 1,0091 1,04
i)
6,9
215,1 424,1
s)
0
0,7
1,302
p(bar)= 72 ; Ts= 287,7ºC
v)
0,9965 1,0089 1,0398
i)
7,3
215,4 424,4
s)
0
0,7
1,301
p(bar)= 76 ; Ts= 291,4ºC
v)
0,9963 1,0088 1,0396
i)
7,7
215,8 424,7
s)
0
0,7
1,301
p(bar)= 80 ; Ts= 295,0ºC
v)
0,9961 1,0056 1,0394
i)
8,1
216,1
425
s)
0
0,7
1,301
p(bar)= 84 ; Ts= 298,4ºC
v)
0,9959 1,0084 1,0392
i)
8,5
216,5 425,3
s)
0
0,7
1,301
p(bar)= 88 ; Ts= 301,7ºC
v)
0,9958 1,0082 1,039
i)
8,9
216,8 425,6
s)
0
0,7
1,3
p(bar)= 92; Ts= 304,9ºC
v)
0,9956 1,0081 1,0388
i)
9,3
217,2 425,9
s)
0
0,699
1,3
p(bar)= 96; Ts= 308,0ºC
v)
0,9954 1,0079 1,0385
i)
9,7
217,5 426,2
s)
0
0,699
1,3
p(bar)= 100; Ts= 310,96ºC
v)
0,9952 1,0077 1,0383
i)
10,1
217,8 426,5
s)
0
0,699 1,299
p(bar)= 110; Ts= 318,04ºC
v)
0,9947 1,0073 1,0378
i)
11,1
218,7 427,3
s)
0
0,699 1,299
p(bar)= 120; Ts= 324,65ºC
v)
0,9942 1,0069 1,0373
i)
12,1
219,6
428
s)
0
0,698 1,298
p(bar)= 130; Ts= 330,81ºC
v)
0,9937 1,0064 1,0368
i)
13,1
220,4 428,8
s)
0,001 0,698 1,297
p(bar)= 140; Ts= 336,63ºC
v)
0,9932 1,006 1,0363
i)
14,1
221,3 429,6
s)
0,001 0,697 1,296
p(bar)= 150; Ts= 342,12ºC
v)
0,9928 1,0056 1,0358
i)
15,1
222,1 430,3
s)
0,001 0,697 1,296
Univ. Erwin Choque Conde
150
200
350
400
450
500
550
600
650
700
1,0866 1,1514 1,246 30,65
636,1 854,6 1085,7 2851
1,835 2,323 2,787 5,961
36,46
3024
6,251
41,21
3162
6,466
45,52
3290
6,649
49,58
3412
6,812
53,49
3532
6,963
57,28
3651
7,103
61
3769
7,235
64,66
3888
7,36
1,0864
636,3
1,834
28,31
2831
5,906
34,05
3013
6,211
38,64
3154
6,431
42,78
3284
6,616
46,66
3407
6,781
50,38
3528
6,933
53,99
3648
7,074
57,22
3766
7,206
60,99
3885
7,331
1,0861 1,1506 1,2446 26,18
636,6 854,9 1085,7 2810
1,834 2,321 2,785
5,85
31,89
3001
6,171
36,35
3147
6,397
40,33
3278
6,585
44,05
3402
6,751
47,6
3524
6,904
51,04
3644
7,046
54,41
3764
7,179
57,71
3833
7,305
1,0859 1,1502 1,2439 24,23
636,8 855,1 1085,7 2787
1,833 2,321 2,784 5,793
29,94
2990
6,133
34,29
3139
6,364
38,12
3272
6,555
41,7
3398
6,723
45,1
3520
6,877
48,39
3641
7,019
51,6
3761
7,153
54,76
3881
7,279
1,0856 1,1498 1,2432 22,43
637,1 855,3 1085,7 2763
1,833
2,32
2,783 5,734
28,16
2977
6,095
32,41
3131
6,332
36,12
3266
6,526
39,57
3393
6,696
42,84
3516
6,851
45,99
3638
6,994
49,07
3758
7,128
52,08
3878
7,254
1,0854 1,1495 1,2426 1,403
637,3 855,4 1085,7 1345
1,832
2,32
2,782 3,254
26,54
2965
6,058
30,7
3122
6,301
34,31
3260
6,498
37,63
3388
6,669
40,78
3513
6,826
43,81
3634
6,969
46,76
3755
7,104
49,66
3876
7,231
1,0851 1,1492 1,2419 1,401
637,6 855,6 1085,7 1344
1,832 2,319 2,781 3,252
25,05
2952
6,021
29,14
3114
6,271
32,65
3253
6,471
35,86
3383
6,644
38,9
3509
6,802
41,82
3631
6,946
44,66
3752
7,081
47,44
3873
7,209
1,0849 1,1487 1,2412 1,399
637,8 855,8 1085,8 1344
1,832 2,318
2,78
3,25
23,68
2939
5,984
27,71
3106
6,243
31,12
3247
6,445
34,24
3378
6,62
37,18
3504
6,778
39,99
3628
6,923
42,73
3749
7,059
45,4
3871
7,187
1,0846 1,1483 1,2405 1,397
638,1
856 1085,8 1343
1,831 2,318 2,779 3,248
22,41
2926
5,947
26,39
3097
6,213
29,72
3241
6,419
32,75
3373
6,596
35,59
3500
6,756
38,31
3624
6,902
40,95
3746
7,038
43,23
3868
7,166
1,084
638,7
1,83
1,393
1342
2,244
19,6
2889
5,856
23,5
3075
6,143
26,66
3225
6,358
29,49
3360
6,539
32,13
3490
6,702
34,65
3616
6,85
37,08
3739
6,988
39,45
3862
7,117
1,0833 1,1464 1,2372 1,389
639,3 856,8 1085,9 1341
1,829 2,315 2,775
3,24
17,19
2849
5,762
21,07
3052
6,076
24,1
3209
6,301
26,77
3348
6,487
29,25
3480
6,653
31,59
3607
6,802
33,85
3732
6,941
36,05
3856
7,072
1,0827 1,1455 1,2356 1,385
639,9 857,3 1085,9 1340
1,828 2,313 2,772 2,326
15,09
2804
5,664
19,01
3028
6,011
21,93
3192
6,246
24,47
3335
6,437
26,81
3470
6,606
29,01
3599
6,758
31,12
3725
6,898
33,18
3850
7,03
1,082
640,6
1,827
1,381
1339
3,231
13,21
2753
5,559
17,22
3003
5,946
20,06
3175
6,193
22,5
3322
6,39
24,71
3459
6,562
26,79
3590
6,716
28,78
3717
6,858
30,71
3843
6,991
1,0814 1,1436 1,2325 1,377
641,2 858,2 1086,1 1338
1,826
2,31
2,768 3,228
11,46
2693
5,443
15,66
2977
5,883
18,44
3157
6,142
20,78
3309
6,345
22,9
3449
6,52
24,87
3581
6,677
26,76
3710
6,82
28,57
3837
6,954
1,151
854,7
2,322
250
1,2453
1085,7
2,786
1,1474 1,2389
856,4 1085,8
2,316 2,777
1,1446 1,2341
857,7 1086
2,312
2,77
300
Página 136
C O N STA N TE S T E RM O D IN AM IC A S D E L V A PO R D E A G U A R E C A L E N T A D O
C o n tin u a ció n
T(ºC)
0
50
100
p(bar)= 160; Ts= 347,32ºC
v)
0,9923 1,0051 1,0353
i)
16,1
223
431,1
s)
0,001 0,696 1,295
p(bar)= 170; Ts= 352,26ºC
v)
0,9918 1,0047 1,0349
i)
17,1
223,8 431,8
s)
0,001 0,696 1,294
p(bar)= 180; Ts= 356,96ºC
v)
0,9914 1,0043 1,0344
i)
18,1
224,7 432,6
s)
0,001 0,695 1,293
p(bar)= 190; Ts= 361,44ºC
v)
0,9909 1,0039 1,0539
i)
19,1
225,6 433,3
s)
0,001 0,695 1,293
p(bar)= 200; Ts= 365,7ºC
v)
0,9904 1,0034 1,0334
i)
20,1
2264 434,1
s)
0,001 0,694 1,292
p(bar)= 210; Ts= 369,8ºC
v)
0,9899 1,003 1,0329
i)
21,1
227,3 434,9
s)
0,001 0,694 1,291
p(bar)= 220; Ts= 373,7ºC
v)
0,9895 1,0026 1,325
i)
22,1
228,1 435,6
s)
0,001 0,693
1,29
Univ. Erwin Choque Conde
150
200
350
400
450
500
550
600
650
700
1,0807 1,1427 1,2309 1,373
641,8 858,6 1086,2 1338
1,825 2,509 2,766 3,224
9,764
2617
5,304
14,27
2949
5,82
17,02
3139
6,093
19,28
3295
6,301
21,31
3438
6,481
23,19
3573
6,639
24,98
3703
6,784
26,7
3831
6,919
1,0801 1,1418 1,2294
642,5 859,1 1086,3
1,824 2,307 2,764
1,37
1337
3,22
1,729
1667
3,771
13,03
2920
5,765
15,76
3121
6,044
17,96
3281
6,26
19,91
3427
6,442
21,71
3564
6,603
23,42
3695
6,75
25,06
3825
886
1,0795 1,1409 1,2279 1,366
643,1 859,6 1086,4 1336
1,823 2,306 2,761 3,216
1,704
1659
3,755
11,91
2888
5,691
14,63
3102
5,997
16,78
3268
6,219
18,66
3417
6,406
20,39
3555
6,569
22,03
3688
6,717
23,59
3818
6,855
1,0788
643,7
1,822
1,683
1653
3,742
10,89
2855
5,625
13,62
3082
5,95
15,72
3254
6,18
17,54
3406
6,371
19,21
3546
6,536
20,78
3680
6,686
22,28
3812
6,825
1,14
860
2,305
250
300
1,2264 1,363
1086,6 1335
2,759 3,213
1,0782 1,1391 1,2249
644,4 860,5 1086,7
1,821 2,303 2,757
1,36
1335
3,209
1,665
1647
3,73
9,95
2819
5,556
12,7
3062
5,904
14,77
3239
6,142
16,54
3395
6,337
18,15
3537
6,505
19,66
3673
6,656
21,1
3806
6,788
1,0776 1,1382 1,2235
645
860,9 1086,9
1,819 2,302 2,755
1,356
1334
3,206
1,649
1642
3,719
9,076
2781
5,484
11,87
3041
5,858
13,9
3225
6,105
15,63
3383
6,303
17,19
3528
6,474
18,65
3665
6,627
20,03
3799
6,768
1,077
645,6
1,818
1,353
1333
3,203
1,635
1637
3,709
8,254
2738
5,409
11,11
3020
5,813
13,12
3210
6,068
14,8
3372
6,271
16,32
3519
6,444
17,73
3658
6,599
19,06
3793
6,742
1,1374 1,2221
861,4
1087
2,3
2,753
Página 137
Anexo D.
U N ID AD ES Y TABLAS DE CONVERSIÓN Y EQUIVALENCIA
Unidades eléctricas
Unidades eléctricas de intensidad, tensión y resistencia
Corriente eléctrica, es el movimiento o paso de electricidad a lo largo del circuito eléctrico desde el generador
de electricidad hasta el aparato donde se va a utilizar, que llamaremos receptor, a través de los conductores.
Para que se origine la corriente eléctrica es necesario que en el generador se produzca una fuerza
electromotriz que cree una diferencia de potencial entre los terminales o polos del generador.
A esta diferencia de potencial se le llama tensión o voltaje y se mide en VOLTIOS (V).
La cantidad de electricidad que pasa por un conductor en un segundo se llama intensidad de la corriente y
se mide en AMPERIOS (A).
La dificultad que ofrece el conductor al paso de una corriente eléctrica se llama resistencia eléctrica y se
mide en OHMIOS ().
Así pues, tras definir estas magnitudes podemos relacionarlas por medio de la llamada LEY DE OHM, que
nos dice que la intensidad es directamente proporcional a la tensión o voltaje e inversamente proporcional a la
resistencia. Es decir que la intensidad crece cuando aumenta la tensión y disminuye cuando crece la
resistencia.
Esto se expresa de la siguiente forma:
TENSION
E
V
INTENSIDAD =
------------= --ó
--RESISTENCIA
R
R
de donde: E ó V = I * R y R = E / I
Sus unidades serán:
1 Amperio = 1 Voltio / 1 Ohmio
1 Voltio = 1 Amperio * 1 Ohmio
1 Ohmio = 1 Voltio / 1 Amperio
La unidad de intensidad es el Amperio (A), nombre dado en honor del físico francés Ampere, como en
electrónica esta es una unidad muy grande para las corrientes que normalmente se controlan, definiremos sus
submúltiplos mas empleados:
-3
1 MILIAMPERIO = 10 Amperios
-6
1 MICROAMPERIO = 10 Amperios
La unidad que nos mide la diferencia de potencial o tensión es el VOLTIO (V) llamado así en honor al físico
italiano Volta, que descubrió la pila eléctrica. Para grandes potenciales se emplea el KILOVOLTIO y en los
pequeños el MILIVOLTIO.
3
1 KILOVOLTIO = 10 Voltios
-3
1 MILIVOLTIO = 10 Voltios
La unidad de medida de la resistencia eléctrica es el OHMIO (), nombre dado en honor del físico alemán
Ohm. Al ser una pequeña cantidad se emplean sus múltiplos:
3
1 KILOOHMIO = 10 Ohmios
6
1 MEGAOHMIO = 10 Ohmios
Unidades eléctricas de potencia
La electricidad puede producir energía de diferentes tipos, siendo la cantidad que produce por unidad de
tiempo, que suele ser el segundo, lo que se llama potencia.
La unidad fundamental que mide la potencia desarrollada por un elemento es el VATIO (W).
El vatio (W) es la potencia que consume un elemento al que se le ha aplicado una tensión de un voltio y
circula por el una intensidad de un amperio.
W=A*VyW=E*I
A = Amperios
V = Voltios
3
Como múltiplo mas usual se emplea el:
1 KILOVATIO = 10 VATIOS
-3
Como submúltiplo se utiliza el:
1 MILIVATIO = 10 VATIOS
Por lo tanto:
1 W = 1.000 mW = 0.001 Kw
Univ. Erwin Choque Conde
Página 138
Unidades eléctricas de capacidad e inducción
Unidades de capacidad
Un condensador es el conjunto formado por dos placas metálicas paralelas (armaduras) separadas entre si
por una sustancia aislante (dieléctrico).
Aplicando una tensión a las placas del condensador, esta hará pasar los electrones de una armadura a otra,
cargando el condensador.
La relación entre la carga eléctrica que adquieren las armaduras del condensador y el voltaje aplicado se
denomina capacidad.
CAPACIDAD = CARGA / VOLTAJE
Siendo sus unidades:
Q = Culombios (1 Culombio = 1 Amperio / 1 Segundo)
V = Voltios
C = Faradios (F), siendo esta la unidad fundamental de capacidad.
Por ser muy grande esta unidad para las capacidades normales empleadas se utilizan sus submúltiplos:
-6
1 MICROFARADIO = 10 FARADIOS
-9
1 NANOFARADIO = 10 FARADIOS
-12
1 PICOFARADIO = 10 FARADIOS
Unidades de inducción
Además de las resistencias, los componentes reactivos, o sea, las bobinas y los condensadores, también se
oponen a las corrientes en los circuitos de corriente alterna.
La INDUCTANCIA (L) es la característica o propiedad que tiene una bobina de oponerse a los cambios de la
corriente.
La cantidad de oposición que presenta una inductancia se llama reactancia inductiva y se mide en ohmios.
La unidad de inductancia es el Henrio (H). Por ser una unidad muy grande, para las medidas usuales se
emplean sus submúltiplos:
-3
1 MILIHENRIO = 1 mH = 10 H
-6
1 MICROHENRIO = 1 uH = 10 H
Sistema Internacional de Unidades SI
Las unidades SI son de tres clases:
1) Unidades básicas o fundamentales. Se refieren a magnitudes independientes.
2) Unidades suplementarias. Son unidades cuyo carácter fundamental no aparece claro a priori. De
momento sólo hay dos, puramente geométricas.
3) Unidades derivadas. Se refieren a todas las demás magnitudes, y se deducen de las fundamentales
y suplementarias de manera coherente.
Magnitud
Longitud.
Definición: El metro es la longitud del trayecto recorrido en el vacío por la luz durante un tiempo de
1/299.792.458 de segundo. (17ª CGPM, 1983, r.1).
Masa.
Definición: El kilogramo es la unidad de masa y es igual a la masa del prototipo internacional del kilogramo. (3ª
CGPM, 1901, p. 70 del acta).
Tiempo.
Definición: El segundo es la duración de 9.192.631.770 periodos de la radiación correspondiente a la transición
entre los dos niveles hiperfinos del estado fundamental del átomo de cesio 133. (13ª CGPM, 1967, r.1).
Intensidad de corriente eléctrica.
Definición: El amperio es la intensidad de una corriente constante que, manteniéndose en dos conductores
paralelos, rectilineos, de longitud infinita, de sección circular despreciable y situados a una distancia de 1 metro
-7
uno de otro, en el vacío, produciría entre estos conductores una fuerza igual 2 x 10 newton por metro de
longitud. (CIPM, 1946, r.2, aprobada por la 9ª CGPM, 1948).
Temperatura termodinámica.
Univ. Erwin Choque Conde
Página 139
Definición: El kelvin es la fracción 1/273,16 de la temperatura termodinámica del punto triple del agua. (13ª
CGPM 1967, r.4).
La 13 CGPM (1967, r.3) decidió así mismo que la unidad kelvin y su símbolo K sean utilizados para expresar un intervalo o una diferencia de
temperaturas.
Además de la temperatura termodinámica, símbolo T, expresada en kelvins, se utliza también la temperatura Celsius, símbolo t, definida por la
ecuación t=T - T0, donte T0 = 273,15 Kpor definición. Para expresar la temperatura Celsius, se utiliza la unidad "grado celsius", que es igual a la
unidad Kelvin; en este caso, el "glado celsius" es un nombre especial utilizado en lugar de "Kelvin", Un intervalo o una diferencia de temperatura
Celsius puede expresarse, indistintamente, en grados Kelvins o Celsius.
Intensidad luminosa.
Definición: La candela es la intensidad luminosa, en una dirección dada, de una fuente que emite una radiación
12
monocromática de frecuencia 540 x 10 hertz y cuya intensidad radiante en dicha dirección es 1/683 vatios por
estereorradián. (16ª CGPM, 1979, r.3).
Cantidad de sustancia.
Definición: El mol es la cantidad de sustancia de un sistema que contiene tantas entidades elementales como
átomos hay en 0,012 kilogramos de carbono 12. Cuando se emplea el mol, las entidades elementales deben
ser especificadas y pueden ser átomos, moléculas, iones, electrones, otras partículas o agrupamientos
especificados de tales partículas. (14ª CGPM, 1971).
Unidades suplementarias
Angulo plano
Angulo sólido
La Ley 3/1985, de 18 de marzo, de Metrología determina como las Unidades Legales de Medida las del Sistema Internacional de Unidades
adoptado por la Conferencia General de Pesas y Medidas. Estas unidades quedaron establecidas en el Real Decreto 1317/1987, de 27 de
octubre, modificado posteriormente por el Real Decreto 1737/1997, de 20 de noviembre
Unidades básicas del Sistema Internacional
Magnitud
Nombre
longitud
metro
masa
kilogramo
tiempo
segundo
corriente eléctrica
ampere, amperio
temperatura termodinámica
kelvin
cantidad de sustancia
mol
intensidad luminosa
candela
Símbolo
m
kg
s
A
K
mol
cd
Hay otras muchas unidades también derivadas (ej.: las de área, volumen, velocidad, etc.) sin nombre especial
que no se incluyen en la siguiente tabla.
Unidades derivadas SI con nombre especial
Magnitud
- Frecuencia
- Fuerza
- Presión, esfuerzo, tensión mecánica
- Energía, trabajo, cantidad de calor
- Potencia, flujo radiante
- Carga eléctrica, cantidad de electricidad
- Potencial eléctrico, diferencia de potencial, tensión, fuerza
electromotriz
- Capacidad eléctrica
- Resistencia eléctrica
- Conductividad, conductancia eléctrica
- Flujo magnético, flujo de inducción magnética
- Intensidad del campo, magnético
- Inducción magnética, densidad de flujo magnético
- Inductancia
- Temperatura
- Flujo luminoso
- Iluminación, iluminancia
Univ. Erwin Choque Conde
Nombre
Símbolo
Expresión
hertz, hercio
newton
pascal
joule, julio
watt, vatio
coulomb,
culombio
volt, voltio
Hz
N
Pa
J
W
C
s
-2
kg·m·s
-2
N·m
N·m
-1
J·s
A·s
V
W·A
farad, faradio
ohm, ohmio
siémens
wéber
lenz
tesla
henry, henrio
grado Celsius
lumen
lux
F
S
Wb
Lz
T
H
ºC
lm
lx
C·V
-1
V·A
-1
A·V
V·s
-1
A·m
-2
Wb·m
-1
Wb·A
K
cd·sr
-2
lm·m
-1
-1
-1
Página 140
- Actividad (radiactiva)
- Dosis energética
- Dosis equivalente
- Angulo plano
- Angulo sólido
becquerel
gray
sievert
radián
estereorradián
Bq
Gy
Sv
rad
sr
-1
s
-1
J·kg
-1
J·kg
Prefijos SI de múltiplos y submúltiplos
Múltiplos y submúltiplos decimales de las unidades SI que designan los factores numéricos decimales
por los que se multiplica la unidad
Prefijo
Símbolo
1 000 000 000 000 000 000 000 000
yotta
Y
1 000 000 000 000 000 000 000
zetta
Z
1 000 000 000 000 000 000
exa
E
1 000 000 000 000 000
peta
P
1 000 000 000 000
tera
T
1 000 000 000
giga
G
1 000 000
mega
M
1 000
kilo
k
100
hecto*
h
10
deca*
da
0.1
deci*
d
0.01
centi*
c
0.001
mili
m
0.000 001
micro
0.000 000 001
nano
n
0.000 000 000 001
pico
p
0.000 000 000 000 001
femto
f
0.000 000 000 000 000 001
atto
a
0.000 000 000 000 000 000 001
zepto
z
0.000 000 000 000 000 000 000 001
yocto
y
* Se recomienda usar sólo los prefijos cuyos factores tengan exponentes múltiplos de 3.
Los señalados con asterisco deben evitarse
Factor
24
10
21
10
18
10
15
10
12
10
9
10
6
10
3
10
2
10
1
10
-1
10
-2
10
-3
10
-6
10
-9
10
-12
10
-15
10
-18
10
-21
10
-24
10
En la siguiente tabla se relacionan otras unidades que no son propiamente del SI, pero cuyo uso se permite
dentro de éste.
Unidades no métricas de uso permitido en el SI
Magnitud
Nombre
Símbolo
Equivalencia SI
Ángulo
grado
º
1º = ( / 180) rad
minuto
'
1' = (1/60)º = ( / 10800) rad
segundo
"
1" = (1/60)' = ( / 648000) rad
Tiempo
minuto
min
1 min = 60 s
hora
h
1 h = 60 min = 3600 s
día
d
1 d = 24 h = 86400 s
3
-3
3
Volumen
litro
loL
1 L = 1 dm = 10 m
3
Masa
tonelada
t
1 t = 10 kg = 1 Mg
2
4
2
Área
hectárea
ha
1 ha = 1 hm = 10 m
Nota. Los prefijos SI no son aplicables a las unidades de ángulo ni a las de tiempo con excepción del segundo
Unidades utilizadas con el SI, cuyos valores se han obtenido experimentalmente
Magnitud
Nombre
masa
energía
Símbolo
unidad de masa atómica unificada
electrovolt, electrovoltio
u
eV
Unidades ajenas al SI que deben mantenerse
Magnitud
Unidad SI
Unidad
2
superficie
m
velocidad
m/s
Univ. Erwin Choque Conde
Unidad ajena
Múlt. y submúlt.
Observaciones
ha (hectárea)
a (área)
km/h
Página 141
-1
frecuencia de rotación
s
presión
Pa
carga eléctrica
C
-1
min
r/min (revoluciones por minuto)
r/s (revoluciones por segundo)
bar (bar) (sólo con fluidos)
mbar
A·h
Normas para el uso de los nombres de unidades SI
Las normas que siguen se refieren exclusivamente al uso de los nombres de las unidades SI, tanto
fundamentales como suplementarias o derivadas. Hay otras normas que afectan a los símbolos y se resumen
en el siguiente apartado.
1) Los nombres de las unidades son los consignados en las tablas. No deben alterarse para acomodarse a las
peculiaridades de cada idioma.
2) Cuando se usa el nombre completo de las unidades fundamentales y derivadas o de sus múltiplos y
submúltiplos, debe escribirse con minúscula incluso si procede de un nombre propio (ej.: pascal, newton, joule).
Se exceptúa Celsius en "grado Celsius".
3) Los nombres de unidades compuestas que son producto de otras unidades, se pueden separar por un
espacio o un guión (v.g.: newton-metro o newton metro). Cuando se trata de cocientes y no de productos se
intercala la preposición "por": así, metro por segundo.
4) Cuando el valor de la magnitud que se menciona es superior a la unidad, se usa el plural (ej.: 300
micrometros, 500 hectopascales; pero 0,5 micrometro). Del plural se exceptúan las unidades hertz, lux y
siemens.
5) Debe evitarse el uso de nombres antiguos y no aceptados en el SI, tales como "micra" (en la actualidad
micrómetro) y angstrom, en cuyo lugar debe usarse el nanómetro (1 nm = 10 A). La antigua redundancia "grado
centígrado", derogada en 1967, debe sustituirse por "grado Celsius".
Normas para el uso de los símbolos SI
Cada unidad SI tiene su propio símbolo, el mismo en cualquier idioma. Las normas aplicables a los símbolos,
que se exponen continuación, no son idénticas de nombres.
1) Los símbolos se escriben con minúscula excepto cuando provienen de un nombre propio (ej.: m para metro,
pero N para newton). Es permisible usar la mayúscula L para litro cuando el símbolo normal, l, puede
confundirse con el dígito 1. Cuando un símbolo de dos letras proviene de un nombre propio, la inicial es
mayúscula (ej.: Pa para pascal y Hz para hertz).
2) Los símbolos de unidades se deben imprimir en tipo redondo (letra romanilla).
3) Los prefijos de múltiplos y submúltiplos se escriben con minúscula excepto en el caso de los múltiplos mega
y superiores. Así, kilómetro se escribirá km pero megahertz se escribirá MHz. Obsérvese que esta norma
deroga la antigua según la cual los prefijos de los múltiplos se escribían con mayúscula y los de los
submúltiplos con minúscula.
4) Cuando el símbolo lleva prefijo, la combinación prefijo y símbolo debe considerarse como un nuevo símbolo,
-1
-1
que se puede elevar a una potencia sin necesidad de paréntesis. Ej.: de cm, cm , y no (cm) .
5) Los símbolos no son abreviaturas, nunca llevan plural y no deben ir seguidos de punto final. Por ejemplo, 1
km y 15 km deben llevar el mismo símbolo.
6) Entre el valor numérico y el símbolo se debe dejar un espacio.
Esto no se aplica a los símbolos grado, minuto y segundo de ángulo, que no van separados. Ej.: 20 cm, pero
40º50'22" de latitud. La temperatura se puede expresar de ambas maneras (tanto 18ºC como 18ºC).
7) Los productos de unidades se expresan mediante un punto a media altura de las minúsculas (así, N·m para
newton-metro), es permisible el punto normal N.m. En los cocientes se usa la barra de fracción o el exponente
-1
-1
negativo (m/s o m·s para metro por segundo: no omitir el punto, pues, en virtud de 4), ms se interpretaría
como inverso de milisegundo). Nunca se debe emplear más de una barra de fracción; así, joule por kelvin y mol
-1
-1
se escribirá J/(K·mol) o J·K ·mol , y no J/K/mol.
8) Aquellos símbolos que no existen en ciertas máquinas de escribir o equipos de tratamiento de textos, tales
como m o W, se deben escribir a mano. Debe evitarse el uso de impresoras antiguas que sólo tienen
mayúsculas.
Reglas referentes a los valores numéricos
1) La coma decimal, usada en Europa, o el punto decimal usado en los EE.UU. son ambos aceptables.
2) La anterior regla excluye el uso de comas o puntos para separar grupos de cifras. Estos deben separarse
con un espacio sin puntuación alguna. No es necesaria la separación de un grupo de cuatro cifras, excepto si
Univ. Erwin Choque Conde
Página 142
forma parte de una tabla en que aparezcan números mayores. Se pueden usar potencias de diez o prefijos
para hacer innecesaria esta regla.
3) Se prefiere la notación decimal al uso de fracciones (ej.: 0,25 preferiblemente a 1/4). Para valores inferiores
a la unidad, el cero debe preceder a la coma o punto decimal.
Unidades. Factores de conversión
- El asterisco (*) indica que el valor de la equivalencia o factor de conversión es exacto, por definición, convenio
o cálculo.
- La correspondencia con unidades utilizadas en países de habla inglesa esta basada en los sistemas
empleados en U.S.A. La inclusión de algunos valores particulares, de uso en Gran Bretaña, se indica
expresamente con (G.B.).
Unidades lineales
Unidad
Milla marina (USA)
*
*
Milla estatuto (terrestre)
*
*
*
*
*
*
Cable
Braza
*
*
*
*
*
*
*
*
*
*
*
Yarda
*
*
Pie
Univ. Erwin Choque Conde
*
*
*
*
*
*
Factor
1.15077945
1.852
8.43904929
1012.68591426
1852
2025.37182852
6076.11548556
0.86897624
1.609344
7.33333333
880
1609.344
1760
5280
63360
0.11849676
0.13636364
0.219456
120
219.456
240
720
8640
1/120
0.00833333
1.8288
2
6
72
0.00049374
0.00056818
0.0009144
1/240
0.00416667
0.5
0.9144
3
36
91.44
1/720
Unidad de conversión
millas estatuto
kilómetros
cables
brazas
metros
yardas
pies
millas
kilómetros
cables
brazas
metros
yardas
pies
pulgadas
millas
millas estatuto
Kilómetros
brazas
metros
yardas
pies
pulgadas
cables
cables
metros
yardas
pies
pulgadas
millas
millas estatuto
kilómetros
cables
cables
brazas
metros
pies
pulgadas
centímetros
cables
Página 143
*
*
Pulgada
*
*
*
*
*
*
*
*
*
*
Kilómetro
*
*
Metro
Centímetro
*
*
*
*
*
Milímetro
*
*
0.00138889
1/6
0.16666667
1/3
0.33333333
12
0.3048
30.48
304.8
1/72
0.01388889
1/36
0.02777778
1/12
0.08333333
0.0254
2.54
25.4
0.53995680
39370
0.62137119
4.55672208
546.80664917
1093.61329834
3280.83989501
1000
1000000
0.00053996
0.00062137
0.00455672
0.54680665
1.09361330
3.28083990
39.37007874
0.001
100
1000
0.01
0.01093613
0.03280840
0.39370079
10
0.03937
0.003281
0.001
0.1
cables
brazas
brazas
yardas
yardas
pulgadas
metros
centímetros
milímetros
brazas
brazas
yardas
yardas
pies
pies
metros
centímetros
milímetros
millas
pulgadas
millas estatuto
cables
brazas
yardas
pies
metros
centímetros
millas
millas estatuto
cables
brazas
yardas
pies
pulgadas
kilómetros
centímetros
milímetros
metros
yardas
pies
pulgadas
milímetros
pulgadas
pies
metros
centímetros
Unidades de velocidad
Unidad
Nudo
*
Univ. Erwin Choque Conde
Factor
0.00027778
Unidad de conversión
millas por segundo
0.01666667
1
millas por minuto
millas por hora
0.51444444
metros por segundo
Página 144
*
Millas por hora
Kilómetro por hora
*
Kilómetro por segundo
Metro por hora
Metro por minuto
Metro por segundo
*
*
*
Centímetros por segundo
Yarda por segundo
*
*
*
*
*
*
Pies por hora
Pies por minuto
Pies por segundo
*
*
*
*
Univ. Erwin Choque Conde
30.86666667
1852
0.56260329
33.75619714
2025.37182852
1.68780986
101.26859143
6076.11548556
44.7
26.82
0.00014999
0.00899993
0.62137
0.53995680
0.27777778
16.66666667
1000
0.30378147
18.22688831
2025.37182852
0.91134442
54.68066492
3280.83989501
2.2369
0.0547
3.2808
0.0373
3.28
0.00053996
0.03239741
1.94384449
0.001
0.06
3.6
1.09361330
65.61679790
3937.00787402
3.28083990
196.85039370
11811.02362205
0.0224
0.00049374
0.02962419
1.77745140
3.29184
0.9144
54.864
3
180
10800
0.3048
182.9
0.305
18.2880
0.59248380
1.09728
0.3048
30.48
18.288
0.33333333
metros por minuto
metros por hora
yardas por segundo
yardas por minuto
yardas por hora
pies por segundo
pies por minuto
pies por hora
centímetros por segundo
metros por minuto
millas por segundo
millas por minuto
millas por hora
nudos
metros por segundo
metros por minuto
metros por hora
yardas por segundo
yardas por minuto
yardas por hora
pies por segundo
pies por minuto
pies por hora
millas por hora
pies por minuto
pies por hora
millas por hora
pies por minuto
millas por segundo
millas por minuto
nudos
kilómetros por segundo
kilómetros por minuto
kilómetros por hora
yardas por segundo
yardas por minuto
yardas por hora
pies por segundo
pies por minuto
pies por hora
millas por hora
millas por segundo
millas por minuto
nudos
Kilómetros por hora
metros por segundo
metros por minuto
pies por segundo
pies por minuto
pies por hora
metros por hora
kilómetros por hora
metros por minuto
metros por hora
nudos
Kilómetros por hora
metros por segundo
centímetros por segundo
metros por minuto
yardas por segundo
Página 145
*
*
Luz en el aire
Luz en el vacío
Sonido en el aire
(A nivel del mar, con presión
normal y en aire seco a 15.5ºC)
Sonido en el agua.
(En agua con el 3.485% de
salinidad y a 15.5ºC)
20
1200
161829
299707
161875
299792.458
661.801
yardas por minuto
yardas por hora
millas por hora
kilómetros por hora
millas por hora
kilómetros por hora
nudos
1225.656
340.460
372.332
2930.054
5426.460
1507.350
1648.458
kilómetros por hora
metros por segundo
yardas por segundo
nudos
kilómetros por hora
metros por segundo
yardas por segundo
Unidades de superficie
Unidad
Milla cuadrada
Milla estatuto cuadrada
*
*
*
*
*
Kilómetro cuadrado
*
*
*
*
Héctarea
*
*
*
Acre
Area
*
*
*
*
*
*
*
Metro cuadrado
*
*
*
*
*
Yarda cuadrada
Univ. Erwin Choque Conde
Factor
Unidad de conversión
3.429904
2.589988110336
640
3097600
27878400
0.29155335
0.38610216
100
247.10538146
10000
1000000
1195990.046301
0.01
2.47105381
100
10000
11959.90046301
107639.1041671
0.0015625
0.0040468564224
4046.8564224
0.4047
4840
43560
0.01
100
0.00000039
0.000001
0.0001
0.00024711
0.01
1.19599005
10.76391042
100
1550.00310001
10000
0.00000032
kilómetros cuadrados
kilómetros cuadrados
acres
yardas cuadradas
pies cuadrados
millas cuadradas
millas estatuto cuadradas
hectáreas
acres
areas
metros cuadrados
yardas cuadradas
kilómetros cuadrados
acres
áreas
metros cuadrados
yardas cuadradas
pies cuadrados
millas estatuto cuadradas
kilómetros cuadrados
metros cuadrados
hectáreas
yardas cuadradas
pies cuadrados
hectáreas
metros cuadrados
millas estatuto cuadradas
kilómetros cuadrados
hectáreas
acres
áreas
yardas cuadradas
pies cuadrados
decímetros cuadrados
pulgadas cuadradas
centímetros cuadrados
millas estatuto cuadradas
Página 146
*
*
*
*
Pie cuadrado
Decímetro cuadrado
*
*
*
*
*
*
Pulgada cuadrada
Centímetro cuadrado
*
*
*
*
*
*
Milímetro cuadrado
0.00020661
0.836127736
9
1296
8361.2736
0.00002296
0.11111111
144
0.09290304
929.0304
92903.04
0.01
100
0.00077160
0.00694444
0.00064516
6.4516
645.16
0.0001
100
0.00011960
0.00107639
0.01
0.15500031
0.00155000
0.01
acres
metros cuadrados
pies cuadrados
pulgadas cuadradas
centímetros cuadrados
acres
yardas cuadradas
pulgadas cuadradas
metros cuadrados
centímetros cuadrados
milímetros cuadrados
metros cuadrados
centímetros cuadrados
yardas cuadradas
pies cuadrados
metros cuadrados
centímetros cuadrados
milímetros cuadrados
metros cuadrados
milímetros cuadrados
yardas cuadradas
pies cuadrados
decímetros cuadrados
pulgadas cuadradas
pulgadas cuadradas
centímetros cuadrados
Unidades de volumen-capacidad
Unidad
Factor
Unidad de conversión
Metro cúbico
1.30795062
35.31466672
264.17205236
220.05
999.97200078
2204.5
1000
1000000
0.764554857984
27
201.97402597
764.53345105
46656
0.028316846592
6.232
62.425
28317
0.03703704
7.48051948
28.31605374
29.92207792
1728
1.20095002
277.41
0.1605
0.00455
4.54596307
yardas cúbicas
pies cúbicos
galones
galones imperiales
litros
libras
decímetros cúbicos
centímetros cúbicos
metros cúbicos
pies cúbicos
galones
litros
pulgadas cúbicas
metros cúbicos
galón imperial
libras
centímetros cúbicos
yardas cúbicas
galones
litros
"quarts"
pulgadas cúbicas
galones
pulgadas cúbicas
pies cúbicos
metros cúbicos
litros
Yarda cúbica
Pie cúbico
*
*
*
*
*
*
*
Galón imperial (GB)
Univ. Erwin Choque Conde
Página 147
*
Galón
*
*
*
*
*
"Quart" (GB)
Litro
*
Decímetro cúbico
*
*
Cuarto - "Quart"
*
*
*
*
*
Pinta (GB)
Pinta
*
*
*
*
*
Pulgada cúbica
Centímetro cúbico
Acre-Pie
Univ. Erwin Choque Conde
*
*
*
10
0.00495113
0.13368056
0.83267412
3.78530580
8.33
0.00378530580
3785.30580
3.785411784
4
8
231
1.13640077
1.20095002
0.00130799
0.03531566
0.21997539
0.26417945
0.87990156
1.000028
1.05671780
1.75980312
2.11343559
61.02545276
0.001
0.26417205
0.99997200
1.056685821
2.11337642
61.02374409
1000
0.03342014
0.25
0.83267412
0.94632645
946.32645
0.946352946
2
57.75
0.56824538
1.20095002
0.125
0.47316322
0.5
0.83267412
28.875
473.176473
0.00057870
0.00432900
0.003607
0.01638661
0.0361
0.01731602
0.03463203
0.000016387064
16.387064
0.001
0.00211376
0.06102374
1233.53
libras
yardas cúbicas
pies cúbicos
galones imperial (GB)
litros
libras
metros cúbicos
centímetros cúbicos
decímetros cúbicos
"quarts"
pintas
pulgadas cúbicas
litros
"quarts"
yardas cúbicas
pies cúbicos
galones imperial.(GB)
galones
"quarts" (GB)
decímetros cúbicos
"quarts" o quarter líquido
pintas (GB)
pintas
pulgadas cúbicas
metros cúbicos
galones
litros
"quarts"
pintas
pulgadas cúbicas
centímetros cúbicos
pies cúbicos
galones
"quarts" (GB)
litros
milímetros cúbicos
decímetros cúbicos
pintas
pulgadas cúbicas
litros
pintas
galones
litros
"quarts"
pintas (GB)
pulgadas cúbicas
centímetros cúbicos
pies cúbicos
galones
galones imperiales
litros
libras
"quarts"
pintas
metros cúbicos
centímetros cúbicos
decímetros cúbicos
pintas
pulgadas cúbicas
metros cúbicos
Página 148
Onzas fluidas (US)
Pecks
Bushels
Cucharada
Cucharadita
Taza
0.029573
0.881
0.3524
5
15
0.24
litros
decalitros
hectolitros
mililitros
mililitros
litros
Unidades de masa
Unidad
"Long ton"
*
*
*
*
*
Tonelada
*
"Short ton"
Kilogramo
*
*
*
*
*
*
*
*
*
*
*
*
*
Libra
*
*
"Hundredweight"
"Stone"
*
*
*
*
*
*
Univ. Erwin Choque Conde
Factor
1.0160469088
1.12
20
160
2240
0.98420653
1.10231131
19.68413055
157.47304442
1000
2204.62262185
0.89285714
0.90718474
17.85714286
142.85714286
2000
0.05
0.056
8
50.80234544
112
0.00625
0.007
0.125
6.35029318
14
224
0.001
2.20462262
35.27396195
1000
1/2240
0.00044643
0.0005
1/112
0.00892857
1/14
0.07142857
0.45359237
16
7000
Unidades de conversión
toneladas
"short tons"
"hundredweights"
"stones"
libras
"long tons"
"short tons"
"hundredweights"
"stones"
kilogramos
libras
"long tons"
toneladas
"hundredweights"
"stones"
libras
"long tons"
"short tons"
"stones"
kilogramos
libras
"long tons"
"short tons"
"hundredweights"
kilogramos
libras
onzas
toneladas
libras
onzas
gramos
"long tons"
"long tons"
"short tons"
"hundredweights"
"hundredweights"
"stones"
"stones"
kilogramos
onzas
"grains"
Página 149
Onza
*
Gramo
*
*
*
*
"Grain"
*
*
1/224
0.00446429
0.0625
28.349523125
437.5
0.001
0.00220462
0.03527396
15.43235835
1/7000
0.00014286
0.00228571
0.06479891
"stones"
"stones"
libras
gramos
"grains"
kilogramos
libras
onzas
"grains"
libras
libras
onzas
gramos
Unidades de presión
Unidad
Atmosfera
Corresponde a la presión
"tipo" al nivel del mar.
*
*
Bar
*
*
*
*
Kilo por centímetro cuadrado
*
*
Libra por centímetro
cuadrado
*
*
Libra por pulgada cuadrada
Pulgada de mercurio
Univ. Erwin Choque Conde
Factor
1.03322745
2.27787662
2116.22
14.69594878
29.92125984
33.89853848
760
1013.25
1033.22745280
1013.250
1000
1000000
1000000
0.96784111
2.20462262
2048.16
14.22334331
980.665
1000
980665
0.43900534
2.92639653
6.4516
13.13559287
14.88163944
333.64405898
444.82216153
453.59237
0.06804596
0.15500031
2.03602097
2.30665873
51.71493257
68.94757293
70.30695796
0.03342105
0.07612903
0.49115408
1.13292484
Unidad de conversión
2
kilos por cm
2
libras por cm
2
libras por pie
libras por pulgada cuadrada
pulgadas de mercurio
pies de agua
milimetros de mercurio
milibares
centímetros de agua
2
dinas por cm
milibares
barias
2
dinas por cm
atmósferas
2
libras por cm
2
libras por pie
libras por pulgada cuadrada
milibares
centímetros de agua
2
dinas por cm
atmósferas
kilos por pulgada cuadrada
libras por pulgada cuadrada
pulgadas de mercurio
pies de agua
milímetros de mercurio
milibares
2
gramos por cm
atmósferas
2
libras por cm
pulgadas de mercurio
pies de agua
milímetros de mercurio
milibares
2
gramos por cm
atmósferas
2
libras por cm
libras por pulgada cuadrada
pies de agua
Página 150
*
Pie de agua
Milímetro de mercurio
*
Milibar
*
*
Gramo por centimetro
cuadrado
*
*
*
Centímetro de agua
*
Dina por centímetro
cuadrado
*
*
*
25.4
33.86388158
34.53154908
0.02949980
0.06719690
0.43352750
0.88267109
22.41984564
29.8906692
30.48
0.00131579
0.00299721
0.01933677
0.03937008
0.04460334
1.33322368
1.35950981
1333.22368421
0.00098692
0.001
0.00224809
0.01450377
0.02952999
0.03345526
0.75006168
1.01971621
1000
0.00096784
0.00220462
0.01422334
0.02895903
0.03280840
0.73555924
0.980665
1
980.665
0.980665
1
0.00000099
0.000001
0.001
0.00101972
1
milímetros de mercurio
milibares
2
gramos por cm
atmósferas
2
libras por cm
libras por pulgada cuadrada
pulgadas de mercurio
milímetros de mercurio
milibares
2
gramos por cm
atmósferas
2
libras por cm
libras por pulgada cuadrada
pulgadas de mercurio
pies de agua
milibares
2
gramos por cm
2
dinas por cm
atmósferas
bar
2
libras por cm
libras por pulgada cuadrada
pulgadas de mercurio
pies de agua
milímetros de mercurio
2
gramos por cm
2
dinas por cm
atmósferas
2
libras por cm
libras por pulgada cuadrada
pulgadas de mercurio
pies de agua
milímetros de mercurio
milibares
centímetro de agua
2
dinas por cm
milibares
2
gramo por cm
atmósferas
bar
milibar
2
gramos por cm
baria
Unidades de potencia
Unidad
Caballos de vapor
Horsepower
Factor
0.9863
1.0139
Unidad de conversión
horsepower
caballos de vapor
Unidades de Flujo o caudal
Unidad
Galones/segundo (gps)
Galones/minuto (gpm)
Univ. Erwin Choque Conde
Factor
3.785
0.00006308
Unidades de conversión
Litros/segundo (lps)
Metros cúbicos/segundo
Página 151
3
Galones/hora (gph)
Galones/día (gpd)
3
Pies cúbicos/segundo (pie /seg)
3
Pies cúbicos/minuto (pie /min.)
Millones de galones/día (mgd)
2
3.785
22824.5
0.0228
15.8508
2.119
0.0005886
0.0021
(m /seg)
3
Metros cúbicos/hora (m /h)
Litros/segundo (lps)
3
Metros cúbicos/hora (m /h)
Millones de litros/día (Mlt/d)
3
Metros cúbicos/día (m /d)
Metros cúbicos/segundo
3
(m /seg)
Litros/minuto (lt/min)
Centímetros cúbicos/segundo
3
(cm /seg)
Litros/segundo (lps)
3
Metros cúbicos/hora (m /h)
Litros/segundo (lps)
3
Metros cúbicos/día (m /d)
Metros cúbicos/segundo
3
(m /seg)
2
Litros/metros cuadrados (lt/m )
Metros cúbicos/hectárea/día
3
(m /ha/d)
Metros cúbicos/metros
3
2
cuadrados/día (m /m /d)
Litros/metros cuadrados/día
2
(lt/m /d)
Metros cúbicos/metros
cuadrados/hora
3
2
(m /m /h)
Litros/metros
2
cuadrados/segundo (lt/m /seg.)
Litros/metros cuadrados/minuto
2
(lt/m /min)
Litros/día/cápita (lt/d per cápita)
Galones/día (gpd)
Millones de galones/día (mgd)
Galones/minuto (gpm)
3
Pies cúbicos/minuto (pie /min)
3
Pies cúbicos/segundo (pie /seg)
3
Pies cúbicos/minuto (pie /min)
35.3147
22.8245
15850.3
0.5886
4.403
264.1720
0.00026417
106.9064
Pies cúbicos/segundo (pie /seg)
Millones de galones/día (mgd)
Galones/minuto (gpm)
3
Pies cúbicos/minuto (pie /min)
Galones/minuto (gpm)
Galones/día (gpd)
Millones de galones/día (mgd)
Galones/Acre/día (gal/A/d)
0.408
Galones/Pie cuadrado/minuto
2
(gal/pie /min)
Galones/Pie cuadrado/día
2
(gal/pie /d)
Galones/Pie cuadrado/minuto
2
(gal/pie /min)
Galones/Pie cuadrado/día
2
(gal/pie /d)
0.277
0.06308
0.003785
0.000003785
0.003785
0.028317
1699
472
0.472
1.6990
43.8126
0.003785
0.043813
Galones/pie cuadrado (gal/pie )
Galones/Acre/día (gal/Ac/d)
40.74
0.0094
Galones/Pie cuadrado/día
2
(gal/pie /d)
0.0407
0.0283
Galones/Pie cuadrado/minuto
2
(gal/pie /min)
2.444
0.679
40.7458
Galones/cápita/día (gpcd)
Litros/segundo (lt/seg)
Litros/minuto (lt/min)
Centímetros cúbicos/segundo
3
(cm /s)
Metros cúbicos/segundo
3
(m /seg)
3
Metros cúbicos/hora (m /h)
3
Metros cúbicos/día (m /d)
Metros cúbicos/hectárea/día
3
(m /ha/d)
Metros cúbicos/metros
3
2
cuadrados/hora (m /m /h)
Metros cúbicos/metros
3
2
cuadrados/día (m /m /d)
Litros/metros
cuadrados/minuto
2
(lt/m /min)
24.5424
0.0245
35.3420
3
Tablas de equivalencia
Univ. Erwin Choque Conde
Página 152
Equivalencia métrica del sistema inglés en tamaños de tuberías
Pulgadas
1/4
3/8
1/2
3/4
1
1-1/4
1-1/2
2
2-1/2
3
3-1/2
4
6
8
10
12
14
Milímetros estimados
8
10
15
20
25
32
40
50
65
80
90
100
150
200
250
300
350
Pulgadas
16
18
20
24
28
30
32
36
40
42
48
54
60
64
72
78
84
Milímetros estimados
400
450
500
600
700
750
800
900
1000
1050
1200
1400
1500
1600
1800
1950
2100
Equivalencias entre unidades de trabajo o energía en sus formas eléctrica, mecánica y térmica
Ergio
(Erg)
Julio
(J)
Ergio
1
10
2.778 10
Julio
10
1
kWh
3.600
13
10
4.186
10
10
2.650
13
10
1.055
10
10
1.055
25
10
3.600
6
10
4.186
3
10
2.650
6
10
1.055
3
10
1.055
18
10
kcal
CV-h
Btu
Quad
-7
7
Kilovatiohora (kWh)
Kilocaloría
(hcal)
Caballo de Vaporhora
(CV-h)
-13
0.377 10
-11
British thermal
unit (Btu)
-14
2.389 10
2.778 10
-7
2.389 10
0.377 10
9.480 10
1
860
1.359
3.413
1.163 10
1
1.581 10
3.969
0.736
6.326 10
1
2.510
-4
-3
-4
2.930 10
2.930 10
-6
2
2.520 10
-3
1
12
10
0.398 10
14
0.398 10
9.480
-26
10
9.480
-19
10
3.413
-12
10
3.969
-15
10
2.510
-12
10
-15
10
-4
-3
0.252
11
-11
9.480 10
Quad
15
1
Macrounidades energéticas
Tm
equivalente de
carbón
(tec)
Tm
equivalente de
carbón
(tep)
Teracalorías
(Tcal)
Termias(Th)
tec
tep
Tcal
Th
1
0.700
0.007
7 10
2.777
7
10
1.428
1
0.010
10
4
3.968
7
10
1.428
2
10
1.428
100
1
10
-4
10
3.968
9
10
3.968
Univ. Erwin Choque Conde
10
3
6
-6
Btu
1
3
10
Barril de
petróleo
5.300 10
3
3
10 m de
GN
1 T de
GLP
0.778
0.569
0.758 10
1.111
0.813
0.758
1.111 10
3
-
2
-
0.758 10
2
-4
1.111 10
0.813
2
10
0.813
Página 153
-4
British
thermal unit
(Btu)
3
10 Barriles
de petróleo *
3
3
10 m
de GN **
1T de GLP
10
0.360
-7
10
3
-
0.252 10
7
2
10
1
-3
0.252
-9
10
0.252 10
1.319
1.319 10
6
4
1.884
2
10
1.285
1.319 10
0.900
0.009
0.900 10
1.757
1.230
1.230
-2
10
1.230 10
6
-4
-
-7
0.191 10
0.277 10
1
0.146 10
9
5.240
9
10
-3
36 10
6.810 10
1
8.68
8.68
1.38 10
-4
-
3
3
3
10
0.019
-6
10
0.115
0.0.724
-3
10
1
* 1 barril de petróleo equivale a 42 galones USA (158.9 litros).
1 barril/día equivalente a 48.2 Tm/año.
** Se considera 0.09 tep por Gcl de poder calorífico superior.
Factores de conversión y principales constantes físicas
Aceleración
Calor específico
Calor latente
Coeficiente de transferencia de materia
Coeficiente de transmisión de energía
Conductividad térmica
Densidad
Densidad de flujo de energía
Difusividad
Energia
Esfuerzo cortante
Flujo másico
Flujo volumétrico
Fuerza
Longitud
Masa
Potencia
Potencia por unidad de volumen
Presión
Superficie
Trabajo
Viscosidad cinemática
Viscosidad dinámica
Volumen
Univ. Erwin Choque Conde
-2
7
-2
1 m s = 4.2520 x 10 ft h
-1 -1
4
-1
-1
1 J kg K = 2.3886 x 10 Btu lbm °F
-1
-4
-1
1 J kg = 4.2995 x 10 Btu lbm
-1
4
-1
1 m s = 1.1811 x 10 ft h
-2 -1
-1 -2
-1
1 W m K = 0.17612 Btu h ft °F
-1 -1
-1 -1
-1
1 W m K = 0.57782 Btu h ft °F
-3
-3
1 kg m = 0.062428 lbm ft
-2
-1 -2
1 W m = 0.3171 Btu h ft
2 -1
4 2 -1
1 m s = 3.875 x 10 ft h
-4
1 J = 9.4787 x 10 Btu
-2
-2
1 N m = 0.020886 lbf ft
-1
-1
1 kg s = 7936.6 lbm h
3 -1
5 3 -1
1 m s = 1.2713 x 10 ft h
3 -1
3 3
-1
1 m s = 2.1189x 10 ft min
3 -1
4
-1
1 m s = 1.5850 x 10 gal min
1 N = 0.22481 lbf
1 m = 39.370 in = 3.2808 ft
1 km = 0.62137 millas (mile)
1 kg = 2.2046 lbm
-1
1 W = 3.4123 Btu h
-3
-1 -3
1 W m = 0.09665 Btu h ft
-2
1 Pa = 0.020886 lbf ft (psia)
-4
-2
1 Pa = 1.4504 x 10 lbf in.
-3
1 Pa = 4.015 x 10 in. water
-4
1 Pa = 2.953 x 10 in. Hg
5
1.0133 x 10 Pa = 1 atm (estándar)
5
1 x 10 Pa = 1 bar
1 atm = 14.696 psia
2
2
2
1 m = 1550.0 in. = 10.764 ft
4
1 J = 9.4787 x 10 Btu
2 -1
4 2 -1
1 m s = 3.875 x 10 ft h
-2
-1 -1
-6
-1
1 N s m = 2419.1 lbm ft h = 5.8016 x 10 lbf h ft
3
4
3
3
1 m = 6.1023 x 10 in. = 35.314 ft
nbsp;
= 264.17 gal (U.S.) = 219.97 gal (Brit.)
Página 154
Constante universal de los gases (R)
Constante de Boltzmann
Constante de Planck
Constante de Stefan-Boltzman
Aceleración de la gravedad al nivel del
mar
Factor de conversión gravitacional
(sistemas ingenieriles)
Peso molecular del aire
Número de Avogadro
Velocidad de la luz en el vacío
2
3
-1
-1
R = 8.205 x 10 m atm kmol K
-2
3
-1 -1
R = 8.314 x 10 m bar kmol K
-1 -1
R = 8.314 kJ kmol K
-1
-1
R = 1545 ft lbf lbmole °R
-1
-1
R = 1.986 Btu lbmole °R
-1 -1
R = 1.987 cal mol K
-23
-1
-1
k = 1.380 x 10 J K molécula
-34
-1
h = 6.625 x 10 J s molécula
-8
-2 -4
= 5.670 x 10 W m K
-8
-1 -2
-4
= 0.1714 x 10 Btu h ft °R
-2
g = 9.807 m s
-2
g = 980.7 cm s
-2
g = 32.174 ft s
-1 -2
gc = 32.1740 lbm ft lbf s
-1 -2
gc = 980.665 gm cm gf s
-1
MA = 28.97 g mol
-1
MA = 28.97 lbm lbmole
-23
-1
NA = 6.024 x 10 moléculas mol
8
-1
c = 2.998 x 10 m s
Constantes de interés
Aceleración media debida a la gravedad de la Tierra (nivel mar)
Albedo medio de la Tierra
Calor específico del agua a 0ºC
Calor específico del aire seco a presión constante y 0ºC
Calor específico del aire seco a volumen constante
Calor específico del hielo a 0ºC
Calor específico del vapor agua a 0ºC (presión constante)
Calor específico del vapor agua a 0ºC (volumen constante)
Calor específico del vapor agua a 15ºC (presión constante)
Calor latente de fusión del hielo a 0ºC
Calor latente de sublimación del agua a 0ºC
Calor latente de vaporización del agua a 0ºC
Calor latente de vaporización del agua a 100ºC
Calor latente de vaporización del agua a 20ºC
Cero absoluto
Constante de Boltzman
Constante de los gases específica del aire seco
Constante de Planck
Constante de Stefan-Boltzmann
Constante de Wien
Constante específica de los gases del vapor de agua
Constante solar
Constante universal de los gases
Declinación del eje de la Tierra
Densidad del agua a presión estándar
Densidad del aire seco a presión estándar
Densidad del hielo a presión estándar
Densidad del mercurio a 20ºC
Densidad media del aire en la troposfera (0-11 km)
Distancia media Sol-Tierra
Distancia Sol.-Tierra más corta (3 enero)
Distancia Sol-Tierra más larga (4 julio)
Factor de Coriolis
Univ. Erwin Choque Conde
9.807 m/s
0.3
4217.6 J/K·kg
1004.67 J/K·kg
717.63 J/K·kg
2106 J/kg·K
1850 J/K·kg
1390 J/K·kg
1875 J/K·kg
6
0.334 · 10 J/kg
6
2.83 · 10 J/kg
6
2.50 · 10 J/kg
6
2.26 · 10 J/kg
6
2.45 · 10 J/kg
273.15ºC
-23
1.38 · 10
J/K
287.053 J/K·kg
-34
6.63 · 10
Js
-8
2 4
5.67 · 10 W/m ·K
-3
2.898 · 10 m·K
461.5 J/K·kg
2
1368 W/m
8.314 J/K·mol
23,45º
3
1000 kg/ m
3
1.29 kg/ m
3
917 kg/ m
3
13546 kg/ m
3
0.689 kg/ m
11
1.49598 · 10 m
11
1.4696 · 10 m
11
1.5196 · 10 m
-4
0.729 · 10 1/s
1 cal/K·g
0.24 cal/K·g
0.171 cal/K·g
0.5 cal/K·g
0.44 cal/K·g
0.331 cal/K·g
80 cal/g
595 cal/g
540 cal/g
585 cal/g
Página 155
Gradiente adiabático seco
Gravedad aparente (aceleración) en el ecuador
Gravedad aparente (aceleración) en los polos
Gravedad aparente (aceleración) media
Luminosidad de la fotosfera del Sol
Masa de la Tierra
Número de Avogadro
Período orbital de la Luna
Período orbital de la Tierra
Peso molecular del agua
Peso molecular del aire seco
Presión superficial estándar
Radio de la Tierra en el Ecuador
Radio medio de la Tierra
Radio medio del Sol
Temperatura de la fotosfera del Sol
Tensión superficial del agua a 20ºC
Velocidad angular de la Tierra
Velocidad de la luz
Velocidad de rotación ecuatorial
Velocidad del sonido
Viscosidad del agua a 20ºC
Anexo E.
9.75 K/km
9.78 m/s
9.83 m/s
9.807 m/s
26
3.9 · 10 W
24
5.9742 · 10 kg
23
-1
6.02 · 10 mol
27.32 días
365.25463 días
18.02 kg/kmol
28.966 kg/kmol
1013.25 hPa
6378 km
6
6.3 · 10 m
8
6.96 · 10 m
5796 K
-3
72.75 · 10 N/m
-5
7.292 · 10 1/s
8
3.00 · 10 m/s
465 m/s
343.15 m/s
1.0 g/m·s
BIBLIOGRAFÍA:
FRANK P. INCROPERA Y DAVID P. DeWITT” Fundamentos de transferencia de calor” EDICION 198
RAMIRO BETANCOURT GRAJALES “Transferencia molecular de calor, masa y/o cantidad
de movimiento” Universidad Industrial de Santander 2004
INGENIERIA TERMICA Y DE FLUIDOS DE Pedro Fernández Díez “DEPARTAMENTO DE INGENIERIA
ELECTRICA Y ENERGETICA UNIVERSIDAD DE CANTABRIA” creado el 23 de lulio del 2003
TRANSFERENCIA DE CALOR de Ing. Gustavo Rojas Ugarte Universidad Técnica de Oruro
http://www.proteccioncivil.org/vademecum/vdm017.htm creado el 09-01-2006 por Arturo
Venavides
Univ. Erwin Choque Conde
Página 156
Anuncio
Documentos relacionados
Descargar
Anuncio
Añadir este documento a la recogida (s)
Puede agregar este documento a su colección de estudio (s)
Iniciar sesión Disponible sólo para usuarios autorizadosAñadir a este documento guardado
Puede agregar este documento a su lista guardada
Iniciar sesión Disponible sólo para usuarios autorizados