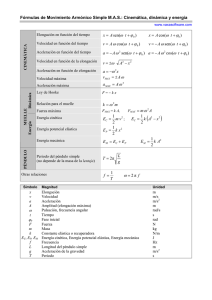
El estudio del oscilador armónico constituye en Física un capítulo muy importante, ya que son muchos los sistemas físicos oscilantes que se dan en la naturaleza y que han sido producidos por el hombre. Definición Una partícula describe un Movimiento Armónico Simple (M.A.S.) cuando se mueve a lo largo del eje X, estando su posición x dada en función del tiempo t por la ecuación x=A·sen(ωt+φ) donde A es la amplitud. la frecuencia angular. t+ la fase. la fase inicial. Las características de un M.A.S. son: Como los valores máximo y mínimo de la función seno son +1 y -1, el movimiento se realiza en una región del eje X comprendida entre A y +A. La función seno es periódica y se repite cada 2, por tanto, el movimiento se repite cuando el argumento de la función seno se incrementa en 2, es decir, cuando transcurre un tiempo P tal que (t+P)+=t++2 . P=2π/ω Cinemática de un M.A.S. En un movimiento rectilíneo, dada la posición de un móvil, obtenemos la velocidad derivando respecto del tiempo y luego, la aceleración derivando la expresión de la velocidad. La posición del móvil que describe un M.A.S. en función del tiempo viene dada por la ecuación x=A·sen(ωt+φ) Derivando con respecto al tiempo, obtenemos la velocidad del móvil Derivando de nuevo respecto del tiempo, obtenemos la aceleración del móvil Este resultado se suele expresar en forma de ecuación diferencial Esta es la ecuación diferencial de un MAS donde x puede ser cualquier magnitud: un desplazamiento lineal, un desplazamiento angular, la carga de un condensador, una temperatura, etc. Puede comprobarse que la solución de esta ecuación diferencial es x=A sen( t+ ) Condiciones iniciales Conociendo la posición inicial x0 y la velocidad inicial v0 en el instante t=0. x0=A·sen v0=A·cos se determinan la amplitud A y la fase inicial φ Dinámica de un M.A.S. Aplicando la segunda ley de Newton obtenemos la expresión de la fuerza necesaria para que un móvil de masa m describa un M.A.S. Esta fuerza es proporcional al desplazamiento x y de sentido contrario a éste. Como la fuerza F es conservativa. El trabajo de dicha fuerza es igual a la diferencia entre el valor inicial y el final de la energía potencial Ep. La expresión de la energía potencial es Donde c es cualquier constante. Se toma como nivel cero de la energía potencial Ep=0 cuando el móvil está en el origen, x=0, por lo que c=0 La energía total E, es la suma de la energía cinética Ek y de la energía potencial Ep que es constante. Curva de energía potencial La función Ep=mω2x2/2 representa una parábola cuyo vértice está en el origen, que tiene un mínimo en x=0 cuyo valor es Ep=0. Las región donde se puede mover la partícula está determinada por la condición de que la energía cinética ha de ser mayor o igual a cero Ek>=0. En otras palabras, que la energía total sea mayor o igual que la energía potencial E>=Ep. Si la partícula tiene una energía total E, la partícula solamente se podrá mover en la región comprendida entre -A y +A, siendo A la amplitud de su M.A.S. El módulo y el sentido de la fuerza vienen dados por la pendiente de la recta tangente cambiada de signo. Por tanto, la fuerza que actúa sobre la partícula es negativa a la derecha del origen y positiva a la izquierda. En el origen la pendiente es nula, la fuerza es nula, una situación de equilibrio, que por coincidir con un mínimo de la energía potencial es de carácter estable. Actividades Se introduce El valor de mω2, actuando en la barra de desplazamiento titulada Constante La energía total de la partícula E, actuando en la barra de desplazamiento titulada Energía. Se pulsa en el botón titulado Empieza Observar los valores de la energía cinética, potencial y la fuerza sobre la partícula, en particular, cuando la partícula pasa por el origen y por las posiciones de máximo desplazamiento. otro DEFINICIÓN del M.A.S. y CARACTERÍSTICAS Conviene aclarar lo que significa periódico, oscilatorio y vibratorio para entender porqué se aplica este término al movimiento armónico simple: Movimiento periódico: un movimiento se dice que es periódico cuando a intervalos iguales de tiempo, todas las variables del movimiento (velocidad, aceleración, etc.) toman el mismo valor. Ej. la Tierra alrededor del Sol. Movimiento oscilatorio: Es el movimiento periódico en el que la distancia del móvil al centro de oscilación, pasa alternativamente por un valor máximo y un mínimo. Ej. un péndulo. Movimiento vibratorio: Es un movimiento oscilatorio que tiene su origen en el punto medio y en cada vibración pasa por él. Las separaciones a ambos lados a ambos lado del centro se llaman amplitud y son iguales. Ej. una varilla que sujeta por un extremo a la que damos un impulso en el otro. La varilla vibra. El Movimiento vibratorio armónico simple -M.A.S- es: un movimiento vibratorio. La ecuación que determina la posición es una función matemática seno o coseno y por ello se las denomina armónicas. No se consideran las atenuaciones del medio por lo que al movimiento así simplificado se le llama simple. ¿Cómo se origina el MAS? Cuando separamos un resorte de su posición de equilibrio, estirándolo o comprimiéndolo, adquiere un M.A.S al soltarlo. La fuerza recuperadora de ese resorte, que varia según la distancia al centro, es la que genera una aceleración, proporcional también a la elongación, la cual le confiere ese movimiento de vaivén llamado M.A.S. Todas las expresiones del M.A.S. de la fuerza, aceleración etc., contienen la función matemática senoidal o cosenoidal. Magnitudes (valores a medir) del fenómeno Observando el movimiento del resorte vemos que se desplaza entre dos puntos, desde la máxima compresión hasta la máxima elongación, pasando por un punto medio de equilibrio. A la distancia desde el punto medio a cualquiera de los extremos le llamamos AMPLITUD y la representamos por A. La distancia desde la posición que ocupa la bola roja en cada momento hasta el punto central es la ELONGACIÓN, x. El valor de x coincide con la coordenada de posición medida desde el centro. El punto O es el punto de equilibrio. Al representar un movimiento que oscila en unos ejes cartesianos al eje vertical le llamamos X (aunque suele llamársele "eje y" ) para que la elongación coincida con la fórmula que viene en la mayoría de los libros de texto. Esto es lo mismo que girar la imagen de la oscilación. El tiempo que emplea en realizar una oscilación completa se llama PERÍODO, se representa por T y se mide en segundos. ¿Tarda lo mismo en recorrer las distancias OP y PM ? ¿En tiempos iguales recorre siempre distancias iguales?. Pulsa aquí para hacer un ejercicios sobre este concepto. La FRECUENCIA es el número de oscilaciones que realiza por segundo y la representamos por CINEMÁTICA del M.A.S. Actividades Teoría Para una partícula que oscila con M.A.S existe una ecuación que permite calcular la posición en función del tiempo. Es senoidal y armónica. Pulsa aquí si quieres saber como se calculó. x = A sen(t + ) siendo x la elongación, A la amplitud, la pulsación o frecuencia angular y el desfase. El desfase nos indica que la partícula no está en el punto medio de la oscilación cuando comienzo a medir el tiempo (t = 0), está en otro lugar. El lugar en que está para t = 0 es xo y su expresión xo= A sen() Es muy común la confusión de alumnos que no entienden porqué unos libros ponen que la posición está dada por: x = A sen(t + ) y otros por x = A cos(t + ). Las dos expresiones son totalmente correctas y el elegir una u otra sólo depende de donde se empiece a observar la oscilación, si partiendo del medio para t = 0 , o partiendo del extremo. De una expresión se puede pasar a la otra añadiendo una fase de/2 Para estudiar las expresiones de la posición de un cuerpo que oscila sin parar, podemos elegir cuando empezamos a contar el tiempo, por lo que si no está en el origen escogido existirá una fase. Vamos a considerar una oscilación sobre el eje de las X. Si empezamos a contar el tiempo cuando pasa por el centro y se dirige a la derecha, la expresión será: x = A sen(t) y en ella vemos quepara t = 0 —> x=0 Si empezamos a contar cuando está ligeramente a la derecha del centro, la expresión será: x = A sen(t + ) y para t = 0 — >xo= A·sen( ) y en general para un tiempo t estará en: x = A sen(t + ) En consecuencia, si empezamos a contar desde el centro, usamos la expresión seno, con o sin desfase. Si empezamos a contar el tiempo cuando pasa por el extremo y comienza a regresar al centro, la expresión será: x = A·cos(t) y para t = 0 —>x = A Si empezamos a contar cuando ya está regresando (por ejemplo en 1, a la izquierda del extremo, ya giró ) para t = 0 está en xo= A cos() y en general para un tiempo t estará en : x = A cos(t + ) Si empezamos a contar desde el extremo, usamos la expresión coseno, con o sin desfase. La expresión de la posición también dependerá del eje sobre el que se está considerando la oscilación. Para ver las expresiones de una oscilación vertical pulsa aquí. Pulsa aquí para realizar actividades de cambio de fase inicial con un applet. El valor de la frecuencia angular está relacionado con la constante recuperadora por la siguiente ecuación: La pulsación, equivale al número de oscilaciones completas que se ejecutan en 6,28 segundos ( = 2· / T). Si en un tiempo "T" se realiza una oscilación completa en 2· segundos se realizan 2·/T VELOCIDAD Y ACELERACIÓN EN EL M.A.S. A partir de la ecuación de la posición o de la elongación y, derivando respecto al tiempo, obtenemos la ecuación de la velocidad en el M.A.S: v = A cos(t + ) v(máx) = ·A Modificando ligeramente esta ecuación encontramos una expresión de la velocidad en función de la elongación, x: Consulta en un libro como se realizó la transformación anterior. ¿Podrías hallar la velocidad media en un período? ¿Cuál es la velocidad media en T/4? Pulsa aquí para realizar actividades y comprobarlo. Derivando la velocidad con respecto al tiempo, obtenemos la ecuación de la aceleración en el M.A.S: a = - A 2 sen(t + ) a(máx) = A 2 de la que podemos obtener también una ecuación que la relaciona con la posición: a = - 2 X Hemos obtenido ecuaciones para la velocidad y la aceleración no sólo en función del tiempo sino también en función de la posición. Con las expresiones de la velocidad y de la aceleración podemos calcular fácilmente los valores máximos de ambas y los puntos de la trayectoria donde se dan estos valores. Quedan resumidos en la siguiente tabla: Magnitud Ecuación en función del tiempo Ecuación en función de la posición Condición de máximo El máximo se da en Velocidad Aceleración v = A cos(t + ) a=A 2 sen(t + ) X = 0 —> Vmax= · A a=- 2 ·x el punto de equilibrio X= A —> amax= en los puntos 2 ·A extremos (X es máximo) Observa que en el punto central de la oscilación (punto de equilibrio) la suma de la fuerza recuperadora más la de la gravedad es cero, pero la velocidad no lo es. Puede, por lo tanto, haber un punto de equilibrio ( F = 0 ) que tiene velocidad distinta de cero. Los signos que aparecen en las fórmulas sólo significan que la magnitud despejada tiene sentido contrario al vector de la derecha ( "a" tiene sentido contrario a x). Los módulos son siempre positivos. ¿Podrías hallar la aceleración media en diferentes intervalos? Pulsa aquí para realizar actividades. Se agradecen todos los comentarios que ayuden a corregir errores y a mejorar la página Autor del tema : José Villasuso Gato Movimiento Armónico Simple (MAS) CONCEPTOS GENE Se llama Movimiento Vibratorio u Oscilatorio al desplazamiento de una partícula entre dos extremos de El Movimiento Armónico Simple (MAS) es un tipo de movimiento vibratorio causado por la proyección La proyección mencionada consiste en tomar un diámetro cualquiera de la circunferencia de un Movimient El movimiento circular se reducirá a un movimiento de vaivén en la recta. NOTA: El movimiento Armónico Simple, se le llama SIMPLE porque proviene de un Movimiento Circula NO tiene velocidad constante (pudiendo ser acelerado o variado); la proyección que genera forma el llama pero teniendo en cuenta el cambio de la velocidad en el tiempo aplicado en las diversas fórmulas del mism Otra forma de ilustrar esta proyección, es en el caso de una partícula que rota en el eje de un motor. El Movimiento Circular Uniforme (MCU) que se genera, es alumbrado desde arriba por una fuente de luz, superficie de la tabla. La luz esta dispuesta de modo que sólo se vea una línea fina del movimiento del vaiv Simple (MAS). NOTA: Este ejemplo, al igual que muchos otros, demuestra que las proyeciones deben de ser perpendicula una recta fina en forma de vaivén. PARTES DE UN MOVIMIENTO A PERIODO (T): Es el tiempo que tarda la partícula en dar una oscilación completa. FRECUENCIA (f): Es la cantidad de oscilaciones completas que la partícula realiza en la unidad de tiemp PUNTO DE EQUILIBRIO: Es el punto central de la trayectoria de la partícula. PUNTO DE RETORNO: Son los extremos de la trayectoria que limitan el movimiento de la partícula. ELONGACIÓN (x): Es la distancia que separa la partícula de su posición de equilibrio. AMPLITUD (A): Es la máxima elongación posible y equivale a la distancia entre el punto de equilibrio y OSCILACIÓN SENCILLA: Es el movimiento de un extremo al otro de la trayectoria. OSCILACIÓN COMPLETA: Es el movimiento de un extremo al otro de la trayectoria y regreso hasta e sencillas. ELONGACIÓN, VELOCIDAD Y ACE Si la elongación del Movimiento Armónico Simple se la representa según avanza el tiempo, se obtiene una tipo SENO o COSENO. Esta es la ley periódica del movimiento vibratorio. De igual modo, si se considera además la Velocidad Lineal y la Aceleración Centrípeta de la partícula al m ECUACIONES. ELONGACIÓN EN EL TIEMPO (t): CASO ESPECIAL: ELONGACIÓN MÁXIMA VELOCIDAD EN EL TIEMPO (t): CASO ESPECIAL: VELOCIDAD MÁXIMA ACELERACIÓN EN EL TIEMPO (t): CASO ESPECIAL ACELERACIÓN MÁXIMA: X = elongación V = velocidad lineal a = aceleración centríp A = amplitud ω = velocidad angula t = tiempo transcurrid NOTA: En la ecuación de aceleración aparece un signo ( - ) el cual indica que apunta siempre en dirección CARACTERISTICAS. La velocidad de la partícula es mayor mientras más lejos se encuentra de los puntos de retorno, siendo má La aceleración de las partículas es mayor mientras más lejos se encuentra del punto de equilibrio, siendo m IMPORTANTE: Las ecuaciones de Velocidad y Aceleración descritas anteriormente, son consecuencias embargo, las mismas ecuaciones también se pueden expresar como: Esto se debe a que: Las gráficas del Seno y del Coseno son iguales en su forma, y sólo se encuentran desfa Por este motivo, se cumple la siguiente regla general: Si la elongación se expresa en forma de Seno, ent si la elongación se expresa en forma de Coseno, entonces su velocidad está en términos de Seno y su acele Decidir entre el uso del Seno o el Coseno para expresar elongación, depende del instante en que se comien gráfica senosoidal, y si se inicia desde algún punto de retorno, la gráfica es del tipo cosenosoidal. En todo caso, cualquier forma de la gráfica describirá el Movimiento Armónico Simple de la partícula y sus