FUERZA DE FRICCION

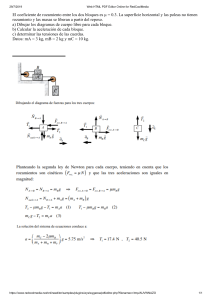
FUERZA DE FRICCION
RESUMEN
⃗⃗⃗⃗ ) es una fuerza que surge por el contacto
La fuerza de rozamiento o de fricción (𝐹𝑟
de
dos
cuerpos
y
se
opone
al
movimiento
(https://www.fisicalab.com/apartado/rozamiento#contenidos / Autor: José L.
Fernández, Gregorio Coronado). En este experimento se utiliza el montaje con una
tabla elevado a ciertos ángulos para comprobar el coeficiente de fricción. Se
trabajó con una tabla, distintos pesos (piedras), una caja. El error porcentual de la
fuerza de fricción fue de 5,26% valor que demuestra la comprobación de que existe
la fuerza de fricción que existe al haber contacto entre dos superficies.
I.
Introducción
La fuerza de rozamiento (o fuerza de fricción) es la fuerza que aparece por el contacto
entre dos cuerpos.
Normalmente parece que el fenómeno del rozamiento produzca efectos negativos. Pero
no siempre es así, ni mucho menos.
Sin el rozamiento no podríamos frenar los automóviles con las pastillas de freno, los
discos de embrague no permitirían transmitir el movimiento a las ruedas, los trenes no
podrían moverse sobre las vías, no podríamos andar y, entre muchísimas acciones
cotidianas más, no podríamos encender una cerilla (o cerillo).
Rozamiento (o fricción)
Aquí se ve una aplicación práctica de las Leyes de Newton, en concreto, de la Segunda
Ley de Newton, según la cual, la resultante de las fuerzas que actúan sobre una masa
producen una aceleración proporcional a dicha resultante.
Cuando dos cuerpos están en contacto, existen, normalmente a nivel microscópico, unas
alteraciones, unas rugosidades que se oponen a que un cuerpo se deslice sobre el otro.
Veamos la siguiente figura, donde
un cuerpo de un cierto material de
masa m descansa sobre una
superficie horizontal, también de
determinado material. Según la
Tercera Ley de Newton, a la fuerza
que ejerce m sobre la superficie se
le opone otra igual y de sentido
contrario, a la que llamaremos
fuerza normal, es decir FN = –mg.
Puede ocurrir que se aplique a m una determinada fuerza en la dirección del plano F, o
bien que inclinemos la superficie de apoyo un cierto ángulo α y, en los dos casos, el
cuerpo no se mueva, que siga en reposo. Esto es debido a que hay una fuerza de
rozamiento estático ocasionada por las características del contacto entre los dos
materiales a las que se han aludido antes (a la que llamaremos Fre) que impide el
movimiento.
Dibujo de la fuerza de rozamiento (o de fricción) en un plano inclinado
Esta fuerza de rozamiento estático es directamente proporcional a la fuerza normal.
Dibujo de la fuerza de rozamiento (o de fricción) estático
Coeficiente de rozamiento estático
En el primer caso, el del plano horizontal, hay una fuerza, a la que llamaremos Femáx tal
que si la aumentásemos mínimamente, el cuerpo de masa m comenzaría a moverse.
Dibujo de la fuerza emáx en la fuerza de rozamiento (o de fricción)
En el segundo caso, al aumentar la inclinación del plano, llegaríamos a un ángulo θ tal
que si lo aumentásemos también mínimamente, el cuerpo comenzaría a desplazarse. La
componente del peso en la dirección del plano también la llamamos Femáx y su valor es
mg · sen θ.
Dibujo de la fuerza de rozamiento estático en un plano inclinado
Se ha alcanzado el llamado ángulo crítico o ángulo de rozamiento.
Como hemos dicho antes, la fuerza de rozamiento estático es directamente proporcional a
la fuerza normal.
A esta proporcionalidad, al coeficiente que relaciona las dos magnitudes le llamaremos
coeficiente de rozamiento estático que tendrá el símbolo: μe.
Fórmula 1 de la fuerza de rozamiento estático en un plano inclinado
El coeficiente de rozamiento estático, o μe será la tangente del ángulo crítico θ.
Fórmula 2 de la fuerza de rozamiento estático en un plano inclinado
Coeficiente de rozamiento dinámico (o coeficiente de rozamiento cinético)
Cuando la fuerza actuante sobre el peso supera a la de rozamiento, el cuerpo empieza a
moverse, bajando en ese instante ligeramente el valor de la fuerza de rozamiento, que
ahora se llamará fuerza de rozamiento cinético (o fuerza de fricción por deslizamiento).
La fricción ha modificado ligeramente a nivel microscópico las superficies de contacto,
rompiéndose cantidades de asperezas moleculares de masa despreciable. Ahora estamos
ante el coeficiente de rozamiento dinámico (o cinético) μd, que es menor que el
coeficiente de rozamiento estático.
Leyes de la fuerza de rozamiento
 La fuerza de rozamiento depende directamente de la fuerza normal que se ejerce
entre las superficies en contacto.
 Depende del tipo de material de las superficies, temperatura y de su acabado.
 No depende de la dimensión de la superficie de contacto.
 No depende de la velocidad de deslizamiento.
 La dirección de la fuerza de rozamiento es de igual dirección pero de sentido
contrario al desplazamiento del cuerpo.
 Para un mismo par de materiales, la fuerza de rozamiento es mayor en el preciso
momento de iniciar el movimiento que cuando el desplazamiento ya se está
produciendo.
(http://www.universoformulas.com/fisica/dinamica/fuerza-rozamiento/ )
En la presente práctica se demostrara experimentalmente la el coeficiente de fricción.
II. Método
Se utilizó una tabla con distintos ángulos cuyo montaje se muestra en la figura 1.
Figura 1.
Se utilizaron los siguientes equipos y/o materiales: Una tabla, un nivel, una caja, distintas masas
(piedras) y un transportador.
Armamos el experimento con la ayuda de una tabla con el nivel por debajo, con ayuda del
transportador levantamos la tabla en distintos ángulos y se puso encima la caja con distintas masas.
II.
Resultados
№
Nµ
1
2
3
4
5
6
7
8
9
Ffs (µ)
1,465
2,556
3,649
4,368
5,063
5,868
6,844
8,036
9,026
Tabla №1
0,93
1,452
2,107
2,264
3,066
3,554
3,983
4,382
5,339
Grafico №1
III.
IV.
Conclusiones
Podemos ver la importancia y entender a fondo sobre lo que es la fuerza de fricción,
entendiéndolo como la fuerza que se genera al haber contacto entre dos superficies ya sea
en una superficie plana o inclinada, entendiendo que para todos los casos se cumple el
rozamiento, a no ser de que una de las superficies sea completamente lisa, haciendo que
no se genere este contacto, mediante este laboratorio y la aplicación de las fórmulas de
fricción.
IV. Bibliografía
[1] https://www.fisicalab.com/apartado/rozamiento#contenidos.
[2] Ruiz I. Apuntes de Clase Física I, UCB 2018.
[3] http://www.universoformulas.com/fisica/dinamica/fuerza-rozamiento/
ANEXOS
№
Nµ
1
2
3
4
5
6
7
8
9
Σ
Ffs (µ)
1,465
2,556
3,649
4,368
5,063
5,868
6,844
8,036
9,026
46,875
lnNµ
lnFfs (µ)
(lnNµ)²
(Ffs (µ))²
lnNµ*lnFfs (µ)
0,93 0,38185524 -0,07257069 0,14581343 0,00526651 -0,0277115
1,452 0,93844354 0,37294192 0,88067627 0,13908567 0,34998493
2,107 1,29445316 0,74526513 1,67560898 0,55542012 0,96471081
2,264 1,47430524 0,81713316 2,17357594 0,6677066 1,2047037
3,066 1,62195919 1,12037378 2,63075162 1,25523741 1,81720055
3,554 1,76951386 1,26807373 3,1311793 1,60801098 2,24387404
3,983 1,92337236 1,3820353 3,69936122 1,91002158 2,6581685
4,382 2,08393145 1,47750524 4,34277028 2,18302174 3,07901964
5,339 2,2001093 1,67503837 4,84048094 2,80575354 3,6852675
27,077 13,6879433 8,78579594 23,520218 11,1295242 15,9752182
Tabla №2
Y=a𝑥 𝑏
r²= 0,9896974133
b= 0,9671229509
a=-0,4949749953
1−0,9671229509
b=
1
∗ 100=3,28770491%
Δ=24,3110748
S=0,02630079
σ²=0,003757256
EA=0,060300059
EB=0,0372951889
a=𝑒 𝐴 =0,3790830381
Ea=𝑒 𝐴 *Ea=0,02274498
b=B
a(0,38±0,02);5,26%
b(0,97±0,04);4,12%
Fs=a𝑁 𝑏
µ=𝑎
µ= 0,38
µ(0,38±0,02)[µ];5,26%
№
Fs(w)
1
2
3
4
5
6
7
8
9
0,55
0,944
1,334
1,588
1,833
2,115
2,455
2,869
3,211
Tabla №3
Grafico №2