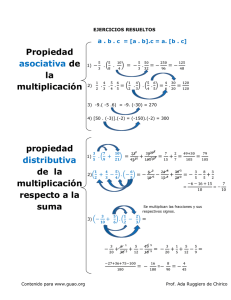
El sistema de números complejos, construido a partir de los números reales, tiene propiedades heredadas de éstos como las propiedades sobre la suma y la multiplicación. Recuerde que dos números complejos, z1=a1+b1i y z2=a2+b2i son iguales si y sólo si son iguales sus partes reales y sus partes imaginarias, a1=a2 y b1=b2. Una idea para demostrar muchas de las propiedades sobre identidades sobre operaciones de suma y multiplicación es efectuar las operaciones de un miembro de la identidad, aplicar las propiedades de los números reales a las partes reales y a las partes imaginarias para llegar al lado derecho de la identidad. De aquí decimos que las propiedades de la suma y la multiplicación son heredadas de las propiedades de los números reales. Pero el sistema de los números complejos no tiene todas las propiedades de los números reales, por ejemplo no se tienen propiedades de orden. Propiedades de la suma Se define la suma de dos números complejos z1=a+bi y z2=c+di como (a+bi)+(c+di)=(a+c)+(b+d)i A partir de esta definición, usando las propiedades de los números reales, podemos probar que se cumplen las siguientes. Propiedad de cierre o cerradura para la suma Para z1,z2∈C se tiene que z1+z2∈C Propiedad conmutativa Para cualesquiera z1,z2∈C se cumple que z1+z2=z2+z1 Propiedad asociativa Para cualesquiera z1,z2,z3∈C se cumple que (z1+z2)+z3=z1+(z2+z3) Propiedades de la multiplicación Se define el producto de dos números complejos z1=a+bi y z2=c+dicomo (a+bi)⋅(c+di)=(ab−bd)+(ad+bc)i PROPIEDADES DE LOS NÚMEROS COMPLEJOS 1 Introducción. 2 Propiedad transitiva 3 Propiedades de la suma 4 Propiedades de la multiplicación 5 Propiedad distributiva 6 Propiedades del conjugado 7 Propiedades del módulo El sistema de números complejos, construido a partir de los números reales, tienen propiedades heredadas de éstos como las propiedades sobre la suma y la multiplicación. Recuerde que dos números complejos, z1=a1+b1i y z2=a2+b2i son iguales si y sólo si son iguales sus partes reales y sus partes imaginarias, a1=a2 y b1=b2. Una idea para demostrar muchas de las propiedades sobre identidades sobre operaciones de suma y multiplicación es efectuar las operaciones de un miembro de la identidad, aplicar las propiedades de los números reales a las partes reales y a las partes imaginarias para llegar al lado derecho de la identidad. De aquí decimos que las propiedades de la suma y la multiplicación son heredadas de las propiedades de los números reales. Pero el sistema de los números complejos no tiene todas las propiedades de los números reales, por ejemplo no se tienen propiedades de orden. En la página se enuncian otras propiedades propias del sistema de números complejos junto con algunas pruebas. Propiedad transitiva Si z1=z2 y z2=z3 entonces z1=z3 Sean z1=a1+b1i, z2=a2+b2i y z3=a3+b3i, Tenemos que ver que las partes reales de z1 y z3 son iguales. Por la igualdad de los números complejos se tiene Si z1=z2 entonces a1=a2 y b1=b2 Si z2=z3 entonces a2=a3 y b2=b3 Entonces por la propiedad transitiva de los números reales como a1=a2 y a2=a3 se cumple que a1=a3 De manera similar, llegamos que b1=b3. Así conluimos que z1=z3. Propiedades de la suma Se define la suma de dos números complejos z1=a+bi y z2=c+di como (a+bi)+(c+di)=(a+c)+(b+d)i A partir de esta definición, usando las propiedades de los números reales, podemos probar que se cumplen las siguientes. Propiedad de cierre o cerradura para la suma Para z1,z2∈C se tiene que z1+z2∈C Propiedad conmutativa Para cualesquiera z1,z2∈C se cumple que z1+z2=z2+z1 Propiedad asociativa Para cualesquiera z1,z2,z3∈C se cumple que (z1+z2)+z3=z1+(z2+z3) Sean z1=a1+b1i, z2=a2+b2i y z3=a3+b3i, Desarrollamos el lado izquierdo, primero sustituímos ((a1+b1i)+(a2+b2i)) + (a3+b3i) Aplicamos la suma de complejos planteada entre paréntesis =((a1+a2)+(b1+b2)i)+(a3+b3i) Sumamos =((a1+a2)+a3)+((b1+b2)+b3)i Aplicamos la propiedad asociativa en la parte real y en la parte imaginaria =(a1+(a2+a3))+(b1+(b2+b3))i Siguiendo el mismo proceso podemos demostrar que la última línea es igual a z1+(z2+z3). Existencia del elemento neutro para la suma 0+0i, abreviado por 0, es el elemento neutro para la suma. Existencia del inverso aditivo u opuesto Todo número complejo z tiene un único inverso aditivo, denotado por −z. Propiedades de la multiplicación Se define el producto de dos números complejos z1=a+bi y z2=c+dicomo (a+bi)⋅(c+di)=(ab−bd)+(ad+bc)i A partir de esta definición, usando las propiedades de los números reales, podemos demostrar que se cumplen las siguientes. Las pruebas son similares a las de la suma. Propiedad de cierre o cerradura para la multiplicación Para z1,z2∈C se tiene que z1⋅z2∈C Propiedad conmutativa Para cualesquiera z1,z2∈C se cumple que z1⋅z2=z2⋅z1 Propiedad asociativa Para cualesquiera z1,z2,z3∈C se cumple que (z1⋅z2)⋅z3=z1⋅(z2⋅z3) Existencia del elemento neutro para la multiplicación 1+0i, abreviado por 1, es el elemento neutro para la multiplicación. Existencia del inverso multiplicativo o recíproco Todo número complejo z, dintinto de 0, tiene un único inverso multiplicativo , denotado por z−1 Propiedad distributiva Para cualesquiera z1,z2,z3∈C se cumple que z1⋅(z2+z3) = z1⋅z2+z1⋅z3 Propiedades del conjugado El conjugado de un número complejo z=a+bi, denotado por z¯¯¯, se define comoz¯¯¯=a−bi Es claro las siguientes El conjugado de un número real es él mismo. El conjugado de un número imaginario puro es el opuesto del número. A continuación otras propiedades del conjugado El conjugado del conjugado Para z∈C se tiene que z¯¯¯¯¯¯=z Propiedades del módulo El módulo o valor absoluto de un número complejo z=a+bi, denotado por |z| , se define como |z|=a2+b2−−−−−−√ El módulo es la raíz cuadrada de zz¯¯¯ El módulo del producto Para cualesquiera z1,z2∈C se cumple que |z1⋅z2|=|z1|⋅|z2|