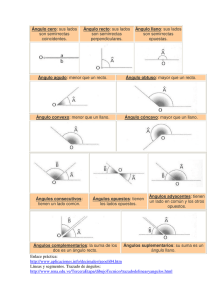
Clasificación de Ángulos Historicidad Como se sabe la matemática es un hecho admirable, hace miles de años los egipcios ya la utilizaban para dividir los terrenos o construir sus templos; ellos no fueron los únicos, todas las poblaciones presentaban un tipo de sistema de numeración y descubrían propiedades especificas a medida que pasaban los años. El pueblo egipcio es la cuna de la geometría, de acuerdo a los sucesos que remontan los libros se puede saber que: “Por las condiciones de su clima, Egipto fue siempre una zona árida, de desierto. Pero el rio Nilo, que lo atraviesa, se desbordaba anualmente y cuando las aguas volvían a su cauce, los terrenos adyacentes a sus márgenes, que habían sido inundados, quedaban cubiertos por una capa de limo, o barro fértil, que permitía cultivar esas zonas con gran provechó ”1 . Ante este suceso los cercos que distribuían las propiedades en parcelas rectangulares, eran arrastrados y debían ser nuevamente trazados por los sacerdotes quienes eran los que recibían los conocimientos geométricos necesarios para esos trabajos de agrimensura. A partir de este hecho proviene el nombre de geometría, ya que epistemológicamente significa medir la tierra. Otro suceso importante, fue la construcción de los templos, los cuales fueron levantados por bloques de piedra traídos en barco por el Nilo; los mismos debían ser tallados, pulidos y respetar las formas exactas, para ello además de contar con instrumentos para su desempeño, fueron exigidos a comprender nociones como perpendiculares, paralelas y ángulos. Paralelamente, Tales de Mileto, quien fue uno de los sabios de Grecia, realizo varios viajes a Egipto, donde por parte de los sacerdotes, recibió todos los conocimientos matemáticos que luego el enseñaría. Por su parte descubrió numerosas propiedades como las de los segmentos proporcionales y los ángulos; nuevamente encontramos la aparición de los mencionados un tanto superficial. 1 REPETTO, LINSKENS Y FESQUET (1996). “Geometría 1”. Matemática Moderna. (pp. 5-10). Editorial kapelusz S.A Sin lugar a dudas el aporte más significativo al origen de los ángulos es el del sistema sexagesimal (que tenía como base el número 60) el cual fue inventado por los babilonios hace miles de años. Ellos dividieron el círculos en 360 partes o ángulos iguales y llamaron a cada uno de esas partes grados con el siguiente símbolo (°). Para que cada uno de esos ángulos sea medido de una forma más precisa, crearon dos unidades de medidas más pequeñas, por lo tanto cada grado se dividió en 60 minutos y cada minuto en 60 segundos. Desarrollo: Un ángulo es la abertura que hay entre dos semirrectas. Ambas semirrectas son los lados del ángulo y el punto de concurrencia es el vértice. La siguiente figura representa el ángulo formado por las semirrectas AB y AC; se suele designar como ángulo. B A C Un ángulo presenta: Un vértice: que es el punto donde se intersectan las dos semirrectas que lo determinan. Dos lados: que son las semirrectas con origen en el vértice. Amplitud: que corresponde a la abertura del ángulo formado, y que es representado en grados (°), minutos (´) y segundos (´´) Para poder medir un ángulo hace falta solo de dos cuestiones: la primera corresponde a la unidad de medida, esta puede ser grados, minutos o segundos, de acuerdo a cuál de todas sea la más conveniente para realizar la medición de un determinado ángulo; y la segunda tiene que ver con el instrumento a medir, el cual debe reproducir la unidad de medida que fue elegida. Ahora bien, no todos los ángulos son iguales, ya que cada uno presenta particularidades. Una de las grandes diferenciaciones es aquella que tiene que ver con su medida en particular, a partir de la amplitud que este tenga se los clasifican en: Ángulo agudo: son todos aquellos que miden menos de 90° y más que 0° Ángulo recto: son los que miden 90° Ángulo obtuso: son todos aquellos que miden más de 90° y menos que 180° Ángulo llano: son los que miden 180° Ángulo nulo: 0° Ángulo reflejo: son todos aquellos que son mayores 180° y menores a 360° Ángulo completo: son los que completan la circunferencia, y por lo tanto miden 360° Tomando como punto de partida al ángulo llano, se puede hacer referencia a los demás ángulos de un modo más general, clasificándolos de la siguiente manera: Ángulo convexo y cóncavo: dos semirrectas de origen común determinan, en realidad dos ángulos: el ángulo interior a las semirrectas, que recibe el nombre de convexo, y el ángulo exterior a las semirrectas, que recibe el nombre de cóncavo. Estas no son las únicas clasificaciones que presentan, ya que según la posición que forman dos o más ángulos pueden clasificarse en: Complementario: dos ángulos con medidas m1 y m2, se dice que son complementarios si y solo si m1 + m2 = 90° Suplementario: dos ángulos con medidas m1 y m2, se dice que son suplementarios si y soló si m1+m2 = 180° Ángulos conjugados: dos ángulos con medidas m1 y m2, se dice que son conjugados si y solo sí m1+m2 = 360° Consecutivo: presentan en común el vértice y un lado. Adyacente: son aquellos que responden a los criterios del ángulo consecutivo pero que su suma da 180° Opuesto por el vértice: dos ángulos son opuestos por el vértice cuando los lados de uno de ellos son semirrectas opuestas a los lados del otro. Cuando dos líneas se cortan en dos puntos por otra recta transversal. Vamos a separar los ocho ángulos que se forman en dos grupos. Si hablamos de angulos en relacion a los poligonos se presenta otro tipo de clasificación la cual corresponde a: Ángulos interiores: se forman de acuerdo a dos lados consecutivos. Ángulos exteriores: se forman de acuerdo a un lado y a la prolongación del lado consecutivo. Teniendo como referencia las siguientes clasificaciones, un solo ángulo puede ser clasificado de varias maneras y la conformación de dos ángulos presenta otras múltiples clasificaciones de acuerdo a su amplitud y sus intersecciones. Recurso no convencional Las aspiraciones del segmento Luel Había una vez un segmento llamado Luel, una simple línea con principio y fin. Él vivía en las profundidades del Bosque y se sentía muy triste, ya que pensaba que no encajaba en aquel lugar. El vagaba deprimido por el bosque preguntándose: - ¿Por qué todos a mí alrededor están completos y yo no? De pronto un árbol muy sabio le pregunto a qué se debía su tristeza. Luel le conto lo que le sucedía y éste le recomendó que se tomará unas vacaciones, recorriera el mundo y le dijo: - Quien no encaja en el mundo, está siempre cerca de encontrarse a sí mismo, ya que a veces hace falta perderse para encontrarse. Luel luego de reflexionar sobre aquellas palabras, decidió hacer su valija y emprender viaje. Un viaje cargado de miedos, emociones pero sobre todo de mucha incertidumbre por lo que vendrá. Después de varios días de viaje llego a una aldea llamada Nilo, como el nombre del rio que la atraviesa. A medida que avanzaba por sus calles observaba fascinado todo a su alrededor. En su paseo, se topó con inmenso templo que le llamo poderosamente su atención y entró, allí vio a un anciano y a sus discípulos, él se acercó y les pregunto: -¿Quiénes son ustedes? ¿Qué están haciendo aquí? ¿Qué es este maravilloso lugar? El anciano se presentó diciendo: - Soy Mileto y ellos son mis estudiantes, aquí desarrollamos conocimientos matemáticos. Qué forma peculiar tienes ¿Qué eres tú? Luel le explica que es un segmento y que no es feliz siendo lo que es. Mileto lo invita a viajar con él y le dijo: - ¡Vamos, te ayudaré en tu búsqueda! Arribaron en Babilonia y allí Luel conoció a otros sabios, y no solo eso, sino que se encontró con otros segmentos, pero estos no estaban libres como él sino que estaban unidos por un punto en común. Miletos, al ver que Luel observaba aquello con mucha curiosidad, le explico que un segmento por sí solo no era nada más que una simple línea, pero que si se emparejaba con su segmento gemelo de esa unión nacerán ángulos. - Mira a Pedro y Catalina ellos son padres de Agudo y Recto, el primero es el más pequeñito ya que mide menos de 90° y su hermano justo 90°. Por allá están los Trianguláis, ellos tuvieron a Obtuso, mayor de 90°, a Llano de 180°, a Nulo de 0° y Completo, el más gordito, mide 360°. Fijémonos también en que dos semirrectas de origen común, determinan dos ángulos: el interior a las semirrectas que se llama Convexo y el exterior a las semirrectas, que recibe el nombre de Cóncavo. - ¡Que asombroso! No todos son iguales ¡cuántas peculiaridades! - Claro, además no todos se relacionan de la misma manera, algunos son consecutivos, complementarios, suplementarios, adyacentes, conjugados y opuestos. Si hablamos de polígonos tenemos familias de ángulos interiores y exteriores que presentan sus conformaciones. - ¡polígonos! ¿Y eso que es? Son las grandes figuras geométricas como el triángulo, el rectángulo y el círculo entre otras, que le dan formas a nuestras estructuras. Luel finalmente comprendió su misión, ya no tenía motivos para estar deprimido. Decidió quedarse para encontrar su amor y formar su propia familia.