Físisca. Movimiento oscilatorio

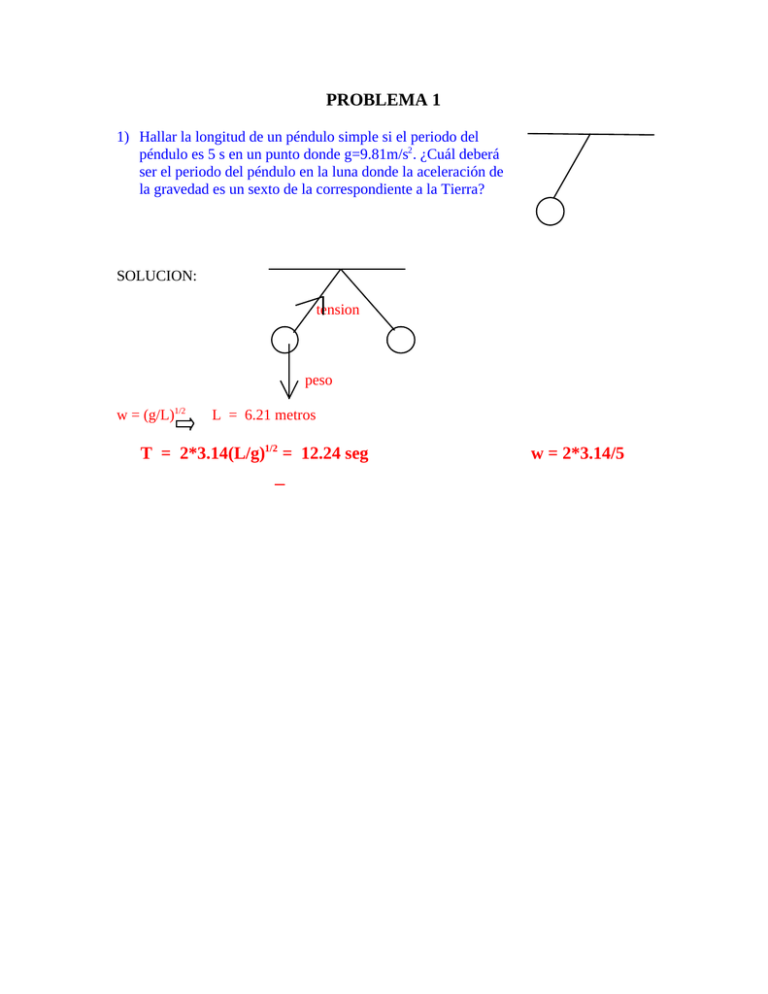
PROBLEMA 1
1) Hallar la longitud de un péndulo simple si el periodo del
péndulo es 5 s en un punto donde g=9.81m/s2 . ¿Cuál deberá
ser el periodo del péndulo en la luna donde la aceleración de
la gravedad es un sexto de la correspondiente a la Tierra?
SOLUCION:
tension
peso
w = (g/L)1/2
L = 6.21 metros
T = 2*3.14(L/g)1/2 = 12.24 seg
w = 2*3.14/5
PROBLEMA 2
En mar gruesa, la proa de un destructor sufre un movimiento de balanceo equivalente a
un movimiento armónico simple de 8 segundos de periodo y 2 metros de amplitud.
a)¿Cuál es la máxima velocidad vertical de la proa del destructor?
b)¿Cuál es su aceleración máxima?
c)Un marinero de 80 Kg. está subido a una báscula en una cámara de proa.
¿Cuáles son la máxima y mínima lectura de la báscula en Newtons?
Como bien indica el enunciado, el destructor sufre un movimiento armónico
simple, luego emplearemos para resolver las dos primeras cuestiones las siguientes
fórmulas:
Y= A.cos(wt)
Vy= A.w.sen(wt)
Ay= -A.w2.cos(wt)
a) Vymáx= A.w= A.(2∏/Τ)= 1,57 m/s
b) Ay= A.w2= A.(2∏/Τ) 2 = 1,23 m/s2
c) N+P= m.a
N-m.g=-m.w2y
N= m.g-m.w2.y= m.(g-w2y)
La fórmula subrayada es la que emplearemos para calcular la máxima y mínima
lectura de la báscula. La lectura mínima se produce cuando la proa se eleva, momento
en el cual la y coincide con la A:
Superior
y= A
N= m.(g-w2A)= 686 N
La lectura máxima se produce cuando la proa del barco desciende, según el
dibujo adjunto:
Inferior
y= -A
N= m.(g+w2A)= 883 N
PROBLEMA 3
En las especificaciones militares es frecuente que exijan de los dispositivos electrónicos,
que sean capaces de resistir aceleraciones de 10g = 98.1 m/s 2 . Para asegurarse que sus
productos cumplen esta especificación, los fabricantes los someten a ensayos en mesas
vibrantes que pueden hacer vibrar un equipo a diversas frecuencias y amplitudes. Si un
determinado dispositivo se somete a una vibración de 1.5 cm de amplitud, ¿Cuál deberá
ser su frecuencia?
Para un movimiento vibratorio la aceleración es:
A=-Aω2 sen(ωt+ϕo )= ω2 A
Si queremos conseguir una aceleración 10g;
10g = ω2 A
10g
918
.
=
−2
A
15
. *10
ω = 2πν
ω2 =
ν=
1
2π
918
.
−1
= 12.45s
−2
15
. *10
Tomamos 10g como aceleración máxima, por eso sustituimos x por su valor máximo A.
Nota: 10g no vale 91.8, sino 9.81, por lo que si utilizamos este valor, el resultado es
-1
ν = 12.87 S .
PROBLEMA 4
Un cuerpo de 2 Kg está unido a un muelle horizontal de constante de fuerza K=5kN/m. Se
alarga 10 cm. el muelle y se deja libre. Hallar a) la frecuencia, b) el periodo y c)Amplitud del
movimiento. d) ¿Cuál es la velocidad máxima? e) ¿cuál es la aceleración máxima. f) ¿Cuándo
alcanza el cuerpo por primera vez su posición de equilibrio?, ¿Cuál es su aceleración en ese
instante? g) Hallar la energía total del cuerpo.
Sol
K= 5kN/m
2
Kg
a) Se trata de un movimiento armónico simple, y, como tal, vamos a utilizar sus fórmulas. Para
hallar la frecuencia primeramente vamos a calcular la velocidad angular.
ω=√ K/m = √ 5000/2 =50 rad/s
T= 2π/ω
fif= ω/2π = 7.96 Hz.
f= 1/T
b) T=2π/ω = 2π/50 = 0.1257 s.
c) Como se ha alargado 10 cm. la A= 0.1m.
d) Para hallar la velocidad máxima usamos la fórmula v= Aωsen(ωt+φ) sabiendo que para que
la velocidad sea máxima sen(ωt+φ) tiene que ser igual a 1. Por lo tanto :
v= Aω= 0.1x50= 5m/s
e) Tal como ocurre en el caso anterior la aceleración se obtiene mediante la fórmula a= Aω 2
cos(ωt+φ) y el cos(ωt+φ)=1.
a= Aω 2 = 0.1x2500= 250m/s2
f) El periodo es lo que tarda el cuerpo desde que se suelta hasta que vuelve a esa misma
posición. Por lo tanto, el tiempo que tarda en llegar a la posición de equilibrio, ya que es 1/4 del
espacio total recorrido es, T/4.
t= T/4= 0.1257/4= 0.0314 s.
En este punto la aceleración es igual a ω 2 x, y como es la posición de equilibrio, x=0.
Por lo tanto la aceleración es igual a cero.
a=0
g) La energía total del muelle se obtiene de la siguiente forma:
ET =1/2kA2= 1/2 5000 (0.01)= 25 J
PROBLEMA 5
Un muelle cuelga verticalmente y en su extremo sin deformar se cuelga, a su vez, un
cuerpo de masa desconocida que se suelta desde el reposo. Cae 3.42 cm antes de que
quede en reposo por primera vez. Hallar el periodo del movimiento.
T es el periodo, M la masa del cuerpo, K la constante de elasticidad del muelle, g la
gravedad (9.8) y h la altura que alcanza el muelle (-3,42 cm sí situamos el sistema de
referencia en la posición 1).
Sabemos que T = 2Π / ω ; Y que ω = (K/M)1/2; por lo que T = 2Π(M/K)1/2. Por tanto
nuestras incógnitas son K y M; las cuales están relacionadas entre sí.
En la posición inicial 1, las energías cinética y potencial (tanto gravitatoria como
elástica) son nulas. Pero en la posición 2 (momento en el que alcanza la elongación
máxima de -3.42 cm) toda la energía potencial gravitatoria que pierde el cuerpo al
descender la longitud indicada, se transforma en energía potencial elástica del muelle.
Como en la posición inicial la energía total es nula, la energía gravitatoria final será
igual a menos la energía elástica final (para que su suma sea cero). Luego:
-Mgh = (1/2)Kh2 ⇒ K = 2Mg/h
Si sustituimos en la ecuación inicial el valor de K obtenido (se simplifica la Masa) y
obtenemos:
T = 2∏(h/2g)1/2 = 0.262s
PROBLEMA 6
Un cuerpo de 1.5 kg. que alarga un muelle en 2.8 cm. respecto a su longitud
natural cuando cuelga de él en reposo, oscila con una amplitud de 2.2 cm.. Hallar:
a) La energía total del sistema.
b) La energía total gravitatoria en el máximo desplazamiento hacia abajo.
c) La energía potencial del muelle en el máximo desplazamiento hacia
abajo.
d) ¿Cuál es la energía cinética máxima del cuerpo?
(Escoger Epg = Epe = 0 cuando el cuerpo cuelga en reposo).
Sabiendo que en el punto de equilibrio, que se
encuentra a 2.8 cm del sistema de referencia, el
cuerpo no se mueve, por lo tanto el sumatorio de las
fuerzas que actúan sobre el cuerpo tiene que ser 0:
F.recuperadora – Peso = 0
k·x - m·g = 0
k· 0.028m – 1.5kg · 9.81m/s2 = 0
k =525.5 N/m
a) Sabiendo que la E. mecánica de un muelle es:
Em=1/2 k·A2 =1/2 ·525.53 · (0.022)2 =0.1272 J
b) Teniendo en cuenta que en el pto. de equilibrio la Ep. gravitatoria es 0. La
Ep. a 0.022m., máximo desplazamiento, será:
Ep= -m·g·h = -1.5kg·9.81m/s2 ·0.022m = -0.32373 J
c) Sabiendo que la Ec. en el máximo desplazamiento es nula y conociendo la ley
de conservación de la energía, en el pto. de máximo desplazamiento sólo tendrá Ep.
gavitatoria y Ep. del muelle, por lo tanto:
Em = Ep + Epe
0.1272 J= -0.32373 J +Epe
Epe= 0.45093 J
También se puede hacer de la siguiente manera:
Epe =1/2·k·(x0 +A)2 - 1/2·k·x0 2 = 0.6569 J – 0206 J = 0.4509 J
d) La Ec. máxima se alcanza en el centro de la trayectoria, que es el pto. donde
la Ep = Epm = 0, por esta razón y teniendo en cuenta ley de conservación de la energía:
Em = Ec.max
Ec.max = 0.1272 J.
PROBLEMA 7
Un objeto de 2 Kg de masa apoyado sobre una superficie horizontal sin rozamiento, se
une a un muelle de constante 600 N/m. Otro objeto de 1 Kg de masa desliza sobre la
superficie acercándose al primero a 6 m/s.
a) Hallar la amplitud de oscilación si el segundo objeto choca de forma
inelástica perfecta quedando unido también al muelle. ¿Cuál es le periodo de
oscilación?
b) Hallar la amplitud y el periodo de oscilación si el choque fuera elástico.
c) Para cada tipo de colisión, escribir una expresión para la posición x en función
del tiempo t para el objeto unido al muelle, suponiendo que el choque se produce en el
t=0.
d) ¿Cuál es el impulso aplicado al cuerpo de 2 Kg en cada caso?
Solución:
m1=2 Kg
m2=1 Kg
e=0
m1v1+m2v2=(m1+m2)V
V=2 (metros/segundo)
a- Según la formula del periodo:
T = 2π ( m / k ) =
Siendo m=3 Kg
K=600 N/m
π=3.14
T=0.444 segundos
Toda la Energía cinética cuando el muelle se comprime se convierte en Energía
potencial elástica .
0.5(m1+m2)v∗2=1/2(kA*2)
A=0,14
e
b- Cuando =1 hay 2 velocidades después del choque:
M1V1+m2V2=m1V´1+m2V´2
e=-(V´2-V´1)/(V2-V1)
6 = V´1+V´2
-6 = V´1-V´2
-------------12 = 3V´2
V´2 = 4 (metros/segundo)
V´1-V´2 = -6
V´1=-2 (metros/segundo)
La ecuación general del movimiento:
Para t=0, suponemos que x=0, suponiendo a la vez que la función va hacia arriba:
X=A sen(wt+ϕ)
Para t=0
x=0, luego ϕ=0
Si lo ponemos en función del cos:
X=A cos(wt-π/2)
es cosπ/2=0
Si hubiésemos considerado como negativa la ecuación del movimiento esta sería:
X=-A sen(wt)= A sen(wt+π)
X=A cos(wt+π/2)
La X va hacía valores negativos. Hay que tener en
cuenta lo que vale la posición inicial.
X=-A cos(wt - π/2)
A medida que aumenta el t, la x va hacia valores
negativos.
Para tiempo=0, el ángulo de desfase tiene que ser 0.
Nota. El problema no tiene resueltos los apartados b, c y d
PROBLEMA 8
Demostrar que en los casos de las figuras a) y b), el objeto oscila con una
frecuencia de
ν = ( 1 / 2π ) • ( Kefec / m ) _ , en donde Kefec viene dado por a) Kefec = K1 + K2 y
b) 1/Kefec = 1/K1 + 1/K2 . Indicación: Hallar la fuerza neta F sobre el objeto para un
pequeño
desplazamiento x y escribir F = − Kefec • x. Obsérvese que en b) los muelles se
deforman cantidades
diferentes cuya suma es x.
a) A Kefec para mayor comodidad la vamos a llamar K a secas, sin
subíndices. Esta será la K
total del ejercicio la cual será suma de K 1 y K2 .
K = K1 + K2
ω=√(K/2)
T = 2π /ω
Como la frecuencia es uno partido del periodo y la velocidad angular es la
raíz cuadrada de la K
total dividida por dos implica que la frecuencia es:
ν = ω / 2π
⇒ ν = [√ ( k / m ) ] / 2π = 1 / 2π • √ ( K / m )
b) 1 / K = 1/ K1 + 1/ K2 ⇒ K = K1 + K 2
Esto quiere decir que la frecuencia del movimiento es la misma al ser igual
tanto la constante como la
masa del cuerpo y la velocidad angular.
Ahora nos pide hallar la fuerza neta sobre el objeto para un pequeño
desplazamiento x. También nos
indica el ejercicio que los muelles se comprimen en cantidades diferentes cuya
suma es x.
La fuerza neta se dirige hacia la izquierda y es la suma de F1 y F2 .
F1 = −K1 x1
F2 = −K2 x2
X = x1 + x2 = − F ( 1 / K1 + 1 / K2 )
F1 = F2 pero sus desplazamientos son diferentes.
Así tenemos que el desplazamiento total es X = − F • 1 / K por lo
que la fuerza neta es :
F = − KX
En la cual X es el desplazamiento total que es la suma de desplazamientos de
cada muelle y K es la
suma de las dos constantes de los de dos muelles.
PROBLEMA 9
*Un bloque de madera cuya densidad es δ tiene dimensiones “a”, “b”, “c”. Mientras
esta flotando en el agua con el lado “a” vertical, se le empuja hacia abajo y se le suelta.
Halle el periodo de las oscilaciones resultantes.(Recuerde que la fuerza de empuje es
igual al peso del fluido desplazado.
E
b
+
-Como queremos calcular el periodo
de las oscilaciones, tenemos que llegar
c
a una expresión en la que la fuerza sea
del tipo F = -KX . Siempre que hay una
a
fuerza con esta forma tendremos un
L
movimiento armónico simple.
-Si el bloque está en la posición de
X
equilibrio con el agua se cumplirá la
igualdad: fuerza de empuje=peso del fluido desplazado
es decir: P=m.g=Empuje=E
P=m.g
-Para determinar el volumen de agua desalojado en la posición de equilibrio
relacionamos:
Vol. = a.b.c ; δ = m/Vol. ; m = Vol..δ = a.b.c.δ
-Y por otro lado la fuerza de empuje será: E =
longitud desplazada en el equilibrio:
L = -a.(δ/δagua)
b.c.(-L).δagua.g
siendo L la
-Si ahora empujamos el bloque
hcia abajo, éste se desplaza de la posición de
equilibrio una longitud X .El bloque entonces comenzará a oscilar en esta nueva
posición, en la que seguirán actuando las mismas fuerzas que antes salvo el empuje,que
será mayor ,porque el volumen de agua desalojado también ha aumentado.Entonces:
∑ F=P+E= -(a.b.c.δ.g)+[b.c-(L+X)].δagua.g

masa
Sustituyendo el primer término por la expresión que habíamos deducido para
la posición de equilibrio queda:
F=-[b.c.(-L).δagua.g]+[b.c-(L+X)δagua.g]
F=(b.c.L.δagua.g)-(b.c.Lδagua.g)-b.c.δagua.g.X
F=-b.c.δagua.g.X=-K.X ,donde K=b.c.δagua.g
-Ahora que ya hemos comprobado que se trata de un movimiento armónico simple,
podemos calcular el periodo de las oscilaciones:
T=(2.π)/ω =(2.π) ⁄ (K/m)_=(2.π). (m/K)_=(2.π).[(a.b.c.δ) ⁄( b.c.δagua.g)]_
T = (2.π).[(a.δ) ⁄(δagua.g)]_
PROBLEMA 10
Un péndulo simple tiene un periodo de 2 s y una amplitud de 2º. Después de 10
oscilaciones completas su amplitud se ha reducido a 1.5º . Halle la constante de
amortiguamiento γ.
Ln(A/Ao) = -γΤ Ln1.5/2 = -γ 20
γ = 0.0144 /s
como hay 10 oscilaciones el tiempo es 20
PROBLEMA 12
Un remolque pequeño que pesa 300 ks. con su carga, se sostiene mediante dos
resortes, ambos de constante 17500N/m. Se tira del remolque sobre un camino cuya
superficie se asemeja a una curva sinusoidal de amplitud 4 cm y 5 m de separación
entre amplitudes máximas positivas sucesivas. Determínese:
a) La velocidad a la que se producirá la resonancia
Es un movimiento oscilatorio en la dirección vertical
L
K t = K1 + K 2 = 17500 + 17500 = 35000 N / m
ω0 =
k
=
m
35000
= 10.8 rad / seg
300
Como la velocidad v es igual al espacio L por el tiempo , que se corresponde con
el periodo T podremos despejar la velocidad de resonancia de la siguiente
ecuación:
ω=
v=
2π
2π
2π v
=
=
L
T
L
v
ωL
2π
Sabemos que la resonancia se produce cuando T = T0
v=
ω 0 L 10.8 ⋅ 5
=
= 8.59 m / s
2π
2π
b) La amplitud de la vibración del remolque a una velocidad de 65 km/h
(Suponer el término de amortiguación despreciable).
Pasamos los 65 km/h a m/s:
v = 65
1000 m
= 18.06 m / s
3600 s
Con esta velocidad hallamos la nueva frecuencia angular:
ω=
2π v 2π 18.06
=
= 22.68 rad / seg
L
5
Aplicando la 2ª Ley de Newton igualamos la Fuerza externa a la periódica dado
que la Fuerza amortiguadora es cero porque el coeficiente de amortiguación b es
nulo:
F = F0 ⋅ cos ω t
− kx = F0 ⋅ cosω t
como x = A ⋅ cosω t entonces
− k ⋅ A ⋅ cosω t = F0 ⋅ cos ω t
F0 = −k ⋅ A = 35000 ⋅ 0.04 = 1400 N / m
En el régimen permanente la T es la de la fuerza y la amplitud es:
A=
F0
m ⋅ (ω − ω 0 ) + b ⋅ ω
2
2
A=
2
2
2
como b=0:
1400
300 ⋅ ( 22.68 − 10.8 ) + 0
2
2
2 2
= 0.0117 m = 1.2 cm