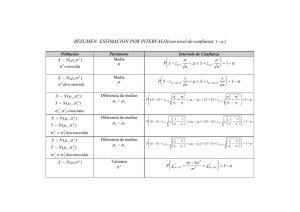
“CONCEPTOS ESTADISTICOS Y INTERVALOS DE CONFIANZA PARA LA DIFERENCIA DE MEDIAS” ESTADISTICA INFERENCIAL Integrantes: Edgardo Barreto Denisse Ortega Grupo: 2 Profesor: Richard Sánchez UNIVERSIDAD DEL ATLÁNTICO BARRANQUILLA/ATLÁNTICO 2016 INTRODUCCIÓN El siguiente trabajo tiene como objetivo comprender algunos conceptos estadísticos y abordar el tema de intervalos de confianza para la diferencia de medias la importancia de ello y como aplicarlos a la administración, para lo cual es necesario realizar un recorrido por distintas ejemplos realizados en el presente trabajo, con el fin de acercarnos de afianzar nuestros conocimientos. VARIABLE ALEATORIA Se denomina variable aleatoria a la función que adjudica eventos posibles a números reales (cifras), cuyos valores se miden en experimentos de tipo aleatorio. Estos valores posibles representan los resultados de experimentos que todavía no se llevaron a cabo o cantidades inciertas. Cabe destacar que los experimentos aleatorios son aquelos que desarrollados bajo las mismas condiciones, pueden ofrecer resultados diferentes. Arrojar una moneda al aire para ver si sale cara o sello es un experimento de este tipo. La varible aleatoria, en definitiva, permite ofrecer una descripción de la probabilidad de que se adoptan ciertos valores. No se sabe de manera precisa qué valor adoptará la variable cuando sea determinada o medida, pero si se puede conocer cómo se distribuye las probabilidades vinculadas a los valores posibles; En dicha distribución incide el azar. La variable aleatoria discreta son aquellas cuyo rango está formado por una cantidad finita de elementos o que sus elementos pueden enumerarse de manera secuencial. Supongamos que una persona arroja un dado tres veces: Los resultados son variables aleatorias discretas, ya que pueden obtenerse valores del 1 al 6. En cambio, la variable aleatoria continua se vincula a un recorrido o rango que abarca, en teoría la totalidad de los números reales, aunque solo sea accesible una cierta cantidad de valores, como la altura de un grupo de personas. La duración de una llamada a un servicio de atención al cliente o el tiempo que un médico tarda en atender a sus pacientes. TÉCNICAS DE MUESTREO La utilidad del muestreo se describen los diferentes tipos de muestreo que se pueden aplicar para tomar una muestra de la población. La selección intencionada o muestreo por conveniencia consiste en un muestreo no aleatorio, por lo que suele presentar sesgos. Las técnicas de muestreo son un conjunto de técnicas estadísticas que estudian la forma de seleccionar una muestra representativa de la población, es decir, que represente lo más fielmente posible a la población a la que se pretende extrapolar o inferir los resultados de la investigación, asumiendo un error mesurable y determinado. Cuando queremos estudiar alguna característica de una población para obtener el máximo de información veraz, se nos plantea un problema relacionado con la elección de los individuos. Puesto que no podemos estudiar a toda la población por varias razones (proceso largo y coste elevado, entre otros), debemos elegir estudiar una muestra que sea representativa y que nos permita extrapolar los resultados que obtengamos a la población de referencia. Sin embargo, debemos considerar que el empleo de técnicas de muestreo implica una serie de ventajas y limitaciones. Entre las ventajas se incluyen una mayor eficiencia en términos económicos y mayor rapidez de obtención de resultados. Por ejemplo, si para realizar nuestro estudio necesitamos una muestra de ‘x’ pacientes, considerando que ésta sea representativa de la población de estudio, y recogemos información acerca de ‘x + 100’, estamos derrochando más dinero y tiempo del necesario. Si empleamos sólo el tamaño muestral necesario, seleccionando la muestra de manera que represente lo más fielmente posible a la población, podremos obtener también mayor validez, puesto que el tiempo y dinero ahorrados se podrán emplear en recoger la información o variables del estudio con mayor precisión y fiabilidad, implicando una mayor validez interna final del estudio. Por otra parte, entre las limitaciones de las técnicas de muestreo se incluyen los errores que se pueden cometer, como son el error aleatorio y el error sistemático o sesgo. Técnicas de muestreo, para que las conclusiones obtenidas a partir de una muestra sean válidas para una población, la muestra debe haberse seleccionado de forma que sea representativa de la población a la que se pretende aplicar la conclusión. Sin embargo, no existe un método de muestreo que garantice plenamente que una muestra sea representativa de la población que sometemos a estudio. La mejor forma de asegurar la validez de las inferencias es seleccionar la muestra mediante una técnica aleatoria. A este tipo de muestreo se le denomina muestreo probabilístico y puede definirse como aquel en que todos los individuos de la población tienen una probabilidad de entrar a formar parte de la muestra (normalmente equi-probable, es decir, con la misma probabilidad). Los diseños en que interviene el azar producen muestras representativas la mayoría de las veces, aunque no garantizan la representatividad de la población que sometemos a estudio. Aunque en muchos estudios no es posible obtenerla rigurosamente de esta forma, es importante seleccionarla intentando que sea lo más parecida posible a la población de interés. En este caso, el muestreo no probabilístico utiliza métodos en que no interviene el azar y por lo tanto, se desconoce la probabilidad asociada a cada individuo para formar parte de la muestra. Normalmente estos métodos se utilizan en estudios exploratorios o intencionales, en los cuales no es necesario proyectar los resultados. El inconveniente de este método es que no puede asegurarse la representatividad de la muestra. Clasificación de los tipos de muestreo probabilístico, el muestreo probabilístico es el que todos los individuos de la población a estudiar tienen una probabilidad conocida asociada al hecho de entrar en el estudio. Entre los métodos de muestreo probabilísticos más utilizados en investigación encontramos los siguientes: Muestreo aleatorio simple, estratificado, sistemático y muestreo en etapas múltiples. Muestreo aleatorio simple se caracteriza porque cada elemento de la población tiene la misma probabilidad de ser escogido para formar parte de la muestra. Una vez censado el marco de la población, se asigna un número a cada individuo o elemento y se elige aleatoriamente. La aleatorización puede realizarse mediante listas de números aleatorios generados por ordenador, aplicándolas para escoger de la población los individuos o sujetos que coincidan con los números obtenidos. Este tipo de muestreo se caracteriza por su simplicidad y fácil comprensión, aunque también posee algunas limitaciones, ya que no siempre es posible disponer de un listado de todos los individuos que componen la población, generalmente cuando son poblaciones grandes. Si se seleccionan muestras pequeñas mediante este método pueden aparecer errores aleatorios, no representando la muestra adecuadamente a la población. Un ejemplo de muestreo aleatorio simple sería la elección de los individuos a través de la elección realizada totalmente al azar de un cierto número de identificación. Muestreo estratificado en este tipo de muestreo la población de estudio se divide en subgrupos o estratos, escogiendo posteriormente una muestra al azar de cada estrato. Esta división suele realizarse según una característica que pueda influir sobre los resultados del estudio. Por ejemplo, en el caso de seleccionar una muestra para evaluar la altura, dada la heterogeneidad entre hombres y mujeres, la variable de género podría ser una variable de estratificación. Si la estratificación se realiza respecto un carácter se denomina muestreo estratificado simple, y si se realiza respecto dos o más características se denomina muestreo estratificado compuesto. Si tenemos constancia o suponemos a priori que la población de estudio presenta variabilidad de respuesta con respecto a alguna característica propia, deberemos tener en cuenta este tipo de muestreo, dado que se producen estimaciones más precisas cuanto más homogéneos sean los elementos del estrato y más heterogeneidad exista entre estratos. Así pues, entre las ventajas de este tipo de muestreo es que tiende a asegurar que la muestra represente adecuadamente a la población en función de la variable de estratificación seleccionada, sin embargo, debe conocerse la distribución de la población en las variables de estratificación, clara desventaja de este muestreo. Para obtener la muestra en cada uno de los estratos pueden aplicarse diferentes fracciones de muestreo, pudiendo ser proporcional al tamaño en relación a la población, es decir, la distribución se realiza de acuerdo con el peso o tamaño de la población de cada estrato. Por ejemplo, si de los 5 millones de hipertensos españoles hay un 35% de pacientes que fuman, podemos estratificar de manera que en nuestra muestra queden representados al igual que en el total de la población, la misma proporción de hipertensos fumadores (35%) y de no fumadores (65%). Muestreo sistemático el muestreo sistemático es muy similar al muestreo aleatorio simple. La diferencia se obtiene en que en este tipo de muestreo se divide el total de la población de estudio entre el tamaño de la muestra, obteniendo una constante de muestreo (k). La primera unidad que formará parte de la muestra debe estar entre 1 y k y se elige al azar; a partir de esta unidad se van seleccionando sistemáticamente uno de los k individuos siguiendo un orden determinado. Por ejemplo, si obtenemos un valor de k=10 y seleccionamos al azar el número 6, deberíamos elegir todas las historias clínicas que finalizaran en «6»: «006», «016», «026».... Es un método de muestreo muy sencillo de realizar y que cuando la población esta ordenada siguiendo una tendencia conocida, asegura una cobertura de unidades de todos los tipos. La principal limitación es que si la constante se asocia al fenómeno de interés puede cometerse un sesgo. Muestreo en etapas múltiples consiste en empezar a muestrear por algo que no constituye el objeto de la investigación (unidades primarias), y obtener una muestra dentro de cada una de ellas (unidades secundarias). Pueden utilizarse sucesivamente tantas etapas como sean necesarias, y en cada una de ellas, una técnica de muestreo diferente. Este método de muestreo se utiliza cuando la población de referencia es muy amplia y dispersa, ya que facilita la realización del estudio. Principalmente, el muestreo en etapas múltiples se utiliza en estudios multicéntricos, donde debemos elegir primero los hospitales y después de haberlos seleccionado, realizamos el muestreo de pacientes dentro del mismo. Entre los métodos de muestreo no probabilísticos, que son aquellos en los que no conocemos la probabilidad de que un elemento de la población pase a formar parte de a muestra ya que la selección de los elementos muéstrales dependen en gran medida del criterio o juicio del investigador. La muestra, en este caso, se selecciona mediante procedimientos no aleatorios. Los métodos anteriores (probabilísticos) no son mejores que los no probabilísticos sino que simplemente nos permiten calcular el error muestral que se está cometiendo. Los tipos de muestreo no probabilístico son: muestreo de conveniencia, muestreo discrecional y muestreo por cuotas. Muestreo de conveniencia. El investigador decide qué individuos de la población pasan a formar parte de la muestra en función de la disponibilidad de los mismos (proximidad con el investigador, amistad, etc.). Muestreo discrecional. La selección de los individuos de la muestra es realizada por un experto que indica al investigador qué individuos de la población son los que más pueden contribuir al estudio. Este muestreo es adecuado si dentro de la población que queremos estudiar, existen individuos que no queremos que se nos escapen por utilizar un método totalmente aleatorio o de conveniencia. Muestreo por cuotas. Si se conocen las características de la población a estudiar, se elegirán los individuos respetando siempre ciertas cuotas por edad, género, zona de residencia, entre otras que habrán sido prefijadas. TEOREMA LÍMITE CENTRAL El teorema del límite central es un teorema fundamental de probabilidad y estadística. El teorema establece que la distribución de , que es la media de una muestra aleatoria de una población con varianza finita, tiene una distribución aproximadamente normal cuando el tamaño de la muestra es grande, independientemente de la forma de la distribución de la población. Muchos procedimientos estadísticos comunes requieren que los datos sean aproximadamente normales, pero el teorema del límite central le permite aplicar estos procedimientos útiles a poblaciones que son marcadamente no normales. El tamaño que debe tener la muestra depende de la forma de la distribución original. Si la distribución de la población es simétrica, un tamaño de muestra de 5 podría generar una aproximación adecuada; si la distribución de la población es marcadamente asimétrica, se requiere un tamaño de muestra de 50 o más. Las siguientes gráficas muestran ejemplos de cómo la distribución afecta el tamaño de la muestra. Distribución uniforme Medias de las muestras Una población que sigue una distribución uniforme es simétrica, pero marcadamente no normal, como lo indica el primer histograma. Sin embargo, la distribución de 1000 medias de la muestra (n=5) de esta población es aproximadamente normal debido al teorema del límite central, como lo demuestra el segundo histograma. Este histograma de medias de la muestra incluye una curva normal superpuesta para ilustrar esta normalidad. Distribución exponencial Medias de las muestras Una población que sigue una distribución exponencial es asimétrica y no normal, como lo demuestra el primer histograma. Sin embargo, la distribución de medias de la muestra de 1000 muestras de tamaño 50 de esta población es aproximadamente normal, debido al teorema del límite central, como lo demuestra el segundo histograma. Este histograma de medias de la muestra incluye una curva normal superpuesta para ilustrar esta normalidad. El teorema del límite central dice que si una muestra es lo bastante grande (n > 30), sea cual sea la distribución de la variable de interés, la distribución de la media muestral será aproximadamente una normal. Además, la media será la misma que la de la variable de interés, y la desviación típica de la media muestral será aproximadamente el error estándar. Una consecuencia de este teorema es la siguiente: Dada cualquier variable aleatoria con esperanza m y para n lo bastante grande, la distribución de la variable (X – m ¤) /(error estándar) es una normal estándar. Ejemplo de aplicación del teorema del límite central. Una empresa de mensajería que opera en la ciudad tarda una media de 35 minutos en llevar un paquete, con una desviación típica de 8 minutos. Supongamos que durante el día de hoy han repartido 200 paquetes. a) ¿Cuál es la probabilidad de que la media de los tiempos de entrega de hoy esté entre 30 y 35 minutos? b) ¿Cuál es la probabilidad de que, en total, para los doscientos paquetes hayan estado más de 115 horas? Consideremos la variable X = “Tiempo de entrega del paquete”. Solución: Sabemos que su media es 35 minutos y su desviación típica, 8. Durante el día de hoy se han entregado n = 200 paquetes. Por el teorema del límite central sabemos que la media muestral se comporta como una normal de esperanza 35 y desviación típica: a) Por lo que respecta a la segunda pregunta, de entrada debemos pasar las horas a minutos, ya que ésta es la unidad con la que nos viene dada la variable, 115 horas por 60 minutos nos dan 6.900 minutos. Se nos pide que calculemos la probabilidad siguiente: b) Y como que sabemos que la media se distribuye aproximadamente como una normal de media 35 y desviación típica 0,566 (supondremos siempre que la distribución de la media es normal, ya sea porque la variable de interés es normal o porque la muestra es lo bastante grande), esta probabilidad se puede aproximar por la probabilidad de una distribución normal estándar Z: INTERVALOS DE CONFIANZA PARA LA DIFERENCIA DE MEDIAS Un intervalo de confianza es un intervalo que tiene a lo menos un extremo aleatorio y es construido de manera tal que el parámetro de interés que se estima está contenido en dicho intervalo con una probabilidad 1 − α, llamada coeficiente de confianza. Un intervalo de confianza puede adoptar una de las siguientes formas: Bilateral: Unilateral: Un intervalo de confianza para la media es un estimador de intervalo que se construye con respecto a la media muestral y que permite especificar la probabilidad de que incluya el valor de la media poblacional. El grado de confianza asociado con un intervalo de confianza señala el porcentaje a largo plazo de esa clase de intervalos que incluirían el parámetro que se estima. Por lo general, se construyen los intervalos de confianza utilizando el estimador no sesgado como punto medio del intervalo. Sin embargo, algunas veces se ilustra la construcción de un intervalo de confianza que se denomina "en un sentido", y para el cual la media muestral no es el punto medio, del intervalo. Cuando puede utilizarse la distribución normal de probabilidad, el intervalo de confianza para la media se determina mediante: Los intervalos de confianza que se utilizan con mayor frecuencia son los de 90,95 y 99%. En la siguiente se presentan los valores de z que se requieren para esos intervalos. Proporciones seleccionadas de áreas bajo la curva normal INTERVALO DE CONFIANZA PARA LA DIFERENCIA DE MEDIAS DE DOS DISTRIBUCIONES NORMALES, VARIANZAS DESCONOCIDAS En el caso en donde se tienen dos poblaciones con medias y varianzas desconocidas, y se desea encontrar un intervalo de confianza para la diferencia de dos medias 1- 2. Si los tamaños de muestras n1 y n2 son mayores que 30, entonces, puede emplearse el intervalo de confianza de la distribución normal. Sin embargo, cuando se toman muestras pequeñas se supone que las poblaciones de interés están distribuidas de manera normal, y los intervalos de confianza se basan en la distribución t. INTERVALO DE CONFIANZA PARA LA DIFERENCIA DE MEDIAS DE DOS DISTRIBUCIONES NORMALES, VARIANZAS DESCONOCIDAS PERO IGUALES Si s12 y s22 son las medias y las varianzas de dos muestras aleatorias de tamaño n 1 y n2, respectivamente, tomadas de dos poblaciones normales e independientes con varianzas desconocidas pero iguales, entonces un intervalo de confianza del 100( la diferencia entre medias es: en donde: ) por ciento para es el estimador combinado de la desviación estándar común de la población con n 1+n2 – 2 grados de libertad. Ejemplos: 1. Un artículo publicado dio a conocer los resultados de un análisis del peso de calcio en cemento estándar y en cemento contaminado con plomo. Los niveles bajos de calcio indican que el mecanismo de hidratación del cemento queda bloqueado y esto permite que el agua ataque varias partes de una estructura de cemento. Al tomar diez muestras de cemento estándar, se encontró que el peso promedio de calcio es de 90 con una desviación estándar de 5; los resultados obtenidos con 15 muestras de cemento contaminado con plomo fueron de 87 en promedio con una desviación estándar de 4. Supóngase que el porcentaje de peso de calcio está distribuido de manera normal. Encuéntrese un intervalo de confianza del 95% para la diferencia entre medias de los dos tipos de cementos. Por otra parte, supóngase que las dos poblaciones normales tienen la misma desviación estándar. Solución: El estimador combinado de la desviación estándar es: Al calcularle raíz cuadrada a este valor nos queda que sp = 4.41 expresión que se reduce a – 0.72 1- 2 6.72 Nótese que el intervalo de confianza del 95% incluye al cero; por consiguiente, para este nivel confianza, no puede concluirse la existencia de una diferencia entre las medias. PRUEBA SOBRE DOS MEDIAS, POBLACIONES NORMALES, VARIANZAS DESCONOCIDAS PERO IGUALES Las situaciones que más prevalecen e implican pruebas sobre dos medias son las que tienen varianzas desconocidas. Si el científico prueba mediante una prueba F, que las varianzas de las dos poblaciones son iguales, se utiliza la siguiente fórmula: donde: Los grados de libertad están dados por: Ejemplos: 1. Para encontrar si un nuevo suero detiene la leucemia, se seleccionan nueve ratones, todos con una etapa avanzada de la enfermedad. Cinco ratones reciben el tratamiento y cuatro no. Los tiempos de sobrevivencia en años, a partir del momento en que comienza el experimento son los siguientes: Con Tratamiento 2.1 5.3 1.4 4.6 Sin Tratamiento 1.9 0.5 2.8 3.1 0.9 ¿Se puede decir en el nivel de significancia del 0.05 que el suero es efectivo? Suponga que las dos poblaciones se distribuyen normalmente con varianzas iguales. Solución: Primero se probará el supuesto de varianzas iguales con un ensayo de hipótesis bilateral utilizando la distribución Fisher. Datos: Con tratamiento s= 1.97 n=5 Sin tratamiento s = 1.1672 n=4 Ensayo de hipótesis: Estadístico de prueba: La sugerencia que se hace es que el numerador sea el de valor mayor . Entonces los grados de libertad uno será el tamaño de la muestra de la población uno menos uno. 1= 5-1 = 4 y 2 = 4-1=3. Regla de decisión: Si 0.10 Fc 15.1 No se rechaza Ho, Si la Fc < 0.10 ó si Fc > 15.1 se rechaza Ho. Cálculo: Decisión y Justificación: Como 2.85 esta entre los dos valores de Ho no se rechaza , y se concluye con un = 0.05 que existe suficiente evidencia para decir que las varianza de las poblaciones son iguales. Con la decisión anterior se procede a comparar las medias: Ensayo de Hipótesis Ho; CT- ST=0 H1; CT- ST >0 Los grados de libertad son (5+4-2) = 7 Regla de decisión: Si tR 1.895 No se Rechaza Ho Si tR > 1.895 se rechaza Ho Cálculos: por lo tanto sp = 1.848 Justificación y decisión: Como 0.6332 es menor que 1.895, no se rechaza Ho, y se concluye con un nivel de significancia del 0.05 que no existe suficiente evidencia para decir que el suero detiene la leucemia. INTERVALO DE CONFIANZA PARA LA DIFERENCIA DE MEDIAS DE DOS DISTRIBUCIONES NORMALES, VARIANZAS DESCONOCIDAS PERO DIFERENTES Consideremos ahora el problema de encontrar una estimación por intervalos de 1- 2 cuando no es probable que las varianzas poblacionales desconocidas sean iguales. La estadística que se usa con más frecuencia en este caso es: que tiene aproximadamente una distribución t con grados de libertad, donde: Como rara vez es número entero, lo redondeamos al número entero más cercano menor. Esto es si el valor de nu es de 15.9 se redondeará a 15. Al despejar la diferencia de medias poblacionales de la formula de t nos queda: Ejemplo: 1. El departamento de zoología de la Universidad de Virginia llevó a cabo un estudio para estimar la diferencia en la cantidad de ortofósforo químico medido en dos estaciones diferentes del río James. El ortofósforo se mide en miligramos por litro. Se reunieron 15 muestras de la estación 1 y se ontuvo una media de 3.84 con una desviación estándar de 3.07 miligramos por litro, mientras que 12 muestras de la estación 2 tuvieron un contenido promedio de 1.49 con una desviación estándar 0.80 miligramos por litro. Encuentre un intervalo de confianza de 95% para la diferencia del contenido promedio real de ortofósforo en estas dos estaciones, suponga que las observaciones vienen de poblaciones normales con varianzas diferentes. Solución: Datos: Estación 1 Estación 2 n1 = 15 n2 = 12 S1= 3.07 S2 = 0.80 Primero se procederá a calcular los grados de libertad: Al usar =0.05, encontramos en la tabla con 16 grados de libertad que el valor de t es 2.120, por lo tanto: que se simplifica a: 0.60 1- 2 4.10 Por ello se tiene una confianza del 95% de que el intervalo de 0.60 a 4.10 miligramos por litro contiene la diferencia de los contenidos promedios reales de ortofósforo para estos dos lugares. PRUEBA SOBRE DOS MEDIAS, POBLACIONES NORMALES, VARIANZAS DESCONOCIDAS PERO DIFERENTES Ejemplo: 1. Un fabricante de monitores prueba dos diseños de microcircuitos para determinar si producen un flujo de corriente equivalente. El departamento de ingeniería ha obtenido los datos siguientes: Diseño 1 n1 = 16 s12 = 10 Diseño 2 n2 = 10 s22 = 40 Con = 0.05, se desea determinar si existe alguna diferencia significativa en el flujo de corriente promedio entre los dos diseños, donde se supone que las dos poblaciones son normales, pero no es posible suponer que las varianzas desconocidas sean iguales. Solución: Primero se probarán varianzas desiguales. Ensayo de hipótesis: Estadístico de prueba: La sugerencia que se hace es que el numerador sea el de valor mayor . Entonces los grados de libertad uno será el tamaño de la muestra de la población uno menos uno. 1= 10-1 = 9 y 2 = 16-1=15. Regla de decisión: Si 0.265 Fc 3.12 No se rechaza Ho, Si la Fc < 0.265 ó si Fc > 3.12 se rechaza Ho. Cálculo: Decisión y Justificación: Como 4 es mayor que 3.12 se rechaza Ho , y se concluye con un = 0.05 que existe suficiente evidencia para decir que las varianza de las poblaciones son diferentes. Con la decisión anterior se procede a comparar las medias: Ensayo de Hipótesis Ho; 1- 2=0 H1; 1- 0 2 Para poder buscar el valor de t en la tabla, se necesita saber el valor de los grados de libertad: Este valor se redondea al próximo menor que sería 11. Regla de decisión: Si –2.201 tR 2.201 No se rechaza Ho Si tR < -2.201 ó si tR > 2.201 se rechaza Ho Cálculos: Justificación y decisión: Como 0.1395 está entre –2.201 y 2.201, no se rechaza Ho y se concluye con un = 0.05, que no existe diferencia significativa en el flujo de corriente promedio entre los dos diseños. CONCLUSIÓN A lo largo del presente trabajo se lograron presentar los conceptos estadísticos solicitados en la investigación demostrándose con ejemplos y situaciones. Se tuvieron en cuenta los teoremas tratados en el aula y se observó la aplicabilidad que se le puede dar a las diferentes alternativas a los problemas y situaciones presentadas para lograr resolver dudas y de ello afianzar los conocimientos. Bibliografía 1. ESTIMACION POR INTERVALOS. [En línea]. Colombia, Disponible en < http://www.mat.uda.cl/hsalinas/cursos/2007/intervalos.pdf > [consulta: 20 de mayo de 2016]. 2. INTERVALO DE CONFIANZA PARA LA DIFERENCIA DE MEDIAS DE DOS DISTRIBUCIONES NORMALES, VARIANZAS DESCONOCIDAS. [En línea]. Colombia, Disponible en < http://www.itchihuahua.edu.mx/academic/industrial/estadistica1/cap03d.html#tres_ic> [consulta: 20 de mayo de 2016]. 3. INTERVALO DE CONFIANZA PARA LA DIFERENCIA DE MEDIAS DE DISTRIBUCIONES NORMALES INDEPENDIENTES. [En línea]. Colombia, Disponible en < http://www.ub.edu/stat/GrupsInnovacio/Statmedia/demo/Temas/Capitulo8/B0C8m1t16.htm> [consulta: 20 de mayo de 2016]. 4. ESTADÍSTICA APLICADA A ADMINISTRACIÓN Y ECONOMÍA, Leonard Kazmier, Alfredo Díaz Mata, Segunda Edición. McGraw-Hill, México 1990.