CUERPOS-SOLIDOS

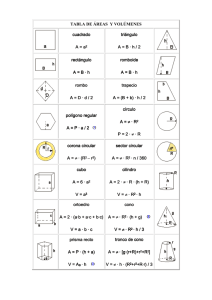
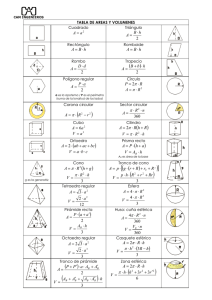
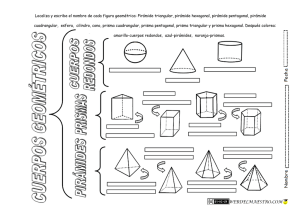
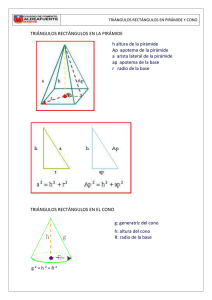
Geometría: Cuerpos
Prof. Marvin Montiel A.
CUERPOS SÓLIDOS
El mundo bidimensional de la geometría plana no es suficiente para explicar el mundo en el que vivimos, pues
esta posee tres dimensiones: largo, ancho y alto. Para explicar este mundo tridimensional se ha desarrollado el ramo de
la matemática denominado geometría del espacio o estereometría. La mayoría del mundo tridimensional se basa en
cinco figuras sólidas familiares: cajas, pirámides, conos, balones y embases. En geometría del espacio se les conoce con
los nombres respectivos: prismas, pirámide, conos, esferas y cilindros.
PRISMA
PIRAMIDE
CONO
ESFERA
CILINDRO
Podemos observar a simple vista que el prisma y la pirámide están limitados completamente por superficies
planas; la esfera está limitada por una sola superficie curva, y el cono y el cilindro están limitados por superficies planas
y curvas.
•
•
Los cuerpos geométricos que están limitados completamente por superficies planas, se llaman poliedros.
Los cuerpos geométricos que están limitados por superficies curvas o por superficies curvas y planas se llaman
cuerpos redondos.
1. POLIEDROS
Se llama poliedro a la porción del espacio limitada solamente por polígonos. Estos polígonos se llaman
caras del poliedro. Los lados y los vértices de estos polígonos se llaman aristas y vértices del poliedro,
respectivamente.
• Cada una de las superficies plana que la limitan
se llama cara del poliedro.
• Cada dos caras se intersecan en un segmento de
recta que se denomina arista del poliedro.
• Cada tres o más aristas se intersecan en un punto
llamado vértice del poliedro.
1
Geometría: Cuerpos
Prof. Marvin Montiel A.
EJERCICIOS
2
Geometría: Cuerpos
Prof. Marvin Montiel A.
a. PRISMAS RECTOS
Los prismas rectos son poliedros limitados por dos polígonos paralelos y congruentes llamados bases y
por caras laterales que son rectángulos perpendiculares a las bases.
Dependiendo del número de lados del polígono de las bases, es el nombre del prisma. El siguiente cuadro,
muestra algunos prismas regulares rectos:
Prisma triangular
Prisma cuadrangular
Prisma pentagonal
Prisma hexagonal
3
Cálculo del área del prisma recto
El área total (
) de un prisma corresponde a la suma del área basal (
=
+
)y el área lateral (
)del prisma.
El área basal ( ) es igual a la suma de las dos áreas de las bases del prisma. El área de la base (
corresponde al área del polígono que determina la base.
)
= 2∙
El área lateral ( ) de un prisma recto es igual a la suma de las áreas de los rectángulos que constituyen las
caras laterales del prisma.
Si ( ) representa el perímetro de la base de un prisma recto y ( ) la medida de su altura, entonces su área
lateral se puede calcular con la siguiente fórmula:
=
∙
Geometría: Cuerpos
Prof. Marvin Montiel A.
Ejemplo:
¿Cuál es el área total del prisma regular recto de la figura?
R/. El área total es de 810 cm2.
Ejemplo:
La apotema de la base del prisma regular de la figura mide 6√3 cm
¿Cuál es el área total del prisma?
Solución:
a. Se calcula la medida del lado de la base ( ).
Como la apotema de la base mide 6√3 ,
entonces 6√3 = √3
b. Se calcula el área basal.
c. Se calcula el área lateral
d. Se calcula el área total
→
= 12
=2∙
=
=
⋅( )
⋅
√3
=2∙
⋅(
)
√3 = 432√3
= 6 ⋅ 12 ∙ 15 = 1080
+
= 432√3 + 1080 ≈ 1828,25
R/. El área total es de aproximadamente 1828,25 cm2
Cálculo del volumen del prisma recto
El volumen de un cuerpo geométrico es la medida del espacio que ocupa. El volumen
calcula multiplicando la longitud de su altura, por el área de una de sus bases ( )
Ejemplo
=
⋅
de un prisma recto, se
4
Geometría: Cuerpos
Prof. Marvin Montiel A.
Ejemplo
Ejercicios
1. Calcule el área total y el volumen de las siguientes figuras:
2. Conteste las siguientes preguntas
3. Resuelva los siguientes ejercicios
5
Geometría: Cuerpos
Prof. Marvin Montiel A.
b. PIRÁMIDES RECTAS
Una pirámide recta, es un cuerpo geométrico, que tiene como base un polígono regular y como cara
laterales triángulos isósceles congruentes, que se unen en un punto llamado vértice de la pirámide. Este punto
pertenece al segmento que es perpendicular a la base y que contiene al centro de la base.
Dependiendo del número de lados del polígono de las bases, es el nombre de la pirámide. El siguiente cuadro,
muestra algunas pirámides rectas:
Pirámides triangular
Pirámides cuadrangular
Pirámides pentagonal
Pirámides hexagonal
En cualquier pirámide regular recta se pueden establecer las siguientes relaciones entre sus elementos,
por medio del teorema de Pitágoras:
(
) =
+
+(
=
)
Ejemplo:
¿Cuál es la medida de la apotema de una pirámide regular recta, si la altura de la pirámide mide 8 cm y el
lado de la base mide 6 cm?
a. Se calcula la apotema de la base, si se sabe que el lado de la base mide 6, se obtiene la siguiente figura:
=
⇒
=3∙
30 ÷
60
⇒
= √3
6
Geometría: Cuerpos
Prof. Marvin Montiel A.
b. Se calcula la apotema de la pirámide mediante el teorema de Pitágoras, así:
Respuesta: La apotema de la pirámide mide √67 cm.
Cálculo del área de una pirámide recta
=
+
Ejemplo
Si la altura de una pirámide regular hexagonal recta mide 12 cm y la arista de su base 16 cm. ¿Cuál es el
área total de la pirámide?
a. Se calcula la medida de la apotema de la base
como el lado de la base mide 16, entonces
⇒
=
=8∙
b. Se calcula la medida de la apotema de la pirámide
60 ÷
30
⇒
, para poder determinar el área lateral
c. Se calcula el área lateral:
d. Se calcula el área total:
=
+
= 8√3
= 384√3 + 192√21 ≈ 1544,96
Respuesta: el área total de la pirámide es aproximadamente 1544,96 cm2
7
Geometría: Cuerpos
Prof. Marvin Montiel A.
Ejemplo:
Si el área basal de una pirámide regular recta es 64√2 dm2 y su altura 9 dm. ¿Cuál es el volumen de la
pirámide?
Solución:
Respuesta: el volumen de la pirámide es 192√2 dm3
Ejemplo:
Si la altura de una pirámide regular cuadrangular recta mide 9 cm y la apotema de su base, 6√2 cm ¿Cuál es el
volumen de esa pirámide?
a. Se debe determinar la medida del lado de la base, como la apotema de un cuadrado mide la mitad de
su lado, podemos afirmar que su lado mide12√2
b. Se calcula el área de la base:
c. Se calcula el volumen de la pirámide:
=
= 12√2
= 288
1
1
∙
∙ = ∙ 288 ∙ 9 = 864
3
3
Respuesta: el volumen de la pirámide es 864 cm3
=
Ejercicios
1. Resuelva los siguientes problemas:
a. Determine el área lateral de una pirámide regular triangular, si la apotema de la pirámide mide 10
cm y el radio de la base mide 8√3 cm.
b. Calcule el volumen de una pirámide regular hexagonal recta, si la apotema de la pirámide mide
4√2 cm y la arista de la base 6 cm
2. Calcular el área total y el volumen de cada pirámide regular recta:
8
Geometría: Cuerpos
Prof. Marvin Montiel A.
3. Complete el cuadro con las medidas solicitadas, los datos corresponden a pirámide regulares rectas
Base de la pirámide
a. triangular
Apotema de la base
Apotema de la pirámide
Arista lateral
8
c. pentagonal
18
2√3
Altura de la pirámide
10
b. cuadrangular
d. hexagonal
Arista basal
10
6
10
4
4. Resuelva los siguientes problemas
5. Conteste las siguientes preguntas:
9
Geometría: Cuerpos
Prof. Marvin Montiel A.
c. CUBO
El cubo es un prisma rectangular recto, que tiene todas sus aristas congruentes. También se llama
hexaedro regular.
Algunos de los elementos que se identifican en el cubo son los siguientes:
•
•
Arista: lados de las caras del cubo
Diagonal: segmento que tiene por extremos dos vértices
opuestos del cubo
Ejemplo
Ejemplo
10
Geometría: Cuerpos
Prof. Marvin Montiel A.
Ejemplo
Ejercicio
1. Complete el siguiente cuadro
CUBO
A
B
C
D
E
F
MEDIDA DE LA ARISTA
0,75 m
AREA DEL CUBO
120 m2
VOLUMEN DEL CUBO
625 m3
5m
8 m2
3√3m3
11
Geometría: Cuerpos
Prof. Marvin Montiel A.
12
Geometría: Cuerpos
Prof. Marvin Montiel A.
2. CUERPOS REDONDOS
a. CILINDRO
El cilindro circular recto es un cuerpo geométrico que se obtiene del giro de un rectángulo alrededor
de uno de sus lados.
Algunos de los elementos que se identifican en un cilindro circular recto son los siguientes:
•
Bases: son los dos círculos que son paralelos y congruentes.
•
Altura del cilindro: es el segmento que une los centros de las bases.
Es perpendicular a los radios de las bases.
•
Radio del cilindro: es un radio de las bases del cilindro
Calculo del área de un cilindro circular recto
Área basal
Es igual a la suma de las áreas de las dos bases del cilindro. El área basal AB de un cilindro recto de radio r
se calcula con la siguiente fórmula:
=2⋅
Área lateral
La superficie lateral de un cilindro circular recto es una superficie curva que si se extiende, forma un
rectángulo como el siguiente:
2r
h
El área lateral es igual al producto del perímetro de una de las bases (2 r) y la longitud de la altura del
cilindro.
El área basal AL de un cilindro recto de radio r se calcula con la siguiente fórmula:
=2⋅
∙ ⋅
Área Total
El área total de un cilindro se calcula sumando el área basal y el área lateral
= 2⋅
+2⋅
∙ ⋅
= 2 ( + )
13
Geometría: Cuerpos
Prof. Marvin Montiel A.
Ejemplo:
Ejemplo:
Si el área lateral de un cilindro circular recto es 24π dm2 y su altura mide 6 dm. ¿Cuál es su área total?
Solución:
Respuesta: el área total del cilindro es 32π dm2
Cálculo del volumen de un cilindro recto
Se calcula multiplicando el área de una de las bases por la medida de la altura del cilindro. El volumen V de
un cilindro de radio r y altura h se calcula con la siguiente fórmula:
Ejemplo:
Ejemplo
=
⋅
⋅
14
Geometría: Cuerpos
Prof. Marvin Montiel A.
Ejercicio
1. Calcule el área total de cada cilindro circular recto. Considere que en todos los cilindros P y Q son los
centros de las bases.
2. Calcule el volumen de cada cilindro circular recto.
3. Conteste las siguientes preguntas:
a. ¿Cuál es el área lateral, en centímetros cuadrados, de un cilindro recto, si su altura mide 20 cm y el
diámetro de una de sus bases 16 cm?
b. ¿Cuántos litros de agua caben en un envase con forma de cilindro circular recto, si tiene 20 cm de
diámetro y 55 de altura? (1litro∼1000 cm3)
c. ¿Cuál es la medida aproximada de la altura de un cilindro circular recto que tiene volumen de
92 cm3 y un radio de 5 cm?
d. ¿Cuál es el área lateral de un cilindro circular recto, si el área de la base es 64π mm2 y la altura mide
8 mm?
4. Calcule el volumen de cada cilindro circular recto, según los datos
15
Geometría: Cuerpos
Prof. Marvin Montiel A.
5. Marque escriba una equis sobre la letra correspondiente a la letra de la opción correcta
16
1.
a. 6,8 cm2 b. 27,5π dm2 c. 64π mm2
2.
a. 1215π cm3 b.
3.
a. 320 cm2 b. 5,5π l c.

4.
a. 2,4π mm3 b. 2π2 cm3 c.
5.
a. D
b. CONO
b. B
c. 5776π cm3

d. 228π mm2

d. 280π dam3
Geometría: Cuerpos
Prof. Marvin Montiel A.
Es un cuerpo geométrico que se obtiene del giro de un triángulo rectángulo alrededor de uno de sus
catetos. En la siguiente figura se muestra el cono que se obtiene del giro del triangulo rectángulo AOB
alrededor del cateto AO:
Algunos de los elementos que se identifican en un cono circular recto son los siguientes:
En cualquier cono circular recto, se pueden establecer las siguientes relaciones entre algunos de sus
elementos:
=√
+
=
−
=
−
Calculo del área de un cono circular recto
Área basal
Es igual al área de la base del cono. El área basal AB de un cono recto de radio r se calcula con la siguiente
fórmula:
=
Área lateral
La superficie lateral de un cono circular recto es una superficie curva que si se extiende forma un sector
circular como el siguiente:
g
superficie lateral
de un cono
2r
El área basal AL de un cono recto de radio r se calcula con la siguiente fórmula:
17
Geometría: Cuerpos
Prof. Marvin Montiel A.
=
∙ ⋅
Área Total
El área total de un cono se calcula sumando el área basal y el área lateral
Ejemplo:
=
⋅
+
∙ ⋅
= ( + )
Ejemplo:
18
Ejemplo:
Ejemplo:
=
1
⋅⋅
3
⋅
Geometría: Cuerpos
Prof. Marvin Montiel A.
Ejemplo:
Ejercicios:
1. Complete las siguientes proposiciones. Considere que g, r y h representan las medidas de una
generatriz, de un radio y de la altura de un cono circular recto, respectivamente:
2. Calcule el volumen de cada cono circular recto según las medidas dadas. Considere que g, r y h
representan las medidas de una generatriz, de un radio y de la altura de un cono circular recto,
respectivamente:
3. Resuelva los siguientes ejercicios
19
Geometría: Cuerpos
Prof. Marvin Montiel A.
4. Marque escriba una equis sobre la letra correspondiente a la letra de la opción correcta
20
c. ESFERA
Geometría: Cuerpos
Prof. Marvin Montiel A.
Se llama esfera a un cuerpo tal que todos los puntos de su superficie están a igual distancia de un
mismo punto fijo llamado centro de la esfera.
Algunas características importantes de la esfera, son:
• El segmento que une cualquier punto de la esfera
con el centro se llama radio; la longitud de este
siempre es fija.
• El diámetro de una esfera es el segmento que pasa
por el centro de la esfera y une dos puntos de ella,
su longitud es igual a la de dos radios.
• La intersección de una esfera con un plano y que
contiene al centro, se llama circunferencia
máxima.
Área de la esfera
La superficie esférica puede considerarse como una zona esférica limitada por la circunferencia
máxima y cuya altura es igual a su diámetro. Entonces el área de una esfera, se obtendrá de multiplicar
la longitud de la circunferencia máxima y la longitud del diámetro.
Ejemplo:
=2
⋅ 2 = 4 ⋅
Volumen de la esfera
El volumen V de una esfera de radio r se puede calcular con la siguiente fórmula:
Ejemplo:
Ejercicios
=
21
Geometría: Cuerpos
Prof. Marvin Montiel A.
3. Marque escriba una equis sobre la letra correspondiente a la letra de la opción correcta
3. a) D b) C
TRABAJO EXTRA CLASE
22
Geometría: Cuerpos
Prof. Marvin Montiel A.
Resuelva tres de los ejercicios propuestos en el tema siguiente:
AREA Y VOLUMEN DE OTROS CUERPOS GEOMETRICOS
UNION DE CUERPOS GEOMETRICOS
Ejercicios
Determinar el área y el volumen de los siguientes cuerpos geométricos
23