aplicaciones de integrales

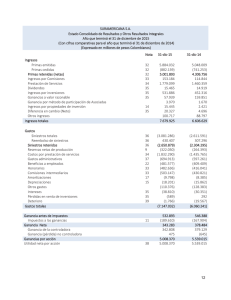
CALCULO II
APLICACIONES A LA ECONOMÍA Y A LOS NEGOCIOS DE LA INTEGRAL DEFINIDA
Se pueden presentar varias situaciones económicas en donde las cantidades pueden expresarse
como integrales definidas y representarse geométricamente como áreas entre curvas.
Veamos el caso de las utilidades netas
Supóngase que dentro de x años un plan de inversión generará utilidades a un ritmo de
R1 x   50  x 2 dólares por año, mientras que un segundo plan lo hará a un ritmo de
R2 x   200  5 x dólares por año.
a.) ¿Cuántos años será más rentable el 2º plan?
b.) ¿Cuál es el exceso de utilidad neta, si se invierte en el 2º plan, en lugar del 1º, durante el
período que éste es más rentable que el 1º?
c.) Explicar y representar, geométricamente, el exceso de utilidad neta calculado en el ítem b.
Solución:
a.) El segundo plan será más rentable hasta que
50  x 2  200  5x
R1 x   R2 x 
 x 2  5x  150  0  x  15 años  no tener en cuenta x  10 
0  x  15 , el ritmo al que las utilidades generadas por el 2º plan exceden las del 1º
es R 2 x   R1 x  dólares por año. Entonces el exceso de utilidad neta que genera el 2º
b) Para
plan durante los 15 años está dado por la integral definida:
Exc . de utilidad

0
c)

R2 x   R1 x  dx

0

15

neta 
15
 x3 5

 x 2  5 x  150 dx   
 x  150 x 
 3

2



200  5 x   50  x  dx 
15
2
0
15
 1 . 687 ,50 dól .
0
Geométricamente, la integral definida antes calculada es el área de la región limitada por
las curvas
yy  R2 x  , y  R1 x  desde x  0 hasta x  15
275
R2 (x)
200
Exc. Util.
R1 (x)
50
0
5
Aplicaciones de la integral definida
10
15
x
1
CALCULO II
Otra aplicación importante es el cálculo de las ganancias netas producidas por una maquinaria
industrial, por ejemplo.
Cuando
tienes
x
años,
una
maquinaria
industrial
genera
ingresos
a
razón
de
Rx   5 . 000  20 x dólares por año, y los costos de operación y mantenimiento se
2
acumulan a razón de
Cx   2 . 000  10 x 2 dólares por año.
a.) ¿Durante cuántos años es rentable el uso de la maquinaria?
b.) ¿Cuáles son las ganancias netas generadas por la maquinaria en ese periodo de tiempo?
c.) Explicar y representar, geométricamente, las ganancias netas calculadas.
Solución:
a) El uso de la maquinaria será rentable en tanto que el ritmo al que se generan los ingresos
sea superior al que se generan los costos. Es decir, hasta que
5000  20 x 2  2000  10 x 2
30 x 2  3000
 no
 x  10 años
tener
Rx   Cx 
en cuenta
x  10 
b) Dado que las ganancias netas generadas por la maquinaria durante cierto período de
tiempo están dadas por la diferencia entre el ingreso total generado por la misma y el
costo total de operación y mantenimiento de ésta, se puede determinar esta ganancia por
la integral definida:


10
Ganancia
neta 
Rx   Cx  dx

0

10


10
5000  20 x   2000  10 x  dx 
2
2
0

3000  30 x 2 dx  3000 x  10 x 3
0

10
 20000 dól .
0
c) En términos geométricos, la ganancia neta calculada en el ítem anterior está representada
por el área de la región limitada entre las curvas
x  10 .
y  Rx  y y  Cx , desde x  0 hasta
y
5000
R(x)
Gan. Neta
3000
2000
C(x)
0
x
Aplicaciones de la integral definida
5
10
x
2
CALCULO II
Otra importante aplicación es el cálculo del excedente de los consumidores y del excedente en
la producción.
La siguiente gráfica muestra una curva de oferta
F q  para un producto, donde p indica el
precio por unidad al que un fabricante venderá o suministrará q unidades.
También se muestra la curva de demanda
Dq  para el producto, donde p indica el precio por
unidad al que los consumidores comprarán o demandarán q unidades del mismo.


El punto q 0 , p 0 es el punto de equilibrio, en el cual se presenta estabilidad en la relación
producto – consumidor.
Suponiendo que el mercado está en equilibrio, en que el precio por unidad del producto es p 0 ,
observando la curva de demanda se puede apreciar que hay consumidores que estarían
dispuestos a pagar más que p 0 por el producto, así como también, si observamos la curva de
la oferta, podríamos concluir diciendo que hay productores que están dispuestos a ofrecer el
producto a un precio inferior que p 0 .
De esta manera ambas partes pueden obtener una ganancia total que llamamos exceso.
En el caso de los consumidores, se denomina excedente o superávit del consumidor, y es la
ganancia total que obtienen los consumidores por el hecho de estar dispuestos a pagar el
producto a un precio superior al del mercado. Este se puede calcular por la integral definida
dada por:
Exc . Cons 




q0
 Dq   p 0  dq 
p
0



q0
Dq  dq 
0

q0
p 0 dq 
0
q0
Dq  dq  p 0 . q
q0
0

D(q)
0
Ex .C
q0
Dq  dq  p 0 . q 0
p0
0
0
q0
q
En el caso de los productores, se denomina excedente o superávit del productor, y es la
ganancia total que obtienen los productores por el hecho de estar dispuestos a ofrecer el
producto a un precio inferior al del mercado. Este se puede calcular por la integral definida
dada por:
Aplicaciones de la integral definida
3
CALCULO II
Exc .P rod 

q0
 p 0  F q  dq 
p
0


q0
p 0 dq 
0
q0
 p0 . q
0



q0
F q  dq  
0
q0
F q  dq 
Ex. P
0
 p0 . q0 

q0
Dq  dq
p0
0
F(q)
0
q
q0
En el caso de que las funciones de oferta y demanda estuviesen representadas cantidades en
función de los precios, el planteo para el cálculo de los excedentes es el siguiente:
Exc . Cons . 

p2
Dp  dp
Exc . Pr od . 
p0

p0
F p  dp
p1
q
q0
Ex P
Ex C
0
p1
p0
Aplicaciones de la integral definida
p2
p
4