GUÍA : Polinomio de interpolación de Lagrange.

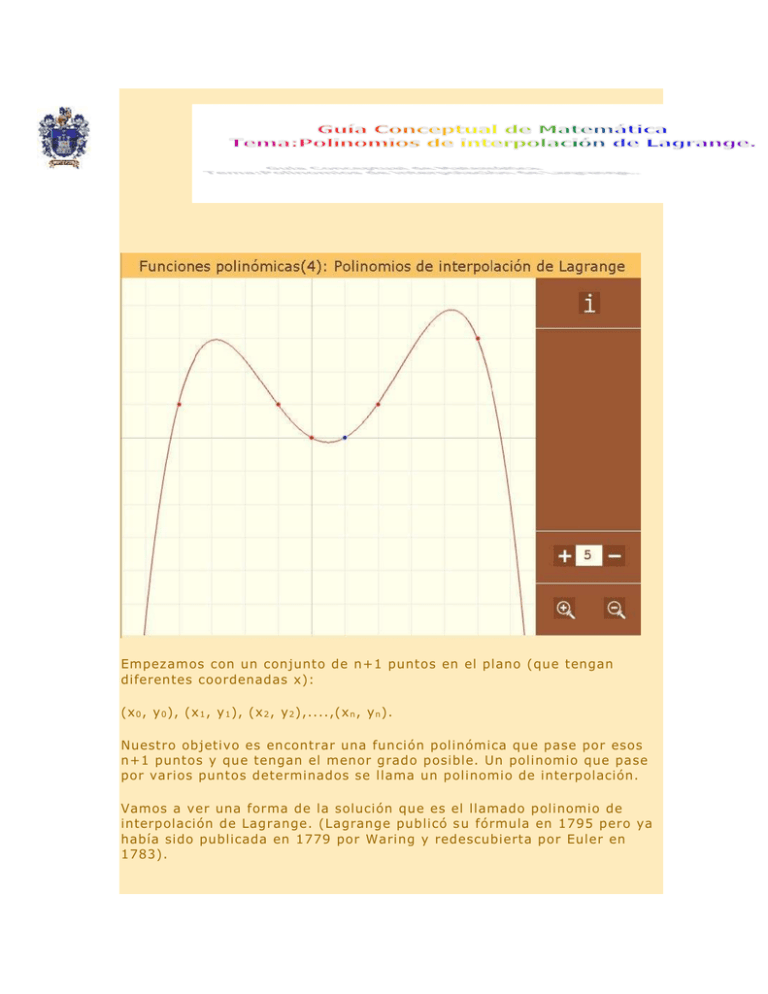
Empezamos con un conjunto de n+1 puntos en el plano (que tengan
diferentes coordenadas x):
(x 0 , y 0 ), (x 1 , y 1 ), (x 2 , y 2 ),....,(x n , y n ).
Nuestro objetivo es encontrar una función polinómica que pase por esos
n+1 puntos y que tengan el menor grado posible. Un polinomio que pase
por varios puntos determinados se llama un polinomio de interpolación.
Vamos a ver una forma de la solución que es el llamado polinomio de
interpolación de Lagrange. (Lagrange publicó s u fórmula en 1795 pero ya
había sido publicada en 1779 por Waring y redescubierta por Euler en
1783).
La fórmula general para el polinomio de interpolación de Lagrange es
Donde usamos polinomios básicos de Lagrange:
Expandiendo el producto para verlo mejor:
Estos polinomios básicos de Lagrange se construyen con una propiedad:
Entonces es muy fácil comprobar que estos polinomios pasan por todos los
n+1 puntos dados (es decir, es un polinomio de interpolación):
El grado del polinomio de interpolación de Lagrange es igual o menor que n.
Es el menor grado posible. El polinomio encontrado es único. Hay otras
maneras de calcular este polinomio (con sus ventajas e inconvenientes). La
forma de Lagrange es sencilla y se comprueba con facilidad q ue es un
polinomio de interpolación y su grado. Pero para conocer los coeficientes
del polinomio hay que simplificar los términos. Otra característica de esta
forma de encontrar el polinomio es que si añadimos o quitamos puntos hay
que recalcularlo otra vez.
Vamos a ver algunos ejemplos. El más sencillo es una recta. Dados dos
puntos (x 0 , y 0 ) y (x 1 , y 1 ) hay exactamente una recta que pasa por esos dos
puntos:
Dados tres puntos (x 0 , y 0 ), (x 1 , y 1 ) y (x 2 , y 2 ), con coordenadas x
diferentes, o bien los tres puntos están en una recta o hay un polinomio
de segundo grado (una parábola) que pasa por esos tres puntos. En
cualquier caso, hay un polinomio de grado como mucho 2 que pasa por
esos tres puntos.
Si tenemos 4 puntos, podemos encontrar un polinomio de grado 3 (o
quizás una parábola o una línea recta en algunos casos) que pasa por
esos 4 puntos:
Un función polinómica de grado 4 pasa a través de 5 puntos:
Usaremos los polinomios de interpolación de Lagrange para construir
aplicaciones interactivas relacionadas con funciones polinómicas,
sus derivadas e integrales.
Las funciones polinómicas con coeficientes reales o complejos de grado n
tienen siempre n raíces (reales o complejas)(Teorema fundamental del
Álgebra):