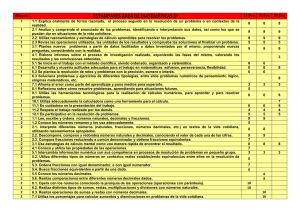
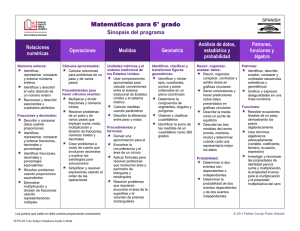
2. Programación de Matemáticas.
Anuncio

Consejería de Educación y Ciencia Colegio de Educación Infantil y Primaria Valdemembra. Quintanar del Rey. CUENCA. Castilla – La Mancha. ESPAÑA. Programación Didáctica. Isaac Peral Nº 2. C.P.16220. [email protected] www.colegiovaldemembra.es Área de Matemáticas 3º Ciclo de Educación Primaria. 5º y 6º cursos. C.E.I.P. Valdemembra. Quintanar del Rey. CUENCA. Curso 2012 - 2012. ÍNDICE: 1. INTRODUCCIÓN. .............................................................................................................. 2 2. OBJETIVOS, COMPETENCIAS BÁSICAS, SECUENCIACIÓN DE CONTENIDOS Y CRITERIOS DE EVALUACIÓN. ............................................................................................... 8 3. MÉTODOS DE TRABAJO. .............................................................................................. 31 4. ACTIVIDADES COMPLEMENTARIAS. .......................................................................... 37 5. EVALUACIÓN DEL ALUMNADO. ................................................................................... 38 6. INDICADORES, CRITERIOS, PROCEDIMIENTOS, TEMPORALIZACIÓN Y RESPONSABLES DE LA EVALUACIÓN DEL PROCESO DE ENSEÑANZA Y APRENDIZAJE. ...................................................................................................................... 57 7.ANEXO I ............................................................................................................................... 59 1 ÁREA: MATEMÁTICAS. 3º CICLO DE EDUCACIÓN PRIMARIA. Niveles: 5º y 6º Cursos. 1. INTRODUCCIÓN. 1.A. ENFOQUE Y NORMATIVA. El área de Matemáticas pertenece al ámbito cuyo contenido acerca al alumnado al conocimiento del mundo que le rodea, tal como queda expresado en el Decreto 68/2007 de la Consejería de Educación de la Comunidad Autónoma de Castilla- La Mancha, de 19 de Mayo por la que se establece y ordena el currículo de la Educación Primaria en esta Comunidad. A través de la enseñanza-aprendizaje de esta área se contribuye de manera más específica al desarrollo de las capacidades incluidas en los objetivos generales de etapa g) y o) que establece la Ley Orgánica 2/2006, de 3 de mayo, en su artículo 17 del Capítulo II. g) Desarrollar las competencias matemáticas básicas e iniciarse en la resolución de problemas que requieran la realización de operaciones elementales de cálculo, conocimientos geométricos y estimaciones, así como ser capaces de aplicarlos a las situaciones de su vida cotidiana Los contenidos quedan organizados en tres bloques: 1. Comprensión, representación y uso de los números: operaciones y medida. En este bloque quedan incluidos los contenidos relacionados con el uso del número y de las operaciones para realizar estimaciones, cálculos y medidas. Este ciclo tiene como finalidad principal consolidar los conocimientos adquiridos en los ciclos anteriores, aunque con mayor grado de formalización e introduciendo otros nuevos que faciliten el paso a la etapa de Educación Secundaria Obligatoria con una sólida base matemática. Se repasa y amplía el conocimiento de los números naturales y se des arrolla la capacidad de operar con ellos; asimismo, se amplía el manejo de las fracciones y se introducen los números decimales, efectuando correspondencias entre fracciones decimales y números decimales. El estudio de fracciones y de números decimales se hace de forma interrelacionada, expresando las fracciones en forma de números decimales. Previamente al estudio de 2 estos últimos, se realizan actividades de lectura, escritura, comparación, ordenación, suma y resta con fracciones sencillas, extraídas de contextos familiares. Se desarrollan nuevas estrategias de cálculo mental, basadas en los nuevos conocimientos adquiridos sobre propiedades numéricas y en el dominio que se tiene de las operaciones aritméticas. Por otra parte, se introduce la utilización de la calculadora de cuatro operaciones como una herramienta que simplifica la realización de cálculos que resuelven un problema o para realizar comprobaciones o investigaciones. La utilización de calculadoras no significa que los estudiantes no tengan que aprender y desarrollar los procedimientos de las operaciones, sino que se maneja como un recurso al alcance del alumnado, quien deberá aprender a estimar cuándo es necesaria su ayuda. Se concede en este ciclo una atención especial a la resolución de situaciones problemáticas. Los alumnos y las alumnas se familiarizarán y habituarán con procesos cada vez más rigurosos que faciliten la exploración y resolución de problemas, tales como: organizar enunciados, asociar a una situación problemática los contenidos matemáticos necesarios para su resolución, elegir las operaciones más indicadas, estimar resultados, expresar oralmente y por escrito los pasos seguidos, los resultados obtenidos y su comprobación. Para ello, el alumnado trabajará de forma sistemática las fases fundamentales del proceso de resolución de problemas: - Comprender la situación problemática planteada. - Concebir un plan de resolución y elegir los procedimientos y estrategias más adecuados para llevar a cabo los cálculos. - Comprobar los resultados obtenidos realizando las sustituciones convenientes. - Analizar el resultado obtenido. - Comunicar el desarrollo y los resultados obtenidos, contrastándolos con sus compañeros y compañeras. Finalmente, mediante la resolución de problemas en pequeños grupos, se desarr ollarán actitudes de cooperación que, a su vez, mejorarán la confianza en las propias capacidades. En este bloque se desarrolla con más profundidad que en el ciclo anterior la necesidad de medir y de expresar la medición con unidades convencionales, fomentando la utilización de los instrumentos de medida con mayor seguridad y precisión, para poder expresar los resultados de forma más ajustada. El desarrollo de la capacidad de medir se incrementa realizando transformaciones de unas unidades a otras de la misma magnitud, utilizando también los números decimales, que favorecen el uso de las unidades de medida más adecuadas en cada situación. En este ciclo, además de estudiar todas las unidades de medida de longitudes, capacidades y masas, se introducen unidades convencionales de medida de superficies: metro cuadrado, decímetro cuadrado y centímetro cuadrado. También, se estudia la medida del volumen. 3 Es importante, además, la transformación de unidades y las equivalencias entre ellas, así como el uso de algoritmos para el cálculo de áreas. Por último, se trabaja con las monedas de euro para contar, agrupar, establecer equivalencias y materializar conceptos numéricos y se realizan operaciones para medir el tiempo. 2. Interpretación y representación de las formas y la situación en el espacio Incluye los contenidos relacionados con la localización un punto y la representación en el plano y en el espacio, y la identificación de formas y cuerpos geométricos. El aprendizaje de los aspectos geométricos sigue fundamentándose en la observación y experimentación mediante el trabajo manipulativo y de construcción, de tal modo que, en primer lugar, se identifican modelos geométricos en la realidad física, y, posteriormente, se pasa al estudio y análisis de los cuerpos y formas, comparándolos y clasificándolos según diversos criterios, para poner de manifiesto la estrecha relación existente entre el espacio y el plano. Se profundiza en el estudio y el análisis de los elementos de las formas planas y espaciales: lados, ángulos, vértices, aristas, etc., y se introducen sistemas de referencia (coordenadas cartesianas) para describir e interpretar itinerarios y recorridos, desplazamientos y giros. El reconocimiento e identificación de cuerpos y formas geométricas sencillas desde perspectivas diferentes, el establecimiento de relaciones entre ellos y sus elementos (superficies, lados, diagonales, radio y diámetro, etc.), la representación de formas y la construcción de cuerpos para llegar a su descripción completa, cobran especial importancia en este ciclo. 3. Recogida de información y resolución de problemas de la vida cotidiana. En este último bloque se utilizan las estrategias y procedimientos matemáticos para interpretar y resolver distintas situaciones partiendo del uso de técnicas elementales de recogida, ordenación, representación y tratamiento de datos, comprensión, interpretación; identificación de operaciones adecuadas y comprobación de resultados. También incluye el entrenamiento en formulación de problemas y el análisis de fenómenos de azar y probabilidad. En este ciclo, ya es posible trabajar con un número mayor de datos y de situaciones. Además, las técnicas de recogida de información son más elaboradas, pudiéndose utilizar 4 tablas de recogida de datos, encuestas, tablas, gráficas, mediciones, etc., y representaciones mediante gráficas de sectores, diagramas de barras, tablas de frecuencias. Se profundiza, también, en la lectura e interpretación de tablas y gráficas, no elaboradas por los escolares. A través de la estadística, los alumnos y las alumnas aprenden a observar, obtener, tratar, organizar y aplicar la información mediante el análisis de situaciones reales de la vida cotidiana. Las técnicas de recogida y recuento de datos son en este ciclo más elaboradas, y los gráficos, más complejos. Además, se obtienen e interpretan la moda y la media aritmética en situaciones familiares. Por otra parte, en este ciclo se inicia una aproximación al concepto de probabilidad, considerando los sucesos más o menos posibles, impos ibles o seguros. El alumnado, mediante la repetición de experiencias, diferenciará unos de otros y calculará la probabilidad de sencillos experimentos aleatorios. Y, asimismo, llegará a saber que la mayor parte del conocimiento científico es probabilístico (que asume un cierto margen de error) y plausible (que es válido como explicación). Finalmente, tiene especial relevancia el desarrollo de la actitud crítica ante las informaciones y mensajes transmitidos de forma gráfica. 1.A. ENTORNO GEOGRÁFICO, SOCIO-ECONÓMICO Y CULTURAL Quintanar del Rey es una localidad situada en la zona de La Manchuela, al sudeste de la provincia de Cuenca, de la que dista unos 98 km; y de Albacete, 45 Km. Ubicado en el centro del eje de comunicaciones de Cuenca, Albacete y Valencia. Está atravesada de norte a sur por el río Valdemembra, del cual toma el nombre nuestro colegio. Ocupa una superficie total de 80 kilómetros cuadrados y una densidad de población aproximada de unos 100 habitantes por kilómetro cuadrado. En los últimos años ha experimentado un gran desarrollo tanto económico como demográfico. En la actualidad cuenta con una población aproximada de 8000 habitantes censados (7845 habitantes, censo de 2009), a los que se unen un importante número de habitantes que por motivos laborales residen en la localidad. El municipio en los últimos años está experimentando un fuerte proceso migratorio en el que se están recibiendo ingentes llegadas de inmigrantes, lo que supone que debamos adaptarnos a una nueva realidad social. Igualmente, en virtud de su desarrollo económico, el municipio cuenta con una alta tasa de natalidad, lo que se refleja en los alumnos matriculados en los centros educativos. 5 La agricultura –principalmente la producción vitícola- es la actividad económica predominante. Es un pueblo con iniciativas empresariales, emprendedor en sectores económicos. Caben señalar las actividades vitivinícolas (entre ellas el proyecto para la elaboración de vinos ecológicos), cultivo y comercialización del champiñón y setas (en el municipio se encuentra la sede del Centro de Investigación, Experimentación y Servicios del Champiñón), transporte (camiones), construcción y estructuras metálicas, pequeño comercio y sector servicios. Su población es joven y el nivel económico medio-alto. Ha sido un pueblo de gran poder adquisitivo, haciéndose visible en las viviendas, vehículos, fiestas…En la actualidad, aquejado por la crisis se percibe el receso de esa prosperidad. A nivel cultural, las gentes de Quintanar del Rey no han aprovechado los recursos, las instituciones y las facilidades que han tenido al alcance para potenciar mucho más la cultura y educación. En los últimos años se está incrementando, aunque lentamente, la participación en actividades culturales cuyo foco dinamizador viene de los centros educativos y de las instituciones (Centro Social, Ayuntamiento, Casa de Cultura, Biblioteca…). Quintanar del Rey reúne las siguientes instalaciones e instituciones: Colegio, Instituto, Escuelas Infantiles, Ludoteca, Biblioteca, Centro Cultural, Aula de Música, Escuela de Música (por inaugurar), Centro de la Mujer, Casa de Cultura, Centro Social, Centro de Salud y otro recientemente construido, Residencia de Ancianos, Piscina Municipal, Campo de fútbol, Polideportivo, Asociaciones de Mujeres. 1.B. CENTRO ESCOLAR El Centro Escolar consta de dos colegios distanciados más de un kilómetro. Uno situado en la zona sur de la localidad. Consta de cuatro edificios diferentes dentro de un mismo recinto y separados entre sí. En él se encuentra ubicada la Dirección del centro y se recogen tres líneas completas. La construcción del edificio más antiguo data del año 1957, con graves deficiencias de mantenimiento y conservación. El resto de inmuebles presentan diferentes grados de conservación. El colegio nuevo, situado en la zona norte del pueblo acoge una línea de nueve unidades y su conservación es buena. Los dos colegios cuentan con gimnasio cubierto, Biblioteca, Aulas de Informática (Althia) y aulas digitalizadas de 5º y 6º de E. Primaria según el Programa Escuela 2.0. En este Centro se imparten Educación Infantil y Educación Primaria, con aulas de Pedagogía Terapéutica, Audición y Lenguaje, Aula de Música, Aula de Psicomotricidad, Aula de usos múltiples, Laboratorio (en el que se habilitará un aula de Inglés), patios y pistas polideportivas 6 En el presente curso 2011-1012 el alumnado se distribuye en 23 aulas de Educación Primaria y 12 de Educación Infantil, agrupados en los diferentes edificios. La ratio oscila entre 20 y 25 alumnos. La población escolar actual es de 779 alumnos, todos censados en la localidad. De ellos, el número de alumnos procedentes de otros países es 122. Este considerable número de alumnos inmigrantes exige la elaboración y el desarrollo de una programación adecuada y específica para facilitar su integración en el entorno. La respuesta a la diversidad se hace desde las medidas recogidas en el Proyecto Educativo. 7 2. OBJETIVOS, COMPETENCIAS BÁSICAS, SECUENCIACIÓN DE CONTENIDOS Y CRITERIOS DE EVALUACIÓN. 2. A. OBJETIVOS y SECUENCIACIÓN DE CONTENIDOS. 1. OBJETIVO GENERAL DE ÁREA: Elaborar y utilizar instrumentos y estrategias personales para cálculo mental, medida y orientación espacial y temporal. OBJETIVOS DE CICLO 1.1. Utilizar los conceptos básicos matemáticos sobre el número, las operaciones básicas de cálculo, la medida y la orientación espacial y temporal para comprender hechos y fenómenos conocidos. 1.2. Comparar cantidades cada vez más complejas, tanto estimando como contando, y expresar el resultado. 1.3. Efectuar operaciones de cálculo mental cada vez más complejas mostrando confianza en las propias capacidades. 1.4. Elaborar y utilizar estrategias personales de estimación, aproximación y cálculo mental, y de orientación espacial para la resolución de problemas sencillos a partir de su conocimiento de los números y de las operaciones. CONTENIDOS: 5º CURSO. 6º CURSO. Sistema de numeración decimal. La utilidad de los números en situaciones reales (contar, identificar, Grafía, lectura y escritura de calcular, medir, ordenar…) números de siete cifras. Uso y grafía de los números de Sistemas de numeración en más de seis cifras. culturas anteriores (romana y egipcia) e Valor de posición de las cifras. influencias en la actualidad. Lectura y escritura de números de Números positivos y negativos; seis cifras. uso en contextos reales. Comparación y ordenación de Jerarquía en las operaciones 8 números de seis cifras. combinadas. Uso del paréntesis. Múltiplos y divisores. Consolidación de las operaciones (suma, resta, multiplicación y división). Las potencias: -Cuadrados y cubos. -Potencias de base diez Desarrollo de las operaciones de Ordenación de números enteros, suma, resta, multiplicación y división con de decimales y de fracciones por distintos tipos de números. comparación y representación gráfica. Propiedad distributiva de la Desarrollo de las operaciones de multiplicación. suma, resta, multiplicación y división con Números decimales: valor de distintos tipos de números. posición de sus cifras. Comparación y Múltiplos y divisores de un ordenación. número: m.c.m., criterios de divisibilidad. Operaciones con números Divisores de un número. Criterios decimales. Uso de los números decimales de divisibilidad. en la vida cotidiana. El porcentaje. Cálculo del tanto Números fraccionarios. Obtención por ciento de una cantidad. de fracciones equivalentes. Correspondencia entre fracciones La fracción como cociente de dos sencillas, decimales y porcentajes. números. Las unidades de medida de Suma y resta de fracciones de longitud, volumen y de superficie del igual denominador. Sistema Métrico Decimal y manejo de sus El metro como unidad principal de equivalencias. medida de longitud, el litro como unidad Las medidas agrarias. de capacidad, el kilogramo como unidad de peso y el metro cuadrado como unidad de superficie. Múltiplos y submúltiplos. Equivalencias entre las unidades de medida de longitud, capacidad , peso y superficie, realizando estimaciones. Desarrollo de estrategias personales para medir figuras de manera exacta y aproximada. Realización de mediciones usando instrumentos y unidades de medida convencionales. Interés por un uso cuidado y con precisión de instrumentos de medida. 9 2. OBJETIVO GENERAL DE ÁREA: Identificar formas geométricas del entorno natural y cultural, utilizando el conocimiento de sus elementos y propiedades para describir la realidad y desarrollar nuevas posibilidades de acción. OBJETIVOS DE CICLO 2.1. Reconocer en el entorno objetos y espacios con diferentes formas geométricas y expresarlo con claridad y precisión. 2.2. Comprender mejor el propio entorno y desarrollar nuevas posibilidades de acción sobre este, utilizando los conocimientos sobre las formas geométricas, sus propiedades y tamaños, describiendo apropiadamente posiciones y trayectorias de objetos en el espacio. 2.3. Definir de forma precisa la propia situación y la de los objetos, utilizando diferentes puntos de vista y sistemas de referencia apropiados. 2.4. Construir e interpretar croquis, planos, mapas y maquetas, reconociendo en ellos elementos importantes y recorridos. CONTENIDOS: 5º CURSO. 6º CURSO. Sistema sexagesimal: el grado. Ángulos según su abertura y según su posición. Medida y dibujo de ángulos con el Polígonos: elementos y perímetro. semicírculo graduado. Triángulos: clasificación. Cuadriláteros: clasificación. Áreas del triángulo, rectángulo y romboide. La escala. Cálculo del área y el perímetro de una figura plana. Áreas del triángulo, cuadrado, cuadrado, rectángulo, rombo, romboide, polígonos regulares y círculo. Estimación del área de figuras planas no poligonales. Cuerpos geométricos: poliedros (prismas y pirámides) y cuerpos de revolución (cono, cilindro y esfera). Explicación oral del significado de los datos, la situación planteada, el proceso seguido y las soluciones obtenidas. 10 3. OBJETIVO GENERAL DE ÁREA: Utilizar técnicas elementales de recogida de datos para obtener información sobre fenómenos y situaciones de su entorno; representarla de forma gráfica y numérica y formarse un juicio sobre la misma. OBJETIVOS DE CICLO 3.1. Utilizar técnicas de recogida de datos de la realidad cotidiana, organizando los resultados en tablas y gráficos. 3.2. Observar y tomar datos sobre hechos, fenómenos y situaciones de la realidad cotidiana para clasificarlos y cuantificarlos, formándose juicios sobre ellos en función de su probabilidad y plausibilidad, y representándolos gráfica y numéricamente. 3.3. Representar datos mediante diagramas de barras e interpretar tablas y gráficas similares contextualizadas CONTENIDOS: 5º CURSO. 6º CURSO. Obtención y utilización de Variables estadísticas: información para la realización de tablas y cuantitativas y cualitativas. gráficos. Frecuencia absoluta y relativa. Elaboración de tablas de frecuencias Representación e interpretación de absolutas y relativas. la información proveniente del recuento Cálculo de la media aritmética de dato. para datos agrupados y sin agrupar. Interpretación de gráficas, Distintas formas de analizando críticamente las representación. informaciones. Lectura de datos representados en Tipos de gráficos: diagramas de distintos gráficos: de barras y de sectores. barras, gráficas de líneas y gráficas Elaboración y presentación de dobles. Gráficos de sectores. gráficos de forma ordenada. Sucesos. Probabilidad de un Representación de tablas de doble suceso. Estimación del grado de entrada. probabilidad de un suceso. Frecuencia. Tablas de frecuencia. El azar en la vida cotidiana. Diferenciación de situaciones La media, la mediana y la moda. aleatorias de las que no lo son. 11 4. OBJETIVO GENERAL DE ÁREA: Expresar mediante fórmulas matemáticas situaciones reales y resolverlas con operaciones matemáticas. OBJETIVOS DE CICLO 4.1. Reconocer situaciones que puedan ser resueltas con la ayuda de códigos, números naturales, fracciones y números decimales. 4.2. Resolver situaciones cuyo tratamiento requiera más de dos operaciones elementales de cálculo, utilizando los algoritmos correspondientes e interpretando el resultado. 4.3. Detectar y resolver problemas del entorno cotidiano, mediante operaciones de geometría y de lógica 4.4. Resolver y plantear problemas matemáticos utilizando un lenguaje correcto y los procedimientos de cálculo, medida, estimación y comprobación de resultados. CONTENIDOS: 5º CURSO. 6º CURSO. Uso en situaciones reales del Utilización de todo tipo de número nombre y grafía de los números de más (enteros, decimales, fracciones, de seis cifras. potencias) en contextos reales. Uso de los números decimales y Aplicación de la jerarquía de las operaciones con ellos en la vida operaciones en la resolución de cotidiana. problemas de la vida real. Desarrollo de estrategias Realización de mediciones reales personales para medir figuras de manera sobre terrenos, obtención de datos y exacta y aproximada. representación a escala. Resolución de problemas de la vida cotidiana en los que se utilicen medidas de longitud, peso, capacidad o tiempo. Resolución de problemas de la vida cotidiana en los que se utilicen medidas de longitud, peso, capacidad o tiempo. Reconocimiento de simetrías en Utilización de construcciones figuras y objetos de nuestro entorno. geométricas, objetos y relaciones espaciales para resolver problemas en 12 Comprensión de enunciados de situaciones reales. problemas. y búsqueda de alternativas Desarrollo de las operaciones de para su resolución. suma, resta, multiplicación y división de Desarrollo de las operaciones de distintos tipos de números para resolver suma, resta, multiplicación y división de situaciones de la vida real. distintos tipos de números para resolver Revisión de los resultados situaciones de la vida real. buscando la lógica en su interpretación. Explicación oral del significado de los datos de un problema, planteamiento para su resolución, proceso a seguir y soluciones obtenidas. Formulación de problemas propios o en equipo. 5. OBJETIVO GENERAL DE ÁREA: Apreciar el papel de las matemáticas en la vida cotidiana, disfrutar con su uso y reconocer el valor de actitudes como la confianza en sus propias capacidades para afrontar los problemas, la exploración de distintas alternativas, la conveniencia de la precisión o la perseverancia en la búsqueda de soluciones y apreciar lo que de positivo tienen lo errores cometidos. OBJETIVOS DE CICLO 5.1. Valorar la necesidad e importancia de las matemáticas en la vida c otidiana 5.2. Mostrar interés y perseverancia en la búsqueda de soluciones a situaciones problemáticas y apreciar lo que tienen de positivo los errores cometidos. 5.3. Manifestar creatividad en la exploración de distintas alternativas en la resolución de problemas cada vez más complejos. 5.4. Afrontar con autonomía situaciones problemáticas cada más complejas sin abandonar las tareas hasta haberlas concluido. CONTENIDOS: 13 5º CURSO. 6º CURSO. Desarrollo de estrategias Desarrollo de estrategias personales de cálculo mental e personales de cálculo mental e interpretación de datos en situaciones interpretación de datos en situaciones reales. reales. Confianza en las propias posibilidades, curiosidad, interés y constancia en la búsqueda de soluciones en problemas de la vida cotidiana. Confianza en las propias posibilidades, curiosidad, interés y constancia en la búsqueda de soluciones en problemas de la vida cotidiana. Interés por la descripción y Interés por la descripción y representación de formas geométricas. representación de formas geométricas. Perseverancia en la búsqueda de Perseverancia en la búsqueda de soluciones en situaciones de soluciones en situaciones de incertidumbre. incertidumbre. Disposición a la elaboración y Disposición a la elaboración y presentación de gráficos y tablas a partir presentación de gráficos y tablas a partir de recogida de datos, de forma ordenada. de recogida de datos, de forma ordenada. Participación activa en el trabajo Valoración de la necesidad de en equipo. reflexión, razonamiento y perseverancia en la resolución de problemas. Respeto por el trabajo de los demás. 14 6. OBJETIVO GENERAL DE ÁREA: Utilizar la lectura y los medios tecnológicos en la búsqueda, tratamiento y representación de informaciones diversas. OBJETIVOS DE CICLO 6.1. Utilizar los medios tecnológicos para el cálculo de medidas de longitud, capacidad, masa y tiempo, sus múltiplos y divisores. 6.2. Explorar y utilizar instrumentos de cálculo (calculadora de cuatro operaciones), analizando su adecuación, ventajas e inconvenientes, y revisando los resultados. 6.3. Explorar y utilizar instrumentos de medida (regla graduada, compás, unidades de longitud, capacidad y masa, reloj, etc.), decidiendo sobre la pertinencia y ventajas que implica su uso y revisando los resultados. 6.4. Fomentar la utilización del lenguaje propio del campo de las Matemáticas con precisión. CONTENIDOS: 5º CURSO. 6º CURSO. Las nuevas tecnologías en el Las nuevas tecnologías en el aprendizaje de las Matemáticas. aprendizaje de las Matemáticas. Representación de gráficos de barras, de La calculadora: herramienta de sectores… cálculo y autocorrección. La calculadora: herramienta de Instrumentos de medida y cálculo y autocorrección. herramientas tecnológicas. Ventajas e inconvenientes. Instrumentos de medida y herramientas tecnológicas. Elección de los instrumentos más adecuados para realizar medidas de Elección de los instrumentos más longitud, peso y capacidad. adecuados para realizar medidas de longitud, peso y capacidad. Uso adecuado del semicírculo graduado en la medida de ángulos. Uso adecuado del semicírculo graduado en la medida y dibujo de ángulos de distinta abertura. 15 2. B. SECUENCIACIÓN DE CRITERIOS DE EVALUACIÓN Y RELACIÓN CON COMPETENCIAS BÁSICAS. Los indicadores marcados con letra cursiva son considerados los mínimos para la superación de los criterios de evaluación correspondiente y la consecución del objetivo programado. Las competencias básicas responden a estas siglas: C1. Competencia en comunicación lingüística C2. Competencia matemática C3. Competencia en el conocimiento y la interacción con el mundo físico. C4. Competencia cultural y artística. C5. Tratamiento de la información y competencia digital. C6. Competencia social y ciudadana. C7. Aprender a aprender. C8. Autonomía e iniciativa personal. C9. Competencia emocional 1. OBJETIVO GENERAL DE ÁREA. Elaborar y utilizar instrumentos y estrategias personales para cálculo mental, medida y orientación espacial y temporal. OBJETIVOS DE CICLO. CRITERIOS EVALUACIÓN. Objetivo.1.1 Criterios evaluación obj. 1.1 Utilizar los conceptos básicos matemáticos sobre el número, las operaciones básicas de cálculo, la medida y la orientación espacial y temporal para comprender hechos y fenómenos conocidos. Leer, escribir, ordenar y realizar operaciones de suma, resta, multiplicación y división con números naturales de hasta siete cifras. Realizar operaciones de suma, resta, multiplicación de números decimales y fracciones. Conocer y utilizar las propiedades de las operaciones suma, resta y COMPETENCIAS BÁSICAS Indicadores. C1. Aumento de la riqueza de vocabulario específico del área y uso de él. C1. Empleo con rigurosidad de los términos. C1. Incorporación de los números al lenguaje habitual. C1. Comprensión global del texto en los enunciados de los problemas. 16 multiplicación. Aplicarlas resolución de problemas. en la Diferenciar números positivos y negativos y aplicarlos a situaciones reales. C1.Descripción verbal de los razonamientos y procesos matemáticos en la resolución de situaciones problemáticas de la vida real. C1.Escucha activa. Resolver problemas con operaciones de números decimales. Multiplicar y dividir por la unidad seguida de ceros. Resolver problemas con el concepto de fracción de una cantidad y calcular el total conociendo el valor de una fracción del mismo. Reconocer el metro como unidad principal de medida de longitud, el litro como unidad de capacidad, el kilogramo como unidad de peso y el metro cuadrado como unidad de superficie. Conocer los múltiplos y submúltiplos de esas unidades y realizar estimaciones. Resolver problemas con operaciones de medidas de longitud, peso, capacidad y superficie. C1.Respeto de las normas intercambio y turno de palabra. de C1. Participación y respeto en las conversaciones. C2.Uso de las operaciones con números naturales, decimales y fraccionarios. C2. Aplicación de las operaciones en la resolución de problemas. C2. Revisión y corrección en los cálculos. C3. Comprensión y uso de matemáticas en el mundo físico. las C3.Búsqueda de alternativas para solucionar situaciones problemáticas relacionadas con nuestro entorno. C3. Utilización de las operaciones matemáticas en situaciones cotidianas fuera del aula. C3. Uso del sistema monetario en situaciones cotidianas. C4. Utilización de algunas obras de arte para trabajar contenidos matemáticos. C5. Utilización de la calculadora y herramientas tecnológicas para facilitar la comprensión de contenidos matemáticos. C5. Uso de internet como fuente de información. C6. Utiliza los números como recurso para analizar los elementos y relaciones de la sociedad en la que vivimos. 17 C7. Descripción del proceso seguido en el aprendizaje de las distintas operaciones matemáticas, corrigiendo posibles errores. C8.Desarrollo de estrategias propias en la resolución de cálculos y problemas. C9.Actuación flexible y dialogante en temas de situaciones problemáticas. C9. Relaciones positivas y colaboración con sus compañeros en la búsqueda de soluciones a problemas planteados. Objetivo.1.2 Criterios evaluación obj. 1.2 Comparar cantidades cada vez más complejas, tanto estimando como contando, y expresar el resultado. Comparar y ordenar números de hasta siete cifras. C1. Incorporación de los números decimales a su lenguaje habitual. Comparar números decimales hasta las centésimas. C1. Interpretación de mensajes que contienen números decimales. Realizar cálculos numéricos mediante diferentes procedimientos. C1.Conocimiento y uso de los términos de la fracción Utilizar los números decimales y fracciones relacionándolos entre ellos. C2. Comparación y orden de números de hasta siete cifras. Realizar porcentajes sencillos en contextos de la vida cotidiana e interpretar la información. C2. Uso de operaciones con números decimales. C2. Revisión y corrección en los cálculos. C3. Uso de los números decimales para expresar cantidades que manejamos todos los días. C3. Reconocimiento de la utilidad de las fracciones para representar, describir y resolver situaciones cotidianas del mundo físico. C5.Utilización de lenguajes gráficos para interpretar la información sobre la realidad. C6. Trabajo en equipo colaborando en las tareas de grupo y aceptando las normas. C7. Comprensión, análisis y resolución 18 de problema potenciando estrategias. Objetivo.1.3 Criterios evaluación obj. 1.3 Efectuar operaciones de cálculo mental cada vez más complejas mostrando confianza en las propias capacidades. Desarrollar mental. estrategias de cálculo Efectuar operaciones mentalmente aumentando la complejidad. C1.Verbalización del proceso de razonamiento seguido en el cálculo mental de operaciones. C2.Cálculo mental de operaciones con números naturales. C2.Reconocimiento de la utilidad del cálculo mental en el manejo de monedas y billetes de curso legal en situaciones cotidianas. C7.Desarrollo de estrategias faciliten el cálculo mental. que C7. Identificación y aceptación de sus limitaciones y posibilidades, así como las de sus compañeros, respetándolas. C8.Confianza para enfrentarse cálculo mental con éxito. al C9. Desarrollo de la interiorización y autocontrol de si mismo. Objetivo.1.4 Criterios evaluación obj. 1.4 Elaborar y utilizar estrategias personales de estimación, aproximación y cálculo mental, y de orientación espacial para la resolución de problemas sencillos a partir de su conocimiento de los números y de las operaciones. Reconocer la importancia de las mediciones y estimaciones en la vida cotidiana. C1.Utilización del vocabulario de medida de longitudes, capacidad y peso en situaciones familiares. Ser capaz de relacionar los problemas con situaciones reales para visualizar una solución lógica. C2. Uso de estrategias de estimación y medida. C3.Establecimiento de relaciones causales en la resolución de problemas relacionados con el medio. C3.Definición de objetivos y metas para una mejor convivencia y trabajo en grupo. C4. Comprensión y uso de relaciones espaciales y temporales. C6.Aceptación de otros puntos de vista diferentes al propio al utilizar estrategias de resolución de problemas. 19 2. OBJETIVO GENERAL DE ÁREA. Identificar formas geométricas del entorno natural y cultural, utilizando el conocimiento de sus elementos y propiedades para describir la realidad y desarrollar nuevas posibilidades de acción. OBJETIVOS DE CICLO. CRITERIOS EVALUACIÓN. Objetivo.2.1 Criterios evaluación obj. 2.1 Reconocer en el entorno objetos y espacios con diferentes formas geométricas y expresarlo con claridad y precisión. Reconocer en el entorno inmediato objetos y espacios con formas de cuerpos geométricos. Reconocer los poliedros, su clasificación, elementos y los principales cuerpos de revolución y elementos. Aplicar los conceptos y nomenclatura relativos a los elementos geométricos para analizar, describir y comprender el entorno real. . COMPETENCIAS BÁSICAS Indicadores. C1.Uso de la terminología geométrica aprendida en el lenguaje habitual. C1.Comprensión y uso relaciones espaciales. de las C1.Descripción precisa de espacios con formas geométricas. C2.Medida, comparación y clasificación de ángulos en objetos y espacios reales. C2.Localización de formas geométricas. espacios con C2. Clasificación de cuerpos geométricos y conocimiento de sus elementos. C3. Enumeración de objetos cotidianos que correspondan a poliedros. C4. Relación de similitud entre los cuerpos geométricos y algunas estructuras artísticas reales. C4.Diseño de un proyecto artístico a partir de cuerpos geométricos. C5. Uso de las nuevas tecnologías para diseño gráfico de fotografías del entorno y su similitud con formas geométricas estudiadas. C6.Colaboración en las tareas de grupo. 20 Objetivo.2.2 Criterios evaluación obj. 2.2 Comprender mejor el propio entorno y desarrollar nuevas posibilidades de acción sobre este, utilizando los conocimientos sobre las formas geométricas, sus propiedades y tamaños, describiendo apropiadamente posiciones y trayectorias de objetos en el espacio. Comprender mejor el entorno utilizando el conocimiento de las formas geométricas. Describir con propiedad y lenguaje preciso la posición de objetos en el espacio. Utilizar las nociones geométricas de paralelismo, perpendicularidad, simetría, perímetro y superficie para describir y comprender situaciones de la vida cotidiana. C1.Uso de la terminología geométrica aprendida en el lenguaje habitual. C1.Comprensión y uso relaciones espaciales. de las C2.Medida, comparación y clasificación de ángulos en objetos y espacios reales. C2.Utilización de las nociones geométricas en la descripción de espacios, trayectorias y posiciones en la vida cotidiana. C3. Aplicación de los conceptos y nomenclatura relativos a los elementos geométricos para analizar, describir y comprender el entorno real. C4.Uso de la experimentación. observación y C4. Relación de similitud entre los cuerpos geométricos y algunas estructuras artísticas reales. C7.Reconocimiento de manipulación, construcción representación como métodos investigación y descubrimiento geometría la y de en C8.Interés por descubrir diferentes formas de construcción y representación de los elementos y figuras geométricas. Objetivo.2.3 Definir de forma precisa la propia situación y la de los objetos, utilizando diferentes puntos de vista y sistemas de referencia apropiados. Criterios evaluación obj. 2.3 Interpretar una representación espacial (croquis, plano…) realizada a partir de un sistema de referencia y de objetos o situaciones familiares. C1.Valoración de la terminología geométrica como recurso expresivo. C2.Aplicación en distintos contextos de los conceptos relativos a los distintos tipos de líneas, a sus posiciones relativas y a los ángulos. C2.Uso adecuado de los conceptos espaciales en relación con puntos de 21 referencia,distancias, desplazamientos. C2. Localización y trazado de puntos, líneas, traslaciones y simetrías. C3.Representación de espacios familiares y puntos de ellos en ejes de coordenadas. Objetivo.2.4 Criterios evaluación obj. 2.4 Construir e interpretar croquis, planos, mapas y maquetas, reconociendo en ellos elementos importantes y recorridos. Realizar croquis, planos y maquetas de espacios conocidos y familiares, trazando recorridos y localizando puntos C3.Representación de espacios del entorno aplicando los conceptos matemáticos. C3.Localización de puntos concretos en mapas y croquis de espacios conocidos. C3.Trazo de recorridos sobre un plano o mapa. C4. Diseño de un proyecto artístico: maquetas sencillas utilizando la escala y la proporción. C5. Búsqueda de información en bibliotecas, TIC´s y observación directa de los espacios trabajados en las maquetas, croquis, mapas… C6.Respeto hacia las obras y las opiniones de los demás. 3. OBJETIVO GENERAL DE ÁREA. Utilizar técnicas elementales de recogida de datos para obtener información sobre fenómenos y situaciones de su entorno; representarla de forma gráfica y numérica y formarse un juicio sobre la misma. OBJETIVOS DE CICLO. Objetivo.3.1 CRITERIOS EVALUACIÓN. COMPETENCIAS BÁSICAS Indicadores. Criterios evaluación obj. 3.1 Realizar encuestas, cuestionarios y C1.Uso de distintas técnicas de 22 Utilizar técnicas de recogida de datos de la realidad cotidiana, organizando los resultados en tablas y gráficos. plasmar los resultados gráficamente. recogida de datos. Obtener datos sobre un tema relacionado con el entorno y representarlos gráficamente. C1. Transmisión oral de informaciones precisas sobre aspectos cuantificables del entorno. Interpretar representaciones gráficas de un conjunto de datos. C2. Obtención de datos cualitativos y cuantitativos plasmando gráficamente los resultados. . Resolver problemas sencillos en los que los datos tengan que ser obtenidos leyendo o interpretando una tabla o gráfico. C3.Recogida y organización de datos relacionados con aspectos de nuestro entorno. C3.Interpretación de gráficas con datos referentes a nuestro entorno, nuestra Comunidad Autónoma, España. C5.Uso del lenguaje gráfico estadístico para interpretar información sobre la realidad. y la C7.Resolución de problemas sencillos partiendo de los datos obtenidos de tablas o gráficos. Objetivo.3.2 Criterios evaluación obj. 3.2 Observar y tomar datos sobre hechos, fenómenos y situaciones de la realidad cotidiana para clasificarlos y cuantificarlos, formándose juicios sobre ellos en función de su probabilidad y plausibilidad, y representándolos gráfica y numéricamente. Realizar estimaciones basadas en la experiencia sobre un resultado posible, imposible, seguro o más o menos probable de pequeños juegos de azar y comprobar el resultado. Recoger datos sobre aspectos de la realidad cotidiana, clasificarlos y cuantificarlos. C1.Uso de distintos tipos de texto que utilicen datos matemáticos. C2.Toma de datos sobre situaciones o fenómenos reales y representación gráfica de los mismos. C2.Cálculo de la probabilidad de un suceso. C2. Comparación de la medida de dos o más fenómenos. C2.Establecimiento causales. de relaciones C6.Valoración de la utilidad de los números como recurso para analizar los elementos y relaciones de la sociedad en la que vivimos. C6.Desarrollo de la colaboración con los demás para la recopilación de datos con el fin de resolver situaciones problemáticas. C7.Reconocimiento de la utilidad de 23 las representaciones gráficas para fijar y aclarar conceptos relacionados con nuestra vida cotidiana. C7. Búsqueda de alternativas. Objetivo.3.3 Criterios evaluación obj. 3.3 Representar datos mediante diagramas de barras e interpretar tablas y gráficas similares contextualizadas Recoger datos y representarlos en diagramas de barras. Comprender y comunicar la información a partir de unos datos recogidos en un diagrama de barras, en tablas y gráficas de distinto tipo. C1.Descripción verbal y por escrito de la interpretación de datos recogidos en una tabla o gráfica. C2.Representación de datos obtenidos en distintos tipos de gráficas. C2.Uso de técnicas de registro y de representación gráfica y numérica. C3.Uso de diagramas, gráficas de barras y de sectores es aspectos relacionados con la geografía de nuestra Comunidad Autónoma y nuestro entorno. C5.Búsqueda de información por distintos medios tecnológicos y bibliográficos para la elaboración de gráficas. C6. Recogida de datos de la realidad social, representación gráfica e interpretación de los mismos. C8.Valoración realista de los resultados desde el esfuerzo realizado. 24 4. OBJETIVO GENERAL DE ÁREA. Expresar mediante fórmulas matemáticas situaciones reales y resolverlas con operaciones matemáticas OBJETIVOS DE CICLO. CRITERIOS EVALUACIÓN. Objetivo.4.1 Criterios evaluación obj. 4.1 Reconocer situaciones que puedan ser resueltas con la ayuda de códigos, números naturales, fracciones y números decimales. Buscar los procedimientos matemáticos adecuados para abordar el proceso de resolución de problemas sencillos, anticipando una solución razonable. Valorar las diferentes estrategias en la resolución de situaciones. Perseverar en la búsqueda de datos y soluciones precisas, tanto en la formulación como en la resolución de un problema. COMPETENCIAS BÁSICAS Indicadores. C1.Incorporación de los números al lenguaje habitual, como elemento expresivo. C1.Interpretación y explicación mensajes que contienen números. de C1.Descripción verbal de los razonamientos y procedimientos matemáticos en la resolución de problemas. C2.Reconocimiento y uso de los números y utilización de códigos numéricos para identificar objetos, situaciones… C2.Uso de estrategias de estimación C6.Respeto hacia las diferentes estrategias de los otros compañeros. C6.Expectativas positivas del trabajo en grupo. C7.Corrección de errores recurso de aprendizaje como Objetivo.4.2 Criterios evaluación obj. 4.2 Resolver situaciones cuyo tratamiento requiera más de dos operaciones elementales de cálculo, utilizando los algoritmos correspondientes e interpretando el resultado. Aplicar el cálculo con dos o más operaciones en la resolución de problemas relacionados con la vida cotidiana. C1. Exposición oral de los pasos seguidos en el proceso de resolución de problemas que requieren más de dos operaciones. Expresar de forma ordena y clara, oralmente y por escrito, el proceso seguido en la resolución del proceso. C2.Uso de las operaciones con números de forma lógica para la resolución de problemas. C3. Resolución de problemas que requieren más de dos operaciones que resuelven situaciones de la vida cotidiana (mediciones, compra, 25 tiempo…) C6.Respeto a los planteamientos distintos de los otros compañeros e igual de válidos para la resolución de problemas. Objetivo.4.3 Criterios evaluación obj. 4.3 Detectar y resolver problemas del entorno cotidiano, mediante operaciones de geometría y de lógica. Resolver de forma lógica y reflexiva, dando importancia al orden y la claridad de los datos y la búsqueda de la solución correcta. Resolver problemas sencillos de la vida cotidiana empleando los conceptos de geometría. C1.Comprensión de los textos que enuncian los problemas. C1. Describir oralmente el orden seguido en el proceso de resolución. C2.Aplicación de las operaciones de todo tipo de números para resolver problemas cotidianos. C2.Planteamientos distintos en la resolución de problemas para conseguir el mismo resultado. C3.Aplicación de los conceptos matemáticos y cálculo en situaciones reales. C7. Definición de objetivos y metas para conseguir resultados lógicos. C8.Desarrollo de la capacidad de reflexión y lógica en la resolución de problemas cotidianos. Objetivo 4.4 Criterios de evaluación obj. 4.4 Resolver y plantear problemas matemáticos utilizando un lenguaje correcto y los procedimientos de cálculo, medida, estimación y comprobación de resultados. Resolver problemas expresando de forma clara y ordenada el procedimiento seguido, detectando los posibles errores en el planteamiento de la resolución. Comprobar los resultados una vez resuelto el problema e interpretar dichos resultados. C1.Redacción de enunciados de problemas a partir de unos datos dados. C2. Formulación y resolución problemas siguiendo un orden. de C2.Descripción e interpretación de los resultados. C3. Comprensión y uso de relaciones espaciales y temporales relacionados con el mundo físico en la resolución de problemas. C3.Formulación de hipótesis. C7.Comprobación de los resultados y corrección de errores como enriquecimiento del aprendizaje. 26 5. OBJETIVO GENERAL DE ÁREA. Apreciar el papel de las matemáticas en la vida cotidiana, disfrutar con su uso y reconocer el valor de actitudes como la confianza en sus propias capacidades para afrontar los problemas, la exploración de distintas alternativas, la conveniencia de la precisión o la perseverancia en la búsqueda de soluciones y apreciar lo que de positivo tienen lo errores cometidos. OBJETIVOS DE CICLO. CRITERIOS EVALUACIÓN. Objetivo.5.1 Criterios evaluación obj. 5.1 Valorar la necesidad e importancia de las matemáticas en la vida cotidiana Mostrar interés por el aprendizaje de las Matemáticas y valorar la importancia que tienen en la vida cotidiana. Aplicar las estrategias aprendidas a la resolución de situaciones problemáticas reales. COMPETENCIAS BÁSICAS Indicadores. C7. Interés por el aprendizaje de las Matemáticas. C7.Valoración de las Matemáticas para resolver situaciones problemáticas en la vida diaria. C8.Desarrollo de aplicación en la problemas. C9.Reconocimiento errores. estrategias resolución verbal de y de los C9.Defensa argumentada en el uso de un planteamiento matemático. Objetivo.5.2 Criterios evaluación obj. 5.2 Mostrar interés y perseverancia en la búsqueda de soluciones a situaciones problemáticas y apreciar lo que tienen de positivo los errores cometidos. Perseverar en la búsqueda de datos y soluciones precisas, tanto en la formulación como en la resolución de un problema. C7.Autocontrol de la atención perseverancia en la tarea Aceptar los errores cometidos como fuente de aprendizaje y reconocimiento de su progreso. C7. Selección de datos y toma de decisión sobre la estrategia más adecuada para la resolución. y C7. Búsqueda de alternativas. C8. Iniciativa para buscar información, leer… C8.Responsabilidad en las tareas. C9. Reconocimiento de los errores 27 cometidos y corrección de los mismos. Objetivo.5.3 Criterios evaluación obj. 5.3 Manifestar Explorar distintas alternativas en la C7. Búsqueda de alternativas. creatividad en la resolución de problemas. C7. Selección de datos y toma de exploración de decisión sobre la estrategia más distintas alternativas adecuada para la resolución. en la resolución de problemas cada vez C9.Defensa argumentada de la alternativa escogida. más complejos. Objetivo 5.4 Criterios de evaluación obj. 5.5 Afrontar con autonomía situaciones problemáticas cada más complejas sin abandonar las tareas hasta haberlas concluido. Terminar las tareas con calidad, aplicando las estrategias y conceptos aprendidos a situaciones cotidianas, cada vez con más autonomía. C2. Revisión responsabilidad realizadas. y corrección con de las tareas C4. Presentación clara y ordenada del trabajo. C6. Respeto hacia las obras y las opiniones de los demás, manifestando el reconocimiento y la alegría con el éxito de sus compañeros. C7. Desarrollo de estrategias que faciliten el trabajo autónomo. C7. Autocontrol y perseverancia en la tarea. 28 6. OBJETIVO GENERAL DE ÁREA. Utilizar la lectura y los medios tecnológicos en la búsqueda, tratamiento y representación de informaciones diversas. OBJETIVOS DE CICLO. Objetivo.6.1 CRITERIOS EVALUACIÓN. COMPETENCIAS BÁSICAS Indicadores. Criterios evaluación obj. 6.1 Utilizar los medios Manejar los medios tecnológicos para tecnológicos para el la búsqueda de información, cálculo cálculo de medidas de medidas… de longitud, capacidad, masa y tiempo, sus múltiplos y divisores. C2.Desarrollo del gusto por la precisión y el rigor utilizando los instrumentos de medida más apropiados. C5.Uso de internet como fuente de información. C5.Uso de la calculadora y de herramientas tecnológicas para facilitar la comprensión de contenidos matemáticos. C5. Uso de cronómetros y relojes digitales. C6. Cumplimiento de los acuerdos adoptados en el grupo clase, prevaleciendo el respeto, aprecio y tolerancia. . Objetivo.6.2 Criterios evaluación obj. 6.2 Explorar y utilizar Conocer el uso de la calculadora y C2.Uso de la calculadora sencilla de cuatro operaciones. instrumentos de utilizarla de forma adecuada. cálculo (calculadora C5.Conocimiento, aplicación y uso de cuatro crítico, positivo y responsable de las operaciones), nuevas tecnologías. analizando su C7.Conocimiento de las ventajas e adecuación, ventajas inconvenientes del uso de la e inconvenientes, y calculadora. revisando los resultados. Objetivo.6.3 Criterios evaluación obj. 6.3 Explorar y utilizar instrumentos de medida (regla graduada, compás, Utilizar adecuadamente diversos recursos didácticos en la resolución de situaciones problemáticas y cálculo. C2.Desarrollo del gusto por la precisión y el rigor utilizando los instrumentos de medida más apropiados. C2. Uso de la regla graduada, metro, 29 semicírculo graduado, compás,. unidades de longitud, capacidad y masa, reloj, etc.), decidiendo sobre la pertinencia y ventajas que implica su uso y revisando los resultados. C6. Desenvolvimiento con autonomía e iniciativa personal en el planteamiento de hipótesis y resolución de problemas Criterios de evaluación obj.6.4 Objetivo 6.4 Fomentar utilización lenguaje propio campo de Matemáticas precisión C5. Uso de cronómetros y relojes digitales. la del del las con Incorporar a su lenguaje habitual la terminología de las Matemáticas. Utilizar el lenguaje preciso en la descripción de los procesos matemáticos. C1.Uso del vocabulario específico. C1. Incorporación del vocabulario del lenguaje matemático en su lenguaje habitual. C1.Uso preciso de los términos matemáticos. C1.Corrección ortográfica. C7. Autoevaluación del uso del lenguaje matemático. 30 3. MÉTODOS DE TRABAJO. 3.1. Metodología didáctica. Matemáticas es un área que necesita para su aprendizaje de una metodología activa, participativa, comunicativa, interactiva y motivadora. En la metodología para la enseñanza de las Matemáticas se tendrá en cuenta: la investigación matemática la realización de proyectos de trabajo el aprendizaje dialógico el aprendizaje cooperativo la utilización de contextos sociales y situaciones globales de aprendizaje la creación de un ambiente matemático en el que el alumno debe hacer hipótesis, investigar, ensayar, equivocarse y aprender en grupo. Es activa porque el alumno debe ser partícipe de su propio proceso de aprendizaje a través de su experiencia directa y manipulación. El aprendizaje del área de Matemáticas parte principalmente de los aprendizajes significativos del alumnos, de todo aquello que ya conoce y relacionarlo con lo que irá aprendiendo. Su principal finalidad es la utilidad en la vida real de todo lo aprendido, consiguiendo una alfabetización matemática a nivel numérico, operacional, geométrico… que será el bagaje matemático que aplicará en la resolución de los problemas que se le presenten en la vida cotidiana, sirviéndole para entender y vivir en la sociedad del conocimiento. Se busca el refuerzo del carácter comunicativo de las matemáticas y la importancia de contextos y textos matemáticos culturales. La metodología participativa se basa en una dinámica de grupos que, a su vez, se apoya en la cohesión entre los miembros que lo componen; para ello es necesario un clima favorable que consiga un afianzamiento y consolidación del grupo. En los primeros trabajos realizados con esta metodología pueden darse momentos de tensión, en cambio, cuando se consigue esa cohesión intergrupal se crea un clima de trabajo agradable que favorece a nivel de relación -personal y en el enriquecimiento de ideas-, y a nivel de acción mejorando la autonomía, la organización, la colaboración y la consecución de los objetivos marcados. Otro método de trabajo adecuado para esta área y apropiado para trabajar y evaluar las competencias es el trabajo cooperativo, que no hay que confundir con trabajar simplemente en grupo. 31 En el trabajo cooperativo los alumnos trabajan juntos para aprender y, a su vez, son responsables de su propio aprendizaje y del aprendizaje de los demás. Se definen unos objetivos para cada alumno, de tal forma que cada uno de ellos podrá lograrlo si todos los demás consiguen el suyo. Los niños con este método discuten, opinan, oyen distintos puntos de vista y a través del diálogo y los debates se buscan soluciones. Desarrollan el sentido crítico, la creatividad y el aprendizaje por descubrimiento. Recogemos unas estrategias metodológicas a tener en cuenta: Impulsar y favorecer la autonomía en el proceso enseñanza-aprendizaje. Dar facilidad para un aprendizaje activo. Motivar hacia el objeto de aprendizaje. Crear un ambiente propicio en el aula. Favorecer el uso de diversas fuentes de información y de las TIC. Impeler lo aprendido fuera del ámbito escolar, dándole funcionalidad. Impulsar la evaluación formativa. Criterios metodológicos en el área de Matemáticas. Posibilitará el paso del pensamiento concreto al abstracto Que los saberes y conocimientos estén orientados al “saber aplicar” Utilización de diferentes agrupamientos de aprendizaje: grupo-clase, individual, parejas, pequeño grupo. Promoverá elaboración de trabajos personales y en equipo, reales y virtuales. Aprovechará objetos, espacios reales y situaciones de la vida cotidiana como objeto de aprendizaje. Propiciará la creatividad del alumnado en su proceso de aprendizaje. Utilizará las TIC de forma continua y sistemática. ¿Cómo podemos darle forma a este método de trabajo en nuestra práctica docente? Concretando la secuenciación de actividades en nuestras programaciones de unidades didácticas siguiendo los siguientes pasos: Presentando una problemática o situación relacionada con algo real 1º.- Planificación: Estableciendo unos objetivos para dar solución Elaborando un esquema de actividades para conseguir los objetivos 2º.- Aprendizaje: 3º.- Aplicación: Puesta en práctica de las actividades anteriores. Llevarlo a situaciones reales 32 Las competencias básicas se adquieren y se evalúan a través de tareas realizadas, utilizando diferente fuentes de información (entrevistas, trabajo del alumnado, exámenes…). En la tarea que nos planteemos tenemos que tener en cuenta: Qué esté vinculada a las competencias. Que exista un contexto donde se aplique. Criterios de evaluación que tiene relación con unos objetivos y, a su vez, con unos conocimientos de nuestro proceso de enseñanza-aprendizaje. Actividades que resuelvan la tarea y nos indiquen el nivel de dominio de la misma. . 3.2. Organización de tiempos El horario lectivo implantado en nuestro Centro está acogido al Anexo II de la Orden de 12-06-2007, de la Consejería de Educación y Ciencia por la que se establece el horario y la distribución de las áreas de conocimiento en la Educación Primaria en la Comunidad de Castillas-La Mancha, aprobado por mayoría en Claustro y ratificado por el Consejo Escolar. Con él se puede adoptar un horario propio de acuerdo con el límite mínimo y máximo semanal para cada área. El intervalo de horas por ciclo correspondientes a esta área es de un mínimo de 8 y un máximo de 10. En 5º se han establecido cinco sesiones semanales de 45 minutos y en 6º, seis sesiones de 45 minutos. La suma total de horas impartidas en el Ciclo entra dentro de ese intervalo recogido en la Orden. Las sesiones se imparten generalmente, salvo casos excepcionales por reajuste de horarios, a primeras horas de la mañana, antes del período de recreo, pues exigen un mayor esfuerzo mental en los alumnos. La temporalización de los contenidos se realiza por niveles y teniendo en cuenta los que trabaja la editorial elegida en el curso en desarrollo (libros del programa de gratuidad de la Consejería), en cada uno de los niveles 5º y 6º cursos. En cada curso, los contenidos están tratados en quince temas que se distribuyen a lo largo de todo el curso, trabajando cinco temas por evaluación. Las evaluaciones no tienen por qué coincidir con los trimestres. Hay cursos escolares en los que se alarga el segundo trimestre y se tiene que comenzar a trabajar en el segundo trimestre, parte de la materia que corresponde al tercero. En la temporalización del temario también se tiene en cuenta la dificultad y densidad de los temas, así como las actividades programadas, para atribuirles más o menos sesiones en su desarrollo. Siempre es flexible, estando supeditada a las características 33 del alumnado, ritmo de aprendizaje, número de altas que se incorporan a lo largo del curso… El reparto de temas en el presente curso para ambos niveles queda de la siguiente manera: 1º Trimestre: 6 temas. 2º Trimestre: 5 temas. 3º Trimestre: 4 temas. 3.3. Agrupamientos y espacios El espacio se adecuará al tipo de agrupamiento y éste, a su vez, al tipo de actividad que estemos realizando en cada instante. Somos conscientes que todavía está muy arraigado el método transmisivoexpositivo convencional y tenemos que ir abriendo paso a un método donde los alumnos tomen protagonismo en su aprendizaje y alimentar esas relaciones entre ellos, ante la pluralidad de culturas que tenemos en nuestras aulas. Los agrupamientos, aunque flexibles, se aplicarán según: Las características de los alumnos Los objetivos que nos proponemos Las características de los contenidos que vamos a trabajar en cada momento. Así coexistirán: El trabajo individual: en las actividades de estudio, memorización, aplicación, refuerzo. Grupos flexibles homogéneos o heterogéneos: en actividades según niveles, o de ayuda de unos compañeros a otros que no dominan bien los contenidos o competencias. Grupos fijos heterogéneos: en actividades de trabajo cooperativo que exija responsabilidad individual y grupal, en resolución de conflictos, realización de tareas trabajando competencias… Grupo clase: en actividades de planteamiento de actividades de interés común, buscar soluciones, sacar conclusiones… La mayoría de las sesiones se llevarán a cabo en el espacio común, aula. En años anteriores también se hacía uso del Aula Althia; desde el curso 2009-2010, con la 34 implantación del programa Escuela 2.0, dotando el aula con pizarra digital y netbook para cada uno de los alumnos, esas actividades se realizan también en la misma clase. Hay sesiones que se realizarán fuera del recinto escolar en función de las actividades que estemos realizando, como son las visitas al entorno, olimpiadas… 3.4. Materiales y recursos didácticos Los materiales curriculares y recursos que se utilizan en esta área son: Libro de texto (del Programa de Gratuidad de la Consejería), exige un cuidado especial por parte del alumnado al no ser de su propiedad. Software educativo de elaboración propia o ya editada. Netbook para cada alumno de 5º y 6º, pizarra digital y material informático (Programa Escuela 2.0). Material bibliográfico (biblioteca de Centro, biblioteca municipal). Material de medición: reglas, metro, probetas, balanza, semicírculo graduado… Material para construcción de objetos con formas geométricas. Fuentes diversas de información: revistas, TIC, encuestas y entrevistas directas… Recursos audiovisuales: vídeos, televisión Recursos multimedia. Páginas webs. 3.5. Medidas de apoyo a la diversidad. La diversidad presente en nuestra realidad escolar nos conduce a planificar medidas educativas adaptadas a las necesidades específicas que presentan los alumnos . Estas medidas deben dar respuesta al alumnado y a su entorno en función de las diferentes capacidades, ritmos y estilos de aprendizaje, motivaciones e intereses, situaciones sociales, étnicas, de inmigración y de salud del alumnado. Los alumnos con alguna necesidad educativa siempre permanecerá integrado en su grupo o clase, poniendo en marcha medidas que cubran esas necesidades en un contexto lo más normalizado posible. En los casos de alumnos con necesidades educativas especiales importantes se hará una adecuación curricular, que condiciona adoptar medidas organizativas, didácticas, personales…para su integración en el grupo-clase. Ello conlleva una organización de trabajo en el aula y contar con la posibilidad de participación de estos niños en situaciones individuales de trabajo, trabajos en grupo, en 35 actividades lúdicas, y se dé un intercambio de intereses y puntos de vista con el resto de compañeros, prestando y recibiendo ayuda. Las respuestas educativas para apoyar otras necesidades en el proceso de enseñanza- aprendizaje de los alumnos para superar sus dificultades serán: - Acción tutorial que favorezca la integración de los alumnos en la vida del centro. - Refuerzo educativo: si el alumno, por motivos circunstanciales, presenta problemas en el aprendizaje, recibirá el apoyo específico para superarlo. Este refuerzo se hace con el profesorado paralelo al nivel o ciclo. Los recursos que se emplean como medidas de atención al alumnado con necesidades de apoyo educativo son: - Fichas de refuerzo. - Fichas de ampliación - Fichas de comprensión. Otras estrategias de respuesta que facilitan la atención individualizada sin modificar los objetivos del ciclo son: - Los agrupamientos flexibles con grupos homogéneos durante un tiempo determinado con adaptación de una parte del aprendizaje. - Talleres que armonicen las necesidades educativas con los interes es del alumnado. - Grupos de enriquecimiento de contenidos para los alumnos más avanzados. - Programas de aprendizaje del idioma para el alumnado de desconocimiento del idioma. - Programa específico para el alumnado que no puede asistir a clase por enfermedad prolongada. En este centro hemos tenido casos de atención domiciliaria por grave enfermedad. - Programa PROA. 36 4. ACTIVIDADES COMPLEMENTARIAS. Las actividades complementarias en el Área de Matemáticas se centran principalmente a talleres en los que se pone en práctica los contenidos trabajados durante el curso. Otras actividades que también se pueden realizar son: MATEMÁTICAS Actividad Olimpiada matemática (Me divierto y aprendo) Salidas a espacios abiertos (parque, campo de fútbol…) Juegos con las matemáticas http://redescolar.ilce.edu.mx/red escolar/act_permanentes/mate/l ugares.htm Visita Museo de Ciencias Taller de construcción (Anexo I) Taller de Matemáticas Recreativas http://www.juntadeandalucia.es/ averroes/iesarroyo/matematicas/ taller/taller.htm Concurso de cifras Concurso “Fotografía matemática” Gymkhana de ingenio matemático Concurso de juegos matemáticos cronometrado. http://www.thatquiz.org/es/ Contenidos Resolución de problemas Desarrollo de la habilidad del calculo mental Medición de longitudes y áreas. Espacio Cuenca Tiempo Un día Recursos CEP Familias y centro. Localidad Media jornada Centro Lógica Reflexión Resolución de problemas Clase Sesiones programadas Centro Cuenca Un día Centro Sesiones programadas Sesiones Centro familias Centro Taller matemáticas Lógica Espacio Cálculo Lógica Geometría Etc de Agilidad de cálculo Cálculo mental Razonamiento Relación del mundo físico con las matemáticas Tema elegido en la gymkhana Agilidad de cálculo Razonamiento Centro Centro Centro Sesiones programadas Centro Cualquier espacio Fuera del horario escolar Centro Familias Centro Sesiones programadas Sesiones programadas Centro Centro Centro 37 5. EVALUACIÓN DEL ALUMNADO. La evaluación debe centrarse en: Qué hacen los alumnos Cómo lo hacen Con qué contenidos. En la evaluación tenemos tres fases: 1ª.- Evaluación Inicial: Nos sirve para valorar los conocimientos previos, las capacidades y las actitudes que tiene el alumnado. Los resultados nos sirven de punto de referencia para programar nuestro proceso de enseñanza- aprendizaje adecuándolo a las características del alumnado y sus posibilidades. 2ª.- Evaluación formativa continua: Registrando el grado de logro de los objetivos y competencias. Según sean los resultados podemos modificar el proceso educativo para mejorarlos. 3ª.- Evaluación sumativa o final: Recoge el resultado de los objetivos conseguidos al término de nivel o de ciclo. En todo momento la evaluación tendrá en cuenta los logros conseguidos por el alumno en relación con la adquisición de las competencias básicas. Tendrá un carácter: Criterial teniendo en cuenta las posibilidades de aprendizaje del alumno con la adquisición de las competencias. Cuantitativo, más que cuantitativo Personalizado, valorando el proceso de cada alumno en particular. La evaluación de las competencias nos debe permitir conocer el grado de aplicación de los conocimientos adquiridos en situaciones reales diversas. Se trata de un proceso complejo que requiere técnicas y recursos diferenciados según la competencia que se evalúa y utilizará mecanismos para reconocer la utilidad de esos aprendizajes para superar las situaciones que se presenten de manera satisfactoria. Las actividades de evaluación estarán enfocadas a la realización de tareas que se refieran a los contenidos de aprendizaje relacionados con una competencia determinada para resolver una situación concreta. Los instrumentos de evaluación pueden ser muy diversos: Observación 38 Pruebas objetivas o escritas En estas pruebas se parte de una situación más o menos cotidiana (un contexto o escenario). A partir de ella se plantean diferentes tareas matemáticas referentes a diferentes ámbitos matemáticos y para resolverlos se utilizan contenidos matemáticos (numéricos, operacionales, geométricos…) Trabajo diario (Cuaderno del alumno, realización y finalización correcta de las actividades.) Trabajos de producción o investigación. Trabajo en equipo Diario de clase Autoseguimientos Comportamiento (interés, colaboración, participación, esfuerzo persona, normas…) En cada evaluación se pondrá una nota media, dependiendo del grado de consecución de objetivos que responda a los criterios: 60% Contenidos: pruebas orales y escritas, proyectos. 20% Esfuerzo, trabajo, interés, motivación, respeto, colaboración y cooperación. 20% Cuaderno de trabajo, fichas, corrección de actividades. Evaluación de diagnóstico: Medidas de mejora En los resultados de la evaluación de diagnóstico del curso 2010-2011 observamos que las Matemáticas está en la media de la Comunidad Autónoma, pero un punto por debajo de los resultados obtenidos en el 2009-2010. Vemos necesario plantear unas medidas de mejora para lograr un mayor conocimiento y aplicación de las Matemáticas a nivel de las Competencias Básicas. 39 El trabajo de las Matemáticas se realizará contextualizando la aplicación de las mismas, presentando escenarios y situaciones reales a nuestros alumnos, en los que deban resolver situaciones problemáticas más cercanas a la realidad que viven. Se debe fomentar el cálculo mental como autoconfianza en el manejo de las matemáticas, ayudando al alumno a buscar estrategias con las que les resulte más fácil realizarlo. Es importante y necesario presentar un plan de resolución de problemas que debe contener un proceso a seguir (pasos o criterios que debe dar siguiendo un orden), y el uso de la lógica y el razonamiento para su consecución (mediante preguntas que le hagan razonar). El trabajo se puede hacer mucho más motivador programando actividades basadas en juegos matemáticos (de lógica, construcción, cálculo, deducción…), en un concurso “Resolvemos problemas” entre clases del mismo nivel al final de cada evaluación. Desde el EOA se propone aplicar desde el inicio de Educación Primaria y a lo largo de toda ella un programa de razonamiento lógico-matemático y resolución de problemas. Otro aspecto que se debe trabajar es la interdisciplinariedad con la competencia lingüística. En general, el alumno no comprende bien lo que lee y eso dificulta el proceso de resolución de problemas. Se trabajará con distintos tipos de textos que contengan información numérica, analizando e interpretando dicha información. CONOCIMIENTOS MÍNIMOS PARA PROMOCIONAR 5º curso. Lectura y escritura, composición y descomposición de números de hasta siete cifras. Establecimiento de equivalencias entre los distintos órdenes de unidades. Operaciones: suma, resta, multiplicación y división con números naturales y decimales. Propiedades de la suma, resta y la propiedad distributiva de la multiplicación. Aplicación en la resolución de problemas. Conocimiento y aplicación de la jerarquía de operaciones en el cálculo y en problemas. Expresión de productos de factores iguales en forma de potencia y viceversa. Lectura y escritura de potencias. Operaciones con números decimales: suma, resta, multiplicación y división. Fracciones: términos y significado. Operaciones con fracciones: suma, resta, multiplicación y cociente. Ángulos: clasificación. Medida y construcción de ángulos con el transportador. 40 Operaciones con ángulos: sumas y restas de ángulos (sistema sexagesimal). Longitud: medición. Múltiplos y submúltiplos del metro. Peso: medición. Múltiplos y submúltiplos del gramo. Capacidad: medición. Múltiplos y submúltiplos del litro. Polígonos: perímetro y área. Áreas de: triángulo, cuadrado, rectángulo, rombo, romboide, polígonos regulares, círculo. Poliedros: identificación. Caras, vértices y aristas. Aplicación de todos los conceptos en la resolución de problemas relacionados con la vida cotidiana. Experiencias aleatorias. Sucesos. Probabilidad de un suceso. 6º curso. Conocimiento y aplicación de la jerarquía de operaciones en el cálculo y en problemas. Expresión de productos de factores iguales en forma de potencia y viceversa. Lectura y escritura de potencias. Reconocimiento de la relación de divisibilidad entre dos números. Obtención de múltiplos y divisores de un número dado. Cálculo del mínimo común múltiplo Resolución de sencillos problemas relacionados con la divisibilidad. Números positivos y negativos. Aplicación en la vida cotidiana. Representación de los números positivos y negativos en la recta numérica. Ordenación y comparación de números positivos y negativos. Suma de números enteros del mismo signo y de distinto signo. Número decimal y fracción decimal. Operaciones con números decimales: suma, resta, multiplicación y división. Fracciones: términos y significado. Operaciones con fracciones: suma, resta, multiplicación y cociente. Proporcionalidad directa. Construcción de tablas. Resolución de sencillos problemas de proporcionalidad directa. Significado de tanto por ciento. Cálculo de porcentajes. Resolución de problemas de porcentajes. Ángulos: clasificación. Medida y construcción de ángulos con el transportador. Operaciones con ángulos: sumas y restas de ángulos (sistema sexagesimal). Longitud: medición. Múltiplos y submúltiplos del metro. Peso: medición. Múltiplos y submúltiplos del gramo. Capacidad: medición. Múltiplos y submúltiplos del litro. Superficie: el metro cuadrado. Volumen: el metro cúbico. Polígonos: perímetro y área. Áreas de: triángulo, cuadrado, rectángulo, rombo, romboide, polígonos regulares, círculo. Cálculo de la longitud de una circunferencia. Poliedros: identificación. Caras, vértices y aristas. Clasificación de poliedros: prismas y pirámides. Cuerpos de revolución: cono, cilindro y esfera. 41 Aplicación de todos los conceptos en la resolución de problemas relacionados con la vida cotidiana. Variables estadísticas: cuantitativas y cualitativas. Frecuencia absoluta y relativa La media aritmética, la moda y el rango. Aplicación a situaciones familiares. Experiencias aleatorias. Sucesos. Probabilidad de un suceso. Los registros de evaluación necesarios para una buena evaluación son: Ficha registro de cada unidad didáctica: Criterios de evaluación e indicadores específicos Dimensiones e indicadores de competencias instrumentales dimensiones de competencias transversales En la siguiente ficha quedan recogidas las competencias, dimensiones de las mismas e indicadores relacionados con los criterios de evaluación expresados en el punto 2 de esta programación, facilitándonos el control y registro del trabajo por competencias realizado en cada unidad didáctica. Registro inventario de dimensiones e indicadores de competencias con todas las unidades didácticas del área. Unidades didácticas Unidad 15 Unidad 14 Unidad 13 Unidad 12 Unidad 11 Unidad 10 Unidad 9 Unidad 8 Unidad 7 Unidad 6 Unidad 5 Unidad 4 Unidad 3 Unidad 2 de evaluación Unidad 1 Competencias, dimensiones e indicadores Competencia en el conocimiento y la interacción con el mundo físico 1.Comprensión e interpretación de la vida, el mundo físico y sus interacciones. Uso del vocabulario específico Comprensión y uso de las matemáticas en el mundo físico. 42 Búsqueda de alternativas para solucionar situaciones problemáticas relacionadas con nuestro entorno. Utilización de las operaciones matemáticas en situaciones cotidianas fuera del aula. Uso del sistema monetario en situaciones cotidianas. Uso de los números decimales para expresar cantidades que manejamos todos los días Reconocimiento de la utilidad de las fracciones para representar, describir y resolver situaciones cotidianas del mundo físico Establecimiento de relaciones causales en la resolución de problemas relacionados con el medio. Enumeración de objetos cotidianos que correspondan a poliedros. Aplicación de los conceptos y nomenclatura relativos a los elementos geométricos para analizar, describir y comprender el entorno real Representación de espacios familiares y puntos de ellos en ejes de coordenadas. Representación de espacios del entorno aplicando los conceptos matemáticos. Localización de puntos concretos en mapas y croquis de espacios conocidos. Recogida y organización de datos relacionados con aspectos de nuestro entorno. Interpretación de gráficas con datos referentes a nuestro entorno, nuestra Comunidad Autónoma, España. Formulación de hipótesis 2.Implementación de los proyectos científicos y tecnológicos. Definición de objetivos y metas. Distribución de un proceso en fases, tareas y responsables Establecimiento de relaciones causales Comprensión y uso de relaciones espaciales y temporales relacionados con el mundo físico en la resolución de problemas. Búsqueda de alternativas. Planteamiento de estrategias, Trazo de recorridos sobre un plano o mapa. Uso de diagramas, gráficas de barras y de sectores es aspectos relacionados con la geografía de nuestra Comunidad Autónoma y nuestro entorno. 3.Práctica de valores de salud y medio ambiente. Definición de objetivos y metas para una mejor convivencia. Competencia Social y ciudadana 1.Relaciones interpersonales Trabajo en equipo colaborando en las tareas de grupo y aceptando las normas. Colaboración en las tareas de grupo. Cumplimiento de los acuerdos adoptados. 43 Expectativas positivas hacia el trabajo del grupo. Respeto hacia las obras y las opiniones de los demás Aceptación de otros puntos de vista diferentes al propio al utilizar estrategias de resolución de problemas. 2.Trabajo cooperativo Elaboración de normas del aula referentes al cuidado corporal y personal. Identificación y rechazo de cualquier tipo de discriminación por diferencias físicas, sociales, religiosas. Colaboración en las actividades de grupo. Desarrollo de la colaboración con los demás para la recopilación de datos con el fin de resolver situaciones problemáticas. Escucha activa en la exposición y expresión de ideas de los diferentes grupos. 3.Ejercicio de derechos y deberes. Respeto hacia las obras y las opiniones de los demás. Respeto hacia las diferentes estrategias de los otros compañeros. Respeto a los planteamientos distintos de los otros compañeros e igual de válidos para la resolución de problemas 4.Práctica de valores sociales. Utiliza los números como recurso para analizar los elementos y relaciones de la sociedad en la que vivimos. Cumplimiento de los acuerdos adoptados en el grupo clase, prevaleciendo el respeto, aprecio y tolerancia. Desenvolvimiento con autonomía e iniciativa personal en el planteamiento de hipótesis y resolución de problemas Respeto hacia las obras y las opiniones de los demás, manifestando el reconocimiento y la alegría con el éxito de sus compañeros. 5.Conocimiento e interpretación de la realidad social. Recogida de datos de la realidad social , representación gráfica e interpretación de los mismos. Cultural y artística 1.Comprensión artística Uso de la de observación y experimentación Comprensión y uso de relaciones espaciales y temporales. Diseño de un proyecto artístico a partir de cuerpos geométricos. 2.Creación artística. Diseño de un proyecto artístico: maquetas sencillas utilizando la escala y la proporción. Presentación clara y ordenada del trabajo. 3.Conocimiento del patrimonio. Utilización de algunas obras de arte para trabajar contenidos matemáticos.. 44 4.Construcción cultural compartida. Relación de similitud entre los cuerpos geométricos y algunas estructuras artísticas reales. Reconocimiento y valoración de la importancia estética y cultural de los paisajes montañosos, del interior de la península, de las costas. Competencia comunicación lingüística 1.Escuchar y comprender mensajes hablados Escucha activa 2.Hablar para que otros escuchen y comprendan Uso de la terminología geométrica aprendida en el lenguaje habitual. Comprensión y uso de las relaciones espaciales. Descripción precisa de espacios con formas geométricas. Valoración de la terminología geométrica como recurso expresivo Interpretación y explicación de mensajes que contienen números. Transmisión oral de informaciones precisas sobre aspectos cuantificables del entorno con fluidez y claridad. Exposición oral de los pasos seguidos en el proceso de resolución de problemas que requieren más de dos operaciones. 3.Conversar Respeto de las normas de intercambio y turno de palabra Participación y respeto en las conversaciones. Utilización del vocabulario de medida de longitudes, capacidad y peso e situaciones familiares. 4.Leer de forma eficaz (expresiva y comprensiva) Lectura y comprensión de textos Uso de distintas técnicas de recogida de datos. Uso de distintos tipos de textos que utilicen datos numéricos. Adquisición del hábito de consultar el diccionario y aumento de vocabulario. Comprensión de los textos que enuncian los problemas. 5.Escribir correctamente Aumento de la riqueza de vocabulario y empleo riguroso del mismo Corrección ortográfica Descripción verbal y por escrito de la interpretación de datos recogidos en una tabla o gráfica. Redacción de enunciados de problemas a partir de unos datos dados. Competencia matemática 45 1.Representación y medida del espacio Uso de las operaciones con números naturales, decimales y fraccionarios. Aplicación de las operaciones en la resolución de problemas. Revisión y corrección en los cálculos. Uso de operaciones con números decimales. Utilización de números, símbolos y formas de expresión y razonamiento matemático. Representación cualitativa y cuantitativamente de los datos obtenidos en distintos tipos de gráficas. Localización de espacios con formas geométricas. Aplicación en distintos contextos de los conceptos relativos a los distintos tipos de líneas, a sus posiciones relativas y a los ángulos. Localización y trazado de puntos, líneas, traslaciones y simetrías. Medida, comparación y clasificación de ángulos. Localización de espacios con formas geométricas. Clasificación de cuerpos geométricos y conocimiento de sus elementos. Utilización de las nociones geométricas en la descripción de espacios, trayectorias y posiciones en la vida cotidiana. Aplicación en distintos contextos de los conceptos relativos a los distintos tipos de líneas, a sus posiciones relativas y a los ángulos. Uso adecuado de los conceptos espaciales en relación con puntos de referencia, distancias, desplazamientos Localización y trazado de puntos, líneas, traslaciones y simetrías Reconocimiento y uso de los números y utilización de códigos numéricos para identificar objetos, situaciones… Reconocimiento de la utilidad del cálculo mental en el manejo de monedas y billetes de curso legal en situaciones cotidianas. Uso de estrategias de estimación y medida. Aplicación de las operaciones de todo tipo de números para resolver problemas cotidianos. Cálculo mental de operaciones con números naturales. 2.Relaciones entre distintas variables Comparación y orden de números de hasta siete cifras. Interpretar gráficos con datos de aspectos relacionados con nuestro entorno. Medida, comparación y clasificación de ángulos Clasificación de cuerpos geométricos y conocimiento de sus elementos. Medida, comparación y clasificación de ángulos en objetos y espacios reales. Obtención de datos cualitativos y cuantitativos plasmando gráficamente los resultados. Uso de técnicas de registro y de representación gráfica y numérica. Toma de datos sobre situaciones o fenómenos reales y representación gráfica de los mismos. 46 Representación de datos obtenidos en distintos tipos de búsquedas. Formulación y resolución de problemas siguiendo un orden. Desarrollo del gusto por la precisión y el rigor utilizando los instrumentos de medida más apropiados. Uso de la regla graduada, metro, semicírculo graduado, compás, Comparación de la medida de dos o más fenómenos. Establecimiento de relaciones causales. Uso de las operaciones con números de forma lógica para la resolución de problemas. Planteamientos distintos en la resolución de problemas para conseguir el mismo resultado. 3.Incertidumbre y azar Cálculo de la probabilidad de un suceso. Tratamiento de la información y competencia digital 1.Búsqueda, tratamiento y comunicación de la información. Utilización de la calculadora y herramientas tecnológicas para facilitar la comprensión de contenidos matemáticos. Uso de internet como fuente de información. Utilización de lenguajes gráficos para interpretar la información sobre la realidad. Uso de las nuevas tecnologías para diseño gráfico de fotografías del entorno y su similitud con formas geométricas estudiadas. Búsqueda de información en bibliotecas, TIC´s y observación directa de los espacios trabajados en las maquetas, croquis, mapas… Uso del lenguaje gráfico y estadístico para interpretar la información sobre la realidad. Uso de cronómetros y relojes digitales. 2.Comunicación social y en el aprendizaje cooperativo. Respeto de las normas de participación en comunidades virtuales. Conocimiento, aplicación y uso crítico, positivo y responsable de las nuevas tecnologías. Aprender a aprender 1.Conocimiento de las propias capacidades y motivaciones. Identificación y aceptación de sus limitaciones y posibilidades, así como las de sus compañeros, respetándolas. Desarrollo de estrategias que faciliten el cálculo mental. Identificación y manejo de diversas respuestas ante una misma situación, utilizando diversas metodologías o estrategias. 47 Resolución de problemas sencillos partiendo de los datos obtenidos de tablas o gráficos. Valoración de las Matemáticas para resolver situaciones problemáticas en la vida diaria Desarrollo de estrategias que faciliten el trabajo autónomo. 2.Planificación y hábitos de estudio. Descripción del proceso seguido en el aprendizaje de las distintas operaciones matemáticas, corrigiendo posibles errores. Comprensión, análisis y resolución de problema potenciando estrategias. Organización de tareas para el cuidado de los recursos tecnológicos comunes (Aula Althia, pizarra digital…) Búsqueda de alternativas. Reconocimiento de la utilidad de las representaciones gráficas para fijar y aclarar conceptos relacionados con nuestra vida cotidiana. Reconocimiento de la manipulación, construcción y representación como métodos de investigación y descubrimiento en geometría Utilización de fuentes bibliográficas y elaboración de informes con planes de mejora. Selección de datos y toma de decisión sobre la estrategia más adecuada para la resolución. 3.Estrategias de aprendizaje y autorregulación. Manipulación, construcción y representación como métodos de investigación y descubrimiento en geometría Capacidad de autoevaluarse y coevaluar. Comprobación de los resultados y corrección de errores como enriquecimiento del aprendizaje. Definición de objetivos y metas para conseguir resultados lógicos Interés por el aprendizaje de las Matemáticas. Autocontrol de la atención y perseverancia en la tarea Autoevaluación del uso del lenguaje matemático. Corrección de errores como recurso de aprendizaje Selección de datos y toma de decisión sobre la estrategia más adecuada para la resolución. Autonomía e iniciativa personal 1.Conocimiento y confianza en uno mismo Confianza para enfrentarse al cálculo mental con éxito. Responsabilidad en las tareas. Valoración realista de los resultados desde el esfuerzo realizado. Valoración realista de los resultados obtenidos. 2.Innovación y creatividad Desarrollo de estrategias propias en la resolución de cálculos y problemas. 48 Interés por descubrir diferentes formas de construcción y representación de los elementos y figuras geométricas. Desarrollo de la capacidad de reflexión y lógica en la resolución de problemas cotidianos. Iniciativa para buscar información, leer… Competencia emocional 1.Conocimiento y control de las propias emociones Desarrollo de la interiorización y autocontrol de si mismo. Reconocimiento verbal de los errores. Defensa argumentada en el uso de un planteamiento matemático. Reconocimiento de los errores cometidos y corrección de los mismos Identificación de las motivaciones que dan lugar a ciertas actuaciones, corrigiendo las negativas y reforzando las positivas. 2.Empatía en las relaciones interpersonales. Actuación flexible y dialogante en temas de situaciones problemáticas. Relaciones positivas y colaboración con sus compañeros en la búsqueda de soluciones a problemas planteados. Leyenda de colores: Competencias específicas Competencias instrumentales Competencias transversales Además de esta ficha, es necesaria otra hoja de registro de alumnos en donde se registrará la evaluación de cada niño en relación a los indicadores de cada una de las competencias básicas trabajada. Superados los mínimos que quedaron reflejados en la tabla del punto 2, el alumno supera los criterios de evaluación y por consiguiente, consigue el objetivo programado. A continuación está el modelo de esta hoja, en la que faltaría expresar los indicadores de las competencias. Se debe intentar evaluar todos los indicadores que aparecen en todos los criterios de evaluación teniendo en cuenta que no todos tienen la misma importancia. 49 Competencia en el conocimiento y la interacción con el mundo físico Competencia Social y ciudadana Cultural y artística Competencia Comunicación Lingüística Competencia matemática Tratamiento de la competencia digital información y Aprender a aprender Autonomía e iniciativa personal Competencia emocional CALIFICACIÓN La autoevaluación y la coevaluación tienen gran importancia en el proceso de evaluación de las competencias. Con la autoevaluación es el propio alumno el que determina en qué medida el trabajo que está realizando está bien o mal. En la coevaluación, los alumnos evalúan el trabajo de sus compañeros de grupo. Ambas evaluaciones deben seguir las instrucciones del profesor. La autoevaluación y la coevaluación ayudan al alumno a: interiorizar los criterios de evaluación consiguiendo adaptar las respuestas a lo que el maestro espera, desarrollar el hábito de la reflexión y concienciarse de los propios errores, esforzarse más motivados por quedar bien ante los compañeros, desarrollar y aceptar una crítica constructiva CRITERIOS DE PROMOCIÓN Se valorará un 40% los objetivos conseguidos, con un 75 % de indicadores mínimos señalados. Datos que podremos recoger a partir de las hojas de registros expuestas anteriormente y por las pruebas escritas de control que se realizarán. 50 Alumno 24 Alumno 23 Alumno 22 Alumno 21 Alumno 20 Alumno 19 Alumno 18 Alumno 17 Alumno 16 Alumno 15 Alumno 14 Alumno 13 Alumno 12 Alumno 11 Alumno 10 Alumno 9 Alumno 8 Alumno 7 Alumno 6 Alumno 4 Alumno 5 Alumno 3 Competencias e indicadores Alumno 2 Alumno 1 Alumnos Un 40 % el trabajo diario, participación, presentación… Un 20% la conducta, el comportamiento y su predisposición en la resolución de conflictos en el espacio de trabajo (aula, Althia, concursos…) 51 Presentamos unos ejemplos de fichas de autoevaluación y coevaluación para realizar con nuestros alumnos. FICHA DE AUTOEVALUACIÓN Nombre y apellidos:…………………………………………………….. Curso……………………Área…………………………………………… INDICADORES SIEMPRE A VECES CASI NUNCA NUNCA Tengo interés al realizar mis tareas Sigo un plan de trabajo para realizar mis tareas. Realizo mis tareas con anticipación y las repaso. Presento mis tareas a tiempo Me esfuerzo por superar mis errores. Me ofrezco voluntariamente en clase para realizar actividades. Participo activamente en clase. Organizo y dirijo el equipo de trabajo Me preocupo por superar mis calificaciones Soy puntual para la entrada a clase Consulto frecuentemente mis dudas al profesor Reviso y estudio el tema todos los días. Cumplo las normas del aula. 52 FICHA DE COEVALUACIÓN (Conducta y convivencia) Nombre del evaluador/a………………………………………………… INDICADORES INTEGRANTES DEL GRUPO Compañero 1 Compañero 2 Compañero 3 Compañero 4 Compañero 5 Respeta la opinión de sus compañeros Comparte sus materiales escolares Cumple con las normas de aula. Ayuda a sus compañeros cuando se lo piden. Respeta a los profesores y compañeros Cuida el material común de clase. Fomenta la integración del grupo Identifica sus logros personales y grupales Utiliza el diálogo para solucionar conflictos. Acepta a todos los compañeros por igual. Tiene reacciones agresivas 53 FICHA DE COEVALUACIÓN (Trabajo en equipo) Nombre del evaluador/a………………………………………………… INDICADORES INTEGRANTES DEL GRUPO Compañero 1 Compañero 2 Compañero 3 Compañero 4 Compañero 5 Participa activamente sugiriendo ideas. Comparte sus materiales escolares Demuestra responsabilidad. Ayuda a sus compañeros cuando se lo piden. Respeta la opinión de los otros compañeros Se comunica de forma clara, concisa y cordial. Fomenta la integración del grupo Identifica los logros como trabajo común de grupo Usa el diálogo en los conflictos que se presentan Acepta a todos los compañeros por igual. 54 FICHA DE COEVALUACIÓN EXPOSICIÓN ORAL DE UN TRABAJO Nombre del evaluador/a……………………………………Curso……………….. Evalúa la exposición de tus compañeros de 1 a 5 atendiendo a los siguientes criterios NOMBRES CRITERIOS Comenzó la exposición con una introducción. No se desvió del tema durante la exposición. La exposición fue clara y precisa El contenido de la exposición fue interesante El grupo estuvo atento durante la exposición. Se dirigía a la audiencia mientras exponía. Respetó el tiempo de exposición Usó apoyos visuales: láminas, fotos… Su tono de voz fue claro La exposición fue fluida La exposición motivó para hacer preguntas. total 55 FICHA DE COEVALUACIÓN EXPOSICIÓN DE UN TRABAJO PRÁCTICO (Construcción con elementos geométricos) Nombre del evaluador/a……………………………………Curso……………….. Evalúa la exposición de tus compañeros de 1 a 5 atendiendo a los siguientes criterios NOMBRES CRITERIOS Comienza la exposición con una introducción. Presenta y describe los elementos necesarios. Utiliza un lenguaje claro y preciso en su explicación Presenta un esquema gráfico de la construcción Explica el montaje para la construcción. La explicación resulta atractiva e interesante. La construcción tiene todos los cuerpos geométricos estudiados. En la explicación requiere a otros compañeros para que prueben el funcionamiento Ha motivado a los oyentes a preguntar. total 56 6. INDICADORES, CRITERIOS, PROCEDIMIENTOS, TEMPORALIZACIÓN Y RESPONSABLES DE LA EVALUACIÓN DEL PROCESO DE ENSEÑANZA Y APRENDIZAJE. La evaluación sirve para recopilar información periódicamente el proceso de enseñanza-aprendizaje. que nos permitirá mejorar 57 58 7.ANEXO I JUEGOS MATEMÁTICOS 59 JUEGOS MATEMÁTICOS 60 http://www.juntadeandalucia.es/averroes/iesarroyo/matematicas/taller/juegos/cubosoma/cubosoma.htm 61 62 63 64 http://www.juntadeandalucia.es/averroes/iesarroyo/matematicas/tall er/juegos/tangram/tangram.htm 65 66 67