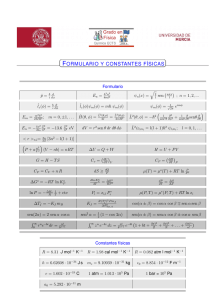
2 knn Π

n −1
Π sin(
k =1
kπ
n
) = n −1
n
2
證明：考慮圓內接正 n 邊形，圓心為 (0, 0) ，且頂點分別為 z1 , z2 ,..., zn
即可視為考慮 x n = 1 之 n 個根；
不失一般性，令 z1 = 1 ，則
f ( x) = x n − 1 = ( x − 1)( x n −1 + x n − 2 + ... + 1)
( x − z2 )( x − z3 )...( x − zn ) = x n −1 + x n − 2 + ... + 1
且
則 z1 z2 × z1 z3 × ... × z1 zn =| z1 − z2 | × | z1 − z3 | ×...× | z1 − zn |
=|1 − z2 | × |1 − z3 | ×...× |1 − zn |
=| (1 − z2 ) × (1 − z3 ) × ... × (1 − zn ) |
=|1n −1 + 1n − 2 + ... + 1|
=n
2(k − 1)π
又 z1 zk = 2 − 2 cos
=2
n
n −1
1
n −1
Π sin(
則得
Sol： sin
2(k − 1)π
(k − 1)π
n
= 2 sin
2
n
n = z1 z2 × z1 z3 × ... × z1 zn = 2n −1 Π sin(
故
例：求 sin
1 − cos
k =1
π
13
π
13
× sin
× sin
kπ
n
) = n −1
n
2
2π
6π
× ... × sin
=?
13
13
2π
12π 13
× ... × sin
=
13
13 212
2π
6π
13
13
× ... × sin
= 12 = 6
13
13
13
2
2
o
o
o
o
例：求 sin1 sin 3 sin 5 ...sin 89 = ?
則 sin
π
kπ
)
n
× sin
179
kπ
180 90
Sol： sin1o sin 2o sin 3o...sin179o = Π sin(
) = 179 = 178
k =1
180
2
2
90
90
= 89
178
2
2
89
kπ
90 45
又 sin 2o sin 4o sin 6o...sin178o = Π sin( ) = 89 = 88
k =1
90
2
2
則 sin1o sin 2o sin 3o...sin 89o =
則 sin 2o sin 4o sin 6o...sin 88o =
故 sin1o sin 3o sin 5o...sin 89o =
45
45
= 44
88
2
2
sin1o sin 2o sin 3o...sin 89o
2
= 45
o
o
o
o
sin 2 sin 4 sin 6 ...sin 88
2
【淵智】