Clase ejes y rodamientos

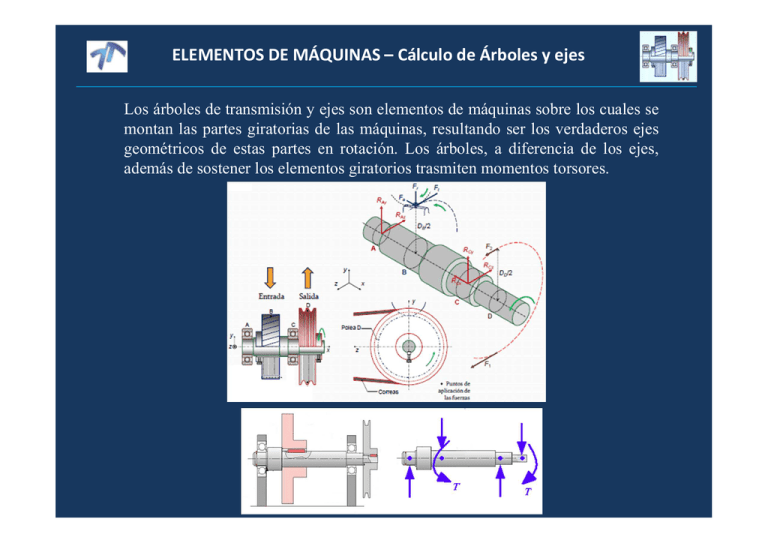
ELEMENTOS DE MÁQUINAS – Cálculo de Árboles y ejes
Los árboles de transmisión y ejes son elementos de máquinas sobre los cuales se
montan las partes giratorias de las máquinas, resultando ser los verdaderos ejes
geométricos de estas partes en rotación. Los árboles, a diferencia de los ejes,
además de sostener los elementos giratorios trasmiten momentos torsores.
ELEMENTOS DE MÁQUINAS – Cálculo de Árboles y ejes
Las cargas son principalmente de torsión debido al par de torsión transmitido o
de flexión proveniente de cargas transversales por engranes, poleas, etc. Estas
cargas suelen ocurrir combinadas, ya que, por ejemplo, el par de torsión
transmitido puede estar asociado con fuerzas en los dientes de engranes. El
carácter de las cargas por par de torsión y de las de flexión puede ser uniforme
(constante) o variar con el tiempo.
Todo eje sometido a flexión y torsión que además se encuentre rotando estará
expuesto a fallas por fatiga.
También pueden estar presentes cargas axiales si el eje de la flecha es vertical o
si incluye engranes helicoidales o tornillos sinfín, con una componente de fuerza
axial, con lo cual también podrían estar sujetos a pandeo e inestabilidades.
ELEMENTOS DE MÁQUINAS – Cálculo de Árboles y ejes
Aunque a veces es posible diseñar flechas de transmisión que en toda su longitud no tenga
modificaciones en el diámetro de la sección, lo mas común es que tengan una diversidad de escalones o
resaltos u hombros donde cambia el diámetro, a fin de adaptarse a elementos sujetos como cojinetes,
ruedas dentadas, engranes, etc. Los escalones o los hombros son necesarios para conseguir una
ubicación axial, precisa y consistente de los elementos sujetos, así como para obtener el diámetro
correcto, adecuado a piezas estándar como los cojinetes.
Se suele recurrir a cuñas, chavetas circulares o espigas atravesada para asegurar elementos que deban ir
sujetos a la flecha, con el fin de transmitir el par de torsión requerido o para fijar la pieza axialmente.
Las cuñas requieren una ranura tanto en la flecha como en la pieza, y pudieran necesitar un tornillo prisionero
para impedir cualquier movimiento axial. Las chavetas circulares ranura las flechas, y las espigas
transversales generan perforaciones en estas. Cada uno de estos cambios de contorno contribuirá ciertas
concentraciones de esfuerzos.
ELEMENTOS DE MÁQUINAS – Cálculo de Árboles y ejes
ELEMENTOS DE MÁQUINAS – Cálculo de Árboles y ejes
ELEMENTOS DE MÁQUINAS – Cálculo de Árboles y ejes
ELEMENTOS DE MÁQUINAS – Cálculo de Árboles y ejes
ELEMENTOS DE MÁQUINAS – Cálculo de Árboles y ejes
Existen diversos criterios de falla para estimar las dimensiones de ejes sometidos a torsión y flexión. Estos
provienen de distintos supuestos. Se debe considerar el criterio cuyos supuestos más se adecúen a las
condiciones de utilización de la pieza a considerar
ELEMENTOS DE MÁQUINAS – Cálculo de Árboles y ejes
ELEMENTOS DE MÁQUINAS – Cálculo de Árboles y ejes
Se debe tener cuidado al aplicar esta ecuación solo en situaciones en las que las
cargas son como se suponer deben ser, es decir, un par de torsión constante y un
momento totalmente alternante. Si en algún caso dado cualquiera de los
componentes de la carga que se suponen iguales a cero son distintos de cero, el
estándar ASME da resultados que no son conservadores.
ELEMENTOS DE MÁQUINAS – Cálculo de Árboles y ejes
Procedimiento de verificación del árbol en TP
1. Desarrollar un diagrama de cuerpo libre, calcular reacciones en apoyos
2. Evaluar los momentos flectores, torsores, esfuerzos axiales en el tramo
completo del eje (trazado de diagramas de momentos flectores y torsores)
3. Seleccionar las secciones más conflictivas y de ellas los puntos más
conflictivos (por lo menos 2)
4. Evaluar los estados tensionales en los puntos conflictivos.
5. Evaluar seguridad de puntos conflictivos (verificar diámetros con ASME)
6. Efectuar un replanteo en términos de diámetro y configuraciones
geométricas o material en tanto que los resultados obtenidos no satisfagan
las condiciones de diseño.
ELEMENTOS DE MÁQUINAS – Cálculo de Rodamientos
Los rodamientos son elementos mecánicos que aseguran un enlace móvil
entre dos elementos de un mecanismo, uno que se encuentra en rotación
con respecto a otro; siendo su función principal el de permitir la rotación
relativa de dichos elementos bajo carga, con precisión y con un
rozamiento mínimo.
En el proceso general de diseño de los rodamientos, deben considerarse
una gran cantidad de factores, tales como rozamiento, transferencia de
calor, fatiga de los materiales, resistencia a la corrosión, propiedades de
los materiales, forma y tipo de lubricación, tolerancia, velocidades de
funcionamiento, tipos de montaje, uso y costo.
ELEMENTOS DE MÁQUINAS – Cálculo de Rodamientos
Los rodamientos se clasifican de acuerdo a:
I.
A la forma como soportan la carga en:
Radiales, Axiales y Combinación de los
anteriores.
II.
A los elementos de rodadura que poseen
en: De bolas, de rodillos
ELEMENTOS DE MÁQUINAS – Cálculo de Rodamientos
ELEMENTOS DE MÁQUINAS – Cálculo de Rodamientos
ELEMENTOS DE MÁQUINAS – Cálculo de Rodamientos
¿Porque fallan los rodamientos?
- Fatiga
- Contaminación
-
Manejo incorrecto
-
Lubricación deficiente
Las superficies de las pistas y los elementos rodantes están constantemente sometidos a
esfuerzos compresivos repetitivos que causan descascarillado de las superficies en
cuestión. Este descascarillado es producto de la fatiga del metal y causa la falla del
rodamiento. La vida efectiva o útil de los rodamientos, se define usualmente en términos del
número total de revoluciones, que un rodamiento puede ejecutar antes de que se presente
el descascarillado de las pistas o de los elementos rodantes.
Debido a la complejidad de su diseño ya que poseen un alto grado de normalización, el
verdadero problema que se presenta en los rodamientos es su selección; para lo cual no
deben establecerse reglas rígidas, pues deben considerarse y ponderarse una gran variedad
de factores dados por los fabricantes y que varían para cada tipo de rodamiento.
ELEMENTOS DE MÁQUINAS – Cálculo de Rodamientos
SELECCIÓN TIPO DE RODAMIENTO
Para la aplicación determinada de rodamientos, entre los factores de
mayor importancia que deben contrastarse entre sí para decidir acerca del
tipo, más adecuado, podrían incluirse los siguientes:
•
•
•
•
•
•
•
•
•
Espacio disponible
Magnitud de la carga
Dirección de la carga
Capacidad de soportar momentos flectores
Capacidad de absorber desalineaciones angulares
Limites de velocidad
Precisión
Rigidez
Montaje y desmontaje
ELEMENTOS DE MÁQUINAS – Cálculo de Rodamientos
SELECCIÓN TAMAÑO DE RODAMIENTO
Para ello se emplearán como criterios fundamentales la capacidad de
carga estática y Capacidad de carga dinámica.
Criterio de deformación: la selección de rodamientos según el
criterio de capacidad de carga estática se realiza cuando la frecuencia
de rotación de este es menor de 10 rpm (velocidad de rotación muy
lenta).
Criterio de vida útil: en caso contrario se emplea el criterio de
capacidad de carga dinámica, si el rodamiento permanece en las
paradas y arranques bajo el efecto de la carga debe realizarse
adicionalmente la comprobación a capacidad de carga estática.
ELEMENTOS DE MÁQUINAS – Cálculo de Rodamientos
Datos del fabricante:
ELEMENTOS DE MÁQUINAS – Cálculo de Rodamientos
El cálculo de la vida útil es dependiente del rodamiento en particular,
esto lo convierte en un cálculo iterativo en el cual se escoge un
rodamiento y se comprueba su vida útil, si el resultado es satisfactorio,
la selección ha terminado, pero si la vida es menor o muy mayor de lo
recomendado debe escogerse otro rodamiento y recalcular la vida.
ESTADO DE CARGA
Una vez definido el estado de carga sobre cada uno de los apoyos, si la
misma es constante en magnitud y dirección-sentido, se define una Carga
Dinámica Equivalente P, la cual expresa una carga imaginaria constante en
magnitud y dirección-sentido, que actuando sobre un rodamiento tiene el
mismo efecto que las cargas reales a las cuales está sometido dicho
rodamiento.
ELEMENTOS DE MÁQUINAS – Cálculo de Rodamientos
Para el caso de una carga constante F en dirección radial (Fr) sobre el
rodamiento radial o axial (Fa) sobre el rodamiento axial respectivamente, se
tiene que:
P=F
Los rodamientos radiales comúnmente están sometidos a cargas que poseen
componentes en las direcciones radial y axial, donde si la magnitud y la dirección
de la carga resultante son constantes, la carga dinámica equivalente se determina a
partir de la expresión:
P = XFr + YFa
Donde:
P: carga dinámica equivalente
X, Y: factores de carga radial y carga axial, respectivamente.
Fr, Fa: cargas radial y axial reales, respectivamente.
ELEMENTOS DE MÁQUINAS – Cálculo de Rodamientos
P = XFr + YFa
En el caso de rodamientos radiales de una hilera de elementos rodantes, la
carga axial no se considera para los cálculos de P si su magnitud no llega a
cumplir que la relación entre ella y la carga radial (Fa/Fr), es menor que
un e especificado por los fabricantes de rodamientos.
Fa
≤e
Fr
En este caso :
X=1 Y=0
Los factores X e Y pueden obtenerse de la Tabla para
la cual se necesita conocer la capacidad de carga
básica estática (Co), la cual viene tabulada en los
catálogos
ELEMENTOS DE MÁQUINAS – Cálculo de Rodamientos
ELEMENTOS DE MÁQUINAS – Cálculo de Rodamientos
Un grupo de rodamientos aparentemente idénticos, sometidos a cargas y
condiciones de operación idénticas, tendrán un amplio rango de durabilidad. Esta
diferencia en la "vida" puede ser explicada por la diferencia en la resistencia a la
fatiga del material de los rodamientos propiamente.
La vida nominal básica se basa en un modelo estadístico al 90%, que se
expresa como el número total de revoluciones que el 90% de los rodamientos de
un grupo idéntico, sometidos a iguales condiciones de operación, alcanzará o
sobrepasará antes de que ocurra el descascarillado por fatiga del metal.
La capacidad básica de carga dinámica muestra la capacidad de un rodamiento
de asimilar carga dinámica. Dicha capacidad expresa la carga constante que un
rodamiento puede soportar por un periodo de 1 millón de revoluciones. La misma
se expresa como carga radial pura para los rodamientos radiales y carga axial
pura para los rodamientos axiales. Las capacidades básicas de carga están
dadas en las tablas de rodamientos de los catálogos.
ELEMENTOS DE MÁQUINAS – Cálculo de Rodamientos
La fórmula de la ISO de la duración o vida nominal. En millones de revoluciones se expresa como:
P
C  C 
1/ p
L10 =   ó  = L10
P P
Donde:
L10 = duración nominal en millones de revoluciones
(C/P) = seguridad de carga requerida para la aplicación.
P = Exponente de la formula de vida nominal
(p = 3, para rodamientos de bolas; p = 10/3, para rodamientos de rodillos)
En muchas oportunidades es conveniente expresar la duración nominal en horas de funcionamiento o
de servicio. Calculándose de la expresión,
10 6  C 
Lh =
 
60n  P 
Donde:
Lh = duración nominal en horas de servicio
n = Velocidad de giro (en min.-1)
P
ELEMENTOS DE MÁQUINAS – Cálculo de Rodamientos
Valores prácticos de duración nominal Lh para diferentes tipos de máquinas
CLASE DE MAQUINA
Lh
Electrodomésticos, maquinas agrícolas, instrumentos y aparatos para uso
medico.
300 - 3000
Maquinas usadas intermitentemente o por cortos periodos, como: maquinas
herramientas portátiles, aparatos elevadores para talleres y maquinas de
construcción.
3000 - 8000
Maquinas para trabajar con alta fiabilidad de funcionamiento por cortos
periodos o intermitentes tales como: ascensores y grúas para mercancías
elevadas.
8000 - 12000
Maquinas para 8 horas de trabajo diario no totalmente utilizadas:
transmisiones por engranes y machacadoras giratorias.
10000 - 25000
Maquinas para 8 horas de trabajo diario totalmente utilizadas, como:
maquinas herramientas, maquinas para trabajar madera, maquinas para
la industria mecánica general, grúas para materiales a granel,
ventiladores, cintas transportadoras, equipos de imprenta, separadores y
centrifugas.
20000 - 30000
ELEMENTOS DE MÁQUINAS – Cálculo de Rodamientos
En los casos donde la capacidad de carga del rodamiento no se determina a partir de la fatiga
del material, sino por la deformación permanente que se origina en los puntos de contacto
entre los elementos rodantes y sus caminos de rodadura, se utiliza lo que se denomina Carga
Estática Equivalente, que se define como la carga (radial para rodamientos radiales y axial
para rodamientos axiales) que si se aplicase a un rodamiento produciría la misma
deformación permanente en aquél que la cargas reales.
Las cargas que poseen componentes radial y axial, deben convertirse en una carga estática
equivalente a partir de:
P0 = X 0 Fr + Y0 Fa
Donde:
Po: carga estática equivalente i
Xo, Yo: factores de carga radial y axial, respectivamente
Fr, Fa : cargas reales radial y axial, respectivamente
ELEMENTOS DE MÁQUINAS – Cálculo de Rodamientos
La carga básica estática Co expresa la carga estática a la que corresponde unos valores de esfuerzos
definidos por los fabricantes para sus diferentes rodamientos y que calculados en un punto específico,
son capaces de producir una deformación permanente total del aro y del elemento rodante del 0.0001
del valor del diámetro del elemento de rodadura.
La carga estática equivalente admisible
se determina tomando en consideración
el factor de seguridad So que se puede
obtener de la Tabla y la ecuación:
ELEMENTOS DE MÁQUINAS – Cálculo de Rodamientos
Designación ISO
ELEMENTOS DE MÁQUINAS – Cálculo de Rodamientos
EJEMPLOS TÍPICOS DE DESIGNACIÓN DE RODAMIENTOS:
ELEMENTOS DE MÁQUINAS – Cálculo de Rodamientos