UNIDAD 2 - PROBLEMA 11

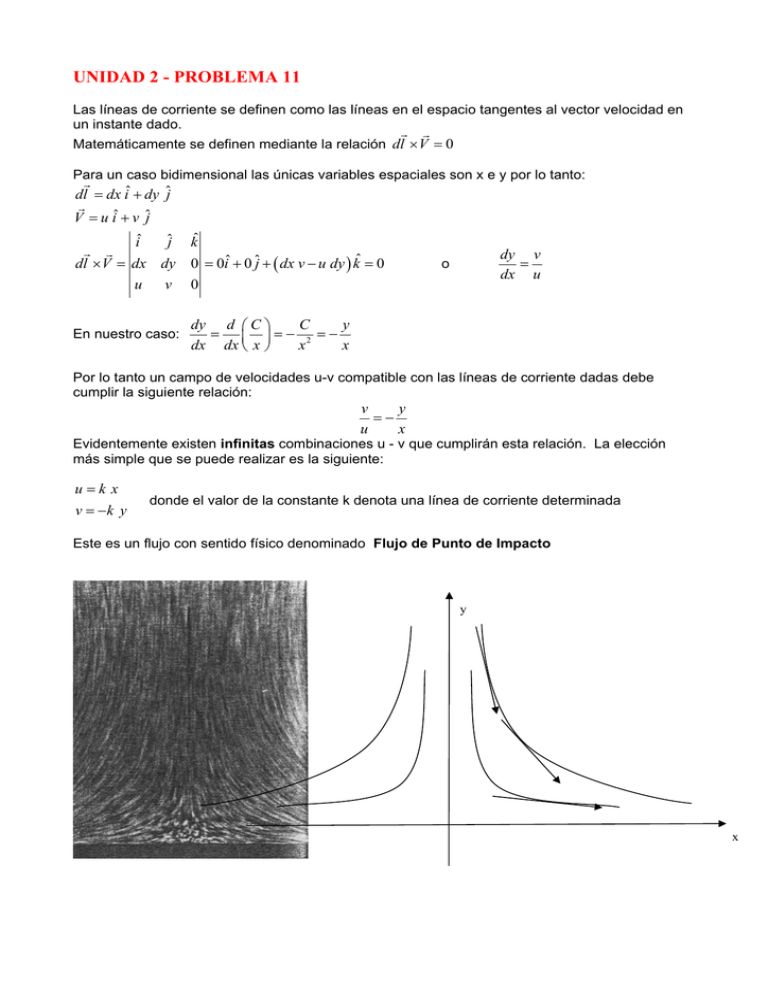
UNIDAD 2 - PROBLEMA 11
Las líneas de corriente se definen como las líneas en el espacio tangentes al vector velocidad en
un instante dado.
G G
Matemáticamente se definen mediante la relación dl × V = 0
Para un caso bidimensional las únicas variables espaciales son x e y por lo tanto:
G
dl = dx iˆ + dy ˆj
G
V = u iˆ + v ˆj
ˆj kˆ
iˆ
G G
dl × V = dx dy 0 = 0iˆ + 0 ˆj + ( dx v − u dy ) kˆ = 0
u v 0
En nuestro caso:
dy v
=
dx u
o
dy d ⎛ C ⎞
C
y
= ⎜ ⎟=− 2 =−
dx dx ⎝ x ⎠
x
x
Por lo tanto un campo de velocidades u-v compatible con las líneas de corriente dadas debe
cumplir la siguiente relación:
v
y
=−
u
x
Evidentemente existen infinitas combinaciones u - v que cumplirán esta relación. La elección
más simple que se puede realizar es la siguiente:
u=k x
v = −k y
donde el valor de la constante k denota una línea de corriente determinada
Este es un flujo con sentido físico denominado Flujo de Punto de Impacto
y
x
UNIDAD 2 - PROBLEMA 12
En coordenadas cilíndricas:
G
dl = dr eˆr + r dθ eˆθ
G
V = Vr eˆr + Vθ eˆθ
eˆr
G G
dl × V = dr
eˆθ
r dθ
Vr
Vθ
eˆx
0 = ( dr Vθ − r dθ Vr ) eˆx = 0
0
o
dr
V
= r
r dθ Vθ
En nuestro caso:
dr
a
=− =k
r dθ
b
dr
= k dθ
r
ln r = k θ + cte
r = K e kθ
r=Ke
a
− θ
b
Las líneas de corriente son espirales logarítmicas desde la periferia hacia el centro
Este es otro flujo con sentido físico empleado como el modelo más elemental de flujo en el plano
horizontal generado por un tornado.
UNIDAD 2 - PROBLEMA 13
UNIDAD 2 PROBLEMA 14
UNIDAD 2 - PROBLEMA 15
El caudal másico neto a través de un área A está dado por el flujo asociado a la velocidad
normal a través de la superficie. Matemáticamente por la siguiente definición:
G
Qm = ∫ ρ Vn dA ≡ ∫ ρ V • nˆ dA
A
A
En nuestro caso se asume que además el flujo posee propiedades uniformes en toda el área de
salida de manera que:
Qm = ( ρ Vn A )e = ρ e Ve sen α Ae = 1.2435 kg / s
Vn
α = 30o
V
UNIDAD 2 - PROBLEMAS 16 y 17
El caudal volumétrico a través de un área circular y con un perfil de velocidades con simetría axial
está dado por:
R
Q = ∫ Vn dA = ∫ u (r ) 2π r dr
A
0
Además la definición de velocidad media está dada por: Q = V A = V π R 2
Para flujo laminar:
⎧
⎛
r2 ⎞ ⎫
=
−
1
m
R
⎪
⎜
2 0
2 ⎟ ⎪
⎛
r2 ⎞
⎪
⎝ R ⎠ ⎪⎬ = −2π U R m dm
Q = 2π ∫ U 0 ⎜1 − 2 ⎟ r dr = ⎨
0
2 ∫1
⎝ R ⎠
2
0
⎪
⎪
⎪⎩dm = − R 2 r dr ⎪⎭
R2 ⎛
1⎞ 1
2
= −2π U 0
⎜ 0 − ⎟ = π U0R
2 ⎝
2⎠ 2
1
V
= 0.5
Q = π U0 R2 = V π R2
De dónde:
U0
2
Para flujo turbulento:
1/ 7
r⎞
⎛
Q = 2π ∫ U 0 ⎜ 1 − ⎟
⎝ R⎠
0
R
r ⎫
⎧
=
x
1
⎪⎪
R ⎪⎪ = 2π R 2 U x 7 1 − x dx
r dr = ⎨
⎬
0 ∫
0
⎪dx = dr ⎪
⎪⎩
⎪
R⎭
La integral se resuelve mediante integración por partes, con el siguiente cambio de variables, para
el caso general de un factor n, con n = 7 en nuestro caso:
1
∫ x (1 − x )
1/ n
0
u=x
du = dx
⎧
⎫
1
1
⎪
⎪
dx = ⎨
n
1/ n
( n +1) / n ⎬ = [ u v ]0 − ∫ v du
0
⎪⎩ dv = (1 − x ) dx v = − n + 1 (1 − x )
⎪⎭
1
n
( n +1) / n ⎤
( n +1) / n
⎡ n
= ⎢−
+
x (1 − x )
dx
(1 − x )
∫
⎥
⎣ n +1
⎦ ^0 n + 1 0
1
1
⎛
⎞
1
n ⎜
(2 n +1) / n ⎟
= 0+
(1 − x )
⎜−
⎟
n + 1 ⎜ 2n + 1
⎜
⎟⎟
n
⎝
⎠0
=+
n2
( n + 1)( 2n + 1)
Por lo tanto:
Q = 2π R 2 U 0
n2
( n + 1)( 2n + 1)
n2
Q = 2π R U 0
= π R2 V
( n + 1)( 2n + 1)
2
de donde:
En nuestro caso n = 7 es representativo del flujo turbulento:
V
2n 2
=
U 0 ( n + 1)( 2n + 1)
V
= 0.817
U0