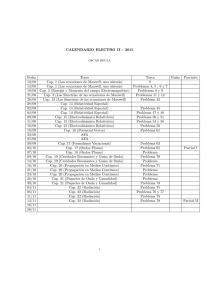
Leyes de los l´ımites Si c es una constante y existen los lımites lim f

Leyes de los lı́mites
Si c es una constante y existen los lı́mites
lim f (x) y
x→a
lim g(x)
x→a
entonces se cumplen las siguientes propiedades:
1. lim [f (x) + g(x)] = lim f (x) + lim g(x)
x→a
x→a
x→a
2. lim [f (x) − g(x)] = lim f (x) − lim g(x)
x→a
x→a
x→a
3. lim [cf (x)] = c lim f (x)
x→a
x→a
4. lim [f (x)g(x)] = lim f (x) lim g(x)
x→a
x→a
lim f (x)
f (x)
= x→a
x→a g(x)
lim g(x)
5. lim
x→a
si
lim g(x) 6= 0
x→a
x→a
h
in
6. lim [f (x)]n = lim f (x)
x→a
x→a
7. lim c = c
x→a
8. lim x = a
x→a
9. lim xn = an donde n es un entero positivo
x→a
10. lim
x→a
√
n
x=
√
n
a donde n es un entero positivo
(si n es par, la expresión es válida cuando a > 0)
11. lim
x→a
p
n
f (x) =
q
n
lim f (x) donde n es un entero positivo
x→a
(si n es par, la expresión es válida cuando lim f (x) > 0)
x→a
12. Si f es contı́nua en b y lim g(x) = b, entonces lim f (g(x)) = f (b) = f
x→a
x→a
lim g(x)
x→a