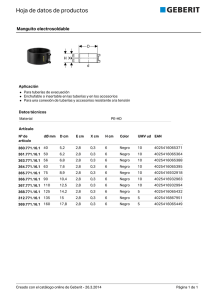
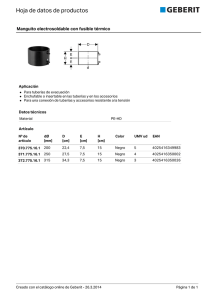
capitulo ii

CAPITULO II
MARCO TEÓRICO
1.
Antecedentes de la Investigación.
Alarcón (2002), en su investigación titulada “Modelo Simplificado del
Proceso de Gas lift para la Optimización de la Producción de Crudo Mediante
Algoritmos Genéticos y Lógica Difusa” tuvo como propósito la optimización
de un sistema simplificado de manejo de gas empleando para ello algoritmos
genéticos con representaciones cromosómicas bajo lógica difusa con el fin
de poder modelar el comportamiento dinámico de un proceso dentro de un
sistema evolutivo, como lo es el algoritmo genético. La investigación fue de
tipo descriptiva y de campo, de diseño no experimental, apoyándose en la
observación como instrumento y utilizando 7 pasos para el diseño; Primero,
identificación de problemas y objetivos en el proceso de manejo de gas para
inyección a los pozos; segundo, se determinación el tipo de información
necesaria para definir y analizar los requerimientos necesarios; tercero,
análisis de las necesidades del sistema; cuarto, diseño del modelo
recomendado; quinto, desarrollo del programa; sexto, simulación del modelo;
séptimo, comparación con otros métodos. Los resultados de esta
13
14
investigación permitieron demostrar la factibilidad de usar lógica difusa como
mecanismo de codificación de los elementos (cromosomas) de una población
resultando en un optimizador híbrido del tipo evolutivo-difuso. Con el empleo
de esta técnica se logro optimizar el proceso de distribución de gas
maximizando la producción de crudo y se demostró a través de simulaciones
y comparaciones con los métodos actualmente utilizados como el
optimizador híbrido no es solo más efectivo en términos de maximización
económica sino también en tiempo computacional.
El aporte de esta investigación, se basa en la semejanza que existe entre
ambos trabajos en cuanto al tipo y diseño de la investigación, ya que resultó
ser descriptiva, de campo y no experimental para ambos. Por otra parte se
puede observar que en el desarrollo de la investigación fue utilizada la lógica
difusa junto a los algoritmos genéticos como optimizador hibrido para mejorar
la inyección de gas a nivel de pozos, de igual forma se utiliza la lógica difusa
en el presente trabajo pero aplicada a mejorar la distribución de gas de alta
presión a nivel de redes de tuberías frente a escenarios operacionales
presentados.
García (2003), en su investigación “Estrategia de Control Inteligente para
la Optimización de la Inyección
automatización
integral
de gas en pozos productores con
subsuelo-superficie”
tuvo
como
propósito
la
optimización de la inyección de gas empleando lógica difusa con el fin de
modelar el comportamiento dinámico del proceso. La investigación fue del
tipo prospectiva y explicativa, de diseño no experimental, apoyándose en las
15
observaciones
como instrumento y utilizando cuatro pasos para su
desarrollo; primero recolección de la información; segundo, determinación de
los requerimientos; tercero, análisis de los sistemas de inteligencia artificial;
cuarto, desarrollo del sistema. Los resultados de esta investigación
permitieron demostrar la factibilidad de usar la lógica difusa como mecanismo
de solución del problema. Con el empleo de esta técnica se logró optimizar el
proceso de inyección de gas, maximizando la producción de crudo y se
demostró a través de simulaciones y comparaciones, que no solo es más
efectivo en términos de maximización económica, sino también en tiempo
computacional.
El aporte de esta investigación se basa fundamentalmente en la
aplicación de la lógica difusa para optimizar el proceso de inyección de gas
en pozos productores maximizando la producción y el tiempo de respuesta,
lo cual de igual forma es aplicado en la presente de investigación en cuanto a
maximizar el tiempo de respuesta ante un evento o falla presentada en la
distribución de gas de alta presión a través de la lógica difusa. A su vez se
puede observar que ambas investigaciones son del tipo prospectiva y de
diseño no experimental, apoyándose en la observación como principal
instrumento.
Por otra parte Rodríguez et.al (2003) en su investigación “Evaluación
integral y optimización de las variables que intervienen en los procesos
hidráulicos de las estaciones de flujo TJ -19 y TJ-22” tuvo como objetivo
general, evaluar integralmente y optimizar las variables que intervienen en
16
los procesos hidráulicos de las estaciones de flujo TJ-19 y TJ-22, a fin de
detectar las posibles restricciones que causan caídas de presiones de los
componentes del sistema para desarrollar recomendaciones que al
implantarse arrojen mejoras de producción. Para la recolección de
información se utilizaron las normas PDVSA para el levantamiento de
isométricos, Aico, Centinela, PI Process Book 2.0 y visitas a campo. La
evaluación hidráulica se desarrolló utilizando el Simulador Hidráulico
Pipephase 7.4 y el Simulador de proceso PRO II 5.6. Los resultados
obtenidos de las simulaciones hidráulicas son en estado estacionario
considerando el esquema actual de operación, donde es simulado el sistema
de llenado, de descarga de crudo y gas. A partir de estas simulaciones no se
encontraron restricciones hidráulicas al flujo bifásico, pero se observó una
distribución desigual de crudo y gas en los separadores generales, además
permitió la determinación y evaluación de posibles mejoras a considerar para
los próximos proyectos que implantará la U.E.L.S. en su infraestructura.
El aporte de este estudio, es el uso de software tales como: Centinela,
Aico, PI Process Book y Pipephase que es un simulador hidráulico en estado
estacionario, los cuales serán utilizados en la investigación.
Así mismo Rodríguez y Valiente (2003), en su investigación titulada
“Evaluación de los Sistemas de Distribución y Recolección de Gas de la
Unidad de Explotación Lagomar”, identificaron mediante el uso de
herramientas computacionales como PIPESIM 2000, restricciones de flujo,
17
problemas de medición y arreglos inadecuados en los gasoductos existentes
en ambos sistemas, garantizando el adecuado transporte del gas desde el
conjunto de Estaciones de Flujo hasta la succión de las plantas compresoras,
así como el transporte del gas hasta los múltiples a una presión adecuada
que maximice el levantamiento de los fluidos, proponiéndose el tendido de
nuevos gasoductos así como arreglos en los existentes, mejorando el
manejo de gas en ambos sistemas.
También, se definieron acciones que se deben tomar en caso de paros de
plantas y ruptura de gasoductos principales, con el fin de obtener el menor
impacto en producción por efecto de la presurización o despresurización del
sistema. A fin de que el personal de la U.E. LAGOMAR pueda efectuar
rápidamente simulaciones de los sistemas de recolección y distribución se
elaboró un Manual de Procedimiento de Referencia Rápida que permite
realizar alguna evaluación de los mismos. Para la recolección de información
se utilizaron los Manuales de Datos de Procesos de Instalaciones de la
industria petrolera venezolana , Centinela, SIMEP, PI Process Book 2.0,
registros anteriores de cromatografía de gas y visitas
a campo.
La
evaluación hidráulica se desarrolló utilizando el Simulador PIPESIM. Los
resultados obtenidos de las simulaciones son en estado estacionario
considerando el esquema actual de operación, donde es simulado el sistema
de recolección y distribución de gas de la U.E. LAGOMAR.
18
El aporte de esta investigación, se basa en las técnicas de recolección de
información utilizadas, ya que Centinela, PI ProcessBook , lo manuales de
datos de las instalaciones de igual forma fueron utilizados en el desarrollo del
estudio, en este caso correspondiente a la segregación Rosa Mediano. A su
vez, se realizaron simulaciones en estado estacionario, lo cual también será
objetivo del estudio.
Ferrer (2004), en su investigación titulada “Sistema de detección de fallas
aplicando técnicas de inteligencia artificial”, su objetivo principal fue el diseño
de un sistema sensible a la detección de fallas operacionales, a través de la
aplicación de técnicas de inteligencia artificial (IA), tomando como caso
particular las redes neuronales. La investigación fue de tipo descriptiva y la
metodología utilizada consideró cuatro pasos: en el primer paso se realizó la
revisión documental para analizar las técnicas de inteligencia artificial y en el
segundo paso se realizó la detección de la técnica para el desarrollo del
sistema., en el tercer paso se desarrolló el sistema de detección de fallas y
finalmente en el cuarto paso se presentaron las pruebas del sistema
desarrollado, demostrando de esta manera que mediante un monitoreo
apropiado
y esquemas de detección de fallas, es posible advertir el
momento de llevar a cabo un mantenimiento preventivo para mejorar la
fiabilidad y seguridad del sistema. Los resultados obtenidos permiten afirmar
que las técnicas de inteligencia artificial (IA) ofrecen una alternativa para el
diagnóstico rápido de fallas.
19
El aporte de esta tesis de grado se basa principalmente en dar a conocer
el uso
de técnicas de inteligencia artificial para el diagnóstico rápido de
fallas, utilizando para ello la aplicación de redes neuronales, lo cual sirve de
antecedente en el presente trabajo de investigación en cuanto a la aplicación
de la lógica difusa (técnica de inteligencia artificial) para el diagnóstico de
evento o fallas presentadas en el proceso de distribución de gas y toma de
decisiones en el menor tiempo posible.
Chávez et..al (2004), en su investigación titulada “Evaluación del sistema
de recolección de gas de la Unidad de Explotación La Salina”, desarrollan la
evaluación técnica orientada a proponer opciones que eliminen la necesidad
de cerrar producción o de recurrir al venteo para manejar el gas recolectado
en la segregación Urdaneta Pesado, en los casos de sobrepresión. La
metodología empleada para este estudio se basó en la simulación del
proceso de recolección de gas a través de la herramienta computacional
PIPEPHASE 9.1, que permite predecir el comportamiento de un sistema ante
cualquier alteración en alguna de las variables que maneje. Inicialmente se
simuló el sistema bajo las condiciones actuales de operación y luego
tomando en cuenta las condiciones implícitas en cada una de las opciones
de manejo de gas propuestas. Con la simulación inicial se determinó la
eficiencia aproximada de las tuberías y se localizó la tubería crítica que
representa una restricción o “cuello de botella” para la red en estudio. Las
simulaciones posteriores se hicieron con la finalidad de demostrar la
factibilidad técnica de cada opción propuesta.
20
El aporte de este antecedente para la investigación, se enfocó
específicamente e n tomar la descripción de los principios básicos del proceso
productivo relacionado a la industria petrolera.
Romero (2004), en su investigación “Alineación
inteligente
para
movimiento de crudo en un patio de tanques de almacenamiento” desarrolló
un sistema inteligente de alineación para movimiento de crudo en un patio de
tanques de almacenamiento con la finalidad de ayudar al operador de la
industria petrolera, en la toma de decisiones. La investigación es de tipo
descriptivo, documental, y el diseño de la investigación es bibliográfico. Las
técnicas de recolección de información fueron el análisis documental y la
observación indirecta. El lenguaje de programación utilizado para desarrollar
el sistema fueron Visual Basic, Visual C y el manejador de base de datos
Access para la base de conocimiento. Se utilizó como método de búsqueda
los algoritmos genéticos. Las pruebas realizadas, por medio de simulaciones
en un patio de tanques, demuestran que este sistema evita errores de
alineación, previene la contaminación del producto y reduce el tiempo en la
toma de decisiones. Adicionalmente, le da la facilidad al operador, luego de
escoger el mejor camino, sugerir las válvulas que deben ser cerradas, y así
evitar contaminación del producto, lo que puede traducir en un ahorro de
tiempo, dinero y recursos humanos. Se recomienda hacer un enlace con el
sistema SCADA existente en la industria petrolera, de esta manera, tener un
mayor control de todos los procesos involucrados en un patio de tanques de
almacenamiento de crudo.
21
El aporte de este antecedente en la investigación, se refiere a la
información obtenida del resultado de las simulaciones realizadas en el patio
de tanques, ya que demuestran que el sistema evita errores y reduce el
tiempo de respuesta en la toma decisiones del proceso, lo cual es uno de los
aspectos a considerar para el estudio.
Camargo et.al (2010) en su investigación titulada “Intelligent Supervisión
Systems for Improving the industrial production performance in oil wells”,
presenta un esquema de supervisión inteligente para la producción en la
industria petrolera, el cual fue probado en pozos con sistema de
levantamiento artificial por gas (Gas Lift). La propuesta se basa en la
evaluación
de
la
producción
probable,
las
variables
de
proceso
(específicamente, la presión en fondo del pozo) y la detección de escenario
operacionales correspondientes al proceso (el caso de estudio, es un pozo
productor de petróleo), con el objetivo de optimizar el rendimiento de la
producción del pozo. La propuesta combina técnicas inteligentes (algoritmos
genéticos, clasificadores difusos, sistemas neodifusos) y balances de masa
y energía. El esquema en este estudio especifico permite establecer el flujo
de gas o petróleo que un pozo pueda producir, tomando en cuenta la
geometría de la completación y el potencial del yacimiento, así como también
los criterios financieros relacionados a la curva de rendimiento del pozo y el
costo de comercialización de petróleo y gas. La posibilidad de poder estimar
en fondo las variables del pozo es de gran importancia para las operaciones
en la propuesta presentada, ya que los costos de instalación de tecnología y
22
mantenimiento para fondo en pozos son muy elevados, resultando esto ser
rentable para la producción del pozo.
El aporte de esta investigación principalmente es la utilización de la lógica
difusa en el desarrollo de un sistema de supervisión inteligente, siendo esto
uno de los objetivos del actual trabajo de grado, al igual que el desarrollo de
balances de masa y energía para la elaboración de un modelo matemático
que se ajuste al comportamiento de producción de pozos de gas lift, siendo
esto una diferencia con respecto a la presente investigación ya que se
desarrollaran de igual forma balances de masa y ene rgía pero con la
finalidad de hallar un modelo matemático que se ajuste a los escenarios
operacionales correspondientes al proceso de distribución de gas de alta
presión a través de redes de tuberías en la industria petrolera.
2.
Bases teóricas.
2.1.
Gas Natural
Se denomina gas natural al formado por los miembros más volátiles de la
serie parafínica de hidrocarburos, principalmente metano, cantidades
menores de etano, propano y butano, y finalmente, puede contener
cantidades muy pequeñas de compuestos más pesados. Además, puede
contener en varias cantidades, gases no hidrocarburos, como dióxido de
23
carbono, sulfuro de hidrógeno (ácido sulfúrico), nitrógeno, helio, vapor de
agua, etc.
El gas natural puede existir como tal, en yacimientos de gas, o asociado
con yacimientos de petróleo y de condensado (porciones volátiles de
petróleo). Particularmente en Venezuela la mayoría del gas proviene de
yacimientos de petróleo (Chavez y Puyosa, 2004)
2.1.1.
Propiedades y Comportamiento del Gas Natural
En la forma más simple, un gas puede considerarse compuesto de
partículas sin volumen y entre las cuales no existen fuerzas de atracción. Es
un fluido homogéneo, generalmente de baja densidad y viscosidad, sin
volumen definido y llena cualquier volumen en el cual se coloca.
La anterior definición de gas, generalmente se cumple a condiciones de
baja presión y temperatura, pero gradualmente se aparta de esta definición
y el comportamiento teórico se aparta del observado. A medida que aumenta
la presión y la temperatura, debe incluirse el volumen de las moléculas y
fuerzas entre ellas. Los gases que cumplen con la definición dada en el
párrafo anterior, se denominan gases perfectos o ideales. Los que no
cumplen esta definición se denominan gases reales.
El gas natural puede existir como tal, en yacimientos de gas libre o
asociado con yacimientos de petróleo y condensado (porciones volátiles de
24
petróleo). En vista de que el gas natural normalmente se encuentra presente
en los yacimientos de hidrocarburos, es de gran importancia el conocimiento
de ciertas propiedades físicas del mismo que son fundamentales en el
análisis del comportamiento de yacimientos de petróleo, gas y condensado.
Las relaciones que describen el comportamiento Presión-VolumenTemperatura, PVT de gases son llamadas ecuaciones de estado. La
ecuación del estado más simple, es llamada la Ley de los Gases Ideales
(Ec.1);
PV = nRT
Ec. 1
donde:
V = volumen del gas.
n = moles de gas.
P = presión.
T = temperatura.
R = constante universal de los gases.
Esta ecuación es el resultado de los esfuerzos combinados de Boyle,
Charles, Avogadro y Gay Lussac, y sólo es aplicable a presiones cercanas a
la presión atmosférica para la cual fue experimentalmente obtenida y a las
cuales los gases se comportan como ideales.
- Densidad y factor de compresibilidad (? g y Z):
25
La densidad de los gases sufren efectos significativos durante el
transporte en tuberías debido a los cambios relativos de presión y
temperatura, por ejemplo; cuando se tienen diferencias de presiones
elevadas esto provoca un aumento del volumen del gas causando una
disminución en su densidad. Así mismo ocurre cuando se tiene un aumento
de la temperatura, la velocidad de las moléculas del gas aumentan y
consecuentemente su volumen.
Se tiene que a presiones moderadamente bajas (= 3 kg/cm2) los efectos a
menudo son pequeños y la hipótesis del flujo compresible con una densidad
constante (promedio) suele ser razonable. Pero cuando se tienen
desviaciones ideales más significativas, la ley de los gases ideales
proporciona una descripción cada vez menos eficiente del comportamiento
del gas (GPSA, 1998).
Cuando se determina la densidad de un gas real es necesario modificar la
ecuación del gas ideal para obtener una aproximación razonable mediante la
inclusión de un término conocido como factor de compresibilidad (Z), este
valor es una corrección para desviaciones a partir del comportamiento ideal,
el cual no depende de la cantidad del flujo y es considerado aceptable para
los requerimientos normales de ingeniería (GPSA, 1998). La determinación
del factor de compresibilidad implica una selección adecuada de una
ecuación de estado: Redlich-Kwong, Soave Redlich-Kwong, Peng Robinson,
entre otros, y que a su vez depende indudablemente del tipo de fluido a
transportar (componentes puros o multicomponentes), sus propiedades
26
físicas y las condiciones de operación (presión y temperatura) a la cual está
sometido.
Así, la determinación de la densidad para un gas real puede obtenerse
mediante la inclusión del factor de compresibilidad Z, resultando la (Ec.2 ):
Ec. 2
Donde:
? g = densidad del gas a la temperatura de operación, lbm/ft3
P = presión absoluta del sistema (Patm + Pman), psia
Pman = presión manométrica de operación, psig
Patm = presión atmosférica o barométrica, psia
PM = masa molecular del gas, lbm/lb-mol
Z = factor de compresibilidad a la presión y temperatura de operación, adim.
27
R = constante de los gases, 10.73 ft3.psia/lb-mol.R
T = temperatura absoluta de operación, R
- Gravedad específica del gas (γg):
La gravedad específica del gas se define como la razón de la densidad del
gas a la densidad del aire, ambas medidas a las mismas condiciones de
presión y temperatura. Como la gravedad del gas se mide generalmente a
condiciones normales, tanto el gas como el aire se comportan como gases
ideales (Chavez y Puyosa, 2004)
A continuación se tiene que (Ec.3):
γg =
ρg
ρa
Ec. 3
Por otra parte, la gravedad específica también puede definirse también
como una relación entre las masas moleculares del gas y aire. Es una
relación de como una medida de la masa del gas es comparado con la masa
del aire a una temperatura en particular, ambas a condiciones estándar
(Ec.4).
Ec. 4
Donde:
28
Sg = gravedad especifica del gas, adimensional
PM = masa molecular del gas, lbm/lb-mol
PMaire = masa molecular del aire a condiciones estándar (60°F, 14.7 psia),
28.9625 lbm/lb-mol.
2.1.2.
Flujo de Gases
- Consideraciones Básicas.
El flujo de Gases en tuberías es más complejo que el de líquido debido a
la dependencia del volumen específico con los cambios en la presión a lo
largo de la línea. Si esta variación es grande, tanto la velocidad como la
densidad
cambiarán
significativamente,
es
decir,
se
necesita
un
conocimiento preciso de la relación P,V,T del gas para poder aplicar la
ecuación de Bernoulli en forma diferencial, y el balance de energía en estado
estacionario. Es importante puntualizar, que el comportamiento de la línea (la
caída de presión) dependerá del tipo de flujo existente en la línea.
Los extremos usuales de flujo son:
• Adiabático (PVk = constante), el cual es el caso de las líneas cortas
aisladas en refinerías y plantas químicas, donde el calor transferido hacia o
desde la línea es despreciable.
29
• Isotérmico (PV = constante) se presenta en líneas largas sin aislar como las
de transmisión de gas natural. A menudo se asume este tipo de flujo, parte
por conveniencia pero en realidad, es porque es lo más cercano al
comportamiento real.
• Politrópico (PVn = constante) es una condición entre adiabático e
isotérmico.
Desde el punto de vista práctico, las diferencias entre los dos extremos son:
• Para caídas de presión, si se conoce el flujo, el diámetro y la longitud de la
tubería.
∆PIsotérmico ≥ ∆ Padiabático
• Si se desea determinar el tamaño de la línea conociendo el flujo y la caída
de presión.
DIsotérmico
≥
Dadiabático
• Si se desea determinar la capacidad (flujo másico) de la línea de proceso
dada, con caída de presión conocida.
°
°
m Isotérmico = m adiabático
Por tanto, cuando la naturaleza del flujo se desconoce, los procedimientos
de la industria petrolera venezolana para dimensionamiento de líneas
recomiendan asumir flujo isotérmico con la finalidad de obtener resultados
más conservadores. Sin embargo, las prácticas de diseño consideran ambos
30
casos, debido a que hay situaciones donde se requiere un diseño más
preciso de flujo adiabático. (PDVSA,1996)
- Flujo de Gases en una Tubería Recta.
Para el flujo de gases en tuberías rectas, el cálculo de caída de presión
para un determinado flujo másico es complicado por la dependencia de la
densidad del gas con la presión. Además para caídas de presión
significativas,
tanto
la
velocidad
como
la
densidad
cambiarán
significativamente. Como resultado, para usar el Teorema de Bernoulli en el
desarrollo de funciones para predecir caídas de presión, se necesita conocer
la relación entre la presión del gas y la densidad en la tubería (PDVSA,1996).
Además el comportamiento de la línea dependerá del tipo de flujo
existente en dicha línea, el cual usualmente existe a condiciones entre
adiabática e isotérmica.
La solución para un fluido compresible a través de una tubería puede
obtenerse utilizando las siguientes ecuaciones con la ayuda de una ecuación
de estado y la ecuación de continuidad para expresar la densidad y la
velocidad en términos de presión (PDVSA,1996).
En general se hace las siguientes suposiciones:
1. Flujo isotérmico.
2. No se aporta ni se realiza trabajo mecánico sobre o por el sistema.
31
3. El cambio en la energía cinética es insignificante y es asumido igual a
cero.
4. La temperatura es constante a un valor promedio para la sección
considerada.
5. El factor de compresibilidad es considerado constante a una temperatura
y presión promedia.
6. La tubería es recta y horizontal entre los puntos extremos.
7. La aceleración puede despreciarse por ser una tubería larga.
Ecuación Isoterma (Ec.5 ).
Wg =
P12 − P22
−

P1
P
* L / D + Loge 1 
P2 
144 * g * A2

Ve f

Donde:
Wg = rata de flujo de gas, lb/seg.
g = ft/ seg2
A = área o sección de tubería ft2.
Ve = volumen especifico de gas a condiciones contra corriente ft3/lb.
f = factor de fricción.
P1 = presión contracorriente, psia ( upstream ).
P2 = presión a factor corriente, psia ( downstream ).
Ec. 5
32
Esta ecuación asume:
1. No se realiza trabajo entre los puntos 1 y 2.
2. No hay compresores.
3. No hay expansión de gas.
4. No existen cambios de elevación.
5. El gas esta fluyendo.
Asunciones para fines prácticos en el campo.
1. Para propósitos de gasoductos (Ec.6).
2 loge ( P1 / P2 ) << fL / D, por lo que puede ser ignorado.
SG * Qg2 * Z * T1 * f * L
P − P = 25.1
d5
2
1
2
2
Donde:
Qg = MMPCD
T1 = temperatura de flujo ( °R ).
f = factor de fricción de Moody
d = diámetro interno tubería, in.
L= longitud de la tubería, ft.
Ec. 6
33
2. El factor Z puede cambiar entre un punto y P1 Y P2, entonces se puede
promediar utilizando la ecuación 7:
2 
P *P 
promedio = * ( P1 + P2 ) − 1 2 
3 
( P1 + P2 ) 
Ec. 7
Para obtener (Ec.8):
(
)
 d P −P

Qg = 0.199 * 

 Z * T1 * f * L * SG 
5
2
1
2
2
1
2
3. Si el cambio de presión es menor al 10 %, entonces (Ec.9):
(P
2
1
)
− P22 ≅ 2 * P1 (P1 − P2 )
Ec. 8
Ec. 9
Ec. 9
Por lo tanto (Ec.10):
SG * Qg * Z * T1 * f * L
∆P =
P1 * d 5
Ec. 10
34
4. Asumo un diámetro para ver el factor de fricción.
El objetivo del diseño es determinar un diámetro que produzca la menor
caída de presión a una tasa de flujo deseada (PDVSA, 1996).
- Regímenes de flujo de fluidos en tuberías
Flujo laminar: Existe a velocidades más bajas que la crítica, se caracteriza
por el deslizamiento de capas cilíndricas concéntricas una sobre otras de
manera ordenada. Se determina que hay flujo laminar cuando el numero de
Re ( Reynolds) es menor de 2000.
Flujo transicional. También llamado flujo critico, existe cuando el caudal se
incrementa después de estar en flujo laminar hasta que las laminas
comienzan a ondularse y romperse en forma brusca y difusa. Se determina
cuando el numero de Re tiene valores entre 2000 y 4000.
Flujo turbulento. Existe a velocidades mayores que la critica, cuando hay un
movimiento irregular e indeterminado de las partículas del fluido en
direcciones transversales a la dirección principal de flujo. Es determinado
cuando el numero de Re tiene valores mayores a 4000 (Crane Co., 1982).
Numero de Reynolds.
El número de Reynolds es un número proporcional que relaciona las fuerzas
dinámicas (energía cinética) y las fuerzas viscosas (resistencia del
35
movimiento del fluido debido a su viscosidad) (Rodríguez, 2008). Para
calcular el número de Re para gases se tiene la siguiente ecuación (Ec.11):
Re =
20100 * Q g * SG
d *µ
Ec. 11
Donde:
SG = gravedad especifica del gas a condiciones standard ( aire = 1)
d = diámetro interior de tubería, in ( pulgadas)
µ = viscosidad del gas, cp
Qg = flujo de gas, en MMSCF ( millones de pies cúbicos standard).
Una vez determinado el tipo de flujo que circula por el interior de la
tubería, con base al número de Reynolds es posible calcular el factor de
fricción de Darcy, f. Para el caso de tuberías lisas o rugosas en régimen
laminar (Re < 2000) puede deducirse matemáticamente por medio de la
ecuación de Hagen-Poiseuille (Ec.12).
Ec. 12
Sin embargo, para el caso del régimen turbulento (Re > 4000) el instituto
de Hidráulica y la mayoría de ingenieros consideran la ecuación de
Colebrook & White (1939), como la más aceptable para calcular f, debido a
su mejor aproximación al comportamiento de las tuberías comerciales. Esta
36
ecuación es válida para tuberías de pequeño y gran diámetro de superficies
lisas o rugosas que manejan caudales de diferentes intervalos y de
viscosidad variada (Howard, 1982), (Swaffield, 1983) (Ec.13).
Ec. 13
Donde:
f = factor de fricción de Darcy, adimensional
e = rugosidad absoluta de la tubería, ft
D = diámetro interior de la tubería, ft
Re = número de Reynolds, adimensional
La mayoría de los textos bibliográficos referente a tuberías proporcionan
abundante información sobre la rugosidad absoluta de los distintos
materiales a diferentes condiciones de servicio. En el Anexo A se muestra
una lista de rugosidades de materiales para tuberías más comunes
empleados en la industria de la refinación.
La expresión implícita de la ecuación de Colebrook & White requiere de
un procedimiento iterativo para su resolución. La consideración de un método
numérico que se adapta mejor a la ecuación para la aplicación en un
programa de computadora es el método de Newton Raphson, debido a su
precisión y convergencia para la obtención de resultados.
37
Esto es con la finalidad de reducir el tiempo para su determinación y
mejorar la fidelidad de este valor en comparación a los que obtendrían
tradicionalmente de forma manual mediante la gráfica de Moody (García,
2003), (Lester, 2003).
Lewis F. Moody (1944), realizó un estudio extenso sobre los datos de
tuberías comerciales consiguiendo representar la expresión de Colebrook &
White en una gráfica de fácil manejo que integra el valor de f para los
distintos tipos de flujo conocido comúnmente como el Diagrama de Moody o
Diagrama universal para el cálculo de tubería, Figura 1.
Figura 1. Diagrama de Moody.
Fuente: Garcia (2003)
38
2.2. Métodos de Levantamiento Artificial
Los estudios realizados en la ingeniería de producción comprenden una
serie de procesos que van desde el comportamiento de afluencia, el
levantamiento de fluidos del pozo, hasta los equipos de superficie tales
como: recolección, separación, tratamientos, almacenamiento y transporte
del crudo y gas. Al poner en producción un pozo se crea una diferencia entre
la presión del yacimiento y la presión de fondo del pozo, esta diferencia de
presión origina el desplazamiento de los fluidos desde la formación hacia el
pozo cuando la presión es mayor en el yacimiento que en el pozo. A su vez
por la diferencia de presión entre el fondo del pozo y la superficie, los fluidos
pueden ser extraídos (García y Quintero, 2005).
El proceso de levantamiento de los fluidos del pozo hacia la superficie,
puede llevarse a cabo mediante producción del pozo por flujo natural o por
métodos de levantamiento artificial.
En Venezuela los programas de explotación masiva han ocasionado una
disminución de las presiones de yacimiento en las diferentes áreas
operacionales del país, lo que ha hecho necesario el uso intensivo de
métodos de Levantamiento Artificial, tales como por inyección de gas (Gas
Lift), por bombeo electrosumergible (BES), por bombeo de cavidad
progresiva (BCP), bombeo mecánico, bombeo hidráulico, bombeo tipo jet y
pistón mecánico.
39
En este caso se estudiará el método de levantamiento artificial por
inyección de gas (Gas Lift), que tiene como principio fundamental levantar el
fluido desde el yacimiento hacia la superficie, mediante inyección de gas,
generalmente en el casing , lo que permite que el fluido ascienda y llegue a
la superficie con suficiente energía.
El sistema de LAG está formado por un sistema de compresión, una red
de distribución de gas a alta presión, equipos de medición y control del gas
comprimido, los pozos conjuntamente con sus mandriles, válvulas de
descarga y válvula operadora, y la red de recolección del gas a baja presión.
A continuación se describen los equipos de superficie principales
relacionados al levantamiento artificial por gas (LAG) (García y Quintero,
2005):
a)
Planta Compresora:
Es donde se realiza el proceso de comprimir el gas de baja a alta presión.
Puede ser Centrífuga (turbina) o Reciprocante (motocompresor). Recibe el
gas de baja, el cual puede provenir de los pozos, lo comprime a su
capacidad, lo envía como gas de alta presión a la red de distribución y, de
allí, a cada pozo.
40
b)
Sistema de Distribución de Gas:
La red de distribución, la cual puede ser del tipo ramificado o poseer un
múltiple de distribución, es la encargada de transportar el gas y distribuirlo a
cada pozo. La presión y el volumen de gas que llega al pozo dependerá de la
presión y el volumen disponibles en la planta compresora, menos la pérdida
que se origina en el sistema de distribución.
2.2.1. Proceso general levantamiento artificial por gas (Gas Lift)
Existe un ciclo básico de producción de crudo y gas que comprende
varias fases. La primera de estas fases es la de inyección de gas en los
pozos, este gas proviene de una planta compresora y se inyecta a los pozos
a alta presión para levantar el crudo que está alojado en el yacimiento, de allí
se extrae una mezcla de crudo y gas (el gas incluye al gas de formación y de
levantamiento), esta mezcla de hidrocarburos va a las estaciones de flujo en
donde se separa y el crudo se envía a un patio de tanques donde se
almacena, mientras que el gas ingresa a un sistema de recolección que lo
lleva nuevamente hasta la planta compresora para reutilizar una parte del
mismo en el proceso de levantamiento por inyección y el resto se utiliza en
otras actividades de interés para la industria (Chávez y Puyosa, 2004) (ver
Figura 2).
41
PATIO DE TANQUES
ESTACIONES
DE FLUJO
PLANTA COMPRESORA
MULTIPLES DE GAS LIFT
POZOS
CRUD
O
GAS DE BAJA PRESIÓN
GAS DE ALTA PRESIÓN
Figura 2. Proceso básico de Producción de crudo y gas.
Fuente: Chavez y Puyosa (2004)
2.3. Redes de Tuberías
2.3.1. Ecuaciones Fundamentales para Redes de Tuberías
Existe una vasta información referente al flujo de un fluido a través de una
tubería o una red de tuberías, dentro de esta información se incluye los
aspectos de interés para el transporte de agua en las redes de suministro y
42
distribución a grandes ciudades, suministro y distribución de fluidos en las
industrias petrolera y eléctrica. (González, 2008)
La mayoría de las situaciones concernientes al flujo de fluidos en tuberías
para el transporte y distribución dentro de la industria petrolera están
relacionadas con el movimiento de estos desde el centro productor hasta los
centros de consumo. Los sistemas de transporte se pueden dividir en:
sistema de recolección, facilidades de compresión y tratamiento, sistema de
tuberías principales y sistema de distribución. (González, 2008)
Las redes principales que comprenden los sistemas de recolección,
troncales principales y los sistemas de distribución constituyen un medio
económico para transportar el gas a largas distancias. Varios factores deben
ser considerados en el diseño de los sistemas de tuberías utilizados para
transportar un fluido a larga distancias, entre ellos tenemos: la naturaleza y
cantidad del fluido a ser transportado, el tipo del terreno a ser recorrido,
material de las tuberías, la distancia entre los extremos de las tuberías, el
medio ambiente que rodea a las tuberías y el perfil del terreno entre otros. La
inversión inicial representa los grandes costos asociados al transporte
(material, instalación entre otros), puesto que los costos de operación son
relativamente bajos. (González, 2008)
Referido a la industria petrolera, la ubicación de las facilidades de
compresión representan una de las actividades de mayor importancia, una
vez que esta sea ubicada, el sistema de recolección es diseñado. Este
comprende el derecho de vía para instalar las tuberías que transportaran el
43
fluido de los pozos productores, la cantidad del fluido y los niveles de presión
entre el campo y la planta de compresión. (González, 2008)
Los pozos en general son agrupados y ubicados alrededor de la
estructura geológica o dentro de los límites del yacimiento productor. Una vez
que esto sea establecido, el problema principal lo constituye el transporte del
fluido hasta el centro de compresión. Los sistemas de recolección están
formados por una serie de tuberías de diámetro pequeño que convergen en
tuberías de mayores diámetros o troncales principales, los cuales deben
tener la capacidad para transportar los crecimientos previstos en el área. El
sistema de distribución está conformado por una serie de tuberías de
diámetro relativamente pequeño de pendiendo de los niveles de presión, que
sirven para conducir el fluido desde el centro de compresión hasta los
centros de consumo o clientes. El diseño de los sistemas de recolección y
distribución involucran estudio de cierta complejidad los cuales son
necesarios para decidir el diámetro, espesor y material de las tuberías que lo
forman, así como la capacidad de compresión y los niveles de presión a los
cuales
estaría
sometido
el
sistema
de
transporte.
Algoritmos
computacionales son utilizados en el proceso de análisis y diseño de estos
sistemas, en vista que es necesario seleccionar la mejor opción desde el
punto de vista hidráulico y económico. (González, 2008)
El transporte de un fluido a través de un sistema tuberías requiere de los
conocimientos relacionados con su comportamiento y movimiento, de hecho
ecuaciones que permitan determinar sus propiedades, los gradientes de
44
presión y temperatura y la capacidad de estos sistemas. En la literatura
técnica se presentan varias ecuaciones para calcular el comportamiento del
flujo de un fluido a través de sistemas de tuberías. En los análisis de los
sistemas de transmisión de fluido debido a la interdependencia de las
propiedades y del factor de fricción con los gradientes de presión y la
temperatura del fluido es necesario realizar un proceso iterativo en el
momento de calcular los gradientes de presión y temperatura, así como
también el calculo de la capacidad de los mismos. Con la finalidad de
suavizar este proceso se utilizan formulas simplificadas para resolver las
ecuaciones fundamentales. Se realizan simplificaciones en lo referente a la
consideración o no del efecto cinético, inclinación de la tubería, factor de
fricción y el impacto de las propiedades del fluido. (González, 2008)
El desarrollo que se presenta está relacionado con el flujo de un fluido a
través de conductos y tubos circulares cerrados y con dispositivos
relacionados con su movimiento. Analizaremos situaciones relacionadas con
el flujo de un fluido en tuberías con la finalidad de calcular las pérdidas de
presión y temperatura necesarias para transportar un fluido desde el extremo
inicial de una tubería hasta el extremo final. De igual manera desarrollaremos
aplicaciones para determinar el flujo o diámetro requerido por una tubería
cuando se establece una pérdida de presión entre los extremos de la misma.
Se presentan ecuaciones que incluyen el efecto cinético considerando o no
considerando el efecto de la presión y la temperatura sobre el factor de
compresibilidad y el factor de fricción. Se estudia la solución de la ecuación
45
general para flujo de un fluido considerando todos sus términos; así como
ecuaciones simplificadas. Los métodos de solución incluyen diferencias
finitas y técnicas de integración numérica donde se considera la división de la
tubería en tramos. (González, 2008)
Tuberías en serie
González 2008, dice que cuando dos tuberías por donde circula el
mismo flujo y fluido de tamaño, rugosidades o inclinación diferentes se
conectan de tal manera que el fluido fluye a través de una tubería y luego a
través de la otra, se dice que las tuberías están conectadas en serie. Un
esquema de tuberías conectadas en serie se muestra en la Figura 3.
Considerando las pérdidas locales en la unión de las tuberías como
despreciables se tiene:
De la ecuación de continuidad (Ec.14):
Ec. 14
De la ecuación del balance de la energía mecánica (Ec.15)
Ec. 15
46
Figura 3. Tubería en Serie
Fuente: González (2008)
Tuberías en paralelo
Una combinación de dos o más tuberías conectadas como se
muestra en la Figura 4, de tal manera que el caudal circulante se divide entre
las tuberías y luego se unen nuevamente, representa un sistema de tuberías
en paralelo. En las tuberías en serie, el mismo caudal fluye por todas las
tuberías y las pérdidas de energía se acumulan, en el caso de tuberías en
paralelo las pérdidas de energía son las mismas en cada uno de las tuberías
y el caudal o flujo de masa se suma. (González, 2008). Al analizar un sistema
de tubería en paralelo, se cumple:
47
De la ecuación de continuidad (Ec. 16).
Ec. 16
Figura 4. Tuberías en Paralelo
Fuente: González (2008)
De la ecuación del balance de la energía mecánica (Ec.17)
Ec. 17
Para el arreglo de tubería (Ec.18)
Ec. 18
Entre las aplicaciones para tuberías paralelas se tiene (1) la
determinación del flujo que circula por cada tubería una vez conocida la
48
diferencia de energía o presión entre sus extremos y (2) determinar el flujo de
masa que circula por cada tubería para un flujo total que alimenta al conjunto
de tuberías paralelas.
Tuberías ramificadas
En la Figura 5 se muestra un simple sistema de tuberías ramificadas. En
esta situación, el caudal en cada tubería se puede determinar cuando se
conocen las elevaciones en los depósitos. Se supone que se conocen los
tamaños y tipo de las tuberías, y las propiedades de los fluidos. La solución
de este problema debe satisfacer las ecuaciones del balance de energía
mecánica en cada tubería y la ecuación de continuidad en la unión de las
diferentes tuberías, así como también en el arreglo de las tuberías.
(González, 2008)
Figura 5. Tuberías ramificadas
Fuente: González (2008)
49
La ecuación de continuidad establece que el flujo hacia la unión J debe
ser igual al flujo hacia fuera de la unión. El flujo debe ser desde el depósito
más elevado hacia él más bajo; por consiguiente, la ecuación de continuidad
es (Ec.19):
Ec. 19
Si el nivel de la energía de la unión J está por encima de las energías de
las superficies libre de los ta nques, entonces el flujo circula hacia esos
tanques, en caso contrario fluye desde el tanque.
De la ecuación del balance de la energía mecánica se tiene:
Ec. 20
Ec. 21
50
Ec. 22
Ec. 23
Redes de tuberías
La interconexión de dos o mas tuberías a través de uno de sus extremo
constituyen lo que se conoce como una red de tuberías, por medio estas
interconexiones se pueden formar redes abiertas en las cuales sus tuberías
no forman lazos, redes cerradas donde todas sus tuberías pertenecen por lo
menos a un lazo y aque llas redes que se forman por la combinación de las
dos anteriores, las cuales son conocidas como redes mixtas. La Figura 6
esquematiza estas descripciones. (González, 2008)
51
Figura 6. Redes de Tuberías
Fuente: González (2008)
2.3.2. Simulador de Redes de Tuberías PIPEPHASE 9.1:
El simulador de flujo multifásico PIPEPHASE® predice en estado
estacionario
presión,
temperatura
del
líquido
compresores, separadores y otras facilidades.
en
pozos,
bombas,
Los tipos de fluidos
manejados por PIPEPHASE® son: líquido, gas, vapor y mezclas multifásicas
de gas y líquido.
Algunas de las capacidades especiales que también están designadas
dentro de PIPEPHASE® incluyen el análisis de pozos, gas lift entre otros.
Esta herramienta puede simular con fluidos definidos composicionalmente o
no. Cuando los fluidos se definen por su composición, las propiedades de
52
todos sus componentes están disponibles en la base de datos del simulador.
(Chávez y Puyosa, 2004).
Un modelo de fluido es composicional cuando éste puede definirse en
término de sus componentes individuales directamente o por medio de una
curva de ensayo. PIPEPHASE® puede predecir las propiedades del fluido
aplicando leyes apropiadas de mezclas a las propiedades del componente
puro. Salvo que se indique lo contrario, éste realizará el cálculo de equilibrio
de fase para el fluido y determinará la cantidad y propiedades de las fases
(líquida
y
vapor).
Para
fluidos
definidos
no
composicionalmente,
PIPEPHASE® usa correlaciones que le permiten determinar todas las
propiedades físicas que el programa requiere para cálculos de caídas de
presión y transferencia de calor. (Chávez y Puyosa, 2004).
PIPEPHASE® resuelve ecuaciones definidas por la relación entre las
caídas de presión y la tasa de flujo, además de poder calcular pérdidas o
ganancias de calor. Cuando se realiza la simulación en una línea única éste
calculará la caída de presión para una
tasa de flujo conocida o
alternativamente se puede fijar la caída de presión y se obtendrá la tasa de
flujo. En simulaciones de redes se deben suministrar las tasas de flujo y los
valores de presión conocidas en cada entrada o salida y éste calculará los
datos restantes (Dado el flujo en las fuentes y la presión en los sumideros,
este calculará la presión e n las fuentes y el flujo en los sumideros), (Chávez y
Puyosa, 2004). A continuación en la Figura 7 se presenta la ventana que
representa el ambiente de trabajo del simulador PIPEPHASE.
53
Figura 7. Ventana del programa PIPEPHASE
Fuente: El Autor (2012)
2.4 Control Proporcional Integral Derivativo (PID)
El control automático asienta sus bases esencialmente en el concepto de
realimentación.
Este concepto se concreta en una estructura de control en la cual el
controlador se puede entender como un operador, que en función de la
salida deseada de la planta, y la salida real medida, proporciona la acción de
control a aplicar sobre el sistema (Alamo, 2009).
Si bien existen muchos tipos de control basados en este principio, el
control proporcional, derivativo e integral (PID), es el que mayor implantación
tiene en la industria de procesos. Dicho control consiste esencialmente en
54
obtener la acción de control como la suma de tres términos: término
proporcional, término derivativo y término i ntegral (Alamo, 2009).
Se pueden obtener variaciones a este esquema consistentes en la no
introducción de los términos derivativo e integral; en dicho caso el control
coincide con el llamado control proporcional. Si solamente se prescinde de la
acción integral, el control se denomina control proporcional derivativo (PD).
Si, por el contrario, el único término que desaparece es el derivativo, el
control se denomina proporcional integral (PI) (Alamo, 2009).
2.4.1 Estructura del PID
Consideremos un lazo de control de una entrada y una salida (SISO) de
un grado de libertad (ver Figura 8):
Figura 8: Diagrama en Bloques del PID
Fuente: Alamo (2009)
55
Los miembros de la familia de controladores PID, incluyen tres acciones:
proporcional (P), integral (I) y derivativa (D). Estos controladores son los
denominados P, I, PI, PD y PID (Mazzone, 2002).
P: acción de control proporcional, da una salida del controlador que es
proporcional al error, es decir: u(t) =KP.e(t),que descrita desde su función de
transferencia queda (Ec. 24):
Ec. 24
donde Kp es una ganancia proporcional ajustable. Un controlador
proporcional
puede
controlar
cualquier
planta
estable,
pero
posee
desempeño limitado y error en régimen permanente (off-set).
I: acción de control integral: da una salida del controlador que es
proporcional al error acumulado, lo que implica que es un modo de controlar
lento (Ec.25 y Ec.26).
Ec. 25 y 26
56
La señal de control u(t) tiene un valor diferente de cero cuando la señal de
error e(t) es cero. Por lo que se concluye que dada una referencia constante,
o perturbaciones, el error en régimen permanente es cero.
PI: acción de control proporcional-integral, se define mediante la Ec.27:
Ec. 27
donde Ti se denomina tiempo integral y es quien ajusta la acción integral. La
función de transferencia resulta (Ec.28):
Ec. 28
Con un control proporcional, es necesario que exista error para tener una
acción de control distinta de cero. Con acción integral, un error peque ño
positivo siempre nos daría una acción de control creciente, y si fuera
negativo la señal de control será decreciente. Este razonamiento sencillo nos
muestra que el error en régimen permanente será siempre cero (Mazzone,
2002).
57
Muchos controladores industriales tienen solo acción PI. Se puede
demostrar que un control PI es adecuado para todos los procesos donde la
dinámica es esencialmente de primer orden. Lo que puede demostrarse en
forma sencilla, por ejemplo, mediante un ensayo al escalón (Mazzone, 2002).
PD: acción de control proporcional-derivativa, se define mediante (Ec.29):
Ec. 29
donde Td es una constante de denominada tiempo derivativo. Esta acción
tiene carácter de previsión, lo que hace más rápida la acción de control,
aunque tiene la desventaja importante que amplifica las señales de ruido y
puede provocar saturación en el actuador. La acción de control derivativa
nunca se utiliza por si sola, debido a que solo es eficaz durante períodos
transitorios. La función transferencia de un controlador PD resulta (Ec.30):
Ec. 30
Cuando una acción de control derivativa se agrega a un controlador
proporcional, permite obtener un controlador de alta sensibilidad, es decir
que responde a la velocidad del cambio del error y produce una corrección
significativa antes de que la magnitud del error se vuelva demasiado grande.
Aunque el control derivativo no afecta en forma directa al error en estado
58
estacionario, añade amortiguamiento al sistema y, por tanto, permite un valor
más grande que la ganancia K, lo cual provoca una mejora en la precisión en
estado estable (Mazzone, 2002).
PID: acción de control proporcional-integral-derivativa, esta acción
combinada reúne las ventajas de cada una de las tres acciones de control
individuales. La ecuación de un controlador con esta acción combinada se
obtiene mediante: (Ec.31)
Ec. 31
y su función de transferencia resulta (Ec.32):
Ec. 32
2.4.2. Método Ziegler-Nichols para Entonamiento de Controladores
En este sentido Ogata (1998) menciona que es posible aplicar técnicas de
diseño para determinar los parámetros del controlador cumpliendo con las
especificaciones de la planta en estado transitorio y estado estable de un
sistema en lazo cerrado, siempre y cuando se pueda obtener un modelo
59
matemático de la planta. Sin embargo, si la planta es complicada no es fácil
obtener el mismo, tampoco es posible obtener un enfoque analítico para el
diseño de un controlador PID. Para esto se debe recurrir a los enfoques
experimentales para el entonamiento de los controladores PID.
Ziegler-Nichols propusieron unas reglas para determinar los valores de la
ganancia proporcional Kc, del Tiempo Integral Ti y el Tiempo Derivativo Td,
con base en las características de respuesta transitoria de una planta
especifica. Tal determinación de los controladores PID o del entonamiento de
los controladores PID la realizan los ingenieros en el sitio mediante
experimentos sobre la planta.
Existen dos métodos o reglas para entonar controladores PID. En ambas
reglas se pretende obtener un sobre paso máximo de 25% en la respuesta
escalón (ver figura 9).
c(t)
25%
1
0
t
Figura 9. Máximo sobrepaso permitido en la respuesta al escalón
Fuente: Ogata (1998)
60
1. Primer Método:
En este método la respuesta de la planta a una entrada escalón se
determina experimentalmente. Si la planta no posee integradores ni polos
dominantes complejos conjugados, entonces, la curva de la respuesta
escalón posiblemente sea en forma de “S” (ver Figura 10 y Cuadro 1).
Recta tangente en
el punto de inflexión
c(t)
k
0
t
L
T
Figura 10. Primer método de entonamiento
Fuente: Ogata (1998)
Cuadro 1.Regla de entonamiento de Ziegler-Nichols basada en la respuesta
escalón de la planta
P
Kc
T
L
Ti
∝
T
L
L
0 .3
T
1.2*
PID
2*L
L
Fuente: Ogata (1998)
PI
0.9*
Td
0
0
0.5*L
61
2. Segundo Método:
En este segundo método se establecen Ti = ∝
y Td = 0. Se utiliza
únicamente una acción proporcional en la que se incrementa la ganancia
desde cero (0) hasta un valor de ganancia crítico (Kcr), y en donde la salida
muestre
primero
oscilaciones
sostenidas,
observando
su
periodo
correspondiente (Pcr). El método sugiere que por medio de estos parámetros
obtenidos y aplicando las relaciones que se muestran en el Cuadro 2 se
obtienen los valores de Kc, Ti y Td (ver Figura 11).
c(t)
Pcr
0
t
Figura 11. Segundo método de entonamiento
Fuente: Fuente: Ogata (1998)
62
Cuadro 2. Regla de entonamiento de Ziegler-Nichols basada en la ganancia
crítica Kcr y en el periodo crítico Pcr
Kc
Ti
Td
∝
P
0.5*Kcr
0
PI
0.45*Kcr
Pcr
1 .2
0
PID
0.6*Kcr
Pcr
2
0.125*Pcr
Fuente: Fuente: Ogata (1998)
2.5 Inteligencia Artificial
Desde siempre el hombre ha adquirido crear e imitar la majestuosidad de
la naturaleza, desde antes de existir la computadora e inclusive antes de
poder imaginar algún mecanismo complejo capaz siquiera de dar la mínima
posibilidad de creatividad.
La Inteligencia Artificial (IA), trata de desarrollar sistemas que parezcan
que se comportan de manera inteligente, estos trabajos se realizan como
una parte de la ciencia de la computación aunque también tiene elementos
de psicología lingüística y matemática (Ferrer, 2004).
La Inteligencia Artificial (IA) trata de abarcar y estudiar muchas de las
capacidades del hombre para poder ofrecérselas a la máquina y también a l
propio hombre en el entendimiento de sus principios de su inteligencia, de lo
63
cual se puede entender el porqué la inteligencia artificial tiene diversas ramas
de estudio tales como: redes neuronales, lógica difusa, algoritmos genéticos,
sistemas expertos, vida artificial, tecnología del habla, visión artificial y robótica, entre otras (Ferrer, 2004).
Por otra parte, según Díez et al.(2001), dada la indefinición de
inteligencia, prácticamente existe una definición de inteligencia artificial por
cada autor que escribe sobre el tema. Tal vez una de las definiciones que se
puede considerar más ajustada en la realidad es la reflejada en la
Encyclopedia Of Artificial Intelligence:
“La IA es un campo de la ciencia y la ingeniería que se
ocupa de la comprensión, desde el punto de vista
informático, de lo que se denomina comúnmente
comportamiento inteligente. También se ocupa de la
creación de artefactos que exhiben este comportamiento”.
Otros autores prefieren otras definiciones como:
“La inteligencia artificial es el estudio de las ideas que
permiten ser inteligentes a los ordenadores” (Winston,
1988).
“Parte de la informática que estudia procesos simbólicos,
razonamientos no
algorítmicos y representaciones simbólicas del
conocimiento” (Buchanan., B y Feigenbaum., E, 1990).
En cualquier caso, desde distintas perspectivas, en el seno de la IA como
ciencia y tecnología se han ido acumulando conocimientos sobre como
emular
las
diversas
capacidades
del
ser
humano
para
exhibir
comportamientos inteligentes y se han desarrollado sistemas cada vez más
perfeccionados que reproducen parcialmente dichas capacidades. Así, el
estudio de sensores y mecanismos de intercambio de información con el
64
exterior constituyen, por sí mismos pujantes áreas de investigación y
aplicaciones prácticas.
2.5.1. Historia de la Inteligencia Artificial
Galán et al (2000), cita que a mediados de los años 80, se produce el
desarrollo teórico por parte de grupos de trabajo universitarios que plantean
el fundamento teórico de este tipo de sistemas desde la perspectiva de la
inteligencia artificial, el control y la interacción de sistemas jerárquicos. Se
desarrollan las primeras aplicaciones de sistemas expertos reales:
- Sistemas de 1° Generación, en los que se logra implantar conocimiento de
control, tomado de operadores expertos, en forma de reglas.
- Sistemas de 2° Generación, basados en modelos de los procesos que
manejan.
En esta época, también, aparecen las primeras herramientas específicas
que permiten el desarrollo eficaz de sistemas inteligentes de control.
Pero ha sido en la década de los 90 cuando el control inteligente ha
alcanzado su desarrollo. Los centros de investigación, libros, conferencias,
congresos y reuniones científicas dedicados al tema son numerosos.
Mención
especial
merecen
los
proyectos
internacionales
de
investigación financiados por entidades europeas o americanas, que han
65
realizado una importante labor de desarrollo de técnicas y transferencia de
tecnología dando lugar a muchas aplicaciones industriales.
El control inteligente es el resultado de la intersección del Control
Automático, la Inteligencia Artificial y los sistemas informáticos distribuidos de
tiempo real (Galán et al, 2000.)
Uno de los objetivos de esta investigación es el desarrollo del modelo
matemático a través de técnicas de inteligencia artificial. Para este caso se
utilizará la lógica difusa, ya que es una técnica que tiene una buena
correspondencia en cuanto al diagnóstico de fallas así como también en la
toma de decisiones a ser aplicada en el mejoramiento de la distribución de
gas de alta presión. A continuación se exponen las características más
resaltantes de esta técnica.
2.6.
Lógica Difusa
Una de las disciplinas matemáticas con mayor número de seguidores
actualmente es la llamada lógica difusa o borrosa, que es la lógica que utiliza
expresiones que no son ni totalmente ciertas ni completamente falsas, es
decir, es la lógica aplicada a conceptos que pueden tomar un valor
cualquiera de veracidad dentro de un conjunto de valores que oscilan entre
dos extremos, la verdad absoluta y la falsedad total. Conviene recalcar que lo
que es difuso, borroso, impreciso o vago no es la lógica en sí, sino el objeto
66
que estudia: expresa la falta de definición del concepto al que se aplica. La
lógica difusa permite tratar información imprecisa, como estatura media o
temperatura baja, en términos de conjuntos borrosos que se combinan en
reglas para definir acciones: si la temperatura es alta entonces enfriar mucho.
De esta manera, los sistemas de control basados en lógica difusa combinan
variables de entrada, definidas en términos de conjuntos difusos, por medio
de grupos de reglas que producen uno o varios valores de salida. (Pérez,
2005).
2.6.1. Breve Reseña Histórica y Aplicaciones
La lógica difusa fue investigada, por primera vez, a mediados de los años
sesenta en la Universidad de Berkeley (California) por el ingeniero Lotfy A.
Zadeh, cuando se dio cuenta de lo que él llamó principio de incompatibilidad:
“Conforme la complejidad de un sistema aumenta, nuestra capacidad para
ser precisos y construir instrucciones sobre su comportamiento disminuye
hasta el umbral más allá del cual, la precisión y el significado son
características excluyentes”. Introdujo entonces el concepto de conjunto
difuso (Fuzzy Set) bajo el que reside la idea de que los elementos sobre los
que se construye el pensamiento humano no son números sino etiquetas
lingüísticas. La lógica difusa permite representar el conocimiento común, que
es mayoritariamente del tipo lingüístico cualitativo y no necesariamente
67
cuantitativo, en un lenguaje mate mático a través de la teoría de conjuntos
difusos y funciones caracterís ticas asociadas a ellos. Permite trabajar a la
vez con datos numéricos y términos lingüísticos; los términos lingüísticos son
inherentemente menos precisos que los datos numéricos pero en muchas
ocasiones aportan una información más útil para el razonamiento humano.
(Pérez, 2005).
El aspecto central de los sistemas basados en la teoría de la lógica difusa
es que, a diferencia de los que se basan en la lógica clásica, tienen la
capacidad
de
reproducir aceptablemente los modos usuales del
razonamiento, considerando que la certeza de una proposición es una
cuestión de grado. Más formalmente se puede decir que si la lógica es la
ciencia de los principios formales y normativos del razonamiento, la lógica
difusa o borrosa se refiere a los principios formales del
razonamiento
aproximado, considerando el razonamiento preciso (lógica clásica) como
caso límite. Así pues, las características más atractivas de la lógica difusa
son su flexibilidad, su tolerancia con la imprecisión, su capacidad para
modelar problemas no -lineales, y su base en el lenguaje natural. (Gutiérrez
et.al, 1992)
Aunque la lógica difusa es conocida con este nombre desde que Zadeh la
bautizó así en 1965, la idea que se esconde tras ella y sus orígenes se
remontan hasta 2.500 años atrás. Los filósofos griegos, Aristóteles entre
ellos, consideraban que existían ciertos grados de veracidad y falsedad y
Platón ya trabajó con grados de pertenencia. (Pérez, 2005).
68
El término borroso aplicado a la lógica y a la teoría de conjuntos y
sistemas procede de la expresión fuzzy sets (conjuntos borrosos) citada por
Lofti A. Zadeh, brillante ingeniero eléctrico iraní nacionalizado en Estados
Unidos, profesor en las más prestigiosas universidades norteamericanas y
doctor honoris causa de varias instituciones académicas. Sus tesis
entroncan, como podemos observar, con la obra de pensadores de distintas
disciplinas que tenían una visión similar de los problemas
alejada de la
lógica tradicional. La paradoja del conjunto de Bertrand Russell, el principio
de incertidumbre de la física cuántica de W. Heisenberg, la teoría de los
conjuntos vagos de Max Black, sin olvidar la fundamental aportación del
polaco Jan Lukasiewicz, creador de la lógica multivaluada, influyeron para
que Zadeh publicase su famoso ensayo "Fuzzy Sets" en "Informations and
Control" en 1965 y más tarde “Fuzzy algorithm” en la misma revista en 1968.
Mientras que Russell y Black utilizaron el término vagueness (vaguedad,
vago) para referirse a la nueva lógica o para calificar a los conjuntos en la
teorización sobre los mismos, Zadeh prefirió el término fuzzy (borroso, difuso)
para denominar a sus conjuntos y a la lógica en la que se apoya su análisis.
(Pérez, 2005).
Aunque en un principio la lógica difusa encontró una fuerte resistencia
entre la comunidad científica, algunos investigadores se convirtieron en
seguidores de las teorías de Zadeh y mientras él siguió ampliando y
asentando los fundamentos de la teoría de conjuntos difusos estos
investigadores exploraron estas nuevas teorías durante la década posterior
69
a su nacimiento. Además de las contribuciones del propio Zadeh, otros
autores como Bellman, Lakoff, Goguen, Kohout, Smith, Sugeno, Chang,
Dunn, Bezdek, Negoita, Mizumoto,Tanaka, Kandel, Zimmermann, entre
otros,
hicieron aportaciones al desarrollo de las bases de esta teoría.
Durante esta primera década, gran parte de estructuras lógicas y
matemáticas son generalizadas en términos de lógica difusa: relaciones
lógicas, funciones, grupos, operaciones, operadores, algoritmos, entre otros.
(Pérez, 2005).
A principios de la década de los setenta, se establecen varios grupos de
investigación en lógica difusa en algunas pequeñas universidades japonesas;
los profesores Terano y Shibata en Tokio y los profesores Tanaka y Asai en
Osaka, y pese a encontrar también un ambiente hostil en estos primeros
años de investigación, hacen grandes contribuciones tanto al desarrollo de la
teoría de la lógica difusa como al estudio de sus aplicaciones. (Pérez, 2005).
Un hito importante en el desarrollo de la lógica difusa fue establecido por
Assilian y Mamdani en 1974 en el Reino Unido
al desarrollar el primer
controlador difuso diseñado para una máquina de vapor, pero la primera
implantación real de un controlador de este tipo fue realizada en 1980 por
F.L. Smidth & Co. en una planta cementera en Dinamarca. En 1983 Fuji
aplica la lógica difusa para el control de inyección química en plantas
depuradoras de agua por primera vez en Japón y en 1987 Hitachi pone en
marcha un controlador fuzzy para el control del tren-metro de Sendai, y la
70
empresa Omron desarrolla los primeros controladores difusos comerciales.
(Pérez, 2005).
Paralelamente al desarrollo de las aplicaciones de la lógica difusa,
investigadores teórico siguen, en la década de los ochenta, el camino
iniciado por Mamdani. Así, Takagi y Sugeno desarrollan la primera
aproximación para construir reglas fuzzy a partir de datos de entrenamiento,
y aunque en un principio no tiene mucha repercusión, más tarde será el
punto de partida para investigar la identificación de modelos fuzzy. Otro de
los factores que contribuye a seguir con la investigación en este campo es el
creciente interés en las redes neuronales y su similitud con los sistemas
fuzzy; la tendencia es buscar vías de relación entre las dos técnicas y los
resultados son los llamados neuro -fuzzy systems, sistemas fuzzy que usan
métodos de aprendizaje basados en redes neuronales para identificar
y
optimizar sus parámetros. B. Kosko es conocido por su contribución a los
sistemas neuro -fuzzy y con sus publicaciones introdujo en la lógica difusa a
muchos lectores interesados en las redes neuronales. (Pérez, 2005).
En la década de los noventa, además de las redes neuronales y los
sistemas
fuzzy, hacen su aparición
los algoritmos genéticos. Estas tres
técnicas computacionales, que pueden combinarse de múltiple maneras y se
pueden considerar complementarias, son herramientas de trabajo muy
potentes en el campo de los sistemas de control en la última década. (Pérez,
2005).
71
En realidad, la intención original del profesor Zadeh era crear un
formalismo para manipular de forma más eficiente la imprecisión y la
vaguedad del razonamiento humano expresado lingüísticamente, sin
embargo causó cierta sorpresa que el éxito de la lógica borrosa llegase en el
campo del control automático de procesos. Esto se debió básicamente al
boom que la lógica borrosa causó en Japón, iniciado en 1987 y que alcanzó
su máximo apogeo a principios de los noventa. Este boom fue el resultado
de una estrecha colaboración entre el gobierno, las universidades y las
industrias japonesas, estableciéndose dos proyectos nacionales a gran
escala llevados a cabo por el Ministerio de Industria y Comercio (MITI) y la
Agencia de Ciencia y Tecnología (STA) en consorcio con el LIFE, Laboratory
for International Fuzzy Research, y en los que se involucraron más de 50
compañas durante seis años.
Desde entonces, han sido infinidad los
productos lanzados al mercado que usan tecnología borrosa, muchos de
ellos utiliza ndo la etiqueta fuzzy como símbolo de calidad y prestaciones
avanzadas. El control difuso ha sido aplicado con éxito en muy diversas
ramas tecnológicas, por ejemplo la metalurgia, robots para la fabricación,
controles de maniobras de aviones, sensores de imagen y sonido (sistema
de estabilización de la imagen en cámaras fotográfica y de video Sony,
Sanyo y Cannon), lavadoras (Panasonic
y Bosch) que son capaces de
autorregular la cantidad de jabón que requiere un lavado dependiendo del
grado de suciedad de la ropa,
aire acondicionado (Mitsubishi) en el que el
sistema fuzzy evita las oscilaciones entre el exceso y el defecto de
72
temperatura ), rice-cooker capaces de elaborar diversas variedades de arroz
regulando la cantidad de agua y la temperatura en cada caso para que el
grano quede cocido y suelto , en automoción, sistemas de frenado ABS
(Mazda
y Nissan), cambio automático de Renault, control automático de
velocidad que
controla la frenada en casos peligrosos y selecciona la
relación de marchas a partir del rendimiento del motor, climatizadores,
fotocopiadoras (ajusta el voltaje del tambor a partir de la densidad de la
imagen, la temperatura y la humedad), lavaplatos (ajusta el ciclo de lavado y
enjuague a partir del número de platos y cantidad de comida adherida),
ascensores (reduce el tiempo de espera a partir del número de personas),
humidificadores (ajusta el contenido de humedad a las condiciones de la
habitación), mejoras en imágenes médicas (ajustando el contraste en los
bordes), sistemas de reconocimiento de escritura, hornos microondas
(establece y afina el programa de energía y cocción), neveras (establece los
tiempos de descongelación y enfriamiento en función del uso que se haga),
televisores (ajusta el color de la pantalla y
la textura de cada imagen),
mecanismos de atraque automático de naves espaciales, sistemas
automáticos de regulación de la cantidad de anestesia que se suministra a
los pacientes en un quirófano aunque bajo supervisión médica, por supuesto ,
sistemas de concesión o denegación automática de créditos según el perfil
económico del solicitante, entre otros. Estas son algunas de las muchísimas
aplicaciones de la lógica difusa, que ya están funcionando en el campo de
73
los llamados sistemas expertos. Todos estos sistemas utilizan información,
esencialmente, imprecisa con el fin de lograr sus cometidos. (Pérez, 2005).
La lógica difusa está teniendo, por lo tanto, bastante éxito en su utilización
sobre los sistemas de control, aplicación que ya podría considerarse como
rutinaria. Sin embargo, los investigadores buscan nuevos campos de
aplicación de esta técnica. Se investiga en áreas como el reconocimiento de
patrones visuales o la identificación de segmentos de ADN, por mencionar
dos
ejemplos.
Además,
según
algunos
de
los
más
prestigiosos
investigadores en Internet, parece que el futuro para abordar la ingente
cantidad de datos, recuperar la información, controlar y gestionar la red, pasa
por el uso de las tecnologías borrosas. Esta intuición parece ser que coincide
con la nueva orientación que, según el profesor Zadeh, debe seguir la lógica
borrosa. Prueba de ello fue la celebración del primer encuentro sobre lógica
borrosa e internet en el año 2001 en la universidad de Berkeley organizado
por el propio Zadeh. (Pérez, 2005).
2.6.2. Conjuntos Difusos y Funciones Características
El primer ejemplo utilizado por Lofti A. Zadeh, para ilustrar el concepto de
conjunto difuso, fue el conjunto “hombres altos”. Según la teoría de la lógica
clásica el conjunto “hombres altos” es un conjunto al que pertenecerían los
hombres con una estatura mayor a un cierto valor, que podemos establecer
74
en 1.80 metros, por ejemplo, y todos los hombres con una altura inferior a
este valor quedarían fuera del conjunto. Así tendríamos que un hombre que
mide 1.81 metros de estatura pertenecería al conjunto hombre altos, y en
cambio un hombre que mida 1.79 metros de altura ya no pertenecería a ese
conjunto. Sin embargo, no parece muy lógico decir que un hombre es alto y
otro no lo es cuando su altura difiere en dos centímetros. El enfoque de la
lógica difusa considera que el conjunto “hombres altos” es un conjunto que
no tiene una frontera clara para pertenecer o no pertenecer a él: mediante
una función que define la transición de “alto” a “no alto” se asigna a cada
valor de altura un grado de pertenencia al conjunto, entre 0 y 1. Así por
ejemplo , un hombre que mida 1.79 podría pertenecer al conjunto difuso
“hombres altos” con un grado 0.8 de pertenencia, uno que mida 1.81 con un
grado 0.85, y uno que mida 1.50 m con un grado 0.1. Visto desde esta
perspectiva se puede considerar que la lógica clásica es un caso límite de la
lógica difusa en el que se asigna un grado de pertenencia 1 a los hombres
con una altura mayor o igual a 1.80 y un grado de pertenencia 0 a los que
tienen una altura menor (ver Figura 12). (Mendel, 1995)
75
Figura 12. Lógica Difusa versus Lógica Clásica
Fuente: Mendel (1995)
Así pues, los conjuntos difusos pueden ser considerados como una
generalización de los conjuntos clásicos: la teoría clásica de conjuntos sólo
contempla la pertenencia o no pertenencia de un elemento a un conjunto, sin
embargo la teoría de conjuntos difusos contempla la pertenencia parcial de
un elemento a un conjunto, es decir, cada elemento presenta un grado de
pertenencia a un conjunto difuso que puede tomar cualquier valor entre 0 y 1.
Este grado de pertenencia se define mediante la función característica
asociada al conjunto difuso: para cada valor que pueda tomar un elemento o
variable de entrada x la función característica µA (x) proporciona el grado de
pertenencia de este valor de x al A conjunto difuso A. (Mendel, 1995)
Formalmente, un conjunto clásico A, en un universo de discurso U, se
puede definir de varias formas: enumerando los elementos que pertenecen al
76
conjunto, especificando las propiedades que deben cumplir los elementos
que pertenecen a ese conjunto o, en términos de la función de pertenencia
µA (x) (Ec. 33):
Podemos además decir que el conjunto A es matemáticamente
equivalente a su función de pertenencia o característica µA (x), ya que
conocer µA (x) es lo mismo que conocer A. (Mendel,1995)
Un conjunto difuso en el universo de discurso U se caracteriza por una
función de pertenencia µA (x) que toma valores en el intervalo [0.1], y puede
representarse como conjunto de pares ordenados de un elemento x y su
valor de pertenencia al conjunto (Ec.31):
Ec. 31
Muchos conceptos de teoría clásica de conjuntos se pueden hacer
extensivos a los conjuntos difusos, otros son exclusivos e inherentes a la
teoría de conjuntos difusos.
Algunos de los más utilizados son los siguientes (Mendel, 1995):
•
El soporte de un conjunto difuso A en el universo de discurso U es un
conjunto “crisp” (numérico) que contiene todos los elementos de U que tienen
un valor de pertenencia distinto de cero en A, esto es (Ec.31),
77
Ec. 31
•
Si el soporte de un conjunto difuso no contiene ningún elemento
tendremos un conjunto difuso vacío. Si el soporte de un conjunto difuso es un
solo punto tendremos lo que se conoce como “singleton” difuso.
•
El punto de cruce de un conjunto difuso es el punto de U cuyo valor de
pertenencia al conjunto es igual a 0.5.
•
Dos conjuntos difusos A y B son iguales si y sólo si sus funciones
características µA (x) y µB(x) son iguales.
•
El conjunto difuso B contiene al conjunto difuso A, esto es A c B, si y
sólo sí, µA (x) = µB (x) para todo x € U.
La función característica proporciona una medida del grado de similaridad
de un elemento de U con el conjunto difuso.
La forma de la función
característica utilizada, depende del criterio aplicado en la resolución de cada
problema y variará en función de la cultura, geografía, época o punto de vista
del usuario. La única condición que debe cumplir una función característica
es que tome valores entre 0 y 1, con continuidad. Las funciones
características más comúnmente utilizadas por su simplicidad matemática y
su manejabilidad son: triangular, trapezoidal, gaussiana, sigmoidal, gamma,
pi, campana, entre otros, (ver Figura 13). Conceptualmente existen dos
aproximaciones para determinar la función característica asociada a un
conjunto: la primera aproximación está basada en el conocimiento humano
78
de los expertos, y la segunda aproximación es utilizar una colección de datos
para diseñar la función (Yen et.al,1999).
Figura 13. Algunas de las funciones características más habituales: (a)
triangular, (b) trapezoidal, (c) gaussiana y (d) sigmoidal.
Fuente: Yen (1999)
El número de funciones características asociadas a una misma variable
es elegido por
el experto: a mayor número de funciones características
tendremos mayor resolución pero también mayor complejidad computacional;
además estas funciones pueden estar solapadas o no, el hecho de estar
solapadas pone de manifiesto un aspecto
clave de la lógica difusa: una
variable puede pertenecer con diferentes grados a varios conjuntos difusos a
la vez , es decir, “el vaso puede estar medio lleno y medio vacío a la vez”
(Yen et.al,1999).
79
2.6.3. Inferencia Difusa
Se llama reglas difusas al conjunto de proposiciones IF -THEN que
modelan el problema que se quiere resolver. Una regla difusa simple tiene la
forma:
“si u es A entonces v es B”
dónde A y B son conjuntos difusos definidos en los rangos de “u” y “v”
respectivamente.
Una regla expresa un tipo de relación entre los conjuntos A y B cuya
función característica sería
y representa lo que conocemos
como implicación lógica.
La elección apropiada de esta función
característica está sujeta a las reglas de la lógica proposicional. (Pérez,
2005)
Como es bien sabido se puede establecer un isomorfismo entre la teoría
de conjuntos, la lógica proposicional y el álgebra booleana que garantiza que
cada teorema enunciado en una de ellas tiene un homólogo en las otras dos.
La existencia de estos isomorfismos nos permitirá traducir las reglas difusas
a relaciones entre conjuntos difusos y éstas a términos de operadores
algebraicos con los que podremos trabajar. (Pérez, 2005)
80
2.6.4. Diagrama de bloques de un sistema basado en lógica difusa.
El esquema de un sistema basado en técnicas de lógica difusa se
presenta en la Figura 14:
Figura 14. Esquema General de un sistema basado en lógica difusa
Fuente: Pérez (2005)
Está compuesto por los siguientes bloques (Pérez, 2005):
- Bloque Difusor: bloque en el que a cada variable de entrada se le asigna un
grado de pertenencia a cada uno de los conjuntos difusos que se ha
considerado, mediante las funciones características asociadas a estos
conjuntos difusos. Las entradas a este bloque son valores concretos de las
variables de entrada y las salidas son grados de pertenencia a los conjuntos
difusos considerados.
- Bloque de Inferencia: bloque que, mediante los mecanismos de inferencia,
relaciona conjuntos difusos de entrada y de salida y que representa a las
reglas que definen el sistema. Las entradas a este bloque son conjuntos
difusos (grados de pertenencia) y las salidas son también conjuntos difusos,
81
asociados a la variable de salida. En esta etapa se crean una serie de
condiciones en lenguaje de programación con estructura IF THEN, las cuales
gobiernan las acciones del controlador según los valores lingüísticos que
tomen las variables.
- Desdifusor: bloque en el cual a partir del conjunto difuso obtenido en el
mecanismo de inferencia y mediante los métodos matemáticos de
desdifusión, se obtiene un valor concreto de la variable de salida, es decir, el
resultado. Los métodos de desdifusión son los siguientes:
Método del Máximo: se elige como valor para la variable de salida aquel para
el cual la función característica del conjunto difuso salida es máxima. En
general, no es un método óptimo, ya que este valor máximo puede ser
alcanzado por varias salidas.
Método del Centroide: utiliza como salida el centro de gravedad de la función
característica de salida. Matemáticamente
Ec. 32
Es el método más utilizado en aplicaciones de lógica difusa a la ingeniería
ya que se obtiene una solución única, aunque a veces es difícil de calcular.
Método de la Altura: se calcula para cada regla el centro de gravedad del
conjunto difuso de salida Bm y después se calcula la salida como la media
ponderada (Ec. 33):
82
Ec. 33
2.6.5. Ventajas y Desventajas en el uso de Lógica Difusa
Ferrer
(2004),
sistemáticamente
señala
trasladar
que
la
lógica
información
difusa
heurística,
puede
facilitar
lingüística
y
y
de
conocimiento cualitativo (preferido por humanos) a números y cantidades
(preferido por las computadora) y viceversa. Esto provee de un método
simple de implementación heurística para realizar la detección de fallas y
para interpretar y analizar sus resultados.
Coli na y Ríos (1998) expresan que el sistema de control lógico difuso es
un tipo de sistema experto basado en el conocimiento que contiene el
algoritmo de control en una base simple de reglas. El conocimiento
codificado en la base de reglas se deriva de la experiencia y de la intuición
humana, además del conocimiento teórico y práctico que se disponga del
controlado. Lo que hace al control difuso especial y conceptualmente
diferente del control convencional es la falta de una descripción analítica.
A continuación se presentan algunas ventajas y desventajas:
Ventajas:
•
Son una forma fácil de codificar un sistema no lineal.
•
Tiene una buena correspondencia a la forma del pensamiento humano
sobre una gran clase de problemas matemáticos.
83
•
Los
sistemas
expertos
difusos
los
ejecutan
a
velocidades
extremadamente altas sobre el hardware especializado.
Desventajas:
•
Es difícil llegar a una función de membresía y a una regla confiable sin
la participación de un experto humano.
•
No hay actualmente un análisis matemático riguroso que garantice
que el uso de un sistema experto difuso para controlar un sistema de
cómo resultado un sistema estable.
•
Son sistemas sin memoria, no poseen la capacidad de aprender.
2.7. Sistemas de Supervisión Inteligente
Según Ramírez (2010), la supervisión inteligente de procesos industriales
es un área de intensos estudios de investigación y se han usado múltiples
enfoques basados en técnicas de inteligencia artificial; que por lo general
conllevan a un esquema resultante basado en un sistema híbrido.
La supervisión inteligente está basada en la evaluación global del punto
actual de operación del proceso (Lunze, 2000); y permite caracterizar la
evolución temporal de los parámetros de un sistema, dentro de la perspectiva
de proveer diagnostico y/o de anticipar posibles cambios no deseados en el
estado de operación en un determinado proceso a través del ajuste de
84
parámetros escalares de controladores o de cambios en la consigna de
operación.
De entre la amplia variedad de esquemas de supervisión inteligente
propuestos en varias publicaciones, como por ejemplo en (Altamiranda et al.,
2002; Ortega et al., 2007; Rodríguez et al., 2003), se pueden determinar tres
elementos fundamentales: el detector de eventos, el modelo del proceso y el
sistema de toma de decisión. El detector de eventos puede ser realizado de
múltiples maneras, en particular, las técnicas más usadas han sido basadas
en la lógica difusa y las redes neuronales; y buscan en esencia la posible
clasificación de los estados de operación de un determinado proceso. Para
determinar el modelo de un proceso existen múltiples alternativas como los
modelos
cualitativos,
ampliamente
recomendados
en
esquemas
de
supervisión o modelos no lineales basados en modelos locales del tipo
Takagi-Sugeno (Ramírez and Colina, 2009). Más aún, existe una alternativa
denominada modelado multiresolucional, la cual, integra un modelo
matemático, un modelo basado en conocimiento y un modelo cualitativo
(Lunze, 2000). Finalmente, el sistema de toma de decisión, en base a una
serie de objetivos y prioridades del proceso, ejecuta ciertas acciones sobre el
proceso y/o sobre los controladores que se traducen en cambios en el punto
de consigna o cambios de parámetros escalares de controladores.
Es importa nte destacar que dentro de una perspectiva general, la
supervisión de procesos suele implicar las siguientes operaciones: (a)
detección de desviación de los parámetros de la planta, (b) sintonización,
85
adaptación y síntesis de controladores y (c) identificación y diagnóstico de
fallas de un proceso.
Por otra parte Camargo et.al (2010), menciona que los sistemas de
supervisión inteligente son aquellos capaces de atribuir las siguientes
cualidades a los sistemas que están supervisados tales como: autonomía en
la toma de decisiones de los procesos, adelanta el efecto de las tareas de
supervisión en sí misma, capacidad de adaptación al posible aprendizaje
sobre la ocurrencia de eventos en el sistema industrial bajo supervisión,
capacidad de auto diagnóstico y posible distribución de inteligencia a nivel de
procesos para la toma de decisiones de manera local, minimizando así el
tiempo de respuesta de las tareas de supervisión, entre otras.
3.- Definición de términos básicos.
BPD: Unidad de medida de petróleo, significa barriles por día.
Control automático de procesos: Es una manera de mantener la
variable controlada en eI punto de control, a pesar de las perturbaciones”.
(Smith-Corripio, 1995)
Gas Natural: fluido en estado gaseoso formado por la acción de la
naturaleza. Mezcla de hidrocarburos que se encuentra en la naturaleza en
estado gaseoso, por sí sola o asociada con el petróleo, y que permanece así
en condiciones normales de temperatura y presión. Se emplea como
86
combustible doméstico, en la generación de electricidad y como insumo
industrial, en petroquímica. En su composición prevalece el metano, aunque
también incluye etano y otros hidrocarburos de la cadena parafínica más
pesados y en menor proporción.
También puede contener otros componentes como nitrógeno, sulfuro de
hidrógeno, helio, dióxido de carbono, agua, etc. Mezcla de hidrocarburos en
estado gaseoso que suele obtenerse por el fraccionamiento de la parte más
liviana del petróleo o porque se encuentre libre en yacimientos. Se consigue
en el subsuelo en su forma natural y se usa sin que intervenga la mano del
hombre en la transformación de la molécula. Combustible que procede de
formaciones geológicas. (Martínez M, 2000)
Gas de levantamiento artificial (LIFT): el usado en el levantamiento
artificial. Método para llevar a la superficie el petróleo o el agua mediante la
inyección de gas en un pozo productor. (Martínez M, 2000)
LPPC: Unidad de medida de presión, significa libras por pulgadas
cuadradas. También se p uede representar como PSI.
MMPCD: Unidad de medida de inyección de gas, significa millones de
pies cúbicos diarios.
Modelo matemático: “Un modelo matemático de un sistema simple sirve
para predecir cambios, diseñar nuevos esquemas de control, para conocer
los parámetros de entrada, predecir las salidas y para simular, para entender
la relación entre las entradas y salidas de un proceso”. (Smith-Corripio,
1995).
87
Modelación: Es el desarrollo de las ecuaciones que describen los
diferentes procesos y se utilizan para aplicaciones avanzadas. (SmithCorripio, 2001).
Modelo: Es la manera como las variables se relacionan entre sí y su
complejidad y el formalismo matemático que lo acompaña en función del uso
que se dará. ( Smith-Corripio, 2001,).
Múltiple de Gas: Es una plataforma o instalación que tiene como función
principal recolectar el flujo gaseoso por medio de manifuel o cañón y
distribuirlo por medio de las escopetas a los pozos por las líneas inyectoras
de gas.(Nava et.al, 2008).
Planta: es el elemento físico que se desea controlar. Planta puede ser: un
motor, un horno, un sistema de disparo, un sistema de navegación, un
tanque de combustible, etc. (Greene, 2005)
Proceso: Es el proceso esencial de un lazo de control. Es una operación
que conduce a un resultado determinado o cualquier operación que se va a
controlar. (Ogata, 1993).
Simulación de procesos: tiene como objetivo la representación de un
proceso por un modelo matemático, que se resuelve a fin de predecir el
comportamiento del sistema y evaluar posibles cambios en las condiciones
de operación,
2004).
basándose en balances de masa y energía.(Chavez et.al,
88
La simulación de procesos en forma computarizada permite estudiar un
sistema en línea, es decir, realizar experimentos con el proceso de la misma
manera como se haría en un caso real.
Sistema:
Consiste
en
un
conjunto
de
elementos
que
actúan
coordinadamente para realizar un objetivo determinado. (Ogata , 1993).
4.- Sistema de Variables
Variable: Sistema de Supervisión Inteligente:
Definición Conceptual:
Según Lunze (2000), la supervisión inteligente está basada en la
evaluación global del punto actual de operación del proceso y permite
caracterizar la evolución temporal de los parámetros de un sistema, dentro
de la perspectiva de proveer diagnostico y/o de anticipar posibles cambios no
deseados en el estado de operación en un determinado proceso a través del
ajuste de parámetros escalares de controladores o de cambios en la
consigna de operación.
Definición Operacional:
La supervisión inteligente es un sistema que proporciona la capacidad de
medir, controlar, diagnosticar, identificar y optimizar el proceso de distribución
89
de gas a través de la línea troncal MLAG-TJ-3-02/MLAG-TJ-3-03 mediante el
modelado de fluidos comprensible por medio de leyes físicas aplicando la
técnica de inteligencia artificial lógica difusa a través de la identificación de
escenarios generadores de inestabilidad para la toma de decisiones de
manera local, logrando por esta vía la entonación del controlador,
minimizando de esta manera el tiempo de respuesta de las tareas de
supervisión del sistema de distribución de gas. Todo esto permitirá que el
sistema supervisado funcione de forma autónoma en la dinámica del entorno ,
alcanzándose los fines antes mencionados.