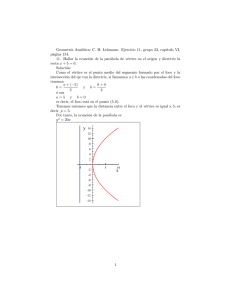
“Planeación de vídeos-tutoriales: Cónicas” Parábola

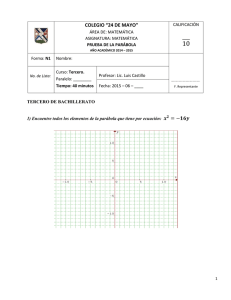
“Planeación de vídeos-tutoriales: Cónicas”
Adriana Serna García; Jonathan E. Martínez Medina; Luis Eduardo Gómez Ojeda
[email protected]; [email protected]; [email protected]
Licenciatura en Matemática Educativa
Universidad Autónoma de San Luis Potosí, Facultad de Ciencias, México.
Parábola
En este tutorial se presentará el concepto, los elementos y las ecuaciones de la parábola.
-Primero se muestra el siguiente concepto de parábola:

El lugar geométrico de todos los puntos en el plano que equidistan de un punto fijo
llamado foco y de una recta fija llamada directriz.
Después de dar la definición se hace una explicación, enfatizando en la propiedad que
caracteriza a la parábola mediante un gráfico:
-Se citan los elementos que conforman a la parábola, dando una explicación de cada uno de
ellos, así como su representación gráfica.
1) Foco (F): punto fijo
2) Directriz (d): recta fija
3) Eje Focal o eje de simetría (FV): recta que pasa por el foco y es perpendicular a la
directriz.
4) Radio focal o radio vector (AF): segmento de recta cuyos extremos son el foco y un
punto que pertenece a la parábola.
5) Cuerda (GH): segmento que une dos puntos cualesquiera de la parábola.
6) Cuerda focal (DE): cuerda que pasa por el foco.
7) Lado recto o ancho focal (IJ): cuerda focal paralela a la directriz.
8) Vértice (V): punto de la parábola que se encuentra en el eje focal.
Se mencionaron otras características, tales como:
1) El vértice y el foco están siempre en el eje focal.
2) La distancia de la directriz al vértice es siempre igual a la distancia del vértice al
foco. A esta distancia le llamaremos p y a la distancia entre el foco y la directriz la
se le llama parámetro y se representa por 2p.
3) En todos los casos la parábola se abre en dirección a foco por lo que nunca toca a la
directriz.
-Por último se presentan las ecuaciones que representan a la parábola, dividiéndose en dos
caso:
1) Ecuaciones de la parábola cuando su vértice esta en el origen de los ejes coordenados:




𝑦 2 = 4𝑝𝑥: Si p>0 y el eje focal es horizontal, entonces la parábola se abre hacia la
derecha.
𝑦 2 = −4𝑝𝑥: Si p<0 y el eje focal es horizontal, entonces la parábola abre hacia la
izquierda.
𝑥 2 = 4𝑝𝑦: Si p>0 y el eje focal es vertical, entonces la parábola abre hacia arriba.
𝑥 2 = −4𝑝𝑦: Si p<0 y el eje focal es vertical, entonces la parábola abre hacia abajo.
2) Ecuaciones de la parábola cuando su vértice esta en otro punto del plano


(𝑦 − 𝑘)2 = ±4𝑝(𝑥 − ℎ): Si el eje focal es paralelo al eje x.
(𝑥 − ℎ)2 = ±4𝑝(𝑦 − 𝑘): Si el eje focal es paralelo al eje y.
Elipse
Vídeo online:http://www.showme.com/sh/?h=mYlfX0K
- Se presenta la definición:

Es el conjunto de puntos en el plano tales que la suma de sus distancias a dos puntos
fijos llamados focos es constante y mayor que la distancia entre los focos.
- Se presentan la gráfica que define a la elipse, y se explica cuáles son los elementos
constitutivos de la elipse y el nombre de cada uno de ellos.
F y F´ son los focos
FF´= 2c es la distancia focal
V y V´ vértices del eje mayor
VV´= 2a es la longitud del eje mayor
B y B´ vértices del eje meno
BB´= 2b es la longitud del eje menor
C (h, k) es el centro de la elipse
P es un punto cualquiera de la elipse
a
B
P
B
c
b
V
V´
F
C
F´
B´
V
V´
F
C
F´
B´
- Se presentan las ecuaciones ordinarias que definen tanto elipses horizontales y verticales
con centro en el origen y ecuaciones ordinarias horizontales y verticales fuera del origen.
Ecuación de elipse horizontal
con centro en el origen
Ecuación de elipse vertical con
centro en el origen
Ecuación de elipse horizontal
fuera del origen
Ecuación de elipse vertical fuera
del origen
- Se muestra la importancia de estudiar a la elipse y se mencionan algunas aplicaciones que
tiene en el mundo real.
Hipérbola
La hipérbola es el lugar geométrico de los puntos del plano tales que la diferencia de sus
distancias a dos puntos fijos llamados focos siempre es constante y menor que la distancia
entre los focos.
Sobre el eje x, la ecuación de la hipérbola con centro(ℎ, 𝑘) y que los focos situados a
𝑐unidades a la izquierda y a la derecho de centro
(𝑥 − ℎ)2 (𝑦 − 𝑘)2
−
=1
𝑎2
𝑏2
Los focos están en ℎ − 𝑐, 𝑘 y (ℎ + 𝑐, 𝑘)
Los vértices están en(ℎ − 𝑎, 𝑘) y (ℎ + 𝑎, 𝑘)
Las asíntotas en
(𝑥 − ℎ) (𝑦 − 𝑘)
−
=0
𝑎2
𝑏2
Sobre el eje y, la ecuación de la hipérbola con centro en(ℎ, 𝑘) y que los focos estan situados
a 𝑐unidadesarriba y abajodelcentro
(𝑦 − 𝑘)2 (𝑥 − ℎ)2
−
=1
𝑏2
𝑎2
Los focos están en ℎ, 𝑘 − 𝑐 y (ℎ, 𝑘 + 𝑐)
Los vértices están en(ℎ, 𝑘 − 𝑎) y (ℎ, 𝑘 + 𝑎)
Las asíntotas en
(𝑦 − 𝑘) (𝑥 − ℎ)
−
=0
𝑏2
𝑎2
En los dos casos
𝑎2 + 𝑏 2 = 𝑐 2
Ejemplo
Hipérbola con centro en el origen
Grafica de hipérbola con centro el origen.
Hiperbola con centroen(3, −2) y ejesen𝑎 = 5 , 𝑏 = 6
La ecuaciones
(𝑥 − 3)2 (𝑦 + 2)2
−
=1
25
36
𝑐 = 61
Los focosestanen 3 − 61, −2 y (3 + 61, −2)
Los vertices estanen(−2, −2) y (8, −2)
Las asintotasen
(𝑥 − 3) (𝑦 + 2)
−
=0
25
36
La grafica
Grafica de hiperbola con centroen(3, −2)