Ejes sólidos y esfuerzos cortantes

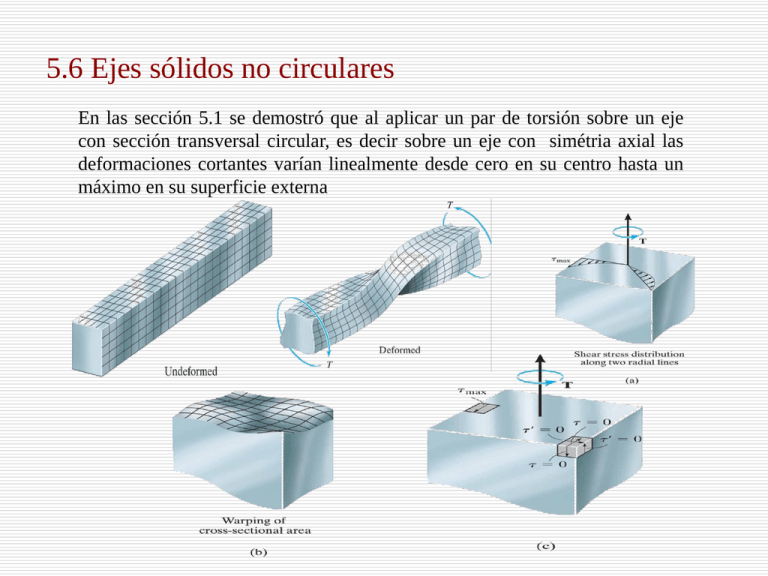
5.6 Ejes sólidos no circulares
En las sección 5.1 se demostró que al aplicar un par de torsión sobre un eje
con sección transversal circular, es decir sobre un eje con simétria axial las
deformaciones cortantes varían linealmente desde cero en su centro hasta un
máximo en su superficie externa
5.6 Ejes sólidos no circulares
Ejemplo 5.10
El eje de aluminio 6061-T6 mostrado tiene una sección transversal con forma de
triangulo equilátero. Determine el mayor par de torsión T que puede aplicarse sobre el
extremo del eje si el esfuerzo cortante permisible es τperm=8ksi y el ángulo de giro en
su extremo esta restringido a Φperm=0.02rad ¿De que tamaño puede ser el par de torsión
aplicado a un eje con sección transversal circular hecho con la misma cantidad de
material?
5.7 Tubos de pared delgada con secciones transversales
cerradas
Los tubos de pared delgada con sección transversal no circular se utilizan a
menudo para construir estructuras ligeras como las empleadas en aviones
Flujo cortante
En las figuras se muestran un pequeño elemento del tubo, con una una
longitud finita ¨s¨ y un ancho diferencial ¨dx ¨
Esfuerzo cortante promedio
El esfuerzo cortante promedio se puede relacionar con el par de torsión T al
considerar el par de torsión producido por este esfuerzo cortante alrededor de
un punto O seleccionado dentro de los limites del tubo
Angulo de giro
El ángulo de giro de un tubo con pared delgada y longitud L puede
determinarse mediante métodos de energía . Si el material se comporta de una
manera elástico-lineal y G es el modulo cortante, entonces este ángulo dado en
radianes puede expresarse como
La integral debe realizarse alrededor del limite del área de la sección
transversal del tubo.
Ejemplo 5.11
Calcule el esfuerzo cortante promedio en un tubo de pared delgada con un sección
transversal circular de radio medio rm y grosor t, el cual esta sometido a un par de torsión T
figura(a). Además ¿Cuál es el ángulo de giro relativo si el tubo tiene una longitud L?
Ejemplo 5.12
El tubo fabricado de bronce C86100 y tiene una sección transversal rectangular como se
muestra en la figura se somete a los dos pares de torsión mostrados en la figura, determine el
esfuerzo cortante promedio en el tubo en los puntos A y B. Además , ¿Cuál es el ángulo de
giro del extremo C? el tubo se encuentra fijo en E
Ejemplo 5.12
El tubo fabricado de bronce C86100 y tiene una sección transversal rectangular como se
muestra en la figura se somete a los dos pares de torsión mostrados en la figura, determine el
esfuerzo cortante promedio en el tubo en los puntos A y B. Además , ¿Cuál es el ángulo de
giro del extremo C? el tubo se encuentra fijo en E
Problema 5.95
Compare los valores del esfuerzo cortante elástico máximo y el ángulo de giro
desarrollados en ejes de acero inoxidable 304 con secciones transversales circular y
cuadrada. Cada eje tiene la misma área de 9 pulg2 y se somete a un para de torsión de
4000lb-pulg.
Máximo esfuerzo cortante
Para eje circular
Para eje rectangular
Problema 5.95
Compare los valores del esfuerzo cortante elástico máximo y el ángulo de giro
desarrollados en ejes de acero inoxidable 304 con secciones transversales circular y
cuadrada. Cada eje tiene la misma área de 9 pulg2 y se somete a un para de torsión de
4000lb-pulg.
Angulo de torsión
Para eje circular
Para eje rectangular
Problema 5.98
El eje esta hecho de latón rojo C83400 y tiene una sección transversal elíptica. Si se
somete a las cargas de torsión mostradas determine el esfuerzo cortante máximo dentro de
las regiones AC y BC, también encuentre el ángulo de giro Φ del extremo B con respecto
al extremo A
Máximo esfuerzo cortante
Problema 5.98
El eje esta hecho de latón rojo C83400 y tiene una sección transversal elíptica. Si se
somete a las cargas de torsión mostradas determine el esfuerzo cortante máximo dentro de
las regiones AC y BC, también encuentre el ángulo de giro Φ del extremo B con respecto
al extremo A
Angulo de torsión
Problema 5.100
Los segmentos AB y BC del eje tienen secciones transversales circular y cuadrada,
respectivamente. Si el extremo A se somete a un par de torsión T= 2kN-m, determine el
esfuerzo cortante máximo absoluto desarrollado en el eje y el ángulo de giro del extremo
A. el eje esta fabricado de acero A-36 y se encuentra fijo en C.
Máximo esfuerzo cortante: en los segmentos AB
Problema 5.100
Los segmentos AB y BC del eje tienen secciones transversales circular y cuadrada,
respectivamente. Si el extremo A se somete a un par de torsión T= 2kN-m, determine el
esfuerzo cortante máximo absoluto desarrollado en el eje y el ángulo de giro del extremo
A. el eje esta fabricado de acero A-36 y se encuentra fijo en C.
segmentos BC
Angulo de torsión
Problema 5.106
El eje de acero tiene 12 pulg de largo y se atornilla a la pared mediante una llave.
Determine el esfuerzo cortante máximo en el eje y cuanto se desplaza cada fuerza de par
si estas tienen una magnitud de F=30lb, Gac=10.8(10)3ksi
Problema 5.115
El tubo esta sometido a un par de torsión de 750N-m. Determine el esfuerzo cortante
promedio en los puntos A y B del tubo.
Refiriéndose ala geometría se muestra en la figura
Problema 5.119
El tubo simétrico esta fabricado de un acero de alta resistencia, con las dimensiones medias
mostradas en la figura y un grosor de 5 mm. Si se somete a un par de torsión de T=40 N·m
determine el esfuerzo cortante promedio desarrollado en los puntos A y B. Indique el
esfuerzo cortante sobre elementos de volumen ubicados en esos puntos
Problema 5.117
Las dimensiones medias de la sección transversal del borde delantero y la caja de torsión del
ala de un avión pueden aproximarse como se muestra en la figura. Si el ala esta fabricada de
una aleación de aluminio 2014-t6 con un esfuerzo cortante permisible de τ =125 Mpa y el
grosor de su pared es de 10 mm, determine el par de torsión máximo permisible y el ángulo
de giro correspondiente por metro de longitud del ala.
Problema 5.118
Las dimensiones medias de la sección transversal del borde delantero y la caja de torsión del
ala de un avión pueden aproximarse como se muestra en la figura. Si el ala se somete a un
par de torsión de 4.5 MN.m y el grosor de su pared es de 10 mm, determine el esfuerzo
cortante promedio desarrollado en el ala y su ángulo de giro por metro de longitud. El ala
esta fabricada de aluminio 2014-t6.
5.8 Concentración del esfuerzo
La formula de la torsión no puede aplicarse a las regiones de un eje que
tienen un cambio repentino en su sección transversal. Aquí las distribución de
esfuerzo cortante y deformación cortante en el eje se vuelven complejas por lo
que solo se pueden obtener mediante el uso de métodos experimentales o
posiblemente por medio de un análisis matemática basada en la teoría de la
elasticidad figura(a) coples , figura(b) cuñeros y figura(c) filetes
Ejemplo 5.13
El eje escalonado que se muestra en la figura(a), esta apoyado sobre cojines en A y B.
determine el esfuerzo máximo en el eje debido a los pares de torsión aplicados. El filete
ubicado en la unión de cada eje tiene un radio r=6mm
5.9 Torsión inelástica
Si las cargas de torsión aplicadas sobre el eje son excesivas, entonces el
material puede presentar cedencia y, en consecuencia debe usarse un
`análisis plástico´ para determinar la distribución del esfuerzo cortante y el
ángulo de giro elástico-lineal
Par de torsión elástoplastico
Considere que el material de un eje exhibe un comportamiento elástico perfectamente
plástico, como se muestra en la figura, este se caracteriza por un diagrama de esfuerzodeformación cortante creciente cuando el esfuerzo cortante alcanza el punto de
cedencia
Par de torsión elástoplastico
Par de torsión plástico
Los aumentos adicionales en T tienden a reducir el radio del núcleo elástico hasta que
todo el material cede. El material del eje estará sometido a un comportamiento
perfectamente plástico y la distribución del esfuerzo cortante se vuelve uniforme
En comparación con el par de torsión elástico TY
El par de torsión plástico es 33 por ciento mayor que
el par de torsión elástico máximo.
5.10 Esfuerzo residual
Cuando un eje se somete a deformaciones cortantes plásticas causadas por torsión, el
retiro del par de torsión hará que algunos esfuerzos cortantes permanezcan en el eje.
5.10 Esfuerzo residual
Como se produce una recuperación elástica, es posible superponer en la distribución del
esfuerzo de torsión plástica de la figura (a), una distribución lineal del esfuerzo causada
por la aplicación del par de torsión plástico Tp en dirección opuesta (b), acá el esfuerzo
cortante máximo se llama modulo de ruptura para la torsión.
Par de torsión ultimo
En general la mayoría de los materiales de ingeniería tendrán un diagrama de esfuerzo deformación cortante como el mostrado a continuación
Ejemplo 5.14
El eje tubular de la figura esta fabricado de una aleación de aluminio la cual se supone tiene
un diagrama τ-γ elastoplástico como se muestra. Determine el par de torsión máximo que
puede aplicarse al eje sin causar que el material ceda, y el par de torsión máximo o el par de
torsión plástico que se puede aplicar al eje. Además ¿Cuál debe ser la deformación cortante
mínima en la pared exterior para que se desarrolle un par de torsión totalmente plástico?
Par de torsión elástico
Ejemplo 5.14
El eje tubular de la figura esta fabricado de una aleación de aluminio la cual se supone tiene
un diagrama τ-γ elastoplástico como se muestra. Determine el par de torsión máximo que
puede aplicarse al eje sin causar que el material ceda, y el par de torsión máximo o el par de
torsión plástico que se puede aplicar al eje. Además ¿Cuál debe ser la deformación cortante
mínima en la pared exterior para que se desarrolle un par de torsión totalmente plástico?
Par de torsión plástico
Deformación cortante del radio
exterior
Ejemplo 5.15
Un eje circular solido tiene un radio de 20 mm y una longitud de 1.5 m. El material tiene un
diagrama τ-γ elastoplastico como se muestra en la figura(a). Determine el par de torsión
necesario para girar el eje un ángulo de Φ=0.6rad
Ejemplo 5.16
El tubo de la figura 5.41a tiene una longitud de 5 pies y su diagrama τ-γ elastoplastico como
se muestra en la figura(a). Determine el par de torsión Tp plástico. ¿Cual es la distribución
del esfuerzo cortante residual si Tp se retira justo después de que el tubo se vuelve totalmente
plástico?
Ejemplo 5.16
El tubo de la figura 5.41a tiene una longitud de 5 pies y su diagrama τ-γ elastoplastico como
se muestra en la figura(a). Determine el par de torsión Tp plástico. ¿Cual es la distribución
del esfuerzo cortante residual si Tp se retira justo después de que el tubo se vuelve totalmente
plástico?
Problema 5.122
El eje compuesto esta diseñado para girar a 540 rpm. Si el radio de la soldadura de filete que
conecta a los ejes es r =7.20 mm y el esfuerzo cortante permisible para el material es
τperm=55 Mpa, determine la potencia máxima que puede transmitir el eje
Problema 5.124
El acero utilizado para fabricar el eje tiene un esfuerzo cortante permisible τperm=8 Mpa. Si
los elementos se conectan entre si mediante una soldadura de filete con un radio r =2.25 mm,
determine el máximo par de torsión T que puede aplicarse
Problema 5.134
El eje hueco esta fabricado de un material elástico perfectamente plástico con un modulo
cortante G y un esfuerzo cortante de cedencia τy. Determine el par de torsión Tp aplicado
cuando el material de la superficie interior esta a punto de ceder (par de torsión plástico).
Además encuentre el ángulo de giro correspondiente y la deformación cortante máxima.
El eje tiene una longitud de L
Par plástico
Problema 5.134
El eje hueco esta fabricado de un material elástico perfectamente plástico con un modulo
cortante G y un esfuerzo cortante de cedencia τy. Determine el par de torsión Tp aplicado
cuando el material de la superficie interior esta a punto de ceder (par de torsión plástico).
Además encuentre el ángulo de giro correspondiente y la deformación cortante máxima.
El eje tiene una longitud de L
Angulo de torsión
Problema 5.134
El eje hueco esta fabricado de un material elástico perfectamente plástico con un modulo
cortante G y un esfuerzo cortante de cedencia τy. Determine el par de torsión Tp aplicado
cuando el material de la superficie interior esta a punto de ceder (par de torsión plástico).
Además encuentre el ángulo de giro correspondiente y la deformación cortante máxima.
El eje tiene una longitud de L
Problema 5.135
El eje hueco tiene diámetros interno y externo de 60 mm y 80 mm respectivamente. Si
esta fabricado de un material elástico perfectamente plástico y tiene el diagrama τ-γ que
se muestra en la figura, determine las reacciones en los soportes fijos A y C.
Problema 5.135
El eje hueco tiene diámetros interno y externo de 60 mm y 80 mm respectivamente. Si
esta fabricado de un material elástico perfectamente plástico y tiene el diagrama τ-γ que
se muestra en la figura, determine las reacciones en los soportes fijos A y C.
Ecuación de equilibrio
Análisis elástico
Problema 5.135
El eje hueco tiene diámetros interno y externo de 60 mm y 80 mm respectivamente. Si
esta fabricado de un material elástico perfectamente plástico y tiene el diagrama τ-γ que
se muestra en la figura, determine las reacciones en los soportes fijos A y C.
Resolviendo ecuación 1 y 2
Problema 5.135
El eje hueco tiene diámetros interno y externo de 60 mm y 80 mm respectivamente. Si
esta fabricado de un material elástico perfectamente plástico y tiene el diagrama τ-γ que
se muestra en la figura, determine las reacciones en los soportes fijos A y C.
Tc > Ty .El resultado obtenido en la zona elástica no es valida. Asumiendo que la
zona BC es plástica podemos decir.
Análisis plástico
Reemplazando en ecuación 1
Problema 5.135
El eje hueco tiene diámetros interno y externo de 60 mm y 80 mm respectivamente. Si
esta fabricado de un material elástico perfectamente plástico y tiene el diagrama τ-γ que
se muestra en la figura, determine las reacciones en los soportes fijos A y C.
Problema 5.136
El eje tubular esta fabricado de un material con endurecimiento por deformación que
tiene diagrama τ-γ como el mostrado en la figura. Determine el par de torsión T que debe
aplicarse al eje para que la deformación cortante máxima sea de 0.01 rad
Problema 5.136
El eje tubular esta fabricado de un material con endurecimiento por deformación que
tiene diagrama τ-γ como el mostrado en la figura. Determine el par de torsión T que debe
aplicarse al eje para que la deformación cortante máxima sea de 0.01 rad
Problema 5.136
El eje tubular esta fabricado de un material con endurecimiento por deformación que
tiene diagrama τ-γ como el mostrado en la figura. Determine el par de torsión T que debe
aplicarse al eje para que la deformación cortante máxima sea de 0.01 rad
Ans
Problema 5.136
El eje tubular esta fabricado de un material con endurecimiento por deformación que
tiene diagrama τ-γ como el mostrado en la figura. Determine el par de torsión T que debe
aplicarse al eje para que la deformación cortante máxima sea de 0.01 rad
Desde el diagrama esfuerzo cortante
Problema 5.138
Un tubo esta fabricado de material elástico perfectamente plástico y tiene el diagrama τ-γ
como el mostrado en la figura. Si el radio del núcleo elástico es ρy = 2.25 pulg, determine
el par de torsión T aplicado. Además, encuentre la distribución del esfuerzo cortante
residual en el eje y el ángulo de giro permanente de uno de los extremos en relación con el
otro al retirarse el par de torsión.